Mixture Modeling Methods for the Assessment of Normal and Abnormal Personality part II: Longitudinal Models

Abstract

Studying personality and its pathology as they change, develop, or remain stable over time offers exciting insight in to the nature of individual differences. Researchers interested in examining personal characteristics over time have a number of time-honored analytic approaches at their disposal. In recent years there have also been considerable advances in person-oriented analytic approaches, particularly longitudinal mixture models. In this methodological primer we focus on mixture modeling approaches to the study of normative and individual change in the form of growth mixture models and ipsative change in the form of latent transition analysis. We describe the conceptual underpinnings of each of these models, outline approaches for their implementation, and provide accessible examples for researchers studying personality and its assessment.

The study of personality is ultimately the study of persons. A central theme in personality research has been the description of interindividual differences (i.e., between-person differences) in characteristic patterns of thoughts, feelings, and behavior. Work in this domain has often focused on identifying the key dimensions on which individuals differ, and factor analysis (both exploratory and confirmatory) has long been the primary data-analytic workhorse. However, it can be argued that characterizing intraindividual (i.e., within-person) differences is equally important for understanding personality (Roberts, Caspi, & Moffitt, 2001; Roberts, Wood, & Caspi, 2008). Leveraging time to study the manner in which personality develops, changes, or remains stable within individuals holds immense promise for psychological research, in part because dynamic processes offer researchers and clinicians a window in to the mechanisms underlying differences among individuals. Indeed, the ultimate goal is to understand between-person differences in within-person change (Nesselroade, 1991).

The manner in which one conceptualizes change and stability dictates the appropriate analytic tools for studying personality and psychopathology over time because distinct analytic approaches speak to different aspects of change (Mortimer, Finch, Kumka, 1982; Roberts & Caspi, 1999; Wright, Pincus, & Lenzenweger, 2012). Moreover, for a given study one analytic approach may better capture the research question than others. Because the general goal of personality assessment is to understand a person, it is worth considering the degree to which the available methods are person-oriented, or otherwise maintain a focus on the individual. Many of the commonly employed longitudinal methods are extensions of cross-sectional methods and are variable-oriented in nature (see e.g., Hallquist & Wright, this issue). That is to say, their emphasis is on identifying the relationships among variables, with the assumption that these relationships are similar across all individuals (Bergman & Magnusson, 1997; Bergman, Magnusson, & El-Khouri, 2003). However, more person-oriented longitudinal methods are also available, which can clarify different patterns of within-person change. These generally fall under the rubric of mixture models and can provide personality researchers the tools necessary to sift through observed heterogeneity to uncover and describe unobserved (i.e., latent) change-groups.

Our goal is to provide an introduction to longitudinal mixture modeling in the context of research on personality and its pathology. We first review common approaches to longitudinal modeling in personality with a focus on models that try to resolve individual heterogeneity in normative change (i.e., the latent growth model; LGM) and models that seek to characterize ipsative stability (i.e., profile stability). In so doing, we outline situations that challenge the suitability of these models and articulate some limitations in the type of information they provide. We then place the LGM within a larger framework of growth mixture models (GMMs) and discuss the benefits of using latent transition analysis (LTA) for investigating transitions among personality profiles. It is our view that these methods can augment the armamentarium of personality scientists and psychopathologists interested in change over time. Finally, we present examples of how to apply and interpret longitudinal mixture models. This is intended to be a non-technical treatment of longitudinal mixture models, focused on the conceptual issues associated with model selection and interpretation. As such, this is more of a menu than a recipe book. Many excellent introductory and advanced texts exist that cover the mathematical underpinnings, estimation, identification, and interpretation of these models in depth (e.g., Collins & Lanza, 2010; Jung & Wickrama, 2007; Kreuter & Muthén, 2008; Muthén, 2002, 2003, 2004; Morin et al., 2011; Nagin, 1999, 2010; Pickles & Croudace, 2010). Readers who intend to use these analytic approaches are encouraged to consult these resources as well.

Studying Personality Longitudinally: Different Conceptions of Change

People are not static entities. Dynamic changes of various types unfold over multiple time scales ranging from momentary shifts and rapid resolutions that reflect brief interactions with environmental stimuli to the gradual but perceptible trends in personality development that reflect maturation across the lifespan (Donnellan et al., 2007; Roberts, Walton, & Viechtbauer, 2006). Regardless of the time-scale, individual dynamics are arguably of central importance to understanding personality and its pathology. For example, young adults who deviate from the normative maturational trend in personality trait development are at risk for personality pathology in early adulthood (e.g., Wright, Pincus, & Lenzenweger, 2011). Some individuals show a remitting course of psychopathology symptoms, whereas others remain chronically impaired (e.g., Hallquist & Lenzenweger, 2013; Stoolmiller, Kim, & Capaldi, 2005). Some patients exhibit rapid shifts in their symptomatic profile over time (e.g., depression gives way to generalized anxiety and back again), whereas others are steady in their form of impairment (Cain, Epler, Steinley, & Sher, 2010; Lanza & Collins, 2008; Read, Bachrach, Wright, & Colder, 2013). Quantifying both the normative pattern of intraindividual change and any interindividual heterogeneity in longitudinal trajectories is important because it can elucidate psychological processes and mechanisms that underlie change. Moreover, being able to predict differences in trajectories of change may inform clinical prognosis.

Five independent ways of operationalizing stability and change over time have become commonplace in the personality literature (De Fruyt et al., 2006; Robins et al., 2001; Wright et al., 2012): structural (i.e., factorial), differential (i.e., rank-order), normative (i.e., mean), individual, and ipsative (i.e., profile) stability. These forms vary in the degree to which they emphasize persons as opposed to variables. Structural stability can be understood as measurement invariance across time and is most frequently tested using structural equation modeling (SEM) where parameters are equated across time points. Structural stability is squarely a variable-oriented technique, as it is fundamentally a question of the manner in which variables covary. Differential stability measures the degree to which individuals maintain their relative standing over time in a given domain compared to others in the sample, and it is typically summarized using a single coefficient (usually a Pearson correlation). As such, differential stability is only indirectly person-oriented, boiling down change to one coefficient per scale or dimension and thereby retaining a focus on the variables.

Normative stability summarizes the average change in a target variable within a sample. For example, how does the average level of Extraversion change between childhood and early adulthood (Roberts, Walton, & Viechtbauer, 2006)? An emphasis on a single normative trajectory may mask distinct trajectories or pathways that characterize latent subgroups. As we articulate below, longitudinal mixture models can be employed to uncover fundamentally different latent subgroup trajectories and the individuals who follow them (e.g., distinct pathways to antisocial behavior; Shaw, Hyde, & Brennan, 2012), thereby increasing the analytic focus on the person. Individual stability is the degree of variability in individual trajectories, and it is by definition a person-oriented approach, especially as conceived in growth models (Singer & Willett, 2003). Yet, because many statistical models assume that individuals in the analysis emerge from the same population, there is the potential to misestimate individual variability when the latent distributions are severely non-normal or when subgroups characterized by distinct patterns of change exist. Finally, ipsative, or within-person profile change, is nothing if not a person-oriented approach, but as we will show, many analytic approaches discard the kind of change that occurs, focusing instead on the degree of change. Certain mixture models can simultaneously estimate the degree and kind of change, making ipsative analyses potentially more informative. Thus, the ultimate goal of person-oriented longitudinal modeling is to better articulate patterns of change by discerning subgroups of individuals who follow fundamentally distinct shapes of change and to identify those who belong to each subgroup. In what follows, we first discuss GMM as a person-oriented approach to normative and individual change followed by a treatment of LTA as an alternative approach to measuring ipsative change.

Part 1: Normative and Individual Change – Latent Growth and Growth Mixture Models

Throughout this section, to place these models on a firmer base, we refer to a hypothetical example of examining the naturalistic trajectories in borderline personality disorder (BPD) symptoms over seven years in early adulthood (e.g., ages 18–25) in an at-risk sample. A large body of research now demonstrates that the DSM-defined symptoms of BPD are not stable over time, but relatively little work has explored the heterogeneity in those trajectories (cf. Hallquist & Lenzenweger, 2013). Below we consider how each longitudinal model represents between-person differences in longitudinal trajectories, culminating in a complete example.

The Latent Growth Model: Parameterizing Normative Change

GMMs build directly on a traditional LGM framework (Bollen & Curran, 2006; McArdle, 2009; Preacher, Wichman, MacCallum, & Briggs, 2008; Singer & Willett, 2003). The LGM has a number of attractive features, but chief among them is that it provides information not only about the mean level of change, as with repeated-measures ANOVA, but also the degree of interindividual heterogeneity in the observed trajectories. Moreover, LGMs can be adapted to model various non-linear patterns of change (Bollen & Curran, 2006; McArdle, 2009; Ram & Grimm, 2009), such as polynomial, exponential, or piecewise growth patterns that capture the unique patterns of the data (McArdle, 1986; McArdle & Bell, 2000).

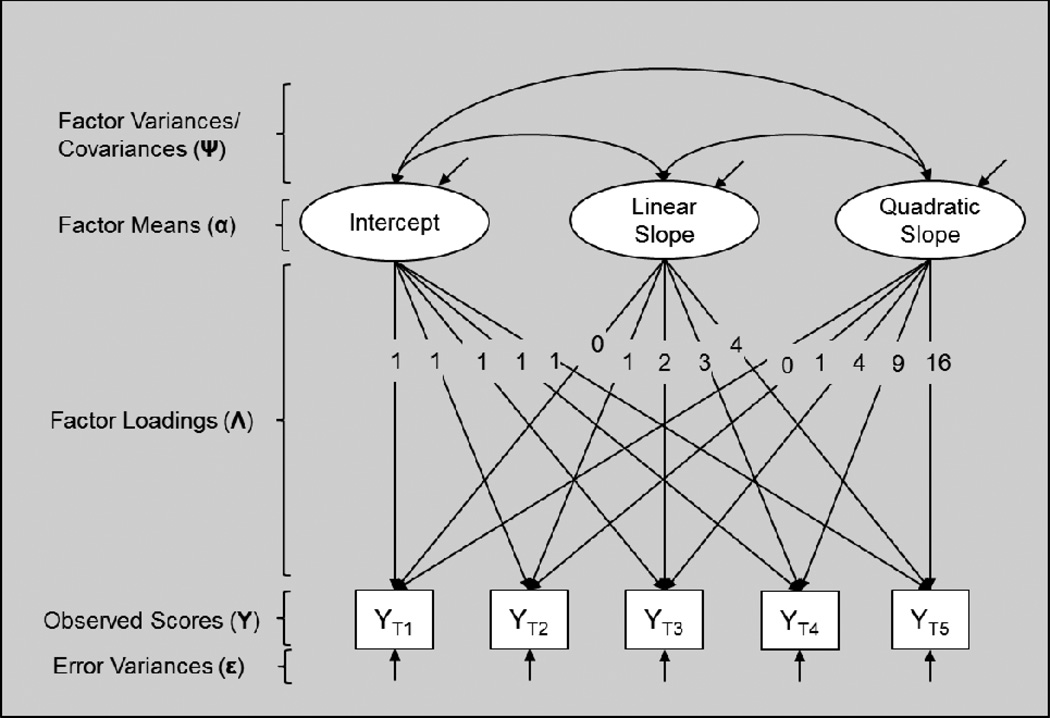
At its most basic level, the LGM is a factor model.¹ Specifically, it is a factor model where the indicators are repeated measures of the same observed variable (e.g., BPD symptoms assessed each year in our example) and which imposes a specific factorial structure. Figure 1 provides an example of a common LGM parameterization, which resembles a standard CFA model. In an LGM, change in the observed variables (Y) over time (i.e., the growth curve) is estimated as a function of growth factors (η). The basic linear LGM includes an intercept factor that reflects the average level of the curve at a given time point (most commonly the initial observation, but this is flexible) and at the minimum one slope factor that reflects a linear rate of change. Alternative shapes of change (e.g., quadratic or cubic) can be captured by adding additional factors. The shape of the estimated growth curve is defined by the pattern of factor loadings (Λ) for all the growth factors, which are fixed by the researcher to specific values.

Figure 1.

A graphical depiction of a LGM parameterized for quadratic change

As shown in Figure 1, the intercept is estimated by fixing all loadings to 1.0, and the slope factor loadings are most commonly fixed to reflect the distance in time between observation points. Time is thus coded in the model by the slope factor loadings, and the mean of the linear slope factor represents the average change in the dependent variable per unit time (e.g., change in BPD symptoms per year). In the case of Figure 1, the slope factor loadings reflect an equal spacing of measurements, with the loading for the first time point fixed to 0.0, and increasing by unit values across the remaining time points. By fixing the slope factor loading for the first time point to 0.0, and all intercept loadings to 1.0, the intercept is assigned to the start of the series and reflects the average level of the variable (e.g., personality trait) at the first time point. This is by no means the only parameterization, and the slope could just as easily be centered on the final time point by fixing the final loading to 0.0, and the remaining loadings to −4.0, −3.0, −2.0, and −1.0, respectively, starting with the initial assessment. Such an approach would lead to an intercept term that would reflect the average level of the trajectory at the end of the study, and as a result the intercept/slope covariance would change, but the estimate of the slope (i.e., mean and variance) would remain identical. Unequal schedules of measurement can be accommodated through uneven spacing of slope loadings (e.g., 1.0, 1.5, 3.0). Quadratic factors are estimated by fixing the factor loadings to the square of the linear slope loadings, and so on (see Figure 1). Residuals (ε) capture time-point specific variability in observed scores unaccounted for by the estimated growth curve.

The key parameters of change in the LGM are the factor means (α) and variances/covariances (Ψ). Factor means capture the average level and rate of change (i.e., normative change) for the sample, whereas the factor variances represent individual variability in the pattern of change (i.e., individual change), which is assumed to be normally distributed. Covariances represent the association between scores at the time-point of the intercept and rate of change over time. Because LGMs model individual differences in change with factor variances, these models are to some degree person-oriented in nature. We note, however, the individual trajectories are not directly estimated, but rather are represented as normally distributed deviations from the mean growth trajectory. The statistical significance of growth factor means can be tested to determine if the average intercept and rate of change are significantly different from zero. Likewise, factor variance estimates can also be tested to determine whether there is significant interindividual variability. It is not uncommon to obtain an LGM with a mean slope that does not differ significantly from zero, but has significant slope variance, indicating that the average level of the construct is stable over time, but some individuals increase, whereas others decrease (e.g., the average severity of BPD symptoms does not change over time, but this reflects remission in some individuals and exacerbation in others). Alternatively, it may be the case that the mean slope is a large positive value, but with a non-significant variance, indicating that change is positive and homogenous across the sample.

If we were to fit a LGM to the hypothetical repeated measurement of BPD scores, we might fix the intercept at age 18, and estimate a linear pattern of growth up until age 25. We would then examine the means of the intercept and linear growth factors. Given that the sample is at risk, the intercept mean and variance may both be significant, suggesting that average symptoms in the sample are above zero, but there is significant variability in symptom severity at baseline. We may also find a significant negative mean for the growth factor and a significant variance, suggesting that individuals typically decline in BPD symptoms from ages 18–25, but they vary in the rates of change. It would not be uncommon to find that on the average symptoms decline, but there are those with steep declines, those that remain stable, and those that increase over the course of the study. Thus the basic LGM is a powerful tool for understanding between-person differences in within-person change.

However, despite its strengths, there are situations when the basic LGM struggles to adequately reflect the true form of change in the sample—for example, in the case where the latent distribution of trajectories is decidedly non-normal, as can be the case when a large portion of the sample retains a score at the extreme (e.g., zero symptoms) over the course of the study. Alternatively, in conventional LGMs the mean curve may be misleading, the model may fit the data poorly, and parameter values may be misestimated when there are unobserved subgroups of individuals who cannot be summarized by the same model of growth. For instance, if there is one group of individuals whose growth trajectory is best described with a quadratic trend, and another group that remains flat, or only changes in a linear fashion, a model that summarizes change using a single average latent trajectory may result in poor fit and misleading results. If scenarios of these types are either predicted by theory, or are suggested based on a visual analysis of longitudinal data plots or by plotting the histograms of the variance components, mixture models may be able to better capture the heterogeneity by estimating a model composed of more homogenous subgroups of change patterns.

Growth Mixture Modeling: A General Framework

Growth mixture models (GMMs) can be understood as a general umbrella term for mixture models applied to the estimation of growth trajectories in latent subgroups. Although specific types of GMMs have been developed, discussed, and evaluated in isolation (e.g., Nagin, 1999), treating these as a general class of models (Muthén, 2004) clarifies their relationship to each other and allows for their flexible application. In particular, we would like to draw a loose parallel to a recent conceptual framework for understanding factor mixture models. Masyn and colleagues (2010) organized factor mixture models along a dimensional-categorical spectrum, ranging from factor analysis, a purely dimensional model at one pole of the spectrum, to latent class analysis (LCA), a purely categorical model at the other extreme (see also Hallquist & Wright, this issue). We extend this organizing approach to GMMs. Recall that the standard LGM is fundamentally a factor analytic model, and so by extension, GMMs are special cases of the factor mixture model with repeated measures data and growth parameterizations. At the dimensional end of the GMM spectrum we find the standard LGM, which is a single-class model (i.e., no latent categories) with a fully dimensional parameterization of variability in change trajectories. At the categorical end of the spectrum, we find the repeated measures latent class analysis (RMLCA; Lanza, 2003; Lanza & Collins, 2006), which captures trajectories of change exclusively by means of a categorical latent variable.² In between these extremes are a virtually infinite number of variations of GMM.

Prior to explicating GMM variants, we briefly cover some basics of mixture models. These models were designed to discern whether there are unobserved subgroups/classes of individuals who share very similar patterns of scores. At the most basic level, a mixture model treats an observed distribution of scores as a mixture of two or more distributions from discrete subpopulations (McLaughlin & Peel, 2000). Mixture models can be extended to mean and covariance structure modeling (i.e., SEM), with the assumption that an observed mean vector and covariance matrix arises from the combination of a finite number of class-specific mean vectors and covariance structures. Maximum likelihood-based estimation can be used to estimate unique growth parameters in several latent trajectory classes, the subgroup size and membership for each class, and the posterior probability that any given individual belongs to a class. This final point warrants some elaboration. Each individual in the sample receives a probability of membership in each estimated class, and these probabilities sum to 1.0 for each individual. In this sense, standard (i.e., non-mixture) latent variable models, which treat the entire sample as arising from the same latent population, can be considered a special case of the mixture model with a single class, for which all individuals have a probability of 1.0 for class membership.

With some basic background in place, we now turn to the description of a series of GMMs. These models differ primarily in how much they constrain patterns of change across growth classes. When estimating a GMM, any of the parameters can be constrained or allowed to vary across classes, including the factor means (α), variances/covariances (Ψ), factor loadings (Λ), and even residual item variances/covariances (ε; Enders & Tofighi, 2008). Here we focus on some of the most scientifically useful models that have emerged in the literature. We start with the most restrictive GMM and progress by describing models with increasing freedom in the form of growth across classes.

The Unique Means GMM: The Latent Class Growth Model

The latent class growth model (LCGM; sometimes referred to as group-based trajectory modeling; Nagin, 1999, 2005) can be understood as a mixture of LGMs in which only the factor means are free to vary across classes, whereas the factor variances and covariances are constrained to be zero in each class. Whereas LGMs accommodate individual differences in change with normally distributed variability around latent growth factors (e.g., intercept, slope, quadratic, etc.), LCGMs account for heterogeneity in growth with discrete latent trajectories (i.e., classes of individuals who are assumed to share the same latent trajectory of change). Any within-class variability in the observed growth curves is understood as error around the true latent scores, which are assumed to be identical across individuals within each class. A typical result for an LCGM applied to our sample of at-risk adults with BPD would be to find an elevated group that maintains their symptoms over time, a group that starts high and quickly remits, a group that starts at a moderate level and remits more slowly, and a group that starts at a moderate level and increases. This result would be interpreted as there being four types of change over time in BPD symptoms among at-risk adults, and within each group the individuals would be assumed to share the same number of initial symptoms and rate of change.

The LCGM is among the most popular of the GMMs due in large part to its early description in the methodological literature, its conceptual accessibility, and its stability in model convergence. At the same time, the LCGM is in many respects a highly constrained model that may not adequately represent the actual heterogeneity in individual growth trajectories—in particular, the assumption of within-class homogeneity in latent trajectories is often not plausible. Moreover, as we demonstrate below, the restricted parameterization can sometimes lead to spurious classes. Thus, limitations in the LCGM motivate more complex GMMs.

The Unique Means Shared Variance GMM

To move beyond the notion that there is complete homogeneity of trajectories within class, GMM growth factor variances and covariances can be estimated, but constrained to equality across classes. Such a model allows for a number of unique latent trajectory classes and also permits interindividual variability within each class, but assumes that the degree of such variability is similar across classes. This parameterization is often more theoretically plausible than LCGM, but also has important model estimation implications. First, by constraining the variances and covariances to be equal across classes, estimation of this type of model is often more stable than GMMs with unique variance estimates in each class (described below), and so a precise estimation of within-class heterogeneities is balanced with the pragmatics of model estimation. As models become more complex (i.e., more parameters are allowed to vary across classes), they can become increasingly difficult to estimate and frequently result in inadmissible or under-identified solutions (Wang, Brown, & Bandeen-Roche, 2005). Second, the constraints across classes in GMM affect the trajectory classes that emerge, and class variances/covariances have important implications for this issue (Morin et al., 2011). Specifically, less constrained models may require fewer classes to model the interindividual differences in growth, and LCGM can often result in an over-extraction of classes to accommodate heterogeneity (Bauer & Curran, 2004; Muthén & Muthén, 2000). For example, a common result in LCGM is to obtain two highly similar trajectory classes that differ only in intercept, but not slope. These may best be collapsed into one class that permits variability around the intercept term, resulting in a more parsimonious solution.

If this type of model were fit to the hypothetical BPD data, a possible result might be to find three growth classes, an initially elevated mean and rapidly declining symptom group, an initially elevated mean but stable symptom group, and initially moderate mean symptoms and stable group. Although the classes differ in their average levels of initial symptoms and rates of change, the magnitude of interindividual variability around these class-specific means is estimated to be equal across classes.

The Unique Means and Variances GMM

Constraining the variances and covariances to be equal across GMM classes may be too restrictive in some instances, and so the next conceptual step is to allow these, too, to vary freely across classes. This may be a desirable approach when there is a large class with considerable variability in one or more of the growth factors, along with a “tighter,” more homogeneous class with a different growth pattern. For example, some individuals may have few, if any, symptoms of personality dysfunction over time, resulting in a low slope variance, whereas a separate latent class may exhibit symptom declines over time, but with significant heterogeneity in the rate of remission. It would be unreasonable to assume that these classes could be considered to have the same slope variance, and this can be accommodated with unique means and variances GMM.

The Unique Means, Variances, and Patterns GMM

Thus far we have considered GMMs that differ in the degree to which they accommodate individual differences in variability across classes. We now consider GMMs that allow for differences in the shape of change, which offer a compelling reason for considering these models. For example, it may be hypothesized, based on theory or past research, that there is a group whose pattern of change is quadratic (e.g., an accelerating rate of change), whereas others in the sample might adopt a linear trajectory. In this instance, it may be worth considering a GMM with differences in pattern across classes. There are two general approaches that can be adopted here. In the first, the researcher can specify a different factor structure across classes (e.g., one includes a quadratic slope factor, the other only a linear slope factor, etc.). This can be specified a priori or, alternatively, by first estimating the most complex form of change under consideration in each class and then trimming the unnecessary parameters from the model (e.g., when there is a non-significant mean and variance for a quadratic term in a given class).

The second approach offers even more flexible possibilities for differences in change trajectories. This type of GMM is based on LGMs with freely estimated factor loadings (Bollen & Curran, 2006; McArdle & Nesselroade, 2003). Above we discussed LGMs that imposed a structure on the growth factors by specifying the factor loadings for the slopes. It is also possible to estimate growth factor loadings to capture unique patterns of change in what has been termed the latent basis model (McArdle & Epstein, 1987; Meredith & Tisak, 1990). Note that for model identification, two loadings must always be specified (i.e., fixed to a value by the researcher). If the pattern of change is expected to be very complex, and not conform to common polynomial models, freeing the factor loadings may be a good option. There are a number of ways to free factor loadings — a topic that is beyond this primer. However, to illustrate one variant of the latent basis model, there is only one slope factor, which has the first loading fixed to 0.0 and the final loading fixed to 1.0. The intermediate loadings are freely estimated, and their values represent the proportion of cumulative change up to that time point (see McArdle & Nesselroade, 2003). To extend this model to GMMs, the factor loadings for the first and final time points are fixed to 0.0 and 1.0, respectively, across each class, and the remaining loadings are allowed to vary across classes, which contributes to different patterns of change across classes (see Ram & Grimm, 2009).

Were we to apply a model that allowed for differing shapes of change across classes to the hypothetical longitudinal BPD data, we might find that the group that previously emerged as having a steep linear decline actually has a quadratic trend, such that there is an initially steep rate of change that decelerates as symptoms remit. In contrast, the remaining classes might maintain their linear shape.

Allowing for differences in shape or pattern of change across classes is an appealing approach in part because a misestimation of the shape of change can lead to improper class structure (Bauer & Curran, 2004; Voelkle, 2008). However, we caution that these models can be difficult to estimate and interpret in some scenarios. For example, freeing the growth factor loadings in GMM can lead to idiosyncratic patterns of change that offer little conceptual clarity, such as trajectories with slight deviations from linear change.

Nonparametric Change: RMLCA

An alternative approach to capturing unstructured patterns of change or non-parametric growth is RMLCA (Lanza, 2003; Lanza & Collins, 2006; Collins & Lanza, 2010). RMLCA applies a standard LCA³ model to repeated measures of the same observed variable as opposed to distinct variables at one time point. In LCA, the relationship among observed variables is represented as differences in mean profiles across latent classes (Collins & Lanza, 2010). In the case of RMLCA, the mean profiles represent distinct non-parametric growth trajectories that describe the repeated-measures data. Compared to the models above, this approach is the least restrictive in terms of structuring change, and the emerging profiles are entirely data-driven (i.e., the investigator imposes no assumptions of a parametric growth curve). Neither did RMLCA emerge from the GMM tradition because it is a fully categorical latent variable model. Nevertheless, there is good reason to include RMLCA within the same conceptual family as GMM because it holds promise for instances when highly nonlinear patterns of change are hypothesized or as an exploratory tool to understand the forms of change in the dataset.

An RMLCA approach to the hypothetical BPD change data might reveal two latent classes, one of which shows a triangular pattern over time (i.e., symptoms that fluctuate above and below the initial level without any linear trend) and the other that exhibits a rapid drop in symptoms between ages 18 and 19, followed by gradual decreases from 19–25.

GMM Model Estimation, Evaluation, and Selection

We briefly cover issues related to model estimation, evaluation, and selection, and refer the reader to our cross-sectional companion piece (Hallquist & Wright, this issue) for a more detailed and technical treatment of these issues.

Given the large number of possibilities for different parameterizations of GMMs, a general heuristic to model estimation and evaluation is warranted. Ideally, the application of GMMs should be motivated by an articulated hypothesis about the class structure that is anticipated to emerge. However, we also recognize that in many instances strong hypotheses are not available, and yet there remains an interest in searching for potentially interesting unobserved growth trajectory classes in an exploratory fashion. Even when this is the case, we recommend that the researcher establish, a priori, which forms of GMM are plausible for their data. As we alluded to above, models can quickly become highly complex, both in terms of computation and interpretation. Therefore our recommendation is that researchers first outline the number of classes that they anticipate to emerge, and how these classes may differ from each other with respect to mean, variance, and trajectory shape (Ram & Grimm, 2009).

There are three basic sources of information that can influence the selection about which forms of GMM might be optimal in terms of the number of classes and within-class variance and shape. Naturally, if there is an available theory about the number and type of classes that might exist, this is the preferred place to start. It is often the case, however, that theory may be mute on the latent trajectory issue, but there exist compelling prior empirical results that warrant clarification in a new sample or with new measures. In either case, the researcher is likely to include among their models the structure dictated by theory or put forward by prior findings. In addition to these, near neighbors in class number or variance structure may warrant consideration (e.g., if a three class structure of depression course was hypothesized, two- and four-class models should also be tested). In the absence of strong theory or prior results, the only option may be to proceed in an exploratory fashion. Given the danger of uncovering growth classes that are spurious or sample specific, we recommend that researchers engaging in exploratory work seek to replicate or cross-validate their class solutions if sample size allows. Options for this include randomly splitting the sample in half, or comparing groupings across which classes would not be expected to differ (e.g., gender, pairs of twins, etc.).

Whether proceeding in a confirmatory or exploratory approach, a third source of information should come from the data itself. We strongly encourage a visual scan of longitudinal plots of the raw data prior to beginning modeling exercises. What does the average pattern of change look like? Are there discernible differences in the patterns of change? In this regard, it is often useful to fit an LGM prior to any of the GMMs, in part because the growth factor variances in LGM are assumed to be normally distributed, an assumption that can be explored visually. If a histogram of the variance estimates for the slope factor is quite bimodal, for example, this may provide initial evidence for a GMM approach. We recommend initially fitting and thoroughly evaluating an LGM first, which can provide important information about model fit, shape of growth, and whether assumptions of variance normality are tenable. Subsequently, we have found that running an RMLCA can be very useful as an exploratory technique to get an initial sense of the potential class structures embedded in the data prior to estimating other forms of GMM.

Once the types of GMMs under consideration have been identified, model estimation and comparison can proceed. It is common to estimate a series of models that vary in the number of classes within each type of GMM. For example, models with two, three, four, and five classes would be estimated for the LCGM, unique variances GMM, and unique shape GMM, for a total of 12 models. Model comparison would then proceed in a two-step approach, where the models of different numbers of classes are first compared within each type of GMM, followed by comparing the preferred model within each type across different types of GMM. However, alternative approaches are viable, and may be better suited for some research questions.

Adjudicating between GMMs can be a complex endeavor. The types of difficulties that arise are not unlike those that arise in factor analyses, where researchers are often faced with conflicting evidence about which model to select. Accordingly, we, like others before us (Bauer & Curran, 2004; Muthén, 2003) want to emphasize that theoretical interpretability should always be the final arbiter of model selection, and blindly following a given fit index or criterion is not advisable. With this in mind, there are a number of tools available to select among models.

Recall that a common statistical approach to comparing nested latent variable models is the likelihood ratio test (LRT; i.e., the χ² difference test; Bollen, 1989). Although mixture models that are equivalently parameterized but that differ only in the number of classes are in fact nested, they violate the assumptions of the standard LRT (i.e., they are at the boundary of parameter space and the differences in their log-likelihoods most likely are not χ² distributed), and therefore these are generally not appropriate (see Collins & Lanza, 2010; McLaughlin & Peel, 2000; and Nylund, Asparouhov, & Muthén, 2007 for detailed discussions). Recent simulation work (Henson, Reise, & Kim, 2007; Nylund et al., 2007; Tofighi & Enders, 2008) supports the use of a variety of indices. These include the Akaike Information Criterion (AIC; Akaike, 1974) and its sample size-corrected variant, the AIC_C (Sugiura, 1978), the Bayesian Information Criterion (BIC, Schwartz, 1978), and the bootstrapped likelihood ratio test (BLRT; McLaughlin & Peel, 2000). We strongly recommend the use of the AIC_C over the AIC for most applications in moderately sized samples (Hurvich & Tsai, 1991).

The AIC_C and BIC rely on information theory and Bayesian inference, respectively (Burnham & Anderson, 2002; Claeskens & Hjort, 2008; Vrieze, 2012), but both seek to balance the ability of the model to fit the data with the parsimony of the model (i.e., the number of estimated parameters). In general, however, when comparing two models, the model that has a lower value for a given information criterion is preferred as having a better complexity-fit tradeoff. The BLRT overcomes the limitations with standard LRTs we reference above. A significant BLRT p-value (conventionally p < .05) indicates that the k-class model fits the data significantly better than the model with k-1 classes, accounting for the additional parameters added by increasing the number of latent classes. Note that the BLRT cannot be used to compare across different types of GMMs.

In practice, it is quite common for these criteria to disagree on which model is best. In this instance, it falls on the researcher to select between models. Various additional considerations must be weighed. These include class sizes, class differentiability (more below), and the pattern of associations with covariates. For example, if fit criteria were split between models that differ by one class (e.g., a three- versus four-class GMM), but the size of the additional class was very small (e.g., 3% of the sample) representing a very rare growth trajectory, it might not be worth considering. Similarly, if the additional class represented a qualitatively similar growth trajectory to one of the other classes, regardless of size, for instance differing only slightly in intercept, this also might not be worth retaining. Finally, if comparisons of the classes on external variables indicate that the additional class was very similar to another in terms of predicting outcomes or correlates of class membership, it might not be worth considering.

Regardless, choosing among GMM solutions can be challenging, and we encourage researchers not to make binary decisions based on arbitrary rules, but rather weigh various statistical and substantive issues when deciding on a final model. It is generally advisable, when theory clashes with model fit in a given sample, for researchers to give emphasis to substantive issues and theory when choosing the optimal model. We now walk through a hypothetical example of comparing GMMs using simulated data before we consider an alternative approach to studying ipsative change as discrete shifts over time.

A Simulated Example: Comparing GMMs

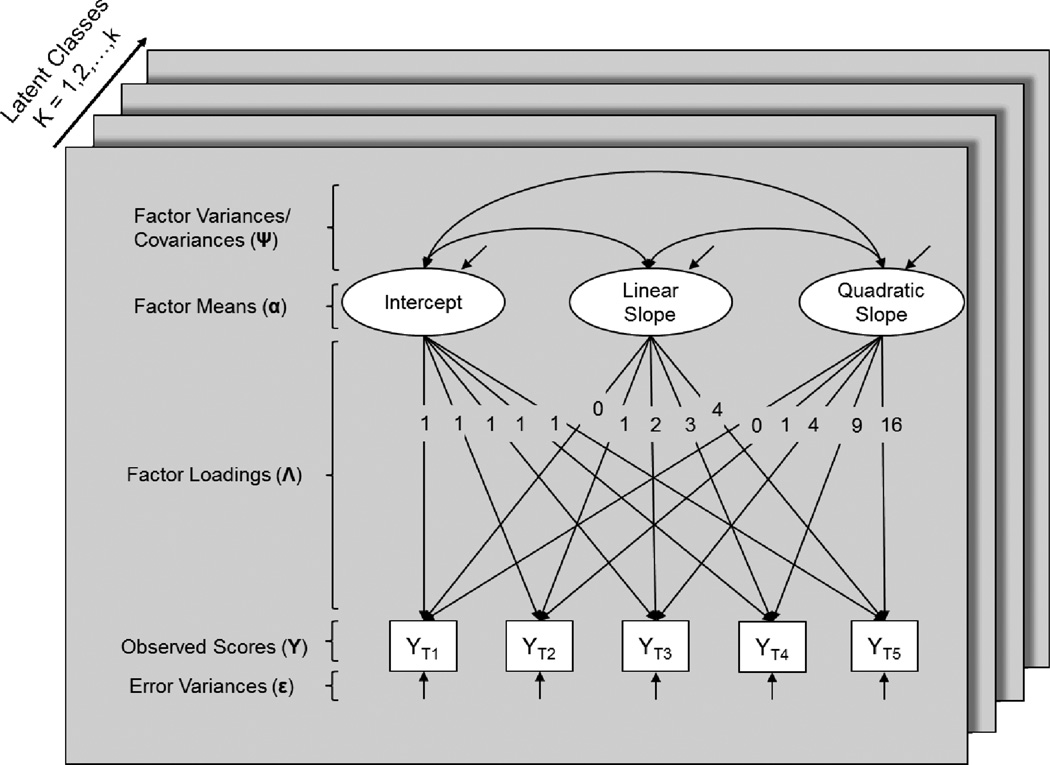
To consolidate the above discussion of model comparison and selection, we now turn to a hypothetical example using simulated data. To fit with our working example, we consider the longitudinal course of BPD features as they might be measured by a semi-structured psychiatric interview, the Revised Diagnostic Interview for Borderlines (DIB-R; Zanarini, Gunderson, Frankenburg, & Chauncey, 1989). Scores on the DIB-R are integer values that can range from 0–44. We generated a data set of 500 individuals measured at 7 time points using the Monte Carlo features of Mplus version 7 (Muthén & Muthén, 2012). The data were simulated from a GMM with four classes of approximately equal size. The raw data can be found on the left panel of Figure 2, and the mean curves of the estimated trajectory classes from the best fitting model can be found in the right panel. We next submitted the simulated data to a series of analyses, as might be the case in a study employing GMM to understand heterogeneity in the longitudinal course of BPD. We treat this example as if we were naïve to the latent structure.

Figure 2.

A Graphical depiction of a general growth mixture model parameterized for quadratic change. Note that any of the parameters listed on the left hand side of the graph could be allowed to vary across classes (k).

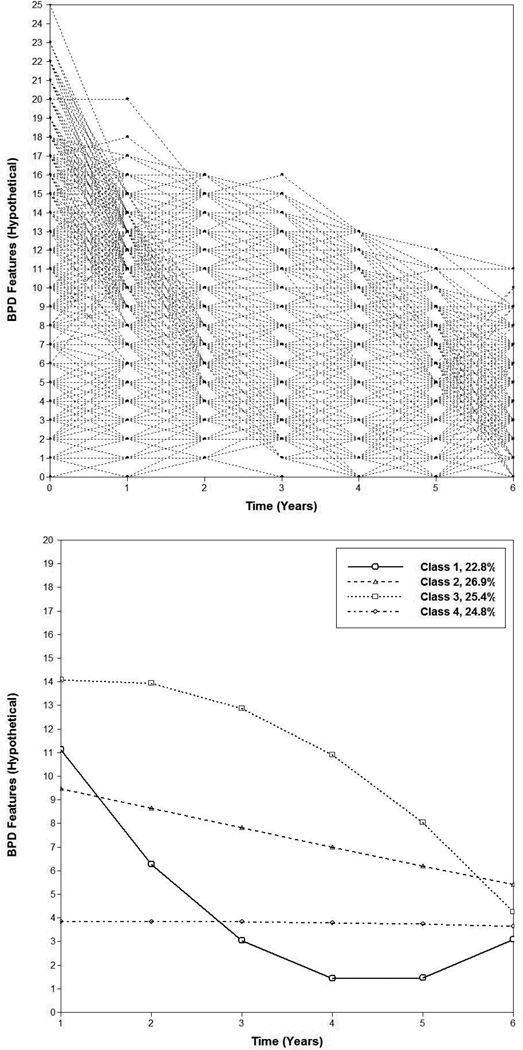
Table 1 contains the models we considered in this analysis and their associated parameters and model fit statistics. Although we knew the class structure beforehand, the pattern of fit statistics in the table along with difficulties in estimation is informative, as described below. However, as a first step we inspected the longitudinal plot of the raw data (Figure 4). The figure suggests a) a high degree of heterogeneity in trajectories, although this can be difficult to directly ascertain with plots of integer values; b) a general decrease in BPD features over time; and c) patterns that might be suggestive of non-linear effects as evidenced by very steep initial declines for those individuals with high values followed by a flattening of the trajectories.

Table 1.

Model Fit Statistics from Simulated GMM Example

Model	K	LL	AIC	AICC	BIC	BLRT	BLRT p
LGM
Linear	12	−7855.11	15734.22	15734.86	15784.79	--	--
Quadratic	16	−6738.50	13509.00	13510.13	13576.44	--	--
RMLCA
1 Class	14	−9494.56	19017.12	19017.98	19076.12	--	--
2 Class	22	−8450.38	16944.77	16946.89	17037.49	2088.35	0.000
3 Class	30	−7916.17	15892.34	15896.30	16018.78	1068.43	0.000
4 Class	38	−7145.70	14367.41	14373.84	14527.56	1540.93	0.000
5 Class	46	−7018.63	14129.27	14138.81	14323.14	254.14	0.000
6 Class	54	−6864.83	13837.67	13851.02	14065.26	307.60	0.000
GMM-UM (LCGM)
1 Class	10	−9494.59	19009.18	19009.63	19051.33	--	--
2 Class	14	−8450.54	16929.07	16929.94	16988.08	2088.11	0.000
3 Class	18	−7916.71	15869.43	15870.85	15945.29	1067.65	0.000
4 Class	22	−7147.43	14338.87	14340.99	14431.59	1538.56	0.000
5 Class	26	−7021.5	14095.00	14097.97	14204.58	251.87	0.000
6 Class	30	−6899.03	13858.06	13862.03	13984.50	244.94	0.000
7 Class	34	−6795.59	13659.18	13664.3	13802.48	206.88	0.000
8 Class	38	−6765.51	13607.03	13613.46	13767.18	50.88	0.000
9 Class	42	−6740.44	13564.87	13572.78	13741.89	50.15	0.000
10 Class	46	−6724.63	13541.25	13550.80	13735.12	53.01	0.000
GMM-UMSV
1 Class (LGM)	16	−6738.50	13509.00	13510.13	13576.44	--	--
2 Class	20	−6460.54	12961.08	12962.83	13045.37	555.92	0.000
3 Class	24	−6312.43	12672.85	12675.38	12774.00	296.23	0.000
4 Class	28	−6166.29	12388.59	12392.03	12506.59	292.27	0.000
5 Class	32	−6130.92	12325.85	12330.37	12460.71	70.74	0.000
6 Class	36	−6066.10	12204.20	12209.95	12355.93	129.64	0.000
7 Class	40	−6040.89	12161.78	12168.93	12330.37	50.42	0.000
8 Class	44	−6024.67	12137.34	12146.04	12322.78	32.44	0.000
9 Class	48	−6011.92	12119.84	12130.27	12322.14	25.50	0.000
10 Class	52	−6000.11	12104.22	12116.55	12323.38	31.92	0.000
GMM-UMUV
1 Class (LGM)	16	−6738.50	13509.00	13510.13	13576.44	--	--
2 Class	26	−6314.27	12680.54	12683.50	12790.12	848.467	0.000
3 Class	36	−6044.89	12161.78	12167.53	12313.50	538.757	0.000
4 Class	46	−5975.14	12042.27	12051.82	12236.14	139.509	0.000
5 Class	56	−5963.18	12038.36	12052.77	12274.37	23.914	0.364
GMM-UMUVUS
4 Class	38	−5983.12	12042.24	12048.67	12202.39	--	--

Note. N = 500. GMM = Growth Mixture Model; K = model parameters; LL = Loglikelihood; AIC = Akaike Information Criterion; AICC = Consistent AIC; BIC = Bayesian Information Criterion; BLRT = Bootstrapped Likelihood Ratio Test; LGM = Latent Growth Model; UM = Unique Means; UMSV = Unique Means, Shared Variance; UMUV = Unique Means, Unique Variance; UMUVUS = Unique Means, Unique Variance, Unique Shape.

Figure 4.

Simulated raw data and mean curves for best fitting LGM

Note. Top panel is the longitudinal plot of the simulated data from the GMM example. Bottom panel presents the mean trajectories for each class of the best fitting model in the GMM example.

As a next step we fitted LGMs to the data. An intercept and linear slope model had a poor global fit (df = 10; χ² = 656.57, p = < .001; RMSEA = .36; CFI = .80; SRMR = .38) and resulted in negative residual error variances (i.e., impossible values). Based on the initial data visualization, we tried to improve the model fit by estimating a quadratic LGM, which had excellent fit to the data (df = 6; χ² = 4.08, p = .67; RMSEA = .00; CFI = 1.00; SRMR = .00) indicating that the mean curve for the sample had a significantly elevated intercept (M = 5.17, p < .001), a significant negative linear slope (M = −1.69, p < .001), and a significant quadratic slope (M = .47, p < .001). Additionally, all of the growth factors had significant variances, suggesting a high degree of heterogeneity in growth trajectories in the sample. We subsequently ran a series of RMLCAs in an exploratory fashion in order to examine the types of heterogeneity in growth patterns in the data set. Up through four classes, unique patterns of growth emerged, but beyond this the additional classes were highly similar in pattern to others, suggesting that the increasing classes might only be capturing subtle variations as opposed to qualitatively different growth patterns. However, relative fit of the RMLCA was poor (even through models with a large number of classes, the fit of which are not presented for space). Importantly, the latent classes appeared to have reasonably parametric growth trajectories (i.e., linear, quadratic) as opposed to unique patterns that could not reasonably be captured by a standard GMM parameterization. This highlights one potentially useful feature of RMLCA, namely that if the resulting classes appear to follow some parametric form, this can be tested by specifying GMMs that best parameterize the RMLCA results.

With these initial findings in mind, we proceeded to test a series of GMMs based on a quadratic growth curve shape, with the expectation that approximately four classes would emerge as the best fitting model. We began with the most restrictive models, the latent means only LCGM approach, followed by increasingly permissive (and more complex) models that allowed for a shared variance/covariance pattern or unique variances. Finally, we tested a model with different shapes of growth across classes. As can be seen in Table 1, the best fitting initial model was (expectably given the known structure in the data) the 4-class GMM with unique means and variances across classes. The AIC_C and BIC were lowest for this model, and the BLRT for a five-class solution was not significant. Adding one class also lead to increases in AIC_C and BIC. Conversely, the AIC suggested adding a class, consistent with its known tendency to prefer overly complex models if not corrected for the low sample size (Hurvich & Tsai, 1991). Based on the output of the model, we determined that two classes had non-significant means and variances for the quadratic slope term, and therefore we fixed these to zero, resulting in a model that had different shapes across classes, which was ultimately was the best-fitting model.

The mean trajectories of the hypothetical BPD growth classes can be seen in the right panel of Figure 2. If these were our empirical findings, we would conclude that there is a group with moderate BPD features that maintain their score over time, there is a group with elevated features that decreases linearly over time, there is an elevated group that shows a quadratic decline such that they have dramatic decreases at the outset of the study but then slow in their symptom remission, and finally, that there is a group of individuals who initially maintain their score, only to show a more precipitous decline late in the study. If these were real data, our next task would be to compare these classes on covariates, perhaps trying to predict class membership based on an initial assessment in order to inform prognostic decision-making. Alternatively, we could look to differences on some outcome of importance measured at the final time-point or beyond—for example, BPD trajectory classes might differ in their social functioning, even though many of their symptoms have remitted. The possibility of linking trajectory classes with additional outcomes can be a compelling reason to employ GMMs, and it can also help determine whether these classes should be treated as meaningfully and qualitatively distinct, as opposed to more continuous interindividual differences in intraindividual change.

It is worth noting that the more restrictive forms of GMM struggled to fit the simulated model. For the unique means only and the unique means/shared variances models, the addition of classes continued to improve model fit, up to our a priori limit of 10 latent classes. For each of these GMMs, often around the seven-class model, very small classes began to emerge (i.e., 1–4% of the sample). Furthermore, an inspection of the model trajectory plots indicated that these additional classes had the same change patterns as other classes, differing slightly in intercept or curvature of the slope. This highlights the point that more restrictive models will tend to account for heterogeneity with additional classes. One should consider moving to a more complex and less constrained within-class structure if “too many” classes begin to emerge. Naturally, this is an extreme and artificial example, and when using real data, the more restrictive variants of GMM can be useful due to their stability in estimation, especially when considering non-linear growth. When means and variances are free, as we mentioned above, problems often emerge in estimation, which require troubleshooting. An additional point we sought to demonstrate here is that the one-class unique means/shared variance and unique means/unique variance GMMs both reduce to the LGM as can be seen from the identical log-likelihood values. Finally, it bears mention that despite having excellent fit by most conventional standards, the quadratic LGM has poor relative fit in comparison to the best GMMs. This illustrates that qualitatively distinct and conceptually interesting latent trajectories can be embedded in a dataset that “fits well” with LGM and argues in favor of at least testing the waters using GMM if one thinks that there may be conceptually meaningful latent trajectories.

Words of Caution

Thus far we have presented an enthusiastic discussion primarily focused on potential advantages of GMMs. We would be remiss if we did not also pause to draw the reader’s attention to some of the drawbacks associated with GMMs and the need to proceed cautiously—especially given that [such?] much modeling is likely to be exploratory in nature. It is important to keep in mind that it is the researcher’s responsibility to bridge the gap between a statistical approximation of the data and the meaning ascribed to it. In this context, it means that the researcher must decide whether a given GMM solution has produced a set of meaningful latent trajectory classes, or whether the classes reflect non-substantive groupings that capitalize on sample features or model misspecification. More generally, because GMM accounts for heterogeneity in growth in part by adding classes, even modest misspecifications in the model can lead to spurious classes (Bauer & Curran, 2003, 2004; Lubke & Neale, 2006). For instance, it is frequently the case that GMMs may identify additional “classes” with only minor violations of normality and other subtle violations of the LGM (Bauer, 2007). Classes that differ quantitatively but not qualitatively are probably best treated within an LGM framework (Bauer & Curran, 2004). Researchers should beware of situations in which modest changes in model specification lead to large changes in conclusions about the class number or structure, suggesting that the classes are not robust.

Others have pointed to the fact that very similar solutions will emerge from LGCMs even across very distinct modeling situations. Sher et al. (2010) provided a dramatic demonstration of this fact by comparing LCGMs of all time points analyzed together versus conclusions reached by analyzing the first half or second half of the series. In each case a similar result emerged, lending little confidence that this technique was extracting “true” classes of individuals. Although one hopes that similar LCGM results would emerge across independent samples, it is troubling that similar results were obtained by exploring different temporal subsets of the same data. A multi-class solution only provides statistical evidence that a mixture distribution fits the data better than a single-class model, not that the classes are necessarily discrete subgroups of the population (Bauer, 2007; Sterba & Bauer, 2010). Even as we encourage researchers to consider the potential for new insights using these models, given the potential pitfalls in exploratory GMMs and the likelihood that many modeling situations will have limited theory to draw on, we urge researchers to be cautious in their approach and seek to replicate and validate solutions.

At various points we have made reference to “difficulties” in estimation. At the current juncture mixture models often require a fair amount of manual attention in the process of model specification and vetting. Furthermore, researchers will undoubtedly run in to instances where models fail to converge, converge but only after a significant amount of estimation time (e.g., days), or provide impossible parameter values. Researchers should closely inspect their output after each model, keeping an eye out for error warnings, impossible parameters, or other evidence of modeling difficulties (e.g., a non-replicating log-likelihood across random starting values, suggestive of numerical instability that may undermine confidence in parameter estimates).

Part 2: A Mixture Approach to Ipsative Change: Latent Transition Analysis

The GMM methods described in the previous sections are able to model, with a high degree of fidelity, individual change in a given content domain (e.g., extraversion, depression, or narcissism). And yet, these approaches are generally limited to capturing change in one dimension at a time. Personality is a multidimensional system, and what is often of interest is not one’s unidimensional standing, but rather a qualitative “profile” of traits. When considered from a longitudinal standpoint, an important question is: to what degree do individuals maintain their profile over time (i.e., what is their ipsative stability)? Investigators interested in ipsative stability have drawn on early and contemporary work in profile analysis (e.g., Biesanz & West, 2000; Cronbach & Gleser, 1953; Furr, 2008) to study the degree and predictors of multidimensional change over time (e.g., Asendorpf & Van Aken, 1991; Donnellan et al., 2007; Robins et al., 2001; Wright et al., 2012). With its focus on the multidimensional trait profile, ipsative stability is the most person-oriented of the traditional approaches to studying personality over time. In this regard, ipsative stability should be of high interest not only to personality psychologists but also clinicians who are often in the business of promoting lasting improvements in multiple if not all domains of an individual’s life. Although traditional measures of profile stability (e.g., q-correlation or D²) capture multidimensional change, they reduce this change to a unitary number, and lose the specifics of the change. That is to say, these methods reduce each individual’s profile similarity across time to one coefficient (e.g., .90), which cannot track which specific aspects changed. What is typically learned in studies of ipsative stability is grossly how stable individual profiles are, or what is predictive of stability, but not the manner in which someone changes over time. Often the average coefficient of ipsative personality stability is high, but individual values vary dramatically, including being negative, beckoning for the development and application of methods that can elucidate not just the degree of change, but the kind of change that is occurring.

Latent transition analysis (LTA) holds promise for the simultaneous study of the degree and kind of change in personality profiles over time. LTA is a longitudinal extension of latent class analysis (LCA; Collins & Lanza, 2010). LCA is a cross sectional mixture model that can be applied to multivariate data to uncover (potentially) distinct latent groupings of individuals who share the same profile of scores across variables within a class, but differ in the profile across classes. LCA models variability in trait profiles at a single time point using latent classes. When there are multivariate data measured at multiple time points, a researcher may be interested to know to what degree individual class membership (i.e., personality profile) is stable over time, and in which ways do individuals transition among classes over time. LTA accomplishes this by predicting an individual’s status at a given time point by his or her previous status (in LTA the term status is used instead of class to reflect the potentially transient nature of latent group membership). Thus, LTA differs from RMLCA, which applies a standard LCA to repeated measures of one variable. To date, LTA has only been used in one longitudinal personality study (Meeus, van de Schoot, Klimstra, & Branje, 2011), although a number of illustrative exemplars exist in psychopathology research (e.g., Cain et al., 2010; Chung, Park, & Lanza, 2005; Read et al., 2013). One likely reason that LTA has been applied to personality data so infrequently is that modern personality research has been overwhelmingly focused on dimensions as opposed to types (see e.g., Hallquist & Wright, this issue). There are instances of typological theories of personality (e.g., Block & Block, 1980) that could only be tested by using LTA. However, more importantly, LTA provides conceptual and analytic features that fill a problematic gap in traditional longitudinal methods by being able to characterize the content in ipsative change.

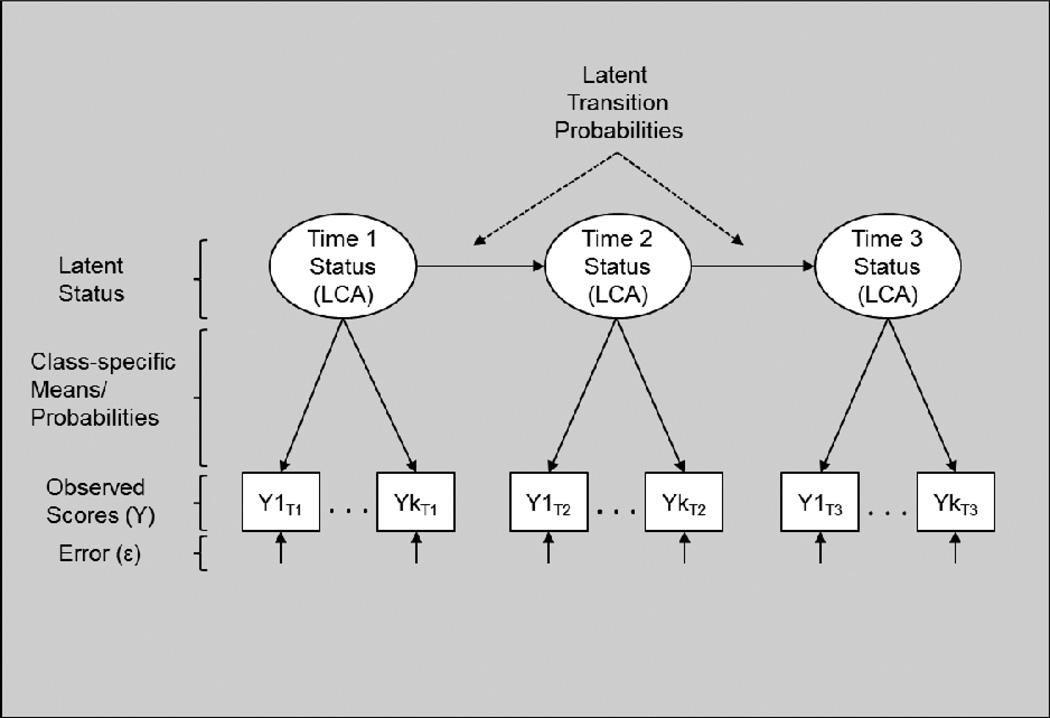
In LTA, an LCA is first fit to the multidimensional data at each time point in order to establish the number and form of personality profiles at each wave. Subsequently, to measure the transition from one profile to another over time, the statuses from later time-points are regressed on earlier time-points using multinomial logistic regression (see Figure 3). There are a number of parameters that emerge from an LTA. First are the standard parameters that emerge from an LCA, which include item means (in the case of continuous observed variables) or probabilities (in the case of categorical observed variables), the number of latent statuses (i.e., time-specific personality profiles), and the proportion of individuals assigned to a given status. The relative levels of the personality variables (i.e., profiles) in each group define the content for each status at each wave. It is incumbent on the researcher to interpret the emerging profiles and choose the best fitting LCA solution for each wave as the first step.

Figure 3.

Graphical depiction of a three time-point latent transition analysis

The second set of parameters, unique to LTA, are the latent transition probabilities, which reflect the likelihood of an individual moving from a one status at a given time-point to another status at a subsequent time-point versus remaining in the same status. Thus, the probability of maintaining one’s class reflects the stability in class membership, and the probability of moving in to another class reflects the instability. In this way, LTA can speak to gross levels of stability and instability, as with more conventional ipsative stability analyses. However, LTA also quantifies the probability that an individual in a given status shifts to another, thereby providing information about the type of change occurring. As an example, consider the possibility that there are two primary psychological states for individuals with narcissistic pathology, one characterized by grandiosity, expansiveness, and hubris, and the other characterized by shame, vulnerability, and withdrawal. Assuming these states could be adequately differentiated using LCA, LTA would provide the probability of shifting from one status to another within a given period of time (e.g., one week), and, as we note below, could also estimate the effect of an external event (e.g., perceived interpersonal insult) on determining one’s later status or state.

Although the number of statuses, variable means, and proportion of individuals assigned to each status are unique to each time-point’s LCA model, and it is frequently advantageous to test for invariance in the number of classes and variable means to ensure that statuses are conceptually identical across time points. This is especially the case when more than two time points are being examined. If the LCA model is not invariant across time points one can still proceed with an LTA, but the statuses will not be conceptually identical at each time point. Depending on the application, a varying class structure across time may make more or less sense. This may make good sense in the event that there are certain statuses that cannot be achieved before a developmental milestone has passed or an intervention is given. For example, in an LTA of depression symptoms among those diagnosed with depression at Time 1, but who have gone through an intervention at Time 2, there may be no “healthy” status that emerges at Time 1, only at Time 2. In this way LTA can be flexibly applied to test theories about change in an intervention or developmental framework.

An additional attractive feature of LTA is that it does not constrain the patterns of change over time a priori. Individuals can shift between statuses and back again with as many patterns of trajectories as there are permutations based on the number of classes and the number of time-points. Admittedly, the number of possible pathways can quickly become staggering, especially with the addition of assessment points, which contribute to geometric growth (e.g., with three statuses at three time-points there are 27 possible trajectories, but with three statuses and four time points there are 81 possible trajectories). Most frequently, however, there are a handful of common pathways that emerge in LTA. For example, if there were three statuses of participants, internalizers, externalizers, and low-pathology (Achenbach, 1966; Krueger, 1999), it is frequently the case that most of the movement between statuses will occur going from the pathology statuses to the low-pathology status. The frequencies of common transitions provide information about the modal patterns of ipsative stability. Yet LTA also provides estimates of the proportion of individuals moving in the opposite direction, from low-pathology to internalizing or externalizing, and between the two pathology classes. In this way it can capture patterns of growth that include waxing and waning symptoms, as well as qualitative shifts in symptom presentation over time.

As the name implies, in LTA the focus is on discrete transitions. The temporal resolution of individual status transitions will only be as good as the frequency of measurement. Thus LTA can only indicate that someone has shifted statuses between two time points, not when during the intermediate time it occurred. It should also be noted that there exists a major tradeoff is imposing a categorical structure on what may better be understood as continuous change. Change that is actually occurring gradually will be treated as if it is all or none. Nevertheless, LTA can be used in conjunction with other approaches to better grasp the full picture of change, and for certain questions discrete change may indeed be the most appropriate model (e.g., the development of a new behavior or skill). An additional consideration that takes on particular importance for LTA, but is also of relevance for GMM, is that like most latent variable models these are ideally “large sample” techniques. Although it is difficult to determine hard-and-fast cutoffs because the necessary sample size is dependent on a number of features (e.g., reliability of measurement, sample homogeneity, model complexity, number of observations per person; Muthén & Curran, 1997), there are situations where models will be inestimable or provide poor parameter estimates due to low sample size. As it pertains to LTA, low sample size can lead to empirical under-identification, which is sometimes evident as a model that fails to converge or takes considerable time reach convergence.

More advanced applications of LTA involve the addition of covariates which can be included as predictors of the probability of time-point specific statuses, but also as moderators of the latent transitions. This feature is particularly advantageous when one is interested in the effect of certain discrete events on the trajectory of change over time, which cannot easily be accommodated in latent growth modeling. To illustrate this point, we briefly consider the results of a recent study by Read and colleagues (2013) examining the trajectory of PTSD symptomatology over the first year of college. A large sample of students (N = 944) was assessed in September, December, and April, covering the full academic year. A three-class LCA was selected for each assessment point, reflecting absent, moderate, and severe PTSD statuses. Controlling for initial levels of neuroticism, the authors demonstrated that new and repeated traumatic events were predictive of shifts into the more severe latent statuses or the stability of the symptomatic statuses over time. Naturally, this was an expected result, but in addition it was shown that engaging in alcohol use was also predictive of transitions over and above trauma. Thus, LTA offers a powerful tool for studying not only qualitative and idiosyncratic patterns of change, but also the effect of covariates on longitudinal changes in a way not easily accomplished using other techniques.

Examining the Results of a Hypothetical LTA

To illustrate the modeling steps in LTA we offer a plausible but hypothetical study. We limit this example to two time-points for clarity. In this hypothetical study, 1,000 adolescents are followed in the transition from middle school to high school. Each participant completed the Multidimensional Personality Questionnaire (MPQ; Tellegen & Waller, 2008) midway through the year during the final year of middle school (i.e., eighth grade) and the first year of high school (i.e., ninth grade). The research questions were a) whether there was evidence of a coherent latent grouping structure of personality in early adolescence and b) whether these classes were stable over the transition from middle school to high school.

Personality profiles were assessed with the higher-order MPQ scales of Positive Emotionality (PEM), Negative Emotionality (NEM), and Constraint (CON). As an initial step, the goal would be to run LCAs for the measurement model at each assessment point. Assuming these were reasonably similar, and agreed in terms of the number of classes suggested, but with relatively minor differences in means for example, measurement invariance could be imposed, constraining the number of classes and mean values across time-points to equality, and the AIC_C and BIC could be compared across solutions. Lower AIC_C and BIC in a more constrained model would provide evidence in support of identical classes emerging across time. Although the indicator means and number of classes can be constrained for the purpose of imposing measurement invariance, it is important that the proportion of individuals in each class is freely estimated to capture movement from one class to another, which is of primary scientific interest in LTA. However, for the sake of this example let us assume that the same status structure emerged at both time points and could be modeled as invariant. In the left side of Table 2 the status specific means are summarized in T-Scores, and appear to conform to a pattern of No Pathology (High PEM, low NEM, moderate CON), Internalizing problems (low PEM, high NEM, average CON), and Externalizing problems (average PEM, moderate NEM, low CON). The Time 1 status proportions were as follows, No Pathology .80 (n = 800), Internalizing .10 (n = 100), and Externalizing .10 (n = 100). The Time 2 class proportions were as follows, No Pathology .65 (n = 648), Internalizing .16 (n = 161), and Externalizing .14 (n = 140).

Table 2.

Example of Parameter Estimates from a Hypothetical Latent Transition Analysis

	Status Specific Means (SDs)			Latent Transition Probabilities
	MPQ Higher-Order Scale					Time 2 Status
	PEM	NEM	CON			Non-Path	Internalizing	Externalizing
Non-Path	60 (8.2)	35 (7.3)	57 (9.5)	Time 1 Status	Non-Path	0.81	0.11	0.08
Internalizing	32 (7.4)	67 (6.2)	52 (9.0)		Internalizing	0.29	0.60	0.11
Externalizing	55 (10.1)	58 (8.7)	30 (5.6)		Externalizing	0.22	0.13	0.65

Note. Hypothetical results for the purpose of illustration, these do not correspond to actual findings. MPQ = Multidimensional Personality Questionnaire; PEM = Positive Emotionality; NEM = Negative Emotionality; CON = Constraint; Non-Path = Non-Pathological. MPQ Means provided in T-Scores. Status specific means fixed to equality (i.e., are measurement invariant) across both time-points. Bolded latent transition probabilities on the diagonal represent stabilities.

Next we would regress the second time point statuses on the initial time point statuses (note the shift in terminology from class to status reflecting the potential transient nature of these latent groupings). This step is done in a single latent variable model that regresses the time 2 categorical latent variable on the time 1 categorical latent variable using multinomial logistic regression. In other words, the entire model is estimated simultaneously. The new results are the latent transition probabilities displayed in the right portion of Table 2. The status-specific stabilities can be found on the diagonal, and the off-diagonals reflect the probability of shifting from one status to another as an adolescent goes from middle school to high school. Here we see that the No Pathology class is the most stable, but sizeable portions of children are moving into the Internalizing (i.e., 88 = 800 × .11) and Externalizing statuses (i.e., 64 = 800 × .08). The Externalizing status was next most stable followed by the Internalizing status. Note how the Time 1–Time 2 transition probabilities (i.e., represented on each row) are required to sum to 1.0 for each Time 1 status, representing a full account of how individuals in the sample change in status between time-points, whereas there is no similar requirement of columns. If one were to multiply the initial proportions of individuals classified to each status by their transition probabilities one would obtain marginal proportions classified in each status at time 2 (note this only works when there is no attrition).

Although this example is hypothetical, it demonstrates that LTA is able to assess ipsative stability while still retaining a focus on the content of each individual’s profile. To be sure, by classifying individuals into a few classes some resolution on the fine-grained change in profiles is lost, but this may be a worthwhile trade-off in many instances. We advocate using multiple approaches to studying change of all types, including ipsative change, and LTA adds a promising complement to the standard approaches. By comparing scientific conclusions across different longitudinal analyses, one may achieve a more informed and hopefully convergent perspective on the form and content of changes over time.

Conclusion

Recent years have seen an increasing emphasis on studying personality over time, and accordingly longstanding questions related to when and if personality becomes stable (James, 1890) have received definitive answers—namely, “it depends.” Indeed, the complex nature of stability and change in personality provides new insight into the psychological mechanisms that undergird who we are. Motivated in part by the complexity of scientific questions about the development and stability of personality, recent advances in longitudinal methods have promoted a better understanding of personality and psychopathology. Mixture modeling approaches have gained considerable traction of late, and their person-oriented emphasis conforms to the scientific and clinical traditions in personality psychology. This primer was intended to give a broad conceptual introduction to longitudinal mixture models and their application. We hope this paper provided a balanced view of the potential utility and potential pitfalls associated with adopting mixture approaches. We look forward to the new discoveries in personality science that may be supported by these models.