3D Whole-Brain Perfusion Quantification using Pseudo-Continuous Arterial Spin Labeling MRI at Multiple Post-Labeling Delays: Accounting for Both Arterial Transit Time and Impulse Response Function

Abstract

Measurement of cerebral blood flow (CBF) with whole-brain coverage is challenging in terms of both acquisition and quantitative analysis. In order to fit the ASL-based perfusion kinetic curves, an empirical 3-parameter model that characterizes the effective impulse response function (IRF) is introduced, which allows determination of CBF, arterial transit time (ATT), and T_1,eff. The accuracy and precision of the proposed model is compared with more complicated models with 4 or 5 parameters through Monte Carlo simulations. Pseudo-continuous arterial spin labeling (PCASL) images were acquired on a clinical 3 Tesla scanner in 10 normal volunteers using a 3D multi-shot gradient- and spin-echo (GRASE) scheme at multiple post-labeling delays to sample the kinetic curves. Voxel-wise fitting was performed using the 3-parameter model and other models that contain 2, 4 or 5 unknown parameters. For the 2-parameter model, T_1,eff values close to tissue and blood were assumed separately. Standard statistical analysis was conducted to compare these fitting models in various brain regions. The fitted results indicate that: 1) the estimated CBF values using the 2-parameter model show appreciable dependence on the assumed T_1,eff values; 2) the proposed 3-parameter model achieves the optimal balance between the goodness of fit and the model complexity when compared among the models with explicit IRF fitting; 3) both the 2-parameter model using fixed blood T₁ values for T_1,eff and the 3-parameter model provide reasonable fitting results. Using the proposed 3-parameter model, the estimated CBF values (46±14 mL/100g/min) and ATT values (ATT = 1.4±0.3 s) averaged from different brain regions are close to the literature reports; the estimated T_1,eff values (T_1,eff = 1.9±0.4 s) are higher than the tissue T₁ values, possibly reflecting a contribution from the microvascular arterial blood compartment.

INTRODUCTION

A general kinetic model (1,2) has been accepted to describe the arterial spin labeling (ASL)-based perfusion weighted signals (difference of label/control) as the convolution between the arterial input function (AIF) and the impulse response function (IRF). In classic tracer kinetic modeling, the AIF is the time dependent function describing the concentration of the labeled tracer within the arterial supply to the imaging voxel, while the IRF is a time-course function describing how much remains in the imaging voxel after a unit of labeled tracer arrives. In ASL images, the accumulation of labeled arterial blood water signal in the imaging voxel and its loss of the tag through relaxation or clearance, produce a kinetic curve as a function of post-labeling delay (PLD). Thus, in order to account for varying AIFs and IRFs across the brain, a reasonable strategy for estimating cerebral blood flow (CBF) is to obtain ASL images with a range of PLDs and then to perform voxel-by-voxel curve fitting with an underlying kinetic model.

Given the inherently low signal-to-noise ratio (SNR) of ASL signals, the multi-PLD approach has not been regularly employed due to the required long acquisition time. Instead, the majority of CBF quantification studies to date only acquire perfusion images at a single long PLD and assume minimal effects due to the spatial variance in arterial transit time (ATT), the transit time of the arterial bolus from the labeling plane to the imaging voxels. This is a reasonable assumption as long as all labeled blood water have arrived in the voxels and the difference of the longitudinal relaxation time constants of arterial blood and tissue, T_1,a and T_1,t, is small (3). However, this assumption may be problematic given the heterogeneous distributions of ATT and T_1,t between different regions in normal brain and between normal and pathological conditions. Recognizing that a spatially varying ATT is one major confounding issue affecting the AIF accuracy for ASL-based CBF quantification, techniques have been developed to measure regional ATT separately (4–6) or to estimate CBF and ATT together (two unknown parameters) with multi-PLD datasets (1,7–12).

Additionally, the IRF for ASL-based CBF quantification has been initially approximated by a single-compartment model of instantaneously fast exchange of labeled arterial tracer from capillary to tissue (13,14). This corresponds to a monoexponential decay function for the IRF with tissue T₁ (T_1,t) as the characteristic time constant (13,14). While there are three unknown parameters in this model: CBF, ATT, T_1,t, local T_1,t values are often taken from either a literature-reported gray matter (GM) T₁ value or from individually measured T₁ maps (3,15,16). However, T₁ values are tissue-dependent and precise T₁ mapping is time-consuming. Moreover, several ASL studies have demonstrated that a substantial fraction of labeled water, after arriving at the imaging voxels, remains in the arterial microvascular compartment for some time (δ_a) before reaching the capillary bed and diffusing into the tissue compartment (3,17–19), which indicates a four-parameter model (CBF, ATT, T_1,t, δ_a) may be more suitable. Furthermore, a two-compartment exchange model for ASL-based CBF quantification may be needed to describe the intermediate exchange regime for water exchange between capillary and tissue compartments (20–22). Sophisticated modeling of the IRF in principle also needs to take into account the fraction of the decay of the labeled signal in the vascular compartment (both arterial and capillary compartments), in addition to the tissue compartment (both extracellular and intracellular compartments). This will significantly increase the complexity of the model for IRF with various parameters including not only T₁ values and residence time corresponding to different compartments, but also extra microscopic parameters such as the exchange rate of water molecules from capillary blood to tissue, K_w, which would lead to a five-parameter model: CBF, ATT, T_1,t, δ_a, K_w, as introduced in a pulsed ASL study (23). However, recent Monte Carlo simulations have shown that, within the limit of the low SNR typically afforded by current ASL techniques, it is difficult to fit all these parameters with acceptable levels of precision (24).

In order to simplify the IRF model, we propose to use an effective T₁ relaxation time constant (T_1,eff) to approximate these elaborate relaxation processes, which describes the IRF as a monoexponential decay function. Using multi-PLD datasets, it then becomes feasible and sufficient to fit the kinetic curves with CBF, ATT and T_1,eff as three unknown parameters. In this work, we first used Monte Carlo simulations to compare the accuracy and precision with 3-parameter (CBF, ATT, T_1,eff, the proposed method), 4-parameter (CBF, ATT, T_1,t, δ_a), and 5-parameter (CBF, ATT, T_1,t, δ_a, K_w) models, respectively. We then acquired 3D pseudo-continuous ASL (PCASL) (25) images with a whole-brain coverage over a range of PLDs at 3T, and fitted the data using the three aforementioned CBF estimation approaches in additional to the 2-parameter method (CBF, ATT). The fitted results using the proposed 3-parameter model in various brain regions were compared with the other fitting results using standard statistical analysis. To our best knowledge, this is the first time the models with IRFs at a full range of degree of complexity are systematically compared using multi-delay ASL data from both simulation and human subjects.

MATERIALS AND METHODS

3-Parameter Model

The AIF c(t) for continuous or pseudo-continuous labeling for a single-compartment model can be described by (1):

$$\mathrm{c}(\mathrm{t})=\{\begin{array}{ll}0,\hfill & \hfill \mathrm{t}<\mathit{ATT}\hfill \\ 2\mathrm{\alpha }{\mathrm{M}}_{0,\mathrm{a}}·\mathrm{f}·\left({\mathrm{e}}^{-\text{ATT}/{\mathrm{T}}_{1,\mathrm{a}}}\right),\hfill & \hfill \text{ATT}\le \mathrm{t}\le \text{ATT}+\mathrm{\tau }\hfill \\ 0,\hfill & \hfill \mathrm{t}>\text{ATT}+\mathrm{\tau }\end{array}$$ [1]

Here t = 0 is defined as the beginning of the labeling pulse, α is the labeling efficiency, τ is the duration of the continuous labeling, and M_0,a is the equilibrium magnetization of arterial blood. Note that CBF (mL/100g/min) = 6000 · f (mL/g/s) and ATT and relaxation time constants are expressed in units of second.

The IRF decay function, r(t), for the 3-parameter model is assumed to be monoexponential with an effective T₁ relaxation time constant (T_1,eff):

$$\mathrm{r}(\mathrm{t})={\mathrm{e}}^{-\mathrm{t}/{\mathrm{T}}_{1,\text{eff}}},\mathrm{t}>0$$ [2]

The ASL signal, as the difference between the control and labeled images, is the convolution between the AIF c(t) (Eq. [1]) and IRF r(t) (Eq. [2]):

$$\mathrm{\Delta }\mathrm{M}(\mathrm{t})=\{\begin{array}{ll}0,\hfill & \hfill \mathrm{t}<\mathit{ATT}\hfill \\ 2\mathrm{\alpha }{\mathrm{M}}_{0,\mathrm{t}}/\mathrm{\lambda }·\mathrm{f}·\hfill & \text{ATT}\le \mathrm{t}\le \text{ATT}+\mathrm{\tau }\hfill \\ \left({\mathrm{T}}_{1,\text{eff}}·{\mathrm{e}}^{-\text{ATT}/{\mathrm{T}}_{1,\mathrm{a}}}·\left(1-{\mathrm{e}}^{-(\mathrm{t}-\text{ATT})/{\mathrm{T}}_{1,\text{eff}}}\right)\right),\hfill \\ 2\mathrm{\alpha }{\mathrm{M}}_{0,\mathrm{t}}/\mathrm{\lambda }·\mathrm{f}·\hfill \\ \left({\mathrm{T}}_{1,\text{eff}}·{\mathrm{e}}^{-\text{ATT}/{\mathrm{T}}_{1,\mathrm{a}}}·\left({\mathrm{e}}^{\mathrm{\tau }/{\mathrm{T}}_{1,\text{eff}}}-1\right)·{\mathrm{e}}^{-(\mathrm{t}-\text{ATT})/{\mathrm{T}}_{1,\text{eff}}}\right),\hfill & \hfill \mathrm{t}>\mathit{ATT}+\mathrm{\tau }\end{array}$$ [3]

Where M_0,t is the equilibrium magnetization of tissue and is related to M_0,a through the brain-blood coefficient, λ = 0.9 ml/g (26).

The derived equations for the 4-parameter and 5-parameter models are listed in the Appendix for comparison.

Simulations

Simulations were performed using Matlab 7.0 (MathWorks, Inc., Natick, MA, USA). Examples of continuous ASL data using 3-parameter, 4-parameter, and 5-parameter were generated with typical values: CBF = 50 mL/100g/min (9), ATT = 1.5 s (5), T_1,eff = 1.6 s, T_1,a = 1.9 s (27), T_1,t = 1.2 s (28), δ_a = 0.7 s (19), K_w = 75 min⁻¹ (29), τ = 1.0 s, α = 1.0, M_0,a = 1.0.

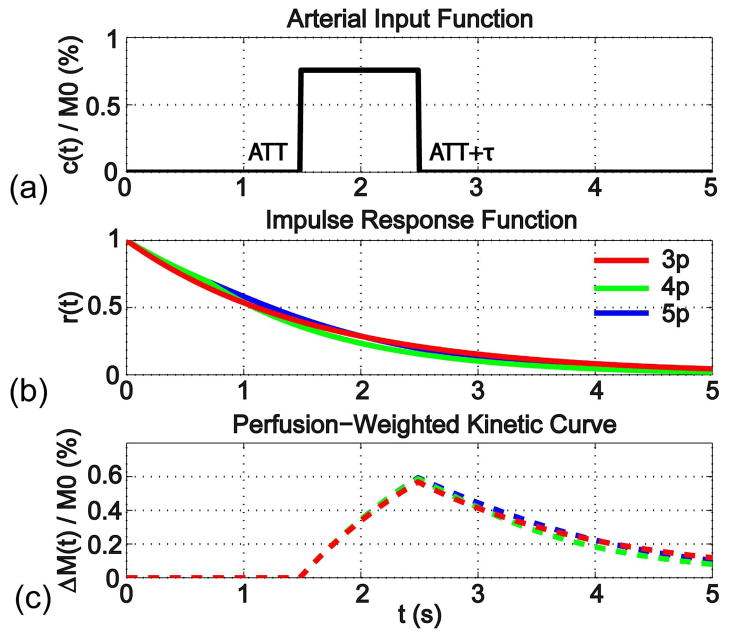
Figure 1a displays the AIF for continuous ASL (Eq. [1]), while Figures 1b and 1c show the IRF of the 3-parameter model (Eq. [2], red line in Figure 1b) and the corresponding perfusion-weighted kinetic curve (Eq. [3], red dashed line in Figure 1c). To compare with the 4-parameter and 5-parameter models, the IRFs (Eq. [A1] and [A4]) and perfusion-weighted kinetic curves (Eq. [A2] and [A5]) are shown in Figures 1b and 1c in green and blue, respectively. It can be seen from Figure 1 that the empirically simplified 3-parameter model, with the T_1,eff chosen from the range between T_1,a and T_1,t, provides a reasonable representation of the perfusion kinetic curves from the more complicated 4-parameter and 5-parameter models.

Figure 1.

(a) The Arterial Input Function (AIF) for continuous ASL is characterized by the lengthening of ATT with the duration τ; (b) The Impulse Response Function (IRF) is compared between the proposed 3-parameter model (3p), which assumes a monoexponential decay function characterized with T_1,eff, and the more sophisticated 4-parameter (4p) and 5-parameter models (5p) (Appendix); (c) The perfusion-weighted kinetic curves are the convolutions of AIF (a) with IRFs of the each model (b), respectively.

The dependencies of the 3-parameter model on CBF, ATT and T_1,eff are illustrated respectively in Figure 2. By varying CBF = [15, 30, 45, 60, 75, 90] mL/100g/min with fixed values of ATT = 1.5 s and T_1,eff = 1.4 s, the perfusion signals are proportional to the CBF values (Figure 2a) as well known. By varying ATT = [1.0, 1.2, 1.4, 1.6, 1.8, 2.0] s with fixed values of CBF = 50 mL/100g/min and T_1,eff = 1.4 s, the perfusion weighted signals show strong sensitivity on ATT values before the bolus arrives (the peak of the curves) and yet little sensitivity on ATT values after it (Figure 2b), which validates the utilization of a long PLD for single PLD approach to reduce the dependence of the result on ATT (3). It is worth noting that data acquired at the longer PLD will have significant signal drop for curves with shorter ATTs due to the T₁ relaxation (Figure 2b). By varying T_1,eff = [1.0, 1.2, 1.4, 1.6, 1.8, 2.0] s with fixed values of CBF = 50 mL/100g/min and ATT = 1.4 s, the perfusion signals demonstrate apparent sensitivity on T_1,eff values after arrival of all the bolus (Figure 2c): longer T_1,eff corresponds to higher perfusion signal.

Figure 2.

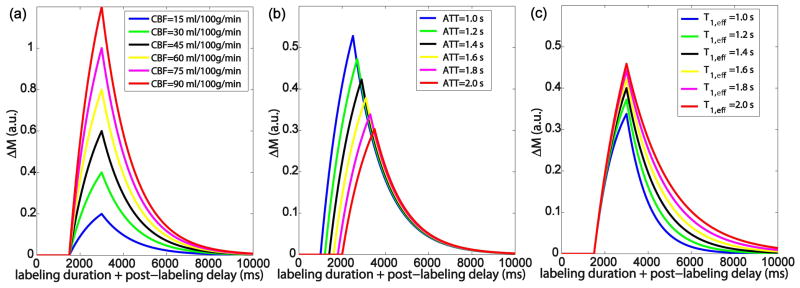
The dependencies of the 3-parameter model for continuous ASL on (a) CBF; (b) ATT; (c) T_1,eff.

To compare the accuracy and precision of these CBF estimation approaches, a Monte Carlo simulation study was performed to compare among 3-, 4-, 5-parameter models. Although none of these are true representations of the reality, the 3-, 4-, and 5-parameter models do increasingly approximate the complex kinetic processes. Here the 5-parameter model is chosen as a description of the real circumstance, albeit still simplified. Each dataset was produced using the 5-parameter model and fitted with the models employing 3 parameters (CBF, ATT, T_1,eff), 4 parameters (CBF, ATT, T_1,t, δ_a), and 5 parameters (CBF, ATT, T_1,t, δ_a, K_w). For each dataset, random noise with normal distribution was added in the curve, with SNR of the peak signal increasing from 5 to 50 in 2.5 intervals. For each noise level, the data generation was repeated 1000 times in order to compute the mean and std of the estimated parameters under the same noise condition.

Fitting was conducted using a nonlinear-least-squares algorithm provided by Matlab (lsqcurvefit) and the correlation coefficient for each fit (R²) was also calculated. The error percentage of the mean of the fitted parameters with respect to the input values was analyzed as an indicator of accuracy of each approach at each SNR level. The corresponding coefficient of variation (fitted std / fitted mean) was measured as an indicator of precision (24).

Experiments

Ten healthy human volunteers (23–48 yrs, six males and four females) were enrolled after providing informed consent in accordance with the Institutional Review Board guideline. Subjects were imaged on a 3T Philips Achieva scanner (Philips Medical Systems, Best, The Netherlands) using the body coil for transmission and a 32-channel head coil for reception.

The pseudo-continuous ASL (PCASL) (25) was applied with the following parameters: labeling duration τ = 1.0 s, RF interval 1 ms, RF duration 0.5 ms, flip angle 18°, maximum gradient strength = 6 mT/m, average gradient strength = 0.6 mT/m (30). The label/control pulse train was followed by different PLDs with separate acquisitions (12 PLDs ranging from 0.5 s to 2.7 s in 0.2 s intervals, the same as in the simulations) in order to adequately sample the perfusion kinetic curves for the different brain regions. The pulse sequence diagram is shown in Figure 3. The rational for the shorter labeling duration, τ = 1.0 s, compared with the 1.5 ~ 2.0 s used by many previous works (25,30–32), is to accommodate the timing of background suppression pulses required for different PLDs, especially for the earlier time points.

Figure 3.

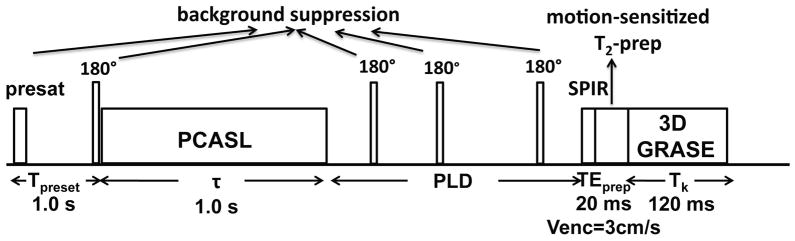
Pulse sequence diagram for 3D mapping of baseline CBF. There are five blocks within each repetition: PCASL (τ = 1 s), background suppression with one preset pulse (T_presat = 1 s) and four inversion pulses (timing as in Table 1), SPIR pulse, motion-sensitized T₂ prep (TE_prep = 20 ms), and 3D GRASE acquisition (T_k = 120 ms). Twelve different PLDs ([0.5, 0.7, 0.9, 1.1, 1.3, 1.5, 1.7, 1.9, 2.1, 2.3, 2.5, 2.7] s) were acquired separately for measuring the perfusion kinetic curves.

Background suppression pulses (33) were applied to suppress the static tissues: a slab-selective presaturation pulse at 1.0 s before PCASL module, one selective inversion pulse right before PCASL and three nonselective inversions after PCASL. The arrangement of these pulses is similar to earlier works (25,33,34). The timing of the four inversion pulses for background suppression were individually tailored for each PLD (supplementary material available online), through a home-made iterative minimization algorithm in Matlab, to achieve residual background signal intensities of less than 1% for a broad range of T_1,t values (from 0.5 s to 4.4 s in 0.3 s interval).

At the end of each PLD, a spectral presaturation with inversion recovery (SPIR) module was used to remove fat artifacts. Then before acquisition, a 20 ms T₂-prep module with inserted motion-sensitized gradients (Venc = 3 cm/s) in three orthogonal directions was utilized to reduce signals from large vessels (35).

The gradient- and spin-echo (GRASE) approach (36) combines high sampling efficiency from EPI or spiral read-outs with low sensitivity to B₀ field inhomogeneity from Fast Spin Echo (FSE) acquisition and has become a natural choice for 3D whole-brain ASL protocols (25,33,37,38). To evaluate the SNR status with different resolutions, multi-PLD PCASL sequences were acquired at 5 × 5 × 5 mm³, 6 × 6 × 6 mm³, and 6.7 × 7.4 × 7 mm³ resolution on a subset of six subjects. On another four subjects, only the 6.7 × 7.4 × 7 mm³ resolution was obtained. The transverse field of view (FOV) was kept at 240 × 240 mm² with 20 partitions along superior-inferior direction, such that a slab thickness of 100 mm, 120 mm and 140 mm were possible for each acquisition resolution. A reconstructed matrix size of 48 × 48 × 20 for each acquisition resolution produced in-plane reconstruction resolutions as low as 5 × 5 mm². An echo train duration (T_k) of 120 ms was chosen for all three resolutions for minimized T₂-decay induced blurring and optimized SNR efficiency (39). Low-high profile ordering ensured a short effective echo time which equals to the echo spacing of 17 ms. For each acquisition resolution, although with different EPI factors (5 mm: 27; 6 mm: 23; 7 mm: 19), the acquisition time at each echo was kept the same by proportionally changing the acquisition bandwidth. Together with other acquisition parameters (FSE factor: 7; SENSE factor: 2; number of interleaves: 3; number of averages: 1), total k-space sampling time was about the same for all three resolutions. Each dataset pair (control and label) at each PLD took from 19 s to 32 s. For all 12 PLDs, total measurement duration was about 5 min for each resolution.

With the same resolution and acquisition scheme, an extra scan without background suppression and PCASL modules was employed (TR = 10 s) to acquire the tissue equilibrium magnetization map (M_0,t), which also provides local receiver sensitivity information. Another series of scans with the same acquisition scheme for different resolutions was acquired with the RF pulse turned off, with the goal of assessing the systematic noise levels. A fast sequence was employed to measure blood T₁ of each subject at the internal jugular vein (27). Each of these scans took about 1 min.

A high-resolution 3D image applying magnetization prepared rapid acquisition with gradient echo (MP-RAGE) (40) was also acquired with 1.1 mm isotropic resolution. Imaging parameters were: FOV = 250 × 250 × 180 mm³, flip angle (FA) = 9°, TR / TE = 12 ms / 3.2 ms, and inversion time = 1110 ms. Using SENSE factors of 2 (Anterior-Posterior) × 2 (Right-Left), the acquisition time was 3.5 min.

Data Analysis

Matlab 7.0 (MathWorks, Inc., Natick, MA, USA) was used for data processing. Fittings of the ASL kinetic curves are based on the 2-, 3-, 4-, and 5-paramaeter models (m = 2 and 3, Eq. [3]; m = 4, A[2] and A[3]; m = 5, A[5] and A[6]), respectively. For the 2-parameter model, T_1,eff = 1.2, 1.6, 2.0 s were assumed separately. For in vivo data, α is set as the labeling efficiency of PCASL, assumed to be 0.8 (32), and multiplied by the factor of perfusion signal loss due to the background suppression, assumed to be 0.8 (41). Voxel-wise fitting of a set of n data pairs (y_i vs. t, i = 1:n, n = 12) was executed using a nonlinear-least-squares algorithm (lsqcurvefit) and each predicted data through the best-fit curve is denoted by Y_i. As in standard regression analysis, the residue for each data pair i is defined as: e_i = y_i – Y_i; the standard error of estimate is calculated as $E_{y,t}=\sqrt{({\sum }_{i=1}^n{e_i}^2)/df}$, where df is the degree of freedom: df = n – m; the standardized residue for each data pair i is e_i/E_y,_t. Since E_y,_t can be approximated as a standard deviation of the actual data relative to the estimated least-squares fit values, 95% e_i should be within −2E_y,_t and 2E_y,_t. The data pair with the maximal standardized residue of each fit and |e_i,max/E_y,_t| > 2 is regarded as an outlier, which might be caused by physiological fluctuation or systematic instability. For each voxel, only up to 2 out of 12 data points could be called as outliers and fit was performed again after each exclusion.

To measure the goodness of the fit, the correlation coefficients of all the fittings, R², were calculated:

$$R^2=1-{SS}_{\mathit{res}}/{SS}_{\mathit{tot}}$$ [4]

where ${SS}_{\mathit{res}}={\sum }_{i=1}^n{e_i}^2$ (sum of squares of residues) and ${SS}_{\mathit{tot}}={\sum }_{i=1}^n{(y_i-{\overline{y}}_i)}^2$ (total sum of squares). Higher R² indicates better fit and R² = 1 corresponds to an ideal fitting of the data (SS_res = 0). It is worth noting here that R² of the fit does not consider the number of parameters (model complexity) used for fitting and presumably an n^th order polynomial (m = n, df = 0) always yield higher R² than models with less parameters and more df.

In order to determine the balance between the goodness of fit and the model complexity, two standard statistical measures of each model fitting were computed: corrected Akaike information criterion (AICc) (42) and Bayesian information criterion (BIC, or sometimes called Schwarz criterion) (43).

$$\mathit{AICc}=n·ln({SS}_{\mathit{res}}/n)+2m+2m(m+1)/(n-m-1)$$ [5]

$$\mathit{BIC}=n·\text{ln}({SS}_{\mathit{res}}/n)+m·ln(n)$$ [6]

The second-order term in Eq. [5] is a correction added on AIC for fitting of small sample size relative to the number of model parameters (n/m ≤ 40) (44). For a given set of data, the model with the lowest AICc or BIC values represents the best balance between goodness of fit and complexity among the considered models. Detailed knowledge of AIC and BIC can be found in (45). These statistical tests have been utilized in studies of tracer kinetic modeling using nuclear medicine (46,47) and dynamic contrast-enhanced MRI (48,49).

FSL (FMRIB Software Library, Oxford, UK) (50) was used on the high-resolution MPRAGE images to remove the skull, and to generate partial volume maps of gray matter, white matter and CSF. The images of brain and segmented tissue were then co-registered with the low-resolution M₀ images. For each subject, five ROIs in the gray matter (frontal lobe, temporal lobe, parietal lobe, occipital lobe, and cerebellum) were manually drawn bilaterally from the co-registered MPRAGE maps.

When comparing results from different models on the same datasets, paired t-test with the two-tailed distribution is used. Difference between any two groups are considered significant for P < 0.05.

RESULTS

Simulations

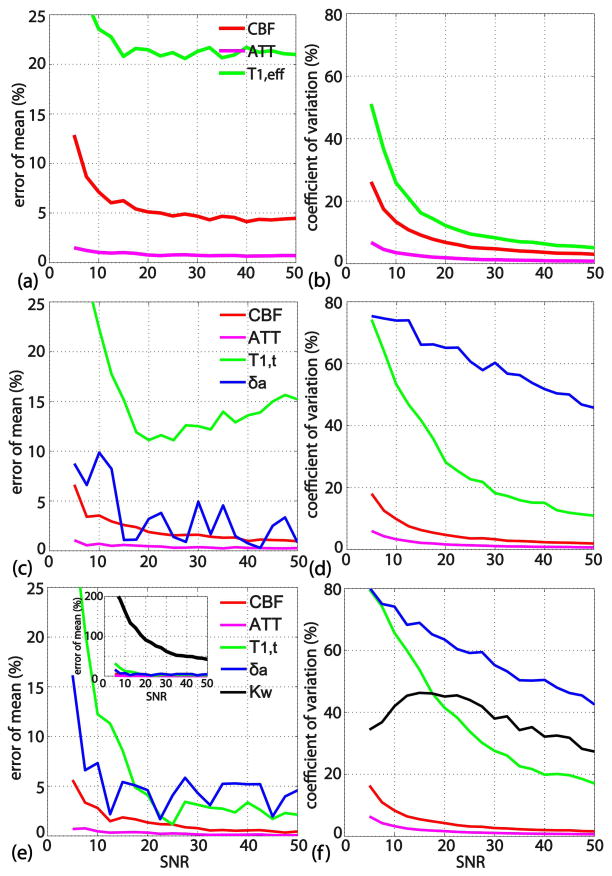
Figure 4 shows the simulation results of the fitting models with 3-parameter (Figure 4a,b), 4-parameter (Figure 4c,d) and 5-parameter (Figure 4e,f), plotting the error percentage of the mean (defined as accuracy) in the left column and coefficient of variation (precision) in the right column, all as a function of SNR. At the same SNR levels, fitted ATT values (pink lines) have higher accuracy and precision than the other parameters. Estimated CBF values (red lines) follow next, and, for the 3-parameter model, exhibit an accuracy of about [13, 7, 6, 5]% and a precision around [25, 13, 9, 7]% when SNR levels are [5 10 15 20], respectively (Figures 4a, b). The accuracy and precision of the CBF values are slightly higher with the 4- and 5-parameter models (Figures 4c–f), with no improvement when going from 4 to 5 parameters. This higher accuracy and precision for CBF estimation from the 4- and 5-parameter approach is expected since the data was generated using the 5-parameter model. Both the 4- and 5-parameter models lead to estimated δ_a values with large coefficients of variation, which reflect low precision (Figure 4d,f). Similar to the result of another Monte Carlo simulation work (24), the estimated K_w values from the 5-parameter model show poor accuracy and precision (Figure 4e,f).

Figure 4.

Monte Carlo simulation results for 3-parameter (a, b), 4-parameter (c, d) and 5-parameter (e, f) models, showing the error percentage of the mean (indicating accuracy) in the left column and the coefficient of variation (indicating precision) in the right column, all as a function of SNR. The precision and accuracies of the 3-, 4-, and 5-parameter models for estimating CBF / ATT is comparable; Additional parameters (δ_a / K_w) in the 4-, 5-parameter models are not estimated with acceptable precision.

Experiments

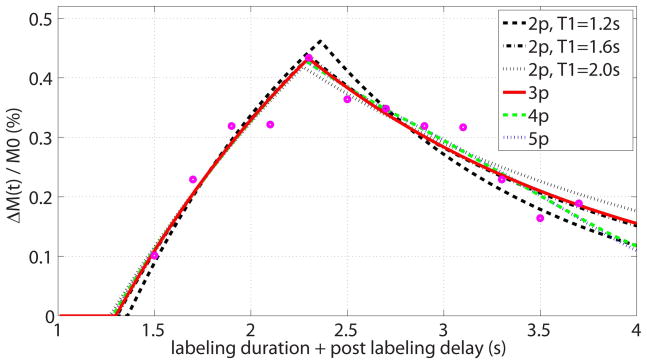
In Figure 5, a representative 3D whole-brain dataset (31 yrs, female) is displayed of the difference images (label-control, due to the 3 inversion pulses implemented post-labeling for background suppression) acquired at multiple PLDs, with the acquisition resolution of 6.7 × 7.4 × 7 mm³. The images are normalized to the maximum signal of the dataset. These data clearly show the effects of a heterogeneous distribution of arterial transit times over various brain regions. Little distortion or blurring effects are apparent in the different cross-sectional views. Typical multi-PLD data points from a gray matter voxel in the temporal lobe and the corresponding fitted curves obtained using the 2-, 3-, 4-, and 5-paramaeter models are shown in Figure 6.

Figure 5.

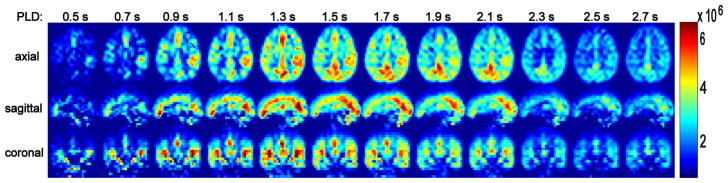
Perfusion weighted images as a function of post-labeling delay, with a representative dataset shown in three orthogonal views. Little distortion or blurring effects can be detected. The images are scaled by the maximal difference signal in the dataset. A heterogeneous distribution of arterial arrival times is visible for different brain regions.

Figure 6.

Representative multi-PLD dataset (open circles) for one voxel in gray matter, fitted by the proposed 3-parameter model (red solid line, the estimated values are: CBF = 52 mL/100g/min, ATT = 1.3 s, T_1,eff = 1.7 s, R² of fit = 0.91, AICc of fit = 316, BIC of fit = 314) and other models including: 2-parameter models with assumed T_1,eff = 1.2 s (black dashed line, CBF = 64 mL/100g/min, ATT = 1.4 s, R² of fit = 0.86, AICc of fit = 317, BIC of fit = 317), assumed T_1,eff = 1.6 s (black dashdot line, CBF = 53 mL/100g/min, ATT = 1.3 s, R² of fit = 0.91, AICc of fit = 312, BIC of fit = 312), and assumed T_1,eff = 2.0 s (black dotted line, CBF = 47 mL/100g/min, ATT = 1.3 s, R² of fit = 0.9, AICc of fit = 314, BIC of fit = 314); 4-parameter model (green dashed line, CBF = 49 mL/100g/min, ATT = 1.3 s, R² of fit = 0.92, AICc of fit = 319, BIC of fit = 315); and 5-parameter model (blue dotted line, CBF = 49 mL/100g/min, ATT = 1.3 s, R² of fit = 0.92, AICc of fit = 325, BIC of fit = 318).

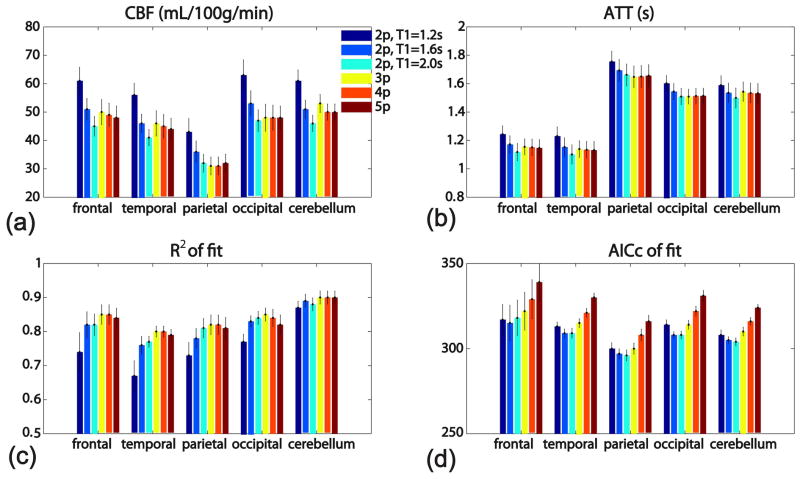
For each of the five ROIs in the gray matter (frontal lobe, temporal lobe, parietal lobe, occipital lobe, and cerebellum), the averaged estimated values (CBF, ATT, R² of fit, and AICc of fit) among 10 healthy subjects using six model fittings are displayed in a bar-graph (Figure 7). Table 1 lists the averaged CBF, ATT, T_1,eff, R2 of fit, AICc of fit and BIC of fit across all five ROIs of all the subjects for each model fitting, respectively, along with the paired statistical comparisons between groups. The BIC values are very close to the corresponding AICc values (Table 1) and are thus not shown in Figure 7. Across all regions, the estimated CBF values using the 2-parameter model vary appreciably with the assumed T_1,eff values (Figure 7a, Table 1); Conversely, relatively consistent CBF values are produced from the 3-, 4-, and 5-parameter models (Figure 7a, Table 1), similar to the Monte Carlo simulation results (Figure 4). ATT values estimated from the 2-parameter model are also slightly depend on the assumed T_1,eff values, as contrast to the almost invariable results from 3-, 4-, and 5-parameter models (Figure 7b, Table 1). The R² numbers always show better goodness of fit using the 3-, 4-, and 5-parameter models than using the 2-parameter models (Figure 7c, Table 1). The AICc numbers of the 3-parameter model are lower than both the 4- and 5-parameter models (Figure 7d, Table 1) (P < 0.05), indicating its optimal balance between goodness of fit and model complexity. Although the AICc numbers of most of the 2-parameter models are slightly lower than those of the 3-parameter model (Figure 7d, Table 1), the strong dependence of the CBF on assumed T_1,eff values (Figure 7a, Table 1) makes them suboptimal. From the proposed 3-parameter model, the averaged values are: CBF = 46±14 mL/100g/min, ATT = 1.4±0.3 s, and T_1,eff = 1.9±0.4 s (Table 1).

Figure 7.

Bar-graphs of the averaged estimated values using six model fittings: (a) CBF, (b) ATT, (c) R² of fit, and (d) AICc of fit, for each of the five ROIs in the gray matter (frontal lobe, temporal lobe, parietal lobe, occipital lobe, and cerebellum), among 10 healthy subjects. Error bars reflect the standard errors across subjects.

Table 1.

The averaged values estimated using different kinetic models, across five ROIs in the gray matter in different brain regions from ten healthy subjects, along with the paired statistical comparisons between groups.

model	CBF (mL/100g/min)	ATT (s)	T1,eff (s)	R2 of fit	AICc of fit	BIC of fit
2p_1.2s	57±16	1.5±0.3	1.2	0.76±0.13	310±15	310±15
2p_1.6s	47±13	1.4±0.3	1.6	0.82±0.09	307±17	306±17
2p_2.0s	42±11	1.4±0.3	2.0	0.82±0.08	307±17	306±17
3p	46±14	1.4±0.3	1.9±0.4	0.84±0.08	312±18	311±18
4p	44±13	1.4±0.3		0.84±0.08	319±19	315±18
5p	44±13	1.4±0.3		0.83±0.09	328±19	320±18
P values from paired t-test
(2p_1.2s, 2p_1.6s)	1.6×10−26	3.2×10−32		7.8×10−9	1.3×10−4	6.9×10−5
(2p_1.6s, 2p_2.0s)	1.7×10−27	3.9×10−29		0.18	0.81	0.97
(2p_2.0s, 3p)	1.1×10−4	2.3×10−3		9.5×10−10	8.8×10−12	5.4×10−9
(3p, 4p)	8.8×10−4	0.12		0.27	1.2×10−22	1.4×10−15
(4p, 5p)	0.15	0.86		9.6×10−6	6.4×10−36	1.4×10−24

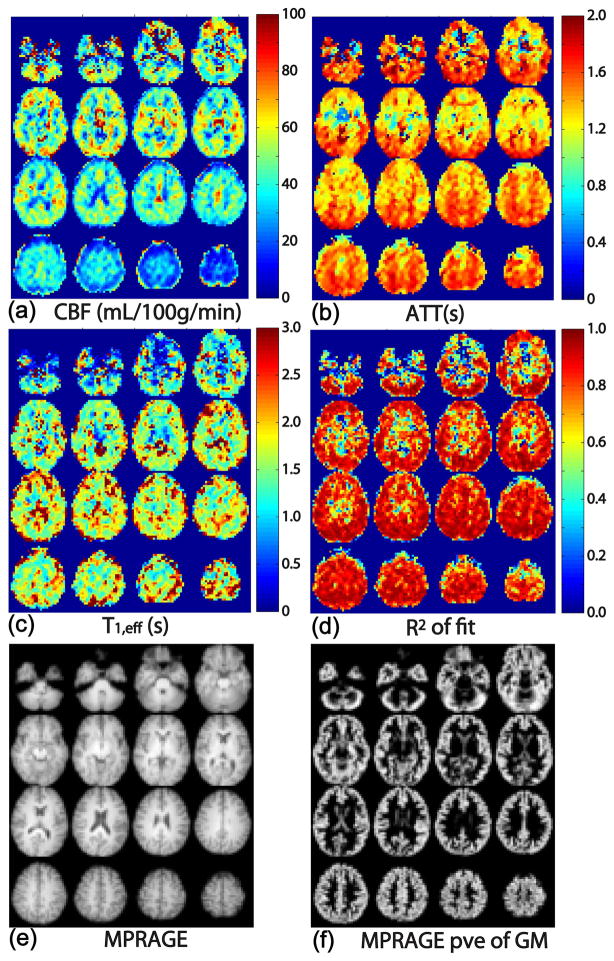
The estimated maps of CBF, ATT, T_1,eff, and R2 of fit using the 3-parameter model are displayed in Figure 8 (excluding the bottom two and top two slices). Figure 8 shows these maps in axial view, respectively, together with a co-registered MPRAGE image for anatomical comparison. For each subject, CBF maps (Figure 8a) were found to be uniform within the gray matter within each slice. CBF is lower in white matter than in gray matter and shows a longer transit time as expected. The CBF values in the inferior and superior slices are likely underestimated due to the imperfect slice profile of the slab excitation pulse. The inter-subject variation of CBF (35–75 mL/100g/min, Figure 8) is typical for the low SNR ASL measurement. ATT maps (Figure 8b) reflect the heterogeneity between different brain regions. ATT values are about 0.3–0.7 s shorter in the temporal lobe and medial frontal lobe, compared to the parietal/occipital lobes and cerebellum (Figure 8b). ATT is also about 0.2–0.5 s longer in white matter than in gray matter. T_1,eff values (1.2–2.5 s, Figure 8c) are found overall higher than reported tissue T₁ values, likely reflecting a contribution from microvascular arterial blood compartment or from CSF partial volume effects. The maps of the R² of fit indicate reasonable fits in most cortical regions, but not in deep gray matter and deep white matter areas (Figure 8d).

Figure 8.

Maps of (a) CBF, (b) ATT, (c) T_1,eff, and (d) the correlation coefficient of the fit, R2. The data show very good fits overall. Co-registered MPRAGE images (e) and segmented gray matter partial volume estimation (pve) (f) are also shown for anatomical comparison.

SNR evaluations were performed for acquisitions at 5 mm, 6 mm and 7 mm isotropic resolutions, respectively, by calculating the ratio of the mean at the peak of the kinetic curve of each ROI to the standard deviation of the noise at the same location in the noise images. Table 2 reports the systematic SNR of different ROIs averaged from six subjects at three acquisition resolutions. As expected, lower spatial resolution leads to higher SNR. The measured SNR values at about 7 mm isotropic resolution are higher than 20 across different regions, suggesting acceptable accuracy and precision can be achieved at this resolution, based on the Monte Carlo simulation results (Figure 4a,b).

Table 2.

The systematic SNR of different ROIs in gray matter averaged from the six subjects at three acquisition resolutions.

resolution	frontal lobe	temporal lobe	parietal lobe	occipital lobe	cerebellum
5 mm	15±5	14±5	11±5	12±6	11±3
6 mm	24±6	24±8	17±6	18±5	19±5
7 mm	41±12	39±13	25±5	28±7	32±13

DISCUSSION

We developed a whole brain quantitative CBF protocol that can be acquired in a short, clinically-relevant time frame (~5 min). The protocol covers the whole brain to allow for a broad range of applications, and it samples at multiple PLDs to obtain perfusion kinetic curves from different brain regions that are adequate for quantification. A simple 3-parameter model (CBF, ATT, T_1,eff) was used for quantification, which took account of both the arterial input function and the impulse response function.

Quantification Models

The multi-PLD approach, although requiring a longer acquisition time than the single-PLD approach, allows more accurate quantification of CBF, by relying less on assumptions such as an assumed ATT or impulse response function. The proposed 3-parameter model is also much simpler than the other more complicated 4-parameter or 5-parameter models, and offers the same level of accuracy and precision on estimating CBF and ATT (Figure 4). The estimated ATT maps, in addition to being helpful for quantification for CBF, may also be relevant to study the pathophysiology of cerebrovascular diseases.

The fitting of a single value of T_1,eff as a characterization for the IRF is an approximation to the complicated relaxation processes for labeled spins during a serial-travel through various compartments (arteries, capillaries, tissue, veins) after arrival at the voxels. Single-compartment models have previously described IRF with T₁ of tissue (3,15,16) or arterial blood (2). Although the treatment with predefined T₁ for IRF is tempting, as it reduces the model complexity, caution should be exercised to its validity.

As our current work indicate, the measured CBF values through the 2-parameter model show considerable dependence on the assumed T_1,eff values (Figure 7a, Table 1). In different gray matter ROIs from our healthy subjects, the measured CBF values using the 2-parameter model with T_1,eff = 1.6 s or 2.0 s are closer to the ones from 3-, 4-, and 5-parameter models with explicit IRF fitting, as compared to values using the other 2-parameter model with T_1,eff = 1.2 s (Figure 7a, Table 1). The estimated mean T_1,eff value of 1.9 s in gray matter ROIs using the proposed 3-parameter model (Table 1) is a little longer than the blood T₁ value measured from the in vitro bovine blood (~1.7 s, (51)), but close to the blood T₁ determined in vivo (~1.9 s, (27)), both conducted at 3T. In addition, the reduction of hematocrit in capillaries can be as low as 70% of that of the large arteries, known as Fahraeus effect (52,53), which would at least counteract the gradual shortening of the T₁ relaxation due to deoxygenation in microvascular network, if not further prolonging it. This suggests that the presence of labeled water within the blood appear to be the major contributor to IRF. Another measuring T₂ values of the ASL signal also demonstrated significant effect within vascular compartment (18). Quantifications using assumed tissue T₁s may cause overestimation of CBF (Figure 7a, Table 1).

Use of a single blood T₁ value for the IRF might provide reasonable quantification for healthy subjects, as suggested by our data, whereas its clinical applications still warrant to be further studied. For instance, certain vascular pathology or blood disorder, such as arteriovenous malformation or sickle cell anemia, may be associated with much faster blood velocity or shorter mean transit time within the cerebrovasculature. This might increase the contribution from the tissue compartment or the venous outflow in the IRF (1).

Although additional physiological parameters, such as arterial microvascular transit time (δ_a) and exchange rate of water from capillary blood to tissue (K_w), are included in those more sophisticated 4-, and 5-parameter models, our simulation results showed that it is not feasible to accurately estimate these values with the typical SNR levels afforded by current ASL techniques.

A model-free ASL quantification approach was applied before using deconvolution algorithm based on locally estimated AIF (54). Accounting for variability in T₁ values of the IRF was also proposed before using Variational Bayes method (55).

SNR Measurement

The measured SNR values (Table 2) are relatively higher than reported in other studies (17,37,56). This is in part due to the use of a larger voxel size (5 mm to 7 mm isotropic) and a 32-channel receive coil. Another reason is the method by which the SNR is calculated. A common method is to calculate the ratio of the mean value in a ROI in the tissue and the standard deviation of a different ROI in the background. This approach suffers the spatially variable noise level resulting from the parallel imaging reconstruction with the use of phased array coils (57,58). In this work, a separate noise measurement was performed with an identical acquisition protocol and RF pulses turned off. This is a more reliable way to measure systematic SNR when using parallel reconstruction (57,58).

Alternative method measures SNR as the ratio of the mean value and the standard deviation of the signal time course from a series of repeatedly recorded images. This also includes the physiological noise, such as cardiac pulsation and respiration (59), which could be a significant source of noise in ASL data. We did not utilize this approach due to the required long measurement duration for repeating multiple times of our segmented 3D GRASE acquisition, which could be sensitive to both subject motion and fluctuation of the brain activity during the scans. The actual SNR present in our data, when accounting for both the systematic noise and physiological noise, is expected to be lower than the values reported in Table 2. With lower SNR within the acquired multi-PLD ASL data, the accuracy and precision of the estimated CBF values using our proposed 3-parameter model would be poorer (Figure 4a, b). It is certainly worth further investigation of respective contribution of each noise source and practical methods to reduce physiological noise in ASL acquisition, which is beyond the scope of this study.

Limitations

Compared to other ASL approaches, the current CBF measurement protocol has a lower spatial resolution (~7 mm isotropic), which is close to the spatial resolution range in PET or SPECT studies (60). This is to attain the required SNR in order to ensure acceptable levels of accuracy and precision for the CBF estimation.

In this work, PCASL was chosen for labeling preparation. Although it provides higher SNR than pulsed ASL, it suffers from lower inversion efficiency and sensitivity to off-resonance and velocity effects (25). In future studies, a quick prescan for each subject to optimize this efficiency parameter of the PCASL technique will help reduce systematic errors caused by imperfect inversion (56,61). Another local parameter, in addition to ATT and T_1,eff, is the partial volume contribution of CSF, which needs to be measured and then corrected for when quantifying CBF (62), especially for the elderly population.

Lower SNR with some geometric distortion was observed in the inferior frontal lobe, temporal lobe, and brain stem areas. We attribute this to the sensitivity of the EPI component of the GRASE acquisition to B0 inhomogeneity in regions near the air cavities.

The proposed 3-parameter model assumes a single arterial transit time for each voxel, which may not be true for the watershed areas of brain, where tissue is at the border zone between arterial distributions. This may contribute to the poor fitting results in regions such as deep gray matter, but a more likely factor that could also explain this is the lower SNR due to the suboptimal 32-channel receive-coil sensitivity in midbrain regions. The AIF model used in this work only considered delay, without taking account of dispersion as some recent papers have performed (63–67), Further improvements of the proposed model by incorporating dispersion is currently under investigation.

CONCLUSION

ASL signal changes are not only proportional to CBF, but also depend on the arterial input function characterized by ATT and the impulse response function characterized by T_1,eff. We have developed a 3D whole-brain multi-PLD PCASL imaging protocol that can be acquired on clinical 3T scanners in five minutes. Both simulation and human brain mapping demonstrated a feasible 3-parameter model that renders simultaneous extraction of CBF, ATT and T_1,eff. The analysis of our multi-PLD data from healthy subjects indicate that both the 2-parameter model using fixed blood T₁ for T_1,eff and the 3-parameter model provide reasonable fitting results. The comparison in various cerebrovascular disorders is worth further studying.

Abbreviation

CBF

cerebral blood flow

ATT

arterial transit time

IRF

impulse response function

PCASL

pseudo-continuous arterial spin labeling

GRASE

the gradient- and spin-echo

APPENDIX

4-Parameter Model

The IRF r(t) for the 4-parameter model with two serial compartments (microvascular arterial and tissue) is:

$$\mathrm{r}(\mathrm{t})=\{\begin{array}{ll}{\mathrm{e}}^{-\mathrm{t}/{\mathrm{T}}_{1,\mathrm{a}}},\hfill & \hfill 0<\mathrm{t}\le {\mathrm{\delta }}_{\mathrm{a}}\\ {\mathrm{e}}^{-{\mathrm{\delta }}_{\mathrm{a}}/{\mathrm{T}}_{1,\mathrm{a}}}·{\mathrm{e}}^{{\mathrm{\delta }}_{\mathrm{a}}/{\mathrm{T}}_{1,\mathrm{t}}}·{\mathrm{e}}^{-\mathrm{t}/{\mathrm{T}}_{1,\mathrm{t}}},\hfill & \hfill \mathrm{t}>{\mathrm{\delta }}_{\mathrm{a}}\end{array}$$ [A1]

Here δ_a is the transit time of the blood in the microvascular arterial tree before entering the tissue compartment.

The ASL signal, as the convolution between the AIF c(t) (Eq. [1]) and IRF r(t) (Eq. [A1]), depends on the relationship between δ_a and τ:

When δ_a < τ,

$$\mathrm{\Delta }\mathrm{M}(\mathrm{t})=\{\begin{array}{ll}0,\hfill & \hfill \mathrm{t}<\mathit{ATT}\hfill \\ 2\mathrm{\alpha }{\mathrm{M}}_{0,\mathrm{a}}·\mathrm{f}·\left({\mathrm{T}}_{1,\mathrm{a}}·\left(1-{\mathrm{e}}^{-(\mathrm{t}-\text{ATT})/{\mathrm{T}}_{1,\mathrm{a}}}\right)\right),\hfill & \hfill \text{ATT}\le \mathrm{t}\le \text{ATT}+{\mathrm{\delta }}_{\mathrm{a}}\hfill \\ 2\mathrm{\alpha }{\mathrm{M}}_{0,\mathrm{a}}·\mathrm{f}·({\mathrm{T}}_{1,\mathrm{a}}·\left(1-{\mathrm{e}}^{-{\mathrm{\delta }}_{\mathrm{a}}/{\mathrm{T}}_{1,\mathrm{a}}}\right)\hfill \\ +{\mathrm{e}}^{-{\mathrm{\delta }}_{\mathrm{a}}/{\mathrm{T}}_{1,\mathrm{a}}}·{\mathrm{T}}_{1,\mathrm{t}}·\left(1-{\mathrm{e}}^{-(\mathrm{t}-\text{ATT}-{\mathrm{\delta }}_{\mathrm{a}})/{\mathrm{T}}_{1,\mathrm{t}}}\right)),& \text{ATT}+{\mathrm{\delta }}_{\mathrm{a}}<t<\mathit{ATT}+\mathrm{\tau }\hfill \\ 2\mathrm{\alpha }{\mathrm{M}}_{0,\mathrm{a}}·\mathrm{f}·({\mathrm{T}}_{1,\mathrm{a}}·\left({\mathrm{e}}^{-(\mathrm{t}-\text{ATT}-\mathrm{\tau })/{\mathrm{T}}_{1,\mathrm{a}}}-{\mathrm{e}}^{-{\mathrm{\delta }}_{\mathrm{a}}/{\mathrm{T}}_{1,\mathrm{a}}}\right)\hfill \\ +{\mathrm{e}}^{-{\mathrm{\delta }}_{\mathrm{a}}/{\mathrm{T}}_{1,\mathrm{a}}}·{\mathrm{T}}_{1,\mathrm{t}}·\left(1-{\mathrm{e}}^{-(\mathrm{t}-\text{ATT}-{\mathrm{\delta }}_{\mathrm{a}})/{\mathrm{T}}_{1,\mathrm{t}}}\right)),& \text{ATT}+\mathrm{\tau }\le \mathrm{t}\le \text{ATT}+\mathrm{\tau }+{\mathrm{\delta }}_{\mathrm{a}}\hfill \\ 2\mathrm{\alpha }{\mathrm{M}}_{0,\mathrm{a}}·\mathrm{f}·({\mathrm{T}}_{1,\mathrm{t}}·{\mathrm{e}}^{-{\mathrm{\delta }}_{\mathrm{a}}/{\mathrm{T}}_{1,\mathrm{a}}}·\left({\mathrm{e}}^{\mathrm{\tau }/{\mathrm{T}}_{1,\mathrm{t}}}-1\right)\hfill \\ ·{\mathrm{e}}^{-(\mathrm{t}-\text{ATT}-{\mathrm{\delta }}_{\mathrm{a}})/{\mathrm{T}}_{1,\mathrm{t}}}),& \hfill \mathrm{t}>\mathit{ATT}+\mathrm{\tau }+{\mathrm{\delta }}_{\mathrm{a}}\end{array}$$ [A2]

When δ_a ≥ τ,

$$\mathrm{\Delta }\mathrm{M}(\mathrm{t})=\{\begin{array}{ll}0,\hfill & \hfill \mathrm{t}<\mathit{ATT}\hfill \\ 2\mathrm{\alpha }{\mathrm{M}}_{0,\mathrm{a}}·\mathrm{f}·\left({\mathrm{T}}_{1,\mathrm{a}}·\left(1-{\mathrm{e}}^{-(\mathrm{t}-\text{ATT})/{\mathrm{T}}_{1,\mathrm{a}}}\right)\right),\hfill & \hfill \text{ATT}\le \mathrm{t}\le \text{ATT}+\mathrm{\tau }\hfill \\ 2\mathrm{\alpha }{\mathrm{M}}_{0,\mathrm{a}}·\mathrm{f}\hfill \\ ·\left({\mathrm{T}}_{1,\mathrm{a}}·\left({\mathrm{e}}^{-(\mathrm{t}-\text{ATT}-\mathrm{\tau })/{\mathrm{T}}_{1,\mathrm{a}}}-{\mathrm{e}}^{-(\mathrm{t}-\text{ATT})/{\mathrm{T}}_{1,\mathrm{a}}}\right)\right),& \text{ATT}+\mathrm{\tau }<t<\mathit{ATT}+{\mathrm{\delta }}_a\hfill \\ 2\mathrm{\alpha }{\mathrm{M}}_{0,\mathrm{a}}·\mathrm{f}·({\mathrm{T}}_{1,\mathrm{a}}·\left({\mathrm{e}}^{-(\mathrm{t}-\text{ATT}-\mathrm{\tau })/{\mathrm{T}}_{1,\mathrm{a}}}-{\mathrm{e}}^{-{\mathrm{\delta }}_{\mathrm{a}}/{\mathrm{T}}_{1,\mathrm{a}}}\right)\hfill \\ +{\mathrm{e}}^{-{\mathrm{\delta }}_{\mathrm{a}}/{\mathrm{T}}_{1,\mathrm{a}}}·{\mathrm{T}}_{1,\mathrm{t}}·\left(1-{\mathrm{e}}^{-(\mathrm{t}-\text{ATT}-{\mathrm{\delta }}_{\mathrm{a}})/{\mathrm{T}}_{1,\mathrm{t}}}\right)),& \text{ATT}+{\mathrm{\delta }}_{\mathrm{a}}\le \mathrm{t}\le \text{ATT}+\mathrm{\tau }+{\mathrm{\delta }}_{\mathrm{a}}\hfill \\ 2\mathrm{\alpha }{\mathrm{M}}_{0,\mathrm{a}}·\mathrm{f}·\left({\mathrm{T}}_{1,\mathrm{t}}·{\mathrm{e}}^{-{\mathrm{\delta }}_{\mathrm{a}}/{\mathrm{T}}_{1,\mathrm{a}}}·\left({\mathrm{e}}^{\mathrm{\tau }/{\mathrm{T}}_{1,\mathrm{t}}}-1\right)·{\mathrm{e}}^{-(\mathrm{t}-\text{ATT}-{\mathrm{\delta }}_{\mathrm{a}})/{\mathrm{T}}_{1,\mathrm{t}}}\right),\hfill & \hfill \mathrm{t}>\mathit{ATT}+\mathrm{\tau }+{\mathrm{\delta }}_{\mathrm{a}}\end{array}$$ [A3]

This 4-parameter, 2-compartment model was first described using formulas with different expressions (17).

5-Parameter Model

By adding on the microvascular arterial compartment to the 2-compartment (capillary bed and tissue) Single-Pass Approximation model (22,29), the IRF r(t) for the 5-parameter, 3-compartment model is expressed as:

$$\mathrm{r}(\mathrm{t})=\{\begin{array}{ll}{\mathrm{e}}^{-\mathrm{t}/{\mathrm{T}}_{1,\mathrm{a}}},\hfill & 0<t\le {\mathrm{\delta }}_{\mathrm{a}}\hfill \\ {\mathrm{e}}^{-{\mathrm{\delta }}_{\mathrm{a}}/{\mathrm{T}}_{1,\mathrm{a}}}·{\mathrm{e}}^{{\mathrm{\delta }}_{\mathrm{a}}/{\mathrm{T}}_{1,\mathrm{t}}}·\mathrm{\beta }·{\mathrm{e}}^{-\mathrm{t}/{\mathrm{T}}_{1,\mathrm{t}}}+{\mathrm{e}}^{-{\mathrm{\delta }}_{\mathrm{a}}/{\mathrm{T}}_{1,\mathrm{a}}}·{\mathrm{e}}^{{\mathrm{\delta }}_{\mathrm{a}}({\mathrm{K}}_{\mathrm{w}}+1/{\mathrm{T}}_{1,\mathrm{a}})}·(1-\mathrm{\beta })·{\mathrm{e}}^{-\mathrm{t}({\mathrm{K}}_{\mathrm{w}}+1/{\mathrm{T}}_{1,\mathrm{a}})},\hfill & \hfill \mathrm{t}>{\mathrm{\delta }}_{\mathrm{a}}\end{array}$$ [A4]

Here K_w is the exchange rate of water from capillary blood to tissue, and β = K_w / (K_w + 1/T_1,a − 1/T_1,t).

The ASL signal, as the convolution between the AIF c(t) (Eq. [1]) and IRF r(t) (Eq. [A4]), also depends on the relationship between δ_a and τ:

When δ_a < τ,

$$\mathrm{\Delta }\mathrm{M}(\mathrm{t})=\{\begin{array}{ll}0,\hfill & \hfill \mathrm{t}<\mathit{ATT}\hfill \\ 2\mathrm{\alpha }{\mathrm{M}}_{0,\mathrm{a}}·\mathrm{f}·\left({\mathrm{T}}_{1,\mathrm{a}}·\left(1-{\mathrm{e}}^{-(\mathrm{t}-\text{ATT})/{\mathrm{T}}_{1,\mathrm{a}}}\right)\right),\hfill & \hfill \text{ATT}\le \mathrm{t}\le \text{ATT}+{\mathrm{\delta }}_{\mathrm{a}}\hfill \\ \begin{array}{l}2\mathrm{\alpha }{\mathrm{M}}_{0,\mathrm{a}}·\mathrm{f}·({\mathrm{T}}_{1,\mathrm{a}}·\left(1-{\mathrm{e}}^{-{\mathrm{\delta }}_{\mathrm{a}}/{\mathrm{T}}_{1,\mathrm{a}}}\right)\\ +{\mathrm{e}}^{-{\mathrm{\delta }}_{\mathrm{a}}/{\mathrm{T}}_{1,\mathrm{a}}}·\mathrm{\beta }·{\mathrm{T}}_{1,\mathrm{t}}·\\ \left(1-{\mathrm{e}}^{-(\mathrm{t}-\text{ATT}-{\mathrm{\delta }}_{\mathrm{a}})/{\mathrm{T}}_{1,\mathrm{t}}}\right)\dots \\ +{\mathrm{e}}^{-{\mathrm{\delta }}_{\mathrm{a}}/{\mathrm{T}}_{1,\mathrm{a}}}(1-\mathrm{\beta })/\left({\mathrm{K}}_{\mathrm{w}}+1/{\mathrm{T}}_{1,\mathrm{a}}\right)·\left(1-{\mathrm{e}}^{-(\mathrm{t}-\text{ATT}-{\mathrm{\delta }}_{\mathrm{a}})({\mathrm{K}}_{\mathrm{w}}+1/{\mathrm{T}}_{1,\mathrm{a}})}\right)),\end{array}\hfill & \text{ATT}+{\mathrm{\delta }}_{\mathrm{a}}<t<\mathit{ATT}+\mathrm{\tau }\hfill \\ \begin{array}{l}2\mathrm{\alpha }{\mathrm{M}}_{0,\mathrm{a}}·\mathrm{f}·({\mathrm{T}}_{1,\mathrm{a}}·\left({\mathrm{e}}^{-(\mathrm{t}-\text{ATT}-\mathrm{\tau })/{\mathrm{T}}_{1,\mathrm{a}}}-{\mathrm{e}}^{-{\mathrm{\delta }}_{\mathrm{a}}/{\mathrm{T}}_{1,\mathrm{a}}}\right)\\ +{\mathrm{e}}^{-{\mathrm{\delta }}_{\mathrm{a}}/{\mathrm{T}}_{1,\mathrm{a}}}·\mathrm{\beta }·{\mathrm{T}}_{1,\mathrm{t}}·\left(1-{\mathrm{e}}^{-(\mathrm{t}-\text{ATT}-{\mathrm{\delta }}_{\mathrm{a}})/{\mathrm{T}}_{1,\mathrm{t}}}\right)\dots \\ +{\mathrm{e}}^{-{\mathrm{\delta }}_{\mathrm{a}}/{\mathrm{T}}_{1,\mathrm{a}}}·(1-\mathrm{\beta })/\left({\mathrm{K}}_{\mathrm{w}}+1/{\mathrm{T}}_{1,\mathrm{a}}\right)·\left(1-{\mathrm{e}}^{-(\mathrm{t}-\text{ATT}-{\mathrm{\delta }}_{\mathrm{a}})({\mathrm{K}}_{\mathrm{w}}+1/{\mathrm{T}}_{1,\mathrm{a}})}\right)),\end{array}\hfill & \text{ATT}+\mathrm{\tau }\le \mathrm{t}\le \text{ATT}+\mathrm{\tau }+{\mathrm{\delta }}_{\mathrm{a}}\hfill \\ \begin{array}{l}2\mathrm{\alpha }{\mathrm{M}}_{0,\mathrm{a}}·\mathrm{f}·({\mathrm{T}}_{1,\mathrm{t}}·{\mathrm{e}}^{-{\mathrm{\delta }}_{\mathrm{a}}/{\mathrm{T}}_{1,\mathrm{a}}}·\mathrm{\beta }·\left({\mathrm{e}}^{\mathrm{\tau }/{\mathrm{T}}_{1,\mathrm{t}}}-1\right)·{\mathrm{e}}^{-(\mathrm{t}-\text{ATT}-{\mathrm{\delta }}_{\mathrm{a}})/{\mathrm{T}}_{1,\mathrm{t}}}\dots \\ +{\mathrm{e}}^{-{\mathrm{\delta }}_{\mathrm{a}}/{\mathrm{T}}_{1,\mathrm{a}}}·(1-\mathrm{\beta })/\left({\mathrm{K}}_{\mathrm{w}}+1/{\mathrm{T}}_{1,\mathrm{a}}\right)\\ ·\left({\mathrm{e}}^{\mathrm{\tau }({\mathrm{K}}_{\mathrm{w}}+1/{\mathrm{T}}_{1,\mathrm{a}})}-1\right)·{\mathrm{e}}^{-(\mathrm{t}-\text{ATT}-{\mathrm{\delta }}_{\mathrm{a}})({\mathrm{K}}_{\mathrm{w}}+1/{\mathrm{T}}_{1,\mathrm{a}})}),\end{array}\hfill & \hfill \mathrm{t}>\mathit{ATT}+\mathrm{\tau }+{\mathrm{\delta }}_{\mathrm{a}}\end{array}$$ [A5]

When δ_a ≥ τ,

$$\mathrm{\Delta }\mathrm{M}(\mathrm{t})=\{\begin{array}{ll}0,\hfill & \hfill \mathrm{t}\le \mathit{ATT}\hfill \\ 2\mathrm{\alpha }{\mathrm{M}}_{0,\mathrm{a}}·\mathrm{f}·\left({\mathrm{T}}_{1,\mathrm{a}}·\left(1-{\mathrm{e}}^{-(\mathrm{t}-\text{ATT})/{\mathrm{T}}_{1,\mathrm{a}}}\right)\right),\hfill & \hfill \text{ATT}\le \mathrm{t}\le \text{ATT}+\mathrm{\tau }\hfill \\ 2\mathrm{\alpha }{\mathrm{M}}_{0,\mathrm{a}}·\mathrm{f}·\left({\mathrm{T}}_{1,\mathrm{a}}·\left({\mathrm{e}}^{\mathrm{\tau }/{\mathrm{T}}_{1,\mathrm{a}}}-1\right)·{\mathrm{e}}^{-(\mathrm{t}-\text{ATT})/{\mathrm{T}}_{1,\mathrm{a}}}\right),\hfill & \text{ATT}+\mathrm{\tau }<t<\text{ATT}+{\mathrm{\delta }}_{\mathrm{a}}\hfill \\ 2\mathrm{\alpha }{\mathrm{M}}_{0,\mathrm{a}}·\mathrm{f}·({\mathrm{T}}_{1,\mathrm{a}}·\left({\mathrm{e}}^{-(\mathrm{t}-\text{ATT}-\mathrm{\tau })/{\mathrm{T}}_{1,\mathrm{a}}}-{\mathrm{e}}^{-{\mathrm{\delta }}_{\mathrm{a}}/{\mathrm{T}}_{1,\mathrm{a}}}\right)\hfill \\ +{\mathrm{e}}^{-{\mathrm{\delta }}_{\mathrm{a}}/{\mathrm{T}}_{1,\mathrm{a}}}·\mathrm{\beta }·{\mathrm{T}}_{1,\mathrm{t}}·\left(1-{\mathrm{e}}^{-(\mathrm{t}-\text{ATT}-{\mathrm{\delta }}_{\mathrm{a}})/{\mathrm{T}}_{1,\mathrm{t}}}\right)\dots \hfill \\ +{\mathrm{e}}^{-{\mathrm{\delta }}_{\mathrm{a}}/{\mathrm{T}}_{1,\mathrm{a}}}·(1-\mathrm{\beta })/\left({\mathrm{K}}_{\mathrm{w}}+1/{\mathrm{T}}_{1,\mathrm{a}}\right)\hfill \\ ·\left(1-{\mathrm{e}}^{-(\mathrm{t}-\text{ATT}-{\mathrm{\delta }}_{\mathrm{a}})({\mathrm{K}}_{\mathrm{w}}+1/{\mathrm{T}}_{1,\mathrm{a}})}\right)),\hfill & \hfill \text{ATT}+{\mathrm{\delta }}_{\mathrm{a}}\le \mathrm{t}\le \text{ATT}+\mathrm{\tau }+{\mathrm{\delta }}_{\mathrm{a}}\hfill \\ 2\mathrm{\alpha }{\mathrm{M}}_{0,\mathrm{a}}·\mathrm{f}·({\mathrm{T}}_{1,\mathrm{t}}·{\mathrm{e}}^{-{\mathrm{\delta }}_{\mathrm{a}}/{\mathrm{T}}_{1,\mathrm{a}}}·\mathrm{\beta }·\left({\mathrm{e}}^{\mathrm{\tau }/{\mathrm{T}}_{1,\mathrm{t}}}-1\right)·{\mathrm{e}}^{-(\mathrm{t}-\text{ATT}-{\mathrm{\delta }}_{\mathrm{a}})/{\mathrm{T}}_{1,\mathrm{t}}}\dots \hfill \\ +{\mathrm{e}}^{-{\mathrm{\delta }}_{\mathrm{a}}/{\mathrm{T}}_{1,\mathrm{a}}}\hfill \\ ·(1-\mathrm{\beta })/\left({\mathrm{K}}_{\mathrm{w}}+1/{\mathrm{T}}_{1,\mathrm{a}}\right)\hfill \\ ·\left({\mathrm{e}}^{\mathrm{\tau }({\mathrm{K}}_{\mathrm{w}}+1/{\mathrm{T}}_{1,\mathrm{a}})}-1\right)·{\mathrm{e}}^{-(\mathrm{t}-\text{ATT}-{\mathrm{\delta }}_{\mathrm{a}})({\mathrm{K}}_{\mathrm{w}}+1/{\mathrm{T}}_{1,\mathrm{a}})}),\hfill & \hfill \mathrm{t}>\mathit{ATT}+\mathrm{\tau }+{\mathrm{\delta }}_{\mathrm{a}}\end{array}$$ [A6]

A more extensive model that includes all three compartments but classifies into four phases has been described using formulas with different expressions (23).