Substrates with Patterned Extracellular Matrix and Subcellular Stiffness Gradients Reveal Local Biomechanical Responses

Both substrate stiffness and the extracellular matrix are key regulators of a large variety of cellular functions, and act as critical checkpoints in regulating cellular development. Substrate stiffness is either directly or indirectly sensed by cells and leads to signaling ^[1] that has been identified to affect migration (durotaxis) ^[2], proliferation ^[3], tissue architecture ^[1], stem cell differentiation ^[4], and phenotype ^[5,6]. Spatial restriction and regulation of extracellular matrix (ECM), or cell patterning, similarly perturbs cell behavior, with noted effects on cell polarity ^[7], proliferation ^[8,9], division ^[10], and differentiation ^[11]. While numerous technological achievements abound in the study of these separated effects, as of yet, there exists few techniques allowing long-term, simultaneous and aligned patterning of stiffness (or force) and ECM cues, especially at sub-cellular resolution ^[12]. In vivo, both single cells and tissues are often subject to local variations in stiffness, forces from neighboring cells and tissues, and matrix organization (particularly in early stages of biological development) ^[13,14], and as such, the capability to explore the steady-state response of cells under controlled combinations of such conditions is of critical importance in both biological understanding and the further development of tools to specify the assembly of biological structures with local microenvironment variations.

A number of technologies exist to pattern stiffness and extracellular matrix proteins on substrates. Stiffness is patterned predominantly by generating a direct material interface between polymeric materials with different cross-linking density, whether by the introduction of chemical gradients in cross-linker, or by differential exposure of photo-sensitive crosslinker ^[2,15–19]. This fundamentally also generates gradients in material properties exposed to the biological systems, as the pore size and surface chemistry can vary significantly across regions of varying cross-linking density. Recently, several approaches have generated stiffness patterns in polyacrylamide gels that instead rely on generating a 3-d molded rigid backbone filled and covered by the less stiff polymer ^[20,21]. Because of the propagation of force through the softer material, regions with lower heights of softer polymer above the stiff backbone are measured to have higher effective stiffness. The material appears chemically continuous to biological structures interacting with the surface, but generates gradients in stiffness due to sensing of the backbone structures underneath ^[22,23]. Extracellular matrix proteins are patterned using a number of approaches including contact printing ^[8], deep UV activation ^[24], and photolithography ^[12,25,26]. These methods are not traditionally amenable to soft substrates: contact printing techniques are commonly unstable, and photolithography relies on plasma treatments ^[27], which generate thin, high elastic modulus silica layers ^[28], significantly increasing the apparent modulus of the substrate. Contact printing substrates pre-gelation ^[29], and deep-UV exposure has been shown to be effective specifically on polyacrylamide substrates ^[30], however, restrictions of this approach make it difficult to align ECM patterns with an underlying stiffness pattern on a substrate.

Here, we introduce an integrated, multilayered, microfabricated substrate with enhanced functionality compared to existing patterned surfaces, allowing the generation of large, stiffness gradients across the material surface, and their integration and alignment with spatially patterned extracellular matrix, both of these with sub-cellular resolution (Fig. 1a). This type of approach can restrict single cell movement and shape, allowing the unique study of single cells in equilibrium with consistent, asymmetric mechanical boundary conditions. This greatly simplifies interpretation of cell response to coincident mechanical signals with larger sample size and statistical accuracy.

Figure 1.

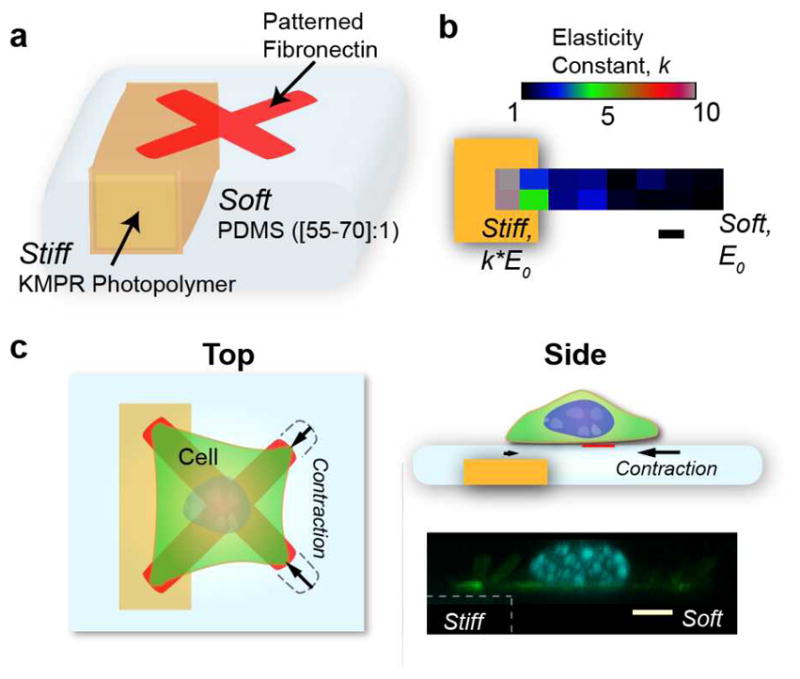
Complex substrates encoding large stiffness gradients with aligned extracellular matrix patterning. a) Simplified schematic of the primary components of the microfabricated system. Photopatterned KMPR forms the stiff backbone defining more rigid surface regions above it, while low Young’s modulus PDMS is spun to cover and planarize this structure. The thinner PDMS regions above the KMPR are designed to be stiffer than the neighboring thick PDMS films. b) Elastic modulus variation spanning the soft to stiff regions as determined from atomic force microscopy for a 1 μm thick PDMS layer over the stiff backbone. Thin PDMS regions have higher effective elastic modulus due to the presence of the underlying backbone. E₀ of our PDMS depends on cross-linker to base ratio (55:1 yield a modulus of around 16 kPa). c) Top and side view of the major elements showing a schematic of patterned cells. The cell contracts soft regions of the surface connected through focal adhesions, while those on stiff regions are accompanied by significantly reduced contraction. A confocal cross-section shows the planar nature of the substrate from stiff to soft. Scale bars are 5 μm.

The structural backbone that corresponds to stiff regions in the final planarized surface is composed of high resolution, high aspect-ratio photo-patterned KMPR (epoxy) resin, as opposed to large beads or micromolded stiff acrylamide, resulting in steeper stiffness gradients. This backbone is covalently grafted to a mechanically soft, 65:1 Polydimethylsiloxane (PDMS) layer via oxygen plasma and subsequent silanization with allyl groups. These functional groups cross-link with the PDMS, and upon curing, bond to form the high resolution stiff-soft structures of our substrates. In contrast to polyacrylamide, whose porosity and surface functionalization can vary strongly with cross-linking concentration^[6,31], PDMS forms a robust, continuous, water-repellant structure, and is commonly integrated in microfabrication techniques. PDMS spinning yields more consistent thicknesses and significantly reduced topology in comparison to acrylamide.

As PDMS expands and shrinks upon cyclic exposure to organic solvents and subsequently water, traditional photolithography steps were modified to reduce PDMS exposure to solvent, and allow aqueous development of the photoresist defining the stiffness gradient-aligned protein patterns (Fig. S1). Final substrates were measured to have negligible topography (PDMS regions with heights down to 1 to 1.5 μm above the backbone varied around 300 nm across the substrate, at the z-resolution limits of confocal microscopes, Movie S1), and exhibit large, subcellular stiffness gradients (Fig. 1b) and high resolution fibronectin patterns. The KMPR backbone fluoresces under excitation by a typical DAPI filter set, and its z-region can be delineated by confocal microscopy (Fig. 1c).

We confirmed that stiffness gradients were present across the patterned surfaces by acquiring force-displacement curves using atomic force microscopy, and fitting to the Hertz model. Due to the smaller size of our backbone structures, the elastic modulus in “stiff” regions increases more slowly with decreasing PDMS thickness than that seen by other groups ^[21], and to achieve apparent moduli increases of 10 times above the surrounding thick PDMS film (30 μm thick, above the 15 μm threshold at which cells no longer sense the underlying substrate), a local PDMS thickness of 1 μm is required. We successfully patterned matrix on 55:1 up to 70:1 ratios, with our 55:1 thick films (30 μm) measuring 16 kPa, and higher ratios being softer.

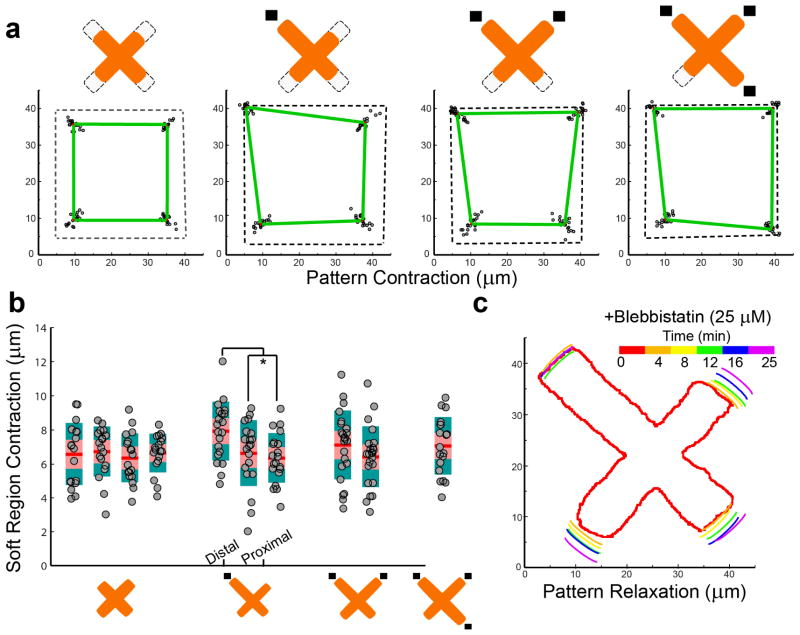
We used local stiffness control at sub-cellular locations across a patterned cell to investigate how a cell integrates disparate mechanical signals to arrive at an overall response. We chose the fibronectin “X” pattern to perform our systematic studies, as in this pattern cell adhesions are focused to four peripheral points, and can be individually addressed with a region of high stiffness. This simplifies the interpretation of the data. Zero to three corners of the “X” were co-located with high local stiffness regions, and the remaining regions of the pattern rested atop the thicker region yielding low local stiffness. We subsequently seeded 3T3 cells and found that cells contract to shapes unique to the defined stiffness constraints (Fig. 2a).

Figure 2.

Cells contract and retract asymmetrically when constrained by extracellular matrix patterns with underlying stiffness gradients. a) Cells patterned to X shapes with corners constrained by either stiff (dark rectangles) or soft regions contract to unique shapes depending on the stiffness boundary conditions. b) Magnitude of contraction for adhesions above soft regions for X-patterned cells. Contraction magnitude is similar across shapes, except for the asymmetric single stiff adhesion condition. Distal adhesions contract slightly higher in comparison to proximal adhesions, significance determined by student’s t-test, p < .031. Contraction of 6.5 μm corresponds to approximately 254 nN of force on soft regions. c) Relaxation of fibronectin patterns upon treatment with 25 μM of blebbistatin was observed by live-cell microscopy.

We found that the presence of stiff regions resulted in asymmetric displacements (and applied forces) on soft regions, yielding new equilibrium deformed ECM shapes. Interestingly, constraining the regions where forces are applied to the substrates with ECM patterning allows mechanical analysis similar to that done for pillar deflection studies ^[32], as the focal adhesion locations are restricted to discrete areas corresponding to extracellular matrix. The underlying elastic modulus can be equated to a pillar spring constant by the equation: E_eff = 9k/(2πD) ^[33], where D is the initial size of the adhesion. In this manner we can approximate the pressures generated by the cell directly from the deflection of the protein pattern, greatly simplifying what typically requires inverse-transform numerical techniques. For substrates with zero, two, and three stiff edges underlying the arms of the “X” ECM pattern we observed a conserved level of deflection of the remaining soft regions of the substrate (Fig. 2b). For the 6.5 μm deflection observed for these systems on 63:1 PDMS substrates (estimated to be 8 kPa) we estimate a force of 254 nN applied by the cell at focal adhesions. This is slightly higher than the 200 nN force reported to be applied by these cells ^[34]. Several factors could account for such a discrepancy, including non-linearities in modeling the PDMS elastic modulus with large deformations and the coupled mechanical system of an elastic sheet. Notably, substrate deflection and applied force at distal anchorages for patterns with a single stiff region were larger than deformations on all soft patterns, indicating that the rigid region seemed to bias the local force balance of the cell. Although here we quantify the x-y contraction of our substrates, it is of note that confocal imaging reveals subtle z-deflections initiated at focal adhesion regions in soft areas (Movie S1). This value is not traditionally accessible in pillar deflection geometries due to large stiffness of pillars in the z-dimension, which become directly coupled to x-y deflection.

We confirmed the absence of substantial plasticity upon substrate deformation, by releasing cell-induced tension with blebbistatin. 3T3 cells constrained to grow on patterns were treated with 25 μM of blebbistatin (a myosin II inhibitor). Cells treated with blebbistatin relaxed from their initial asymmetric structures, and the pattern correspondingly retracted (Fig. 2b, Movie S2). Although cell patterns did not completely relax, the final tension in the structure is similar with previous relaxation experiments ^[30], and indicates that the substrate retains elastic characteristics.

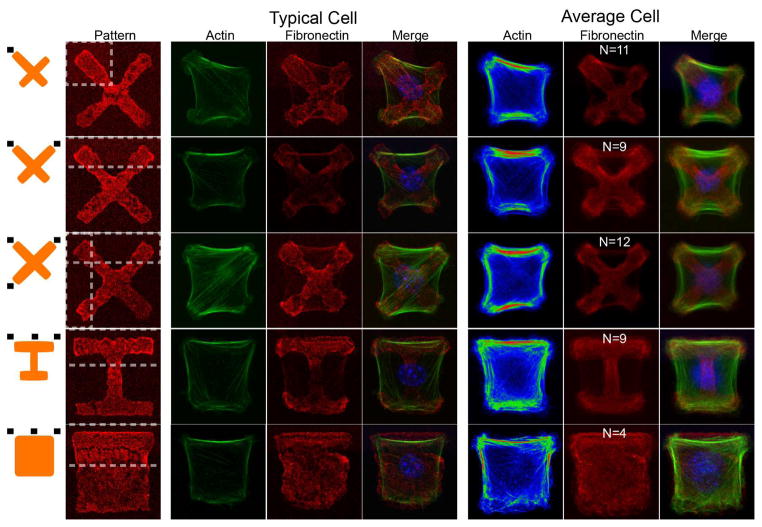
Underlying sub-cellular actin architecture also reflected the asymmetric rigidity of the substrates. Numerous studies have tracked phenotypic changes of cells grown on PDMS substrates as stiffness is increased. In general, these studies demonstrated that isolated cells on soft substrates exhibit thinner, shorter stress fibers, and more rounded cell-morphology ^[4,5]. In contrast to acrylamide-based studies, existing studies have noted that cell size does not typically change with PDMS substrate stiffness ^[5,31], possibly due to differences in presentation of matrix. When cells were patterned on X, square, and I ECM patterns along with asymmetric substrate stiffnesses, we found that the actin cytoskeleton polarized to match the underlying substrate (Fig. 3). Soft regions of the pattern displayed significant contraction specifically where actin cables terminated. Underlying stress fiber distributions similarly shifted with increased intensity and number of stress fibers originating from stiffer regions, which subsequently decay as they terminate in regions of high contraction and low stiffness. We note that in the special case of cells with a single stiff anchorage, average cells display a net polarity in internal stress fibers from stiff anchorages to the distal soft anchorage, which may explain our observed contractility asymmetry. It is also possible that the stiff region shifts the cell center point, where distance from cell center has been shown, and modelled to have an effect on cell contractility in freely spread cells ^[35,36]. In cells grown on stiff substrates (Fig. S3) with symmetric ECM patterns, stress fibers originate symmetrically around all corners and do not appear directed. Cells patterned under all-soft conditions display notably thinner and more irregular exterior and interior stress fibers (Fig. S3). Our results seem consistent with studies and theory that have shown that low to moderate traction forces (up 100 to 200 pN, as mediated from the substrate) can increase focal adhesion intensity and size ^[37,38], which subsequently reinforce the actin cytoskeleton ^[39]. Together, these results imply that the cell is sensitive to local stiffness which directs the active assembly of actin stress fibers locally, suggesting diffusible signaling molecules are not part of this pathway.

Figure 3.

Single-cell actin cytoskeleton polarizes to match the stiffness gradients of the underlying matrix. Shown are typical and average cell actin substructure for X, I, and square fibronectin shapes with varying stiffness stimuli from the substrate. Black rectangles near orange schematics on the left represent stiff regions. Interior stress fibers preferentially orient towards contracted regions, initiating at regions of high stiffness, and terminating at regions of low stiffness. Of particular note are stress fibers in the single stiff adhesion case, which preferentially orient diagonally and terminate across the sample, and may be the source of the increased contraction of distal adhesions for this case. Scale bar is 5 μm.

We finally attempted to decouple the contributions of substrate stiffness gradients from deformed cell shape. Following observations of the deformed ECM patterns, we developed new patterns that replicated the contracted extracellular matrix shapes but onto an all stiff substrate. Fluorescent microscopy averages of these shapes appear alongside fluorescent microscopy averages of initially square patterns with sub-cellular stiffness gradients, subsequently contracted by the cells (Fig. S4). Besides polarity in actin, edge stress fibers on the all stiff substrates have a larger radius of curvature, and possess less asymmetric inflection. This is consistent with a larger fiber tension (and substrate pulling force) acting to stretch out the local cortex, appearing to flatten out the shape and asymmetry of stress fibers.

In total, we demonstrate a novel, integrated material allowing high precision, decoupled control of the extracellular matrix pattern and local apparent stiffness to cells. Cells simultaneously process an enormous number of extracellular cues when making decisions. Isolated control of factors such as stiffness, contractility, and matrix shape allows unique insight into the biophysics of cellular response to stiffness cues. In particular, such control allows exploration of how cells integrate information from surroundings, make decisions, and subsequently stabilize in accordance to mechanical cues presented from the surrounding tissue. While the presented methodology allows scientists significant control for mechanotransduction studies in unique, constrained circumstances, the use of PDMS and a modified lithographical approach allow the direct integration of the technique with more complex, MEMS-based underlying sub-structures ^[12,40]. Particularly interesting directions would be in novel interfaces with devices that actively modulate light, electricity, and/or mechanical motion. The PDMS layer itself, due to its low elasticity, can also provide feedback through quantification of the deflections of the layer, and can facilitate the development of tools to better deliver and extract information from biological structures

Experimental

Substrate Preparation

The stiff backbone substructure for substrates with gradients in stiffness was directly patterned through standard photolithography. KMPR 1025 was spun onto portioned glass slides to a goal thickness of 28 μm. Samples were then oxidized in oxygen plasma, and silanized overnight (in vacuum) with 200 μL of allyltriethoxysilane (Sigma). PDMS was vortexed at base to crosslinker ratios of 55:1 to 70:1 depending on desired base elastic modulus (63:1 for experiments in manuscript), degassed, and spun onto samples in successive 2500 rpm spins until a proper thickness of 1 to 2 μm above features was achieved. Samples were then cured at room temperature over a minimum of 4 days, before 10:1 PDMS spacers were spun onto edges. S1805 photoresist was patterned using a modified process. Resist was spun onto the PDMS substrate (3000 rpm, 1700 rpm/s, 5 s), and soft-baked for one minute. Substrates were subsequently exposed under an aligner with a mask (note that small features directly over and adjacent to the KMPR substructures must be dilated by 2 μm), developed with AZ400K developer, and carefully washed and dried. Samples were finally flood exposed, before being hard-baked for 1 minute at 80 °C. Within 1 hour of photoresist patterning, substrates were covered with 30 μg/mL fibronectin (Sigma) and 30 μg/mL fibrinogen-alexa fluor 568 (Invitrogen) in PBS, and allowed to incubate for 45 minutes before being washed and left in PBS. Remnant resin was developed in aqueous AZ400K, KOH developer (45 s with high agitation and partial ultrasonic), and samples replaced in PBS. Samples were then kept overnight before subsequent processing.

All-stiff control substrates were generated according to previously described protocols ^[12]. Briefly, PSR resin (4 GPa) was processed according to protocol. Hard-baked samples were subsequently processed with standard S1805 lithography, and incubated with extracellular matrix proteins. Remnant resin was stripped in 100 % ethanol, before incubation in Pluronics F127, and washing in PBS.

Cell culture

3T3 fibroblasts (ATCC) were grown in flasks at 5 % CO₂ and 37 °C, using complete medium (DMEM, 10 % FBS, 1 % Pencillin/Streptomycin). Cells were grown in subconfluent conditions, trypsinized, and pelleted before deposition onto substrates.

Directly before cell culture, substrates were incubated in 0.4 % Pluronics F127 (Sigma) solution for 45 minutes before being washed in PBS, and transfered into petri-dishes with complete medium. Cells resuspended from trypsinization were subsequently pipetted above the substrate at approximately 10 cells per 10000 μm², and allowed to incubate. Substrates were inspected every 20 minutes for sufficient pattern coverage, before being washed in warm complete medium, and allowed to settle.

Imaging and analysis

Live-cell imaging occured at 3 hours subsequent to the final washing of the substrate, using a Nikon inverted microscope with a 20x objective, within an In-Vivo Scientific microscope incubator. For single-cell asymmetric relaxation studies, 25 μM blebbistatin (Sigma) was applied to the petri dish medium, and cells were subsequently imaged every two minutes in bright-field and green-excitation/red-fluorescent channels to examine cell and substrate relaxation over time.

Cytoskeleton imaging and contraction studies were performed on fixed-cell samples. At 5 hours subsequent to final washing of the substrate, cells were fixed in initially warm 3 % formaldehyde (Fisher) over 15 minutues. Cells were subsequently washed in PBS, and incubated in 0.2 % Triton-X 100 and phalloidin-alexa fluor 488 conjugate for 30 minutes. Samples were finally washed in PBS, and mounted in Slowfade with DAPI (Invitrogen), and sealed. Fluorescent microscopy occured in the same manner as in live-cell conditions. Confocal microscopy images were captured with a Leica SP2 confocal microscope with a 63x oil-immersion objective.

Grayscale images were analyzed using a custom MATLAB program to track fluorescent pattern edge points, align samples, average cells, and convert these back into grayscale images.

Elastic modulus characterization

Force-displacement curves were obtained from a Bruker Catalyst AFM aligned above a Leica inverted microscope. AFM probes with a 5 μm polystyrene bead attached and a spring constant of 0.7 N m⁻¹ (Novascan), generated indentation curves in force control mode. Elastic modulus was extracted by fitting the Hertz model to our acquired data.