Nonparametric modeling and analysis of association between Huntington’s disease onset and CAG repeats

Abstract

Huntington’s disease (HD) is a neurodegenerative disorder with a dominant genetic mode of inheritance caused by an expansion of CAG repeats on chromosome 4. Typically, a longer sequence of CAG repeat length is associated with increased risk of experiencing earlier onset of HD. Previous studies of the association between HD onset age and CAG length have favored a logistic model, where the CAG repeat length enters the mean and variance components of the logistic model in a complex exponential-linear form. To relax the parametric assumption of the exponential-linear association to the true HD onset distribution, we propose to leave both mean and variance functions of the CAG repeat length unspecified and perform semiparametric estimation in this context through a local kernel and backfitting procedure. Motivated by including family history of HD information available in the family members of participants in the Cooperative Huntington’s Observational Research Trial (COHORT), the methodology is developed in the context of mixture data, where some subjects have a positive probability of being risk free. We also allow censoring on the age-at-onset of disease and accommodate covariates other than the CAG length. We study the theoretical properties of the proposed estimator and derive its asymptotic distribution. Finally, the proposed methods are applied to the COHORT data to estimate the HD onset distribution using a group of study participants and the disease family history information available on their family members.

1 Motivating Study and the Existing Model

1.1 Huntington’s Disease Study

Huntington’s disease (HD) is a severe hereditary neurodegenerative disorder caused by an expansion of CAG repeats at a gene on chromosome 4 that codes the protein named hunt-ingtin (Huntington’s Study Investigators 1993 [1]). Typically neurological and physical symptoms express around 30–50 years of age in affected individuals, although sometimes the symptoms can develop much earlier (pre-teen) or much later in life (in the 80s; See for example, [2]). Patients eventually die from complications such as pneumonia, heart failure, or other complications, usually 15–20 years after the disease onset although the duration of the disease also varies depending on the onset age [3]. Clinical studies suggest that an individual with a CAG repeat length (denoted as X) smaller than 36 is risk free of HD (no risk of developing HD at any given age; [2, 4]). Otherwise, for an individual with CAG repeat length greater than or equal to 36, the CAG length is an important factor that is inversely correlated with the age-at-onset (AAO) of HD (denoted as T), where subjects with longer stretches of CAG repeat length tend to have earlier onset.

To further study the association between CAG length and the onset time of HD, various large epidemiological studies on HD were conducted worldwide. One particular study is the Cooperative Huntington’s Observational Research Trial (COHORT), an observational study organized by 42 Huntington Study Group research centers in North America and Australia. In COHORT, the initial participants (probands) undergo a clinical evaluation where blood samples are sequenced for CAG repeat length [5]. Since 2005, the study has expanded to collect family members’ morbidity and mortality information (e.g., AAO of HD) through systematic family history interviews administered to the probands [5, 6]. However, due to the high cost of conducting in-person interviews of family members, the blood samples of the family members were not collected. This kind of studies are referred as kin-cohort study in [7]. The COHORT study with family history data can be classified as a kin-cohort design. A complexity arising from COHORT is that whether a relative shares the same CAG expansion status with a proband (e.g., whether a child has inherited the mutation allele with CAG expansion from a parent) is not available. Instead, we can obtain a relative’s probability of carrying a mutation allele, which is calculated through Mendelian law using the relative’s relationship with the proband and the proband’s mutation status (e.g., Section 8.4 in [8]; and [9, 10]). This calculation yields a probability p (0 ≤ p ≤ 1), indicating the probability that the relative shares the same mutation allele as his or her proband so that the relative’s CAG repeat length is the same as the proband, and he or she is at risk of HD. For example, parents, children and siblings of an at risk proband have at risk probabilities of p = 0.5 under the Mendelian law. Thus the relative has a probability of 1 − p = 0.5 to share the normal allele with his or her proband, in which case the relative will have a CAG length value < 36 and will not be at risk of HD. We assume that the CAG repeat length does not change in the gamete transmission process, i.e., a child will inherit an expanded allele with the same repeat length from a parent. This assumption is used in literature [6], and implications of this assumption are discussed in Section 5.

Another complexity arising from the COHORT study is that HD onset time is not observed for all study subjects, and some study subjects are censored because of loss to follow-up or death due to other causes before developing HD.

1.2 Existing Model

The functional form of the association between the onset time T and CAG repeat length X has been debated in the clinical literature and multiple parametric models have been proposed [11, 12]. Currently, the accepted model captures the relation between the AAO of HD and the CAG length through a logistic link and assumes that the CAG length affects both the mean and the variance components of AAO through an exponential-linear form in [11]. Specifically, the model specifies the conditional distribution $F(t,x)\stackrel{\text{def}}{=}\text{pr}(T<t\mid X=x)$ as

$$F(t,x)=\frac{1}{1+e^{-\{t-\mu (x)\}/s(x)}},$$ (1)

where

$$\mu (x)={\mu }_1+exp({\mu }_2-{\mu }_{3}x),s(x)=\sqrt{{\sigma }_1+exp({\sigma }_2-{\sigma }_{3}x)},$$

and μ₁, μ₂, μ₃, σ₁, σ₂, σ₃ are six unspecified parameters to offer model flexibility and will be estimated from data.

Although (1) is the accepted model in the current clinical literature for describing the association between CAG length and HD onset, it does impose some rather strong assumptions. For example, the specific functional forms of both the mean and variance are pre-specified to be exponential-linear, which can be an advantage if they happen to reflect the true biological relationship between CAG length and onset time, but can also be misleading otherwise. In addition, this global parametric model may not fit well for certain ranges of the CAG lengths and ages (e.g., for smaller CAG length values; [11]). At the values of μ_i and σ_i (i = 1, 2, 3) fitted using data from [11], the corresponding additive and multiplicative coefficient functions for t has the form

$$F(t,x)=\frac{1}{1+e^{-{\alpha }_2(x)t-{\alpha }_1(x)}}$$ (2)

where, using the relation α₁(x) = − μ(x)/s(x), α₂(x) = 1/s(x), we get

$$\begin{array}{l}{\alpha }_1(x)=-\pi /\sqrt{3}\{21.54+exp(9.56-0.146x)\}{\{35.55+exp(17.72-0.327x)\}}^{-1/2},\\ {\alpha }_2(x)=\pi /\sqrt{3}{\{35.55+exp(17.72-0.327x)\}}^{-1/2}.\end{array}$$

Thus α₁(x) is not a monotonically increasing function of x (see Figure 1, upper-left plot). As a result, for some t values, such as t ≤ 22, F(t, x) is not an increasing function of x (see Figure 1, lower-left plot). This may not agree with the clinical conjecture that greater CAG expansion length increases the risk of HD at a given age, i.e., F(t, x) is an increasing function of x at a fixed time point t. While it is still unclear whether the clinical impression is fully supported by data, the assumption that an exponential-linear functional form in both the mean and variance captures the true CAG length effect on HD onset globally in the entire range of x and t can be strong. It may be desirable to relax this parametric model assumption, by using a more flexible nonparametric or semiparametric model that is capable of fitting local changes in certain ranges of x. In addition, no covariates other than CAG length are modeled in (1).

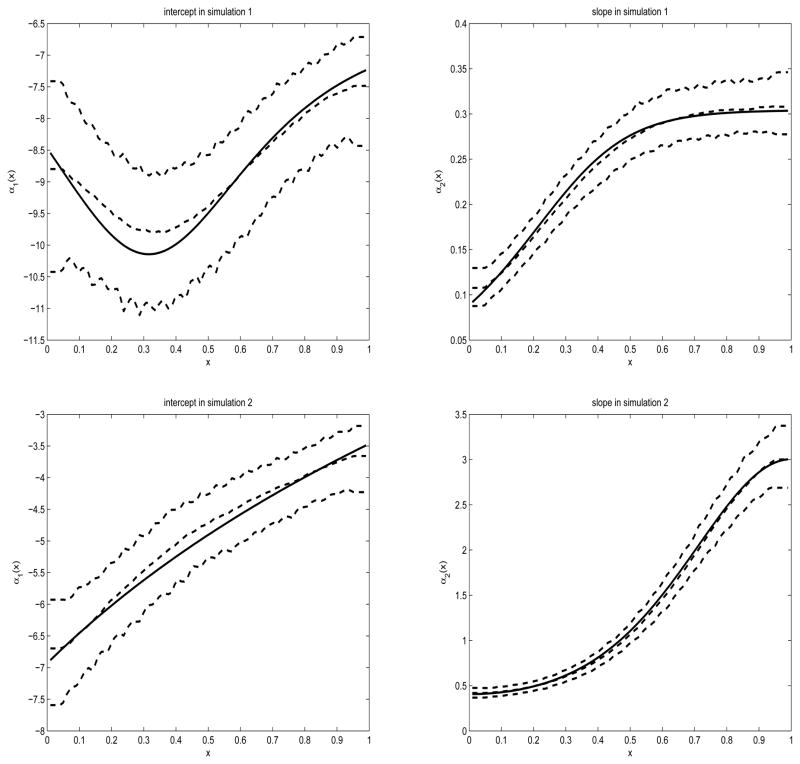
Figure 1.

Plots of the true (solid) and estimated (dashed) curves of the intercept α₁(x) (left) and slope α₂(x) (right) in simulation 1 (upper) and simulation 2 (lower). The dashed curves contain the median, 5% quantile and 95% quantile of the 1000 estimated curves.

2 Proposed Model and its Estimation Procedure

Due to restrictions of a parametric model, we propose to relax the specification of CAG length effect to nonparametric functions by leaving both α₁(x) and α₂(x) in (2) unspecified. Since F(t, x) is a cumulative conditional distribution function, it is required to be an increasing function of t at any value of x. To satisfy this assumption, the slope α₂(x) should be positive. This can be taken into account through a reparameterization such as writing $exp\{{\alpha }_2^{\ast }(x)\}$ instead of α₂(x) with the aim of estimating ${\alpha }_2^{\ast }(x)$. However, in our numerical experiments reported in Sections 3 and 4, such reparameterization does not seem necessary since α₂(x) is estimated to be positive without any constraints. Thus, throughout this article, we simply consider α₂(x) directly. In addition, if the clinical consensus that higher CAG length values are associated with earlier onset times is to be enforced, α₁(x)+ α₂(x)t should be an increasing function of x for any possible HD onset time t. However, we estimate α₁(x) and α₂(x) without forcing the monotonicity constraint. Thus, the resulting fitted functions under the more flexible model can serve as empirical evidence on whether or not the clinical consensus holds.

To express model (2) on the logit scale, note that

$$\text{logit}\{F(t,x)\}={\alpha }_1(x)+{\alpha }_2(x)t,$$

which is a logistic model with varying coefficients. Thus, although our problem is motivated by relaxing the parametric model in [11], it is very general and is applicable to modeling distribution of other disease onset as well. Under this varying-coefficient logistic model, other patient-specific covariates such as gender or baseline symptom severity measures can be easily introduced. Since these covariates are not of primary interest and misspecification of their functional form is less of a concern, we can simply use several linear terms to capture their effects. Collecting these additional covariates into a vector Z, we can extend model (2) to a partially linear varying-coefficient logistic model

$$F\{t,x,\mathit{z},\mathit{\beta },\mathit{\alpha }(x)\}=\frac{1}{1+e^{-\{{\mathit{z}}^{\mathrm{T}}{\mathit{\beta }}_2+{\alpha }_2(x)\}t-\{{\mathit{z}}^{\mathrm{T}}{\mathit{\beta }}_1+{\alpha }_1(x)\}}},$$ (3)

where $\mathit{\beta }={\left({\mathit{\beta }}_1^{\mathrm{T}},{\mathit{\beta }}_2^{\mathrm{T}}\right)}^{\mathrm{T}}$ and α(x) = {α₁(x), α₂(x)}^T are unknown parameters and functions to be estimated from data.

2.1 Likelihood and Estimation

To introduce the likelihood, we start by defining some notation. We use C to denote the censoring time and use f_C(c, x, z) and F_C(c, x, z) to denote the censoring probability density function (pdf) and cumulative distribution function (cdf) conditional on the covariates (X, Z). We assume the censoring to be conditionally independent of HD onset time given a set of covariates. Let Δ = I(T ≤ C) and Y = min(T, C). We denote the ith observation as (p_i, X_i, Z_i, Y_i, Δ_i). Here p_i is the probability of the ith subject having an expanded CAG calculated from the relation between the proband-relative relation, and is known. We use p_i = 1 or p_i = 0 if the ith subject’s CAG expansion status is certain. Taking into consideration the uncertainty in a relative’s CAG expansion status and censoring, the likelihood is

$$\begin{array}{l}L\{\mathit{\beta },\mathit{\alpha }(·)\}=\prod _{i=1}^n{[p_{i}f\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i)\}]}^{{\mathrm{\Delta }}_i}{[1-p_{i}F\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i)\}]}^{1-{\mathrm{\Delta }}_i}{\{1-F_C(Y_i,X_i,{\mathit{Z}}_i)\}}^{{\mathrm{\Delta }}_i}{f}_C{(Y_i,X_i,{\mathit{Z}}_i)}^{1-{\mathrm{\Delta }}_i}{f}_{X,\mathit{Z},p}(X_i,{\mathit{Z}}_i,p_i)\\ \propto \prod _{i=1}^{n}f{\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i)\}}^{{\mathrm{\Delta }}_i}{[1-p_{i}F\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i)\}]}^{1-{\mathrm{\Delta }}_i},\end{array}$$

where F{y, x, z, β, α(x)} is given in (3) and

$$\begin{array}{l}f\{t,x,\mathit{z},\mathit{\beta },\mathit{\alpha }(x)\}=\frac{\partial F\{t,x,\mathit{z},\mathit{\beta },\mathit{\alpha }(x)\}}{\partial t}\\ =\frac{e^{-\{{\mathit{z}}^{\mathrm{T}}{\mathit{\beta }}_2+{\alpha }_2(x)\}t-\{{\mathit{z}}^{\mathrm{T}}{\mathit{\beta }}_1+{\alpha }_1(x)\}}\{{\mathit{z}}^{\mathrm{T}}{\mathit{\beta }}_2+{\alpha }_2(x)\}}{{[1+e^{-\{{\mathit{z}}^{\mathrm{T}}{\mathit{\beta }}_2+{\alpha }_2(x)\}t-\{{\mathit{z}}^{\mathrm{T}}{\mathit{\beta }}_1+{\alpha }_1(x)\}}]}^2}.\end{array}$$

Due to the inclusion of unspecified nonparametric functions α(x), directly maximizing the above likelihood is difficult. Thus, instead of using the maximum likelihood estimator (MLE) or nonparametric MLE, we propose the following backfitting procedure based on local kernel smoothing estimator of α(x). Let the score function with respect to β be

$${\mathit{S}}_{\beta }\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i)\}={\mathrm{\Delta }}_i\frac{\partial f\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i)\}/\partial \mathit{\beta }}{f\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i)\}}-(1-{\mathrm{\Delta }}_i)\frac{p_i\partial F\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i)\}/\partial \mathit{\beta }}{1-p_{i}F\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i)\}}.$$

Replace α(X) with a = (a₁, a₂)^T locally at X = x₀, and let the score function with respect to a be

$${\mathit{S}}_a(Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{a})={\mathrm{\Delta }}_i\frac{\partial f(Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{a})/\partial \mathit{a}}{f(Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{a})}-(1-{\mathrm{\Delta }}_i)\frac{p_i\partial F(Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{a})/\partial \mathit{a}}{\{1-p_{i}F(Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{a})\}}.$$

The backfitting procedure consists of iterating between the following two steps.

1. Obtain β̃ at a fixed α̃(·) through solving

   $$\mathbf{0}=\sum _{i=1}^n{\mathit{S}}_{\beta }\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\stackrel{\sim }{\mathit{\alpha }}(X_i)\}.$$
2. Obtain α̃(x₀) at x₀ = x₁, …, x_n at a fixed β̃ through solving

   $$\mathbf{0}=\sum _{i=1}^n{K}_h(X_i-x_0){\mathit{S}}_a(Y_i,X_i,{\mathit{Z}}_i,\stackrel{\sim }{\mathit{\beta }},\mathit{a}).$$

   Here K(·) is a symmetric kernel function, h is a bandwidth and K_h(x) = K(x/h)/h for any bandwidth h.

The above two steps can use the MLEs as starting values by treating α(x) as constants, and is iteratively performed until convergence is reached. This type of backfitting method adopts the local constant idea for the nonparametric estimation of α₁(·) and α₂(·). When desirable, more sophisticated methods such as local polynomial can also be used. Note that in the second step, the maximization is repeatedly performed for n different x₀ values, thus the computation can be quite involved.

2.2 Asymptotic Properties

To study the asymptotic properties of the backfitting estimator, we first define some notation. Let S_ββ be the partial derivative of S_β with respect to β, S_βα be the partial derivative of S_β with respect to α, S_αα be the partial derivative of S_α with respect to α and S_αβ be the partial derivative of S_α with respect to β. Also define Ω(X) = E[S_αα{Y, X, Z, β, α(X)}|X], α_β (X) = −Ω(X)⁻¹E[S_αβ{Y, X, Z, β, α (X)}|X] and U(X) = E[S_βα{Y, X, Z, β, α(X)}|X]Ω(X)⁻¹. Furthermore, define

$$\mathcal{F}=E[{\mathit{S}}_{\beta \beta }\{Y,X,\mathit{Z},\mathit{\beta },\mathit{\alpha }(X)\}+{\mathit{S}}_{\beta \alpha }\{Y,X,\mathit{Z},\mathit{\beta },\mathit{\alpha }(X)\}{\mathit{\alpha }}_{\beta }(X)].$$

Then we have the following results.

Theorem 1

Assume that the bandwidth h satisfies nh⁴ → 0 and nh² → ∞. Then the backfitting estimator β̂ has the asymptotic expansion

$$-\mathcal{F}{n}^{1/2}(\widehat{\mathit{\beta }}-\mathit{\beta })=n^{-1/2}\sum _{i=1}^n[{\mathit{S}}_{\beta }\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i)\}-\mathit{U}(X_i){\mathit{S}}_{\alpha }\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i)\}]+o_p(1).$$ (4)

Hence, n^1/2(β̂ − β) is asymptotically normally distributed with mean zero and covariance matrix 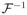Σ 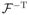, where Σ = cov [S_β{Y, X, Z, β, α (X)} − U(X)S_α{Y, X, Z, β, α(X)}].

Remark 1

In Theorem 1, the requirement that nh⁴ → 0 is the undersmoothing condition typically required for backfitting, and a direct consequence of the bias of the local constant estimator. The undersmoothing requirement does not lead to difficulty in practice because we can easily rescale a selected optimal bandwidth h_opt to obtain the undersmoothed bandwidth $h=h_{\text{opt}}^{3/5}$. In addition, the estimation of β is often insensitive to the bandwidth choice. There are various methods proposed in the literature to avoid undersmoothing as well, including using a projection augmentation on S_β or profiling, see Van Keilegom and Carroll (2007) [13] for details.

Remark 2

There are various possibilities to perform inference about β in our context. Note [14] describes conditions under which the bootstrap will be asymptotically valid for backfitting estimators. Alternatively, one can use the asymptotic results given in Theorem 1. This entails approximating the terms in 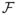and Σ by their sample versions. Specifically, $\widehat{\mathcal{F}}=n^{-1}{\sum }_{i=1}^n[{\mathit{S}}_{\beta \beta }\{Y_i,X_i,{\mathit{Z}}_i,\widehat{\mathit{\beta }},\widehat{\mathit{\alpha }}(X_i)\}+{\mathit{S}}_{\beta \alpha }\{Y_i,X_i,{\mathit{Z}}_i,\widehat{\mathit{\beta }},\widehat{\mathit{\alpha }}(X_i)\}{\widehat{\mathit{\alpha }}}_{\beta }(X_i)]$ and $\widehat{\mathbf{\sum }}=n^{-1}{\sum }_{i=1}^n{[{\mathit{S}}_{\beta }\{Y_i,X_i,{\mathit{Z}}_i,\widehat{\mathit{\beta }},\widehat{\mathit{\alpha }}(X)\}-\widehat{\mathit{U}}(X){\mathit{S}}_{\alpha }\{Y_i,X_i,{\mathit{Z}}_i,\widehat{\mathit{\beta }},\widehat{\mathit{\alpha }}(X)\}]}^{\otimes 2}$. Here and throughout the text, a^⊗2 stands for aa^T for any vector or matrix a. In these calculations, α̂_β(X) = −Ω̂(X)⁻¹Ê[S_αβ{Y, X, Z, β, α̂(X)}|X], Û(X) = Ê[S_βα{Y, X, Z, β̂, α̂(X)}|X]Ω̂(X)⁻¹ and Ω(X) = Ê[S_αα{Y, X, Z, β̂, α̂ (X)}|X], where all the conditional expectations are estimated nonparametrically.

Since our main interest is in estimating α (·), after obtaining the root-n consistent estimator β̂, we need to perform an additional nonparametric estimation step using the usual bandwidth to obtain the final estimates for α̂(X). Because Theorem 1 guarantees the root-n rate for β̂, which is faster than the nonparametric rate, hence the final α̂(X) has the same classic bias and variance properties of the standard nonparametric estimator under a known β. We state the asymptotic property of α̂(·) in Theorem 2.

Theorem 2

Assume that the bandwidth used in the last local linear estimation step is h, and h = O(n^−1/5). Then α̂(x, β̂) satisfy

$$\begin{array}{l}\widehat{\mathit{\alpha }}(x,\widehat{\mathit{\beta }})-\mathit{\alpha }(x)\\ =-h^{2}E{\{{\mathit{S}}_{aa}(Y,X,\mathit{Z},\mathit{\beta },\mathit{a})\mid x\}}^{-1}\frac{d^2[E\{{\mathit{S}}_a(Y,X,\mathit{Z},\mathit{\beta },\mathit{a})\mid x\}{f}_X(x)]}{2f_X(x){dx}^2}\int t^{2}K(t)dt\\ -E{\{{\mathit{S}}_{aa}(Y,X,\mathit{Z},\mathit{\beta },\mathit{a})\mid x\}}^{-1}\frac{1}{{nf}_X(x)}\sum _{i=1}^n{K}_h(X_i-x){\mathit{S}}_a\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i)\}\\ +o(h^2)+o_p\{{(nh)}^{-1/2}\}.\end{array}$$

Thus, it has bias

$$\mathit{bias}\{\widehat{\mathit{\alpha }}(x)\}=-h^2\mathbf{\Omega }{(x)}^{-1}\frac{d^2\{E[{\mathit{S}}_{\alpha }\{Y,X,\mathit{Z},\mathit{\beta },\mathit{\alpha }(X)\}\mid X=x]f_X(x)\}}{2f_X(x){dx}^2}\int t^{2}K(t)dt+o(h^2)$$

and variance

$$\mathit{var}\{\widehat{\mathit{\alpha }}(x)\}=-\frac{\int K^2(t)dt}{{\mathit{nhf}}_X(x)}\mathbf{\Omega }(x)+o\{{(nh)}^{-1}\}.$$

Remark 3

Once the estimation of β̂ and α̂ is obtained, we can plug these estimates in (3) to obtain the estimation of the distribution of the onset time, F{t, x, z, β̂, α̂(x)}. Using the delta method and considering that α̂(x) converges at a slower nonparametric rate than β̂, we can easily obtain that F{t, x, z, β̂, α̂(x)} estimates the true distribution function F{t, x, z, β, α(x)} with leading order bias

$$\frac{\partial F\{t,x,\mathit{z},\mathit{\beta },\mathit{\alpha }(x)\}}{\partial \mathit{\alpha }{(x)}^{\mathrm{T}}}\mathit{bias}\{\widehat{\mathit{\alpha }}(x)\}$$

and leading order variance

$$\frac{\partial F\{t,x,\mathit{z},\mathit{\beta },\mathit{\alpha }(x)\}}{\partial \mathit{\alpha }{(x)}^{\mathrm{T}}}\mathit{var}\{\widehat{\mathit{\alpha }}(x)\}\frac{\partial F\{t,x,\mathit{z},\mathit{\beta },\mathit{\alpha }(x)\}}{\partial \mathit{\alpha }(x)},$$

where bias{α̂(x)} and var{α̂(x)} are given in Theorem 2. Thus, the distribution function is also estimated at the classical nonparametric rate as if β were known.

3 Simulation Study

We conducted simulation studies to investigate the finite sample performance of the proposed estimators. Two simulations were conducted with sample size n = 4000 and repeated 1000 times. Here n = 4000 is the approximate sample size in the COHORT study. We generated the standardized CAG length values X from a uniform distribution between 0 and 1. In many clinical studies of HD, additional information such as gender, inheritance of CAG expansion through mother or father, verbal fluency score, and presence of psychiatric symptoms, type of relatives (e.g., parents, siblings, and children) are also recorded [15]. Thus, in the simulations we generated four additional covariates to form Z, where two are continuous and two are discrete. Specifically, Z₁ is generated from a uniform distribution between [−0.5, 0.5], Z₂ is generated from a uniform distribution between [−1, 1], Z₃ is generated from a Bernoulli distribution with probability 0.5 to be one, and Z₄ is generated from a Bernoulli distribution with probability 0.4 to be one. Our at risk probability p is generated from a Bernoulli type distribution, where p = 1 with probability 0.3, and p = 0.5 with probability 0.7. This is approximately the distribution of the at-risk indicators in the COHORT data. We generated the HD onset time following two different models. The first model is the model in [11] presented in (2), while the second one has the true α functions being

$${\alpha }_1(x)=5\text{log}\{(1+x)\},{\alpha }_2(x)exp\{sin(\pi x-\pi /2)+0.1\}.$$

Note that the second model thus has monotonically increasing α(x) functions. We further generated the censoring times from uniform distributions for both models, so that the censoring rate is approximately 65%, again reflecting the scenario of the COHORT study data structure.

The simulation results for β and α are provided in Table 1 and Figure 1, respectively, where the bandwidth is chosen via cross-validation, i.e., maximizing

Table 1.

Simulation results on β. Mean, median, standard deviation (std), mean absolute deviations (Mad1) and median absolute deviation (Mad2) are reported.

	β11	β12	β13	β14	β21	β22	β23	β24
	Simulation 1
truth	−0.5	0.5	−1	1	0.02	−0.02	0.04	−0.04
Mean	−0.4842	0.4999	−0.9161	1.0636	0.0197	−0.0199	0.0372	−0.0420
Median	−0.4693	0.4999	−0.9212	1.0634	0.0193	−0.0199	0.0371	−0.0420
Std	0.3787	0.1921	0.2279	0.2304	0.0098	0.0050	0.0058	0.0060
Mad1	0.3794	0.1939	0.2273	0.2308	0.0098	0.0051	0.0058	0.0060
Mad2	0.3823	0.1980	0.2296	0.2306	0.0104	0.0054	0.0059	0.0061
	Simulation 2
truth	−0.5	0.5	−1	1	0.1	−0.1	0.2	−0.2
Mean	−0.4977	0.5024	−0.9928	1.0195	0.1008	−0.1009	0.1964	−0.2069
Median	−0.4972	0.5034	−0.9915	1.0181	0.1013	−0.1007	0.1964	−0.2071
Std	0.2221	0.1136	0.1363	0.1384	0.0278	0.0147	0.0180	0.0188
Mad1	0.2205	0.1139	0.1365	0.1371	0.0276	0.0147	0.0179	0.0187
Mad2	0.2123	0.1114	0.1386	0.1383	0.0277	0.0143	0.0179	0.0183

$$\sum _{i=1}^n\left({\mathrm{\Delta }}_i\text{log}[f\{Y_i,X_i,{\mathit{Z}}_i,\widehat{\mathit{\beta }},{\widehat{\mathit{\alpha }}}_{-i}(X_i,h)\}]+(1-{\mathrm{\Delta }}_i)\text{log}[1-p_{i}F\{Y_i,X_i,{\mathit{Z}}_i,\widehat{\mathit{\beta }},{\widehat{\mathit{\alpha }}}_{-i}(X_i,h)\}]\right)$$

as a function of h. Here α̂_−i(X_i, h) means we estimate α(x) at x = X_i using bandwidth h and all the data except the ith observation. From the results, we can see that in both models, the nonparametric modeling allows us to retrieve the shape of the α functions reasonably well, and the estimation of β has small bias. It is interesting to note that the estimation procedure in the second simulation model seems to perform better than in the first model, in the sense that the biases are much smaller across all parameters in β in model 2. In addition, the estimation variance is smaller in absolute value in model 2 for all β components that appear in the intercept term, and are also smaller in relative value for all β components that appear in the slope term. Furthermore, the biases and confidence bands for α are also narrower in simulation model 2. The similarity between the mean and median of the estimates for β, as well as between the standard deviation, mean absolute deviation and median absolute deviation indicates that the computation in both models are quite stable.

4 Application to COHORT Data

We now analyze the COHORT data which motivated this work. As introduced in Section 1, COHORT is an observational study collecting genetic (e.g., CAG repeat length) and clinical data on symptomatic and pre-manifest HD patients (probands), and clinical data on their family members and care givers. In the COHORT study, ascertainment of probands does not depend on family history [5]. The probands include subjects clinically diagnosed with HD or subjects who pursued genetic testing prior to baseline, carry an CAG expanded allele, but did not have clinically diagnosed HD. It is known that HD is a dominant genetic disease, (e.g., having one expanded allele is sufficient to cause HD) [16]. Subjects with a CAG repeat length ≥ 36 are considered to be HD mutation positive and have highly elevated risk of developing the disease, while subjects with CAG repeat length < 36 do not develop HD [2, 17, 18]. In this analysis, each proband participant has his or her CAG repeat value between 41 and 56 (hence at risk of HD with the at risk probability p = 1).

For family members of the proband, as discussed in Section 1, no blood sample was collected. Thus for those who have not experienced HD, it is unknown whether they share the same mutation allele with the proband. Family members’ HD onset information was collected through a family history interview administered to the probands. All the first-degree relatives with available family history information are included in the analysis. These relatives are not selected based on their HD status or possible mutation carrier status, so there is little obvious ascertainment issue for including relative data. There are 34% parents, 38% siblings and 28% children. The distribution of the at risk probabilities in the whole sample is 1196 individuals having p = 1 and 2768 having p = 0.5. This yields 3964 observations. Here, we assume that inclusion of a family member in the study is independent of the family member’s risk status. Note that among the 1196 individuals, some are relatives who developed HD, hence we can obtain their CAG status under the assumption of no interference and thus they share the same repeat length as their probands. The onset times in the COHORT data range from 11 to 82, with a censoring rate about 19% in probands and 62% overall. Some of the relatives are censored if they have not experienced HD at the time of family history interview. The censoring rate in family members depends on the relative type. Since children are younger, they are more likely to have not experienced HD especially children of probands with shorter CAG repeats. We account for the covariate gender by including it in Z.

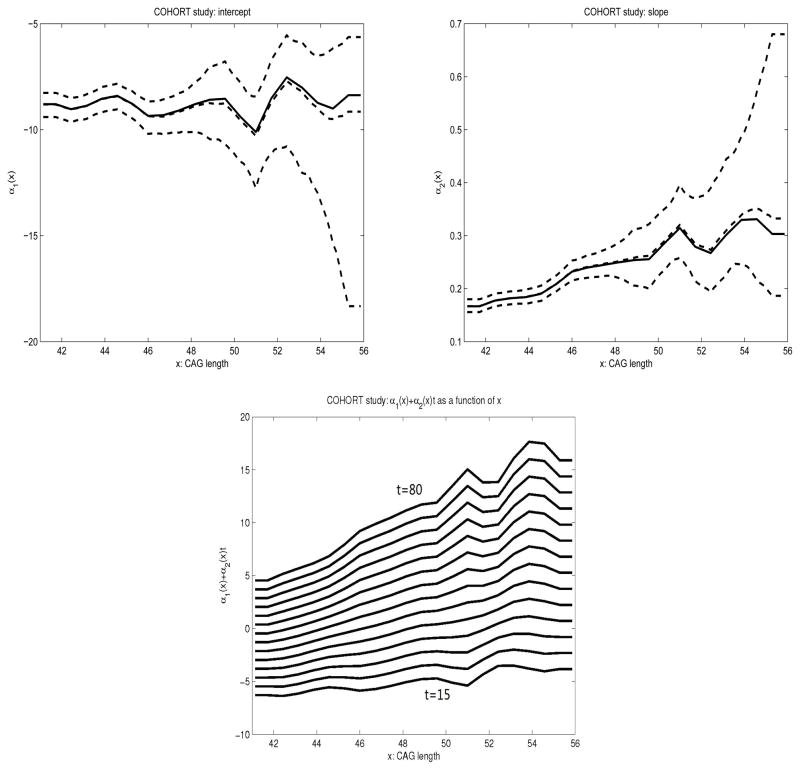
We analyzed the COHORT data using model (3) and the method described in Section 2.2, with the bandwidth 1.33, selected through a cross-validation procedure. The estimated α(x) and their confidence intervals are provided in Figure 2. We can see that the estimation of α(x) is much more reliable for CAG length value x < 48 than for CAG length value x ≥ 48. This is because the majority of the COHORT observations contain relatively small (< 48) CAG length values. Although the slope function (i.e., α₂(x)) exhibits an increasing trend, it is not sufficient to confirm that it is indeed monotone especially in the large CAG length region, where the estimation variability is very high. At the onset time ranging from t = 15 to t = 80, the intercept and slope functions translate to a set of functions α₁(x) + α₂(x)t, which appear to show an increasing relation with x for x between 41 and 50, while they then slightly deviate from this trend for a CAG length value beyond 50. This suggests that in general the cumulative risk of HD onset by age t increases with longer sequence of CAG repeat length across different values of t.

Figure 2.

Plots of the estimated (solid) curves of the intercept α₁(x) (upper-left) and slope α₂(x) (upper-right) and α₁(x) + α₂(x)t for t = 15, 20, 25, …, 80 (lower) in COHORT data. The dashed curves contain the median, 5% quantile and 95% quantile of the 1000 bootstrap estimation results.

Comparing the estimated intercept and slope functions with the plots in Figure 1 with parameters fitted in [11] suggests that the intercept and slope components can be different from what are estimated from the nonparametric method here. To better compare the parametric model of [11] and our nonparametric model, while eliminating the effect of using different data, we re-fit the exponential linear model (1) with the COHORT data stratified by gender. The fitted parametric functions are

$$\mu (x)=16.92+exp(7.90-0.103x),s(x)=\sqrt{44.49+exp(13.64-0.225x)}$$

for females, and

$$\mu (x)=19.08+exp(8.73-0.125x),s(x)=\sqrt{12.40+exp(13.63-0.213x)}$$

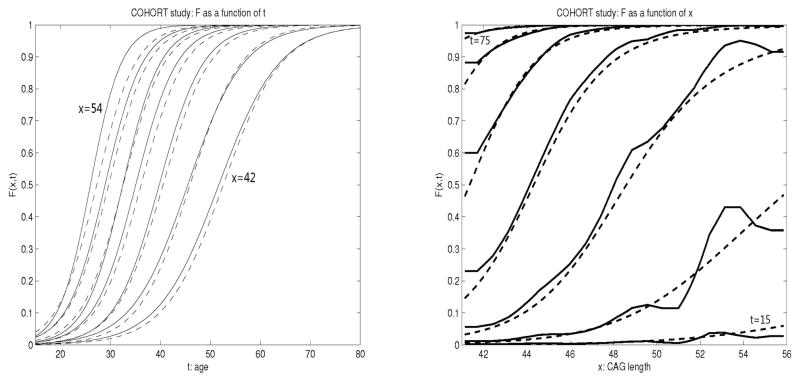
for males. In the left panel of Figure 3, we plot the estimated cdf, F̂(t, x), as a function of t at different values of CAG repeats x using both the parametric and nonparametric methods in females. The figures for males show similar trend and are therefore omitted. Comparing results obtained under a nonparametric model with that of a parametric model, we see that at a given CAG repeat length, the shapes of the estimated cdfs are similar, which is expected since at each value of x, model (1) belongs to the class of nonparametric/semiparametric models used here. However, we do not assume a parametric relationship of F(t, x) across different values of x, and therefore our model is less restrictive. The fitted values of the cdfs differ, especially for higher CAG length values (left curves). The largest difference appear to be when the CAG repeat length is 54, where the cumulative risk is estimated to be slightly higher with the nonparametric method than the parametric method.

Figure 3.

Plots of the F̂(t, x) from COHORT data analysis as a function of t at x = 42, 44, 46, ···, 54 (left), and as a function of x at t= 15, 25, 35, …, 75 (right) in females. Plots of males are similar and therefore omitted. The solid curves are estimated from the nonparametric model and the dashed curves are estimated from the parametric model.

The right panel of Figure 3 shows F̂(t, x) as a function of CAG repeats x at different values of age t. It is clearly seen from the figure that the CAG length has a larger influence on cumulative risk for the middle age range (e.g., between 25 and 65). By age 75, almost all subjects with a CAG length greater than 40 will develop disease regardless of their actual CAG repeats (cumulative risk approximates 100%). By age 65, subjects with a CAG length greater than 45 will develop disease. At the ages plotted in Figure 3, the parametric model imposes a constraint of F(t, x) being an increasing function of x. Although there is such an increasing trend in general, it is not necessarily supported by the data at certain local ranges, especially for younger ages such 15, 25 and 35 (lower three curves) as shown from fitting a more flexible semiparametric model; for certain ranges of CAG repeat values, the cumulative disease risk F(t, x) may be a constant and does not necessarily increase with x. Therefore the impression that a longer sequence of CAG repeats increases risk of disease at any given age does not necessarily hold and needs to be investigated further in future studies especially in the population with more extreme lengths of CAG repeats.

In the right panel of Figure 3, there seems to be a plateau effect for large t. This is due to the nature of cumulative risk function F(t, x) for HD subjects with expanded CAG repeats. It is suggested that most subjects at risk of HD will develop the disease by a certain age regardless of the CAG repeats length. Therefore, when t is large, say t = 75, F(t, x) approaches one quickly for any fixed x, and creates a visual plateau effect.

Regarding the gender effect, our analysis shows an estimate of β̂₁ = 0.3387, β̂₂ = −0.0055, with the standard errors 0.3517 and 0.0078 respectively. This indicates that gender is not a significant risk factor for HD onset, which agrees with the current clinical literature.

5 Discussion

We have developed a flexible partially linear varying-coefficient model under the logit link function to model the onset of Huntington’s disease. Existing parametric models are parsimonious and efficient if the functional form is correctly specified. However, in practice there is usually not sufficient biological information to suggest a particular parametric model to be correct. For example, the logistic-exponential model with six parameters [6] may be somewhat arbitrary. In contrast, the nonparametric approach proposed here is more flexible and not subject to model misspecification. It is also useful for revealing the underlying functional relation and constructing goodness-of-fit test for parametric models. The proposed methods here are sufficiently general to be applied to other known link functions through a similar backfitting maximization procedure. The methods account for random censoring and take advantage of the family history of disease information reported by the study participants without requiring the mutation status of the family members to be known.

Here, we assumed Mendelian transmission of CAG repeat length without interference so that the CAG length does not change from parents to offspring. In reality, CAG lengths can vary somewhat among family members, and those with paternal inheritance have, on average, a slightly longer stretch of CAG repeats than their fathers. A possible explanation may be that there are many more biological opportunities for the CAG repeat length to change in a paternal process of sperm formation than in a maternal process of egg formation [6]. Although these processes have been studied extensively [19], there is no validated population genetics models for such processes. Assuming the CAG length does not change from father to offspring may lead to a slightly lower estimated risk for affected fathers of probands. The transmission from mother to offspring is thought to be more stable [19].

Our methodology relies on the assumption of no ascertainment bias in recruiting probands. All the estimation and inference are developed under this assumption. The issue of ascertainment bias is best treated in the sampling design stage (e.g., selecting a random sample of probands from the population), and adjusting for potential ascertainment bias in the estimation stage needs to be treated separately. The COHORT study did not recruit probands through a positive family history, which avoided one of the major sources of ascertainment bias.

There are several reasons the estimated cdfs obtained here are different from [11] other than that we do not assume an exponential-linear form of logit {F(t, x)}. The age-at-onset (AAO) for probands in COHORT is age-at-diagnosis of HD, while in [11] it was earliest age at which a clinician observed an irreversible objective sign of the illness. This may occur earlier than the point at which an actual diagnosis of manifest HD is given. Thus, the two versions of AAO may be slightly different. Furthermore, here we included family history information in the relatives in the analysis, whereas [11] focuses only on proband participants. Also the AAO for the family members in COHORT study is the AAO of the first symptom of HD, potentially reported by a subject, not necessarily by the clinician. Although including family members’ age at onset data increases the sample size, a practical limitation is that relative data may be less reliable than the data directly collected from the probands. Thus, if additional information can be obtained to ascertain the potential uncertainty involved in a relative’s age at onset information, then further analysis incorporating such randomness can be pursued.

Lastly, we present some final remarks about the COHORT data analysis. One reason that prevents us from concluding that a larger CAG length value is associated with an increased risk of earlier HD onset across all ages is the absence of other covariates. There can be other risk factors that affect the age-specific risk of HD onset. Since data on these factors are unavailable (especially in family members), we cannot incorporate them into the model and this could distort the estimation of α(x), especially if these factors are correlated with CAG repeat length as well. Since in practice, it is often difficult to obtain these covariates especially for relatives, modeling and studying the potential association of these covariates and the CAG length values is of importance. Such knowledge will allow us to treat the relatives’ risk factors as missing covariates, and develop appropriate methods to make use of the covariate information on the proband and handle such problems in the missing covariate framework.

Although the work is motivated from COHORT study, the nonparametric/semiparametric methodology developed based on the likelihood here can be used in other studies with a similar kin-cohort design, for example, the studies reviewed in [20] on estimating risk of LRRK2 mutation on Parkinson’s disease.

Appendix

Proof of Theorem 1

We provide only a sketch of the proof. Precise conditions that justify our calculations and the general backfitting algorithm have been given by Claeskens and Van Keilegom (2003) [21] and Chen et al. (2003) [14].

We assume that X has compact support and that its density function is positive on the support. We also assume that α̂(x,β) has the usual properties uniformly in x in neighborhoods of {β, α(·)}, and in particular that α̂(x, β) = α(x) + o_p(n^−1/4) uniformly in x, this follows because nh⁴ → 0.

Usual expansion around β yields

$$\begin{array}{l}\mathbf{0}=n^{-1/2}\sum _{i=1}^n{\mathit{S}}_{\beta }\{Y_i,X_i,{\mathit{Z}}_i,\widehat{\mathit{\beta }},\widehat{\mathit{\alpha }}(X_i,\widehat{\mathit{\beta }})\}\\ =n^{-1}\sum _{i=1}^n\left[{\mathit{S}}_{\beta \beta }\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\widehat{\mathit{\alpha }}(X_i,\mathit{\beta })\}+{\mathit{S}}_{\beta \alpha }\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\widehat{\mathit{\alpha }}(X_i,\mathit{\beta })\}\frac{\partial \widehat{\mathit{\alpha }}(X_i,\mathit{\beta })}{\partial {\mathit{\beta }}^{\mathrm{T}}}\right]\sqrt{n}(\widehat{\mathit{\beta }}-\mathit{\beta })+n^{-1/2}\sum _{i=1}^n{\mathit{S}}_{\beta }\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\widehat{\mathit{\alpha }}(X_i,\mathit{\beta })\}+o_p(1)\\ =n^{-1}\sum _{i=1}^n\left[{\mathit{S}}_{\beta \beta }\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i,\mathit{\beta })\}+{\mathit{S}}_{\beta \alpha }\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i,\mathit{\beta })\}\frac{\partial \mathit{\alpha }(X_i,\mathit{\beta })}{\partial {\mathit{\beta }}^{\mathrm{T}}}\right]\sqrt{n}(\widehat{\mathit{\beta }}-\mathit{\beta })+n^{-1/2}\sum _{i=1}^n{\mathit{S}}_{\beta }\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\widehat{\mathit{\alpha }}(X_i,\mathit{\beta })\}+o_p(1).\end{array}$$ (A.1)

Note that for all β^*, E[S_α{Y, X, Z, β^*, α(X, β^*)} | X] = 0, hence taking derivative with respect to β^*, we have

$$\mathbf{0}=E[{\mathit{S}}_{\alpha \beta }\{Y,X,\mathit{Z},{\mathit{\beta }}^{\ast },\mathit{\alpha }(X,{\mathit{\beta }}^{\ast })\}\mid X]+E[{\mathit{S}}_{\alpha \alpha }\{Y,X,\mathit{Z},{\mathit{\beta }}^{\ast },\mathit{\alpha }(X,{\mathit{\beta }}^{\ast })\}\mid X]\frac{\partial \mathit{\alpha }(X,{\mathit{\beta }}^{\ast })}{\partial {\mathit{\beta }}^{\ast \mathrm{T}}}.$$

Letting β^* = β, we have

$$\frac{\partial \mathit{\alpha }(X,\mathit{\beta })}{\partial {\mathit{\beta }}^{\mathrm{T}}}=-E{[{\mathit{S}}_{\alpha \alpha }\{Y,X,\mathit{Z},\mathit{\beta },\mathit{\alpha }(X,\mathit{\beta })\}\mid X]}^{-1}E[{\mathit{S}}_{\alpha \beta }\{Y,X,\mathit{Z},\mathit{\beta },\mathit{\alpha }(X,\mathit{\beta })\}\mid X]={\mathit{\alpha }}_{\beta }(X).$$

Inserting this relation in (A.1), we have

$$\begin{array}{l}\mathbf{0}=n^{-1}\sum _{i=1}^n[{\mathit{S}}_{\beta \beta }\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i,\mathit{\beta })\}+{\mathit{S}}_{\beta \alpha }\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i,\mathit{\beta })\}{\mathit{\alpha }}_{\beta }(X_i)]\sqrt{n}(\widehat{\mathit{\beta }}-\mathit{\beta })+n^{-1/2}\sum _{i=1}^n{\mathit{S}}_{\beta }\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\widehat{\mathit{\alpha }}(X_i,\mathit{\beta })\}+o_p(1)\\ =\mathcal{F}{n}^{1/2}(\widehat{\mathit{\beta }}-\mathit{\beta })+n^{-1/2}\sum _{i=1}^n{\mathit{S}}_{\beta }\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i,\mathit{\beta })\}+n^{-1/2}\sum _{i=1}^n{\mathit{S}}_{\beta \alpha }\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i,\mathit{\beta })\}\{\widehat{\mathit{\alpha }}(X_i,\mathit{\beta })-\mathit{\alpha }(X_i,\mathit{\beta })\}+o_p(1),\end{array}$$

thus we obtain the expansion

$$-\mathcal{F}{n}^{1/2}(\widehat{\mathit{\beta }}-\mathit{\beta })=n^{-1/2}\sum _{i=1}^n[{\mathit{S}}_{\beta }\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i,\mathit{\beta })\}+{\mathit{S}}_{\beta \alpha }\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i,\mathit{\beta })\}\{\widehat{\mathit{\alpha }}(X_i,\mathit{\beta })-\mathit{\alpha }(X_i)\}]+o_p(1).$$ (A.2)

Performing standard expansion with local constant estimation, taking into account that nh⁴ → 0 and nh² → ∞, we have

$$\begin{array}{l}\mathbf{0}=n^{-1}\sum _{i=1}^n{K}_h(X_i-x_0){\mathit{S}}_a(Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\widehat{\mathit{\alpha }})\\ =n^{-1}\sum _{i=1}^n{K}_h(X_i-x_0){\mathit{S}}_a(Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{a})\\ +n^{-1}\sum _{i=1}^n{K}_h(X_i-x_0){\mathit{S}}_{aa}(Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{a})(\widehat{\mathit{a}}-\mathit{a})+o_p(n^{-1/2})\\ =n^{-1}\sum _{i=1}^n{K}_h(X_i-x_0){\mathit{S}}_a\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i)\}\\ +n^{-1}\sum _{i=1}^n{K}_h(X_i-x_0)[{\mathit{S}}_a(Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{a})-{\mathit{S}}_a\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i)\}]\\ +E\{{\mathit{S}}_{aa}(Y,X,\mathit{Z},\mathit{\beta },\mathit{a})\mid X=x_0\}{f}_X(x_0)(\widehat{\mathit{a}}-\mathit{a})+o_p(n^{-1/2}).\end{array}$$ (A.3)

Note that

$$E[K_h(X-x_0){\mathit{S}}_a\{Y,X,\mathit{Z},\mathit{\beta },\mathit{\alpha }(X)\}]=E(K_h(X-x_0)E[{\mathit{S}}_a\{Y,X,\mathit{Z},\mathit{\beta },\mathit{\alpha }(X)\}\mid X])=\mathbf{0},$$

and

$$\begin{array}{l}E\{K_h(X-x_0){\mathit{S}}_a(Y,X,\mathit{Z},\mathit{\beta },\mathit{a})\}=\int K(t)E\{{\mathit{S}}_a(Y,X,\mathit{Z},\mathit{\beta },\mathit{a})\mid X=x_0+ht\}{f}_X(x_0+ht)dt\\ =E\{{\mathit{S}}_a(Y,X,\mathit{Z},\mathit{\beta },\mathit{a})\mid X=x_0\}{f}_X(x_0)+{\frac{d^2[E\{{\mathit{S}}_a(Y,X,\mathit{Z},\mathit{\beta },\mathit{a})\mid X=x\}{f}_X(x)]}{2{dx}^2}|}_{x=x_0}{h}^2\int t^{2}K(t)dt+o(h^2)\\ ={\frac{d^2[E\{{\mathit{S}}_a(Y,X,\mathit{Z},\mathit{\beta },\mathit{a})\mid X=x\}{f}_X(x)]}{2{dx}^2}|}_{x=x_0}{h}^2\int t^{2}K(t)dt+o(h^2).\end{array}$$ (A.4)

In the last equality, we used the fact that S_a(Y, X, Z, β, a) = S_a{Y, X, Z, β, α(X)} at X = x₀ and E{S_α{Y, X, Z, β, α(X)} | X] = 0.

In addition, we have

$$\begin{array}{l}var(K_h(X-x_0)[{\mathit{S}}_a(Y,X,\mathit{Z},\mathit{\beta },\mathit{a})-{\mathit{S}}_a\{Y,X,\mathit{Z},\mathit{\beta },\mathit{\alpha }(X)\}])\\ \le \int K_h^2(x-x_0)E({[{\mathit{S}}_a(Y,X,\mathit{Z},\mathit{\beta },\mathit{a})-{\mathit{S}}_a\{Y,X,\mathit{Z},\mathit{\beta },\mathit{\alpha }(X)\}]}^{\otimes 2}\mid X=x)f_X(x)dx\\ =\int h^{-1}{K}^2(t)E({[{\mathit{S}}_a(Y,X,\mathit{Z},\mathit{\beta },\mathit{a})-{\mathit{S}}_a\{Y,X,\mathit{Z},\mathit{\beta },\mathit{\alpha }(X)\}]}^{\otimes 2}\mid X=x_0+ht)f_X(x_0+ht)dt\\ =\int h^{-1}{K}^2(t)E({[{\mathit{S}}_a(Y,X,\mathit{Z},\mathit{\beta },\mathit{a})-{\mathit{S}}_a\{Y,X,\mathit{Z},\mathit{\beta },\mathit{\alpha }(X)\}]}^{\otimes 2}\mid X=x_0)f_X(x_0)dt\\ +\int {tK}^2(t)\frac{d}{dx}\{E({[{\mathit{S}}_a(Y,X,\mathit{Z},\mathit{\beta },\mathit{a})-{\mathit{S}}_a\{Y,X,\mathit{Z},\mathit{\beta },\mathit{\alpha }(X)\}]}^{\otimes 2}{\mid x)f_X(x)\}\mid }_{x=x_0}dt\\ +\int {ht}^2{K}^2(t)\frac{d^2}{2{dx}^2}\{E({[{\mathit{S}}_a(Y,X,\mathit{Z},\mathit{\beta },\mathit{a})-{\mathit{S}}_a\{Y,X,\mathit{Z},\mathit{\beta },\mathit{\alpha }(X)\}]}^{\otimes 2}{\mid x)f_X(x)\}\mid }_{x=x_0}dt+o(h)\\ =\mathbf{0}+\mathbf{0}+O(h)=O(h).\end{array}$$

Here, in the last equality, we used S_a(Y, X, Z, β, a) = S_a(Y, X, Z, β, α(X)} at X = x₀ and ∫ tK²(t)dt = 0. Thus

$$n^{-1}\sum _{i=1}^n{K}_h(X_i-x_0)[{\mathit{S}}_a(Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{a})-{\mathit{S}}_a\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i)\}]=O(h^2)+O_p\{{(h/n)}^{1/2}\}=o_p(n^{-1/2})$$

when nh⁴ → 0. Thus we have obtained

$$\widehat{\mathit{\alpha }}(x,\mathit{\beta })-\mathit{\alpha }(x)=-\frac{1}{{nf}_X(x)}\sum _{i=1}^n{K}_h(X_i-x)E{\{{\mathit{S}}_{aa}(Y,X,\mathit{Z},\mathit{\beta },\mathit{a})\mid X=x\}}^{-1}{\mathit{S}}_a\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i)\}+o_p(n^{-1/2}).$$ (A.5)

Substituting the right hand side of the (A.5) into (A.2), we have

$$\begin{array}{l}-\mathcal{F}{n}^{1/2}(\widehat{\mathit{\beta }}-\mathit{\beta })\\ =n^{-1/2}\sum _{i=1}^n{\mathit{S}}_{\beta }\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i)\}\\ +n^{-1/2}\sum _{j=1}^n{\mathit{S}}_{\beta \alpha }\{Y_j,X_j,{\mathit{Z}}_j,\mathit{\beta },\mathit{\alpha }(X_j)\}\{\widehat{\mathit{\alpha }}(X_j,\mathit{\beta })-\mathit{\alpha }(X_j)\}+o_p(1)\\ =n^{-1/2}\sum _{i=1}^n{\mathit{S}}_{\beta }\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i)\}-n^{-1/2}\sum _{i=1}^n[\sum _{j=1}^n{\mathit{S}}_{\beta \alpha }\{Y_j,X_j,{\mathit{Z}}_j,\mathit{\beta },\mathit{\alpha }(X_j)\}\frac{1}{{nf}_X(X_j)}\\ E{\{{\mathit{S}}_{aa}(Y,X,\mathit{Z},\mathit{\beta },\mathit{a})\mid X=X_j\}}^{-1}{K}_h(X_i-X_j)]{\mathit{S}}_a\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i)\}+o_p(1)\\ =n^{-1/2}\sum _{i=1}^n{\mathit{S}}_{\beta }\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i)\}-n^{-1/2}\sum _{i=1}^{n}E[{\mathit{S}}_{\beta \alpha }\{Y,X_i,\mathit{Z},\mathit{\beta },\mathit{\alpha }(X_i)\}\mid X_i]\\ E{\{{\mathit{S}}_{aa}(Y,X,\mathit{Z},\mathit{\beta },\mathit{a})\mid X=X_i\}}^{-1}{\mathit{S}}_a\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i)\}+o_p(1)\\ =n^{-1/2}\sum _{i=1}^n{\mathit{S}}_{\beta }\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i)\}-n^{-1/2}\sum _{i=1}^n\mathit{U}(X_i){\mathit{S}}_a\{Y_i,X_i,{\mathit{Z}}_i,\mathit{\beta },\mathit{\alpha }(X_i)\}+o_p(1).\end{array}$$

This completes the proof of Theorem 1.

Proof of Theorem 2

Because β̂ has a root-n convergence rate, we replace β̂ by β inside α̂. Working through the same derivation following (A.3), while maintaining the bias term in (A.4), we can obtain a refined version of (A.5), which is exactly the expansion in Theorem 2.

Because S_a{Y, X, Z, β, α(X)} is a score function, we have

$$E[{\mathit{S}}_a\{Y,X,\mathit{Z},\mathit{\beta },\mathit{\alpha }(X)\}{\mathit{S}}_a^{\mathrm{T}}\{Y,X,\mathit{Z},\mathit{\beta },\mathit{\alpha }(X)\}\mid x]=-E[{\mathit{S}}_{aa}\{Y,X,\mathit{Z},\mathit{\beta },\mathit{\alpha }(X)\}\mid x].$$

This yields the variance to be

$$\frac{\int K^2(t)dt}{{\mathit{nhf}}_X(x)}E{[{\mathit{S}}_a\{Y,X,\mathit{Z},\mathit{\beta },\mathit{\alpha }(X)\}{\mathit{S}}_a^{\mathrm{T}}\{Y,X,\mathit{Z},\mathit{\beta },\mathit{\alpha }(X)\}\mid x]}^{-1}+O\{{(nh)}^{-1}\}=-\frac{\int K^2(t)dt}{{\mathit{nhf}}_X(x)}\mathbf{\Omega }(x)+o\{{(nh)}^{-1}\}.$$

This completes the proof of Theorem 2.