Longitudinal Image Registration with Temporally-Dependent Image Similarity Measure

Abstract

Longitudinal imaging studies are frequently used to investigate temporal changes in brain morphology and often require spatial correspondence between images achieved through image registration. Beside morphological changes, image intensity may also change over time, for example when studying brain maturation. However, such intensity changes are not accounted for in image similarity measures for standard image registration methods. Hence, (i) local similarity measures, (ii) methods estimating intensity transformations between images, and (iii) metamorphosis approaches have been developed to either achieve robustness with respect to intensity changes or to simultaneously capture spatial and intensity changes. For these methods, longitudinal intensity changes are not explicitly modeled and images are treated as independent static samples. Here, we propose a model-based image similarity measure for longitudinal image registration that estimates a temporal model of intensity change using all available images simultaneously.

I. Introduction

Longitudinal imaging studies are important to study changes that occur during brain development, neurodegeneration, or disease progression in general. Spatial correspondences almost always need to be established between images for longitudinal analysis through image registration. Most image registration methods have been developed to align images which are similar in appearance or structure. If such similarity is not given (e.g., in case of pathologies or pre- and post-surgery images) cost function masking [4] is typically used to discard image regions without correspondence from the registration. Such strict exclusion is not always desirable. When investigating brain development (or neurodevelopment) for example (our target application in this paper) valid correspondences for the complete brain are expected to exist. However, brain appearance changes continuously over time (see Figure 1) due to biological tissue changes, such as the myelination of white matter [2], [24], and adversely affects image registration results [17].

Fig. 1.

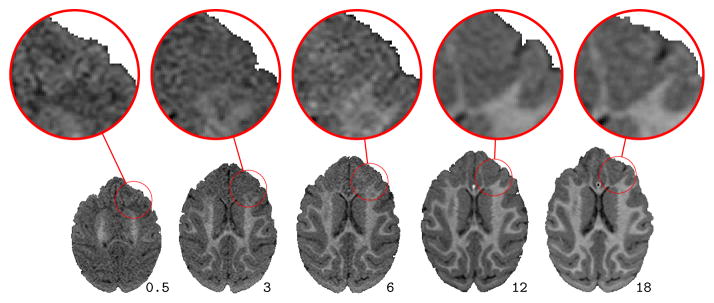
Brain slices and magnifications from T1 weighted magnetic resonance images for a monkey at ages 2 weeks, 3, 6, 12, and 18 months. White matter appearance changes locally as axons are myelinated during brain development.

The effect of appearance change on the result of an image registration depends on the chosen transformation model and the chosen image similarity measure. Generally, transformation models with few degrees of freedom (such as rigid or affine transformations) are affected less by local changes in image appearance than transformation models which can capture localized spatial changes, such as elastic or fluid models. In particular, in Section IV-C we show that affine methods perform well even in the presence of strong non-uniform appearance change, while deformable methods introduce erroneous local deformations in order to resolve inconsistencies in appearance. However, transformation models which can capture local deformations are desirable for many longitudinal studies as changes in morphology tend to be spatially non-uniform.

For longitudinal registration, temporal regularization of the transformation model has been explored recently. This is motivated by the assumption that unrealistic local changes can be avoided by enforcing temporal smoothness of a transformation [10], [12], [31]. It has been shown that various anatomical structures in the brain follow distinct growth patterns over time [16]. Temporal regularization can introduce bias by smoothing the deformation of all anatomical structures equally at all time-points. This can be especially problematic during periods of rapid growth at the early stages of development. The longitudinal processing stream in Freesurfer [22] aims to avoid such over-regularization by initializing the processing for each time-point with common information from a subject template without a temporal smoothness constraint on the deformation therefore allowing for large temporal deformations. However, it is developed for MR images of adult subjects with minimal appearance change compared to brain maturation studies.

The longitudinal registration algorithm 4-dimensional HAMMER [27] establishes alignment by searching for corresponding regions with similar spatio-temporal attributes. While this method is less sensitive to appearance change, it suffers from the previously mentioned problems associated with the temporal smoothness constraint of the deformation. DRAMMS [20] further improves attribute based registration by choosing more discriminative attributes that reduce matching ambiguity. The longitudinal segmentation algorithm CLASSIC [33] jointly segments a longitudinal image sequence and estimates the longitudinal deformation of anatomy using HAMMER. The spatial and temporal segmentation constraints are adaptive and can accommodate relatively local intensity changes, but the temporal smoothness constraints are the same as in HAMMER.

Several methods have been developed for the longitudinal registration of the cortical surfaces in developing neonates. In [32] the difficulty due to appearance change is circumvented by registering pairs of inflated cortical surfaces. The method establishes correspondence for the cortex and not the whole brain volume. The authors in [14] propose a registration method that combines surface based and tissue class probability based registration. The method relies on tissue class priors and surfaces of the tissue boundaries and the cerebellum. While this method defines a transformation over the whole brain it does not address the problem of aligning the unmyelinated and myelinated white matter at different time-points.

In [25] the authors construct a spatio-temporal atlas capturing the changes in anatomical structures during development. The atlas provides the missing anatomical evolution between two time-points. The source image is registered to the closest age snapshot of the atlas and transformed to the age of the target image using the atlas information. The transformed image is then registered to the target image. The method relies on an atlas with dense temporal sampling. Constructing the spatio-temporal atlas during early brain maturation, however, requires the registration of longitudinal images at different stages of myelination. The atlas construction [26] relies on normalized mutual information and B-spline based free-form deformation to align the longitudinal image sequence, but the appropriateness of the method for aligning images undergoing contrast inversion is not addressed.

Approaches which address non-uniform intensity changes have mainly addressed registration for image-pairs so far and either rely on local image uniformities [17], [29] or try to estimate image appearance changes jointly with an image transform [13], [18], [21], [23]. Often (e.g., for bias field compensation in magnetic resonance imaging), image intensity changes are assumed to be smooth. This assumption is not valid for certain applications, including longitudinal magnetic resonance (MR) imaging studies of neurodevelopment.

In this paper we focus on the complementary problem of determining an appropriate image similarity measure for longitudinal registration in the presence of temporal changes in image intensity.

In [3] the authors derive a Bayesian similarity measure for simultaneous motion correction and pharmacokinetic model parameter estimation in dynamic contrast-enhanced MR image sequences. The intensity model parameters are estimated individually for each voxel. In our method we spatially regularize the model parameters and show that it is beneficial to mitigate errors during parameter estimation and improves registration accuracy (Section IV-D1).

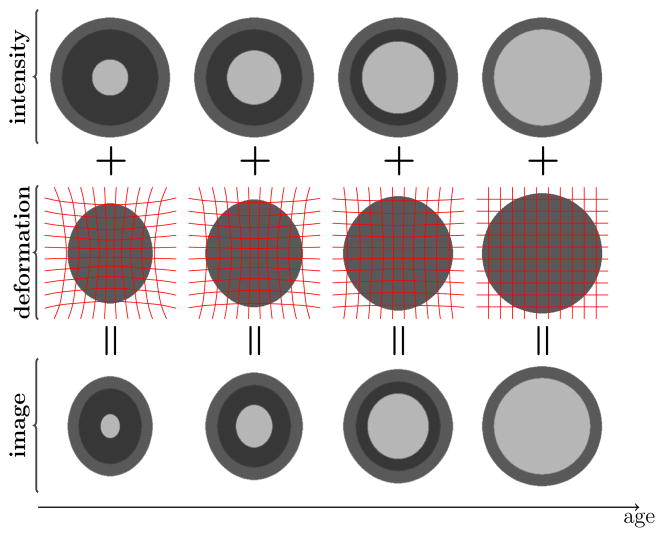
The changes seen on the MR images during neurodevelopment result from a variety of parallel biological processes. Changes in various factors of tissue composition, such as myelin and water content, are coupled with both tissue generation and tissue loss [6]. The majority of the changes seen on MR images, however, can be attributed to the myelination of the neuronal axons and morphological changes due to growth. In a simplified model of neurodevelopment, these two processes can be decoupled and modeled separately as shown in Figure 2. Our goal is to register the images in the bottom row. Existing deformable registration algorithms can resolve the morphological differences between source and target images if the image intensities within tissue classes remain constant or vary slowly. Therefore, if the model of intensity change is known the intensity change can be modded out and the only remaining task of the registration method is to recover the spatial transformation (middle row), reducing the original problem to registering each source image in the bottom row to the corresponding intensity adjusted target image in the top row.

Fig. 2.

Simplified model of neurodevelopment. The outer ring represents gray matter, the bright central ring is the myelinating white matter surrounded by darker, unmyelinated white matter. The overall changes (bottom row; age increases to the right) can be decomposed into intensity changes due to the myelination process (top row) and morphological changes due to growth (middle row).

Our proposed approach estimates local longitudinal models of intensity change using all available images. Once the intensity model is known, existing deformable registration methods can be used to find the spatial transformation between the images. Our approach alternates between parameter estimation for the local models of intensity change and estimation of the spatial transformation. Image similarities are computed relative to the estimated intensity models, hence accounting for local changes in image intensities. While our motivating application in this paper is studying brain maturation, the proposed method is general and can be applied to any longitudinal imaging problem with non-uniform appearance change (for example, time-series imaging of contrast agent injection).

This paper is an extension of our previous conference papers [7], [8]. In [8] we showed derivation of the model-based similarity measure with a quadratic intensity model and region based spatial regularization of the model parameters. The method was compared to commonly used global similarity measures on 2D synthetic data sets. In [7] we introduced the logistic intensity model with improved spatial regularization of the model parameters. We validated our method against mutual information (MI) on real data with manually chosen landmarks. In this paper, we extended the previous conference papers with (i) a simplified model of neurodevelopment for motivating our similarity measure, (ii) an experimental section comparing various polynomial and logistic intensity models (Section IV-B), (iii) a longitudinal deformation model between time-points for the synthetic test data sets to better approximate the deformations during development, (iv) an experimental section on the effect on the registration accuracy of the median filter size used for the spatial regularization of the intensity model parameters (Section IV-D1), (v) and an experimental section on the effect of the white matter segmentation accuracy on the registration (Section IV-D2).

Section II introduces the model-based image similarity measure, sum of squared residuals (SSR). Section III discusses parameter estimation. Section IV describes the performed experiments and discusses results. The paper concludes with a summary and outlook on future work.

II. Model-Based Similarity Measure

Assume we have an image intensity model Î(x, t; p) which for a parameterization, p, describes the expected intensity values for a given point x at a time t (x can be a single voxel or a region). This model is defined in a spatially fixed target image. Then, instead of registering a measured image I_i at t_i to a fixed target image I_T we can register it to the corresponding intensity-adjusted target image Î(x, t_i; p), effectively removing temporal intensity changes for a good model and a good parameterization, p. Hence,

$$\text{Sim}(I_i\circ {\mathrm{\Phi }}_i,I_T)\text{is}\text{replaced}\text{by}\text{Sim}(I_i\circ {\mathrm{\Phi }}_i,\widehat{I}(\mathbf{x},t_i;\mathbf{p})),$$

where Sim(·, ·) is any chosen similarity measure (e.g., sum of squared differences (SSD), normalized cross correlation, or mutual information), and Φ_i is the map from image I_i to the spatially fixed target space. Since our method aims to create an intensity adjusted model Î that matches the appearance of the source image, we use SSD in this paper. We call the intensity-adjusted SSD similarity measure a sum of squared residual (SSR) model, where the residual is defined as the difference between the predicted and the measured intensity value.

A. General Local Intensity Model Estimation for SSD

Since SSR is a local image similarity measure, for a given set of N measurement images {I_i} at times {t_i} we can write the full longitudinal similarity measure as the sum over the individual SSRs, i.e.,

$$\mathit{SSR}(\{I_i\};\mathbf{p})=\sum _{i=0}^{N-1}{\int }_{\mathrm{\Omega }}{(I_i\circ {\mathrm{\Phi }}_i(\mathbf{x})-\widehat{I}(\mathbf{x},t_i;\mathbf{p}))}^{2}dx,$$ (1)

where Ω is the image domain of the fixed image. For given spatial transforms Φ_i, 1 is simply a least-squares parameter estimation problem given the measurements {I_i ∘ Φ_i(x)} and the predicted model values {Î(x, t_i; p)}. The objective is to minimize 1 while, at the same time, estimating the model parameters p. We use alternating optimization with respect to the intensity model parameters, p, and the spatial transformations Φ_i to convergence (see Section III). Note that looking at only two images at a time without enforcing some form of temporal continuity would lead to independent registration problems and discontinuous temporal intensity models. However, this potential problem is avoided by using all available images in the longitudinal set to estimate the intensity model parameters.

B. Logistic Intensity Model with Elastic Deformation

SSR can be combined with any model for intensity change, ranging from a given constant target image (the trivial model) and linear models to nonlinear models that are more closely adapted to the myelination process during neurodevelopment. Since the myelination process exhibits a rapid increase in MR intensity (in T1 weighted images) during early brain development followed by a gradual leveling off [9], nonlinear appearance models are justified. In this paper we use the logistic model for the experiments which is often used in growth studies [11], but also investigate various polynomial models in Section IV-B. The logistic model is defined as

$$\widehat{I}(\mathbf{x},t;\alpha ,\beta (\mathbf{x}),k(\mathbf{x}))=\frac{\alpha }{1+e^{-k(\mathbf{x})(t-\beta (\mathbf{x}))}},$$ (2)

where α is a global parameter, β and k are spatially varying model parameters. We can attribute biological meaning to these parameters, k being the maximum rate of intensity change, α the maximum increase of white matter intensity during myelination (intensities are normalized to a zero lower asymptote during the fitting process), and β is related to the onset time of myelination (see Figure 3). Assuming that both unmyelinated and fully myelinated white matter intensities are spatially uniform we keep α constant as the difference between myelinated (upper asymptote) and unmyelinated (lower asymptote) white matter intensities. This is a simplifying, but reasonable assumption since intensity inhomogeneities in unmyelinated or myelinated white matter are small compared to the white matter intensity change due to the myelination process itself [2]. The unmyelinated and myelinated white matter intensities defining α are estimated from the white matter voxels (as defined by the white matter segmentation) as the 1^st percentile of the first image (mostly unmyelinated) and the 99^th percentile of the last image (mostly myelinated), respectively.

Fig. 3.

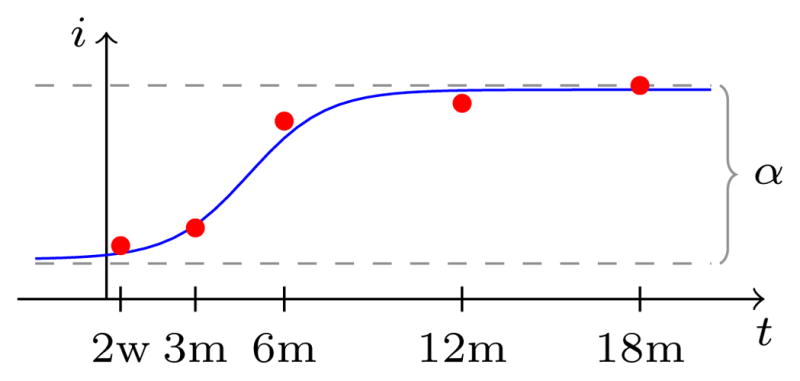
Logistic intensity model.

III. Parameter Estimation

Once the parameters for the local intensity models are known, SSR can be used to replace the image similarity measure in any longitudinal registration method. Here, we use an elastic deformation model (Section III-A) and jointly estimate the parameters for the intensity model (Section III-B).

A. Registration model

The growth process of the brain not only includes appearance change but complex morphological changes as well, hence the need for a deformable transformation model. To single out plausible deformations, we use (for simplicity) an elastic regularizer [5] defined on the displacement field u as

$$S[u]={\int }_{\mathrm{\Omega }}\frac{\mu }{4}\sum _{j,k=1}^d\underset{\text{rigidity}}{\underbrace{{({\partial }_{x_j}{u}_k+{\partial }_{x_k}{u}_j)}^2}}+\frac{\lambda }{2}\underset{\text{volume}\text{change}}{\underbrace{{(\text{div}u)}^2}}dx,$$

where μ (set to 1) and λ (set to 0) are the Lamé constants that control elastic behavior, and the div is the divergence operator defined as ∇·u, where ∇ is the gradient operator. The behavior of the elastic regularizer might be better understood if we convert the Lamé constants to Poisson’s ratio ν (=0) and Young’s modulus E (=2). The given Poisson’s ratio allows volume change such that the change in length in one dimension does not cause expansion or contraction in the other dimensions. This is a desirable property in our case, since tissue is both generated and destroyed during development resulting in volume change over time. Young’s modulus, on the other hand, describes the elasticity of the tissue and was chosen experimentally to allow large deformations while limiting the amount of folding and discontinuities.

Registration over time then decouples into pairwise registrations between the intensity-adjusted target image Î and given source images I_i. This is sufficient for our test of the longitudinal image similarity measure, but could easily be combined with a spatio-temporal regularizer which would then directly couple the transformations between the images of a time-series (instead of only having an indirect coupling through the model-based similarity measure).

B. Model Parameter Estimation

We estimate the intensity model parameters only within the white matter where image appearance changes non-uniformly over time; for simplicity, gray matter intensity was assumed to stay constant. The methods for obtaining the white matter segmentations for each data set are described in the corresponding experimental sections. In addition, we investigate the effect of white matter segmentation accuracy on the model-based registration in Section IV-D2.

Instead of estimating the parameters independently for each voxel, spatial regularization was achieved by estimating the medians of the parameters from overlapping local 3 × 3 × 3 neighborhoods (the effect of various neighborhood sizes on registration accuracy is investigated in Section IV-D1).

The algorithm is defined as follows

1. Initialize model Î parameters to p = p₀ (constant in time intensity model if no prior is given).

2. Affinely pre-register images {I_i} to {Î(t_i)}.

3. Estimate model parameters p from the pre-registered images.

4. Estimate the appearance of Î at times {t_i}, giving {Î(t_i)}.

5. Estimate displacement fields {u_i} by registering images {I_i} to {Î(t_i)}.

6. Estimate p from the registered images {I_i ∘ u_i}.

7. Repeat from step 3 until convergence.

The parameterization p for the logistic intensity model is estimated with generalized linear regression. The algorithm terminates once the SSR registration energy (1) decreases by less than a given tolerance between subsequent iterations. In all our experiments only few iterations (typically less than 5) were required. A more in-depth numerical convergence analysis should be part of future work. If desired, a prior model defined in the target image (a form of intensity model parameter atlas) could easily be integrated into this framework.

IV. Experimental Results

The validation of the model-based similarity measure requires a set of longitudinal images with known ground truth transformations between the source images and the target images. We used three different types of data sets for validation:

• Synthetic (2D)

• Simulated brain images (3D)

• Real monkey data (3D)

For the synthetic and simulated data sets known longitudinal deformations can be added to the generated images in order to simulate growth over time. The deformations are generated as follows. We start with an identity spline transformation with 4 × 5 equally spaced control points for the target image (thus the target image has the same geometry as the original synthetic or simulated image). We then generate the deformation for the next time-point by randomly perturbing the spline control points of the current time-point by a small amount. We iteratively repeat this step until a new deformation is generated for each time-point. The deformation between any two time-points is small, but the cumulative deformation between the first and last time-points is considerable.

Since the ground truth transformations are known the accuracy of the registration method can be determined by registering each source and target image pair and comparing the resulting transformations to the ground truth transformations. Registration accuracy was determined by computing the distance between the ground truth and the recovered transformation. The root mean squared (RMS) error of the voxel-wise distance within the mask of the target image then yielded the registration error.

For the real data sets, however, the ground truth transformations are not known and cannot be easily determined. Therefore, instead of using a ground truth deformation, we use manually defined landmarks in the source and target images to measure how well they are aligned after registration. For this data set, registration error was computed as the average Euclidean distance between the target and the registered landmarks.

Imaging for the monkey data was performed on a 3T Siemens Trio scanner at the Yerkes Imaging Center, Emory University with a high-resolution T1-weighted 3D magnetization prepared rapid gradient echo (MPRAGE) sequence (TR = 3,000ms, TE = 3.33ms, flip angle = 8, matrix = 192 × 192, voxel size = 0.6mm³, some images were acquired with TE = 3.51ms, voxel size = 0.5mm³).

In this section we describe several experiments that test the proposed similarity measure with progressively more difficult registration problems. In addition, we performed experiments that compare our method to three of the commonly used similarity measures: sum of squared difference (SSD), normalized cross correlation (NCC), and mutual information (MI).

Image registration was performed with the publicly available registration toolbox, FAIR [19]. The same elastic regularizer parameters were used for all experiments (described in Section III-A). The parameters for the similarity measures were chosen to allow deformations with similar magnitude and smoothness.

A. White Matter Intensity Distributions from Real Data

An important part of the registration experiments is testing the similarity measures on realistic appearance change while knowing the ground truth deformations. To this end, we calculated the spatial and temporal intensity changes from the MR images of 9 rhesus monkeys during the first 12 months of life. The white matter intensity trajectories acquired from the real monkey data were then used to generate the synthetic images for Experiment 2 (Sect. IV-C).

The spatial white matter distributions were calculated for each time-point (2 week, 3, 6, 12 month) of the 9 monkeys. The early time-points have low gray-white matter contrast, therefore the white matter segmentation of the 12 month image was transferred to the earlier time-points (this is often the case for longitudinal studies of neurodevelopment where good tissue segmentation might only be available at the latest time-point [28]). For the purpose of a simplified simulation, we averaged the white matter intensity change of the whole brain orthogonal to the posterior-anterior direction (most of the intensity change is along this direction [15]). Figure 4 shows the mean and variation of the white matter intensity profiles from all four time-points. Myelination starts in the posterior and central regions of the white matter and continues towards the periphery and, dominantly, towards the anterior and posterior regions. These findings agree with existing studies on myelination [15]. Of note is the strong white matter intensity gradient in the early time-points due to the varying onset and speed of the myelination process.

Fig. 4.

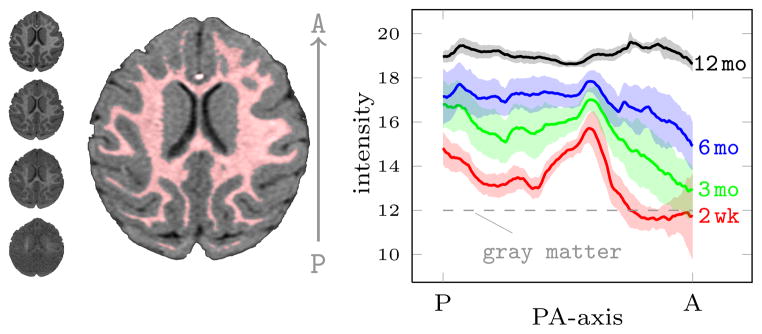
Spatio-temporal distribution of white matter intensities in 9 monkeys. A single slice from each time-point is shown in order in the left column (2 week at the bottom), and the white matter segmentation (red) at 12 months is shown in the middle. Plotted, for each time-point, the mean (line) ± 1 standard deviation (shaded region) of the spatial distribution of the white matter intensities averaged over the whole brain of each monkey orthogonal to the PA direction. The images were affinely registered and intensity normalized based only on the gray matter intensity distributions (gray matter is assumed to stay constant over time).

B. Experiment 1: Model Selection

In this experiment we investigated the choice of the parametric intensity model for Î on registration accuracy given data sets generated with various intensity models. While the logistic model described in Section II-A is a reasonable model for the intensity change seen due to myelination, the true intensity model of the data is a result of complex biological processes and might not be known. The image intensity model therefore is an approximation of the true underlying model and the choice of this approximation can affect registration accuracy.

Four intensity models were investigated: constant, linear, quadratic, and logistic. Five 128 × 128 2D synthetic longitudinal image sets were generated with 10 time-points each (I₀, …, I₉). The synthetic images consist of three concentric rings, the outer ring resembling gray matter, the middle ring white matter going through myelination, and the inner ring myelinated white matter. The outer and inner rings have constant intensity over time (69 and 143 respectively, based on average tissue intensities from the monkey data) while the intensity of the ring representing myelinating white matter was set according to one of five intensity profiles (with unmyelinated white matter = 46 and myelinated white matter = 143): constant, linear, quadratic, unsaturated logistic, and saturated logistic (see Figure 5 for the five data sets). The last time-point I₉ was designated as the target image and the earlier time-points as the source images. The source images were then registered to the target image with deformable elastic registration using one of the four intensity models for the model image Î (constant, linear, quadratic, logistic). There is no displacement between the source and target images thus the ground truth transformation is the identity.

Fig. 5.

Synthetic data sets with 10 time-points generated with various intensity models. The outer ring resembling gray matter and the inner ring resembling myelinated white matter stay constant over time. The middle ring representing myelinating white matter changes over time according to the intensity models shown in the first column.

Figure 6 shows an extreme case of the model-based registration experiment with a saturated logistic intensity model used for generating the original longitudinal images and a constant model used for the model estimation step. The constant model cannot capture the simulated logistic intensity change within the white matter, therefore, considerable deformation is introduced (the correct deformation is the identity).

Fig. 6.

The influence of the intensity model on the registration is shown. Top row: images generated with the saturated logistic intensity profile. The goal is to register the source images I₀, …, I₈ to the target image I₉ with SSR. The following rows show the intensity-adjusted model images {Î (t_i)} and the SSR registration results with the deformation field u overlaid (red grid) for constant, quadratic, and logistic intensity models. Note that the source images are registered to the corresponding intensity-adjusted model images. The correct deformation field is the identity, but the constant model cannot capture the logistic intensity change.

Table I shows the registration errors for all 20 combinations between the five different intensity profiles used to generate the longitudinal images and four model types used for the intensity model estimation. Each row shows the registration error for one of the five generated data sets (lowest errors for each set are highlighted). The columns show the model used for estimating the intensity change over time for Î. The results show that quadratic model is a good choice if the underlying true model is polynomial or the logistic model is not saturated, however, the logistic model is necessary when the true model is logistic and the time-points are far enough to saturate the model.

TABLE I.

Model selection experiment results. In each row, the data for the experiment was generated by the type of intensity model shown. Each column shows the registration error (RMS) obtained when using that model in the column for the model-based similarity measure (best values are highlighted).

	constant	linear	quadratic	logistic
constant	0.04	0.04	0.04	0.04
linear	0.68	0.07	0.07	0.13
quadratic	0.60	0.10	0.05	0.16
logistic (unsaturated)	1.63	0.10	0.09	0.12
logistic (saturated)	2.36	0.16	0.16	0.12

C. Experiment 2: Synthetic Data

In this experiment, we created sets of 64 × 64 2D synthetic images (based on the Internet Brain Segmentation Repository (IBSR) [1] synthetic dataset). Each set consisted of 11 time-points (I_i, i = 0, …, 10). I₀ was designated as the target image and all subsequent time-points as the source images. The gray matter intensities of all 11 images were fixed ( $I_i^{\text{gm}}=80$). For the source images, I₁, …, I₁₀, we introduced two types of white matter appearance change:

1. Uniform white matter appearance change over time, starting as dark (unmyelinated) white matter ( $I_1^{\text{wm}}=20$) and gradually brightening (myelinated) white matter ( $I_{10}^{\text{wm}}=180$) resulting in contrast inversion between gray and white matter. The target white matter intensity was set to 100.

2. White matter intensity gradient along the posterior-anterior direction with increasing gradient magnitude over time. The target image had uniform white matter ( $I_0^{\text{wm}}=50$). For the source images the intensity gradient magnitude increased from 1 to 7 intensity units per pixel (giving $I_1^{\text{wm}}=\{50,\dots ,70\}$ up to $I_{10}^{\text{wm}}=\{50,\dots ,200\}$). These gradients are of similar magnitude as observed in the real monkey data (see Figure 4).

We tested the similarity measures for two types of transformation models: affine; and deformable with elastic regularization. Figure 7 shows the experimental setup with deformable transformation model (for the affine registration experiments Φ_i was an affine transform; for the deformable registration experiment Φ_i was a longitudinal spline deformation with 20 control points). The aim of the experiment was to recover the ground truth inverse deformation, ${\mathrm{\Phi }}_i^{-1}$, by registering the 10 source images to I₀ (giving ${\widehat{\mathrm{\Phi }}}_i^{-1}$) with each of the four similarity measures (SSD, NCC, MI, SSR). We repeated each experiment 100 times for each transformation model with different random deformations giving a total of 16000 registrations (2 white matter change × 2 transformation model × 10 source image × 4 measure × 100 experiment). Significance was calculated with Welch’s t-test (assuming normal distributions, but unequal variances) at a significance level of a = 0.01.

Fig. 7.

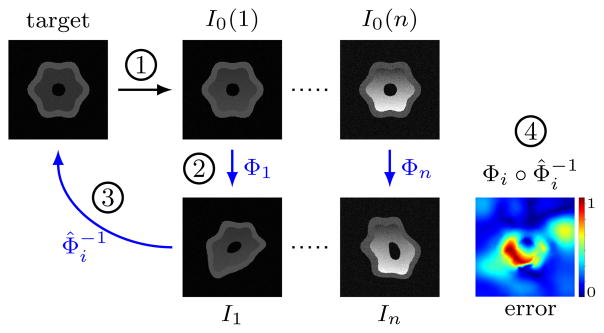
Experimental setup: 1) Increasing white matter intensity gradient is added to the target, I₀. 2) Adding known random longitudinal deformations yields the source images, 3) which are registered back to the target. 4) Registration error is calculated from the known (Φ_i) and recovered ( ${\widehat{\mathrm{\Phi }}}_i^{-1}$) transformations.

Next, we describe the results of the experiments for each transformation model.

1) Affine transformation model

Affine registration is often appropriate for images from the same adult subject. In our case, it is only a preprocessing step to roughly align the images before a more flexible, deformable registration. Nevertheless, the initial alignment can greatly affect the initial model estimation and the subsequent deformable solution. Therefore we first investigate the sensitivity of affine registration to white matter appearance changes separately from deformable registration.

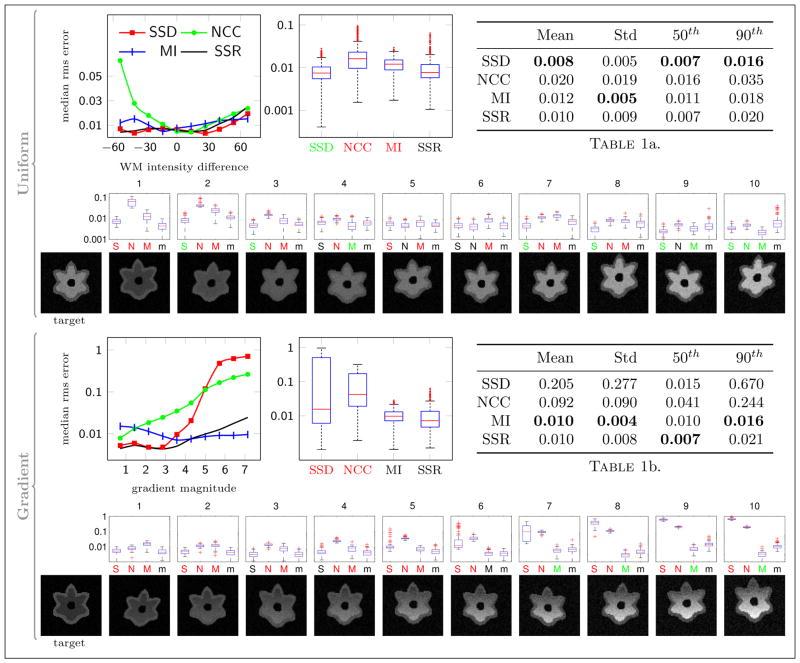
Figure 8 shows the results for registering I₁ through I₁₀ to the target image I₀ from multiple sets (n = 100, giving 1000 pair-wise registrations for each similarity measure) of longitudinal images with both uniform and gradient spatial white matter intensity profiles.

Fig. 8.

Results for Experiment 2 with affine transformation, uniform and gradient white matter intensity change. For uniform white matter, the line plot shows the median RMS error vs. the white matter intensity difference between the source and the target images ( $I_i^{\text{wm}}-I_0^{\text{wm}}$) for each time-point (0 means the images have the same contrast). For the gradient white matter, the x-axis of the line plot is the magnitude of the gradient. The boxplots and the tables summarize the aggregate results over all time-points (the box is the 25^th and 75^th percentile, the red line is the medium, the whiskers are 1.5 × interquartile range, and the red marks are outliers). The small boxplots show results for each time-point (S, N, M, and m are SSD, NCC, MI, and SSR respectively). For each boxplot, the x-label is highlighted in red/green if SSR performed significantly better/worse than that particular measure. The row of images shows the target and source images for a single trial. Note that all box plots and the bottom line plot have log y scales.

With uniform white matter, all four measures performed well when the contrast of the source image was close to the contrast of the target image (near 0 white matter intensity difference in the first plot of the median root mean squared registration error). The results for the gradient white matter profiles show that the performance of both SSD and NCC declined as the gradient magnitude increased, while MI and SSR aligned the images well even with the strongest gradient. Overall, SSR significantly outperformed NCC and MI but not SSD; however, the differences between the overall registration errors are on the order of 0.001 voxels for SSD, MI, and SSR (see Table 1a. in Figure 8).

The experiments suggest that affine registration can be reliably achieved by SSD, MI or SSR, but for simplicity MI should be used if affine alignment is the only objective.

2) Deformable registration

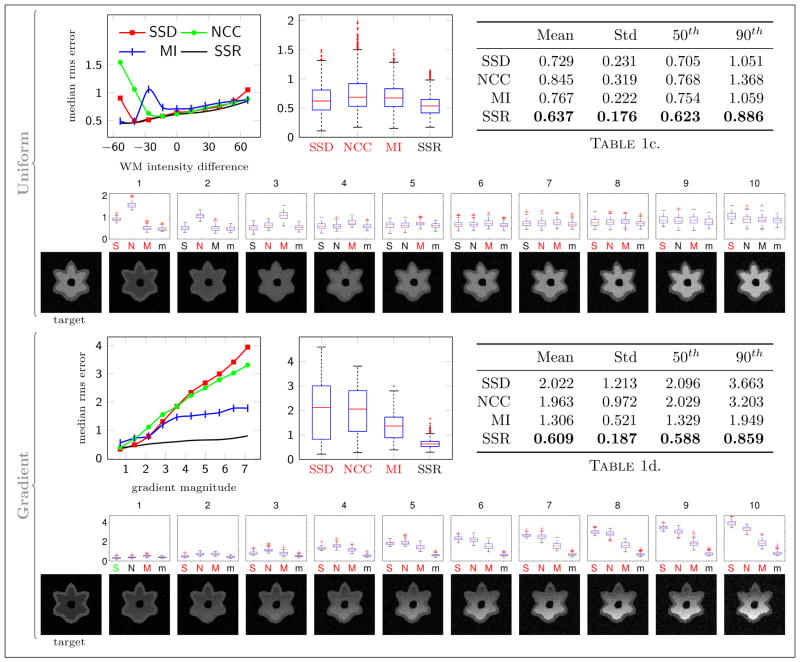
Similarly to the affine experiment, Figure 9 shows the error plots for deformable registrations in the presence of white matter intensity change. For uniform white matter, SSD again produced small registration errors when the contrast difference was small, but fared worse than MI and SSR in the presence of large intensity differences between the target and the source images. SSR performed slightly better than MI for all time-points.

Fig. 9.

Experiment 2 results with deformable transformation. The graphs are set up similarly as in Figure 8 except all plots have linear y scales. The last setup with deformable transformation model and gradient white matter intensity is the most challenging and relevant to the real world problem.

The setup with deformable registration and white matter gradient resembles the real problem closely and therefore is the most relevant. Here, SSD and NCC introduced considerable registration errors with increasing gradient magnitude. The registration error of MI remained under 2 voxels (mean = 1.62 ± 0.45), while SSR led to significantly less error (mean = 1.25 ± 0.35) for all time-points.

D. Experiment 3: Simulated Brain Data

The next set of experiments used simulated 3D brain images with white matter intensity distributions based on the monkey data. The images were preprocessed as described in Section IV-A. First, we estimated the voxel-wise longitudinal intensity model within the white matter from the four time-points of a single subject using SSR with a logistic intensity model. The estimated intensity model was then applied to each white matter voxel of the 12 month image to generate four different time-points I₀, …, I₃ with the same geometry as the 12 month image, but with different white matter intensity distributions. The time-points were random perturbations of the original image time-points (0.5, 3, 6, and 12 months) with normal distribution 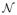(μ = 0, σ² = 1 week). The final source images were obtained by adding known longitudinal random deformations to the generated images I₀, …, I₂ (see Figure 10). 100 sets of longitudinal images were generated for the following experiments with different random time perturbations and spatial deformations.

Fig. 10.

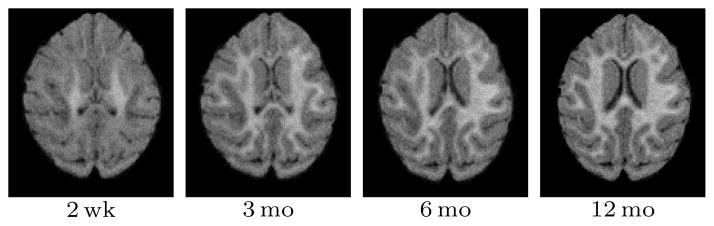
Simulated brain images with white matter intensity distributions estimated from the monkey data.

1) Smoothing filter size

In this experiment we investigated the effect of the smoothing filter size on the registration accuracy of SSR. In addition to no smoothing, four isotropic filters with sizes 3, 5, 7, and 9 voxels were used to smooth the model parameters.

The size of the smoothing filter had no significant influence on the global registration error (see Figure 13), even though, larger filters tend to over smooth the salient features of the model, such as the boundary between the unmyelinated and myelinated white matter. No smoothing, on the other hand, allows areas of poor model estimation, due to misregistration between the time-points, to remain in the intensity model. Most noticeably, initial misregistration near the gray matter white matter boundary can lead to a boundary shift.

Fig. 13.

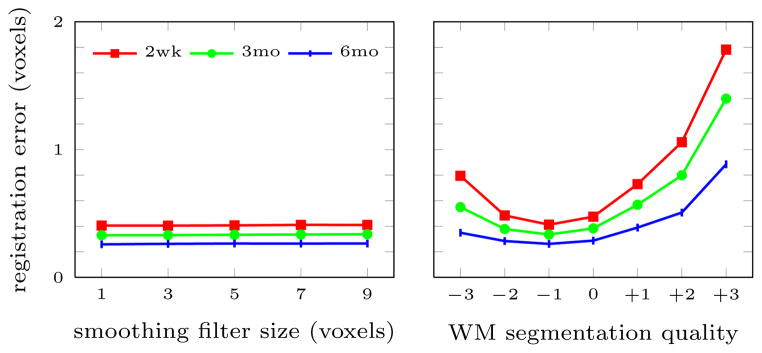
Results for SSR registration with different smoothing filter sizes (left) and varying quality white matter segmentations (right; x-axis shows the amount of erosion (−) or dilation (+) applied to the accurate (0) white matter mask).

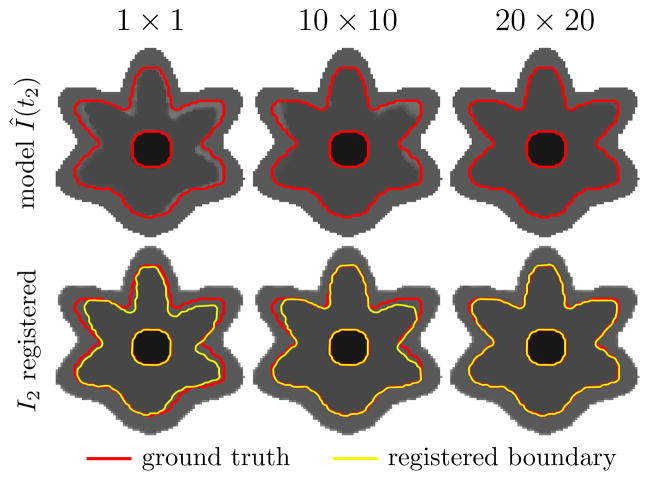
Next, we illustrate this boundary shift with a 2D synthetic longitudinal data set with a small misalignment between the time-points shown in Figure 11. Assuming that this is the best initial alignment between the time-points, the top row of Figure 12 shows the model images estimated from the data set at time t₂ with three different filter sizes; the bottom row shows the registration results between the source (I₂) and model images (Î(t₂)). As the filter size increases, the model better approximates the true tissue intensities near the boundary and the registration error (boundary shift) decreases. While a large smoothing filter is advantageous near the boundary, a smaller filter is less likely to smooth out salient features within the white matter. Finding the best fixed filter size or smoothing with an adaptive filter size will be investigated as part of future work.

Fig. 11.

Synthetic data set with logistic white matter intensity change and longitudinal deformation over time. I₀, …, I₅ are source images, I₆ is the target image. The outline shows the white matter gray matter boundary of the target image.

Fig. 12.

The effect of various smoothing filter sizes on the intensity model estimation and the subsequent registration (data set is shown in Figure 11). Top row: shows the estimated model from the misaligned synthetic longitudinal data set with 1 × 1, 10 × 10, and 20 × 20 voxel filters (the red outline is the correct tissue boundary). Bottom row: shows the results of elastically registering time-point I₂ to the models Î(t₂) in the top row (the yellow outline is the boundary after the registration).

2) White matter segmentation

Since the intensity change over time occurs in the white matter, the current algorithm estimates the model parameters only within the white matter segmentation. Reliable white matter segmentations, however, may not be available. In order to test the registration accuracy with various quality white matter segmentations, we registered each of the 100 longitudinal sets of the 3D simulated brain images using SSR with 7 white matter masks with varying quality, shown in Figure 14 (from an empty mask (M₋₃) through the accurate (M₀) white matter mask and a full brain mask). The mask under/over estimating the white matter were generated by eroding/dilating the accurate white matter mask (M₀) of the 12 month image. Figure 13 shows the registration accuracy for each of the masks. The registration error is lowest when the white matter mask is accurate or slightly underestimated, therefore, accurate white matter segmentation is necessary.

Fig. 14.

White matter segmentations used to investigate the influence of segmentation accuracy on SSR registration (erosion (M_−.) and dilation (M_+.) are applied to the accurate (M₀) segmentation).

E. Experiment 4: Monkey Data

We compared the model-based similarity measure to mutual information and sum of squared differences (SSR reduces to SSD when a constant in time intensity model used with no spatial regularization) on sets of longitudinal magnetic resonance images of 9 monkeys, each with 4 time-points (2 week, 3, 6, and 12 month). Each time-point was affinely pre-registered to an atlas generated from images at the same time-point (the atlas images for the four time-points were affinely registered) and intensity normalized so that the gray matter intensity distributions matched after normalization (gray matter intensity generally stays constant over time). The tissue segmentation was obtained at the last time-point with an atlas-based segmentation method [30].

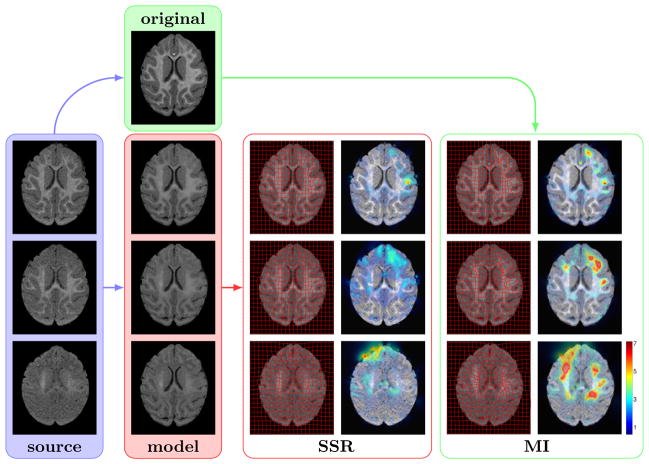
We registered 3D images of the three early time-points I_2wk, I_3mo, I_6mo to the target image I_12mo with an elastic registration method. Here, the target image is I_12mo as white matter segmentation is easily obtained given the good gray matter white matter contrast, but other time-points could be used. Since the ground truth deformations were not known, manually selected landmarks (Figure 15) identified corresponding regions of the brain at the different time-points (10–20 landmarks in a single slice for each of the 4 time-points in all 9 subjects; the landmarks were selected by IC based on geometric considerations after without consulting the deformable registration results, but after affine pre-registration). The distance between transformed and target landmarks yielded registration accuracy. Figure 16 shows the experimental setup for comparing MI to SSR.

Fig. 15.

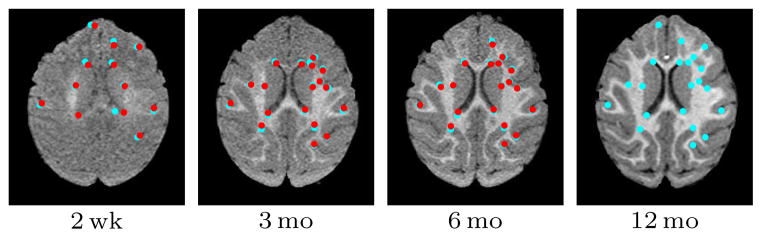
Corresponding target (cyan) and source (red) landmarks for a single subject.

Fig. 16.

Experimental setup and results for a single subject out of 9. To test MI, the source images (blue; from bottom: I_2wk, I_3mo, I_6mo) are registered to the latest time-point I_12mo (green). The resulting deformation field and the magnitude of the deformations (in pixels) is shown in the right panel. For SSR, the source images are registered to the model (red) that estimates the appearance of I_12mo at the corresponding time of each source image (results in middle panel).

Note that for the model-based method the target image is not I_12mo but the model Î_12mo(t) which is based on the geometry of I_12mo but appearance of the white matter is estimated at time t of the source image. The last time-point I_12mo was chosen since white matter segmentation is easily obtained given the good gray matter white matter contrast, but other time-points could be used.

With MI, the registration method accounts for both the non-uniform white matter appearance change and the morphological changes due to growth through large local deformations. This is not desirable since the registration method should only account for the morphological changes. These local deformations are especially apparent for registrations between I_2wk (and to a lesser extent I_3mo) and the target I_12mo and suggests large local morphological changes contradictory to normal brain development [9]. The landmark mismatch results (Figure 17) show that both mutual information and the model-based approach perform well in the absence of large intensity non-uniformity, however, SSR consistently introduces smaller erroneous deformations than MI.

Fig. 17.

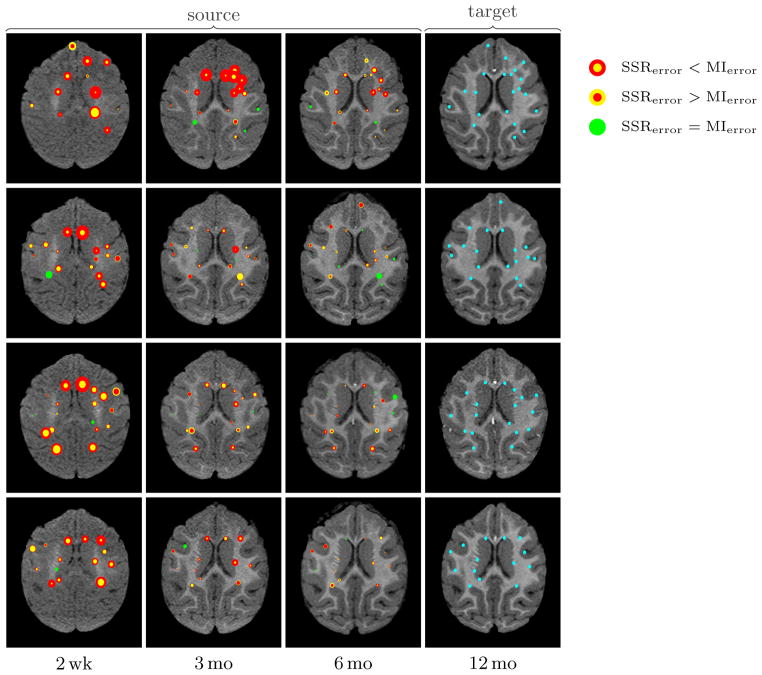
Landmark distance mismatch for 4 subjects out of 9. Each row shows a single subject. The last column shows the target images and landmarks (cyan). Columns 1–3 are the source images: each target-source landmark pair is marked as a circle (red: mutual information; yellow: SSR) with size proportional to the distance (mismatch) after registration between the landmark pair (the smaller circle is always on top). That is, the size of the circles are proportional to registration accuracy (smaller is more accurate) in that particular location.

Table II shows the aggregate results of the landmark mismatch calculations for SSD, MI, and SSR. The model-based approach SSR can account for appearance change by adjusting the intensity of the model image (see the estimated model images in Figure 16) and therefore is most beneficial when the change in appearance between the source and target image is large (for I_2wk SSR significantly outperformed SSD and MI, for I_3mo SSR significantly outperformed MI).

TABLE II.

Average landmark registration error (in voxels) between target I_12mo and source images I_2wk, I_3mo, I_6mo for all 9 subjects (significance level is α = 0.05; the smallest mean SSR registration errors are highlighted in bold; for SSD and MI significantly larger than SSR mean errors are shown in italics).

	I2wk				I3mo				I6mo
	mean	std	50th	90th	mean	std	50th	90th	mean	std	50th	90th
SSD	2.23	1.12	2.14	3.95	0.97	0.69	0.80	1.70	0.77	0.46	0.69	1.34
MI	2.84	1.58	2.76	4.87	1.64	1.10	1.31	3.49	1.01	0.66	0.90	1.82
SSR	1.54	0.83	1.43	2.73	0.91	0.48	0.84	1.61	0.85	0.52	0.73	1.56

We also compared 1^st and 2^nd degree polynomial intensity models to the logistic model and found no significant difference. This agrees with our findings from Section IV-B with only 4 time-points even the 1^st degree model can reasonably estimate the local appearance changes. However, similarly to the earlier model selection experiment, the logistic model should outperform the simpler models in larger studies with more time-points or when the model appearance needs to be extrapolated (e.g., if new images are acquired later in a longitudinal study after the previous time-points have been aligned).

V. Conclusions

We proposed a new model-based similarity measure which allows the deformable registration of longitudinal images with appearance change. This method can account for the intensity change over time and enables the registration method to recover the deformation due only to changes in morphology. We compared the model-based approach to mutual information and demonstrated that it can achieve higher accuracy than mutual information in cases when there is a large appearance change between source and target images. We used a logistic model of intensity change and an elastic deformation model, however, the formulation is general and can be used with any other appearance or deformation model. In the future we will investigate the use of prior models to inform the estimation step in regions with high uncertainty (e.g., due to poor initial alignment) and combine SSR with a registration method incorporating spatio-temporal regularization of displacements.