Inclusion of multiple fragment types in the Site Identification by Ligand Competitive Saturation (SILCS) approach

Abstract

The Site Identification by Ligand Competitive Saturation (SILCS) method identifies the location and approximate affinities of small molecular fragments on a target macromolecular surface by performing Molecular Dynamics (MD) simulations of the target in an aqueous solution of small molecules representative of different chemical functional groups. In this study, we introduce a set of small molecules to map potential interactions made by neutral hydrogen bond donors and acceptors, and charged donor and acceptor fragments in addition to nonpolar fragments. The affinity pattern is obtained in the form of discretized probability or, equivalently, free energy maps, called FragMaps, which can be visualized with the target surface. We performed SILCS simulations for four proteins for which structural and thermodynamic data is available for multiple, diverse ligands. Good overlap is shown between high affinity regions identified by the FragMaps and the crystallographic positions of ligand functional groups with similar chemical functionality, thus demonstrating the validity of the qualitative information obtained from the simulations. To test the ability of FragMaps in providing quantitative predictions, we calculate the previously introduced Ligand Grid Free Energy (LGFE) metric and observe its correspondence with experimentally measured binding affinity. LGFE is computed for different conformational ensembles and improvement in prediction is shown with increasing ligand conformational sampling. Ensemble generation includes a Monte Carlo sampling approach that uses the GFE FragMaps directly as the energy function. The results show some, but not all experimental trends are predicted, and warrant improvements in the scoring methodology. In addition, the potential utility of atom-based free energy contributions to the LGFE scores and the use of multiple ligands in SILCS to identify displaceable water molecules during ligand design are discussed.

INTRODUCTION

Structure based drug design (SBDD) uses the 3D structure of a macromolecular target to discover or rationally design molecules that can bind to it with high affinity to achieve the desired biological outcome. While experimentally determined target 3D structures serve as the starting point of SBDD and are a critical element in all phases of SBDD initiatives, computational methods have played important and complimentary roles.¹ The statistical thermodynamic connection between the binding affinity and molecular configurations provides an attractive avenue for classical molecular mechanics methods in SBDD. However, computational methods are challenged by: (i) The large conformational space of the target (protein), solvent and ligands included in the calculations and (ii) the large chemical space of drug-like molecules. In an attempt to overcome these difficulties, many docking methods use the approximations of rigid protein geometries and approximate treatment of aqueous solvation to estimate the binding affinity typically of a million or more drug-like molecules, a number that is minuscule compared to the estimated chemical space of such molecules at 10⁶⁰ to 10¹⁰⁰.^{2, 3} Alternatively, there are free energy perturbation techniques in which more rigorous treatment of protein flexibility and aqueous solvation is performed, but at a significant computational cost, thereby further limiting the chemical space accessible to these related approaches.^{4, 5}

The site identification by ligand competitive saturation (SILCS) methodology,^6–9 and related methods,^10–17 approach the SBDD problem from a different direction, borrowing concepts from Fragment Based Drug Discovery (FBDD) in an attempt to solve the problems of conformational space and chemical space simultaneously. The SILCS method is exploratory in nature and involves molecular dynamics (MD) simulations of the macromolecular target in an aqueous solution of small molecules representative of chemical fragments to obtain extensive conformational sampling of both macromolecule conformation and small molecule distributions. The small molecule distributions are converted to residence probability maps of fragment atoms that are then Boltzmann transformed into a free energy representation, termed grid free energy (GFE) fragment maps (FragMaps). Notably, the GFE FragMaps are normalized for the distributions of the small molecules in solution in the absence of the macromolecule, such that they implicitly include the free-energy penalty for small molecule desolvation. GFE FragMaps can provide information about the affinity pattern of the macromolecule for different kinds of functional groups, which can be useful in various stages of SBDD as illustrated previously.⁷ Thus, the SILCS approach includes protein flexibility and aqueous solvation contributions to fragment binding by performing a series of upfront, computationally demanding MD simulations. However, once the GFE FragMaps are obtained, they may be used both qualitatively and quantitatively in a computationally efficient fashion to facilitate ligand design.

In our previous studies, benzene and propane were used as molecular probes for non-polar functionalities with explicit water used as the probe for both hydrogen bond donors and acceptors. Using that setup, we demonstrated the predictive ability of the four categories of FragMaps by recapitulating the crystallographic location of ligand functional groups of the corresponding chemical type in a dataset of 31 protein-ligand complexes.⁷ In this article, we extend the SILCS method by introducing SILCS Tier II, which includes explicit probes for hydrogen bond donors and acceptors. Seven chemically representative fragments were chosen to obtain the affinity pattern of the protein for different functionalities. The molecules are: benzene, propane, methanol, formamide, acetaldehyde, methylammonium and acetate. Having such a diverse mixture allows for competition between them, as well as for water, for macromolecular binding sites. Benzene and propane serve as probes for non-polar functionalities. Methanol, formamide and acetaldehyde are neutral molecules that participate in hydrogen bonding. Since our mapping method is atom-based, methanol and formamide serve both as probes for hydrogen bond donors and acceptors based on the 3D probability of the polar hydrogen and oxygen atoms, respectively. The positively charged methylammonium and negatively charged acetate molecules serve as probes for charged donor and acceptor functionalities, respectively. The presence of both fragments in approximately equal concentration is also important to maintain an uncharged fragment solution. In the present study, using the 7 probes, we construct 5 FragMaps representing unique chemical functionality, namely (1) generic non-polar - NGEN (benzene, propane carbons), (2) generic neutral donor - DGEN (methanol and formamide polar hydrogens), (3) generic neutral acceptor . AGEN (methanol, formamide and acetaldehyde oxygens), (4) positive donor - DPOS (polar methylammonium hydrogens) and (5) negative acceptor . ANEG (acetate oxygens). It is also possible to construct maps from the individual molecules and the functionalities present in them, resulting in 9 possibilities, but we reserve this analysis for a future study.

To evaluate the potential utility of the method in SBDD, we chose a set of 4 diverse proteins for which structural and thermodynamic data is available for multiple ligands in the literature. The proteins were Factor Xa (24 ligands), P38 MAP kinase (6 ligands), RNase A (5 ligands) and HIV protease (6 ligands). The ligands included in the present study are generally structurally diverse such that congeneric series of ligands are not investigated. Analysis focuses on both the qualitative and quantitative information contents in the SILCS FragMaps. Quantitatively, the SILCS method may be used to estimate the relative binding affinity of ligands through a scoring scheme, as is commonly performed by computational chemistry methods. In addition, the information content in SILCS may be used to estimate the individual contribution of ligand atoms to the overall binding affinity as well as the overall contribution of the different classes of functional groups to ligand binding. Finally, as the fragments are competing for water during the SILCS simulations the method intrinsically identifies water molecules that are thermodynamically unfavorable to displace upon ligand binding.^{18, 19} This additional information content in SILCS may be of further utility in ligand design.

METHODS

SILCS system setup

Protein coordinates for the studied protein-ligand complex crystal structures were used following deletion of the crystallographic ligand. The following Protein Data Bank (PDB)²⁰ structures were used to initiate the calculations: 1FJS²¹ (Factor Xa), 1OUY²² (P38 MAP kinase), 1JVT²³ (RNase A) and 1G2K²⁴ (HIV protease). Crystal water molecules were retained, as were any structurally important ions. The Reduce software²⁵ was used to place missing hydrogens and to choose optimal Asn, Gln, and His side chain ring orientations. An in-house preparation script utilized GROMACS²⁶ utilities to generate the simulation system involving protein, water and small molecules included in the simulation system. The protein was aligned based on the principal axes and centered in the simulation box, the size of which was chosen so as to have the protein extrema separated from the edge by 8 Å on all sides. An aqueous solution of the small molecules was created by overlaying a waterbox of suitable size with seven types of randomly positioned fragments at approximately 0.25 M each and deleting overlapping waters. This small molecule solution box was overlaid on the protein and the overlapping fragments and water molecules were deleted if the distance between the atoms was found to be less than the sum of their van der Waals (vdW) radii. Ten protein-small molecule-water systems were generated for each protein with each system differing in the initial position and orientation of the molecules. The seven small molecules used were benzene (benz), propane (prpa), methanol, formamide, acetaldehyde, methyl-ammonium (mamm) and acetate (acet). As done in previous implementations,⁶ repulsive inter-molecule interactions were introduced between the following pairs: benz:benz, benz:prpa, prpa:prpa, mamm:acet, mamm:mamm, and acet:acet. The latter two terms were only included for technical ease; as the same-charged groups are not expected to be found close to each other, the repulsion is not expected to perturb the interaction of these groups with the protein. Secondly, the repulsive interactions are cut-off at 8 Å, such that small molecules occupying two protein sites separated by greater than this distance would not repel each other. Analagous rectangular systems, of size 80 Å X 60 Å X 50 Å, were setup in the absence of protein as required to calculate the fragment distributions in solution. The average system volume obtained from these NPT simulations were used to calculate bulk fragment concentrations used to normalize the FragMaps.

SILCS MD simulations

All simulations were performed using the GROMACS simulation program²⁶(version 4.5). The CHARMM22 protein force field²⁷ with CMAP backbone correction²⁸ and the TIP3P water model²⁹ modified for the CHARMM force field³⁰ was used in the simulations. Small molecules (ligands and fragments) were based on the CHARMM General Force Field (CGenFF).³¹ vdW interactions were switched off smoothly in the range of 5–8 Å and the particle mesh Ewald method³² was used to treat long range electrostatics with a real space cut off of 10 Å, with the order of B-spline interpolation set to 4 and the maximum grid spacing set to be 1.2 Å. Long-range dispersion correction to the energy and pressure was applied. MD simulations were performed with the leap-frog integrator (GROMACS integrator "md") with a time step of 2 fs. During production, the Nose-Hoover method^{33, 34} was used to maintain the temperature at 298 K with the protein and the remainder of the system separately coupled to the heat bath. Pressure was maintained at 1 bar using the Parrinello-Rahman barostat.³⁵ The time constant used for temperature and pressure coupling was uniformly 1ps. The LINCS algorithm³⁶ was used to constrain water geometries and all covalent bonds involving a hydrogen atom. The system in the presence of periodic boundary conditions was minimized for 500 steps with the steepest descent (SD) algorithm.³⁷ The systems were equilibrated for 100ps during which temperature was adjusted by velocity rescaling.³⁸ During the minimization and equilibration harmonic positional restraints with a force constant of 2.4 kcal mol⁻¹ A⁻² were applied to protein non-hydrogen atoms. During production the position restrains were removed and replaced by weak restraints only on the backbone C-alpha carbon atoms with a force constant (k in 1/2 kδx²) of 0.12 kcal mol⁻¹ A⁻². This was done to prevent the rotation of the protein in the simulation box and potential denaturation due to the presence of a highly concentrated fragment solution.⁶ Solution simulations in the absence of protein were performed following the same protocol.

FragMap preparation

3D probability distributions of the selected atoms from the small molecules, called “FragMaps”, from the SILCS simulations were constructed for the following atom types: benzene carbons, propane carbons, methanol polar hydrogen, methanol oxygen, formamide polar hydrogens, formamide oxygen, acetaldehyde oxygen, methylammonium polar hydrogens and acetate oxygens. Atoms from snapshots output every 10 ps from each SILCS simulation trajectory were binned into 1 Å × 1 Å × 1 Å cubic volume elements (voxels) of a grid spanning the entire system, and the voxel occupancy for each FragMap atom type was calculated. For the purpose of normalization, a bulk voxel occupancy for each fragment type was calculated from a simulation involving only the small molecules in aqueous solution. The voxel occupancies of the 9 atom types were merged in the following manner to create the following 5 FragMap types: (1) generic non-polar - NGEN (benzene and propane carbons), (2) generic neutral donor - DGEN (methanol and formamide polar hydrogens), (3) generic neutral acceptor - AGEN (methanol, formamide and acetaldehyde oxygens), (4) positive donor - DPOS (methylammonium polar hydrogens) and (5) negative acceptor . ANEG (acetate oxygens). The voxel occupancies computed in the presence of the protein were divided by the value in bulk to obtain a normalized probability. Normalized distributions were converted to free energies via a Boltzmann-based transform of the normalized probability to yield a “Grid Free Energy (GFE)” for each fragment type T for the coordinates x,y,z, referred to as GFE FragMaps.

$${\mathit{\text{GFE}}}_{xyz}^T=\mathit{\text{min}}\{-RT{\text{log}}_e\frac{{\mathit{\text{occupancy}}}_{x,y,z}^T}{\langle \mathit{\text{bulk occupancy}}\rangle },3\}$$ (1)

All GFE values were capped at 3 kcal/mol, in contrast to our previous study where they were capped at 0 kcal/mol. FragMaps were visualized as isocontour surfaces at a GFE value of −1.2 kcal/mol, unless otherwise noted. All visualizations were prepared using Visual Molecular Dynamics (VMD).³⁹

The convergence of the FragMaps was monitored by calculating Overlap Coefficients (OC). The ten trajectories were divided into two groups (group 1: trajectories 1–5, group 2: trajectories 6–10) and FragMaps of each group were separately computed. OC relates the overlap between group 1 and group 2 FragMaps to a number between 0 and 1, with 1 reflecting completely identical maps. In all cases, OC was computed for a sub region centered on the binding pocket of size 20 Å × 20 Å × 20 Å.

$$OC=\sum _{i=1}^N\text{min}(\frac{Q_i^1}{\sum _{j=1}^N{Q}_j^1};\frac{Q_i^2}{\sum _{j=1}^N{Q}_j^2})$$ (2)

Where, N is the number of voxels in the FragMaps and Q¹_i and Q²_i are occupancies for the ith voxel from group 1 and 2 generated FragMaps, respectively. The ratios in the parantheses are computed to normalize the occupancy of each voxel by the sum of occupancies of all voxels in the corresponding FragMap. For each voxel, the smaller value (the conserved part) from group 1 and 2 is summed over all voxels to get the OC. It should be noted that the OC index does not behave linearly, such that a relatively small difference in the two distributions leads to a decrease from 1 to approximately 0.8 and values of > 0.6 indicate a high degree of similarity.

LGFE scoring

In order to calculate LGFE scores, ligand atoms were classified into FragMap types, for which an assignment map was created. The assignment map consists of a rule file which translates CGenFF atom types³¹ into the FragMap classes. A subset of atoms was not included in the LGFE calculation, such as aromatic hydrogen atoms, indicated by NCLA, since their contribution is implicitly accounted for by their parent carbon atoms. In addition to the CGenFF type, a charge criterion and a connectivity criterion were implemented to make the classification unambiguous. These additional criteria were required only for two atom types namely HGR52 and OG2P1, where specification of CGenFF type alone was not enough for classification. The rules are presented in the Supporting Information Table S1. An in-house Python implementation which reads all the FragMaps, CGenFF topology and a PDB file containing the conformations was used to calculate the LGFE scores as shown in Equations 3 and 4. As shown, the LGFE is based on a summation over all GFE FragMap types, T, and applicable atoms assigned to specific FragMap types, i_T. Two variants of the score were computed for all conformational sets. The first one, termed “unweighted” scoring, simply summed the GFE contributions of the classified ligand atoms (c_T = 1, for all T). The second variant, termed “weighted” scoring, multiplied the GFE contribution of each atom by prefactors, c_T, of 0.25, 0.75, 2, 0.3, and 0.5 for NGEN, DGEN, AGEN, DPOS, and ANEG, respectively, with the motivation for the prefactors discussed below. For each conformation k, LGFE(k) is computed as

$$\mathit{\text{LGFE}}(k)=\sum _{\mathit{\text{FragMaps}},T}{c}_T\sum _{\mathit{\text{atoms}},i_T}{\mathit{\text{GFE}}}_{x_i,y_i,z_i}^T(i_T)$$ (3)

For each conformational ensemble {k}, LGFE is then obtained as a Boltzmann average over all LGFE(k) values.

$$\mathit{\text{LGFE}}=-kT{\text{log}}_e{\langle \text{exp}(-\frac{\mathit{\text{LGFE}}(k)}{kT})\rangle }_{\{k\}}$$ (4)

The correlation of LGFE with experimental binding affinity is measured as the square of the correlation coefficient (R²). In order to quantify the ability of the method to rank order ligands by binding free energy, we use the Predictive Index (PI) metric developed by Pearlman and Charifson.⁴⁰

$$PI=\frac{\sum _{j>i}\sum _i{w}_{ij}{C}_{ij}}{\sum _{j>i}\sum _i{w}_{ij}}$$ (5)

$$w_{ij}=|E(j)-E(i)|$$

$$C_{ij}\{\begin{array}{c}\hfill -1\mathit{\text{if}}[E(j)-E(i)]/[\mathit{\text{LGFE}}(j)-\mathit{\text{LGFE}}(i)]<0\hfill \\ \hfill 1\mathit{\text{if}}[E(j)-E(i)]/[\mathit{\text{LGFE}}(j)-\mathit{\text{LGFE}}(i)]>0\hfill \\ \hfill 0\mathit{\text{if}}[\mathit{\text{LGFE}}(j)-\mathit{\text{LGFE}}(i)]=0\hfill \end{array}$$

In Equation 5 E(i) and LGFE(i) are the experimental affinity and LGFE of ligand i, respectively. By definition, PI can assume values between −1 and 1. A value of 1 implies all data points were ranked correctly pairwise, −1 implies all pairs were incorrectly ranked and 0 implies random predictions.

Generation of the ligand MD conformational ensemble

Initial ligand conformations for the calculation of LGFE scores were extracted from the corresponding co-cystal coordinate PDB files and the automated CHARMM General force-field (CGenFF) parametrization algorithm^{41, 42} was used to obtain the topology and parameters for the small molecules in the context of CGenFF.³¹ Table 1 provides the PDB IDs of the co-crystal structures. Short minimizations and MD simulations of the protein-ligand complexes were performed using the CHARMM program⁴³ to obtain conformational ensembles for LGFE scoring. Three conformational sets were generated for each ligand - (i) minimized , (ii) single-dynamics and (iii) multi-dynamics. To obtain the minimized conformation, the ligand conformation from the co-crystal structure was extracted and aligned with the protein conformation from which the SILCS simulations were initiated. The alignment was done based on optimal alignment of the backbone Cα carbon atoms in the two protein structures. The complex was minimized using the SD algorithm for 50 steps. In all visualizations presented in this work, the minimized conformation is used to depict the ligand overlap with the FragMaps. To generate the single-dynamics trajectory, the minimized conformation was subject to a 10 ps gas-phase MD simulation using Langevin Dynamics with a friction coefficient of 50 ps⁻¹, with snapshots output every 0.2 ps. During the dynamics, all protein atoms further than 8 Å from any ligand atom were restrained using a force constant of 1 kcal mol⁻¹ Å⁻². To obtain the multi-dynamics set, the same procedure was employed as for single-dynamics set, but on 40 protein conformations obtained from the SILCS simulations by selecting 4 snap shots equally spaced in time from each of the 10 trajectories.

Table 1.

Dataset of ligands used to validate the method. The four proteins and the co-crystal structure PDB IDs are indicated.

Protein	Ligand PDB IDs
Factor Xa	1EZQ49, 1F0R49, 1F0S49, 1FJS21, 1G2M50, 1KYE51, 1LQD52, 1MQ553, 1MQ653, 1NFU54, 1NFW54, 1NFX54, 1NFY54, 1Z6E55, 2BOH56, 2BOK57, 2BQ756, 2BQW56, 2CJI58, 2FZZ59, 2J2U60, 2J3460, 2J3860, 2J4I61
P38 MAP kinase	1OUY22, 1W8462, 1A9U63, 1BL763, 1DI964, 1WBW62
RNase A	1O0H65, 1O0O65, 1O0M65, 1O0N65, 1QHC66
HIV Protease	1G2K24, 1HVI20, 1HBV67, 1DMP68, 1D4L69, 1B6K70

SILCS-MC sampling

In addition to the MD sampling, sampling of the ligand was performed in the “field” of the GFE FragMaps using Metropolis Monte Carlo (MC) steps, starting from the crystallographic conformation. An in-house suite of programs was used to setup and run the MC simulations. The ligands had rotational, translational and select intra-molecular degrees of freedom. No rotational restraints were present, but the ligand center of mass (CoM) was restrained to lie within 2.5 Å of the CoM of the ligand crystal conformation using a flat bottom restraint. Intramolecular degrees of freedom consisted of rotatable bonds, which were assigned automatically. All acyclic non-terminal bonds were considered rotatable, with the exception of bonds ending in methyl or NH₃⁺ groups. The force-field terms corresponding to the intra-molecular degrees of freedom comprised of dihedral (dihe), vdW and electrostatic (elec) terms were based on the CGenFF parametrization. Due to the absence of the protein and solvent during these simulations a distance dependent dielectric (=4|r|) was used to evaluate the intramolecular electrostatic contributions to prevent their overestimation. The energy computed during the Metropolis MC was calculated as:

$$E=E_{\mathit{\text{vdw}},\mathit{\text{intra}}}+E_{\mathit{\text{elec}},\mathit{\text{intra}}}+E_{\mathit{\text{dihe}},\mathit{\text{intra}}}+\mathit{\text{LGFE}}$$ (6)

For each ligand, 10⁶ MC steps were attempted with snapshots output every 1000 steps

RESULTS

The goal of our study is to investigate the ability of the SILCS Tier-II approach to qualitatively identify chemically diverse interaction sites that can be informative in SBDD as well as quantitatively evaluate relative ligand binding affinities. We applied the approach on 4 proteins for which structure and affinity data were available in the literature. Several changes were introduced compared to our previous studies.⁷ Firstly, methanol, formamide, acetaldehyde, methylammonium and acetate were included in addition to benzene and propane in the SILCS simulations. Secondly, during calculation of the FragMaps a distance cutoff of 5 or 2.5 Å from the protein surface was not included as we did previously yielding GFE FragMaps that extend away from the protein surface. Third, we explored the effect of including multiple ligand conformations generated using MD or MC simulations to calculate LGFE scores, as opposed to using the single crystallographic geometry. Fourth, unfavorable GFEs were included in the LGFE score. Previously, all unfavorable GFE values were set to zero. This modification was made possible partly due to the FragMaps being built without distance cut-offs. For each protein, 10 trajectories, each 40ns long, were obtained and GFE FragMaps were constructed. In our previous studies,⁷ we had used the last 5ns segments of 20ns long trajectories. Our preliminary calculations with the Tier II approach indicated a larger segment of sampling time necessary due to the lower concentrations of fragments present. Accordingly, the whole 40ns segment was used for FragMap preparation, which marks the fifth modification.

Validation of the extent of convergence of the SILCS simulations in the context of the output FragMaps was performed by calculating OCs as described in Eq. 2. Table S2a in the Supporting Information shows the OC computed for the 5 FragMaps for all four proteins. The NGEN FragMaps are generally the best converged with OC values near 0.8. Barring two exceptions, the OC values for the neutral and charged donor/acceptor FragMaps is greater than 0.6. The better convergence of NGEN maps may be associated with the larger number of atoms assigned to that class of FragMaps. For example, benzene contains 6 aromatic carbons, while methanol only contains one neutral hydrogen bond donor, such that the non-polar NGEN fragments are effectively at a higher concentration versus the DGEN fragments. The low OC value of NACC FragMap for P38 MAP kinase is not significant because the region surrounding the binding site of the protein does not show a marked density of that FragMap type (Figure 2). Taking Factor Xa as an example, in Figure S2b we show better convergence by using the complete 0–40ns trajectories to calculate the OCs as opposed to the 35–40ns segment as done in our previous study of Tier I fragments. Finally, to obtain a qualitative picture of the meaning of the OC values, in Figure S1 we present the two groups of GFE FragMaps overlaid with the protein. The NGEN maps show the best visual overlap (panel a), which is consistent with the high OC of 0.83. The DGEN and AGEN FragMaps displayed in panels b and c, respectively show many regions of overlap and a few regions which are mapped by only one of the two groups. The DGEN FragMap is also displayed at a higher GFE cutoff of −0.6 kcal/mol in panel f, which shows a larger number of identified sites. The DPOS and ANEG FragMaps (panels d,e) show better overlap than DGEN and AGEN. The general observation is that surface exposed sites show better overlap than buried sites. For example, panel d shows a DPOS site in the S1 pocket (green arrow), which is identified only by group 1 FragMap. It is noted that better convergence is desirable and may be obtained through longer and/or additional simulations and enhanced sampling methods.

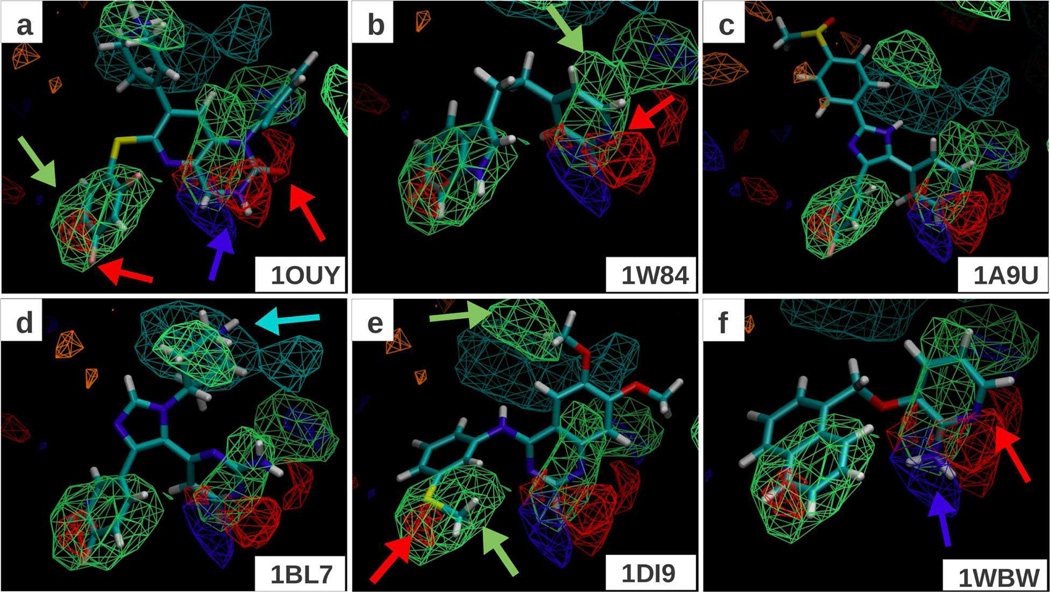
Figure 2.

FragMaps obtained for P38 Map kinase; the protein surface is not shown in order to make a clear presentation. All FragMaps are drawn at an isocontour cutoff of −1.2 kcal/mol. The 6 panels show the minimized crystal conformation of four ligands (PDB IDs indicated on bottom right). The color of the FragMaps for generic non-polar (NGEN), neutral donor (DGEN), neutral acceptor (AGEN), positive donor (DPOS) and negative acceptor (ANEG) are green, blue, red, cyan and orange respectively.

In the remainder of the results both the qualitative and quantitative utility of the Tier II Fragmaps are presented for the four studied proteins. Qualitative predictions involve the ability of the GFE FragMaps to recapitulate the location of ligand functional groups in various ligand-protein crystal structures. Quantitative estimates focus on the ability of the method to rank order ligands in accordance with experimental binding affinity. We quantify the overlap of functional groups with FragMaps based on LGFE scores, following equations 1, 3 and 4. GFE is an atom-based metric, which assigns a free energy score to a ligand atom based on its overlap with its corresponding FragMap. The LGFE metric thus does not have a formal relationship to ligand binding affinity, but may be used as an empirical score. This motivated us to explore introducing empirical prefactors specific for each FragMap type. In the weighted LGFE scheme, GFEs were divided by the number of atoms present in the small molecule used to define the corresponding FragMap. The logic behind this choice is explained in the Discussion. For example, the multiplicative prefactor for a benzene FragMap would be 1/6. For generic FragMaps an average prefactor of the composing FragMap prefactors was computed. For example, for generic non-polar FragMap the composite prefactor was (1/6 + 1/3)/2 = 0.25. The values therefore are 0.25, 0.75, 2, 0.3, and 0.5 for NGEN, DGEN, AGEN, DPOS, and ANEG. The AGEN FragMap is the exception to the above rule, which would set it at 1. Instead it was set to be 2 based on our empirical observations in terms of better predicting the Factor Xa affinities. The set of prefactors, c_T in equation 3, determines the relative contribution of the different FragMap types to the LGFE. For each of the ligand datasets analyzed below, we report both the unweighted and weighted LGFEs. In the former the c_T values are uniformly set to unity. Final quantitative analysis involves determining the correlation between experimental binding affinities for the studied ligands and their weighted and unweighted LGFE scores.

Factor Xa

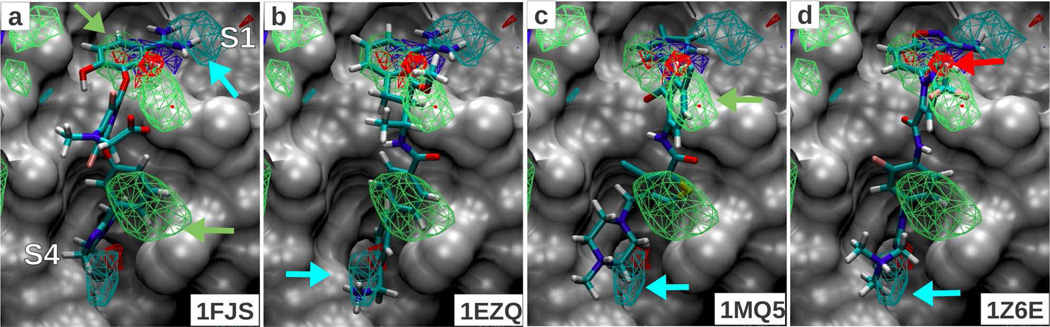
Qualitative analysis was performed based on visual inspection of Figure 1 which shows selected regions of the protein surface of Factor Xa overlaid with the FragMaps and four representative ligand conformations from structures 1FJS, 1EZQ, 1MQ5, 1Z6E in panels a, b, c and d, respectively. Panels a and b show a positively charged benzamidine group of the ligands in the S1-pocket, which is a common functional group across Serine protease inhibitors. The positive donor (DPOS) FragMap (cyan) maps this interaction correctly as shown by the cyan arrow in panel a. In addition, there is another DPOS region identified in the S4-pocket, which shows overlap with the ammonium group in the 1EZQ, 1MQ5 and 1Z6E ligands (lower region of panels b,c,d). The generic non-polar (NGEN) FragMap identifies three regions, two of which are exploited by all four ligands shown here through aromatic ring interactions in the S1 and S4 pockets, indicated in Figure 1a. An additional NGEN region present between the S1 and S4 pockets marked by the green arrow in panel c shows overlap with the phenyl ring in the 1MQ5 ligand and the trifluoro group in 1Z6E ligand. A generic acceptor (AGEN) interaction site shown by the red arrow in panel d overlaps with the trifluoro group as well, which could act as an acceptor. These observations show that the locations of different types of functional groups in ligands bound to Factor Xa are captured by the Tier II FragMaps.

Figure 1.

FragMaps overlaid on the protein surface of Factor Xa crystal conformation (PDB 1FJS); protein atoms occluding the view of the binding pocket were removed for a clear visualization. All FragMap contours are displayed at a cutoff of −1.2 kcal/mol. The four panels show the minimized crystal conformation of four ligands (PDB IDs indicated on bottom right). The color of the FragMaps for generic non-polar (NGEN), neutral donor (DGEN), neutral acceptor (AGEN) and positive donor (DPOS) FragMaps are green, blue, red and cyan, respectively.

Quantitative analysis for the 24 Factor Xa ligands is presented in Table 2 and Figure S2 of the supporting information. Experimental affinity data was obtained from the data compiled by Abel et al.¹⁸ LGFEs were computed for the dataset using the minimized, single-dynamics, multi-dynamics and SILCS-MC conformational sets using both the unweighted and weighted scoring schemes. Correlation plots of the unweighted LGFE scoring are shown in panels a, c, e and g of Figure S2. Panels b, d, f and h show the weighted LGFE scores computed for those sets. Analysis shows the predictions to be poor based on minimization alone. Improvements are seen when multiple conformations are introduced via MD simulations. The SILCS-MC sampling results in further improvement. Comparison of the unweighted and weighted scores shows the weighted LGFE scores to systematically better predict the experimental trends as evidenced by the correlation R² value (Table 2). While the R² values are relatively poor, the predictive indexes may be considered reasonable, with the value for the SILCS-MC sample with unweighted and weighted LGFE being 0.43 and 0.50, respectively. This is, in part, due to the ranking of pairs that are well separated in experimental values being better predicted than the ones that have similar values. The cluster of data points between experimental values of −10 to −12 kcal/mol represent a difficult set of affinities to rank as they are very close to each other.

Table 2.

Correspondence between computed LGFEs and experimental affinities for the four proteins quantified in terms of (a) R² and (b) Predictive index (PI) values. Correlation metrics are computed for the 4 conformational sets of minimized, single-dynamics, multi-dynamics and SILCS-MC, using both the weighted and unweighted LGFE scoring schemes.

a) R2	Minimized		Single-dynamics		Multi-dynamics		SILCS-MC
Protein	unweighted	weighted	unweighted	weighted	Unweighted	weighted	unweighted	weighted
Factor Xa	0.02	0.09	0.08	0.14	0.08	0.28	0.13	0.33
P38MK	0.03	0.17	0.05	0.16	0.02	0.09	0.73	0.39
Rnase A	0.06	0.45	0.34	0.64	0.65	0.43	0.79	0.64
HIV Protease	0.05	0.20	0.63	0.61	0.55	0.68	0.23	0.62
Average R2*	0.04	0.24	0.16	0.31	0.25	0.27	0.55	0.45

b) PI	Minimized		Single-dynamics		Multi-dynamics		SILCS-MC
Protein	unweighted	weighted	unweighted	weighted	Unweighted	weighted	unweighted	weighted
Factor Xa	0.13	0.20	0.31	0.34	0.32	0.49	0.43	0.50
P38MK	0.10	0.18	0.19	0.50	−0.02	0.50	0.91	0.57
Rnase A	0.05	0.50	0.66	0.73	0.73	0.50	0.73	0.73
HIV Protease	−0.01	−0.59	−0.57	−0.66	−0.64	−0.83	−0.60	−0.81
Average PI *	0.10	0.29	0.39	0.53	0.34	0.50	0.69	0.60

^*The average values indicate the trend, but do not include HIV Protease data as the predictions are incorrect.

P38 MAP Kinase

To judge the predictability of the FragMaps in the context of P38 alpha MAP Kinase (P38MK), a set of 6 ligands was selected from the PDB. P38MK is known to exhibit extraordinary flexibility in the ATP-binding site resulting in two well characterized family of conformations known as DFG-in and DFG-out.^{44, 45} Since the 1OUY structure is from the DFG-in family, and 40 ns of MD simulation time is not adequate to permit transitions between the two different states, co-crystal structures to validate our method were chosen to be in the DFG-in family only. 6 such structures with affinity data in the form IC₅₀ values reported in the PDB were thus obtained and are indicated in Table 1. Figure 2 shows the FragMaps overlaid with these ligands. The non-polar FragMaps identify a few regions that are matched by aromatic rings of all the inhibitors. An aromatic group common to all ligands is located in the site shown in panel a by a green arrow. Overlapping with this is a hydrogen bond acceptor site (red arrow on the left side of panel a), which overlaps with the fluorine atom shown in panels a, c and d. In panel e, the acceptor region is occupied by a sulfur atom, which acts as an acceptor. Other hydrogen bond donor and acceptor regions identified by blue and red arrows shown in panel a match the location of donor and acceptor atoms incorporated in the aromatic rings of all inhibitors. Finally, the positive donor FragMap site is matched by the ligand shown in panel d.

Table 2 includes the P38MK correlation results and Figure S3 in the Supporting Information presents the correlation plots of the experimental affinities, computed from IC₅₀ values, versus the LGFE scores. LGFE based on minimization alone yields no significant correlation though it predicts the trend for 4 out of the 6 inhibitors (Figure S3), but overestimates the affinity of the two ligands with the lowest affinities (1WBW, 1W84). Inclusion of additional ligand conformations in the single-dynamics set marginally improves the correlations (Table 2). Panels (c,d) and (e,f) in Figure S3 refer to the ligand conformations obtained from dynamics with single and multiple protein conformations, respectively. The problem observed in the minimized structures is present in these large ensembles as well. LGFE computed from the SILCS-MC sampling shows improvement both when using the unweighted and weighted scoring schemes (Table 2 and Figure S3g,h) with the predictive index for the SILCS-MC sample with weighted LGFE being 0.57. Interestingly, unlike Factor Xa, the unweighted scoring scheme performs better than the weighted with a predictive index of 0.91.

RNase A

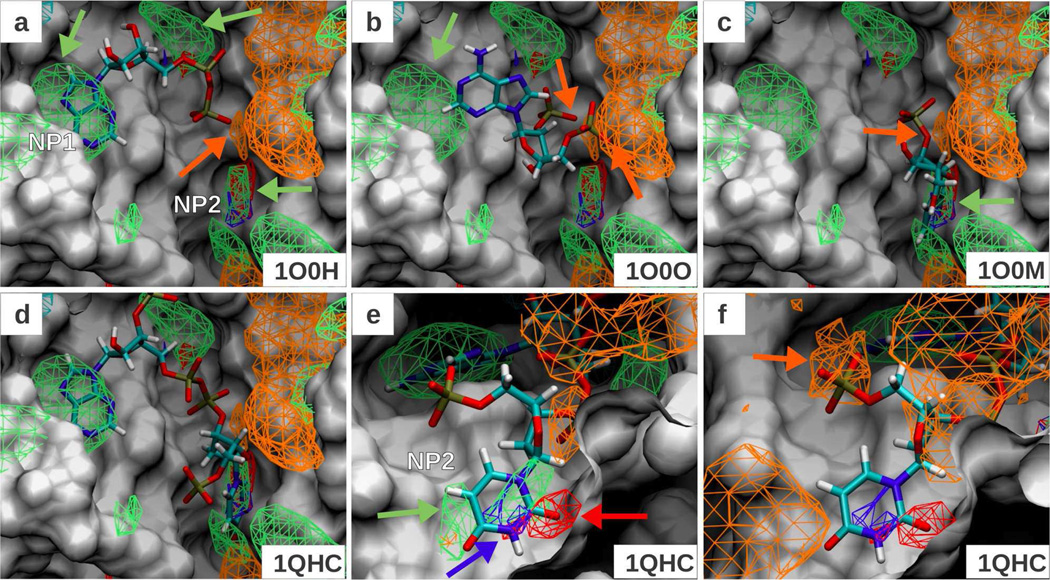
To judge the predictability of the FragMaps, a set of 5 ligands bound to RNase A was selected from the PDB. Figure 3 shows the FragMaps overlaid with four of the five ligand conformations. The GFE cutoff of the ANEG FragMap was increased from −1.2 to −0.8 kcal/mol in order to show the overlaps. Three non-polar pockets are identified in the binding site, which are shown in panel a by green arrows. Two of them, labeled “NP1” and “NP2” in the same panel are pockets that make contact with RNase A ligands. In the 1O0H ligand (5'-ADP) shown in panel a, NP1 is occupied by the adenine base. The terminal phosphate overlaps with the negative acceptor FragMap region shown by an orange arrow. The binding mode of 1O0O ligand (2',5-ADP) shown in panel b is similar to 5'-ADP, but the adenine base no longer resides in the NP1 site. Secondly, both phosphate groups show overlap with the negative acceptor FragMap. The binding modes of the 1O0M ligand (uracil-2'-phosphate) shown in panel c is very similar to that of 1O0N (uracil-3'-phosphate; not shown). Both ligands place the uracil base in the NP2 non-polar site and the single phosphate group in them shows overlap with the negative acceptor FragMap as pointed by the orange arrow in panel c. Finally, the 1QHC ligand shown in panel d combines functionalities from these other ligands and extends from NP1 to NP2, occupying the binding pocket fully. The uracil base, which is common to 1O0M, 1O0N and 1QHC ligands, binds in a very similar orientation in all cases. Taking the 1QHC ligand as an example, we show another view of the ligand to highlight the overlap of the uracil base with FragMaps in panel e, where acceptor and donor maps are shown to overlap with the ligand atoms having those functionalities. The ANEG maps at the displayed cutoff of −0.8 kcal/mol do not show overlap with many of the phosphate groups in the ligands. When the GFE cutoff is further reduced to −0.6 kcal/mol, the ANEG FragMap now overlaps with 2’ phosphate group of the 1QHC ligand, as shown in panel f. This is an example of how FragMap contour levels can be adjusted during visualization to identify additional sites of lower affinity.

Figure 3.

FragMaps overlaid on the protein surface of Rnase A crystal conformation (PDB 1JVT). All FragMap contours are displayed at a cutoff of −1.2 kcal/mol, except the NGEN, which is shown at −0.8 kcal/mol. Panels a-d show the minimized crystal conformation of the four ligands (PDB IDs indicated on bottom right). Panel e shows the 1QHC ligand in a different orientation than shown in d. Panel f shows the same data as e, but with ANEG FragMap cutoff at −0.6 kcal/mol. The color for generic nonpolar (NGEN), neutral donor (DGEN), neutral acceptor (AGEN), positive donor (DPOS) and negative acceptor (ANEG) FragMaps are green, blue, red, cyan and orange, respectively.

Included in Table 2 are the correlation coefficients and predictive indices for the RNase A dataset, with the correlation plots shown on Figure S4. The LGFEs computed using the minimized ligand conformations show poor correlation with experiment, although improvements are obtained with GFE weighting. The dynamics sets perform significantly better in most cases. Consistent with the previous proteins, SILCS-MC ensemble provides good correlation at an R² of 0.64 and a predictive index of 0.73 in the weighted scoring scheme. As with P38 MAP kinase, the unweighted scoring scheme with an R² of 0.79 and a predictive index of 0.73 performs better than the weighted one. The relatively poor performance of the minimized set highlights the importance of sampling in our scoring method. A closer look at the 1O0O ligand (2',5-ADP), which is predicted to be highly unfavorable in the minimized set reveals the adenine base not overlapping with the non-polar NP1 site (Figure 3b). An examination of the crystal packing of this structure revealed close contacts of the adenine base of the ligand with an adjacent protein molecule in the crystal envirionment, which is not the case for the very similar 1I0H ligand (data not shown). This is consistent with the fact that the 1O0O ligand shows the maximum deviation over all ligands from the crystal conformation during the SILCS-MC simulations, reaching values up to 7 Å. The RMSD with respect to the crystal conformation as a function of MC steps is presented in Figure S6 of the Supporting Information for all ligands. This observation further emphasizes the importance of including ligand conformational sampling in our approach.

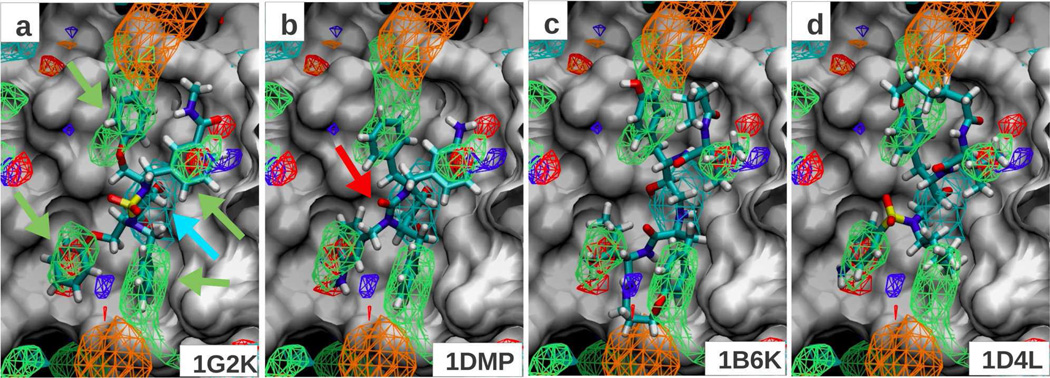
HIV protease

To judge the predictability of the FragMaps on HIV Protease, a set of 6 ligands was selected from the PDB (Table 1). The FragMaps overlaid with the 6 ligand conformations are shown in Figure 4. Four non-polar pockets are identified and are indicated by the four green arrows in Figure 4a. Panels a-d show these four pockets being occupied by aromatic/aliphatic groups of 4 representative ligands. The identification of these 4 pockets is consistent with the same regions being identified using the Tier-I SILCS in our previous study (Figure 8 in Raman et al.⁷). Two additional regions in the binding pockets make thermodynamically important interaction with ligands as judged by experimental affinity measurement following chemical modification.⁴⁶ The “bottom” of the pocket is lined with two Asp residues and acts as a site for accepting hydrogen bonds from the ligands. The “top” of the pocket on the other hand has two Ile residues in the flap region, which can act as a backbone H-bond donor either directly (PDB 1DMP) or through a water-mediated interaction (PDB 1G2K). In our previous study, consistent with these observations from the literature, we found the bottom and top of the binding pocket to be highly occupied by hydrogen bond donor and acceptor FragMaps, respectively. Using the Tier II fragments, we observe a positive-donor (DPOS) FragMap at the bottom of the pocket (Figure 4a, cyan arrow), which is at odds with most inhibitor atoms having a neutral donor classification; most inhibitors analyzed in this study place an alcohol hydrogen in the pocket and one ligand places an amine group. The neutral donor (DGEN) FragMap is not visible in the pocket even after reducing the isocontour cutoff value to −0.3 kcal/mol. One reason for this discrepancy could be the observation that only one of the Asp residues has been predicted to be in the negatively charged ionization state in the presence of an inhibitor⁴⁷ as opposed to both in the apo-state as used in our simulations. The top of the pocket displays a generic acceptor (AGEN) density upon increasing the cutoff from −1.2 to −1 kcal/mol (not shown). In addition, a water oxygen FragMap occurs in the same site at a GFE cutoff of −0.7 kcal/mol (not shown), suggesting competition between acceptors and water.

Figure 4.

FragMaps overlaid on the protein surface of HIV protease crystal conformation (1G2K); protein atoms occluding the view of pocket were removed from the visualization. All FragMap contours are displayed at a cutoff of −1.2 kcal/mol. The panels show the minimized crystal conformation of 4 ligands (PDB IDs indicated on bottom right). The color for generic non-polar (NGEN), neutral donor (DGEN), neutral acceptor (AGEN), positive donor (DPOS) and negative acceptor (ANEG) FragMaps are green, blue, red, cyan and orange, respectively.

Predictive indices for the HIV protease systems are included in Table 2 and Figure S5 plots the experimental affinities, computed from K_i values, versus the LGFE values. The correlation coefficients shown in Table 2 are not relevant because the predictions are anti-correlated with experimental affinity as shown by the negative predictive indices. Clearly, the LGFE scores in this case do not predict the experimental trends in affinities. Since the correlation does not improve with increasing sampling, the ligand geometries are unlikely to be the source of the poor predictions. Qualitatively, the FragMaps identify the non-polar and H-bond acceptor interactions, but not the neutral donor interactions expected in the bottom of the pocket. This result points to a limitation of the scoring function and is elaborated in Discussion.

DISCUSSION

The SILCS Tier-II approach applied to the 4 proteins resulted in their affinity pattern for non-polar, neutral and charged donors and acceptor functional groups based on the GFE FragMap representation. Overall, the FragMaps captured crystallographically identifed interactions of functional groups in ligands with the protein as shown in Figures 1–4. The significance of the mapped interaction sites is evidenced by the placement of functional groups of similar chemical type as the FragMaps in those sites across multiple ligands. For example, two of three non-polar sites identified in the Factor Xa binding pocket are occupied by almost all 24 ligands by an aromatic group and the third one is similarly occupied by many, though not all, of the ligands. Similar observations can be made for P38 MAP Kinase and HIV protease.

While validation of the methodology is based on the GFE FragMaps recapitulating the location of functional groups on known ligands, the location of FragMaps beyond the ligands should be noted. For example, in the upper left corner of the Factor Xa maps (Figure 1) a NGEN region is present, suggesting that the addition a non-polar group to the benzene ring may improve affinity. In another example, with P38MK 1BL7 (Figure 2d) there is a generic nonpolar FragMap indicated beyond the amine of the 2-aminopyrimidine group on the right side of the panel. This is qualitative information that can be used to direct ligand design. Indeed, in the P38MK 1OUY (panel a) structure this region is occupied by a phenyl ring and we note that the experimental affinity of the 1OUY ligand is −0.9 kcal/mol more favorable than that of 1BL7, suggesting that the GFE FragMaps are of utility to qualitatively direct ligand design. The potential modifications may then be quantitatively assessed via the calculation of LGFE. For example, the ΔLGFE (unweighted) computed using the multi-dynamics and SILCS-MC conformational sets for this pair is −6.2 and −3.1 kcal/mol, thus predicting the trend. However, the analogous values for the weighted ÄLGFE are −1.2 and 3.0 kcal/mol, suggesting potential limitations in that scoring method. The ability of FragMaps to qualitatively recapitulate the location of functional groups in known ligands as well as inform lead optimization emphasizes the utility of the approach in SBDD.

The choice of the probe molecules is also validated by the many non-overlapping FragMaps at the significant cutoff of −1.2 kcal/mol, which is selected based on 2kT energy. The S1-pocket in Factor Xa shows a marked density of DPOS FragMap near the catalytic Asp residue (Figure 1a; cyan arrow) in agreement with the presence of a positively charged group in many ligands. Another example is the presence of neutral donor and acceptor densities in P38MK pocket (Figure 2a; blue and red arrows, respectively) as opposed to that of charged probes, which is in agreement with the neutral donor and acceptor ligand atoms located in that region. The RNase A binding pocket on the other hand shows mostly ANEG charged acceptors among all polar probes in agreement with the presence of phosphates of the ligands. This distinguishing ability of the FragMaps between different polar classes is not just due to the nature of the protein sites but also due to the small molecule desolvation penalty that is included in our method by design.

The ability to visualize the FragMaps at different GFE values allows for the visual inspection of regions with differential affinities for a specific fragment type. Visualization based on GFE values more favorable than −1.2 kcal/mol identifies high affinity sites for a particular fragment type, while sites with less favorable affinity may be observed contouring the GFE values at levels less favorable than −1.2 kcal/mol. Indeed, it is possible to visualize regions that are unfavorable for a given fragment type by contouring the FragMaps by positive GFE values.

Fragment competition with bound water

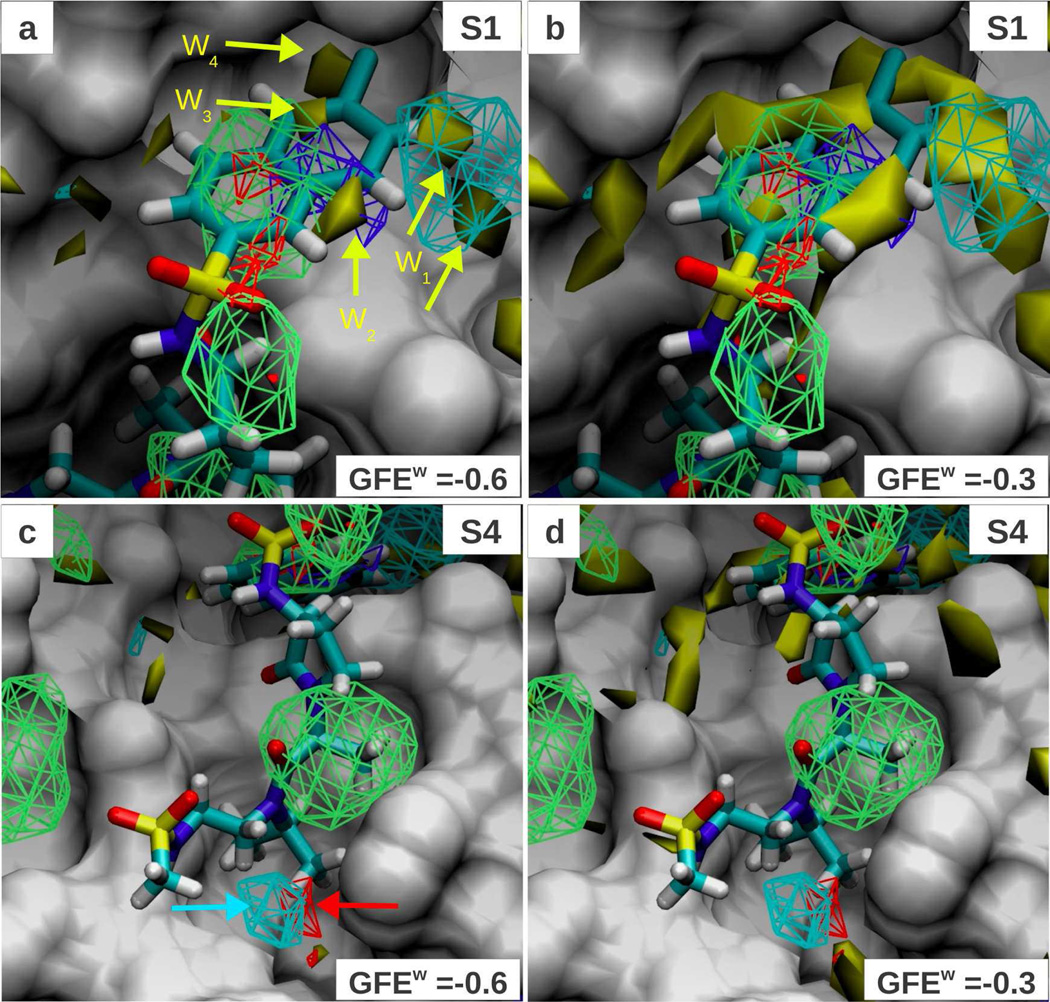
One of the key aspects of protein-ligand interactions is the displacement of water from the binding site upon ligand binding. An important step towards understanding this phenomena was the development of inhomogeneous solvation theory (IST),⁴⁸ which has been extended into a scoring function to direct ligand design.¹⁸ In that approach, high occupancy water sites are characterized as either favorable or unfavorable for displacement by a prospective ligand based on the excess energy, entropy or both. One of the assumptions is that the free energy cost of water displacement is the governing factor driving ligand binding and is enough to predict affinity. This approach, without accounting for other contributions, does not consider the chemical group that will replace the water molecule(s) at those sites. In principle, the SILCS Tier II approach should provide this information due to the inclusion of explicit water in the simulations, such that the small molecules in the SILCS simulations have to compete with water to favorably interact with regions on the protein surface. To evaluate this hypothesis, we calculated a FragMap corresponding to the occupancy of water oxygen atoms using the same approach as applied for other FragMaps. Figure 5 plots the water oxygen FragMap (yellow solid contour) at cutoffs of −0.6 kcal/mol (panels a, c) and at −0.3 kcal/mol (panels b, d) and shows pockets S1 (panels a, b) and S4 (panels c, d) of Factor Xa. The yellow arrows in panel a point to favorable water binding regions. The sites W1, W2 and W3 are favorable regions for water, but are overlapped by DPOS, DGEN and NGEN FragMaps, respectively at a GFE < −1.2 kcal/mol. This indicates that these functional groups can effectively compete with those water sites. The two W1 sites are adjacent to the catalytic residue Asp189 and lie approximately in the same location as the 3 sites previously identified to be enthalpically unfavorable to displace (Figure 2 in Abel et al.¹⁸). Consistent with this observation is the lack of overlap of the DGEN maps with the W1 sites, indicating that neutral donors cannot favorably compete with water for that site. However, the DPOS FragMap does overlap with region W1, and identifies this site to potentially result in an affinity gain when a positively charged group is placed into this region, but not a neutral donor. Indeed, this region in the S1 pocket is contacted by the positively charged amidinium groups in a large number of Factor Xa ligands as seen in Figures 1a and b. Similarly W2 and W3 are sites that can be favorably displaced by a neutral donor or non-polar group. The fact that these water sites are occupied by many of the crystallographic ligands and are overlapped at a higher affinity (<−1.2 kcal/mol GFE) by the probe fragments shows the ability of SILCS to locate displaceable water sites. Figure 5b shows the same data with the only difference being water oxygen FragMap displayed with a GFE cutoff of −0.3 kcal/mol, which reinforces the fact that the water densities even at a low cutoff in the non-polar ring system of the inhibitor are replaced by FragMap occupancies (NGEN, DGEN), showing the ability of the maps to point to displaceable waters by competition.

Figure 5.

FragMaps overlaid on the protein surface of Factor Xa crystal conformation (PDB 1FJS); protein atoms occluding the view of the binding pocket were removed for clear visualization. All FragMap contours are displayed at a cutoff of −1.2 kcal/mol. The water oxygen FragMap is displayed at −0.6 kcal/mol cutoff in panels a and c and at −0.3 kcal/mol in panels b and d, and is shown as yellow solid contour. Panels a and b show a close-up view of the S1 pocket and panels c and d show the S4-pocket. The ligand from PDB 2J4I is shown to demarcate the binding site. The color of the FragMaps for generic non-polar (NGEN), neutral donor (DGEN), neutral acceptor (AGEN) and positive donor (DPOS) FragMaps are green, blue, red and cyan, respectively.

Region W4 on the other hand is predicted to be a “stable water” based on the absence of any overlapping FragMaps, which is at odds with the WaterMap prediction. A large number of ligands in the dataset place a chlorine atom at the W4 site (site 12 in Figure 2 from Abel et al.¹⁸), which is predicted to be both enthalpically and entropically unstable by IST. There could be many reasons behind the fragments not displacing water at this site : (i) the shape of the fragments being not amenable to occupying this site (eg. Benzene), (ii) the site being very buried in the protein such that 40ns of MD may not be long enough to exchange the water with a fragment, (iii) the water getting more stabilized (compared to apo) owing to the presence of fragments nearby, as opposed to a pure water environment in WaterMap calculations, or (iv) contributions from changes in protein conformation that are included in SILCS and may play a role in water binding energetics.

In the example of the S4 pocket, due to its hydrophobic nature, we observe the FragMaps to significantly out compete water. This is indicated by the lack of water FragMaps overlapping with the small molecule FragMaps as shown in panels 5c and d. The red and cyan arrows in panel c point to AGEN and DPOS densities, respectively. Based on ligand atom overlap for ligands in PDBs 2J4I and 1MQ6, we determined this region to coincide with WaterMap identified sites 13, 1 and 20 reported in Abel et al.¹⁸, which are predicted to be favorably displaced by the method. This finding is further corroborated in panel d where even at GFE cutoff of −0.3 kcal/mol, the water oxygen density barely contacts the visible AGEN FragMap region. The AGEN and DPOS FragMaps thus correctly identify these sites to be more favorably occupied by fragment or ligand atoms than water. These two examples show that in addition to identifying the favorable regions for water displacement, FragMaps could suggest the chemical composition of the substituting group in a prospective ligand.

Exploration of surface buried sites

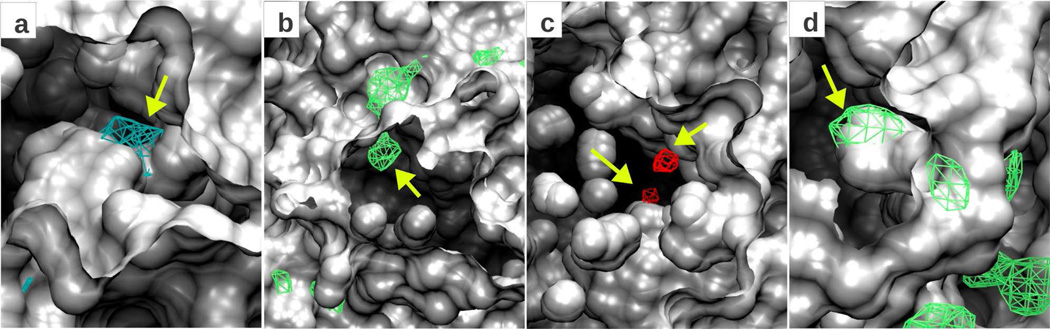
The ability of the SILCS methodology to identify binding regions below the surface of the protein has been previously reported.⁹ In Figure 6 we show several examples where this is observed using the Tier II fragment set, by overlaying the FragMaps with the protein surface representation based on the structure used to initiate the SILCS simulations. Panel a shows the S1 pocket of Factor Xa overlaid with the DPOS FragMap, where the methyl ammonium molecules have penetrated the pocket, which is associated with conformational flexibility of the catalytic aspartate. Panel b shows the NGEN FragMap at another region of Factor Xa having significant occupancy at a site that is buried in the apo-structure. Panels c and d show two additional such examples for P38 MAP kinase for FragMaps AGEN and NGEN, respectively. These observation indicate the ability of the method to sample conformations of pocket different from the initial conformation, thereby identifing potential binding pockets that would not be evident from analysis of the crystal structure alone.

Figure 6.

FragMaps penetrating the protein surface. Presented are Z-clipped protein surface representations such that the central regions of the figures that include the FrapMaps are on the interior of the protein based on the starting conformation used in the SILCS simulations. (a) Factor Xa with DPOS FragMap, (b) Factor Xa with NGEN FragMap, (c) P38MK with AGEN FragMap and (d) P38MK with NGEN FragMap. All FragMap contours are displayed at a cutoff of −1.2 kcal/mol. Yellow arrows point to buried sites identified by the FragMaps.

Quantitative scoring

In addition to qualitative mapping, we attempted to predict quantitative trends by using the LGFE metric to predict experimental binding affinities using a dataset of ligands for the 4 proteins. In the present study, we did not make attempts to choose congeneric ligands because this problem may be addressed by methodologies such as Free energy perturbation (FEP).⁴⁰ However, FEP methodologies are not practical for absolute free energy calculations for large datasets. For this important problem, we think the SILCS based scoring can attempt to fill the gap between computationally-demanding FEP methods and highly approximate docking-scoring approaches. The choice of an extremely diverse ligand set also poses an additional problem for validation and that is the availability of accurate experimental data. Ligands that are not from congeneric series are typically studied in different laboratories, and affinity measurement experiments are carried out under different conditions and practices. However, within our chosen datasets there exist ligands with large differences in affinities increasing the confidence in the experimental data and allows us to use the datasets for method validation. Indeed, we observe better predictability of larger experimental affinity differences than smaller, which is captured by the predictive index metric, as seen for Factor Xa. The central assumption behind the use of the LGFE score as a sole predictor of binding affinity is that the interactions of functional groups with the target as mapped by isolated fragments are a dominant contributor to affinity. We note here that LGFE is not a predictor based purely on the enthalpy of the bound state, as the GFEs include the desolvation penalties of the fragments as well as of the protein and include changes in conformational mobility of the protein and loss of translational and rotational degrees of the small molecules. However, LGFE does not consider the contributions of strain energy and configurational entropy of the ligands to the binding free energy and therefore departs from the rigorous statistical thermodynamics formulation of binding affinity.⁵ The wrong predictions obtained for the HIV protease may be due to the limitation of the assumption of idealized interactions predicting affinity, as well as by difficulties associated with treatment of the ionization of the Asp residues located in the binding pocket and possible difficulties associated with sampling the partially occluded active site of the protein.

The GFE is influenced by the number of atoms present in the fragment and the amount of smearing of the probability distributions, which is dependent on the nature of the binding pocket. Secondly, during the LGFE calculation, the GFEs of each atom is simply added, which may result in over counting, because each voxel in principle implicitly contains the probability of the full fragment being present in the pocket. The empirical GFE prefactors were thus introduced to attempt to correct for these effects. The rationale behind the prefactors was that fragments with a larger number of probe atoms (such as benzene) would result in overly favorable GFEs due to multiple atoms being close together in space, and thus resulting in higher probability voxels than fragments with few probe atoms (eg. six benzene carbons versus the single acetaldehyde oxygen). However, ligand functional groups may present these functionalities with different number of atoms (benzene and naphthalene, for example) and a uniform prefactor within a FragMap type may not be appropriate. Therefore, we used an empirical analysis of the 24 ligand dataset of Factor Xa to adjust our choice of prefactors, which resulted in an adjustment of the AGEN prefactor from 1 to 2. We note that automated fitting of prefactors did not result in predictive models. While the prefactors result in modest improvements in predictions for Factor Xa ligands when calculated for all conformational sets, for other proteins, the results are ambiguous. For example, for the SILCS-MC ensemble of ligands of P38MK and RNase A, the predictive indices obtained with unweighted scoring are significantly higher than the weighted scoring. However, for RNase A the weighted scoring method performs better for the minimized and single-dynamics sets. These observations highlight the limitations in our scoring scheme and warrant further investigation. The possibility of improving the scoring function by supplementing it with molecular mechanics terms may represent a potential solution to this problem.

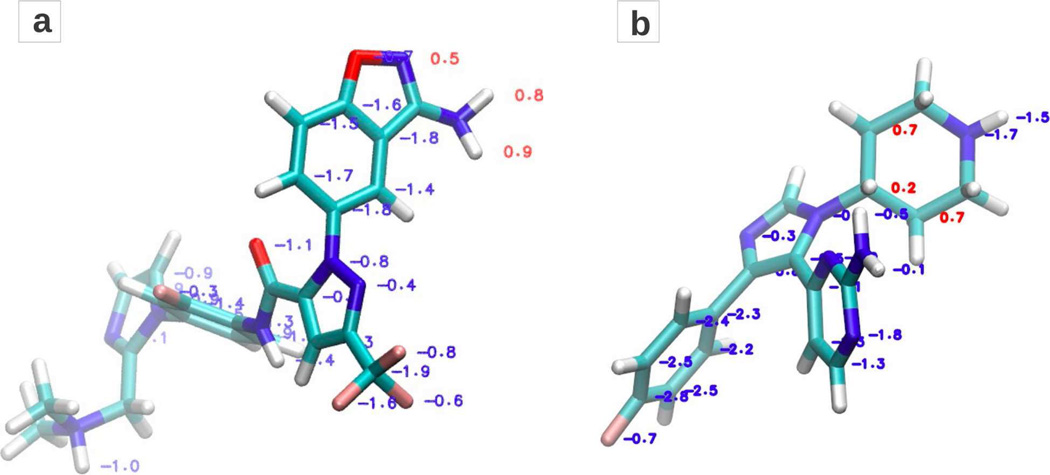
The atom-based nature of the LGFE scoring approach has the benefit of predicting parts of ligands that contribute favorably or unfavorably to ligand binding. Figure 7 shows two example ligands 1Z6E of Factor Xa and 1BL7 of P38 MAP kinase with Boltzmann averaged GFE values over the multi-dynamics conformational set plotted for each classified atom. The average GFE(a) for each atom a over k conformations in the set is computed as follows.

$$\mathit{\text{GFE}}(a)=\frac{\sum _k\mathit{\text{GFE}}(k,a)\text{exp}(-\mathit{\text{LGFE}}(k)/kT)}{\sum _k\text{exp}(-\mathit{\text{LGFE}}(k)/kT)}$$ (7)

Where, GFE(k,a) is the GFE of atom a in conformation k. GFE values plotted in red color show atoms which overlap with unfavorable regions of the FragMap of the similar chemical type and thus regions that are not contributing to binding but may have a role in acting as a scaffold between moieties on the ligand that do make favorable contributions to binding. In addition, such regions could potentially be modified to result in increased affinity. For example the amine group in 1Z6E ligand occupies a sub-region in the S1 pocket, which has exclusively a DPOS density. Being a neutral donor group, the GFE(a) of the donor atoms is calculated to be unfavorable. Similarly, the aliphatic carbons in the 1BL7 ligand of P38MK are identified as potential sites of modification for increased affinity because that region is not populated with the non-polar NGEN FragMap. In a more general sense, analysis of the atom GFE scores allows for identification of atoms and regions of the ligands that make favorable versus unfavorable contributions to ligand binding, information that can be of utility for SBDD.

Figure 7.

Boltzmann averaged Grid Free Energies (GFE) shown for the atoms comprising ligands from PDB structures (a) 1Z6E and (b) 1BL7 of proteins Factor Xa and P38 MAP kinase, respectively. Favorable GFE values are displayed in blue and unfavorable in red.

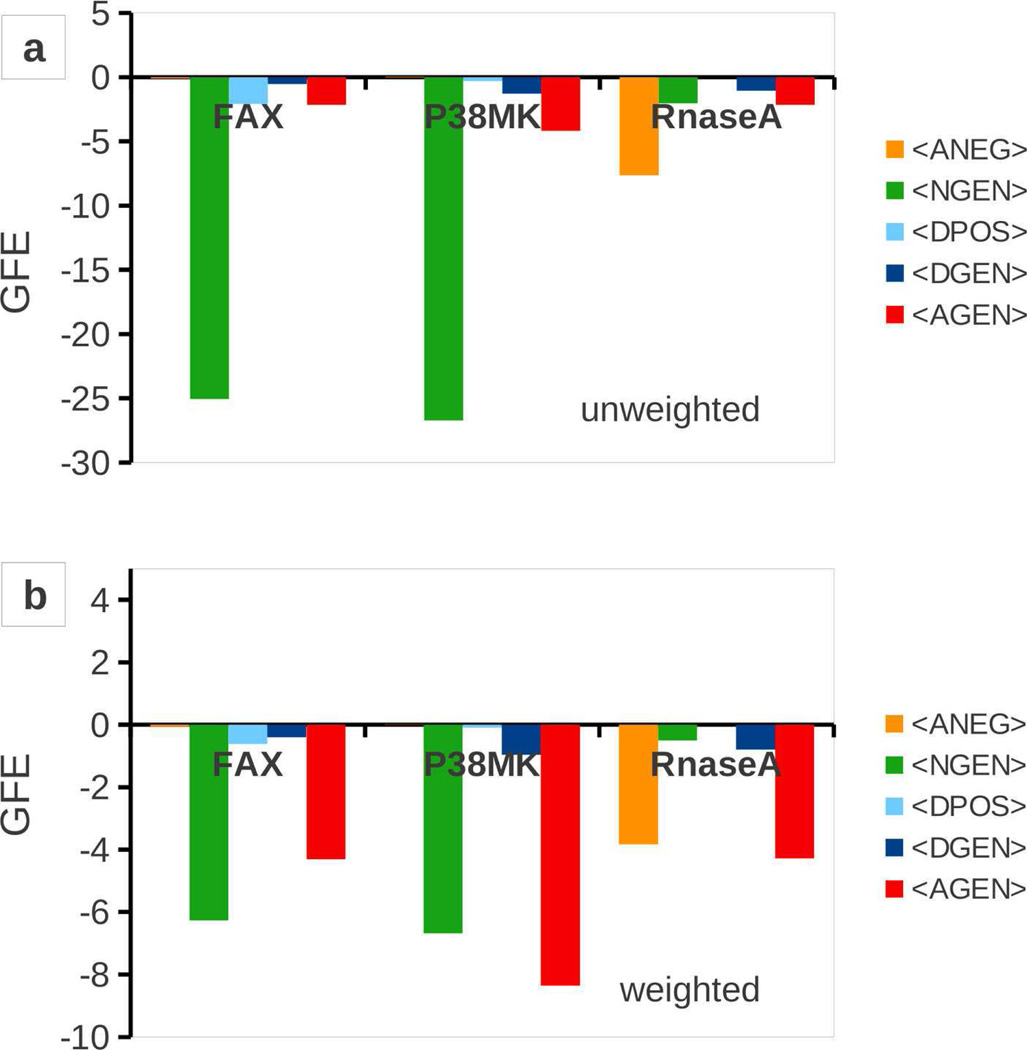
In addition to the GFE contribution of individual atoms in ligands to the binding affinity, the contributions of the different FragMap types to LGFE may be informative for ligand design (Figure 8). To that end, we computed the average of the GFE contributions from the different FragMap types T, over all ligands analyzed for each protein separately.

$$\langle {\mathit{\text{GFE}}}^T\rangle =c^T{\langle \frac{\sum _k{\mathit{\text{GFE}}}^T(k)\text{exp}(-\mathit{\text{LGFE}}(k)/kT)}{\sum _k\text{exp}(-\mathit{\text{LGFE}}(k)/kT)}\rangle }_{\mathit{\text{ligands}}}$$ (8)

Where, GFET(k) is the sum of GFEs of all atoms classified into FragMap type T in conformation k. Presented in panel a are the average unweighted <GFE^T> (c^T=1, for all T) calculated from the SILCS-MC ensemble separately for each FragMap type, with the average computed separately over the 3 different ligand sets of Factor Xa, P38 MAP kinase and RNase A. The extremely favorable values of NGEN reflects the dominant contributions of the non-polar atoms to ligand binding. For Factor Xa, this arises from the two heteroaromatic ring systems present in most ligands in the set. P38 MAP kinase follows this trend with a slightly more pronounced AGEN contribution. On the other hand, the LGFE of RNase A ligands is dominated by ANEG owing to the phosphate groups in the ligands. Panel b shows the weighted contributions. Notable is the overall reduction in the contributions in the scale of the plot, with the trends generally being similar. The prefactor (c^T) of 0.25 for the NGEN FragMap brings the dominating contribution lower in the weighted LGFE. The AGEN prefactor of 2 makes the FragMap contribution more significant in Factor Xa and the dominating contribution in P38MK and RNase A. Our motive behind using these prefactors is to show that their introduction is capable of reproducing experimental binding trends better. We see a marked improvement for Factor Xa predictions, but for P38MK and RNaseA, the unweighted score predictions already reproduce the experimental trends and the weighting does not make the ranking better. On the contrary for these sets, there is a slight loss in predictability with the weighted scoring scheme. We note here that the value of the prefactors could be further adjusted based on (i) availability of more accurate experimental data and (ii) use of more accurate FragMaps that are obtained after significantly longer simulation times or better sampling methodologies.

Figure 8.

Average GFE contributions computed for each ligand set for the three proteins Factor Xa (FAX), P38 MAP kinase (P38MK) and RNase A. Panel (a) shows the averages that are unscaled and correspond to the unweighted LGFEs. Panel (b) shows the averages of GFEs multiplied by the prefactors as explained in the text. All GFEs are in kcal/mol units.

CONCLUSION

The SILCS Tier II approach applied to four proteins showed the ability of the method to qualitatively map protein-ligand interactions. The affinity pattern obtained identifies the location of different classes of hydrogen bond donor and acceptor interactions in addition to the non-polar interactions. Such information may be used to inform ligand design. We also showed that the predictability of LGFE metric of experimental affinity improves with increasing ligand sampling, although limitations in the method are present as evidenced by the predictions being incorrect for HIV-protease ligands. It is noted that the use of LGFE scoring may represent a middle ground between rapid, but highly approximate docking methods and computationally intensive, but more accurate FEP methods.