Abstract
The Rosenberg Self-Esteem Scale (RSES) is a widely used measure for assessing self-esteem, but its factor structure is debated. Our goals were to compare 10 alternative models for RSES; and to quantify and predict the method effects. This sample involves two waves (N=2513 ninth-grade and 2370 tenth-grade students) from five waves of a school-based longitudinal study. RSES was administered in each wave. The global self-esteem factor with two latent method factors yielded the best fit to the data. The global factor explained large amount of the common variance (61% and 46%); however, a relatively large proportion of the common variance was attributed to the negative method factor (34 % and 41%), and a small proportion of the common variance was explained by the positive method factor (5% and 13%). We conceptualized the method effect as a response style, and found that being a girl and having higher number of depressive symptoms were associated with both low self-esteem and negative response style measured by the negative method factor. Our study supported the one global self-esteem construct and quantified the method effects in adolescents.
Keywords: Self-esteem, measurement model, method effect, response style
Introduction
Self-esteem is the evaluative component of an individual's self-concept which is associated with overall health, well-being (DuBois & Flay, 2004) and even mortality (Stamatakis et al., 2004). The Rosenberg Self-Esteem Scale (RSES, Rosenberg, 1965) is the most widely used instrument for measuring global self-esteem, and has been translated into numerous languages (Schmitt & Allik, 2005). Having the advantage of a long history of use, an uncomplicated language and brevity, the RSES is a convenient and thus popular device for measuring self-esteem, especially in large, population-based quantitative studies (e.g. Swallen et al., 2005).
Although self-esteem was originally conceptualized as a one-dimensional construct (Rosenberg, 1965), there is an ongoing debate about the factor structure of the Rosenberg Self-Esteem Scale which is substantively important, influencing the interpretation of responses and also the construct validity of global self-esteem (Corwyn, 2000). Although the scale is routinely handled as a one-factor measure, some exploratory and confirmatory factor analyses have resulted in two oblique factors implying two meaningful dimensions: one of positive and one of negative images of self (Owens, 1994; Roth et al, 2008; Mimura & Griffiths, 2007). Furthermore, an alternative two-factor model was proposed which includes self-acceptance and self-assessment factors based on a theoretical consideration (Tafarodi & Milne, 2002). On the other hand, some studies have reported one main factor following reversed recoding of negatively worded items (Schmitt & Allik, 2005). Many researchers have assumed that the two-factor solution is owed merely to the method effect being derived from the item wording and thus the scale includes only one substantive dimension (Carmines & Zeller, 1979; Corwyn, 2000; DiStefano & Motl, 2009; Greenberger, Chen, Dmitrieva, & Farruggia., 2003; Horan, DiStefano, & Motl, 2003; Marsh, 1996; Marsh et al., 2010; Tomás & Oliver, 1999; Wu, 2008).
Method effect refers to variance that is attributable to the method of measurement – in this case negative and positive wording of the items – rather than to the construct of interest (Fiske, 1982; Podsakoff, MacKenzie, Lee, & Podsakoff, 2003). Unlike exploratory factor analysis, confirmatory factor analysis provides an opportunity to compare alternative measurement models and also to specify the method effects (Brown, 2006). Two different approaches were used to model the method effects within a confirmatory analysis framework (Lindwall et al., 2012). One approach is correlated traits, correlated uniqueness (CTCU) which models the method effects with the error covariances, the other is correlated traits correlated methods (CTCM) which models the method effects with implying one or more latent method factors. In four studies it is revealed that the one-factor structure with method effect modeled by the covariances between positively worded items yielded the best fit among other competing models (Dunbar et al., 2000; Wang et al., 2001; Martin-Albo et al., 2007; Aluja et al., 2007). Only one study demonstrated that the best fit was yielded by one global self-esteem factor and correlated uniqueness between negatively worded items and between positively worded items (Vasconcelos-Raposo et al, 2011), however because of an identification problem, some minor modification was needed. In favor of CTCM models, a recent study involving a large number of alternative models provided support for the model with one global self-esteem factor and two latent method factors in a sample of boys (Marsh et al., 2010). This study is based on an exclusively male sample however, so more research is needed to evaluate whether gender does indeed affect method factors. The CTCM approach was bolstered by other previous studies supporting one global self-esteem and one latent method factor from the negatively worded items (DiStefano & Motl, 2009). Furthermore, Tafarodi and Milne (2002) proposed a five factor model which included their new theoretical factors (self-acceptance and self-assessment), global self esteem, and two method factors.
The advantage of CTCM models is that the method effects can be quantified and predicted by other variables, something that is not possible when using the CTCU model (Lindwall, et al, 2012). A significant question regarding method effect is whether it merely reflects systematic measurement errors or whether it represents response styles (DiStefano & Motl, 2006; Lindwall, et al, 2012; Quilty et al. 2006). Response style is defined as “a personality trait that involves the predisposition toward interpreting and endorsing items based on a certain tone or valence” (DiStefano & Motl, 2009, p.310).
In recent research, method effects associated with negatively phrased items are treated as a response style and correlated or predicted by other variables (DiStefano & Motl, 2006; DiStefano & Motl, 2009; Lindwall, et al, 2012; Quilty et al. 2006). A response style occurring with the negatively phrased items is positively associated with depression (Lindwall, et al, 2012) reward responsiveness in women only (DiStefano & Motl, 2009), and negatively associated with life satisfaction (Lindwall, et al, 2012), conscientiousness and emotional stability (Quilty et al. 2006), tendency towards risk taking behaviors in both genders, fear of negative evaluation, and private self-consciousness only in women (DiStefano & Motl, 2009). One study demonstrated that response style linked with positively worded items is associated with life satisfaction (Lindwall, et al, 2012). These studies supported the proposition that the negative and probably the positive response styles can be affected by personality traits and demographic factors, and it is worth examining their associations in order to clarify whether self-esteem per se or the response style or both are associated with other constructs and variables. For example the question might be whether gender difference in self-esteem reflects differences in the evaluative component of self-concept or if it only reflects different response styles. In the first case gender difference should be present when response style is statistically controlled, in the second case when controlling response style gender difference should disappear and response style should be different in boys and girls.
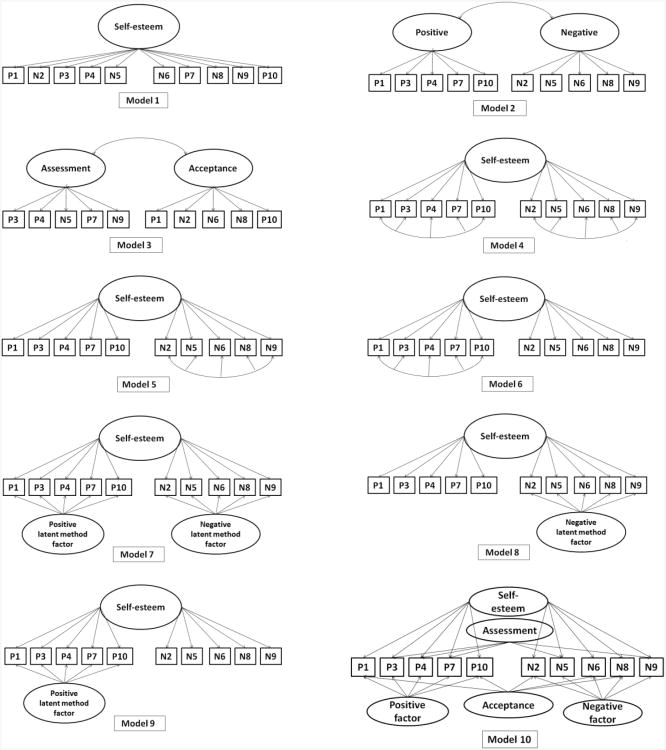
The goals of this report are threefold. The first goal was to contrast the competing measurement models depicted in Figure 1 to identify the best-fitting model in a large adolescent sample. This comparison was informative for at least two reasons. On the one hand we could contrast the global one-factor model with a two-factor model including negative and positive aspects of self-esteem. On the other hand, we could also contrast the original global self-esteem approach and the two-factor approach including the acceptance and assessment factors and also the five-factor model proposed by Trafordi and Milne (2002). The second goal was to test the longitudinal stability of the measurement model of self-esteem in order to make valid conclusion regarding the temporal change in self-esteem. The third goal was to quantify the size and stability of method effects due to positive and negative wording of items, using the explained common variance approach, and to test whether gender, depressive symptoms, average grade and subjective academic performance predict method effects in RSES.
Figure 1.
Ten competing measurement models of Rosenberg Self-Esteem Scale.
Method
Participants and procedure
This analysis involved two waves (second and third) from a school-based longitudinal study. The two-stage cluster sampling method is described in more detail elsewhere (Urbán, 2010). The second wave (between March and May 2009) comprised 2513 ninth-grade adolescents (51% girls; mean age=15.7 SD=0.55) and the third wave (between October and December 2009) comprised 2370 tenth-grade adolescents (52% girls; mean age=16.4 SD=0.68). A total of 1857 adolescents participated in both waves. The average time between the two waves was 5.9 months.
Instruments
Self-Esteem Scale
The Hungarian version of Rosenberg's Self-Esteem Scale (RSES-HU, Elekes, 2009) was administered in two forms. This scale contains five positively and five negatively worded items. In the first form, positively worded items were 1, 3, 4, 7 and 10. In the second form, these items were 1, 2, 4, 6 and 7. The first form was administered in Wave 2, and the second form was used in Wave 3. The items on the scale are listed in Table 2. The internal consistency of the scale was adequate in both waves (α=0.87 in Wave 2 and α= 0.86 in Wave 3) and in both genders (in boys: α=0.87 in both waves, and in girls α=0.86 in both waves). Test-retest correlation of RSES-HU in this study was excellent (r=0.67).
Table 2. Standardized factor loadings in the best fitting model containing one trait factor and positive and negative latent method factors.
| Item | GSE | Positive method factor | Negative method factor | |||
|---|---|---|---|---|---|---|
|
| ||||||
| Time 1 | Time 2 | Time 1 | Time 2 | Time 1 | Time 2 | |
| Positively phrased items | ||||||
| I take a positive attitude toward myself. | 0.86 | 0.85 | −0.10ns | 0.09ns | ||
| On the whole, I am satisfied with myself. | 0.71 | 0.83 | −0.05ns | 0.06ns | ||
| I feel that I have a number of good qualities. | 0.66 | 0.55 | 0.30 | 0.63 | ||
| I feel that I'm a person of worth, at least on an equal plane with others. | 0.62 | 0.55 | 0.29 | 0.44 | ||
| I am able to do things as well as most other people. | 0.56 | 0.49 | 0.38 | 0.29 | ||
| Negatively phrased items | ||||||
| I certainly feel useless at times. | −0.51 | −0.52 | 0.62 | 0.69 | ||
| All in all, I am inclined to feel that I am a failure. | −0.48 | −0.46 | 0.58 | 0.43 | ||
| At times I think I am no good at all. | −0.47 | −0.51 | 0.54 | 0.66 | ||
| I feel I do not have much to be proud of. | −0.41 | −0.45 | 0.42 | 0.29 | ||
| I wish I could have more respect for myself. | −0.34 | −0.42 | 0.46 | 0.47 | ||
|
| ||||||
| Explained common variance (%) | 61% | 46% | 5% | 13% | 34% | 41% |
|
| ||||||
| Omega | 0.84 | 0.87 | 0.82 | 0.84 | ||
|
| ||||||
| Omega hierarchical | 0.04 | 0.14 | 0.48 | 0.45 | ||
Note: Time 1 (Wave 2): N=2340 and Time 2 (Wave 3): N=2288. The significant (p < .05) factor loadings are boldfaced. Explained common variance is calculated with the formula provided by Bentler, 2009 and Berge & Sočan (2004).
Depressive symptoms
The Hungarian version of Centre for Epidemiological Studies Depression scale (CES–D; Radloff, 1977) was used to measure depressive symptoms recorded during the past week. The CES-D consists of 16 negative affect and 4 positive affect items, such as “I felt depressed”, “I felt tearful”, and “I enjoyed life”. Participants had to answer how often they felt this way in the past week on a 4-point scale ranging from 1 to 4 with overall scores ranging between 20 and 80. Positive affect items were reversed when computing the sum score of the scale. CES-D is widely used to assess depressive symptoms in non-clinical adolescent and adult populations. The internal consistency of the scale was adequate (α = .82 in Wave 2 and 0.80 in Wave 3). Test-retest correlation in this study was excellent (r=0.61).
Academic performance variables
One question was constructed to measure average grades during the last semester. Self-reported average grades reflect adequately the objective average grade, even though the validity of the self-reported value is somewhat lower in students with lower average grade. In general, the correlation between self-reported average grade and the objective value is r=.82 as estimated in a meta-analysis (Kuncel, Credé, & Thomas, 2005). Another question was used to measure relative performance in school compared to other students. A five-point scale was provided to answer this question from 1 (Far above the average) and 5 (Far below the average). Due to the negative direction of this scale, we call this a measure of relative under-achievement in school.
Data Analysis Strategy
We used structural equation modeling with Mplus 7.0 to estimate the degree of fit of ten prior measurement models to the data in both waves. We performed all analyses with maximum likelihood parameter estimates with standard errors and chi-square test statistics that were robust to nonnormality and nonindependence of observation (Muthén & Muthén, 1998–2007, p. 484). We used the full information maximum likelihood estimator to deal with missing data (Muthén &Muthén, 1998–2007).
A satisfactory degree of fit requires the comparative fit index (CFI) and the Tucker-Lewis Index (TLI) to be higher than or close to 0.95 (Brown, 2006). The next fit index was root mean squared error of approximation (RMSEA). RMSEA below 0.05 indicates excellent fit and a value above 0.10 indicates poor fit. Closeness of model fit using RMSEA (CFit of RMSEA) is a statistical test (Browne & Cudeck, 1993), which evaluates the statistical deviation of RMSEA from the value 0.05. Non-significant probability values (p > .05) indicate acceptable model fit (Brown, 2006). The last fit index is the standardized root mean square residual (SRMR). An SRMR value below 0.08 is considered a good fit (Kline, 2011). Aikaike information criteria (AIC) was use in case of comparison of non-nested models, a model with lower AIC value is regarded to fit the data better in relation to alternative models (Brown, 2006).
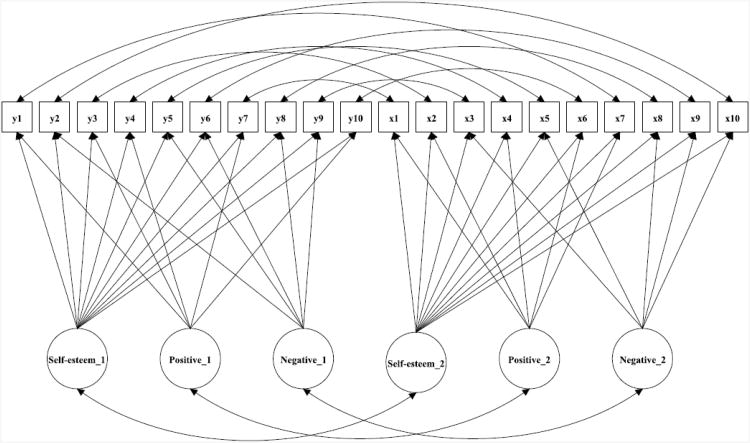
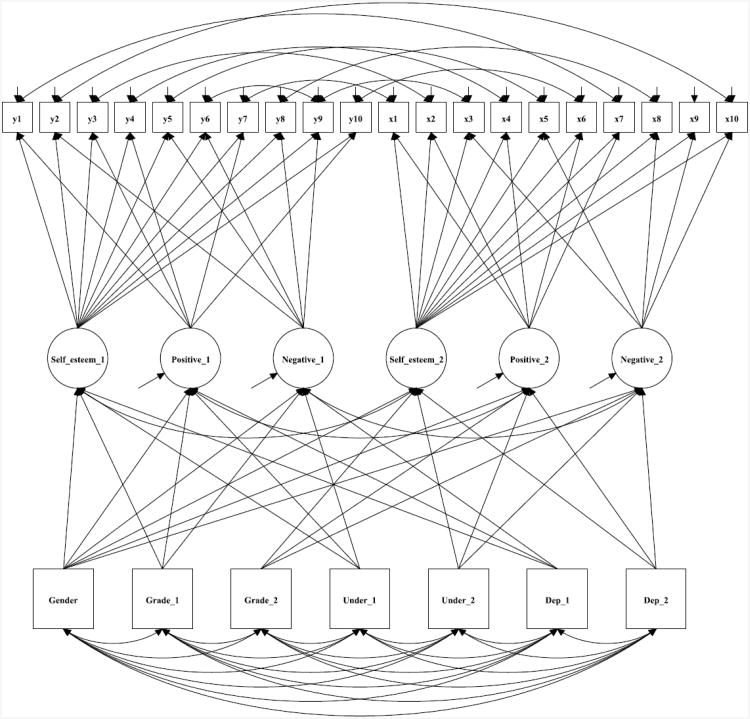
In order to quantify the size and stability of method effects due to positive and negative wording of items we applied a longitudinal CFA model (see Figure 2, Vandenberg & Lance, 2000, Little, 2013). In addition, to identify the correlates of the main factor and the method factors, we applied another longitudinal CFA with covariates model (see Figure 3).
Figure 2. Longitudinal CFA model of Rosenberg Self-Esteem Scale.
Note: Self-esteem=global self-esteem factor. Positive=Positive latent method factor. Negative= Negative method factor.
Figure 3.
Longitudinal CFA model of Rosenberg Self-Esteem Scale with covariates.
Note: Grade=Average Grade; Under=Relative underachievement; Dep=Depression; Positive=Positive method factor; Negative=Negative method factor.
Results
Comparing measurement models
In order to compare alternative models, we tested ten measurement models of self-esteem in both waves including (1) one trait factor with no correlated uniqueness, (2) two correlating trait factors: positive and negative trait factors, (3) two correlating trait factors: one acceptance and one assessment factor as proposed by Trafordi and Milne (2002) (4) one trait factor with correlated uniqueness among both positive and negative items, (5) one trait factor with correlated uniqueness among negatively worded items, (6) one trait factor with correlated uniqueness among positively worded items, (7) one trait factor and positive and negative latent method factors, (8) one trait factor plus a negative method factor and (9) one trait factor plus a positive method factor. (10) Finally we tested a five-factor model proposed by Trafordi and Milne (2002), which included one trait factor, one acceptance, one assessment factor, and positive and negative latent method factors. The fit indices for each model are presented in Table 1.
Table 1.
Confirmatory factor analysis of different measurement models of the Rosenberg Self-Esteem Scale.
| χ ² | df | CFI | TLI | RMSEA | Cfit of RMSEA | ||
|---|---|---|---|---|---|---|---|
|
| |||||||
| Model 1. One trait factor: no correlated uniqueness* | |||||||
| Time 1 | 1188.6 | 35 | .80 | .74 | .119 | <.001 | .075 |
| Time 2 | 1750.6 | 35 | .73 | .65 | .146 | <.001 | .086 |
|
| |||||||
| Model 2. Two correlating trait factors: positive and negative trait factors* | |||||||
| Time 1 | 187.3 | 34 | .97 | .97 | .044 | .986 | .026 |
| Time 2 | 436.8 | 34 | .94 | .92 | .072 | <.001 | .046 |
|
| |||||||
| Model 3. Two correlating trait factors: an acceptance and an assessment factor** | |||||||
| Time 1 | 1195.3 | 34 | .80 | .73 | .121 | <.001 | .076 |
| Time 2 | 1825.0 | 34 | .72 | .63 | .152 | <.001 | .086 |
|
| |||||||
| Model 4. One trait factor with correlated uniqueness among both positive and negative items* | |||||||
| Time 1 | The model is not identified | ||||||
| Time 2 | The model is not identified | ||||||
|
| |||||||
| Model 5. One trait factor with correlated uniqueness among negatively worded items* | |||||||
| Time 1 | 155.7 | 25 | .98 | .96 | .047 | .723 | .023 |
| Time 2 | 327.3 | 25 | .95 | .91 | .073 | <.001 | .037 |
|
| |||||||
| Model 6. One trait factor with correlated uniqueness among positively worded items* | |||||||
| Time 1 | 68.7 | 25 | .99 | .99 | .027 | 1.000 | .015 |
| Time 2 | 181.5 | 25 | .98 | .96 | .052 | .284 | .031 |
|
| |||||||
| Model 7. One trait factor and positive and negative latent method factors* | |||||||
| Time 1 | 66.2 | 25 | .99 | .99 | .027 | 1.000 | .013 |
| Time 2 | 151.7 | 25 | .98 | .96 | .047 | .736 | .026 |
|
| |||||||
| Model 8. One trait factor plus a negative method factor* | |||||||
| Time 1 | 180.2 | 30 | .97 | .96 | .046 | .819 | .024 |
| Time 2 | 386.6 | 30 | .94 | .92 | .072 | <.001 | .039 |
|
| |||||||
| Model 9. One trait factor plus a positive method factor* | |||||||
| Time 1 | 160.1 | 30 | .98 | .97 | .043 | .957 | .022 |
| Time 2 | 382.6 | 30 | .94 | .92 | .072 | <.001 | .038 |
|
| |||||||
| Model 10. Five factor model: one trait factor, one acceptance, one assessment factor, positive and negative latent method factors** | |||||||
| Time 1 | 34.7 | 15 | 1.00 | .99 | .024 | 1.000 | .009 |
| Time 2 | 89.1 | 15 | .99 | .97 | .046 | .717 | .012 |
Note: Time 1 (Wave 2): N=2340 and Time 2 (Wave 3): N=2288.
Measurement models are depicted in Figure 1.
Tafordi and Milne (2002). χ²=chi-square test statistic; df = degrees of freedom; CFI = comparative fit index; TLI = Tucker–Lewis index; RMSEA = root mean square error of approximation; Cfit = closeness of fit; SRMR = standardized root mean square residual.
Only three models (Model 6, 7, 10) satisfied our predefined decision criteria (CFI> .95; TLI> .95, RMSEA≤ .05 and SRMR < .08) in both waves (see Table 1). Model 10, the five-factor model yielded the closest model fit in both waves; however in the first wave the negative method factor and the acceptance factor did not have any significant factor loadings, and the assessment factor had only three significant loadings, and in the second wave the acceptance factor did not have any significant loadings, and the assessment factor had only one significant loading, therefore the interpretability of these factors is unclear. We can conclude that our data does not support the five-factor model.
The model (Model 7 in Table 1) containing one trait factor and positive and negative latent method factors also yielded an excellent fit to the data in both waves. In this model all three factors were also identified by significant factor loadings. The degree of fit of Model 7 (in Table 1) and Model 6 are, however, quite close in the single wave analyses. We also performed a longitudinal CFA, in which the models included the same measurement model at both assessment points, and the related latent variables and the error of the same items from two time points were allowed to freely covariate (see for example Figure 2). The degree of fit of both models was acceptable (Model 6: χ²=631.8 df=139; RMSEA=0.035 Cfit=1.00, CFI=0.97 TLI=0.95 SRMR=0.065 Akaike Information Criterion (AIC): 91105; and Model 7: χ²=402.7 df=137; RMSEA=0.026 Cfit=1.00, CFI=0.98 TLI=0.97 SRMR=0.035 Akaike Information Criterion (AIC): 90820). Model 7, however, performed somewhat better fit than Mode 6. In sum, Model 7 provided a somewhat better solution of the measurement model of RSES, but the difference of degree of fit is very moderate.
The factor loadings of Model 7 are presented in Table 2. The loadings are very similar in both waves. In order to quantify the degree of unidimensionality of the Rosenberg Self-Esteem scale, we applied the percentage of common variance attributable to the global factor with the use of explained common variance index (ECV, Bentler, 2009; Berge & Sočan, 2004). The ECV of the global factor was 61% in Wave 2 and 46% in Wave 3 supporting the theory that the majority of variance is explained by the global self-esteem factor, however a relatively large proportion of ECV was attributed to the negative method factor (34 % and 41%), and a small proportion of common variance is explained by the positive method factor (5% and 13%).
Longitudinal CFA model: measurement invariance and temporal stability
In order to test temporal stability or test-retest correlation of the global self-esteem and response style measured by positive method and negative method factors we tested a longitudinal CFA model (see Figure 2). The degree of fit was excellent (χ²=402.7 df=137; RMSEA=0.026 Cfit=1.00, CFI=0.982 TLI=0.975 SRMR=0.032). Before further analysis, we tested the longitudinal measurement invariance hypothesis with a series of longitudinal CFA. Fit indices and their difference tests are reported in Table 3. The configural invariance model that does not contain any constrains yielded excellent degree of fit. We applied increasing equality constrains to test the longitudinal invariance. To compare the nested models with increasing constrains we used the traditional Δχ²-test and we followed the recommendations of Cheung and Rensvold (2002) and Chen (2007) for comparing two nested models who suggest cut-off values at ΔCFI ≤ 0.01 and ΔRMSEA ≤ 0.015. Testing metric invariance of GSE factor, we constrained appropriate factor loadings to be equal at both time points. Although the conservative χ²-difference test indicated significant decrement in degree of fit, but the changes in CFI and RMSEA were less than the cutoff values. We also tested metric invariance of method factors applying equality constrains on factor loadings of adequate items, which also yielded significant change in χ²-difference test, and the change in CFI was larger than the cut-off value but as for RMSEA, this change is still less than the cut-off value. Therefore the metric invariance conclusion of method factors could not be supported. To test the scalar invariance, we constrained the intercepts of the same items to be equal. Again, the conservative χ²difference test indicated significant decrement in degree of fit, but the changes in CFI and RMSEA were less than the cutoff values. These results supported the longitudinal scalar invariance of global self-esteem factor of RSES, but questioned the metric invariance of method factors which is likely to be due to the different order of items in the two waves.
Table 3.
Tests of Longitudinal invariance of measurement model of RSES with longitudinal CFA method.
| Model | χ² | df | RMSEA | CFI | TLI | SRMR | Δχ² | Δdf | p | ΔRMSEA | ΔCFI | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. | Configural invariance | 402.7 | 137 | .026 | .982 | .975 | .032 | |||||
| Model 1 versus Model 2.a. | 70.1 | 10 | <.0001 | .002 | .004 | |||||||
| 2.a. | Metric invariance of global(GSE) factor* | 473.1 | 147 | .028 | .978 | .971 | .040 | |||||
| Model 2.a. versus Model 2.b. | 350.5 | 10 | <.0001 | .009 | .022 | |||||||
| 2.b. | Metric invariance of both positive and negative method factors** | 791.0 | 157 | .037 | .956 | .947 | .043 | |||||
| Model 2.b. versus Model 3 | 210.9 | 10 | <.0001 | .003 | .009 | |||||||
| 3. | Scalar invariance | 951.1 | 167 | .040 | .947 | .939 | .046 | |||||
Note: RMSEA = root mean squared error of approximation; CFI = comparative fit index; TLI = Tucker-Lewis index; SRMSR = standardized root mean squared residual. Δχ²= Satorra-Bentler scaled (S-B scaled) χ²difference test. The latent variables were identified with fixing one factor loading being equal with 1.
The factor loadings on global factors are constrained to be equal in Time 1 and Time2.
The factor loadings of both method factors are constrained to be equal in Time 1 and Time 2.
The test-retest correlation of global self-esteem was 0.74 p<0001, the test-retest correlations of method factors were 0.41 p<.0001 for negative and 0.48 p<.0001 for the positive method factors. We also tested the equality of latent means in the current longitudinal model, and fixing the two means to be equal resulted in significant increase in the χ² value (Δχ²=5.9 df=1 p<016), however other fit indices did not change (ΔRMSEA=0.000; ΔCFI=.001), therefore by using newly proposed criteria we can support the temporal stability of the latent mean of global self-esteem factor.
Correlates of global and method effects: determinants of response style
In order to understand the covariates of global and method effects we applied longitudinal CFA with covariates approach which is depicted in Figure 3. We performed the analysis in the total sample, and also by gender. The fit indices of the three model were satisfactory: (in total sample: χ²=634.3 df=253; RMSEA=0.034 Cfit=1.00, CFI=0.965 TLI=0.954 SRMR=0.053; in boys: χ²=386.9 df=239; RMSEA=0.033 Cfit=1.00, CFI=0.965 TLI=0.954 SRMR=0.063; in girls: χ²=444.6 df=239; RMSEA=0.035 Cfit=1.00, CFI=0.965 TLI=0.954 SRMR=0.055). The standardized regression coefficients are presented in Table 4. Gender is negatively associated with global self-esteem, with girls scoring lower on global self-esteem. Gender was positively associated with negative method effect, which highlighted that girls were more likely to endorse negatively worded items. Depression score was negatively associated with global self-esteem, and positively associated with negative method factor. Adolescents with a higher depression score are more likely to attain a higher score on negatively phrased items and therefore more likely to endorse these items. These associations were present in the boys and girls separately. School grade is not associated with neither global self-esteem nor negative method effect in both waves and was linked with positive method effects only in girls in Wave 3. Relative under-achievement in school is negatively related to self-esteem in total sample.
Table 4.
Standardized regression weights between predictors and Rosenberg Self-Esteem Scale latent factors in a longitudinal CFA model.
| Global self-esteem | Positive method factor | Negative method factor | ||||
|---|---|---|---|---|---|---|
| Time 1 | Time 2 | Time 1 | Time 2 | Time 1 | Time 2 | |
| Total sample | ||||||
| Genderđ | −0.24*** | −0.20*** | 0.08 | 0.07 | 0.14*** | 0.15*** |
| Depression$ | −0.44*** | −0.38*** | 0.10 | −0.01 | 0.36*** | 0.41*** |
| Average grade | 0.01 | 0.04 | −0.05 | −0.12** | 0.03 | 0.02 |
| Relative under-achievement | 0.09** | 0.08* | −0.12* | −0.08 | 0.07 | −0.01 |
| R² | 30% | 24% | 3% | 1% | 17% | 22% |
| Boys | ||||||
| Depression$ | −0.32*** | −0.35*** | −0.04 | −0.08 | 0.38*** | 0.44*** |
| Average grade | −0.04 | −0.02 | −0.02 | −0.07 | −0.03 | 0.03 |
| Relative under-achievement | −0.06 | −0.11* | −0.15 | −0.10 | 0.05 | −0.03 |
| R² | 12% | 15% | 2% | 2% | 16% | 19% |
| Girls | ||||||
| Depression$ | −0.55*** | −0.44*** | 0.17 | 0.02 | 0.33*** | 0.40*** |
| Average grade | 0.02 | −0.07 | −0.11 | −0.15 | 0.09 | 0.01 |
| Relative under-achievement | −0.11* | 0.05 | −0.08 | −0.04 | 0.09 | −0.01 |
| R² | 34% | 19% | 4% | 2% | 11% | 16% |
Note:
Boys were coded 0 and girls were coded 1.
Measured with the Center for Epidemiological Studies Depression scale.
p < .05.
p < .01.
p < .001.
Discussion
Our study supported the model that included one global self-esteem factor and two latent method factors for the Rosenberg Self-Esteem Scale in a large sample of Hungarian adolescents. We compared several different models and, similarly to an earlier study (Marsh et al., 2010), the global self-esteem model with positive and negative method factors yielded a superior degree of fit. However, other measurement models also had acceptable level of model fit, and the model containing a trait factor and correlated uniqueness among positively worded items – an example for correlated traits, correlated uniqueness (CTCU) models – had a degree of model fit very close to our chosen model with one global self-esteem factor and two latent method factors that can be regarded as a correlated traits correlated methods (CTCM) model. Recent recommendations regarding the use of CTCM and CTCU models concluded that CTCM model is generally preferred model, and the CTCU model should be applied only when the CTCM model fails (Lance, Noble & Scullen, 2002). A simulation study presented evidence that CTCU models would imply biased estimation of trait factor loadings when the method factor loadings are high (Conway, Lievens, Scullen, & Lance, 2004). In the present case, the sizes of factor loadings of method factors are in the medium or large range, therefore a CTCU model would be less appropriate.
Our result not only provides evidence of the factorial structure of the Rosenberg Self-Esteem Scale in an adolescent population, but also supports the theory that self-esteem as measured by the Rosenberg Self-Esteem Scale should be viewed as a global and one-dimensional construct which could be defined as a positive or negative attitude toward the self (Rosenberg, 1965) or simply as a favorable global evaluation of oneself (Baumeister, Smart, & Boden, 1996).
Although the unidimensionality of RSES is supported in this study, a large proportion of common variance is explained by the method effect, due to negatively and positively phrased items. Because the size of method effect is not negligible (36% and 54%) it may have an impact on the reliability of the measurement of self-esteem. Several previous studies have reported method effects in adolescents, young adults and older samples (DiStefano & Motl, 2006; DiStefano & Motl, 2009; Lindwall, et al, 2012; Marsh et al., 2010; Quilty et al. 2006), however in this study we quantified these effects using an estimation of the proportion of common method variance due to method effects, and found that while the method effects related to positively worded items explain only a small amount, method effects linked to negatively worded items explain a large proportion of common variance. This result is also in line with earlier research which placed emphasis mainly on method effect related to negatively phrased items (DiStefano & Motl, 2009). We also found that the degree of method effect also depends on the order of the items. Due to the fact that we used the same items in different orders in two waves, we found that the explained common variances of method effects were different. Further research should clarify the role of item order in method effects. Although method effects related to wording of the items are regarded as a source of bias (Podsakoff, MacKenzie, & Podsakoff, 2012), they also provides the possibility of grasping a stable personality trait, namely the style of response to positively and negatively worded items.
We also tested the longitudinal stability of the measurement model. For longitudinal studies, it is important to demonstrate the longitudinal alpha, beta, and gamma change (Chan, 1998). Alpha change refers to true score change in the given construct such as self-esteem, beta change refers to change when the measurement properties of indicators change over time, and finally gamma change refers to the situation where the construct changes over time. Based on a longitudinal CFA approach, we demonstrated the temporal stability of the global self-esteem factor, however the factor loadings of the method factors are not invariant in time. While our result is consistent with a previous study (Motl and DiStefano, 2002), it is still not known whether the construct of self-esteem changes over a longer period of time.
We found that the method effects due to different affective valence of the items are relatively stable. In this study, we provided evidence for the temporal stability of response style demonstrating the moderate test-retest correlations of latent method factors through a six month follow-up. This result is in line with research on the stability of response style (Motl and DiStefano, 2002) which presented evidence suggesting that response styles have an important stable component. Furthermore, in this study we also demonstrated that the response style related to negatively worded items is associated with gender and depressive symptoms, this result is also in line with a previous study of older samples (Lindwall et al., 2012). This and previous studies (Lindwall et al., 2012) equivocally demonstrated that research participants with higher depressive symptoms are more likely to endorse negatively worded items, another study also reported that people with higher avoidance motivation and neuroticism are more likely to endorse negative items (Quilty et al. 2006). In comparison, one study reported that individuals with a higher score for the self-consciousness trait are less likely to show method effects. The evidence that the response style is a stable characteristic and can be predicted by other variables supports the idea that response style can be regarded as a personality trait (e.g. DiStefano & Motl, 2006; Horan et al., 2003, Lindwall et al., 2012). The global self-esteem is associated with a school-related variable. The relative under-achievement in school is negatively related to global self-esteem.
The main limitation of this study is that the present sample only involved urban adolescents with a narrow age range, therefore the generalizability to rural and minority adolescents and also to adults is limited. On the other hand, one of the strengths of this study is that it included two waves of data, therefore we could test the longitudinal stability of global and method effects in a relatively large representative sample of adolescents.
Acknowledgments
Funding information: This publication was supported by Grant Number 1 R01 TW007927-01 from the Fogarty International Center, the National Cancer Institute, and the National Institute on Drug Abuse, within the National Institutes of Health (NIH). Its contents are solely the responsibility of the author and do not necessarily represent the official view of the NIH. The project was also supported by the European Union and the European Social Fund under Grant Agreement No. TÁMOP 4.2.1./B-09/1/KMR-2010-0003.
Zsolt Demetrovics and Gyöngyi Kökönyei acknowledge the financial support of the János Bolyai Research Fellowship awarded by the Hungarian Academy of Sciences.
Footnotes
All authors agreed to submit this paper.
References
- Aluja A, Rolland JP, García LF, Rossier J. Dimensionality of the Rosenberg Self-Esteem Scale and its relationships with the three - and the five-factor personality models. Journal of Personality Assessment. 2007;88:246–249. doi: 10.1080/00223890701268116. [DOI] [PubMed] [Google Scholar]
- Baumeister R, Smart L, Boden J. Relation of threatened egotism to violence and aggression: The dark side of self-esteem. Psychological Review. 1996;103:5–33. doi: 10.1037/0033-295x.103.1.5. [DOI] [PubMed] [Google Scholar]
- Bentler P. Alpha, dimension-free, and model-based internal consistency reliability. Psychometrika. 2009;74(1):137–143. doi: 10.1007/s11336-008-9100-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berge JMF, Sočan G. The greatest lower bound to the reliability of a test and the hypothesis of unidimensionality. Psychometrika. 2004;69(4):613–625. [Google Scholar]
- Brown TA. Confirmatory factor analysis for applied research. New York: Guilford Press; 2006. [Google Scholar]
- Browne MV, Cudeck R. Alternative ways of assessing model fit. In: Bollen KA, Long JS, editors. Testing structural equation models. Newbury Park, CA: Sage; 1993. pp. 136–162. [Google Scholar]
- Carmines EG, Zeller RA. Reliability and validity assessment. Beverly Hills, CA: Sage; 1979. [Google Scholar]
- Chan D. The conceptualization and analysis of change over time: An integrative approach incorporating longitudinal mean and covariance structures analysis and multiple indicator latent growth modeling. Organizational Research Methods. 1998;1:421–483. [Google Scholar]
- Chen FF. Sensitivity of goodness of fit indexes to lack of measurement invariance. Structural Equation Modeling. 2007;14:464–504. [Google Scholar]
- Cheung GW, Rensvold RB. Evaluating goodness-of-fit indexes for testing measurement invariance. Structural Equation Modeling. 2002;9:233–255. [Google Scholar]
- Conway JM, Lievens F, Scullen SE, Lance CE. Bias in the correlated uniqueness model for MTMM data: A simulation study. Structural Equation Modeling. 2004;11:535–559. [Google Scholar]
- Corwyn RF. The factor structure of global self-esteem among adolescents and adults. Journal of Research in Personality. 2000;34:357–379. [Google Scholar]
- DiStefano C, Motl RW. Further investigating method effects associated with negatively worded items on self-report surveys. Structural Equation Modeling. 2006;13:440–464. [Google Scholar]
- DiStefano C, Motl RW. Personality correlates of method effects due to negatively worded items on the Rosenberg Self-Esteem Scale. Personality and Individual Differences. 2009;46:309–313. [Google Scholar]
- DuBois DL, Flay BR. The healthy pursuit of self-esteem: Comment on and alternative to the Crocker and Park (2004) Formulation. Psychological Bulletin. 2004;130:415–420. doi: 10.1037/0033-2909.130.3.415. [DOI] [PubMed] [Google Scholar]
- Dunbar M, Ford G, Hunt K, Der G. Question wording effects in the assessment of global self-esteem. European Journal of Psychological Assessment. 2000;16:13–19. [Google Scholar]
- Elekes Zs. ESPAD 2007. Budapest: L'Harmattan Kiadó; 2009. Egy változó kor változó ifjúsága. Fiatalok alkohol- és egyéb drogfogyasztása Magyarországon –. Changing youth in changing times. Alcohol and other substance use among school children in Hungary – ESPAD 2007. [Google Scholar]
- Fiske DW. Convergent–discriminant validation in measurements and research strategies. In: Brinbirg D, Kidder LH, editors. Forms of validity in research. San Francisco: Jossey-Bass; 1982. pp. 77–92. [Google Scholar]
- Greenberger E, Chen C, Dmitrieva J, Farruggia SP. Item-wording and the dimensionality of the Rosenberg Self-Esteem Scale: do they matter? Personality and Individual Differences. 2003;35:1241–1254. [Google Scholar]
- Horan PM, DiStefano C, Motl RW. Wording effects in self-esteem scales: Methodological artifact or response style? Structural Equation Modeling. 2003;10:435–455. [Google Scholar]
- Kline RB. Principles and practice of structural equation modeling. 3rd. New York, NY: Guilford Press; 2011. [Google Scholar]
- Kuncel NR, Credé M, Thomas LL. The validity of self-reported grade point average, class ranks, and test scores: A meta-analysis and review of the literature. Review of Educational Research. 2005;75:63–82. [Google Scholar]
- Lance CE, Noble CL, Scullen SE. A critique of the correlated trait-correlated method and correlated uniqueness models for multitrait-multimethod data. Psychological Methods. 2002;7:228–244. doi: 10.1037/1082-989x.7.2.228. [DOI] [PubMed] [Google Scholar]
- Lindwall M, Barkoukis V, Grano C, Lucidi F, Raudsepp L, Liukkonen J, Thøgersen-Ntoumani C. Method Effects: The Problem With Negatively Versus Positively Keyed Items. Journal of Personality Assessment. 2012;94:196–204. doi: 10.1080/00223891.2011.645936. [DOI] [PubMed] [Google Scholar]
- Little TD. Longitudinal Structural Equation Modeling. New York: Guilford Press; 2013. [Google Scholar]
- Marsh HW. Positive and negative global self-esteem: A substantively meaningful distinction or artifacts? Journal of Personality and Social Psychology. 1996;70:810–819. doi: 10.1037//0022-3514.70.4.810. [DOI] [PubMed] [Google Scholar]
- Marsh HW, Scalas LF, Nagengast B. Longitudinal tests of competing factor structures for the Rosenberg Self-Esteem Scale: Traits, ephemeral artifacts, and stable response styles. Psychological Assessment. 2010;22:366–381. doi: 10.1037/a0019225. [DOI] [PubMed] [Google Scholar]
- Martín-Albo J, Núñez JL, Navarro JG, Grijalvo F. The Rosenberg Self-Esteem Scale: translation and validation in university students. The Spanish Journal of Psychology. 2007;10:458–467. doi: 10.1017/s1138741600006727. [DOI] [PubMed] [Google Scholar]
- Mimura C, Griffiths P. A Japanese version of the Rosenberg Self-Esteem Scale: translation and equivalence assessment. Journal of Psychosomatic Research. 2007;62:589–594. doi: 10.1016/j.jpsychores.2006.11.004. [DOI] [PubMed] [Google Scholar]
- Motl RW, DiStefano C. Longitudinal invariance of self-esteem and method effects associated with negatively worded items. Structural Equation Modeling. 2002;9:562–578. [Google Scholar]
- Muthén LK, Muthén BO. Mplus user's guide. 5th. Los Angeles, CA: Author; pp. 1998–2007. [Google Scholar]
- Owens TJ. Two dimensions of self-esteem: Reciprocal effects of positive self-worth and self-deprecation on adolescent problems. American Sociological Review. 1994;59:391–407. [Google Scholar]
- Podsakoff PM, MacKenzie SB, Lee JY, Podsakoff NP. Common method biases in behavioral research: A critical review of the literature and recommended remedies. Journal of Applied Psychology. 2003;88:879–903. doi: 10.1037/0021-9010.88.5.879. [DOI] [PubMed] [Google Scholar]
- Podsakoff PM, MacKenzie SB, Podsakoff NP. Sources of method bias in social science research and recommendations on how to control it. Annual Review of Psychology. 2012;65:539–569. doi: 10.1146/annurev-psych-120710-100452. [DOI] [PubMed] [Google Scholar]
- Quilty LC, Oakman JM, Risko E. Correlates of the Rosenberg Self-Esteem Scale method effects. Structural Equation Modeling. 2006;13:99–117. [Google Scholar]
- Radloff LS. The CES–D Scale: A self-report depression scale for research in the general population. Applied Psychological Measurement. 1977;1:385–401. [Google Scholar]
- Rosenberg M. Society and the adolescent self-image. Princeton, NJ: Princeton University Press; 1965. [Google Scholar]
- Roth M, Decker O, Herzberg PY, Brähler E. Dimensionality and norms of the Rosenberg Self-Esteem Scale in a German general population sample. European Journal of Psychological Assessment. 2008;24:190–197. [Google Scholar]
- Schmitt DP, Allik J. Simultaneous administration of the Rosenberg Self-Esteem Scale in 53 nations: Exploring the universal and culture-specific features of global self-esteem. Journal of Personality and Social Psychology. 2005;89:623–642. doi: 10.1037/0022-3514.89.4.623. [DOI] [PubMed] [Google Scholar]
- Stamatakis KA, Lynch J, Everson SA, Raghunathan T, Salonen JT, Kaplan GA. Self-esteem and mortality: Prospective evidence from population-based study. Annals of Epidemiology. 2004;14:56–85. doi: 10.1016/s1047-2797(03)00078-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swallen KC, Reither EN, Haas SA, Meier AM. Overweight, obesity, and health-related quality of life among adolescents: The National Longitudinal Study of Adolescent Health. Pediatrics. 2005;115:340–347. doi: 10.1542/peds.2004-0678. [DOI] [PubMed] [Google Scholar]
- Tafarodi RW, Milne AB. Decomposing global self-esteem. Journal of Personality. 2002;70:443–483. doi: 10.1111/1467-6494.05017. [DOI] [PubMed] [Google Scholar]
- Tomás JM, Oliver A. Rosenberg's Self-Esteem Scale: Two factors or method effects. Structural Equation Modeling. 1999;6:84–98. [Google Scholar]
- Urbán R. Smoking outcome expectancies mediate the association between sensation seeking, peer smoking, and smoking among young adolescents. Nicotine and Tobacco Research. 2010;12:59–68. doi: 10.1093/ntr/ntp174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vandenberg RJ, Lance CE. A review and synthesis of the measurement invariance literature: Suggestions, practices, and recommendations for organizational research. Organizational Research Methods. 2000;3:4–69. [Google Scholar]
- Vasconcelos-Raposo J, Fernandes HM, Teixeira CM, Bertelli R. Factorial validity and invariance of the Rosenberg Self-Esteem Scale among Portuguese youngsters. Social Indicator Research. 2011 doi: 10.1007/s11205-011-9782-0. Advance online publication. [DOI] [Google Scholar]
- Wang J, Siegal HA, Falck RS, Carlson RG. Factorial structure of Rosenberg's Self-Esteem Scale among crack-cocaine drug users. Structural Equation Modeling. 2001;8:275–286. [Google Scholar]
- Weijters B, Geuens M, Schillewaert N. The stability of individual response styles. Psychological Methods. 2010;15:96–110. doi: 10.1037/a0018721. [DOI] [PubMed] [Google Scholar]
- Wu CH. An examination of the wording effect in the Rosenberg Self-Esteem Scale among culturally Chinese people. The Journal of Social Psychology. 2008;148:535–551. doi: 10.3200/SOCP.148.5.535-552. [DOI] [PubMed] [Google Scholar]