Abstract
The purpose of this study is to investigate the feasibility and impact of incorporating deliverable monitor unit (MU) constraints into spot intensity optimization in intensity modulated proton therapy (IMPT) treatment planning. The current treatment planning system (TPS) for IMPT disregards deliverable MU constraints in the spot intensity optimization (SIO) routine. It performs a post-processing procedure on an optimized plan to enforce deliverable MU values that are required by the spot scanning proton delivery system. This procedure can create a significant dose distribution deviation between the optimized and post-processed deliverable plans, especially when small spot spacings are used. In this study, we introduce a two-stage linear programming (LP) approach to optimize spot intensities and constrain deliverable MU values simultaneously, i.e., a deliverable spot intensity optimization (DSIO) model. Thus, the post-processing procedure is eliminated and the associated optimized plan deterioration can be avoided. Four prostate cancer cases at our institution were selected for study and two parallel opposed beam angles were planned for all cases. A quadratic programming (QP) based model without MU constraints, i.e., a conventional spot intensity optimization (CSIO) model, was also implemented to emulate the commercial TPS. Plans optimized by both the DSIO and CSIO models were evaluated for five different settings of spot spacing from 3 mm to 7 mm. For all spot spacings, the DSIO-optimized plans yielded better uniformity for the target dose coverage and critical structure sparing than did the CSIO-optimized plans. With reduced spot spacings, more significant improvements in target dose uniformity and critical structure sparing were observed in the DSIO- than in the CSIO-optimized plans. Additionally, better sparing of the rectum and bladder was achieved when reduced spacings were used for the DSIO-optimized plans. The proposed DSIO approach ensures the deliverability of optimized IMPT plans that take into account MU constraints. This eliminates the post-processing procedure required by the TPS as well as the resultant deteriorating effect on ultimate dose distributions. This approach therefore allows IMPT plans to adopt all possible spot spacings optimally. Moreover, dosimetric benefits can be achieved using smaller spot spacings.
1. Introduction
State-of-the-art intensity-modulated proton therapy (IMPT) is performed today using the active spot scanning technique. In this modality, a proton pencil beam can be scanned magnetically in two-dimensional directions perpendicular to the beam direction in order to form an irradiating field. Monoenergetic pencil beams with different energies can then be used to produce the desired dose distributions to cover the three-dimensional tumor target (Lomax et al., 2004; Lomax, 1999). By individually modulating the intensity of each scanning spot, an IMPT plan thus can be delivered (Zhu et al., 2010). The scanning scheme can be either continuous or discrete. The continuous scanning system sweeps a beam in a raster manner, whereas the discrete scanning system employs a stop-and-shoot process whereby the beam is turned off between spots (Smith et al., 2009). The spot scanning system used at The University of Texas MD Anderson Cancer Center employs the discrete scanning scheme and is capable of generating protons with 94 non-equispaced energies from 72.5 MeV to 221.8 MeV using a scanning nozzle (Hitachi, Ltd., Tokyo, Japan and Hitachi America Ltd., Tarrytown, NY, USA) (Zhu et al., 2010). Proton beams range from 4 cm to 30.6 cm in steps of 1 mm for lower energies and up to 6 mm for higher energies. This study focuses on the discrete scanning system at MD Anderson, although other discrete scanning systems would function using similar principles.
The positioning of spots is predetermined to cover the target volume in the current treatment planning system (Eclipse, Varian Medical Systems, Palo Alto, CA, USA) at MD Anderson. In all energy layers, a set of discrete spots is located with defined spacing between spots.
The default setting of the Eclipse treatment planning system assigns the value of spot spacing for each field as a fraction α (0 < α < 1) of the spot size at the isocenter for the highest energy used for the field. The spot size, specified by the full width at the half maximum (FWHM) of the single spot in air, ranges from approximately 12 mm for the 221.8 MeV energy to approximately 34 mm for the 72.5 MeV energy (Gillin et al., 2010). For example, the spot spacing can be 6 mm for a field if α is 0.5 and the highest energy used for this field is 221.8 MeV. The intensity of each spot from each treatment field is optimized based on the arrangement of spots (Varian Medical Systems, 2007).
Smaller spot spacing has been shown to increase target dose homogeneity and lower the organ-at-risk (OAR) dose, but it also results in many low-intensity spots and reduces plan optimality (Zhu et al., 2010; Robertson et al., 2009). There are minimum monitor unit (MU) constraints for delivering each pencil beam (spot) for the scanning spot system. A MU is defined by a fixed number of output pulses from the main dose monitor ion chamber in the scanning nozzle (Zhu et al., 2010); hence, one MU value is used to represent spot intensity and its resolution at MD Anderson is 0.0001. To ensure delivery accuracy, the minimum MU (0.005 at MD Anderson) must be set with regard to two considerations: 1) the spot dose should be higher than the expected delayed dose, which is the dose delivered after the scanning termination signal is sent; and 2) the accuracy of spot position measurement would be reduced if a lower minimum MU were used (Gillin et al., 2010). Note that at the Bragg peak, the dose delivered by a single spot with 0.005 MU is approximately 0.08 to 0.2 Gy, depending on different energies. However, deliverable minimum MU constraints are not considered in the current treatment planning system. Instead, a post-processing procedure is performed to satisfy those constraints. MU values over 0.0025 are rounded up to 0.005 and MU values below 0.0025 are rounded down to 0. Rounding errors in this procedure can result in significant distortion from the optimized dose distributions to the delivered dose distributions (Zhu et al., 2010). Distortion is exacerbated when there are more spots with small MU values, which can be caused by small spot spacing. Therefore, when designing a treatment plan, a threshold value for spot spacing needs to be set in order to resolve the tradeoff between the dosimetric advantage and delivery constraints (Zhu et al., 2010); hence, using spot spacings smaller than the threshold value is to be avoided when designing IMPT plans owing to the dose distribution deterioration caused by rounding errors.
Whereas the incorporation of MU constraints into inverse treatment planning for IMPT has not been discussed by far, the problem of limiting excessive MUs has been extensively studied in the inverse treatment planning for intensity modulated radiation therapy with photons (IMXT). Most previous studies have focused on including beam segmentation constraints in the IMXT optimization process so that more continuous fluence maps can be generated in an optimized plan (Siebers et al., 2002; Cotrutz and Xing, 2003; Romeijn et al., 2005; Bedford and Webb, 2006; Men et al., 2010). Coselmon et al specifically discussed a strategy that assigns maximum intensity limits in IMXT optimization to improve delivery efficiency without significantly degrading plan quality (Coselmon et al., 2005). Overall, approaches proposed for IMXT optimization have to address the question of deliverability with a multi-leaf collimator (MLC) and are therefore not applicable to IMPT, in which intensities for all proton scanning spots can be modulated independently. Therefore, only a minimum MU constraint is needed to guarantee the deliverability of IMPT spot scanning. To the intensity optimization problem, this study focuses on a linear program with a piecewise convex objective function. Similar models have been discussed for both IMXT and IMPT optimization (Cao et al., 2012; Romeijn et al., 2006). Two of the most important features of linear optimization, or so-called L1 minimization, are that constraints can be imposed strictly (Gass, 1958) and optimal solutions are more likely to be sparse (Candès et al., 2008).
We approach the deliverable IMPT optimization problem in two stages: 1) optimizing spot intensities with sparse and large values using linear programming (LP); and 2) re-solving the LP problem by imposing strict minimum MU constraints only on non-deliverable spot intensities. Thus, the two-stage LP approach simultaneously optimizes spot intensities and incorporates minimum MU constraints. Unlike the conventional optimization used by commercial treatment planning systems, this method allows any setup of smaller spot spacing to achieve dosimetric advantages by means of reliable delivery. The deliverable optimization model and testing cases are described in Section 2. Results on characteristics of optimized treatment plans are presented in Section 3. Insights for implementing the proposed method are discussed in Section 4 and the study is summarized in Section 5.
2. Methods
2.1. Spot intensity optimization with MU constraints
We introduce a two-stage LP model to solve the spot intensity optimization (SIO) problem by means of incorporated minimum deliverable MU constraints, i.e., a deliverable spot intensity optimization (DSIO) model. A subset of pre-arranged candidate spots is selected without MU constraints in the first stage of LP optimization and the intensities of selected spots are optimized with MU constraints in the second stage of LP optimization. The primary LP SIO model is implemented on the basis of our previous study on fluence map optimization (Lim and Cao, 2012; Cao et al., 2012).
The influence matrix dij is calculated on the basis of our in-house dose calculation algorithm (Li et al., 2011; Li et al., 2012; Zhang et al., 2011), where dij denotes the dose contributed by the jth spot per unit weight and received by voxel i with j ∈ J and i ∈ V, given that V is the set of all voxels in the treatment volume and J is the set of all pre-arranged candidate scanning spots available. Assuming that the decision variable is xj, i.e., the intensity of the spot j, the total dose in voxel i is
| (1) |
If T, Sk, and N denote the set of all voxels in the target, the kth organ at risk (OAR) and normal tissues, respectively, then . The objective function that penalizes dose deviation on target voxels and OAR voxels is formulated as follows:
| (2) |
where (·)+ represents max{·, 0}, and eT and eSk represent vectors of ones. Given that θ+ is the overdosing control parameter for the target, θ− and ϕSk are under-dosing control parameters for the target and OAR k. The values of these control parameters are not necessarily the prescription or organ tolerance doses. We chose tighter soft bounds for setting those values in our implementation of prostate cases in this paper. Specific values are generally based on trial and error. Additionally, , , and λSk are weighting factors for different objectives.
Because the LP model is generally flexible in adding hard constraints and the optimal solution is guaranteed to satisfy those constraints, dose limits on target and OAR voxels can be assigned by adding the following constraints:
| (3) |
| (4) |
| (5) |
where UB and LB represent lower and upper bounds, respectively, for different voxels. By first solving an LP (1)-(5) with appropriate parameters verified, a tentatively optimized IMPT plan can be created. Meanwhile, only a subset of pre-arranged spots is selected, i.e., optimized spot intensities greater than zero; the remaining spots are dropped, i.e., optimized spot intensities equal to zero. Assume that J1 is the set of the selected spots and J0 is the set of the dropped spots, i.e., J1 = {j : xj ≥ 0, j ∈ J}, and J0 = J\J1. In order to ensure the minimum MU constraint, a second LP (1)-(7) can be formed by adding two constraints to the first LP:
| (6) |
| (7) |
where LBMU is the lower bound for spot intensity, which is a fraction of the real minimum MU value; and ε is a very small positive value such that the feasibility of the model can be guaranteed. Feasibility would remain in the second LP mainly because only a minimal number of spots are constrained by (6) and (7), and the majority of spot intensities satisfy the MU constraint preemptively. Although the two-stage LP model is solved consecutively, most of the CPU time is spent on the first stage, whereas the second stage runs fast due to a warm start strategy.
We compared the DSIO model with a conventional spot intensity optimization (CSIO) model (Zhang et al., 2004) defined as
| (8) |
The least-square based objective function penalizes dose deviation on all voxels in the target and the OARs. As a nonlinear programming (NLP) model, the model does not contain hard constraints such as those for the minimum MU or OAR dose upper bounds; only soft constraints are included. In this CSIO, scanning spots whose MU values violate the minimum MU constraint will be post-processed to ensure a deliverable IMPT treatment plan according to the requirement of the current treatment planning system.
2.2 Patient planning setup
We studied four representative prostate cancer cases with prostate glands ranging from small to large volumes. The patients had been treated with IMPT at MD Anderson previously. The prescribed dose was 78 Gy for 39 fractions for all patients. Two parallel-opposed lateral fields were used in this study—one from the right and the other from the left. Table 1 lists proton range and energy level settings. Note that the scanning treatment volume (STV) was used in optimization according to the planning procedure for IMPT prostate cancer treatment at MD Anderson. The STV was defined using the distal margin (defined by a function of the most distal range for the clinical target volume (CTV), usually 0.9-1.1 cm for the prostate) for the patient's lateral anatomic expansion, 0.6 cm for the posterior expansion, and 0.8 cm for the expansion from the CTV to all other directions (Zhu et al., 2010). Volumes of both CTVs and STVs are also listed in Table 1. Intensities of scanning spots from both fields are simultaneously optimized by both the DSIO and CSIO models. Treatment plans with Eclipse default spot spacings (a fraction of spot size, 6-7 mm, varying between patients) and uniform spot spacings (3, 4, 5, 6, and 7 mm) were created to evaluate the proposed methods. In this study, the LP models were solved using the interior point method in CPLEX v12.1 (IBM, Armonk, New York, USA). The NLP models were solved using the limited-memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) method (Li et al., 2011). According to our previous study (Zhu et al., 2010), post-processing on spot intensities over the maximum MU (0.04) threshold has no evident impact on deviating spot scanning IMPT plan quality. We consider only the minimum MU constraint in this study.
Table 1.
Patient and treatment planning data for four prostate cancer cases.
| Right lateral field | Left lateral field | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Patient | CTV (cc) | STV (cc) | Prescription (Gy) | Max energy (Mev) | Nominal range (g/cm2) | No. of energy layers | Max energy (Mev) | Nominal range (g/cm2) | No. of energy layers |
| 1 | 29.3 | 90.3 | 78 | 198.3 | 25.2 | 19 | 195.6 | 24.6 | 18 |
| 2 | 45.7 | 120.1 | 78 | 193.0 | 24.1 | 20 | 193.0 | 24.1 | 19 |
| 3 | 69.8 | 157.3 | 78 | 195.6 | 24.6 | 23 | 198.3 | 25.2 | 24 |
| 4 | 99.1 | 233.2 | 78 | 203.7 | 26.4 | 21 | 201.0 | 25.8 | 23 |
3. Results
3.1. Treatment planning with Eclipse default spot spacing
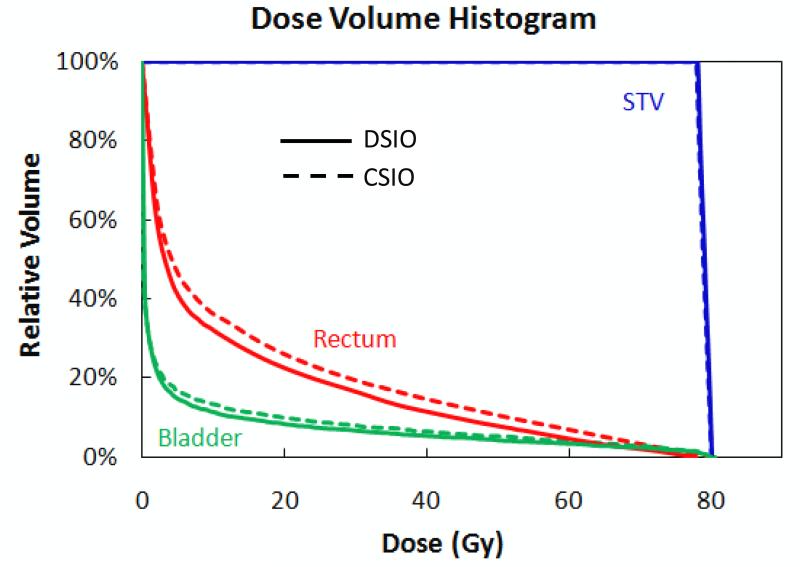
A comparison of dose volume histograms (DVHs) for the DSIO- and CSIO-optimized plans with the Eclipse default spot spacing (6.07 mm for the right field and 6.13 mm for the left field) for patient 1 is shown in Figure 1. Both the DSIO- and CSIO-optimized plans performed very similarly in terms of uniformity of STV coverage. The DSIO-optimized plan demonstrated better OAR dose sparing to both the rectum and the bladder than did the CSIO-optimized plan. Note that we consider a CSIO plan as the solution optimized by CSIO (8) with the post-processing in this study. For other patient cases with default spot spacings, we observed that the dosimetric advantage of the DSIO model over CSIO was consistent as what is shown in Figure 1.
Figure 1.
Dose volume histograms for STV, rectum, and bladder of IMPT treatment plans optimized by DSIO (solid lines) and CSIO (dashed lines) models for prostate cancer patient 1. Both plans are based on Eclipse default spot spacing settings (6.07 mm for the right field and 6.13 mm for the left field).
3.2. Treatment planning with decreased spot spacing
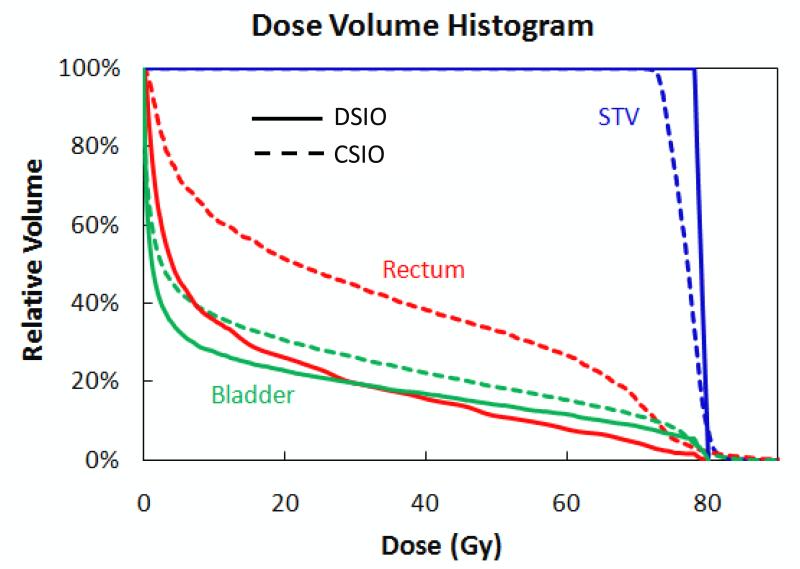
Figure 2 compares the DSIO- and CSIO-optimized plans (both with 3 mm uniform spot spacing) for patient 2. The DSIO-optimized plan was markedly superior to the CSIO-optimized plan in STV dose uniformity and rectum and bladder sparing. It is clear that the plan quality was significantly differentiated by DSIO and CSIO. This difference was greater in the 3 mm spot spacing scenario than in the default spot spacing scenario (Figure 1) mainly because the deterioration effect of CSIO post-processing increased when smaller spot spacing was used.
Figure 2.
Dose volume histograms for STV, rectum, and bladder of IMPT treatment plans optimized by DSIO (solid lines) and CSIO (dashed lines) models for prostate cancer patient 2. Both plans are based on 3 mm spot spacing settings.
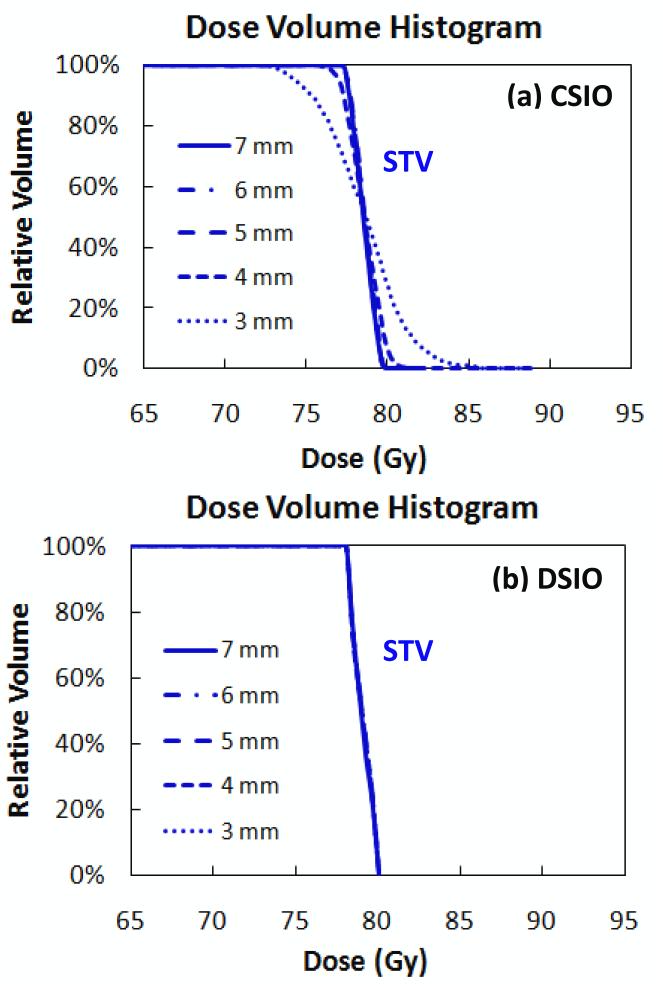
Figure 3 shows DVHs for patient 3 for the STV in both DSIO- and CSIO-optimized plans with five different uniform spot spacings, ranging from 7 mm to 3 mm. For the CSIO-optimized plans, STV dose uniformity decreased with decreased spot spacings—most markedly with the 3 mm spot spacing—whereas for the DSIO-optimized plans, STV dose uniformity was maintained, albeit with minimal variation. Dose volume statistics for the rectum and the bladder in both DSIO and CSIO plans with different spot spacings are shown in Table 2. The values used here are means calculated from the four patient cases. The DSIO model outperformed the CSIO model on rectum and bladder sparing for all dose volume measurements (V30, V40, V50, V60, and V70) and spot spacings. Moreover, with decreased spot spacings, each dose volume measurement improved in DSIO-optimized plans, while corresponding measurements were degraded in CSIO-optimized plans.
Figure 3.
Dose volume histograms for STV in IMPT treatment plans optimized by (a) CSIO and (b) DSIO models for prostate cancer patient 3. Plans are based on spot spacings of 7 mm, 6 mm, 5 mm, 4 mm, and 3 mm.
Table 2.
Mean dose volumes for four prostate cancer cases for rectum and bladder in the DSIO- and CSIO-optimized IMPT plans with different spot spacings.
| 7 mm | 6 mm | 5 mm | 4 mm | 3 mm | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ROI | Statistic | CSIO | DSIO | CSIO | DSIO | CSIO | DSIO | CSIO | DSIO | CSIO | DSIO |
| Rectum | V30 | 27.8 | 23.6 | 28.2 | 23.0 | 28.4 | 22.5 | 29.0 | 22.5 | 34.8 | 22.3 |
| V40 | 22.0 | 18.2 | 22.6 | 17.8 | 22.7 | 17.1 | 23.3 | 17.1 | 29.0 | 17.0 | |
| V50 | 17.5 | 14.5 | 17.8 | 13.7 | 17.7 | 12.8 | 18.3 | 12.8 | 23.8 | 12.7 | |
| V60 | 12.6 | 10.9 | 13.2 | 10.5 | 13.2 | 9.7 | 14.1 | 9.7 | 18.4 | 9.5 | |
| V70 | 7.9 | 6.8 | 8.5 | 6.6 | 8.6 | 6.1 | 9.1 | 6.1 | 12.4 | 5.6 | |
| Bladder | V30 | 17.9 | 16.2 | 18.0 | 15.8 | 18.2 | 15.6 | 18.8 | 15.4 | 19.8 | 15.3 |
| V40 | 15.0 | 13.5 | 15.2 | 13.2 | 15.5 | 13.0 | 15.9 | 12.9 | 16.6 | 12.8 | |
| V50 | 12.3 | 11.2 | 12.6 | 11.0 | 12.8 | 10.9 | 13.2 | 10.8 | 13.8 | 10.4 | |
| V60 | 9.7 | 9.0 | 9.9 | 8.8 | 10.1 | 8.8 | 10.6 | 8.6 | 11.2 | 8.4 | |
| V70 | 6.9 | 6.6 | 7.2 | 6.5 | 7.4 | 6.4 | 7.9 | 6.3 | 8.7 | 6.1 | |
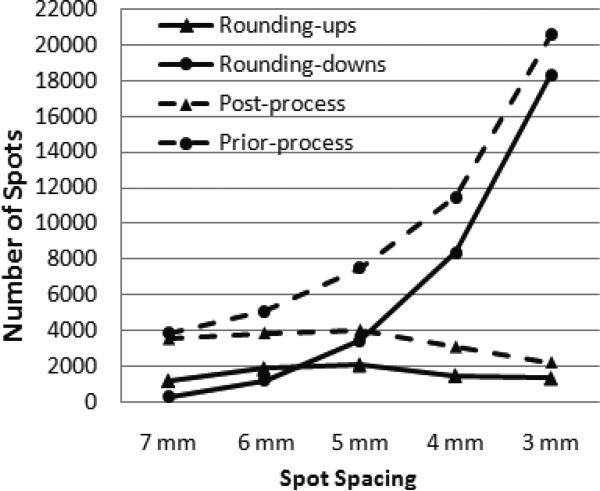
For the CSIO model, the deterioration in final dose distributions as an effect of post-processing is mainly caused by the elimination of scanning spots. One example of the scanning spot elimination is shown in Figure 4, which illustrates the number of scanning spots pre- and post-processing and the number of scanning spots associated with rounding up and down for patient 4. When spot spacing decreased from 7 mm to 3 mm, the number of pre-processed spots continued to increase, but the number of post-processed spots only increased until spot spacing decreased to 5 mm. For smaller spot spacings, such as 4 mm and 3 mm, the number of post-processed spots decreased with decreases in spot spacings. This indicated that, when spot spacing was 4 mm and 3 mm, a significant number of undeliverable spots with less than 0.0025 MU were eliminated by post-processing. Meanwhile, the number of rounding up and down is generally positively correlated with the number of post- and pre-processing scanning spots when the spot spacing decreases.
Figure 4.
Numbers of spots processed by rounding up and rounding down during post-processing (solid lines), and numbers of spots available before and after post-processing (dashed lines), in CSIO-optimized IMPT treatment plans with different spot spacings (i.e., 7 mm, 6 mm, 5 mm, 4mm, and 3 mm) for prostate cancer patient 4.
Although spot spacing decreased and the number of available scanning spots increased, deliverable scanning spots from DSIO consistently made up small subsets of default spots. When the spot spacing was relatively big (e.g., 7 mm and 6 mm), CSIO used more deliverable scanning spots than did DSIO. For example, with the decreased spot spacings of 7, 6, 5, 4, and 3 mm, the fraction of the used spots over the total number of scanning spots was 88.0%, 72.2%, 58.1%, 31.8%, and 7.4% for the CSIO plans; and 28.6%, 21.9%, 14.7%, 9.9% and 5.4% for the DSIO plans for patient 2.
The time used for either CSIO or DSIO increased when smaller spot spacings were used. Although the selection of spots and optimization of spot intensity can be computed by DSIO simultaneously, solution times were much longer for cases with smaller spot spacings. Solution times ranged from approximately 5 minutes to 1 hour for spot spacings from 7 mm to 3 mm in this prostate study.
3.3. Optimized sparse spot selection
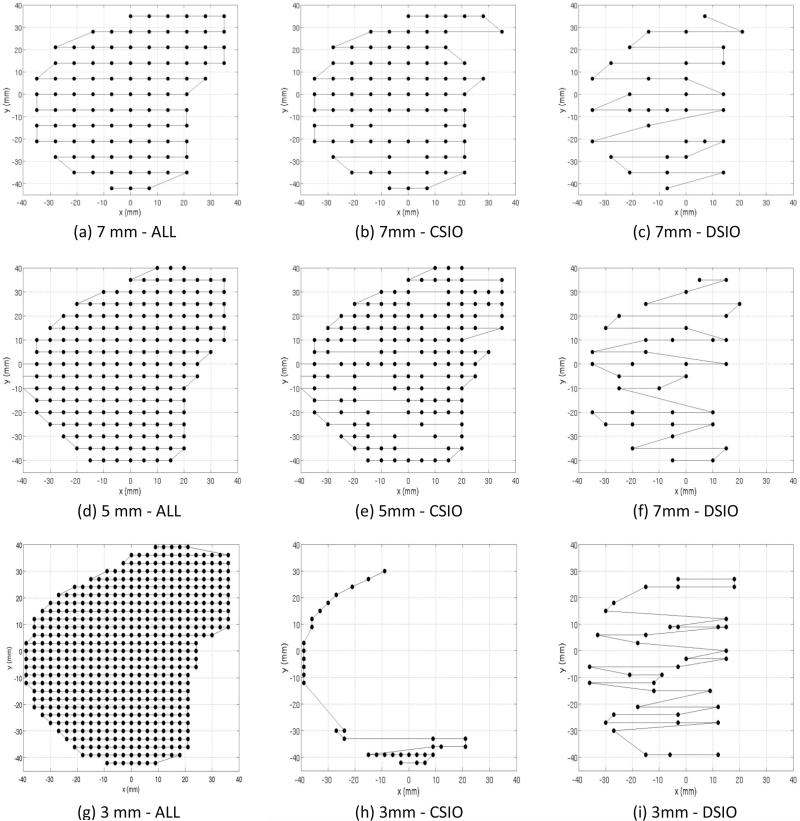
In our study, DSIO-optimized treatment plans exhibited an inhomogeneous spatial distribution of spots. Whereas pre-arranged scanning spots were generally set by a uniform arrangement and deliverable scanning spots in CSIO-optimized plans were positioned by non-optimal post-processing, a sparse spot selection was optimized by the DSIO model. As an example, Figure 5 shows spot arrangements in one energy layer (with 173.7 MeV of energy from the right field) in pre-optimized and CSIO- and DSIO-optimized plans with 7, 5, and 3 mm spot spacings for patient 2. Prior to spot intensity optimization, uniformly pre-arranged scanning spots were located more densely as spot spacing decreased. In CSIO-optimized plans, more reductions of deliverable scanning spots were seen when spot spacing decreased. A majority of spots were dropped, with the rest only positioned on the edge of the energy layer when spot spacing was 3 mm. In DSIO-optimized plans, with decreased spot spacing, the number of spots showed no pronounced increase and spot arrangements remained inhomogeneous. All energy layers in all patient cases exhibited a similar pattern as shown in Figure 5.
Figure 5.
Scanning spot positions of one energy layer (176.25 MeV) for pre-optimization (in panels [a], [d], and [g]), CSIO-optimized plans (in panels [b], [e], and [h]) and DSIO-optimized plans (in panels [c], [f], and [i]) with three different spot spacings (7mm, 5mm, and 3mm) for prostate cancer patient case 2.
4. Discussion
Whereas deliverable MU constraints can be included in a two-stage IMPT optimization approach, they have yet been considered in the optimization process in the current mainstream treatment planning system. A post-optimization process for rounding non-deliverable MU values is no longer needed in the proposed approach. The distortion between optimized and the delivered dose distributions caused by rounding errors can also be avoided. It is recommended that spot spacing be at least 6 mm to prevent excessive rounding errors in IMPT plans with two lateral fields for prostate cancer patients at MD Anderson (Zhu et al., 2010). When the proposed deliverable optimization approach is applied, different spot spacing settings can be realized in IMPT planning, thereby improving plan quality. In studies on patients with prostate cancer with the two lateral fields, as smaller spot spacing was used, improved target dose uniformity and OAR sparing were achieved. Most importantly, a common strategy for creating more complex dose distributions is to employ more scanning spots, initially arranged by smaller uniform spot spacings, thus allowing more degrees of freedom for modulation. The proposed DSIO approach therefore provides an important tool to improve IMPT plan quality for other more complex patient cases in addition to prostate as studied in this work. The optimal spot spacing for specific cancer sites and individual patients has still not been determined in IMPT treatment planning. A planner currently has to use trial and error to determine the best spot spacing for maximizing dosimetric benefits for each individual patient. With the proposed approach, the planner can safely choose smaller spot spacing as long as manageable optimization time is retained.
In IMPT treatment planning, the spatial arrangement of scanning spots in a tumor target is critical to treatment plan quality. Different spot intensity optimization methods, including both mathematical programming models and solution algorithms, result in different optimal solution characteristics. Nonlinear models, such as CSIO with a least-square based objective, and gradient-based algorithms are prevailing for optimizing spot intensity in IMPT treatment planning in clinical practices (Albertini et al., 2010; Liu et al., 2012; Unkelbach et al., 2007), which is an application similar to conventional IMXT treatment planning (Spirou and Chui, 1998; Aleman et al., 2010; Bortfeld, 1999; Wu and Mohan, 2000; Zhang et al., 2004). In this study, we have demonstrated that in both the commercial treatment planning system (Varian Medical Systems, 2007) and an in-house optimization routine (Li et al., 2011), intensities of all scanning spots pre-arranged with uniform spot spacing are optimized with positive values by such nonlinear approaches. Ideally, these results indicate that all pre-arranged spots will be delivered if no MU constraint exists. In contrast, the LP based DSIO model would create improved dose distributions (as with the nonlinear CSIO model) with only a fraction of the pre-arranged spots required for delivery. In fact, only a fraction of spots are optimized by DSIO with positive intensities and others are with zero intensities. This pattern of sparse solutions is mainly due to the modeling choice of DSIO.
One potential benefit of the DSIO approach is that it maximally reduces IMPT delivery time by both reducing scanning spots together with the optimized scanning path (Kang et al., 2007) and reducing energy layers (Kang et al., 2008). Another advantage of using the DSIO model to optimize spot intensities in IMPT treatment planning is that it allows for automatic sparse selection of scanning spots in a non-uniform arrangement. Without designated extra optimization for spot arrangement, an inhomogeneous distribution of deliverable scanning spots is automatically determined to “represent” all candidate spots with uniform spacing. Thus, when creating desired dose distributions, unnecessary spots can be identified and dropped for delivery with the DSIO model, whereas unnecessary spots cannot be identified with the CSIO model. Most importantly, with any given spot spacing from 3 mm to 7 mm, the DSIO can create a dose distribution superior to that of the CSIO model and uses fewer delivered spots. Incorporating objectives or constraints on specific spot arrangement requirements into a conventional spot intensity optimization model (e.g., reducing the number of spots or arranging spots with non-uniform spacing) requires integer variables to form a mixed-integer program (MIP) or a mixed-integer nonlinear program (MINLP); model complexity and computational difficulty would increase dramatically. Using a linear model such as the one implemented in this study could incur the lowest computational cost among other alternative methods.
5. Conclusions
We have introduced a two-stage optimization approach to simultaneously optimize spot intensities and incorporate minimum deliverable MU constraints in IMPT treatment planning. Unlike current commercial treatment planning systems, this approach allows treatment planners to use small spot spacings to improve dosimetric performance of IMPT plans without diminishing delivery reliability. Our study of four prostate cancer cases demonstrated that when decreased spot spacings are used for IMPT plans, the better plan quality in terms of target dose uniformity and normal sparing can be achieved. The proposed approach avoids the troublesome post-processing routine required by current IMPT treatment planning systems. More importantly, the use of trial-and-error to determine appropriate spot spacing can be eliminated. In addition, the deliverable spot intensity optimization model can automatically generate a sparse selection of deliverable scanning spots in a non-uniform arrangement. Therefore, deliverable scanning spots are selected as part of the optimization process without a post-processing step.
Acknowledgments
The authors thank Radhe Mohan, Wei Liu, and Kazumichi Suzuki for their helpful comments. We are also very grateful to Amelia Scholtz for her editorial assistance to improve the presentation of manuscript. This research is supported through National Cancer Institute grant P01CA021239 and The University of Texas MD Anderson Cancer Center support grant CA016672. Part of this work was presented at the 54th American Association of Physicists in Medicine (AAPM) Annual Meeting as an oral presentation.
Contributor Information
Wenhua Cao, Department of Industrial Engineering, University of Houston, Houston, Texas 77204.
Gino Lim, Department of Industrial Engineering, University of Houston, Houston, Texas 77204.
Xiaoqiang Li, Department of Radiation Physics, The University of Texas MD Anderson Cancer Center, Houston, Texas 77030.
Yupeng Li, Department of Radiation Physics, The University of Texas MD Anderson Cancer Center, Houston, Texas 77030.
X. Ronald Zhu, Department of Radiation Physics, The University of Texas MD Anderson Cancer Center, Houston, Texas 77030.
Xiaodong Zhang, Department of Radiation Physics, The University of Texas MD Anderson Cancer Center, Houston, Texas 77030.
References
- Albertini F, Hug EB, Lomax AJ. The influence of the optimization starting conditions on the robustness of intensity-modulated proton therapy plans. Phys. Med. Biol. 2010;55:2863. doi: 10.1088/0031-9155/55/10/005. [DOI] [PubMed] [Google Scholar]
- Aleman DM, Glaser D, Romeijn HE, Dempsey JF. Interior point algorithms: guaranteed optimality for fluence map optimization in IMRT. Phys. Med. Biol. 2010;55:5467–82. doi: 10.1088/0031-9155/55/18/013. [DOI] [PubMed] [Google Scholar]
- Bedford JL, Webb S. Constrained segment shapes in direct-aperture optimization for step-and-shoot IMRT. Med. Phys. 2006;33:944–58. doi: 10.1118/1.2163832. [DOI] [PubMed] [Google Scholar]
- Bortfeld T. Optimized planning using physical objectives and constraints Seminars in Radiation. Oncology. 1999;9:20–34. doi: 10.1016/s1053-4296(99)80052-6. [DOI] [PubMed] [Google Scholar]
- Candès E, Wakin M, Boyd S. Enhancing sparsity by reweighted l1 minimization. Journal of Fourier Analysis and Applications. 2008;14:877–905. [Google Scholar]
- Cao W, Lim GJ, Lee A, Li Y, Liu W, Zhu XR, Zhang X. Uncertainty incorporated beam angle optimization for IMPT treatment planning. Med. Phys. 2012;39:5248–56. doi: 10.1118/1.4737870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coselmon MM, Moran JM, Radawski JD, Fraass BA. Improving IMRT delivery efficiency using intensity limits during inverse planning. Med. Phys. 2005;32:1234–45. doi: 10.1118/1.1895545. [DOI] [PubMed] [Google Scholar]
- Cotrutz C, Xing L. Segment-based dose optimization using a genetic algorithm. Phys. Med. Biol. 2003;48:2987. doi: 10.1088/0031-9155/48/18/303. [DOI] [PubMed] [Google Scholar]
- Gass SI. Linear programming: methods and applications. McGraw-Hill; 1958. [Google Scholar]
- Gillin MT, Sahoo N, Bues M, Ciangaru G, Sawakuchi G, Poenisch F, Arjomandy B, Martin C, Titt U, Suzuki K, Smith AR, Zhu XR. Med. Phys. Vol. 37. Anderson Cancer Center, Proton Therapy Center; Houston: 2010. Commissioning of the discrete spot scanning proton beam delivery system at the University of Texas M.D. pp. 154–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang JH, Wilkens JJ, Oelfke U. Demonstration of scan path optimization in proton therapy. Med. Phys. 2007;34:3457–64. doi: 10.1118/1.2760025. [DOI] [PubMed] [Google Scholar]
- Kang JH, Wilkens JJ, Oelfke U. Non-uniform depth scanning for proton therapy systems employing active energy variation. Phys. Med. Biol. 2008;53:N149. doi: 10.1088/0031-9155/53/9/N01. [DOI] [PubMed] [Google Scholar]
- Li Y, Zhang X, Mohan R. An efficient dose calculation strategy for intensity modulated proton therapy. Phys. Med. Biol. 2011;56:N71–84. doi: 10.1088/0031-9155/56/4/N03. [DOI] [PubMed] [Google Scholar]
- Li Y, Zhu RX, Sahoo N, Anand A, Zhang X. Beyond Gaussians: a study of single spot modeling for scanning proton dose calculation. Phys. Med. Biol. 2012;57:983–97. doi: 10.1088/0031-9155/57/4/983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lim GJ, Cao W. A two-phase method for selecting IMRT treatment beam angles: Branch-and- Prune and local neighborhood search European. Journal of Operational Research. 2012;217:609–18. [Google Scholar]
- Liu W, Zhang X, Li Y, Mohan R. Robust optimization of intensity modulated proton therapy. Med. Phys. 2012;39:1079–91. doi: 10.1118/1.3679340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lomax A. Intensity modulation methods for proton radiotherapy. Phys. Med. Biol. 1999;44:185–205. doi: 10.1088/0031-9155/44/1/014. [DOI] [PubMed] [Google Scholar]
- Lomax A, Böhringer T, Bolsi A, Coray D, Emert F, Goitein G, Jermann M, Lin S, Pedroni E, Rutz H, Stadelmann O, Timmermann B, Verwey J, Weber DC. Treatment planning and verification of proton therapy using spot scanning: Initial experiences. Med. Phys. 2004;31:3150–7. doi: 10.1118/1.1779371. [DOI] [PubMed] [Google Scholar]
- Men C, Jia X, Jiang SB. GPU-based ultra-fast direct aperture optimization for online adaptive radiation therapy. Phys. Med. Biol. 2010;55:4309. doi: 10.1088/0031-9155/55/15/008. [DOI] [PubMed] [Google Scholar]
- Robertson D, Zhang X, Li Y, Lee A, Gillin M, Zhu X, Mohan R. Optimizing spot spacing and margin for intensity-modualted proton therapy planning. Med. Phys. 2009;36:2554. [Google Scholar]
- Romeijn HE, Ahuja RK, Dempsey JF. A new linear programming approach to radiation therapy treatment planning problems. Operation Research. 2006;54:201–16. [Google Scholar]
- Romeijn HE, Ahuja RK, Dempsey JF, Kumar A. A column generation approach to radiation therapy treatment planning using aperture modulation. SIAM J. on Optimization. 2005;15:838–62. [Google Scholar]
- Siebers JV, Lauterbach M, Keall PJ, Mohan R. Incorporating multi-leaf collimator leaf sequencing into iterative IMRT optimization. Med. Phys. 2002;29:952–9. doi: 10.1118/1.1477230. [DOI] [PubMed] [Google Scholar]
- Smith AR, Gillin M, Bues M, Zhu XR, Suzuki K, Mohan R, Woo S, Lee A, Komaki R, Cox J, Hiramoto K, Akiyama H, Ishida T, Sasaki T, Matsuda K. The M. D. Anderson proton therapy system. Med. Phys. 2009;36:4068–83. doi: 10.1118/1.3187229. [DOI] [PubMed] [Google Scholar]
- Spirou SV, Chui C-S. A gradient inverse planning algorithm with dose-volume constraints. Med. Phys. 1998;25:321–33. doi: 10.1118/1.598202. [DOI] [PubMed] [Google Scholar]
- Unkelbach J, Chan TCY, Bortfeld T. Accounting for range uncertainties in the optimization of intensity modulated proton therapy. Phys. Med. Biol. 2007;52:2755. doi: 10.1088/0031-9155/52/10/009. [DOI] [PubMed] [Google Scholar]
- Varian Medical Systems Proton algorithm reference guide, Chapter 6: Eclipse proton optimizer for modulated scanning. 2007 P/N B500299R01C.
- Wu Q, Mohan R. Algorithms and functionality of an intensity modulated radiotherapy optimization system. Med. Phys. 2000;27:701–11. doi: 10.1118/1.598932. [DOI] [PubMed] [Google Scholar]
- Zhang X, Liu H, Wang X, Dong L, Wu Q, Mohan R. Speed and convergence properties of gradient algorithms for optimization of IMRT. Med. Phys. 2004;31:1141–52. doi: 10.1118/1.1688214. [DOI] [PubMed] [Google Scholar]
- Zhang X, Liu W, Li Y, Li X, Quan M, Mohan R, Anand A, Sahoo N, Gillin M, Zhu XR. Parameterization of multiple Bragg curves for scanning proton beams using simultaneous fitting of multiple curves. Phys. Med. Biol. 2011;56:7725–35. doi: 10.1088/0031-9155/56/24/003. [DOI] [PubMed] [Google Scholar]
- Zhu XR, Sahoo N, Zhang X, Robertson D, Li H, Choi S, Lee AK, Gillin MT. Intensity modulated proton therapy treatment planning using single-field optimization: The impact of monitor unit constraints on plan quality. Med. Phys. 2010;37:1210–9. doi: 10.1118/1.3314073. [DOI] [PMC free article] [PubMed] [Google Scholar]