Coastal flood damage and adaptation costs under 21st century sea-level rise

Significance

Coastal flood damages are expected to increase significantly during the 21st century as sea levels rise and socioeconomic development increases the number of people and value of assets in the coastal floodplain. Estimates of future damages and adaptation costs are essential for supporting efforts to reduce emissions driving sea-level rise as well as for designing strategies to adapt to increasing coastal flood risk. This paper presents such estimates derived by taking into account a wide range of uncertainties in socioeconomic development, sea-level rise, continental topography data, population data, and adaptation strategies.

Abstract

Coastal flood damage and adaptation costs under 21st century sea-level rise are assessed on a global scale taking into account a wide range of uncertainties in continental topography data, population data, protection strategies, socioeconomic development and sea-level rise. Uncertainty in global mean and regional sea level was derived from four different climate models from the Coupled Model Intercomparison Project Phase 5, each combined with three land-ice scenarios based on the published range of contributions from ice sheets and glaciers. Without adaptation, 0.2–4.6% of global population is expected to be flooded annually in 2100 under 25–123 cm of global mean sea-level rise, with expected annual losses of 0.3–9.3% of global gross domestic product. Damages of this magnitude are very unlikely to be tolerated by society and adaptation will be widespread. The global costs of protecting the coast with dikes are significant with annual investment and maintenance costs of US$ 12–71 billion in 2100, but much smaller than the global cost of avoided damages even without accounting for indirect costs of damage to regional production supply. Flood damages by the end of this century are much more sensitive to the applied protection strategy than to variations in climate and socioeconomic scenarios as well as in physical data sources (topography and climate model). Our results emphasize the central role of long-term coastal adaptation strategies. These should also take into account that protecting large parts of the developed coast increases the risk of catastrophic consequences in the case of defense failure.

Although increased coastal flood damage and corresponding adaptation may be one of the most costly aspects of climate change (1), few studies have assessed this impact globally. The first of these studies considered flood risk to people under a 1-m sea-level rise and adaptation via dikes, but without socioeconomic change (2). Follow-up studies refined this analysis in several directions: (i) adding a range of sea-level scenarios and a single socioeconomic scenario (3, 4), (ii) applying a range of socioeconomic scenarios (5), (iii) extending the resolution of the coastal zone to subnational levels (6, 7), and (iv) including regional patterns of climate-induced sea-level rise (6). These studies further differ in the digital elevation model (DEM) and spatial population datasets used, as well as the adaptation strategies applied. No study has, however, explored all of these dimensions together.

This paper addresses this gap and assesses the impacts of increased coastal flooding on population and assets by comparing results attained using various available data sources and adaptation strategies under a comprehensive sample of state-of-the-art socioeconomic and sea-level rise scenarios. Flood risk is considered in terms of expected annual damage to assets, expected annual number of people flooded, and adaptation costs in terms of dike investment and additional maintenance costs. We apply the Dynamic Interactive Vulnerability Assessment (DIVA) model (8) that currently offers, to our knowledge, both the most detailed global scale representation of the coastal zone and the most comprehensive and advanced representation of relevant processes at global scale.

To explore the role of input data uncertainty, multiple input datasets are used. For DEM data, we use the Global Land One-kilometer Base Elevation (GLOBE) (9) dataset and the Shuttle Radar Topography Mission (SRTM) (10). For population data, we use the population density grid of the Global Rural–Urban Mapping Project (GRUMP) (Version 1) (11), and the LandScan high-resolution global population dataset (12).

For adaptation, we follow earlier studies and consider a common protection approach using dikes (2, 4, 7, 13, 14) contrasting two strategies. In the constant protection strategy, dikes are maintained at their height, but not raised, so flood risk increases with time as relative sea level rises. In the enhanced protection strategy, dikes are raised following both relative sea-level rise and socioeconomic development (i.e., dikes are raised as the demand for safety increases with growing affluence and increasing population density).

For sea-level rise, we generate regional state-of-the-art projections of the four main contributors: oceanic thermal expansion (15), mass changes from glaciers (16), and the Greenland (17) and Antarctic ice sheets (18). The scenarios produced span three representative concentration pathways (RCPs 2.6, 4.5, and 8.5), four general circulation models (GCMs) (HadGEM2-ES, IPSL-CM5A-LR, MIROC-ESM-CHEM, and NorESM1-M) and a low, medium and high land-ice scenario. For socioeconomics, we use five population and gross domestic product (GDP) growth scenarios based on the shared socioeconomic pathways (SSPs 1–5) taken from ref. 19 (Table 1).

Table 1.

Global population and GDP in 2050 and 2100 under different SSPs

	Population in millions		GDP, billion US$/y
SSP	2050	2100	2050	2100
SSP1	8,400	7,200	295,000	771,000
SSP2	9,300	9,800	260,000	685,000
SSP3	10,300	14,100	169,000	355,000
SSP4	9,400	11,800	242,000	462,000
SSP5	8,500	7,700	348,000	1,207,000

Results

Exposure.

The areas exposed to coastal flooding estimated with the SRTM DEM are smaller than those estimated with the GLOBE DEM (Table 2). This difference is largely due to SRTM being a surface model where elevation values in low-lying areas may be offset due to land cover (e.g., a mangrove forest or built environment) (20). Exposed population and assets are lower under LandScan than under GRUMP. The reason for this is that LandScan tends to distribute population in a more concentrated way than GRUMP, with less people being in close proximity to the coastline (20). The lower exposure under LandScan is more pronounced for SRTM, which is a surface model and therefore it is likely that coastal areas with concentrated population are not captured as low-lying due to the presence of built environment.

Table 2.

Global exposed area, population, and assets below the 100-y flood event in 2010

DEM	Population data	Exposure below 100-y flood
		Area, 103 km2	Population in millions	Assets, billion US$
GLOBE	GRUMP	1,200	310	11,000
GLOBE	LandScan	1,200	290	9,600
SRTM	GRUMP	660	160	4,700
SRTM	LandScan	660	93	3,100

Sea-Level Projections.

All sea-level projections are given with respect to the 1985–2005 reference period. While the median global mean sea-level rise is projected as 35 cm for RCP2.6 and 74 cm for RCP8.5 (Table 3), the highest projected global mean sea-level rise across all models and emission scenarios is 123 cm. The greatest median contribution comes from oceanic thermal expansion, closely followed by mountain glaciers and ice caps, but if considered as a whole, land-ice is projected to contribute most to future sea-level rise. Similar to the Fifth Assessment Report (AR5) of the Intergovernmental Panel on Climate Change (21), the most uncertain contribution by far comes from the Antarctic ice sheet, with a long-tailed risk of very-high sea-level rise (up to 41 cm in the RCP8.5 scenario, whereas the median lies around 10 cm, and the lower bound around 2 cm). Our projections for Antarctica sample uncertainties associated with ice-shelf melting and ice flow in a comprehensive manner, thereby yielding a broader sea-level rise range than in AR5. Uncertainty in the GCM forcing is also substantial: under the RCP8.5 scenario, median sea-level projections for each GCM range from 64 to 86 cm (Table 3).

Table 3.

Global mean sea-level rise in 2100 with respect to 1985–2005

			Land-ice, cm
Scenario	Model	Steric, cm	Glacier	Antarctica	Greenland	Sum	Total, cm
RCP2.6	HadGEM2-ES	14	14 (14,15)	7 (2,23)	0 (0, 0)	21 (16,39)	35 (29,52)
	IPSL-CM5A-LR	12	12 (12,12)	7 (2,23)	0 (0, 0)	19 (13,36)	30 (25,47)
	MIROC-ESM-CHEM	19	13 (13,13)	7 (2,23)	0 (0, 0)	20 (14,36)	39 (34,56)
	NorESM1-M	15	11 (11,12)	7 (2,23)	0 (0, 0)	18 (13,35)	34 (28,50)
	ALL	15	13 (12,13)	7 (2,23)	0 (0, 0)	20 (14,36)	35 (29,51)
RCP4.5	HadGEM2-ES	18	17 (16,19)	8 (2,29)	7 (5, 8)	32 (23,56)	50 (41,75)
	IPSL-CM5A-LR	18	14 (14,15)	8 (2,29)	8 (7, 10)	30 (22,53)	48 (40,71)
	MIROC-ESM-CHEM	25	15 (14,16)	8 (2,29)	9 (7, 11)	32 (24,56)	57 (48,81)
	NorESM1-M	20	13 (13,14)	8 (2,29)	3 (2, 4)	24 (17,49)	44 (37,67)
	ALL	20	15 (14,16)	8 (2,29)	7 (5, 8)	29 (21,53)	50 (42,73)
RCP8.5	HadGEM2-ES	29	22 (20,26)	10 (2,41)	12 (10, 14)	44 (31,81)	72 (60,110)
	IPSL-CM5A-LR	30	18 (17,20)	10 (2,41)	15 (12, 18)	43 (31,79)	73 (61,109)
	MIROC-ESM-CHEM	38	19 (18,21)	10 (2,41)	19 (15, 23)	49 (36,85)	86 (74,123)
	NorESM1-M	32	16 (16,17)	10 (2,41)	6 (5, 8)	33 (23,66)	64 (55,97)
	ALL	32	19 (18,21)	10 (2,41)	13 (10, 16)	42 (30,78)	74 (62,110)

The median as well as the 5% and 95% quantiles (in parentheses) are provided.

In addition to the global mean projections used here, we apply a regional distribution that accounts for gravitational and rotational effects from changes in ice masses (22) and changes in ocean circulation (23). As a consequence sea-level rise is generally higher in the tropics than it is at high latitudes (24). These projections are based on process-based models. Whereas higher projections may be obtained from semiempirical models (25), we follow here the approach of AR5 of using process-based models only as there is low agreement on the reliability of semiempirical models (21).

Impacts.

We present impacts from 2000 to 2100 relative to the global mean temperature anomaly with respect to 1985–2005. All costs are reported in 2005 US$ and not discounted. For clarity, the figures only show results attained using GRUMP as the LandScan results are similar. We also disregard SSP4 as its intermediate population and GDP numbers do not contribute to the uncertainty ranges.

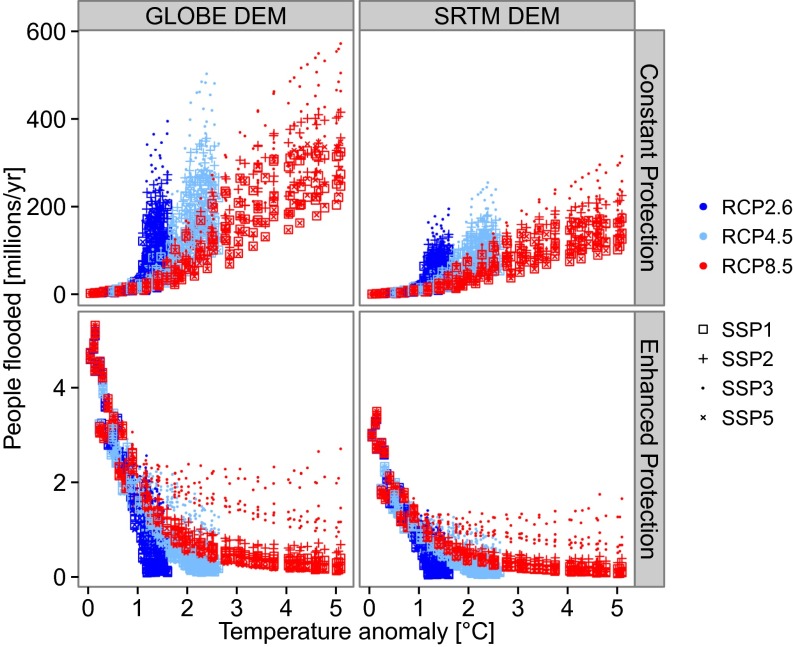
The expected annual number of people flooded is highest under SSP3 and lowest under SSP1, reflecting the highest and lowest population numbers under these scenarios (Fig. 1). Under constant protection, impacts grow throughout the century under all socioeconomic scenarios despite decreasing population under SSP1 and SSP5 from 2050 onwards (see SI Text, Results over Time). Using the GLOBE DEM, impacts are about two times higher than those estimated using the SRTM DEM. Under constant protection, 0.2–2.9% of the global population is expected to be flooded annually in 2100 under RCP2.6 and 0.5–4.6% under RCP8.5. Enhanced protection reduces impacts by about 2 orders of magnitude. In this case, the influence of the socioeconomic scenario on people flooded is smaller compared with the influence under constant protection. This is because the effect of increasing exposure due to socioeconomic development is compensated by increasing wealth and hence higher dikes. An exception is the extreme scenario SSP3, under which population grows fastest, but GDP and hence dike height grow the slowest.

Fig. 1.

Global expected annual number of people flooded from 2000 to 2100 versus global mean temperature anomaly with respect to 1985–2005.

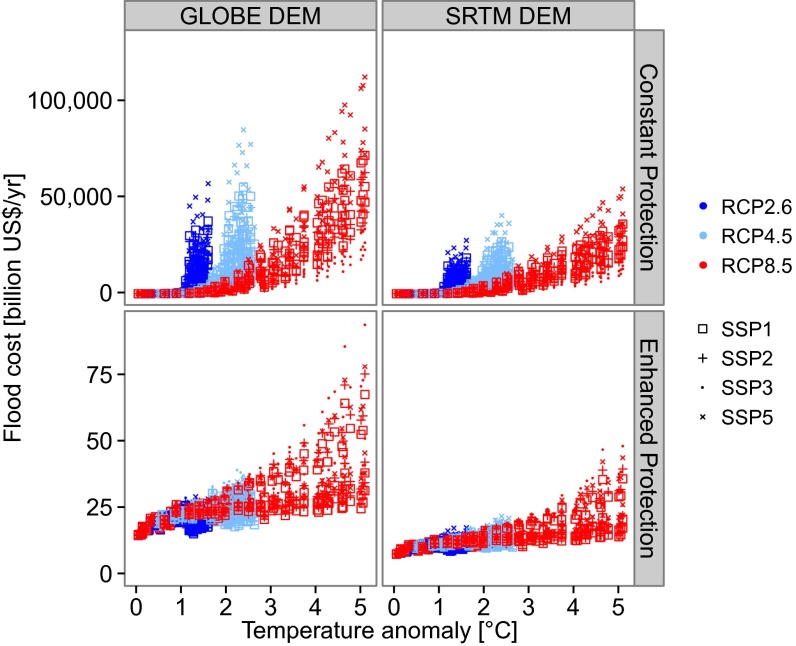
The picture for flood costs is similar to the one for people flooded. Impacts increase significantly and in similar magnitudes throughout the century under constant protection (see SI Text, Results over Time). Flood costs grow a bit slower at the beginning of the century, but then accelerate faster than the number of people flooded, as GDP per capita grows faster than population. The value of assets below the height of the 100-y flood event reaches US$ 17–180 trillion under RCP2.6 and US$ 21–210 trillion under RCP8.5 in 2100. Under constant protection damage, costs are 0.3–5.0% of global GDP in 2100 under RCP2.6 and 1.2–9.3% under RCP8.5.Under enhanced protection, impacts are about 2–3 orders of magnitude lower, but this time also increase slightly during the century (again as income grows faster than population). With constant protection, flood costs are highest under SSP5 and lowest under SSP3 (Fig. 2). With enhanced protection and particularly for GLOBE, flood costs are highest under SSP3. This scenario has the lowest GDP and hence the lowest capacity to adapt, so dike heights are also lowest and therefore damages increase.

Fig. 2.

Global expected annual flood cost from 2000 to 2100 versus global mean temperature anomaly with respect to 1985–2005.

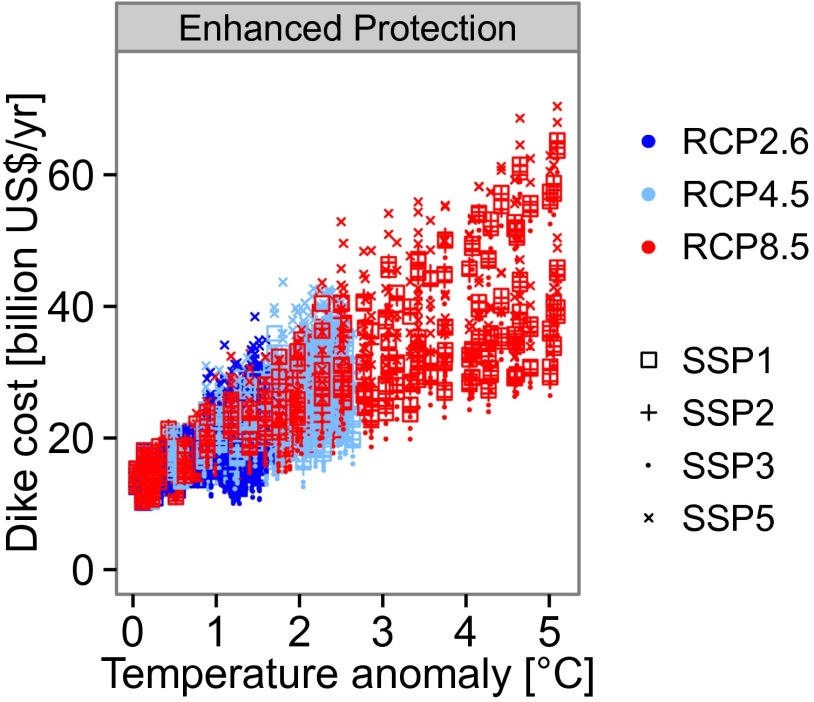
Dike costs comprise annual investment cost (for building and upgrading dikes) and the cost of maintaining the additional dike stock built since the base year of 1995. In 2100, these costs range from US$ 12–31 billion under RCP2.6 to US$ 27–71 billion under RCP8.5. Maintaining the dikes existing in 1995 will involve substantial additional costs, too, but these are not ascribed to sea-level rise. Dike costs are identical under GLOBE and SRTM, as, in our model, building dikes does not depend on the exposed area, but only on population density and GDP per capita. Dike costs are highest under SSP5 as this is the richest world with the highest demand for safety and hence highest protection level. Conversely, dike costs are lowest under SSP3, which reflects the poorest world. When following the enhanced protection strategy, dike costs level off toward the mid- and end of the century for RCP2.6 and to some extent also for RCP4.5 (in particular combined with low population world of SSP5), whereas for RCP8.5 they rise until the end of the century (and beyond). The additional costs of protecting against sea-level rise via dikes are proportional to sea level rise, which itself is roughly linear in temperature at this time scale (Fig. 3).

Fig. 3.

Global annual dike cost (capital and additional maintenance cost) from 2000 to 2100 versus global mean temperature anomaly with respect to 1985–2005.

Impacts are most sensitive to the variation of the adaptation strategy (Table 4). This is not surprising as the constant protection adaptation strategy constitutes illustrative but implausible assumptions, which are that development continues in the coastal flood plain under rising sea levels and no protection upgrade (7). In reality, societies will adapt. Growing flood risk would either lead to higher protection standards or divert new development to other locations and displace existing people and development without protection. Hence, damages would not grow to the values shown in the model. We included the no-protection strategy because it is widely used in climate impact literature and corresponds to the notion of potential impacts.

Table 4.

Sensitivity of impacts in 2100 to the seven uncertainty dimensions considered

Dimension	No. of people flooded, millions/y	Flood cost, billion US$/y	Dike cost, billion US$/y
DEM	75	9,500	0.6
Population data	20	2,200	0.2
SSP	60	12,000	3.1
RCP	57	9,800	12.0
GCM	17	3,100	3.3
Land-ice scenario	43	7,600	7.8
Adaptation strategy	170	22,000	30.0

Sensitivity is calculated as average difference between the maximum and minimum impacts in 2100 attained through varying inputs along a single uncertainty dimension while fixing the other six dimensions.

Of the other six dimensions, DEM, SSP, RCP, and the land-ice model uncertainty are roughly of equal importance, with the SSP being relatively more important for flood cost as GDP growth rates differ more between the SSPs than population growth rates. The sensitivities to the GCMs and variations in population distribution data are relevant but smaller.

Discussion

The results attained here are in the same range as those of national studies (SI Text, Flood Model Validation), but a number of uncertainties inherent to the nature of global socioeconomic coastal analysis remain. Although elevation data can be improved at local scales through high-accuracy field measurements or using land-use datasets to correct the offset in surface models (26), such corrections cannot currently be applied on a global scale due to logistical and computational constraints. Hence, this is likely to remain a significant constraint on global analyses and the analyses of relative impacts are more robust than the absolute results which should be taken as indicative.

For many locations it is observed that coastal population and asset exposure are growing faster than the national average trends assumed here due to coastward migration and urbanization (27). This process is expected to continue in the coming decades, but capturing this in global scenarios would be a major research undertaking as the drivers of migration and urbanization are complex and variable (28). Moreover, we neglect to account here for groundwater depletion for human use, which was projected to contribute up to about 8 cm to global sea-level rise by the end of the century (29). In addition to sea-level rise, possible changes in storminess and potential increases in cyclone intensity may alter flood damage (25) but are not considered here.

Another major source of uncertainty is human-induced subsidence as a result of the withdrawal of ground fluids, in particular within densely populated deltas, which may lead to rates of local relative sea-level rise that are 1 order of magnitude higher than current rates of climate-induced global-mean sea-level rise (30, 31). Unlike natural glacial isostatic adjustment where global models are available (32), it is difficult to model how this trend will continue as information on annual rates of human-induced subsidence is extremely limited and both the drivers and responses are localized (33). Indirect damages in terms of disruption of economic growth are not considered. These might be significant, in particular for poor countries and major events (34).

Adaptation as modeled here and in all earlier global assessments is stylized. Adaptation costs are thus indicative and would increase with, for example, higher estimates of the defended length of coast. Additional costs would arise for protecting developments along the lower reaches of rivers susceptible to flooding from the sea. More adaptation options are available for flood risk management than dikes, and global adaptation in the real world is the sum of a myriad of local and likely diverse adaptation decisions. Previous studies have contrasted retreat with protection options but only considering permanent dry land loss due to submergence and not flood damage (13, 35). More comprehensive analyses of global adaptation options are required, with a realistic next step to be a comparison of stylized protection, accommodation, and retreat options for flood risk.

Materials and Methods

Sea-Level Rise Scenarios.

Steric contributions for the sea-level rise projections are taken from four GCMs from the Coupled Model Intercomparison Project Phase 5 (CMIP5) archive. The contribution of glaciers and ice caps to global mean sea-level rise was taken from ref. 16. They model the past and future mass balance of all glaciers contained in the Randolph Glacier Inventory based on air temperature and precipitation anomalies obtained from the CMIP5 climate models, added to the observed climatologies of ref. 36. Although ice loss by calving is not included in the method, the dataset used for validation includes calving glaciers such that the error estimate includes the uncertainty derived from the omission of ice loss by calving.

Sea-level rise estimations coming from mass changes of the Greenland ice sheet and peripheral ice caps are based on surface mass balance (SMB) estimates from ref. 17, extended to more CMIP5 models, and augmented by to account for missing dynamic processes. These are the elevation feedback (i.e., the thinning of the ice sheet causing an additional warming; 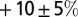) (17) and changes in ice dynamics (iceberg calving; 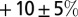) (37). The remaining 10% uncertainty represents the skill of the SMB model to simulate the current SMB rate over Greenland.

In contrast to other contributions, Antarctic sea-level projections are driven by 19 CMIP5 comprehensive climate models. Their global mean temperature change is scaled to the oceanic subsurface outside the ice-shelf cavities. These reduced temperature changes are then translated into basal ice-shelf melting via an interval of observed melting-sensitivity parameters. These basal-melt rates are then used to force five continental ice sheet models. To obtain a probability distribution, switch-on experiments within the Sea-level Response to Ice Sheet Evolution project are combined with linear-response theory (18). Through this approach it is possible to compute 50,000 combinations of climate, ocean, basal-melt, and ice-model combinations. Here we use the 5%, 50%, and 95% quantiles as reported in ref. 18. This approach clearly neglects any contribution that results from changes in basal lubrication. Furthermore we do not account for changes in SMB. This can be justified by the fact that the amount of surface melting is going to be relatively small even under future warming and that a large portion of the snowfall on Antarctica is compensated by snowfall-induced ice discharge (38). We thus consider a zero contribution from Antarctic SMB to be an upper estimate of the SMB contribution but we do not include this relatively small uncertainty in the reported error intervals.

We create a low, medium, and high land-ice scenario by summing up the three land-ice components along percentiles (5th, 50th, and 95th) to create a “very-likely” range. The overestimate of the total uncertainty, in comparison with using root mean square, is only marginal because most of the uncertainty comes from the Antarctic ice sheet. Global mean sea-level change contributions from the Greenland and Antarctic ice sheets are then combined with their gravitational–rotational fingerprints to obtain the regional contributions. We consider uniform mass loss over the ice sheets, using the same model as ref. 39. The fingerprints also include instantaneous, local land uplift in the vicinity of the ice sheets due to the elastic response of the solid earth upon melting (not to be mistaken with long-term glacial isostatic adjustment), thus also describing relative sea level changes. A uniform pattern is assumed for mountain glaciers and ice caps.

We also account for vertical land movement due to (i) glacial isostatic adjustment (resulting from the loading and unloading of ice sheets during the last Ice Age) (32) and (ii) an assumed 2-mm/y subsidence of natural origin in coastal segments comprising deltas (2). Enhanced human-induced subsidence (e.g., due to ground fluid abstraction or drainage) is not considered due to the lack of consistent observations or future scenarios. We also neglect additional global sea-level rise as a consequence of groundwater depletion (29).

Flood Risk.

Flood risks are assessed using the DIVA model (8) with a refined flooding algorithm (Version 5.0.0). People and assets exposed to coastal flood events are computed using a global coastal segmentation that divides the world’s coast into 12,148 variable-length coastal segments (40) based on the Digital Chart of the World (41).

For each coastline segment, a cumulative people exposure function (e_p) that gives the number of people living below a given elevation level x is constructed by superimposing a DEM with a spatial population dataset and interpolating piecewise linearly between the given data points. Only those grid cells that are hydrologically connected to the coast are considered. From areas below 1 m of elevation we subtract the areas covered by coastal wetlands, as these are uninhabitable. Also for each segment, a cumulative asset exposure function (e_a) is obtained by applying subnational per capita GDP rates to the population data (40) multiplied by an empirically estimated assets:GDP ratio of 2.8 (42). Future exposure is attained by applying national population and GDP growth rates of the socioeconomic scenarios to the coastal segments.

For people and assuming no dikes, the damage function is identical to the cumulative exposure function 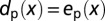. For assets, the damage also depends on the depth by which the asset is submerged. Following ref. 43, we assume a logistic depth-damage function (giving the fraction of assets damaged for a given flood depth) with a 1-m flood destroying 50% of the assets: 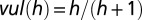. Depth-damage functions tend to have a declining slope, reflecting that additional damage declines with additional water depth. The selection of a 1-m depth is a good indicative value based on the available information.

The damage to assets done by a flood of height x is computed by integrating from elevation level 0 to x over the product of the depth-damage function applied to the water depth 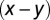and the derivative of the cumulative exposure function 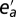applied to the elevation level y:

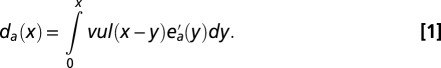In the case that there are dikes, we assume that the damage is 0 for floods with a height below the top of the dike.

Finally, we compute the people flooded and the flood cost as a mathematical expectation of the people and assets damage functions:

where f is the probability density function of extreme water levels, 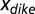the dike height, and 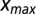is the maximum extreme water level to be taken into account in the integration. Extreme water-level probability density functions are derived based on extreme water levels given for different return periods in ref. 40. Future extreme water levels are obtained by uniformly displacing the distribution with relative sea-level change following 20th century global observations of extreme sea levels (44). Hence, no change in storm characteristics is assumed. We set 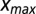to the height of the water level with the 10,000-y return period and solve the integral numerically.

Adaptation.

Because there is limited empirical data on actual defense levels or other adaptation around the world, we model adaptation assuming that the defenses are always provided by dikes (2, 3, 5, 13, 14). The dikes in 1995 around the world’s coast are estimated using the methods explained below to define the baseline situation. Without adaptation, dike heights are maintained, but not raised, so flood risk increases with time as relative sea level rises. With adaptation, dikes are raised following a demand function for safety derived as follows: let the benefits B of coastal protection with a design return period F be given by

where Y is GDP, y is (scaled) per capita income, S is sea-level rise, and P is population density. Greek letters are parameters. Eq. 3 can be interpreted as follows: without protection (F = 0), the benefits of protection are 0; if F grows, benefits grow, but ever slower. The costs of coastal protection are

where β and ϕ are positive parameters and 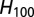is the extreme water level; if the extreme water level is higher, one would need to build a higher dike for the same return period. We here use the 100-y extreme water level as an indicator for the extreme water level regime.

The optimal protection (F*) follows from equating the marginal costs and benefits:

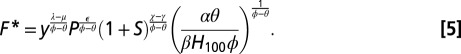χ equals γ, so S drops out. Let us assume that 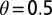and 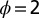. The empirical evidence reported in ref. 45 suggests that the elasticity of coastal protection to per capita income is 1.02 (with a SD of 0.17). The dike unit costs reported for all coastal countries in ref. 2 suggest that these costs are not very sensitive to income levels; the estimated elasticity μ is only 0.1. We can thus estimate λ from 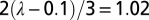, which gives 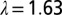. In ref. 45 it is further estimated that 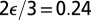(with an SD of 0.10), that is, 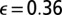. If 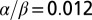, then the optimal level of protection is against the 1,400-y storm if per capita income and population density are as in Germany; if protection against the 10,000-y flood costs 0.5% of GDP, then 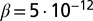and .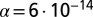

Following Eq. 5, we build and upgrade dikes for each coastline segment in each time step (5 y). A threshold of 1 person per square kilometer is assumed, below which no dikes are built. Dike capital costs are computed based on the attained dike height, coastal segment length, and dike unit costs taken from ref. 2, which are assumed to be constant over time and linear in dike height. Following ref. 33, we also calculate the maintenance costs of dikes which are at 1% per annum of the construction costs of the dikes.