Hybrid-fuel bacterial flagellar motors in Escherichia coli

Significance

The bacterial flagellar motor is a rotary nano-machine that is driven by an electrochemical ion gradient across the cytoplasmic membrane, either H⁺ or Na⁺ ions. Natural Escherichia coli cells have only H⁺-driven motors. We demonstrate a genetically engineered hybrid-fuel flagellar motor in E. coli that runs on both types of ion gradient, H⁺ and Na⁺. The hybrid motors switch between the two types of ion automatically and dynamically in response to external conditions, by swapping the stator components that determine their ion selectivity. These hybrid motors combine biological components with specific functions from different organisms that do not naturally coexist but demonstrate that natural hybrid motors could exist in other species.

Abstract

The bacterial flagellar motor rotates driven by an electrochemical ion gradient across the cytoplasmic membrane, either H⁺ or Na⁺ ions. The motor consists of a rotor ∼50 nm in diameter surrounded by multiple torque-generating ion-conducting stator units. Stator units exchange spontaneously between the motor and a pool in the cytoplasmic membrane on a timescale of minutes, and their stability in the motor is dependent upon the ion gradient. We report a genetically engineered hybrid-fuel flagellar motor in Escherichia coli that contains both H⁺- and Na⁺-driven stator components and runs on both types of ion gradient. We controlled the number of each type of stator unit in the motor by protein expression levels and Na⁺ concentration ([Na⁺]), using speed changes of single motors driving 1-μm polystyrene beads to determine stator unit numbers. De-energized motors changed from locked to freely rotating on a timescale similar to that of spontaneous stator unit exchange. Hybrid motor speed is simply the sum of speeds attributable to individual stator units of each type. With Na⁺ and H⁺ stator components expressed at high and medium levels, respectively, Na⁺ stator units dominate at high [Na⁺] and are replaced by H⁺ units when Na⁺ is removed. Thus, competition between stator units for spaces in a motor and sensitivity of each type to its own ion gradient combine to allow hybrid motors to adapt to the prevailing ion gradient. We speculate that a similar process may occur in species that naturally express both H⁺ and Na⁺ stator components sharing a common rotor.

Molecular motors are tiny machines that perform a wide range of functions in living cells. Typically each motor generates mechanical work using a specific chemical or electrochemical energy source. Linear motors such as kinesin on microtubules or myosin on actin filaments and rotary motors such as F₁-ATPase, the soluble part of ATP-synthase, run on ATP, whereas the rotary bacterial flagellar motor embedded in the bacterial cell envelope is driven by the flux of ions across the cytoplasmic membrane (1–4). Coupling ions are known to be either protons (H⁺) or sodium ions (Na⁺) (5, 6).

The bacterial flagellar motor consists of a rotor ∼50 nm in diameter surrounded by multiple stator units (7–10). Each unit contains two types of membrane proteins forming ion channels: MotA and MotB in H⁺ motors in neutrophiles (e.g., Escherichia coli and Salmonella) and PomA and PomB in Na⁺ motors in alkalophiles and Vibrio species (e.g., Vibrio alginolyticus) (1, 11). Multiple units interact with the rotor to generate torque independently in a working motor (9, 10, 12, 13). The structure and function of H⁺ and Na⁺ motors are very similar, to the extent that several functional chimeric motors have been made containing different mixtures of H⁺- and Na⁺-motor components (11). One such motor that runs on Na⁺ in E. coli combines the rotor of the H⁺-driven E. coli motor with the chimeric stator unit PomA/PotB, containing PomA from V. alginolyticus and a fusion protein between MotB from E. coli and PomB from V. alginolyticus (14).

In most flagellated bacteria, motors are driven by ion-specific rotor–stator combinations. However, some species (e.g., Bacillus subtilis and Shewanella oneidensis) combine a single set of rotor genes with multiple sets of stator genes encoding both H⁺ and Na⁺ stator proteins, and it has been speculated that these stator components may interact with the rotor simultaneously, allowing a single motor to use both H⁺ and Na⁺. An appealing hypothesis that the mixture of stator components is controlled dynamically depending on the environment has arisen from the observation that the localization of both stator components depends upon Na⁺ (15). However, despite some experimental effort there is as yet no direct evidence of both H⁺ and Na⁺ stator units interacting with the same rotor (16).

The rotation of single flagellar motors can be monitored in real time by light microscopy of polystyrene beads (diameter ∼1 μm) attached to truncated flagellar filaments (17). Under these conditions, the E. coli motor torque and speed are proportional to the number of stator units in both H⁺-driven MotA/MotB and Na⁺-driven PomA/PotB (17–19) motors. The maximum number of units that can work simultaneously in a single motor has been shown to be at least 11 by “resurrection” experiments, in which newly produced functional units lead to restoration of motor rotation in discrete speed increments in an E. coli strain lacking functional stator proteins (19). Stator units are not fixed permanently in a motor: Each dissociates from the motor with a typical rate of ∼2 min⁻¹, exchanging between the motor and a pool of diffusing units in the cytoplasmic membrane (20). Removal of the relevant ion gradient inactivates both H⁺ and Na⁺ stator units, most likely leading to dissociation from the motor into the membrane pool (2, 21, 22).

Here we demonstrate a hybrid-fuel motor containing both H⁺-driven MotA/MotB and Na⁺-driven PomA/PotB stator components, sharing a common rotor in E. coli. We control the expression level of each stator type by induced expression from plasmids, and the affinity of Na⁺-driven stator units for the motor by external [Na⁺]. Units of each type compete for spaces around the rotor, and the motor torque is simply the sum of the independent contributions, with no evidence of direct interaction between units. Thus, we demonstrate the possibility of modularity in the E. coli flagellar motor, with ion selectivity determined by the choice of stator modules interacting with a common rotor. Our artificial hybrid motor demonstrates that species with multiple types of stator gene and a single set of rotor genes could contain natural hybrid motors that work on a similar principle (15, 16, 23).

Results

Control of Stator Unit Number.

An E. coli strain with a genomic deletion of motA/motB, carrying two separate plasmids encoding MotA/MotB and PomA/PotB, was used for all experiments. We controlled expression levels of these proteins independently by adding various concentrations of the inducers arabinose or isopropyl-β-D-thiogalactopyranoside (IPTG) to the growth medium, or in some cases by adding IPTG after harvesting cells. Expression from these plasmids without inducer was very low: We typically counted ∼100 times fewer rotating tethered cells (4) in a given sample area without inducer than at saturating inducer concentration. We measured motor rotation speeds as previously described (17, 24) by tracking the position of 1-μm polystyrene beads, attached to genetically modified sticky flagellar filaments, using back-focal-plane interferometry (Fig. 1B, Inset). MotA/MotB motors rotate 1-μm beads at an average speed of 6.1 Hz per stator unit and PomA/PotB motors at 8.3 Hz per unit in 85 mM Na⁺. Thus, we determined the number of units in either type of motor by dividing motor speed by the appropriate unitary speed. Fig. 1A shows the dependence of stator unit number on the concentration of each inducer, added to the growth medium in the absence of the other inducer. MotA/MotB was half-saturated at ∼15 μM arabinose and PomA/PotB at ∼10 μM IPTG.

Fig. 1.

Control of stator unit numbers. (A) Average numbers of H⁺ or Na⁺ stator units in cells expressing only one stator type, in 85 mM Na⁺, showing saturation at inducer concentrations of ∼30 μM arabinose and ∼20 μM IPTG, respectively. Symbols and error bars show the mean and SD of 17–50 motors for each point. (B) Typical example of Na⁺ resurrection at 12 μM IPTG. Speed vs. time of a 1-µm polystyrene bead attached to a flagellar motor (Inset), tracked using back-focal-plane interferometry. Shading indicates the presence of Na⁺ at either 1 mM or 85 mM. Na⁺ was added and removed by flow (hatched regions). Red arrowheads indicate stepwise speed increments following Na⁺ addition.

For a given expression level, the number of PomA/PotB stator units can be controlled by transient removal of Na⁺ (25). Fig. 1B shows the Na⁺ response of a motor containing only PomA/PotB (no arabinose and 12 μM IPTG). The motor speed of ∼80 Hz at time (t) = 0 in 85 mM [Na⁺] indicates ∼10 Na⁺ units interacting with a rotor, close to the maximum number possible (18). When we introduced Na⁺-free medium around t = 30 s the motor speed fell steeply to zero, because chimeric Na⁺ motors generate no torque without sodium-motive force (SMF). When we restored 85 mM [Na⁺] around t = 100 s, speed increased in eight equal steps (Fig. 1B, Left, red arrowheads), as reported previously (25). The procedure was repeated with the same motor, but with 1 mM rather than 85 mM [Na⁺] restored (Fig. 1B, Right). Speed increments were smaller than in 85 mM [Na⁺], reflecting the reduced SMF, but Na⁺ stator units were still recruited to the motor by restoring Na⁺—a process we call “Na⁺ resurrection.”

Motors with No Stator Units.

Fig. 2A shows angle vs. time for a tethered cell (Fig. 2A, Inset, top left) in an experiment similar to that shown in Fig. 1B, grown without arabinose and therefore expressing no H⁺ stator components. Na⁺ (85 mM) was removed 10–30 s before and replaced ∼110 s after the record was started. Initially the motor was locked except for discrete steps between two angles separated by ∼10°; later, it showed free rotational diffusion. The mean-square displacement (MSD) over integer numbers of video frames is plotted vs. the corresponding elapsed time, τ, for 10-s periods beginning at t = 0 (Fig. 2A, Inset, left) and t = 40 s (Fig. 2A, Inset, right). For t = 0–10 s the cell exhibited restricted diffusion: The MSD tends to a fixed value at large time and the line fit (red) is poor. For t = 40–50 s the cell exhibited free diffusion: MSD = 2Dτ, with diffusion coefficient D = 0.12 rad²⋅s⁻¹. Fig. 2 B and C quantifies the changing behavior of this cell vs. time. Filled circles in Fig. 2B show diffusion coefficients D(¹/₆₀ s) estimated as the MSD between successive frames divided by 2τ₁, where τ₁ = ¹/₆₀ s, the time between frames. Open circles show D(¹/₂ s), estimated as the slope of a least-squares linear fit of MSD vs. 2τ for intervals between 1 and 30 frames. Fig. 2C shows the ratio D(¹/₂ s)/D(¹/₆₀ s), which is equal to 1 for free diffusion where the linear fit is good and MSD = 2Dτ, less than 1 for restricted diffusion where the displacement at long times is confined by a locked motor, and more than 1 for active rotation. The change from restricted to free diffusion around t = 40 s is visible as an increase in both estimates of D and an increase in their ratio from less than 1 to ∼1.

Fig. 2.

Rotational diffusion without Na⁺. (A) Angle vs. time of a tethered cell from video tracking; 85 mM Na⁺ was removed 10–30 s before the recording and restored at ∼110 s. Initially the cell showed restricted diffusion and stepping between two angles, then it showed free diffusion, and finally after restoration of Na⁺ it resumed rotation. The motor was stalled by flow during the exchange of medium that restored Na⁺. The insets show MSD vs. time with linear fits (red) for two selected 10-s periods. (B) Estimates of the rotational diffusion coefficient on two different timescales: D(¹/₆₀ s) = (MSD over one frame)/(2 × frame time) (filled circles) and D(¹/₂ s) = (slope of line fit)/2 (open circles). (C) The ratio of these two estimates vs. time for successive 10-s periods. Around t = 40 s both estimates of D increase and their ratio tends to 1, marking the transition to free diffusion. (D) Average ratios (median and interquartile interval) of diffusion coefficient estimates for the 10 out of 15 cells measured that did not show free diffusion (ratio ≥1) in either of the first two 10-s windows.

We repeated the experiment of Fig. 2 A–C with a total of 15 cells. Five of these showed free diffusion at the start of the record. Fig. 2D shows average ratios as in Fig. 2C for the remaining 10 cells, which showed a variety of diffusive behaviors. The rising trend confirms that cells are increasingly likely to show free diffusion with time following removal of Na⁺. Thus, it seems that motors change from restricted to free diffusion on a timescale of minutes following the removal of Na⁺, similar to the timescale of changes in stator unit number observed here and elsewhere (20, 22, 25).

Hybrid-Fuel Motors.

Fig. 3A shows the speed vs. time of a flagellar motor driving a 1-μm polystyrene bead in a cell expressing both MotA/MotB and PomA/PotB at just below half-saturating levels. At t = 0 there was no Na⁺ in the medium, under which condition Na⁺ stator units detach from the motor as shown Figs. 1B and 2. The motor speed of ∼12 Hz at t = 0 indicates two H⁺ units (Fig. 3 B and C, Upper) and no Na⁺ units generating torque in this motor. Around t = 35 s, a new medium containing 1 mM Na⁺ was introduced. The subsequent stepwise speed increments (Fig. 3A, red arrowheads) are typical of Na⁺ resurrection. Removing Na⁺ at t = 180 s returned the motor to the initial state with two H⁺ and no Na⁺ units, and adding 85 mM Na⁺ at t = 760 s initiated a second Na⁺ resurrection. This motor was unusual in having two H⁺ units in all data shown—typically the number of H⁺ units changed stochastically on a timescale of minutes (19, 20). Speed histograms for the resurrections in 1 mM (gray) and 85 mM Na⁺ (black) are shown in Fig. 3A, Right. The speed increments, defined as the separations between peaks in a multiple-Gaussian fit, are indicated with arrows. Note that the first increment in the 85 mM resurrection was too short-lived to be recorded using this method (Fig. 3A, open arrowhead).

Fig. 3.

Hybrid fuel motors. (A) Speed vs. time of a hybrid motor with low expression level of both stator components (8 µM arabinose and 10 µM IPTG). Color marking is same as in Fig. 1B. Speed histograms with multiple-Gaussian fits (Right) quantify the speed increments following the addition of 1 mM (gray) and 85 mM (black) Na⁺. (B) Speed vs. time of a hybrid motor as in A, but with greater expression of stator proteins (10 µM arabinose and 25 µM IPTG). Black line shows data Chung–Kennedy-filtered with a 1-s window; blue arrowheads indicate stepwise speed increments corresponding to H⁺ resurrection. (C) Speed increment distributions for 0 mM, 1 mM, and 85 mM Na⁺, for a total of 56, 56, and 79 increments (21, 14, and 17 separate motors), respectively. (Inset) Speed increment (ordinate, hertz) vs. external Na⁺ concentration (abscissa, millimolar), compared with previous results with PomA/PotB motors (26), red line). The size of speed increments did not depend upon expression levels. (D) Schematic of the transition between a proton motor and a hybrid fuel motor upon the addition of Na⁺.

Fig. 3B shows the response of a motor expressing MotA/MotB at approximately half-saturating and PomA/PotB at saturating levels to the removal of Na⁺, in an experiment similar to that shown in Fig. 3A. The speeds immediately before and after Na⁺ removal show that this motor started with three H⁺ and five or six Na⁺ stator units. Stepwise speed increments following the removal of Na⁺ show the addition of seven more H⁺ units (Fig. 3B, blue arrowheads), presumably filling space vacated by the departing Na⁺ units. This indicates that both types of stator unit competitively interact with the rotor. H⁺ resurrection in Fig. 3B indicates that the expression level of H⁺ stator components in this cell was considerably higher than in the cell of Fig. 3A, despite the relatively small increase in concentration of the inducer of MotA/MotB expression. This may reflect the large cell-to-cell variation in stator expression at a given inducer concentration (Fig. 1A). Fig. 3C shows histograms of speed increments observed in 0 mM, 1 mM, and 85 mM Na⁺. The speed increment of 6.1 ± 0.20 Hz per unit (mean ± SEM) in 0 mM Na⁺ is characteristic of the turnover of H⁺ stator units (19), and those of 5.0 ± 0.24 Hz and 8.3 ± 0.36 Hz in 1 mM and 85 mM Na⁺ are characteristic of Na⁺ units (26) (Fig. 1D, Inset), confirming our identification of speed steps as H⁺ and Na⁺ resurrections.

Kinetics of Stator Dynamics.

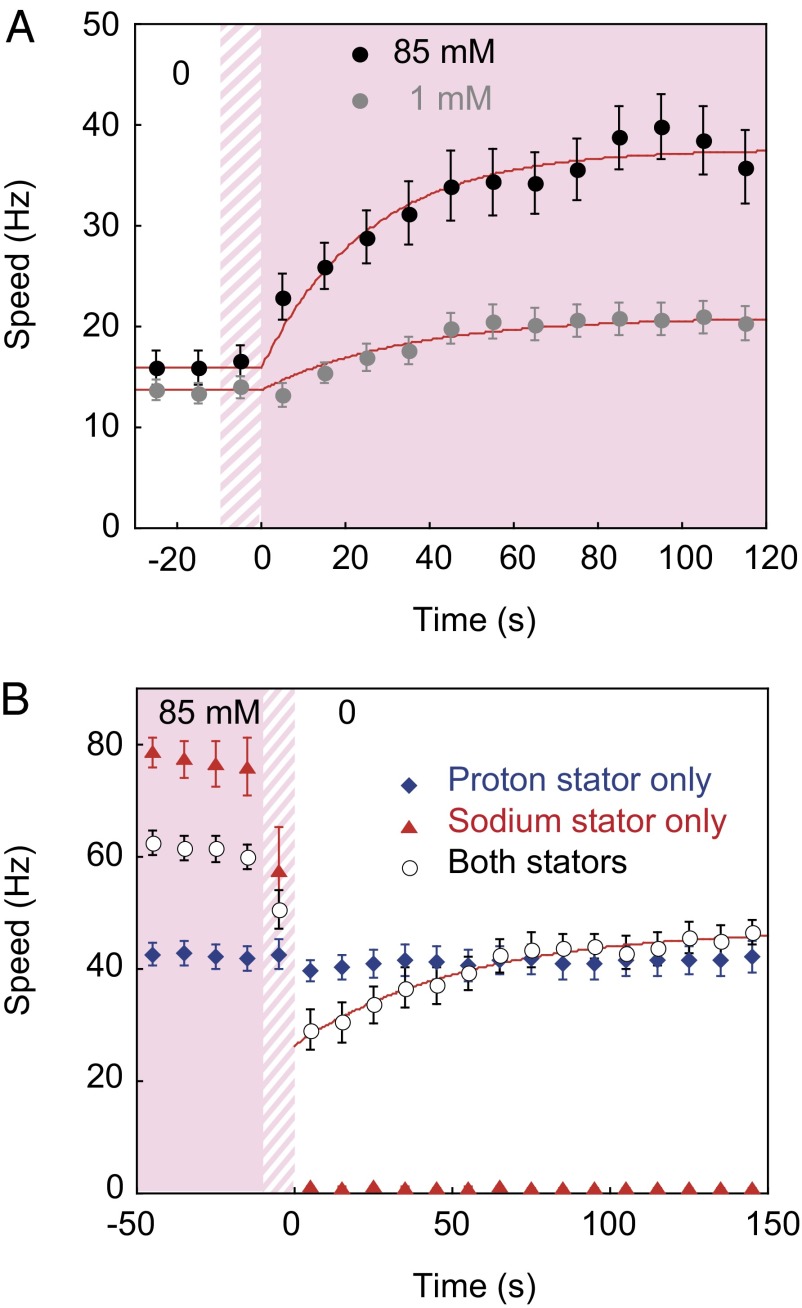
Fig. 4A shows the average speed of motors vs. time after the addition of Na⁺ in multiple repeats of the experiment illustrated in Fig. 3A. Exponential fitting (Fig. 4A, red lines) gives recovery time constants of 34 ± 6 s and 26 ± 3 s for 1 mM and 85 mM Na⁺, respectively. The slower time constant and lower final level in 1 mM compared with 85 mM Na⁺ suggests that stator units’ affinity for the motor is an increasing function of SMF, consistent with the observation of sodium de-resurrection. Fig. 4B (circles) shows the average response to removal of Na⁺ as in Figs. 1B and 3B, with a recovery time constant of 54 ± 8 s for H⁺ stator units upon removal of competing Na⁺ units. Controls (Fig. 4B, diamonds and triangles) confirm the dependence of Na⁺ but not H⁺ units on sodium concentration. Recovery time constants are similar to the rates of turnover of H⁺ stator components observed using fluorescent microscopy (20). The longer recovery time for H⁺ stator units may include effects of the requirement for Na⁺ units to leave the motor before H⁺ units can replace them.

Fig. 4.

Average speed of motors vs. time after the addition (A) or removal (B) of Na⁺ in multiple repeats of the experiments of Fig. 3. Red lines are exponential fits. B shows responses of motors in cells expressing both types of stator (circles), H⁺ stator components only (diamonds), and Na⁺ stator components only (triangles). Data points are mean ± SEM of (A) 19 and 22 speed traces from 14 and 17 cells in 1 mM and 85 mM, respectively, and (B) 23, 16, and 15 speed traces from 18, 16, and 15 cells expressing both, H⁺, and Na⁺ stator components, respectively.

Discussion

The bacterial flagellar motor is driven by ion flux across the cytoplasmic membrane. The motor can contain 10 or more independent stator units, each of which pushes against a ring of FliG proteins in the rotor (1, 2, 27, 28) with a high duty ratio (17). Stator units leave the motor when the relevant ion-motive force (21, 22, 25, 29) is removed and also when the load on the motor is reduced (22, 30). Our results show that coexpression of MotA/MotB and PomA/PotB proteins produces hybrid-fuel motors that run simultaneously on both ion gradients, at a speed that is simply the sum of the independent contributions of each type of stator (Fig. 3 A and B). The balance between the two types of stator can be controlled either via the sodium-motive force (Na⁺ concentration in this work) or the expression levels. A detailed understanding of stator dynamics will require extensive measurements of the type shown in Figs. 3 and 4, combined with fluorescence microscopy of labeled stator components, under a wide range of expression levels and ion-motive forces.

Free Brownian motion after stator unit detachment following Na⁺ removal (Fig. 2) indicates that the rotor bearing in the cell envelope is smooth, lacking energy barriers significantly larger than the thermal energy k_BT. We measured diffusion coefficients in the range D = 0.1–0.2 rad²⋅s⁻¹, essentially the same range as predicted from hydrodynamic estimates of the viscous drag coefficient f of a tethered cell rotating close to a surface using the Einstein relation D = k_BT/f. The twofold uncertainty in estimates of f combines variations in cell size and tether position with uncertainty in estimating the effect of proximity to the surface. For example, hydrodynamic calculations give a value of D = 0.2 rad²⋅s⁻¹ for the cell illustrated in Fig. 2 if surface effects are neglected (31). Surface effects are expected to increase f, and therefore decrease D, by up to twofold (32, 33), giving close agreement with the measured value of D = 0.12 rad²⋅s⁻¹. Thus, it is likely that the bearing lacks any significant energy barriers.

Some tethered cells showed restricted rotation shortly after Na⁺ removal, presumably before detachment of all stator components. Furthermore, 3 out of 15 cells showed clear steps between distinct angles similar to Fig. 2A, but without a consistent step size from cell to cell (the range was 10° to 40°). This indicates there are static interaction potentials between the rotor and de-energized stator units. A cycle that alternates between a set of periodic potentials is a key element in models of the motor mechanism (34, 35), raising the possibility that de-energized stator units are locked in one of the motor’s working states (25). Periodic, static rotor–stator interactions have been reported before in de-energized motors (36) and in the stop state of the Rhodobacter sphaeroides motor (37). Stator loss offers an explanation of reports of both locked and free rotation in de-energized motors (36, 38, 39). However, as before, we saw a range of step sizes in locked motors, and the structural origin of the interaction potentials remains elusive. It has been proposed that steps observed in flagellar rotation (25) may have been due not to steps in the torque-generating cycle, but to other interactions (possibly involving the LP ring) that give rise to a periodic interaction potential (40). Our results point to stator units rather than other components as a possible source of such potentials. Application of external torque to de-energized motors before stator loss might allow more systematic investigation of the phenomenon in future.

Our hybrid-fuel motors combine biological components with specific functions that do not naturally coexist in either E. coli or V. alginolyticus. The results shown in Figs. 3 and 4 show that the characteristics of a motor can be controlled automatically and dynamically by changing the external conditions. Other bacteria, such as B. subtilis and S. oneidensis, express both H⁺ and Na⁺ stator proteins, but only a single rotor in nature (15, 23). These motors have been suggested to use both H⁺ and Na⁺, allowing bacteria to swim without interruption by changes in ion-motive forces; however, whether the B. subtilis and S. oneidensis motors are hybrid-fuel motors remains to be seen (16). Our result shows that it is possible.

Materials and Methods

Bacteria and Culture.

E. coli strain JHC36 was derived from YS34 by replacement of chromosomal fliC::Tn10 with the fliC-sticky gene and transformed with plasmids pYS13 (pomApotB, IPTG-inducible, Cm^R) and pDFB27 (motAmotB, arabinose-inducible, Amp^R). Cells were grown from frozen aliquots (0.1 mL, grown overnight in LB medium and stored at −80 °C with DMSO, 10% vol/vol) in 5 mL of T-broth [1% Bacto tryptone (Difco) and 0.5% sodium chloride] at 30 °C for 4.5 h. Chloramphenicol (25 µg/mL) and ampicillin (50 µg/mL) were added to preserve the plasmids. Inducers IPTG and arabinose were added to the growth medium at various concentrations: up to 10 µM in the experiments of Fig. 4A; 20–25 and 10–15 µM, respectively, in experiments to demonstrate competition between H⁺ and Na⁺ stator units in Fig. 4B; and 30 µM and 12 µM for expression of Na⁺ or H⁺ stator components only in Fig. 4B.

Speed Measurements.

Cells were immobilized on poly-lysine–coated glass coverslips in custom-made flow chambers, and 0.992-µm-diameter polystyrene beads (Polysciences, Inc.) were attached to the truncated flagellar filaments and tracked by back-focal-plane interferometry as described (24). Experiments were performed in motility buffer [10 mM potassium phosphate (pH 7.0), 0.1 mM EDTA, X mM sodium chloride, and (85-X) mM potassium chloride, where X = 0, 1, or 85]. Flow chambers had three input channels containing sodium concentrations, 0, 1, and 85 mM, which were opened one at a time to exchange buffers, using gravity to drive the flow. Buffer exchange was achieved by flowing 25–40 μL (two to three times flow chamber volume), which required 5–20 s depending on the dimensions of individual hand-made channels. All experiments were carried out at 23 °C.

Speed Analysis.

Speeds were calculated from power spectra of back-focal-plane data as described (19, 24), using data windows of length 1 s at 0.1-s intervals with a median filter of rank 4. Speed histograms for each sodium concentration (including ∼5 s before and after buffer exchange) were constructed with 1-Hz bins, and speed increments were calculated as the difference between the means of adjacent Gaussians in a multiple-Gaussian fit to the speed histogram. For Fig. 4, speed traces were aligned by eye as follows. If the speed changed suddenly during flow, marking the arrival of the new buffer at the cell, the time of this change was taken as t = 0. Otherwise, the end of the flow was defined as t = 0.

Tethered Cell Assay and Image Analysis.

Cells were immobilized on glass coverlips via sticky filaments. Exchange of medium was achieved as in the bead assay. Bright-field images of rotating cells were acquired at 60 frames per second (FASTCAM-1024PCI; Photron). Cell angle was determined by a custom made algorithm using LabVIEW and IMAQ VISION. Mean-square angle deviation was calculated as described (41).