Observational determination of albedo decrease caused by vanishing Arctic sea ice

Significance

The Arctic sea ice retreat has been one of the most dramatic climate changes in recent decades. Nearly 50 y ago it was predicted that a darkening of the Arctic associated with disappearing ice would be a consequence of global warming. Using satellite measurements, this analysis directly quantifies how much the Arctic as viewed from space has darkened in response to the recent sea ice retreat. We find that this decline has caused 6.4 ± 0.9 W/m² of radiative heating since 1979, considerably larger than expectations from models and recent less direct estimates. Averaged globally, this albedo change is equivalent to 25% of the direct forcing from CO₂ during the past 30 y.

Abstract

The decline of Arctic sea ice has been documented in over 30 y of satellite passive microwave observations. The resulting darkening of the Arctic and its amplification of global warming was hypothesized almost 50 y ago but has yet to be verified with direct observations. This study uses satellite radiation budget measurements along with satellite microwave sea ice data to document the Arctic-wide decrease in planetary albedo and its amplifying effect on the warming. The analysis reveals a striking relationship between planetary albedo and sea ice cover, quantities inferred from two independent satellite instruments. We find that the Arctic planetary albedo has decreased from 0.52 to 0.48 between 1979 and 2011, corresponding to an additional 6.4 ± 0.9 W/m² of solar energy input into the Arctic Ocean region since 1979. Averaged over the globe, this albedo decrease corresponds to a forcing that is 25% as large as that due to the change in CO₂ during this period, considerably larger than expectations from models and other less direct recent estimates. Changes in cloudiness appear to play a negligible role in observed Arctic darkening, thus reducing the possibility of Arctic cloud albedo feedbacks mitigating future Arctic warming.

The Arctic has warmed by nearly 2 °C since the 1970s, a temperature change three times larger than the global mean (1). During this period, the Arctic sea ice cover has retreated significantly, with the summer minimum sea ice extent decreasing by 40% (2). This retreat, if not compensated by other changes such as an increase in cloudiness (3–6), should lead to a decrease in the Arctic planetary albedo (percent of incident solar radiation reflected to space), because sea ice is much more reflective than open ocean. Such an amplified response of the Arctic to global warming was hypothesized and modeled in the 1960s by Budyko (7) and Sellers (8). As per the Budyko–Sellers hypothesis, an initial warming of the Arctic due to factors such as CO₂ forcing will lead to decreased ice cover which exposes more of the underlying darker ocean and amplifies the warming. In 1975, this phenomenon was simulated in a 3D climate model by Manabe and Wetherald (9), who showed that under conditions of a doubling of CO₂, tropospheric warming in the polar regions was much larger than in the tropics, due in part to the albedo decrease from shrinking snow/ice area. Previous studies have addressed aspects of this question using a combination of radiative transfer models and indirect albedo change estimates (10–13), but this study uses satellite measurements of both the region’s radiation budget (14) and the sea ice fraction (15) to quantify the radiative effects of ice retreat.

Empirical measurements determining the response of planetary albedo to sea ice decline are critical for assessing the radiative impacts of Arctic changes and for evaluating climate models. The Clouds and Earth’s Radiant Energy System (CERES) satellite program (14), which includes global measurements of incident and reflected solar radiation, provides an ideal tool to address this issue. In this study, we analyze CERES clear-sky and all-sky planetary albedo data (0.2–4.5-μm wavelength range) as well as sea ice observations inferred from passive microwave satellite instruments [the Special Sensor Microwave Imager (SSM/I) and its predecessor and successor (15)]. Using these datasets, we assess the magnitude of planetary darkening due to Arctic sea ice retreat, providing a direct observational estimate of this effect. We then compare our estimate with simulation results from a state-of-the-art ocean–atmosphere global climate model (GCM) to determine the ability of current models to simulate these complex processes.

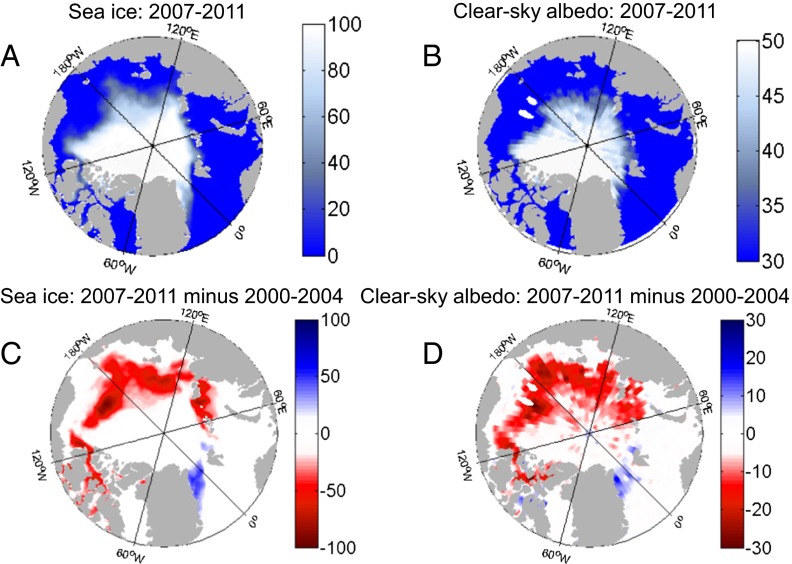
Comparing spatial patterns of the CERES clear-sky albedo with SSM/I sea ice concentration patterns, we find a striking resemblance (Fig. 1), revealing that the spatial structure of planetary albedo is dominated by sea ice cover both in terms of the time average (Fig. 1 A and B) and the changes over time (Fig. 1 C and D). Fig. 1 focuses on the month of September, when the year-to-year sea ice decline has been most pronounced, although there is also agreement between sea ice cover and planetary albedo during every other sunlit month of the year (Fig. S1). There is also a smaller effect associated with diminishing albedo in central Arctic regions which have nearly 100% sea ice cover throughout the record (Fig. 1D and Fig. S1), as would be expected from a warming ice pack experiencing more surface melt (16).

Fig. 1.

(A) Sea ice concentration and (B) CERES clear-sky albedo averaged over each September during the last 5 y of the CERES record (2007–2011) and the change in (C) sea ice and (D) clear-sky albedo between the mean of the last five Septembers (2007–2011) and the mean of the first five Septembers (2000–2004) of the CERES record. Results for other months are included in Fig. S1.

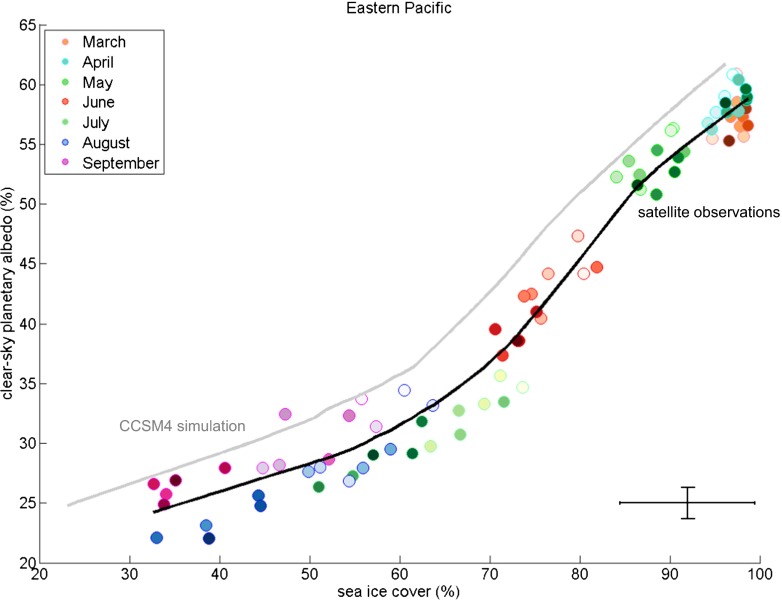
To further probe the relationship between planetary albedo and sea ice cover, we split the Arctic into six regions (Fig. S2) and examine changes in the sea ice cover and albedo averaged over each region. As anticipated from Fig. 1, monthly mean values of the clear-sky planetary albedo demonstrate a close relationship with sea ice cover, which is illustrated in Fig. 2 for the Eastern Pacific region (Figs. S3 and S4 illustrate other regions).

Fig. 2.

Monthly mean CERES clear-sky planetary albedo versus SSM/I sea ice cover for the months March through September during 2000–2011 in the Eastern Pacific (EP) region. Different colors indicate different months, and lighter shading indicates earlier years. The thick black line indicates smoothing with a lowpass moving average filter with a span of 41 points. NCAR CCSM4 model output for the same region is also included (gray line), using simulation years 1985–2005 smoothed with a lowpass moving average filter with a span of 82 points (widened to account for the longer time series). The error bar in the bottom right corner indicates the instrumental uncertainty of both datasets (Supporting Information).

This relationship, however, is not linear: the slope of the curve in Fig. 2 is steeper for months with more ice. Because the presence of snow gives ice-covered regions a higher albedo in winter and spring, whereas melt ponds contribute to lower albedos in summer and fall, we hypothesize that the nonlinearity in Fig. 2 arises due to the seasonal evolution of the ice albedo itself. To test this interpretation, we generate an estimate of the seasonal cycle in the albedo of ice-covered regions by linearly extrapolating the CERES clear-sky planetary albedo to 100% ice cover (Methods). This isolates what seasonal changes in ice albedo would be required to produce the nonlinearity in Fig. 2. We then use an empirical relationship (17) to estimate the sea ice surface albedo from the clear-sky planetary albedo associated with ice-covered regions (Methods). The CERES-inferred surface albedo is consistent with in situ measurements (18) of the seasonal cycle of sea ice surface albedo (Fig. 3), suggesting that the nonlinearity in Fig. 2 is indeed the result of the seasonal cycle in sea ice surface albedo. The same basic structure of the relationship between CERES albedo and SSM/I ice cover (Fig. S3) and between the observations and model (Fig. S4) applies to each individual region and to the Arctic as a whole, and we see a similar seasonal cycle in sea ice surface albedo inferred for each region (Fig. S5).

Fig. 3.

The mean seasonal cycle in sea ice surface albedo during 2000–2011 derived from the CERES data in the region 80–90°N (blue line) and from in situ surface albedo measurements from the Surface Heat Budget of the Arctic (SHEBA) project (18) of 1997–1998 (black line). Blue error bars indicate one SD of CERES 2000–2011 year-to-year variability, and gray shading indicates one SD of SHEBA spatial variability along a 200-m survey line.

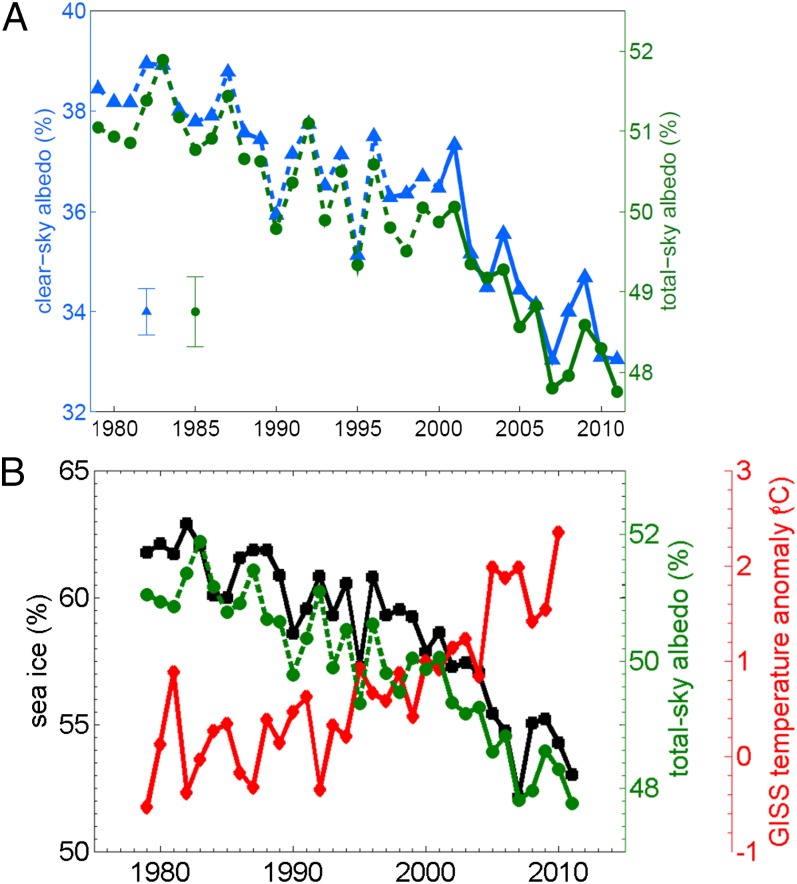
The CERES albedo observations allow us to directly estimate the total darkening of the Arctic during the 2000–2011 CERES period. Fig. 4A shows the annual clear-sky and all-sky albedos during this period (solid lines). The change in all-sky albedo implies that the darkening of the Arctic has caused an increase in solar absorption of 4.2 W/m² during this 12-y period (Methods). The close relationships between all-sky and clear-sky planetary albedo (Fig. 4A) and between clear-sky planetary albedo and sea ice cover (Figs. 1 and 2) implies that much of this darkening and associated increase in solar energy input can be attributed to the declining Arctic sea ice cover.

Fig. 4.

(A) Observed annual-mean clear-sky and all-sky planetary albedo for the entire Arctic region. Solid lines are direct CERES observations, and dashed lines are estimates derived from sea ice observations. The error bars in the Bottom Left corner indicate the uncertainty in the pre-CERES clear-sky and all-sky albedo values (Supporting Information). (B) All-sky albedo as in A compared with annual-mean observed sea ice area (as a fraction of the ocean in the Arctic region) and surface air temperature averaged over the ocean in the Arctic region.

These relationships also suggest that the longer 1979–2011 sea ice dataset can be used to estimate the all-sky and clear-sky planetary albedos during the period before the CERES instruments were online. Thus, we estimate the magnitude of the long-term increase in solar energy into the Arctic using the observed pre-CERES (1979–1999) ice cover paired with a linear approximation of the relationship between albedo and ice constructed from observations during the CERES period (2000–2011) for each month and each region, as illustrated in Fig. S6. We apply these relationships to the monthly regional sea ice observations, and then we average over the regions and months to derive the Arctic annual albedo (Methods). Note that the linear relationships effectively function as a monthly and regionally varying empirical “kernel,” in analogy with model-based kernels typically used in feedback analyses (19).

The results are indicated by the dashed lines in Fig. 4A. For the clear-sky case, we observe a decrease in albedo from 0.39 to 0.33 during the 33-y period from 1979 to 2011. The change in all-sky albedo, which is less pronounced due to clouds masking some of the decrease (12), declines by 0.04 ± 0.006, from 0.52 to 0.48, during this period. This change in all-sky albedo corresponds to an increase of 6.4 ± 0.9 W/m² over the Arctic Ocean during this period. Here the error bar is based on uncertainty in the linear relationships used to estimate the albedo during 1979–1999 (Supporting Information discusses sources of error). This is equivalent to an increase of 0.43 ± 0.07 W/m² averaged over the Northern Hemisphere, or 0.21 ± 0.03 W/m² averaged over the globe. The radiative forcing is largest in June, coinciding with the maximum solar input; it is smaller by a factor of 5 in September, when the sea ice retreat is largest but solar input is reduced (Fig. S7).

Fig. 4B includes a time series of the surface air temperature in the Arctic (Methods) as well as the total Arctic sea ice cover. Although this does not necessarily represent a causal relationship, the warming surface temperature (red), retreating sea ice (black), and planetary darkening (green) have evolved approximately in step during the past 3 decades and together paint a consistent picture for the Arctic climate.

The relationship between Arctic sea ice and planetary albedo can be directly compared with climate models, and to this end these observations provide an independent metric for evaluating current models. We illustrate this point by comparing the observations with simulation results from one of the GCMs participating in the most recent Climate Model Intercomparison Project (CMIP5), the National Center for Atmospheric Research Community Climate System Model version 4 (NCAR CCSM4) (20) (Methods). The CCSM4 simulation (gray lines in Fig. 2 and Fig. S4) displays a basic structure similar to that of the observations, with the slope being steeper for larger ice covers, although there are substantial quantitative differences for each region, and the scatter of individual monthly points in CCSM4 (Fig. S8) is less continuous than in the observations (Fig. 2).

The simulated model albedo in CCSM4 is systematically higher than the observed albedos for the Eastern Pacific (EP) region shown in Fig. 2, but for some of the other regions the simulated albedos are lower (Fig. S4), such that, when averaged over the entire Arctic, the simulated and observed albedos are much closer (Fig. S4, Bottom Right). Furthermore, the uncertainty in the observed albedos is about 1.3% (in albedo units) (21), and retrieval accuracy for the SSM/I sea ice fraction (22) is about 7.5% (in ice fraction units; Supporting Information provides a more detailed discussion of uncertainties). As a result, the difference between the observation and model curves is within the instrumental uncertainty for all six regions (Fig. S4), and this difference is less pronounced when considering the variability of the individual points about the smoothed curve (Fig. S8).

The radiative forcing from Arctic darkening that we compute from CERES and SSM/I is consistent with the CCSM4 simulation results given the level of observed sea ice retreat. The change in annual total-sky albedo per change in annual-mean fractional sea ice area, calculated using a regression between the two quantities averaged over the Arctic Ocean poleward of 60°N (Supporting Information), is 0.36 in CCSM4 (using simulation years 1985–2005) and 0.39 in our observational results (using years 2000–2011). This implies that if CCSM4 simulated a rate of sea ice retreat consistent with observations, then it would also simulate a change in total-sky albedo consistent with observations. The rate of Arctic sea ice retreat in this CCSM4 simulation is near the middle of the spread of the CMIP5 models (23, 24), which substantially underpredict the observed sea ice retreat (23); our results suggest that this is not due to the sensitivity of planetary albedo to changes in sea ice, because this is well-captured by the model we analyze.

The albedo changes that we find are substantially larger than previously published estimates. A recent study by Flanner et al. (10) used a synthesis of measurements and atmospheric models to assess the Northern Hemisphere cryosphere radiative forcing during 1979–2008. They found an increase in solar energy input from sea ice changes of 0.15–0.32 W/m², with a mean estimate of 0.22 W/m² (their table 2). This estimate, which relied on atmospheric models, is about half as large as our observationally based result of 0.43 ± 0.07 W/m². It should be noted that their value has a wide uncertainty range and, as pointed out by Flanner et al. (10), was intended as a lower bound due to biases in their analysis.

We also find a larger radiative forcing than a recent study by Perovich et al. (11) which used passive microwave sea ice observations, reanalysis products, and field measurements. They calculated an increase in the spatial-mean solar energy absorbed into just the ice-free areas of the Arctic Ocean of 5.6 W/m² during 1979–2005. Although this is smaller than our value of 6.4 W/m², it is not a straightforward comparison because our study applies to the entire Arctic Ocean area. Furthermore, we consider the increase in solar absorption at the top-of-atmosphere rather than at the surface.

These results indicate that the clear-sky planetary albedo is 0.31 higher in ice-covered regions than in ice-free regions, which is determined by extrapolating the monthly relationships in Fig. S6 to 100% ice cover and then calculating the annual albedo. This is larger than the estimate of 0.25 from the previous generation of satellite radiation measurements (25). Similarly, our sea ice surface albedos (Fig. 3) are somewhat higher throughout the year than albedos derived from the Advanced Very High Resolution Radiometer (AVHRR) satellite instrument (26). However, the AVHRR analysis (26) considered the average albedo of all pixels with at least 50% multiyear ice cover, rather than only completely ice-covered regions, which was noted to lead to a lower albedo due to the presence of open water in some pixels.

We next speculate on the implications of the observed albedo decrease for the climate feedback parameter associated with changes in surface albedo. The change in annual-mean global-mean surface temperature is 0.69 °C during 1979–2011 (Methods). If we make the extreme assumption that all of the observed decrease in Arctic albedo is due to warming, then we obtain an estimate of the feedback parameter associated with changes in Arctic Ocean albedo of 0.31 ± 0.04 W/m²/K (change in global forcing of 0.21 W/m² divided by the global temperature change). This estimate is an upper bound because some of the decrease in albedo may be due to natural variability (e.g., ref. 24) and the darkening effect of black carbon deposition (e.g., ref. 27), neither of which can be estimated reliably solely from current observations. Nonetheless, it is instructive to compare this observational estimate with those based on climate models. This upper-bound estimate of the Arctic Ocean contribution to the global surface albedo feedback parameter is substantially larger than model-based estimates of 0.11 ± 0.04 W/m²/K for the current generation of GCMs (CMIP5) and 0.10 ± 0.03 W/m²/K for the previous generation (CMIP3) (Methods). In fact, this observational estimate of just the Arctic Ocean contribution is comparable to the model-based estimate of the total global surface albedo feedback parameter, which is 0.31 ± 0.07 W/m²/K in CMIP5 (28) and 0.26 ± 0.08 W/m²/K in CMIP3 (19).

The present results are also consistent with a time-invariant cloud albedo field. We can relate clear-sky albedo (α_cs), all-sky albedo (α_as), and overcast albedo (α_cld) to the cloud fraction (f_c) as α_as = α_cs (1 − f_c) + α_cld f_c, which implies that if the cloud fraction and overcast albedo remain approximately constant, then a change in clear-sky albedo (Δα_cs) will cause a change in all-sky albedo (Δα_as) as Δα_as = Δα_cs (1 − f_c). Given that the all-sky albedo trend during 2000–2011 in Fig. 4A (solid lines) is about 30% as large as the clear-sky albedo trend, and the Arctic cloudiness is observed to be about 70% (3), this is consistent with the cloud fraction remaining approximately constant. Although not a comprehensive analysis of cloud feedbacks, this approximate calculation suggests that cloud albedo feedbacks are not playing a substantial role in the observed Arctic warming.

In summary, this study demonstrates a close relationship between SSM/I sea ice cover and CERES planetary albedo during the CERES record (2000–2011), thereby independently corroborating the passive microwave satellite observations of sea ice retreat. We find consistent agreement between these satellite observations, a climate model, and in situ surface observations. Using the relationship between SSM/I and CERES measurements to extend the albedo record back in time, we find that during 1979–2011 the Arctic darkened sufficiently to cause an increase in solar energy input into the Arctic Ocean region of 6.4 ± 0.9 W/m², equivalent to an increase of 0.21 ± 0.03 W/m² averaged over the globe. This implies that the albedo forcing due solely to changes in Arctic sea ice has been 25% as large globally as the direct radiative forcing from increased carbon dioxide concentrations, which is estimated to be 0.8 W/m² between 1979 and 2011 (29). The present study shows that the planetary darkening effect of the vanishing sea ice represents a substantial climate forcing that is not offset by cloud albedo feedbacks and other processes. Together, these findings provide direct observational validation of the hypothesis (7, 8) of a positive feedback between sea ice cover, planetary albedo, and global warming.

Methods

In this work the Arctic is defined as the area north of 60°N, and only nonland area is considered. Observed albedo is calculated from CERES Single Satellite Footprint (SSF) top-of-atmosphere (TOA)/Surface Fluxes and Clouds Terra Level 3 Edition 2.6 shortwave radiation (0.2–4.5 μm) on a 1° × 1° grid during March 2000 through December 2011. By subdividing the larger Arctic Ocean into smaller regions (Fig. S2) and averaging over these spatial areas, we minimize the effects of the contamination of individual retrievals by the neighboring pixels. We use monthly gridded sea ice concentration data (15) on a 25 × 25 km polar stereographic grid during January 1979 through December 2011; ice cover in each region is computed as the mean of the ice concentration weighted by grid cell area. A detailed discussion of the sources of bias and uncertainty of both CERES and sea ice data may be found in Supporting Information. We use CCSM4 simulation result from years 1985–2005 of Ensemble Member #1 of the 1° 20th Century simulation, acquired from the Earth System Grid (case name b40.20th.track1.1deg.005). The temperature in Fig. 4B is from the Goddard Institute of Space Studies (GISS) 2° × 2° surface temperature record (30). We used the annual-mean (January–December) global-mean temperature product from this same dataset for the feedback analysis, where we estimated the total change during 1979–2011 as the product of the linear trend and the time interval.

The annual-mean albedo is computed as the ratio of annual-mean solar fluxes (rather than the average of the monthly albedo values), and spatial-mean albedos are calculated in the same way. For the pre-CERES period, we use a constant solar incidence equal to the value averaged over the CERES period. Spatial points with missing values are ignored in our calculation of the spatial means. Of the 420 regional-mean monthly mean clear-sky albedo values considered, 83% had less than 10% of grid boxes with missing data, and 98% had less than 20% with missing data. Due to the onset of polar night, only the months March through September are considered for albedo, and we calculate annual albedo values assuming zero solar flux during October through February.

The sea ice surface albedo is estimated using two steps. First, the clear-sky planetary albedo associated with 100% sea ice cover is computed from an ordinary least squares linear regression between albedo and sea ice cover for each month constrained to go through an ocean albedo of 0.175 (cf . ref. 25) at 0% sea ice cover. For this calculation, a region containing all ocean grid cells between 80 and 90°N is used to reduce the extrapolation to 100% ice calculation and to focus on multiyear ice for comparison with the in situ observations. Next, surface albedo (α_sfc) is calculated from this clear-sky planetary albedo (α_cs) based on a linear estimate, α_sfc = (α_cs − a)/b, with empirically derived seasonally varying monthly parameter values of a and b adopted from a previous study (17).

The clear-sky albedo during 1979–1999 is computed from sea ice using a total least squares linear regression between 2000 and 2011 clear-sky albedos and sea ice. All-sky albedos during 1979–1999 are similarly computed from clear-sky albedos using a total least squares linear regression between the two albedos during 2000–2011. In both regressions, the quantities are normalized by their uncertainties, and error bars are estimated based on the regression confidence intervals (details provided in Supporting Information).

We estimate the Northern Hemisphere ocean contribution to the global surface albedo feedback parameter by drawing on the results of previous studies. An analysis of CMIP3 models under an idealized emissions scenario showed that 37 ± 9% of the total surface albedo feedback was due to changes in the Northern Hemisphere ocean (31). We assume that this fraction does not change, scaling the CMIP3 and CMIP5 albedo feedback parameters by this number to obtain the estimates reported in the text.