Form, function, and evolution of living organisms

Significance

Understanding the origin and evolution of the shapes observed in nature remains an exciting challenge. Even from a cursory inspection, it is clear that the shapes of animals and plants, as determined by the distribution of mass over volume, are distinct. Animals are able to move and are approximately homogeneous in their mass distribution. Plants are rooted organisms endowed with heterogeneous self-similar geometry where the mass is concentrated in the stem and branches rather than in the leaves. By addressing the fundamental physics underlying the relation between form and physiology and the origins of Kleiber’s law, we discuss how the two divergent life forms of plants and animals may have independently evolved to achieve equivalent energetic efficiencies.

Abstract

Despite the vast diversity of sizes and shapes of living organisms, life’s organization across scales exhibits remarkable commonalities, most notably through the approximate validity of Kleiber’s law, the power law scaling of metabolic rates with the mass of an organism. Here, we present a derivation of Kleiber’s law that is independent of the specificity of the myriads of organism species. Specifically, we account for the distinct geometries of trees and mammals as well as deviations from the pure power law behavior of Kleiber’s law, and predict the possibility of life forms with geometries intermediate between trees and mammals. We also make several predictions in excellent accord with empirical data. Our theory relates the separate evolutionary histories of plants and animals through the fundamental physics underlying their distinct overall forms and physiologies.

Understanding the origin and evolution of the geometries of living forms is a formidable challenge (1, 2). The geometry of an object can be characterized by its surface−volume relationship—the surface area S of an object of volume V can scale at most as 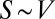and at least as 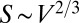(3). These geometries have been used by nature in space-filling trees and animals, respectively. Here, our principal goal is to explore how it is that both geometries of life coexist on Earth, whether intermediate geometries are possible, and what all this implies for evolution of life on Earth.

Living organisms span an impressive range of body mass, shapes, and scales. They are inherently complex, they have been shaped by history through evolution and natural section, and they continually extract, transform, and use energy from their environment. The most prevalent large multicellular organisms on Earth, namely plants and animals, exhibit distinct shapes, as determined by the distribution of mass over the volume. Animals are able to move and are approximately homogeneous in their mass distribution—yet they have beautiful fractal transportation networks. Plants are rooted organisms with a heterogeneous self-similar (fractal) geometry—the mass of the tree is more concentrated in the stem and branches than in the leaves.

The approximate power law dependence of the metabolic rate, the rate at which an organism burns energy, on organism mass has been carefully studied for nearly two centuries and is known as allometric scaling (4–32). From the power law behavior, with an exponent around 3/4, one can deduce the scaling of characteristic quantities with mass and, through dimensional analysis, obtain wide-ranging predictions often in accord with empirical data. However, what underlies this ubiquitous quarter-power scaling, and with a dominant exponent of 3/4?

In an influential series of papers, West and coworkers (11, 12, 14–16) suggested that fractality was at the heart of allometric scaling. Inspired by these papers, a contrasting view was presented (13), which argued that, although fractal circulatory networks may have advantages, quarter-power scaling came built in with the directed transport of nutrients. However, this latter paper was necessarily incomplete because it did not address the distinct geometries of animals and trees. More recently, members of both groups joined together to construct explicit models for animals, which showed (24) that “quarter-power scaling can arise even when there is no underlying fractality.” Here, we take a fresh look at the problem and derive quarter-power scaling quite generally for all living organisms. We then turn to a consideration of the sharp differences in the geometries of animals and trees and argue that the evolution of organismal forms follows from a rich interplay of geometry, evolutionary history, developmental symmetry, and efficient nutrient acquisition.

Despite their independent evolution and different metabolisms, vascular plants and bilaterian animals share major design features, namely, an internal mass comprising organized cells capable of metabolic and bioenergetic activities, a transport mechanism for distributing molecules and energy within itself, and a surface capable of exchanging matter and energy with the environment. Regardless of the shape differences observed between these two groups, the physics associated with the transformation, transport, and exchange of matter and energy must unavoidably impose physical constraints on their designs. An organism is akin to an engine—part of the energy obtained from nourishment is used for organism function, growth, reproduction, while the rest is dissipated through its surface. We consider the hypothesis of the survival of the fittest in terms of energy metabolism and postulate that an organism with a higher energy intake would have a competitive advantage over another organism of similar mass performing energetically suboptimally, and explore its consequences.

Consider an isotropic 3D organism of spatial extent h whose volume V scales as 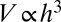. Generalization to organisms with distinct scaling along the three different directions is straightforward. We make the simplifying assumption that the consumption and metabolic activity is distributed uniformly in space and in time or suitable averaging is used. We denote the basal metabolic rate of the organism by B and its mass by M. B is a measure of the energy being delivered to the organism per unit time and ought to be proportional to the energy dissipated through its surface. There is no evidence of size selection in empirical data, and this lends support to the assumption that the efficiency of the engine is independent of the organism’s size. We will derive Kleiber’s law based on energy intake considerations and study the role of geometry, as captured in the surface−volume relationship, on considering the expelled energy.

Our goal is to understand the ideal dependence of B on M in the scaling regime. The characteristic time scale associated with the organism is known to scale as 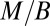—it is a measure of how long it would take for energy proportional to M to be dissipated at a rate of B. Henceforth, proportionality constants, which serve to fix the correct units of various quantities related through scaling relations, will be omitted for the sake of simplicity.

The number of metabolites, N, consumed in the organism per unit time is proportional to B. Let us define 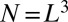, so that a single metabolite is consumed per unit time in the local region surrounding each site of an 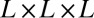grid. Each of these sites can be thought of as being within a service volume, in which one metabolite is consumed per unit time, of linear spatial extent 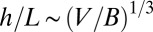. At the local level, the metabolites need to be transported this distance over unit time, and one immediately finds (24) that the transport velocity 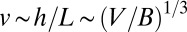. Another measure of the transport velocity is obtained by noting that it is a characteristic length scale of the organism divided by the corresponding characteristic time scale and therefore scales as 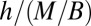. Setting the two measures to be proportional to each other, one obtains Kleiber’s law .

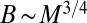An alternative way of deriving the same result in a more rigorous manner is through the consideration of the properties of efficient transportation networks. The goal is to determine the minimum number of metabolites in transit, a measure of the organism mass, to ensure that 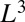metabolites are delivered in unit time within the organism volume. One can prove that the mass scales at least as 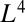with the optimality arising for efficient directed networks with no large-scale backtracking (13). This again leads to Kleiber’s law.

Remarkably, the idealized metabolic rate−mass relationship is predicted to be algebraic with a 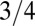exponent independent of the geometry of the organism. Such competitive equivalence explains the coexistence of animals with a homogeneous tissue density and fractal plants on Earth. The mass-specific metabolic rate, 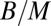, scales as 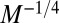, whereas the transit time scales as 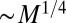. 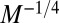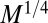Indeed, characteristic biological rates (such as the heart beat and mutation rates) and characteristic biological times (such as circulation times or lifetimes) scale as and , respectively (6, 7, 9–12, 14–16).

Results and Discussion

We now turn our attention to geometry and the constraints it imposes on the physiology of an organism. The link arises from the well-known observation that the metabolic rate is proportional to the surface area. The crucial point, which seems to have been overlooked in the literature, is that the proportionality constant includes the velocity of nutrient delivery and/or energy transport at the surface. Thus, the two quantities that determine the metabolic rate, B, are the surface area, S, and the velocity of transport at the surface, v: 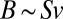. A pure power law in the relationship would be expected only when the product of the surface area and the transport velocity at the surface scales precisely as a power law of the organism mass. One would expect that the transportation ability at the surface could vary from species to species depending on the conditions of the surface as well as on ambient conditions. Thus, pure power law behavior would only hold in an idealized situation.

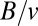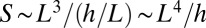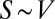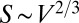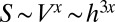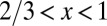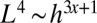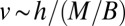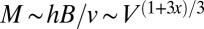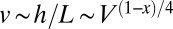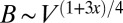The surface area of the organism, S, is given by , and therefore . The surface area of an object of volume V can scale at most as or at least as . More generally, with , and thus . Noting that , one finds that , , and . The 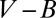relationship is different for different geometries, leading to profound consequences for life (Table 1). The two limiting cases of geometry have been exploited by nature: 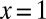in trees, and 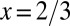in animals.

Table 1.

Summary of predictions of the theoretical analysis

	Tree,	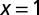Animal,	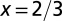Intermediate geometry
Metabolic rate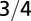
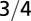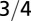Characteristic length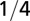
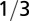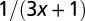Characteristic time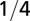
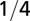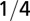Characteristic rate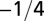
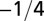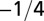Organism volume		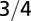1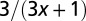
Transport velocity	0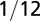
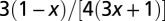Need for pump	No	Yes	Yes
Density		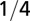0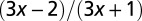
Surface area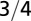
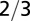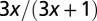Recirculation network	No	Yes	Yes
Fractality of organism	Yes	No	Yes
Service volume density	0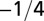
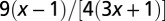Trunk radius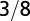

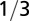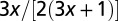The geometry of the organism enters through the scaling of its surface area S with volume V, 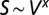. The exponents characterize the scaling of the quantity in the first column with organism mass M. The idealized scaling of the basal metabolic rate, the characteristic time (as reflected in circulation times and life times), and the characteristic rate (such as mutation rates or pump rates) do not depend on the geometry and are universal. Many of the predictions for trees and animals have been observed empirically (10–12, 14–16, 19, 20). The results for organisms with intermediate geometry interpolate between the results for animals and trees.

For a tree, the volume is all surface 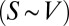with the leaves acting as terminal units from which water transported from the ground evaporates. The transport velocity is independent of the organism mass. This is convenient because water has to be transported upwards against gravity. The organism mass 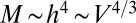and implies a density which increases with organism mass (see Methods). This geometry is tantamount to an organism in three dimensions having an effective dimensionality (12) of 4. Interestingly, a value lower than 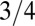of the metabolic rate−mass exponent is predicted if the tree is not isotropic, i.e., its crown diameter scales sublinearly with tree height (22). The mass of the tree is not uniformly distributed but rather is concentrated in the trunk and the branches in a self-similar manner (19, 20).

In contrast, an animal has a uniform density—mass and volume are proportional. The positive scaling (24) of the blood velocity with animal mass as 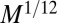requires the presence of a pump, the heart (33, 34). A fractal tree is a rooted organism because of its branching, whereas the nonfractal animal has the advantage of being able to move. The density of service volumes is independent of tree volume, whereas it decreases with increase in animal size, as does the mitochondrial density.

An organism with an intermediate geometry, although matching a tree and a mammal in metabolic efficiency, would require a complex circulation network because not all volume elements lie at the surface. Such organisms would not be as easily mobile because of their fractal geometry, and require a pump because the transport velocity increases with organism mass as 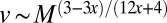. Table 1 shows the key predictions of our analysis and highlights the commonalities and differences between the geometries and physical attributes of plants and animals.

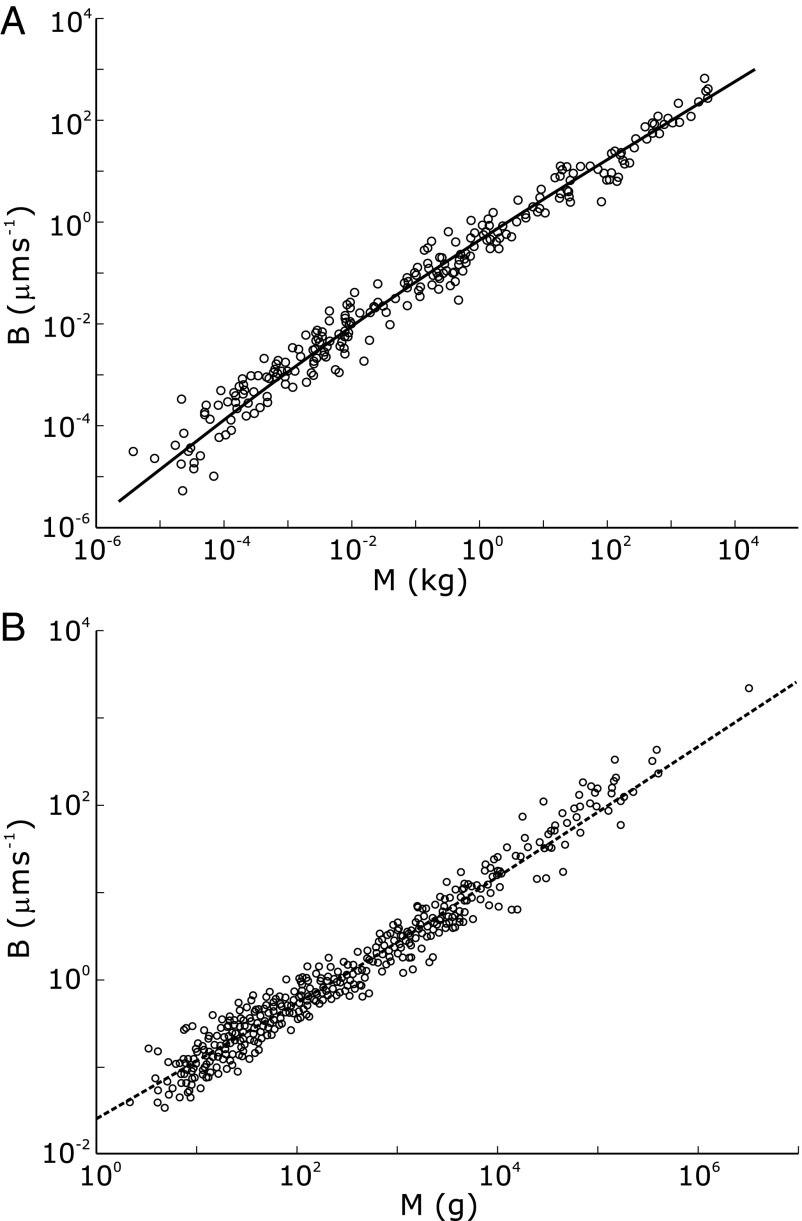
Given the richness of nature’s adaptive strategies and differences in life history, climate, metabolic strategies, and habitat of multicellular organisms, a remarkable result is that, despite deviations and variations, robust trends are observed in the relationship between metabolic rates and body mass. Fig. 1 shows interspecies log-log plots of the metabolic rate−mass relationships for trees [data from Mori et al. (21)] and mammals [from McNab (18) and presented in ref. 23]. Even though the curvatures of the two plots are distinct, in the large mass limit, both trees and mammals approximately follow Kleiber’s law 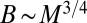, where B is the basal metabolic rate of an organism of mass M. The observations of such scaling behavior have been accompanied by vigorous debate on the specific form of the relationship as well as on the reasons underlying such behavior. Much of the debate has stemmed from the exponent value of 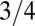. As noted above, the 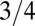exponent arises for a tree essentially from an effective dimensionality of the tree being 4 instead of 3. How can the effective dimensionality of an object be greater than the dimensionality of space it resides in? The constraint of packing a mass (scaling as the tree volume to the 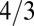power) within the tree volume requires a density that scales as 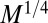. This is facilitated through a heterogeneous distribution of mass over a range of scales. The mass of a tree is not uniformly distributed but is rather concentrated within the trunk and the branches. 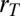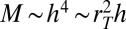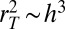Denoting the tree height and trunk radius by h and , respectively, we obtain or and 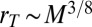. In order for this mass to be contained within a volume of size 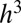, the mass M cannot be greater than 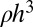, and this can be satisfied only when 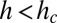, the upper cutoff scale for tree size. Here ρ is an upper bound on the density of a tree component and can be thought of as the mass density of the trunk.

Fig. 1.

Log-log plots of metabolic rate versus mass for trees and animals show deviations from pure power law behavior. The plot suggests that the curvatures (23) in the data sets are opposite to each other. Shigeta Mori (21) provided the tree data (A), and the mammal data (B) are taken from ref. 18. The curvatures are explained as arising from the crossover of exponent values. (A) The solid line shows a fit to 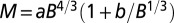. The adjusted 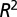value is 0.979, 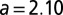with SE 0.220 and P value of 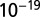, and 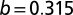with SE 0.0602 and P value of 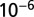. Interestingly, one obtains a leading exponent indistinguishable from 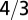if one chooses to make it an adjustable parameter. (B) Motivated by the lack of consensus of the exponent associated with pure power law behavior of the metabolic rate with mass, Kolokotrones et al. (23) carried out extensive analysis of several data sets, principally one due to McNab (18), and showed that the data exhibit curvature on a log-log plot. The analysis was carried out twice, excluding and including the effects of body temperature on metabolic rate. In both cases, the authors used an empirical quadratic fit in which the logarithm of the metabolic rate was expanded in terms of the logarithms of the body mass, measured in grams. The dashed line is a fit to 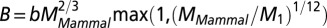. The adjusted 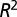value is 0.961 comparable to the quality of fit presented in (23), 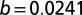with SE 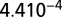and P value of 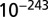, and 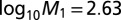with SE 0.162 and P value of .

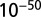By definition, 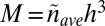where 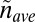is the average mass density (apart from a numerical factor that takes into account the specific tree geometry—the numerical factor is 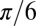for a sphere of diameter h). Because 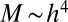, 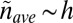(apart from a constant with units that fixes the correct dimensionality). From the obvious bound 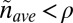, the trunk density, we deduce that 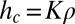, where the constant K has units of length⁴/mass. One would expect that K would depend on details and not be universal.

The 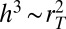result is known to occur in two contexts: (i) It describes the relationship between tree height and diameter (see figure on p. 142 of ref. 6 for interspecies scaling, and figure on p. 143 for intraspecies scaling); and (ii) because of the self-similar nature of a tree, it also describes the tapering of a tree trunk (22). Interestingly, the tapering has been derived previously (6) in a completely different manner using solid mechanics by asking how tall a column of a given diameter could become before it buckles under its own weight.

During the seedling stage of tree growth, most of the mass is composed of metabolically active tissues (17). When the mass of the leaves (which is responsible for the metabolism) accounts for a constant fraction of the total mass, M would be expected to be proportional to B. The crossover between the two distinct behaviors (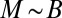 and Kleiber’s 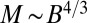) can be simply captured by the expression

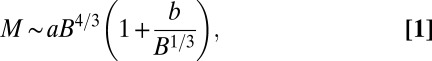where 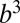sets the scale of B at which the crossover occurs corresponding to a crossover mass of 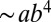. The distinct linear scaling for juveniles was underscored by Reich et al. (17), and a somewhat similar crossover relationship was presented by Enquist et al. (29) and more recently by Mori et al. (21). Fig. 1A shows a log-log plot of B versus M for trees (data from ref. 21) along with a fit to Eq. 1.

We now consider the other limiting case of organism geometry corresponding to a minimal surface area for a given volume: an animal with 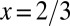, , 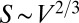and 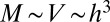. To match the metabolic efficiency of animals with trees, one now requires 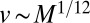. In the simple situation of a single velocity scale (i.e., the velocities in various parts of the mammal body all being proportional to each other with a proportionality constant independent of organism mass), one would expect that the mean blood velocity also scales as 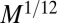. This is supported by empirical data (9)—a velocity increasing with organism mass necessitates the use of a mechanical pump such as a heart. Unlike in trees, the service volumes being nourished in an animal do not all reside at its surface. Thus, one requires a more complex circulation network because, nonetheless, dissipation occurs at the surface. Unlike trees, which are fractal and rooted, compact organisms have the distinct advantage of being able to move. Again, assuming a single velocity scale, the aorta cross-sectional area ought to scale as the ratio of B to the transport velocity or as 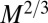. One would expect then that the aorta radius scales as 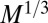, again in accord with empirical data (24, 35). When Kleiber’s law holds, the mass-specific metabolic rate, 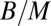, scales as 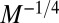, whereas the transit time scales as .

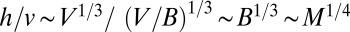The linear size of the service volume and the transport velocity at the surface become smaller in an animal as its mass decreases. One would therefore expect that below a certain threshold mass, 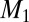, mechanisms such as diffusion, which are body mass independent (recall that the velocity in trees is indeed independent of mass), become operative. Our approach allows one to incorporate velocity variation with organism size in a natural way leading to:

Fig. 1B shows a log-log plot of mammal metabolism data [from McNab (18) and presented in ref. 23] along with a fit to Eq. 2. In this simple scenario, the opposite curvatures in a log-log plot of B versus M arise because the exponent crosses over from 1 to 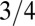as tree size increases whereas the crossover occurs from 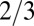to 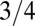as mammal mass goes up.

We turn now to a discussion of the prevalence of separate convergent forms in animals and plants, which is diagnostic of physical and metabolic factors serving as selective pressures affecting the overall evolution of form. Developmental perspectives (36–38) provide the fundamental insight that the patterns of organismal symmetry are established during the earliest developmental stages for most multicellular organisms, including plants and animals. Subsequently, these organisms often grow into complex forms through independently evolved mechanisms including modularity, fractal structure, and segmentation. Despite the diversity of life forms, the approximate validity of Kleiber’s law (4, 6, 7, 9–25) provides a remarkable unifying feature. This allometric scaling pertains to biological structures ranging from unicellular organisms to the tallest trees and has direct implications for characteristic rates and time scales.

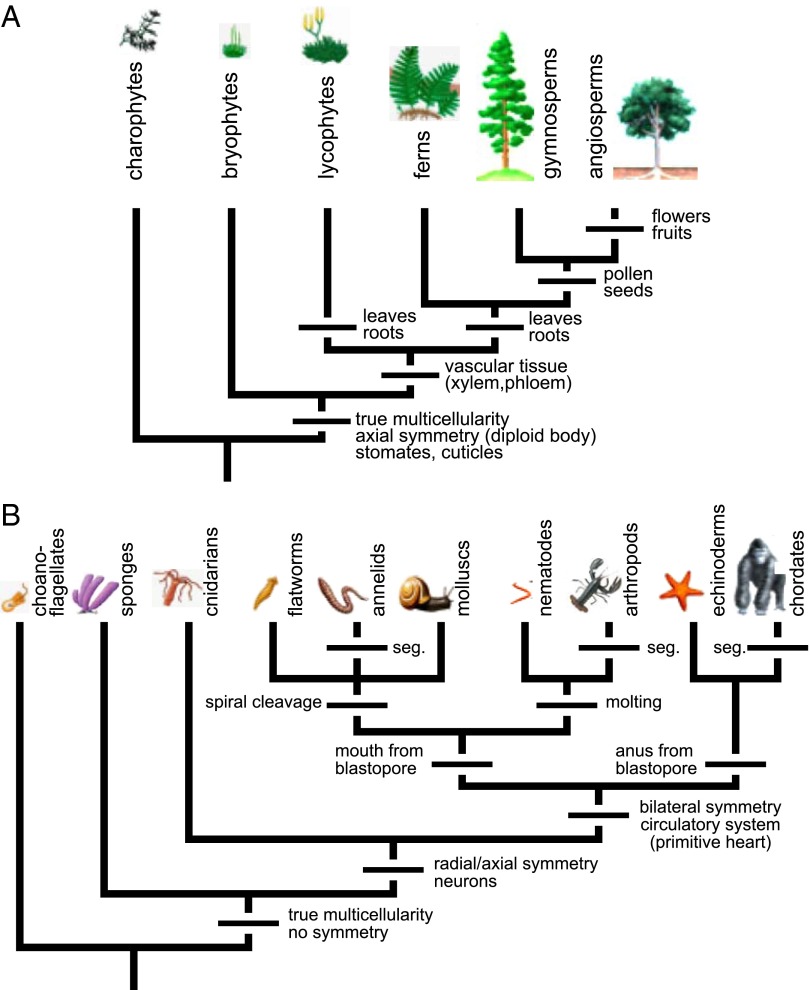
Animals and plants evolved from different ancestral unicellular eukaryotes (37), and their characteristic developmental symmetries, transport systems, and complex forms have evolved independently from each other (Fig. 2). Interestingly, basal lineages of either plants or animals do not exhibit the characteristics of transport tissues and complex structures observed in later-evolved species of both groups. This implies that various selection pressures, including physical constraints, have been favoring the evolution of overall forms and transport structures that are better adapted to carry out particular energetic strategies.

Fig. 2.

Consensus phylogenetic trees for the evolution of the major lineages of modern plants (A) and animals (B) underscore the role of physics as a major selective pressure for driving the evolution of the design of multicellular organisms. (Adapted from refs. 36, 39, and 40.) The origins of the major innovations in organismal form are also plotted on these trees. The earliest diverging lineages of multicellular animals (e.g., sponges and cnidarians) and of multicellular plants (e.g., bryophytes) lack complex transport tissues. The later-arising groups of vascular plants and bilateral animals evolved complex transport tissues, namely, xylem and phloem, and circulatory systems, respectively. In terms of species numbers, vascular plants and bilateral animals dominate modern ecosystems, but it is important to consider the simpler forms of the basal lineages to understand the selection pressures driving the evolution of complex organismal forms. Organism drawings are intended to associate the names of different groups with representative organisms. Due to their size range of 7 orders of magnitude, they are not presented in proper scale. seg, segmentation. (Reprinted by permission of Pearson Education, Inc., Upper Saddle River, NJ.)

Bilaterian animals with circulatory systems are characterized by higher metabolic and transport rates than simpler basal animals, such as barrel sponges and large cnidarians, of the same mass. In the fruit fly Drosophila, a gene called tinman functions as the master control switch for initiating the development of the simple insect heart. Despite the profound differences in the circulatory systems and cardiac structures of insects vs. vertebrates, the homologous gene designated as 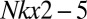plays the same role in vertebrate heart development (33). The presence of these homologous genes and associated regulatory networks in the principal bilaterian lineages argues that the bilaterian common ancestor had evolved a major innovation in animal design, namely a rudimentary circulatory system having a pump whose development was regulated by the ancestral 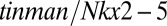gene (34).

The earliest plants evolved from simple algal relatives to become the first successful multicellular invaders of terrestrial environments. They—and their modern bryophyte descendants—lack complex transport systems, i.e., water-conducting xylem and sugar-conducting phloem. In a manner analogous to what happened in animal evolution, the evolution of these complex transport systems in vascular plants accompanied a dramatic change in organismal form (36, 38). Then several lineages of early vascular plants independently evolved bilateral leaves specialized for photosynthesis and evapotranspiration, as well as cylindrical roots specialized for water and ion absorption (36, 38). The basic form of these ancient plants is replicated by the fractal stem and root systems of modern plants. Interestingly, this fractal form has permitted many vascular plant lineages to achieve great heights, as evidenced by repeated evolution of tree-like plants ranging from the arborescent lycopods and horsetails in Carboniferous forests 360–300 million years ago to the coniferous and angiosperm trees of today (38). Furthermore, the evolution of space-filling leaves has allowed vascular plant trees to effectively improve their energetic efficiency.

Methods

We postulate that Kleiber’s law represents a central tendency capturing joint fluctuations in the measurement protocol of metabolic rates (26) (field, basal, maximum, etc.) and body sizes (27). To illustrate the key mathematical idea, we present an analytic derivation of Kleiber’s law for the idealized situation of a spherical organism of radius h and volume 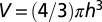. Consider an organism in steady state uniformly nourished from a single source located at its center. Denoting the metabolic rate as B, the source produces B metabolites per unit time. The amount of nutrients consumed per unit volume in unit time is therefore given by 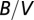. 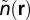Let and 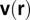denote the density of metabolites and their velocity at position r (measured from the center) within the organism (metabolites are carried in a fluid). The current of metabolites is then given by:

with 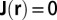at the boundary, i.e., at 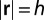, because the nutrients are all used within the organism. The uniform nourishment of the organism leads to the conservation law:

Note that the metabolically active sites (the leaves) are distributed uniformly in a tree just as the metabolically active tissues are distributed uniformly in an animal—it is the mass of the tree which is inhomogenously distributed, unlike in an animal. As a byproduct of this nourishment, heat is generated uniformly within the organism, which is then dissipated at its surface. This heat is transported from within the organism by the fluid, and the nonzero velocity at the surface plays a pivotal role. Solving Eq. 4 with the condition of no flow at the boundary, one obtains

where 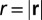. One can proceed to derive Kleiber’s law from the above equation by recalling that the mean velocity scales as the service volume length (24), 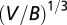. The mean velocity can also be deduced using Eq. 3 and the definition:

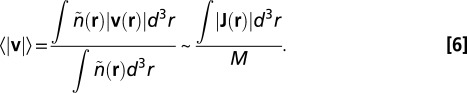Equating the two measures of the mean velocity, one finds universally, for animals and trees as well as intermediate life forms, Kleiber’s law. Of course, deviations from the 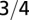exponent would arise when the two measures of the velocity do not coincide. An exact result pertaining to the behavior of optimal directed networks has been presented as supplementary material in ref. 13.