Anomalous water diffusion in salt solutions

Significance

Liquid water remains one of the most important environments in which physical, chemical, and biological processes occur. One such process involves the solvation of ions. Understanding the perturbation that ions make on the hydrogen bond network of water remains an open question. Here, using state-of-the-art simulation methods, we show that treating the electronic degrees of freedom explicitly is required to reproduce the experimentally observed water diffusion trends in CsI and NaCl solutions, where ab initio water is characterized by dynamic heterogeneity. We find that the ions do not disrupt the network in any significant manner and provide some nuances to classical ideas in physical chemistry regarding the “structure-making” and “structure-breaking” properties of ions.

Abstract

The dynamics of water exhibits anomalous behavior in the presence of different electrolytes. Recent experiments [Kim JS, Wu Z, Morrow AR, Yethiraj A, Yethiraj A (2012) J Phys Chem B 116(39):12007–12013] have found that the self-diffusion of water can either be enhanced or suppressed around CsI and NaCl, respectively, relative to that of neat water. Here we show that unlike classical empirical potentials, ab initio molecular dynamics simulations successfully reproduce the qualitative trends observed experimentally. These types of phenomena have often been rationalized in terms of the “structure-making” or “structure-breaking” effects of different ions on the solvent, although the microscopic origins of these features have remained elusive. Rather than disrupting the network in a significant manner, the electrolytes studied here cause rather subtle changes in both structural and dynamical properties of water. In particular, we show that water in the ab initio molecular dynamics simulations is characterized by dynamic heterogeneity, which turns out to be critical in reproducing the experimental trends.

Despite being one of the most-studied liquids, the properties of water and the nature of its interactions with other physical systems continue to be at the forefront of current research in many fields of science (1–8). One important facet of this vast research is the role of water in the solvation of ions. Thus, understanding the effect that ions have on the structural and dynamical properties of water has been a subject of numerous experimental and theoretical studies (6, 9–23). Besides being a classical textbook problem in physical chemistry, the coupling between solutes such as ions and molecules and the surrounding solvent has deep implications on a plethora of biologically relevant processes (24–26).

Over six decades ago, Gurney introduced the notion of “structure makers” and “structure breakers” within the context of how different ions would perturb water’s hydrogen bond (HB) network (27). These ideas have generally been accepted and applied to explain various phenomena observed in electrolyte solutions (6, 28). One such example is the celebrated Hofmeister series, a list of cations and anions empirically discovered by Hofmeister, who found that different ions have varying tendencies to salt-out proteins from solution (6, 26). Although there exist some similarities between this series and various phenomenological measures of structure making and breaking, how exactly the structure of water and the extent of hydrogen bonding should be measured remains an open problem. Experimental studies from the Bakker group (13, 23) probing the rotational mobility of water, for example, have in fact suggested that the presence of ions does not even result in the enhancement or breakdown of the HB network of liquid water.

Perhaps more interesting are questions concerning the connection between structural perturbations and the changes that ions induce on the dynamical properties of water. One important measure of this effect that will form the focus of this study is the self-diffusion coefficient of water molecules (D_W) in electrolyte solutions. In particular, NMR experiments have shown that below 3 M salt concentration, D_W for electrolytes like CsI increases as a function of concentration whereas the opposite trend is observed for NaCl (29). Our interest in these experiments is also piqued by the fact that recent molecular dynamics (MD) simulations using both fixed charge and polarizable force fields (FF) of the same systems do not succeed in even qualitatively predicting the experimental trends––D_W decreased with salt concentration for all of the systems studied (29)! We cannot exclude the possibility that an empirical potential can be constructed to reproduce these phenomena. However, our results from this work raise serious concerns about the use of empirical potentials in simulating electrolyte solutions in different applications and hence fail to provide a model that could be used to get a better understanding of the microscopic origins behind the anomalous water diffusion.

Herein we revisit this problem using state-of-the-art ab initio molecular dynamics (AIMD) simulations where the electronic degrees of freedom are explicitly treated. Unlike the empirical simulations, we find that the AIMD qualitatively reproduce the trends observed in the experimental D_W. First, our analysis of various dynamical properties, such as residence times, unequivocally shows that there is a characteristic dynamic heterogeneity in the water ensemble that is present in the AIMD but absent in the empirical simulations. Rather than inducing significant perturbations to the dynamical properties, we find that the ions result in subtle but measurable changes in the tails of the dynamical ensemble. Although our analysis of various structural features indicates that there are effects that could be likened to structure making and breaking, the HB network is not disrupted or broken in any significant manner. In similar spirit to some recent work from our group that looked at directional correlations in the HB network relevant for proton and hydroxide diffusion (7), we show that ions such as Na⁺, Cl⁻, Cs⁺, and I⁻ substitute the role of water molecules in the network participating in directed ring structures with similar “network rules” present in neat water. The AIMD and empirical HB network exhibit qualitative differences which provide clues into the origins of the discrepancies previously noted.

Self-Diffusion of Water

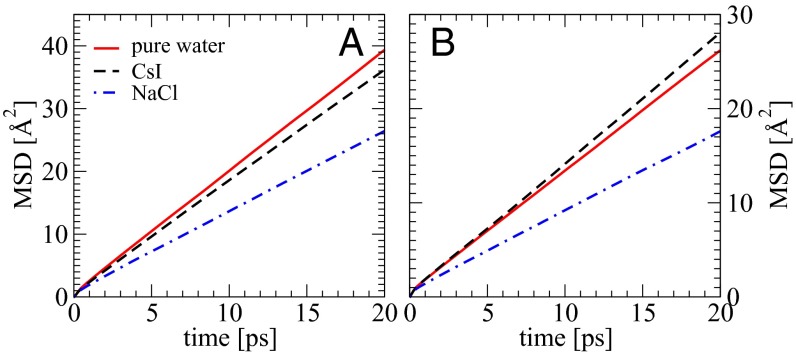
AIMD simulations using the CP2K package (30) were conducted for three systems: pure water, 3 M NaCl, and 3 M CsI. Similar calculations were also performed for these systems using an empirical FF. See Materials and Methods, Computational Methods for more details on the protocols used to setup the calculations. We note that obtaining converged diffusion coefficients, particularly from the AIMD simulations, is quite challenging, and very long simulations (∼170 ps) are needed. We begin first by comparing the D_W for the three systems using AIMD and the empirical FF. In experiment, at 3 M concentration, the D_W for CsI solution is accelerated by ∼23% compared with pure water, whereas the D_W for NaCl solution is slowed down by ∼19% (29). Here, D_W is calculated using the standard relationship between the diffusion coefficient and the slope of the mean-squared displacement (MSD), which is averaged over all of the snapshots with a time interval of 10 fs. To obtain D_W, a linear regime between 2 and 20 ps of the MSD curve was used. Fig. 1A illustrates the MSD curves obtained from the empirical simulations. Consistent with previous studies, we see that the slope of the curves for both salt solutions is less than that of pure water. The D_W for NaCl and CsI is smaller than pure water by ∼32% and 8%, respectively. In contrast, Fig. 1B shows that the MSD curves obtained from the AIMD simulations reproduce the qualitative trends observed in the experiments. More specifically, we find that water in CsI has a D_W that is larger than pure water by ∼8%, whereas in NaCl it is significantly slower by 34%. Although, in absolute terms, there are differences between the experimental and AIMD D_W, the qualitative trends are reproduced and hence our simulations provide a model in which the origins of the effects can be examined. For clarity, D_W for all systems is listed in Table 1.

Fig. 1.

Mean-squared displacement of O atoms in pure water (red solid line), 3 M CsI (black dashed line), and NaCl (blue dashed and dotted line) solutions simulated with classical FF (A) and AIMD (B).

Table 1.

Water and ion self-diffusion coefficients for both AIMD and classical simulations

	Dw(× 10−5 cm2/s)
Components	AIMD	Classical
Pure water	2.135	3.208
Water (3 M CsI)	2.305	2.961
Water (3 M NaCl)	1.412	2.139
Cs+	1.144	1.451
I−	1.296	1.284
Na+	0.799	0.723
Cl−	1.215	0.769

The preceding results are quite striking and highlight the critical requirement of treating these relatively simple electrolyte systems from first principles. Our next task is to try to understand the origins of the different D_W obtained for these three systems. In doing so, we introduce some nuances to the ideas of structure breakers and makers and at the same time provide some clues into the origins of the discrepancies between the AIMD and empirical calculations.

Structural Perturbations to the Network

We first examine the radial and angular distribution functions which are standard probes of the effects of the ions on the water network.

Radial and Angular Distribution Functions.

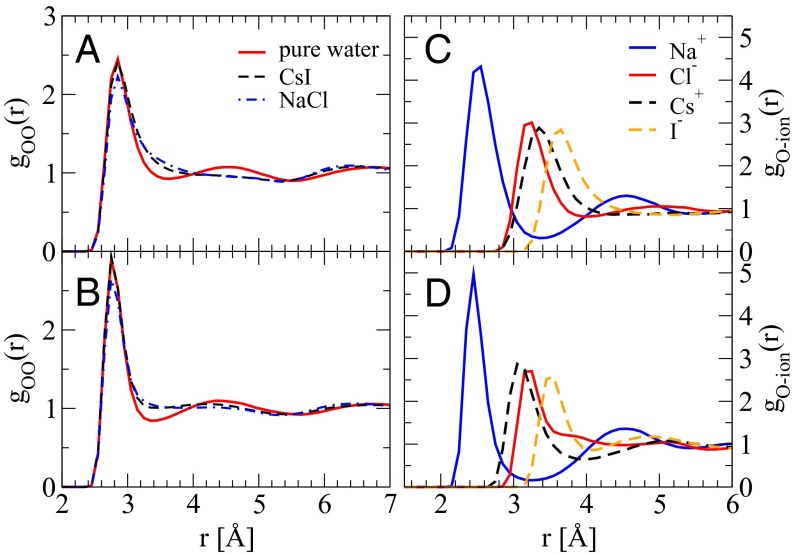
The radial distribution function [g(r)] between a pair of tagged species provides a measure into the extent and the length scales of the structural correlations that exist in the system. It is well appreciated that most standard density functionals tend to overstructure ab initio water (31). This feature is also invoked to explain why the diffusive dynamics of ab initio water tends to be more sluggish compared with the experimental D_W (32). However, as we will see now, extracting correlations between features of the g(r) and dynamics is not so obvious. Take, for example, the g_OO(r) for the three simulated systems in the AIMD shown in Fig. 2A. The g_OO(r) of pure water exhibits more pronounced oscillations between 3 and 6 Å and is hence more structured. However, we see that in both NaCl and CsI solutions this regime is completely washed out. The flattening of the second solvation shell is often interpreted as a structure-breaking effect and subsequently used to rationalize a speed-up in diffusive water dynamics (33). However, as we have seen earlier, the D_W of pure water, which has the most structured g_OO(r), is sandwiched between the D_W of CsI and NaCl in AIMD simulations. Besides these features, we also note that despite the differences in D_W between the AIMD and empirical simulations, their g(r)s do not even reveal any striking differences (Fig. 2). More revealing insights into the perturbation that the ions induce on the HB network can be obtained by examining the ion–water g(r) illustrated in Fig. 2 C and D. Physically this measures how strongly water molecules are bound to the ions. First we see that owing to their larger van der Waals’ radii, the excluded volume around both Cs⁺ and I⁻ is larger than that around Na⁺ and Cl⁻ in the AIMD runs. This feature is not captured using the empirical potentials. Besides underestimating the excluded volume around Cs⁺, the empirical simulations also lead to much longer range structural correlations compared with the AIMD. In the latter case, after the first peak we observe an immediate flattening of the g(r) for the fatter ions that is clearly not featured around Na⁺ and Cl⁻. This provides one of the first signatures that the fluctuations of water molecules around the ions in the two electrolytes CsI and NaCl are quite different. We will see later that these differences do not require a significant disruption or enhancement of the HB network. Note that the empirical simulations carried out in this work are plagued by clustering effects where the positive and negative ions form close contact pairs (see Materials and Methods, Computational Methods for more details). This artifact is quite strongly manifested in the size of the hydration shell of the ions which tend to be severely undercoordinated (Table S1) in the empirical simulations.

Fig. 2.

Radial distribution functions of O–O (A and B) and O–ion (C and D) in pure water, 3 M CsI and NaCl solutions simulated with AIMD (A and C) and classical FF (B and D).

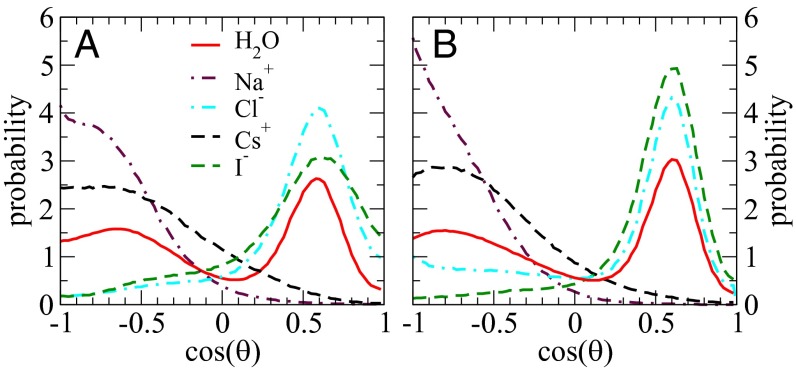
Due to the inherent directionality of the HBs, we were interested in determining whether the water molecules around the ions had specific orientational preferences around the different electrolytes. To this end we looked at the orientational distribution between O_NS_C and the bisector of the water molecule H₂O_N. S_C represents an oxygen atom or an ionic center and O_N corresponds to the oxygen atom of a neighbor water molecule within the first solvation shell of S_C. Fig. 3 compares this distribution obtained around different species and between the AIMD and empirical simulations. The distribution in pure water exhibits two peaks, one positive and the other negative, corresponding to water molecules acting as either an HB donor or acceptor, respectively, to the central O_C water. Much to our surprise, the distributions in the electrolyte systems with S_C as a water molecule are very similar, implying that the orientational organization of the water network is not impacted in any significant manner in the electrolyte solutions compared with neat water (Fig. S1). When the central atom is substituted by the ions, only one peak is observed, which tends to be more pronounced compared with those around water. Furthermore, the orientational fluctuations of water around the fatter ions Cs⁺ and I⁻ appear to be occurring on a much softer underlying potential than those around Na⁺ and Cl⁻. Overall, the empirical simulations tend to damp these fluctuations compared with what is seen in the AIMD. Despite these effects, we will see shortly that the ions effectively take on the donating and accepting functions of water’s HBs, thereby substituting the role of water molecules without disrupting the water network.

Fig. 3.

Angular distributions of ∠S_CO_N p (S_C could be O atom in pure water, or Na⁺, Cl⁻, Cs⁺, and I⁻ centers, whereas O_N p represents the bisector of the neighboring water molecules in the first solvation shell) for simulations carried out with AIMD (A) and classical FF (B).

Ring Statistics.

In a recent work we have shown that water’s HB network is made up of a union of interconnected rings (7). The directionality of the HBs results in rather specific directional correlations within the ring structures. We also demonstrated that structural defects like the excess proton and hydroxide ion perturb the distribution of rings that thread them and are incorporated into the water network without significantly altering the directional correlations. We begin our analysis by examining the perturbation that the electrolytes make on the rings where the directionality is first neglected. In the ensuing analysis of the properties of the network, we focus the discussion on the AIMD network.

The HB network and the perturbation induced by the electrolytes can be probed at several levels. First we can look at the overall distribution of the size of different rings. Note that in the salt systems, the rings are made up of both water molecules and ions. Pure water, for example, is dominated by 5–7-membered (M) rings, with a much smaller population of 3–4 and 8–10 M rings (7). Both electrolytes alter the relative populations of these rings, significantly increasing the proportion of 3–4 M rings. However, there are no striking differences observed between NaCl and CsI. Another more local measure of the perturbation that the ions make on the network is the change in the distribution of the rings that thread individual water molecules. Here we see that both the mean and fluctuations in the number of rings around waters increase for both electrolytes, and that this increase is much more pronounced for CsI. These effects arise from the lack of restriction of tetrahedral geometry that is present in neat water.

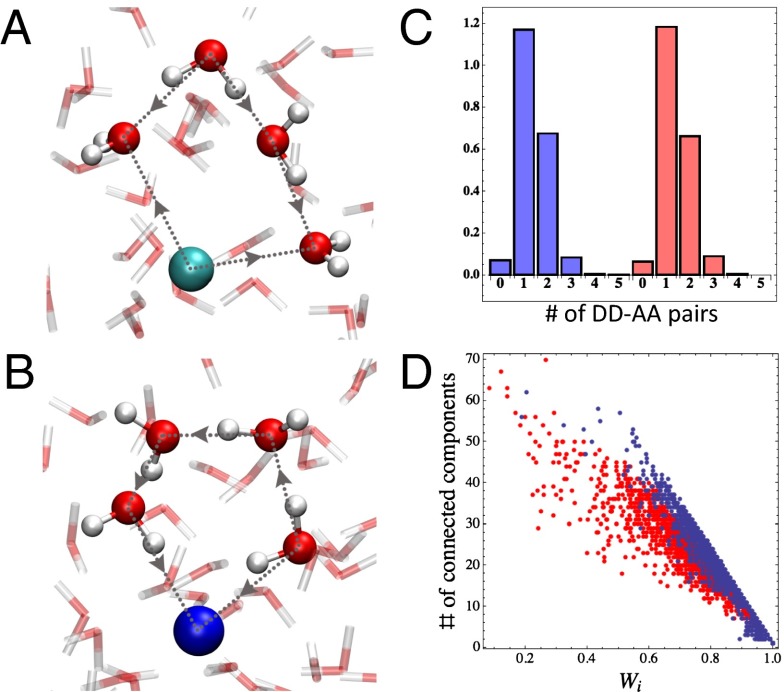
To address this issue in more detail, we examined the directional correlations in the rings composed of ions and water molecules. In our earlier study (7), we found that closed rings consisted of three types of water molecules that perform specific HB patterns: double donors (DD) that donate two HB within a ring, double acceptors (AA) that accept two HB within a ring, and single donor–acceptors (DA) that donate and accept a single HB. In pure water we found that DD and AA water molecules always occurred in pairs within the ring, and that finding a single DD–AA pair was the most dominant motif. Within the context of the electrolytes in this work, the results of Fig. 3 strongly suggest that the positive Na⁺ and Cs⁺ can be thought of as nodes that play the role of DD in all of the rings in which they participate. On the other hand, the negative Cl⁻ and I⁻ act solely as AA. Illustrative examples of these types of rings are shown in Fig. 4 A and B. With these rules, we examined the distribution of the number of DD–AA pairs within the directed rings for the NaCl and CsI systems. Fig. 4C compares this distribution for the two electrolytes. These distributions are strikingly similar to what we observe in pure water: the number of DD–AA pairs ranges between mostly 0 and 3 and the dominant motif is made up of a single DD–AA pair (7). Essentially in these electrolyte solutions, the ions seem to be accommodated within the network and subscribe to the same topological rules. The aforementioned results already suggest that the notion of making or disrupting the network needs to be revisited. To further bolster this point, we can take our analysis beyond a local measure within the ring and examine the global extent of the HB network for the different electrolytes. To do this, we first constructed a global directed graph made up of the union of rings consisting of only water molecules (see Materials and Methods, Computational Methods for more details). The spatial extent of the network is probed by examining the distribution of the number of strongly connected components in the system (N_comp) and an effective weight of the largest connected cluster (W_i). A strongly connected component is defined as a group of waters, where a bidirected path can be found between every pair of water molecules in the cluster. W_i measures the total percentage of water molecules in the system that are hosted by the largest connected cluster. Fig. 4D illustrates the distribution of W_i and N_comp for the NaCl and CsI solutions. First, we notice that although N_comp can take on quite a broad distribution of values, the vast majority of water molecules are comfortably accommodated within the largest connected component. This implies that despite the presence of the ions, a spanning or rather percolating HB network still exists. Another interesting feature of Fig. 4D is that CsI is characterized by moderately larger fluctuations in the effective size of the largest component, as revealed by a higher density of red points toward lower values of W_i. This reveals some signal of “higher disorder” of the directed water network in CsI.

Fig. 4.

(A) Ring with two DD–AA pairs consisting of a Cs⁺ and four water molecules. (B) Ring with one DD–AA pair consisting of a Cl⁻ and four water molecules. Note how the Cs⁺ and Cl⁻ play the role of a DD and an AA, respectively, within the ring. Ball and stick, and line models are used to represent water molecules with O atoms in red and H atoms in white, whereas Cs⁺ and Cl⁻ are in cyan and blue, respectively. (C) DD–AA pair distributions in both CsI (red bars) and NaCl (blue bars) solutions within a single ring. (D) N_comp and W_i distributions in CsI (red dots) and NaCl (blue dots) solutions.

Perturbations to Dynamical Properties

Up to this point, we have established that the electrolytes induce rather subtle structural changes in water without causing significant disruption of the HB network. More importantly, the changes that we observe reflect perturbations to the degree of the fluctuations rather than drastic changes in the average properties. In this regard, studying changes in the dynamical properties becomes essential. We begin by discussing the water residence times and then move on to the HB kinetics and the reorientational dynamics.

Residence Times.

We computed the residence time correlation function 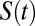around both the ions as well as water molecules in all of the simulated systems using a procedure that has been previously used to compute residence times of waters around proteins (34). The 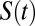measures the average number of water molecules that continuously remain around the tagged site of interest (an ion or water molecule). Because the time interval between two snapshots is 10 fs, water molecules can diffuse out of the solvation shell and then return within this time interval. In all our simulations, 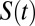decays in an exponential manner, and the time constant associated with this decay gives a measure of the residence time of water around a specific site.

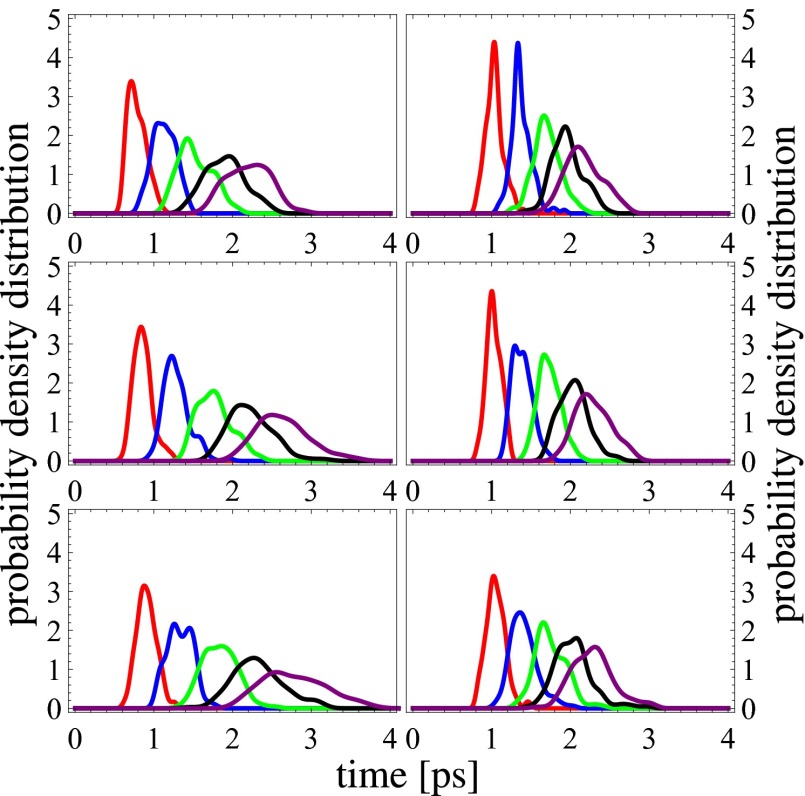
Fig. 5 compares the distribution of residence times obtained from exponential fits to 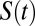for each water in the system using different cutoffs for the first solvation shell. We begin by first comparing the distributions obtained for pure water with AIMD and the empirical simulations (Fig. 5, Middle). For all cutoffs larger than 3.3 Å, we observe that the residence times for AIMD water have a broader distribution compared with those of TIP4P water model (35), which tend to be more localized. This reflects the dynamic heterogeneity of the AIMD ensemble where residence times with a tail up to 4 ps are observed. As we will discuss later, part of the origin of this feature comes from the underlying electronic heterogeneity of the water molecules which is absent in the empirical models. Comparing the residence times in the electrolyte systems to those in pure water reveals that CsI is characterized by a more pronounced tail to shorter residence times and hence faster dynamics (Fig. 5, Top), whereas in NaCl the tail is bigger for longer residence times, reflecting more sluggish dynamics (Fig. 5, Bottom). This trend is consistent with what we observe for the self-diffusion of water discussed earlier. On the other hand, in the classical simulations the residence time distributions tend to be rather insensitive to the presence of the electrolyte and are much more localized around a similar average value.

Fig. 5.

Smoothed probability density distributions of water residence time around water in 3 M CsI solution (Top), pure water (Middle), and 3 M NaCl solution (Bottom) obtained from AIMD (Left) and classical FF (Right) simulations. The distributions are plotted in different colors according to different cutoffs used for the solvation shell. Red, cutoff 3.2 Å. Blue, cutoff 3.3 Å. Green, cutoff 3.4 Å. Black, cutoff 3.5 Å. Purple, cutoff 3.6 Å.

Besides the heterogeneous polarization effects that water molecules feel with respect to other waters in the system, they are also subject to strong electric fields from the ions. In a similar way as above, the residence times of water molecules around ions were also examined (Fig. S2). The residence time of water around Na⁺ is significantly longer compared with that around Cs⁺ and I⁻. Although the empirical simulations seem to reproduce these trends, the residence times around Cs⁺ and I⁻ are much longer than in AIMD. Furthermore, the separation in timescales between Cl⁻ and CsI is also much less pronounced in the empirical simulations.

HB Kinetics.

The residence time correlation functions previously described are “history dependent” and in some sense give a lower bound of the relaxation times associated with the translational dynamics of water. To investigate the HB dynamics and the changes observed in different electrolytes we examined the history-independent correlation function 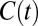, which has been previously examined in literature (36, 37). To construct this correlation function we use standard definitions of the HB which simultaneously satisfy three criteria: O…O distance is less than 3.4 Å, H…O distance is less than 2.5 Å, and the ∠HOO is no more than 30°. Fig. 6 A and B compares the 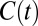obtained for the AIMD and empirical simulations. 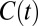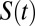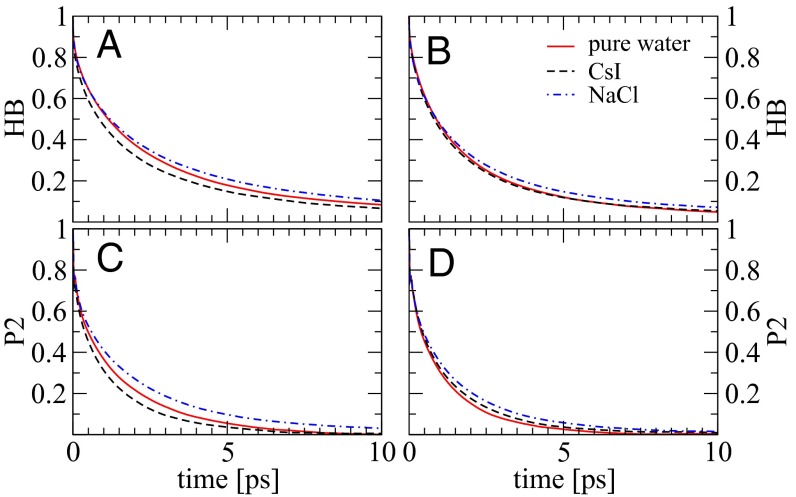First, we note that as expected, is characterized by longer decay times than and is best described by a series of two exponential decay functions (Table S2). Although the trends are not as pronounced as in 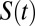, the HB dynamics of water in CsI is faster than in pure water whereas that around NaCl is slower. This feature is not captured by the empirical simulations and reinforces the notion that the effects that the ions have on the dynamics are rather subtle, and is consistent with the extent of the perturbations we observe in the structural and network properties.

Fig. 6.

Hydrogen bond (A and B) and P2 (C and D) correlation functions of water molecules in pure water (red solid line), 3 M CsI solution (black dashed line), and 3 M NaCl solution (blue dashed and dotted line) simulated in AIMD (A and C) and classical FF (B and D).

Reorientational Dynamics.

The correlation functions 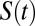and 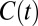primarily probe the translational diffusion of water molecules. Earlier, we alluded to the fact that the orientational fluctuations of water around the ions had some characteristic differences. To quantify the dynamics associated with these fluctuations, we examined the first and second Legendre polynomials of the correlation function (P1 and P2) (8, 20, 38) associated with the bisector of a water molecule which is very close to the direction of the dipole moment. The trends in the decay dynamics from the AIMD reinforce the results for the self-diffusion: water reorientation in NaCl is the most sluggish whereas that in CsI is faster than pure water. Once again, the empirical simulations do not succeed in reproducing these trends (Fig. 6 and Fig. S3). Recently Stirnemann et al. (8) have studied the reorientation dynamics of ions in both diluted and concentrated salt solutions and concluded that all of the concentrated salt solution will retard the water dynamics. This conclusion seems to contradict our findings and the experimental data on CsI solutions (29). However, an important role might be played by the ionic concentration. For instance, in this very same paper, it is found that in NaClO₄ solution at 1 M and 2 M there is an acceleration in the reorientational dynamics that eventually gets retarded at a higher concentration of 8 M.

Electronic Heterogeneity of Water Molecules

The preceding results make quite a convincing case that, at least on the timescales relevant for diffusion in the systems we have studied, water molecules in the AIMD are characterized by a form of dynamic heterogeneity. This feature appears to be crucial in reproducing the trends observed in D_W for pure water and electrolyte solutions. Previous AIMD simulations of ab initio water have speculated that this feature arises from the many-body electronic polarization of the HB network (39). To obtain a more quantitative measure of the implications of this effect, we looked for possible correlations between the average dipole moment of water molecules and some of the structural and dynamical properties previously discussed. Dipole moments were computed using the maximally localized Wannier functions (40) that were determined for each water molecule by sampling snapshots from the trajectories using a time interval of 0.1 ps.

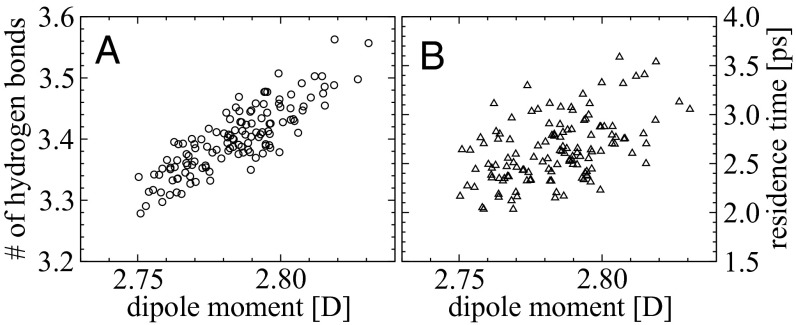
As in previous studies (41), the dipole moment distribution in ab initio water is quite broad. The instantaneous dipole moment of a water molecule exhibits enormous fluctuations in the AIMD ranging between 1.7 and 4.0 D (Fig. S4). Fig. 7A shows a scatter plot of the average dipole moment of each water molecule vs. the number of HBs that it participates in, for simulations without the ions. Despite the large fluctuations in the instantaneous dipole moment, the correlation between these two variables is significant––water molecules involved in more HBs on average tend to be more polarized. It seems reasonable to think that water molecules with a larger dipole moment on average will induce longer residence times for waters in their vicinity. Fig. 7B indeed shows that although this correlation is weaker than that observed for the number of hydrogen bonds, there is still a nontrivial relationship between these quantities.

Fig. 7.

Correlation between average dipole moments and average number of hydrogen bonds (A, correlation coefficient 0.82), as well as correlation between average dipole moments and the residence times (B, correlation coefficient 0.46) in pure water simulated with AIMD. The correlation coefficients are calculated based on Spearman’s rank formula.

Extracting similar types of correlations for the electrolyte systems poses many more challenges. Water molecules in the salt solutions face both dynamically evolving water and ionic environments which influence the diffusion in different ways. In particular, we find that both electrolyte solutions, for example, result in an overall decrease in the average dipole moment of the water molecules compared with pure water. Furthermore, this effect is induced predominantly on water molecules that reside in the vicinity of the ions. The polarization of “bulk-like” water molecules in the electrolyte systems is strikingly similar to those in pure water (Fig. S4).

Discussion and Conclusions

In this work we examined the origins of the anomalous diffusion of water in different electrolyte solutions. Although there exist differences in the absolute value of the diffusion coefficients between ab initio and experiments, our results demonstrate that ab initio water is qualitatively more realistic than the empirical potential used in the present work. We have shown here that even for rather simple electrolytes, AIMD simulations of pure water, 3 M CsI, and NaCl solutions successfully reproduce the qualitative trends of the self-diffusion observed experimentally (29) which the empirical models so far tested fail. One of the key ingredients that appears to be essential in reproducing these features is that the ab initio water ensemble is characterized by dynamic heterogeneity. The origin of this behavior lies in the electronic diversity of water molecules in different environments, which in turn results in significant variability in the way water molecules polarize their surroundings. This is then manifested in dynamical properties such as the residence times.

The commonly accepted descriptions of how ions perturb the water network invoke some notion of structure making or structure breaking, although the microscopic origins of this behavior remain elusive. Here we have attempted to provide a more nuanced understanding of these ideas by describing the perturbation in terms of structural, dynamical, and electronic properties of the water network. The picture that emerges is that even at very high salt concentrations, the ions do not disrupt the HB network in any significant manner. Instead, the ions adapt to the topological rules of water’s directed HB network and induce rather subtle changes to the dynamical and electronic properties of water which ultimately lead to the change in the self-diffusion of water.

Clearly, even for the rather simple electrolyte systems like CsI and NaCl that we have studied here, an explicit treatment of the electronic degrees of freedom within an AIMD approach seems mandatory. Although more work is needed to parameterize better empirical potentials, exploring the degree of dynamic heterogeneity in other aqueous systems, for example water near proteins and DNA with first-principle simulations is also required at this point. This will allow for more meaningful comparisons with experiments. Recent advances in linear-scaling density functional theory are already making these types of calculations possible (42).

Materials and Methods

Computational Methods.

AIMD simulations were performed with the CP2K package (30). We use a hybrid Gaussian and plane waves (43) or Gaussian and augmented plane waves (GAPW) (44) scheme, in which, the electronic density is expanded in the form of plane waves with a cutoff of 280 Ry. The GAPW scheme is only applied for Na⁺ and Cl⁻ ions to obtain well-converged forces. In addition, Grimme’s empirical dispersion corrections are also included (45). Previous studies (46, 47) have shown that better bulk water properties could be achieved with Grimme’s correction. We choose revised Perdew-Burke-Ernzerhof (48) as the exchange and correlation functional. Goedecker–Teter–Hutter pseudopotentials (49) are used to treat the core electrons. In particular, the semicores of Na⁺ and Cs⁺ are treated explicitly, which involves nine valence electrons. Double-zeta split valance basis sets are used for all atomic kinds. The motion of nuclei follows Newton’s equation of motion and is propagated based on the velocity Verlet algorithm with a time step of 0.5 fs. At each time step, the wavefunction is optimized based on the orbital transformation method, and the self-consistent field convergence criterion is set to 1.0 × 10⁻⁶ a.u. All systems are first equilibrated with TIP4P water model (35) and OPLS force field (50) for the ions for periods of at least 800 ps.

Simulations of NaCl solution with certain empirical potentials are plagued by artifacts involving clustering of Na⁺ and Cl⁻ ion pairs (51). Hence, for the equilibration phase, the ions are fixed at a distance of at least 6 Å from each other. Thereafter the last snapshot is chosen as the initial structure in the AIMD simulations. Generally in each AIMD run, we first equilibrate the system in the canonical ensemble (NVT) using the Nosé–Hoover thermostat at 298 K for at least 15 ps. Then the simulations are continued with energy-conserving dynamics in the microcanonical ensemble (NVE) for ∼170 ps. The empirical simulations for pure water, 3 M NaCl, and CsI solutions are carried out with the LAMMPS MD package (52). We first equilibrate the systems with at least 800-ps NVT runs at 298 K, and then NVE simulations are carried out for another 800 ps. The first 600 ps is treated as equilibration and the last 200 ps is used for analysis.

Experimental densities are used for pure water and NaCl solution at 298 K (53). A cubic box with a side length of 15.6465 Å is used to simulate pure water containing 128 water molecules. Seven NaCl ion pairs and 120 water molecules are simulated in a cubic box of 15.6489³ ų, which corresponds to a concentration of 3 M. The density of 3 M CsI solution is extrapolated from the experiment densities of KCl, KI, and CsCl at the same concentration (53). We use the same simulation box as NaCl solution for 7 Cs⁺ and I⁻ ion pairs, which contains 105 water molecules. Although much larger system sizes could be afforded with the empirical simulations, we use the same system sizes as in the AIMD to allow for a 1-to-1 comparison of the calculations.

To probe the perturbation that the ions make on the directed network, we examined various distributions of both undirected and directed rings of the whole network as well as rings threading individual water molecules. Rings were constructed in a similar fashion as in our previous study and the reader is referred to this earlier work (ref. 7) for more details. One important difference is how to consider the directionality between the ions and water molecules. For negatively charged ions such as the Cl⁻ and I⁻, water molecules donate hydrogen bonds to the anionic species and hence the ion plays the topological role of an AA site. On the other hand, for positive ions such as Cs⁺ and Na⁺ the directionality is less obvious. Within the framework of our topological analysis, the cations essentially play the role of DD sites and hence we insert a directed edge from the ion to the neighboring water. Cutoffs for the water–water and ion–water interactions were chosen where physically meaningful coordination numbers for the species of interest were obtained (Table S1).