First look at changes in flood hazard in the Inter-Sectoral Impact Model Intercomparison Project ensemble

Abstract

Climate change due to anthropogenic greenhouse gas emissions is expected to increase the frequency and intensity of precipitation events, which is likely to affect the probability of flooding into the future. In this paper we use river flow simulations from nine global hydrology and land surface models to explore uncertainties in the potential impacts of climate change on flood hazard at global scale. As an indicator of flood hazard we looked at changes in the 30-y return level of 5-d average peak flows under representative concentration pathway RCP8.5 at the end of this century. Not everywhere does climate change result in an increase in flood hazard: decreases in the magnitude and frequency of the 30-y return level of river flow occur at roughly one-third (20–45%) of the global land grid points, particularly in areas where the hydrograph is dominated by the snowmelt flood peak in spring. In most model experiments, however, an increase in flooding frequency was found in more than half of the grid points. The current 30-y flood peak is projected to occur in more than 1 in 5 y across 5–30% of land grid points. The large-scale patterns of change are remarkably consistent among impact models and even the driving climate models, but at local scale and in individual river basins there can be disagreement even on the sign of change, indicating large modeling uncertainty which needs to be taken into account in local adaptation studies.

Climate change due to anthropogenic greenhouse gas emissions is expected to change the distribution and variability of precipitation (1, 2). As the water holding capacity of the atmosphere is increasing with temperature, global warming is expected to increase the intensity of precipitation events (3–5). Such an increase in precipitation intensity is likely to have an impact on the frequency of (pluvial and fluvial) flooding.

Although an increase in flooding under climate change is often speculated on, few studies have actually provided projections of fluvial flooding at a continental or global scale (for examples see refs. 6–9). Most studies that have appeared to date focus on individual river basins or countries (e.g., refs. 10–13), and the use of different models and scenarios makes it impossible to generalize the results, to compare regional sensitivities, or to make global-scale risk assessments. Assessing the impact of climate change on fluvial flooding is furthermore hampered by biases and uncertainties in both climate and impact models.

The InterSectoral Impact Model Intercomparison Project (ISI-MIP, ref. 14) provides the opportunity to explore these uncertainties in projections of changes in flood hazard at a global scale. ISI-MIP offers a framework for comparing multiple climate impact models within and across different sectors, based on consistent climate and (where appropriate) socioeconomic scenarios, providing a quantitative estimate of impacts and uncertainties. The fast-track phase of the project involves 34 global impact models across 5 sectors. The aim of this paper is to look specifically at the relative importance of climate and impact model uncertainty in projected changes of flood characteristics, as well as the consistency in these projections. We use results from nine global hydrology and land surface models (hereafter referred to as impact models, IMs) that provided simulations of daily river discharge at a global 0.5° grid (Table 1). Each IM was driven by five global climate models (GCMs) that were selected to represent the range of global mean temperature change and relative precipitation changes in the Coupled Model Intercomparison Project Phase 5 (CMIP5) simulations (see ref. 14 for further details). In this paper we only include simulations using representative concentration pathway RCP8.5, giving us an ensemble of 45 experiments, each consisting of a historical and future period.

Table 1.

Overview of models used in this paper

Hydrology and land surface models	Climate models
LPJmL	GFDL-ESM2M
JULES	HadGEM2-ES
VIC	IPSL-CM5A-LR
H08	MIROC-ESM-CHEM
Mac-PDM.09	NorESM1-M
WBM
MPI-HM
PCR-GLOBWB
MATSIRO

For references, see ref. 14. Further details on most of the IMs used in the present study can also be found in ref. 19. GFDL-ESM2M, Geophysical Fluid Dynamics Laboratory Earth System Model; HadGEM2-ES, Hadley Centre Global Environment Model version 2 - Earth System; IPSL-CM5A-LR, Institut Pierre Simon Laplace Climate Model 5A Low resolution; JULES, Joint UK Land Environment Simulator; LPJmL, Lund-Potsdam-Jena managed Land Dynamic Global Vegetation and Water Balance Model; Mac-PDM.09, Macro-scale-Probability-Distributed Moisture model version 09; MATSIRO, Minimal Advanced Treatments of Surface Interaction and RunOff; MIROC-ESM-CHEM, Model for Interdisciplinary Research on Climate - Earth System Model - Coupled Atmospheric Chemistry; MPI-HM, Max Planck Institute - Hydrology Model; NorESM1-M, Norwegian Earth System Model version 1-M; PCR-GLOBWB, PCRaster Global Water Balance Model; VIC, Variable Infiltration Capacity model; WBM, Water Balance Model.

As an indicator of flood hazard we estimated the 30-y return level of river flow (Q30) at each grid cell for two 30-y periods (1971–2000 and 2070–2099). The Q30 is a moderately extreme discharge level that will be exceeded only very infrequently. Whereas the probability of exceedance (Pe) in any given year is 1/30, in any given 10-y period it amounts to almost one-third (0.29). In flood risk management it is therefore common to take even higher flow levels (such as the 100-y return level) as a threshold for protection measures or planning regulations.

Results

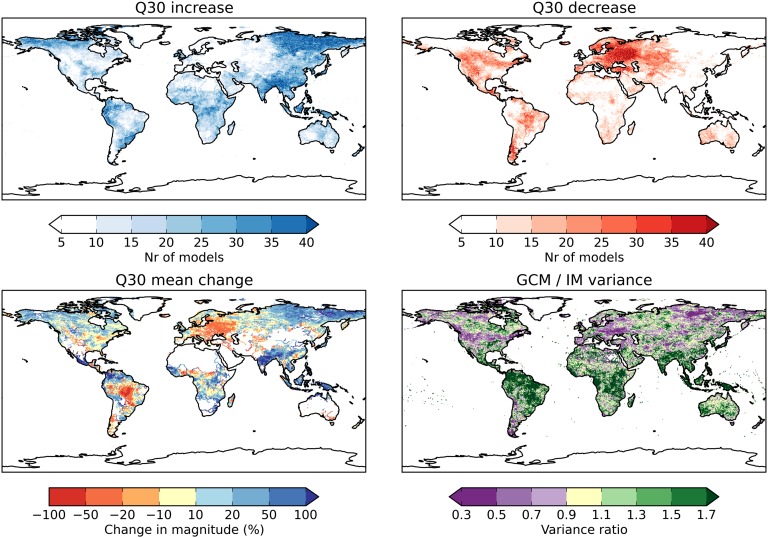
The large-scale pattern of regions with projected increases and decreases in flood hazard is remarkably robust across the IMs and even the GCMs. Fig. 1 (Upper) shows the number of experiments that agree on an increase or decrease in the magnitude of Q30 by more than 10%. The magnitude of change in each GCM/IM combination is shown in Figs. S1–S5). Broadly speaking, increases in flood hazard are projected consistently in central and eastern Siberia and parts of Southeast Asia, including India. Likewise, the Q30 is generally projected to decrease in northern and eastern Europe, and parts of northwestern North America. The relatively large agreement between GCMs may be the result of consistent changes in flood-generating precipitation (2), as well as similar responses to change in the IMs. It cannot be ruled out that the bias correction applied to the climate simulations also has an influence, but this needs further investigation.

Fig. 1.

(Upper) Number of experiments (out of 45 in total) showing an increase (Left) or decrease (Right) in the magnitude of Q30 of more than 10% in 2070–2099 under RCP8.5, compared with 1971–2000. (Lower Left) Average change in the magnitude of Q30 across all experiments. (Lower Left) Ratio of GCM variance to IM variance. GCM variance was computed as the variance of the change in Q30 across all GCMs for each individual IM, and then averaged over the nine IMs; IM variance was computed as the variance of the change in Q30 across all IMs for each individual GCM, and then averaged over the nine GCMs. In dark green (purple) areas GCM (IM) variance predominates.

The pattern described above resembles to some extent the findings of earlier studies (6, 9) that were based on a much smaller number of models. Both these studies noted that especially at northern higher latitudes, decreases in flood hazard can occur even in areas where the intensity and/or frequency of precipitation events is projected to increase, and attributed this to a decrease in snow accumulation in winter under warmer climate conditions. Some high-latitude areas in Fig. 1, however, show a consistent increase in Q30 magnitude, tentatively reflecting an increase in snow accumulation over winter. Clearly, in rivers where the annual hydrograph is dominated by snowmelt any changes in the magnitude of the peak flows depend on a fine balance between warmer and possibly shorter winters, and increases or decreases in the total amount of precipitation during the winter season. Similar patterns were also found for northern Europe by refs. 7 and 8.

Although the global pattern of changes in flood hazard shows a relatively large degree of consistency across the experiments, at the scale of individual river basins there can be important differences, and projections can disagree even on the sign of change. This can be seen for example in the River Nile, where IM simulations driven by the Geophysical Fluid Dynamics Laboratory Earth System Model (GFDL-ESM2M) show a relatively robust increase in Q30 magnitude, whereas the Hadley Centre Global Environment Model version 2 - Earth System (HadGEM2-ES) simulations generally show a decrease. This highlights the fact that at regional and local scale the impact of climate change on fluvial flood hazards can be highly uncertain.

This uncertainty has various causes, including climate and impact modeling uncertainty. An estimate of GCM and IM uncertainty can be obtained by looking at the variance across both types of models (Fig. 1, Lower). Especially (but not exclusively) in areas with snowmelt, IM uncertainty can predominate over GCM uncertainty, and outside the tropics there are few areas where GCM uncertainty is considerably larger than the uncertainty brought about by the different IMs.

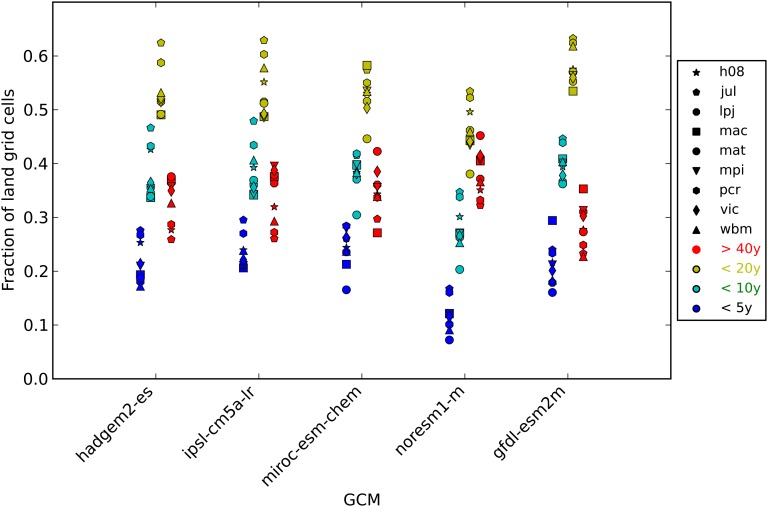
Changes in the magnitude of the Q30 translate into an increase or decrease of the probability of occurrence of the historical 30-y discharge level. Fig. 2 summarizes the extent that the return period of the historical Q30 is expected to become longer or shorter, indicating a decrease or increase in the probability of flooding, respectively. The corresponding plots for each GCM/IM combination can be found in Figs. S6–S10). The results suggest that under these climate scenarios the historical Q30 will occur more frequently in large parts of the world: whereas at roughly one-third of the land grid points of the IMs the future return period is projected to lengthen to more than 40 y, at around 40–60% it is estimated to be less than 20 y and at 20–45% it is less than 10 y, suggesting that here the historical Q30 discharge level is 3 times more likely to occur by the end of this century. At a smaller fraction of land grid points (between 5% and 30%) the future return period is even estimated to be less than 5 y, which would mean that the current Q30 flow level can be expected to be exceeded every few years. The fraction of land where this occurs depends to some extent on the GCM/IM combination that is used, but it is worth noting that at the global scale the range in impact between IMs is of similar magnitude to the range between GCMs (Fig. 2).

Fig. 2.

Fraction of land grid points where the estimated future return period of the historical Q30 is more than 40 y (red colors), less than 20 y (light green), less than 10 y (cyan), and less than 5 y (blue), grouped by driving GCM (horizontal axis). Results from individual impact models (denoted by their first three letters) are indicated with different symbols. Note that the exact number of land points can be different for each GCM/IM combination.

Discussion

The results presented in the previous section suggest that under conditions of climate change flood hazard is not increasing uniformly across the globe. Decreases in the magnitude of Q30 occur particularly (but not exclusively) in areas where the hydrograph is dominated by snowmelt in spring. Nevertheless, in most model experiments an increase in flood hazard was found in more than half of the global land grid points. At a much smaller fraction (between 5% and 30%) the current 30-y flood peak is expected to occur more than once every 5 y in the future. This includes areas that are currently sparsely populated (e.g., eastern Siberia), but also some densely populated regions such as Southeast Asia. It should also be emphasized that these projections are for a high-end climate change scenario (RCP8.5), which means that a comparison with any observed trends (refs. 15 and 16) is not yet feasible.

The large-scale pattern of changes in flood hazard presented above resembles, to some extent, those found in earlier studies (in particular refs. 6 and 9) that were based on a much smaller number of experiments. At the same time our analysis demonstrates that both climate and impact model uncertainty contribute to the spread in the projected changes, especially at the regional scale. A large contribution of IM uncertainty has also been found in analyses of the ISI-MIP hydrological simulations (e.g., refs. 17 and 18) Further work is necessary to better understand and explain some of these uncertainties, and tentatively relate them to model performance under present-day conditions. Note that IM uncertainty seems to be large especially in regions that are dominated by snowmelt, albeit not everywhere. Ref. 19 found that the scheme used for simulating snow is an important cause for differences in model performance between land surface and hydrological models, and potentially this also affects projections of future changes in peak flows in these areas.

Also note that not all sources of uncertainty are taken into account in our analysis; for example, we have only looked at one scenario of future greenhouse gas concentrations. The subset of five GCMs used in ISI-MIP may not sample the full uncertainty in projections of extreme precipitation in the CMIP5 ensemble. Estimates of the Pe of extreme flow levels are inherently uncertain as well, especially for return periods beyond the length of the data (here 30 y). For a more extreme discharge level, ref. 8 found that natural variability in the climate simulations can yield differences in the estimated Pe even without a change in climate. Here this effect might be smaller because we use a less extreme flow level as indicator of flood hazard, but its exact importance may only be determined by including more ensemble members of the same climate model simulations, where available. We also have not explored to what extent the bias correction method that was applied to the GCM simulations (Materials and Methods) has influenced the results, but this is likely to add further uncertainty to the projections (20, 21). Finally, no attempt has been made here to weigh the models according to their skill in simulating present-day conditions.

The analysis presented in this paper explores uncertainties in the potential impacts of climate change on flood hazard, and is not meant to provide specific guidance on adaptation to climate change in an individual river basin. The models used in this paper all have a global scope and may not provide an accurate description of the climatological and hydrological system at a given location. Vulnerability is also not taken into account in the current analysis (for examples of this see, e.g., refs. 22–24). Actual changes in flood hazard and indeed flood risk may depend on socioeconomic factors such as land use changes, flow control structures, flood defenses, and changes in exposure, as much as climate change, and although these human factors may dominate the response in individual river basins, they could not be taken into account in a global-scale study like this. However, the results may have a clear implication for local adaptation: studies that are based on only one, or a limited set of model simulations, may underestimate the uncertainty in the climate change signal, and the corresponding change in flood hazard. It should also be noted that large uncertainty even about the direction of change does not equate to no change. It may be worth approaching this uncertainty from a risk management perspective: if all of the model simulations can be regarded as possible or even plausible scenarios of changes in flood hazard due to climate change, those model solutions that appear less likely but nevertheless carry high risk may not simply be ignored. In those regions where even the sign of changes is uncertain, adaptation plans may therefore need to be flexible to changes in both directions (25).

Materials and Methods

The ISI-MIP Setup.

We used natural river flow simulations from nine global hydrology and land surface models (here referred to as IMs; Table 1). With the exception of PCRaster Global Water Balance Model (PCR-GLOBWB) and Water Balance Model (WBM), these models participated previously in the Water Model Intercomparison Project (WaterMIP), and more information on the model characteristics and general hydrological performance can be found in ref. 19. A more thorough evaluation of how well these IMs are able to reproduce observed flood characteristics and trends would be desirable, but is difficult to achieve due to a lack of suitable river flow data in many regions of the world, and the simple fact that many river systems are heavily influenced by human interference such as water extraction, reservoir construction, and structural engineering works. However, the models used here can be considered state-of-the-art in global hydrological simulations.

Each IM was driven by five GCMs that were selected to represent the range of global mean temperature change and relative precipitation changes in the CMIP5 simulations (26); see ref. 14 for further details. Each GCM in turn was driven by up to four scenarios of future levels of atmospheric greenhouse gas concentrations [representative concentration pathways (RCPs); ref. 27]. In this paper we only include simulations using scenario RCP8.5, assuming that higher levels of global warming will result in stronger hydrological changes (although locally and regionally this may not always be the case, e.g., ref. 7). We thus have an ensemble of 45 experiments, each consisting of a historical and future period.

The output of each GCM was bias corrected to ensure statistical agreement with the observational data set of ref. 28 over the period 1960–1999, and downscaled to the same 0.5 × 0.5° grid. The bias correction method that was used preserves the absolute trends in globally averaged temperature and relative trends in land-averaged precipitation (29), and is a modification of the transfer function approach that has been used in WaterMIP. Ref. 30 found that applying bias correction to the output from a regional climate model can improve the realism of subsequent hydrological simulations and result in a better reproduction of observed flood statistics. However, good model performance in the present day does not necessarily imply plausible projections into the future, and it has been argued that bias correction hides rather than reduces the uncertainty of the predictions (20). An implicit assumption in bias correction is that biases in the climate simulations remain the same into the future, which is probably not very realistic. Bias correction may therefore add further uncertainty to climate impact projections (e.g., ref. 21), but this is not explored further in this paper.

Analysis of Flood Hazards.

For each experiment (that is, each GCM/IM combination), the time series of simulated daily river discharge at each land grid cell was smoothed to 5-daily running averages, which were thought to be more appropriate than daily values considering the typically generalized routing parameters used in global models. For each year, the annual maximum 5-daily flow was determined for both the historical and the future period. For each grid cell we thus have two distributions of 30 annual peak flows. To estimate the Q30 a generalized extreme value distribution (GEV) (31, 32) was fitted separately to these two sets of peak flows using a maximum likelihood approach. The goodness of fit was tested by calculating the Kolmogorov–Smirnov and Anderson–Darling statistics. Grid points with annual maxima close to 0 m³⋅s⁻¹ were excluded from the analysis as these generally resulted in poor fits. This occurs mostly in desert areas, but not in all IMs. The total number of land points that was included in the analysis is therefore slightly different in each experiment. Finally, a likelihood ratio test (31) was performed to test whether the shape parameter of the GEV is significantly different from zero, or if a Gumbel distribution should be used instead. Note that the Q30 (technically the 31-y return level) can, in principle, also be estimated directly from a 30-y time series, but a GEV-based estimate is more robust as the shape of the distribution is based on all peak flows during this period.

Changes in Q30 may be expressed as a change in magnitude between the historical and future period, suggesting higher or lower flood levels. Alternatively, the future return period (based on the future GEV) of the historical Q30 can be calculated, suggesting a change in probability and thus frequency. Although estimates of return levels can be uncertain, especially beyond the period of the data, it is important to keep in mind that any changes in the Q30 are caused by changes in the underlying set of peak flows between the historical and future period that determines the shape of the GEV.