Joint Analysis of Binomial and Continuous Traits with a Recursive Model: A Case Study Using Mortality and Litter Size of Pigs

Abstract

This work presents a model for the joint analysis of a binomial and a Gaussian trait using a recursive parametrization that leads to a computationally efficient implementation. The model is illustrated in an analysis of mortality and litter size in two breeds of Danish pigs, Landrace and Yorkshire. Available evidence suggests that mortality of piglets increased partly as a result of successful selection for total number of piglets born. In recent years there has been a need to decrease the incidence of mortality in pig-breeding programs. We report estimates of genetic variation at the level of the logit of the probability of mortality and quantify how it is affected by the size of the litter. Several models for mortality are considered and the best fits are obtained by postulating linear and cubic relationships between the logit of the probability of mortality and litter size, for Landrace and Yorkshire, respectively. An interpretation of how the presence of genetic variation affects the probability of mortality in the population is provided and we discuss and quantify the prospects of selecting for reduced mortality, without affecting litter size.

MIXED linear models (Henderson 1984) are broadly used in livestock and plant breeding and play an important role in evolutionary and theoretical quantitative genetics (Lande 1979; Cheverud 1984; Walsh 2003). The classical approach for a multiple-trait analysis is to use models posing that the nature of the correlation between response variables (phenotypes) is due to linear associations between unobservables, such as additive genetic values or nongenetic sources, like permanent or temporary environmental effects.

Structural equation models represent an extension of the standard linear model to account for links (feedback and/or recursiveness) involving either the phenotypes directly or latent variables; they are well established in econometrics and sociology (Goldberger 1972; Jöreskog 1973; Duncan 1975). These models were discussed in the early genetics literature by Wright (1921) but this work has not received much attention in quantitative genetics. Xiong et al. (2004) proposed the use of structural equation models for modeling and identifying genetic networks. In a quantitative genetics context, Gianola and Sorensen (2004) studied the consequences of the existence of simultaneous and recursive relationships between phenotypes on genetic parameters and presented statistical methods for inference. An application to study the relationship between somatic cell score and milk yield in goats is in de los Campos et al. (2006). Varona et al. (2007) present a recursive model for the joint analysis of litter size and average litter weight in Danish pigs. These studies were concerned with normally distributed traits. Here the methodology is developed further for the joint analysis of a binomial and a continuous trait and it is shown that a computationally simple implementation can be arrived at by appropriate choice of the recursive specification. The method is illustrated using mortality and litter size in two breeds of Danish pigs.

Litter size is basically determined by ovulation rate and embryo mortality (Blasco et al. 1995); these processes take place mainly at the early stages of gestation. Piglet weight at birth is determined mostly by growth in late gestation and is importantly related to piglet survival. It is then reasonable to postulate a one-way causal path establishing an effect of litter size on piglet mortality. This specification defines a recursive two-trait system. On the other hand, simultaneity occurs when trait 1 affects trait 2 and vice versa.

Litter size has been under selection in the Danish pig-breeding program since the early nineties and resulted in considerable increase in total number born and also in the proportion of stillborn piglets (Sorensen et al. 2000; Su et al. 2007). Sorensen et al. (2000) report an increase in the observed proportion of piglets born dead at higher-litter-size values. This has raised a number ethical and economic concerns and has led to measures designed to reduce mortality. A recently implemented approach in the Danish pig-breeding program is based on changing the emphasis of selection from total number born to total number of piglets alive 5 days after farrowing (Su et al. 2007). Despite the fact that this selection strategy is not addressing the problem of mortality directly, it seems to have had a beneficial effect on both litter size and mortality (Nielsen et al. 2013).

A number of studies have reported genetic variation for mortality with heritabilities ranging from 0.03 to 0.17. These studies have assumed normality of the sampling model for mortality (e.g., Van Arendonk et al. 1996), based inferences on a variety of threshold models (e.g., Roehe and Kalm 2000; Arango et al. 2006), or implemented mixed models for count data (Varona and Sorensen 2010). Mortality data, regarded as a trait of the mother, show typically a large proportion of “zeros” (many litters do not have stillborn piglets). The study of Varona and Sorensen (2010) included a variety of models that accounted for this feature of the data and concluded that the best fit was achieved with a hierarchical binomial logit mixed model. In this work we extend this model in two directions. First, the probability of mortality is assumed to be a function of the total number of piglets born in the litter. This is achieved by assigning a recurrent relationship between the logit of the probability of mortality and litter size. Linear and higher-order functions of litter size are investigated, and the quality of fit of the models is studied. The second extension allows for a joint analysis of mortality and litter size. The recursive parameterization implemented has the attractive feature that the joint posterior distribution of the two traits factorizes into two independent posterior distributions, one for each trait, whereby the computational burden of implementation is reduced.

The article is organized as follows. Material and Methods introduces the models, including the prior and posterior distributions, the method used to compare the models, and a brief description of the data. This is followed by Results, where the focus is on mortality but results for litter size are briefly reported. A Discussion comprises the final section of the paper and the Appendix sketches technical details regarding the model and the Markov chain Monte Carlo algorithm.

Material and Methods

Model and prior distributions

Total number of dead piglets at birth (called mortality hereinafter, treated as a trait of the mother) and total number of piglets born (called litter size hereinafter, treated as a trait of the mother) are analyzed jointly using a model that exploits the factorization of their joint distribution. The conditional binomial model for mortality in litter i, Y_i, given litter size in litter i, t_i is

$$f\left(Y_i=y_i|t_i,{\phi }_i\right)=\left(\begin{array}{c}{t}_i\\ y_i\end{array}\right){\phi }_i^{y_i}{\left(1-{\phi }_i\right)}^{t_i-y_i},\hspace{0.17em}{Y}_i=0,1,\dots ,t_i,$$ (1)

where φ_i is the probability that a piglet dies (referred to as the probability of mortality hereinafter) in litter i, which is assumed to vary over the observations as an inverse logistic deterministic function of unknown parameters. Thus, the linear structure of the logit of φ_i is assumed to be equal to

$$\text{logit }{\phi }_i=x_i^{\prime }{\alpha }_y+z_i^{\prime }{\tilde{u}}_y+w_i^{\prime }{\tilde{p}}_y+g_j\left(t_i\right),$$ (2)

where $x_i^{\prime }$, $z_i^{\prime }$, and $w_i^{\prime }$ are vectors of observed incidence matrices X, Z, and W, α_y is a vector of systematic effect parameters affecting mortality (herd-year and parity), ${\tilde{u}}_y$ is a vector of residual additive genetic values affecting mortality defined in the Appendix, ${\tilde{p}}_y$ is a vector of residual permanent environmental effects affecting mortality (see also the Appendix for an explanation), and g₁(t₁) = λ₁t_i (j = 1 for Model 1), $g_2\left(t_i\right)={\lambda }_1{t}_i+{\lambda }_2{t}_i^2$ (j = 2 for Model 2), $g_3\left(t_i\right)={\lambda }_1{t}_i+{\lambda }_2{t}_i^2+{\lambda }_3{t}_i^3$ (j = 3 for Model 3), where the λ′s are recurrent parameters. In the case of Model 1 it is easy to see that two possible partitions are

$$\begin{array}{c}\text{logit}\hspace{0.5em}{\phi }_i=x_i^{\prime }{\alpha }_y+z_i^{\prime }{\tilde{u}}_y+w_i^{\prime }{\tilde{p}}_y+{\lambda }_1{t}_i\\ =x_i^{\prime }{\alpha }_y+z_i^{\prime }{u}_y+w_i^{\prime }{p}_y+{\lambda }_1{x}_i^{\prime }{\alpha }_t+{\lambda }_1{e}_{t_i},\end{array}$$

where $u_{y_i}=E\left(u_{y_i}|u_{t_i}\right)+{\tilde{u}}_{y_i}$ and $p_{y_i}=E\left(p_{y_i}|p_{t_i}\right)+{\tilde{p}}_{y_i}$ (see Appendix) represent draws from the marginal distributions of additive genetic values and permanent environmental effects affecting mortality.

Given vectors of systematic effects α_t (herd-year and parity), of additive genetic values u_t and of permanent environmental effects p_t, litter size records are conditionally independent and assumed to follow the Gaussian process

$$t_i|{\alpha }_t,u_t,p_t\sim N\left(x_i^{\prime }{\alpha }_t+z_i^{\prime }{u}_t+w_i^{\prime }{p}_t,{\sigma }_{e_t}^2\right).$$ (3)

In the Appendix it is shown that the structure of $\left({\tilde{p}}_{y_i},p_{t_i}\right)$ is

$$\left({\tilde{p}}_{y_i},p_{t_i}\right)\sim N\left[\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{cc}{\sigma }_{{\tilde{p}}_y}^2& 0\\ 0& {\sigma }_{p_t}^2\end{array}\right)\right]$$

and also in the Appendix it is shown that under the recursive parameterization employed,

$$\left({\tilde{u}}_{y_i},u_{t_i}\right)\sim N\left[\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{cc}{\sigma }_{{\tilde{u}}_y}^2& 0\\ 0& {\sigma }_{u_t}^2\end{array}\right)\right].$$

The covariance matrix of the joint distribution of the vectors ${\tilde{u}}_y$ and u_t is G ⊗ A, where $G=\text{diag}\left({\sigma }_{{\tilde{u}}_y}^2,{\sigma }_{u_t}^2\right).$ Therefore the joint distribution factors into the product of the marginal distributions; that is,

$$\tilde{p}\left(u_y,u_t|A,{\sigma }_{{\tilde{u}}_y}^2,{\sigma }_{u_t}^2\right)=p\left({\tilde{u}}_y|A,{\sigma }_{{\tilde{u}}_y}^2\right)p\left(u_t|A,{\sigma }_{u_t}^2\right)$$

and similarly,

$$p\left({\tilde{p}}_y,p_t|{\sigma }_{{\tilde{p}}_y}^2,{\sigma }_{p_t}^2\right)=p\left({\tilde{p}}_y|{\sigma }_{{\tilde{p}}_y}^2\right)p\left(p_t|{\sigma }_{p_t}^2\right).$$

In these expressions, A is the additive genetic relationship matrix, ${\sigma }_{{\tilde{u}}_y}^2$ is the residual additive genetic variance for mortality (conditional variance of the additive genetic value for mortality, given the additive genetic value of liter size), ${\sigma }_{u_t}^2$ is the additive genetic variance for litter size, ${\sigma }_{p_y}^2$ is the variance of permanent environmental effects for mortality, and ${\sigma }_{p_t}^2$ is the variance of permanent environmental effects for litter size. The phenotypic variance for litter size is ${\sigma }_t^2={\sigma }_{u_t}^2+{\sigma }_{p_t}^2+{\sigma }_{e_t}^2$, where ${\sigma }_{e_t}^2$ is the variance of the conditional distribution of litter size.

The variance component parameters, the recurrent parameters, and the vectors α_y and α_t are assigned independent improper uniform distributions a priori.

Posterior distributions

Given the likelihood models (1) and (3) and the prior distributions of the parameters, the joint posterior distributions corresponding to Model 1, say, are

$$\begin{array}{l}p\left({\alpha }_y,{\tilde{u}}_y,{\tilde{p}}_y,{\alpha }_t,u_t,p_t,{\lambda }_1,{\sigma }_{{\tilde{u}}_y}^2,{\sigma }_{{\tilde{p}}_y}^2,{\sigma }_{u_t}^2,{\sigma }_{p_t}^2,{\sigma }_{e_t}^2|y,t\right)\\ \propto f\left(y|t,{\alpha }_y,{\tilde{u}}_y,{\tilde{p}}_y,{\lambda }_1\right)p\left(t|{\alpha }_t,u_t,p_t\right)\times p\left({\tilde{u}}_y|{\sigma }_{{\tilde{u}}_y}^2\right)p\left({\tilde{p}}_y|{\sigma }_{{\tilde{p}}_y}^2\right)p\left(u_t|{\sigma }_{u_t}^2\right)p\left(p_t|{\sigma }_{p_t}^2\right),\end{array}$$ (4)

where y and t are vectors with elements y_i and t_i, respectively and

$$\begin{array}{l}f\left(y|t,{\alpha }_y,{\tilde{u}}_y,{\tilde{p}}_y,{\lambda }_1,{\lambda }_2,{\lambda }_3\right)={\displaystyle \prod _{i=1}^{n}f\left(Y_i=y_i|t_i,{\phi }_i\right)}={\displaystyle \prod _{i=1}^n\left(\begin{array}{c}{t}_i\\ y_i\end{array}\right){\phi }_i^{y_i}{\left(1-{\phi }_i\right)}^{t_i-y_i}},\\ p\left(t|{\alpha }_t,u_t,p_t\right)={\left(2\pi {\sigma }_{e_t}^2\right)}^{-n/2}\text{exp}\left[-\frac{1}{2{\sigma }_{e_t}^2}{\left(t-X{\alpha }_t+Z{u}_t+W{p}_t\right)}^{\prime }\left(t-X{\alpha }_t+Z{u}_t+W{p}_t\right)\right].\end{array}$$

Note that in (4), the joint posterior distribution factorizes into two independent posterior distributions, one for each trait.

Model comparison

The models are compared using the pseudo-log-marginal probability of the data. The pseudo-log-marginal probability of the data is a standard measure of model comparison (Gelfand 1996) and is defined and computed as follows. Consider data vector $y\prime =\left(y_i,y_{-i}^{\prime }\right)$, where y_i is the ith datum, and y_−i is the vector of data with the ith datum deleted. The conditional predictive distribution can be interpreted as the probability of each data point given the remainder of the data and has probability density

$$\begin{array}{c}p\left(y_i|y_{-i}\right)={\displaystyle \int p\left(y_i|\mathit{\theta },y_{-i}\right)f\left(\mathit{\theta }|y_{-i}\right)d\theta },\\ \theta ={\left\{{\theta }_i\right\}}_{i=1}^n,\end{array}$$ (5)

where θ is the vector of parameters. The actual value of p(y_i|y_−i) is known as the conditional predictive ordinate (CPO) for the ith observation. The pseudo-log-marginal probability of the data are given by

$${\displaystyle \sum _i\ln p\left(y_i|y_{-i}\right)}.$$ (6)

A Monte Carlo approximation of the CPO (5) for observation i is given by (Gelfand 1996)

$$\widehat{p}\left(y_i|y_{-i},M_k\right)=N{\left[{\displaystyle \sum _{j=1}^N\frac{1}{p\left(y_i|{\theta }_i^{\left(j\right)},M_k\right)}}\right]}^{-1},$$ (7)

where N is the number of MCMC draws, M_k is a label for model k, and ${\theta }_i^{\left(j\right)}$ is the jth draw from the posterior of θ_i under model k corresponding to the ith observation. The so-called Log CPOs reported below are based on

$${\displaystyle \sum _i\ln \widehat{p}\left(y_i|y_{-i},M_k\right)}.$$

MCMC algorithm

The fully conditional posterior distributions associated with mortality do not all have closed forms, except for the variance components ${\sigma }_{{\tilde{u}}_y}^2$ and ${\sigma }_{{\tilde{p}}_y}^2$, which are scaled inverted chi-square distributions and can therefore be easily updated. For the remaining parameters of the model, ${\alpha }_y,{\tilde{u}}_y$, and ${\tilde{p}}_y$, a random walk single-site Metropolis–Hastings algorithm was chosen as updating strategy. This required a little preliminary experimentation to tune the input parameters. For ${\tilde{u}}_y$ and ${\tilde{p}}_y$, the random walk proposal consisted of a draw from a uniform distribution centered at the current value, and with lower and upper bounds given by plus and minus the updated draw from ${\sigma }_{{\tilde{u}}_y}$ and ${\sigma }_{{\tilde{p}}_y}$, respectively. For α_y the uniform was also centered at the current value and the bounds were given by ±0.15. In the case of the recursion parameters, the bounds were as follows: for λ₁, ±0.015, for λ₂, ±0.0015, and for λ₂, ±0.00015. The final inference was based on single chains of length 5 million (several were run with different starting values as checks and the convergence of the chains to their posterior distributions was studied by visual inspection of trace plots of chosen parameters). The effective chain sizes for the dispersion parameters for mortality varied from ∼750 to 3600 in Landrace and from 400 to 4600 in Yorkshire. For the best fitting models, the effective chain sizes associated with the regression parameter(s) were 3700 in Landrace (Model 1) and varied from 40 to 90 in Yorkshire (Model 3).

Data

Data were obtained from an existing database of performance records collected from nucleus farms of Danish Landrace and Danish Yorkshire during the period from May 2002 until December 2004. Pedigrees were traced back five generations or more. For Landrace, the data comprised records from 5178 litters and a pedigree file of 8800 individuals. The Yorkshire data consisted of records from 3938 litters and a pedigree file of 7143 individuals. Sows were kept under commercial conditions and all matings took place using artificial insemination. More details can be found in Su et al. (2007).

Results

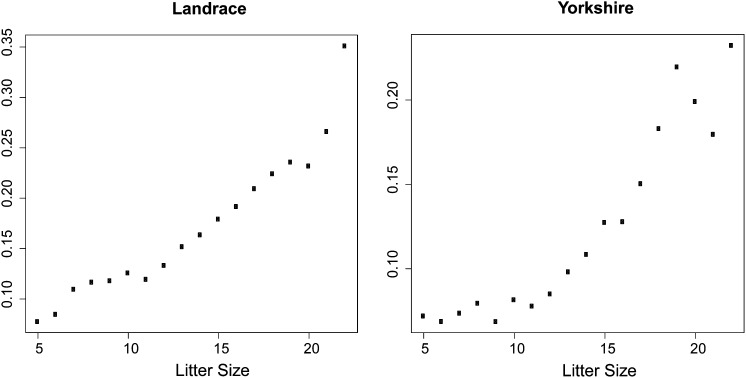
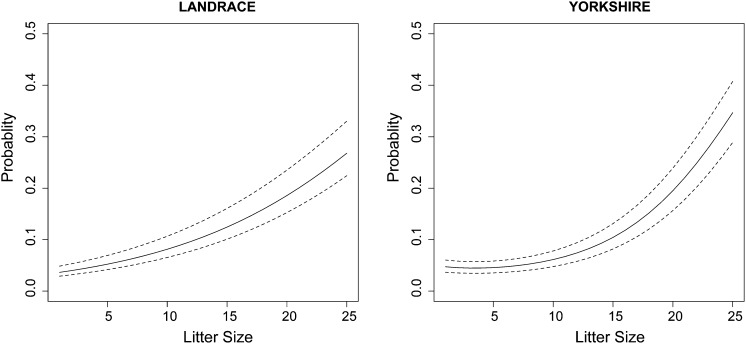
The raw means for litter size for parities 1, 2, 3, and >4 are as follows: 13.4, 15.3, 16.1, and 16.3 for Landrace and 12.3, 14.1, 14.5, and 14.6 for Yorkshire. The average observed proportion of dead-born piglets in parities 1, 2, 3, and >4 are 0.17, 0.17, 0.20, and 0.23 in Landrace and 0.11, 0.09, 0.12, and 0.17 in Yorkshire. Figure 1 shows the raw mortality proportions for a given litter size, across the range of values of litter size of the data sets, in Landrace and Yorkshire. The figures provide a rough illustration for the phenotypic relationship between mortality and litter size, especially within the range defined by litter sizes between 7 and 20 in Landrace and between 6 and 19 in Yorkshire. Within this range each point is represented with a minimum of 100 observations, and outside this range, especially at litter sizes <3 and >23 in Landrace, and 4 and 21 in Yorkshire, with <20 observations. The figures indicate that the proportions increase nonlinearly with the size of the litters, but the relationships are a little different in the two breeds (this is more clearly visualized in Figure 4, which displays the probability of mortality as a function of litter size, based on the best-fitting models—Model 1 for Landrace and Model 3 for Yorkshire).

Figure 1.

Raw phenotypic averages of the proportion of dead-born piglets as a function of litter size, for Landrace and for Yorkshire.

Figure 4.

Posterior means of the average probability of mortality (solid lines) vs. litter size. For a given litter size, the range (dashed lines) is defined by the average posterior means of the probability of mortality of the top and bottom 20% selected.

The Monte Carlo estimates of Log CPO (best model has the largest value) indicate that in both breeds, the poorest fit is obtained with Model 0, which assumes that the probability of mortality does not depend on litter size. The differences in the quality of fit are not very marked among the remaining models. For Landrace, the results in Table 1 indicate that a linear relationship (Model 1) gives the best overall fit. The regression parameters differ in Yorkshire (Table 2) and the Log CPO indicates that for this breed a cubic relationship (Model 3) between the logit of mortality and litter size gives the best overall fit.

Table 1. Posterior means and standard deviations (in brackets) of variance components, recursive parameters and of LogCPO in Landrace, for mortality.

	Model 0a	Model 1	Model 2	Model 3
${\sigma }_{{\tilde{u}}_y}^2$	0.168 (0.035)	0.162 (0.032)	0.162 (0.031)	0.157 (0.031)
${\sigma }_{{\tilde{p}}_y}^2$	0.344 (0.032)	0.281 (0.028)	0.283 (0.028)	0.288 (0.029)
λ1		0.094 (0.005)	0.087 (0.017)	0.075 (0.016)
λ2 × 10−3			0.278 (0.570)	1.530 (1.010)
λ3 × 10−4				−0.314 (0.248)
Log CPO	−10164	−9930	−9934	−9949

^aFor Model 0, ${\sigma }_{{\tilde{u}}_y}^2={\sigma }_{u_y}^2$ and ${\sigma }_{{\tilde{p}}_y}^2={\sigma }_{p_y}^2$.

Table 2. Posterior means and standard deviations (in brackets) of variance components, recursive parameters and of Log CPO in Yorkshire, for mortality.

	Model 0a	Model 1	Model 2	Model 3
${\sigma }_{u_y}^2$	0.170 (0.044)	0.165 (0.046)	0.163 (0.045)	0.168 (0.053)
${\sigma }_{p_y}^2$	0.585 (0.051)	0.494 (0.049)	0.484 (0.049)	0.487 (0.053)
λ1		0.121 (0.007)	−0.0094 (0.0362)	−0.191 (0.046)
λ2 × 10−2			0.473 (0.129)	1.943 (0.306)
λ3 × 10−3				−0.371 (0.076)
Log CPO	−6363	−6185	−6181	−6176

^aFor Model 0, ${\sigma }_{{\tilde{u}}_y}^2={\sigma }_{u_y}^2$ and ${\sigma }_{{\tilde{p}}_y}^2={\sigma }_{p_y}^2$.

Shown in Table 1 are Monte Carlo estimates of posterior means and posterior standard deviations of various parameters in Landrace. In the case of mortality, the figures in the table indicate that ∼37% of the total variance of the logit of mortality (total variance is equal to ${\sigma }_{{\tilde{u}}_y}^2+{\sigma }_{p_y}^2=0.443$) is accounted for by the residual additive genetic variance (for the best-fitting model, Model 1 for Landrace). These results imply that at the level of the logit for mortality, the additive genetic correlation between mortality and litter size based on Model 1 is ∼0.20 in both breeds [calculated from (9), using estimates of posterior means of the additive genetic variance for litter size, ${\widehat{\sigma }}_{u_t}^2\approx 0.8$, retrieves an estimate of the genetic correlation ${\lambda }_1\left({\widehat{\sigma }}_{u_t}/{\widehat{\sigma }}_{u_y}\right)\approx 0.09{\left(0.80/0.16\right)}^{0.5}=0.20$]. Similar calculations show that the estimate of the correlation between permanent environmental effects is ∼0.13 in both breeds. Nielsen et al. (2013) report estimates of the genetic correlation between mortality and litter size ranging between 0.22 and 0.28. However, their analysis treats mortality as a Gaussian trait and the figures are not directly comparable with the results reported here.

For Yorkshire (see Table 2), estimates of variances for mortality are broadly similar although the additive genetic variance comprises a somewhat smaller proportion of the total variance of the logit of mortality (26% for Model 3, the best-fitting model in Yorkshire).

The estimates of heritability for litter size in both breeds are very similar. The posterior mean is equal to 0.077 with a posterior standard deviation of 0.020. These estimates are similar to those reported by Su et al. (2007).

We have also studied how predictions of residual additive genetic values for mortality (based on posterior means) differ among the four models. In both breeds, the three product moment correlations between the predictions based on Model 0 and those based on each of the other three models are in the vicinity of 0.96. The three product moment correlations between predictions derived from Models 1, 2, and 3 are all >0.99.

Discussion

In previous work we performed genetic analyses of count data using a number of discrete models (Varona and Sorensen 2010) with an illustration using mortality in pigs. Mortality data show overdispersion, due to a high proportion of litter records with an absence of mortality and heterogeneity induced by covariation among observations. The models accounted for both sources of overdispersion and the study confirmed the presence of genetic variation for mortality. The model that showed the best global fit was a hierarchical binomial logit model and was therefore chosen in this work. In contrast with the models implemented by Varona and Sorensen (2010), in this work the logit of the probability of mortality is assumed to be functionally related to litter size. Both linear and nonlinear functions at the level of the logit were studied and the results indicate that in Landrace, the linear relationship leads to the best global fit. In Yorkshire, quadratic and cubic relationships produce better global fits and all the models translate into nonlinear relationships between the probability of mortality and litter size.

In mixed linear models the interpretation of variance components is straightforward because the random effects operate on the same scale as the values of the response variable. This is not the case in generalized mixed models. One way of studying the direct impact of the variances on the probability of mortality is as follows. Consider first the simplified version (excluding “random effects”) of the model defined in (2), with g₁(t_i) = λ₁t_i,

$$\text{ln}\left(\frac{{\phi }_i}{1-{\phi }_i}\right)={\mu }_i+\lambda t_i,$$

where μ_i is the mean of the ith record (that includes the sum of the effects herd-year and parity) and t_i is the effect of litter size. For example, in Landrace, replacing the values of the parameters for parity 1 and herd-year 1 by their posterior means (resulting in a value of μ_i ≈ −2.5), and using the posterior mean of λ (0.094), translates into a value of the probability

$${\widehat{\phi }}_i=\frac{\text{exp}\left({\widehat{\mu }}_i+\widehat{\lambda }{t}_i\right)}{1+\text{exp}\left({\widehat{\mu }}_i+\widehat{\lambda }{t}_i\right)}$$

equal to 0.17 for t_i = 10 and 0.21 for t_i = 17. The extended “mixed model” version of the logit for the ith record is

$$\text{ln}\left(\frac{{\phi }_i}{1-{\phi }_i}\right)={\mu }_i+\lambda t_i+q_i,$$

where the random effect $q_i\sim N\left(0,{\sigma }_q^2\right)$ is the sum of the residual additive genetic effect and of the residual permanent environmental effect, with ${\sigma }_q^2={\sigma }_{{\tilde{u}}_y}^2+{\sigma }_{{\tilde{p}}_y}^2$. Given μ_i and t_i the probability φ_i is a function of q_i,

$${\phi }_i=f\left(q_i\right)=\frac{\text{exp}\left({\mu }_i+\lambda t_i+q_i\right)}{1+\text{exp}\left({\mu }_i+\lambda t_i+q_i\right)}.$$

The inverse function is $f^{-1}\left({\phi }_i\right)=\text{ln}\left[{\phi }_i/\left(1-{\phi }_i\right)\right]-{\mu }_i+\lambda t_i$ and the Jacobian is equal to (φ_i(1 − φ_i))⁻¹. Therefore the probability density of φ_i is

$$p\left({\phi }_i\right)=\frac{1}{\sqrt{2\pi {\sigma }_q^2}}\text{exp}\left[-\frac{{\left(\text{ln}\left[{\phi }_i/\left(1-{\phi }_i\right)\right]-{\mu }_i+\lambda t_i\right)}^2}{2{\sigma }_q^2}\right]\frac{1}{{\phi }_i\left(1-{\phi }_i\right)}.$$ (8)

The effect of the variance component on the probability of mortality can be studied using the density (8).

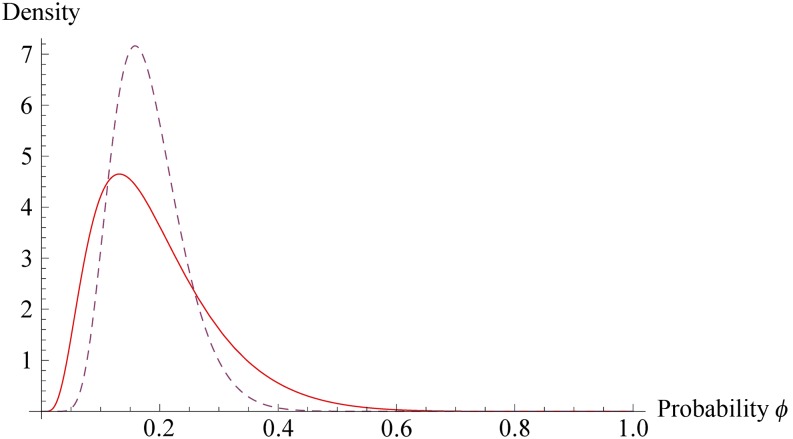
Figure 2 displays the distribution of φ_i for t_i = 10, where ${\sigma }_q^2$ is replaced by its posterior mean ${\widehat{\sigma }}_q^2=0.443$ (computed as 0.162 + 0.281; see Table 1). The variance parameter ${\widehat{\sigma }}_q^2$ defines the range and shape of the distribution in a manner that depends on the value of μ_i + λt_i. For example, for t_i = 10, the 0.1, 0.5, and the 0.9 quantiles are φ_i = 0.082, 0.173, and 0.330, respectively, with a mode at φ_i = 0.131. As ${\sigma }_q^2$ tends to zero, the distribution of φ_i becomes a point mass at a value of φ_i given by the solution to $\text{ln}\left({\phi }_i/\left[1-{\phi }_i\right]\right)={\mu }_i+\lambda t_i$ (resulting in ${\phi }_i\approx 0.17$). The figure shows also the distribution of the probability of mortality evaluated at the posterior mean of the residual additive genetic variance for mortality ${\widehat{\sigma }}_{{\tilde{u}}_y}^2=0.162$ (dashed lines).

Figure 2.

Probability distribution of the probability of mortality for t_i = 10. Solid line, ${\sigma }_q^2=0.443$; dashed line ${\sigma }_{{\tilde{u}}_y}^2=0.162$.

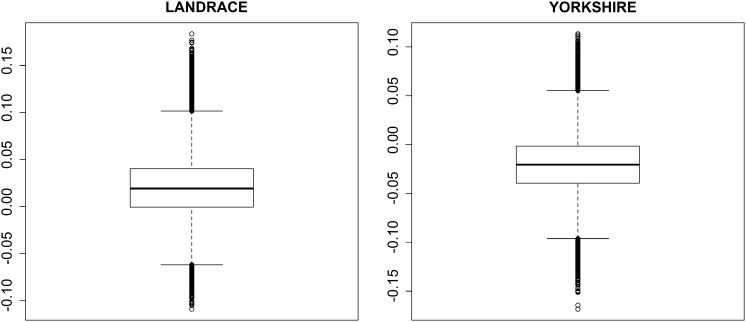
The model specified by Equations 1 and 2 leads to a simple strategy to reduce mortality, without affecting litter size. Given the model, the residual additive genetic values of mortality are independent of the additive genetic values of litter size. The model predicts, therefore, that selecting on the basis of residual additive genetic values for mortality should not lead to correlated changes in litter size. This lack of association is supported by Figure 3, which discloses the posterior distribution of the product moment correlation between the residual additive genetic values of mortality and the additive genetic values of litter size. The value of zero is in a region of very high-density mass.

Figure 3.

Monte Carlo posterior distribution (in form of boxplots) of the product moment correlation between residual additive genetic values for mortality and additive genetic values for litter size in Landrace and Yorkshire.

To give an idea of the likely response to selection to reduce mortality that is expected under the model, we plotted in Figure 4 the range and mean of values of the probability of mortality based on the top and bottom 20% of the distribution of the posterior means of the residual additive genetic values of mortality, for a given value of litter size. The range is governed by the selection pressure and the variability of the posterior means among individuals. For example, Figure 4 indicates that in the Yorkshire population, for a value of litter size of 14 piglets, the average probability of mortality is ∼9.14%, and selecting for reduced mortality from the lowest 20% of the distribution changes this probability to 8.16% [a relative change in the proportion of mortality equal to (9.14% − 8.16%)/9.14% ≈ 11%]. At a value of litter size of 17, the average probability of mortality is ∼13.24% and selecting from the lowest 20% changes the probability to 11.88% [a relative change in the proportion of mortality equal to (13.24% − 11.88%)/13.24% ≈ 10%]. It is of course possible to retrieve from the MCMC output draws from the marginal distribution of the additive genetic values for mortality $u_{y_i}$ using Equation 10 and base selection on these instead.

The classical analysis involving two or more traits is based on a description of their correlation structure at the level of additive genetic and environmental correlations. In this work a recursive parameterization as in Varona et al. (2007) was chosen instead. In this parameterization, a one-way causal path establishes a direct effect of the size of the litter on mortality, omitting the details of the underlying nature of this relationship. A graphical representation of this relationship is in Figure 4. The models that condition the logit of mortality on litter size retrieve estimates of residual (additive genetic and permanent environmental) variances, in contrast to Model 0, which provides estimates of marginal variances. The figures in Table 1 and Table 2 illustrate this, especially for the total variance of the logit of mortality (given by ${\sigma }_{{\tilde{u}}_y}^2+{\sigma }_{{\tilde{p}}_y}^2$). Although the signal is not strong for each of the terms taken separately, their sum is clearly larger for Model 0 (which yields instead estimates of ${\sigma }_{u_y}^2+{\sigma }_{p_y}^2$) than for the remaining models, in both breeds.

From a practical point of view it is relevant to compare the predictive ability of this model with the one currently in operation in the Danish pig-breeding program. In the latter, the traits analyzed are total number born and total number born alive, from which parameters associated with number of piglets dead are derived. The model is based on multivariate normality and ignores the truncated nature of one of the traits (number born alive is smaller or equal to total number born). However, it has the appeal of ease of implementation, from the point of view of both computing requirements and data collection. Details of this model can be found in Su et al. (2007) and Nielsen et al. (2013). The comparison presented here for each breed is based on a 10-fold cross-validation (for example, Hastie et al. 2009), whereby the total number of sows with records were divided into 10 groups of equal size. Phenotypic records of each fold were excluded in the training phase, predicted in the validating data set, and the correlation between observed and predicted number of dead piglets in the validating data set was computed. The predictions of the number of dead piglets using both models are obtained conditional on observed total number of piglets born. We label the model currently in operation by MVN (multivariate normal), and the binomial-normal model by BN. The average correlations (over the 10 folds) in Landrace based on MVN and on BN are 0.52 and 0.57, respectively. In Yorkshire, the correlations are 0.46 (MVN) and 0.50 (BN). The figures indicate that the BN model has a small advantage in terms of predictive ability. However, a breeding program involves a large number of traits and further work is needed, including refinements of the model to account for possible effects of the sire on mortality (Strange et al. 2013), to study the feasibility of incorporating the BN model into a system that can yield routine predictions of aggregate genotypes in a computationally efficient manner.

We have investigated the properties of the logit model for mortality and the Gaussian model for litter size using a modestly sized data set. In this investigation no attempt was made at exploring efficient MCMC algorithms. An implementation on a larger scale requires more attention to algorithmic details, especially if the model is extended to include dense genetic marker information. This should be the subject of future studies.

The Landrace and Yorkshire data and pedigree files as well as the FORTRAN code used for fitting the models can be found in supporting information, File S1.

Appendix

The model for the joint distribution of additive genetic and permanent environmental values for mortality and litter size

The independence of the residual additive genetic values for mortality and additive genetic values for litter size is based on the following result. A recurrent formulation for the additive genetic values for mortality and litter size for an individual is (Varona et al. 2007)

$$\left(u_{y_i},u_{t_i}\right)\sim N\left[\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{cc}{\sigma }_{u_y}^2& \lambda {\sigma }_{u_t}^2\\ \lambda {\sigma }_{u_t}^2& {\sigma }_{u_t}^2\end{array}\right)\right],$$ (A1)

where λ is a recurrent parameter that describes the linear relationship between mortality and litter size. Then,

$$\left(u_{y_i}|u_{t_i}\right)\sim N\left[\lambda u_{t_i},{\sigma }_{u_y}^2-{\lambda }^2{\sigma }_{u_t}^2\right].$$

We can write

$$u_{y_i}=E\left(u_{y_i}|u_{t_i}\right)+{\tilde{u}}_{y_i},$$ (A2)

where ${\tilde{u}}_{y_i}$ is the residual term in the additive genetic regression of mortality on litter size and is referred to as the residual additive genetic value of mortality. Then,

$$\left({\tilde{u}}_{y_i},u_{t_i}\right)\sim N\left[\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{cc}{\sigma }_{{\tilde{u}}_y}^2& 0\\ 0& {\sigma }_{u_t}^2\end{array}\right)\right],$$ (A3)

where ${\sigma }_{{\tilde{u}}_y}^2={\sigma }_{u_y}^2-{\lambda }^2{\sigma }_{u_t}^2$. The covariance matrix of the joint distribution of the vectors ${\tilde{u}}_y$ and u_t is G ⊗ A, where $G=\text{diag}\left({\sigma }_{{\tilde{u}}_y}^2,{\sigma }_{u_t}^2\right)$ is the diagonal covariance matrix of (A3). Therefore the joint distribution factors into the product of the marginal distributions; that is,

$$p\left({\tilde{u}}_y,u_t|A,{\sigma }_{{\tilde{u}}_y}^2,{\sigma }_{u_t}^2\right)=p\left({\tilde{u}}_y|A,{\sigma }_{{\tilde{u}}_y}^2\right)p\left(u_t|A,{\sigma }_{u_t}^2\right).$$

In the case of the permanent environmental values, the starting point is

$$\left(p_{y_i},p_{t_i}\right)\sim N\left[\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{cc}{\sigma }_{p_y}^2& \lambda {\sigma }_{p_t}^2\\ \lambda {\sigma }_{p_t}^2& {\sigma }_{p_t}^2\end{array}\right)\right],$$ (A4)

which in a similar manner leads to

$$\left({\tilde{p}}_{y_i},p_{t_i}\right)\sim N\left[\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{cc}{\sigma }_{{\tilde{p}}_y}^2& 0\\ 0& {\sigma }_{p_t}^2\end{array}\right)\right].$$ (A5)

Sketch of the MCMC algorithm

The fully posterior distributions of the parameters, except for the variance components, do not have closed forms. For example, updating the jth element of α_y requires the computation of its fully conditional posterior distribution

$$\begin{array}{l}p\left({\alpha }_{y,j}|\text{all},y,t\right)\propto {\displaystyle \prod _{i=1}^n{\left[\frac{\text{exp}\left(x_i^{\prime }{\alpha }_y+z_i^{\prime }{\tilde{u}}_y+w_i^{\prime }{p}_y+g\left(t_i\right)\right)}{1+\text{exp}\left(x^{\prime }{\alpha }_y+z_i^{\prime }{\tilde{u}}_y+w_i^{\prime }{p}_y+g\left(t_i\right)\right)}\right]}^{y_{i}I\left(x_i^{\prime }{\alpha }_y={\alpha }_{y,j}\right)}}\\ \times {\left[1-\frac{\text{exp}\left(x_i^{\prime }{\alpha }_y+z_i^{\prime }{\tilde{u}}_y+w_i^{\prime }{p}_y+g\left(t_i\right)\right)}{1+\text{exp}\left(x_i^{\prime }{\alpha }_y+z_i^{\prime }{\tilde{u}}_y+w_i^{\prime }{p}_y+g\left(t_i\right)\right)}\right]}^{\left(t_i-y_i\right)I\left(x_i^{\prime }{\alpha }_y={\alpha }_{y,j}\right)},\end{array}$$ (A6)

where I(⋅) is the indicator function that takes the value 1 if the argument is satisfied, and zero otherwise. This distribution is not of standard form and an updating strategy based on a uniform random walk Metropolis–Hastings algorithm was chosen. A similar strategy was adopted to update the residual additive genetic and permanent environmental effects.