Intraventricular vortex properties in nonischemic dilated cardiomyopathy

Abstract

Vortices may have a role in optimizing the mechanical efficiency and blood mixing of the left ventricle (LV). We aimed to characterize the size, position, circulation, and kinetic energy (KE) of LV main vortex cores in patients with nonischemic dilated cardiomyopathy (NIDCM) and analyze their physiological correlates. We used digital processing of color-Doppler images to study flow evolution in 61 patients with NIDCM and 61 age-matched control subjects. Vortex features showed a characteristic biphasic temporal course during diastole. Because late filling contributed significantly to flow entrainment, vortex KE reached its maximum at the time of the peak A wave, storing 26 ± 20% of total KE delivered by inflow (range: 1–74%). Patients with NIDCM showed larger and stronger vortices than control subjects (circulation: 0.008 ± 0.007 vs. 0.006 ± 0.005 m²/s, respectively, P = 0.02; KE: 7 ± 8 vs. 5 ± 5 mJ/m, P = 0.04), even when corrected for LV size. This helped confining the filling jet in the dilated ventricle. The vortex Reynolds number was also higher in the NIDCM group. By multivariate analysis, vortex KE was related to the KE generated by inflow and to chamber short-axis diameter. In 21 patients studied head to head, Doppler measurements of circulation and KE closely correlated with phase-contract magnetic resonance values (intraclass correlation coefficient = 0.82 and 0.76, respectively). Thus, the biphasic nature of filling determines normal vortex physiology. Vortex formation is exaggerated in patients with NIDCM due to chamber remodeling, and enlarged vortices are helpful for ameliorating convective pressure losses and facilitating transport. These findings can be accurately studied using ultrasound.

intraventricular vortex dynamics may have an important role in cardiac hemodynamics. During early filling and atrial contraction, strong jets entering the left ventricle (LV) lead to the formation of vortex rings near the tips of the mitral valve leaflets. Due to the chiral configuration formed by the LV inflow tract, main chamber, and LV outflow tract (LVOT), these vortex rings evolve into large rotational flow structures that occupy a large fraction of the ventricle. Recent clinical data in patients with diastolic dysfunction indicate that LV vortices may facilitate flow from the left atrium to the LV apex (6). Also, vortical structures may increase ejection efficiency by conserving the momentum of blood built up during filling (1). Finally, vortices may contribute to blood mixing inside the ventricle, avoiding stasis (6, 19, 30, 32, 33, 40). Because impaired diastolic function, reduced mechanical efficiency, and risk of thrombosis characteristically concur in patients with nonischemic dilated cardiomyopathy (NIDCM), addressing the physical properties of intraventricular vortices is particularly relevant in this condition.

Recent ultrasound (1, 19, 29), computational (28), and phase-contrast magnetic resonance (PC-MR) (3, 6, 11–13) studies have described intraventricular flow characteristics in small numbers of patients with normal and dilated hearts. We hypothesized that significant physiological insights can be gained by comprehensively studying the temporal dynamics and correlates of intraventricular vortex development. We also hypothesized that impaired chamber properties in patients with NIDCM may be associated with modified vortex physiology. Therefore, the present study was designed to characterize the dynamics of vortex position, size, and strength along the cardiac cycle in patients with NIDCM and age-matched healthy control subjects. The physiological relevance of vortices relative to the global LV kinetic energy (KE) balance was also analyzed in detail. We used a custom-developed method that allowed us to measure two-dimensional (2-D) flow using conventional color-Doppler ultrasound (17). Because most previous evidence in this field has been reported using PC-MR, the ultrasound-based method was compared in vivo against this technique in a subset of NIDCM patients.

METHODS

Patients.

Sixty-one patients with NIDCM were included prospectively (Table 1). The inclusion criteria for enrollment were as follows: 1) diagnosis of chronic NIDCM with a LV ejection fraction of ≤0.40, 2) angiographically proven absence of significant coronary artery disease, and 3) sinus rhythm. Sixty-one healthy volunteers were matched for age and enrolled as control subjects. Control subjects were voluntarily recruited among our institution employees or their first-degree relatives. The inclusion criteria as suitable healthy controls were as follows: 1) lack of a prior history of cardiovascular disease, hypertension, or diabetes mellitus; 2) sinus rhythm; 3) normal ECG tracing; and 4) a normal echocardiographic examination. This study was approved by the Institutional Review Board, and all participants provided written informed consent for the study.

Table 1.

Demographic and echocardiographic data

	NIDCM Patients	Control Subjects	P Value
No. of subjects	61	61
Sex, no. of subjects			0.4
Men	33	38
Women	28	23
Age, yr	56 ± 12	58 ± 13	0.4
Heart rate, beats/min	66 ± 13	64 ± 13	0.4
QRS duration > 120 ms
No. of subjects	31	0
Percent	51	0
LV chamber
End-diastolic volume, ml	163 ± 77	84 ± 22	<0.0001
End-systolic volume, ml	122 ± 71	31 ± 9	<0.0001
Stroke volume, ml	41 ± 15	53 ± 15	<0.0001
Ejection fraction	0.27 ± 0.09	0.63 ± 0.05	<0.0001
LV mass, g	215 ± 73	129 ± 35	<0.0001
Long-axis diastolic diameter, cm	9.2 ± 1.1	8.3 ± 0.8	<0.0001
Short-axis diastolic diameter, cm	6.0 ± 1.0	4.5 ± 0.5	<0.0001
Sphericity index	0.7 ± 0.1	0.5 ± 0.1	<0.0001
Vortex formation time	1.43 ± 0.83	3.95 ± 1.78	<0.0001
Conventional Doppler
Mitral regurgitation III–IV/IV
No. of subjects	22	0
Percent	36	0
Isovolumic relaxation time, ms	117 ± 37	94 ± 25	0.002
E wave velocity, m/s	0.65 ± 0.23	0.66 ± 0.14	0.79
A wave velocity, m/s	0.67 ± 0.23	0.64 ± 0.18	0.32
E/A	1.07 ± 0.67	1.13 ± 0.46	0.57
E wave deceleration time, ms	163 ± 52	198 ± 52	0.0003
e′ wave velocity, m/s	0.06 ± 0.02	0.10 ± 0.03	<0.0001
E/e′	13 ± 6	7 ± 2	<0.0001
Diastolic intraventricular pressure gradients
Total early DIVPD, mmHg	1.1 ± 0.4	1.1 ± 0.6	0.78
Inertial early DIVPD, mmHg	1.5 ± 0.5	1.6 ± 0.6	0.65
Convective early DIVPD, mmHg	−1.3 ± 0.7	−1.0 ± 0.6	0.02
Late DIVPD, mmHg	1.4 ± 0.5	0.7 ± 0.5	<0.0001

NIDCM, nonischemic dilated cardiomyopathy; LV, left ventricular; DIVPD, diastolic intraventricular pressure difference.

Image acquisition and conventional analysis.

A comprehensive 2-D echocardiographic examination was performed using a Vivid 7 scanner and a phase-array 2- to 4-MHz transducer (General Electric Healthcare). LV volumes and ejection fraction were measured using the biplane Simpson method. LV mass was measured from short-axis and long-axis 2-D views. Pulsed-wave Doppler-flow spectrograms were obtained at the level of the mitral tips and LVOT. Pulsed-wave tissue Doppler spectrograms were recorded at the septal and lateral mitral annulus. Ventricular sphericity was computed as the ratio between LV long and short axes measured from the apical four-chamber and parasternal long-axis views at end systole. Using EchoPac analysis software (version 110.1.2, GE), the following temporal events of the cardiac cycle were identified from the pulsed-wave Doppler spectrograms: aortic valve opening, aortic valve closing, mitral valve opening, peak E wave velocity, A wave onset, peak A wave velocity, and mitral valve closure. We forwarded these time stamps automatically to our in-house fluid mechanics solver using the QRS onset as a reference (see below). Color-Doppler M-mode (CDMM) tracings were obtained from the transmitral flow and processed to measure intraventricular diastolic pressure differences using previously described and validated acquisition and processing methods (2). The methods used to estimate total KE related to filling and ejection are described in appendix a.

The vortex formation time was calculated from LV end diastole and averaged mitral annulus diameters, end-diastolic volume, and the proportion of the atrial contribution to total filling time velocity integral (18, 38); the latter was measured by manual identification of the A wave onset from the decoded CDMM filling velocity.

2-D flow image acquistion and processing.

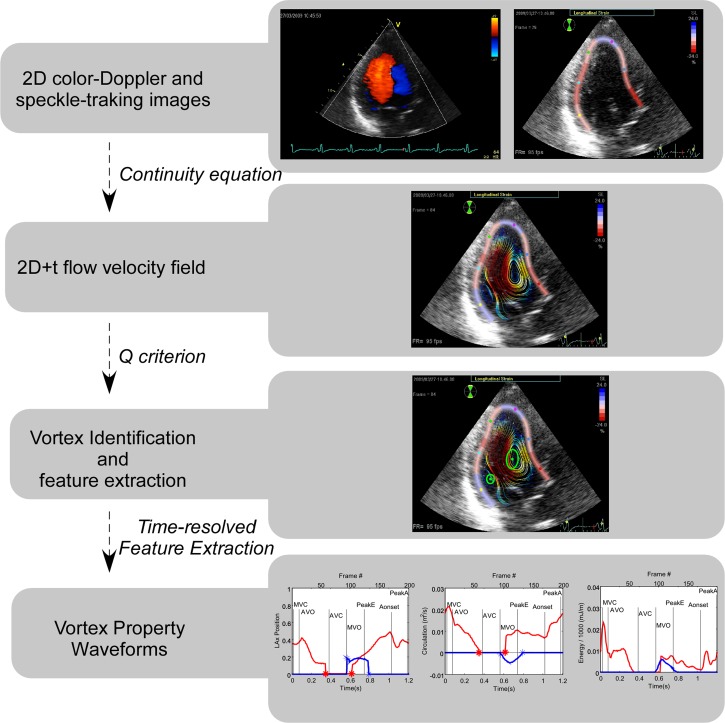
The image acquisition and processing methods to estimate 2-D velocity fields have been previously reported in detail and validated in vitro using particle image velocimetry in our previous work (17). An overall perspective of these methods is shown in Fig. 1. Images were obtained from the long-axis apical view with special care to enclose the full LV in the color-Doppler sector. The color-Doppler (8–14 beats) and harmonic 2-D (4 beats) sequences were carefully recorded consecutively without displacing the probe during two consecutive apneas. The respective frame rates were 30 ± 8 and 100 ± 10 Hz. The ECG signal was used for temporal registration, frame interleaving, and matching B-mode and color-Doppler data (17). Cross-beam (azimuthal) velocities are calculated using the continuity equation under a planar flow assumption (i.e., by neglecting mass fluxes across the imaging plane). In polar coordinates, radial (V_r) and azimuthal (V_θ) velocities are related as follows:

$${\partial }_{\theta }{\text{V}}_{\theta }=-r{\partial }_r{V}_r\left(r,\theta \right)-V_r\left(r,\theta \right)$$ (1)

Fig. 1.

Overview of the methods used for image processing.

where r is the radius and θ is the azimuth. The myocardium-blood boundary position obtained by speckle-tracking (EchoPAC) was used to impose nonpenetration conditions and solve Eq. 1. The width of the myocardial speckle-tracking region of interest was carefully adjusted to delimit the endocardial boundary. A specific accuracy analysis performed in the full database (n = 122) showed very good accuracy for this method of endocardial tracking when compared against blinded manual segmentation [intraclass correlation coefficient (R_ic) = 0.95 and 0.94 for end-systolic and end-diastolic LV area values, respectively].

The redundant information provided by boundary conditions from opposite LV walls was used to minimize the error related to the planar flow assumption (17). To increase the temporal resolution of the 2-D velocity fields, we retrospectively interleaved frames from consecutive beats into a synthetic cardiac cycle based on the offset from ECG signal features yielding 150–200 frames/cardiac cycle. Beats with a >5% variation in cycle length were automatically rejected.

Vortex feature extraction.

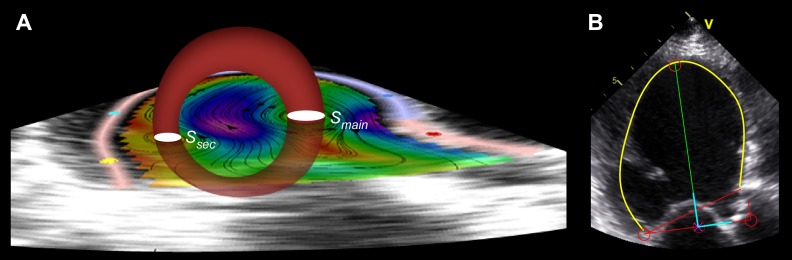
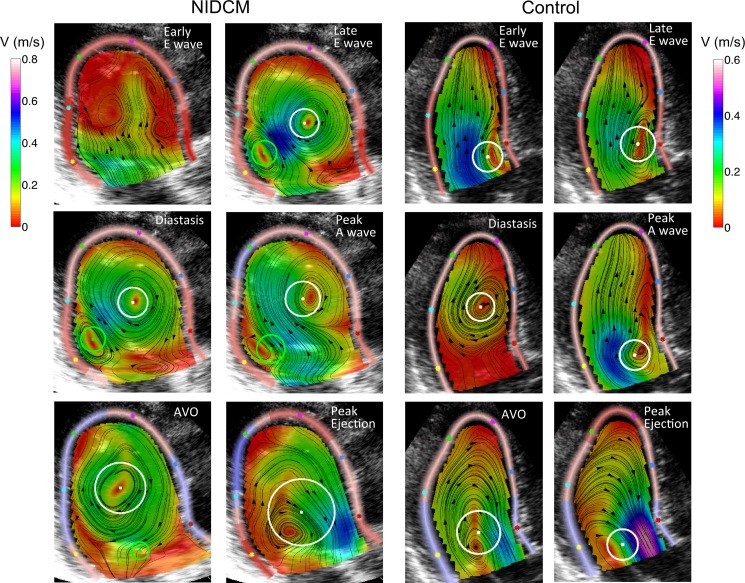
In 2-D, the three-dimensional (3-D) LV vortex ring is visualized as two cores corresponding to the intersections between the ring and the imaging plane, with the clockwise rotating (main) section directed toward the anteroseptal wall and the counterclockwise (secondary) section close to the inferolateral LV wall (Fig. 2A). Vortex core sections were tracked in a threshold-independent manner using the second invariant of the velocity gradient tensor of the reconstructed 2-D velocity fields, the Q criterion, as described elsewhere (5, 10, 17, 43). In-plane properties of the tracked vortex cores were determined from the flow data obtained on the imaging plane. We measured the in-plane circulation (Γ; in m²/s), trajectory, and radius of each core from the zero-, first-, and second-order moments of the vorticity distribution, respectively. The Reynolds number (Re) of each vortex core was estimated from the following ratio: Re = Γ/ν, where ν is the kinematic viscosity of blood (taken as ν = 4 × 10⁻⁶ m²/s). This nondimensional parameter indicates the relative importance of flow inertia compared with viscous forces in the fluid, and it is a major determinant of the dynamics of vortices. Roughly speaking, a free vortex will rotate a number of times equal to its Re before it decays under the effect of viscosity (35). To account for differences in preload, the circulation was additionally normalized for LV end-diastolic area and expressed in s⁻¹. For noncircular and circular vortex core sections, the radius was defined from the vortex area (A_v) as follows: r = (A_v/π)^1/2. The area of vortex cores was also normalized to total LV end-diastolic area. Vortex symmetry was calculated as the ratio between the radii of the secondary and main vortex cores. In-plane vortex KE was determined from the data available on the imaging plane, whereas total vortex KE was estimated by assuming a linearly tapered toroidal shape for the 3-D vortex ring. These methods are described in appendix a.

Fig. 2.

Geometric reference systems. A: main (S_main) and secondary (S_sec) vortex sections as well as the asymmetric toroidal geometric model used to estimate out-of-plane vortex distribution for the calculation of total vortex energy, overlaid on the two-dimensional (2-D) velocity distributions of a patient with nonischemic dilated cardiomyopathy (NIDCM; see text for details). B: internal moving coordinate system used for the analysis of vortex trajectories along the cardiac cycle. v, flow velocity.

We defined an internal orthogonal LV moving reference system from the short and long axis of the LV as the intersection of the long axis of the ventricle with the line defining the mitral annulus (Fig. 2B). Vortex positions in this system were normalized by the long (range: 0–1) and short (−0.5 to +0.5) axes. The temporal waveforms for the radius, position, normalized area, circulation, and in-plane KE were obtained for the full cardiac cycle. Mean values for the cardiac cycle as well as instantaneous values at each event were measured from these waveforms. The instants of peak A wave transmitral flow velocity and aortic valve opening were selected for a detailed study of KE with the aim of characterizing the potential effects of the LV vortex on late-diastolic performance and ejection energy transfer, respectively.

We analyzed the test-retest reliability of the method in 10 unselected patients referred for conventional echocardiographic examination. The full image acquisition and processing procedure was blindly repeated by two independent observers >5 min apart. Values of R_ic for the main vortex core radius, position, circulation, and in-plane energy were 0.78, 0.86, 0.70, and 0.69, respectively. For the secondary vortex core, these values were 0.44, 0.72, 0.45, and 0.52, respectively.

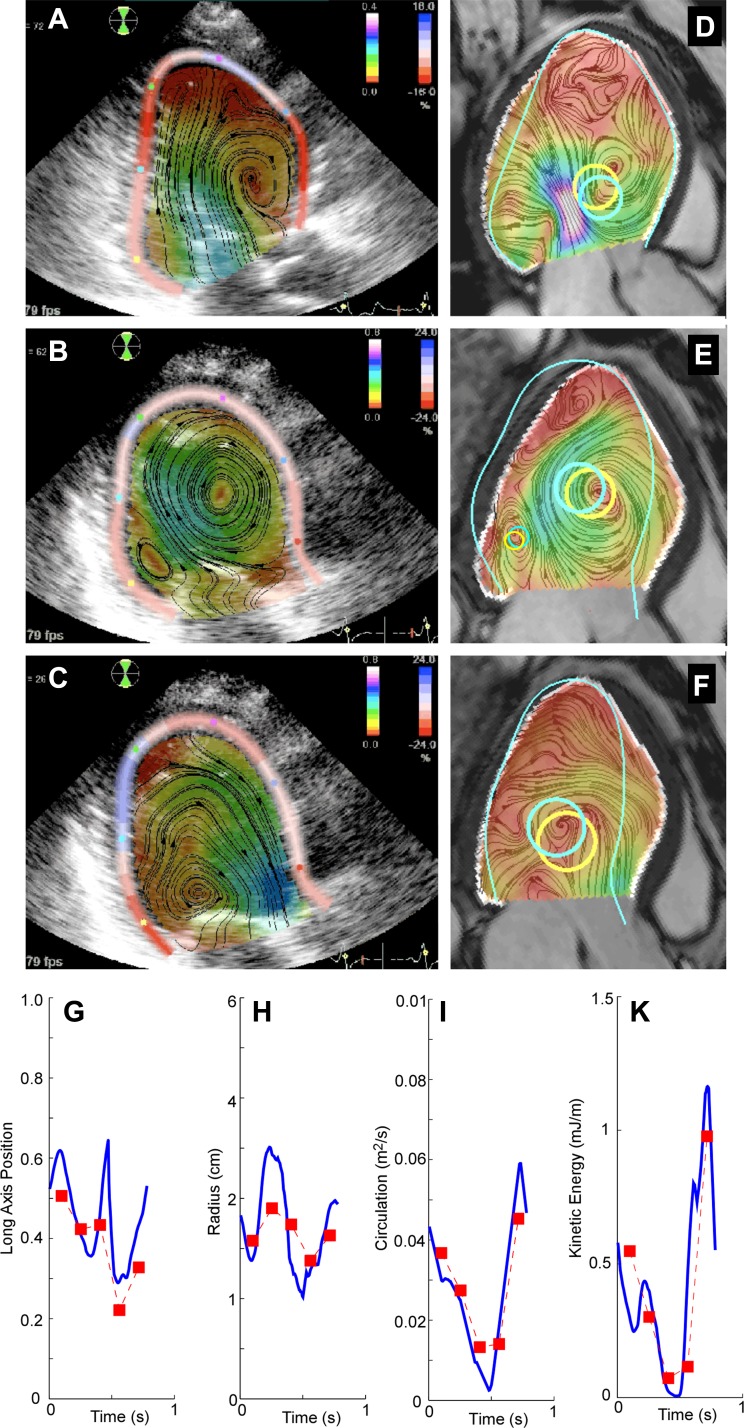
A Doppler and PC-MR head-to-head clinical comparison study performed in a subgroup of 21 NIDCM patients (see appendix b) showed close agreement between the Doppler method and PC-MR for the circulation and in-plane KE of the main vortex core (R_ic = 0.82 and 0.76, respectively; Fig. 3 and Table 2). However, for the radius and position, the agreement was moderate. The agreement between techniques was worse for properties of the secondary vortex core.

Fig. 3.

A–F: head-by-head comparison between echocardiography and phase-contrast magnetic resonance (PC-MR) for vortex size and position in a patient with NIDCM for early filling (A and D), late filling (B and E), and ejection (C and F) phases. A–C: results of the ultrasound-based 2-D velocity fields. The distributions of flow velocity and longitudinal myocardial strain are overlaid on the raw B-mode tissue images. D–F: time-matched PC-MR frames. The endocardial boundary from the MR is overlaid in white, whereas the endocardial boundary from the ultrasound is overlaid in cyan, normalized for the same long-axis length. Automatically identified vortex structures are overlaid as yellow and cyan for the PC-MR and ultrasound methods, respectively. The secondary vortex structure could only be identified during late filling (B and E). G–K: vortex properties along the cardiac cycle, as measured by ultrasound (blue line) and PC-MR (red squares) in another patient with NIDCM.

Table 2.

Head-by-head comparison study against phase-contrast magnetic resonance in a subgroup of 21 NIDCM patients

	Pearson Correlation Coefficient	Intraclass Correlation Coefficient	Absolute Error	Relative Error, %
Main vortex core
Radius	0.42	0.37	−0.035 ± 0.494 cm	−7 ± 36
Position	0.71	0.69	0.022 ± 0.087	6 ± 32
Circulation	0.82	0.82	0.001 ± 0.005 m2/s	−4 ± 47
In-plane kinetic energy	0.76	0.75	−1 ± 13 mJ/m	−12 ± 71
Secondary vortex core
Radius	0.10	0.15	−0.005 ± 0.01 cm	−39 ± 65
Position	0.02	0.03	0.048 ± 0.273	4 ± 72
Circulation	0.31	0.10	−0.008 ± 0.008 m2/s	−80 ± 57
In-plane kinetic energy	0.41	0.28	−8 ± 17 mJ/m	−63 ± 93
Total
Total vortex energy	0.50	0.49	−0.1 ± 1.0 mJ	2 ± 72

Statistical analysis.

Variables are shown as means ± SD. We used Bland-Altman analysis as well as Pearson correlation coefficients (R) and R_ic to assess validation and reproducibility. Proportions between groups were compared using Pearson's χ²-tests. Quantitative variables between groups were compared using paired and unpaired t-tests where appropriate. Determinants of total vortex energy were assessed by Pearson correlation and multivariate linear regression analysis of significant predictors followed by backwards stepwise elimination based on Alkaike's selection criteria (S-Plus, TIBCO software). Standardized regression coefficients were calculated for variables entered in the final models. Statistical significance was established at the P < 0.05 level.

RESULTS

Time evolution of intraventricular vortices.

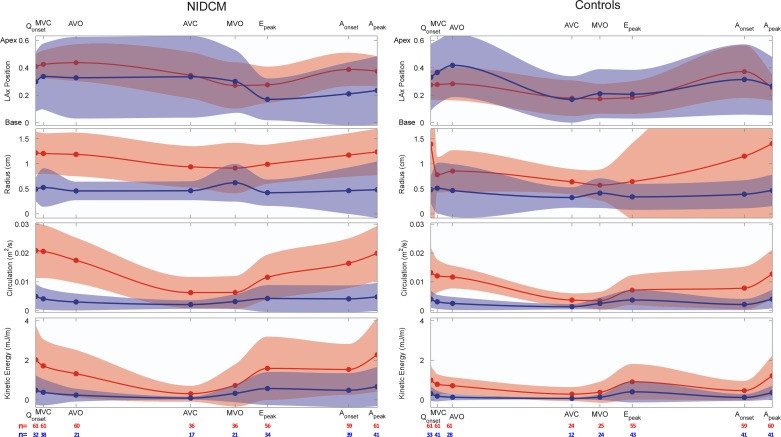
Main vortex properties are shown in Table 3 and Figs. 4 and 5. By the time of mitral valve closing, the main vortex core was identified in all patients and control subjects, whereas the secondary core was only identified in roughly half of the total population (Fig. 4). The time evolution of the main and secondary cores during diastole followed a characteristic pattern in both populations. During rapid filling, the vortex developed rapidly after mitral valve opening, progressively increasing its circulation [0.005 ± 0.005 to 0.009 ± 0.007 m²/s from mitral valve opening to the peak E wave, P < 0.001 (main core, pooled populations)] and its in-plane KE (0.6 ± 0.8 to 1.1 ± 1.3 mJ/m, P < 0.001). During E wave deceleration, circulation significantly increased, reaching 0.012 ± 0.009 m²/s at the A wave onset (P < 0.001 vs. at the peak E wave). KE did not change significantly (0.9 ± 1.1 mJ/m at the A wave onset, P = 0.1). The vortex moved apically during this phase. Visual inspection of the flow field time-lapse sequences revealed a second vortex ring being generated during late filling. In most control subjects, the early filling vortex had weakened by the A wave onset, causing the late filling jet to destroy those residual vortices and creating a new and stronger vortex ring close to the mitral tips (Figs. 4 and 5, control case). Consequently, late filling caused circulation and KE to reach their highest values in the cardiac cycle at the time of peak A wave velocity (0.016 ± 0.01 m²/s and 1.7 ± 1.6 mJ/m at peak A velocity, P < 0.001 for both vs. A wave onset values). During A wave deceleration and isovolumic contraction, the vortex weakened, loosing circulation and KE (0.014 ± 0.007 m²/s and 1.0 ± 0.9 mJ/m at aortic valve opening, P = 0.01 and P < 0.001 vs. peak A wave values, respectively). During ejection, vortices were eventually vanished by the time of aortic valve closing, either disappearing or holding very low circulation (0.005 ± 0.005 m²/s, P < 0.001 vs. aortic valve opening values) and KE (0.6 ± 0.9 mJ/m, P < 0.001; Fig. 4).

Table 3.

Main vortex properties in NIDCM patients and control subjects

	NIDCM Patients	Control Subjects	P Value
Main vortex core
Vortex duration, %cycle	86 ± 13	81 ± 13	0.09
Mean radius, cm	1.1 ± 0.3	0.9 ± 1.1	0.2
Peak radius, cm	1.8 ± 0.5	1.4 ± 0.7	0.0004
Mean relative vortex area	0.09 ± 0.05	0.07 ± 0.06	0.02
Peak relative vortex area	0.25 ± 0.14	0.20 ± 0.12	0.02
Peak long-axis position (normalized)	0.55 ± 0.09	0.51 ± 0.14	0.07
Long-axis postion at AVO (normalized)	0.43 ± 0.14	0.28 ± 0.12	<0.0001
Peak short-axis position (normalized)	0.28 ± 0.18	0.30 ± 0.15	0.5
Mean circulation, m2/s	0.0144 ± 0.0046	0.0092 ± 0.0036	<0.0001
Mean normalized circulation, ×10−12 s−1)	3.2 ± 1.0	2.8 ± 1.1	0.05
Mean Reynolds number	3600 ± 1150	2300 ± 900	<0.0001
Mean in-plane energy, mJ/m	14 ± 8	8 ± 4	<0.0001
Secondary vortex core
Vortex duration, %cycle	55 ± 28	57 ± 29	0.79
Mean radius, cm	0.66 ± 0.55	0.54 ± 0.74	0.32
Peak radius, cm	1.23 ± 0.9	0.99 ± 0.57	0.08
Mean relative vortex area	0.06 ± 0.07	0.04 ± 0.04	0.115
Peak relative vortex area	0.13 ± 0.14	0.13 ± 0.13	0.82
Peak long-axis position (normalized)	0.46 ± 0.25	0.45 ± 0.26	0.9
LAx position at AVO	0.26 ± 0.30	0.33 ± 0.27	0.35
Peak short-axis position (normalized)	0.18 ± 0.17	0.21 ± 0.19	0.45
Mean circulation, m/s2	0.0081 ± 0.007	0.0055 ± 0.005	0.02
Mean normalized circulation, ×10−12 s−1	1.9 ± 1.8	1.7 ± 1.5	0.5
Mean Reynolds number	2025 ± 1750	1375 ± 1250	0.02
Mean in-plane energy, mJ/m	7 ± 8	5 ± 5	0.04
Global properties
Cases with new vortex during late filling			<0.0001
No. of subjects	14	50
Percent	23	80
Filling jet diameter at peak E wave, cm	3.3 ± 2.8	4.0 ± 2.5	0.14
Filling jet diameter at peak A wave, cm	2.6 ± 2.9	3.1 ± 2.8	0.38
Vortex symmetry	0.58 ± 0.54	0.63 ± 1.25	0.83

AVO, aortic valve opening.

Fig. 4.

Mean (solid curves) and SD (light ribbons) values of vortex properties along the cardiac cycle for patients with NIDCM (left) and control subjects (right). Properties are shown for the main and secondary vortex cores (red and blue, respectively). The horizontal axes have been scaled for average times of cardiac events in each population. The number of subjects in which the main (red) and secondary (blue) cores were identified in each phase is shown at the bottom. Q_onset, onset of the Q wave; MVC, mitral valve closure; AVO, aortic valve opening; AVC, aortic valve closure; MVO, mitral valve opening; E_peak, peak of the E wave; A_onset, onset of the A wave; A_peak, peak of the A wave; LAx, long axis.

Fig. 5.

Snapshots of 2-D intraventricular flow along the cardiac cycle in a representative NIDCM patient and a control subject. The position and radius of the main vortex core section is indicated by the white circle; the position and radius of the secondary vortex core section is indicated by the green circle.

Vortex properties in NIDCM patients.

These time evolution patterns were different in NIDCM patients than in control subjects, particularly during the flow deceleration phases (Figs. 4 and 5). From the peak E wave to A wave onset, the main vortex core became stronger in the NIDCM group (change in KE: +0.2 ± 1.3 mJ/m and change in circulation: +0.004 ± 0.007 m²/s), whereas it was weakened in the control group (change in KE: −0.2 ± 1.0 mJ/m and change in circulation: −0.000 ± 0.008 m²/s, P < 0.001 vs. the NIDCM group for both). The interaction of the vortex generated during late filling with the early filling vortex was different in NIDCM patients than in control subjects (Table 3). In most NIDCM patients, the early diastolic vortex ring was still strong at the A wave onset and the late filling jet did not destroy it but reinforced it instead (Fig. 5, NIDCM case). As a result, the strengthened diastolic vortex kept its location near the apex. The vortex reinforcing pattern during the A wave was observed in 77% of NIDCM cases and in 20% of control cases (P < 0.001; Table 3). Throughout ejection, the vortex was still detected in 60% of NIDCM patients but only in 40% of control subjects (P = 0.04; Fig. 4). Overall, these different evolution patterns caused the main vortex core NIDCM patients to have a larger size and to contain a higher circulation than in control subjects, even when corrected for their larger chamber area (Table 3 and Figs. 4–6). The larger vortices in NIDCM patients caused the inflow jet to be of similar width than in control subjects (Table 3). The vortex Re was higher in the NIDCM group by >50% (P = 0.02; Table 3).

Fig. 6.

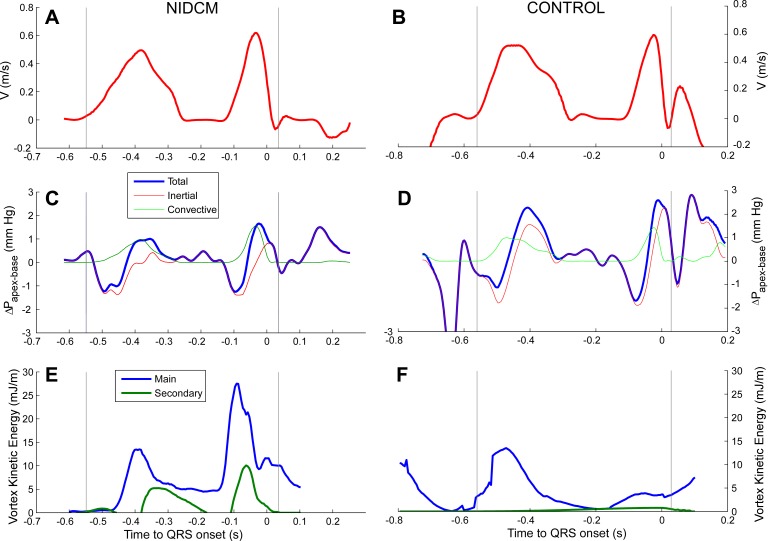
Physiological analysis of vortex energy during diastole in a patient with NIDCM (A, C, and E) and a control subject (B, D, and F). Waveforms are shown for transmitral filling velocity (A and B), the intraventricular pressure difference (C and D), and vortex kinetic energy (E and F). Vertical lines represent mitral valve opening and closing. Notice the impact of late filling flow on vortex kinetic energy.

Kinetic energy analysis.

Patients with NIDCM developed higher KE during filling than control subjects (Table 4). KE during diastasis progressively decreased in control subjects but remained almost constant in NIDCM patients. This resulted in higher vortex KE, both at the time of peak A wave velocity and at the time of aortic valve opening. At peak A velocity, KE stored by the vortex represented 26–27% of inflow KE, with NIDCM patients and control subjects showing almost identical values. Remarkably, values were as high as 90% in some cases. There were no significant differences in the amount (20–24%) of KE released during ejection (Table 4). Mean values of vortex KE closely correlated with those of vortex circulation both for the main (R = 0.86, pooled populations) and secondary (R = 0.94) sections.

Table 4.

Analysis of vortex energy relative to inflow and outflow jet global KE

	NIDCM Patients	Control Subjects	P Value
Inflow KE, mJ	9.0 ± 6.6	6.2 ± 4.8	0.02
Outflow KE, mJ	8.6 ± 9.3	5.0 ± 3.6	0.01
Vortex energy
Vortex KE at peak A wave, mJ	2.5 ± 2.6	1.3 ± 1.5	0.003
Vortex KE at AVO, mJ	1.3 ± 1.1	0.7 ± 0.7	0.005
Stored KE at peak A wave			0.77
Percentage of inflow KE	26 ± 20	27 ± 29
Range	1–74	1–98
Stored KE at AVO			0.81
Percentage of inflow KE	15 ± 17	16 ± 17
Range	1–73	1–69
Released KE			0.48
Percentage of outflow KE	24 ± 26	20 ± 23
Range	1–92	1–93

KE, kinetic energy.

A number of chamber and flow-velocity variables correlated with total vortex energy both at peak A wave velocity and at aortic valve closure (Table 5). By multivariate analysis, the duration of filling, inflow KE, and ventricular geometry were the most important determinants of vortex KE. The vortex formation time was considerably lower in NICDM patients than in control subjects (Table 1), but it was not found to be independently associated with vortex KE (Table 5).

Table 5.

Determinants of total vortex KE in univariate and multivariate analysis

	At Peak A Wave Velocity				At AVO
	Univariate		Multivariate		Univariate		Multivariate
	Pearson correlation coefficient	P value	Standardized regression coefficient	P value	Pearson correlation coefficient	P value	Standardized regression coefficient	P value
Heart rate	0.32	0.001			0.16	0.11
Duration of filling	−0.37	<0.001	−0.22	0.04	−0.17	0.08
LV ejection fraction	−0.31	0.001			−0.29	0.003
LV stroke volume	−0.11	0.26			−0.04	0.68
LV end-diastolic volume	0.21	0.04			0.33	<0.001
LV short-axis diameter	0.24	0.01			0.40	<0.001	0.40	<0.001
LV sphericity index	0.24	0.02			0.39	<0.001
Peak E wave velocity	−0.04	0.68			−0.02	0.81
Peak A wave velocity	0.27	0.007			0.14	0.18
Transmitral flow deceleration time	−0.19	0.06			−0.24	0.02
Transmitral E/A ratio	0.17	0.09			−0.05	0.65
E/e′	0.24	0.02			0.24	0.04
Vortex formation time	−0.25	0.01			−0.20	0.06
Inflow KE	0.35	0.002	0.31	0.004	0.07	0.52
Total peak early DIVPD	−0.07	0.51			−0.02	0.82
Total peak late DIVPD	0.29	0.006			0.10	0.33
Full model adjusted R2			0.15	<0.001			0.15	<0.001

DISCUSSION

Despite growing interest in intracardiac flow dynamics (22, 31, 36), the present study is the first to quantitatively describe the evolution of vortex properties along the full cardiac cycle in a relatively large clinical population. The analysis of vortex dynamics provided interesting novel insights on chamber physiology of the normal and dilated heart.

Vortex Dynamics

The chiral geometry of the LV generates a complex flow pattern during filling, causing a rotational fluid motion close to the mitral leaflet tips. Flow entrainment allows the filling vortex to progressively grow while moving apically. When fully developed, the vortex is highly asymmetrical, with a larger main core directed anteroseptally and a secondary core close to the inferolateral wall. Asymmetry has been classically related to the geometry of mitral and noncoaxial flow orientation along the ventricular long axis (20). The results of our study additionally reveal the importance of the interaction of the vortex with the ventricular wall, as previously suggested (37). Here, we show that, by the time of aortic valve opening, the major determinant of vortex KE was the ventricular short-axis diameter. Consequently, not only size but also chamber geometry modulate vortex development. The temporal evolution of vortex structures showed that vortex-wall interactions can strengthen the main vortex core during E wave deceleration and diastasis, particularly in dilated ventricles. Interestingly, this finding has been predicted by numeric computations demonstrating that the collision of a vortex ring with a flat wall at shallow angles amplifies the circulation of the vortex ring in cross-sections opposite from the interacting wall (i.e., the main vortex core) (7). Furthermore, the observation of significantly higher vortex Re in ventricles from NIDCM patients indicates that the vortices in these hearts are less affected by blood viscosity and offers an explanation for their higher temporal persistence throughout diastole compared with control subjects.

Impact of vortices on diastolic function.

Our findings suggest that vortex structures heavily influence chamber diastolic properties by two mechanisms. The first mechanism is related to the capability of the vortex to facilitate blood transport from the left atrium. Notice that the interaction between the vortex and inflow jet is reciprocal, as vortices, once developed, are capable of transporting flow per se. The second mechanism was first described in the right ventricle (32, 33) and is related to the capacity of the vortex to ameliorate the adverse pressure gradient caused by convective deceleration by channeling the inflow jet inside the ring (6). The resultant of these two effects is that vortex-flow interactions generate pressure forces inside the ventricle that facilitate transferring the filling volume in an organized way toward the apex along the long axis of the chamber (6, 7). In NIDCM patients, this would be particularly relevant, as larger and stronger vortices would transport more fluid volume while at the same time avoiding pressure losses despite their larger LV cavity. The enhanced vortex formation in NIDCM could be partially responsible for the abnormally low LV chamber stiffness characteristic of this condition (27). Interestingly, ventricular dilatation could be associated with reduced operative chamber stiffness, not only due to changes in the myocardial mechanical properties but also because of modifications in chamber intraventricular flow dynamics.

Paradoxically, in a previous work (44), our group has reported an adverse effect of intraventricular flow phenomena on diastolic suction in NIDCM patients. We showed that immediately after mitral valve opening, convective pressure losses are increased in dilated ventricles (44). We believe this is not incompatible with our present findings. As demonstrated here, the intraventricular vortex is not well developed until E wave deceleration. Either very weak or completely absent during early diastole, vortex-mediated effects must be irrelevant while filling is driven by diastolic suction. Only once vortex structures are fully built are they capable of providing their positive effects on chamber operative stiffness, mostly during E wave deceleration and late filling. This is supported by our finding that it was only the late diastolic intraventricular pressure difference that correlated with vortex KE. Surprisingly, this interaction between the vortex and late filling flow has been overlooked by previous PC-MR studies (25, 40).

Vortex energetics and ejection efficiency.

The external work of the LV is predominantly conditioned by chamber pressurization, with total KE accounting for only 0.5–3% of this work (4). During late filling, the total KE inside the LV has been measured in the range of 5–6 mJ in healthy subjects (4). Our average results suggest that rotational vortex motion accounts for 20% of this total KE, and our estimations of KE in control subjects are very close to a previous approximation using single-plane PC-MR (25). We showed that vortices of NIDCM patients charge a greater amount of KE than normal subjects. This is in agreement with the four-dimensional PC-MR finding of LV volume as a major determinant of total ventricular vortices (4). However, as previously discussed, vortex strength was not only related to LV size but also to different chamber geometry and inflow KE. Remarkably, the proportion of this inflow KE stored by the vortex was identical in NIDCM patients and control subjects, close to 30% in both cases. However, the proportion of stored KE could be even higher than we estimated for two reasons. First, we did not correct for a nonflat inflow spatial profile in Eq. 3 (15). Second, we only accounted for the KE contained inside the vortex cores, but vortices induce rotational velocities away from their cores (whose magnitude decreases as the inverse distance to the vortex core).

The intraventricular vortex facilitates flow transit toward the outflow tract and may help coupling filling and ejection phases by conserving momentum (3, 14, 24). Remarkably, we found a huge variability of the amount of KE stored by the intraventricular vortex, a matter that deserves further research. How storing KE can facilitate systolic performance is a matter of debate (26, 42). It has been suggested that diastolic vortices increase chamber efficiency by forwarding momentum from filling to ejection (14, 42). However, using simulations, it has been reported that the overall external work of the normal heart is almost unaffected by this potential energy-saving mechanism (42). Future in vivo studies are necessary to definitely establish the impact of intracardiac vortex dynamics on ventricular mechanical efficiency.

We also found that increased inertia of the main vortex core in NIDCM patients sustained the vortex through E wave deceleration and diastasis, leading to particularly effective late diastolic boosting in this population. This observation suggests that the vortex provides a constructive interference between the rotational motions generated during the two filling waves, which may be particularly relevant during exercise (23), as diastasis duration and A wave inflow peak velocity are inversely and directly correlated with heart rate, respectively, during exercise (8). Therefore, we believe that future studies are necessary to clarify the impact of the intraventricular vortex on systolic efficiency of the heart, particularly during exercise.

Ultrasound-based methods for studying vortical structures.

To our knowledge, this is the first clinical study comparing PC-MR against an ultrasound-based technique implemented for the analysis of intracardiac vortices. Recently, several echocardiographic methods have been proposed (36). Particle-tracking velocimetry applied to contrast ultrasound sequences has shown to be relatively accurate in vitro (21). However, this technique is semi-invasive, and the technical requirements may not be easy to meet (16). Color-Doppler-based methods have been also validated numerically (41) and in vitro using particle image velocimetry in normal-shaped ventricles (17). Our results show that the main vortex core features obtained using this method correlate reasonably well with PC-MR measurements, despite data not being acquired simultaneously. The lower agreement observed for secondary vortex properties was probably related to their smaller magnitude, which renders them particularly sensitive to noise using either imaging modality. Because PC-MR has its own well-characterized limitations in the measurement of intracardiac flow velocity (34, 36), our head-to-head analysis should not be interpreted as a formal validation study.

Limitations.

The mathematical basis for the method used in this study assumes a planar distribution of flow along the long-axis plane of the LV. This is conceptually incompatible with a 3-D vortical structure and a given out-of-plane geometry. However, notice that this planar flow assumption is also present in all ultrasound (17, 21, 29, 41) and some MR (39) methods of flow visualization. Importantly, in our method, the theoretical planar flow limitation is relaxed by the availability of additional information obtained from tracking the LV walls, which is incorporated into the algorithm to minimize the error of the planar approximation (17). A number of further model simplifications were taken for the purpose of our study. Known to be asymmetrical and morphologically complex, main and secondary vortex sections were assumed to be circular. Additionally, an asymmetric toroidal model was used to estimate total vortex energy. True time-evolving 3-D geometry is far more complex, and exact values of total energy must be interpreted with caution. However, we believe that the toroidal approach is useful to estimate an order of magnitude of the relative energetic aspects of intracardiac vortex formation. Although a certain degree of inaccuracy must be present in our 2-D approach, similar geometric simplifications have been universally used for years in the field of clinical cross-sectional ultrasound and have proven to be extremely useful in terms of physiological insights and patient care.

Vortex size and strength were related to chamber size and filling duration. These findings translate to some degree of preload and heart rate dependency of vortex features, properties that are not ideal for physiological cardiovascular metrics sensu stricto. To clarify the physical basis of intracardiac vortex formation, we provided absolute values of vortex indexes such as the radius, circulation, and energy, despite that the fact that they are obviously influenced by larger chamber sizes in NIDCM. Nevertheless, the majority of vortex indexes estimated in our study were nondimensional (relative position, relative size, symmetry, Re, normalized circulation, and relative stored and released vortex KE) and, therefore, should be relatively preload independent. The performance of these or additional preload- and rate-corrected vortex metrics in terms of clinical efficacy should be addressed in further studies. Additionally, vortices are highly unsteady structures, and, thus, their time-evolving properties and their nonlinear interactions may be missed using average property values. However, notice that our mechanistic analysis of determinants was based on instantaneous values obtained at a given time instant.

We obtained only moderate reproducibility results. However, notice that, for the first time in the field of clinical ultrasound-based intracardiac flow visualization, reliability was assessed including blinded reacquisition and reprocessing. Future technical implementations such as obtaining color-Doppler and boundary data from a single ultrasound sequence are promising approaches to increase reproducibility.

Conclusions and clinical implications.

For the purpose of understanding the physiological foundations of vortex development in the LV, the time-evolving properties of intraventricular vortices are described along the full cardiac cycle. We believe that vortices may help coupling the rapid and late filling phases useful for buffering the intermittent nature of cardiac phases. For this purpose, vortices make use of approximately one-fourth of KE entering the LV.

How this type of analysis of vortex dynamics can be translated into useful information in terms of guiding patient care is a challenging field of future research. A number of clinical scenarios deserve particular focus. First, the assessment of mechanical properties of intraventricular flow could be helpful to triage which patients with NIDCM are at an increased risk of intraventricular stasis and thrombosis therefore benefiting most of anticoagulation therapy. Second, because we have shown that late filling is a major determinant of normal vortex physiology, atrial fibrillation and atrioventricular dysynchrony must lead to some degree of LV inefficiency and increased stasis. Consequently, the assessment of vortex physiology may be useful to understand the unsolved issue of response variability to cardiac resynchronization therapy. Third, the direct relationship between LV geometry and vortex function may be particularly important in situations of abnormally small chamber size, as in extreme concentric remodeling. Finally, the analysis of intraventricular vortices anticipates useful information to fully understand the impact of chamber remodeling therapies or assist devices on ventricular mechanics. These relevant aspects of ventricular physiology can now be mechanistically addressed in patients using ultrasound.

GRANTS

This work was supported by Instituto de Salud Carlos III-Ministerio de Economía y Competitividad Grants PIS09/02603, PI12/02885, RD12/0042 (RIC), and CM12/00273 (to C. Pérez del Villar) and BA11/00067 (to J. Bermejo). A. González-Mansilla and C. Pérez del Villar were partially supported by grants from the Fundación para Investigación Biomédica Gregorio Marañón. J. Bermejo, P. Martínez-Legazpi, and J. C. del Álamo were partially supported by National Heart, Lung, and Blood Institute Grant 1-R21-HL-108268-01 (to J. C. del Álamo).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: J.B., R.Y., and J.C.d.A. conception and design of research; J.B., Y.B., M.A., R.Y., P.M.-L., E.P.-D., A.G.-M., C.S.-M., A.B., and J.C.d.A. performed experiments; J.B., Y.B., M.A., R.Y., P.M.-L., A.G.-M., A.B., and J.C.d.A. analyzed data; J.B., R.Y., P.M.-L., C.P.d.V., and J.C.d.A. interpreted results of experiments; J.B., P.M.-L., C.P.d.V., and J.C.d.A. prepared figures; J.B., R.Y., C.P.d.V., and J.C.d.A. drafted manuscript; J.B., P.M.-L., and J.C.d.A. edited and revised manuscript; J.B., F.F.-A., and J.C.d.A. approved final version of manuscript.

APPENDIX A: METHODS OF KE ESTIMATION

Estimation of inflow and outflow KE.

The time rate of change of any scalar quantity, such as KE in a chamber due to fluid fluxes in and out of the chamber, is as follows:

$${\left(\frac{\delta \text{KE}}{\delta t}\right)}_{\text{flux}}={\displaystyle {∯}_s\hspace{0.17em}k\text{e}}(\overrightarrow{\mathit{v}}\hspace{0.17em}·\hspace{0.17em}\overrightarrow{\mathit{n}})\hspace{0.17em}dS$$ (2)

where t is time, S is the outer surface that delimits the chamber, ke is the density of KE per unit volume, $\overrightarrow{\mathit{n}}$ is the vector normal to S (pointing outward), $\overrightarrow{\mathit{v}}$ is the flow velocity, and dS is a differential element of that surface. In turn, ke = 1/2ρ$\mid \overrightarrow{\mathit{v}}\mid$², where ρ is blood density. Because ventricular walls and heart valves are impermeable, $\overrightarrow{\mathit{v}}$ · $\overrightarrow{\mathit{n}}$ can only differ from zero either at the mitral annulus during filling or at the outflow tract during ejection. Thus, during inflow, the rate of change in KE can be estimated as follows:

$${\left(\frac{\delta \text{KE}}{\delta t}\right)}_{\text{inflow}}={\displaystyle {∯}_{\mathrm{m}\mathrm{i}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{l}\hspace{0.17em}\mathrm{a}\mathrm{n}\mathrm{n}\mathrm{u}\mathrm{l}\mathrm{u}\mathrm{s}}}\frac{1}{2}\rho {\mid \overrightarrow{\mathit{v}}\mid }^2\left(\overrightarrow{\mathit{v}}·\overrightarrow{\mathit{n}}\right)dS\approx \frac{1}{2}\rho \pi r_{\text{An4Ch}}{r}_{\text{An2Ch}}{V}_{\text{inflow}}^3$$ (3)

where it is assumed that ν_inflow = −($\overrightarrow{v}$ × $\overrightarrow{n}$) = $\mid \overrightarrow{v}\mid$, as the flow velocity is practically one-dimensional at the filling jet crossing the mitral annulus. It is also assumed that the mitral annulus has an elliptical shape with orthogonal axes equal to measurements obtained at the four- and two-chamber views (r_An4Ch and r_An2Ch), respectively. By integrating Eq. 5 in time, we can obtain the amount of KE entering the LV during filling (ΔKE_inflow), as follows:

$$\Delta {\text{KE}}_{\text{inflow}}={\displaystyle {\int }_{\text{MVO}}^{\text{MVC}}}{\left(\frac{\partial \text{KE}}{\partial t}\right)}_{\text{inflow}}\text{d}t=\frac{1}{2}\rho \pi r_{\text{An4Ch}}{r}_{\text{An2Ch}}{\displaystyle {\int }_{\text{MVO}}^{\text{MVC}}}{\text{V}}^3\text{d}t$$ (4)

where MVC is mitral valve closure and MVO is mitral valve opening. Using the same assumptions except a circular shape for the LVOT, the amount of KE leaving the ventricle during ejection (ΔKE_outflow) can be obtained as follows:

$$\Delta {\text{KE}}_{\text{outflow}}={\displaystyle {\int }_{\text{AVO}}^{\text{AVC}}}{\left(\frac{\partial \text{KE}}{\partial t}\right)}_{\text{outflow}}\text{d}t=\frac{1}{2}\rho \pi r_{\text{LVOT}}{\displaystyle {\int }_{\text{AVO}}^{\text{AVC}}}{\text{V}}^3\text{d}t$$ (5)

where AVC is aortic valve closure and AVC is aortic valve opening. To solve Eqs. 6 and 7, we used inflow and outflow instantaneous velocities obtained from CDMM inflow and outflow recordings. CDMM velocity decoding offers the advantage over conventional annulus pulsed-wave Doppler of allowing correction for annulus longitudinal displacement during diastole and has been previously validated by our group (2).

Estimation of vortex KE.

In-plane KE contained in the main core (in mJ/m) was estimated from the surface integral as follows:

$${\text{KE}}_{\text{main}}=\frac{1}{2}\rho {\displaystyle {\iint }_{S_{\text{main}}}}{\mid \overrightarrow{v}\mid }^{2}dS$$ (6)

where S_main is the region of the imaged plane occupied by the main vortex, as obtained from the Q-identification method described above (Fig. 2), and $\left|\overrightarrow{v}\right|$ is the modulus of the 2-D velocity vector in that plane, obtained by integration of Eq. 1. The in-plane KE of the secondary vortex core was obtained in an analogous manner.

The term “in plane” is used here because the thus-obtained energies account only for the velocity and spatial extent of the vortex sections included in the imaged plane. To characterize the total energetic aspects of vortex development, we attempted to obtain an estimate of the total KE stored by the 3-D vortical structure (in mJ). Lagrangian methods applied to volumetric PC-MR data have demonstrated complex time-evolving geometries of the intraventricular vortex ring, which are obviously impossible to capture using a planar imaging modality (19, 40). For the purpose of the present study, this was simplified using an arbitrary geometrical approximation based on an asymmetric toroid (ring) linearly tapering from the main to secondary vortex core sections (Fig. 2A), as follows:

$${\text{KE}}_{\text{total}}=\pi {\text{R}}_{\text{toroid}}\left({\text{KE}}_{\text{main}}+{\text{KE}}_{\text{sec}}\right)$$ (7)

where R_toroid is the half-distance between the centers of the main and secondary vortex cores, KE_main is the KE of the main section, and KE_sec is the KE of the secondary section. Although this model represents a basic vortex 3-D geometry that should be interpreted with caution, we believe it provides an order of magnitude useful to assess the importance of vortex generation in terms of the KE of intraventricular flow. Notice that Eq. 7 was only applied at the time instants of peak A wave velocity and aortic valve closing, two given moments of the cardiac cycle when the vortex is fully developed. Due to the highly unsteady nature of vortex geometry, the toroid model of Eq. 7 is probably highly inaccurate during other phases of the cardiac cycle. Filling jet diameter was obtained as the inside section of the torus as follows: 2R_toroid − r_main − r_sec, where r_main and r_sec are the radii of the main and secondary vortex cores, respectively.

APPENDIX B: PC-MR COMPARISON STUDY

Patients.

Twenty-one patients (13 men and 8 women, age: 56 ± 12 yr old) were selected for the head-to-head comparison study and underwent PC-MR scanning within 3 h of the ultrasound examination. The ultrasound-based method used in this study has been previously validated for normal (symmetric) ventricular geometries against particle image velocimetry, the accepted gold standard technique for flow mapping. Therefore, all subjects used for comparison against PC-MR were selected from the NIDCM population. Values of end-diastolic volume and ejection fraction in this subpopulation were 202 ± 96 ml and 0.28 ± 0.12, respectively.

Image acquisition and image processing.

We used a 1.5-T MR system (software package release 9, Philips Intera) with a five-element phased array dedicated cardiac coil and retrospective ECG gating. PC-velocity measurements were performed using a segmented fast gradient echo sequence [repetition time (ms/echo)/time: 8.8/5.2, flip angle: 15°, section thickness: 8 mm, matrix: 304 × 300]. Two direct orthogonal within-plane velocity measurements were obtained in scout-guided long-axis views using predefined upper velocity limits of 100 and 50 cm/s for directions closest to the long and short axes of the LV, respectively. Five temporal phases were acquired randomly distributed along the cardiac cycle, yielding a total of 105 frames suitable for analysis from the 21 patients studied. Additionally, cine steady-state free precession images of the LV were obtained (sense × 2, repetition time: 2.4 ms, echo time: 1.2 ms, average in-plane spatial resolution: 1.6 × 2 mm, 30 phases/cycle, 8-mm slice thickness without gap). PC sequences in this system were calibrated using a custom in vitro system. Images of a long-tube system filled with 40% glycerol in water (dynamic viscosity: 3.5 mPs·s, density: 1.10 g/cm³) and connected to a continuous flow roller pump at different rates (0.85–5.96 l/min) of steady-state laminar flow (Re = 512–4,100) were obtained using the same PC-MR setting applied for the clinical study (9).

To analyze the PC-MR data, we semiautomatically segmented the LV chamber using the cine sense sequences (QMASS, version 7.2, MEDIS). Contours were then registered and temporally matched to the velocity magnitude of PC-MR frames. Orthogonal velocities inside the LV chamber were automatically decoded and dealiased if necessary. Vortex structures were identified and characterized from the 2-D velocity field adapting the same algorithms used for ultrasound. Time instants of ultrasound and PC-MR frames were automatically matched based on their timing in the cardiac cycle and visually checked (35% ejection phase, 16% isovolumic relaxation, 36% filling, and 8% isovolumic contraction). Three cases showing a >15% variation in the cardiac cycle between ultrasound and MR studies were discarded and are not included in this report.