High-Resolution Multi-Shot Spiral Diffusion Tensor Imaging with Inherent Correction of Motion-Induced Phase Errors

Abstract

Purpose

To develop and compare three novel reconstruction methods designed to inherently correct for motion-induced phase errors in multi-shot spiral diffusion tensor imaging (DTI) without requiring a variable-density spiral trajectory or a navigator echo.

Theory and Methods

The first method simply averages magnitude images reconstructed with sensitivity encoding (SENSE) from each shot, whereas the second and third methods rely on SENSE to estimate the motion-induced phase error for each shot, and subsequently use either a direct phase subtraction or an iterative conjugate gradient (CG) algorithm, respectively, to correct for the resulting artifacts. Numerical simulations and in vivo experiments on healthy volunteers were performed to assess the performance of these methods.

Results

The first two methods suffer from a low signal-to-noise ratio (SNR) or from residual artifacts in the reconstructed diffusion-weighted images and fractional anisotropy maps. In contrast, the third method provides high-quality, high-resolution DTI results, revealing fine anatomical details such as a radial diffusion anisotropy in cortical gray matter.

Conclusion

The proposed SENSE+CG method can inherently and effectively correct for phase errors, signal loss, and aliasing artifacts caused by both rigid and nonrigid motion in multi-shot spiral DTI, without increasing the scan time or reducing the SNR.

Introduction

Diffusion tensor imaging (DTI) is a powerful neuroimaging technique for investigating the structural connectivity of the brain noninvasively, but is typically performed with single-shot echo-planar imaging (EPI), which is limited by a relatively low spatial resolution and signal-to-noise ratio (SNR), even when combined with parallel imaging and partial-Fourier encoding. Multi-shot spiral DTI, on the other hand, is a promising alternative because of its potential for achieving a higher resolution and SNR (1–7), but is also challenging because subject motion causes phase errors among different shots, leading to signal loss and aliasing artifacts in the reconstructed images as well as subsequent errors in the resulting DTI metrics and fiber tracts (8,9).

Previous multi-shot spiral DTI techniques have used a variable-density spiral trajectory oversampling the central k-space (1–6) or a single-shot spiral navigator echo (7–9) to generate a low-resolution estimate of the motion-induced phase error for each shot and to correct for such artifacts. However, these methods all require a longer scan time (e.g., up to a factor 2 for a variable-density spiral acquisition with a typical oversampling factor of 4 (1–5)), which may hamper their ability to achieve both a high spatial and angular resolution, particularly in pediatric or clinical populations.

To address these issues, we recently proposed an iterative phase correction method for multi-shot spiral DTI that can inherently correct for the motion-induced phase errors without requiring any additional data acquisition or increasing the scan time (10,11). Specifically, a series of low-resolution images are iteratively reconstructed with different phase values added to each shot, resulting in different amounts of aliasing, and the background signal intensity of these images is minimized to determine and correct for the motion-induced phase errors. However, the current implementation of this method remains limited by a relatively long computation time for high-resolution DTI and, as a result, only corrects for spatially linear phase errors caused by rigid-body motion (12), but not for nonlinear phase errors caused by nonrigid motion, such as pulsatile brain motion during the cardiac cycle (13).

In the present study, we propose three alternative reconstruction methods for multi-shot spiral DTI, designed to both inherently and more efficiently correct for linear and nonlinear motion-induced phase errors, and we compare their performance in numerical simulations and in vivo experiments performed on healthy volunteers.

Theory

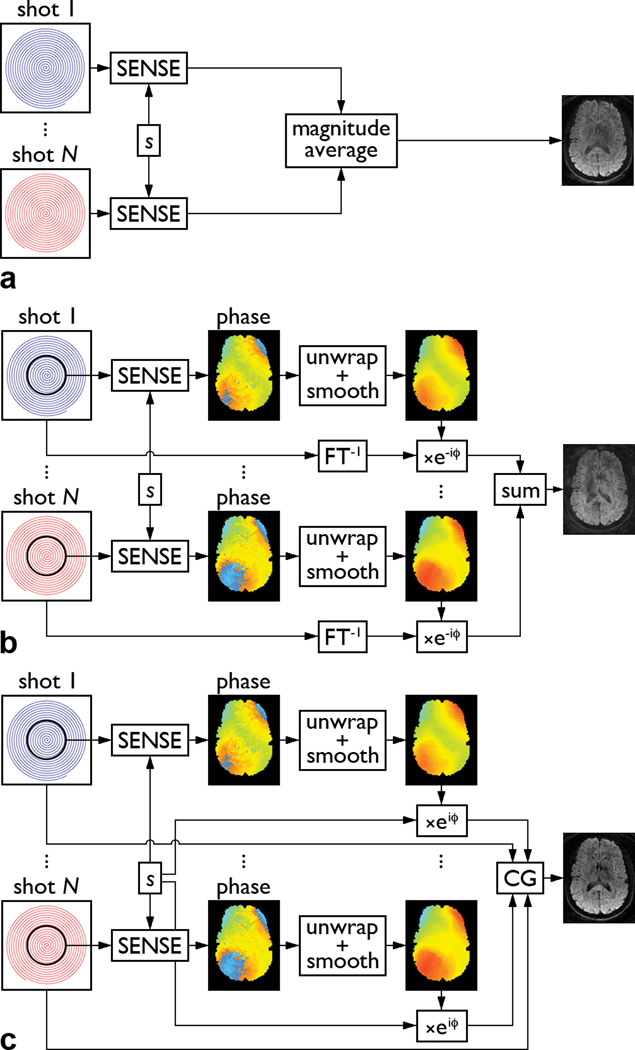
The first and simplest method consists in reconstructing a magnitude image from the k-space data of each shot, by using a sensitivity encoding (SENSE) reconstruction method based on an iterative conjugate gradient (CG) algorithm (14), and averaging the resulting images from all shots (Fig. 1a). For an N-shot spiral acquisition, this method is equivalent to averaging N separate single-shot spiral acquisitions with a SENSE acceleration factor N. Since each magnitude image is only reconstructed from a single shot, this method is not affected by signal loss and aliasing artifacts due to motion-induced phase errors among different shots. However, it suffers from an SNR loss due to the g-factor penalty inherent in parallel imaging (15) as well as from a potential bias due to the Rician noise distribution in the magnitude average of images with very low SNR (i.e., less than 2) (16), both of which increase with the number of shots.

Figure 1.

Schematic diagrams of the SENSE+avg (a), SENSE+DPS (b), and SENSE+CG (c) methods (s: coil sensitivity, FT⁻¹: gridding + inverse Fourier transform, ϕ: motion-induced phase error).

The second method consists in reconstructing a phase image from the k-space data of each shot, also by using a SENSE reconstruction algorithm (14), to estimate the motion-induced phase error (Fig. 1b). Additional steps are used to improve the phase estimation, particularly for acquisitions with a large number of shots (resulting in a high acceleration factor in the SENSE reconstruction of each individual shot) or a high spatial resolution or b-factor (resulting in a low SNR). Since the motion-induced phase errors are typically spatially slowly varying, only the central k-space data of each shot are used for the SENSE reconstruction, such that the resulting phase images have a twice lower spatial resolution, but a higher SNR. The phase images are then unwrapped, smoothed with a 9×9 median filter, and interpolated to the full spatial resolution. These parameters were empirically found to provide good results for the DTI data acquired in this study.

Once the motion-induced phase errors are known, the phase correction then consists in reconstructing a complex image from the full k-space data of each shot (by zero-filling the missing data from the other shots), subtracting the corresponding phase error, and adding the resulting images from all shots (Fig. 1b). This so-called direct phase subtraction (DPS) method has also been used to reconstruct multi-shot variable-density spiral DTI images, whereby the motion-induced phase errors are estimated from the oversampled central k-space data (1). One limitation of this method is that since each shot undersamples k-space, the phase error at one location is aliased to other locations and cannot be completely corrected with a simple phase subtraction, resulting in residual aliasing artifacts in the reconstructed images (2,4).

The third method is identical to the second one, except that it uses an iterative CG algorithm (2) instead of a simple phase subtraction to address this issue and improve the phase correction. Specifically, the coil sensitivity profiles are combined with the motion-induced phase errors, estimated as described above, to form composite sensitivity profiles that vary with each shot (Fig. 1c). The full k-space data and composite sensitivity profiles of all shots are then supplied to an iterative CG algorithm, mathematically similar to that used in the SENSE reconstruction for arbitrary k-space trajectories (14), to reconstruct the final image. This CG method has also been used to reconstruct multi-shot variable-density spiral DTI images, whereby the motion-induced phase errors are estimated from the oversampled central k-space data, and is discussed in more detail in (2). For simplicity, the three reconstruction methods described above will hereafter be referred to as the SENSE+avg, SENSE+DPS, and SENSE+CG methods, respectively.

Methods

Simulations

We first performed numerical simulations to validate the proposed methods. Specifically, a non-diffusion-weighted 6-shot spiral image, acquired as described below and unaffected by motion artifacts, was used as a reference image. Simulated data were generated by reconstructing a complex image from the k-space data of each shot, adding a random spatially nonlinear phase (comparable to the motion-induced phase errors measured experimentally) to each image, and transforming these images back to k-space. The resulting data were then reconstructed with the SENSE+avg, SENSE+DPS, and SENSE+CG methods, and the normalized root mean square error (NRMSE) between the reference image and each reconstructed image was computed to quantitatively assess the performance of these methods.

Furthermore, to assess their dependence on the number of shots and the SNR, both of which can potentially affect the estimation of the motion-induced phase errors, simulations were performed for different spiral k-space trajectories (with a number of shots ranging from 4 to 10) and with different amounts of Gaussian noise added to the simulated data (corresponding to an SNR ranging from 5 to 20, which includes the range of values measured experimentally in the diffusion-weighted images). For each of these conditions, simulations were performed for 10 different sets of random phase errors and 6 different slices across the brain.

Experiments

We studied four healthy adult volunteers, who provided written informed consent as approved by our Institutional Review Board, on a 3T MR750 MRI scanner (GE Healthcare, Milwaukee, WI) equipped with a 32-channel phased-array head coil and a gradient system with 50 mT/m maximum amplitude and 200 T/m/s maximum slew rate. Foam padding was used to restrain the head within the coil and the subjects were instructed to remain still. High-order static shimming was performed using the scanner’s software to reduce the global B₀ inhomogeneity.

Axial DTI images of the whole brain were acquired with a single spin-echo spiral imaging pulse sequence and the following parameters: repetition time = 5.2 s, echo time = 51 ms, field of view = 20.8×20.8 cm, matrix size = 208×208, slice thickness = 3 mm, number of slices = 44, b-factor = 800 s/mm², number of diffusion-weighting directions = 15, and number of averages = 1. A spatial-spectral pulse was used for fat suppression and the k-space trajectory was a 6-shot constant-density spiral-out trajectory with a readout duration of 25.2 ms.

The images were reconstructed without any phase correction and with the SENSE+avg, SENSE+DPS, and SENSE+CG methods. A B⁰ map was acquired on each volunteer to correct for residual blurring artifacts caused by susceptibility effects near air/tissue interfaces, whereas B₀ maps were acquired on a phantom with the same diffusion-weighting gradients as in the DTI scan to correct for blurring artifacts caused by eddy currents, as described in (17). Finally, fractional anisotropy (FA) maps were computed and color-coded according to the direction of the principal eigenvector. All image reconstruction and post-processing were performed in Matlab (The MathWorks, Natick, MA) and in parallel (for each slice and each diffusion-weighting direction) on a Linux cluster with 460 CPU cores and 4.45 TB of memory. Due to a global memory limit per user, about 100 jobs, each using 8 GB of memory, were run in parallel.

Results

Simulations

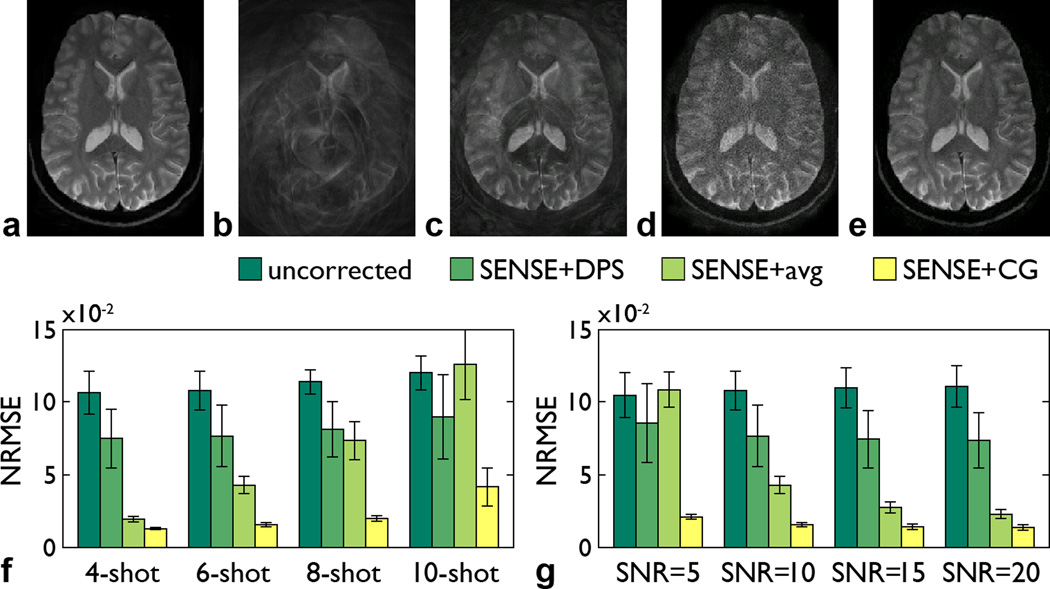
Representative results are shown in Fig. 2. The image simulated by adding random phase errors is affected by severe signal loss and aliasing artifacts (Fig. 2b). The SENSE+DPS method can largely, but not fully, correct for them (Fig. 2c), whereas the SENSE+avg method is not affected by such artifacts, but suffers from a reduced SNR due to the g-factor penalty (Fig. 2d). In contrast, the SENSE+CG method can effectively correct for these artifacts with no SNR loss (Fig. 2e), resulting in an image that is virtually identical to the reference image (Fig. 2a).

Figure 2.

Reference image (a), image simulated by adding random spatially nonlinear phase errors (b), and images reconstructed from the simulated data with the SENSE+DPS (c), SENSE+avg (d), and SENSE+CG (e) methods for a 6-shot spiral trajectory and SNR = 10. NRMSE (mean ± standard deviation) between the reference image and each reconstructed image as a function of the number of shots for SNR = 10 (f) and as a function of the SNR for a 6-shot spiral trajectory (g).

For all conditions tested, the SENSE+CG method consistently performs better than both the SENSE+DPS and SENSE+avg methods (Figs. 2f,g). The NRMSE increases with the number of shots (i.e., with the acceleration factor in the SENSE reconstruction of each individual shot) for all three methods, as expected, but the increase is much larger for the SENSE+avg method than for the SENSE+CG method (Fig. 2f). The NRMSE also increases as the SNR decreases for all three methods, as expected, but the increase is again much larger for the SENSE+avg method than for the SENSE+CG method (Fig. 2g).

Experiments

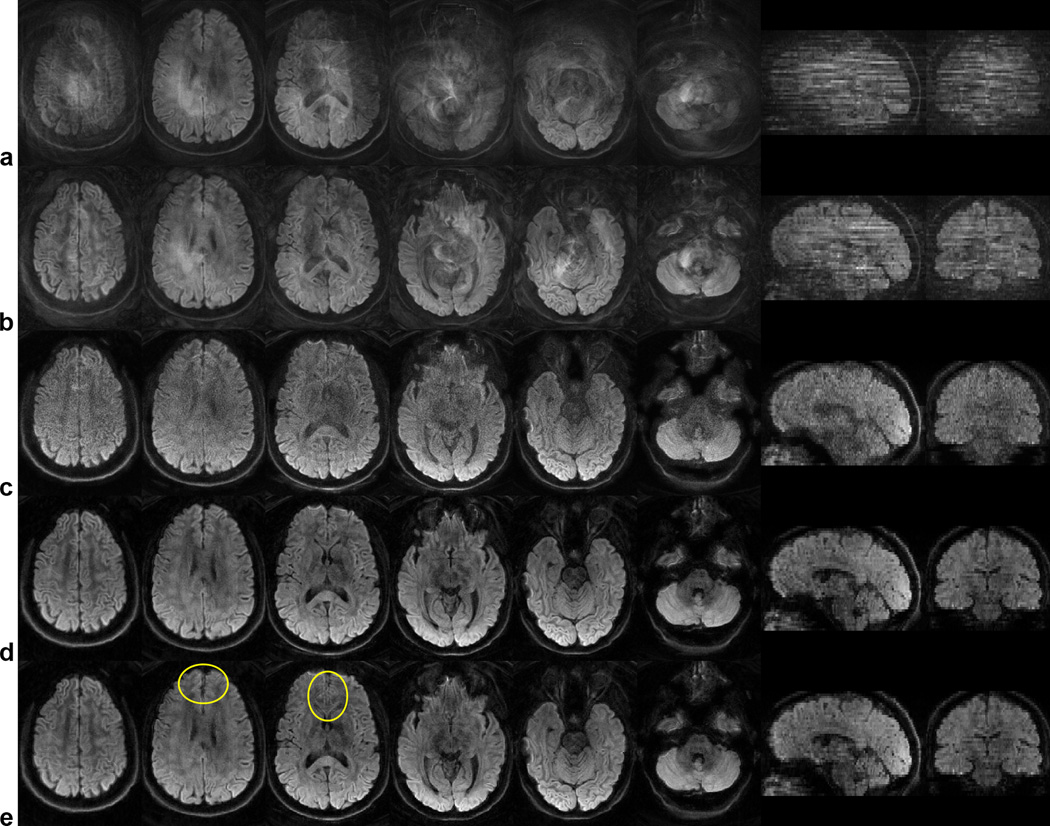
Representative diffusion-weighted images and color-coded FA maps are shown in Figs. 3 and 4, respectively. Even though padding was used to restrain the head within the coil and the subjects were instructed to remain still, residual motion still causes extensive aliasing artifacts in the diffusion-weighted images (Fig. 3a) and subsequent errors in the FA maps (Fig. 4a) throughout the brain. Note that motion-induced phase errors among different shots cause the signal in one pixel to be aliased to other pixels in the image, which, depending on whether these phase errors add up constructively or destructively, can lead to a signal increase or decrease.

Figure 3.

Diffusion-weighted images in six axial slices and two reformatted sagittal and coronal slices uncorrected (a) and reconstructed with the SENSE+DPS (b), SENSE+avg (c), and SENSE+CG (d,e) methods, with (a–d) and without (e) off-resonance correction.

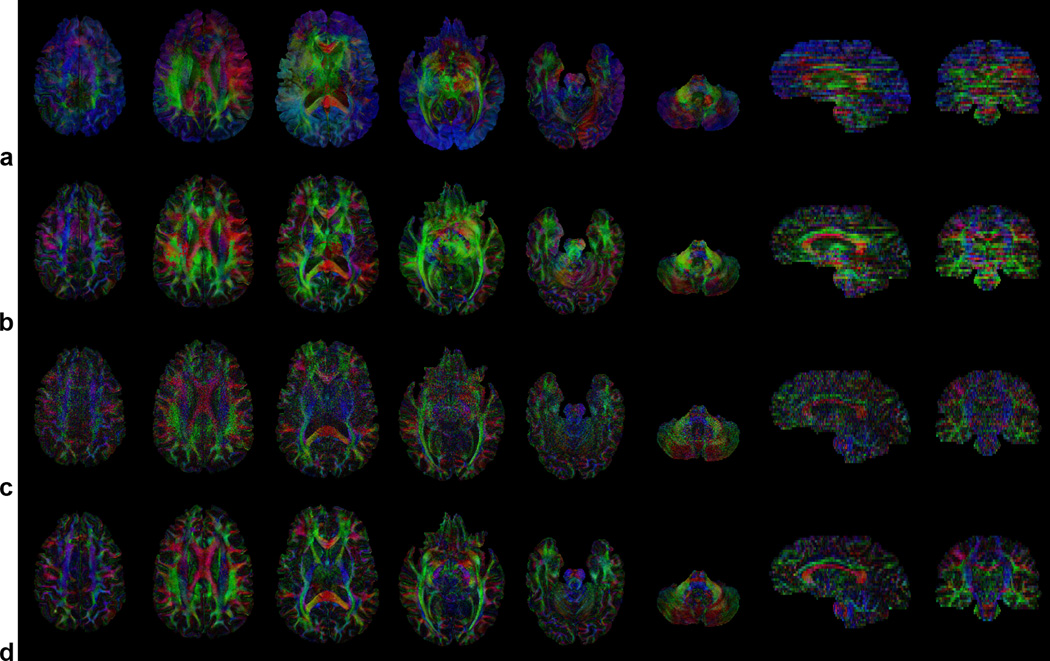
Figure 4.

Color-coded FA maps in the same slices as in Fig. 3 uncorrected (a) and reconstructed with the SENSE+DPS (b), SENSE+avg (c), and SENSE+CG (d) methods, all with off-resonance correction (red: right–left, green: anterior–posterior, blue: superior–inferior).

As in the simulations, the SENSE+DPS method can only partially, but not completely, correct for these artifacts (Figs. 3b, 4b), whereas the SENSE+avg method is not affected by such artifacts, but suffers from a low SNR (Figs. 3c, 4c). On the other hand, the SENSE+CG method can effectively correct for these artifacts and substantially improve the image quality, while providing a much higher SNR than the SENSE+avg method (Figs. 3d, 4d). This SNR improvement is spatially varying and can reach up to 50% in the center of the image (i.e., further away from the coil), in contrast to the simulations where the added noise was spatially uniform by design. Similar results were obtained for all slices, diffusion-weighting directions, and subjects. A comparison between images reconstructed with (Fig. 3d) and without (Fig. 3e) off-resonance correction shows a clear reduction of blurring artifacts, particularly in the inferior frontal regions (outlined in Fig. 3e), where strong localized B₀ inhomogeneities cannot be corrected with shimming alone.

In this work, the iterative CG algorithm stopped when the accuracy reached a threshold of 10⁻⁴ (14), resulting in an average number of iterations of 28 for the SENSE reconstruction in the SENSE+avg method, 19 for the SENSE reconstruction in the SENSE+DPS and SENSE+CG methods, and 5 for the phase correction in the SENSE+CG method. The average reconstruction time for a single image was 2.5, 1.2, and 1.5 min, whereas the total reconstruction time was 17.7, 8.3, and 10.7 min for the SENSE+avg, SENSE+DPS, and SENSE+CG methods, respectively, but these reconstruction times could be further reduced by using more efficient programming languages (e.g., C/C++ instead of Matlab). The reconstruction times are shorter for the SENSE+DPS and SENSE+CG methods than for the SENSE+avg method, despite the additional phase correction step, because the SENSE reconstruction used to estimate the motion-induced phase errors in the SENSE+DPS and SENSE+CG methods is only performed on the central k-space data, whereas the SENSE reconstruction used to reconstruct the magnitude images in the SENSE+avg method is performed on the full k-space data.

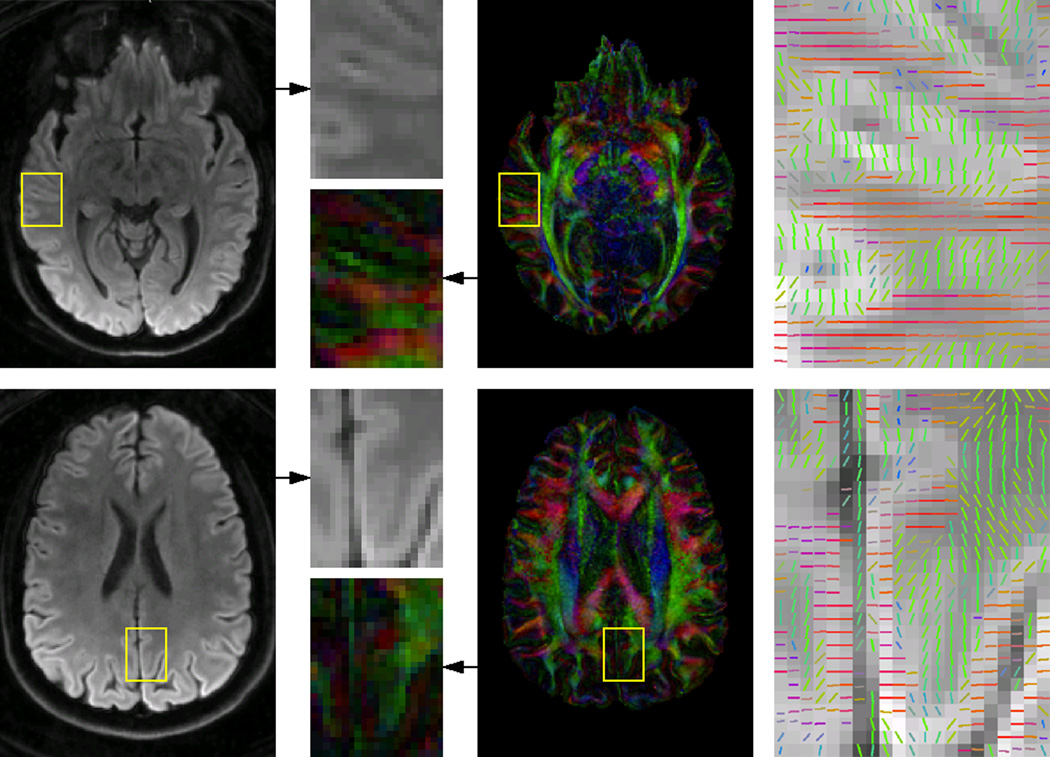
The high-resolution DTI results obtained with the SENSE+CG method reveal a high level of anatomical detail typically not observed in conventional DTI data acquired at 3T. For example, Fig. 5 clearly shows cortical gray matter regions with an anisotropic diffusion and a principal eigenvector approximately orthogonal to that of adjacent white matter regions.

Figure 5.

Mean diffusion-weighted images (left), color-coded FA maps (middle), and direction of the principal eigenvector, color-coded as in the FA maps and overlaid on the mean diffusion-weighted images in two regions-of-interest (right), all reconstructed with the SENSE+CG method and with off-resonance correction.

Discussion and Conclusions

The numerical simulations and in vivo experiments performed in this study demonstrate that the proposed SENSE+CG method can inherently and effectively correct for linear and nonlinear motion-induced phase errors and for the resulting signal loss, aliasing artifacts, and FA errors in multi-shot spiral DTI. As expected, it performs better than both the SENSE+DPS and SENSE+avg methods, which are limited by residual artifacts or by a low SNR, respectively.

This method benefits from significant advantages over previously proposed methods. Unlike multi-shot spiral DTI techniques based on a variable-density spiral trajectory (1–6) or a navigator echo (7–9), it does not require any additional data acquisition and does not increase the scan time, which is particularly critical for pediatric and clinical populations. Furthermore, in contrast to the iterative phase correction method (10,11), it is not limited by a long computation time and can correct for phase errors caused by both rigid and nonrigid motion, thus avoiding the need to use cardiac gating to minimize pulsatile artifacts, which would otherwise increase the scan time (4,5,7,10,11).

This method also shares some common limitations with other two-dimensional motion correction methods (1–5,8,10,11) in that it can correct for in-plane motion, but not for through-plane motion or spin history effects, and with other retrospective motion correction methods (1–7,10,11) in that it cannot correct for large subject motion from uncooperative subjects, which causes not only phase errors, but also misregistration, among different shots. Nevertheless, it is fully compatible with alternative methods designed to address these issues (8,9).

Parallel imaging has previously been used to correct for motion artifacts rather than to speed up the acquisition. For example, one method uses parallel imaging to detect and discard motion-corrupted k-space data and to regenerate the missing data, but results in a reduced SNR and is only applicable if a small region of k-space is corrupted (18). Another method also uses parallel imaging to detect and correct for motion-corrupted k-space data, but can only correct for in-plane rigid-body translations (19). These methods are, however, fundamentally different from those used in this work. The proposed SENSE+avg method uses parallel imaging to reconstruct an image from the k-space data of each shot, but does not discard or replace any data, since this method is not affected by phase errors among different shots. The SENSE+DPS and SENSE+CG methods only use parallel imaging to estimate the motion-induced phase errors, but not to reconstruct the final images. Furthermore, neither of these three methods is restricted to the correction of localized k-space errors or to the correction of one particular type of motion.

The reduction of blurring artifacts observed between Figs. 3e and 3d suggests that the improvement in image quality between the multi-shot variable-density spiral DTI results shown in (1,2) and our results is at least partly due to the fact that off-resonance correction was used in this work but not in (1,2), although other differences, such as the field strength (1.5T vs. 3T) and TE (67 vs. 51 ms), may also be contributing factors. Furthermore, applying the iterative phase correction method (10) and the SENSE+CG method to the same data provided similar results (Fig. S1), indicating that the improvement in image quality between the results shown in (10) and our results, both of which used the same off-resonance correction method, is primarily due to the difference in spatial resolution (2.5 vs. 1 mm).

Our simulations show that the SENSE+CG method remains effective even under very low SNR conditions for the 6-shot spiral trajectory used in this study, which was sufficient to achieve a 1×1 mm in-plane resolution with full brain coverage. As the number of shots increases, more advanced reconstruction algorithms such as phase-constrained (20) or regularized (21) SENSE may be used to further improve the estimation of the motion-induced phase errors (and to reduce the g-factor penalty in the SENSE+avg method). The maximum number of shots is ultimately limited by the number of coil elements, although this may not be a limitation in practice, as highly parallel phased-array coils become increasingly available. Finally, even though the SENSE+CG method was applied to unaccelerated multi-shot spiral DTI data in this study, it is in principle also applicable to undersampled data, as was previously shown for multi-shot variable-density spiral DTI (2), as well as to other multi-shot diffusion-weighted imaging sequences.

The SENSE+CG method can provide high-quality, high-resolution multi-shot spiral DTI results, thereby revealing features typically not seen in conventional DTI data acquired with single-shot EPI or in previous multi-shot spiral DTI studies (1–9). In particular, our results obtained in vivo at 3T show cortical gray matter regions with a radial diffusion anisotropy, which has also been observed in recent high-resolution DTI studies performed in vivo at 7T (22,23) or ex vivo at 3T (24,25). However, more systematic studies performed with a higher and/or isotropic resolution are needed to reduce partial volume effects and further investigate these findings, which is beyond the scope of this work.

In conclusion, the proposed SENSE+CG method can inherently and effectively correct for phase errors caused by both rigid and nonrigid motion in multi-shot spiral DTI, without increasing the scan time or reducing the SNR. This method should facilitate a wider adoption of multi-shot spiral DTI for high-resolution studies in basic neuroscience research and clinical applications.