Multidimensional Methods for the Formulation of Biopharmaceuticals and Vaccines

Abstract

Determining and preserving the higher order structural integrity and conformational stability of proteins, plasmid DNA and macromolecular complexes such as viruses, virus-like particles and adjuvanted antigens is often a significant barrier to the successful stabilization and formulation of biopharmaceutical drugs and vaccines. These properties typically must be investigated with multiple lower resolution experimental methods, since each technique monitors only a narrow aspect of the overall conformational state of a macromolecular system. This review describes the use of empirical phase diagrams (EPDs) to combine large amounts of data from multiple high-throughput instruments and construct a map of a target macromolecule's physical state as a function of temperature, solvent conditions, and other stress variables. We present a tutorial on the mathematical methodology, an overview of some of the experimental methods typically used, and examples of some of the previous major formulation applications. We also explore novel applications of EPDs including potential new mathematical approaches as well as possible new biopharmaceutical applications such as analytical comparability, chemical stability, and protein dynamics.

Introduction

The pharmaceutical uses of proteins, nucleic acids and higher order macromolecular complexes such as viruses, virus-like particles, plasmid and polymer associations, and adjuvanted antigens represent the major advance in the biotechnology and vaccine industries in the last 30 years. Due to their more natural biological character, macromolecules offer a degree of safety and efficacy that has resulted in their continuously increased use for a wide variety of therapeutic and prophylactic applications.

Traditional analytical methods of ensuring the structural integrity and conformational stability of these macromolecules have not, however, kept up with this progress. For example, due to the inability of individual experimental methods to monitor all aspects of the structural integrity of macromolecules, biological potency assays are required to ensure overall structural properties have been maintained. Moreover, in the case of protein-based drugs including monoclonal antibodies, loss of conformational integrity leading to aggregation during manufacturing and storage has raised potential safety concerns due to immunogenicity.^1,2 This problem has become especially acute not only in terms of defining shelf life and ensuring proper administration, but it arises frequently as a comparability issue during the biopharmaceutical drug development process. For example, some of the challenges of establishing analytical comparability for different monoclonal antibodies during early and late stage development have recently been highlighted.³ With the advent of biosimilars, the ability to better define the higher order structure of proteins, nucleic acids, and macromolecular complexes in pharmaceutical dosage forms over time will most likely emerge as a critical analytical challenge.

Although at one time it was thought that it might be possible to build a “frame-work” type structure (especially with monoclonal antibodies) that would behave in a sufficiently uniform and reproducible fashion that a similar characterization and subsequent formulation process could be used with all homologues, it is clear that this is often not the case. This is actually evident when one considers that single mutations (think of sickle cell hemoglobin, cryommunoglobulins, many genetic diseases, etc.) can completely alter the physical properties of a macromolecule. Thus, each macromolecule, despite its apparent similarity to related molecules, must be treated as a physically independent agent.

Because the more complex three dimensional structures of macromolecules (typically involving tens of thousands of atoms or more) often play the key role in defining their biological activity and efficacy, characterization of higher order secondary, tertiary and quaternary structures remains a significant barrier to their pharmaceutical development. The problem is simple enough to state, although it remains difficult to address experimentally: How does one demonstrate that pharmaceutical macromolecular systems are sufficiently structurally similar (at the beginning and end of shelf life or in comparison to an analogous macromolecular systems) that they can for all intents and purposes be considered sufficiently identical for therapeutic use in terms of their safety, efficacy, and stability?

A number of standard methods currently exist with the ability to obtain high resolution structural information for proteins, nucleic acids and their complexes, resulting in commonly used representations such as stick and ball models, ribbon diagrams and van der Waals and electrostatic surface maps. Such three dimensional images of structure are the most common way to think of macromolecular systems. Among the experimental methods used to generate these images are X-Ray crystallography, nuclear magnetic resonance (NMR), cryo-electron microscopy and molecular mechanics calculations based on detailed force potentials. At present, however, these approaches are seldom directly applicable to biopharmaceutical dosage forms due to practical limitations. For example, X-Ray crystallography requires crystallization, while NMR spectroscopy requires isotopic labeling and high concentrations. Moreover, complete structural characterization is most appropriate when it serves the overall goal of developing formulations. For these reasons, lower resolution biophysical methods are commonly employed to monitor structural integrity and hydrodynamic properties. These techniques include circular dichroism (CD), fluorescence, differential scanning calorimetry (DSC), chromatography, and light scattering, among others (see Table 1).

Table 1.

Lower resolution biophysical techniques commonly used to characterize and monitor higher order structure as well as aggregates of biomolecules and macromolecular complexes.

Method	2° Structure Ratios	2° Structure Transitions	3° Structure Transitions	4° Structure Transitions	Aggregate Presence	Aggregate Size	Aggregate Populationd	Dynamics	References
Neara UV Absorbance (UVAS)		°	•		•			•	4, 6, 31–35
Farb UV Absorbance	•	•	•						31
Neara UV Circular Dichroism (CD)			•						36, 37
Farb UV Circular Dichroism	•	•	°						35–38
Intrinsic Fluorescence (IF)		°	•					•	39
Extrinsicc Fluorescence (EF)			•		•				40–45
Red Edge Excitation (REES)								•	46, 47
Time Resolved Fluorescence (TRFS)								•	48, 49
Fourier Transform Infrared (FTIR)	•	•			•				50–52
Raman spectroscopy (RS)	•	•	•						53
Differential Scanning Calorimetry (DSC)		•	•	•	•				54, 55
Pressure Perturbation Calorimetry (PPC)								•	55–57
High Res. Ultrasonic Velocimetry (HRUS)								•	55, 58
Dynamic Light Scattering (DLS)				•	•	•	•		59
Static Light Scattering (SLS)				•	•	•			60
Optical Density (OD)				•	•				60
High Perf. Liquid Chromatography (HPLC)		•	•	•	•	•	•		61, 62

^a240-320nm.

^b190-260nm.

^cDie conjugated.

^dSize distribution profile.

^°Limited data.

Unfortunately, no one method provides sufficient information to establish the identity and integrity of complex macromolecular systems. Therefore, the use of more than one of these methods is generally preferred to better characterize these entities. The multidimensional nature of such data sets makes adequate characterization of higher order structural integrity problematic. To develop stable dosage forms, formulation scientists typically collect data on stress-induced transitions in macromolecular structure under varying solution conditions and in the presence of different excipients. The data analysis is performed utilizing techniques that look at the data locally, such as visual inspection and/or mathematical fitting of thermal unfolding curves to sigmoidal functions. Unfortunately, the global features of high-dimensional data spaces are not always revealed by such local data inspection. A more comprehensive analysis of the complex behavior typically observed is clearly desirable.

We review here the use of a global mathematical analysis technique developed for evaluation of large data sets generated from the biophysical analysis of biopharmaceuticals and vaccines. The mathematical methodology analyzes datasets, finding and quantifying multidimensional regularities that often are difficult to detect with local inspection. The mathematical information is converted into a visual map that serves to better define and investigate structural integrity and conformational stability of biomolecules and macromolecular complexes.

From the dozens of test cases to date, we find that these maps tend to be segmented into regions of distinct structural behavior. We call areas of a single contiguous color on these maps “apparent” phases, and the related diagram an empirical phase diagram (EPD). The word “empirical” serves to distinguish the diagrams from thermodynamic phase diagrams, in which the phase transformations are necessarily reversible. In spite of a common lack of reversibility in many protein transformations, the word “phase” to describe a physically distinctive form of a substance reasonably applies to a pharmaceutical usage, as described in more detail below.

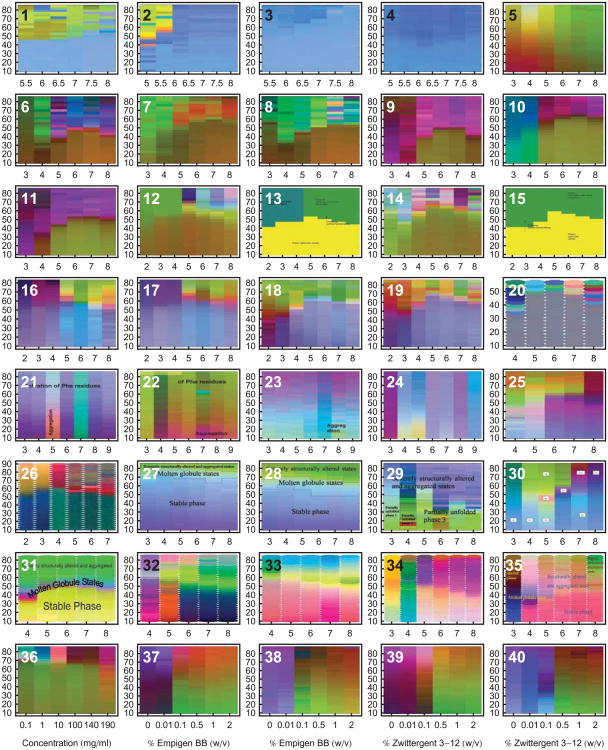
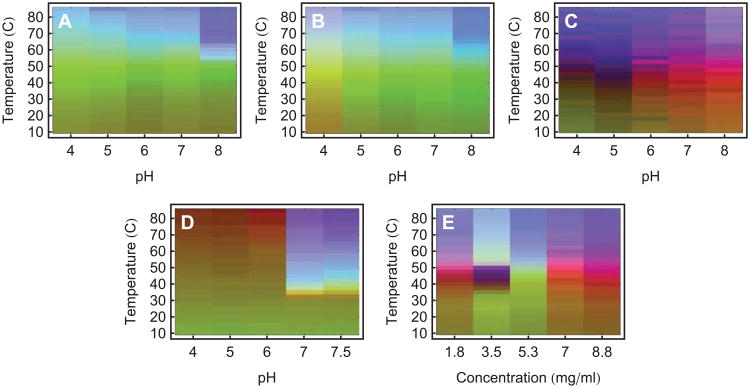
An example is shown in Figure 1 of a representative dataset generated for a monoclonal antibody (IgG1), along with the resulting EPD. Various analytical methods were used to monitor both the structural integrity as well as the dynamic properties of the immunoglobulin as a function of temperature and solution pH.⁴ These data sets are then summarized for analysis in the form of an EPD. This approach has been applied widely by our laboratory to different proteins, plasmid DNA-lipid complexes, virus like particles and viruses. As shown in Figure 2, dozens of EPDs have been generated and published over the past 7-8 years. (Refer to Table 2 for references and more detailed information concerning each EPD. All EPDs in this article have been reformatted for uniform layout.)

Figure 1.

An empirical phase diagram (EPD) assists in the visualization of a data set resulting from the methods listed in Table 1. Figures A-F show measurements of an IgG1 monoclonal antibody collected at pH 3 (black), 4 (red), 5 (green), 6 (yellow), 7 (blue), and 8 (magenta). (A) CD molar ellipticity at 218 nm, (B) UV intrinsic fluorescence (UV-IF) peak position and (C) intensity, (D) tryptophan fluorescence lifetime, (E) static light scattering (SLS), and (F) ANS extrinsic fluorescence (ANS-EF) intensity. Error bars in (A-C and E-F) are from three independent experiments.⁴ Figure (G) shows an EPD based on the above data. Figure (H) shows an EPD based on protein dynamics measurements (data not shown, see the applications section for more information).

Figure 2.

Empirical phase diagrams have found many uses in the optimization of various types of formulations. Many case studies have been published concerning their application to various systems and their extension by the addition of measurement techniques and search space variables. The EPDs in this figure are only from papers published in the Journal of Pharmaceutical Sciences. Many more EPDs have been published in other journals or generated in proprietary studies. Refer to Table 2 for more information concerning each EPD. All EPDs in this diagram have temperature (°C) as the vertical axis. Diagrams 1-35 use pH on the horizontal axis, and diagrams 36-40 have the indicated stress variables on the horizontal axis. All EPDs in this article have been reformatted for uniform layout.

Table 2.

Biomolecules and larger macromolecular complexes, analytical techniques and environmental stress conditions evaluated by empirical phase diagrams. See Table 1 for definitions of the technique abbreviations.

Target	Techniques	Search Space	Figure	Ref.
Measles virus	CD, DLS, SLS, EF	pH, Ta	10	24
Human respiratory syncytial virus	CD, UVAS, OD350, UV-IF	pH, T		25
Live atten. Ty21a bacterial typhoid vaccine	CD, EF	pH, T		29
Adenovirus type 5 (Ad5)	UVAS, DLS, UV-IF, EF	pH, T	2.32, 2.33	26
Recombinant ricin toxin A-Chain vaccine	CD, UF-IF, EF	pH, T	2.20, 2.31	73
Adenovirus type 2 (Ad2)	CD, UVAS, OD350, DLS…	pH, T	2.34	27
Hepatitis C virus envelope glycoprotein E1	CD, DLS, UV-IF, EF	pH, T, Sa	2.37 - 2.40	21
Clostridium difficile toxins and toxoids	CD, OD350, UV-IF, EF	pH, T	8	16
Type III secretion system tip proteins	CD, UVAS, UV-IF, EF	pH, T		14
Type III secretion system needle proteins	CD, UVAS, EF	pH, T		17
Malaria antigen EBA-175 RII-NG	CD, UV-IF, EF	pH, T		15
H1N1 influenza virus-like particles	CD, DLS, EF	pH, T	2.25	22
Norwalk virus-like particles	CD, UVAS, UV-IF, EF	pH, T	9	23
Nonviral gene delivery complexes	CD, DLS, EF	pH, Ia	11	28
Human Inteferon-β-1a	CD, UVAS, UV-IF, EF	pH, T	2.12, 2.19	5
Bovine granulocyte colony stim. factor	UVAS	pH, T	2.26	6
Immunoglobulin-G (IgG)	CD, EF, PPC, HRUS, TRFS…	pH, T	1	4
Pramlintide (antihyperglycemic peptide)	CD, UVAS, OD350, UV-IF	pH, T, Ca	7	7
Monoclonal antibodies	CD, UVAS, OD350, UV-IF	T, C	2.36	8
Clostridium botulinum type A neurotoxin	CD, UV-IF, EF	pH, T		9
Molecular chaperones Hsc70 and gp96	CD, UVAS	pH, T		10
Human fibroblast growth factor 1 (FGF-1).	CD, UVAS, UV-IF, EF	pH, T, S	2.6 - 2.11	11
Fibroblast growth factor 20 (FGF-20)	CD, UVAS, UV-IF	pH, T		12
rPA of B. anthracis	CD, UV-IF, EF	pH, T	2.31, 2.35	13
Recombinant vault particles	CD, UV-IF, EF	pH, T	2.30	18
Recombinant human gelatins	CD, UV-IF, UVAS	pH, T	2.21 - 2.24	19
EC5 domain of E-Cadherin	CD, UV-IF, UVAS	pH, T, N/Ra	2.27 - 2.29	20

^aT = Temperature, I = Ionic Strength, C = Concentration, S = Stabilizer, N/R = Native/Reduced

The EPD method has found many uses in the development and optimization of various types of biopharmaceutical and vaccine formulations. Empirical phase diagrams serve as guides to the interpretation of multidimensional data, determining regularities that may be difficult to visualize otherwise. These data sets are presented in an easy to inspect format, assisting in the determination of protein state and transition points as a function of environmental conditions such as temperature and solution pH. Many case studies have been published concerning not only the application of EPDs to various macromolecular systems, but also their extension by the addition of new biophysical measurement techniques and search space variables. Common pharmaceutical applications have been to aid in selecting stress conditions for excipient screening, finding optimal ranges of stabilizing solution conditions, and investigating the overall physical behavior of large macromolecular complexes. EPDs have been applied to the characterization, stabilization and formulation of proteins,^4-21 virus like particles,^22,23 viruses,^24-27 nucleic acids and their complexes with lipid delivery vehicles,²⁸ as well as whole bacterial cells.²⁹ In principle, one can incorporate almost any kind of information into EPDs, including measurements of structural dynamics, chemical integrity or biological function. Empirical phase diagrams have also been shown to contain information concerning the functional and evolutionary relationships of proteins.^10-12,16,17 These applications will be discussed in more detail below.

The greatest potential application of the EPD method from a formulation development point of view, however, may be to drastically reduce the size of high throughput screening searches to identify stabilizing excipients. The accelerated time-lines of modern drug formulation efforts, and the complexity and size of the search spaces involved, typically result in suboptimal screening.^5,30 The limited procedures available to screen a wide formulation design space can often result in suboptimal formulations or potentially even product failure during long term storage. A brute-force approach would test conformational and chemical stability at every relevant solvent condition. This approach is, however, cost prohibitive because of the exponentially large number of solvent conditions to test. For example, if one tested 5 different excipients at 4 different concentrations each, the number of combinations to test would be 4⁵, or 1024 experiments. The use of empirical phase diagrams permits the size of these high throughput screening search spaces to be reduced in a very natural and pragmatic way. Using EPDs, macromolecule identity has been found to be conserved over contiguous regions of search space. The identification of unique and/or consistent conformational states reduces the search space from an exponentially large and unexplorable one to one that is much smaller yet adapted to the system of interest. More time consuming and extensive excipient screening and analytical characterization tests can then subsequently be performed on the smaller set of conditions to better design and develop optimized formulation conditions.

Experimental Methods

X-Ray Crystallography (XRC) and Nuclear Magnetic Resonance (NMR)

Since these two methods have the potential to determine the full three dimensional structure of macromolecules, they would be ideal were it not for confounding factors. Both methods require costly instrumentation and highly trained support staff. XRC requires the preparation of crystals, which cannot always be grown, and do not necessarily represent structure in the solution state. The experimental procedure typically takes at least days to weeks to optimize and perform. Full structure determination by NMR currently takes a similar length of time, but only works for small to medium size proteins (thus not including monoclonal antibodies). Furthermore, isotopic labeling is necessary for full structural determination. These limiting aspects of NMR may, however, be reduced in the future.^63,64 Both methodologies are also difficult to apply to pharmaceutical dosage forms due to interfering effects of excipients. The goal in the work described here is primarily to find transitions in higher order structure as a function of environmental conditions (e.g. temperature and pH in the presence of different excipients), which requires far less information than that required for full structure determination.

A wide variety of lower resolution biophysical techniques are available for characterization of biomolecules and their macromolecular complexes. In general, these methods can be employed over a wide range of concentrations (from a few micrograms to hundreds of milligrams per milliliter), although interference by factors such as light scattering, absorbance flattening and solute interference can sometimes be a problem. Very brief descriptions of many of these techniques now follow. References and a summary of the capabilities of each method are shown in Table 1.

Near and Far Ultraviolet Absorbance Spectroscopy (UVAS)

Both proteins and nucleic acids contain a number of environmentally sensitive chromophores which absorb in the UV region. While the peptide bonds of proteins display intense absorbance in the far UV (180-220nm) region, thus yielding secondary structure information, analysis in this region is normally done by circular dichroism or FTIR due to their better resolution (see below). In contrast, derivative analysis of protein spectra in the near UV typically provides 5 to 6 well resolved peaks from the three aromatic residues (Trp,Tyr,Phe), which are quite sensitive to structural changes. Nucleic acids also produce distinct spectra from the bases in the same spectral region, which can be used to follow structural alterations. Conveniently, when a macromolecular system aggregates, optical density (OD) in non-absorbing regions (>340nm) can be used to monitor this phenomenon simultaneously with near UV spectral analysis.

Near and Far Ultraviolet Circular Dichroism (CD)

Due to the high optical activity of helical structures, CD can be used to detect changes in both nucleic acid and protein secondary structure in the far-UV region for proteins and mid-UV region for nucleic acids. The optical asymmetry of the environment of the aromatic side chains in proteins also produces distinct signals typically of some complexity in the near-UV region. Thus by monitoring both regions, structural changes in secondary and tertiary structure can be detected. Deconvolution analysis of CD spectral shape in the far UV region also allows fairly accurate estimates (within 2-3%) of actual secondary structure content. The induced CD of certain dyes can also be used to determine structural information, especially with nucleic acids and polysaccharides.

Intrinsic and Extrinsic Fluorescence

The intrinsic UV fluorescence (UV-IF) of proteins is dominated by emission from indole side chains when Trp residues are present and not endogenously quenched. Such fluorescence is very environmentally sensitive, making the peak position and intensity of Trp fluorescence a particularly useful probe of protein structural change. The use of extrinsic fluorescence (EF) probes is applicable to virtually all forms of macromolecules and their complexes, including proteins, nucleic acids, and membranes. For example, dyes are available which are particularly attracted to apolar regions in proteins as well as the characteristic intermolecular β-structures which often form when proteins associate. A wide variety of fluorophores bind both within nucleic acid grooves as well as between bases (intercalation). In addition, there exist a large number of dyes that interact with lipid bilayers such as those present in some viruses and virus-like particles as well as bacterial cells. Some of the most commonly used dyes are 8-anilino-1-naphthalenesulfonate (ANS), used in protein studies; laurdan, used for lipid bilayers; and YOYO-1, used for DNA. In all of the above cases, large changes in fluorescence intensity, peak position, and polarization often occur as these dyes bind to their various targets. Thus, they can be used to probe a plethora of aspects of macromolecular structure and associated changes.

Infrared and Raman Spectroscopy

The complex series of vibrational transitions present in macromolecules can be used to obtain structural information from either infrared or Raman spectroscopy. Infrared spectroscopy is performed almost exclusively in a Fourier transform mode (FTIR). While FTIR is an absorptive technique and Raman is a scattering measurement, both have significant although sometimes different utility. Each can be used to examine the secondary structure of both proteins and nucleic acids (as well as complexes such as viruses) through deconvolution of constituent amide bands (signals from peptide bonds and various nucleic acid base signals). FTIR is the more widely used technique due to instrument availability and sensitivity. In contrast, signals from side-chains tend to be much better detected in Raman spectra.

Static and Dynamic Light Scattering (SLS, DLS)

The size and shape of macromolecules both in their monomeric and associated forms can be characterized by static and dynamic light scattering. In the former, the intensity of the scattered light is measured (often as a function of angle), while in the latter, fluctuations in intensity of scattered light due to Brownian motion are analyzed. Size and shape information obtained are model dependent and complicated by the presence of non-homogeneous scatterers, although various data analysis methods exist to produce useful numerical values from both methods. Imposition of an external electromagnetic field can be used to obtain zeta-potential values. A method we do not discuss here is analytical ultra-centrifugation (AUC). Although AUC is very information rich in terms of evaluating hydrodynamic properties of biomolecules and macromolecular complexes, this methodology is not available in a high throughput mode, unlike the scattering based methods.

Differential Scanning Calorimetry (DSC)

By measuring differential heat capacities in macromolecules, transitions in state can be detected. Virtually every biomolecule from proteins and nucleic acids to membranes and viral particles undergo thermally induced transitions that can be detected by this method and used as indicators of thermal stability. Like the methods described above, DSC is now available in a high throughput mode making it useful for the formulation and stability purposes discussed below.

High Performance Liquid Chromatography (HPLC)

Although not generally adaptable to a high throughput mode in the sense of the above methods (i.e. one cannot easily and rapidly perform measurements over a wide range of pH and temperatures), the use of auto-samplers does permit a variety of chromatographic methods to be used after exposure to a wide range of conditions. Probably the three most useful to the formulation scientist are size-exclusion (SEC), ion-exchange (IE), and reversed phase (RP) chromatography. All three methods will be well known to most readers so we just mention their applicability to size, charge, and polarity changes, respectively. To characterize chemical degradation (oxidation, deamidation, hydrolysis, etc.), RP-HPLC is commonly used in combination with fragmentation and mass spectrometry to characterize sites of covalent alteration. Methods such as capillary isoelectric focusing are also commonly used for this purpose.

Measurements sensitive to intramolecular dynamics

It has become increasingly apparent that macromolecular stability is dependent on the various types of internal molecular motions present in macromolecular systems, such as side-chain movements, breathing modes, domain motions, etc. Thus, measurements of such motions should ultimately be included in a thorough analysis of stability. A number of methods are available for this purpose, and can sample a wide range of such motions. Methods specifically designed for this purpose such as isotope exchange and various forms of NMR are not generally applicable to high-throughput applications, although this may change in the future. In contrast, a number of high-throughput methods are available, including ultrasonic spectroscopy (to measure compressibility), pressure perturbation DSC (to measure coefficients of thermal expansion), as well spectral approaches such as temperature induced pre-transition peak shifts in second derivative UV absorbance spectra, fluorescence anisotropy (rotational correlation times), red-edge fluorescence excitation, and fluorescence and UV absorbance solute-induced spectral shifts.

Multi-mode Machines (“Protein Machines”)

Instruments are currently being developed by several vendors that simultaneously collect data using several of the above methods. For example, the Chirascan from Applied Photophysics collects near and far UV CD and near and far UV absorbance. Fluorescence emission spectra can also be collected, although not simultaneously with the other techniques. The Protein Machine from Olis Instruments collects far UV CD, near UV absorbance, fluorescence emission and excitation spectra, and red-edge excitation spectra. Both instruments can also acquire light scattering signals during several of these measurements.

Simultaneous near and far UV measurements require intermediate path lengths and concentrations. In the far UV region, peptide bonds yield very strong absorbance. Longer path lengths or higher concentrations produce excess absorbance, causing absorbance flattening in far UV measurements. To avoid absorbance flattening in this region one must use short path lengths or low concentrations. The near UV absorbance spectra of aromatic residues are comparatively weak, so short path lengths or low concentrations yield too little signal, resulting in a significant amount of noise in near UV measurements. It is not possible in principle to find an optimum tradeoff between path length and concentration, because both have the same effect on absorbance. Changing slit widths can overcome these problems to only a very limited extent. Thus, the existence of conflicting requirements makes it technically difficult, but not impossible, to simultaneously collect data in the near and far UV regions. Nevertheless, these instruments do permit simultaneous collection of data from multiple techniques with good to excellent resolution. In combination with multiple sample holders, EPDs can be obtained directly from such instruments over periods of 3-12 hours.

Currently, the only way to simultaneously collect data in the near and far UV is to use very long integration times in the near UV, to reduce excessive noise. These long integration times offset the time saved by simultaneous collection. Short of waiting for instruments with lower noise to be developed, there is at least one possible option to be considered: variable path length cells would permit automatic adjusting of absorbance for each wavelength range. This feature is available in a few UV-Vis absorbance instruments built for measuring concentrations, and could potentially be applied to multi-modal spectrometers.

Data Interpretation Challenges

One accumulates a wealth of data when several of the above methods are employed under varying environmental conditions. Figure 1A-F shows one of these data sets for an IgG molecule.⁴ Data were collected as a function of temperature and pH, from pH 3 to 8 at one pH unit increments (6 different conditions), and temperatures from 20 to 90°C at 2.5°C intervals (29 different conditions), resulting in a 6×29 assay grid. At each point on this grid, measurements were taken of CD molar ellipticity at 218 nm (Panel A), intrinsic fluorescence peak position and intensity (Panels B and C), tryptophan fluorescence lifetime (Panel D), static light scattering (Panel E), and ANS fluorescence intensity (Panel F).

The data set shown in Figure 1A-F presents challenges as well as opportunities. Traditionally, we look for evidence of conformational changes, unfolding, and aggregation, then estimate transition temperatures. This approach suffers three major drawbacks. First, experimental methods sometimes disagree on transition temperatures and protein state. Second, plots like Figure 1A do not convey much information to the non-expert. Third, important variations and/or regularities in the data may not carry through to the final analysis when they are unexplained, too complex to easily observe, or partially hidden by noise.

Each experimental technique provides a picture of one or more different aspects of a protein or other macromolecular system. The formulation scientist must assemble this information into an overall picture of the behavior of the protein. The situation is similar to the tale of the blind men and the elephant (e.g., “The Blind Men and the Elephant: A Hindu Fable”, a poem by John Godfrey Saxe), where the macromolecular drug is the elephant, and the experimental methods are the blind men touching different parts of the elephant (tusk, trunk, ear, tail, etc). The formulation scientist is the one who must assemble the information from the others and decide what the elephant looks like. When experimental methods disagree, the formulation scientist must make an educated guess. Sometimes even a single method will report conflicting information, as when transition temperatures between folded and unfolded conformations of a biomolecule differ for measurements from two different wavelengths during the same circular dichroism temperature melt experiment.

Although each experimental method is sensitive to different aspects of protein behavior, different methods often provide overlapping information as well. This manifests itself as regularities in the combined data sets. One would not expect these regularities to always be easily visible in data such as that shown in Figure 1A-F. In these plots we show the results from six biophysical methods to monitor the higher order structure of an IgG molecule as a function of pH and temperature. Similar experiments can generate even larger data sets with many more instruments and/or environmental conditions. To find the regularities, we would need to find patterns in a high dimensional space. This is not possible in the simple plots of Figure 1A-F. An empirical phase diagram of the data in Figure 1A-F is shown in Figure 1G (Figure 1H will be discussed in the applications section). The red region of Figure 1G tells us that high temperature behavior is clearly different between low and high pH (pH values above 4). Inspecting the data, the distinction appears to be subtle and complex, but the EPD shows us that in the multidimensional space, the difference is actually pronounced. Furthermore, focusing on measurements at pH 3 (shown in black), we see that the positions of transitions near 40°C are not well defined. On the phase diagram, the transition is sharper and positioned near 40°C.

Formulation scientists must often resort to educated guesses when further information is hidden in the complex data sets generated from a series of measurements.EPDs use the results of a global analysis, increasing the use of information and reducing the role of guesswork. Such plots present the results in a simple format, so the eye of a non-expert can pick out regularities and transitions with little difficulty.

Mathematical Methods

Search space, protein phase space, and measurement phase space

To better understand the mathematical aspects of generating empirical phase diagrams, we first review terms and concepts that arise naturally from the quantitative characterization of large data sets. Each mathematical term can be made as formal as desired, which we avoid here. Instead, our emphasis is on conveying relevant concepts by using precise mathematical terms in a manner as informal and pictorial as possible.

Search space

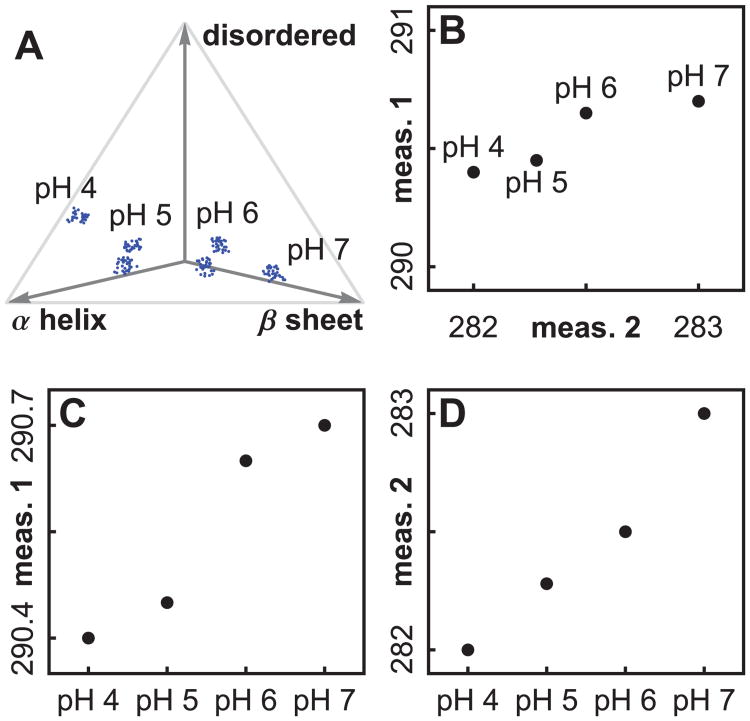
The seach space is defined by the experimental control variables. One may use virtually anything as a control variable, such as concentrations of excipients, temperature, pH, or variables describing protein history. We cannot test every point in the space, so one usually forms a grid of points to test. We will call this the “search grid”. The terms “search space” and “search grid” are borrowed from the field of protein crystallization. In Figure 3A, a one dimensional grid has been chosen consisting of 4 pH values. If we had varied both solution pH and temperature, we would have needed two variables to define the solvent state, and we would have tested points in a two dimensional grid (as will be discussed later in Figure 6A).

Figure 3.

An illustration of three types of spaces, using simulated data. In Figure (A), four pH values define a one dimensional search grid in search space, and ratios of secondary structure type illustrate a protein phase space. Figure (B) shows how two measurement types define a measurement phase space. The transition pH values disagree when we plot measurements separately, as in Figures (C) and (D). A plot in measurement phase space (B) synthesizes the information, but will not work as a visual aid for high dimensional data.

Figure 6.

Illustration of the steps in the Empirical Phase Diagram method, using simulated data. (A): Choose a search space and a search grid. In this case, the search space is 2 dimensional, varying temperature and pH. In each dimension, two values have been chosen, forming a grid. (B): Collect data at each point of the search grid. The data in this example is 5 dimensional. (C): Standardize the data and project it into 3 dimensions. (D): Rescale to the range (0,1), and express as a color. (E): Transform the colors into an image.

Macromolecule phase space

The state of a target biomolecule or macromolecular complex can be described by a list of numbers. For example, we can use a long list of the positions of all the atoms in a protein.⁶⁵ If we consider each list as a point in a high dimensional phase space, then changes in protein shape equate to movement of the corresponding point in phase space. In Figure 3A we have illustrated a protein phase space with ratios of secondary structure. An exhaustively complete protein phase space would require thousands of variables to completely describe a protein state.

Preferred molecule states correspond to equilibrium points caused by energy minima in phase space. Due to thermal vibrations, the molecular states fluctuate around these energy minima, and can be visualized as a cloud of points around each minimum, usually described by a Boltzmann distribution^56,65,66.

For a given solvent condition, there can also be more than one accessible stable protein state, due to the existence of multiple minima in the protein energy landscape.⁶⁵ Instead of a single cloud of points for the given solvent condition, there may be several (see Figure 3A, pH 5 and 6). When we collect spectroscopic data, we see the average of the contributions from all the protein states.

Measurement phase space

This space is defined by all of the measurements used to probe a macromolecular state. For example, in Figure 3B we show how 2 measurements define a 2 dimensional measurement space. If we collect CD data at 3 wavelengths and UVAS data at 2 wavelengths, we can join these into a single 5 dimensional vector (as will be discussed in more detail later; see Figure 6B).

The measurements in a data set contain information generated by multiple physical processes. The types of information derived from these physical processes possess varying levels of prominence in the data. Some stand out on their own, while others require extensive processing to isolate.

We also attribute varying levels of significance to the different types of information. For example, for formulation purposes, information concerning aggregation is highly significant, while information concerning protonation may be less so.

Since the data are generated by physical processes, one cannot expect prominence to be related to significance. Thus, data usually require a certain amount of preprocessing.

Data preprocessing

Data preprocessing steps are designed to extract significant information from data in which it may be hidden in complex ways amid less important information. Preprocessing usually consists of finding the position, width, or intensity of spectral or calorimetric peaks, using methods such as second derivative processing, Fourier self deconvolution, or determination of the spectral center of mass. Another preprocessing practice is the hand-selection of data that is deemed to be pertinent, information rich, and sufficiently free of noise.

For example, the simulated data in Figure 3B is similar to preprocessed data from near UVAS second derivative peak position analysis. A spectrum would have been collected and preprocessed for each pH value, yielding the positions of several peaks. Selection of two of the peaks would have resulted in a data set like the one plotted in Figure 3B.

Typically, on the order of ten measurements remain after preprocessing. It is best to not overdo preprocessing, which may erase information about transitions. Preprocessing constitutes a bias concerning the significance of types of information, so it must be applied judiciously. An example of extreme preprocessing would be to take an FTIR absorbance spectrum measured at 3000 frequencies and reduce it to a single frequency. The global analysis we will describe is capable of finding optimal low-dimensional representations of high dimensional data, and tends to perform better when a large number of measurements are used.

Data standardization

Preprocessing results in a collection of numbers that cannot be expected to have appropriate units, scales, or dimensions. The units of most data are standardized by scientific and engineering conventions that have no relation to their significance for formulation development. For example, fluorescence emission photon peak counts of proteins tend to range from 10⁴ to 10⁶, but absorbance values tend to be kept below 1 AU. The scale of data must be adjusted so that artificial unit conventions do not cause one type of data to overwhelm another. Furthermore, mathematics alone does not contain knowledge of formulation, so it cannot in principle determine the scale choices, preprocessing, and standardization that will lead to useful summaries. Perhaps surprisingly, once these choices are made by the user, mathematics can determine optimal low dimensional representations of data. Fortunately, the adjustment of scale variables is straightforward as described below and rather robust outcomes are not difficult to obtain.

We now discuss an example of the influence of scales on estimates of transition values. Figures 3C and 3D illustrate how measurements can disagree on the position of transitions. Plotting the measurements separately, measurement 1 (Figure 3C) shows a transition between pH 5 and 6, but measurement 2 (Figure 3D) shows a transition between pH 6 and 7. The two dimensional plot (3B) shows the largest transition between pH 6 and 7. Measurement 2 dominates the two dimensional plot since that peak's variation stretches over a larger range.

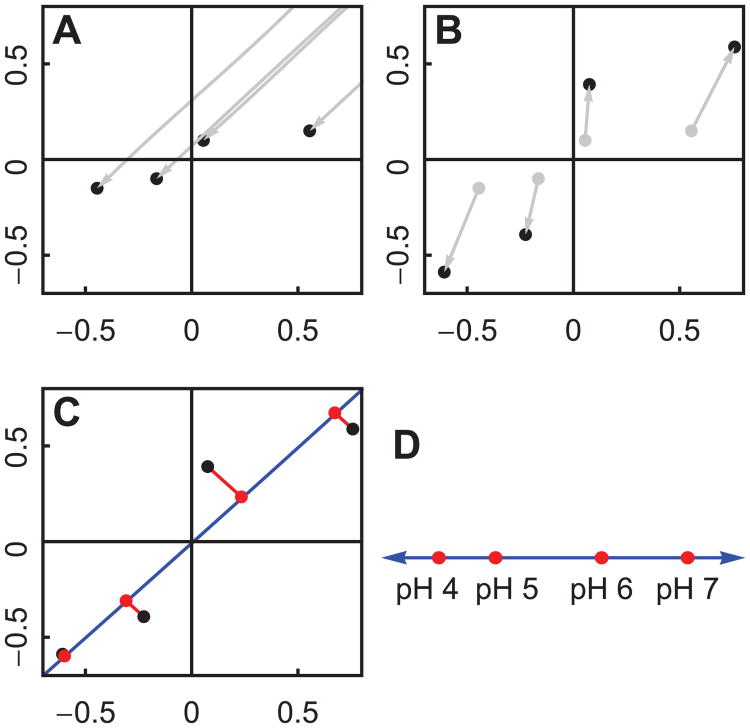
Our current approach to resolving the conflict is to resize the variation in each measurement so that they have equal magnitude. There are many ways to do this, and we show only one of them. Since we are only interested in transitions, we begin by centering the measurements at the origin by subtracting the mean measurement within each measurement type (Figure 4A). This is done separately for each measurement type. Then we can normalize each measurement to equalize their variation (Figure 4B). This is also done separately for each measurement type. We see in Figure 4B that the largest transition occurs between pH 5 and 6.

Figure 4.

Principal Components Analysis can be used to project two dimensions into one. The procedure works the same way for high dimensional data (see Figure 5 and 6). We will use the simulated data shown in Figure 3B. (A): First we center the measurements at the origin, since we are interested in transitions, not average values. (B): Next we normalize each measurement so that they have equal influence on the result. (C): Finally, we use the Singular Value Decomposition (SVD) to find the optimal line for projection (shown in blue). (D): If we plot the position along the blue line, we see that the difference is greatest between pH values 5 and 6.

Singular Value Decomposition

Once the data has been processed and standardized, we seek a way to visualize and inspect it. Since the data set is high dimensional (usually around 10 numbers per search grid point) the human eye cannot find its patterns. Humans prefer two-dimensional diagrams. Thus, a method is required to lower the dimensionality of data for visual representation.

Hypothetically speaking, if humans could only perceive one dimension, we would want to represent the data in one dimension while preserving the information content as much as possible. A standard way to reduce the dimensionality of data is called the Singular Value Decomposition (SVD). Figure 4C conceptually illustrates the result of applying SVD to a data set. We begin with points in a 2 dimensional space (the black dots), and we seek to project the data onto an optimal 1 dimensional space. The term “optimal” is defined by minimizing the projection error, indicated by the red lines. SVD gives us the optimal 1 dimensional space, shown as a blue line. This is still, however, a 2 dimensional plot. For a 1 dimensional plot, we can plot the distance along the blue line (the position inside the 1 dimensional space). This is shown in Figure 4D.

The entire procedure we use to project data is known as Principal Components Analysis (PCA). PCA consists of subtracting the mean from a data set and applying SVD. These steps are shown in Figure 4A and 4C. The extra step of normalizing the measurements, shown in 4B, is a known extension to PCA.

We illustrate higher dimensional SVD with another simple example (Figure 5). Some familiarity with linear algebra will assist the reader, but the following discussion should also be accessible to a general audience. Suppose we are given the following measurements of a protein at different temperatures.

Figure 5.

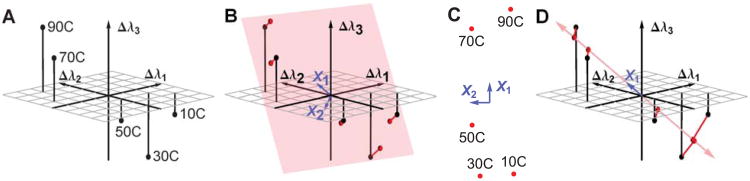
An example of the Singular Value Decomposition (SVD) using simulated data. (A) is a plot of three simulated peak shifts Δλ₁, Δλ₂, and Δλ₃ as a function of temperature. If we could perceive two dimensions but not three, the transition between 50°C and 70°C might be difficult to see. Therefore, we would want to reduce the data to two dimensions in a way that optimally retains the information in the original data set. (B) shows the plane (in pink) which gives the optimum 2D projection. This plane is determined by SVD, and is defined by the vectors X₁ and X₂(in blue). The projection error is shown as red lines. (C) is a 2 dimensional plot of the same data, using the positions within the pink plane. This is a plot of matrix A (see text). (D) shows the optimal one dimensional projection, demonstrating that the error is larger. This plot uses the first column of matrix A (see text).

	Δλ1	Δλ2	Δλ3
10°C	3	−2	−1
30°C	2	−1	−3
50°C	0	−1	−1
70°C	−3	1	2
90°C	−2	3	3

For instance, the data might represent second derivative ultraviolet absorbance peak shifts in hundredths of a nanometer.

A plot of this data is shown in Figure 5A. Each row is plotted as a point in three dimensions, and each point corresponds to a different temperature. The data is three dimensional in the sense that at each temperature we have three numbers, Δλ₁, Δλ₂, and Δλ₃, which represent the state of the target molecule.

If we could perceive two dimensions but not three, the transition between 50°C and 70°C might be difficult to see. So we would want to reduce the data to two dimensions in a way that optimally retains the information in the original data set. To see how to do this, refer to Figure 5B. The black points are the data points, and the pink area represents a plane. The red points are the positions within the plane that are nearest to the data points. They are two dimensional approximations to the data points. The red lines represent the error in the approximation. We seek the plane which minimizes the total error, defined as the sum of the squares of the lengths of all of the red lines.

To show how this works, we first express the data as a matrix:

$$D=\left(\begin{array}{ccc}3& -2& -1\\ 2& -1& -3\\ 0& -1& -1\\ -3& 1& 2\\ -2& 3& 3\end{array}\right)$$

SVD finds an optimal, unique two dimensional approximation, which we will call D̃

$$\stackrel{\sim }{D}=AX$$

$$=\left(\begin{array}{cc}-3.5& -1.2\\ -3.6& 0.46\\ -1.1& 0.85\\ 3.6& 0.88\\ 4.5& -1.0\end{array}\right)\left(\begin{array}{ccc}-0.63& 0.48& 0.61\\ -0.77& -0.28& -0.57\end{array}\right)$$

(For readers familiar with the terms, we note that the matrix A consists of the left singular vector matrix multiplied by the singular value matrix, and retains only the top 2 singular vectors. We have done this to simplify the presentation. For a summary of the properties of SVD, see the appendix.)

The two rows of the matrix X are perpendicular to each other. In Figure 5B, the two rows of X are represented as blue vectors. They are axes in a two dimensional plane (shown in pink), and serve to define that plane. This plane is the unique plane that minimizes the total error. When we perform the matrix multiplication AX, each row of A specifies a linear combination of the rows of X. The matrix multiplication places the approximated data points within the plane defined by the row vectors of X.

In this example, SVD actually returned three optimal axii and we have chosen and shown only the two most important ones (the two rows of X, shown as blue vectors in Figure 5B). When we choose optimal axii to define the lower dimensional space, we generally discard the other axii returned by linear algebra. If we had used only the first row of X, we would have approximated the data within a one dimensional space (Figure 5D). In that case, the error would have been larger. (On the other hand, the optimal one dimensional axis may well encompass most of the data, depending on the relative magnitude of the singular values.)

When we use all of the axii given by SVD, there is no error, and the approximation D̃ is equal to the original matrix D. Error results from excluding axii, as we have done in Figures 5D and 5B. If we exclude axii that only result in a small increase in error, the approximation D̃ can be very close to the original matrix D.

For many data sets, the most common result is that only a few of the axii are important, resulting in a large increase in error when they are dropped. The rest of the axii can usually be eliminated with very little effect on the approximation. We can choose in advance the number of axii to use. In this example, we have three dimensional data that we want to reduce to two dimensions. We can minimize the error for a two dimensional projection by using the two most important axii returned by SVD.

Since we want a true two dimensional representation of D, it is self-consistent to use the positions within the optimal plane instead of the three dimensional positions. The two dimensional positions within the plane are given by the matrix A, and are plotted in Figure 5C. Each point in Figure 5C represents a row of A.

The error in the approximation from D to D̃ can be defined numerically. It is the sum of the squares of the lengths of all the error vectors (the red lines in Figure 5B). This is the error that SVD minimizes. It can be expressed as

$$\sqrt{\sum _{i=1}^5\sum _{j=1}^3{|D_{ij}-{\stackrel{\sim }{D}}_{ij}|}^2}$$

To quantify how well the data has been approximated we compute the percent error, defined as:

$$E(D,\stackrel{\sim }{D})=100\times \frac{\sqrt{\sum _i\sum _j{|D_{ij}-{\stackrel{\sim }{D}}_{ij}|}^2}}{\sqrt{\sum _i\sum _j{\left|D_{ij}\right|}^2}}$$ (1)

It is important to note that the procedure gains its power from the fact that it works the same way in higher dimensions. Instead of three peak shifts, as in the previous example, we might be given 5 measurements at each temperature. These are vectors in a five dimensional space. After standardization, we apply SVD to the matrix of data, returning up to 5 axii. The most significant axii are then used to define a lower dimensional space. The projection onto that space is the best possible approximation to the data that can be made based on the number of dimensions retained. Just as in the example above, the approximated matrix still appears high dimensional. Yet we can get a true low dimensional view of the data by using the data point positions within the space defined by the retained axii (as illustrated for two dimensional projections in Figure 5C).

The Empirical Phase Diagram

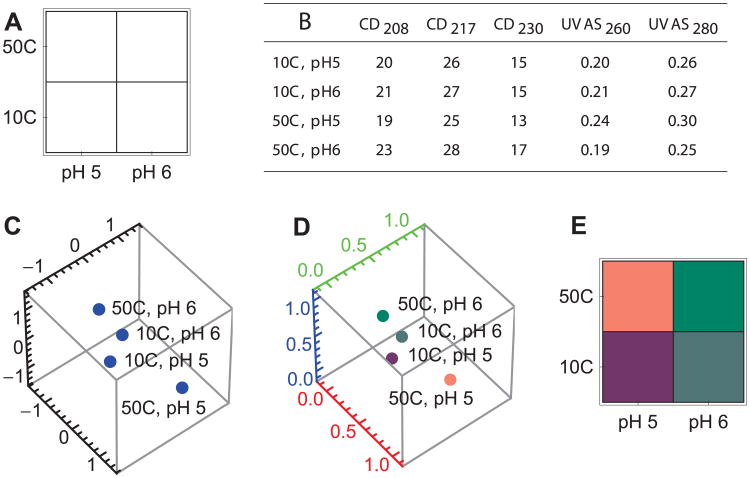
We begin by choosing a search grid (Figure 6A). The most common search grid previously used for protein phase diagrams covers pH values from 3 to 8 in one pH unit increments and temperatures from 10 to 85°C in 2.5°C increments. Measurements typically include a series of biophysical techniques such as CD, fluorescence, and UV absorbance spectroscopy as well as light scattering. In this simulated example, we choose a simpler case of two pH values (5 and 6) and two temperature values (10°C and 50°C) as measured by CD (at 3 wavelengths) and UVAS (at 2 wavelengths).

After collecting and preprocessing the data, a matrix is created in which the rows correspond to all search grid positions and the columns correspond to all measurement types (Figure 6B). The matrix is standardized and projected down to 3 dimensions (as described in the previous section). The result of standardization and projection is shown in Figure 6C. The number of rows remains the same but the number of columns has been reduced to 3.

To provide a convenient visual image, the resulting 3 dimensional positions are converted into ratios of red, green and blue color. First the data is shifted and resized so that all the numbers fit in the range (0,1) (Figure 6D). Then the 3 dimensional positions are expressed as colors. To create the phase diagram, the colors are reorganized into a grid and plotted (Figure 6E).

History

It should be mentioned that the singular value decomposition is attributed to the mathematicians Beltrami and Jordan, who discovered a version in the 1870's. The physicist Carl Eckhart is credited with extending the procedure to non-square matrices. It seems to have been re-discovered many times, and is sometimes associated with Householder and Karhunen-Loeve⁶⁷.

A technique similar to our procedure was used in 1989 to merge satellite imagery.⁶⁸ It is called “PCA based image fusion”, is widely employed in geo-sensing and in-vivo imaging,^69,70 and is spreading to other areas such as art conservation and astronomy.^71,72 Unaware of this history, we first applied PCA in 2003 to characterize transitions in higher order protein structure under different environmental stresses⁶.

Interpreting Empirical Phase Diagrams

Once the empirical phase diagram has been generated, the mathematical work is done. What remains is interpretation. The first step is to inspect the phase diagram to determine regions of conserved structure. Areas of search space that produce similar measurements in the abstract 3-dimensional space manifest themselves on the phase diagram as areas of a single contiguous color. Transitions are then manifested as changes in color, with noise showing as irregular and often quite subtle color variation. When clear structural transitions are not evident, the phase diagram can be dominated by effects unrelated to the higher order structure of the target macromolecule, such as a decrease in absolute fluoresence intensity with rising temperature.

Once the EPD has been inspected to determine regions of conserved structure, one tries to determine as much as possible about the actual physical state of the protein or macromolecular complex within those regions. To do this, one must refer to the original measurements and consider the physical processes that generated them. To reiterate, the best one can hope from quantitative analysis is optimal projection, which still needs expert scientific evaluation of the original biophysical data, and perhaps further targeted experimentation. By referring back to the source data, empirical phase diagrams can usually be segmented into the following types of structure: low temperature inactive, active form, molten globule states, high temperature or acidic pH unfolded forms, and forms which are aggregated or dissociated to various extents. Sometimes, however, a region of an EPD may have no ready interpretation, indicating that the data and mathematics have found something the expert does not readily recognize.

The color of an area is itself a “code”, not universally meaningful information. To get an idea of why this is, refer to Figures 5B and 5C. PCA gave the two vectors X₁ and X₂, defining a plane for the optimal two dimensional projection. An entirely different data set projected into 2 dimensions will also give an optimal plane whose absolute orientation relative to the first cannot be known without comparing the sets with each other. Thus, two different meanings can (and generally will) be applied to a given color code. This is not a matter of much concern, because the color code is not actually used in a quantitative analysis. The colors serve no purpose other than to identify areas of different behavior. One might just as well have labeled contiguous regions with names or numbers, as in traditional thermodynamic phase diagrams.

While the results of PCA are unique for any given data set, small changes in a data set can sometimes result in rotation of the principal axii. That will occur when two large, important singular values are nearly equal. Then distinguishing them by size-ordering can hinge on small variations. The result of swapping the order of axes is a swap of two colors. The shapes of the regions and transitions will, however, remain the same, because the projection plane in question is an absolute concept that does not depend on the labeling. Notice in Figure 5C that a deliberate rotation of X₁ and X₂ does not alter any information about the transition.

In a study of Clostridium difficile toxins and toxoids, discussed below, phase diagrams were generated jointly to achieve uniform meaning of their colors.¹⁶ In such an analysis, the target macromolecule becomes one of the control variables. For example, if the control variables had been pH and temperature, they will now also include the target macromolecule. The matrix shown in Figure 6B will contain additional rows to incorporate the increased number of combinations of control variable positions. The matrix is then standardized, projected into 3 dimensions, rescaled, and interpreted as colors, as shown in Figures 6C and 6D. Finally, the colors are made into multiple phase diagrams, one for each target macromolecule.

Applications and Case Studies

Here we summarize some applications and case studies using empirical phase diagrams to formulate and stabilize various biomolecules and larger macromolecular complexes. As highlighted earlier, common pharmaceutical applications have been to select stress conditions for high throughput excipient screening, to find ranges of solution conditions resulting in optimized stability, and to investigate the overall structural integrity and conformational stability behavior of large macromolecular complexes.

Selection of stress conditions for excipient screening

Screening compounds and polymers for stabilization of a liquid formulation of a biomolecule or macromolecular complex is a time consuming process due to both the large number of excipients that should be tested, and the time it takes to complete each test. The latter can be reduced by selecting conditions which accelerate degradation processes (although the danger always exists that the degradation reactions induced may not be directly relevant to actual storage conditions). The EPD approach can be used to select these accelerated conditions. Since each region of color in an EPD represents a different state of the system, it is presumably related to a local minimum in the energy landscape. Thus, at transitions between these regions, the system may have a somewhat higher energy and be farther from equilibrium. This makes it more likely (but not guaranteed) that the system can access other minima in the energy landscape under these conditions. By selecting transition conditions within pharmaceutically accessible regions, it seems probable that relevant degradation mechanisms during real time storage will be enhanced under these accelerated conditions. This basic concept has been applied to many formulation projects with significant success as described below, and is a commonly used general assumption in pharmaceutical preformulation and formulation efforts.

Finding stabilizing conditions

By the same argument, we can also find stabilizing solution conditions (e.g. pH and ionic strength) for a liquid formulation by selecting conditions distant from EPD boundaries. More routinely, EPDs have assisted in the more standard stabilization and formulation process, in which one finds solution conditions that increase stability as measured by the elevation of thermal unfolding/melting temperatures or reduction of aggregation^24,73.

Using EPDs to investigate the similarity of two proteins

In the construction of EPDs, we perturb the system by varying solution conditions such as temperature, pH, and ionic strength, while measuring the system's response. Rather than focusing on transitions, we can also use an EPD in its entirety to gain additional information about the identity of the system's native form. We have found that EPDs of proteins of similar function do indeed appear similar.^10-12,16,17 For example, the two heat shock proteins Hsc70 and gp96 have very little sequence homology, but demonstrate apparent phase changes in their EPDs which are nearly identical¹⁰.

Investigating protein dynamics

The intramolecular mobility of large molecular systems is a critical factor in their behavior, and a role in molecular recognition and enzymatic catalysis is now generally recognized.^74-77 The relationship of the dynamic behavior of such systems to their stability remains, however, poorly understood.⁵⁵ In this regard, EPDs have been employed to characterize the intramolecular dynamics of an IgG1 monoclonal antibody on a temperature-pH perturbation grid.⁴ This study employed measurements sensitive to protein dynamic motions such as molecular tumbling, domain movement, and the degree of solvation. A combination of the following measurements was used: adiabatic compressibility determined from PPC, coefficient of thermal expansion determined from HRUS, REES, and rotational correlation times determined by TRFS anisotropy (see Table 1 for instrument abbreviations). An EPD was also generated based on the following time averaged methods: steady-state UV-IF, far-UV CD, light scattering, and ANS-EF. The latter methods are sensitive to alterations in protein secondary and tertiary structure. The EPDs from the dynamic and static measurements are shown in Figures 1G and 1H, respectively. In both EPDs, a very different conformational state was observed at pH values 3 and 4. The EPD based on the dynamics measurements is more complex overall, with low temperature events seen that are not present in the static EPD. This study indicates that measurements of protein dynamics potentially provide a more sensitive probe of protein stability and the effect of potential stabilizers. Related approaches are under further development in our laboratories.

Evaluating a Peptide Drug (Pramlintide)

The EPD method has not yet been used with small molecule pharmaceutical drugs, but it has been employed to characterize peptides. An analogue of amylin, the 37-residue peptide Pramlintide is currently used as an antihyperglycemic agent to treat diabetes. This peptide was characterized using a combination of CD, intrinsic Tyr fluorescence, second derivative UV absorbance, and optical density as a function of pH, temperature, and peptide concentration.⁷ Despite the fact that the data shows that the peptide is primarily unstructured at low concentration (confirmed by isotope exchange NMR), the EPDs are still surprisingly complex with distinct pH and temperature dependence reflecting very gradual structural alterations and some limited aggregation (Figure 7A-C). When the characterization was conducted over a wide range of Pramlintide concentrations, much more distinctive changes in color were observed with transitions shifted to much lower temperatures and a narrower range of pH (Figure 7D-E).

Figure 7.

Empirical phase diagrams(EPDs) of the peptide drug pramlintide at low and high concentration,⁷ and concentration dependence at pH 4. Low concentrations (0.088 mg/ml) are represented in A-C. The experimental techniques used to construct A-C were as follows: (A) second derivative UV absorbance peak shift and OD₃₅₀, (B) same as (A), adding fluorescence intensity and peak shift, (C) same as (B), adding the CD change at 204 nm. The peptide at high concentration (8.8 mg/mL) is represented in (D), using the same experimental techniques as (B). An EPD at pH 4 as a function of peptide concentration is shown in (E), using the same experimental techniques as (B).

Investigating the behavior of larger macromolecular complexes

The EPD approach enables visualization of high dimensional data, assisting in the determination of regularities and transition points. For the EPD approach to work, only two conditions are necessary, including that the system under study possess a well-defined structural identity, and that transitions in this identity are manifested in the data. A complete physical understanding of the processes governing the transitions is not necessary.

For example, viruses, virus like particles (VLPs), carbohydrate-conjugates, gene delivery vehicles, and other related macromolecular complexes have defined shapes, sizes, structural features and stability profiles. With selection of appropriate techniques, transitions in structure will be manifested in the data as multidimensional transitions in the measured values. These transitions can reflect significant structural changes that may be associated with changes in biological activity.

Signals obtained from such large systems, however, are the sum of signals from many subsystems which are themselves large. Thus, unlike smaller biomolecules such as purified proteins, it is unlikely that one will be able to directly relate the changes seen to actual molecular events in these larger macromolecular complexes. It may well be, however, that the experimental signals observed are due to subsystems that are present in multiple copies, and therefore reflect stress induced changes in key components of the complexes (for example, many copies of a viral coat protein within an intact virus.) Thus, such EPD data may still be quite useful in characterization studies. The EPD approach has, in fact, been applied successfully to the development and stabilization of numerous vaccines, including live attenuated bacterial vaccines,²⁴ inactivated and live viruses and VLPs,^{21-23,25-27,29} as well as gene deliver complexes^28,35.

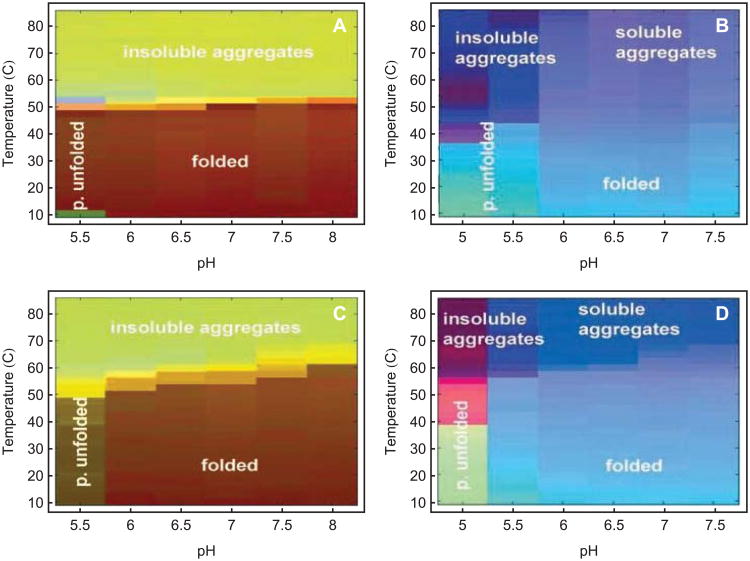
Clostridium difficile Toxins and Toxoids

To further describe the EPD approach, we present a few representative examples of applications to biopharmaceutical drugs and vaccines based on proteins and larger macromolecular complexes. For example, studies using the EPD method were conducted of the A and B toxoids of Clostridium difficile, which are in clinical trials as a diarrheal vaccine.¹⁶ The proteins were characterized with CD, intrinsic and extrinsic (ANS) fluorescence, optical density, UV absorbance, and DLS. Clearly defined regions corresponding to folded protein, partially unfolded states as well as both soluble and unsoluble aggregates are observed (Figure 8A-B).¹⁶ Differences in EPDs are seen when the two toxins are crosslinked with formaldehyde to produce toxoids for use as vaccines (Figure 8C-D) including enhanced thermal stability. Further utility of EPDs is illustrated by their use in pre-formulation characterization studies of the toxoid. Based on the apparent phase boundaries observed in the initial studies, a high throughput screening study was developed based on thermally induced aggregation of the proteins at low pH. A collection of 30 GRAS compounds was then screened and a number were identified which inhibited aggregation. To differentiate effects on conformational stability and aggregation, the proteins were also studied with spectroscopic methods in the presence of presumptive stabilizers. Finally, stabilization studies of the toxoids on the surface of an aluminum salt adjuvant were conducted using DSC. Thus, a series of stabilizers were identified which were successfully employed in final formulations of a candidate C. difficile vaccine.

Figure 8.

An empirical phase diagram for two toxins and toxoids of Clostridium difficile, created using OD₃₅₀, UV-IF, ANS-EF, and CD data.¹⁶ Data were normalized simultaneously for the corresponding toxin and toxoid. (A) Toxin A; (B) Toxin B; (C) Toxoid A; (D) Toxoid B.

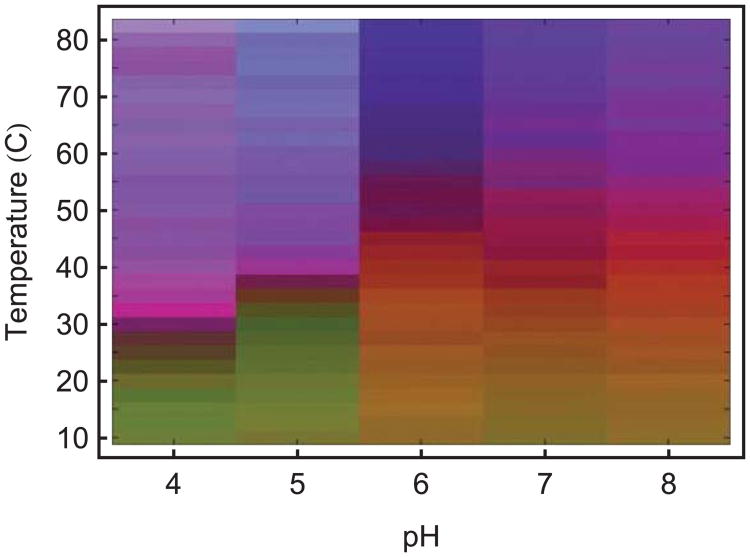
Norwalk Virus-like Particles

Multimeric biocomplexes can also be analyzed by use of EPDs. The most successful recombinant protein vaccines are, in fact, of the virus-like particle (VLP) type (i.e. Hepatitis B vaccine, HBV, and the human papillomavirus vaccine, HPV). One recent example of a candidate vaccine based on VLP technology is that of the Norwalk virus. This VLP consists of an icosahedral assembly of 180 copies of the VP1 capsid protein of the native virus with only a few copies of the VP2 protein also present. The resultant 38 nm particle was characterized by a combination of CD, DSC, intrinsic and extrinsic fluorescence, near UV absorbance and DLS, as a function of pH and temperature.²³ A series of apparent phases could be identified in the EPD corresponding to a variety of conformational and aggregative states (Figure 9), including various states of dissociation of the particles. The precise nature of the latter was established by complementary transmission electron microscopy (EM) experiments. (This research and EPD were originally published in the Journal of Biological Chemisty. Ausar SF, Foubert TR, Hudson MH, Vedvick TS, Middaugh CR. 2006. Conformational stability and disassembly of Norwalk virus-like particles: Effect of pH and temperature. J Biol Chem 281:19478–88. © the American Society for Biochemistry and Molecular Biology.) Again, the EPD was used as a basis to select conditions to analyze the aggregation state of, in this case, the virus like particles. Compounds which were found to inhibit aggregation were also examined for their effects on ANS-EF, DSC and CD, with sucrose, trehalose, glutamate, and chitosan all found to both inhibit aggregation and conformationally stabilize the Norwalk VLP's.⁷⁸ This study led to formulation of a candidate vaccine which has been successful in Phase II trials^79,80.

Figure 9.

Empirical phase diagram for Norwalk virus-like particles (NV-VLPs) based on UV absorbance, intrinsic and extrinsic fluorescence and CD results.²³ Four distinct phases (P) of the NV-VLP were observed: P1, native, intact form; P2, disassembled; P3, soluble VP1 oligomers; P4, aggregated. The nature of the protein in the various phases was confirmed by transmission electron microscopy studies.

Stabilization of Measles Virus

Larger macromolecular complexes such as killed and live viruses have also been characterized by the EPD approach. For example, the relatively unstable attenuated measles virus which is the basis for the important live virus measles vaccine has been examined using EPDs.²⁴ This enveloped attenuated virus contains multiple copies of six different proteins as well as a ssRNA genome. Analysis is further complicated by the fact that the vast majority of viral particles have been inactivated during large scale preparation of the virus. Thus, the potential utility of biophysical studies is based on the assumptions that any change that affects the biological activity (immunogenicity in this case) of immediate interest is still detectable in a significant number of the remaining complexes and that individual measurements detect significant amounts of altered components (presumably due to their presence in multiple copies). While this is no doubt not always true, we have found such assumptions in most cases to be reliable. The measles virus was first purified from its crude vaccine preparation and then examined by the usual combination of spectroscopic and light scattering techniques.²⁴ One additional EPD method not previously described involved the use of the fluorescent dye laurdan, a probe of membrane fluidity. The resulting EPD displays at least 6 regions of differing structure (Figure 10). (This research and EPD were originally published in Kissmann J, Ausar SF, Rudolph A, Braun C, Cape SP, Sievers RE, Federspiel MJ, Joshi SB, Middaugh CR. 2008. Stabilization of measles virus for vaccine formulation. Human Vaccines 4:350–59.) An excipient screening method based on aggregation of the virus was used to identify potential stabilizers as determined by melting temperatures with the generalized polarization of laurdan fluorescence used as a confirmatory method. The compounds identified were then examined in cellular infectivity assays and served as a basis for a significant improvement in the thermal stability of the vaccine.

Figure 10.

Empirical phase diagram of attenuated Measles virus.²⁴ Data used to generate the EPD were measurements of mean effective diameter by DLS, intensity of 562 nm light scattered at 90°, CD at 222 nm, intrinsic fluorescence intensity at 322 nm, ANS peak position, ANS fluorescence intensity at 469 nm and generalized polarization of laurdan fluorescence.

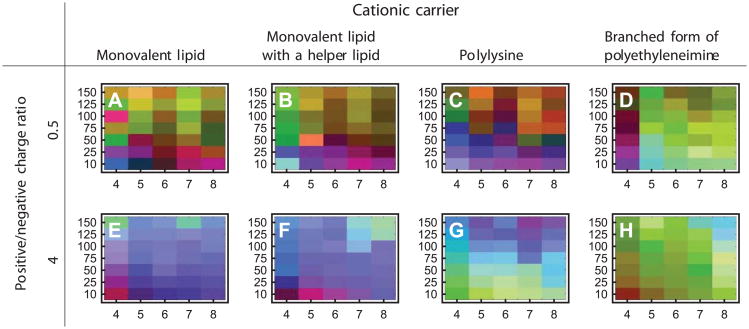
Polymeric and Liposomal Gene Delivery Systems

As a final example, polyplexes and lipoplexes containing plasmid DNA molecules complexed to various polymers and cationic lipids, respectively, were examined by the EPD method. Because of the high thermal stability of the DNA component, pH and ionic strength (rather than temperature) were used as the stress variables. Due to the electrostatic nature of the complexes, they were characterized over a wide range of positive and negative nitrogen to phosphate ratios using circular dichroism, extrinsic fluorescence with a DNA intercalating dye (YOYO-1) and dynamic light scattering.²⁸ The EPDs derived for the polyplexes and lipoplexes lacked the sharp definition of those obtained in the proteinaceous systems described above, but still manifested distinct structural phases which were more complex than plasmid DNA alone (Figure 11). Application of EPD analyses to plasmid DNA and their delivery vehicle systems is still in its infancy, but appears to be a promising approach.

Figure 11.

Ionic strength-pH empirical phase diagrams of various nonviral gene delivery complexes formed between plasmid DNA and four cationic carriers.²⁸ Each EPD has pH as the horizontal axis and ionic strength (mM) as the vertical axis. The experimental techniques used were DLS, CD, and YOYO-1 EF.

Current Research

The development and use of EPDs has provided a high throughput method to quickly determine relative higher order conformational states of biomolecules and larger macromolecular complexes over a large “search space” using multiple biophysical techniques. The optimal determination of regions of conserved structure in the EPD can, however, be hindered by several factors including the presence of noise in the measurements, transitions (during exposure to varying stress conditions) that occur very gradually and are thus difficult to detect, or the presence of important structural information from multiple measurements that cannot be readily reduced to 3 dimensions for display in the EPD.

The EPD method's speed of data collection can also be hindered by the size of the search space. Its practicality can be further limited by the complexity of data processing. In addition, in the absence of reliable automated pattern recognition, the need for an expert scientist to interpret the biophysical data to assign structural meaning to the various phases observed in the EPD, often on the basis of limited information, can also inhibit the method's speed, accuracy, and utility. Here we report on tactics under investigation in our laboratory to tackle and diminish such current limitations of the EPD approach.

A number of new pharmaceutical applications of EPDs are also being explored. These areas include extensions of the current approach to different stresses and a variety of pharmaceutical and vaccine dosage forms. In addition, possible applications of EPDs to describe the chemical stability of macromolecules will also be discussed. Finally, the EPD methodology could potentially be applied to analytical comparability due to its ability to generate and analyze a large amount of biophysical data assessing the overall higher-order (secondary, tertiary and quaternary) structure of biomolecules as a function of solution conditions.

Maximum use of data

One typically provides the EPD method with a limited selection of peak positions, widths, or intensities, obtained from various experimental techniques. This results in a drastic reduction of the potential data set that precedes any global analysis. Data reduction in advance of processing is undesirable, since the excluded data may contain significant information concerning individual structural states and the transitions between them. More information would also allow the mathematical steps (PCA) to better distinguish signal from noise. To address these issues, one seeks a way to pass all of the data through a global analysis first, using minimal preprocessing. The first approach one might consider is to pass unprocessed spectra directly to the empirical phase diagram method. We have attempted this with FTIR and UV absorbance spectra, but the results do not resemble EPDs obtained by using the usual peak parameters (data not shown). Instead, the pH columns in the diagram show very large color differences from each other, dominating much smaller transitions in temperature or pH. The very large pH dependent signal is presumably due to changes in the charge state of amino acids.

We might also apply preprocessing methods that are known to highlight useful information without explicitly dropping data. The second derivative of a spectrum contains information on peak position and width. We can therefore use it to highlight information involving peak parameters. Another method is the use of a mid-pass Fourier filter to emphasize mid-size spectral features, while suppressing offsets and noise. To apply these methods, one simply filters spectra and passes them to the EPD method. A preliminary result is shown in Figure 12E, in which the Fourier mid-pass method has been applied to the FTIR spectra of an IgG molecule. The spectra covered the 900 to 4000cm⁻¹ range, and were measured over the temperature-pH search grid shown in the EPD.

Figure 12.

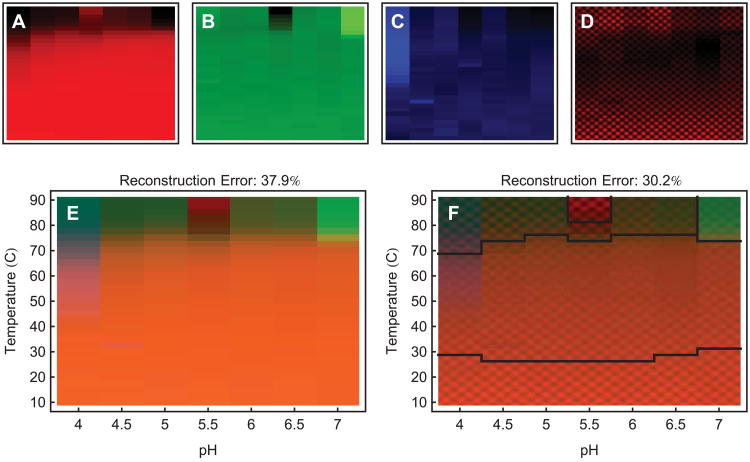
When the projection error is large it can be reduced by incorporating more dimensions. In (A)-(C), we show the primary color images (red, green and blue) of an empirical phase diagram. They are ordered by descending significance from left to right. For axis information, see (E) and (F). After solid red, green, and blue, we can use images containing structure that is smaller than the individual phase diagram blocks. This will represent high dimensional information as changes in texture. Such an image is shown in (D). (E) is a 3 dimensional empirical phase diagram of IgG, using FTIR spectra which have been preprocessed with a Fourier filter to emphasize mid-size spectral features. (F) is a 4 dimensional empirical phase diagram of the same data as (E), showing fourth dimensional information as changes in texture. Notice that the reconstruction error has decreased. The diagram has also been automatically segmented into 5 parts (see text).

Representing more than three dimensions

The error given by equation 1 can sometimes be large. Some criterion for what is too large, such as an error of 20% or greater, must be assigned and validated by the user. Large errors signal the presence of information that cannot be reduced to 3 dimensions. The color-coded EPD are limited by the colors the eye can perceive, given as ratios of red, green, and blue intensities. This is not due to a limitation in PCA or SVD: data can just as easily by projected into more than 3 dimensions. The challenge is to represent the extra dimensions. To represent more than 3 dimensions in each pixel, we can use the eye's ability to recognize shapes, textures, or other signals.

This is not to say that the number of phases that can be shown on an EPD is limited by the number of primary colors used to generate the EPD. Different ratios of red, green, and blue can generate a multitude of colors. Therefore a color coded EPD can display a multitude of phases. The goal of displaying more than 3 dimensions in each pixel of an EPD is to reduce the role of projection and the accompanying error.

We show an example of 4-dimensional visualization in Figure 12F. In Figures 12A-C, we show the primary color images (red, green and blue) of an empirical phase diagram. They are ordered by descending significance from left to right. For axis information, see Figures 12E and F. After solid red, green, and blue, we can use images containing structure that is smaller than the EPD pixels. This will represent information as changes in texture. Perhaps the easiest way to generate these images with small scale structure is through the use of different 2 dimensional harmonic modes, which is what we have done here. The projection error of the example in Figure 12 is significantly smaller for the four dimensional EPD than for the 3-dimensional one. In this case, the fourth principal component shows an additional transition between low and mid range temperatures.

The main reason for expressing information from the EPD method with three colors or selected textures is to exploit the visual processing power of the human eye and brain to segment the EPD into different phases. The traditional “black and white” representation of different regions in a phase diagram is also perfectly acceptable. It amounts to assigning a name, or number, for each distinctly observed and coherent region of the system's physical properties. The 15 known phases of ice are conventionally represented by 15 numbers labeling regions of the pressure-temperature diagram.

Machine learning techniques exist and are being developed to perform the task of segmenting an image. Among the techniques are clustering, support vector machines (SVM's), and Kohonen networks. The main advantage of these techniques is that they can operate on high dimensional data, reducing the role of projection and its accompanying error. In Figure 12F we show the results of a simple image segmentation. We have selected 5 characteristic points on the phase diagram to represent the 5 visible phases. Then, the remaining temperature-pH points have been categorized by their euclidean distance from the characteristic points, where the distance is calculated in measurement space. This is one example; mathematics and computer science possess an abundance of methods designed to recognize and organize information.

Information management

After an EPD is generated, the colors must be assigned meaning based on the information in the experimental data. The standard approach is for a scientist to assign meaning to the colors based on inspection of the original experimental data and the principal components given by PCA. As discussed earlier, however, local inspection of multidimensional data is difficult and does not maximize its utility. It should be better to pursue the assignment of meaning within a general mathematical framework, allowing data to be automatically correlated with observables of interest, such as aggregation pathways and known protein conformational states. Working within a general mathematical framework will also allow determination of the significance of types of information for a given task, so that data collection can be streamlined by the selection of optimal techniques, wavelengths, and integration times.

Relevant mathematics will need to be provided with a starting point. Fortunately, much is known about the determination of protein conformational state from spectroscopic techniques. Also, many proteins have been fully characterized with the EPD approach. The main difficulty in getting started with an automated approach is that raw multi-instrument digital data sets from different experiments tend to be organizationally very complex. They involve multiple data formats and missing data points due to instrument hiccups and differing experimental protocols. The interpretation of an archived data set often requires additional information that must be located. Without an organizing software framework it is difficult to enforce uniform, comprehensive documentation and organization of different biophysical data from diverse sources.

We are working on two solutions to address this issue. One approach consists of a point-and-click program, used for generating phase diagrams. In this interface the user organizes the data and generates phase diagrams. The data are automatically saved with full documentation in the desired format. The other approach is automated, consisting of a framework for importing, processing, and plotting complex information. This automated approach is guided by a short user-programmable script.

Automation

As described in the introduction, modern biopharmaceutical drug formulation challenges, including accelerated time-lines and limited material availability, can result in suboptimal formulations or even product failure due to instability. Because of these challenges, one wishes to explore as much of a search space as possible, using mathematical techniques to obtain the maximum possible amount of information from the data. This collection of techniques can also automate the interpretation of data. Machines and mathematics excel at quickly obtaining and processing massive amounts of data. To this end, it is our goal to automate data collection and interpretation as much as possible, so that the formulation scientist's participation will consist primarily of determining goals, methods, preparing experiments and designing final formulations based on the results. In the next level of automation, scientists would still determine goals and methods, but the machine would choose and prepare its own experimental test cases.

An automated method would potentially work roughly as follows. The equipment would consist of a modern liquid handler, such as the Labcyte Echo^®, robotically coupled to a microplate reader, and controlled via a suitable programming interface. First, spectroscopic measurements of the native form of a macromolecule would be characterized over a region in search space. By characterize we mean finding the simplest accurate mathematical description. This would be akin to a more sophisticated version of the empirical phase diagram. To cover the search space we would use an advanced “Design of Experiment” technique known as “adaptive sampling”.⁸¹ Essentially, the customary grid of points in search space (the test cases) would be replaced by a growing set of points, in which each new point is chosen based on the information contained in previous points. Next, measurements of the macromolecule after accelerated stress would be characterized. In this second step, prior information would be available from both the initial characterization and from the characterization of other macromolecular systems. The prior information would be used to optimally distribute the test cases in search space, reducing the required number of such studies. We mention this idea because it is the natural end point of current research. At present, however, it is only hypothetical.

New pharmaceutical applications of EPDs

Several new pharmaceutical applications for EPDs are currently being explored in our laboratories. One straight forward new application is the extension of the current EPD approach to different stresses and different dosage forms. As shown in Table 2, most EPDs generated to date have evaluated liquid formulations using temperature, solution pH, ionic strength and macromolecular concentration as the primary stresses to perturb the structure of a biomolecule or macromolecular complex. Additional environmental stresses that could easily be adapted to EPD analysis include freeze-thaw, lyophilization and shaking/agitation. For example, in terms of development of a frozen liquid or lyophilized dosage form, the effect of multiple freeze/thaw steps as well as the effect of freeze-drying cycles and reconstitution could be evaluated using the same biophysical techniques described above. Measurements of protein conformational integrity and stability in the solid state itself could also be explored by EPDs using FTIR and Raman spectroscopies, as well as DSC. Identification of phase transition regions could then be used to setup an excipient screening approach for these stresses.

The EPD approach could also be applied to develop a better understanding of different degradation pathways as a function of environmental conditions. In the case of shaking or agitation stress, different shaking speeds, or rotations per minute, could replace temperature as a stress factor. Moreover, new biophysical analytical approaches could be added including detection of protein particles by multiflow digital imaging (MFI) or Nanosight technology. If combined with SE HPLC and OD₃₅₀ measurements, an EPD could be generated to better characterize protein aggregation and subvisible particle formation. In addition, the EPD approach could also be used to examine chemical stability of macromolecules. For example, the rate and extent of specific Asn deamidations or Met oxidations in a protein could be mapped as a function of temperature and solution pH. These “chemical” EPDs could also be overlaid with conformational EPDs to better understand the inter-relationships(s) between chemical and physical stability.

Finally, the unique ability of the EPD method to use a wide variety of biophysical techniques to generate and analyze a large amount of data assessing overall structural integrity and conformational stability of biomolecules could potentially be applied to analytical comparability during development of different biopharmaceutical drugs and vaccines. For example, since the EPD method does not require much protein (1-10 mg), and since availability of protein is often a limiting factor in early formulation development, the generation of EPDs for different candidate molecules could be used as a tool to select the best candidate in terms of “developability” properties such as stability and solubility profiles. Moreover, during later development, process and product changes are usually required to scale up the process for commercial use. These changes often lead to subtle or more dramatic changes in the biomolecules post-translational modifications or degradation profiles (e.g., glycosylation pattern or extent of oxidation of a specific Met residue). The ability to monitor the effect of these changes on the overall structural integrity and conformational stability of biomolecules remains an area of ongoing interest, especially as a possible surrogate for more complex assessments of conformation such as biological assays. The ability of the EPD approach to compare the same biomolecule with differing glycosylation patterns and/or chemically altered amino acid residues is currently being evaluated.

One challenge with this approach is to better assess the precision of the phase identification stage of the EPD methodology. For example, it is important to establish if the differences observed between two protein preparations is greater than the differences observed between multiple measurements of the same protein preparation. In addition, as described in Figure 12 in the previous section, additional higher dimensional information can be added to the standard EPD through the use of changes in texture. This approach, although not routinely used to date, could eventually provide additional structural information for EPDs being generated for the purpose of analytical comparability. Finally, multiple environmental stresses could be utilized (temperature, pH, ionic strength, agitation) to build up a more comprehensive database to compare the structural integrity and conformational stability of a biomolecule prepared from different cell-lines or cell culture/purification/formulation processes.

Conclusion

Modern biopharmaceutical drug development time-lines, combined with limited availability of sufficient material, can result in a variety of challenges for the formulation scientist attempting to rapidly design and develop stable dosage forms for clinical use. Our quest is to enable faster and more thorough screening searches of stabilizing agents and solution conditions by more fully utilizing the information contained in data sets from experimental methods which examine the structural integrity and conformational stability of macromolecules and their complexes. We strive to explore as much of the available search space as possible, using mathematical techniques to obtain the maximum amount of information from the data.

The interpretation of large data sets is made difficult by high dimensionality and the existence of conflicting information. Formulation scientists typically determine transitions in macromolecular structure by using techniques that look at the data locally. Unfortunately, global features on high-dimensional data spaces are not always revealed by such local data inspection. Each experimental method provides a picture of one or more different aspects of the target macromolecule. As indicated previously, this situation is similar to the tale of the blind men and the elephant, where the the elephant represents the macromolecular drug or vaccine, and the various blind men touching different parts of the elephant represent the different experimental methods. The formulation scientist must assimilate all of the conflicting information into a single picture of what an elephant must look like. The lack of an accessible global picture of the data can result in an undesirable degree of approximation of macromolecular transition points brought on by different environmental stresses.

A standard way to reduce the dimensionality of data is by use of the singular value decomposition (SVD). SVD returns a number of spatial axii, defining spaces on which the data can be approximated. The approximation error can be minimized by using a space defined by the most important spatial axii. The projection onto that space is the best possible approximation to the data that can be made on the number of dimensions retained. To provide a convenient visual image, the resulting low-dimensional positions can be converted into colors or textures and presented as an image. Such an image is called an empirical phase diagram (EPD). The empirical phase diagram method guides the formulation scientist by assisting in the visualization of high dimensional information, the determination of macromolecule identity and transition points, and a reduction of the size of search spaces. This approach is quite different from that of the commonly used “Design of Experiment” approach which lacks high density data and produces holes in the picture produced.

The EPD method has found many uses in the optimization of various types of formulations, and many case studies have been published concerning their application to various macromolecular complexes such as viruses and lipoplexes. The EPD approach has been extended over time to include the addition of multiple biophysical measurement techniques and different search space variables. The use of empirical phase diagrams is not limited to proteins and plasmid DNA molecules, but includes larger macromolecular complexes such as viruses and whole cells. One can potentially incorporate almost any kind of information, including measurements of structural dynamics, aggregation kinetics, chemical stability or biological function as well as other common pharmaceutical variables of stress such as agitation and freeze/thaw cycles. Empirical phase diagrams have also been demonstrated to contain information concerning the functional and evolutionary relationships of proteins.^10-12,16,17 Using EPDs, macromolecule identity has been found to be conserved over contiguous regions of search space.

The use of EPDs has brought us to a vantage point where we see clear evidence for a previously unrealized treasure trove of hidden information concerning the higher order structural integrity and conformational stability of biomolecules and larger macromolecular complexes such as viruses and lipoplexes. Much work remains, however. Data consists of combinations of different types of information. Each type is mixed with other types in complex ways, and has its own meaning, prominence in the data, and significance for the task at hand. The inter-relationships between these factors is complex, requiring systematic study within a mathematical framework. However, the journey will be worth the effort. The exhaustion of information in macromolecular data sets suggests a future in which access to new information leads to novel formulation and stabilization methods.

Appendix

In this Appendix we state the properties of the singular value decomposition (SVD) and the connection between the singular values and the reconstruction error. Many mathematical software packages have a command for calculating SVD's.

Standardization and preprocessing of data produces an l×m matrix D_ij of data, where indices i=1…l, j=1…m. The singular value decomposition of D is

$$D_{ij}=\sum _{\alpha =1}^d{U}_{i\alpha }{W}_{\alpha }{V}_{\alpha j},$$ (2)

where d=Min(l, m). The decomposition exists for any matrix, whether real or complex, square or rectangular. The matrices U_iα and V_αj are calculated by solving for the eigenvectors of the covariance matrices DD^T and D^TD:

$$D{D}^T\cdot U_{\alpha }={W_{\alpha }}^2{U}_{\alpha },$$

$$V_{\alpha }\cdot D^{T}D={W_{\alpha }}^2{V}_{\alpha },$$

where U_α is a column of the matrix U_iα, and V_α is a row of the matrix V_αj. For complex matrices replace the transpose D^T by the adjoint D^†.

Both DD^T and D^TD are real symmetric, or complex self-adjoint, and positive definite. The numbers W_α, called singular values, are by convention real and positive by a choice of sign (or complex phase) of the eigenvectors. Also by convention, the singular values are sorted in order of decreasing size, and the eigenvectors are sorted accordingly.

The rows of V_αj are normalized. Since they are eigenvectors, they are orthogonal to one another:

$$V{V}^T=I_{d\times d}.$$

Likewise for the columns of U_iα:

$$U^{T}U=I_{d\times d}.$$

The rows of V and the columns of U are called singular vectors. When D is real, U and V are also real.

The decomposition is unique up to a complex factor chosen for each pair of eigenvectors:

$$D_{ij}=\sum _{\alpha =1}^d(U_{i\alpha }{e}^{-i{\theta }_{\alpha }})W_{\alpha }(e^{i{\theta }_{\alpha }}{V}_{\alpha j}).$$

Even when D is real, the signs of the singular vectors are not uniquely determined by the decomposition. This is an additional reason why similar data sets can produce phase diagrams with different colors.

Equation 2 can be read either as a matrix product or as a sum of matrices, each identified by the index α. The second interpretation is helpful. These summand matrices exist in the vector space of l×m matrices. The natural vector norm in this space is the Frobenius (or Hilbert-Schmidt) norm ║M║, which for an l×m matrix M is defined as

$$\Vert M\Vert =\sqrt{\sum _{i=1}^l\sum _{j=1}^m{\left|M_{ij}\right|}^2}$$

The norm of each summand in Equation 2 is W_α :

$$\Vert U_{i\alpha }{W}_{\alpha }{V}_{\alpha j}\Vert =W_{\alpha }.$$

Since the numbers W_α are sorted in decreasing order, Equation 2 is a series of corrections decreasing in size. For many data sets, the most common result is that the data can be approximated well by a sum over just the top few summands α, since the largest singular values tend to be much larger than the rest. If we use the top n singular values, where 1≤n<d, Equation 2 becomes

$${\stackrel{\sim }{D}}_{ij}=\sum _{\alpha =1}^n{U}_{i\alpha }{W}_{\alpha }{V}_{\alpha j},$$

where D̃ is the approximated data.

In the vector space of l×m matrices, the summands are orthogonal:

$$\sum _{i=1}^l\sum _{j=1}^m\left(U_{i\alpha }{V}_{\alpha j}\right)\left(U_{i\beta }{V}_{\beta j}\right)={\delta }_{\alpha \beta }.$$

Since the summands are orthogonal and their individual norms are W_α, the norm of the partial sum D̃ is the same as the ordinary vector norm of the W_α included in the sum:

$$\Vert \stackrel{\sim }{D}\Vert =\sqrt{\sum _{\alpha =1}^n{W_{\alpha }}^2},$$

The RMS reconstruction error, directly expressed as

$$\Vert D-\stackrel{\sim }{D}\Vert =\Vert D-\sum _{\alpha =1}^n{U}_{i\alpha }{W}_{\alpha }{V}_{\alpha j}\Vert ,$$

can also be expressed as

$$\Vert D-\stackrel{\sim }{D}\Vert =\sqrt{\sum _{\alpha =n+1}^d{W_{\alpha }}^2}.$$