Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Mar 11;4:4346. doi: 10.1038/srep04346

Ultrafast optical control of group delay of narrow-band terahertz waves

Fumiaki Miyamaru 1,a, Hiroki Morita 1, Yohei Nishiyama 1, Tsubasa Nishida 1, Toshihiro Nakanishi 2, Masao Kitano 2, Mitsuo W Takeda 1
PMCID: PMC3949247  PMID: 24614514

Abstract

We experimentally demonstrate control over the group delay of narrow-band (quasi continuous wave) terahertz (THz) pulses with constant amplitude based on optical switching of a metasurface characteristic. The near-field coupling between resonant modes of a complementary split ring resonator pair and a rectangular slit show an electromagnetically induced transparency-like (EIT-like) spectral shape in the reflection spectrum of a metasurface. This coupling induces group delay of a narrow-band THz pulse around the resonant frequency of the EIT-like spectrum. By irradiating the metasurface with an optical excitation pulse, the metasurface becomes mirror-like and thus the incident narrow-band THz pulse is reflected without a delay. Remarkably, if we select the appropriate excitation power, only the group delay of the narrow-band THz pulse can be switched while the amplitude is maintained before and after optical excitation.

Terahertz (THz) technologies have rapidly developed in the last two decades1. Recently, the possibility of THz applications has spread to various research fields and industries, e.g. medical diagnosis2,3,4,5,6,7, drug inspection8, security applications9, chemical analysis10,11, etc. In particular, THz technology is extremely important for wireless telecommunications12. Higher speed is critical for wireless communications and the THz frequency region is promising for this purpose. However, there are few optical components available in the THz region. Although spectral filters13,14,15, waveguides16,17, and polarization components18,19 have been developed thus far, optical components based on new concepts are critically needed.

For wireless communication applications, optical components that can temporarily control THz waves are extremely important. Many attempts to slow down the speed of THz pulses have been reported. An analog of electromagnetically induced transparency (EIT) is a very promising approach for slow-light implementations. Although EIT was originally conceived as a quantum phenomenon that occurs through destructive interference between two radiative transitions amongst three electron energy levels20,21,22, the EIT phenomena can be mimicked with two coupled resonators23 because EIT is essentially a wave phenomenon. Many demonstrations for realizing EIT-like phenomena were reported with metamaterial (metasurface) structures using microwaves24,25,26,27,28,29,30,31, THz waves32,33,34,35,36,37,38,39,40,41,42,43,44,45, and in the near infrared region46,47,48,49,50,51,52,53,54,55. Very recently, the optical modulation of the EIT spectrum was demonstrated experimentally in the THz region56. However, in Ref. 56 a decrease in transparency of the transmission band, where THz pulses decelerate, was observed along with modulation of group delay of the THz pulses by externally irradiating the metasurface. It is important to control group delay of THz pulses while also maintaining THz pulse intensity before and after irradiation with external light.

Here, we propose and experimentally demonstrate that it is possible to control the group delay of a narrow-band THz pulse while maintaining pulse intensity through ultrafast optical switching of metasurface characteristics. Our metasurface consists of an array of complementary split ring resonators (CSRRs) and rectangular slits (RSs) deposited on a gallium arsenide (GaAs) substrate. In the reflection spectrum, the metasurface shows an EIT-like spectral shape in which the relatively sharp reflection peak appears within a broad reflection dip, indicating that the large group delay for the reflected THz wave is realized around the reflection peak frequency. Here we note that the group delay occurs within narrow frequency band about 0.05 THz centered at EIT peak frequency. Correspondingly, the time duration of the THz pulse called the “narrow-band THz pulse” in this paper is about 20 ps. By illuminating the metasurface with optical light, a sufficient density of photo-excited carriers transforms the metasurface into a mirror. Therefore, incident narrow-band THz waves are reflected without a delay. In this group delay switching process, if we select the appropriate power for optically excited light, the amplitude of the THz wave around the EIT peak frequency can be maintained before and after switching. Our proposed technique to control the group delay of narrow-band THz pulses demonstrates great potential for a variety of THz applications, in particular for wireless communications and THz sensing technologies.

Results

Fabrication and design of metasurface

The metasurface used in our experiment consists of an array of CSRRs and RSs deposited on a 640 μm thick GaAs substrate with a refractive index of nGaAs = 3.58 at around 1.0 THz. A photograph and the geometrical parameters of our metasurface are shown in Fig. 1(a). An array of CSRRs and RSs was fabricated by a photolithographic technique. In Ref. 56, EIT characteristics were observed in transmission spectrum for the combination of two split ring resonators (SRRs) and a cut-wire (CW) geometry. For incident polarization parallel to the longitudinal length of the cut-wire and SRR gap, a relatively sharp transmission peak was observed within a broad transmission dip. On the other hand, in our experiment we require a sharp reflection peak within a broad reflection dip. Therefore, we used the combination of CSRRs and RS where metallic and non-metallic parts are inverted relative to those of SRRs and CW57,58,59. According to Babinet's principle60,61, the transmission or reflection behavior of complementary and original structures are interchanged. Since the incident electric and magnetic fields should also be interchanged, in our experiment the incident polarization is perpendicular to the longitudinal length of the RS and CSRR gap. The relation between the incident polarization and metasurface structure is depicted in Fig. 1(b).

Figure 1. Photograph and schematic of metasurface on GaAs substrate.

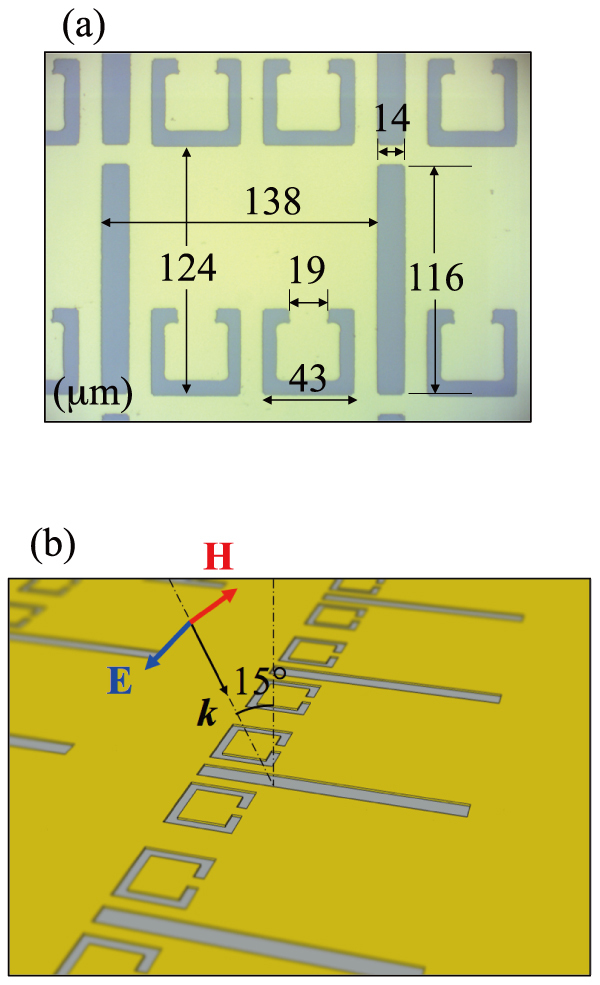
Figure 1

Open in a new tab

(a) A photograph of our metasurface, with a unit cell consisting of rectangular slits sandwiched between two complementary split ring resonators. Geometrical parameters are also shown in the figure. (b) Schematic of the optical configuration of the incident terahertz wave and the metasurface.

Measurement of reflection spectra of metasurface and switching the characteristic of metasurface with optical light

We measured the waveform of THz waves reflected from the metasurface using reflection-type THz time-domain spectroscopy62. This measurement allows us to obtain the waveform of a terahertz wave directly in the time domain, indicating that we can obtain both amplitude and phase information of the reflected THz wave simultaneously. The optical configuration around the metasurface is shown in Fig. 2. The incident terahertz wave was emitted from a 3-mm-thick ZnTe (110) crystal illuminated by a femtosecond optical pump pulse (100 fs, 150 μJ/pulse at 800 nm with an 1 kHz repetition rate). The emitted THz wave was focused on the metasurface with an incident angle of 15 degrees. THz waves reflected from the sample were collected and refocused on a detector plate (a 3-mm-thick ZnTe (110) crystal), which was illuminated by an optical gate pulse to measure the electric field amplitude through the electro-optic sampling technique63. The time variant electric field amplitude of the reflected THz waves was measured by changing the delay time of the gate pulse with respect to the pump pulse. The intensity and phase shift spectra of the reflected THz wave in the frequency domain can be obtained by performing a Fourier transform of the temporal waveform. The period of time window in time domain signal is about 55 ps, so that the spectral resolution of our experiment is about 0.018 THz. For switching the reflection characteristics of the metasurface, the optical excitation pulse, which was also divided from the pump pulse, illuminated the metasurface at normal incidence 40 ps before the THz wave. As the carrier lifetime in GaAs is several tens of picoseconds, the majority of the photoexcited carriers are present during THz waveform measurements, and so the refractive index of GaAs can be considered to be constant during this time. Photo-excited electron-hole pairs induce a change in refractive index of the GaAs substrate, and therefore change the reflection spectrum since the reflection characteristic of the metasurface depends on the refractive index of the substrate.

Figure 2. Terahertz wave reflection measurement.

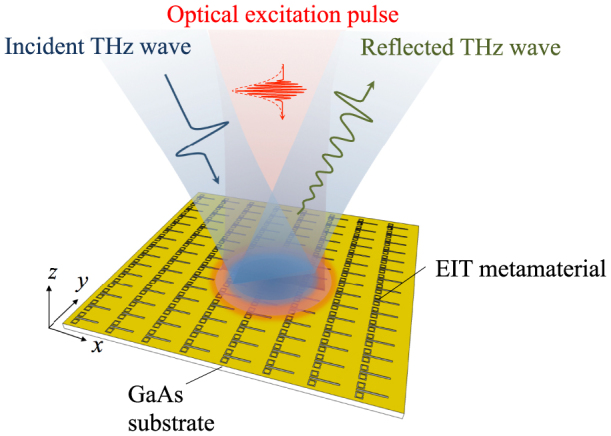
Figure 2

Open in a new tab

Schematic of the optical configuration of our experiment.

First, we measured the reflection characteristics of our metasurface. Figure 3 shows the measured reflectance spectra for various excitation power densities between pexc = 0.00 and 6.40 μJ/cm2. In Fig. 3, we took the THz wave signal reflected from gold mirror as a reference and plot the ratio of reflected power between the sample and reference. When pexc = 0.00 μJ/cm2 (black line), a clear sharp reflection peak is observed at 0.48 THz, which is located within the relatively broad reflection dip ranging from 0.4 to 0.6 THz. Such a spectral shape is a typical characteristic of EIT-like phenomenon. The reflectance at 0.48 THz decreases and simultaneously the reflection peak broadens with increasing pexc from 0.00 to 2.56 μJ/cm2. Further increasing the power causes the reflectance at 0.48 THz to increase again, reaching 0.8 for pexc = 6.4 μJ/cm2, which is comparable to that for pexc = 0.00 μJ/cm2. This spectral change is attributed to a change in dielectric constant in the GaAs substrate induced by photo-excited carriers. As the photo-excited carrier density increases, the plasma frequency in GaAs increases and exceeds the observed frequency range. Therefore, GaAs begins to behave in a similar way as a metal. Consequently, the metasurface behaves as a flat metal surface. These results indicate that the reflectance at 0.48 THz changes only slightly with and without irradiation of an excitation pulse of pexc = 6.4 μJ/cm2.

Figure 3. Reflection spectra of metasurface.

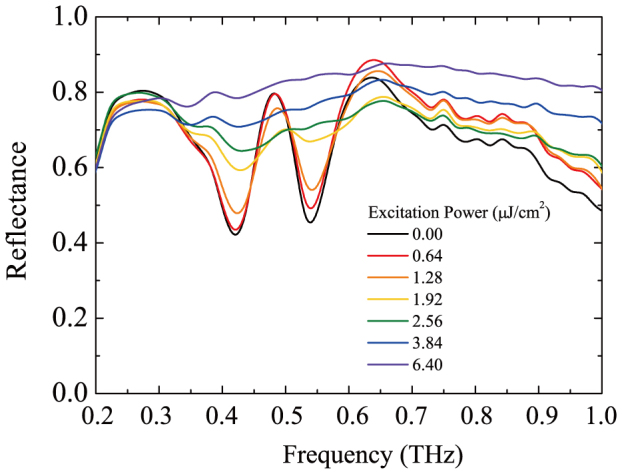
Figure 3

Open in a new tab

Reflection spectra are shown for various levels of photoexcitation power. The excitation pulse timing with respect to the incident terahertz wave was −40 ps.

Here, we briefly mention the peak frequency of the EIT-like spectrum. With increasing excitation pulse power from 0.00 to 1.92 μJ/cm2, the peak frequency shifts slightly to higher frequencies. Such a blue-shift in the resonant frequency of the metasurface structure was observed in previous studies64. Reference 64 attributes this blue-shift to an increase in carrier concentration in GaAs, resulting in a change in complex permittivity in the THz region. In particular, the relatively high value of the imaginary part of the permittivity plays an essential role in the blue-shift characteristic. In Ref. 64, carrier concentration is estimated from the irradiated optical density to calculate the complex permittivity of GaAs. Using the estimated carrier concentration, the resonance frequency of the metasurface was simulated and a characteristic blue-shift was observed, consistent with experimental results.

Measurement of phase shift and group delay spectra of metasurface and switching the characteristic with optical light

Next, we describe the phase shift and group delay spectra. In addition to measuring reflectance, we were also able to retrieve phase information of the reflected THz wave through THz time-domain spectroscopy. In general, the phase shift spectrum is derived by θsam – θref, where θsam is the phase spectrum of the reflected THz wave from the sample and θref is that from a reference material, typically a metal mirror as used in Fig. 3. However, for reflection measurements, the accuracy of the absolute value of the phase is always a serious problem because the reference mirror cannot be located in the same position as the sample material. Thus, in order to avoid deviations caused by replacement, we adopted the phase spectrum of the THz wave reflected from the sample metasurface as a reference when irradiated by optical excitation pulses with pexc = 6.40 μJ/cm2. As determined from the reflection spectrum in Fig. 3, since the reflectance at pexc = 6.40 μJ/cm2 is more than 80% over broad frequency region, and therefore the metasurface can be largely regarded as a flat mirror, it is appropriate to use the signal as a reference.

Figure 4(a) shows phase shift spectra of reflected THz waves from the metasurface with various pexc. When pexc = 0.00 μJ/cm2, the spectral shape characteristic of EIT-like phenomenon is observed. A relatively linear and steep gradient is observed around 0.48 THz where a resonant reflection peak is observed in Fig. 3. The phase shift spectrum broadens with increasing pexc, and becomes almost flat for pexc = 3.84 μJ/cm2. From these phase shift spectra, we can calculate the group delay tg as shown in Fig. 4(b). When pexc = 0.00 μJ/cm2, a group delay of about 1 ps can be observed at 0.48 THz. This group delay decreases with increasing pexc, and becomes almost zero in the entire frequency range for pexc = 3.84 μJ/cm2.

Figure 4. Phase shift and group delay spectra.

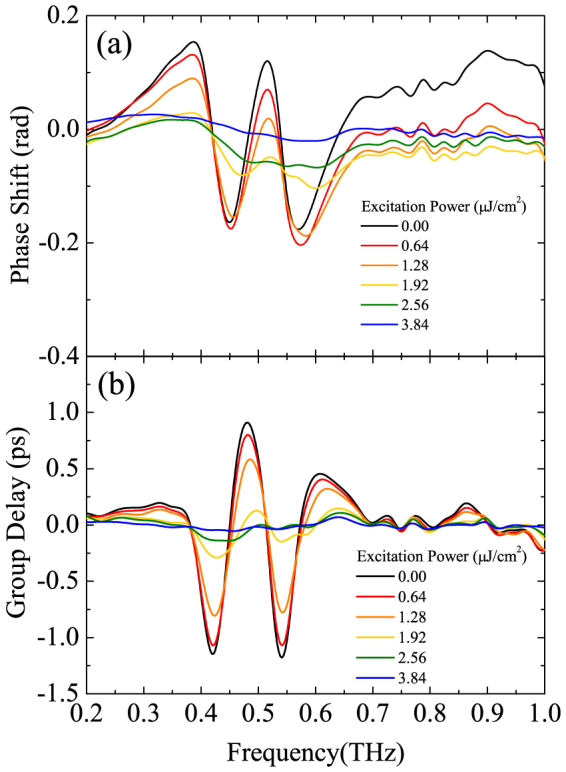
Figure 4

Open in a new tab

(a) Phase shift and (b) group delay spectra for various levels of photoexcitation power.

Discussion

From the measured reflectance spectra in Fig. 3 and group delay spectra in Fig. 4(b), the behavior of the reflected narrow-band THz wave with and without excitation pulses can be explained from the viewpoint in time domain as follows. The followed explanation is based on the reversible principle of the Fourier transform from time domain and frequency domain and vice versa. When a narrow-band THz pulse (orange line in Fig. 5), with a peak frequency of 0.48 THz and a bandwidth of about 0.05 THz, is incident on the metasurface, it is reflected with a group delay of about 1 ps (green line in Fig. 5). When the excitation pulse is irradiated externally, the metasurface becomes a metallic mirror, and correspondingly the incident narrow-band THz wave is reflected back without any group delay (blue line in Fig. 5). Note that the reflectance of the narrow-band THz pulse does not change substantially, indicating that we can control only the group delay of the THz pulse without influencing pulse amplitude.

Figure 5. Group delay switching of a narrow-band THz pulse.

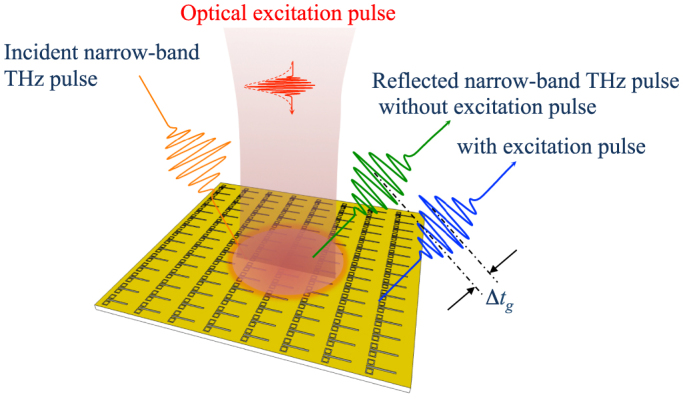
Figure 5

Open in a new tab

Schematic of optical switching of the group delay for a narrow-band THz pulse.

In conclusion, we have shown that the group delay of narrow-band THz pulses reflected from a metasurface can be switched by optically pumping a metasurface with an EIT-like reflection spectrum. By illuminating the metasurface with an optical pulse, we can change the characteristic of the metasurface to that of a mirror. Therefore, the EIT-like phenomenon disappears, resulting in narrow-band THz pulse reflection without delay. Remarkably, in this process only the group delay of the narrow-band THz pulse is switched while the reflection amplitude is maintained when the pump power of the optical light is appropriately selected. Our proposed technique for controlling group delay of narrow-band THz pulses enables temporal control for a variety of THz applications, in particular for wireless communications.

Methods

Terahertz time domain spectroscopy with optical excitation pulse

To measure the waveform of THz waves reflected from the metasurface, we conducted reflection-type THz time-domain spectroscopy combined with the optical pulse to switch the characteristic of the metasurface. By using this spectroscopy, we can obtain the waveform of a terahertz wave directly in the time domain, allowing us to obtain both amplitude and phase information of the reflected THz wave simultaneously. The incident terahertz wave was emitted via optical rectification in a 3-mm-thick ZnTe (110) nonlinear crystal illuminated by a 100 fs optical pump pulse with a beam power of 150 μJ/pulse at 800 nm delivered from a 1 kHz repetition rate Ti:sapphire regenerative amplifier (Spectra Physics, Spitfire-Pro-TU1k-E). The emitted THz wave was focused with a 50-mm focal-length THz lens (Pax Co., Tsurupica) onto the metasurface with an incident angle of 15 degrees. THz waves reflected from the metasurface were collected and refocused with a 50-mm focal-length THz lens on a 3-mm-thick ZnTe (110) crystal, which is illuminated by the gate pulse separated from the pump pulse, to detect the reflected THz field via electro-optic (EO) sampling. The time-domain waveform of the reflected THz wave was measured by recording EO signal with varying the delay time of the gate pulse with respect to the pump pulse. The intensity and phase shift spectra of the reflected THz wave in the frequency domain can be calculated by performing a Fourier transform of the measured temporal waveform. To switch the reflection characteristics of the metasurface, the optical excitation pulse, which was also divided from the pump pulse, illuminated the metasurface at normal incidence. The beam diameter of the optical excitation pulse was 8 mm, which could cover the THz beam diameter of about 3 mm at the metasurface. All measurements were performed at room temperature.

Author Contributions

F.M. proposed the optical switching of group delay of THz pulses. H.M. and Y.N. fabricated the metamaterials. F.M., H.M. and Y.N. performed all the measurements. T.N. performed the analysis of data. T.N., M.K. and M.W.T. supervised theory and experiments. F.M. wrote the paper.

Acknowledgments

This work was partially supported by the Ministry of Education, Science, Sports and Culture, a Grant-in-Aid for Scientific Research on Innovative Areas No. 22109003, a Grant-in-Aid for Scientific Research (B) No. 25287072, and Inamori Foundation.

References

  1. Tonouchi M. Cutting-edge terahertz technology. Nature Photonics 1, 97–105 (2007). [Google Scholar]
  2. Nakajima S., Hoshina H., Yamashita M., Otani C. & Miyoshi N. Terahertz imaging diagnostics of cancer tissues with a chemometrics technique. Appl. Phys. Lett. 90, 041102 (2007). [Google Scholar]
  3. Brucherseifer M. et al. Label-free probing of the binding state of DNA by time-domain terahertz sensing. Appl. Phys. Lett. 77, 4049 (2000). [Google Scholar]
  4. Sim Y. C., Park J. Y., Ahn K.-M., Park C. & Son J.-H. Terahertz imaging of excised oral cancer at frozen temperature. Biomed. Opt. Express 4, 1413 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Hoshina H., Hayashi A., Miyoshi N., Miyamaru F. & Otani C. Terahertz pulsed imaging of frozen biological tissues. Appl. Phys. Lett. 94, 123901 (2009). [Google Scholar]
  6. Woodward R., Wallace V., Arnone D., Linfield E. & Pepper M. Terahertz pulsed imaging of skin cancer in the time and frequency domain. Journal of Biological Physics 29, 257–259 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Titova L. V. et al. Intense THz pulses down-regulate genes associated with skin cancer and psoriasis: a new therapeutic avenue? Sci. Rep. 3, 2363 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Kawase K., OGAWA Y., Watanabe Y. & Inoue H. Non-destructive terahertz imaging of illicit drugs using spectral fingerprints. Opt. Express 11, 2549–2554 (2003). [DOI] [PubMed] [Google Scholar]
  9. Yamamoto K. et al. Noninvasive inspection of C-4 explosive in mails by terahertz time-domain spectroscopy. Jpn. J. Appl. Phys. 43, L414–L417 (2004). [Google Scholar]
  10. Kiwa T. et al. Laser terahertz emission system to investigate hydrogen gas sensors. Appl. Phys. Lett. 86, 261102 (2005). [Google Scholar]
  11. Kiwa T. et al. Terahertz chemical microscope for label-free detection of protein complex. Appl. Phys. Lett. 96, 211114 (2010). [Google Scholar]
  12. Kleine-Ostmann T. & Nagatsuma T. A review on terahertz communications research. J. Infrared, Millimeter, and Terahertz Waves 32, 143–171 (2011). [Google Scholar]
  13. Bingham C. et al. Planar wallpaper group metamaterials for novel terahertz applications. Opt. Express 16, 18565–18575 (2008). [DOI] [PubMed] [Google Scholar]
  14. Drysdale T. D. et al. Transmittance of a tunable filter at terahertz frequencies. Appl. Phys. Lett. 85, 5173 (2004). [Google Scholar]
  15. Lee J. W. et al. Shape resonance omni-directional terahertz filters with near-unity transmittance. Opt. Express 14, 1253–1259 (2006). [DOI] [PubMed] [Google Scholar]
  16. Gallot G., Jamison S. P., McGowan R. W. & Grischkowsky D. Terahertz waveguides. J. Opt. Soc. Am. B 17, 851–863 (2000). [Google Scholar]
  17. Pandey S., Gupta B. & Nahata A. Terahertz plasmonic waveguides created via 3D printing. Opt. Express 21, 24422 (2013). [DOI] [PubMed] [Google Scholar]
  18. Miyamaru F., Kondo T., Nagashima T. & Hangyo M. Large polarization change in two-dimensional metallic photonic crystals in subterahertz region. Appl. Phys. Lett. 82, 2568 (2003). [Google Scholar]
  19. Miyamaru F. & Hangyo M. Strong optical activity in chiral metamaterials of metal screw hole arrays. Appl. Phys. Lett. 89, 211105 (2006). [Google Scholar]
  20. Field J. E., Hahn K. H. & Harris S. E. Observation of electromagnetically induced transparency in collisionally broadened lead vapor. Phys. Rev. Lett. 67, 3062 (1991). [DOI] [PubMed] [Google Scholar]
  21. Boller K. J., Imamolu A. & Harris S. Observation of electromagnetically induced transparency. Phys. Rev. Lett. 66, 2593–2596 (1991). [DOI] [PubMed] [Google Scholar]
  22. Fleischhauer M., Imamoglu A. & Marangos J. Electromagnetically induced transparency: Optics in coherent media. Rev. Mod. Phys. 77, 633–673 (2005). [Google Scholar]
  23. Litvak A. & Tokman M. Electromagnetically induced transparency in ensembles of classical oscillators. Phys. Rev. Lett. 88, 095003 (2002). [DOI] [PubMed] [Google Scholar]
  24. Shao J. et al. Analogue of electromagnetically induced transparency by doubly degenerate modes in a U-shaped metamaterial. Appl. Phys. Lett. 102, 034106 (2013). [Google Scholar]
  25. Zhang L. et al. Large group delay in a microwave metamaterial analog of electromagnetically induced transparency. Appl. Phys. Lett. 97, 241904 (2010). [Google Scholar]
  26. Lu X., Shi J. & Liu R. Highly-dispersive electromagnetic induced transparency in planar symmetric metamaterials. Opt. Express 20, 17581 (2012). [DOI] [PubMed] [Google Scholar]
  27. Tamayama Y., Nakanishi T. & Kitano M. Variable group delay in a metamaterial with field-gradient-induced transparency. Phys. Rev. B 85, 073102 (2012). [Google Scholar]
  28. Tamayama Y. et al. Electromagnetic response of a metamaterial with field-gradient-induced transparency. Phys. Rev. B 82, 165130 (2010). [Google Scholar]
  29. Tassin P. et al. Electromagnetically induced transparency and absorption in metamaterials: The radiating two-oscillator model and its experimental confirmation. Phys. Rev. Lett. 109, 187401 (2012). [DOI] [PubMed] [Google Scholar]
  30. Papasimakis N., Fedotov V., Zheludev N. & Prosvirnin S. Metamaterial analog of electromagnetically induced transparency. Phys. Rev. Lett. 101, 253903 (2008). [DOI] [PubMed] [Google Scholar]
  31. Nakanishi T., Otani T., Tamayama Y. & Kitano M. Storage of electromagnetic waves in a metamaterial that mimics electromagnetically induced transparency. Phys. Rev. B 87, 161110 (2013). [Google Scholar]
  32. Yin X. et al. Tailoring electromagnetically induced transparency for terahertz metamaterials: From diatomic to triatomic structural molecules. Appl. Phys. Lett. 103, 021115 (2013). [Google Scholar]
  33. Liu X. et al. Electromagnetically induced transparency in terahertz plasmonic metamaterials via dual excitation pathways of the dark mode. Appl. Phys. Lett. 100, 131101 (2012). [Google Scholar]
  34. Singh R. et al. Observing metamaterial induced transparency in individual Fano resonators with broken symmetry. Appl. Phys. Lett. 99, 201107 (2011). [Google Scholar]
  35. Li Z. et al. Manipulating the plasmon-induced transparency in terahertz metamaterials. Opt. Express 19, 8912–8919 (2011). [DOI] [PubMed] [Google Scholar]
  36. Dong Z., Liu H., Xu M., Li T. & Wang S. Role of asymmetric environment on the dark mode excitation in metamaterial analogue of electromagnetically-induced transparency. Opt. Express 18, 22412 (2010). [DOI] [PubMed] [Google Scholar]
  37. Tassin P., Zhang L., Koschny T., Economou E. N. & Soukoulis C. M. Planar designs for electromagnetically induced transparency in metamaterials. Opt. Express 17, 5595 (2009). [DOI] [PubMed] [Google Scholar]
  38. Cao W. et al. Low-loss ultra-high-Q dark mode plasmonic Fano metamaterials. Opt. Lett. 37, 3366 (2012). [DOI] [PubMed] [Google Scholar]
  39. Chiam S.-Y. et al. Analogue of electromagnetically induced transparency in a terahertz metamaterial. Phys. Rev. B 80, 153103 (2009). [Google Scholar]
  40. Singh R., Rockstuhl C., Lederer F. & Zhang W. Coupling between a dark and a bright eigenmode in a terahertz metamaterial. Phys. Rev. B 79, 085111 (2009). [Google Scholar]
  41. Wu C., Khanikaev A. & Shvets G. Broadband slow light metamaterial based on a double-continuum Fano resonance. Phys. Rev. Lett. 106, 107403 (2011). [DOI] [PubMed] [Google Scholar]
  42. Tassin P., Zhang L., Koschny T., Economou E. N. & Soukoulis C. M. Low-loss metamaterials based on classical electromagnetically induced transparency. Phys. Rev. Lett. 102, 053901 (2009). [DOI] [PubMed] [Google Scholar]
  43. Fedotov V. A., Rose M., Prosvirnin S. L., Papasimakis N. & Zheludev N. I. Sharp trapped-mode resonances in planar metamaterials with a broken structural symmetry. Phys. Rev. Lett. 99, 147401 (2007). [DOI] [PubMed] [Google Scholar]
  44. Zhu Z. et al. Broadband plasmon induced transparency in terahertz metamaterials. Nanotechnology 24, 214003 (2013). [DOI] [PubMed] [Google Scholar]
  45. Roy Chowdhury D., Singh R., Taylor A. J., Chen H.-T. & Azad A. K. Ultrafast manipulation of near field coupling between bright and dark modes in terahertz metamaterial. Appl. Phys. Lett. 102, 011122 (2013). [Google Scholar]
  46. Dong Z.-G. et al. Enhanced sensing performance by the plasmonic analog of electromagnetically induced transparency in active metamaterials. Appl. Phys. Lett. 97, 114101 (2010). [Google Scholar]
  47. Liu N. et al. Plasmonic analogue of electromagneticallyinduced transparency at the Drude damping limit. Nature Materials 8, 758–762 (2009). [DOI] [PubMed] [Google Scholar]
  48. Wang J. et al. Double Fano resonances due to interplay of electric and magnetic plasmon modes in planar plasmonic structure with high sensing sensitivity. Opt. Express 21, 2236–2244 (2013). [DOI] [PubMed] [Google Scholar]
  49. Chen J. et al. Plasmonic EIT-like switching in bright-dark-bright plasmon resonators. Opt. Express 19, 5970–5978 (2011). [DOI] [PubMed] [Google Scholar]
  50. Zhang J., Xiao S., Jeppesen C., Kristensen A. & Mortensen N. A. Electromagnetically induced transparency in metamaterials at near-infrared frequency. Opt. Express 18, 17187–17192 (2010). [DOI] [PubMed] [Google Scholar]
  51. Lu Y., Rhee J., Jang W. & Lee Y. Active manipulation of plasmonic electromagnetically-induced transparency based on magnetic plasmon resonance. Opt. Express 18, 20912–20917 (2010). [DOI] [PubMed] [Google Scholar]
  52. Lu Y. et al. Plasmonic electromagnetically-induced transparency in symmetric structures. Opt. Express 18, 13396–13401 (2010). [DOI] [PubMed] [Google Scholar]
  53. Zentgraf T., Zhang S., Oulton R. F. & Zhang X. Ultranarrow coupling-induced transparency bands in hybrid plasmonic systems. Phys. Rev. B 80, 195415 (2009). [Google Scholar]
  54. Yannopapas V., Paspalakis E. & Vitanov N. Electromagnetically induced transparency and slow light in an array of metallic nanoparticles. Phys. Rev. B 80, 035104 (2009). [Google Scholar]
  55. Zhang S., Genov D. A., Wang Y., Liu M. & Zhang X. Plasmon-induced transparency in metamaterials. Phys. Rev. Lett. 101, 47401 (2008). [DOI] [PubMed] [Google Scholar]
  56. Gu J. et al. Active control of electromagnetically induced transparency analogue in terahertz metamaterials. Nature Comm. 3, 1151–6 (2012). [DOI] [PubMed] [Google Scholar]
  57. Chen H. et al. Complementary planar terahertz metamaterials. Opt. Express 15, 1084–1095 (2007). [DOI] [PubMed] [Google Scholar]
  58. Bitzer A., Ortner A., Merbold H., Feurer T. & Walther M. Terahertz near-field microscopy of complementary planar metamaterials: Babinet's principle. Opt. Express 19, 2537–2545 (2011). [DOI] [PubMed] [Google Scholar]
  59. Liu N. et al. Planar metamaterial analogue of electromagnetically induced transparency for plasmonic sensing. Nano Lett. 10, 1103–1107 (2010). [DOI] [PubMed] [Google Scholar]
  60. Booker H. G. Slot aerials and their relation to complementary wire aerials (Babinet's principle). Journal of the Institution of Electrical Engineers-Part IIIA: Radiolocation 93, 620–626 (1946). [Google Scholar]
  61. Nakata Y., Urade Y., Nakanishi T. & Kitano M. Plane-wave scattering by self-complementary metasurfaces in terms of electromagnetic duality and Babinet's principle. Phys. Rev. B 88, 205138 (2013). [Google Scholar]
  62. Hangyo M., Tani M. & Nagashima T. Terahertz time-domain spectroscopy of solids: A review. Int. J. Infrared and Millimeter Waves 26, 1661–1690 (2005). [Google Scholar]
  63. Gallot G. & Grischkowsky D. Electro-optic detection of terahertz radiation. J. Opt. Soc. Am. B 16, 1204–1212 (1999). [Google Scholar]
  64. Manceau J.-M., Shen N.-H., Kafesaki M., Soukoulis C. M. & Tzortzakis S. Dynamic response of metamaterials in the terahertz regime: Blueshift tunability and broadband phase modulation. Appl. Phys. Lett. 96, 021111 (2010). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES