Abstract
We investigated the capability of molecular triads, consisting of two strong fluorophores that were covalently linked to a photochromic molecule, for optical gating. Therefore we monitored the fluorescence intensity of the fluorophores as a function of the isomeric state of the photoswitch. From the analysis of our data we develop a kinetic model that allows us to predict quantitatively the degree of the fluorescence modulation as a function of the mutual intensities of the lasers that are used to induce the fluorescence and the switching of the photochromic unit. We find that the achievable contrast for the modulation of the fluorescence depends mainly on the intensity ratio of the two light beams and appears to be very robust against absolute changes of these intensities. The latter result provides valuable information for the development of all-optical circuits which would require to handle different signal strengths for the input and output levels.
The ongoing demand for more computational power and faster rates for data transfer and storage are the driving force for the development of all-optical devices, i.e. devices where signalling occurs via photons rather than electrons. Even though optical data transfer using glass fibres are highly efficient, the requirement of electro-optical or opto-electrical conversion to adapt it to periphery limits the transfer rate. All-optical devices require to control light from one source by light from another source, avoiding intermediate conventional electronic connections. First steps towards the development of such devices have been set by exploiting nonlinear optical materials1. Alternatively, organic fluorophores and their ability to strongly interact with a light field attracted researchers to demonstrate an optical transistor at the single molecule level2. However, in all these experiments it needed many photons to control a few photons, and not the other way round as it would be desirable for designing an all optical circuit.
An alternative strategy to accomplish devices that run on photons rather than electrons is based on the exploitation of photochromic molecules, i.e. molecules that can be interconverted between two bistable forms induced by light. Photochromic systems based on cis-trans isomerisation (stilbenes, azobenzenes)3,4,5, or photocyclization reactions (fulgides, diarylalkenes, azulenes, spiropyrans)6,7,8,9,10,11,12, have been studied intensively in the past. It has been found that photochromic molecules of the dithienylcyclopentene type feature a high fatigue resistance, and that these molecules are thermally stable in either conformation, which supresses unwanted non-optical back-reactions. However, the molecules of this family feature only a very weak contrast between the optical signals registered in their two conformations, which is a serious drawback when aiming at data processing at the molecular level.
As a way out of this, Irie and coworkers synthesized more complex tailor-made molecules that consisted of highly fluorescent chromophores covalently linked to a photochromic building block13,14,15. This approach combined the requested properties of high-fatigue resistance and high fluorescence quantum yield16,17,18. Following the same strategy as Irie et al. we have demonstrated the functionality of an optical transistor, recently19. In order to do so, we studied a photochromic system that corresponds to a molecular triad consisting of two perylene bisimide (PBI) units that are covalently linked to a 1,2-bis(2-methyl-5-phenyl-3-thienyl)perfluorocyclopentene (DCP), see fig. 1. The DCP unit undergoes a photocyclization reaction from the open to the closed form upon irradiation with light in the UV spectral range (280 nm–350 nm) and vice versa upon irradiation with light in the visible spectral range (500 nm–650 nm). In these experiments the photochromic molecule was switched between its bistable conformations using light in the UV (300 nm) and red (635 nm) spectral range, respectively, and the fluorescence intensity of the PBI chromophores was probed with a laser operated in the green (514 nm) spectral range17,18,19,20. This illumination scheme enabled us to modulate the fluorescence output from the PBI with high contrast ratio. An order of magnitude estimate yielded that a few hundred to thousand photons in the conversion beams were sufficient to controll the emission/suppresion of hundreds of millions of photons from the chromophores.
Figure 1. Chemical structure of the photochromic triad consisting of two perylene bisimide (PBI) linked to a 1,2-bis(2-methyl-5-phenyl-3-thienyl)perfluorocyclopentene (DCP).
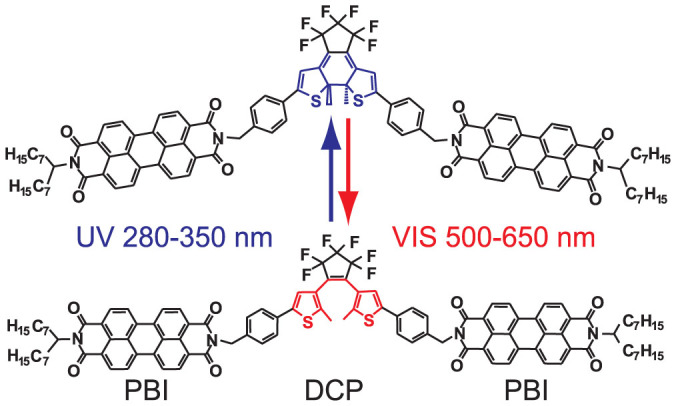
The DCP unit undergoes a photocyclization reaction from the open (bottom) to the closed form (top) upon irradiation with light in the spectral range of 280 nm to 350 nm (blue arrow) and vice versa upon irradiation with the light in the spectral range of 500 nm to 650 nm (red arrow).
However, it turned out that the excitation light in the green spectral range (514 nm) not only induced the fluorescence from the PBIs but also triggered the photocyclization reaction of the photoswitch, i.e. there was substantial crosstalk between one of the conversion channels and the read out channel. Accordingly, the PBI fluorescence intensity can also be modulated without the conversion beam in the red (635 nm) spectral range. Here we demonstrate that for a proper choice of the mutual intensities of the UV and the green light, a modulation of the perylene fluorescence with a contrast ratio of more than 60% can be accomplished. For this simplified two-beam experiment we present a thorough experimental characterisation of the achievable fluorescence intensity modulation depth as a function of the intensity ratio of the conversion and the probe beam. In order to quantify the evolution of the photoreaction of photochromic molecules a lot of efforts have been taken during the last two decades. Most of this work was based on experiments that monitored the absorption signals6,7,8,21,22,23,24,25,26,27,28,29. However, a simple relation between the macroscopic absorbance of the sample and the concentration of the photochromes, as for example provided by Lambert Beer's law, does not hold, because the concentration of the absorbing species varies in time (and space) due to the photoreaction, which in turn leads to uncontrollable variations of the light intensity that is “seen” by the photochromic molecules. This can be overcome by working with absorption cells where the solution is continuously stirred29, but remains an obstacle for immobilised samples and complicates to find an analytical description of the kinetics of the photoconversion as a function of the irradiation intensities22,23,30. On first sight, using the emitted fluorescence for monitoring the photoconversion seems to be even worse, because the number of photons emitted from a fluorophore depends on the number of photons that have been initially absorbed. However, detecting fluorescence instead of absorbance offers superior sensitivity (as has been testified by many single-molecule spectroscopy papers31,32,33,34), which allows to reduce the optical thickness of the sample to very low concentrations of the emitters. This allows us to neglect any spatial dependence of the excitation intensity across the sample and to use a uniform excitation intensity to model the photoreaction. Following this route, we have developed a kinetic model that describes quantitatively the fluorescence modulation depth as a function of the intensities of the conversion and probe beam.
Results and Discussion
In order to study the influence of the probe beam on the modulation of the fluorescence signal we fixed the intensity of the UV light (300 nm) to 0.124 W/cm2 and varied the intensity at 514 nm between 0.030 W/cm2 and 4.448 W/cm2. Four typical examples are shown in fig. 2a as a function of the intensity of the UV beam. Applying the illumination scheme as sketched in the inset of fig. 2a, i.e. alternating time intervals of 7.2 s duration with either the probe and conversion beams simultaneously or with the probe beam only, yields a telegraph-style modulation of the fluorescence intensity such that the high-signal levels correspond to the time intervals without UV irradiation. Moreover, the higher the intensity of the 514 nm radiation is chosen, the faster is the recovery to the high-signal level upon blocking the UV. For the highest intensity of the probe beam, trace 4 in fig. 2a, the high-signal level shows a plateau, which indicates that the photocyclization reaction of the DCP reaches a steady state. All modulation traces are overlaid by a gradual decrease of the total fluorescence intensity indicating the photobleaching of the PBI units.
Figure 2.
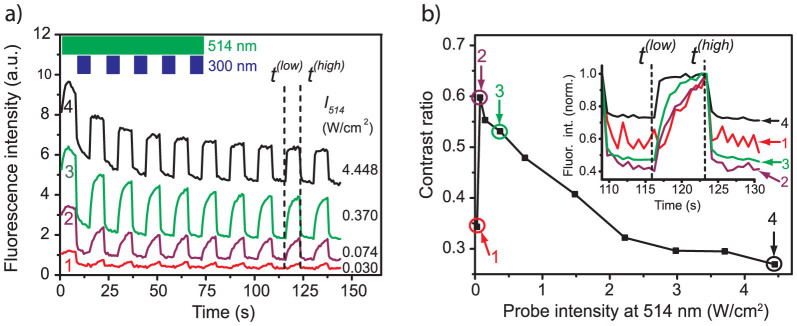
(a) Examples for the modulation of the fluorescence intensity as a function of the intensity of the probe beam at 514 nm. The intensity at 300 nm has been fixed to 0.124 W/cm2. The vertical axis has been normalised to 10 arbitrary units and is valid for trace 4. For better visibility traces 1 and 2 have been multiplied by a factor of 25 and trace 3 has been multiplied by a factor of 10. The inset top left shows the timing sequence of the conversion and the probe beams. The dashed vertical lines indicate the points in time that have been used to determine the contrast ratio of the fluorescence modulation, see text. (b) Contrast ratio of the fluorescence modulation determined at times t(low) and t(high) as a function of the intensity of the probe beam at 514 nm. The data points numbered 1–4 have been calculated from the corresponding traces shown in (a). The inset displays the normalised fluorescence intensity of the traces 1–4 from part (a) around the considered time interval.
For a more quantitative analysis of the fluorescence modulation depth we define the fluorescence contrast ratio as
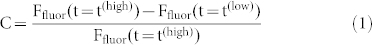 |
where Ffluor(t = t(high)) refers to the fluorescence intensity at t = t(high) and Ffluor(t = t(low)) to the fluorescence intensity at t = t(low), respectively. In order to avoid artifacts due to initial photobleaching we have chosen t(low) and t(high) such (i.e. after eight modulation cycles, see fig. 2a) that the fluorescence signal between successive high-signal periods does not change by more than the shot noise which amounts to 10%. The resulting contrast ratio is displayed in fig. 2b as a function of the intensity of the probe beam. It uncovers a steep rise of the contrast for probe intensities below 0.074 W/cm2 to a value of about C ≈ 0.6 followed by a monotonic decrease to C ≈ 0.25 for the highest applied probe intensity. The relatively low contrast of about 0.35 that is observed for the lowest probe intensity, marked 1 in fig. 2b, demonstrates that this probe intensity is insufficient to drive the photoreaction into steady state during the observation interval of about 7 s. Although the total fluorescence intensity increases for the higher probe intensities, the contrast ratio decreases, because the background fluorescence, which is not affected by the illumination sequences, increases as well. In other words, the modulation rests on an increasing background leading to a relative decrease of the amplitude of the modulation. This becomes clearly visible in the inset of fig. 2b, which shows the observed fluorescence intensities around the considered times on a normalised scale.
Next we reversed the concept of the experiment and fixed the intensity of the probe beam to 1.48 W/cm2 and studied the modulation of the fluorescence intensity as a function of the intensity of the UV conversion beam that was varied between 0.011 W/cm2 and 0.698 W/cm2. Three typical examples are displayed in fig. 3a which follows a similar setup as fig. 2a. Again we observe a telegraph-style modulation of the fluorescence intensity which is more pronounced for higher UV intensities. At the begin of the experiments traces 2 and 3 show a gradual decrease of the overall fluorescence intensity, whereas trace 1 features a slight increase of the fluorescence. As before, the decrease of the fluorescence can be understood in terms of bleaching of the PBI units. The increase of the fluorescence for low UV intensities is due to the fact that the sample has not been preinitialised to the high-signal level prior to the experiment. Therefore the subpopulation of the triads that reside in the closed state is gradually converted to the open state during the first few modulation cycles. This effect is overcompensated by the bleaching in traces 2 and 3. In fig. 3b the contrast ratio is displayed as a function of the intensity of the UV conversion beam, which reveals a monotonic rise for increasing the intensity of the UV beam. This is clearly visible in the inset which shows the fluorescence modulation on a normalised scale.
Figure 3.
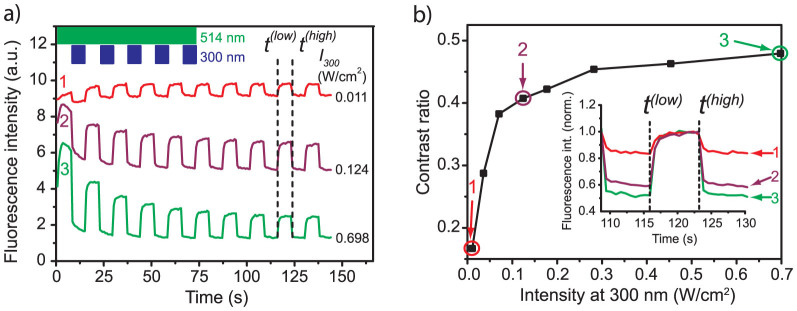
(a) Examples for the modulation of the fluorescence intensity as a function of the intensity of the conversion beam at 300 nm.The intensity at 514 nm has been fixed to 1.482 W/cm2. The vertical axis has been normalised to 10 arbitrary units and is valid for trace 3. For clarity, traces 1 and 2 have been offset by 5.6 and 2.8 units, respectively. The inset top left shows the timing sequence of the conversion and the probe beams. The dashed vertical lines indicate the points in time that have been used to determine the contrast ratio of the fluorescence modulation, see text. (b) Contrast ratio of the fluorescence modulation determined at times t(low) and t(high) as a function of the intensity of the conversion beam at 300 nm. The data points numbered 1–3 have been calculated from the corresponding traces shown in (a). The inset displays the normalised fluorescence intensity of the traces 1–3 from part (a) around the considered time interval.
Kinetic model
In the following we will develop a model that allows for a quantitative description of the fluorescence modulation as a function of the intensities of the conversion and the probe beam. Therefore we first model the photoreaction kinetics of the triads, and then connect the result to the fluorescence intensity of the triads in the open and closed state. In order to keep things simple we treat the total number of triads during the experiments as a constant.
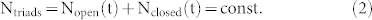 |
Hence the change of the number of triads in either conformation is given by
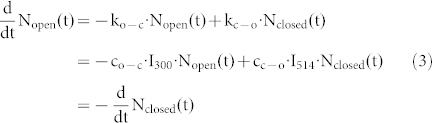 |
where ko-c (kc-o) refers to the rate for the open → closed (closed → open) photocyclization reaction of the DCP upon irradiation with light at 300 nm (514 nm). For convenience, we have extracted the illumination intensities at 300 nm and 514 nm, referred to as I300 and I514, from the rate constants in the second line of eq.(3). Given the low optical thickness of the sample we neglect any spatial dependence of the intensities of I300 and I514 across the sample and assume that all triads in the focal spot experience the same intensity of the respective light beams. For steady-state conditions, 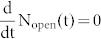 , this yields together with eq.(2),
, this yields together with eq.(2),
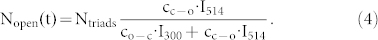 |
This corresponds to the number of open triads in the presence of both radiations, i.e. to Nopen(t = t(low)). The corresponding Nopen(t = t(high)) is obtained from eq.(4) for I300 = 0, and yields Nopen(t = t(high)) = Ntriads.
The fluorescence intensity Ffluor(t) that can be detected from the triads is given by
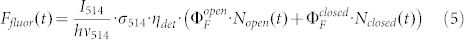 |
where 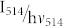 corresponds to the photon flux at 514 nm, σ514 to the absorption cross section at this wavelength, ηdet to the overall fluorescence detection efficiency of the setup, and
corresponds to the photon flux at 514 nm, σ514 to the absorption cross section at this wavelength, ηdet to the overall fluorescence detection efficiency of the setup, and 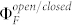 to the fluorescence quantum yield of the triad in the open/closed state of the DCP, respectively. Using eq.(2) and inserting the expressions derived for Nopen(t = t(low)) and Nopen(t = t(high)) into eq.(5), yields the contrast ratio as a function of the illumination intensities
to the fluorescence quantum yield of the triad in the open/closed state of the DCP, respectively. Using eq.(2) and inserting the expressions derived for Nopen(t = t(low)) and Nopen(t = t(high)) into eq.(5), yields the contrast ratio as a function of the illumination intensities
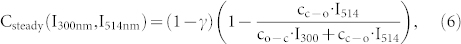 |
where 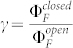 denotes the ratio of the fluorescence quantum yields of the triads in the open and closed state, respectively. Rewriting eq.(6) as
denotes the ratio of the fluorescence quantum yields of the triads in the open and closed state, respectively. Rewriting eq.(6) as
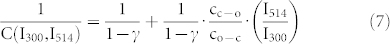 |
yields a simple linear relation between the inverse fluorescence contrast ratio and the ratio of the illumination intensities at 514/300 nm. In fig. 4 the data obtained for 1/C are plotted as a function of 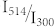 together with two fits that will be discussed later. In general the data from the different experiments follow the expected linear trend, confirming that indeed the ratio
together with two fits that will be discussed later. In general the data from the different experiments follow the expected linear trend, confirming that indeed the ratio 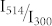 is the relevant parameter that determines the achievable fluorescence contrast ratio.
is the relevant parameter that determines the achievable fluorescence contrast ratio.
Figure 4.
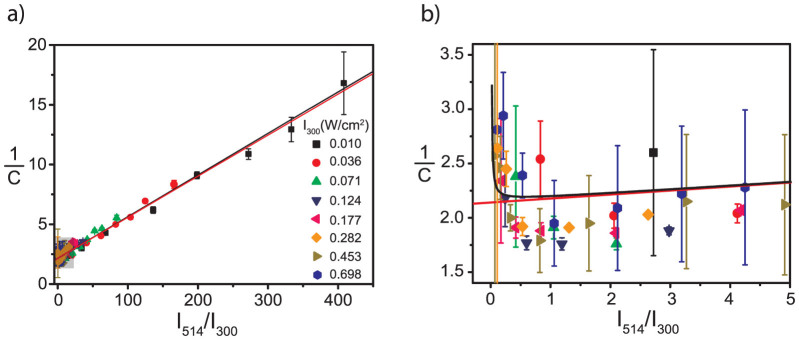
(a) Inverse fluorescence contrast ratio as a function of intensity ratio 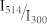 . Different symbols refer to different absolute values of the excitation intensity at 300 nm. (b) An expanded view of the data for small
. Different symbols refer to different absolute values of the excitation intensity at 300 nm. (b) An expanded view of the data for small 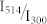 ratios boxed in (a). The red line corresponds to a fit of the data using eq.(8) which yields b = 0.86(±0.08) and
ratios boxed in (a). The red line corresponds to a fit of the data using eq.(8) which yields b = 0.86(±0.08) and 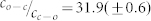 ; and the black line corresponds to a fit of the data using eq.(10) which yields b = 0.85(±0.08) and
; and the black line corresponds to a fit of the data using eq.(10) which yields b = 0.85(±0.08) and 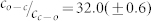 .
.
However, a linear fit of the data to eq.(7) that leaves both the intersection and the slope as a free parameter yields γ = 0.52(±0.02) (Fig. S1a, supporting information), which is in striking contrast with previous work19. There it was found that the ratio of the fluorescence quantum yields of the triads in the open and closed state is about 0.05–0.1. Therefore, we fixed the value of γ to 0.1 and left only the slope as a free parameter. Unfortunately, this approach was not successful (Fig. S1b, supporting information). Yet, closer inspection of fig. 3a (see also Fig. S2, supporting information) reveals that the envelope of the high-signal levels decays faster with respect to the envelope of the low-signal levels. Moreover, these decays are generally the faster the higher the applied UV intensity. Both observations hint for an additional background that contributes to the signal and that does not bleach as fast as the signal from the triads. As shown in more detail in the supporting information such an additional background leads to an offset in the inverse contrast ratio. As long as the contribution from the additional background does not change during the time interval between t(high) and t(low) this can be taken into account pragmatically by adding an offset, here denoted as b, to the inverse contrast ratio,
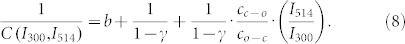 |
Essentially, this modification decouples the fit parameters intersection and slope from each other. Again we kept γ = 0.1 and the resulting fit is shown as the red line in fig. 4. Except for very small values of 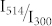 , see fig. 4b, we find a very good agreement between the fit and the data. However, for small values of the intensity ratio the inverse contrast ratio increases, which is not reflected by the model. This discrepancy might have two origins: i) Low I514 intensities are not sufficient to drive the photoconversion of the triads into steady state, see for example fig. 2a trace 1, and the prerequisites of our model calculation are not fulfilled. ii) High I300 intensities might also induce fluorescence from the PBI units which corresponds to crosstalk, which is also not considered in the model. However, the latter can easily be incorporated into the model by modifying eq.(5) to
, see fig. 4b, we find a very good agreement between the fit and the data. However, for small values of the intensity ratio the inverse contrast ratio increases, which is not reflected by the model. This discrepancy might have two origins: i) Low I514 intensities are not sufficient to drive the photoconversion of the triads into steady state, see for example fig. 2a trace 1, and the prerequisites of our model calculation are not fulfilled. ii) High I300 intensities might also induce fluorescence from the PBI units which corresponds to crosstalk, which is also not considered in the model. However, the latter can easily be incorporated into the model by modifying eq.(5) to
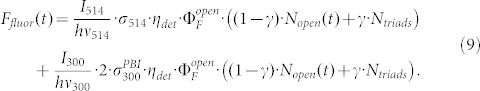 |
Here 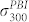 denotes the absorption cross section of the PBI unit at 300 nm which has been determined from a pure PBI sample to 9.8·10−18 cm2. Following the same formalism as above this yields
denotes the absorption cross section of the PBI unit at 300 nm which has been determined from a pure PBI sample to 9.8·10−18 cm2. Following the same formalism as above this yields
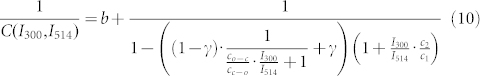 |
for the inverse fluorescence contrast ratio. In eq.(10) we have used the abbreviations 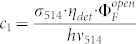 and
and 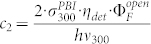 . The fit of the data to eq.(10) for γ = 0.1 is shown in fig. 4 by the black line and reproduces the increase of 1/C if
. The fit of the data to eq.(10) for γ = 0.1 is shown in fig. 4 by the black line and reproduces the increase of 1/C if 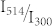 approaches zero. The values that can be extracted for b and
approaches zero. The values that can be extracted for b and 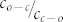 from either fit (eq.(8) or eq.(10)) are given in the figure caption and do not show significant differences. From the latter value we can obtain the relative yield for the photocyclization reaction of the DCP unit. The rates for these conversions ko-c and kc-o, see eq.(3) can be rewritten in the following form
from either fit (eq.(8) or eq.(10)) are given in the figure caption and do not show significant differences. From the latter value we can obtain the relative yield for the photocyclization reaction of the DCP unit. The rates for these conversions ko-c and kc-o, see eq.(3) can be rewritten in the following form
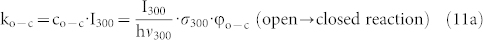 |
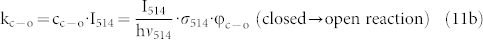 |
where 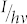 corresponds to the photon flux at the respective wavelength, σ to the absorption cross section at that wavelength, and φ to the quantum yield of the respective photoconversion process. From eqs.(11) it follows
corresponds to the photon flux at the respective wavelength, σ to the absorption cross section at that wavelength, and φ to the quantum yield of the respective photoconversion process. From eqs.(11) it follows
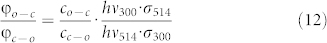 |
for the ratio of the quantum yields. Using 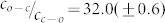 as obtained from the fit, we find
as obtained from the fit, we find 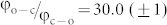 for the ratio of the reaction yields of the photocyclization reaction. This number is in accordance with the value of about 10 that was obtained from a rough estimate in previous work19.
for the ratio of the reaction yields of the photocyclization reaction. This number is in accordance with the value of about 10 that was obtained from a rough estimate in previous work19.
Conclusions
We have demonstrated that photochromic PBI-DCP-PBI triads can be used to modulate optical signals with high contrast ratio. A kinetic model has been developed that allows to describe quantitatively the fluorescence modulation of the triads as a function of the intensity of the probe and the conversion beam. This reveals that the achievable contrast of the fluorescence modulation is very robust against variations of the absolute intensities of both irradiations as long as the ratio of their intensities is fixed with respect to each other. This is an important finding with regard to the development of all-optical circuits that require different signal strength for the input levels of the subunits.
Methods
Sample preparation
The PBI-DCP-PBI triads were synthesized according to the protocols published in19. For quantitative photoconversion experiments the triads were immobilized in a low molecular weight polystyrene matrix. Therefore two 100 μl solutions of toluene, one containing 3·10−6 mol/l of the triads, and one containing a polystyrene/toluene mixture in a mass ratio of 1:3 were prepared. Equal volume fractions of these two solutions were mixed. From the mixture about 30 μl were dropped on a microscope coverslip. After a waiting time of about 5 minutes a second coverslip was put on top of the sample producing a polystyrene film with a thickness in the order of 10 μm that contains the triads at a concentration of about 1.4·10−5 mol/l, which corresponds to an estimated optical density of about OD ≈ 1.1 ·10−3.
The samples where mounted in a home-built inverted microscope and illuminated with light at two different wavelengths. Radiation in the visible at 514 nm is provided by an Ar ion laser (ALC 60, Laserlight Showdesign) and referred to as the probe beam. Light at 300 nm stems from fourth-harmonic generation in two consecutive steps. In the first step a fequency doubler (SHG Autotracker, APE Angewandte Physik & Elektronik GmbH) generates the second harmonic from the output of an optical parametric oscillator (OPO, APE Angewandte Physik & Elektronik GmbH) that is pumped by a pulsed Titanium:Sapphire laser (Tsunami, Spectra Physics). In the second step the output of this unit is frequency doubled in a home-built device that contains a type 1 beta borium borate (BBO) crystal. The radiation at 300 nm is referred to as the conversion beam. The conversion beam was weakly focused onto a elliptical spot with the area of 4.2·10−3 mm2 on the sample using a lens of f = 50 mm. The probe beam is reflected via a dichroic mirror DM (Q520LP, AHF) and focused into the backfocal plane of a microscope objective MO (Microthek 20×, NA = 0.5) by a lens with a long focal length (f = 250 mm) which yields a spot with a diameter of 0.17 mm (corresponding area 2.3·10−2 mm2) on the sample. The fluorescence from the sample is collected by the same objective, transmitted through the dichroic mirror and passes a bandpass filter (AHF, HQ 525 LP, transmission 525–725 nm, AHF) to suppress residual stray light. The sample was illuminated continuously by the probe beam and every 7.2 s it was illuminated for 7.2 s by both beams using an electromechnical shutter that could be operated with about 2 ms temporal accuracy. The resulting emission is registered with a back-illuminated EMCCD camera (iXon DV877ECS, Andor) that was read out every 720 ms (frame rate 1.4 Hz). The exposure time of the camera was 100 ms per frame.
Author Contributions
M.P. constructed the setup, M.G. and M.P. performed the optical experiments, K.G. and P.B. synthesised the triads, M.T. supervised the chemical synthesis, J.K. supervised the optical experiments, and J.K. and M.T. designed the research. M.P., M.T. and J.K. wrote the paper.
Supplementary Material
Supporting materials
Acknowledgments
We thank S. Frank and Prof. Dr. S. Kümmel for fruitful discussions. Financial support from the German Science Foundation (DFG/GRK 1640) and the Bavarian State Ministry of Science, Research, and the Arts for the Collaborative Research Network “Solar Technologies go Hybrid” is gratefully acknowledged.
References
- Chang D. E., Sřrensen A. S., Demler E. A. & Lukin M. D. A single-photon transistor using nanoscale surface plasmons. Nat. Phys. 3, 807–812 (2007). [Google Scholar]
- Hwang J. et al. A single-molecule optical transistor. Nature 460, 76–80 (2009). [DOI] [PubMed] [Google Scholar]
- Sension R. J., Repinec S. T., Szarka A. Z. & Hochstrasser R. M. Femtosecond laser studies of the cis-stilbene photoisomerization reactions. J. Chem. Phys. 98, 6291–6315 (1993). [Google Scholar]
- Ichimura K., Suzuki Y., Seki T., Hosoki A. & Aoki K. Reversible change in alignment mode of nematic liquid crystals regulated photochemically by command surfaces modified with an azobenzene monolayer. Langmuir 4, 1214–1216 (1988). [Google Scholar]
- Fischer T., Ruhmann R. & Seeboth A. Photochemically induced structure transfer from analogous azobenzenes and stilbenes onto a liquid crystalline phase. J. Chem. Soc., Perkin Trans. 2, 1087–1090 (1996). [Google Scholar]
- Yokoyama Y. Fulgides for Memories and Switches. Chem. Rev. 100, 1717–1739 (2000). [DOI] [PubMed] [Google Scholar]
- Handschuh M., Seibold M., Port H. & Wolf H. C. Dynamics of Cyclization Reaction in Photochromic Furyl Fulgides. J. Phys. Chem. A 101, 502–506 (1997). [Google Scholar]
- Brust T. et al. Increasing the efficiency of the ring-opening reaction of photochromic indolylfulgides by optical pre-excitation. Chem. Phys. Lett. 489, 175–180 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gobbi L. et al. Photoswitchable Tetraethynylethene-Dihydroazulene Chromophores. Helv. Chim. Acta 84, 743–777 (2001). [Google Scholar]
- De Waele V., Schmidhammer U., Mrozek T., Daub J. & Riedle E. Ultrafast Bidirectional Dihydroazulene/Vinylheptafulvene (DHA/VHF) Molecular Switches: Photochemical Ring Closure of Vinylheptafulvene Proven by a Two-Pulse Experiment. J. Am. Chem. Soc. 124, 2438–2439 (2002). [DOI] [PubMed] [Google Scholar]
- Berkovic G., Krongauz V. & Weiss V. Spiropyrans and Spirooxazines for Memories and Switches. Chem. Rev. 100, 1741–1754 (2000). [DOI] [PubMed] [Google Scholar]
- Zhang J., Zou Q. & Tian H. Photochromic Materials: More Than Meets The Eye. Adv. Mater. 25, 378–399 (2013). [DOI] [PubMed] [Google Scholar]
- Kawai T., Kim M.-S., Sasaki T. & Irie M. Fluorescence switching of photochromic diarylethenes. Opt. Mater. 21, 275–278 (2003). [Google Scholar]
- Irie M., Fukaminato T., Sasaki T., Tamai N. & Kawai T. Organic Chemistry: A Digital Fluorescent Molecular Photoswitch. Nature 420, 759–760 (2002). [DOI] [PubMed] [Google Scholar]
- Fukaminato T. et al. Photochromism of Diarylethene Single Molecules in Polymer Matrices. J. Am. Chem. Soc. 129, 5932–5938 (2007). [DOI] [PubMed] [Google Scholar]
- Lang E., Würthner F. & Köhler J. Photophysical Properties of a Tetraphenoxy-Substituted Perylene Bisimide Derivate Characterized by Single-Molecule Spectroscopy. ChemPhysChem 6, 935–941 (2005). [DOI] [PubMed] [Google Scholar]
- Lang E. et al. Comparison of the Photophysical Parameters for Three Perylene Bisimide Derivatives by Single-Molecule Spectroscopy. ChemPhysChem 8, 1487–1496 (2007). [DOI] [PubMed] [Google Scholar]
- Würthner F. Perylene Bisimide Dyes as Versatile Building Blocks for Functional Supramolecular Architectures. Chem. Commun. 1564–1579 (2004). [DOI] [PubMed] [Google Scholar]
- Pärs M. et al. An Organic Optical Transistor Operated under Ambient Conditions. Angew. Chem. Int. Ed. Engl. 50, 11405–11408 (2011); Angew. Chem. 123, 11607–11610 (2011). [DOI] [PubMed] [Google Scholar]
- Pärs M., Gräf K., Bauer P., Thelakkat M. & Köhler J. Optical gating of perylene bisimide fluorescence using dithienylcyclopentene photochromic switches. Appl. Phys. Lett. 103, 221115–221118 (2013). [Google Scholar]
- Ulrich K. et al. Photochromic thiophenefulgides. Photokinetics of two isopropyl derivatives. Chem. Phys. 154, 311–322 (1991). [Google Scholar]
- Maafi M. & Brown R. G. The kinetic model for AB(1 Φ) systems: A closed-form integration of the differential equation with a variable photokinetic factor. J. Photochem. Photobiol., A 187, 319–324 (2007). [Google Scholar]
- Sworakowski J., Janus K. & Nešpůrek S. Kinetics of photochromic reactions in condensed phases. Adv. Colloid Interface Sci. 116, 97–110 (2005). [DOI] [PubMed] [Google Scholar]
- Maafi M. The potential of AB(Φ) systems for direct actinometry. Diarylethenes as successful actinometers for the visible range. Phys. Chem. Chem. Phys. 12, 13248–13254 (2010). [DOI] [PubMed] [Google Scholar]
- Vorobiev A. Kh. & Menshykau D. Kinetics of photochemical reactions in optically dense media with reagent diffusion. J. Photochem. Photobiol., A 199, 303–310 (2008). [Google Scholar]
- Florea L., Diamond D. & Benito-Lopez F. Photo-Responsive Polymeric Structures Based on Spiropyran. Macromol. Mater. Eng. 297, 1148–1159 (2012). [Google Scholar]
- Dürr H. Perspectives in Photochromism: A novel System based on the 1,5-Electrocyclization of heteroanalogous Pentadienyl Anions. Angew. Chem. Int. Ed. Engl. 28, 413–431 (1989). [Google Scholar]
- Vázquez A. & Nudelman N. S. Photokinetics of two novel photochromic diarylethenes derived from benzothiophene. Int. J. Chem. Kinet. 44, 736–744 (2012). [Google Scholar]
- Maafi M. Useful Spectrokinetic Methods for the Investigation of Photochromic and Thermo-Photochromic Spiropyrans. Molecules 13, 2260–2302 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pariani G., Bianco A., Castagna R. & Bertarelli C. Kinetics of Photochromic Conversion at the Solid State: Quantum Yield of Dithienylethene-Based Films. J. Phys. Chem. A 115, 12184–12193 (2011). [DOI] [PubMed] [Google Scholar]
- [Basché T. h., Moerner W. E., Orrit M. & Wild U. P. E. (Eds.)] Single Molecule Optical Detection, Imaging and Spectroscopy. (Wiley-VCH, Weilheim, Germany, 1997). [Google Scholar]
- [Rigler R. & Vogel H. (Eds.)] Single Molecules and Nanotechnology. (Springer, Berlin Heidelberg, Germany, 2008). [Google Scholar]
- [Zander, C., Enderlein, J. & Keller, R. A. (Eds.)] Single Molecule Detection in Solution, Methods and Application. (Wiley-VCH, Berlin, Germany, 2003). [Google Scholar]
- [Gräslund A., Rigler R. & Widengren J. (Eds.)] Single Molecule Spectroscopy in Chemistry, Physics and Biology. (Springer, Heidelberg, Germany 2010). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting materials


