Constructing molecular structures on periodic superstructure of graphene/Ru(0001)

Abstract

We review the way to fabricate large-scale, high-quality and single crystalline graphene epitaxially grown on Ru(0001) substrate. A moiré pattern of the graphene/Ru(0001) is formed due to the lattice mismatch between graphene and Ru(0001). This superstructure gives rise to surface charge redistribution and could behave as an ordered quantum dot array, which results in a perfect template to guide the assembly of organic molecular structures. Molecules, for example iron phthalocyanine and C₆₀, on this template show how the molecule–substrate interaction makes different superstructures. These results show the possibility of constructing ordered molecular structures on graphene/Ru(0001), which is helpful for practical applications in the future.

1. Introduction

Graphene has been a hot subject in the scientific world since its discovery in 2004 [1,2]. It is an ideal two-dimensional material that consists of only one layer of carbon atoms and has so many amazing properties that are not only extremely important in science [3–5], but also show great potential in future applications such as stretchable electrodes [6] and high-performance transistors [7]. The original method to obtain graphene was to peel off graphite by adhesive tapes [1,2]. However, this method is suitable only for a small amount of production with a lateral size of several micrometres, which cannot meet the needs of applications in real industry. In order to solve this problem, other preparation methods have been extensively developed in the past few years [8–13]. Among them, epitaxial growth on Ru(0001) substrate can produce high-quality, single crystalline graphene on the centimetre scale [8], thus being an excellent candidate for future industrial consideration. Moreover, the periodically corrugated surface owing to lattice mismatch between graphene and Ru(0001) has been proved to be a good template to guide the adsorption and assembly of functional nanostructures, including organic molecular structures, which may provide a fundamental way for fabricating functional devices [14–17].

In this review, we mainly focus on how the moiré pattern of graphene/Ru(0001) affects the behaviours of different molecules and the physics beneath. We begin with a brief description of the experimental details for graphene/Ru(0001) production and its basic geometrical structure in §2. Then, in §3, we talk about the ordered quantum dot array character of the corrugated graphene sheet, which is closely related to its unique moiré structure on Ru(0001). As we reveal the nanostructured and inhomogeneous nature of graphene, §§4–6 discuss step-by-step its effect on adsorption and assembly behaviours of different organic molecules. We analyse in detail the physics behind these phenomena and then close with a brief summary in §7.

2. Epitaxial growth of graphene on Ru(0001)

The Ru crystal was commercially obtained, with its (0001) surface being polished to a roughness of less than 0.03 μm. After being cleaned ultrasonically in high-purity acetone and ethanol several times to remove organic contamination on the surface, the Ru crystal was transferred into an ultrahigh vacuum chamber for cycles of argon-ion sputtering. The epitaxial graphene layer was fabricated using the following process: ethylene (purity 99.9%) was filled into the vacuum chamber and kept at a pressure of 1×10⁻⁵ Pa and then the temperature was slowly raised to 1300 K, where it was maintained for 20 min, after which the sample was slowly cooled down to room temperature (RT). Graphene gradually formed during the thermal annealing process, as characterized in situ by low-energy electron diffraction (LEED) and scanning tunnelling microscopy (STM).

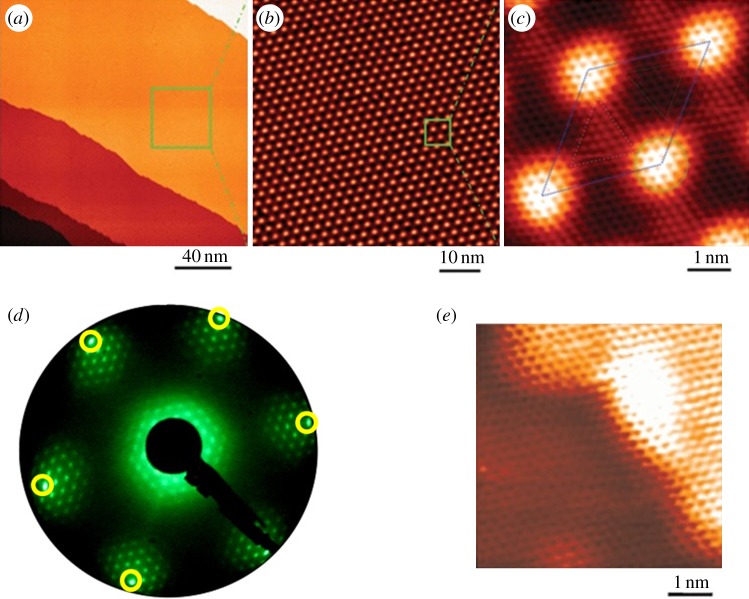
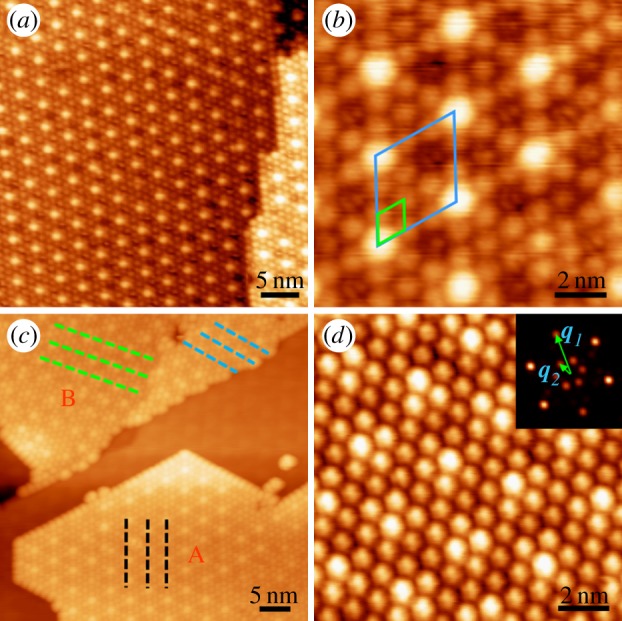
Figure 1a shows a large-scale STM topography of epitaxial graphene on Ru(0001) (G/Ru in the following) [8]. The metal surface is fully covered by atomically flat, single-layer graphene. A zoom-in image is shown in figure 1b, which clearly displays the hexagonal moiré pattern in real space. The average distance between the neighbouring moiré spots is 3 nm, that is, about 12 times the lattice constant of graphene and 11 times that of Ru. Figure 1c is an atomic resolution image showing one unit cell of the moiré pattern. In figure 1c, 12 graphene atoms can be counted between the centres of the bright moiré spots, which is consistent with the measurement from figure 1b.

Figure 1.

STM and LEED characterization of epitaxial graphene on Ru(0001) surface. (a) The atomically flat graphene flake extends over the entire Ru(0001) surface. (b) The hexagonal moiré pattern formed owing to lattice mismatch between graphene and Ru substrate. (c) Atomic-resolution image of one unit cell of the moiré pattern. (d) LEED pattern indicates the single crystalline nature of the graphene sheet. (e) Atomic resolution STM image taken at step edges indicates the continuous growth of graphene across whole Ru terraces. (Online version in colour.)

The lattice mismatch between graphene and the Ru(0001) surface causes the graphene overlayer to have a corrugated surface (with a corrugation of approx. 0.1 nm), producing a strained superlattice with an average in-plane tension of ca +0.81%. Within each unit cell, the superlattice consists of three structural regions: the bright region (marked by the circle in figure 1c) is bowed up into a ridge, the dark region (marked by the dashed triangle in figure 1c) is bowed down into a valley and the intermediate region (marked by the dash-dotted triangle in figure 1c) is of medium height. In the valley region, each atom of the six-member C ring sits right on top of the corresponding Ru atoms underneath, whereas, in the medium height region, the six-member C ring sits on top of one Ru atom. Owing to the different atomic stacking modes of the three typical regions, we call them atop site (bright region), fcc site (intermediate region) and hcp site (dark region), respectively. It is necessary to mention that at the atop sites, the honeycomb lattice of graphene can be clearly resolved. However, at the fcc and hcp sites, the overlayer is seen to have a hexagonal instead of honeycomb lattice, because these sites are closer to the substrate and exhibit diatomic resolution [18].

Figure 1d displays the LEED pattern of G/Ru [8]. The circled diffraction spots originate from the Ru(0001) substrate, and the surrounding spots are contributed by the periodic moiré structure. When the electron beam spot is moved across the whole sample surface, no appreciable change and/or rotation of the diffraction pattern is observed, which means that the epitaxial graphene stretches across the whole sample surface and is single crystalline. The atomic resolution STM image at surface steps (figure 1e) further demonstrates that the graphene overlayer remains perfectly crystalline over the steps without bond breakage or defects.

By combining the STM and LEED results, we can see that high-quality, centimetre scale, continuous and single crystalline graphene sheet is obtained epitaxially on Ru(0001) surface using the above-described thermal annealing technique. Considering the decomposition of ethylene molecules on Ru surface, the growth of graphene is also expected to be self-limited, thus offers an easy controlled way for graphene production.

3. Graphene-based quantum dot array

The unique corrugated moiré structure results in inhomogeneous physical and chemical properties at different sites across the surface. It has been shown that the hills (atop sites) have a 0.25 eV higher local work function compared with the valley regions (fcc and hcp sites), where the graphene sheet is closely bound to the substrate [19]. Photoemission results also reveal a splitting in the C 1s core-level spectrum, indicating the existence of two species of carbon on G/Ru owing to the corrugation, where about one-third has a 0.6 eV lower binding energy [20]. However, splitting in the valence bands owing to surface corrugation was not found [19]. This problem may be resolved if we treat the hills as isolated quantum dots, without dispersion.

In order to illustrate the quantum-dot-like behaviour of the hills in the moiré structure, we did dZ/dV spectroscopy at 5 K [21]. The spectra were acquired with engaged loop gain using a lock-in technique with a 10 mV sinusoidal modulation signal at 793 Hz which is superposed to the bias voltage U. Bias voltage is imposed on the sample, and positive bias voltages correspond to the tunnelling of electrons from the tip to unoccupied states in the sample.

Figure 2a shows the spectra taken at hills (orange, grey curve) and valleys (black curve). Each curve was averaged from more than 30 data points and can be considered as typical spectrum. A series of resonances at distinct tunnelling voltages are clearly displayed in both curves but the peak position and intensity differ dramatically. One of these peaks, the second lowest one, shows a behaviour that deviates from the others, which are the well-known field emission resonances (FERs), sometimes called image potential states, ubiquitous at tip–surface junctions [22,23]. The FER energies may be used to determine the local work function, whereby a decrease in energy indicates a decrease of the work function of the probed surface region [24,25], which is consistent with a previous photoemission study [19]. The peak that opposes the trend of the FERs is assigned to a quantum well resonance (QWR), which indicates the quantum dot nature of the hills. It can be seen that this resonance undergoes, within less than 1 nm, an abrupt decrease in energy (0.5 eV) in going from the valley to the hill of the superstructure. In the following, we propose a simplified physical model to resolve the phenomenon.

Figure 2.

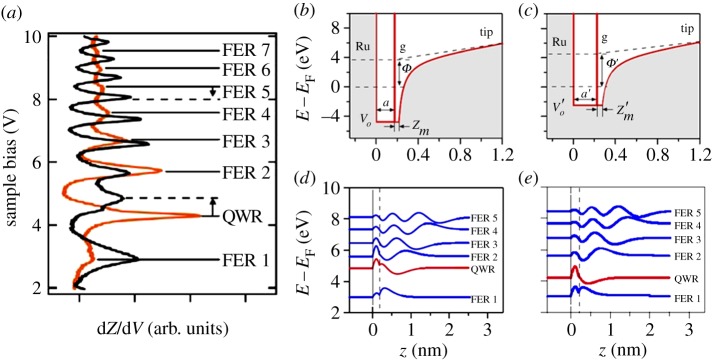
(a) dZ/dV spectra taken on the hill (orange, grey) and the valley (black). The one-dimensional potential models for the QWR and the FERs on G/Ru are shown in (b) for the valley and (c) for the hill. The corresponding energies and amplitudes of the normalized wave functions are displayed in (d,e). The dashed lines indicate the positions of the delta-function potentials. (Online version in colour.)

Figure 2b,c shows one-dimensional models of the potential for the tip–G/Ru junction with positive bias voltages at valley and hill, respectively. The potential in the vacuum is modelled as the work function plus an image potential U(z) proportional to 1/4(z−z_i), with z_i being the position of the image potential plane, plus a linear term that mimics the potential gradient between the tip and the sample. The essential ingredient of the model, the interface between the graphene and the vacuum, is described with a delta-function potential centred on the image plane γδ(z−z_i) [26]. It accounts for the transmission and reflectivity of low-energy electrons approaching graphene along z [27,28] and gives rise to the distinction between QWR and FER. The graphene is a rectangular quantum well with a width a and a′, and a depth V _o and V ′_o for valley and hill, respectively. The substrate is a perfect hard wall mirror, which is justified with the large gap in the relevant energy window along Γ [29]. More considerations on the model itself and calculation details can be found in our published paper [21]. The calculated result (figure 2d,e) well reproduces both the upwards shift of the FERs and the downwards shift of the QWR in going from the valley to the hill, confirming the validity of our one-dimensional model. The FERs are mainly localized in the vacuum/graphene side, and the QWRs are localized in the graphene/ruthenium interval, which demonstrates the vertical confinement of the electrons.

To substantiate the quantum dot picture, further evidence is needed to verify the lateral confinement of the hill regions. We note that FER1 on the hills is much weaker compared with the valleys. This is likely to have an electrostatic explanation, indicating the importance of the lateral dimensions: on the hills, the electrostatic potential is convex in shape owing to the higher local work function that defocuses the electrons out of the resonator cavity, while they are focused into the resonator cavity in the concave potential of the valleys. On the other hand, the QWR on the hill is the strongest. Because the electrons in the QWR are mainly localized in the graphene, the above defocusing argument does not apply, but the decoupling of the graphene from the substrate increases the resonance lifetime. Hence, the geometry of the graphene sheet plays an important role in the lateral localization of electrons at the hills.

Given both the vertical and lateral confinement of the electrons, it is applicable to assign the hills to quantum dots and the whole graphene surface can be treated as a moiré structure-induced quantum dot array. The structures are small enough (made from about 90 carbon atoms) and may have significant potential for new applications in single-electron quantum devices.

4. Site and orientation preferential adsorption behaviour of organic planar molecules on G/Ru

While we have demonstrated above the inhomogeneous nature of electronic properties in the corrugated surface, it is intuitive to expect charge redistribution at different sites of the moiré pattern, which may induce localized lateral electric field. In the following, we describe the influence of the lateral electric field on adsorbed organic species using combined STM and density functional theory (DFT) study.

Iron phthalocyanine (FePc) and pentacene molecules (Aldrich, 98+%) are chosen here due to several considerations: (i) they both are small flat organic molecules which may respond to the electric field applied parallel to sample surface and (ii) they both have potential applications in fields such as organic solar cells and single molecule devices. The molecules were thermally (approx. 540 K) deposited onto G/Ru surface at RT. Subsequently, the sample was slowly cooled down to 5 K for STM characterization. For DFT calculation, the local density approximation [30] for the exchange-correlation energy, projector augmented waves [31] and a planewave basis set as implemented in the Vienna ab initio simulation package [32] were used. The superstructure of the 12×12 graphene cells on 11×11 Ru(0001) cells is fully optimized.

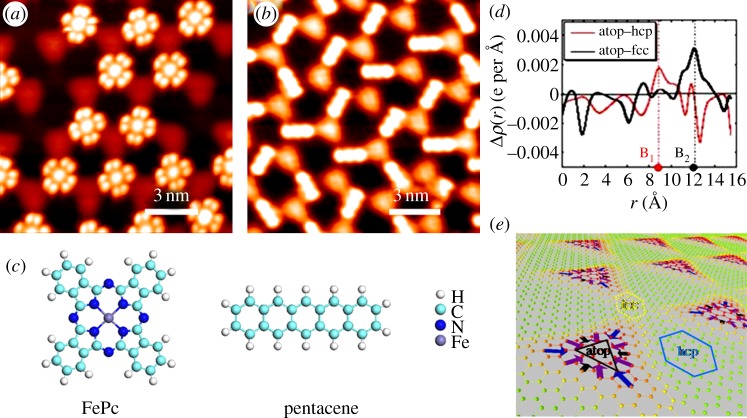
As revealed in the STM images in figure 3a,b, FePc molecule is featured as four lobes with a bright centre, whereas pentacene molecule is featured as a rod. At small molecular coverage, both types of these molecules share similar adsorption behaviour: they preferentially occupy fcc sites. More specifically, they both show orientational character at fcc sites, i.e. the centre of two adjacent lobes of FePc molecule points towards one neighbouring atop site, whereas the body of pentacene lies along the top–fcc direction.

Figure 3.

STM images showing the preferential adsorption of (a) FePc and (b) pentacene molecules at fcc sites on the surface. (c) Schematic drawing showing the structures of the two molecules. (d) DFT calculation of the averaged electron density difference along the top–hcp and top–fcc directions. (e) The perspective view of the inhomogeneous lateral dipole moments created by the G/Ru superstructure. (Online version in colour.)

In the present case, two possible mechanisms might be responsible for the site and orientation preference: the variation of local work function [33], and charge redistribution-induced lateral electric field. Our DFT calculation rules out the former one, because its effect on both types of molecules is inconsistent with the experimental observations [16]. For the second case, we first calculated the spatial variation of the electron density difference Δρ(r) along two different lateral directions, top to hcp and top to fcc, as shown in figure 3d. B₁ and B₂ label the boundary points in the two directions. Significantly, the electron density difference at B₂ is much higher than that at B₁. In other words, a larger lateral dipole is expected to exist in the top–fcc direction than in top–hcp direction, which is qualitatively consistent with our experimental results. More detailed calculation [16,34] suggests that the lateral dipole is indeed the largest along top to fcc direction (figure 3e); hence, fcc site is energetically more favourable to the adsorbing molecules and becomes the preferential site for trapping molecules. Besides, these lateral dipoles create transverse electrostatic fields, whose interaction with the polarized (FePc) or polarizable (pentacene) molecule can provide additional binding energy that accounts for the orientation preference. Our calculation also shows that after the fcc regions are occupied, the slightly smaller dipoles in the top–hcp direction then kick in, leading to the trapping of molecules, again in agreement with experimental observation.

One thing to mention is that the spatial charge redistribution also induces vertical dipoles. However, the calculation shows that they are much smaller than the lateral ones. From the above descriptions, it is safe to conclude that the lateral dipole field and the corresponding polarization of the molecule are the dominant driving forces for the molecular assembly. This finding provides a new route to control the orientation of anisotropically shaped molecules on the surface and might be useful in future single molecule functional devices. We also emphasize that the dipole-driven assembly mechanism is rather general and may be applicable to similar molecular systems on graphene monolayers (MLs) formed on other transition metal surfaces and could lead to a viable route to large-scale, well-defined molecule–graphene interfaces.

5. Kagome lattice formation on G/Ru

In §4, we show that on the periodically corrugated surface of G/Ru, some foreign species such as FePc and pentacene molecules exhibit site- and orientation-specific occupation behaviour at fcc sites during initial adsorption. In fact, the charge redistribution induced by the unique moiré structure plays an important role in guiding molecular adsorption. By following the tendency described above, it should be expected that further incoming molecules occupy hcp sites and atop sites sequentially, which might result in the formation of an ordered molecular layer.

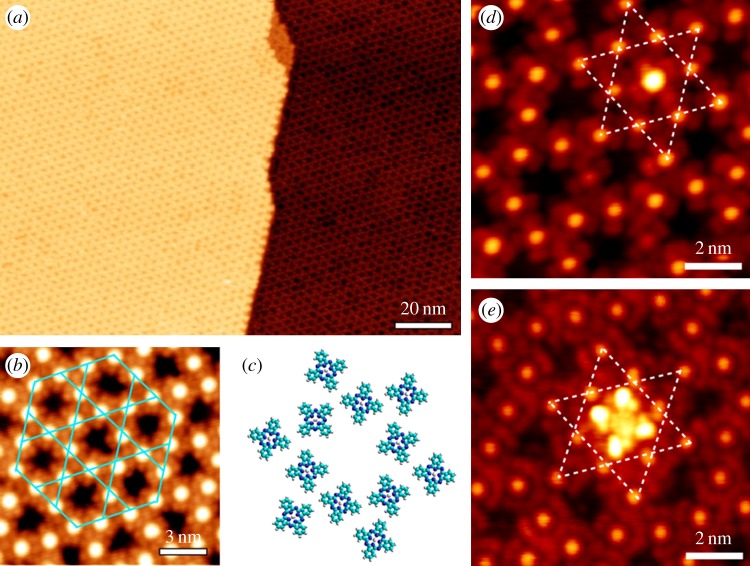
After FePc coverage reaches approximately 0.75 ML, regular hexagonal open networks are clearly resolved by STM (figure 4a) with a pore-to-pore distance of approximately 3 nm, precisely matching the lattice constant of the moiré pattern of G/Ru [15]. The pores are in fact the atop sites where adsorption energy is the lowest for FePc molecules according to DFT calculations, thus left unoccupied. Despite the presence of Ru(0001) terraces with a typical width of several hundred nanometres, the open networks of FePc illustrate an identical lattice orientation on different terraces. Because graphene epitaxy on Ru(0001) yields a continuous single crystal with a lateral size on the millimetre scale, the fact that the open networks of FePc follow the periodicity of the moiré pattern of MG highlights the key role that the G/Ru template plays in the self-organization of FePc molecules.

Figure 4.

(a) Large-scale STM image of the kagome lattice of FePc. (b) Zoom-in image showing the details of the kagome lattice of FePc. The unit cell of the kagome lattice is marked with blue solid lines. (c) Structural model of the kagome lattice showing molecular orientation disorder. (d,e) STM images of single-guest FePc and (t-Bu)₄–ZnPc molecules hosted by FePc kagome lattice, respectively. Dashed lines highlight the underlying kagome lattice. (Online version in colour.)

Figure 4b is a higher resolution image of the molecular lattice. It can be resolved that each FePc molecule is attached to four neighbouring molecules, whereas three molecules form a three-branch joint, thus constructing a so-called kagome lattice structure. Figure 4c further shows the structural model of the kagome lattice. A molecular orientation disorder can be revealed, because (i) the molecules are fourfold symmetric, whereas the template is threefold symmetric and (ii) the molecule–molecule interaction also comes into effect under such a high coverage which might complicate the orientation ordering. Apart from this planar orientation disorder, the centres of the molecules (bright protrusions in STM images) are perfectly aligned, as outlined by the blue solid lines in figure 4b. Further experiments (not shown here) suggest that other kinds of phthalocyanine molecules such as H₂Pc and NiPc show similar assembly behaviour on G/Ru surface.

Kagome lattice is a well-known two-dimensional system in studying spin frustration and has long been a toolkit for theorists, but molecular kagome lattices are very rare. The self-assembly of phthalocyanine molecules on G/Ru provides good candidates: the magnetic atoms offer residual spin right at the centre of the molecules, which are well aligned in the kagome lattice structure. Through changing the central magnetic metal atom, we are able to adjust the molecule spin [35]. Besides, it has been shown that the corrugations and lattice constants of the moiré patterns of epitaxial graphene can be tuned by the underlying metal substrates [36–38], which in turn might result in fine tailoring of the lattice constant of the kagome lattices of phthalocyanine molecules. The possibility of tuning the molecular spins of phthalocyanine molecules and the lattice constant of the kagome lattices, in combination with the decoupling of the magnetic molecules from the metal substrates by graphene sheet, makes the template-guided supramolecular kagome lattices of magnetic phthalocyanine molecules on epitaxial graphene excellent model systems for studying frustration physics.

As we have demonstrated the formation of kagome lattice by phthalocyanine molecules under the guidance of the underlying periodically corrugated substrate surface, we further illustrate that the kagome lattice itself may also act as a template to trap the incoming guest molecules [39]. Figure 4d,e shows STM images after the deposition of approximately 0.01 ML FePc and tert-butyl zinc phthalocyanine ((t-Bu)₄–ZnPc) molecules upon the prepared kagome lattice of FePc on G/Ru, respectively. The four lobes of the two guest molecules show rather similar apparent height, suggesting that they adopt flat configurations with the molecular plane parallel to the surface. We note that all guest molecules are trapped at the pore sites of the kagome lattice and no guest molecule is adsorbed on top of individual FePc molecules constituting the kagome lattice, demonstrating the capability of the porous kagome lattice to site-specifically accommodate guest molecules, and might be used in host–guest supramolecular complexes as well as future organic functional devices.

Overall, we have elaborated in this section the template effect of G/Ru moiré pattern under the guidance of which phthalocyanine molecules are found to align into kagome lattice structure. As the phthalocyanine family can be considered as tuneable molecular magnets owing to different residual spin provided by central metal atoms, the kagome lattices formed on G/Ru are good candidates to study frustration physics. Besides, the molecular kagome lattice itself also exhibits a template effect as the host–guest supramolecular systems. These systems might be beneficial in future molecular spin electronics or organic functional devices.

6. The growth of C₆₀ molecules on G/Ru

As we have mentioned above, some organic species such as pentacene and phthalocyanine molecules show site- and orientation-specific adsorption on G/Ru surface owing to the existence of lateral local electric field, which also influences the assembly behaviour during further molecular dosing. However, there are also species such as C₆₀ and perylene-3,4,9,10-tetracarboxylic dianhydride showing different adsorption and assembly behaviour [40,41]. To explore in depth the effect of G/Ru substrate on adsorption species, it is useful to study these kinds of molecules. C₆₀ is chosen in this study given its all-carbon chemical constituents, unique geometrical structure [42] and potential applications in a variety of fields [43–45]. The molecule powder is commercially obtained (99.5% purity, Aldrich) and is thermally deposited (approx. 600 K) onto G/Ru surface using the same technique as previous molecules.

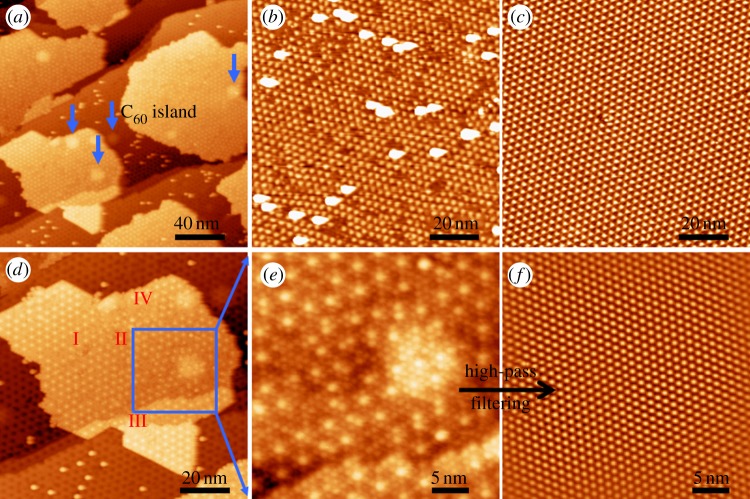
Large-area STM topography of C₆₀ submonolayer on under-annealed (approx. 1100 K) G/Ru substrate is shown in figure 5a [40]. The under-annealed sample surface possesses many imperfections and/or defects which may act as random additional adsorption sites for the adsorbates, and is helpful in investigating the molecule–substrate interactions. Contrary to the planar organic molecules described in the last two sections which show preferential adsorption behaviour, the C₆₀ molecules are observed to form islands on the surface. However, around these islands, there are many randomly isolated molecules also appearing as small bright protrusions. To clarify the difference between these isolated C₆₀ molecules and the site-specific adsorbed planar molecules, an image at lower molecular coverage is displayed in figure 5b, revealing that the isolated molecules are always found adjacent to areas where moiré spots are distorted or missing. A regular moiré pattern is also shown in figure 5c for direct comparison. Hence, this kind of isolated adsorption behaviour does not suggest a relatively strong C₆₀–substrate interaction or preferential adsorption on G/Ru. In fact, on the defect-free areas, we hardly find any isolated molecules. Besides, when samples are heated to 370 K, most C₆₀ molecules desorb from the surface, leaving only some that reside near imperfections. The formation of molecular islands on graphene, free of preferential adsorption and with a low desorption temperature, indicates that interactions between adsorbed molecules and the substrate are rather weak.

Figure 5.

STM topography of C₆₀ molecules adsorbed on under-annealed G/Ru surface. (a) Large-area STM image showing C₆₀ islands and isolated C₆₀ molecules. Five larger bright protrusions owing to argon gas bubbles are pointed out by the arrows. (b) Low-coverage image showing defect-induced isolated adsorption. (c) Regular moiré pattern of G/Ru. (d) Zoom-in image of the lower left part of (a). Four kinds of typical template surface conditions are distinguished: (I) regular moiré pattern, (II) disordered or imperfect areas, (III) steps and (IV) corrugations. (e) Zoom-in image of the area inside the blue square in (d). (f) High-pass filtered image of (e). (Online version in colour.)

In addition, we examine the packing of C₆₀ molecules in the islands. It can be seen that the surface in figure 5a contains four different types of areas: a regular moiré pattern, imperfections, steps and large protrusions induced by argon atoms residing (indicated by the arrows). These are labelled in figure 5d as I, II, III and IV, respectively. C₆₀ molecular island extends over all the four types of surface areas smoothly. To investigate the arrangement of the C₆₀ molecules, we further zoom-in part of the island (figure 5e) and find that they adopt a closely packed hexagonal growth mode. After high-pass filtering, the molecular lattice was successfully made visible in figure 5f. Surprisingly, the lattice is rather well ordered, indicating that the hexagonal packing behaviour is retained, regardless of underlying imperfections, protrusions or steps. These experimental results suggest again a strong C₆₀–C₆₀ interaction compared with the C₆₀–substrate interaction.

Our DFT calculations also provided information for quantitative analysis on molecule–molecule and molecule–substrate interactions. The adsorption energy of C₆₀ (hexagon upward) on three different types of surface sites is −267 meV (atop site), −294 meV (hcp site) and −336 meV (fcc site), whereas the interaction energy between two free C₆₀ molecules is −514 meV. The similar adsorption energies on different surface sites and the strong C₆₀–C₆₀ interactions are consistent with the island growth mode of C₆₀ on G/Ru surface.

After the island growth mode of C₆₀ on G/Ru has been well illustrated, we further show that the template effect of the moiré structure still acts on this system, but under a mechanism different from the previously described lateral electric field. Figure 6a shows typical STM topography of a C₆₀ ML grown on well-prepared (sufficiently annealed under approx. 1300 K) G/Ru surface. The substrate-commensurate, closely packed hexagonal molecular growth can be clearly identified and the bright protrusions are attributed to the superimposition of the underlying atop sites of the graphene moiré structure. Zoom-in image is displayed in figure 6b for better resolving the supramolecular structure. The neighbouring C₆₀–C₆₀ distance is measured to be 0.98±0.04 nm, which is very close to the values of other kinds of surface phase C₆₀ reported previously [46,47]. A small (large) rhombus is used to outline the unit cell of the molecular lattice (G/Ru template). This kind of growth is interpreted in terms of two aspects. On the one hand, the corrugated G/Ru surface has a periodical surface potential, which may influence the molecules to some extent in order to minimize energy. On the other hand, given that the distance between two nearest moiré spots is 3 nm, almost exactly three times the distance between two neighbouring C₆₀ molecules in the solid phase, commensurate overlayers can easily form on such a surface. The lattice periodicity is similar to the one reported by Corso et al. [48] but with a different supramolecular structure. In addition, the defects of the molecular layer on G/Ru surface are much fewer, and the molecular film is continuous and uniform even when there are moiré spots missing (figure 6b).

Figure 6.

(a) The substrate-commensurate growth of C₆₀ molecules on G/Ru. (b) Zoom-in image of the supramolecular structure. The unit cells of the underlying substrate and molecular lattice are outlined by large and small rhombuses, respectively. (c) STM image showing both substrate-commensurate (lower right, marked with ‘A’) and substrate-incommensurate (upper left, marked with ‘B’) growth structure of C₆₀ molecules on G/Ru. The dotted lines in different orientations indicate different molecular domains. (d) Zoom-in image of an incommensurate area. Inset shows its Fourier transformation and the angle between vector q₁ and q₂ is about 26^°. (Online version in colour.)

Occasionally, especially on the surfaces of under-annealed samples, we also observed incommensurate or disordered growth mode (figure 6c,d). We simply classify the growth modes of C₆₀ into type A—growth commensurate with the substrate—and type B—growth that seems disordered. Type B areas occur less frequently and are most likely to appear upon or adjacent to imperfections and domain boundaries of the moiré pattern, which we suppose to cause their formation. In figure 6d, a typical domain-related type B area is displayed. Because the positions of graphene moiré spots cannot be clearly resolved in this case, we applied a Fourier transform (FT) to the initial image, as shown in the inset. The outer six points correspond to the C₆₀ molecular lattice and the inner ones represent the moiré pattern's periodicity. By measuring the angle between vectors q₁ and q₂ in the FT image, we found that the two periodic lattices are rotated by 26^° with respect to each other. However, this is not the only rotation value we obtained. Among the samples we investigated, such angles range from 4^° to 26^°, indicating a random relationship between the orientations of the two lattices. This further supports our supposition that incommensurate growth is related to domains, which also show random directions in our samples.

By using combined STM characterization and DFT calculation, we find that the interaction between C₆₀ molecular film and the substrate is rather weak, but by no means negligible, because it is still enough to guide the commensurate growth of C₆₀ molecules. Compared with FePc and pentacene molecules, C₆₀ seems less sensitive to G/Ru surface corrugation, which can be assigned to a stronger molecule–molecule interaction compared with molecule–substrate interaction. Hence, understanding and tailoring molecule–substrate interactions is important in studying and constructing graphene–organic molecule-based functional devices.

7. Concluding remarks

We have successfully fabricated large-scale, high-quality and single crystalline graphene on Ru(0001) surface. Owing to the lattice mismatch between graphene and Ru(0001) substrate, a moiré pattern with a period of approximately 3 nm is formed, whose atop sites can be assigned to ordered quantum dot arrays. Our spectroscopic measurements reveal a charge inhomogeneity across different surface regions, which results in preferential adsorption behaviour of small planar organic molecules on the surface. In addition, the G/Ru substrate is proved to be a good template to guide the assembly of organic molecules. For that, understanding and manoeuvering molecular–substrate interactions are crucial to obtain different superstructures, such as kagome lattice formed by FePc molecules and commensurate supramolecular structure formed by C₆₀ molecules. Considering the large scale, high quality and the ability to form regular compounds with adsorbed organic species, we believe graphene on Ru(0001) has a bright future in industrial applications.

Funding statement

This work was financially supported by grants from National Science Foundation of China (nos. 61274011, 10834011, 61222112 and 11104109), National ‘973’ projects of China (nos. 2013CBA01600, 2010CB923004 and 2011CB932700), the Chinese Academy of Sciences and SSC.