Pressure-induced planar N₆ rings in potassium azide

Abstract

The first-principles method and the evolutionary algorithm are used to identify stable high pressure phases of potassium azide (KN₃). It has been verified that the stable phase with space group I4/mcm below 22 GPa, which is consistent with the experimental result, will transform into the C2/m phase with pressure increasing. These two phases are insulator with 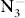anions. A metallic phase with P6/mmm symmetry is preferred above 40 GPa, and the N atoms in this structure form six-membered rings which are important for understanding the pressure effect on 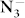anions and phase transitions of KN₃. Above the studied pressure (100 GPa), a polymerization of N₆ rings may be obtained as the result of the increasing compactness.

Metal azides have drawn considerable attention for their interesting chemical and physical properties. Under external influences (impact, heat, irradiation, etc), they become unstable and decompose into metal and nitrogen¹. Their practical applications include explosives, pure nitrogen sources and photographic materials. Additionally, metal azides are structurally simple among solids that deflagrate or detonate, so they are potentially model systems for theories of the fast reactions². Being different from the extensively studied alkali halides, metal azides are ionic compounds containing internal molecular structure which makes them the candidates for understanding the complex nature of chemical bonding. On the other hand, the polymerization of nitrogen may form a high-energy-density material because the transformation from the N–N single bond (160 kJ/mol) to the N≡N triple bond (954 kJ/mol) is accompanied by a large energy release. The non-molecular nitrogen under high pressure was first predicted theoretically by A. K. McMahan et al.³. A single-bonded cubic gauche form of N₂ (cg-N) was also successfully synthesized by M. I. Eremets et al.⁴,⁵. It is suggested that cg-N can be stabilized in compounds with other elements or by introducing impurities⁴. Recently, metal azides have been proposed to be a precursor in the formation of polymeric nitrogen. It could be expected that the 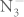anion will create polymeric single-covalent-bond networks more easily than diatomic nitrogen because the 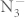anion is more weakly bonded than the diatomic triple-bonded nitrogen⁶. Alkali azides are one class of compound among metal azides. Pressure-induced phase transitions in alkali azides have been reported by both experimental⁶,⁷,⁸,⁹,¹⁰,¹¹ and theoretical investigations¹²,¹³,¹⁴,¹⁵,¹⁶. Previous study reported that sodium azide undergoes a set of phase transitions⁶,⁸, and the 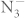anions in NaN₃ transform to polymeric nitrogen net above 120 GPa⁶. Lithium azide, which is isostructural to the low-temperature phase of NaN₃ at ambient condition, is stable up to the pressure of 60 GPa at room temperature⁷. Recent high-pressure study of CsN₃ up to 55.4 GPa reveals three phase transitions approximately at 0.5, 4.4, and 15.4 GPa¹¹. Strikingly, theoretical studies have predicted polymerization of nitrogen in LiN₃¹⁴,¹⁵ and NaN₃¹⁶. Thus, a study of the high-pressure behavior of KN₃ would provide more insights into the mechanism of pressure-induced rearrangement of azide anions. It is helpful to investigate theoretically the pressure effect on potassium azide which might result in the formation of polymeric nitrogen.

At ambient condition, potassium azide crystallizes in a body-centered tetragonal lattice with I4/mcm symmetry, and the 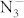ion in the lattice is a straight chain of three nitrogen atoms. Raman scattering up to 4.0 GPa¹⁷ and single-crystal x-ray diffraction up to 7.0 GPa¹⁸ show that no phase transition is found at these measured pressures. Recently, a structural phase transition at 15.5 GPa is revealed by X-ray diffraction study⁹,¹⁰. A Raman scattering study of KN₃ up to 55.0 GPa suggests that a first-order phase transition starts at 13.6 GPa and completes at 32.2 GPa¹⁰. However, a detailed structure of solid KN₃ under high pressure has been unsolved yet. In this paper, we employ the first-principles study to understand the phase transitions and properties of KN₃ under high pressure.

In the present work, KN₃ is compressed up to 100 GPa. The phase transition from I4/mcm to C2/m is determined at a pressure about 22 GPa. In addition, we have defined another high-pressure phase with P6/mmm symmetry in which the 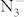ions transform to N₆ rings, and the hexagonal phase is metallic. We have just noticed the discussion on the P6/mmm phase by Li et al. recently¹⁹. The three phases of this crystal are stable against decomposition of KN₃ into 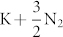under pressure up to 100 GPa. The results provide an insight into the formation of polymeric nitrogen in metal azides.

Computational details

To find the lowest energy structures of KN₃ under extreme conditions, the USPEX code based on the evolutionary algorithm²⁰,²¹ is employed for the search where the VASP code²² is used as an external ab initio code for the underlying structural optimizations. Evolutionary variable-cell structure prediction simulations are performed at 20, 60, and 100 GPa with 1, 2, and 4 KN₃ formula units per unit cell. The first generation is produced randomly. All newly generated structures are relaxed at constant pressure and ranked by their enthalpy value. The lowest-enthalpy 60% structures of each generation are used to produce the next generation through heredity (70%), atomic permutation (10%), atom position mutation (10%) and lattice mutation (10%). The structures are relaxed by using density-functional theory with the Perdew-Burke-Ernzerhof (PBE) exchange correlation functional²³, and projector augmented wave (PAW) method²⁴ is also adopted. The 3s²3p⁶4s¹ for K and 2s²2p³ for N are treated as valence electrons. Having selected the lower enthalpy structures, we recalculate their enthalpies with increased accuracy between 0 and 100 GPa. An energy cutoff of 520 eV is used for the plane-wave basis sets, and the total energy is converged to 1.0 × 10⁻⁶ eV in the self-consistent loop. The atomic positions, lattice parameters, and cell volume are fully optimized by using a conjugate-gradient algorithm. The iterative relaxation of the atomic positions stop when all forces are smaller than 0.001 eV/Å, and the total stress tensor is reduced to the order of 0.01 GPa. The phonon calculations are performed using the Quantum ESPRESSO code based on density functional perturbation theory²⁵, where vanderbilt ultrasoft pseudopotentials are used for K and N. Before the application, the pseudopotentials are tested by comparing the relaxed structural parameters and electronic structure with the results obtained from VASP code. All cases concerned are zero-temperature ground state.

Results and discussion

The analysis of the predicted structures gives us a list of candidate structure with space groups I4/mcm, C2/m, P2₁, Cmc2₁, P6/mmm, 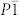, and Imma, which are depicted in Fig. 1. In order to exam the difference between theoretical results and experimental data, the theoretical lattice constants and unit cell volume are compared with experimental I4/mcm structure at ambient condition (Table I). The LDA calculations underestimate a, c, and V by 3.3%, 5.2%, and 11.4%, whereas GGA calculations overestimate a, c, and V by 1.5%, 2.0%, and 5.2%, respectively. The GGA results are closer to the experimental results than the LDA ones. Therefore the GGA exchange-correlation functional is adopted for the further calculations. The C2/m structure detected from the simulations has the same space group as in LiN₃⁷, NaN₃²⁶ and CsN₃¹¹. The I4/mcm, C2/m, P2₁ and Cmc2₁ structures possess linear molecular 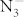anions, while the structures with 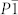and Imma symmetries display the characteristic of the N-atom chains and are radically different from the structures containing 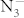anions (see Fig. 1 and supplementary Table S1). In variable-cell simulations at 100 GPa, the P6/mmm structure is clearly identified as the most stable one and it is assigned to a new structure type for alkali metal azides. Interestingly, this is a layer-like structure with six N atoms forming a planar N₆ ring. Additionally, polynitrogen molecules as clean high energy density materials have been extensively explored for several years²⁷,²⁸,²⁹. A lot of theoretical work on N₆ has shown that the planar hexagonal (D_6h) ring is not minimum³⁰,³¹,³². However, the six-membered nitrogen rings can be stabilized by coordinate covalent to oxygen³³ and by the incorporation of metal atom in metal-N₆ molecules³⁴. We now obtain the N₆ rings in bulk materials. It reveals that extra atoms play an important role in stabilizing N₆ ring. More recently, a P6/m structure containing N₆ ring has been also predicted in LiN₃¹³,¹⁴,¹⁵ and NaN₃¹⁶. Thus, the P6/m structure is considered in KN₃. The results show that the P6/m structure becomes P6/mmm phase after structure optimization. Parameters describing the C2/m and P6/mmm structures are listed in Table II.

Figure 1. The structures computed for KN₃ in the pressure range 0–100 GPa.

The purple spheres are potassium atoms and grey are nitrogen atoms. The 2 × 1 × 2 supercell of the 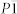structure and the 2 × 1 × 1 supercell of the Imma structure are viewed along b-axis.

Table 1. Theoretical lattice constants and unit cell volumes V at ambient pressure compared with experimental data for I4/mcm structure.

		Present work
Parameter	Experiment (ref. 9)	LDA	GGA
a = b(Å)	6.11094	5.90883	6.20556
c(Å)	7.09755	6.72696	7.24091
V(Å3)	265.043	234.867	278.841

Table 2. Optimized structural parameters of C2/m phase at 30 GPa and P6/mmm phase at 100 GPa from the first-principles calculations.

Pressure(GPa)	Space group	Lattice parameters(Å,°)	Atomic coordinates(fractional)
30	C2/m	a = 4.293, b = 4.360, c = 4.767	K 2a (0.0000, 0.0000, 0.0000)
		α = 90, β = 107.969, γ = 90	N 2d (0.0000, 0.5000, 0.5000)
			N 4i (0.6272, 0.0000, 0.3151)
100	P6/mmm	a = b = 5.376, c = 2.366	K 2d (0.6667, 0.3333, 0.5000)
		α = β = 90, γ = 120	N 6j (0.0000, 0.2396, 0.0000)

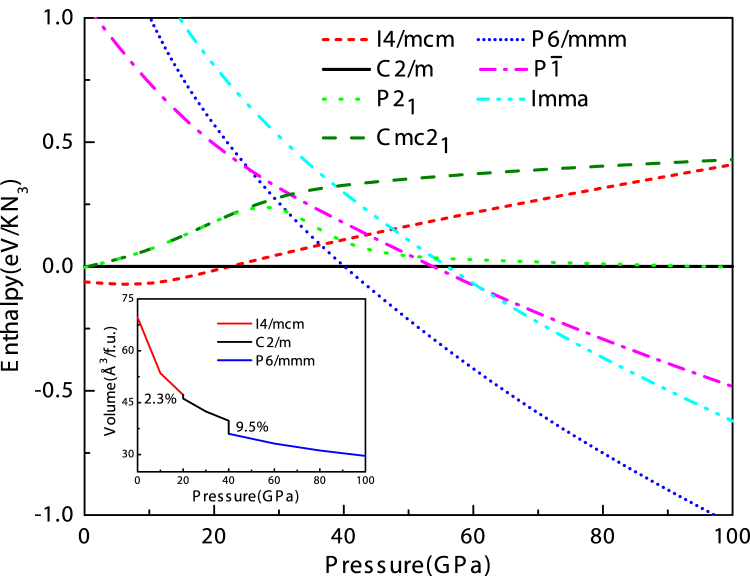
The enthalpies of the most energetically competitive structures are compared over the pressure range 0-100 GPa as shown in Fig. 2. The most stable structure is a tetragonal phase with I4/mcm symmetry from ambient pressure up to 22 GPa, which is then replaced by a lower-enthalpy C2/m structure. Actually, at 13.6 GPa, Raman spectra¹⁰ have identified a phase transition that completes at 32.2 GPa, which is in agreement with the C2/m phase being stable above 22 GPa. The I4/mcm-C2/m sequence has also been observed in CsN₃¹¹. During I4/mcm-C2/m transition, the tetragonal lattice is distorted under pressure, and the orientation of 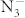anions changes between the two K layers. The 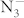anion in the C2/m structure is parallel to one another. Moreover, compression induces a symmetry reduction and 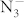anions are still in a molecular state in this transition, which are consistent with the experimental results¹⁰. Above 40 GPa, a hexagonal structure with P6/mmm symmetry is favored over other structures and remains the lowest-enthalpy phase up to 100 GPa. We find that the crystal structures of KN₃ containing the 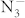ions are energetically favorable at lower pressure, while at higher pressure, there is a tendency to the N chains or rings. Although pressure induces the rearrangement of azide ions, the formation of N–N single bond needs further compression. The dependence of volume on pressure is shown in the inset of Fig. 2. The volume reductions of ~2.3% and ~9.5% are found for the I4/mcm–C2/m and C2/m–P6/mmm transitions, respectively. The discontinuous change in volume indicates that the two phase transitions are first order. As the transformation from C2/m to P6/mmm involves the forming of N-N bonds and is reconstructive, there is a large kinetic barrier. In addition, the possibility of decomposition formula of 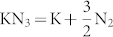is checked by the enthalpies of decomposition, where we consider 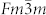, Pnma, I4₁/amd, and Cmca structures for K³⁵,³⁶ and the cubic gauche (I2₁3) structure for the N₂⁴,³⁷. It turns out that the enthalpies of 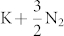are much higher than that of KN₃ at the concerned pressure range (>3.2 eV). Thus the KN₃ crystal keeps stable against decomposition over the 0–100 GPa pressure range.

Figure 2. Calculated enthalpies per KN₃ unit as the function of pressure.

The enthalpies are referenced to that of C2/m. Inset: the pressure dependence of volume for I4/mcm, C2/m and P6/mmm phases of KN₃.

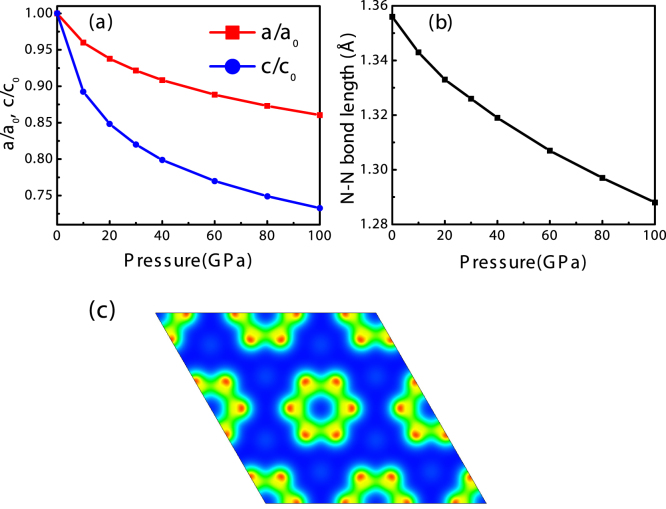
Since the high-pressure P6/mmm phase is novel for alkali metal azides, it is essential to investigate the properties of P6/mmm structure in detail. The ratios of a/a₀ and c/c₀ for the P6/mmm structure seen in Fig. 3a exhibit that the compression is anisotropic with the reduction of lattice parameter a by 13.97% over the pressure studied, while lattice parameter c decreases by 26.73%. This implies that it is more compressive along interlayer direction than intralayer direction for the layer-like P6/mmm phase. The N₆ ring with D_6h symmetry possesses benzene-like characteristics. The charge density of N₆ ring in Fig. 3c suggests that each nitrogen atom forms two σ bonds with its two nearest neighbors by overlapping two sp² hybrid orbitals, which is similar to the C-C bonds of C₆H₆. Additionally, for covalent bonds, there is a general trend in that the shorter the bond length, the stronger the bond strength. As shown in Fig. 3b, the N-N bond length of N₆ ring is longer than that of N = N double bond (1.25Å) but shorter than that of N–N single bond (1.45Å). This means that the σ bond of N₆ ring is weaker than the N = N double bond but stronger than the N–N single bond. In general, pressure induces the destabilization of intramolecular bonds. The structure with N₂ and N₆ units has been reported around 60 GPa by first-principles simulations for pure nitrogen³⁸. Recently, a diamondoid structure of the polymeric nitrogen is predicted above 263 GPa³⁹. These findings also provide a basis for understanding the high-pressure behavior of nitrogen-related materials. As pressure increases, there is a competition among the σ bond, ionic bond, and van der waals. Thus, it is probably fair to say that N₆ rings in P6/mmm phase will transform to polymeric nitrogen networks under further compression.

Figure 3.

(a) Variation of normalized lattice parameters of P6/mmm structure with pressure. a₀ and c₀ are the lattice parameters of the equilibrium volume structure at zero pressure. (b) Pressure dependence of the N-N bond length of N₆ ring. (c) Total charge density plotted in the (001) plane for P6/mmm phase at 100 GPa.

The ambient-pressure phase I4/mcm is insulating with a calculated band gap of 4.2 eV at 0 GPa (see supplementary Fig. S1), and the C2/m structure is also found to be an insulator with a band gap of 4.1 eV at 30 GPa (see supplementary Fig. S2). On further compression, KN₃ transforms to a metallic state with P6/mmm symmetry at 40 GPa. Besides, the 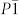and Imma structures are metastable above 60 GPa. The Imma structure is metal (see supplementary Fig. S3), and the 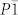structure is a semiconductor with narrow band gap (0.78 eV, see supplementary Fig. S4). Fig. 4 presents the band structure and the density of states of P6/mmm phase at 100 GPa. It reveals that P6/mmm structure is a weak metal with a small density of states at the Fermi level (0.07 states/eV/cell) which are associated with the N-2p electrons. The bands across the Fermi level are highly dispersive along the c-axis (G → A, H → K, and M → L). In addition, the Bader method⁴⁰ is chosen to analyze the charge transfer as implemented in the algorithm developed by Henkelman et al.⁴¹. The Bader charges of the P6/mmm phase are around +0.73 and −0.24 for potassium and nitrogen, respectively, which suggests that the high-pressure P6/mmm phase has ionic characteristics for K-N chemical bonds. It means that the N₆ anion in P6/mmm phase has nearly 8 π-electrons. Six P_z orbitals form three bonding π orbitals and three antibonding π* orbitals. Thus, the π* orbitals are partially occupied by two electrons, accompanied by two conduction bands crossing the Fermi level. Furthermore, the dynamical stability of the P6/mmm structure is established from the phonon calculations. As shown in Fig. 5, the absence of any imaginary frequency confirms the stability of the P6/mmm phase. The lower bands, ranging up to 620 cm⁻¹, are formed by a significant mixing of K and N vibrations, while the higher bands are mostly attributed due to N-atom.

Figure 4. Electronic band structure and projected density of states (PDOS) for P6/mmm phase at 100 GPa.

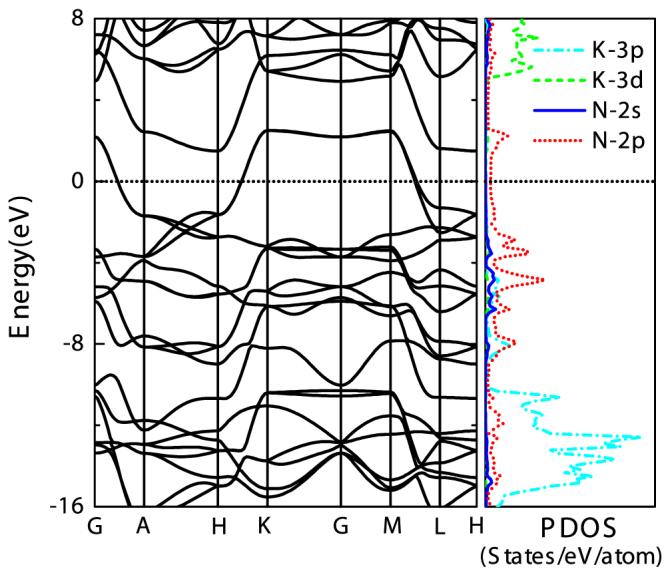
Figure 5. Phonon dispersion curve and phonon density of states (PHDOS) for P6/mmm phase at 100 GPa.

Conclusion

In summary, an evolutionary algorithm in conjunction with first-principles electronic structure computations has been used to predict the stable high-pressure phases of potassium azide. Our calculations indicate that the experimental I4/mcm phase of KN₃ transforms to C2/m structure at 22 GPa and then to a hexagonal P6/mmm structure at 40 GPa. The planar N₆ ring is formed in the metallic P6/mmm phase. This phase of KN₃ is dynamically stable. Further compression could lead to the polymerization of N₆ rings, which can be used as a potential high-energy-density material.

Author Contributions

J.Z. and Z.Z. conceived the research. J.Z. carried out the calculations. J.Z., Z.Z., H.-Q.L. and Y.-L.L. analyzed the data. J.Z. and Z.Z. wrote the paper.

Supplementary Material

Supplementary Information

supplementary information