SIOMICS: a novel approach for systematic identification of motifs in ChIP-seq data

Abstract

The identification of transcription factor binding motifs is important for the study of gene transcriptional regulation. The chromatin immunoprecipitation (ChIP), followed by massive parallel sequencing (ChIP-seq) experiments, provides an unprecedented opportunity to discover binding motifs. Computational methods have been developed to identify motifs from ChIP-seq data, while at the same time encountering several problems. For example, existing methods are often not scalable to the large number of sequences obtained from ChIP-seq peak regions. Some methods heavily rely on well-annotated motifs even though the number of known motifs is limited. To simplify the problem, de novo motif discovery methods often neglect underrepresented motifs in ChIP-seq peak regions. To address these issues, we developed a novel approach called SIOMICS to de novo discover motifs from ChIP-seq data. Tested on 13 ChIP-seq data sets, SIOMICS identified motifs of many known and new cofactors. Tested on 13 simulated random data sets, SIOMICS discovered no motif in any data set. Compared with two recently developed methods for motif discovery, SIOMICS shows advantages in terms of speed, the number of known cofactor motifs predicted in experimental data sets and the number of false motifs predicted in random data sets. The SIOMICS software is freely available at http://eecs.ucf.edu/∼xiaoman/SIOMICS/SIOMICS.html.

INTRODUCTION

Systematic discovery of transcription factor binding sites (TFBSs) and binding motifs is crucial for the study of gene transcriptional regulation (1). TFBSs are 6–14-bp-long DNA segments that can be bound by transcription factors (TFs) (2–4). A TF usually binds to similar TFBSs. The pattern of the TFBSs bound by a TF is called a motif, commonly represented as a position weight matrix or a consensus sequence (5). The binding of TFBSs by TFs can activate or repress the transcription of genes near the TFBSs, and can thus modulate gene expression (6). In eukaryotes, it is often the TFBSs of multiple TFs in a short DNA region that determine the temporal spatial expression pattern of a gene (6). The short DNA regions of several hundred base pairs long that contain TFBSs of multiple TFs are called cis-regulatory modules (CRMs). Correspondingly, we define a motif module as a group of TFs, with their TFBSs co-occurring in significantly many CRMs. In other words, a motif module has the TFBSs of all its motifs co-occurring in at least a given number of sequences and has a P-value of motif co-occurring smaller than a given threshold. Because the possibility that a short DNA region is a CRM of a motif module is much smaller than the possibility that a short DNA segment is a TFBS of a motif, the identification of TFBSs and motifs through the identification of CRMs and motif modules is likely less error-prone than that through the identification of TFBSs of individual TFs (2,7,8).

The chromatin immunoprecipitation (ChIP) followed by massive parallel sequencing (ChIP-seq) experiments provides a great opportunity for computational identification of TFBSs and motifs (1,9). ChIP-seq experiments can define DNA regions that are enriched with TF binding for a TF under a specific condition on the genome scale. These DNA regions are often called ChIP-seq peak regions. ChIP-seq peak regions, which are, on average, several hundred base pairs long, can be identified from ChIP-seq experiments through peak-calling algorithms (10,11). Depending on the TF used for the ChIP-seq experiments, there could be several hundreds to thousands of peak regions defined in one ChIP-seq experiment. Effective computational methods are necessary to systematically discover motifs and TFBSs of the TF and those of its cofactors. Here and in the rest of the paper, a cofactor is a TF that regulates its target genes with the TF used to do the ChIP-seq experiment.

Several computational methods identify motifs in top ChIP-seq peak regions (12,13). Such type of approach is likely to miss many potential motifs because TFBSs of cofactors may only occur in some ChIP-seq peaks (14). A few methods attempt to identify TFBSs and motifs in all peak regions, by using known motifs to scan (extended) ChIP-seq peak regions to identify significantly co-occurring motifs (15,16). This type of approach has achieved success in identifying motifs of certain cofactors (15). Because current knowledge of known motifs is still limited, these methods may miss TFBSs and motifs of many cofactors. There are also methods for de novo discovery of TFBSs and motifs in all peak regions from a ChIP-seq experiment (14,17–19). Almost all of these types of methods consider individual motifs separately. Note that TFBSs of some cofactors may only occur in a small number of peaks (14,20). Motifs of these cofactors may thus be underrepresented in all peak regions from a ChIP-seq experiment (statistically insignificant individually), as shown in the following analyses. The currently available de novo motif discovery methods may thus miss motifs and TFBSs of many cofactors, especially these underrepresented motifs and TFBSs.

Here we developed a novel computational approach SIOMICS (systematic identification of motifs in Chip-seq data) for de novo discovery of motifs and TFBSs from all peak regions of a ChIP-seq experiment. Instead of considering individual motifs separately, SIOMICS simultaneously considers motif modules, i.e. combinations of any number of motifs that co-occur in at least a predefined number of peak regions and have P-value of statistical significance smaller than a given threshold. In this way, an individually underrepresented motif may be overrepresented in all peak regions when this motif and its cofactor motifs are considered as a group, and may thus be identified by SIOMICS. Tested on 13 ChIP-seq data sets, SIOMICS identified many known motifs, new motifs and their TFBSs. Tested on 13 simulated random data sets that were obtained by permuting the experimental sequence data, SIOMICS did not predict any motif. Compared with two recent methods, Dreme (14) and Peak-motifs (18), SIOMICS identified more known cofactor motifs in ChIP-seq data sets and the same or fewer motifs in random data sets, and had a comparable or better time efficiency.

MATERIALS AND METHODS

ChIP-seq experimental data and simulated data

We obtained ChIP-seq data for 13 TFs from Chen et al. (21), which were widely used as the benchmark data sets for evaluating motif identification methods (14,18). We first downloaded the mapped reads from GSE11431 in the Gene Expression Omnibus database (22). We then defined ChIP-seq peaks for each data set using the peak-calling software Model-based Analysis of ChIP-Seq (MACS) (11). Finally, we obtained the repeat-masked DNA sequences for the defined peak regions of each TF using the University of California, Santa Cruz genome browser (23). During this step, to enable TFBSs of more cofactors to be considered, we extended the peaks equally on the two sides of each peak region such that each extended peak region is at least 800-bp long. With these experimental sequence data sets, we obtained 13 simulated data sets by permuting nucleotide positions in every obtained sequence in each data set. In brief, for a given sequence, say it is n-bp long, we randomly generated a permutation of (1, 2, 3, … , n), say (a₁, a₂, … , a_n). We then moved the ith nucleotide in this sequence to the a_ith position of the new sequence, for i from 1 to n. In this way, we obtained a new sequence. We repeated this process for every sequence in each data set, using an independent permutation each time, to generate a random data set.

Generation of motif candidates

SIOMICS identifies motifs by simultaneously considering multiple motifs corresponding to a TF and its cofactors. Because the majority of motifs are unknown (4), SIOMICS first obtains motif candidates and then considers the co-occurrence of the motif candidates to define final putative motifs. To generate motif candidates, SIOMICS uses k-mers (k-bp-long DNA segments) in input sequences in a ChIP-seq data set. Here, k = 8 was used in the following analyses because an 8-mer can already account for an essential portion of a motif that is commonly 6–14-bp long (4). For each k-mer occurring in input sequences, SIOMICS defines it as a k-mer motif candidate by assuming all k-mers in input sequences that are different from this k-mer at most at one position as its TFBSs. SIOMICS then ranks motif candidates in a ChIP-seq data set by the following score schema used previously (24), from the one with the largest score to the one with the smallest score:

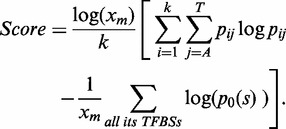Here 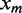is the number of TFBSs of a motif candidate, 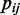is the frequency of the nucleotide j at position i of the motif candidate and 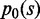is the probability of generating TFBSs based on background nucleotide frequencies. Other score schemas (25,26) have also been tested and do not change the results significantly, which may be due to the fact that final motifs are obtained based on the significance of motif modules instead of that of the individual motifs. Because many motif candidates may be highly similar to each other, SIOMICS removes redundant candidates with lower ranks such that the consensus sequence of a remaining candidate is different from that of other remaining candidates at least at two positions. All remaining motif candidates are used in the following to identify putative motifs.

Putative motif identification by SIOMICS

With the motif candidates, SIOMICS modifies a frequent pattern mining approach (3,15) to discover motifs through the identification of motif modules. The basic idea is to represent motif candidates as nodes in a tree such that more frequent candidates are represented at top level (close to the root) and each branch represents the co-occurrence of a group of candidates in one or multiple sequences. Next, an idea similar to the conditional probability is applied to discover groups of co-occurring motif candidates that contain a specific candidate and have their TFBSs co-occurring in at least s input sequences (3,15). We called s the support of a group of motif candidates. Finally, a Poisson clumping heuristic strategy (27,28) is implemented to measure the significance of each obtained group of co-occurring motif candidates and output motif modules. The basic idea of this significance calculation is to approximate the occurrence of each motif candidate in sequences by an independent Poisson process and measure how likely we will observe a group of candidates co-occurring in x input sequences, where x ≥ s (28). So a motif module predicted by SIOMICS is a group of motif candidates with their TFBSs co-occurring in at least s input sequences and with the multiple comparison-corrected P-value of co-occurrence smaller than a significance cutoff. The motif candidates in these predicted motif modules are output as the final putative motifs.

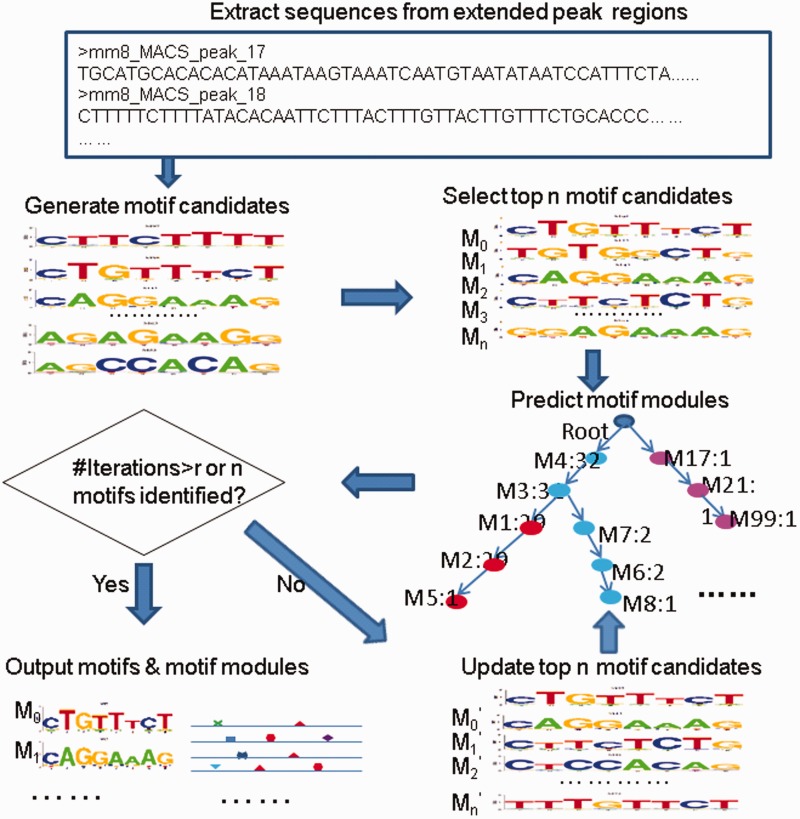
Because of the large number of input sequences, the number of motif candidates obtained above can be large. To deal with the potential large number of motif candidates above and minimize the time cost, SIOMICS applies the following strategy to discover motifs (Figure 1). In brief, with a user-specified maximal number of motifs to be identified, say m, first, SIOMICS considers the top m motif candidates to discover motif modules. Assume there are m1 distinct motif candidates included in the predicted motif modules. SIOMICS outputs these m1 candidates as putative motifs. Next, SIOMICS iteratively identifies other candidates that form motif modules with the identified putative motifs, by considering different groups of m motif candidates each time. Each group of m candidates always includes all putative motifs discovered so far. Finally, if m putative motifs are predicted or no new putative motifs are identified after a certain number of iterations, say r iterations, SIOMICS reports all predicted putative motifs, motif modules and TFBSs and stop. See the following algorithm for details.

Figure 1.

The procedure in SIOMICS.

Algorithm: iterative identification of motifs

Input: ChIP-seq sequences, ranked motif candidates, m, r, s

Output: motifs, motif modules and TFBSs.

Procedure:

1. (Initialization) set iteration = 0.

2a. (Prediction phase)

 Discover motifs and motif modules with the top m motif candidates by the above frequent pattern mining approach, with the support s. Output the m1 motifs included in the predicted motif modules.

2b. Iteration++.

3. (Updating phase)

  If (m1<m) and (iteration <r)

   Choose a new set of top m motif candidates that includes the m1-predicted motifs in the prediction phase and the next (m-m1) ranked top motif candidates that have not been considered with the m1-predicted motifs. Go back to 2a.

  Else

   Output predicted motifs, motif modules, TFBSs from the current prediction phase.

Cofactors of 13 TF

We obtained known cofactors of the 13 TFs in two ways. One was to extract all cofactors mentioned in (14), which used the 13 TFs and their cofactors. The other was to obtain all interacting TFs for each of the 13 TFs from the BioGRID database (29), and then confirm each TF by literature search, if they were predicted as a cofactor by any of the three software: SIOMICS, Dreme and Peak-motifs (Supplementary Table S1).

Comparisons of predicted motifs with known motifs

For the predicted motifs, we compared them with known motifs in two public databases, TRANSFAC V11.3 (4) and JASPAR 2010 (30). We applied the STAMP tool (31) with two E-value cutoffs used in previous studies (7,8), 1E-4 and 1E-5, for the comparisons of predicted motifs with known motifs.

RESULTS

SIOMICS identifies known and new motifs in each ChIP-seq data set

We applied SIOMICS with the default parameters to identify motifs in the 13 ChIP-seq data sets and 13 random data sets. The command used is as follows: python SIOMICS.py -i seq_fasta -o output_directory -w 8 -m 100 -s 1%*n -r 20 -c 0.01, which means to discover at most 100 motifs of length 8 contained in motif modules that occur in at least 1% of the n peak regions, with the motif module P-value cutoff of 0.01 and the iteration number of 20 to stop. Here, n is the total number of input sequences, and the parameter s specifies the required minimum number of sequences containing putative TFBSs of all motifs in a motif module. That is, each predicted motif module has TFBSs of all its motifs co-occur in at least s input sequences. SIOMICS identified >21 known and new motifs in each ChIP-seq data set. In addition, SIOMICS predicted no motif in any random data set, representing a high specificity (Table 1).

Table 1.

Predicted motifs by SIOMICS in 13 ChIP-seq data sets and 13 random data sets

Data set	Number of peaks	Number of predicted motifs	Number of predicted motif modules	Percentage motifs similar to known motifs (Evalue < 1E-5)	Percentage motifs similar to known motifs (Evalue < 1E-4)	Percentage motifs not in original 100	Number of motifs predicted in random data sets
Sox2	7761	99	889	78/99 = 78.8%	96/99 = 97.0%	51/99 = 51.5%	0
E2f1	20 670	99	2510	79/99 = 79.8%	94/99 = 94.9%	55/99 = 55.6%	0
Stat3	5347	91	1256	72/91 = 79.1%	85/91 = 93.4%	39/91 = 42.9%	0
Nanog	17 834	99	1131	76/99 = 76.8%	96/99 = 97.0%	58/99 = 58.6%	0
Oct4	6915	73	719	64/73 = 87.7%	69/73 = 94.5%	42/73 = 45.2%	0
c-Myc	6462	96	1901	74/96 = 77.1%	94/96 = 97.9%	77/96 = 80.2%	0
Klf4	18 144	99	2052	83/99 = 83.8%	96/99 = 97.0%	52/99 = 52.5%	0
Ctcf	49 114	99	784	78/99 = 78.8%	94/99 = 94.9%	38/99 = 38.4%	0
Zfx	17 201	98	1945	75/98 = 76.5%	93/98 = 94.9%	76/98 = 77.6%	0
Tcfcp2l1	45 885	71	782	55/71 = 77.5%	68/71 = 95.8%	41/71 = 57.8%	0
Esrrb	49 127	43	308	35/43 = 81.4%	41/43 = 95.3%	30/43 = 69.8%	0
n-Myc	10 987	94	1766	72/94 = 76.6%	91/94 = 96.8%	80/94 = 85.1%	0
Smad1	2185	21	33	21/21 = 100%	21/21 = 100%	16/21 = 76.2%	0

SIOMICS identified many known motifs in each ChIP-seq data set. Compared with the known motifs in the TRANSFAC and JASPAR databases (4,30), in each data set, >76.0% of the predicted motifs are similar to known motifs, demonstrating that the predicted motifs by SIOMICS are likely to be biologically meaningful instead of arbitrary 8-mer patterns (Table 1). On average, in each data set, >62.9% of motifs corresponding to the known cofactors of the TF under consideration are predicted by SIOMICS. Take the Nanog data set as an example. SIOMICS identified the Nanog motif in this data set, which occurs in 5.8% of peak regions. In addition, SIOMICS identified six motifs for TFs Sox2, Oct4, Zic3, Klf4, Elf5 and Tead1, all of which are known to cooperate with Nanog to regulate their target genes (Supplementary Table S1). Note that the Zic3 and Elf5 TFBSs occur only in 4.5% and 5.2% of peaks, respectively, and are individually not statistically significant enough to be identified if we take the multiple comparisons into account. Because SIOMICS considers multiple motifs simultaneously, it identifies these individually insignificant motifs. For this data set, SIOMICS identified motifs of seven out of eight known cofactors, demonstrating the success of the systematic discovery motifs in ChIP-seq data by SIOMICS. The only motif missed by SIOMICS is the Essrb motif, which is similar to one of the predicted motifs in this data set, did not satisfy the required STAMP E-value cutoff when comparing similarity of the predicted motifs with known motifs.

In addition to motifs corresponding to known cofactors, SIOMICS also identified motifs of potential new cofactors. For instance, SIOMICS identified a motif TTTTAAAA in three data sets (Sox2, E2f1 and Nanog). In each data set, this motif forms a motif module with the same two motifs GAAAGAAA and CAAAACAA, corresponding to the TFs Hsf (STAMP E-value: 5.3E-06) and Fox (STAMP E-value 2.5E-05), respectively. Hsf has been shown to interact with Fox (32), and Fox has the function ‘regulation of RNA splicing’ (33). Consistently, we found that the closest genes to the peak regions containing TFBS of all motifs in this motif module (potential target genes of this motif module) significantly share the same gene ontology term: regulation of RNA splicing (corrected P-value: 0.0052). Thus, it is likely that the unknown TF corresponding to this new motif may play an important role in regulation of RNA splicing together with Hsf and Fox.

To show that SIOMICS can identify motifs that may be underrepresented in all peak regions, we checked the percentage of predicted motifs that were not from the original top 100 motif candidates. As mentioned above, motif candidates were ranked according to their individual statistical significance, from the most significant ones to the least significant ones. We found that on average >60% of predicted motifs were from candidates that were ranked higher than 100, implying that many individually insignificant motifs may play important functional roles (Table 1). It also indicates that considering individual motifs separately in motif discovery may miss many functional motifs. For instance, in the Oct4 data set, SIOMICS identified a motif M67 with motif consensus TCCACCCC, which is insignificant by itself (corrected P = 1). However, this motif M67 is similar to the motif of the TF Zic2 (NACCACCC, STAMP E-value 1.7E-6), and Zic2 is a known cofactor of Oct4 (34).

SIOMICS identifies meaningful motif modules in each ChIP-seq data set

SIOMICS discovered a large number of motif modules in each ChIP-seq data set and no motif module in any random data set (Table 1). The number of motifs is from 2 to 4 in a motif module, with the average of 2.15 motifs per motif module. We investigated the functions of the predicted motif modules and found that at least 51.5% (65.2% on average) of motif modules in a data set are partially supported by at least one source of functional evidence.

First, we focused on the predicted motifs that are similar to known motifs to see whether TFs corresponding to their similar known motifs interact. We collected 648 491 known interacting TF pairs from the BioGRID database (29). For each data set, we then examined whether motifs of these interacting TF pairs are significantly enriched in the predicted motif modules. We found that the corrected P-value of known interacting TF pair enrichment in the predicted motif modules in all 13 data sets is smaller than 1E-10 (Table 2, columns 2 and 3), suggesting TFs corresponding to motifs in the same motif module do interact with each other.

Table 2.

Predicted motif modules are supported

Data set	Motif modules contain at least a pair of interacting TF pairs from BioGRID	P-value of Enrichment of TF pairs from BioGRID	Shared motif modules across data sets	Motif modules with preferred motif order (corrected P-value < 0.05)	Motif modules supported by at least one type of evidence
Sox2	343/889 = 38.6%	0	261/889 = 29.4%	208/889 = 23.4%	582/889 = 65.6%
E2f1	1373/2510 = 54.7%	0	408/2510 = 16.3%	1452/2510 = 57.8%	2039/2510 = 81.2%
Stat3	469/1256 = 37.3%	0	289/1256 = 23.0%	244/1256 = 19.4%	755/1256 = 60%
Nanog	348/1131 = 30.8%	0	273/1131 = 24.13%	428/1131 = 37.8%	712/1131 = 62.3%
Oct4	254/719 = 35.3%	2.2E-271	110/719 = 15.3%	179/719 = 24.9%	406/719 = 56.6%
c-Myc	715/1901 = 37.6%	0	331/1901 = 17.4%	506/1901 = 26.6%	1166/1901 = 61.3%
Klf4	955/2052 = 46.5%	0	357/2052 = 17.4%	1044/2052 = 50.8%	1517/2052 = 73.4%
Ctcf	299/784 = 38.2%	0	181/784 = 23.1%	402/784 = 51.3%	584/784 = 74.5%
Zfx	535/1945 = 27.5%	0	321/1945 = 16.5%	762/1945 = 39.2%	1207/1945 = 62.1%
Tcfcp2l1	169/782 = 21.6%	8.8E-136	154/782 = 19.7%	345/782 = 44.1%	495/782 = 63.3%
Esrrb	105/308 = 34.1%	3.2E-106	51/308 = 16.6%	125/308 = 40.6%	204/308 = 66.2%
n-Myc	807/1766 = 45.7%	0	311/1766 = 17.6%	723/1766 = 40.1%	1249/1766 = 70.1%
Smad1	11/33 = 33.3%	4.8E-12	9/33 = 27.3%	3/33 = 9.1%	17/33 = 51.5%

Next, we investigated whether a motif module was predicted in multiple data sets. Because the majority of peak regions in the 13 data sets do not overlap with each other, the repeated prediction of a motif module in different data sets implies the functionality of this motif module. For each data set, we found a large number of predicted motif modules were shared in at least two data sets (Table 2). We provided an example of a motif module consisting of an unknown motif together with the motifs of the interacting TFs Hsf and Fox above. Here is another example. The motif module composed of three motifs, CCTTCCTG, CAAAACAA and CTGCTGGG, was found in the Stat3 and E2f1 data sets, which are similar to the Stat3 motif (STAMP E-value 4.7E-8), the Sox2 motif (STAMP E-value 4.2E-6) and the Ctcf motif (STAMP E-value 2.2E-4), respectively. The interaction between Stat3 and Sox2 was reported previously (35). Sox2 was also shown to be co-working with Ctcf (36). In addition to the interactions of Stat3, Sox2 and Ctcf, the three TFs also share similar functions. For instance, Stat3 has the function related to system development (37). So does Sox2 (38). By analyzing the closest genes to peak regions containing TFBSs of all motifs in this motif module, we found that these genes significantly share the function ‘system development’ (multiple comparison corrected P = 0.03). The functions of the TFs in this motif module are thus consistent with the functions of these closest genes. All these observations on the TF interactions, the TF functional similarity and the function consistency of the TFs and the closest genes support the functionality of this motif module.

Finally, we examined the relative order of the TFBSs of a pair of motifs in every predicted motif module. The rationale is that if a motif pair has its TFBSs in certain preferred order in peak regions, TFs corresponding to this motif pair likely interact and the motif module may thus be biologically meaningful. Similar to our previous study (3), for a given motif pair in a motif module, we counted in how many peaks the preferred order occurs and then assessed the significance by a binomial test. We found that at least 9.1% of motif modules (or 35.8% on average) have TFBSs of at least a pair of motifs with preferred order of occurrence in ChIP-seq peak regions in each data set, after multiple comparison correction to define the preferred motif orders (Table 2). For instance, in the aforementioned example about the interacting TFs Hsf and Fox, we find that TFBSs of Hsf prefer to bind to the downstream of TFBSs of the Fox motif (corrected P-value 2.47E-12). The two TFs have been shown to interact (32).

Comparison with Dreme and Peak-motifs

We compared SIOMICS with Dreme and Peak-motifs on the 13 ChIP-seq data sets and 13 random data sets. We used the above default parameters for SIOMICS to output at most 100 motifs. For Dreme and Peak-motifs, we used the following commands to output at most 100 motifs as well: python dreme.py -P <input_seq> -m 100 -o <output directory>; peaks-motifs -i <input_seq> -prefix peak_motifs -nmotifs 100 -outdir <output directory>. SIOMICS showed advantages over the two methods in terms of speed and the number of predicted motifs in experimental and random data sets.

We first compared the sensitivity of SIOMICS with that of Dreme and Peak-motifs based on known cofactors of each TF (Table 3). In 11 of the 13 ChIP-seq data sets, SIOMICS did better than, or at least the same as, Dreme. Only in the Klf4 and Esrrb data sets, Dreme predicted motifs of more known cofactors. Similarly, in 12 of the 13 data sets, SIOMICS did at least the same as Peak-motifs. Only in the Esrrb data set, Peak-motifs predicted motifs of more known cofactors. To see whether SIOMICS can identify motifs of more cofactors in the Klf4 and Esrrb data sets, we applied SIOMICS to predict motif modules that occur in at least 0.5% of the peak regions instead of the default 1% of the peak regions: SIOMICS identified 2 and 3 motifs of more cofactors in the Klf4 and Esrrb data sets, respectively. For instance, SIOMICS did not identify Stat3, Sox2 and Ewsr1 in the Esrrb data set at the default 1% cutoff, but identified these motifs when the cutoff 0.5% was used.

Table 3.

Comparison of three methods on prediction of known cofactor motifs

TF	Known motifs found (primary and cofactors) E-value cutoff E-4
	SIOMICS	DREME	Peak-motifs
Sox2	8/9 (Sox2,Klf4, Stat3, Zic3, Hoxa5, Tcf3, Tead1,Oct4)	8/9 (Sox2, Oct4, Klf4, Stat3,Esrrb, Zic3, Tcf3, Tead1)	4/9 (Sox2,Oct4, Klf4, Esrrb)
E2f1	7/10 (E2f1,Stat3, Klf4, Fox, Sp1, Nfkb1, Tbp)	6/10 (E2f1,Stat3, Myc, Klf4, Creb, Sp1)	3/10 (Klf4, Creb, Sp1)
Stat3	6/8 (Stat3,Klf4, Sox2, Myc, Sp1, Irf)	6/8 (Stat3,Klf4, Esrrb, Sox2, Myc,Sp1)	6/8 (Stat3,Klf4, Sox2, Esrrb, Myc, Sp1)
Nanog	7/8 (Nanog,Sox2,Oct4, Zic3, Klf4, Elf5, Tead1)	4/8 (Nanog,Sox2, Klf4, Esrrb)	4/8 (Sox2, Oct4, Klf4, Esrrb)
Oct4	8/10 (Oct4,Sox2, Klf4, Sox10, Ewsr1, Nanog, Zic2, Esrrb)	7/10 (Oct4,Sox2, Klf4, Esrrb, Sox10, Ewsr1, Nanog)	5/10 (Oct4,Klf4,Creb, Esrrb, Sox10)
c-Myc	3/4 (Stat3, Egr1, Sp1)	3/4 (c-Myc,Stat3, Sp1)	3/4 (c-Myc,Egr1, Sp1)
Klf4	4/10 (Klf4,Stat3, Sox2, Sp1)	6/10 (Klf4,Stat3,Esrrb, Sox2, Sp1, Myc)	3/10 (Klf4,Stat3, Sp1)
Ctcf	5/6 (Ctcf,Stat3,Gabpa, Yy1, Smad3)	4/6 (Ctcf,Stat3,Gabpa, Smad3)	2/6 (Ctcf,Myc)
Zfx	2/4 (Zfx,Stat3)	2/4 (Zfx,Stat3)	2/4 (Zfx,Stat3)
Tcfcp2l1	7/12 (Tcfcp2l1,Stat3,Klf4, sox2, Esrrb, Fox, Sp1)	6/12 (Tcfcp2l1,Stat3, Klf4, Esrrb, Fox, Sp1)	5/12 (Klf4, Esrrb, Egr1, Fox, Sp1)
Esrrb	4/10 (Esrrb,Klf4, Rxra, Sp1)	8/10 (Esrrb,Klf4, Sox2, Stat3, Myc, Rxra, Ewsr1, Sp1)	5/10 (Esrrb,Klf4, Stat3, Rxra, Sp1)
n-Myc	2/5 (Stat3,Creb)	2/5 (n-Myc,Stat3)	1/5 (n-Myc)
Smad1	5/9 (Sox2, Oct4, Esrrb, Klf4, Stat3)	4/9 (Sox2, Esrrb, Klf4, Stat3)	4/9 (Sox2,Esrrb, Zic3, Klf4)

We next compared SIOMICS with Dreme and Peak-motifs based on shared motifs predicted by the three methods. This is because we currently have limited knowledge of cofactors of a TF, and thus the above comparison of known cofactors may be limited. In addition, if a motif is predicted by at least two of the three independent methods, this motif may be a true motif. To determine whether two predicted motifs by two methods are similar, we required their STAMP comparison E-value be smaller than 1E-5, a more stringent cutoff used in previous studies (7,8). We found that for every data set, SIOMICS predicted much more shared motifs than both Dreme and Peak-motifs (Supplementary Table S2). Because Dreme and Peak-motifs discover one motif at one time, this comparison implies the advantage of considering multiple motifs simultaneously instead of individual motifs separately.

We then compared the specificity of the three methods on 13 random data sets (Supplementary Table S3). Because these random data sets were obtained by permuting ChIP-seq peak sequences, they represent sequences with no biological meaning and thus are expected to contain no motif. SIOMICS and Dreme predicted no motif in any of these data sets. The fact that no motif was predicted by SIOMICS indicates the small false-positive rate can be achieved by simultaneously considering multiple motifs. Although Dreme considers individual motifs separately, it compares the occurrence of a pattern in a ChIP-seq sequence data set and that in the corresponding permuted data set (14), which also reduces the false-positive rate here. We also found that, on average, Peak-motifs identified 8.62 motifs in a random data set (Supplementary Table S3). We observed that the five data sets with the largest sizes have the larger number of predicted positives by Peak-motifs, which, at least partially, suggests better false-positive control strategies in large data sets by SIOMICS and Dreme.

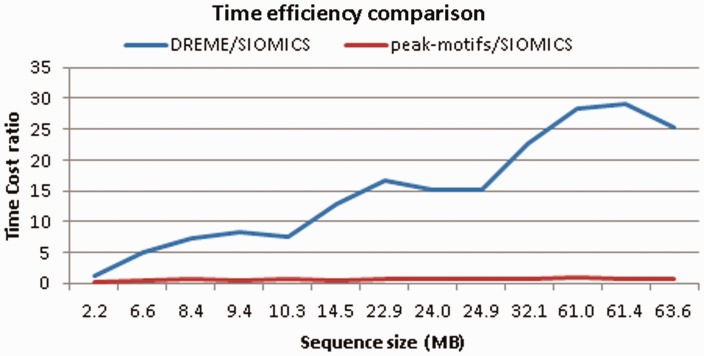
Finally, we compared the speed of the three methods to discover motifs in the 13 ChIP-seq data sets (Supplementary Table S4). All comparisons were done on the same computer with the following configuration: Intel ® Core™ 2 Duo CPU E7500 @ 2.93 GHz and 4 G RAM. We found that Peak-motif is ∼1.43 times faster than SIOMICS, which is 15 times faster than Dreme (median). In addition, when the data set size is small, such as several thousand sequences, the speed difference of SIOMICS and Peak-motifs is large (around three times); when the data set size is large, the speed difference of the two methods is small (around one time). On the contrary, when the data set size is large, the difference of the speed of SIOMICS and that of Dreme is large (>15 times); when the data set size is small, the speed difference of SIOMICS and Dreme is small (around five times for 5347 peaks). These observations demonstrate the efficiency of SIOMICS in dealing with large data sets (Figure 2). It also implies that when the number of peaks in a ChIP-seq experiment is large, SIOMICS will not only predict motifs of more cofactors than the other two methods, but also have the time efficiency advantage compared with the two methods.

Figure 2.

The time cost comparison of SIOMICS with Dreme and Peak-motifs.

DISCUSSION

We developed a novel approach SIOMICS to systematically discover motifs and TFBSs from ChIP-seq data. Different from available methods, SIOMICS does not depend on limited information of known motifs and simultaneously considers multiple motifs. Tested on experimental and simulated data, we show that SIOMICS identifies motifs of more known cofactors and identifies more shared motifs in the experimental data. At the same time, SIOMICS has a low false-positive rate when tested in the simulated data. In addition, we show SIOMICS is as fast as other methods, especially when the ChIP-seq data sets are large. Thus, SIOMICS is a useful alternative method for motif discovery.

We applied SIOMICS on the extended 800-bp-long sequence around the central ChIP-seq peak regions. This is because the central peak regions may not always contain the TFBSs of a cofactor. For instance, for the E2f1 data set, if we only considered the central peak regions defined by the MACS software (11), we could have missed the motif of the E2f1 cofactor, Tbp. In the extended E2f1 ChIP-seq peak sequences, SIOMICS identified Tbp as the cofactor of E2f1 (STAMP E-value 1.77E-07). A critical question is how long we should extend the peak regions. Our experience suggests extension of the central peaks such that each peak is at least 800-bp long is a good choice. In fact, it has been shown that the majority CRMs are shorter than 800 bp (2,3).

In addition to Dreme and Peak-motifs, we also compared SIOMICS with CPModule (16) and CisModule (39). CPModule discovers motif modules using known motifs. Note that one reason that SIOMICS was developed is that the number of known motifs is limited. Even with the same set of known motifs as input, SIOMICS predicted more known cofactor motifs within a shorter time in most of the 13 ChIP-seq data sets (Supplementary file S5). CisModule, a classical de novo CRM discovery method, was not developed for the ChIP-seq data analysis. Thus, we compared it with SIOMICS on sequences from the top 100 peak regions in each ChIP-seq data set. We found that SIOMICS identified more cofactor motifs and was much faster than CisModule (Supplementary File S6).

Users can tune several parameters in the SIOMICS software to optimize the results. The first one is the motif length w. We recommend use w = 8. The second parameter is the support parameter s, which is the minimum number of sequences a motif module needs to occur. We used 1% of the number of input sequences in a data set as the default s, for the speed of the tool. The smaller the s is, the more motifs and motif modules may be predicted. Note that if the number of the input sequences is small (<100), we recommend setting s to be at least 2. The third parameter is the number of motif candidates considered in an iteration of motif module discovery, the parameter m. Users can increase m if ∼100 motifs are predicted, as what was shown in several data sets such as the Sox2 and E2f1 data sets (Table 1). We kept m = 100 for the convenience of the comparisons with other methods. We also tried m = 150 for several data sets and obtained more motifs of known cofactors. For instance, in the Klf4 data set, we identified the motif of an additional Klf4 cofactor Tp53 (STAMP E-value 1.7E-05) (40), which was not discovered with m = 100.

With the input parameters, SIOMICS will output at most m motifs. We believe these motifs are meaningful because of the high sensitivity suggested in Table 3 and the high specificity implied by the fact of no prediction in random data sets. We sorted the predicted motifs from the most reliable ones to the least reliable ones in the output motif files (with a suffix name.otifs). We recommend users take the P-values of motif modules containing a motif and the number of motif modules containing this motif into account when assessing its biological meaning.

In summary, we developed a novel method for de novo systematic discovery of motifs in ChIP-seq data. This method is shown to predict motifs of more known cofactors than available methods and has comparable speed as the fastest method, especially on large data sets. The tool implementing the developed method, SIOMICS, is freely available at http://www.cs.ucf.edu/∼xiaoman/SIOMICS/SIOMICS.html.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Science Foundation [1149955, 1125676 and 1218275]. Funding for open access charge: The National Science [1125676 to H.H.].

Conflict of interest statement. None declared.