Abstract
Under a tension of ∼65 pN, double-stranded DNA undergoes an overstretching transition from its basic (B-form) conformation to a 1.7 times longer conformation whose nature is only recently starting to be understood. Here we provide a structural and thermodynamic characterization of the transition by recording the length transient following force steps imposed on the λ-phage DNA with different melting degrees and temperatures (10–25°C). The shortening transient following a 20–35 pN force drop from the overstretching force shows a sequence of fast shortenings of double-stranded extended (S-form) segments and pauses owing to reannealing of melted segments. The lengthening transients following a 2–35 pN stretch to the overstretching force show the kinetics of a two-state reaction and indicate that the whole 70% extension is a B-S transition that precedes and is independent of melting. The temperature dependence of the lengthening transient shows that the entropic contribution to the B-S transition is one-third of the entropy change of thermal melting, reinforcing the evidence for a double-stranded S-form that maintains a significant fraction of the interstrand bonds. The cooperativity of the unitary elongation (22 bp) is independent of temperature, suggesting that structural factors, such as the nucleic acid sequence, control the transition.
INTRODUCTION
When stretched under forces <60 pN, double-stranded (ds) DNA maintains its basic conformation (B-form) and displays the elastic response of an extensible worm-like chain (1–4). At pulling forces >60 pN, however, the molecule abruptly deforms (overstretching transition), shifting within a few piconewtons to an extended conformation 1.7 times longer than the B-form (5,6). Although the overstretching phenomenon has long been known, its nature is still hotly debated. In a series of studies (7–12), the elongated conformation of DNA was interpreted as merely due to a force-induced melting with strand separation, based on the evidence that (i) the interphosphate distance along the chain in overstretched DNA is the same as that in single-stranded DNA (ss-DNA), (ii) the free energy difference between B-form and overstretched DNA matches the melting requirement, (iii) the overstretched state is able to react with ss-DNA binding proteins and glyoxal, as if it had exposed base pairs (bp). The direct observation of the occurrence of melting during overstretching was more recently obtained using a combination of mechanical manipulation and fluorescence spectroscopy (13). In contrast, the idea of an elongated state of the ds-DNA (S-form) was supported by the evidences that the overstretched molecule is characterized by a defined reduced helicity (14–16) and its stiffness is higher than expected for ss-DNA (17,18).
A growing body of evidence suggests that the melted and S-form of DNA can coexist. Initially the presence of melted DNA in overstretched molecules was inferred from the occurrence of hysteresis in consecutive stretching and shortening cycles. According to this characterization, it was shown that the extent of melting taking place during overstretching varies widely depending on the bp sequence, DNA topology (open or closed), solution conditions (ionic strength, pH and temperature) and manipulation of the molecule (19,20).
Recent experiments on covalently closed DNA molecules (21) prove that the presence of free ends is not a necessary requirement for DNA overstretching and that a double-stranded (S-) form can account for the 1.7 times elongation. Conversely, using molecules with only one end closed, it has been shown that the 1.7 longer form can be generated without hysteresis (and thus without peeling at the free end), provided that the temperature is <18°C and the ionic strength and pH are in the physiological range (22). At higher temperature or at lower ionic strength the reaction becomes hysteretic and is accompanied by a positive entropy change (similar to that found with thermal melting), providing the evidence for melting by peeling at the free ends. Also using molecules with both ends closed, temperature and ionic strength determine whether overstretching is accompanied by melting, which, in this case, is limited to inside strand separation (23,24). A more refined method to distinguish between melted and S-DNA has been recently proposed based on the combined use of multiple fluorescent dyes (24). The results confirmed both the coexistence of melted and S-form of DNA and the dependence of their relative proportions on DNA topology and solution conditions. However, the evidence from calorimetric analysis (23) that internal melting is linked to the appearance of hysteresis is contradicted by the finding obtained with fluorescence microscopy (24) that the progressive increase in the proportion of the internally melted form at the expenses of the S-form is not accompanied by an increase in hysteresis. This weakens the link between melting and hysteresis and in turn poses the question of whether the calorimetric methods provide an accurate description of the complex events occurring during the overstretching transition.
While so much research has been devoted to characterizing the nature of the overstretching transition by its equilibrium force-extension relation, until recently no experiments have been conducted using rapid changes in load to determine nonequilibrium kinetics of the transition, which would represent a much more powerful tool. In fact, the transition elicited by a force step followed by clamp of force at the new level occurs with a potential energy landscape that remains constant, and the reaction is followed through the change in length, which serves at the same time as the reaction coordinate. The application of this approach, however, was limited by the finite response time of the feedback loop, which depends not only on the frequency response of the actuator, but also on the compliance of the specimen under study (25–27). Only recently has a sufficiently fast force-clamp method been developed that allows the transient kinetics of the DNA overstretching to be investigated (25,27). It has been shown that the elongation elicited by a force step of 0.5–2 pN (complete in ∼2 ms), imposed on a molecule with ends opened, in the region of the overstretching transition is characterized by an exponential time course. This implies that the main transition mechanism cannot be force-induced melting starting at the free ends and then propagating inward (13), since this process would have linear kinetics. A two-state model was proposed, which was able to reproduce not only the U-shaped dependence of the rate constant of elongation on force and its independence of the size of the force step, but also the length fluctuations just measured in short DNA segments (20).
The two-state transition kinetics defined at 25°C appear per se to contradict the conclusion from recent equilibrium force-extension experiments (22) that, at physiological ionic strength (150 mM salt concentration), in the range of temperatures ≥18°C the overstretching transition is both hysteretic and associated with the entropy change of thermal melting. Another question raised by the transient kinetics experiments is the finding that the rate and size of elongation following a force step are apparently not affected by the development of melting, as revealed by the hysteresis on relaxation [see Figure 2B–D in (27)]. In contrast with this conclusion, recent work using equilibrium kinetics indicates that the molecular elongation changes according to the appearance of hysteresis: in GC-rich segments, which undergo a nonhysteretic transition, the elongation is shorter than in AT-rich segments, which undergo an hysteretic transition (28). However, this finding is contradicted by other recent equilibrium experiments, showing that, in the presence of melting, the overstretched DNA extension is similar (24) to, or even shorter (23) than, that without melting.
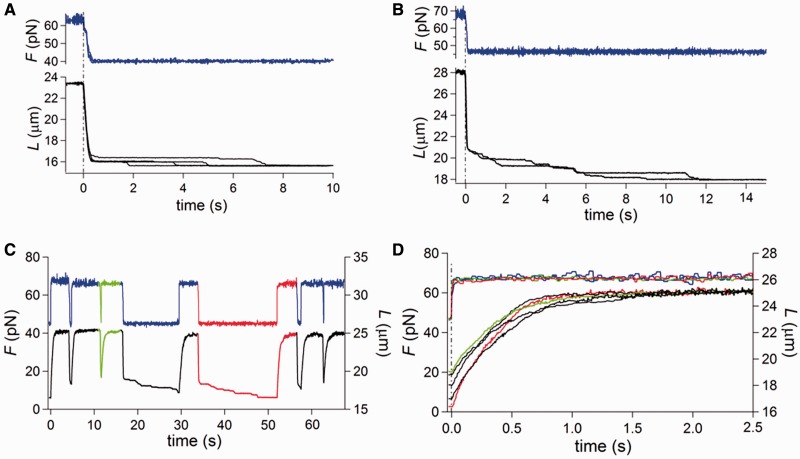
Figure 2.
Shortening and lengthening transients in response to a 20–35 pN square wave at 25°C. Force is blue and length is black unless specified. (A and B) Superimposed shortening transients elicited by a force step bringing the force from 63 to 40 pN (A) and from 67 to 47 pN (B). (C) Lengthening and shortening responses to a square wave of force steps of 20 pN, starting from a low force level of 46 pN, with the force pull imposed at different times following the force drop. The traces of the shortest time are marked in green, those of the longest time are marked in red. (D) Superimposed lengthening transients elicited by the 20 pN force pulls shown in (C) on a faster time scale. Same color code as in (C).
Here the fast force-clamp method is extended to protocols that allow two fundamental questions to be answered: (i) We demonstrate that melting follows the B- to S-form transition and that different degrees of melting do not affect the rate and size of elongation undergone by the double-stranded fraction following a stepwise increase in force. This is achieved by imposing on molecules of λ-DNA an ∼30 pN square wave that cyclically brings the force to, or just above, the overstretching transition region, so that different proportions of B-form and melted single-stranded form are obtained just before the force stretch. (ii) From the temperature dependence of the two-state transition kinetics, obtained by applying the 2 pN step staircase at different temperatures (10–25°C), we determine the enthalpic and entropic contributions to the free energy difference of the B-S transition and extract the enthalpic contribution to the transition barrier. We conclude that the formation of the extended state implies an entropic contribution to the free energy change that at room temperature is one-third of the entropy change of thermal melting. This thermodynamic result represents a fundamental step toward the characterization of the structure of the S-form of DNA, as it indicates that the S-form maintains a higher number of interstrand bonds than melted DNA, as expected from a double-stranded conformation. The equilibrium force-extension curves extracted from the same experiments provide a more limited set of thermodynamic parameters, though in perfect agreement with those from the kinetic analysis, demonstrating in turn that our force-clamp has a response time that is adequate to resolve the kinetics of the overstretching transition.
MATERIALS AND METHODS
Preparation of DNA and mechanical apparatus
Mechanical manipulation of single λ-phage ds-DNA molecules is achieved by means of a Dual Laser Optical Tweezers with two counter-propagating 845 nm laser beams (5). The DNA molecule is held between two streptavidin-coated polystyrene beads by means of biotinilated 3′ ends free to rotate, as previously described (27). While the bead at one end is trapped in the focus of the lasers, acting as a force transducer, the other one is attached to a micropipette integral with the microfluidic chamber carried by a piezoelectric stage (PDQ375, Mad City Lab, Madison, WI, USA), providing movements with subnanometric precision. The system operates in either length- or force-clamp mode with a frequency response of at least 1 kHz. The DNA molecule is first stretched in length-clamp mode at constant pulling velocity (1.4 µm/s) from the starting unstressed length, until a preset force level is reached, at which point the control is switched to force-clamp mode. At the end of the force-clamp protocols detailed below, the system is switched back to the length-clamp mode and the molecule is released at constant velocity to the initial length.
Two mechanical protocols are used in force-clamp mode. In the first protocol, a staircase of force steps of 2 pN separated by 5 s intervals are delivered, either in the shortening direction (negative staircase), starting from a force level above the overstretching transition force, or in the lengthening direction (positive staircase), starting from a force level below the overstretching transition force. In the second protocol, a square wave oscillation is superposed on a force level 20–30 pN below the overstretching transition region, with the first step in the lengthening direction of amplitude (20–35 pN), which is adequate to attain or just overcome the overstretching transition force. In the experiments devised to define the equilibrium force-extension relation, lengthening and shortening at the constant velocity of 1.4 µm/s were imposed on the molecule in length-clamp mode throughout the overstretching transition region (27).
Optimization of the frequency response of the system in force-clamp mode
The force-clamp system was composed of proportional, integrative and differential amplifiers, the gain of which had to be separately optimized for each force step to minimize the error between the command signal and the actual force step imposed on the molecule. The need for accurate modulation of feedback gain tuning arises from the large changes in the compliance of the molecule in the force range investigated (27). In the overstretching transition region, the complex compliance of the molecule (the sum of the changes in length during and shortly after the force step) becomes large, and the gain of the proportional amplifier, set for the stiffer region of the molecule response below or above the overstretching region, becomes insufficient to maintain the stepwise change in force. On the other hand, presetting from the beginning the feedback gain to the value necessary for the compliant region of the molecule response would lead the system to oscillate because the gain would be too high for the early stiffer region. For this reason, the gain had to be adjusted in real time with procedures specifically devised for either the staircase or the square wave protocol (see Supplementary Data). The performance of the system provides that the risetime of the force step (t95%, ranging between 2 and 20 ms) is in any case at least one order of magnitude shorter than the time constant of the corresponding length response.
Temperature control system
The temperature is controlled in a range 4–40°C by means of two copper jackets, which allow thermostated fluid to be circulated around the objectives (29). The response time of the apparatus for temperature equilibration was <8 s (see Supplementary Figure S2A). The thermostat does not add any significant force noise (see Supplementary Figure S2B).
RESULTS
Kinetics of the lengthening transient following 2–35 pN force steps
Figure 1A summarizes how the lengthening of ds-DNA (free ends, 25°C and physiological salt composition) in response to a 2 pN step varies in relation to the steady force at which the step is imposed (27). Below ∼60 pN or above ∼70 pN, the molecule responds elastically with a compliance of ∼30 nm/pN. In contrast, in the region of the overstretching transition the elongation response is at least an order of magnitude larger and has an exponential time course. Five to eight steps are necessary to acquire 100% of the overstretched state. The rate constant (r) of the elongation following the force step is larger at the beginning and at the end of the overstretching transition (range 2–80 s−1), so that the dependence of r on the force attained after the step (F) is U-shaped (black triangles in Figure 1D) with a minimum in the middle of the overstretching force range (∼66.5 pN). It was found that, on reducing the step to 0.5 pN, the amplitude of each elongation transient decreases, but the r–F relation is unchanged (27). Moreover, the size and the rate of lengthening did not depend on the appearance of hysteresis in the subsequent release, and thus on the occurrence of some degree of melting.
Figure 1.
Length changes following 2–35 pN force steps at 25°C. Force is blue and length is black unless specified. (A) Elongation responses to a staircase of force steps of 2 pN separated by 5-s intervals imposed throughout the overstretching region from 47 to 72 pN. (B) Lengthening and shortening transients elicited by a force square wave of progressively increasing size (from 29 pN—first cycle, red—to 31 pN—fifth cycle, green) imposed on the molecule from a starting force of 36 pN. (C) Superimposed lengthening transient, normalized for the maximum length change attained for each pull ( ) from the square wave protocol in (B). The force attained by the step and r, estimated by the exponential fit of the length transient, are 65 pN and 7.7 s−1 (red), 66 pN and 2.8 s−1 (black) and 67 pN and 6.8 s−1 (green). Inset: superimposed fits (dashed line) and traces (continuous line), identified by the color and shifted vertically for clarity. (D) r–F relations determined with different protocols as indicated by the symbols: black triangles from the staircase of 2 pN steps (protocol in A); red squares from the square wave made of force steps of increasing size (protocol in B); green circles from the square wave of constant size and the force during the interval between subsequent pulls increased by 0.5–1 pN; blue squares from the square wave of 20 pN and variable times, from 100 ms to 15 s, between release and pull. (E) Force-length points concerning the first force square wave (red and pink for lengthening and shortening, respectively) and the fifth force square wave (green and light green for lengthening and shortening, respectively) from (B) superimposed on the equilibrium force-extension relation, obtained imposing on the same molecule ramp-faced lengthening (black) and shortening (gray). The asterisk marks the force level (36 pN) at which the square wave is imposed.
) from the square wave protocol in (B). The force attained by the step and r, estimated by the exponential fit of the length transient, are 65 pN and 7.7 s−1 (red), 66 pN and 2.8 s−1 (black) and 67 pN and 6.8 s−1 (green). Inset: superimposed fits (dashed line) and traces (continuous line), identified by the color and shifted vertically for clarity. (D) r–F relations determined with different protocols as indicated by the symbols: black triangles from the staircase of 2 pN steps (protocol in A); red squares from the square wave made of force steps of increasing size (protocol in B); green circles from the square wave of constant size and the force during the interval between subsequent pulls increased by 0.5–1 pN; blue squares from the square wave of 20 pN and variable times, from 100 ms to 15 s, between release and pull. (E) Force-length points concerning the first force square wave (red and pink for lengthening and shortening, respectively) and the fifth force square wave (green and light green for lengthening and shortening, respectively) from (B) superimposed on the equilibrium force-extension relation, obtained imposing on the same molecule ramp-faced lengthening (black) and shortening (gray). The asterisk marks the force level (36 pN) at which the square wave is imposed.
Figure 1B shows an alternative protocol that gives the same kinetic results on stretch, but allows the interplay between overstretching and melting to be defined in the subsequent release (described in the next section). A square wave of 20–35 pN force with 10 s period is applied at 25°C and physiological salt composition. Each pull produces a force (60–70 pN) that is within or just above the overstretching region and is followed after 5 s by a force drop to a value (40–55 pN) in the intrinsic elasticity region, far below the overstretching region. The 5-s interval between force steps allows the molecule to reach the equilibrium extension. The square wave starts with a 29 pN step in the stretch direction superimposed on a steady force of 36 pN (∼30 pN lower than that for the overstretching transition). The size of the stretch–release cycle is increased by 0.5 pN in each cycle. The amplitude of the lengthening response following each pull increases with the force step size, and thus with the force attained after the step (F). Moreover, the lengthening transient displays an exponential time course with a rate that first decreases, as F approaches the middle of the overstretching transition (∼66 pN), and then increases again at larger F. This is emphasized in Figure 1C, in which the lengthening responses, normalized for their maximum value (ΔLe), to three force steps to 65 pN (red, the first in Figure 1B), 66 pN (black, the third) and 67 pN (green, the fifth) are superimposed. It is evident that the rate constant of the elongation, r (estimated from single exponential fits to the length traces, dashed lines in the inset), depends on F in the same U-shaped way as the rate constant of the elongation transient elicited by 2 pN force steps. In fact, the r–F relation from the square wave protocol (red squares in Figure 1D) exactly superposes on the r–F relation from the 2 pN staircase (black triangles).
The monotonic increase in ΔLe of each subsequent transient (Figure 1B) is accounted for by considering that the corresponding force step starts from the region of intrinsic elasticity and attains a larger final F in the overstretching region. Thus, the equilibrium force–extension point attained at the end of the transient implies a progressively larger lengthening. This can be better appreciated in Figure 1E, where the force-length traces of the largest and shortest lengthening transients from Figure 1B (red and green traces) are superimposed on the equilibrium force-extension curve, which was obtained, using the same molecule and the same temperature, with isovelocity lengthening and shortening (black trace, lengthening phase; gray trace, shortening phase). Starting from the first point on the left (marked by asterisk, and corresponding to the low force level of the square wave in Figure 1B), the trajectory of the lengthening transient shows two orthogonal portions, according to the two phases of the response, the first in the vertical direction, corresponding to the elastic response, and the second in the horizontal direction, corresponding to the exponential elongation under force clamp.
In an alternative protocol, the square wave amplitude was held constant and the final force progressively increased by applying 1 pN steps during the low force phase between subsequent pulls (see Figure 3 for a detailed example of this protocol at a lower temperature). Green circles in Figure 1D are the r–F points obtained (at 25°C) with the alternative protocol consisting of a 25 pN pull superimposed on a starting force of 40 pN and increased by 1 pN before each subsequent pull. r depends on F in the same way as in the protocol shown in Figure 1B. We conclude that r depends only on the force at which the elongation occurs and is independent of the starting force, the force step size and the amplitude of the elicited lengthening, as expected from a response that is governed by the kinetics of a two-state reaction.
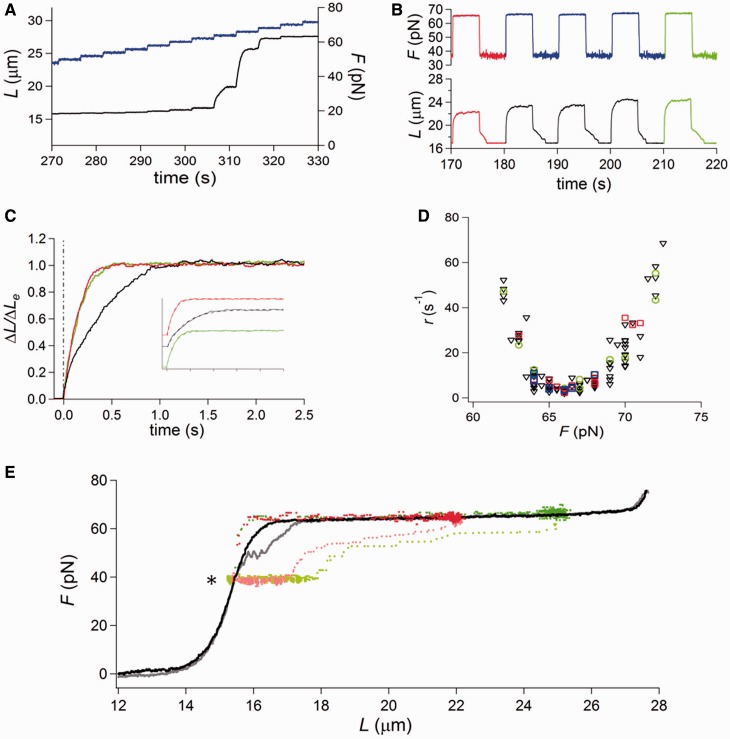
Figure 3.
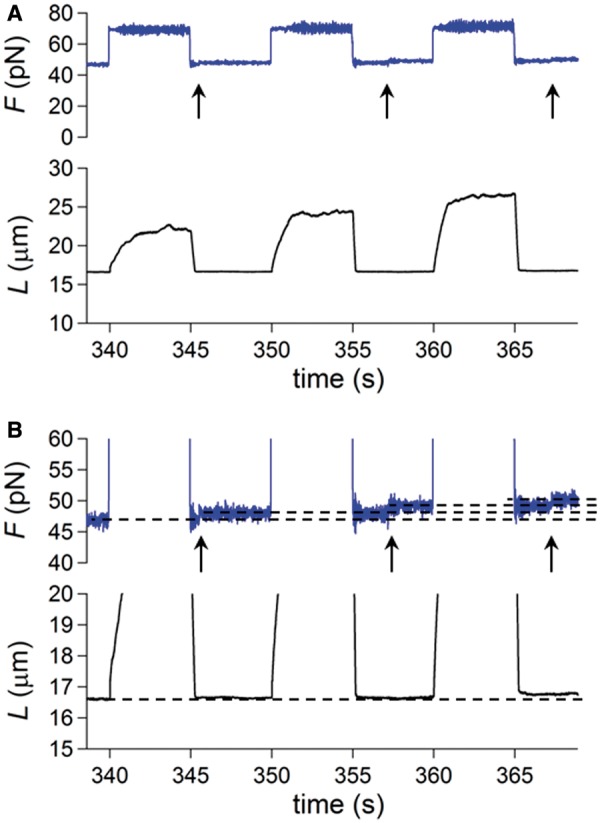
Lengthening and shortening responses to a square wave of 23 pN imposed on a molecule at 10°C. (A and B) are the same records with vertical magnification of traces in (B) four times larger than in (A). Force is gray and length is black. The starting force for the first pull is 47 pN and is increased by 0.5 pN at a time (marked by the arrow) during the low force phase before each subsequent pull.
The shortening transient following 20–35 pN force drop
At 25°C, the release phase of the 20–35 pN square wave protocol shows several striking features. The shortening occurs in two phases, a partial stepwise shortening (simultaneous with the force step attained within the limits of the time resolution of the system—see ‘Materials and Methods’ section) and a subsequent slower shortening, which is the sign of a hysteretic response and terminates with the complete recovery of the molecule length characteristic of the equilibrium force-extension relation (Figure 1B). This can be appreciated also in Figure 1E from the superimposition of the force-length points of the shortening transients from Figure 1B (pink from the first shortening transient and light green from the last shortening transient) and the equilibrium force-extension curve. In Figure 1E, pink and light green are used in place of red and green, which are the colors of the corresponding transient in Figure 1B, to distinguish the force-length points belonging to the stretch phase from those belonging to the release phase. In the force-length plots in E, the rapid phase of the corresponding transient is characterized by a sparse distribution of points (at 1 kHz sampling rate, see ‘Materials and Methods’ section) and the slow phase by a dense distribution of points. In this way, it can be appreciated that the rapid phase of the shortening transient starting from the high force level on the right (65 pN pink, 67 pN light green) is followed by a high density region of horizontally aligned points, due to the hysteretic phase of the response, before attaining the equilibrium low force-extension point on the left (marked by asterisk).
Shortening transients from two other molecules are shown on an expanded time scale in Figure 2A and B. In each panel, two responses to the same force drop (from 63 to 40 pN in A and from 67 to 47 pN in B) are superimposed to stress the stochastic nature of the response. The duration of the hysteretic phase depends on the level of force at which it occurs. The equilibrium force-extension condition is attained within 4 s in Figure 1B (low force level 36 pN), within 8 s in Figure 2A (low force level 40 pN) and within 12 s in Figure 2B (low force level 47 pN). The acceleration of the recovery from the melted state at lower forces suggests that tension on the ss-DNA plays a crucial role in determining the reannealing kinetics.
The most striking feature made evident by the expanded time scale of Figure 2A and B is that the slow phase of the shortening transient is composed of a sequence of stepwise shortenings separated by pauses. This behavior can be compared with the bursts in the force traces under length-clamp conditions reported by Gross and collaborators (30) during the shortening phase of smaller DNA constructs (∼8000 bp) with only one free end. The observed discontinuous shortening in our force-clamp experiments can be explained by the contribution of two processes occurring sequentially at several points along the overstretched molecule: (i) a rate limiting reannealing of melted segments, which does not imply shortening but leads to the double-stranded S-form; (ii) the consequent abrupt (stepwise) recovery of the shorter length characteristic of the B-form. In agreement with Gross and collaborators, the extent of the pause during reannealing may be influenced by the formation of secondary structures within the melted segments.
The kinetics of the lengthening transient in a partially melted molecule
To test the interpretation of the fast and slow process observed during the shortening transients in Figure 2A and B, the square wave protocol was further elaborated by holding constant the starting and final forces and introducing variable waiting times before each pull. In Figure 2C, a 20 pN pull starting from 46 pN is imposed at different times after the 20 pN drop. In this way, the overstretching transition is elicited at different stages of the shortening transient and thus with different degrees of melting. Green and red colors identify the traces corresponding to the earliest pull (the molecule has the largest melted fraction) and the latest pull (the molecule has recovered the equilibrium force-extension condition), respectively. The elongation response exhibits an exponential shape with an amplitude that is smaller when the pull is imposed earlier. At the end of the lengthening transient, the molecule always attains the same length, which is characteristic of the equilibrium force-extension relation, showing that the elongation involves only the fraction of the molecule that has shortened at the time of the pull.
As shown by the superposition of the lengthening transients (Figure 2D), the rate constant r of the exponential elongation is roughly the same independently of both the time of the force pull and the amplitude of the elongation. r–F data obtained with this protocol are plotted in Figure 1D (blue squares) and lie on the same U-shaped relation determined with the protocols of Figure 1. Again, in agreement with the kinetics of a two-state reaction (the B-S transition), r depends only on the force at which the elongation occurs.
The finding that the elongation has the characteristics of the B-S transition and its amplitude increases in direct proportion to the cumulative contribution of the stepwise shortenings during the interval preceding the pull (Figure 2A and B) is a clear indication that the stepwise shortening is the manifestation of the B-form regeneration, which occurs as soon as the reannealing of a segment that had melted during the preceding high-force period, has restored its double-stranded conformation. In this force range (35–45 pN), the S-B transition appears to be almost instantaneous, in contrast to the exponential shape shown in the overstretching force range. This observation is in full agreement with the previous kinetic characterization of the B-S transition because, as expected from the U-shaped r–F relation, at these forces the backward rate constant is orders of magnitude larger than the forward and backward rates in the force range of the overstretching transition.
Thus, the whole shortening transient elicited by a 20–35 pN force drop from the overstretching region (or just above it) (Figure 2A and B) can be explained by the combination of two processes: (i) stepwise shortening due to the S-B transition, which occurs first in proportion to the amount of the double-stranded S-form present in the overstretched state and afterward as a consequence of reannealing, and (ii) rate-limiting reannealing of the melted segments during the isometric phases between shortening events.
The shortening transient in the absence of melting
The above interpretation of the shortening response recorded with the square wave protocol has been verified by eliciting the shortening transient at a lower temperature, at which the probability of melting on stretch is minimized (22,29). In Figure 3, the square wave protocol has been applied to a molecule at 10°C (A and B are the same records with vertical magnification in B four times larger than that in A). The records show the lengthening–shortening responses to a 23 pN square wave. The first force pull is superimposed on a starting force of 47 pN, then the force is increased by 1 pN during each low force phase preceding every pull (arrows), so that a correspondingly higher force is attained in the overstretching region following the 23 pN pull. At the low force value at which the 1 pN step is imposed, the molecule exhibits only its elastic response, which is not resolved on the micrometer scale of the length trace. The shortening transient following the force drop to 47 (first cycle), 48 (second cycle) and 49 pN (third cycle) is always composed of a unique stepwise shortening, without any sign of hysteresis.
At 10°C, the lengthening transient following the force pull also has the exponential shape of the two-state reaction characterizing the B-S transition (Figure 3A), and its rate progressively increases as F increases from 70 (first cycle) to 72 (third cycle) pN, as expected if the r–F points belong to the right branch of the U-shaped relation.
In conclusion, the 20–35 pN square wave protocol with the upper force within or just above the overstretching region has the advantage of providing information on the elongation kinetics while allowing at the same time an estimate of the degree of melting and strand separation elicited by the preceding force pull. The results confirm the finding from the 0.5–2 pN staircase protocol (27) that the amplitude and kinetics of overstretching are not influenced by some degree of melting and are defined solely by the two-state reaction.
Temperature dependence of the transition rates
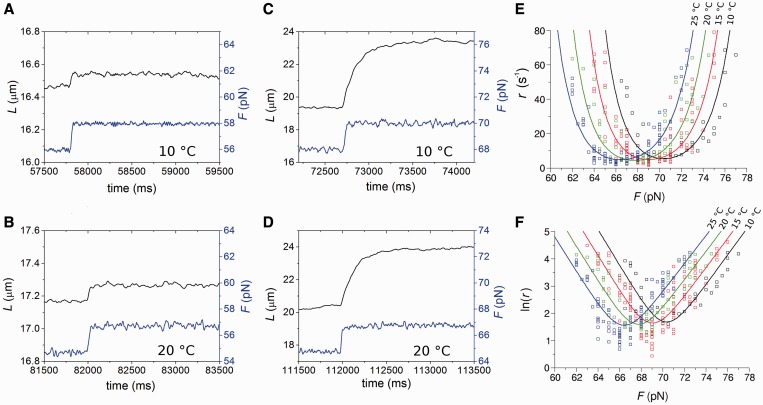
The effect of the temperature on the kinetics of the elongation transient was determined by using the 2 pN step staircase protocol at 10, 15, 20 and 25°C. This protocol was preferred to the square wave protocol because, while it provides the same kinetic information (see Figure 1D), it has a much larger data collection efficiency, allowing the whole r–F relation to be determined with a single overstretching transition. In agreement with the results obtained at 25°C (27), (i) below a force of ∼60 pN, the molecule responds elastically (Figure 4, left column, A: 10°C, B: 20°C), (ii) in the overstretching region (middle column) at either 10°C (Figure 4C) or 20°C (Figure 4D), the elongation response is at least an order of magnitude greater and exhibits an exponential time course, reaching a new steady value in several tens of milliseconds. In the whole range of temperature tested, the rate of elongation (r) following a force step in the overstretching region varies with the force attained after the step between ∼2 and ∼80 s−1, in agreement with the U-shaped relation determined at 25°C (Figure 4E). The minimum of this relation is similar at each temperature, but it is shifted progressively to higher forces at lower temperature. This emerges clearly in Figure 4 from the comparison of both the lengthening transients in Figure 4C (10°C) and Figure 4D (20°C), and the r–F data in Figure 4E (black squares, 10°C, and green squares, 20°C). The elongations with the minimum rate constant (rmin) at 10 and 20°C are similar in both amplitude and speed, the only difference being the force at which they are attained, ∼71 pN at 10°C and ∼67 pN at 20°C. The mean values of rmin from 57 molecules at four temperatures are reported in Table 1, together with the range of F values for which they are calculated (Fmin). rmin (4–6 s−1) does not vary significantly with temperature in the whole temperature range and the only effect of temperature is the progressive reduction of Fmin (from ∼71 to ∼66 pN) with the increase in temperature. Moreover, at each temperature, as at 25°C (27), the relation between the amplitude of the elongation ΔLe and the force is the mirror image of the rate–force relation, so that the maximum elongation (∼4 µm), similar at all temperatures, occurs at a force Fmin progressively larger as the temperature decreases (Table 1).
Figure 4.
Lengthening responses following 2 pN force steps at different temperatures. (A–D) Time course of elongations (black) following force steps (blue) at forces below (A and B) and at the plateau (C and D) of the overstretching transition at 10°C (A and C) and 20°C (B and D). (E) Relation between rate of elongation (r) following 2 pN force steps and the force attained at the end of the step (F) at four temperatures: 10 (black), 15 (red), 20 (green) and 25°C (blue). (F) Relation between ln(r) and F at different temperatures. Same data and color code as in (E). Lines in (E) and (F) are the multi-curve fits with Equation (3) with the same color code for temperature as data points.
Table 1.
Kinetic and mechanical parameters of the overstretching transition at the four temperatures using the protocol shown in Figure 1A
 (°C) (°C) |
 (pN) (pN) |
 (s−1) (s−1) |
 (µm) (µm) |
Number of molecules |
|---|---|---|---|---|
| 10 | 70.0–71.5 | 6.5 ± 0.6 | 4.0 ± 0.2 | 14 (0) |
| 15 | 68.5–70.0 | 3.9 ± 0.4 | 4.8 ± 0.3 | 14 (3) |
| 20 | 67.0–68.5 | 5.4 ± 0.5 | 3.4 ± 0.4 | 12 (6) |
| 25 | 65.5–67.0 | 3.9 ± 0.4 | 3.6 ± 0.5 | 17 (13) |
| 4.9 ± 0.2 | 3.9 ± 0.2 |
Mean values (± SE) of the temperature-independent parameters are reported in the last row. The last column indicates the number of molecules used at each temperature (in brackets the number of molecules showing hysteresis on relaxation).
In Figure 4F, the logarithm of r is plotted versus force for the four temperatures. In agreement with previous findings at room temperature (27), the ln(r)–F relation has a V profile, with its vertex, corresponding to Fmin, progressively shifted to lower forces as temperature is increased from 10 to 25°C.
In terms of the two-state reaction model, Fmin roughly represents the coexistence force Fe, that is, the force at which the work done in the elongation (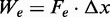 ) equals the free energy difference between the compact and the extended states, and its decrease with temperature suggests a significant entropic contribution to the stability of the extended state.
) equals the free energy difference between the compact and the extended states, and its decrease with temperature suggests a significant entropic contribution to the stability of the extended state.
In the 2 pN step staircase protocol, the hysteresis on relaxation, which underlies melting and strand separation during the extended phase, becomes progressively less frequent at lower temperature (Table 1): hysteresis occurs in 75% of molecules at 25°C, 50% at 20°C, 21% at 15°C and does not occur at 10°C. In this respect it must be noted that, in contrast to the 2 pN step staircase, the 20–35 pN square wave protocol per se increases the probability of melting and strand separation at the same temperature and ionic strength. In fact, with the square wave protocol, the hysteresis was always present at 25°C (Figures 1 and 2), whereas with the staircase protocol, it was present in only 75% of the molecules (Table 1). In agreement with (27), the hysteretic behavior, which underlies melting during overstretching, does not imply any effect on the amplitude and rate of the elongation undergone by the B-form following the 2 pN pull. In fact, rmin is independent of temperature (Table 1).
The nature of the transition barrier
To take into account the effect of temperature on the kinetics of the overstretching transition, the free energy must be defined according to the equations:
| (1) |
and
| (2) |
Where 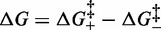 (see Supplementary Figure S1) and analogous relations define ΔE and ΔS, the enthalpy and entropy differences between the two states. Although both entropic and enthalpic differences depend on temperature, in this case, due to the limited temperature range analyzed, we can consider them to be constant and make a linear approximation of the free energies in the interval of interest.
(see Supplementary Figure S1) and analogous relations define ΔE and ΔS, the enthalpy and entropy differences between the two states. Although both entropic and enthalpic differences depend on temperature, in this case, due to the limited temperature range analyzed, we can consider them to be constant and make a linear approximation of the free energies in the interval of interest.
As previously shown at room temperature (27), for any temperature in the range 10–25°C, the relationship between r and ln (F) has a V-shaped profile (Figure 4F). Thus, the unidirectional rate constants that characterize the two branches of the V-shaped profile have a linear dependence on ln (F), with a slope that, according to Kramers–Bell theory (31–33), depends on the distances 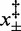 from the starting and final states of the reaction to the transition state. The slopes of the branches of the V-shaped relation are not significantly affected by temperature, while the relation is progressively shifted rightward as the temperature is reduced. At any temperature, the dependence of the rate of elongation on the force can be expressed by an equation that results from the combination of Supplementary Equations (S1–S3) and Equation (2):
from the starting and final states of the reaction to the transition state. The slopes of the branches of the V-shaped relation are not significantly affected by temperature, while the relation is progressively shifted rightward as the temperature is reduced. At any temperature, the dependence of the rate of elongation on the force can be expressed by an equation that results from the combination of Supplementary Equations (S1–S3) and Equation (2):
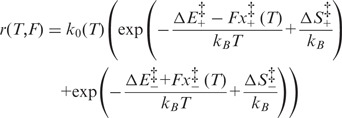 |
(3) |
where the kinetic prefactor, 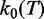 , has the temperature dependence defined in Supplementary Equation (S5).
, has the temperature dependence defined in Supplementary Equation (S5).
The entropic barrier terms 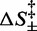 are not independent of each other, and one of them can be made explicit in Equation (3), for instance
are not independent of each other, and one of them can be made explicit in Equation (3), for instance 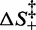 , which provides a multiplicative factor
, which provides a multiplicative factor 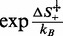 to the elongation rate constant r. As shown by Supplementary Equation (S5),
to the elongation rate constant r. As shown by Supplementary Equation (S5), 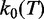 depends on a coefficient α, which provides another multiplicative factor to r. It is, therefore, impossible to distinguish between the two contributions, so that they can be combined in a single parameter
depends on a coefficient α, which provides another multiplicative factor to r. It is, therefore, impossible to distinguish between the two contributions, so that they can be combined in a single parameter 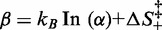 , which describes an effective entropic barrier incorporating both entropic and kinetic factors. Consequently, the entropic component of the transition energy barrier cannot be determined. Taking into account also that the two enthalpy barriers
, which describes an effective entropic barrier incorporating both entropic and kinetic factors. Consequently, the entropic component of the transition energy barrier cannot be determined. Taking into account also that the two enthalpy barriers 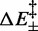 are not independent of each other, Equation (3) can be shown to depend on only 12 different parameters,
are not independent of each other, Equation (3) can be shown to depend on only 12 different parameters, 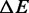 ,
, 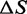 ,
, 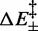 ,
, 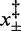 (10°C),
(10°C), 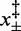 (15°C),
(15°C), 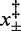 (20°C) and
(20°C) and 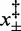 (25°C), plus the additional parameter β. All parameters can be simultaneously estimated by fitting the four different sets of data belonging to the four temperatures analyzed by means of a multi-curve fitting procedure. The results of the fit are shown by the lines in Figure 4E and F. As shown in Supplementary Figure S4), the introduction in Equations (1) and (2) of higher order parameters of T dependence slightly improves the fit. However, due to the limits of precision of the experimental data, the error associated with the additional parameters does not make them significantly different from zero.
(25°C), plus the additional parameter β. All parameters can be simultaneously estimated by fitting the four different sets of data belonging to the four temperatures analyzed by means of a multi-curve fitting procedure. The results of the fit are shown by the lines in Figure 4E and F. As shown in Supplementary Figure S4), the introduction in Equations (1) and (2) of higher order parameters of T dependence slightly improves the fit. However, due to the limits of precision of the experimental data, the error associated with the additional parameters does not make them significantly different from zero.
Table 2 reports the parameters of the transition estimated by the multi-curve fit. Note that Fe, the coexistence force, decreases in steps of ∼2 pN as the temperature increases from 10 (71 pN) to 25°C (66 pN). This behavior is similar to that of Fmin reported in Table 1. Also the numerical values for Fe and Fmin are in good agreement. This result would not be obtained if the energy landscapes were asymmetric (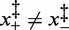 ), in which case the coexistence force and the force corresponding to the minimum elongation rate should differ (27); in the present case, however, the magnitude of the asymmetry correction, a fraction of piconewton, is negligible within the experimental error. The structural parameters
), in which case the coexistence force and the force corresponding to the minimum elongation rate should differ (27); in the present case, however, the magnitude of the asymmetry correction, a fraction of piconewton, is negligible within the experimental error. The structural parameters 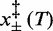 , which represent the distances between the transition state and the compact and extended states (Supplementary Figure S1), are remarkably independent of temperature (Table 2). This implies that at all temperatures (i) the transition state lies almost midway between the compact and extended states, slightly displaced toward the former, (ii) the cooperativity index q is constant (mean: 22 ± 2) and in good agreement with the value previously reported in (27) at room temperature.
, which represent the distances between the transition state and the compact and extended states (Supplementary Figure S1), are remarkably independent of temperature (Table 2). This implies that at all temperatures (i) the transition state lies almost midway between the compact and extended states, slightly displaced toward the former, (ii) the cooperativity index q is constant (mean: 22 ± 2) and in good agreement with the value previously reported in (27) at room temperature.
Table 2.
Mechanical and structural parameters of the transition at the four temperatures as estimated by the multi-curve fit of r–F relations with Equation (3)
 (°C) (°C) |
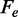 (pN) (pN) |
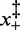 (nm) (nm) |
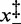 (nm) (nm) |
q |
|---|---|---|---|---|
| 10 | 71 ± 3 | 2.1 ± 0.2 | 3.0 ± 0.3 | 22 ± 2 |
| 15 | 69 ± 3 | 2.1 ± 0.2 | 3.1 ± 0.3 | 22 ± 2 |
| 20 | 68 ± 3 | 2.1 ± 0.1 | 3.1 ± 0.3 | 22 ± 2 |
| 25 | 66 ± 3 | 2.2 ± 0.2 | 3.1 ± 0.3 | 22 ± 2 |
The estimates of the energetic parameters per bp are ΔE: 8.2 ± 0.3 kBT, ΔS: (14.9 ± 0.5) × 10−3kBT/K, 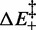 : 3.2 ± 0.3 kBT, β: −0.41 kBT/K.
: 3.2 ± 0.3 kBT, β: −0.41 kBT/K.
As far as the energetics of the transition are concerned, the enthalpy difference ΔE between the compact and extended states is 8.2 ± 0.3 kBT (or 5.1 ± 0.2 kcal/mol), while the entropy difference ΔS amounts to (14.9 ± 0.5) × 10−3 kBT/K (or 9.2 ± 0.3 cal/Kmol), which at 20°C corresponds to a free energy contribution of 4.36 ± 0.14 kBT (or 2.7 ± 0.1 kcal/mol). Thus, in the overstretching transition there is a significant entropic contribution (half of that of the enthalpy) to the stability of the extended state.
About the nature of the transition energy barrier, it is worth noting that 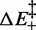 , 3.2 ± 0.3 kBT per bp, is significantly lower than
, 3.2 ± 0.3 kBT per bp, is significantly lower than 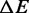 (8.2 kBT per bp), which implies that the height of the backward enthalpy barrier
(8.2 kBT per bp), which implies that the height of the backward enthalpy barrier 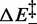 is negative (−5.0 ± 0.3 kBT per bp) and, practically, that a proper enthalpy barrier is absent. As a consequence, the enthalpy increases monotonically without generating a major energy barrier during the transition from the compact to the extended state.
is negative (−5.0 ± 0.3 kBT per bp) and, practically, that a proper enthalpy barrier is absent. As a consequence, the enthalpy increases monotonically without generating a major energy barrier during the transition from the compact to the extended state.
The absence of an enthalpy barrier helps to clarify why rmin is almost independent of T, while, as a general rule, reaction rates are expected to increase with T. Instead, as shown in Figure 4E and F, while the right branch of the r–F relation, dominated by r+, is shifted upward at higher T, the left branch, dominated by r−, is shifted downward at higher T. The reason of this atypical behavior lies in the negative value of 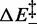 , which causes r− to decrease with temperature, leaving rmin approximately constant.
, which causes r− to decrease with temperature, leaving rmin approximately constant.
Comparison with equilibrium data
The entropic contribution ΔS to the overstretching transition determined here using transient kinetics analysis is approximately one-third of that reported in (7,34), where the transition was investigated by analyzing equilibrium force-extension curves at much higher temperatures, but it appears to be consistent with that shown at the lower end (∼20°C) of the temperature spectrum explored in those studies.
A recent paper (22) shows that (i) at temperatures >18°C, the force-clamp stretch–release responses are hysteretic and the threshold force for the overstretching transition decreases with temperature, with a slope that indicates an entropy contribution to the transition similar to that of thermal melting (35); (ii) at temperatures <18°C, the responses did not show hysteresis and the threshold force increases with temperature, indicating a decrease in the entropy with the overstretching transition. On the contrary, the transition kinetics analysis described here shows that, in the whole range of temperature used (10–25°C), the coexistence force Fe decreases with temperature (Table 2 and open squares in Figure 5C), with a slope that indicates an entropy contribution to the transition of ∼9 cal/Kmol. This entropy change is approximately one-third of that for the thermal melting (35) that characterizes the hysteretic transition reported in (22).
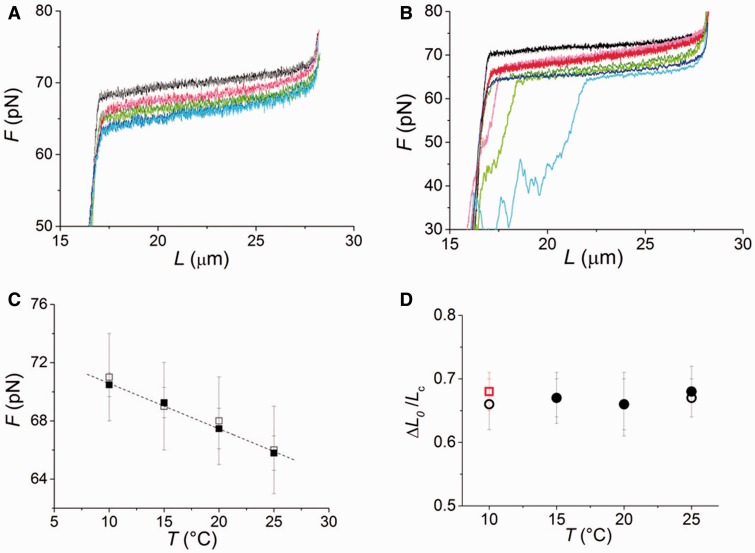
Figure 5.
Temperature dependence of equilibrium force-extension relations. (A) Equilibrium force-extension relations near the overstretching transition at the four temperatures in four molecules from those not showing any hysteresis at all temperatures: 10 (black lengthening, gray shortening), 15 (red lengthening, pink shortening), 20 (green lengthening, light green shortening) and 25°C (blue lengthening, cyan shortening). (B) Equilibrium force-extension relations near the overstretching transition at the four temperatures in four molecules from those showing hysteresis at temperatures >10°C. Color code of the traces as in (A). (C) Comparison of the Fe-temperature relation obtained by fitting Equation (4) to the equilibrium force-extension relations in (A and B) (filled squares, mean and SE from 57 molecules, with at least 12 molecules for each temperature) with that obtained by the multi-curve fitting of the rate-force relations in Figure 4E with Equation (3) (open squares). The larger errors associated to data from multi-curve fitting are due to the simultaneous estimate of a higher number of free parameters, thus increasing the error on the final estimates. The slope of the linear fit to equilibrium data is −0.27 ± 0.03 pN/°C (dashed line) and ΔS calculated from this slope is 9.8 ± 1.1 cal/Kmol. (D) Elongation induced by the overstretching transition, relative to the contour length of the molecule before the transition, (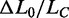 ) versus temperature. Black circles: 150 mM NaCl, open circles from molecules without hysteresis at temperatures >10°C, filled circles from molecules with hysteresis at temperatures >10°C. Red square: 1.5 M NaCl.
) versus temperature. Black circles: 150 mM NaCl, open circles from molecules without hysteresis at temperatures >10°C, filled circles from molecules with hysteresis at temperatures >10°C. Red square: 1.5 M NaCl.
To clear the matter, we determined the equilibrium force-extension relations at the four different temperatures (10, 15, 20 and 25°C) from eight of the same molecules as in Figures 1 and 2. Isovelocity lengthenings and shortenings were imposed as detailed in ‘Materials and Methods’ section. Results are plotted in Figure 5A for four molecules that did not show hysteresis in the whole temperature range, and in Figure 5B for four molecules that showed hysteresis at temperatures >10°C. The color code for the temperature is the same as in Figure 4; the lengthening and shortening phases of the mechanical protocol are identified by modulating the same color from normal (lengthening) to light (shortening), as detailed in the Figure legend. It is evident that, independently of the presence of hysteresis on relaxation and in agreement with transient kinetics analysis, the plateau force decreases with temperature, while the extension of the overstretching transition remains constant. A quantitative estimate of the temperature dependence of the coexistence force 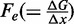 is obtained by fitting each force-extension relation with the force-extension equation of a two-state reaction:
is obtained by fitting each force-extension relation with the force-extension equation of a two-state reaction:
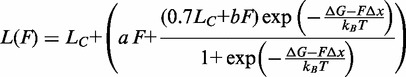 |
(4) |
where 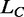 is the contour length of the double-stranded DNA before the transition,
is the contour length of the double-stranded DNA before the transition, 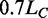 is the corresponding overstretching elongation, the second term on the right side of the equation represents the elongation at a given pulling force F and a and b are linear terms that must be added to take into account the enthalpic elasticity in the basic conformation and in the extended conformation. Equation (4) shows that for the equilibrium data, the only free parameters are
is the corresponding overstretching elongation, the second term on the right side of the equation represents the elongation at a given pulling force F and a and b are linear terms that must be added to take into account the enthalpic elasticity in the basic conformation and in the extended conformation. Equation (4) shows that for the equilibrium data, the only free parameters are 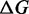 and
and 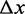 , both related to the difference between the basic and the extended conformation, any information on the barrier being lost. Fitting of Equation (4) to the equilibrium force-extension relations provides the estimates of
, both related to the difference between the basic and the extended conformation, any information on the barrier being lost. Fitting of Equation (4) to the equilibrium force-extension relations provides the estimates of 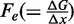 , reported versus temperature in Figure 5C (filled squares). The Fe-temperature relation from equilibrium data practically superimposes on that estimated from transient kinetics analysis (open squares, see also Table 2). The linear fit of the equilibrium Fe data provides an estimate of the entropy of the overstretching transition,
, reported versus temperature in Figure 5C (filled squares). The Fe-temperature relation from equilibrium data practically superimposes on that estimated from transient kinetics analysis (open squares, see also Table 2). The linear fit of the equilibrium Fe data provides an estimate of the entropy of the overstretching transition, 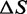 , of (15.8 ± 1.7) × 10−3
kBT/K (or 9.8 ± 1.1 cal/Kmol), which is not significantly different from the estimate obtained by transient kinetics analysis (Table 3).
, of (15.8 ± 1.7) × 10−3
kBT/K (or 9.8 ± 1.1 cal/Kmol), which is not significantly different from the estimate obtained by transient kinetics analysis (Table 3).
Table 3.
Comparison of the thermodynamic parameters at 150 mM ionic strength
| Data source |
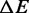 (kcal/mol) (kcal/mol) |
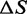 (cal/Kmol) (cal/Kmol) |
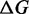 (kcal/mol) (20°C) (kcal/mol) (20°C) |
|---|---|---|---|
| Transient kinetics | 5.1 ± 0.2 | 9.2 ± 0.3 | 2.4 ± 0.3 |
| Equilibrium | 5.0 ± 0.2 | 9.8 ± 1.1 | 2.45 ± 0.01 |
| Williams et al. (7) | 4.57 | 11.76 | 1.12 |
| Zhang et al. (22) | 7.7 ± 1.6 | 21.2 ± 3.5 | 1.48 |
First and second rows report our data from transient and equilibrium kinetics, respectively; third row from Williams and coworkers (7) in the same range of temperature as ours; fourth row from Zhang and coworkers (22) in the temperature range 18–33°C. Note that in both (7) and (22) the parameters are referred to melting and errors are absent where they are not directly reported.
The match between the estimates from kinetic and equilibrium data emphasizes the importance of this work in several respects: (i) the definition of an entropic contribution to the overstretching transition, which is only one-third of that implied in thermal melting (35); (ii) the demonstration of the validity of the proposed two-state mechanism of the overstretching transition, by showing that the same process is responsible for both kinetics and thermodynamics; and (iii) from a methodological point of view, the demonstration that our force clamp has a response time that is adequate to resolve the kinetics of the overstretching transition (26,27). In this respect, it is worth noting here that only the transient kinetics analysis allows 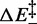 and the two structural parameters
and the two structural parameters 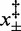 to be defined.
to be defined.
The elongation induced by the overstretching transition (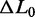 ) is independent of both the temperature and the appearance of hysteresis on relaxation (Figure 5A and B). This is shown more quantitatively in Figure 5D (black circles), where ΔL0, expressed as a fraction of the contour length of the ds-DNA before the transition (
) is independent of both the temperature and the appearance of hysteresis on relaxation (Figure 5A and B). This is shown more quantitatively in Figure 5D (black circles), where ΔL0, expressed as a fraction of the contour length of the ds-DNA before the transition (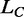 ), is plotted versus temperature for both the 14 molecules that did not show hysteresis in the whole temperature range (open circles) and the 22 molecules that showed hysteresis at temperatures >10°C (filled circles).
), is plotted versus temperature for both the 14 molecules that did not show hysteresis in the whole temperature range (open circles) and the 22 molecules that showed hysteresis at temperatures >10°C (filled circles). 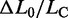 does not vary significantly either with temperature or with the presence of hysteresis, having an average value of 0.67 ± 0.04 (mean ± SE for the eight molecules). This result is in contrast with the recent results for much shorter molecules (28), where the elongation is found to increase from 51 to 67% going from the nonhysteretic to the hysteretic transition. The possibility that some degrees of melting and strand separation could have influenced our conclusion has been further tested, and excluded, by measuring the extension obtained in melting-averse conditions such as 1.5 M NaCl (10 times higher than the physiological ionic strength) and 10°C (red square in Figure 5D).
does not vary significantly either with temperature or with the presence of hysteresis, having an average value of 0.67 ± 0.04 (mean ± SE for the eight molecules). This result is in contrast with the recent results for much shorter molecules (28), where the elongation is found to increase from 51 to 67% going from the nonhysteretic to the hysteretic transition. The possibility that some degrees of melting and strand separation could have influenced our conclusion has been further tested, and excluded, by measuring the extension obtained in melting-averse conditions such as 1.5 M NaCl (10 times higher than the physiological ionic strength) and 10°C (red square in Figure 5D). 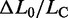 was 0.68 ± 0.03 (eight molecules), identical to that at physiological ionic strength. We conclude that the equilibrium force-extension data, in agreement with transient kinetic data, prove that the 67% extension induced by the overstretching transition is due to the nonhysteretic reaction.
was 0.68 ± 0.03 (eight molecules), identical to that at physiological ionic strength. We conclude that the equilibrium force-extension data, in agreement with transient kinetic data, prove that the 67% extension induced by the overstretching transition is due to the nonhysteretic reaction.
DISCUSSION
Two-state reaction and melting during DNA overstretching
The resolution of the transient kinetics under our rapid force clamp allows the overstretching transition of ds-DNA to be described in terms of a two-state reaction between the B-form and the 70% more extended S-form and to be discriminated from the possible development of different degrees of melting and strand separation. When force steps of 2–30 pN, imposed on the molecule at room temperature and physiological salt concentration, attain the range of forces of the overstretching transition (60–70 pN), they elicit elongation transients, the rate of which depends solely on the final level of force (Figure 1) and which can be explained in terms of a reversible transition from the basic B-form to the extended S-form. Melting and strand separation is a subsequent process that does not imply further increase in length, so that the whole 67% lengthening of the overstretching transition is accounted for by the two-state reaction. Accordingly, a 20–35 pN stepwise drop bringing the force down from the overstretching region far below it (40–50 pN) elicits an almost simultaneous shortening that is proportional to the fraction of the molecule in the S-form. This is expected from the fact that in this case the two-state S-B transition occurs at forces much lower than the coexistence force. The final length, characteristic of the equilibrium force-extension relation, can be attained only following the reannealing of the melted segments, which is the rate-limiting process of the response and explains the pauses separating the shortening steps (Figure 2). Thus the square wave protocol allows a dynamic identification of the hysteretic and reversible components of the relaxation. The conclusion that the hysteretic component does not contribute to the length change is confirmed by the finding that when the 20 pN drop is applied in the absence of melting (at 10°C, Figure 3), the only response following the force step is a simultaneous shortening to the length consistent with the equilibrium force-extension relation.
The finding in recent studies that the length of the overstretched state changes according to the appearance of hysteresis is in apparent contradiction with our results. On the other hand, in one study it is concluded that the elongation is shorter in the nonhysteretic transition (28), while in another it is concluded that the shorter elongation occurs if the transition is hysteretic (23). The discrepancies are probably due to the differences in length and bp composition of the preparations and in the mechanical protocols used in the different experiments. In this respect, it must be noted that the discrepancy cannot be attributed to the difference in time resolution of the experiments, as our equilibrium force-extension data confirm the results from the transient kinetics approach that the 67% extension is totally accounted for by the nonhysteretic reaction (Figure 5). This conclusion in turn explains why the lengthening transient provides the constraints for determining a self-consistent reaction model with well defined kinetics and energetics and also why the equilibrium force-extension relation is the same irrespective of whether the hysteretic behavior appears on relaxation [see also (27)].
Transition thermodynamics
The effect of temperature on the overstretching transition has been determined by recording the elongation transient following force steps of 2 pN in the temperature range 10–25°C. The analysis of the force and temperature dependence of the responses (Figure 4) allows both a precise characterization of the enthalpy profile along the reaction coordinate and the definition of the entropic contribution to the global stability of the overstretched state. We demonstrate that the nature of the free energy difference between the compact and the extended state is mainly enthalpic. In fact, ΔE for the transition is 8.2 ± 0.3 kBT (or 5.1 ± 0.2 kcal/mol). The overstretched state, however, is more disordered than the B-form, as we find a positive entropy difference (TΔS at 20°C is 4.36 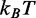 or 2.7 kcal/mol), which favors the transition by lowering by one half the total free energy difference ΔG. The resulting ΔG is 3.8
or 2.7 kcal/mol), which favors the transition by lowering by one half the total free energy difference ΔG. The resulting ΔG is 3.8 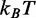 (or 2.4 kcal/mol) and agrees with the value obtained from the equilibrium force-extension relation (Table 3). The free energy for the elementary reaction is increased to 84
(or 2.4 kcal/mol) and agrees with the value obtained from the equilibrium force-extension relation (Table 3). The free energy for the elementary reaction is increased to 84 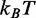 (53 kcal/mol) by the cooperative mechanism, which rises the number of bp involved in the elementary reaction (q, the cooperativity index) to 22.
(53 kcal/mol) by the cooperative mechanism, which rises the number of bp involved in the elementary reaction (q, the cooperativity index) to 22.
These conclusions disagree in many respects with those attained by Zhang and collaborators (22,23). In those studies, it is shown that at physiological salt concentration, the temperature dependence of the transition force changes slope at ∼18°C: at temperatures <18°C the slope is positive, so that ΔS is negative; at temperatures >18°C the slope becomes negative, so that ΔS for the transition is positive and close to the value determined for thermal melting (35). Our transient kinetic data, in contrast, show a monotonic temperature-dependent reduction in the coexistence force 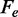 that is independent of the appearance of hysteresis in relaxation and underlies a constant positive
that is independent of the appearance of hysteresis in relaxation and underlies a constant positive 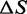 approximately one-third of the value expected from thermal melting. The discrepancy cannot be simply explained by the different time resolution of the experiments, as in the present work the temperature dependence of
approximately one-third of the value expected from thermal melting. The discrepancy cannot be simply explained by the different time resolution of the experiments, as in the present work the temperature dependence of 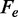 from transient kinetics analysis is confirmed by equilibrium force-extension results (Figure 5C).
from transient kinetics analysis is confirmed by equilibrium force-extension results (Figure 5C).
Previous studies of the force-extension relation in a much higher temperature range (7,34) reported an entropic contribution three times larger than ours, although at the lower end of the temperature range (20°C) the entropy change was much smaller and compatible with ours (Table 3). However, more recently (22), for temperatures >18°C and with physiological salt concentration, a three times larger value for the ΔS of the hysteretic transition is reported, in agreement with that of the thermal melting in (35) (∼24 cal/Kmol). Thus, as made evident from the comparisons in Table 3, there is a contradiction between earlier and recent calorimetric estimates from equilibrium force-extension experiments. This discrepancy depends on the choice of the parameter ΔCP (difference in specific heat on melting), which was assumed near 0 in (22) [in agreement with (35)] and 60 cal/(Kmol) (according to the fitting procedure) in (7). The estimates for ΔS and ΔH from our experiments are close to the values obtained in (7) because the slope of the relations between transition force and temperature are similar in the same temperature range. The difference, however, appears evident considering ΔG, which is larger by a factor of two in our experiments (Table 3). In this respect it must be noted that, while in (7) ΔG is estimated on the basis of the melting assumption (that is assuming that the final state is ss-DNA), in our case ΔG is a free parameter estimated by fitting the experimental rate–force relations.
As far as (22) is concerned, it is also worth noting that the three times larger positive entropy change at temperatures >18°C is strictly associated with a hysteretic reaction, while, under similar conditions, a companion study (24) indicates that the overstretching with internal strand separation does not imply hysteresis. Our experiments demonstrate that, in the temperature range 10–25°C, the kinetics and energetics of the overstretched state do not imply hysteresis and are not affected by hysteresis.
The result in the present study that both transient kinetics and equilibrium data of the overstretching transition indicate a positive 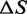 approximately one-third of that of thermal melting strongly supports the existence of an overstretched S-form of ds-DNA that precedes melting and strand separation. The smaller value of
approximately one-third of that of thermal melting strongly supports the existence of an overstretched S-form of ds-DNA that precedes melting and strand separation. The smaller value of 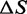 indicates that the S-form is more ordered than ss-DNA and retains a higher number of intramolecular bonds. Those must be mainly interstrand bonds because bonds between bases belonging to the same strand, as hydrogen bonds or base stacking interactions, would lead to a contraction of the molecule, contradicted by the observed molecular extension. Therefore, this thermodynamic result reinforces the evidence for a double-stranded state of the S-form, indicating that only a fraction of the bonds contributing to strand cohesion is broken.
indicates that the S-form is more ordered than ss-DNA and retains a higher number of intramolecular bonds. Those must be mainly interstrand bonds because bonds between bases belonging to the same strand, as hydrogen bonds or base stacking interactions, would lead to a contraction of the molecule, contradicted by the observed molecular extension. Therefore, this thermodynamic result reinforces the evidence for a double-stranded state of the S-form, indicating that only a fraction of the bonds contributing to strand cohesion is broken.
In conclusion, the thermodynamic parameters obtained in this study show the existence of an extended double-stranded S-form of DNA, but do not allow the atomistic details of this form to be characterized. Questions such as the number of hydrogen bonds or base staking interactions broken or retained, as well as the presence of any nonnative interstrand interaction, have to be addressed by other means. Moreover, the result that under force-clamp melting and reannealing do not influence per se either the kinetics of the transient or the length of the molecule opens the question of the relation between the extended ds-DNA and the melted ss-DNA. Further characterization of melting beyond the S-state is needed to determine whether the stabilization of the S-state is thermodynamic or kinetic in nature.
The profile of the activation energy barrier
A direct consequence of the observation that the elongation rate ( ) at the coexistence force does not depend on temperature is that the transition state does not show a real enthalpy barrier. Within the limits of the present approach, it is impossible to determine the entropic contribution to the free energy barrier governing the transition because its effect is indistinguishable from that of the kinetic prefactor affecting the transition rate. Our results are compatible with either the presence of a nonzero time-limiting entropic barrier or with the emergence of a barrier only as a consequence of rise in force. On the other hand, the emergence of a free energy barrier in the absence of an enthalpic barrier, can be justified by breaking of chemical bonds (base pairing hydrogen bonds and stacking interactions between adjacent bases). In this case, the free energy profile is given by the sum of a monotonically increasing enthalpy and an equally monotonically increasing entropy that after the transition state increases even more steeply, thus determining the presence of a free energy saddle. This interpretation is supported by the positive entropy change accompanying the B-S transition. A contribution to the free energy barrier for the transition might also be represented by the change of the solvation properties of the molecule or of its coordination with the solvent ions. To discriminate between these different possibilities, alternative approaches are necessary, such as the investigation of the free energy profile along the activation coordinate by means of molecular dynamics simulations.
) at the coexistence force does not depend on temperature is that the transition state does not show a real enthalpy barrier. Within the limits of the present approach, it is impossible to determine the entropic contribution to the free energy barrier governing the transition because its effect is indistinguishable from that of the kinetic prefactor affecting the transition rate. Our results are compatible with either the presence of a nonzero time-limiting entropic barrier or with the emergence of a barrier only as a consequence of rise in force. On the other hand, the emergence of a free energy barrier in the absence of an enthalpic barrier, can be justified by breaking of chemical bonds (base pairing hydrogen bonds and stacking interactions between adjacent bases). In this case, the free energy profile is given by the sum of a monotonically increasing enthalpy and an equally monotonically increasing entropy that after the transition state increases even more steeply, thus determining the presence of a free energy saddle. This interpretation is supported by the positive entropy change accompanying the B-S transition. A contribution to the free energy barrier for the transition might also be represented by the change of the solvation properties of the molecule or of its coordination with the solvent ions. To discriminate between these different possibilities, alternative approaches are necessary, such as the investigation of the free energy profile along the activation coordinate by means of molecular dynamics simulations.
Transition cooperativity and its structural basis
A final important conclusion of this work arises from the finding that the two structural parameters 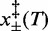 , which describe the distances from the compact and the extended states to the transition state, do not depend on temperature. Accordingly,
, which describe the distances from the compact and the extended states to the transition state, do not depend on temperature. Accordingly, 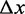 , the total elongation of a single two-state unit, and therefore q, the index of the cooperativity of the reaction, do not depend on temperature. This is an indication that the microscopic mechanism governing the transition is determined by factors that are unaffected by temperature such as the nucleic acid sequence of the molecule.
, the total elongation of a single two-state unit, and therefore q, the index of the cooperativity of the reaction, do not depend on temperature. This is an indication that the microscopic mechanism governing the transition is determined by factors that are unaffected by temperature such as the nucleic acid sequence of the molecule.
It has been recently demonstrated that CG-rich islands, which form more stable hydrogen bonds, contribute to preserving the double-stranded structure of the extended form of DNA (20,28). Instead, short AT repeating sequences could be candidates for triggering the overstretching transition foci. It is worth noting, in this respect, that along the λ-phage DNA molecule AT repeats of more than three consecutive bps appear at an average distance of ∼22 bp.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
Istituto Italiano di Tecnologia [SEED-2009] and Ente Cassa di Risparmio di Firenze [2010-1402], Italy. Funding for open access charge: PRIN 2010/11, Ministero dell'Istruzione, dell'Università e della Ricerca (Italy).
Conflict of interest statement. None declared.
Supplementary Material
AKNOWLEDGEMENTS
The authors thank Mario Dolfi for technical assistance and Malcolm Irving and Gabriella Piazzesi for comments on the manuscript.
REFERENCES
- 1.Smith SB, Finzi L, Bustamante C. Direct mechanical measurements of the elasticity of single DNA molecules by using magnetic beads. Science. 1992;258:1122–1126. doi: 10.1126/science.1439819. [DOI] [PubMed] [Google Scholar]
- 2.Bustamante C, Marko JF, Siggia ED, Smith S. Entropic elasticity of lambda-phage DNA. Science. 1994;265:1599–1600. doi: 10.1126/science.8079175. [DOI] [PubMed] [Google Scholar]
- 3.Marko JF, Siggia ED. Stretching DNA. Macromolecules. 1995;28:8759–8770. [Google Scholar]
- 4.Wang MD, Yin H, Landick R, Gelles J, Block SM. Stretching DNA with optical tweezers. Biophys. J. 1997;72:1335–1346. doi: 10.1016/S0006-3495(97)78780-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Smith SB, Cui Y, Bustamante C. Overstretching B-DNA: the elastic response of individual double-stranded and single-stranded DNA molecules. Science. 1996;271:795–799. doi: 10.1126/science.271.5250.795. [DOI] [PubMed] [Google Scholar]
- 6.Cluzel P, Lebrun A, Heller C, Lavery R, Viovy JL, Chatenay D, Caron F. DNA: an extensible molecule. Science. 1996;271:792–794. doi: 10.1126/science.271.5250.792. [DOI] [PubMed] [Google Scholar]
- 7.Williams MC, Wenner JR, Rouzina I, Bloomfield VA. Entropy and heat capacity of DNA melting from temperature dependence of single molecule stretching. Biophys. J. 2001;80:1932–1939. doi: 10.1016/S0006-3495(01)76163-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Williams MC, Wenner JR, Rouzina I, Bloomfield VA. Effect of pH on the overstretching transition of double-stranded DNA: evidence of force-induced DNA melting. Biophys. J. 2001;80:874–881. doi: 10.1016/S0006-3495(01)76066-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wenner JR, Williams MC, Rouzina I, Bloomfield VA. Salt dependence of the elasticity and overstretching transition of single DNA molecules. Biophys. J. 2002;82:3160–3169. doi: 10.1016/S0006-3495(02)75658-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Rouzina I, Bloomfield VA. Force-induced melting of the DNA double helix 1. Thermodynamic analysis. Biophys. J. 2001;80:882–893. doi: 10.1016/S0006-3495(01)76067-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rouzina I, Bloomfield VA. Force-induced melting of the DNA double helix. 2. Effect of solution conditions. Biophys. J. 2001;80:894–900. doi: 10.1016/S0006-3495(01)76068-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Shokri L, McCauley MJ, Rouzina I, Williams MC. DNA overstretching in the presence of glyoxal: structural evidence of force-induced DNA melting. Biophys. J. 2008;95:1248–1255. doi: 10.1529/biophysj.108.132688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.van Mameren J, Gross P, Farge G, Hooijman P, Modesti M, Falkenberg M, Wuite GJ, Peterman EJ. Unraveling the structure of DNA during overstretching by using multicolor, single-molecule fluorescence imaging. Proc. Natl Acad. Sci. USA. 2009;106:18231–18236. doi: 10.1073/pnas.0904322106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Léger JF, Romano G, Sarkar A, Robert J, Bourdieu L, Chatenay D, Marko JF. Structural transitions of a twisted and stretched DNA molecule. Phys. Rev. Lett. 1999;83:1066. [Google Scholar]
- 15.Sarkar A, Leger JF, Chatenay D, Marko JF. Structural transitions in DNA driven by external force and torque. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2001;63:051903. doi: 10.1103/PhysRevE.63.051903. [DOI] [PubMed] [Google Scholar]
- 16.Bryant Z, Stone MD, Gore J, Smith SB, Cozzarelli NR, Bustamante C. Structural transitions and elasticity from torque measurements on DNA. Nature. 2003;424:338–341. doi: 10.1038/nature01810. [DOI] [PubMed] [Google Scholar]
- 17.Whitelam S, Pronk S, Geissler PL. There and (slowly) back again: entropy-driven hysteresis in a model of DNA overstretching. Biophys. J. 2008;94:2452–2469. doi: 10.1529/biophysj.107.117036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cocco S, Yan J, Leger JF, Chatenay D, Marko JF. Overstretching and force-driven strand separation of double-helix DNA. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2004;70:011910. doi: 10.1103/PhysRevE.70.011910. [DOI] [PubMed] [Google Scholar]
- 19.Fu H, Chen H, Marko JF, Yan J. Two distinct overstretched DNA states. Nucleic Acids Res. 2010;38:5594–5600. doi: 10.1093/nar/gkq309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Fu H, Chen H, Zhang X, Qu Y, Marko JF, Yan J. Transition dynamics and selection of the distinct S-DNA and strand unpeeling modes of double helix overstretching. Nucleic Acids Res. 2011;39:3473–3481. doi: 10.1093/nar/gkq1278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Paik DH, Perkins TT. Overstretching DNA at 65 pN does not require peeling from free ends or nicks. J. Am. Chem. Soc. 2011;133:3219–3221. doi: 10.1021/ja108952v. [DOI] [PubMed] [Google Scholar]
- 22.Zhang X, Chen H, Fu H, Doyle PS, Yan J. Two distinct overstretched DNA structures revealed by single-molecule thermodynamics measurements. Proc. Natl Acad. Sci. USA. 2012;109:8103–8108. doi: 10.1073/pnas.1109824109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zhang X, Chen H, Le S, Rouzina I, Doyle PS, Yan J. Revealing the competition between peeled ssDNA, melting bubbles, and S-DNA during DNA overstretching by single-molecule calorimetry. Proc. Natl Acad. Sci. USA. 2013;110:3865–3870. doi: 10.1073/pnas.1213740110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.King GA, Gross P, Bockelmann U, Modesti M, Wuite GJ, Peterman EJ. Revealing the competition between peeled ssDNA, melting bubbles, and S-DNA during DNA overstretching using fluorescence microscopy. Proc. Natl Acad. Sci. USA. 2013;110:3859–3864. doi: 10.1073/pnas.1213676110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bianco P, Dolfi M, Lombardi V. Mechanics of the unwinding of DNA helix under force clamp. Acta Physiologica. 2008;194 48, P17. [Google Scholar]
- 26.Elms PJ, Chodera JD, Bustamante CJ, Marqusee S. Limitations of constant-force-feedback experiments. Biophys. J. 2012;103:1490–1499. doi: 10.1016/j.bpj.2012.06.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bianco P, Bongini L, Melli L, Dolfi M, Lombardi V. Piconewton-millisecond force steps reveal the transition kinetics and mechanism of the double-stranded DNA elongation. Biophys. J. 2011;101:866–874. doi: 10.1016/j.bpj.2011.06.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bosaeus N, El-Sagheer AH, Brown T, Smith SB, Akerman B, Bustamante C, Norden B. Tension induces a base-paired overstretched DNA conformation. Proc. Natl Acad. Sci. USA. 2012;109:15179–15184. doi: 10.1073/pnas.1213172109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Mao H, Arias-Gonzalez JR, Smith SB, Tinoco I, Jr, Bustamante C. Temperature control methods in a laser tweezers system. Biophys. J. 2005;89:1308–1316. doi: 10.1529/biophysj.104.054536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Gross P, Laurens N, Oddershede LB, Bockelmann U, Peterman EJG, Wuite GJL. Quantifying how DNA stretches, melts and changes twist under tension. Nat. Phys. 2011;7:731–736. [Google Scholar]
- 31.Kramers HA. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica. 1940;7:284–304. [Google Scholar]
- 32.Bell GI. Models for the specific adhesion of cells to cells. Science. 1978;200:618–627. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- 33.Evans E. Probing the relation between force - lifetime - and chemistry in single molecular bonds. Annu. Rev. Biophys. Biomol. Struct. 2001;30:105–128. doi: 10.1146/annurev.biophys.30.1.105. [DOI] [PubMed] [Google Scholar]
- 34.Clausen-Schaumann H, Rief M, Tolksdorf C, Gaub HE. Mechanical stability of single DNA molecules. Biophys. J. 2000;78:1997–2007. doi: 10.1016/S0006-3495(00)76747-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.SantaLucia J., Jr A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics. Proc. Natl Acad. Sci. USA. 1998;95:1460–1465. doi: 10.1073/pnas.95.4.1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.