MM Algorithms for Geometric and Signomial Programming

Abstract

This paper derives new algorithms for signomial programming, a generalization of geometric programming. The algorithms are based on a generic principle for optimization called the MM algorithm. In this setting, one can apply the geometric-arithmetic mean inequality and a supporting hyperplane inequality to create a surrogate function with parameters separated. Thus, unconstrained signomial programming reduces to a sequence of one-dimensional minimization problems. Simple examples demonstrate that the MM algorithm derived can converge to a boundary point or to one point of a continuum of minimum points. Conditions under which the minimum point is unique or occurs in the interior of parameter space are proved for geometric programming. Convergence to an interior point occurs at a linear rate. Finally, the MM framework easily accommodates equality and inequality constraints of signomial type. For the most important special case, constrained quadratic programming, the MM algorithm involves very simple updates.

1 Introduction

As a branch of convex optimization theory, geometric programming is next in line to linear and quadratic programming in importance [4,5,15,16]. It has applications in chemical equilibrium problems [14], structural mechanics [5], integrated circuit design [7], maximum likelihood estimation [12], stochastic processes [6], and a host of other subjects [5]. Geometric programming deals with posynomials, which are functions of the form

$$f(\mathit{x})={\displaystyle \sum _{\mathit{\alpha }\in S}}{c}_{\mathit{\alpha }}{\displaystyle \prod _{i=1}^n}{x}_i^{{\alpha }_i}.$$ (1)

Here the index set S ⊂ ℝⁿ is finite, and all coefficients c_α and all components x₁, …, x_n of the argument x of f(x) are positive. The possibly fractional powers α_i corresponding to a particular α may be positive, negative, or zero. For instance, $x_1^{-1}+2x_1^3{x}_2^{-2}$ is a posynomial on ℝ². In geometric programming we minimize a posynomial f(x) subject to posynomial inequality constraints of the form u_j(x) ≤ 1 for 1 ≤ j ≤ q, where the u_j(x) are again posynomials. In some versions of geometric programming, equality constraints of posynomial type are permitted [3].

A signomial function has the same form as the posynomial (1), but the coefficients c_α are allowed to be negative. A signomial program is a generalization of a geometric program, where the objective and constraint functions can be signomials. From a computational point of view, signomial programming problems are significantly harder to solve than geometric programming problems. After suitable change of variables, a geometric program can be transformed into a convex optimization problem and globally solved by standard methods. In contrast, signomials may have many local minima. Wang et al. [20] recently derived a path algorithm for solving unconstrained signomial programs.

The theory and practice of geometric programming has been stable for a generation, so it is hard to imagine saying anything novel about either. The attractions of geometric programming include its beautiful duality theory and its connections with the arithmetic-geometric mean inequality. The present paper derives new algorithms for both geometric and signomial programming based on a generic device for iterative optimization called the MM algorithm [9,11]. The MM perspective possesses several advantages. First it provides a unified framework for solving both geometric and signomial programs. The algorithms derived here operate by separating parameters and reducing minimization of the objective function to a sequence of one-dimensional minimization problems. Separation of parameters is apt to be an advantage in high-dimensional problems. Another advantage is ease of implementation compared to competing methods of unconstrained geometric and signomial programming [20]. Finally, straightforward generalizations of our MM algorithms extend beyond signomial programming.

We conclude this introduction by sketching a roadmap to the rest of the paper. Section 2 reviews the MM algorithm. Section 3 derives MM algorithm for unconstrained signomial program from two simple inequalities. The behavior of the MM algorithm is illustrated on a few numerical examples in Section 4. Section 5 extends the MM algorithm for unconstrained problems to the constrained cases using the penalty method. Section 6 specializes to linearly constrained quadratic programming on the positive orthant. Convergence results are discussed in Section 7.

2 Background on the MM Algorithm

The MM principle involves majorizing the objective function f(x) by a surrogate function g(x | x_m) around the current iterate x_m (with ith component x_mi) of a search. Majorization is defined by the two conditions

$$f({\mathit{x}}_m)=g({\mathit{x}}_m|{\mathit{x}}_m)$$ (2)

$$f(\mathit{x})\le g(\mathit{x}|{\mathit{x}}_m),\mathit{x}\ne {\mathit{x}}_m.$$

In other words, the surface x ↦ g(x | x_m) lies above the surface x ↦ f(x) and is tangent to it at the point x = x_m. Construction of the majorizing function g(x | x_m) constitutes the first M of the MM algorithm.

The second M of the algorithm minimizes the surrogate g(x | x_m) rather than f(x). If x_m+1 denotes the minimizer of g(x | x_m), then this action forces the descent property f(x_m+1) ≤ f(x_m). This fact follows from the inequalities

$$f({\mathit{x}}_{m+1})\le g({\mathit{x}}_{m+1}|{\mathit{x}}_m)\le g({\mathit{x}}_m|{\mathit{x}}_m)=f({\mathit{x}}_m),$$

reflecting the definition of x_m+1 and the tangency conditions (2). The descent property makes the MM algorithm remarkably stable. Strictly speaking, the validity of the descent property depends only on decreasing g(x | x_m), not on minimizing g(x | x_m).

3 Unconstrained Signomial Programming

The art in devising an MM algorithm revolves around intelligent choice of the majorizing function. For signomial programming problems, fortunately one can invoke two simple inequalities. For terms with positive coefficients c_α, we use the arithmetic-geometric mean inequality

$${\displaystyle \prod _{i=1}^n}{z}_i^{{\alpha }_i}\le {\displaystyle \sum _{i=1}^n}\frac{{\alpha }_i}{{\Vert \mathit{\alpha }\Vert }_1}{z}_i^{{\Vert \mathit{\alpha }\Vert }_1}$$ (3)

for nonnegative numbers z_i and α_i and ℓ₁ norm ${\Vert \mathit{\alpha }\Vert }_1={\displaystyle {\sum }_{i=1}^n}|{\alpha }_i|$ [19]. If we make the choice z_i = x_i/x_mi in inequality (3), then the majorization

$${\displaystyle \prod _{i=1}^n}{x}_i^{{\alpha }_i}\le \left({\displaystyle \prod _{i=1}^n}{x}_{\mathit{\text{mi}}}^{{\alpha }_i}\right){\displaystyle \sum _{i=1}^n}\frac{{\alpha }_i}{{\Vert \mathit{\alpha }\Vert }_1}{\left(\frac{x_i}{x_{\mathit{\text{mi}}}}\right)}^{{\Vert \mathit{\alpha }\Vert }_1},$$ (4)

emerges, with equality when x = x_m. We can broaden the scope of the majorization (4) to cases with α_i < 0 by replacing z_i by the reciprocal ratio x_mi/x_i whenever α_i < 0. Thus, for terms $c_{\mathit{\alpha }}{\displaystyle {\prod }_{i=1}^n}{x}_i^{{\alpha }_i}$ with c_α > 0, we have the majorization

$$c_{\mathit{\alpha }}{\displaystyle \prod _{i=1}^n}{x}_i^{{\alpha }_i}\le c_{\mathit{\alpha }}\left({\displaystyle \prod _{j=1}^n}{x}_{\mathit{\text{mj}}}^{{\alpha }_j}\right){\displaystyle \sum _{i=1}^n}\frac{|{\alpha }_i|}{{\Vert \mathit{\alpha }\Vert }_1}{\left(\frac{x_i}{x_{\mathit{\text{mi}}}}\right)}^{{\Vert \mathit{\alpha }\Vert }_1\text{sgn }({\alpha }_i)},$$

where sgn(α_i) is the sign function.

The terms $c_{\mathit{\alpha }}{\displaystyle {\prod }_{i=1}^n}{x}_i^{{\alpha }_i}$ with c_α < 0 are handled by a different majorization. Our point of departure is the supporting hyperplane minorization

$$z\ge 1+\text{ln }z$$

at the point z = 1. If we let $z={\displaystyle {\prod }_{i=1}^n}{(x_i/x_{\mathit{\text{mi}}})}^{{\alpha }_i}$, then it follows that

$${\displaystyle \prod _{i=1}^n}{x}_i^{{\alpha }_i}\ge {\displaystyle \prod _{j=1}^n}{x}_{\mathit{\text{mj}}}^{{\alpha }_j}(1+{\displaystyle \sum _{i=1}^n}{\alpha }_i\text{ ln }{x}_i-{\displaystyle \sum _{i=1}^n}{\alpha }_i\text{ ln }{x}_{\mathit{\text{mi}}})$$ (5)

is a valid minorization in x around the point x_m. Multiplication by the negative coefficient c_α now gives the desired majorization. The surrogate function separates parameters and is convex when all of the α_i are positive.

In summary, the objective function (1) is majorized up to an irrelevant additive constant by the sum

$$g(\mathit{x}|{\mathit{x}}_m)={\displaystyle \sum _{i=1}^n}{g}_i(x_i|{\mathit{x}}_m)$$

$$g_i(x_i|{\mathit{x}}_m)={\displaystyle \sum _{\mathit{\alpha }\in S_{+}}}{c}_{\mathit{\alpha }}({\displaystyle \prod _{j=1}^n}{x}_{\mathit{\text{mj}}}^{{\alpha }_j})\frac{|{\alpha }_i|}{{\Vert \mathit{\alpha }\Vert }_1}{\left(\frac{x_i}{x_{\mathit{\text{mi}}}}\right)}^{{\Vert \mathit{\alpha }\Vert }_1\text{sgn }({\alpha }_i)}+{\displaystyle \sum _{\mathit{\alpha }\in S_{-}}}{c}_{\mathit{\alpha }}({\displaystyle \prod _{j=1}^n}{x}_{\mathit{\text{mj}}}^{{\alpha }_j}){\alpha }_i\text{ln }{x}_i,$$ (6)

where S₊ = {α : c_α > 0}, and S₋ = {α : c_α < 0}. To guarantee that the next iterate is well defined and occurs on the interior of the parameter domain, it is helpful to assume for each i that at least one α ∈ S₊ has α_i positive and at least one α ∈ S₊ has α_i negative. Under these conditions each g_i(x_i | x_m) is coercive and attains its minimum on the open interval (0, ∞).

Minimization of the majorizing function is straightforward because the surrogate functions g_i(x_i | x_m) are univariate functions. The derivative of g_i(x_i | x_m) with respect to its left argument equals

$$g_i^{\prime }(x_i|{\mathit{x}}_m)={\displaystyle \sum _{\mathit{\alpha }\in S_{+}}}{c}_{\mathit{\alpha }}({\displaystyle \prod _{j=1}^n}{x}_{\mathit{\text{mj}}}^{{\alpha }_j}){\alpha }_i{x}_i^{-1}{\left(\frac{x_i}{x_{\mathit{\text{mi}}}}\right)}^{{\Vert \mathit{\alpha }\Vert }_1\text{sgn}({\alpha }_i)}+{\displaystyle \sum _{\mathit{\alpha }\in S_{-}}}{c}_{\mathit{\alpha }}({\displaystyle \prod _{j=1}^n}{x}_{\mathit{\text{mj}}}^{{\alpha }_j}){\alpha }_i{x}_i^{-1}$$

Assuming that the exponents α_i are integers, this is a rational function of x_i, and once we equate it to 0, we are faced with solving a polynomial equation. This task can be accomplished by bisection or by Newton’s method. In practice, just a few steps of either algorithm suffice since the MM principle merely requires decreasing the surrogate functions g_i(x_i | x_m).

In a geometric program, the function $g_i^{\prime }(x_i|{\mathit{x}}_m)$ has a single root on the interval (0, ∞). For a proof of this fact, note that making the standard change of variables x_i = e^y_i eliminates the positivity constraint x_i > 0 and renders the transformed function h_i(y_i | x_m) = g_i(x_i | x_m) strictly convex. Because |α_i| sgn(α_i)² = |α_i|, the second derivative

$$h_i^{″}(y_i|{\mathit{x}}_m)={\displaystyle \sum _{\mathit{\alpha }\in S_{+}}}{c}_{\mathit{\alpha }}({\displaystyle \prod _{j=1}^n}{x}_{\mathit{\text{mj}}}^{{\alpha }_j})\frac{|{\alpha }_i|\cdot {\Vert \mathit{\alpha }\Vert }_1}{x_{\mathit{\text{mi}}}^{{\Vert \mathit{\alpha }\Vert }_1\text{sgn }({\alpha }_i)}}{e}^{{\Vert \mathit{\alpha }\Vert }_1\text{sgn }({\alpha }_i)y_i}$$

is positive. Hence, h_i(y_i | x_m) is strictly convex and possesses a unique minimum point. These arguments yield the even sweeter dividend that the MM iteration map is continuously differentiable. From the vantage point of the implicit function theorem [8], the stationary condition $h_i^{\prime }(y_{m+1,i}|{\mathit{x}}_m)=0$ determines y_m+1,i, and consequently x_m+1,i, in terms of x_m. Observe here that $h_i^{″}(y_{\mathit{\text{mi}}}|{\mathit{x}}_m)\ne 0$ as required by the implicit function.

It is also worth pointing out that even more functions can be brought under the umbrella of signomial programming. For instance, majorization of the two related functions − ln f(x) and ln f(x) is possible for any posynomial $f(\mathit{x})={\displaystyle {\sum }_{\mathit{\alpha }}}{c}_{\mathit{\alpha }}{\displaystyle {\prod }_{i=1}^n}{x}_i^{{\alpha }_i}$. In the first case,

$$-\text{ln }f(\mathit{x})\le -{\displaystyle \sum _{\mathit{\alpha }}}\frac{a_{m\mathit{\alpha }}}{b_m}[{\displaystyle \sum _{i=1}^n}{\alpha }_i\text{ln }{x}_i+\text{ln }(\frac{c_{\mathit{\alpha }}{b}_m}{a_{m\mathit{\alpha }}}\left)\right]$$ (7)

holds for $a_{m\mathit{\alpha }}=c_{\mathit{\alpha }}{\displaystyle {\prod }_{i=1}^n}{x}_{\mathit{\text{mi}}}^{{\alpha }_i}$ and b_m = Σ_α α_mα because Jensen’s inequality applies to the convex function − ln t. In the second case, the supporting hyperplane inequality applied to the convex function − ln t implies

$$\text{ln }f(\mathit{x})\le \text{ln }f({\mathit{x}}_m)+\frac{1}{f({\mathit{x}}_m)}[f(\mathit{x})-f({\mathit{x}}_m)].$$

This puts us back in the position of needing to majorize a posynomial, a problem we have already discussed in detail. By our previous remarks, the coefficients c_α can be negative as well as positive in this case. Similar majorizations apply to any composition ϕ ◦ f(x) of a posynomial f(x) with an arbitrary concave function ϕ(y).

4 Examples of Unconstrained Minimization

Our first examples demonstrate the robustness of the MM algorithms in minimization and illustrate some of the complications that occur. In each case we can explicitly calculate the MM updates. To start, consider the posynomial

$$f_1(\mathit{x})=\frac{1}{x_1^3}+\frac{3}{x_1{x}_2^2}+x_1{x}_2$$

with the implied constraints x₁ > 0 and x₂ > 0. The majorization (4) applied to the third term of f₁(x) yields

$$x_1{x}_2\le x_{m1}{x}_{m2}\left[\frac{1}{2}{\left(\frac{x_1}{x_{m1}}\right)}^2+\frac{1}{2}{\left(\frac{x_2}{x_{m2}}\right)}^2\right]=\frac{x_{m2}}{2x_{m1}}{x}_1^2+\frac{x_{m1}}{2x_{m2}}{x}_2^2.$$

Applied to the second term of f₁(x) using the reciprocal ratios, it gives

$$\frac{3}{x_1{x}_2^2}\le \frac{3}{x_{m1}{x}_{m2}^2}\left[\frac{1}{3}{\left(\frac{x_{m1}}{x_1}\right)}^3+\frac{2}{3}{\left(\frac{x_{m2}}{x_2}\right)}^3\right]=\frac{x_{m1}^2}{x_{m2}^2}\frac{1}{x_1^3}+\frac{2x_{m2}}{x_{m1}}\frac{1}{x_2^3}.$$

The sum g(x | x_m) of the two surrogate functions

$$g_1(x_1|{\mathit{x}}_m)=\frac{1}{x_1^3}+\frac{x_{m1}^2}{x_{m2}^2}\frac{1}{x_1^3}+\frac{x_{m2}}{2x_{m1}}{x}_1^2$$

$$g_2(x_2|{\mathit{x}}_m)=\frac{2x_{m2}}{x_{m1}}\frac{1}{x_2^3}+\frac{x_{m1}}{2x_{m2}}{x}_2^2$$

majorizes f₁(x). If we set the derivatives

$$g_1^{\prime }(x_1|{\mathit{x}}_m)=-\frac{3}{x_1^4}-\frac{x_{m1}^2}{x_{m2}^2}\frac{3}{x_1^4}+\frac{x_{m2}}{x_{m1}}{x}_1$$

$$g_2^{\prime }(x_1|{\mathit{x}}_m)=-\frac{6x_{m2}}{x_{m1}}\frac{1}{x_2^4}+\frac{x_{m1}}{x_{m2}}{x}_2$$

of each of these equal to 0, then the updates

$$x_{m+1,1}=\sqrt[5]{3(\frac{x_{m1}^2}{x_{m2}^2}+1)\frac{x_{m1}}{x_{m2}}},x_{m+1,2}=\sqrt[5]{6\frac{x_{m2}^2}{x_{m1}^2}}$$

solve the minimization step of the MM algorithm. It is also obvious that the point $\mathit{x}={(\sqrt[5]{6},\sqrt[5]{6})}^t$ is a fixed point of the updates, and the reader can check that it minimizes f₁(x).

It is instructive to consider the slight variations

$$f_2(\mathit{x})=\frac{1}{x_1{x}_2^2}+x_1{x}_2^2$$

$$f_3(\mathit{x})=\frac{1}{x_1{x}_2^2}+x_1{x}_2$$

of this objective function. In the first case, the reader can check that the MM algorithm iterates according to

$$x_{m+1,1}=\sqrt[3]{\frac{x_{m1}^2}{x_{m2}^2}},x_{m+1,2}=\sqrt[3]{\frac{x_{m2}}{x_{m1}}}.$$

In the second case, it iterates according to

$$x_{m+1,1}=\sqrt[5]{\frac{x_{m1}^3}{x_{m2}^3}},x_{m+1,2}=\sqrt[5]{2\frac{x_{m2}^2}{x_{m1}^2}}.$$

The objective function f₂(x) attains its minimum value whenever $x_1{x}_2^2=1$. The MM algorithm for f₂(x) converges after a single iteration to the value 2, but the converged point depends on the initial point x₀. The infimum of f₃(x) is 0. This value is attained asymptotically by the MM algorithm, which satisfies the identities $x_{m1}{x}_{m2}^{3/2}=2^{3/10}$ and x_m+1,2 = 2^2/25x_m2 for all m ≥ 1. These results imply that x_m1 tends to 0 and x_m2 to ∞ in such a manner that f₃(x_m) tends to 0. One could not hope for much better behavior of the MM algorithm in these two examples.

The function

$$f_4(\mathit{x})=x_1^2{x}_2^2-2x_1{x}_2{x}_3{x}_4+x_3^2{x}_4^2={(x_1{x}_2-x_3{x}_4)}^2$$

is a signomial but not a posynomial. The surrogate function (6) reduces to

$$g(\mathit{x}|{\mathit{x}}_m)=\frac{x_{m2}^2}{2x_{m1}^2}{x}_1^4+\frac{x_{m1}^2}{2x_{m2}^2}{x}_2^4+\frac{x_{m4}^2}{2x_{m3}^2}{x}_3^4+\frac{x_{m3}^2}{2x_{m4}^2}{x}_4^4-2x_{m1}{x}_{m2}{x}_{m3}{x}_{m4}(\text{ln }{x}_1+\text{ln }{x}_2+\text{ln }{x}_3+\text{ln }{x}_4)$$

with all variables separated. The MM updates

$$x_{m+1,1}=\sqrt[4]{\frac{x_{m1}^3{x}_{m3}{x}_{m4}}{x_{m2}}},x_{m+1,2}=\sqrt[4]{\frac{x_{m2}^3{x}_{m3}{x}_{m4}}{x_{m1}}}$$

$$x_{m+1,3}=\sqrt[4]{\frac{x_{m3}^3{x}_{m1}{x}_{m2}}{x_{m4}}},x_{m+1,4}=\sqrt[4]{\frac{x_{m4}^3{x}_{m1}{x}_{m2}}{x_{m3}}}$$

converge in a single iteration to a solution of f₄(x) = 0. Again the limit depends on the initial point.

The function

$$f_5(\mathit{x})=x_1{x}_2+x_1{x}_3+x_2{x}_3-\text{ln}(x_1+x_2+x_3)$$

is more complicated than a signomial. It also is unbounded because the point $\mathit{x}=(m,\frac{1}{m},\frac{1}{m})$ satisfies f₅(x) = 2 + m⁻² − ln(m + 2/m). According to the majorization (7), an appropriate surrogate is

$$g(\mathit{x}|{\mathit{x}}_m)=(\frac{x_{m2}}{2x_{m1}}+\frac{x_{m3}}{2x_{m1}})x_1^2+(\frac{x_{m1}}{2x_{m2}}+\frac{x_{m3}}{2x_{m2}})x_2^2+(\frac{x_{m1}}{2x_{m3}}+\frac{x_{m2}}{2x_{m3}})x_3^2-\frac{x_{m1}}{x_{m1}+x_{m2}+x_{m3}}\text{ln }{x}_1-\frac{x_{m2}}{x_{m1}+x_{m2}+x_{m3}}\text{ln }{x}_2-\frac{x_{m3}}{x_{m1}+x_{m2}+x_{m3}}\text{ln }{x}_3$$

up to an irrelevant constant. The MM updates are

$$x_{m+1,i}=\sqrt{\frac{x_{\mathit{\text{mi}}}^2}{({\displaystyle {\sum }_{j\ne i}}{x}_{\mathit{\text{mj}}})(x_{m1}+x_{m2}+x_{m3})}}.$$

If the components of the initial point coincide, then the iterates converge in a single iteration to the saddle point with all components equal to $1/\sqrt{6}$. Otherwise, it appears that f₅(x_m) tends to −∞.

The following objective functions

$$f_6(\mathit{x})=x_1^2{x}_2^6+x_1^2{x}_2^4-2x_1^2{x}_2^3-x_1^2{x}_2^2+5.25x_1{x}_2^3-2x_1^2{x}_2+4.5x_1{x}_2^2+3x_1^2+3x_1{x}_2-12.75x_1$$

$$f_7(\mathit{x})={\displaystyle \sum _{i=1}^{10}}{x}_i^4+2{\displaystyle \sum _{i=1}^9}{x}_i^2{\displaystyle \sum _{j=i+1}^{10}}{x}_j^2+({10}^{-5}-0.5){\displaystyle \sum _{i=1}^{10}}{x}_i^2-(2\times {10}^{-5}){\displaystyle \sum _{i=7}^{10}}{x}_i+\frac{1}{16}$$

$$f_8(\mathit{x})=x_1{x}_3^2{x}_6^{-1}{x}_7^{-1}+x_1^2{x}_3^{-1}{x}_5^{-2}{x}_6^{-1}{x}_7+x_1^3{x}_2^2{x}_5^{-2}{x}_6^2+x_2^{-1}{x}_4^{-1}{x}_6^2+x_3{x}_5^3{x}_6^{-3}$$

$$f_9(\mathit{x})=x_1{x}_4^2+x_2{x}_3+x_1{x}_2{x}_3{x}_4^2+x_1^{-1}{x}_4^{-2}$$

from the reference [20] are intended for numerical illustration. Table 1 lists initial conditions, minimum points, minimum values, and number of iterations until convergence under the MM algorithm. Convergence is declared when the relative change in the objective function is less than a pre-specified value ε, in other words, when

$$\frac{f({\mathit{x}}_m)-f({\mathit{x}}_{m+1})}{|f({\mathit{x}}_m)|+1}\le \epsilon .$$

Optimization of the univariate surrogate functions easily succumbs to Newton’s method. The MM algorithm takes fewer iterations to converge than the path algorithm for all of the test functions mentioned in [20] except f₆(x). Furthermore, the MM algorithm avoids calculation of the gradient and Hessian and requires no matrix decompositions or selection of tuning constants.

Table 1.

Numerical examples of unconstrained signomial programming. Test functions f₄(x), f₆(x), f₇(x), f₈(x) and f₉(x) are taken from [20]. P: posynomial; S: signomial; G: general function.

Fun	Type	Initial Point x0	Min Point	Min Value	Iters (10−9)
f1	P	(1,2)	(1.4310,1.4310)	3.4128	38
f2	P	(1,2)	(0.6300,1.2599)	2.0000	2
f3	P	(1,1)	diverges	0.0000
f4	S	(0.1,0.2,0.3,0.4)	(0.1596,0.3191,0.1954,0.2606)	0.0000	3
f5	G	(1,1,1)	(0.4082,0.4082,0.4082)	0.2973	2
		(1,2,3)	diverges	−∞
f6	S	(1,1)	(2.9978,0.4994)	−14.2031	558
f7	S	(1, …, 10)	0.0255x0	0.0000	18
f8	P	(1, …, 7)	diverges	0.0000
f9	P	(1,2,3,4)	(0.3969,0.0000,0.0000,1.5874)	2.0000	7

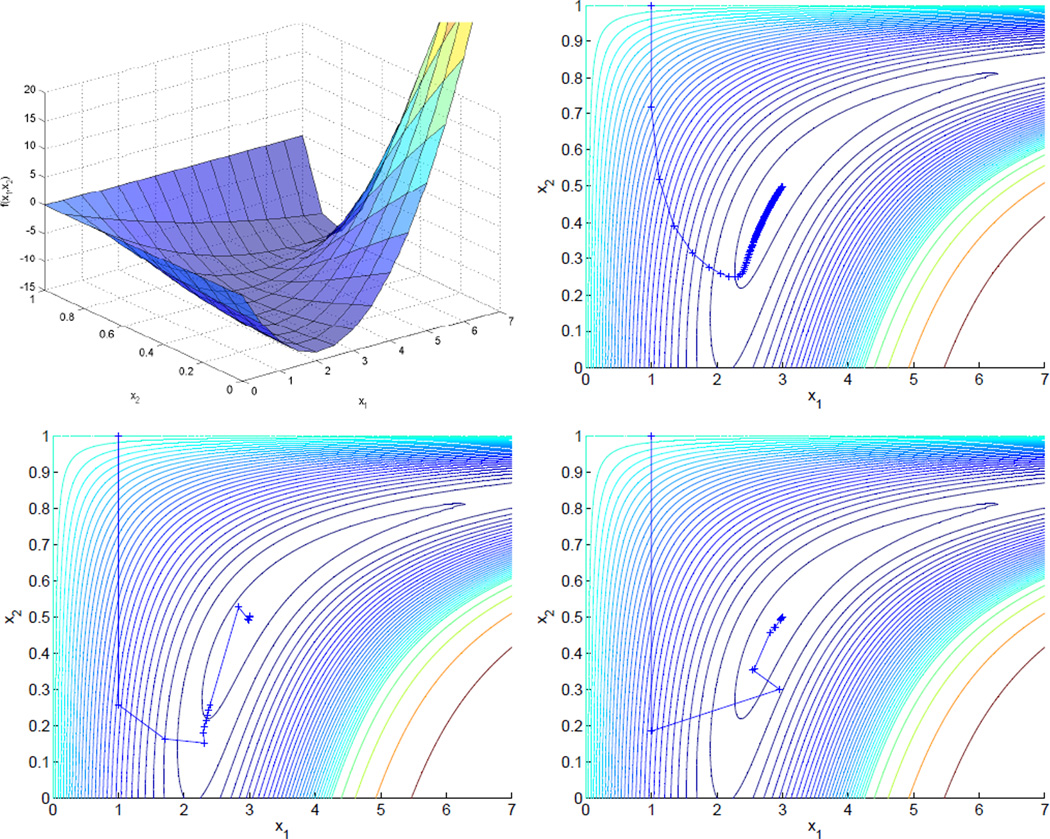
As Section 7 observes, MM algorithms typically converge at a linear rate. Although slow convergence can occur for functions such as the test function f₆(x), there are several ways to accelerate an MM algorithm. For example, our published quasi-Newton acceleration [21] often reduces the necessary number of iterations by one or two orders of magnitude. Figure 1 shows the progress of the MM iterates for the test function f₆(x) with and without quasi-Newton acceleration. Under a convergence criterion of ε = 10⁻⁹ and q = 1 secant condition, the required number of iterations falls to 30; under the same convergence criterion and q = 2 secant conditions, the required number of iterations falls to 12. It is also worth emphasizing that separation of parameters enables parallel processing in high-dimensional problems. We have recently argued [25] that the best approach to parallel processing is through graphics processing units (GPUs). These cheap hardware devices offer one to two orders of magnitude acceleration in many MM algorithms with parameters separated.

Fig. 1.

Upper left: The test function f₆(x). Upper right: 558 MM iterates. Lower left: 30 accelerated MM iterates (q = 1 secant conditions). Lower right: 12 accelerated MM iterates (q = 2 secant conditions).

5 Constrained Signomial Programming

Extending the MM algorithm to constrained geometric and signomial programming is challenging. Box constraints a_i ≤ x_i ≤ b_i are consistent with parameter separation as just developed, but more complicated posynomial constraints that couple parameters are not. Posynomial inequality constraints take the form

$$h(\mathit{x})={\displaystyle \sum _{\mathit{\beta }}}{d}_{\mathit{\beta }}{\displaystyle \prod _{i=1}^n}{x}_i^{{\beta }_i}\le 1.$$

The corresponding equality constraint sets h(x) = 1. We propose handling both constraints by penalty methods. Before we treat these matters in more depth, let us relax the positivity restrictions on the d_β but enforce the restriction β_i ≥ 0. The latter objective can be achieved by multiplying h(x) by $x_i^{{\text{max}}_{\mathit{\beta }}\{-{\beta }_i,0\}}$ for all i. If we subtract the two sides of the resulting equality, then the equality constraint h(x) = 1 can be rephrased as r(x) = 0 for the signomial $r(\mathit{x})={\displaystyle {\sum }_{\mathit{\gamma }}}{e}_{\mathit{\gamma }}{\displaystyle {\prod }_{i=1}^n}{x}_i^{{\gamma }_i}$, with no restriction on the signs of the e_γ but with the requirement γ_i ≥ 0 in effect. For example, the equality constraint

$$\frac{1}{x_1}+\frac{x_1}{x_2^2}=1$$

becomes

$$x_1^2+x_2^2-x_1{x}_2^2=0.$$

In the quadratic penalty method [1,13,17] with objective function f(x) and a single equality constraint r(x) = 0 and a single inequality constraint s(x) ≤ 0, one minimizes the sum $f_{\lambda }(\mathit{x})=f(\mathit{x})+\lambda r{(\mathit{x})}^2+\lambda s{(\mathit{x})}_{+}^2$, where s(x)₊ = max{s(x), 0}. As the penalty constant λ tends to ∞, the solution vector x_λ typically converges to the constrained minimum. In the revised objective function, the term r(x)² is a signomial whenever r(x) is a signomial. For example, in our toy problem the choice $r(\mathit{x})=x_1^2+x_2^2-x_1{x}_2^2$ has square

$$r{(\mathit{x})}^2=x_1^4+x_2^4+x_1^2{x}_2^4+2x_1^2{x}_2^2-2x_1{x}_2^4-2x_1^3{x}_2^2.$$

Of course, the powers in r(x) can be fractional here as well as integer. The term $s{(\mathit{x})}_{+}^2$ is not a signomial and must be subjected to the majorization

$$s{(\mathit{x})}_{+}^2\le \{\begin{array}{cc}{[s(\mathit{x})-s({\mathit{x}}_m)]}^2\hfill & s({\mathit{x}}_m)<0\hfill \\ s{(\mathit{x})}^2\hfill & s({\mathit{x}}_m)\ge 0\hfill \end{array}$$

to achieve this status. In practice, one does not need to fully minimize f_λ(x) for any fixed λ. If one increases λ slowly enough, then it usually suffices to merely decrease f_λ(x) at each iteration. The MM algorithm is designed to achieve precisely this goal. Our exposition so far suggests that we majorize r(x)², s(x)², and [s(x) − s(x_m)]² in exactly the same manner that we majorize f(x). Separation of parameters generalizes, and the resulting MM algorithm keeps all parameters positive while permitting pertinent parameters to converge to 0. Section 7 summarizes some of the convergence properties of this hybrid procedure.

The quadratic penalty method traditionally relies on Newton’s method to minimize the unconstrained functions f_λ(x). Unfortunately, this tactic suffers from roundoff errors and numerical instability. Some of these problems disappear with the MM algorithm. No matrix inversions are involved, and iterates enjoy the descent property. Ill-conditioning does cause harm in the form of slow convergence, but the previously mentioned quasi-Newton acceleration largely remedies the situation [21]. As an alternative to quadratic penalties, exact penalties take the form λ|r(x)| + λs(x)₊. Remarkably, the exact penalty method produces the constrained minimum, not just in the limit, but for all finite λ beyond a certain point. Although this desirable property avoids the numerical instability encountered in the quadratic penalty method, the kinks in the objective functions f(x) + λ|r(x)| + λs(x)₊ are a nuisance. Our recent paper [24] on the exact penalty method shows how to circumvent this annoyance.

6 Nonnegative Quadratic Programming

As an illustration of constrained signomial programming, consider quadratic programming over the positive orthant. Let

$$f(\mathit{x})=\frac{1}{2}{\mathit{x}}^t\mathit{\text{Qx}}+{\mathbf{c}}^t\mathit{x}$$

be the objective function, Ex = d the linear equality constraints, and Ax ≤ b the linear inequality constraints. The symmetric matrix Q can be negative definite, indefinite, or positive definite. The quadratic penalty method involves minimizing the sequence of penalized objective functions

$$f_{\lambda }(\mathit{x})=\frac{1}{2}{\mathit{x}}^t\mathit{\text{Qx}}+{\mathit{c}}^t\mathit{x}+\frac{\lambda }{2}{\Vert {(\mathit{\text{Ax}}-\mathit{b})}_{+}\Vert }_2^2+\frac{\lambda }{2}{\Vert \mathit{\text{Ex}}-\mathit{d}\Vert }_2^2$$

as λ tends to ∞. Based on the obvious majorization

$$x_{+}^2\le \{\begin{array}{cc}{(x-x_m)}^2\hfill & x_m<0\hfill \\ x^2\hfill & x_m\ge 0\hfill \end{array},$$

the term ${\Vert {(\mathit{\text{Ax}}-\mathit{b})}_{+}\Vert }_2^2$ is majorized by ${\Vert \mathit{\text{Ax}}-\mathit{b}-{\mathit{r}}_m\Vert }_2^2$, where

$${\mathit{r}}_m=\text{min}\{{\mathit{\text{Ax}}}_m-\mathit{b},\mathbf{0}\}.$$

A brief calculation shows that f_λ(x) is majorized by the surrogate function

$$g_{\lambda }(\mathit{x}|{\mathit{x}}_m)=\frac{1}{2}{\mathit{x}}^t{\mathit{H}}_{\lambda }\mathit{x}+{\mathit{\upsilon }}_{\lambda m}^t\mathit{x}$$

up to an irrelevant constant, where H_λ and υ_λm are defined by

$${\mathit{H}}_{\lambda }=\mathit{Q}+\lambda ({\mathit{A}}^t\mathit{A}+{\mathit{E}}^t\mathit{E})$$

$${\mathit{\upsilon }}_{\lambda m}=\mathit{c}-\lambda {\mathit{A}}^t(\mathit{b}+{\mathit{r}}_m)-\lambda {\mathit{E}}^t\mathit{d}.$$

It is convenient to assume that the diagonal coefficients $\frac{1}{2}{h}_{\lambda \mathit{\text{ii}}}$ appearing in the quadratic form $\frac{1}{2}{\mathit{x}}^T$ H_λx are positive. This is generally the case for large λ. One can handle the off-diagonal term h_λijx_ix_j by either the majorization (4) or the majorization (5) according to the sign of h_λij. The reader can check that the MM updates reduce to

$$x_{m+1,i}=\frac{x_{\mathit{\text{mi}}}}{2}\left[-\frac{{\upsilon }_{\lambda \mathit{\text{mi}}}}{h_{\lambda \mathit{\text{mi}}}^{+}}+\sqrt{{\left(\frac{{\upsilon }_{\lambda \mathit{\text{mi}}}}{h_{\lambda \mathit{\text{mi}}}^{+}}\right)}^2-4\frac{h_{\lambda \mathit{\text{mi}}}^{-}}{h_{\lambda \mathit{\text{mi}}}^{+}}}\right],$$ (8)

where

$$h_{\lambda \mathit{\text{mi}}}^{+}={\displaystyle \sum _{j:h_{\lambda \mathit{\text{ij}}}>0}}{h}_{\lambda \mathit{\text{ij}}}{x}_{\mathit{\text{mj}}},h_{\lambda \mathit{\text{mi}}}^{-}={\displaystyle \sum _{j:h_{\lambda \mathit{\text{ij}}}<0}}{h}_{\lambda \mathit{\text{ij}}}{x}_{\mathit{\text{mj}}}.$$

When $h_{\lambda \mathit{\text{mi}}}^{-}=0$, the update (8) collapses to

$$x_{m+1,i}=x_{\mathit{\text{mi}}}\text{ max }\left\{-\frac{{\upsilon }_{\lambda \mathit{\text{mi}}}}{h_{\lambda \mathit{\text{mi}}}^{+}},0\right\}.$$ (9)

To avoid sticky boundaries, we replace 0 in equation (9) by a small positive constant ε such as 10⁻⁹. Sha et al. [18] derived the update (8) for λ = 0 ignoring the constraints Ex = d and Ax ≤ b.

For a numerical example without equality constraints take

$$f_{10}(\mathit{x})=\frac{1}{2}{x}_1^2+x_2^2-x_1{x}_2-2x_1-6x_2$$

$$\mathit{A}=\left(\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \\ \hfill -1\hfill & \hfill 2\hfill \\ \hfill 2\hfill & \hfill 1\hfill \end{array}\right),\mathit{b}=\left(\begin{array}{c}\hfill 2\hfill \\ \hfill 2\hfill \\ \hfill 3\hfill \end{array}\right).$$

The minimum occurs at the point (2/3, 4/3)^t. Table 2 lists the number of iterations until convergence and the converged point x_λ for the sequence of penalty constants λ = 2^k. The quadratic program

$$f_{11}(\mathit{x})=-8x_1-16x_2+x_1^2+4x_2^2$$

$$\mathit{A}=\left(\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right),\mathit{b}=\left(\begin{array}{c}\hfill 4\hfill \\ \hfill 3\hfill \end{array}\right)$$

converges much more slowly. Its minimum occurs at the point (2.4, 1.6)^t. Table 3 lists the numbers of iterations until convergence with (q = 1) and without (q = 0) acceleration and the converged point x_λ for the same sequence of penalty constants λ = 2^k. Fortunately, quasi-Newton acceleration compensates for ill conditioning in this test problem.

Table 2.

Iterates from the quadratic penalty method for the test function f₁₀(x). The convergence criterion for the inner loops is 10⁻⁹.

log2 λ	Iters	xλ
0	8	(0.9503,1.6464)
1	6	(0.8580,1.5164)
2	5	(0.8138,1.4461)
3	23	(0.7853,1.4067)
4	32	(0.7264,1.3702)
5	31	(0.6967,1.3518)
6	30	(0.6817,1.3426)
7	29	(0.6742,1.3380)
8	28	(0.6704,1.3356)
9	26	(0.6686,1.3345)
10	25	(0.6676,1.3339)
11	23	(0.6671,1.3336)
12	22	(0.6669,1.3335)
13	21	(0.6668,1.3334)
14	19	(0.6667,1.3334)
15	18	(0.6667,1.3334)
16	16	(0.6667,1.3333)
17	15	(0.6667,1.3333)

Table 3.

Iterates from the quadratic penalty method for the test function f₁₁(x). The convergence criterion for the inner loops is 10⁻¹⁶.

log2 λ	Iters (q = 0)	Iters (q = 1)	xλ
0	18	5	(3.0000,1.8000)
1	2	2	(2.8571,1.7143)
2	56	6	(2.6667,1.6667)
3	97	5	(2.5455,1.6364)
4	167	5	(2.4762,1.6190)
5	312	5	(2.4390,1.6098)
6	541	6	(2.4198,1.6049)
7	955	5	(2.4099,1.6025)
8	1674	4	(2.4050,1.6012)
9	2924	3	(2.4025,1.6006)
10	4839	3	(2.4013,1.6003)
11	7959	4	(2.4006,1.6002)
12	12220	4	(2.4003,1.6001)
13	17674	4	(2.4002,1.6000)
14	21739	3	(2.4001,1.6000)
15	20736	3	(2.4000,1.6000)
16	8073	3	(2.4000,1.6000)
17	111	3	(2.4000,1.6000)
18	6	4	(2.4000,1.6000)
19	5	2	(2.4000,1.6000)
20	3	2	(2.4000,1.6000)
21	2	2	(2.4000,1.6000)

7 Convergence

As we have seen, the behavior of the MM algorithm is intimately tied to the behavior of the objective function f(x). For the sake of simplicity, we now restrict attention to unconstrained minimization of posynomials and investigate conditions guaranteeing that f(x) possesses a unique minimum on its domain. Uniqueness is related to the strict convexity of the reparameterization

$$h(\mathit{y})={\displaystyle \sum _{\mathit{\alpha }\in S}}{c}_{\mathit{\alpha }}{e}^{{\mathit{\alpha }}^t\mathit{y}}$$

of f(x), where ${\mathit{\alpha }}^t\mathit{y}={\displaystyle {\sum }_{i=1}^n}{\alpha }_i{y}_i$ is the inner product of α and y and x_i = e^y_i for each i. The Hessian matrix

$$d^{2}h(\mathit{y})={\displaystyle \sum _{\mathit{\alpha }\in S}}{c}_{\mathit{\alpha }}{e}^{{\mathit{\alpha }}^t\mathit{y}}\mathit{\alpha }{\mathit{\alpha }}^t$$

of h(y) is positive semidefinite, so h(y) is convex. If we let T be the subspace of ℝⁿ spanned by {α}_α∈S, then h(y) is strictly convex if and only if T = ℝⁿ. Indeed, suppose the condition holds. For any υ ≠ 0, it then must be true that α^tυ ≠ 0 for some α ∈ S. As a consequence,

$${\mathit{\upsilon }}^t{d}^{2}h(\mathit{y})\mathit{\upsilon }={\displaystyle \sum _{\mathit{\alpha }\in S}}{c}_{\mathit{\alpha }}{e}^{{\mathit{\alpha }}^t\mathit{y}}{({\mathit{\alpha }}^t\mathit{\upsilon })}^2>0,$$

and d²h(y) is positive definite. Conversely, suppose T ≠ ℝⁿ, and take υ ≠ 0 with α^tυ = 0 for every α ∈ S. Then h(y+tυ) = h(y) for every scalar t, which is incompatible with h(y) being strictly convex.

Strict convexity guarantees uniqueness, not existence, of a minimum point. Coerciveness ensures existence. The objective function f(x) is coercive if f(x) tends to ∞ whenever any component of x tends to 0 or ∞. Under the reparameterization x_i = e^y_i, this is equivalent to h(y) = f(x) tending to ∞ as ‖y‖₂ tends to ∞. A necessary and sufficient condition for this to occur is that max_α∈S α^tυ > 0 for every υ ≠ 0. For a proof, suppose the contrary condition holds for some υ ≠ 0. Then it is clear that h(tυ) remains bounded above by h(0) as the scalar t tends to ∞. Conversely, if the stated condition is true, then the function q(y) = max_α∈S α^ty is continuous and achieves its minimum of d > 0 on the sphere {y ∈ ℝⁿ : ‖y‖₂ = 1}. It follows that q(y) ≥ d‖y‖₂ and that

$$h(\mathit{y})\ge \underset{\mathit{\alpha }\in S}{\text{max}}\{c_{\mathit{\alpha }}{e}^{{\mathit{\alpha }}^{t}y}\}\ge \left(\underset{\mathit{\alpha }\in S}{\text{min}}{c}_{\mathit{\alpha }}\right)e^{d{\Vert \mathit{y}\Vert }_2}.$$

This lower bound shows that h(y) is coercive.

The coerciveness condition is hard to apply in practice. An equivalent condition is that the origin 0 belongs to the interior of the convex hull of the set {α}_α∈S. It is straightforward to show that the negations of these two conditions are logically equivalent. Thus, suppose q(υ) = max_α∈S α^tυ ≤ 0 for some vector υ ≠ 0. Every convex combination Σ_α p_αα then satisfies (Σ_α p_αα)^t υ ≤ 0. If the origin is in the interior of the convex hull, then ευ is also for every sufficiently small ε > 0. But this leads to the contradiction $\epsilon {\mathit{\upsilon }}^t\mathit{\upsilon }=\epsilon {\Vert \mathit{\upsilon }\Vert }_2^2\le 0$. Conversely, suppose 0 is not in the interior of the convex hull. According to the separating hyperplane theorem for convex sets, there exists a unit vector υ with υ^tα ≤ 0 = υ^t0 for every α ∈ S. In other words, q(υ) ≤ 0. The convex hull criterion is easier to check, but it is not constructive. In simple cases such as the objective function f₁(x) where the power vectors are α = (−3, 0)^t, α = (−1, −2)^t, and α = (1, 1)^t, it is visually obvious that the origin is in the interior of their convex hull.

One can also check the criterion q(υ) > 0 for all υ ≠ 0 by solving a related geometric programming problem. This problem consists in minimizing the scalar t subject to the inequality constraints α^ty ≤ t for all α ∈ S and the nonlinear equality constraint ${\Vert \mathit{y}\Vert }_2^2=1$. If t_min ≤ 0, then the original criterion fails.

In some cases, the objective function f(x) does not attain its minimum on the open domain ${ℝ}_{>0}^n=\{\mathit{x}:x_i>0,1\le i\le n\}$. This condition is equivalent to the corresponding function ln h(y) being unbounded below on ℝⁿ. According to Gordon’s theorem [2,10], this can happen if and only if 0 is not in the convex hull of the set {α}_α∈S. Alternatively, both conditions are equivalent to the existence of a vector υ with α^tυ < 0 for all α ∈ S. For the objective function f₃(x), the power vectors are α = (−1, −2)^t and α = (1, 1)^t. The origin (0, 0)^t does not lie on the line segment between them, and the vector (−3/2, 1)^t forms a strictly oblique angle with each. As predicted, f₃(x) does not attain its infimum on ${ℝ}_{>0}^n$ .

The theoretical development in reference [10] demonstrates that the MM algorithm converges at a linear rate to the unique minimum point of the objective function f(x) when f(x) is coercive and its convex reparameterization h(y) is strictly convex. The theory does not cover other cases, and it would be interesting to investigate them. The general convergence theory of MM algorithms [10] states that five properties of the objective function f(x) and MM algorithmic map x ↦ M(x) guarantee convergence to a stationary point of f(x): (a) f(x) is coercive on its open domain; (b) f(x) has only isolated stationary points; (c) M(x) is continuous; (d) x^* is a fixed point of M(x) if and only if x^* is a stationary point of f(x); and (e) f[M(x^*)] ≥ f(x^*), with equality if and only if x^* is a fixed point of M(x). For a general signomial program, items (a) and (b) are the hardest to check. Our examples provide some clues.

The standard convergence results for the quadratic penalty method are covered in the references [1,10,13,17]. To summarize the principal finding, suppose that the objective function f(x) and the constraint functions r_i(x) and s_i(x) are continuous and that f(x) is coercive on ${ℝ}_{>0}^n$. If x_λ minimizes the penalized objective function

$$f_{\lambda }(\mathit{x})=f(\mathit{x})+\lambda {\displaystyle \sum _i}{r}_i{(\mathit{x})}^2+\lambda {\displaystyle \sum _j}{s}_j{(\mathit{x})}_{+}^2,$$

and x_∞ is a cluster point of x_λ as λ tends to ∞, then x_∞ minimizes f(x) subject to the constraints. In this regard observe that the coerciveness assumption on f(x) implies that the solution set {x_λ}_λ is bounded and possesses at least one cluster point. Of course, if the solution set consists of a single point, then x_λ tends to that point.

8 Discussion

The current paper presents novel algorithms for both geometric and signomial programming. Although our examples are low dimensional, the previous experience of Sha et al. [18] offers convincing evidence that the MM algorithm works well for high-dimensional quadratic programming with nonnegativity constraints. The ideas pursued here – the MM principle, separation of variables, quasi-Newton acceleration, and penalized optimization – are surprisingly potent in large-scale optimization. The MM algorithm deals with the objective function directly and reduces multivariate minimization to a sequence of one-dimensional minimizations. The MM updates are simple to code and enjoy the crucial descent property. Treating constrained signomial programming by the penalty method extends the MM algorithm even further. Quadratic programming with linear equality and inequality constraints is the most important special case of constrained signomial programming. Our new MM algorithm for constrained quadratic programming deserves consideration in high-dimensional problems. Even though MM algorithms can be notoriously slow to converge, quasi-Newton acceleration can dramatically improve matters. Acceleration involves no matrix inversion, only matrix times vector multiplication. In our limited experiments with large-scale problems [22,23], MM algorithms with quasi-Newton acceleration can achieve comparable or better performance than limited-memory BFGS algorithms. Finally, it is worth keeping in mind that parameter separated algorithms are ideal candidates for parallel processing.

Because geometric programs are convex after reparameterization, it is relatively easy to pose and check sufficient conditions for global convergence of the MM algorithm. In contrast it is far more difficult to analyze the behavior of the MM algorithm for signomial programs. Theoretical progress will probably be piecemeal and require problem-specific information. A major difficulty is understanding the asymptotic nature of the objective function as parameters approach 0 or ∞. Even in the absence of theoretical guarantees, the descent property of the MM algorithm makes it an attractive solution technique and a diagnostic tool for finding counterexamples. Some of our test problems expose the behavior of the MM algorithm in non-standard situations. We welcome the help of the optimization community in unraveling the mysteries of the MM algorithm in signomial programming.