A risk prediction algorithm based on family history and common genetic variants: application to prostate cancer with potential clinical impact

Abstract

Genome Wide Association Studies have identified several Single Nucleotide Polymorphisms (SNPs) that are independently associated with small increments in risk of prostate cancer, opening up the possibility for using such variants in risk prediction. Using segregation analysis of population-based samples of 4390 families of prostate cancer patients from the UK and Australia, and assuming all familial aggregation has genetic causes, we previously found that the best model for the genetic susceptibility to prostate cancer was a mixed model of inheritance that included both a recessive major gene component and a polygenic component (P) that represents the effect of a large number of genetic variants each of small effect, where $P\sim N(0,{\sigma }_P^2)$. Based on published studies of 26 SNPs that are currently known to be associated with prostate cancer, we have extended our model to incorporate these SNPs by decomposing the polygenic component into two parts: a polygenic component due to the known susceptibility SNPs, $P_K\sim N(0,{\sigma }_K^2)$, and the residual polygenic component due to the postulated but as yet unknown genetic variants, $P_U\sim N(0,{\sigma }_U^2)$. The resulting algorithm can be used for predicting the probability of developing prostate cancer in the future based on both SNP profiles and explicit family history information. This approach can be applied to other diseases for which population-based family data and established risk variants exist.

Introduction

Prostate cancer is the most common non-skin cancer in males living in developed countries, and incidence has been increasing since the early 1990s [AIHW (Australian Institute of Health and Welfare) & AACR (Australasian Association of Cancer Registries) 2007; Parkin, et al. 2003]. Other than advancing age, the strongest risk factor for the disease is having a family history of prostate cancer. The risk of prostate cancer for first degree relatives of men with prostate cancer is approximately 2.5-fold greater than for men without a family history, which suggests that familial factors are important for the disease development [Johns and Houlston 2003].

In the last few years, several prostate cancer susceptibility variants have been identified. Other than mutations in BRCA2 [Agalliu, et al. 2007; Edwards, et al. 2003; The Breast Cancer Linkage Consortium 1999; Willems, et al. 2008], no other genes with high-penetrant variants have been discovered. Genome Wide Association Studies (GWAS) have identified several common variants (SNPs) that individually are associated with small increments in risk of prostate cancer. Taken together these loci explain 22% of the familial risk of prostate cancer [Eeles, et al. 2009]. This opens up the possibility for using SNPs in risk prediction.

Risk prediction algorithms are an important tool for identifying individuals at high risk of developing the disease who can then be offered individually tailored clinical management. They are also useful in the planning of clinical and screening trials or for estimating the population burden of disease [Freedman, et al. 2005].

Recently, an empirical risk model for prostate cancer was published which included the cumulative association of eleven genetic variants and first degree family history with prostate cancer risk using data from a Swedish study [Zheng, et al. 2008]. All the associations were combined using a logistic regression model. A disadvantage of this approach is that it does not deal adequately with different types of family history of prostate cancer and it does not take into account information on all available relatives. An alternative approach is to base predictions on a genetic risk model that explicitly models family history and can provide consistent risks for families with any disease structure [Antoniou and Easton 2006].

In a previous article, we described the development of a genetic model for familial prostate cancer using segregation analysis [MacInnis, et al. 2010]. We demonstrated that genetic susceptibility to prostate cancer can be explained by a mixed model of inheritance that includes the effects of a recessively inherited major gene and a polygenic component representing the effects of a large number of genetic variants each of small effect on risk. In this article, we further develop the model by incorporating the explicit effects of the identified common prostate cancer susceptibility variants. We investigate the predictions of this model and demonstrate the potential clinical utility of risk profiling based on common polymorphisms.

Subjects and Methods

Subjects: Australian Prostate Cancer Case-Control Study

Eligible cases were men diagnosed with a first primary invasive adenocarcinoma of the prostate under the age 70 years, between 1993 and 1998 while resident in Melbourne, Sydney, or Perth in a population-based case-control study of risk factors for prostate cancer. Data on prostate cancer family history in all first -degree relatives were collected by face-to-face interview. In this analysis, only data from cases (1,832 probands) and their relatives were used. This dataset is described in detail elsewhere [Giles, et al. 2001; MacInnis, et al. 2010]

Subjects: Royal Marsden NHS Foundation Trust, U.K

Eligible participants were men diagnosed with prostate cancer at any age, identified through a systematically collected series of patients from prostate cancer clinics in the urology unit at the Royal Marsden NHS Foundation Trust, UK, between 1992 and 2006. 2,558 participants completed a questionnaire that recorded family history of prostate cancer for all first degree relatives. More details can be found in [MacInnis, et al. 2010].

Segregation analysis

A number of different genetic models were previously investigated for the genetic susceptibility to prostate cancer using complex segregation analysis [MacInnis, et al. 2010]. The most parsimonious model was a mixed recessive model, which incorporated a major gene effect that was recessively inherited combined with a polygenic component representing the multiplicative effects of multiple genetic variants with small effect on risk. Under this model, the prostate cancer incidence λ_i(t) for individual i at age t is assumed to depend on the underlying genotype through a model of the form λ_i(t) = λ₀(t) exp(G_i + P_i(t)), where λ₀(t) is the baseline incidence at age t, G_i is the natural logarithm of the relative risk (RR) associated with the major genotype of individual i, and P_i(t) is the polygenic component that is assumed to be normally distributed with mean 0 and variance ${\sigma }_P^2(t)$. This is analogous to a Cox model with the genetic components represented by random effects. The polygenic component was approximated by the Hypergeometric Polygenic Model (HPM), such that

$$P=\frac{(R-N){\sigma }_P}{\sqrt{\frac{N}{2}}}$$ (1)

where R has a binomial distribution (2N, 1/2) and N was the number of loci used in the HPM [Fernando, et al. 1994; Lange 1997]. The model was implemented using the pedigree analysis software MENDEL [Lange, et al. 1988].

Incidences within this model are calendar period and cohort specific, and the overall incidence of prostate cancer is constrained to agree with the national incidences. The model incorporates incidences for England and Wales (1960-2004) [Office for National Statistics 2006; Parkin, et al. 2003] and for Australia (1982-2003) [AIHW (Australian Institute of Health and Welfare) & AACR (Australasian Association of Cancer Registries) 2007] and individuals were assumed to be at risk of disease from birth and censored at the earliest of the following events: age at diagnosis of any cancer, age at death, age at last follow-up, or age 80 years.

In this analysis, we fitted additional models in which the polygenic variance was assumed to be age dependent ${\sigma }_P^2(t)$. Maximum likelihood estimation was used to estimate the model parameters and we maximized the conditional likelihood of observing the family phenotypes given the disease phenotype of the index patient. Nested models were compared using likelihood ratio tests. The Akaike's A Information Criterion [Akaike 1974] [AIC = −2 log Lik + 2×(no. of parameters)] was used to discriminate between non-nested models [Elston 1990], where log Lik equals the total log likelihood across all families.

Genetic variants

At the time of commencement of analyses, 26 SNPs were identified as being associated with prostate cancer susceptibility [Al Olama, et al. 2009; Easton and Eeles 2008; Eeles, et al. 2009] in 24 distinct regions. We used estimates of minor allele frequencies and odds ratios from a case-control study of UK and Australian men [Al Olama, et al. 2009; Eeles, et al. 2009]. SNPs rs721048 and rs4430796 were not genotyped in this study; instead we used other published results [Gudmundsson, et al. 2008; Gudmundsson, et al. 2007]. SNP rs16901979 was also not genotyped in this study, but genotype data were available for a perfectly correlated SNP (rs1050548, r²=1 based on HapMap data). For SNPs in the same region we used the ORs from the joint analyses of the SNPs.

Incorporating common genetic variants

To incorporate information on the genetic variants known to confer increased prostate cancer risk, we decomposed the total polygenic component of the model above (P) into two parts: a polygenic component due to the known susceptibility loci P_K and an unknown residual polygenic component P_U. We assumed that both were independent and normally distributed with mean 0 and variance ${\sigma }_K^2$ and ${\sigma }_U^2$ respectively. Under this model, P=P_K +P_U, where $P\sim N(0,{\sigma }_P^2)$ is given from the fitted models above, and ${\sigma }_P^2={\sigma }_K^2+{\sigma }_U^2$. Given a set of known genetic variants and their joint RR distribution, it is possible to determine ${\sigma }_K^2$ (see below). As ${\sigma }_P^2$ is known, we can therefore solve for ${\sigma }_U^2$. To compute P_K, we assumed that the known genetic loci interact multiplicatively. Therefore for each individual i,

$$P_{K,i}=\sum _j{\beta }_{ij}-\mu$$

where β_ij is the log RR associated with the genotype of individual i at SNP j, and μ is the mean of the log-RR distribution across all SNPs. The polygenic variance due to the set of known-genotyped loci ${\sigma }_K^2$ was computed as:

$${\sigma }_K^2={\sum }_j{\sigma }_j^2$$

where ${\sigma }_j^2=log\left(\frac{{(1-f_j)}^2+2(1-f_j)f_j{e}^{2{\beta }_{1j}}+f_j^2{e}^{2{\beta }_{2j}}}{{({(1-f_j)}^2+2(1-f_j)f_j{e}^{{\beta }_{1j}}+f_j^2{e}^{{\beta }_{2j}})}^2}\right)$ and f_j is the minor allele frequency at locus j, exp(β_1j) is the RR at locus j for carriers of a single copy of the minor allele and exp(β_2j) the RR at locus j for carriers of 2 copies of the minor allele. Note that $exp\left({\sigma }_j^2\right)$ is the coefficient of variation in disease incidence due to SNP j [Antoniou and Easton 2003].

The proportion of the variance explained by each SNP was computed by dividing the variance contribution of each SNP ${\sigma }_j^2$ by the total variance of the polygenic component ( ${\sigma }_P^2$).

Risk of developing prostate cancer in the future

Let $y_1^{\ast }$ denote the event that the proband will develop prostate cancer between ages t₀ and t₁, where t₀ is the current age and t₁>t₀. The probability of the proband developing the disease between ages t₀ and t₁, conditional on the observed SNP genotypes and family phenotypes is given by:

$$P(y_1^{\ast }|P_{K_1},\underset{\_}{y})=\frac{P(\underset{\_}{y}\ast ,P_{K_1})}{P(\underset{\_}{y},P_{K_1})}$$ (2)

where y represents the vector of all the family phenotypes at age t₀, y* represents the vector of family phenotypes including the proband diagnosed with prostate cancer between ages t₀ and t₁ and P_K1 is the known polygenic component for the proband such that P₁ = P_K1 + P_U1 ⋅ P_U1 is the residual (unknown) polygenic component for the proband and P₁ is the total polygenotype. Therefore, P(y*, P_K1) represents the probability of observing all family phenotypes, the known polygenic component for the proband and the proband developing the disease between ages t₀ and t₁.

In equation (2), the denominator can be expressed in terms of $P_1^n$, the n^th “total polygenotype” for the proband, as follows:

$$P(\underset{\_}{y},P_{K_1})=\sum _{n=0}^{2N+1}P(P_{K_1}|P_1^n,\underset{\_}{y})$$ (3)

where the summation is over all possible polygenotypes and N is the number of loci in the HPM. Note that this is possible due the discrete nature of $P_1^n$ under this model (as approximated by equation (1)). In these calculations N was assumed to be equal to 5. $P(P_{K_1}|P_1^n)$ is the conditional normal density function given by:

$$P_{K_1}|P_1^n~N(P_1^n\frac{{\sigma }_K^2}{{\sigma }_K^2+{\sigma }_U^2},\frac{{\sigma }_K^2{\sigma }_U^2}{{\sigma }_K^2+{\sigma }_U^2})$$ (4)

$P(P_1^n,\underset{\_}{y})$ is the probability of observing all family phenotypes at current age t₀ for the proband and the proband having a total polygenotype $P_1^n$. When the polygenic variance is age dependent, expression (3) is evaluated at age t₀.

The numerator of (2) incorporates the probability of developing the disease from age t₀ to age t₁ for the proband and can be computed as follows

$$P({\underset{\_}{y}}^{\ast },P_{K_1})=\sum _{t=t_0}^{t=t_1}P({\underset{\_}{y}}_t^{\ast },P_{K_1})$$

Where ${\underset{\_}{y}}_t^{\ast }$ represents the event of observing the family phenotypes with the proband diagnosed with prostate cancer at age t. Following equation (3):

$$P({\underset{\_}{y}}^{\ast },P_{K_1})=\sum _{t=t_0}^{t=t_1}P({\underset{\_}{y}}_t^{\ast },P_{K_1})=\sum _{t=t_0}^{t=t_1}\sum _{n}P(P_{K_1}|P_1^{n,t})P(P_{K_1}|P_1^{n,t},{\underset{\_}{y}}_t^{\ast })$$

Where $P_1^{n,t}$ is the total polygenotype of the proband at age t.

Hence, the probability of developing prostate cancer in the future can be computed in terms of a series of likelihood functions computed in MENDEL [Lange, et al. 1988].

Descriptive statistics were calculated using Stata 10.

Results

Segregation analysis models

Prior to incorporating the effects of the prostate cancer susceptibility SNPs, we fitted additional models to the family data to investigate in more detail the behavior of the polygenic component (Table I). The most parsimonious model was the one with two age groups for the polygenic variance and this formed the basis for developing the risk prediction algorithm. Under this model, the risk allele of the major gene component was estimated to have a population frequency of 0.165 with a RR for the rare homozygotes compared with common homozygotes of 65. The polygenic variance for age group 35-59 was estimated to be 26.82, and for age group 60-79 2.15.

Table I. Segregation analysis models fitted for the polygenic variance ^a.

Parameter	Age (years)	Estimate	(95% CI)	qA	95% CI	RR	95% CI	AICd
Constant models
σP2	35-79	3.36	(2.22,5.09)	0.145	(0.111,0.190)	100	(51,196)	6562.5
σP2	35-59	26.82	(13.59,52.9)	0.165	(0.125,0.216)	65	(33,129)	6547.7
σP2	60-79	2.15	(1.33,3.46)
σP2	35-59	27.25	(13.56,54.77)	0.161	(0.109,0.239)	69	(23,205)	6549.7
σP2	60-69	2.33	(0.79,6.91)
σP2	70-79	2.10	(1.20,3.65)
Linear modelb
α	35-79	40.1	(15.1,65.0)	0.124	(0.105,0.146)	764	(146,3996)	6553.1
β	35-79	-0.50	(-0.81,-0.19)
Linear/Constant model c
α	35-59	538.5	(108.1,968.9)	0.169	(0.132,0.216)	60	(35,104)	6548.1
β	35-59	-8.94	(-16.11,-1.77)
σP2	60-79	2.15	(1.33,3.46)

^aFive models with different assumptions about the polygenic variance were investigated. In the first model, the polygenic variance was constrained to be equal across all age ranges. Subsequent models were then fitted to allow for the polygenic variance to vary by two age groups (<60, ≥60 years), by three age groups (<60, 60-69, ≥70 years), and as a linear function of age. All models with an age dependent polygenic variance fitted significantly better than the model with a constant polygenic variance (all P<0.001).

^bPolygenic variance σ_p²(t) = α + βt, where t is age in years

^cPolygenic variance σ_p²(t) = α + βt for ages 35-59, and is constant for ages 60-79

^dAkaike's A Information Criterion AIC = -2 × (Log Likelihood) + 2 × (number of estimated parameters)

Known prostate cancer susceptibility SNPs

The allele frequencies, odds ratios and the amount of total polygenic variance explained for each of the 26 SNPs considered are shown in Table II. In practice, it is possible that only a subset of the known prostate cancer susceptibility variants is measured on an individual. In our model formulation we transform the observed SNP profile into the observed polygenic scale and therefore each combination of typed SNPs defines a separate observed polygenic distribution. σ_K for having all 26 SNPs typed is 0.45, which explains about 14% of the total polygenic variance (for ages 60-79).

Table II.

Summary statistics for the 26 prostate cancer susceptibility variants incorporated into the model (data from [Al Olama, et al. 2009; Eeles, et al. 2009; Gudmundsson, et al. 2008; Gudmundsson, et al. 2007]).

Marker	Chromosome	Frequency high-risk allelea	Per allele Odds Ratio	Variance	% variance explained b
rs721048	2	0.19	1.15	0.007	0.30%
rs1465618	2	0.21	1.13	0.005	0.25%
rs12621278	2	0.94	1.49	0.013	0.59%
rs2660753	3	0.11	1.11	0.002	0.11%
rs17021918c	4	0.65	1.14	0.007	0.33%
rs12500426c	4	0.44	1.08	0.003	0.12%
rs7679673	4	0.61	1.14	0.008	0.35%
rs9364554	6	0.30	1.16	0.010	0.45%
rs10486567	7	0.77	1.09	0.003	0.12%
rs6465657	7	0.46	1.11	0.005	0.26%
rs10505483	8	0.03	1.49	0.014	0.66%
rs6983267	8	0.51	1.26	0.026	1.19%
rs1447295	8	0.10	1.43	0.029	1.36%
rs2928679d	8	0.46	1.12	0.006	0.30%
rs1512268d	8	0.42	1.13	0.007	0.34%
rs10086908	8	0.70	1.15	0.008	0.36%
rs620861	8	0.63	1.11	0.005	0.23%
rs10993994	10	0.40	1.25	0.024	1.13%
rs4962416	10	0.30	1.05	0.001	0.04%
rs7931342	11	0.52	1.15	0.010	0.47%
rs7127900	11	0.18	1.27	0.019	0.91%
rs4430796	17	0.49	1.22	0.020	0.91%
rs1859962	17	0.47	1.24	0.024	1.10%
rs2735839	19	0.85	1.20	0.007	0.34%
rs5759167	22	0.50	1.21	0.017	0.80%
rs5945619	X	0.36	1.21	0.009	0.41%

^aBased on the control population

^bVariance for each SNP divided by the total polygenic variance for ages 60-79 ( ${\sigma }_{p60-79}^2=2.15$)

^cOdds ratios are from the joint analysis of rs17021918 and rs12500426

^dOdds ratios are from the joint analysis of rs2928679 and rs1512268

Based on the combined genotypes at all 26 SNPs, the 10% and 1% of the population at highest risk were 2.0 and 3.5 times respectively more likely to develop prostate cancer compared with the population average (i.e., no SNPs measured). Conversely, the 10% and 1% of the population at lowest risk had RRs of 0.5 and 0.3 respectively compared with the population average.

Risk prediction examples

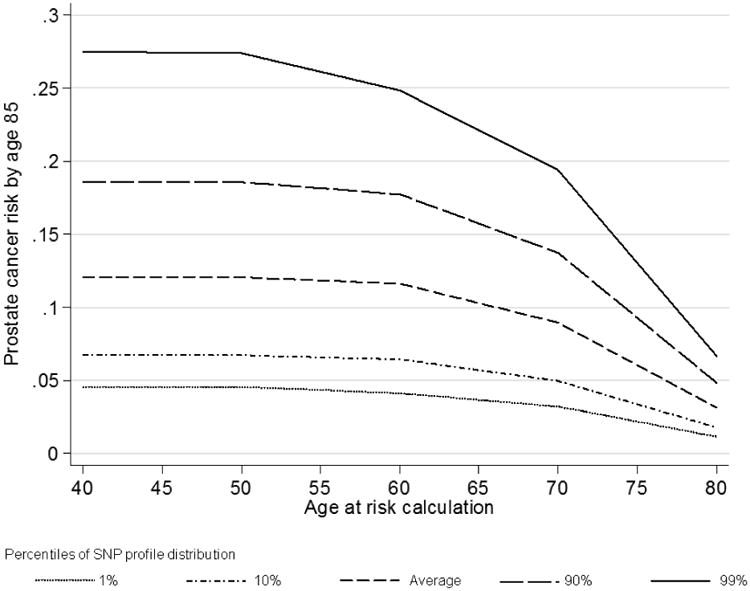
Figure 1 shows the risk of developing prostate cancer by age 85 years by percentile of the SNP profile, for a random individual between 40-80 years old. In the absence of SNP or family history information, based on our model, such an individual would be susceptible to the population prostate cancer incidence. At young ages (40-60 years), the lifetime risk was over 6% higher for those in the top 10^th percentile of the SNP profile compared with the average population. The risk of prostate cancer by age 85 for a 40 year old male who was in the top 10^th percentile of the SNP profile distribution was estimated to be 19%, while for a male in the bottom 10^th percentile it was 7%.

Figure 1. Predicted remaining lifetime risks of prostate cancer for a random individual by current age and percentile of the SNP profile (assuming UK incidences after 1924, all 26 SNPs in Table II typed).

To further illustrate the results of the model and impact of considering jointly SNP profile and family history information, we computed the remaining cumulative lifetime risk (to age 85) of prostate cancer by percentile of the SNP profile, assuming all 26 SNPs are measured under different scenarios (Figure 2). An UK male in the top 10^th percentile of the SNP profile distribution, whose father was diagnosed with prostate cancer at age 70 had a cumulative risk of 33% of developing prostate cancer by age 85, while the equivalent risk for a male in the bottom 10^th percentile was 12%. If we had no SNP information available for this person, then their remaining cumulative lifetime risk would be 22%. The difference in absolute risk between the top and bottom 10^th percentiles of the SNP profile distribution for a 50 year old UK male with a father and brother affected at age 60 was 47%. The magnitude of the difference between SNP risk groups were similar for Australian men (results not shown).

Figure 2.

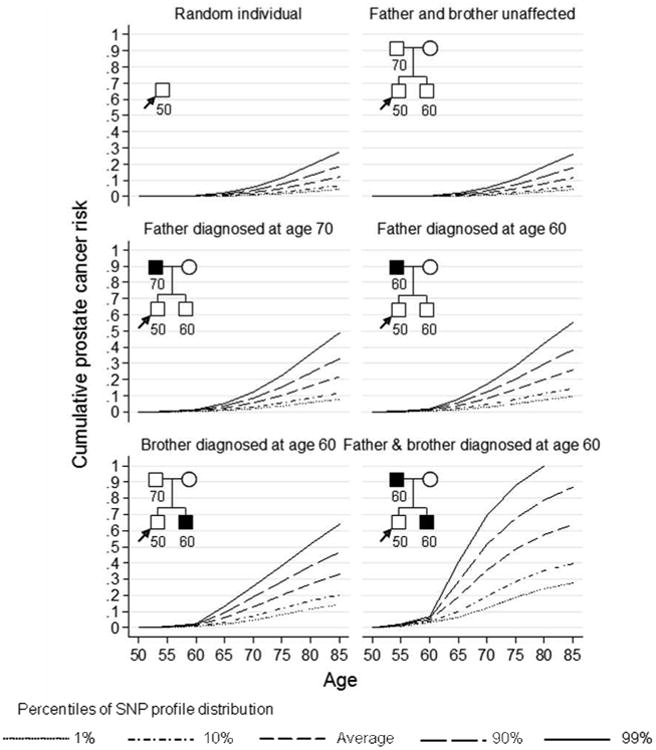
Predicted cumulative risk of prostate cancer for a 50 year old male by percentile of the SNP profile (assuming UK incidences after 1924, all 26 SNPs in Table II typed).

The size of the difference between the percentiles of the SNP profile distribution depended on the percent of polygenic variance explained by the known SNPs, which in turn depended on how many SNPs are measured. As the proportion of polygenic variance explained increased, the absolute difference in risk between the extreme tails of the SNP profile distribution increased (Figure 3). For example, the difference in remaining lifetime risk for a UK male aged 50 with no information on family history of prostate cancer between the top and bottom 10^th percentiles of the SNP profile was only about 3% if the percent polygenic variance explained (for age 60 and older) equaled 1%, whereas the difference increased to 12% if the percent polygenic variance explained equaled 14% (based on the currently known prostate cancer susceptibility SNPs). If 30% of the polygenic variance is explained, then the difference would be 17%.

Figure 3.

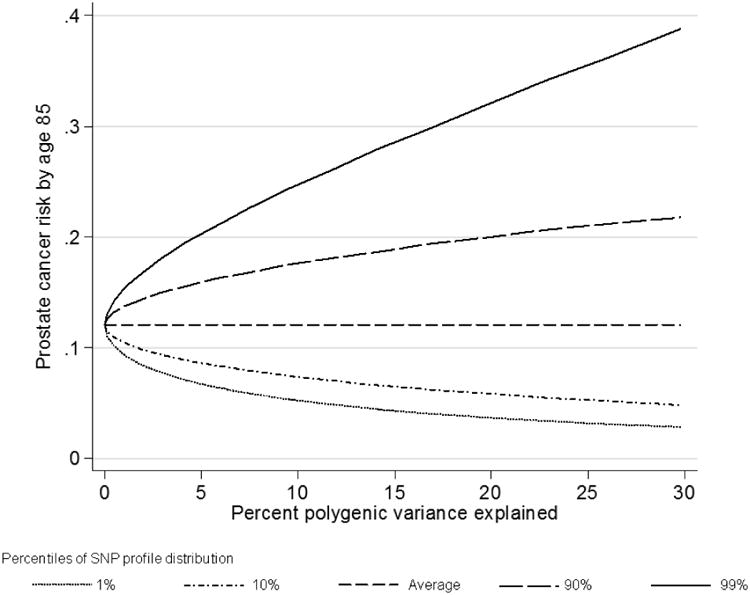
Remaining lifetime risk for a 50 year old random individual by percent polygenic variance (age 60-79) explained and percentile of the SNP profile (assuming UK incidences after 1924).

Discussion

We have developed a risk prediction algorithm for familial prostate cancer which takes into account 26 common variants identified through GWAS. The residual familial clustering of the disease is explained by a mixed model of inheritance that includes an age-dependent polygenic component and a recessive major gene component. The algorithm takes into account explicit family history information on both affected and unaffected relatives and their relationship and can be used on pedigrees of an arbitrary size or structure. To our knowledge, this is the first genetic risk prediction model for prostate cancer that considers the simultaneous effects of the known susceptibility SNPs and residual familial effects. The algorithm can be easily extended to incorporate further polymorphisms as they are identified and confirmed in the literature. Moreover, the approach is quite general and should be straightforward to apply to other cancers with both known and unknown genetic components, such as breast or colorectal cancer, or other diseases with familial component.

The algorithm we have implemented depends on two key assumptions. The first is that the effect of the known genetic variants can be modeled to good approximation by a normal distribution (combining additively with the unknown polygenic component). This will be true provided the known genetic variants interact multiplicatively. Analyses to date for prostate cancer have found little evidence of non-multiplicative interactions. One study found that the combined effect of seven SNPs was close that predicted by a simple multiplicative model, suggesting that this is a reasonable assumption [Kote-Jarai, et al. 2008].

In turn, the total polygenic component in our model is approximated by the HPM [Fernando, et al. 1994; Lange 1997]. This transforms the continuous distribution of risk into a discrete distribution, where the number of loci used in the approximation defines the number of risk categories. Increasing the number of loci in the HPM gives greater precision for risk estimation, particularly in the extremes of the risk distribution. The penalty for increasing the number of loci used in the HPM is an increase in the computation time. The current algorithm assumes that the number of loci is equal to 5, which provides enough precision to discriminate between individuals in the extreme 1% of the SNP profile distribution.

The second assumption is that the known SNP genotypes are assessed on the consultand. This essentially allows the pedigree likelihood to be factorized, conditional on the polygenotype of the proband, and hence for pedigree likelihoods to be computed using the Elston-Stewart algorithm [Lange, et al. 1988]. This is likely to suffice for most practical situations. If more than one individual is genotyped, the same factorization does not apply. In principle it would be possible to consider the segregation of the known and unknown polygenotypes through the pedigree separately (provided that the same SNPs were genotyped for each individual), but currently this appears computationally prohibitive and improvements to the computational algorithms will be required to generalize to this case.

The use of systematic PSA blood tests and digital rectal examinations to predict prostate cancer risk in asymptomatic men is controversial. Currently, there are no official screening programmes for prostate cancer in the UK or Australia and this is unlikely to change unless there is a shift in the evidence or better screening tests become available. Results from large randomized clinical trials are still inconclusive, and it is uncertain whether screening will help reduce mortality from prostate cancer [Andriole, et al. 2009; Schroder, et al. 2009]. Our risk prediction model could potentially be used in conjunction with results from clinical trials to plan future public health policies for PSA screening. For example, the median 10 year risk of prostate cancer at age 65 in the UK population is 3.7%. Assuming that this defines the risk threshold for referring individuals for PSA screening and that all the 26 SNPs can be genotyped, (explaining 14% of the polygenic variance), predictions based on our proposed model suggest that the age for screening could be reduced to 61 for the top 10% and raised to age 77 for the bottom 10% of the SNP profile distribution. If we were to identify more SNPs associated with prostate cancer which explain for example 28% of the polygenic variance, then the age for screening, according to the SNP profile distribution, for the top 10% would be 60 years, while the bottom 25% would be 74 years, and the bottom 10% would never reach a 10 year risk of 3.7%. These age differences will only increase as more SNPs associated with prostate cancer risk are identified. While such an approach would improve the efficiency of a screening program, it could also help reduce mortality from prostate cancer by targeting those at higher risk. It may also potentially help to target those who may warrant more invasive methods of screening such as primary biopsy.

There are several directions that our model can be extended. As more loci are identified, they will be incorporated into the algorithm. It is likely that the number of susceptibility SNPs will increase rapidly over the next few years as results from further large GWAS are reported. In addition, high throughput sequencing technologies may allow rarer susceptibility variants missed by GWAS to be identified [Easton and Eeles 2008]. The current model can be extended straightforwardly to incorporate further variants, providing that their effects can be modeled within polygenic distribution (simply increasing ${\sigma }_K^2$). Rarer variants conferring higher risks may be more problematic; if many such variants need to be incorporated individually into the model, further improvements in computational efficiency will be required. Given the populations where GWAS have been conducted to date were mostly over 60 years, estimates of the SNPs for men less than 60 years would also help improve the model. The model can also be extended to incorporate the effects of the causal variants as these are identified through fine mapping and experimental studies.

The current model does not take into account prostate cancer aggressiveness but none of the confirmed markers identified to date have been clearly shown to be associated with prostate cancer aggressiveness [Easton and Eeles 2008; Witte 2009]. Inclusion of BRCA2 carrier status would also improve predictions; several studies have cindicated that BRCA2 mutations predispose to aggressive prostate cancer [Mitra, et al. 2008; Tryggvadottir, et al. 2007]. It should also be possible to extend the model to incorporate PSA levels as a covariate, although this is complicated by the fact that at least two of the susceptibility loci (MSMB and KLK3) are also associated with PSA levels.

In conclusion, we have derived a general model of prostate cancer susceptibility that has the ability to provide accurate predictions of prostate cancer risk based on the genotypes at all known susceptibility SNPs and family history of the disease. However, it will be important to evaluate the accuracy of the predictions in independent populations, and preferably in prospective studies and to determine the potential benefit of use of such a model in prostate cancer screening studies.