Using Transmural Regularization and Dynamic Modeling for Non-Invasive Cardiac Potential Imaging of Endocardial Pacing with Imprecise Thoracic Geometry

Abstract

Cardiac electrical imaging from body surface potential measurements is increasingly being seen as a technology with the potential for use in the clinic, for example for pre-procedure planning or during-treatment guidance for ventricular arrhythmia ablation procedures. However several important impediments to widespread adoption of this technology remain to be effectively overcome. Here we address two of these impediments: the difficulty of reconstructing electric potentials on the inner (endocardial) as well as outer (epicardial) surfaces of the ventricles, and the need for full anatomical imaging of the subject’s thorax to build an accurate subject-specific geometry. We introduce two new features in our reconstruction algorithm: a non-linear low-order dynamic parameterization derived from the measured body surface signals, and a technique to jointly regularize both surfaces. With these methodological innovations in combination, it is possible to reconstruct endocardial activation from clinically acquired measurements with an imprecise thorax geometry. In particular we test the method using body surface potentials acquired from three subjects during clinical procedures where the subjects’ hearts were paced on their endocardia using a catheter device. Our geometric models were constructed using a set of CT scans limited in axial extent to the immediate region near the heart. The catheter system provides a reference location to which we compare our results. We compare our estimates of pacing site localization, in terms of both accuracy and stability, to those reported in a recent clinical publication [1], where a full set of CT scans were available and only epicardial potentials were reconstructed.

I. Introduction

There is a growing interest in both research and industry in cardiac electrical imaging, that is, in technology and algorithms to reconstruct cardiac electrical activity based on remote potential measurements. One focus of significant clinical attention is the pre-procedure planning and real-time guidance of ablation procedures to treat atrial or ventricular arrhythmias. One limitation of most current techniques for imaging heart surface electrical potentials, including current commercial devices [2]–[4], is that they exclusively image the inner or the outer surface of the chamber(s), whichever is nearer to the probe. This implies a clinical dilemma: while body surface measurements are preferable for planning and may have clinical advantages during procedures, compared to catheter-based measurements, imaging activity on the inner surface, or endocardium, is arguably more important from a clinical standpoint than imaging the outer surface, the epicardium. To emphasize the importance of this problem, in a recent study it was proposed to use non-invasive images of cardiac motion as the input to a machine learning algorithm to reconstruct both endocardial and epicardial electrical activation times from patient-specific electromechanical models [5], [6]. Thus techniques to reconstruct the endocardial potential distribution from electrical body surface measurements, which in principle are more directly connected to the electrical activity to be estimated than mechanical measurements, could be of considerable clinical interest.

A second potential impediment to clinical adoption of cardiac electrical imaging is the typical use of full anatomical imaging of the thorax to build an accurate model of the subject’s thoracic geometry. From a technical point of view, X-ray computed tomographic (CT) imaging is the method of choice, as employed for example in the only current commercial system for imaging from body surface potentials [4], but has obvious drawbacks in terms of radiation exposure, in addition to time and cost. Magnetic resonance imaging (MRI) is another modality to acquire full torso geometry that does not involve ionizing radiation. However, it is still relatively time consuming and it also cannot be used on a significant number of patients with implantable devices which are not MRI compatible. Thus techniques which could achieve sufficient potential reconstruction accuracy with a reduced set of CT images would be helpful. In addition, the use of other imaging methods that produce limited views of the relevant anatomy, such as cardiac ultrasound, might also be enabled by this development.

In this work we present results of potential reconstructions from body surface measurements acquired during clinical procedures which address both of these limitations: we jointly reconstruct the electrical potentials on both endocardial and epicardial surfaces, while using CT sections limited to the immediate region of the heart, which is common clinical practice. We introduce two new features into our reconstruction algorithm: non-linear low-order dynamic parameterization of the potential time series, and joint regularization of both surfaces. Our results depend on both modifications. We report on the method’s performance on clinical body surface recordings from 3 volunteer subjects, consisting of a total set of 2135 endocardially paced beats, distributed over 75 pacing sites on both the right and left ventricles (RV and LV respectively). For each subject, we use a model constructed from CT slices from that subject, covering between 12 and 17.7 centimeters along the cranial-caudal axis centered on the heart, augmented by a coarse morphing of a single standardized anatomical model. We compare our potential reconstructions to measurements of the pacing locations made using a widely-adopted catheter-based clinical system, which we take as ground truth. In our work, we note that paced beats are used here primarily as a surrogate for endogenous ectopic beats, allowing us to validate our reconstructions. Although our results are not yet sufficiently accurate for clinical use, we believe that these are the first results showing that endocardial potentials can be reconstructed from clinical body surface measurements and a limited-slice model. There are many avenues for further technical improvement, some of which we describe in Sec. V.

While our extension of surface regularization to operate transmurally is conceptually fairly straightforward, our use of dynamic model parameterization may require some further context in terms of other approaches towards using temporal constraints for cardiac electrical imaging. One long-standing approach adopts a very strong non-linear temporal model based on a priori restriction of transmembrane potential waveforms to a smoothed step function of known height, so that the only remaining unknown is the wavefront arrival – or activation – time at each node on the heart surface model [7]. This approach is generically known as activation-time imaging [8], [9]. It has several advantages, including the ability to reconstruct activity on both endocardium and epicardium and some degree of robustness to limited imaging and to a limited number of body surface measurement locations. However its a priori restriction does not accurately describe the full temporal behavior of the heart surface potentials and can be especially problematic in the case of conditions such as prior infarctions or ischemia. The other popular approach to dynamic modeling is to use some sort of spatio-temporal regularization. Among several methods presented in the literature [10]–[12], perhaps the most popular method in the community has been the linear subspace “isotropy method” of Huiskamp and Greensite [13]. The isotropy method uses the eigenstructure of the sample temporal correlation estimate of the body surface measurements as a temporal pre-whitener before reconstruction (and thus can be described as a data-driven approach, in contrast to the a priori design of activation imaging). The approach we propose here uses a data-driven non-linear dynamic parameterization which we believe offers a more direct, flexible, and stable representation of the temporal dynamics than the isotropy approach.

Other efforts to reconstruct both epicardial and endocardial potentials from body surface measurements have been reported in the context of so-called “3D” source models, which model the sources in the myocardial wall as well as those on the cardiac surfaces [14]–[19]. An advantage of these models over surface-only models is that they are more directly constrained to have connections between the endocardial and epicardial surfaces, because of the ability to impose smoothness of the solution through the myocardium. One approach also imposes dynamic constraints, through the use of a reduced-parameter propagation model [17]–[19]. However these methods, while very promising, have not reached the same level of maturity and acceptance as surface-based models and require significantly more imaging and computational machinery than the methods reported here. Reports on the application of cardiac electrical imaging in the clinical setting have primarily focused on reconstruction of epicardial potentials (recent examples include [1] and [20]). One notable exception by Nielsen et al., on the identification of transmural ischemic regions, is concerned with estimating sources during the ST segment, when the waveforms are relatively static in time [21]. The present study also differs from the work cited above because full anatomical imaging was unavailable for our experiments. In particular we report that our method achieves generally comparable pacing site localization accuracy and stability on the endocardium to that reported for epicardial reconstruction in [1], which we take as a representation of the state of the art in terms of academic evaluation of the clinical status of cardiac electrical imaging.

In Sec. II, we provide a brief review of the forward and inverse problems of electrocardiography as they pertain to the present work, and then explain the methods used in our proposed estimation procedure in Sec. III. Experiments using this estimation procedure and an overview of the results are presented in Sec. IV. In the Discussion, Sec. V, we provide more detailed analysis of our results and connections to the proposed approach.

II. Background: Forward and Inverse Problems

We use a standard approach to modeling the relationship between the potentials on a surface which encloses the actual cardiac sources and potentials measured on the body surface. In particular, our heart surface model, rather than the more standard “capped” epicardial surface, is a union of the endocardium and epicardium, joined mathematically by a connecting surface at the base, mimicking the electrically insulating boundary which separates the ventricular myocardium from the atria [8], [9], [22]. Using standard assumptions of linearity and quasi-statics, and a standard Boundary Element Method (BEM) discretized numerical solution to Laplace’s Equation (the governing PDE), we arrive at a linear algebraic relationship between the electric potentials of a finite number of equivalent sources on the cardiac surfaces and the potentials at point measurement locations on the body surface at any time t:

$$y(t)=Ax(t),$$ (1)

where x(t) and y(t) are vectors whose elements are the cardiac source potentials and body surface measurement potentials, respectively, at sets of discrete nodes on each surface at time t, and the matrix A is the so-called “forward matrix,” resulting from the BEM solution. Note that here we use x(t) and y(t) to denote time-dependence of the signals, but in line with the usual assumptions, time-dependence of A is ignored. Thus for a finite number of sample times, t = t₁, … , t_T, we may equivalently express equation (1) as:

$$Y=[y(t_1)\dots y(t_T)]X=[x(t_1)\dots x(t_T)]$$

$$Y=AX$$ (2)

where columns of X and Y are x(t) and y(t), respectively, at the sample times. In practice, we always assume that equation (2) is perturbed by unknown measurement noise, N, such that Y = AX + N.

In the associated inverse problem, the goal is to estimate X given Y and A. It is well-known that this problem is ill-posed [23], and thus the matrix A is ill-conditioned with a smoothly decaying singular spectrum. Consequently, estimates of X are highly sensitive to both noise in the measured Y and errors in the forward model A. The standard approach to reducing this sensitivity is Tikhonov regularization, which solves for the columns of X separately. That is, for each i = 1, … , T, one solves:

$$\underset{x(t_i)}{\text{min}}{\Vert y(t_i)-Ax(t_i)\Vert }_2^2+{\lambda }_i{\Vert Rx(t_i)\Vert }_2^2$$ (3)

given a regularization matrix, R, and regularization parameter, λ_i ≥ 0. The regularization parameter controls a trade-off between fitting the data and minimizing the regularization term, and may be different for each i = 1, … , T. In practice, this parameter is usually chosen based on a heuristic criterion for the “best” trade-off (e.g. by the L-curve method) [24].

III. Methods

First we describe the two technical advances we are introducing here that underpin our inverse solution method – transmural derivative regularization and low-order dynamic approximation. Based on that description we then formulate our solution method for the inverse problem, followed by an explanation of a procedure to localize earliest activation sites in our surface potential reconstructions.

A. Transmural Gradient Regularization

Our group has previously described a method to estimate derivatives of functions defined on discretized manifold surfaces embedded in ℝ³ [25]. We have extended this method here to estimate derivatives transmurally across cardiac ventricular surfaces. We explain below the features of this approach most relevant to our inverse solution method, and we refer the reader to Appendix A for details on the derivative estimation. The method simultaneously estimates the gradient and Hessian of a scalar function given point measurements of function values. The basic assumption is that a locally quadratic surface fit to the function is a suitable approximation. We can estimate the coefficients of each local fit and differentiate. To some degree the approach can be seen as an extension of the Laplacian estimation methods presented in [26], [27]. Our procedure relies on a definition of local neighborhoods, which we define to include nearby points from both the endocardial and epicardial ventricular surfaces by using appropriate weighting functions. We solve for the coefficients of each local quadratic model by incorporating the weighting functions into a weighted least squares fit. We only use the gradient vectors for regularization, so we only use the submatrix G, as explained in the Appendix.

B. Low-Order Multichannel Signal Approximation

We recently proposed a method for averaging multi-channel electrocardiographic signals based on grouping spatially-similar patterns and imposing a low-order piecewise cubic model of the signals in the time domain [28]. The underlying intuition conceptualizes the multichannel time series corresponding to a single beat as a trajectory, or curve, in a high dimensional vector space. Here, we apply this approach to find a low-order parameterized approximation of an individual beat rather than to averaging multiple beats. The result is a fit of the entire set of multielectrode torso measurements over a single heartbeat by a multivariate piecewise cubic spline curve parameterized by a relatively small number of knot points, occurring at irregular temporal intervals. We will then use this parameterization in the inverse solution to provide a low-dimensional temporal model for the reconstructions. The reason for the irregular intervals is that, despite the fact that the final result of the procedure is a temporal spline model, the locations of the knot points are found by a non-linear fitting procedure which initially ignores the sample times of the data, rather fitting their locations in the high dimensional space, and then solving for their timings afterwards. We also emphasize that this space is not the physical location of the electrodes on the body surface, but rather an abstract signal space whose dimension is the number of electrodes. The number of knot points is an input parameter to that procedure, and controls the order of the model. Details are described in Appendix B.

The spline curve is defined in terms of a pseudo-time parameter, which represents position along the curve. This curve position parameter is effectively a warping of time, and the fitting procedure returns a map from this pseudo-time to actual time that we can use to “un-warp” the approximation. To fully determine the curve, the fitting procedure also returns the derivatives of the curve at its endpoints, so that a fit with κ knots has in effect κ+2 free parameters. The choice of a value for κ trades off between data fidelity and solution stability. Here we consistently used 12 knot points (i.e. κ = 12). We verified that our results were robust to the choice of this parameter. It will be important in the sequel to note that through this procedure we obtain a linear representation of the approximated signal in terms of the spline coefficients.

C. Transmurally Regularized Reconstruction of Low-Order Approximation of Heart Surface Potentials

In this subsection we describe how we use the spline-based approximation of the body surface potentials to provide temporal regularization for the estimated heart surface potentials. To start, we note that we can write the spline approximation to the body surface potentials as a factorized approximation of the body surface potential matrix Y (Eq. 2). Specifically, we let K_Y be a matrix that contains the coefficients of the knot points and endpoint derivatives obtained by our fitting procedure, and let P = P₁P₂ be a matrix that combines two operations: spline interpolation in the pseudo-time parameter (P₁), and then mapping the pseudo-time parameter to actual time (P₂). Then the matrix Y can be approximated by:

$$Y\approx K_{Y}P=K_Y{P}_1{P}_2.$$ (4)

For a curve with κ knot points, K_Y will have one row for each body surface measurement and κ + 2 columns. Correspondingly P₁ will have κ + 2 rows and one column for each sample of the warped time parameter; typically we will interpolate to a much higher sampling rate in pseudo-time than was used to sample the actual measurements. Indeed, in practice we always interpolate at a high enough rate that the “un-warping” performed by P₂ simply reduces to choosing columns of K_YP₁ to keep. Therefore P₂ will have one column for each original time sample; each column will contain one 1, and the rest of its elements set to 0. Thus K_Y maps the set of body surface waveforms, as temporal signals, to the spline coefficients, and P maps the spline coefficients to time.

We then assume that the same time-warping and knot locations, with different coefficients, will provide a reasonable approximation to the unknown heart surface potentials. Similar to the assumption behind the isotropy method [13], [29], we rely on the idea that, since the forward problem is quasi-static, the torso volume conductor filters in space but not in time, and thus that our parameterization of the body surface potentials will give us a reasonable basis to approximate the heart surface potentials as well. Therefore we factor the matrix of unknown heart surface potentials X in an analogous way, using the same time-warping, encoded in the matrix P. Then the inverse problem reduces to solving for the corresponding coefficient matrix K_X: X ≈ K_XP.

Combining these categorizations with the forward relationship in (2) we obtain:

$$Y\approx K_{Y}P=A{K}_{X}P$$ (5)

$$K_Y=A{K}_X.$$ (6)

To summarize: given K_Y, P, and A, the inverse problem is to estimate K_X To do this, we apply Tikhonov regularization to solving (6), estimating each column of K_X separately, each with its own regularization parameter, λ_i, chosen using its own L-curve [24]. We use the gradient vector approximation matrix G from Sec. III-A as the regularization matrix R. Since κ + 2 << T (for example, we used κ = 12 and T is on the order of 300), many fewer regularization parameters need to be estimated than with a straightforward application of Tikhonov regularization. Finally, collecting all the estimated columns of K_X, we use our interpolation scheme to obtain an estimate of the heart surface potentials, X = K_XP.

D. Pacing Site Localization

In order to evaluate our results, we wanted to compare the estimated heart surface potentials to the catheter-based localization of the pacing sites obtained from the CARTO XP system (Biosense Webster, Diamond Bar, California). To do so requires a method to estimate the location of the earliest activation from the reconstructed potentials. Due to noise in the reconstructed potentials, a simple search or interpolation based only on the reconstructed waveforms did not return earliest activation locations which matched well with visual inspection of isochrone maps (images of contour lines of constant activation times) calculated from the reconstructions. Therefore we carried out a post-reconstruction smoothing step on the estimated activation times before searching for earliest activation. Specifically, given our estimated heart surface potentials, we first obtained a naive estimate of the activation time at each node as the time sample with the most negative derivative (estimated numerically) [30], [31], collected into a vector τ. We then extracted the dominant propagation pattern from the resulting activation time estimates by smoothing their spatial distribution as follows: given a vector of activation times, τ, and a surface Laplacian approximation matrix, L, [25] (note this is different from the transmural gradient estimator described in Sec. III-A), we solved the following problem:

$$\underset{{\tau }_D}{\text{min}}{\Vert \tau -{\tau }_D\Vert }_2^2+\gamma {\Vert L{\tau }_D\Vert }_2^2.$$

The parameter γ controls the smoothness of the resulting propagation pattern. When γ is small, τ_D ≈ τ, and as γ grows, τ_D → 0. We chose γ automatically in an a posteriori fashion. We computed both terms in the minimization over a wide range of values of γ and plotted them against each other in a parametric manner. Our experience is that for γ above a certain value γ_c, ||Lτ_D||₂ rapidly tended to zero while ||τ − τ_D ||₂ changed very little. The largest value of γ less than that corner value γ_c typically corresponded to a good tradeoff point. In our algorithm we find that value automatically in a manner similar to an L-curve corner-picking routine [24]. The node on the heart surface corresponding to the minimum element of τ_D is the estimated pacing site. We examined both the location of the minimizing node across all nodes on both the endocardium or epicardium, and also the minimizing node with the search constrained to the endocardium.

IV. Experiments

We evaluated this method using data recorded from three subjects (2 males and 1 female) during clinical procedures in the electrophysiology laboratory. The subjects were patients that were admitted for routine ablation procedures to suppress paroxysmal fibrillation in the atria. The patients were consented for an add-on experimental procedure involving ventricular pacing, performed according to a protocol approved by the ethical committee of Charles University Hospital, Prague, Czech Republic. The patients had no known ventricular abnormalities. Beats were endocardially paced using the tip of an ablation catheter (Biosense Webster, Diamond Bar, California), with a sequence of 18–34 consecutive beats initiated from each pacing site, at a rate of approximately 100 beats per minute. Subjects’ respiration was not controlled and atrial electrical activity was not controlled for. Pacing-induced potentials were measured with a 2 kHz sampling rate from 120 electrodes on the body surface of the subject. Data were collected while stimulating 2135 heartbeats at 75 pacing sites in total. The numbers of beats from each pacing site in subjects 1, 2, and 3 can be seen in Tables I, II, and III, respectively, as well as in which ventricle each pacing site was located. The location of the catheter tip was tracked using the CARTO XP electroanatomical mapping system (Biosense Webster, Diamond Bar, California). The CARTO pacing locations were mapped manually to their corresponding heart surface model by the fourth author, an expert electrophysiologist physician, before carrying out the inverse solution, thus providing the “ground truth” localization comparison (referred to in the sequel as “CARTO points”) for our inverse procedure.

TABLE I.

Subject 1: Means and Standard Deviations of Localization Errors Per Pacing Site

Pacing Site		Endocardium & Epicardium		Constrained to Endocardium
LV	#of Beats	Mean (in mm)	Std Dev (in mm)	Mean (in mm)	Std Dev (in mm)
1	33	21	9	29	3
2	33	22	0	3	5
3	28	42	6	39	6
4	33	54	5	38	8
5	29	43	10	54	6
6	34	65	9	31	9
7	33	47	13	29	6
8	21	51	13	29	6
9	20	22	9	19	9
10	28	39	4	53	6
11	33	31	9	46	8
12	31	35	7	39	6
13	24	30	5	24	1
14	26	30	11	29	10
15	21	33	14	26	12
16	18	61	5	49	4
17	22	32	11	44	18
RV
1	28	46	0	34	11
2	24	53	15	42	10
3	25	51	0	45	0
4	25	54	15	51	12
5	25	36	5	31	9

TABLE II.

Subject 2: Means and Standard Deviations of Localization Errors Per Pacing Site

Pacing Site		Endocardium & Epicardium		Constrained to Endocardium
LV	#of Beats	Mean (in mm)	Std Dev (in mm)	Mean (in mm)	Std Dev (in mm)
1	43	24	1	40	1
2	18	24	2	30	2
3	38	50	5	41	7
4	41	24	0	26	1
5	35	34	13	34	4
6	35	40	22	51	20
7	27	34	7	22	3
8	14	24	0	24	0
9	29	40	13	38	11
10	32	26	17	13	14
11	33	33	14	17	7
12	37	35	8	37	10
13	30	32	2	30	10
14	21	54	6	47	11
15	28	40	9	42	13
16	35	46	9	46	7
17	33	32	12	23	11
18	32	39	9	24	10
19	35	35	17	49	20
20	24	33	1	38	15
21	34	25	4	21	4
RV
1	17	40	14	39	15
2	12	25	6	24	7
3	30	46	12	50	14
5	35	52	16	40	24
6	34	48	6	51	12
7	34	37	12	33	10
8	31	54	17	48	19
9	7	37	1	32	0
10	33	36	13	47	14
11	13	39	8	43	10
12	27	36	16	24	12
13	17	42	3	40	3

TABLE III.

Subject 3: Means and Standard Deviations of Localization Errors Per Pacing Site

Pacing Site		Endocardium & Epicardium		Constrained to Endocardium
LV	#of Beats	Mean (in mm)	Std Dev (in mm)	Mean (in mm)	Std Dev (in mm)
1	33	38	3	32	4
2	35	40	0	35	0
3	15	24	13	18	10
4	32	38	0	32	0
5	34	38	1	34	5
6	35	55	17	54	18
7	23	35	6	24	9
8	35	28	4	32	1
9	38	29	6	22	4
10	38	33	11	39	4
11	11	20	12	21	24
12	34	39	9	33	9
13	15	16	4	22	12
14	22	31	16	30	11
RV
1	34	66	4	65	5
2	35	34	3	31	3
3	39	38	4	31	6
4	12	46	2	46	7
5	17	35	6	30	2
6	22	39	13	31	10

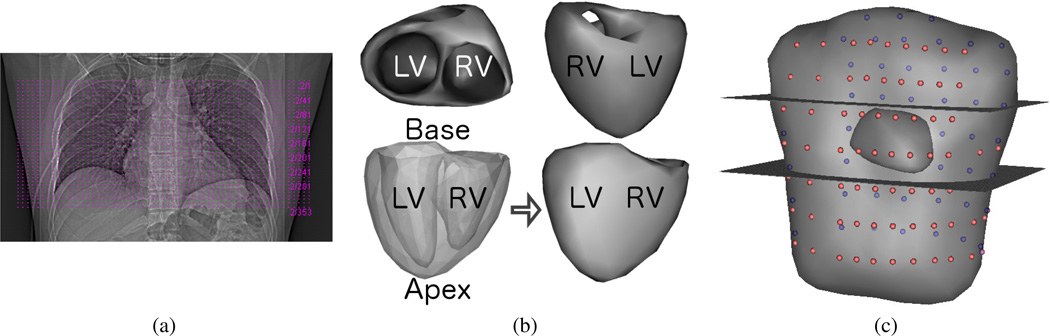
X-ray CT imaging of the torso was restricted to a limited number of slices. Subject 1 had 353 slices covering 17.7 centimeters along the cranial-caudal axis centered on the heart. Subjects 2 and 3 had 329 slices covering 16.5 centimeters, and 120 slices covering 12 centimeters, respectively. Fig. 1 (a) shows the axial CT slice locations for subject 1, marked by dashed horizontal lines, on an anteroposterior X-ray projection of the supine patient’s chest. Surface meshes of the ventricles of these subjects were obtained by manually segmenting these images, extracting an initial surface mesh, and performing mesh decimation and refinement. First a regular lattice mesh of the ventricular volume was constructed from the segmented CT images. Then an initial surface mesh was extracted as an isosurface using the volume mesh and labels obtained from segmentation. Mesh decimation and refinement were performed using the Matlab function “reducepatch” (Mathworks, Natick, Massachusetts) and SCIRun module “FairMesh” [32], respectively, and applied iteratively in succession until a suitably smooth mesh was obtained (usually 2–3 total iterations). Using this procedure we obtained 350 node surface meshes of the ventricles for each of the three subjects, with 123, 181, and 177 of those nodes on the epicardial surfaces of subjects 1, 2, and 3, respectively, and the rest on the endocardial surfaces. Visualizations of the resulting surface mesh for this subject, shown from different views with key anatomical labels, are shown in Fig. 1 (b). The 352 node torso mesh, along with electrode locations, was obtained by manually rotating, scaling, and translating the standardized Dalhousie torso surface mesh and electrodes to fit the torso surface as seen in the limited set of CT images available [33]. This procedure was performed separately for each of the three subjects in this study, resulting in a closely fit heart surface and a roughly approximated torso geometry for each. The electrode locations were assumed to be placed at a standard set of locations on this surface mesh, and thus their locations were also approximately determined using this procedure. Again using subject 1 as an example, a visualization of the limits of the X-ray CT imaging relative to the transformed standardized torso, along with the assumed locations of the measurement electrodes (pink and purple spheres on the near and far surfaces, respectively), is shown in Fig. 1 (c).

Fig. 1.

X-ray CT Slices and Anatomical Geometric Models of Subject 1: (a) Anteroposterior X-ray projection in supine position with axial CT slice locations, spanning 17.7 cm in the axial direction, marked by dashed horizontal lines (b) Model of ventricular surfaces, shown from different views used in Figs. 2 & 3, with the left and right ventricles labeled LV and RV respectively to indicate the orientation of the ventricles in each view. The lower two views are the same, but transparency was used in the lower left view to show the epicardial and endocardial surfaces together. The base and apex of the ventricles are also labeled in this view. (c) Generic torso model with patient-specific model of ventricles. Cutting planes are illustrative of the upper and lower axial limits of the available X-ray CT images of the patient’s anatomy. Colored spheres on the generic torso surface (pink in front, purple in back) mark the model locations of measurement electrodes.

The potential reconstruction method as described was applied to the QRS complex of each beat separately and the pacing site estimate was obtained from the reconstructions using the procedure described in Sec. III-D. Specifically, we took the start of QRS to be immediately following (but not including) the time of the pacing stimulus, and the end of QRS was manually delineated by the fourth author.

First, to characterize the accuracy of the fit to the torso measurements obtained by the low-order spline model, we took the maximum over time and over all electrodes of the absolute value of the difference between the measured data and our approximation for all of the 594 beats measured from subject 1, and then computed the mean and standard deviation of this metric over all beats paced from each of the ventricles. The maximum absolute error was 0.069 ±0.021 millivolts in the LV and 0.074±0.021 millivolts in the RV. For comparison, the maximum absolute value of the same measured signals was 2.008±0.519 millivolts in the LV and 2.538±0.855 millivolts in the RV.

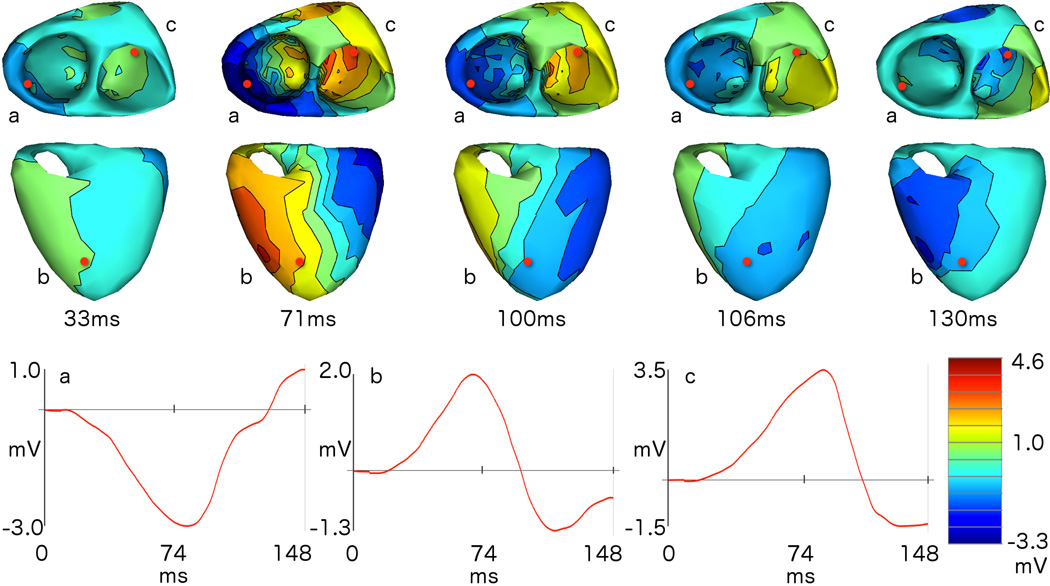
Turning now to the inverse solutions, an example of a reconstructed sequence of heart surface potentials is reported in Fig. 2, which shows selected temporal snapshots of reconstructed isopotential maps (that is, interpolated equipotential contours at a given time sample) for the LV pacing site belonging to subject 1 labeled as LV 1 in our dataset. We show two different views of the heart to illustrate the behavior of the reconstructed potentials on both the epicardial and endocardial surfaces. The three red dots visible on the heart surfaces, labeled a, b, and c, correspond to the respectively labeled reconstructed waveforms at the bottom of the figure. The red dot labeled “a” is placed at the location of the mesh node nearest to the CARTO point. The respective timing is indicated below each isopotential map and can be referenced to the axis markings on the time waveforms.

Fig. 2.

Reconstructed time-varying potentials: snapshots from the sequence of reconstructed potentials for a beat paced from location “LV1” in subject 1, shown as isopotential maps (interpolated equipotential contours) from two different views of the endocardial (first row) and epicardial (second row) surfaces. The time for each snapshot, in ms relative to the stimulus, is reported below each pair of views, and the colormap is scaled globally across snapshots and views. The letters a, b, and c are used to label the nearest heart surface mesh node, marked in red, whose reconstructed potentials over time are shown in the similarly labeled plots below the isopotential maps. Source “a” is the node nearest to the pacing location on the heart surface, and thus the propagation of electrical excitation is expected to originate from near this point.

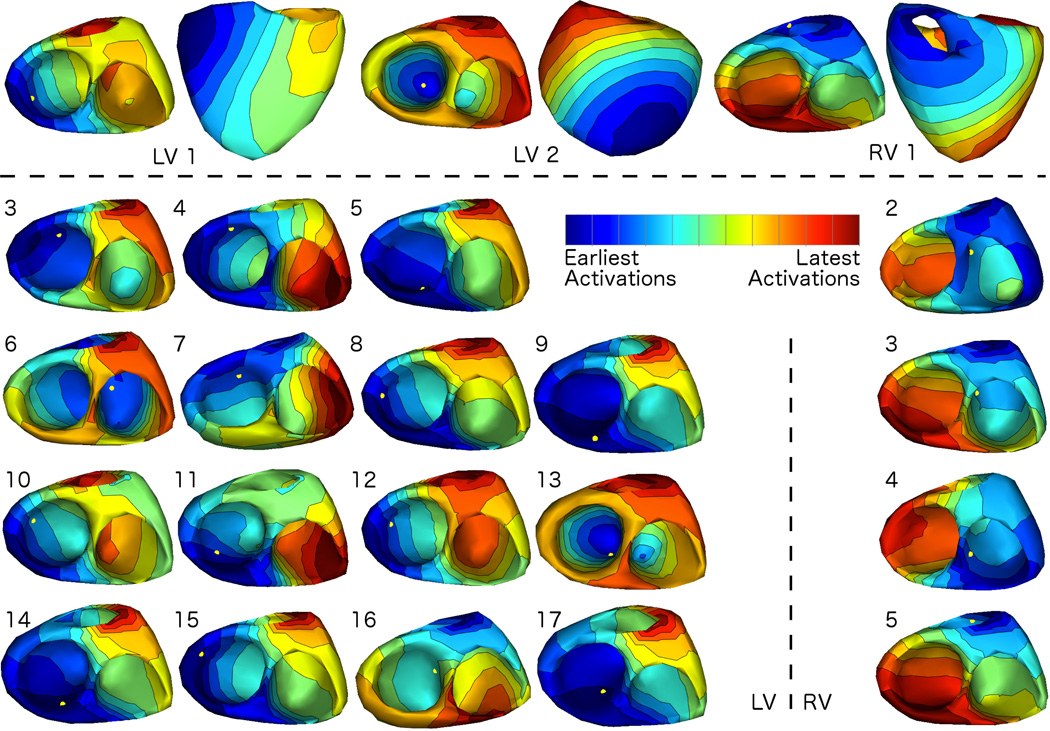
In Fig. 3, we present summary results from one beat each from all 22 pacing sites from subject 1. Specifically, we show activation isochrone maps (i.e. interpolated contours of constant activation time), as computed during the pacing site localization procedure. We normalized the maps so that the entire propagation across all beats is shown using individually scaled color maps, to aid in visual comparison across sites, which have significantly different QRS durations. We show two views of the heart for three sites only, LV1, LV2, and RV1, at the top of the figure, and then show only the endocardial surfaces for the rest. The remaining 15 LV locations are shown on the left and the remaining 4 RV locations in the right column. On each map, we have marked the location of the CARTO point for that pacing site with a yellow dot.

Fig. 3.

Activation Patterns of Reconstructed Potentials for Subject 1: Isochrone maps of activation times (interpolated contours of constant activation time), calculated as described from the potential reconstructions, show the pattern of propagating electrical excitation recovered from reconstructed potentials. Results from one beat per pacing location are shown here. For visualization purposes, maps were normalized to have the same duration; thus the earliest activation time is blue and the latest activation time is red in each map. As a reference, the pacing location reported by the electroanatomical mapping system is marked by a yellow dot in each visualization.

We summarize the accuracy of the localization experiments for each of the three subjects in Tables I–III. As described above, we estimated pacing sites in two different ways: unconstrained (i.e. allowing the site to be on either the endocardial or epicardial surface) and constrained, presuming advance knowledge that it must be on the endocardial surface. For both estimates, we quantified pacing site localization error as their Euclidean distance to the measured CARTO point. In Tables I–III, we report the means and standard deviations of the localization errors over all the beats from each pacing site in mm, for both unconstrained and constrained estimates.

In Fig. 4 we present a visual summary of the mean localization results reported in Tables I–III. That is, for each subject, we mark the locations of the CARTO points with spheres on the corresponding mesh of the ventricular surfaces. Using a colormap scaled globally across all cases, we visualize the mean localization errors over all beats paced from each location using color, such that blue represents relatively small errors and red represents large errors. In the same visualizations, we use blue, white, and red coloring of the meshes to show a segmentation of each subject’s ventricles into “left ventricular (LV) free wall”, “septum”, and “right ventricular (RV) free wall” segments. This segmentation was performed manually by placing two cutting planes through each geometry, and then we assigned mesh nodes to the appropriate segments based on their position relative to these planes. Using the same classification approach, we assigned each pacing site to one of these segments, and then reported statistics of the localization results per subject according to this spatial categorization in Table IV.

Fig. 4.

Mean Errors By Pacing Location: visualizations of the pacing site locations and the mean localization errors for all three subjects, which are also reported in Tables I, II, and III. The colors of the mesh show the rough segmentation of each of the hearts into three segments using cutting planes: the left ventricular free wall (blue), septum (white), and right ventricular free wall (red). These are the segments used to group the pacing locations for the statistics reported in Table IV.

TABLE IV.

All Subjects: Means and Standard Deviations of Localization Errors Per Ventricular Segment

Pacing Site		Endocardium & Epicardium		Constrained to Endocardium
Subject 1	#of Beats	Mean (in mm)	Std Dev (in mm)	Mean (in mm)	Std Dev (in mm)
LV Free Wall	351	38	8	35	7
Septum	218	43	9	34	9
RV Free Wall	25	54	15	51	12
Subject 2
LV Free Wall	390	32	14	32	16
Septum	547	41	13	38	15
RV Free Wall	7	37	1	32	0
Subject 3
LV Free Wall	207	35	8	32	9
Septum	368	35	19	32	18
RV Free Wall	22	39	13	31	10

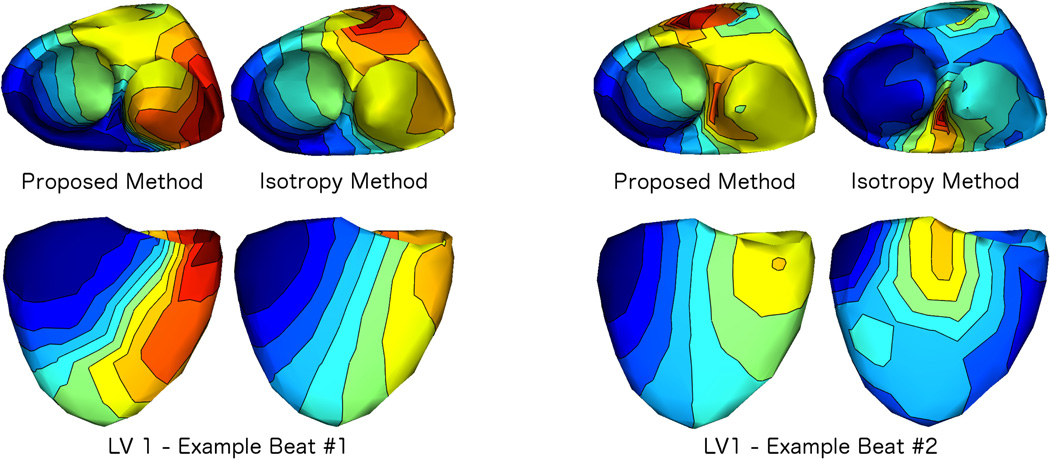
We also compared our proposed method to the isotropy method. To do this, we began applying the isotropy method to the beats from subject 1 using the same transmural gradient regularizer as used in our method . Then activation times were estimated as described in Sec. III-D. We encountered difficulties in applying the isotropy method to many of these beats. The primary difficulty was instability of the solutions to choice of the isotropy method’s truncation parameter (which controls the number of temporal modes to retain after whitening), even across beats paced from the same location. We discuss this experience more in Sec. V, but to illustrate these difficulties, in Fig. 5 we present two examples of the isotropy results compared to those from the spline approximation method. We show isochrone maps from two views (top row: endocardial view, bottom row: epicardial view). As in Fig. 3, the colormaps in Fig. 5 are normalized to the full range of that reconstruction. The examples shown in Fig. 5 are from consecutive beats paced from the same location, LV1, from subject 1.

Fig. 5.

Comparison of the Proposed Method to the Isotropy Method: We applied our proposed method and the isotropy method to all beats from all pacing locations, using the same transmural gradient regularization in both methods. As an example, we show two views (top: endocardial, bottom: epicardial) of isochrone maps of results from each method applied to two consecutive beats paced from the same location (subject 1, LV 1). As in Fig. 3, maps were normalized to have the same duration, thus the earliest activation time is blue and the latest activation time is red in each map (see Fig. 3 for colormap). Example beat #1 is a case where results from the isotropy method and our proposed method were similar. Example beat #2 shows the next subsequent beat from the same pacing site, where the results from the two methods were dissimilar.

V. Discussion

In this work, we presented an approach for reconstructing electric potentials on both surfaces of the ventricular chambers from body surface potential measurements. The approach builds on many recent advances in the field. We have added two technical developments—a low-order approximation of the temporal dynamics, and estimation of the transmural gradients—with which we regularize both the spatial and temporal behaviors of solutions simultaneously. We found that this combined regularization enabled the method to address, to some degree, two obstacles with current methods for heart surface potential reconstruction that could be impediments to more widespread clinical adoption of electrical imaging: the difficulty of full anatomical imaging of every patient’s torso, and the difficulty of reconstructing meaningful endocardial behavior in a potential surface based model of the sources.

We tested the algorithm’s performance on a large collection of endocardially stimulated heartbeats spread across both ventricles of three subjects. For the most part, our results suggest that the reconstructions are able to generally localize the stimulus location. For example, in the sequence of snapshots shown in Fig. 2, depolarization starts from near the point labeled “a”, which is the nearest node to the stimulus point as localized by the CARTO mapping system. An encouraging feature of this reconstruction is that the region of depolarized surface tissue appears to “grow” outward, starting from the initial site of depolarization, in a manner that is consistent with the expected spread of depolarization due to a propagating wavefront of electrical excitation. On the other hand, a shortcoming of this reconstruction is that spatial transition regions – regions that separate depolarized from yet-to-be depolarized regions – are broader than expected and, at some time instants, it is difficult to identify their boundaries. In general the propagation patterns, examples of which are shown as activation isochrone maps in Fig. 3, are largely similar in behavior to the single reconstruction whose selected frames were shown in Fig. 2. The activation patterns are evidence that, for the most part, the method finds earliest activations in a region which contains the CARTO point and then they spread smoothly away from that point in a manner consistent with cardiac propagation. For this subject, the most notable exceptions occurred when the stimulus was on or near the the walls of the septum in both the LV (sites LV16 and LV17) and the RV (RV3 and RV4). Indeed, as we will discuss below, localization of the pacing sites on the septum proved to be challenging in all three subjects.

We also presented quantitative evaluation of these observations in Table I. Similarly, a summary of the quantitative analyses performed for subjects 2 and 3 can be found in Tables II and III. We take, as a measure of localization accuracy, the mean distance between estimated earliest activation location and the manually registered CARTO point. For most of the pacing sites, our estimates were more accurate when we only considered candidate pacing location estimates on the endocardium. However in some cases the mean error was smaller when we allowed epicardial pacing site candidates as well. We note that the fact that we can localize the pacing to a smaller Euclidean distance in these cases suggests that the reconstructed endocardial behavior is not simply an interpolation of epicardial reconstructions. Moreover we note that in most cases tested, the standard deviation of the distance to the earliest activation found, computed over anywhere from as few as 7 to as many as 43 stimuli, ranged from 0 to 24 mm, with the majority 9 mm or less, suggesting the algorithm’s ability to localize activation times is quite robust to noise and other random variability from beat to beat, such as from respiration and atrial electrical activity. This in turn supports the supposition that the reconstructed endocardial activity is truly extracted from the measurements.

The visualization of the mean localization errors in Fig. 4 shows the relationship between localization performance and the spatial locations of pacing sites. This figure shows that not all of the beats paced from septal locations were poorly localized, but also that many of the poorly localized sites were on the septum. We support this observation statistically in Table IV where we have reported the means and standard deviations of the localization errors based on whether the pacing sites were located on the LV free wall, septum, or RV free wall. For example, comparing the mean errors of the LV free wall sites to those of the septum, we can see that the values were typically comparable or greater on the septum as compared to the LV free wall. In the case of subject 3, where the reported means show no differences between LV free wall and septum, the standard deviations of the errors on the septum are still greater than those of the LV free wall. We note here that, unfortunately, the number of pacing sites in the dataset located on the RV free wall (only 1 site per subject) was insufficient to provide a reliable characterization of the algorithm’s performance for this spatial region, but we still report them for completeness. We also note that where the method performs best, it is notably consistent across subjects. For example ,the LV free wall mean error results across the three subjects differ less than the smallest LV free wall standard deviation, and the same is true for results on the septum. Thus our method of constructing an accurate heart model but only a rough torso model seems to be robust across the three subjects tested.

The localization accuracies reported here are comparable with those recently reported by Sapp et al.. In that study epicardial pacing sites were tested. The heart model only contained an epicardial surface, closed across the base of the heart, with no endocardium, and thus the method, in effect, implicitly took into account the prior knowledge that the pacing sites were on the epicardium [1]. The mean localization accuracy was reported for different subsets of the cases, ranging between 13 and 67 mm. Moreover the variability over beats, as measured by the standard deviation of the pacing site localization accuracy, averaged 9 and 11 mm for the least variable subset of cases studied and was considerably larger for the other cases. This suggests that the joint spatial and temporal regularization we introduced in this work both extends the abilities of existing methods to be able to localize endocardial pacing sites, even with the limited range of CT images available, with little loss of accuracy, while maintaining or even improving stability. At the same time, both the mean errors and their standard deviations, especially for the worst cases studied here, do suggest a need for further methodological improvement before adoption for clinical use. This is especially true for inter-ventricular septal locations. Nonetheless we believe that the results are accurate enough to strongly encourage such further development.

We initially tested the use of the transmural gradient and our low-order temporal modeling separately. However we found that neither, by itself, was sufficient to allow reliable reconstruction of endocardial activity. In particular, without the transmural gradient, results suffer from the well-known tendency of standard Tikhonov regularization approaches to localize sources on the epicardium. Such sources are attenuated less before reaching the body surface, and since these methods constrain the amplitude or rate of spatial change of the reconstructions, they typically minimize their combined objective function by lowering regularization cost with superficially biased reconstructions. At the same time, without a temporal model, “wavefront-like” behavior, encoded in the form of temporal waveforms which reflect propagation, is lost to the noise amplification that is inherent in solutions to ill-posed problems. The geometric inaccuracies in our model enhance this tendency to lose temporal coherence. By both encouraging endocardial activity and encouraging realistic waveforms, we were able to push the reconstructions towards accurate localization of endocardial activity.

In principle, temporal stability of reconstructed waveforms has been achieved with other approaches, as noted in the introduction. Among them, our approach is perhaps closest to the isotropy method in the sense that uses a low-order truncation of a basis set which is derived directly from the measured data. We compared the results from our method to those from the isotropy method. Two examples of this comparison are shown in Fig. 5. The isotropy method requires determination of a truncation parameter, in effect analogous to the knot order κ in the spline method. To ensure fair comparisons, in addition to using the same transmural gradient regularizer with both temporal approximations, we tested a range of values for this truncation parameter to obtain the best results. When we were able to obtain stable solutions with this search, as in “Example Beat #1”, the propagation patterns from the isotropy approach were similar to those obtained using our method. However, if we used that same truncation parameter in other cases, even with consecutive beats from the same pacing site, we found that the reconstructions were often inconsistent. As an example we show a case when the same parameter was used on consecutively stimulated beats, Example Beats #1 & #2 in Fig. 5. We found that this inconsistency was quite typical, which made presentation of an extensive comparison difficult, since we are not aware of any established method to objectively choose the truncation parameter in an effective way.

We speculate that the combination of accuracy and stability of our spline approximation function stems at least in part from the fact that its parameters are themselves the values of the function (i.e. knot points exist on the curve they parameterize) or its derivatives, and therefore can be effectively regularized as such. More formally, the isotropy method is derived from an assumption that spatial and temporal behavior of the underlying cardiac propagation are decoupled; specifically that the spatial and temporal correlation of the underlying unknown sources are separable, that is, that the spatial correlation is the same at all time instants except for a scale factor and that the temporal correlation is similarly the same at all spatial locations except for its own set of scale factors. This assumption does not correspond well to highly organized, spatio-temporally coupled phenomena like cardiac propagation [12]. In effect, in our spline method, we assume that the spatial and temporal behavior may be decoupled locally in time, because of the local support of the spline basis functions. The isotropy method is an optimal solution, but only if the separability assumption holds; in practice our results suggest that the spline approximation appears to be better able to reconstruct actual propagation behavior stably, even on the endocardium.

We believe that we will be able to extend the low-order spline approximation to model spatial structure as well temporal structure. In previous work our group reported that we were able to improve wavefront localization in a somewhat similar fashion on the epicardium [34], by using a method which encouraged “wavefront-like” spatial patterns. However the approach described in that work is difficult to extend to more irregular and curved surfaces such as the endocardium. A surface spline method to describe the spatial patterns may help to overcome this limitation. We also plan to further study the effect of geometric model inaccuracy on the solution method presented in this work to identify the limiting factors in required anatomical imaging, as well as to study the robustness of the approach when fewer body surface leads are used. Through these studies, we believe that the potential for clinical adoption of cardiac electrical imaging as an aid to ventricular ablation planning, execution, and cardiac excitation assessment can be made even stronger.

Appendix A

Transmural Derivative Estimation

In this Appendix we describe how we compute the transmural derivative used in our regularization scheme. We assume that both the endocardial and epicardial surfaces are represented by a meshed discretization into piecewise planar segments such as triangles. Let ${\left\{x_i\right\}}_{i=1}^K$ be the collection of nodes on both surfaces, and υ be the potentials at those nodes. Also, for any x_i, let ${\left\{p_i\right\}}_{i=1}^{K_p}\subset {\left\{x_i\right\}}_{i=1}^K$, be the nodes in some definition of x_i’s local neighbors. To estimate the gradient at x_i, denoted Dυ̂(x_i), we can linearly approximate the data at x_i and its local neighbors by a second-order Taylor polynomial:

$$[\upsilon (p_1)-\upsilon (x_i)\dots \upsilon (p_{K_p})-\upsilon (x_i)]=[D\widehat{\upsilon }(x_i)\text{vec}{(D^2\widehat{\upsilon }(x_i))}^T].$$

$$\left[\begin{array}{ccc}\hfill {\tilde{p}}_1\hfill & \hfill \dots \hfill & \hfill {\tilde{p}}_{K_p}\hfill \\ \hfill \frac{1}{2}\text{vec}({\tilde{p}}_1{\tilde{p}}_1^{\mathrm{T}})\hfill & \hfill \dots \hfill & \hfill \frac{1}{2}\text{vec}({\tilde{p}}_{K_p}{\tilde{p}}_{K_p}^{\mathrm{T}})\hfill \end{array}\right]$$

where p̃_r ≡ p_r − x_i, for r = 1, … , K_p. We also define ϕ_i(x) to be a function whose support is confined to the local neighbors of $x_i,{\left\{p_i\right\}}_{i=1}^{K_p}$. We found it useful to use ϕ_i as a “weighting function”, weighting each residual of the equation by ϕ_i(P_r) and solving for Dυ̂(x_i) and D²υ̂(x_i) in the weighted least squares sense. We force D²υ̂(x_i) to be symmetric by consolidating variables when they are identical.

The functions ϕ_i used in this work are identical (i.e. ∀i, ϕ_i = ϕ radially-symmetric inverse exponential functions that are truncated to have finite support around any particular point x₀:

$$g(x)=\text{exp}(-\frac{{\Vert x-x_0\Vert }_2^2}{{\sigma }^2})\varphi (x)=\{\begin{array}{ccc}\hfill g(x)\hfill & \hfill ,\hfill & \hfill g(x)\ge \epsilon \hfill \\ \hfill 0\hfill & \hfill ,\hfill & \hfill g(x)<\epsilon .\hfill \end{array}$$

σ controls the decay of the function’s values for points moving away from x₀, and є is the truncation threshold for the inverse exponential, controlling the edge of the support region. The choices of these parameters that lead to effective transmural local neighborhoods will be specific to a given geometry. In the present work, we chose

$$\sigma =0.05\sum _{i=1}^K\sum _{j=1}^K{\Vert x_i-x_j\Vert }_2^2/K^2,$$

5% percent of the average pairwise distances between nodes, and є = 0.1. We made these choices by visualizing the weighting functions on the heart surfaces and ensuring that their supports at all nodes included nodes from both endocardial and epicardial surfaces, while suitably restricting the size of the “local neighborhood” on each surface to be relatively small. In this case, this choice meant that roughly 10–15 nodes on the same surface as the center of the weighting function were chosen as neighbors, along with 7–13 nodes on the opposite surface.

A key observation is that, given a function υ on a predefined set of nodes ${\left\{x_i\right\}}_{i=1}^K$, the method described solves for D_υ and D²υ at each node using only linear operations. Suppose that we define a vector V є ℝ^K of function values of υ at the nodes ${\left\{x_i\right\}}_{i=1}^K$:

$$V={[\upsilon (x_1)\dots \upsilon (x_K)]}^{\mathrm{T}}$$

and a collection of the consolidated forms of their respective gradients and Hessians:

$${\upsilon }_{\mathrm{g}\mathrm{h}}(x_i)=[D\upsilon (x_i)\text{vec}{(D^2\upsilon (x_i))}^{\mathrm{T}}]V_{\mathrm{g}\mathrm{h}}={[{\upsilon }_{\mathrm{g}\mathrm{h}}(x_1)\dots {\upsilon }_{\mathrm{g}\mathrm{h}}(x_K)]}^{\mathrm{T}}.$$

Then the linearity of the method means that it can be simplified to multiplication by a matrix F:

$$V_{\mathrm{g}\mathrm{h}}=FV$$

We extract the matrix F by applying the gradient and Hessian method at every node for the canonical basis functions ${\left\{e_i\right\}}_{i=1}^K\in {ℝ}^K$. Thus column i of the matrix F is the result of the gradient and Hessian method applied to the vector with element i equal to 1 and zeros elsewhere. Furthermore, one can isolate a matrix for calculation of just the gradient, G, or just the Hessian, H, by keeping only the relevant rows from the matrix F.

Appendix B

Multivariate Curve Approximation

Our conceptual approach to approximation of electrocardiographic signals is to exploit their geometric properties in signal space, modeling them as trajectories on a manifold. Ignoring the rate at which a particular set of signals, corresponding to a single heartbeat, traverses the manifold along this path, we approximate the underlying set which was traversed by the signals. This set, 𝒞, may be described as all the possible points along a curve, c:

$$𝒞=\left\{x\right|\exists \theta \in [0,1]s.t.x=c(\theta )\}.$$

Here θ is the pseudo-time curve parameter and, because the interval over which it is defined is arbitrary, we have chosen [0, 1]. For electrocardiographic data y(t), ∀t ∈ [0, T], our goal is to find a curve c that solves the minimization problem:

$$\underset{c}{\text{minimize}}{\int }_0^T{\Vert y(t)-{\text{proj}}_{𝒞}(y(t),c)\Vert }_2^{2}dt\text{subject to}𝒞=\left\{x\right|\exists \theta \in [0,1]s.t.x=c(\theta )\}$$

where we use proj_𝒞(y(t), c) to denote the projection of y(t) onto the set 𝒞, given a particular choice of the curve c. In words, the goal of this problem is to find the curve that minimizes the integral of all projected distances to it.

In the above form, the problem is too general to be solved because the curve c has infinitely many degrees of freedom and we only have discrete samples of the electrocardiographic signal. Instead, we approximate the problem with a finite dimensional parameterization. We choose a smooth space for the curves c by using piecewise cubic spline interpolation of a pre-determined number, κ, of knot points at unknown locations in the vector space, but occurring at values of θ corresponding to boundaries of regular subintervals of [0, 1]. Thus the knot points are assumed to occur at κ values of θ that satisfy 0 = θ₁ ≤ … ≤ θ_κ = 1. In addition to the knot points, to fully define the spline we need to specify two other conditions. Here we specify the first-order derivatives of the curve with respect to the curve parameter at the first and last knot points c′(θ₁) and c′(θ_κ) – the “complete spline” boundary conditions. We approximate the curve projection operator, proj_𝒞, by interpolating the curve at a predetermined high sampling rate, and projecting onto the resulting discrete set. Also, since we have a finite set of discrete time samples, we modify the minimization problem to be a summation over these discrete sample times instead of an integral over the continuous time interval. We optimize over the knot points, c(θ₁), … , c(θ_κ), and the derivatives, c′(θ₁) and c′(θ_κ). We solve the resulting optimization problem with a custom derivative-free solver based on the Expectation-Maximization algorithm, where the “Expectation” step involves projecting data points to the spline curve, and the “Maximization” step updates the spline parameters. We have verified that other derivative-free solvers, based on the Nelder-Mead algorithm, reach a similar end result. With the resulting minimizing cubic spline curve, ĉ, one can obtain a “filtered” version, ŷ(t), of the original signals, y(t), by using the approximated curve projection, ŷ(t) = proj_𝒞(y(t), ĉ). The projection can also be seen as estimating a pseudo-time curve parameter θ̂_i(t) for every discrete time t, and thus the time warping t → θ.