On Nonstable and Stable Population Momentum

Abstract

This article decomposes total population momentum into two constituent and multiplicative parts: “nonstable” momentum and “stable” momentum. Nonstable momentum depends on deviations between a population’s current age distribution and its implied stable age distribution. Stable momentum is a function of deviations between a population’s implied stable and stationary age distributions. In general, the factorization of total momentum into the product of nonstable and stable momentum is a very good approximation. The factorization is exact, however, when the current age distribution is stable or when observed fertility is already at replacement. We provide numerical illustrations by calculating nonstable, stable, and total momentum for 176 countries, the world, and its major regions. In short, the article brings together disparate strands of the population momentum literature and shows how the various kinds of momentum fit together into a single unifying framework.

Introduction

The concept of population momentum refers to the fact that a population typically does not stop growing (or declining) the instant its fertility reaches replacement. Instead, in a closed population, growth or decline gradually slows until a stationary population is attained, in much the same way that a car gradually comes to a complete stop after a driver’s foot is lifted from the accelerator pedal (Schoen and Kim 1991). The relative amount of momentum is usually measured by the ratio of the size of the long-run stationary population to that of the population when replacement fertility is first achieved. Momentum coefficients for individual countries in 1935 ranged from 1.08 for Austria, Belgium, and France to 1.60 for Puerto Rico and Honduras (Vincent 1945). By 2005, momentum coefficients across all United Nations countries stretched from 0.81 in Bulgaria to 1.76 in Oman (authors’ calculations). In several cases, including Georgia, the Netherlands, and Poland, total momentum was essentially zero. These examples illustrate that population momentum can be positive (coefficient greater than 1) or negative (coefficient less than 1), and that it can play a large or small role in population dynamics (Knodel 1999; Preston and Guillot 1997).

One reason for further study of population momentum is that it contributes importantly to future population growth in developing countries. Bongaarts (1994, 1999) has estimated that momentum accounts for nearly one-half of projected future growth in the developing world over the next century. For the period between 2000 and 2100, momentum is the most important factor in projected future growth for the world and all major regions except Europe and sub-Saharan Africa. For every region in the developing world except sub-Saharan Africa, momentum is a more important contributor to future population growth than all other factors combined (Bongaarts and Bulatao 1999). During the next half-century, momentum is projected to account for 58% of future population growth in the developing world (Bongaarts 2007).

In addition, one should not overlook the contribution of negative momentum to population decline in the developed world. Even with an immediate fertility rebound back to replacement, Europe’s population (ignoring migration) is projected to fall by 7% from current numbers before leveling off. And, in addition to Bulgaria, 11 other countries (all of which, except Japan, are in Europe) are projected to decline by more than 10%owing to negative momentum, even if fertility were to rise instantaneously and permanently to replacement.

The purpose of this article is to convey a deeper understanding of how age composition contributes to long-term population size. We decompose total population momentum into two constituent and multiplicative parts: “nonstable” momentum and “stable” momentum. Nonstable momentum captures deviations between a population’s current age distribution and the stable age distribution implied by current fertility and mortality. Stable momentum reflects deviations between the stable age distribution and the stationary age distribution produced by replacement fertility. In addition, by showing how total, nonstable, and stable momentum fit together into a single theoretical and empirical framework, the article integrates a number of disparate and seemingly unrelated concepts in the population momentum literature.¹

Total, Nonstable, and Stable Momentum

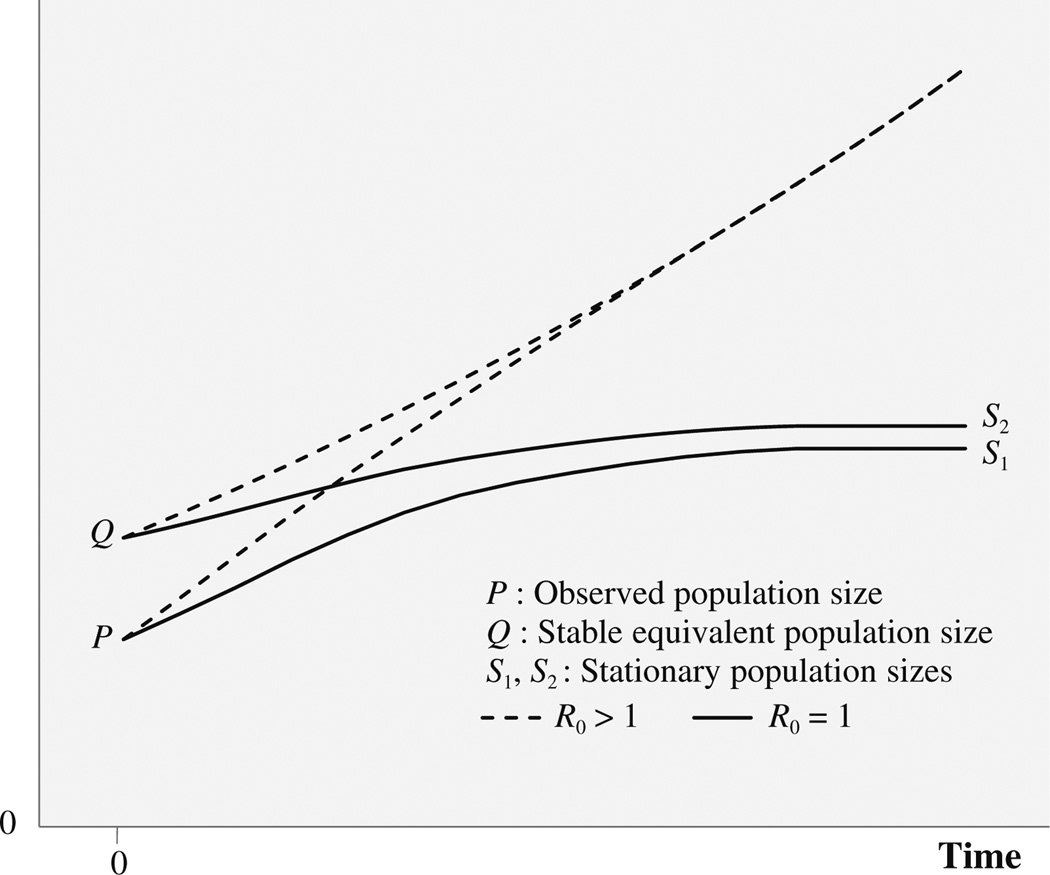
The stylized ingredients of a unified framework are shown in Fig. 1. Let P be the size of an arbitrary initial population—arbitrary with respect to size, age structure, fertility, and mortality. Assume only that the population is closed to migration and consists entirely of females, some women are younger than the oldest age of childbearing, and fertility and mortality are bounded by the range of contemporary human experience. For the sake of illustration, fertility in Fig. 1 is above replacement. Suppose that birth rates are lowered instantaneously to replacement at time t = 0 by dividing the observed fertility schedule by the net reproduction rate (R₀) and that fertility and mortality are then held constant. As shown by the lower solid line, the population eventually converges to a stationary population with size S₁. The ratio S₁ / P is the usual measure of total population momentum.

Fig. 1.

Framework for understanding total, nonstable, and stable population momentum

Suppose instead that the observed population P is projected holding current fertility and mortality constant. It will ultimately converge to a stable population as indicated by the trajectory of the lower dashed line in Fig. 1. Once a stable state has been attained, imagine using the stable growth rate to reverse project the size of the stable population back to t = 0. The reverse projection follows an exponential curve represented by the upper dashed line. The new population is the stable equivalent population. It has size Q, and its age distribution is the stable age distribution implied by the indefinite continuation of current fertility and mortality. It is asymptotically equivalent to the observed population in the sense that if both are projected forward from t = 0 holding current fertility and mortality constant, they will eventually become indistinguishable with respect to population size and age composition. We measure nonstable momentum with the ratio Q / P.

Finally, consider a projection of the stable equivalent population using the same constant replacement-level fertility and mortality used to produce the lower solid line in Fig. 1. The size of the population begins at Q and follows the upper solid curve before leveling off at a stationary population of size S₂. Stable momentum is measured by the ratio S₂ / Q. The stationary populations represented by the endpoints of the two solid lines have the same proportionate age distributions, but they do not necessarily have the same size.

We may write total momentum as the identity

$$\text{Total Momentum}=\frac{S_1}{P}\equiv \frac{Q}{P}\times \frac{S_2}{Q}\times \frac{S_1}{S_2}.$$

In words, total momentum is the product of nonstable momentum, stable momentum, and an offset factor represented by the ratio S₁ / S₂. If, however, S₁ = S₂, then

$$\frac{S_1}{P}=\frac{Q}{P}\times \frac{S_2}{Q},$$ (1)

and we would have accomplished an exact factorization of total population momentum into the product of nonstable and stable momentum. Moreover, under these conditions, the observed population P and its stable equivalent Q are asymptotically equivalent not only with respect to current fertility and mortality but also with respect to replacement fertility and mortality. Our interest will center on the relation between S₁ and S₂ and the conditions under which they might be equal. It is important first to explain how the three types of momentum are related to deviations between pairs of age distributions.

Total Momentum

The concept of the stable equivalent population plays a central and unifying role in our analysis. If an arbitrarily chosen population at t = 0 has size P with fertility schedule m(a) and survival function p(a), then the stable equivalent population is a stable population whose age distribution and vital rates are determined by m(a) and p(a). The size of the stable equivalent population at t = 0 is given by

$$Q=\frac{{\int }_0^{\mathrm{\beta }}n(x)\nu (x)dx}{b·A_r},$$ (2)

where n(x)dx is the number of females between exact ages x and x + dx; b and A_r are, respectively, the birth rate and the mean age of childbearing in the stable equivalent population; and β is the oldest age of childbearing. In Eq. 2, v(x) is Fisher’s reproductive value function (Fisher 1930:27–30) defined for a woman at exact age x as

$$\nu (x)=\frac{1}{p(x)}{\int }_x^{\mathrm{\beta }}{e}^{-r(a-x)}p(a)m(a)da.$$ (3)

One may interpret v(x) as the present discounted value (using the stable growth rate r as the discount rate) of the average expected number of daughters remaining to be born per woman at age x. When the observed population and the stable equivalent population are projected from t = 0 holding constant both m(a) and p(a), they will eventually converge and become indistinguishable.

In Fig. 1, when the observed population P is projected with fertility set at replacement, it converges to a stationary population whose size is S₁. In other words, S₁ is the size of the stable/stationary population that is equivalent to P with respect to replacement fertility. We can express this formally, using Eqs. 2 and 3, as

$$S_1={\int }_0^{\mathrm{\beta }}\frac{n(x)}{p(x)}{\int }_x^{\mathrm{\beta }}p(a)m_0(a)dadx/(b_0·A_0).$$ (4)

The subscript 0 is used to indicate replacement values in the stationary population, where r = 0 by definition. Assume that m₀(a) is obtained by normalizing the fertility schedule m(a) with the net reproduction rate (R₀). We may rewrite n(x) as P · c(x), where c(x) is the observed proportionate age distribution. And because the stationary population age distribution c₀(x) = b₀ · p(x), Eq. 4 becomes

$$S_1={\int }_0^{\mathrm{\beta }}\frac{Pc(x)}{c_0(x)}{\int }_x^{\mathrm{\beta }}p(a)m_0(a)dadx/A_0,$$

from which it follows that

$$\text{Total Momentum}=\frac{S_1}{P}={\int }_0^{\mathrm{\beta }}\frac{c(x)}{c_0(x)}{\int }_x^{\mathrm{\beta }}p(a)m_0(a)dadx/A_0.$$ (5)

An identical expression for total momentum appears in Preston and Guillot (1997:20–21), and it was anticipated in somewhat different form by Keyfitz (1985:155–157).²

Equation 5 shows that the total momentum contained in a population’s age structure depends on the ratio c(x) / c₀(x), which reflects deviations between the proportionate current and stationary age distributions below the oldest age of childbearing. In particular, total momentum is a weighted average of these deviations, where the age-specific weight is ${\int }_x^{\mathrm{\beta }}p(a)m_0(a)da/A_0$ (Preston and Guillot 1997). These weights sum to unity, as can be seen by reversing the order of integration in the double integral. Moreover, because the weights are largest prior to the onset of childbearing and then decline toward zero (Preston and Guillot 1997), deviations between c(x) and c₀(x) in the early part of life matter most in determining total momentum. Finally, if the observed population is already stationary so that there is no difference between c(x) and c₀(x), then all momentum has been wrung out of the age distribution and the total momentum coefficient equals 1.0 (Preston and Guillot 1997).³

Nonstable Momentum

It may not be clear from Fig. 1 why the ratio Q / P is a measure of population momentum, especially because most discussions of momentum occur in the context of replacement fertility. Suppose we separate the observed population growth rate at time t, r(t), into two parts as

$$r(t)=r+\mathrm{\rho }(t),$$

where r is the stable growth rate produced by m(a) and p(a), and ρ(t) is the residual. Then r reflects the contribution of fertility and mortality to r(t), and ρ(t) measures the contribution of the age distribution at time t (Espenshade 1975).

Espenshade and Campbell (1977) showed that

$$\frac{Q}{P}=\underset{\mathrm{T}\to \infty }{\text{lim}}\left\{e^{{\int }_0^T\mathrm{\rho }(t)dt}\right\}.$$ (6)

The limit in Eq. 6 exists because ρ(t) is the transient part of r(t), and ρ(t) → 0 as the observed population converges to a stable population. Equation 6 tells us how large P would eventually become if age composition were the only source of future population growth or decline. In other words, the ratio Q / P is the long-term relative change in population size owing to nonstable momentum if current fertility and mortality are held constant until a stable population is attained. We call it “nonstable” momentum because its value depends on a fluctuating non-equilibrium age distribution.

Nonstable momentum can be expressed in a form similar to Eq. 5. To find the size of the stable equivalent population, Q, that corresponds with P, use Eqs. 2 and 3 in conjunction with m(a), p(a), and the observed age distribution n(x). It follows that

$$Q=P{\int }_0^{\mathrm{\beta }}\frac{n(x)}{P}·\frac{1}{b{e}^{-rx}p(x)}{\int }_x^{\mathrm{\beta }}{e}^{-ra}p(a)m(a)dadx/A_r.$$ (7)

By writing n(x) / P as c(x) and recognizing that the proportionate stable age distribution c_r(x) = be^−rxp(x), Eq. 7 becomes

$$\text{Nonstable Momentum}=\frac{Q}{P}={\int }_0^{\mathrm{\beta }}\frac{c(x)}{c_r(x)}{\int }_x^{\mathrm{\beta }}{e}^{-ra}p(a)m(a)dadx/A_r.$$ (8)

Equation 8 says that nonstable momentum is a function of deviations between the current and implied stable proportionate age distributions below the oldest age of childbearing. If the observed population is stable so that there are no deviations, then c(x) = c_r(x) at all ages, there is no nonstable momentum, and Q / P = 1 as can be verified by reversing the order of integration in Eq. 8. The same process shows that nonstable momentum is a weighted average of disparities between c(x) and c_r(x), where the weights are ${\int }_x^{\mathrm{\beta }}{e}^{-ra}p(a)m(a)da/A_r$ and sum to 1. Equation 8 gives equal weight to deviations up to the age when childbearing begins and monotonically declining weight thereafter until the weight becomes zero at the highest age of childbearing.

The ratio Q / P appears at other places in the momentum literature. Bourgeois-Pichat (1971) introduced the concept of the “inertia of a population” and developed the “coefficient of inertia” (Q / P) to measure it. He went on to suggest a further decomposition of nonstable momentum into the effects of fertility and mortality on the one hand and those of age distribution on the other. In reformulating the concept of the stable equivalent population, Keyfitz (1969) calculated Q / P for several empirical examples without relating it to population momentum. The closest he came is referring to Q as “a simple measure of the favorability of the age distribution to reproduction, given the current regime of mortality and fertility” (Keyfitz 1969:264). Schoen and Kim (1991:456) argued, “The momentum concept need not be limited to cases in which the ultimate stable population has zero growth. More generally, momentum can be defined as the size of a population relative to the size of its stable equivalent.” Finally, Feeney (2003:648) claimed, “The momentum of the given age distribution with respect to the given age schedules of fertility and mortality is the ratio [Q / P]” (first emphasis in the original; second emphasis added).

Stable Momentum

The last kind of momentum in Fig. 1 is stable momentum, defined by the ratio S₂ / Q. Because P and its proportionate age distribution, c(x), can be chosen arbitrarily, let the initial observed population be stable with size Q and age distribution c_r(x) = be^−rxp(x). Then set fertility at replacement and project until the population becomes stationary with growth rate r = 0 and fixed size S₂. The formula in Eq. 5 for total momentum may be invoked and applied in this new situation to yield an expression for stable momentum as

$$\text{Stable Momentum}=\frac{S_2}{Q}={\int }_0^{\mathrm{\beta }}\frac{c_r(x)}{c_0(x)}{\int }_x^{\mathrm{\beta }}p(a)m_0(a)dadx/A_0.$$ (9)

We call it “stable” momentum because, just like other stable population concepts, it depends only on fertility and mortality and not on the current age distribution.

Once again, the amount of momentum depends on deviations between pairs of proportionate age distributions. In the case of stable momentum, what matters are the deviations between the stable and stationary age distributions, weighted by the same age-specific weights used in Eq. 5. These weights are constant prior to the onset of childbearing and then decline steadily to zero by age β. If fertility is already at replacement in the observed population, then the stable age distribution will be stationary, c_r(x) = c₀(x) at all ages, S₂ / Q = 1, and there will be no stable momentum.

Stable momentum is identical to what we might call “Keyfitz” momentum. Keyfitz (1971) considered the long-term size of an initially stable population if fertility rates are set immediately to replacement by normalizing the fertility schedule, m(a), with the net reproduction rate (R₀). To see the equivalence between Eq. 9 and the Keyfitz formula, rewrite Eq. 9 as

$$\frac{S_2}{Q}={\int }_0^{\mathrm{\beta }}\frac{b{e}^{-rx}p(x)}{b_{0}p(x)}{\int }_x^{\mathrm{\beta }}p(a)m(a)dadx/(A_0·R_0),$$ (10)

where b is the birth rate in the initial stable population; b₀ is the birth rate in the ultimate stationary population and equal to the reciprocal of life expectancy at birth $(e_0^o)$. Simplifying Eq. 10 and reversing the order of integration, we have

$$\frac{S_2}{Q}=\frac{b{e}_0^o}{A_0{R}_0}{\int }_0^{\mathrm{\beta }}{\int }_0^a{e}^{-rx}p(a)m(a)dxda.$$ (11)

But because

$${\int }_0^a{e}^{-rx}dx=-\frac{1}{r}{\int }_0^a{e}^{-rx}(-r)dx=\frac{1}{r}(1-e^{-ra}),$$

Eq. 11 becomes

$$\frac{S_2}{Q}=\frac{b{e}_0^o}{r{A}_0{R}_0}(R_0-1),$$

which is exactly the formula in Keyfitz (1971:76) for momentum in a stable population.

In related work, Kim and Schoen (1993) derived momentum in an initially stable population as a simple ratio of proportions in the stable and stationary age distributions at an age determined by the crossover point of reproductive value functions. A further decomposition of momentum in a stable population is given in Kim and Schoen (1997). Much of the work on momentum in populations with gradually declining fertility assumes initial stability. Schoen and Jonsson (2003) decomposed this momentum into a part that reflects the effect of growth continuing at the original stable rate for half the period of decline and an offsetting factor that reduces momentum and the number of births in the long-run stationary population because of population aging (if fertility is falling). Finally, Goldstein and Stecklov (2002) developed a simple analytic formula for estimating population momentum in a stable population when fertility declines gradually and linearly to replacement. Their analysis suggests that differences between an observed population and its stable equivalent are sufficiently small that they can be ignored (Goldstein and Stecklov 2002:136–137). In other words, their analysis assumes that nonstable momentum is inconsequential to an understanding of total momentum and that only stable momentum matters for all practical purposes.

Examples

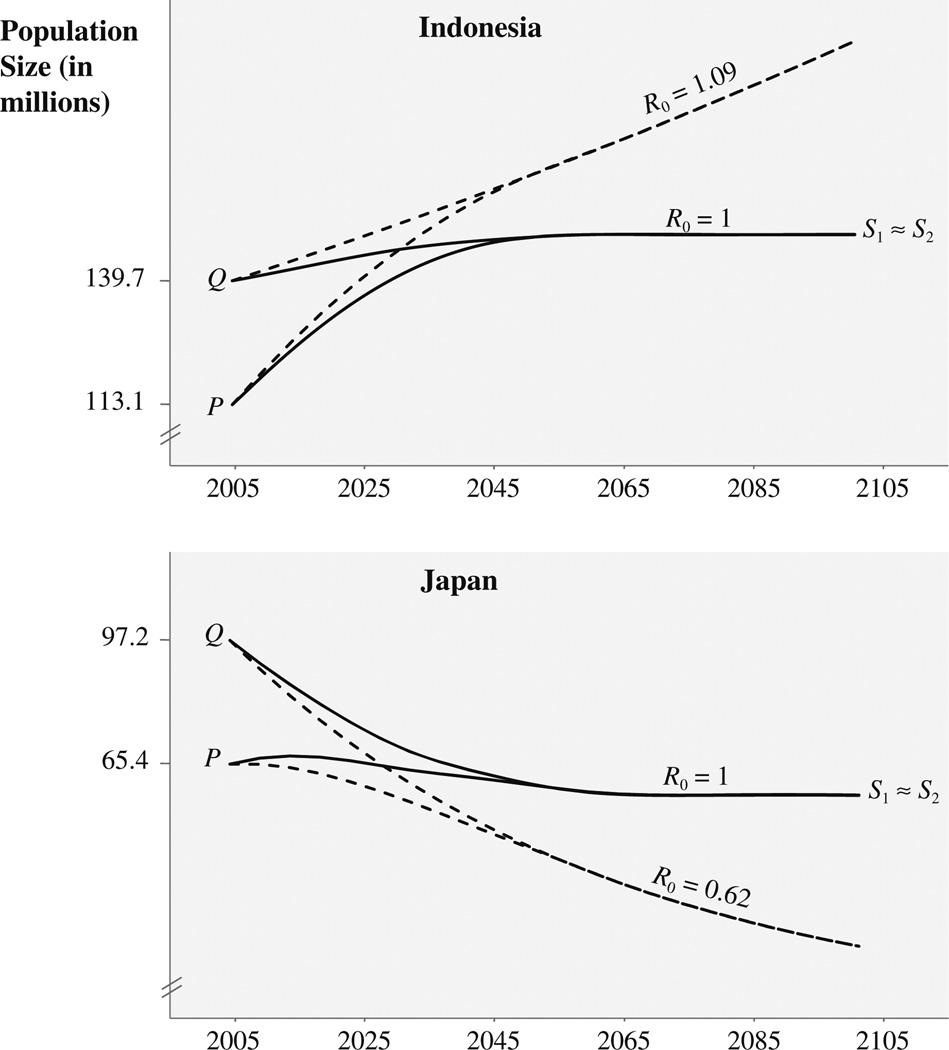
To add empirical content to our analysis and anticipate later results, we show projections of the female populations for two countries in Fig. 2. The top portion illustrates the case of Indonesia, a population with above-replacement fertility. Females numbered 113.1 million in 2005, and the size of the stable equivalent population is 139.7 million. When both populations are projected assuming replacement fertility, it is not possible to detect any visual distance between S₁ and S₂. They are both very close to 150 million. A similar situation arises in the case of Japanese women shown in the bottom portion of Fig. 2. Here the example is chosen to reflect fertility below replacement. But once again, it appears that the observed population and its stable equivalent are asymptotically equivalent with respect to both current and replacement fertility. In this example, S₁ and S₂ are approximately 57.5 million. For Indonesian and Japanese women in 2005, the data in Fig. 2 suggest that total momentum is exactly the product of nonstable and stable momentum, or very nearly so. In the next section we investigate analytically whether S₁ = S₂ in all situations.

Fig. 2.

Projections of the female populations of Indonesia and Japan, 2005–2105

A Unified Analytic Framework

Because population projections usually rely on discrete formulations of age and time, it is convenient to develop an analytic solution using matrix algebra. Relevant introductions are contained in Finkbeiner (1960:23–43) and Keyfitz (1968:27–73).

The General Case

Let {P} be an n × 1 vector for the age distribution of an arbitrarily chosen population at time t = 0. The elements in the vector represent the number of females in successive discrete (say, five-year) age intervals. Suppose that current fertility and mortality are captured by a standard n×n Leslie matrix L, which is assumed to be primitive. Let the Leslie matrix L₀ reflect replacement fertility, and assume that L₀ is obtained from L by dividing fertility rates by the net reproduction rate. Then we may write

$$\{\mathbf{P}\}=\{\mathbf{Q}\}+\{\mathbf{V}\},$$ (12)

where {Q} is the age distribution of the stable equivalent population and {V} is the deviation of {P} from {Q}. When Eq. 12 is projected forward infinitely with L, the part associated with {V} is dominated by the other term and hence can be neglected.

Next consider the infinite projection of Eq. 12 using replacement fertility:

$$\underset{t\to \infty }{\text{lim}}{\mathbf{L}}_0^t\left\{\mathbf{P}\right\}=\underset{t\to \infty }{\text{lim}}{\mathbf{L}}_0^t\left\{\mathbf{Q}\right\}+\underset{t\to \infty }{\text{lim}}{\mathbf{L}}_0^t\left\{\mathbf{V}\right\}.$$ (13)

But because $\underset{t\to \infty }{\text{lim}}{\mathbf{L}}_0^t\left\{\mathbf{P}\right\}$ is the stationary population vector {S₁} and $\underset{t\to \infty }{\text{lim}}{\mathbf{L}}_0^t\left\{\mathbf{Q}\right\}$ is the stationary population vector {S₂} with the same proportionate age distribution as {S₁}, we have from Eq. 13 the quantity of interest, which is

$$\left\{{\mathbf{S}}_1\right\}-\left\{{\mathbf{S}}_2\right\}=\underset{t\to \infty }{\text{lim}}{\mathbf{L}}_0^t\left\{\mathbf{V}\right\}.$$ (14)

Now change bases and rewrite {V} as a linear combination of the eigenvectors {Z_j} of L₀, specifically as

$$\{\mathbf{V}\}=k_1\{{\mathbf{Z}}_1\}+k_2\{{\mathbf{Z}}_2\}+\cdots +k_n\{{\mathbf{Z}}_n\},$$

or more compactly as

$$\{\mathbf{V}\}=k_1\{{\mathbf{Z}}_1\}+\{\mathbf{W}\}.$$ (15)

In Eq. 15, k₁{Z₁} is the stationary part of {V}. In particular, k₁{Z₁} is the stationary equivalent population, where k₁ is the stationary population size and {Z₁} is the proportionate stationary age distribution. {Z₁} is also the principal eigenvector of L₀ associated with the principal or dominant eigenvalue λ₁=1.

Finally, consider the infinite projection of Eq. 15 using L₀, whereupon

$$\underset{t\to \infty }{\text{lim}}{\mathbf{L}}_0^t\left\{\mathbf{V}\right\}=\underset{t\to \infty }{\text{lim}}{\mathbf{L}}_0^t{k}_1\left\{{\mathbf{Z}}_1\right\}+\underset{t\to \infty }{\text{lim}}{\mathbf{L}}_0^t\left\{\mathbf{W}\right\}.$$ (16)

The second term on the right-hand side of Eq. 16 can be ignored in the limit because {V} and k₁{Z₁} are asymptotically equivalent under L₀. Moreover, L₀ k₁{Z₁}=k₁{Z₁}. That this is true is immediately obvious from demography, because projecting an already stationary population using replacement-level fertility simply reproduces the original population. In addition, however, because {_Z1} is an eigenvector of L₀,

$${\mathbf{L}}_0{k}_1\left\{{\mathbf{Z}}_1\right\}=k_1{\mathbf{L}}_0\left\{{\mathbf{Z}}_1\right\}=k_1{\mathrm{\lambda }}_1\left\{{\mathbf{Z}}_1\right\}=k_1\left\{{\mathbf{Z}}_1\right\}.$$

It follows from Eq. 16 that $\underset{t\to \infty }{\text{lim}}{\mathbf{L}}_0^t\left\{\mathbf{V}\right\}=k_1\left\{{\mathbf{Z}}_1\right\}+\left\{\mathbf{0}\right\}$ and, therefore, from Eq. 14, that

$$\{{\mathbf{S}}_1\}-\{{\mathbf{S}}_2\}=k_1\{{\mathbf{Z}}_1\}.$$ (17)

Because k₁ ≠ 0 in general, it follows that, in general, {S₁} ≠ {S₂}. We conclude that when an observed population and its stable equivalent are projected on the assumption of replacement-level fertility, the stationary populations to which they converge are usually different. In other words, the factorization of total population momentum into the product of nonstable and stable momentum typically is not exact, but only approximate.

Special Cases

There are, however, three special cases in which the factorization is exact. First, suppose the observed age distribution is stable. Then S₁ = S₂, as can be verified by substituting c(x) = c_r(x) into the main momentum formulas 5, 8, and 9. The least-developed countries are most likely to be described by this condition. Second, suppose current fertility is at replacement. To see that the factorization is exact, substitute r = 0, m(a) = m₀(a), and c_r(x) = c₀(x) into Eqs. 5, 8, and 9. Fertility at or near replacement is more likely to characterize developed countries than developing ones. Third, there is the degenerate case. If fertility is at replacement and the age distribution is stationary, there is no momentum of any kind—neither total, nor stable, nor nonstable. Each of the ratios in Eq. 1 is 1.0.

Evaluating the Approximation

Our analysis has shown that apart from a few special cases, the sizes of the ultimate stationary populations in Fig. 1, S₁ and S₂, are generally not identical. But are they close in practice? The better is the agreement between S₁ and S₂, the more nearly total momentum factors into the product of stable and nonstable momentum. In other words, if S₁ and S₂ are very close, the decomposition gives us a new way of thinking about population momentum and understanding differences among countries and regions of the world.

We investigate the relationship between S₁ and S₂ for each of 176 United Nations countries. Projections are made using a standard cohort-component methodology applied to recent United Nations (2007) data. The baseline population comes from an estimate for July 1, 2005, for females, disaggregated by five-year age groups from 0–4 up to 100 years and older. Fertility rates and sex ratios at birth are based on estimates for the period 2000–2005, and projections that assume replacement fertility are constructed by dividing age-specific fertility rates by the net reproduction rate. Estimates of death rates by five-year age groups up to 100 years and older come from the World Health Organization (2008). All projections are carried out for 300 years assuming a closed population.⁴

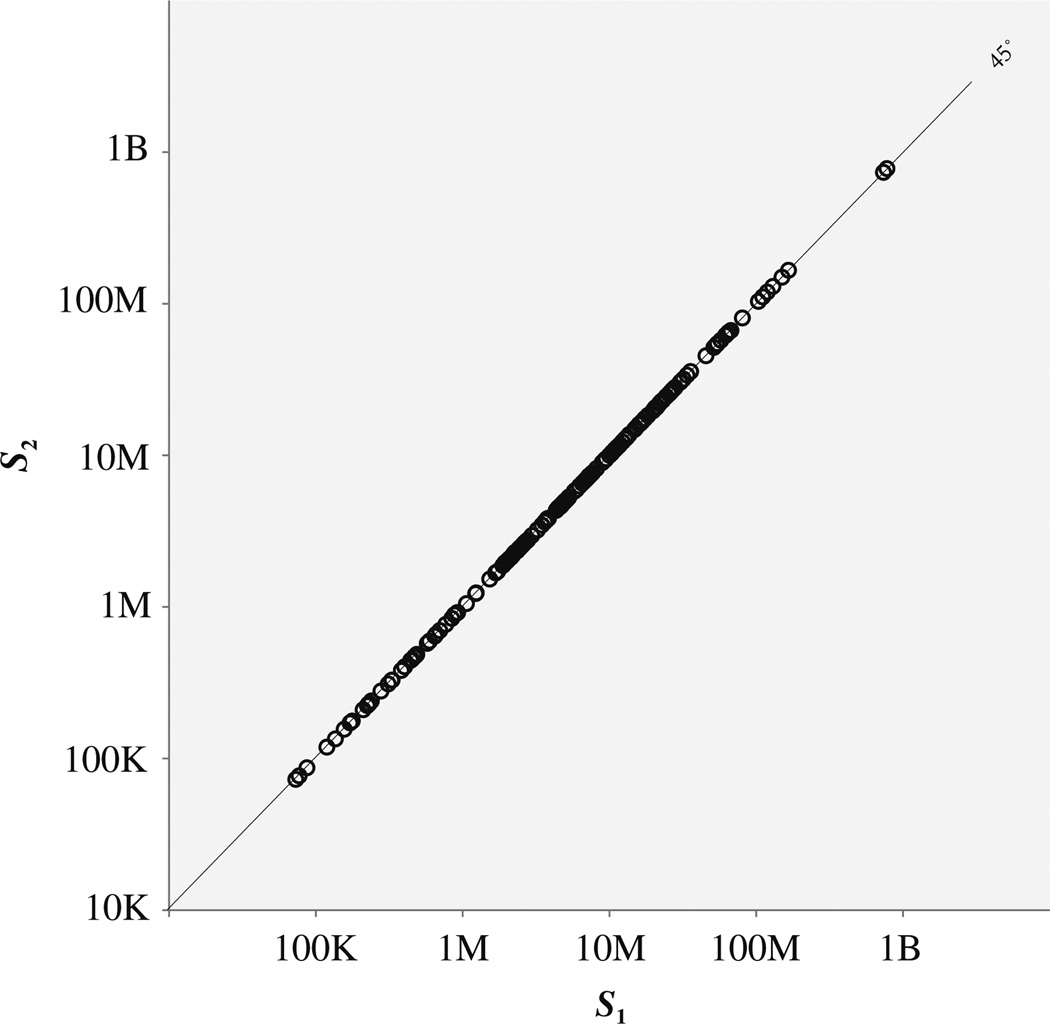
We graph on a logarithmic scale in Fig. 3 values of S₁ and S₂ for the female populations of 176 U.N. countries. Values of S₁ range from 73 million for Tonga and 77 million for Grenada to 736 million for China and 777 million for India. But the most striking feature of Fig. 3 is that all the points appear to lie on the 45-degree line. If S₁ and S₂ are not equal to each other, then the deviation between them is very small. The simple correlation coefficient between S₁ and S₂ is .9999. The correlation is identical to four decimal places when population size is measured on a logarithmic scale in base 10. The data in Fig. 3 reinforce an important conclusion: when the factorization of total momentum into the product of stable and nonstable momentum is not exact, the approximation is extremely good.

Fig. 3.

Relationship between S₁ and S₂ (N = 176 countries)

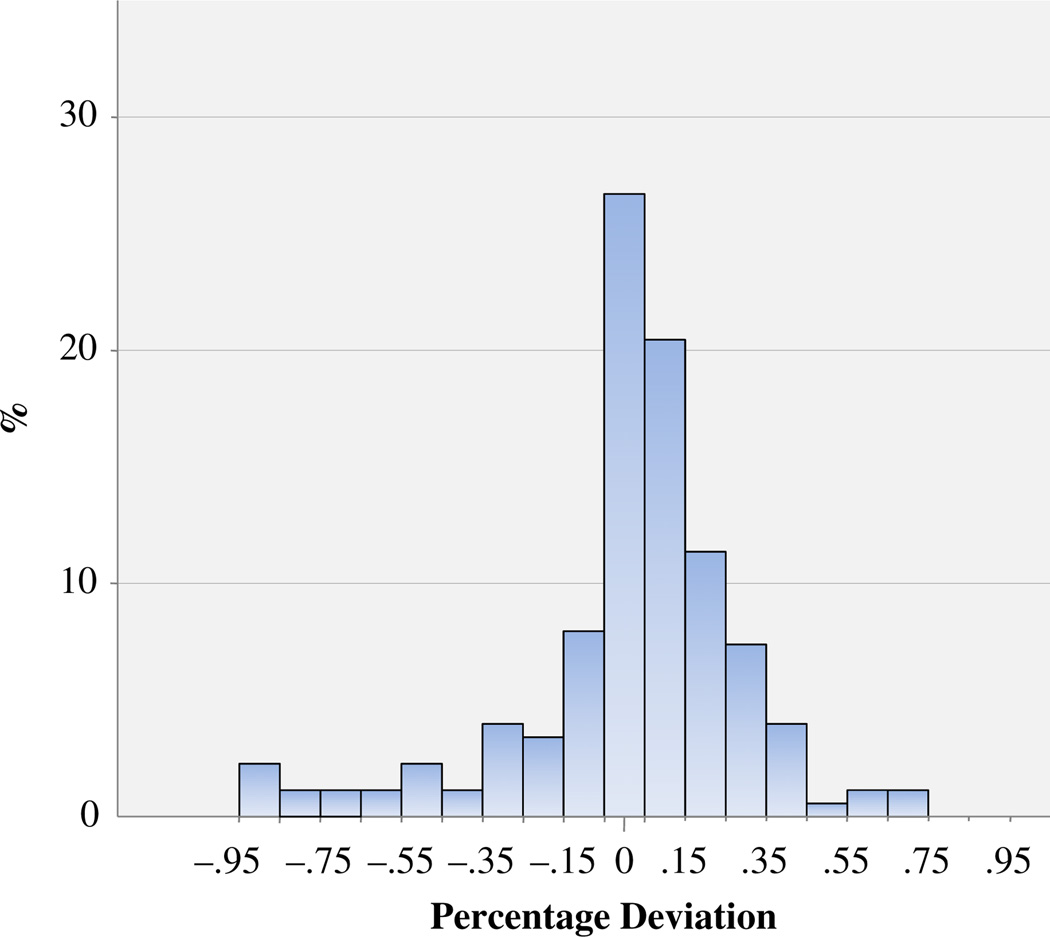
Figure 4 examines the relationship between S₁ and S₂ in another way. Here we show the distribution of the percentage deviation of S₂ from S₁ for the same 176 countries. Most of the deviations cluster in a tight pattern around zero, and only a small number fall outside the range of ±0.5%. Roughly two out of every five cases (39.2%) fall within 0.1% of the origin. In two-thirds of the cases (64.8%), the deviations are contained within 0.2%. And in three-fourths of all cases (74.4%), the relative difference between S₁ and S₂ lies within 0.3%.⁵

Fig. 4.

Distribution of percentage deviations between S₁ and S₂ (N = 176 countries). Deviations are calculated as [(S₂ − S₁) / S₁] × 100. Five countries fall outside the interval (−0.95, 0.95), ranging from Russia (−1.014) to Eritrea (1.168)

The data in Figs. 3 and 4 point to one overarching conclusion. When S₁ and S₂ are compared, only one of two outcomes is possible. Either S₁ = S₂ or S₁ ≈ S₂. This means that total momentum is either identically equal to the product of nonstable and stable momentum or very close to it. And we now know why this is the case: because for many of the world’s countries, either current fertility is close to replacement or the age distribution is nearly stable. It is only in instances of a joint departure from replacement fertility and age distribution stability that the exact factorization begins to dissolve into an approximation.

Momentum in Global Perspective

We calculate values for total, nonstable, and stable momentum for each of 176 United Nations countries, broad regional aggregates, and the world. Results for the world and its major regions are reported in Table 1. Notice first that there is excellent agreement between the numbers in columns 1 and 4. Any differences are usually limited to the third decimal place, which suggests that the product of nonstable and stable momentum is an unusually good approximation to total momentum. Moreover, our estimates indicate that world population would grow by an additional 40% if global fertility rates had moved instantaneously to replacement in 2005. Nonstable and stable momentum contribute roughly equal shares to world population momentum. Taking natural logarithms shows that nonstable momentum accounts for about 53% of total world momentum, and stable momentum contributes roughly 47%.

Table 1.

Total, nonstable, and stable momentum for the world and major regions, 2005

Region	Total Momentum	Nonstable Momentum	Stable Momentum	Nonstable × Stable
World	1.398	1.193	1.173	1.399
More-developed regions	0.971	1.302	0.745	0.969
Less-developed regions	1.437	1.178	1.220	1.438
Least-developed countries	1.513	1.033	1.468	1.515
Less-developed regions, excluding least-developed countries	1.395	1.234	1.131	1.396
Less-developed regions, excluding China	1.494	1.131	1.322	1.496
Sub-Saharan Africa	1.463	1.011	1.449	1.465
Africa	1.503	1.033	1.458	1.506
Asia	1.388	1.265	1.098	1.388
Europe	0.929	1.383	0.669	0.926
Latin America and the Caribbean	1.486	1.257	1.182	1.486
Northern America	1.110	1.157	0.960	1.110
Oceania	1.299	1.159	1.120	1.299

Source: Authors’ calculations.

Europe and the least-developed countries represent two extremes on the global momentum scale. The least-developed countries possess the largest values for total and stable momentum in Table 1 and have one of the lowest values for nonstable momentum. On the contrary, Europe has the lowest values for total and stable momentum but the largest value for nonstable momentum. Because total momentum is a function of the ratio between proportions in the observed population and the stationary population at young ages, it will be influenced by the recent history of crude birth rates. High rates induce large values for total momentum; low birth rates predict low values for total momentum. Europe’s crude birth rate was 10.2 per 1,000 for 2000–2005, in contrast to a birth rate of 37.6 per 1,000 for the least-developed countries during the same period (United Nations 2007). Data in Table 1 suggest that if replacement fertility had been adopted in 2005 and remained constant, the populations of the least-developed countries would eventually grow by more than one-half (51.3%) before becoming stationary. Even with an increase in fertility to replacement in 2005, Europe’s population would ultimately decline by 7%. The only other region exhibiting negative total momentum is the group of more-developed countries. Several regions have positive total momentum coefficients in the neighborhood of 1.50.

Nonstable momentum depends largely on relative proportions in the current and stable age distributions before the onset of childbearing. Populations whose fertility is substantially below replacement and whose age distributions have not had time to adjust fully to the new fertility regime will tend to have high values for nonstable momentum. With a net reproduction rate of 0.69 for 2000–2005, Europe has the largest value in Table 1 for nonstable momentum (1.383). On the other hand, populations with high and relatively constant fertility will have age distributions that are approximately stable. This condition produces nonstable momentum coefficients near unity. The least-developed countries, sub-Saharan Africa, and Africa as a whole all have nonstable momentum values close to 1.0. And each has a history of high fertility, with modest declines occurring only recently (United Nations 2007).

Values for stable momentum involve a comparison between a population’s stable and stationary age distributions in the earliest part of life. When fertility is substantially above replacement, the stable age distribution will be young relative to its stationary counterpart. Coefficients of stable momentum should be large in this situation. But if fertility is dramatically below replacement, the opposite circumstance will arise and values for stable momentum will be less than 1. As seen in Table 1, stable momentum is greatest (at or above 1.45) in regions with high fertility. Europe’s coefficient of stable momentum is just 0.67—the lowest for any region.

Notice finally in Table 1 that the same value for total momentum can be produced with different combinations of nonstable and stable momentum. The total momentum coefficient is either 1.49 or 1.50 for Latin America and the Caribbean, less-developed regions excluding China, and all of Africa. Nonstable momentum is larger than stable momentum in Latin America. These roles are reversed for less-developed regions excluding China. Stable momentum accounts for practically all of total momentum in Africa.

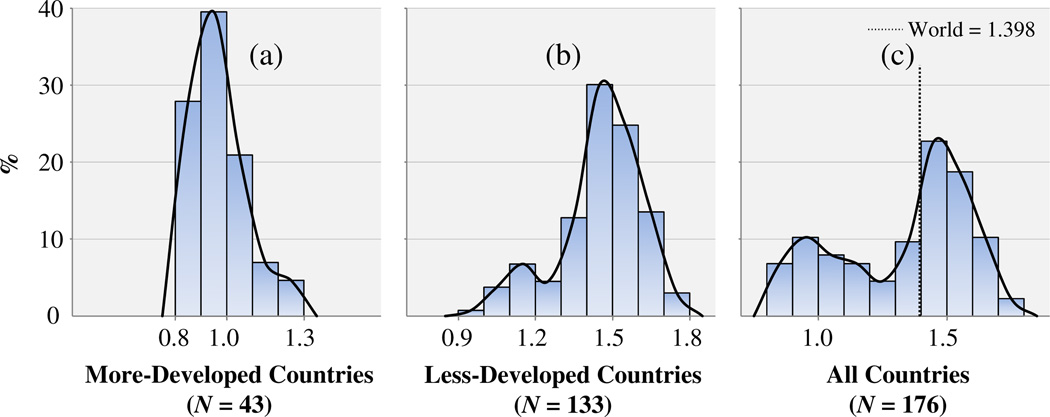
Table 1 suggests that results depend on the level of development. To clarify this relationship, Fig. 5 shows the distribution of values for total momentum for a group of 43 more-developed countries, 133 less-developed countries, and for all countries. For more-developed countries in panel (a), modal values fall between 0.9 and 1.0, indicating that negative population momentum is not uncommon in richer countries. Total momentum values for less-developed countries in panel (b) cluster near 1.5. The distribution in panel (c) for all countries exhibits a somewhat bimodal shape, but it is weighted toward values near 1.5 because of the greater number of less-developed countries. For added perspective, panel (c) also contains a vertical line to indicate total momentum for the entire world.⁶

Fig. 5.

Distribution of total momentum by level of development, 2005

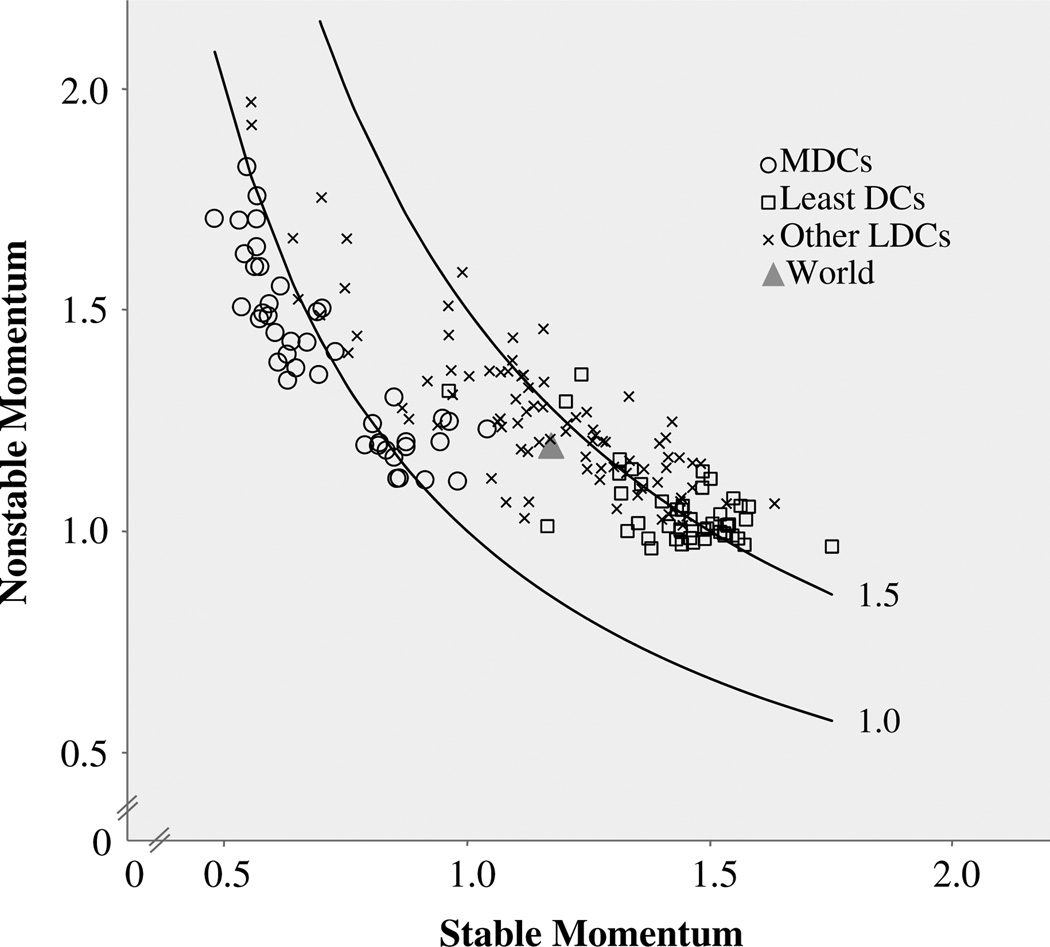
Finally, we consider nonstable and stable momentum values for individual countries. Figure 6 contains a scatterplot of points whose coordinates correspond to stable and nonstable momentum for 176 countries. Stable momentum ranges between 0.48 and 1.75. Countries with the largest values include Timor-Leste (1.751), Guatemala (1.633), Yemen (1.580), Madagascar (1.574), and Guinea-Bissau (1.571). The five smallest values belong to Ukraine (0.479), Czech Republic (0.530), Bulgaria (0.535), Belarus (0.541), and Slovakia (0.546). The level of the net reproduction rate (R₀) is an important determinant of stable momentum. In the five countries where stable momentum is greatest, R₀ values are 2.1 or higher. By contrast, R₀ values do not exceed 0.60 among the five countries with the smallest coefficients for stable momentum.

Fig. 6.

Plot of nonstable and stable momentum for individual countries by level of development, 2005 (N = 176 countries). MDCs = more-developed countries; LDCs = less-developed countries

Nonstable momentum varies between 0.96 and 1.97. Countries with the smallest values include Sierra Leone (0.961), Timor-Leste (0.965), Guinea-Bissau (0.969), Mozambique (0.970), and Malawi (0.974). A history of high and relatively constant fertility is a good predictor of nonstable momentum near 1.0. Each of these countries has a total fertility rate above 5.5 for the period 2000–2005 (United Nations 2007). On the other hand, fertility that has fallen recently to low levels is indicative of large values for nonstable momentum. Countries with the highest values include Republic of Korea (1.970), Armenia (1.918), Slovakia (1.824), Poland (1.758), and Azerbaijan (1.754). Fertility experienced a recent collapse in each of these cases (United Nations 2007).⁷

Total momentum values of 1.0 and 1.5, respectively, are shown by points along the two hyperbolic curves in Fig. 6. It is clear from the graph that multiple combinations of stable and nonstable momentum are compatible with the same total momentum. Most countries lie near or between the two curves, as panel (c) in Fig. 5 suggests they should. Oman has the largest total momentum (1.760), followed by Nicaragua (1.737), Guatemala (1.732), and Honduras (1.703). In each case, population would be expected to grow by more than 70% if replacement fertility had been adopted in 2005. The lowest values for total momentum belong to Bulgaria (0.811), Ukraine (0.824), Germany (0.844), and Italy (0.845). For these countries, even if fertility rebounded immediately to replacement, population losses between 15% and 20% could be expected.

Countries in Fig. 6 are distinguished by their level of development. There are some overlapping circles, squares, and crosses in the graph, and the respective scatterplots for more-developed countries and less-developed countries are not totally distinct. But in general, the least-developed countries are distributed around the 1.5 total momentum curve, and more-developed countries are located near or somewhat below the 1.0 curve. That there are so many points beneath the 1.0momentum curve emphasizes how important negative population momentum is among more-developed countries (Preston and Guillot 1997). Points for other less-developed countries are more dispersed between the two total momentum curves.

All of the more-developed countries lie above an imaginary 45-degree line drawn from the origin. For each of the more-developed countries, nonstable momentum is greater than stable momentum.⁸ Most of the less-developed countries appear to lie below the 45-degree line, meaning that for them, stable momentum outweighs nonstable momentum. The point for the world is indicated by a shaded triangle. This point lies on or close to the 45-degree line, which suggests in another way that on a global scale, nonstable and stable momentum are roughly equal in magnitude. The takeaway message is this: as the level of development increases in Fig. 6, fertility is generally lower, overall population momentum is less, stable momentum becomes weaker, and nonstable momentum becomes stronger.

Discussion

This article has described a decomposition of overall population momentum into two constituent and multiplicative parts: nonstable and stable momentum. The value for nonstable momentum reflects a country’s recent trend in fertility. In a stable population where fertility has been constant for a long time, nonstable momentum is nonexistent. But countries that have a history of fertility decline, especially a recent and sharp decline, will have larger values for nonstable momentum. The value for stable momentum is dictated by a population’s current level of fertility in relation to mortality. A high (low) net reproduction rate corresponds to a large (small) value for stable momentum. This decomposition gives us a new way of thinking about the determinants of overall population momentum. In addition, it allows us to integrate disparate strands of the population momentum literature and see how the various kinds of momentum that researchers have considered fit together into a single analytic and empirical framework.

Our empirical work shows that the factorization of total momentum into the product of stable and nonstable momentum is an extremely good approximation—much better, in fact, than most approximations in demography. At a global level, stable and nonstable momentum are roughly equal in importance. On a regional basis, however, a partitioning of the world by levels of development corresponds not only to different values for overall momentum but also to different roles played by stable and nonstable momentum. Among more-developed countries, total momentum is close to zero or slightly negative. For these countries, positive nonstable momentum is offset by negative stable momentum. By contrast, in less-developed regions, and especially among the least-developed countries, total momentum values of 1.5 or greater are common. For the poorest countries, nonstable momentum is only slightly positive. Stable momentum dominates the overall projection and gives by far the larger impetus to future population growth. In short, among the 176 countries we have examined, as the level of development increases and fertility subsides, values for total momentum decline, stable momentum becomes weaker, and nonstable momentum becomes stronger.

The research raises a number of questions for further work. First, we have identified two special cases in which the factorization of total momentum is exact. But are there more? If so, these additional examples might help to explain why the simple product of nonstable and stable momentum is such a good approximation to total momentum.

Second, the factorization of overall momentum is inexact whenever k₁ ≠ 0 in Eq. 17. This corresponds to situations in Fig. 1 in which S₁ ≠ S₂. What are the conditions that determine the magnitude and direction of k₁?

Third, work by Li and Tuljapurkar (1999, 2000) has opened up new avenues of inquiry concerning momentum in populations with gradually declining fertility (e.g., see Goldstein 2002; Goldstein and Stecklov 2002; O’Neill et al. 1999; Schoen and Jonsson 2003; Schoen and Kim 1998). Might it be useful in this context to contemplate the roles of nonstable and stable momentum?

Fourth, how does our understanding of stable and nonstable momentum change if populations are no longer assumed to be closed to migration? Migrants modify a population’s age distribution (Guillot 2005:293), but they can also affect levels of fertility and mortality.

Fifth, our analysis has been largely static, relying on estimates of momentum in 2005 for individual countries, the world, and major regions. There is a need to put nonstable and stable momentum in a more dynamic context and consider what happens within populations over time. In Fig. 6, for example, European countries are clustered in the upper left-hand corner of the diagram. But if one assumes that fertility and mortality as measured in 2005 are held constant, one can imagine the circles for European countries gradually drifting downward toward a nonstable momentum value close to 1.0 when momentum values are recalculated periodically after 2005. More generally, it would be useful to trace the arc of nonstable and stable momentum across the demographic transition. From this dynamic perspective, one could conjecture that nonstable momentum is something that emerges during a time of fertility transition and then begins to disappear after birth rates reach relatively low levels. In this sense, nonstable momentum is the transitory part of total population momentum.

Finally, different combinations of stable and nonstable momentum are compatible with the same amount of overall population momentum. For example, in 2005, total momentum measured 1.46 in Chad and 1.45 in Mongolia. Both countries could be expected to grow by nearly 50% if fertility had gone immediately to replacement. In Chad, stable momentum (1.49) outweighed nonstable momentum (0.98). But these roles were reversed in Mongolia, where stable and nonstable momentum were estimated at 0.96 and 1.51, respectively. Apart from implications that their respective life expectancies have for long-run stationary age distributions, does the particular mix of stable and nonstable momentum in the two countries matter for the paths taken to stationarity?⁹ Does the time required to achieve a stationary population depend on the relative strength of nonstable and stable momentum? What about the ripples that are created in various age groups along the way? Carlson (2008) showed for the United States not only that successive generations measured by 20-year birth cohorts vary in size but also that there have been substantial booms and busts in their relative sizes. These oscillations have impacts throughout the life course, affecting schooling, labor and housing markets, political attitudes and participation, health care, and pension systems. For a given level of overall momentum, what are the corresponding implications of varying combinations of nonstable and stable momentum as cohorts of fluctuating sizes pulse through institutional arteries?