Analysis of Point Based Image Registration Errors With Applications in Single Molecule Microscopy

Abstract

We present an asymptotic treatment of errors involved in point-based image registration where control point (CP) localization is subject to heteroscedastic noise; a suitable model for image registration in fluorescence microscopy. Assuming an affine transform, CPs are used to solve a multivariate regression problem. With measurement errors existing for both sets of CPs this is an errors-in-variable problem and linear least squares is inappropriate; the correct method being generalized least squares. To allow for point dependent errors the equivalence of a generalized maximum likelihood and heteroscedastic generalized least squares model is achieved allowing previously published asymptotic results to be extended to image registration. For a particularly useful model of heteroscedastic noise where covariance matrices are scalar multiples of a known matrix (including the case where covariance matrices are multiples of the identity) we provide closed form solutions to estimators and derive their distribution. We consider the target registration error (TRE) and define a new measure called the localization registration error (LRE) believed to be useful, especially in microscopy registration experiments. Assuming Gaussianity of the CP localization errors, it is shown that the asymptotic distribution for the TRE and LRE are themselves Gaussian and the parameterized distributions are derived. Results are successfully applied to registration in single molecule microscopy to derive the key dependence of the TRE and LRE variance on the number of CPs and their associated photon counts. Simulations show asymptotic results are robust for low CP numbers and non-Gaussianity. The method presented here is shown to outperform GLS on real imaging data.

I. Introduction

Image registration is the process of overlaying two or more images of the same scene [1]. From a theoretical stance, registration is the process of establishing the geometric transformations between two or more data sets such that they can be viewed in a single coordinate system. These images could arise from different times (multitemporal), different viewpoints (multiview), or different sensors (multimodal).

Broadly speaking, image registration techniques can be divided into two categories. The first is intensity-based registration where gray scale values in both images are correlated to match the images, e.g. [2], [3]. Here we are concerned with the alternative method, feature-based registration, whereby correspondence between the two images is determined through the matching of distinct features common in both images e.g. [4], [5], (although there exist methods that combine both feature and intensity-based approaches to registration e.g. [6]). Specifically we are concerned with the case where the features used for matching are points in the image where pair correspondence is certain. In this case they are known as control points (CPs). It is common that these points are created with the use of fiducial markers, e.g. beads in microscopy [7], [8], or infrared emitting diodes in computer aided surgery [9].

We consider an image to capture a subset of the space ℝ^d, d = 2 or 3. Given two image spaces ℐ₁ ⊆ ℝ^d and ℐ₂ ⊆ ℝ^d, say, registration is concerned with estimating the mapping T : ℐ₁ → ℐ₂. It is typical to consider T to be an affine transformation e.g. [10]–[13]. In this circumstance, for x ∈ ℐ₁, T(x) = Ax + s where A ∈ ℝ^d×d is a square invertible matrix and s ∈ ℝ^d is a translation vector. This includes the well studied subclass of rigid transformations where the matrix A is a rotation transformation [11], [12], [14], [15]. Registration involves using the CP locations in ℐ₁ and their corresponding mapped positions in ℐ₂ to find T.

In general, due to noisy signals, the location of the CPs in at least one of the images can not be measured exactly and instead are perturbed by random errors. Commonly these error terms are not identically distributed (heteroscedastic) and/or directional (anisotropic). Consequently it is not possible to exactly match the CPs in both images. With this problem in mind, two key questions arise. Firstly; what is the procedure for estimating A and s that correctly accounts for the measurement errors in localizing the CPs? Secondly; how accurately can we determine the transformation and hence what errors arise from the registration process? In response to the second of these questions, it has been common in the literature to define the target registration error (TRE) as a measure of accuracy for a registration and its distributional properties are of keen interest e.g. [10]–[12], [14]–[16].

One of the most widely researched and applied methods of image registration has been the traditional least squares estimator [13], [14], [17]. Given that the CP locations are precisely known without error in one of the images, and the errors in their localization in the second image are independent and identically distributed (iid) then this provides a proper method of registration. In the case of rigid transformations (A represents rotation only) [14] provides an approximation to the root mean square of the TRE that has been corroborated with simulated data. This was extended to an approximate distribution of the TRE in [15] and [16]. For rigid transforms when errors are only present in one set of CPs then several papers have attempted to extend distributional results for the TRE to the case where errors are heteroscedastic and anisotropic based on a number of different approaches, including maximum likelihood procedures [12], and a spatial stiffness model [10].

In most registration scenarios measurement errors will exist in both sets of CP locations rendering these methods insufficient. In this circumstance the problem is known as an errors-in-variables (EIV) problem and it is well known the that traditional least square method provides inconsistent estimators [18]. If all measurement errors are iid then the total least squares (TLS) method (see [19]–[21]) is the correct procedure and [22] provides distributional results for the parameter estimators in the Gaussian case. Under the assumption that measurement errors are iid and white then [23] (corrected by [24]) takes a maximum likelihood (ML) approach to the EIV problem associated with image registration and Cramér-Rao lower bounds are derived for the variance of parameter estimators. However the reality is iid is a rare luxury and any deviation from this render the TLS and ML methods inconsistent. It is therefore necessary to consider the broader class of model called heteroscedastic EIV (HEIV).

In this paper we will use fluorescence microscopy as a motivating example. Using fiducial markers to perform image registration is an important pre-processing step when correcting for drift between successive frames (multitemporal) e.g. [7], or combining a pair of different colored monochromatic images captured through different sensors (multimodal) e.g. [8], [25]. Localization accuracy depends on the brightness of the light emitting object (see [26]–[30]) and hence each fiducial marker is localized with varying degrees of accuracy. This presents us with a typical HEIV model. It is useful to define a new measure of registration error that we will call the localization registration error (LRE). Recent advances in microscopy have made it possible to detect single molecules in a cellular environment, e.g. [31]–[33]. Localizing a feature (e.g. a single molecule) in ℐ₁ typically has its own errors associated with it. The LRE measures the combined effect of this localization error and the registration error to give the localization error of the feature registered in the second image, and is of importance to researchers [8], [25].

There have been recent attempts to tackle the EIV approach to rigid image registration for heteroscedastic errors in [34], [35] with the heteroscedastic EIV (HEIV) algorithm; an iterative procedure that finds an optimal solution to the HEIV model. Numerical Monte Carlo estimates of the TRE for the HEIV algorithm are considered in [11] and compared with a spatial stiffness model approach to the HEIV problem.

In this paper we consider the HEIV model for CP registration, the most general form of the registration problem (under the affine assumption). In Section II we rigorously formulate CP based image registration and formally define the TRE and LRE measures. In Section III, by taking the generalized maximum likelihood approach introduced in [36] as a starting point, we are able to show its equivalence to a heteroscedastic formulation of generalized least squares (GLS) and an EIV analogy of the least squares approach, here called ordinary least squares (OLS) in keeping with the terminology of [22] for iid EIV. In the case where error covariance matrices for each CP are a scalar multiple of a known matrix (e.g. multiples of the identity), we derive the closed form solution. In Section IV, asymptotic results derived in [36] are used to derive distributions for the registration parameters. In Section V these distributions are used to derive asymptotic distributions for the TRE and LRE. In Section VI we derive the asymptotic second order moments of the TRE and LRE in a microscopy setting, giving neat closed form expressions in terms of photon counts and experimental parameters. We verify these results in Section VII with numerical simulations and show asymptotic results are appropriate for relatively low (realistic) numbers of CPs. The method presented here is shown in Section VIII to outperform the traditional GLS method (that assumes homoscedastic measurement errors) when applied to real fluorescence microscopy imaging data. This paper represents a significant development upon the preliminary results first reported in [37].

A comprehensive list of abbreviations and notations used in this paper can be found in Tables II–V in Appendix A.

Table II. Abbreviations.

CP(s)	control point(s)
TRE	target registration error - Definition II. 1
EIV	errors-in- variables - (1)
TLS	total least squares
ML	maximum likelihood
HEIV	heteroscedastic errors-in-variables
LRE	localization registration error - Definition II.2
GLS	generalized least squares - Definition III. 1
OLS	ordinary least squares - Definition III.l
SPD	symmetric positive definite
WCGLS	weighted covariance generalized least squares - Section III-A

II. Formulating the Problem

Suppose K CPs are located in at true locations in ℐ₁ ⊆ ℝ^d at true locations {x_1,k ∈ ℐ₁,k = 1, …, K}, and in ℐ₂ ⊆ ℝ^d at true locations, such that {x_2,k ∈ ℐ₂,k = 1, …, K}, such that x_2,k = T(x_1,k) = Ax_1,k + s, k = 1, …, K, where A ∈ ℝ^{d × d} and s ∈ ℝ^d. In reality the positions of the CPs cannot be known exactly and must instead be measured. Consequently we observe the CP locations as {y_1,k ∈ ℐ₁,k = 1, …, K} and {y_2,k ∈ ℐ₂,k = 1, …, K}, where y_j,k = x_j,k + ∊_j,k, k = 1, …, K, j = 1, 2. The term ∊_j,k ∈ ℝ^d is a random variable known as the measurement error. Each measurement error is assumed zero mean and to have individual symmetric positive definite covariance matrix Ω_j,k. It is assumed that all measurement errors are pairwise independent across the CPs.

We define the ℝ^{d × K} matrices X_j ≡ [x_j,1, …, x_j,K], Y_j ≡ [y_j,1, …, y_j,K] and ℰ_j ≡ [∊_j,1, …, ∊_j,K], j = 1,2, and further define the stacked ℝ^{2d × K} matrices $X\equiv {[X_1^T,X_2^T]}^T$, $Y\equiv {[Y_1^T,Y_2^T]}^T$ and $ℰ\equiv {[{ℰ}_1^T,{ℰ}_2^T]}^T$. With this notation the system of equations can be conveniently represented as the single matrix equation

$$Y=\mathrm{\Lambda }{X}_1+\alpha {\mathbf{1}}_K^T+ℰ,$$ (1)

where ^T is the matrix transpose, α = [0^T, s^T]^T, Λ = [I_d, A^T]^T and 1_K is a column vector of length K with every element taking the value 1. The columns of X₁ are known as the independent variables and the columns of X₂ are the dependent variables. Models of type (1) where observations of both the dependent and independent variables contain measurement errors are EIV models.

If covariance matrices differ across CPs then they must be known [36]. (In [34] the covariance matrices are unknown, but still require estimation through bootstrapping methods). It is convenient at this point to assume the errors in model (1) follow two possible, but different statistical frameworks. The first shall be called the second-order framework .

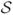Assumption I

Under 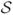, the columns of ℰ are independent with kth column ${∊}_k\equiv {[{∊}_{1,k}^T,{∊}_{2,k}^T]}^T$ having mean zero and known symmetric positive definite (SPD) covariance matrix

$${\mathrm{\Omega }}_k\equiv cov\{{∊}_k\}=\left[\begin{array}{cc}{\mathrm{\Omega }}_{1,k}& 0\\ 0& {\mathrm{\Omega }}_{2,k}\end{array}\right],$$ (2)

where cov{v} denotes the covariance matrix of a vector v.

The alternative framework shall be called the distributional framework .

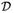Assumption II

Under 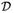, the columns of ℰ are independent and of known distribution with the kth column ${∊}_k\equiv {[{∊}_{1,k}^T,{∊}_{2,k}^T]}^T\underset{=}{\mathrm{d}}{N}_{2d}(\mathbf{0},{\mathrm{\Omega }}_k)$ where the SPD covariance matrix Ω_k is again known and of form (2). (Notation 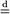means ‘equal in distribution’ and N_p(μ, Σ) denotes the p-variate normal distribution with mean μ and covariance Σ.)

With both 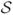and 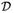, matrices {Ω_k, k = 1, …, K} are in general not equal. In this circumstance (1) is a HEIV model.

Given measurements Y, and assuming (1) models the system, the image registration process involves constructing estimators  and ŝ for parameters A and s, respectively. The method of estimation will be discussed in Section III.

A. Image Registration Errors

Suppose we have registered the pair of images with estimators  and ŝ, we need a measure of how successful the registration procedure has been. We begin by defining the commonly used target registration error [10]–[12], [14]–[16]. For anisotropic noise it is important to consider the error as a vector, rather than just its magnitude.

Definition II.1

The target registration error (TRE) τ : ℐ₁ → ℝ^d for an arbitrary point x₁ ∈ ℐ₁ with corresponding mapped position in ℐ₂ of x₂ = Ax₁ + s is given as τ(x₁) ≡ x₂−(Âx₁ + ŝ) = Ax₁ + s − (Âx₁ + ŝ).

We may find it more helpful to consider a related measure. Suppose we are interested in registering a specific feature (e.g. a single molecule) in ℐ₁ with true position x_1,F ∈ ℐ₁, in the second image the true position of this feature is x_2,F ∈ ℐ₂, with x_2,F = Ax_1,F + s. However, as with the CPs, the position of the feature in ℐ₁ is actually measured to be at y_1,F = x_1,F + ∊_1,F, where ∊_1,F is a measurement error with zero mean and covariance Ω_1,F. Therefore our estimator for the position of the feature in ℐ₂ is Ây_1,F + ŝ. A key question is; what is the error associated with localizing the feature in ℐ₂? To quantify this we define a new measure that we will call the localization registration error.

Definition II.2

For a feature in ℐ₁ with true and measured locations x_1,F and y_1,F = x_1,F + ∊_1,F respectively, the localization registration error (LRE) ℓ_F is defined as the difference between the true position and the registered position, i.e. ℓ_F ≡ x_2,F − (Ây_1,F + ŝ) = Ax_1,F + s − (Ây_1,F + ŝ).

Let us define the difference between the true and estimated values of the transform parameters as ΔA ≡ Â − A and Δs ≡ ŝ − s. It can be shown that

$$\tau (x_1)=-\mathrm{\Delta }A{x}_1-\mathrm{\Delta }s$$ (3)

$${\ell }_F=-A{∊}_{1,F}-\mathrm{\Delta }A{∊}_{1,F}-\mathrm{\Delta }A{x}_{1,F}-\mathrm{\Delta }s.$$ (4)

We can connect the two as ℓ_F = −Aε_1,F − ΔAε_1,F + τ(x_1,F). When localization of the feature in ℐ₁ can be achieved exactly, i.e. ∊_1,F = 0, then ℓ_F = τ(x_1,F). To derive the distribution of the TRE and LRE, and importantly their respective covariance matrices Ω_τ and Ω_ℓ, it is necessary to know the distributional properties of the terms ΔA and Δs.

III. Parameter Estimation

Parameter estimation for EIV models of type (1) when the columns of the measurement error matrix ℰ are iid is well established. The multivariate total least squares (TLS) (see [19]–[21]) or the multivariate generalized least squares (GLS) method [22] solve different but equivalent minimization problems. The parameter estimators that solve the respective minimization problems are exactly known and [22] also derived their asymptotic distributions for Gaussian measurement errors.

The reality is that the covariance matrices {Ω_k, k = 1, …, K} for the stacked measurement errors {∊_k, k = 1, …, K} are, in general, not identical and as such the iid assumption is invalid (although pointwise independence is still assumed). Hence, these estimators and the distributional results derived for the iid case are unsuitable for the image registration problem posed here. It is therefore necessary to take a more general approach to formulating the minimization problem and parameter estimation that can take into account heteroscedastic measurement errors. Definition III.1(i) is given in [36] and Definitions III.1(ii)–(iii) are given here as a generalization to the minimization problems considered in [22].

Definition III.1

Consider the observation matrix Y of measured CP locations that is assumed to arise from model (1) under Assumption I (second-order framework ).

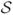1. Define likelihood function ℒ(A, s, X₁; Y) ≡ p(Y; A, s, X₁), where $p(Y;A,s,X_1)={\prod }_{k=1}^{K}p(y_k;A,s,x_{1,k})$ is the joint probability density function (pdf) for the columns $y_k\equiv {[y_{1,k}^T,y_{2,k}^T]}^T$ of observation matrix Y = [y₁, …, y_K]. The ML estimators ŝ^ml, Â^ml and ${\widehat{X}}_1^{\mathit{\text{ml}}}$ are defined as $\underset{s,A,X_1}{arg\; max}\mathcal{ℒ}(A,s,X_1;Y)$.

2. For any given A and s, the residual vectors r_k ≡ y_k − Λx_1,k − α are zero mean and have covariance matrix Ω_k, k = 1, …, K. Let $R(s,A,X_1;Y)=[{\mathrm{\Omega }}_1^{-\frac{1}{2}}{r}_1,\dots ,{\mathrm{\Omega }}_K^{-\frac{1}{2}}{r}_K]$ and let ║ · ║_F represent the Frobenius matrix norm, the ordinary least squares (OLS) estimators ŝ^ols, Â^ols and ${\widehat{X}}_1^{\mathit{\text{ols}}}$ are defined as $\underset{s,A,X_1}{\text{arg min}}{\Vert R(s,A,X_1;Y)\Vert }_F=\underset{s,A,X_1}{\text{arg min}}{\sum }_{k=1}^K{r}_k^T{\mathrm{\Omega }}_k^{-1}{r}_k$.

3. For any given A and s, the residual vectors q_k ≡ y_2,k − Ay_1,k − s are zero mean and have covariance matrix Φ_k = UΩ_kU^T, k = 1, …, K, where U = [−A, I_d]. Let $Q(s,A;Y)=[{\mathrm{\Phi }}_1^{-\frac{1}{2}}{q}_1,\dots ,{\mathrm{\Phi }}_K^{-\frac{1}{2}}{q}_K]$, the generalized least squares (GLS) estimators ŝ^gls, Â^gls are defined as $\underset{s,A}{\text{arg min}}{\Vert Q(s,A;Y)\Vert }_F=\underset{s,A}{\text{arg min}}{\sum }_{k=1}^K{q}_k^T{\mathrm{\Phi }}_k^{-1}{q}_k$.

The maximum likelihood solutions for models of type (1) are discussed in [36]. The number of unknown nuisance parameters {x_1,k, k = 1, …, K} increases linearly with the number of observations {y_k, k = 1, …, K} and are known as incidental parameters [38]. [36] adopts the generalized likelihood approach of [39] to estimate the structural parameters A and s in models containing incidental parameters and an iterative procedure for computing the estimators is given. Let vec(Z) for a r × s matrix Z = [z₁, …, z_s] be defined as the rs × 1 vector $[z_1^T,\dots ,z_s^T]$ and define β ≡ [s^T, vec(A)^T]^T.

Assumption III

Let D be a matrix with (m, n)th element given as E{∂² ℒ(A, s, X; Y)/∂β_m∂β_n}. All elements of D exist and D is non-singular.

Under Assumption III, these estimators of A and s are consistent [36], [40]. We now present the key result of this section, the proof of which is found in Appendix B.

Theorem III.2

Consider model (1) under Assumption I (second-order framework 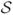), where the random vectors {∊_k, k = 1, …, K} are pairwise independent and vector ∊_k has covariance Ω_k, k = 1, …, K, then the solutions to the OLS and GLS minimization problems (see Definitions III.1(ii) and III.1(iii)) are identical to the ML estimators for the likelihood function under Assumption II (distributional framework 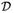) (i.e. Â^ml = Â^ols = Â^gls, ŝ^ml = ŝ^ols = ŝ^gls and ${\widehat{X}}_1^{\mathit{\text{ml}}}={\widehat{X}}_1^{\mathit{\text{ols}}}$), where ${∊}_k\underset{=}{\mathrm{d}}{N}_{2d}(\mathbf{0},{\mathrm{\Omega }}_k)$.

We note the OLS and GLS estimators do not depend on having Gaussian distributed measurement errors.

A. Weighted Covariance Generalized Least Squares

While iterative procedures are required to compute the ML/OLS/GLS estimators—see Definitions III.1(i),(ii) and (iii)—in the general case of heteroscedastic noise it is possible to derive an exact closed form expression for the ML/OLS/GLS estimators when we consider the following special case, which we term weighted covariance.

Assumption IV

For all k = 1, …, K, the SPD covariance matrix Ω_k of ∊_k—the kth column of the measurement error matrix ℰ—is given by Ω_k = η_kΩ₀ where Ω₀ is a known SPD matrix and η_k ∈ ℝ⁺ is known.

Assumption IV will be shown to be suitable in fluorescence microscopy image registration—see Section VI-A—and from a theoretical stance includes the important case of ${\mathrm{\Omega }}_k={\sigma }_k^2{I}_{2d}$. We introduce a further set of assumptions that are necessary for consistency of the estimators presented in Theorem III.3.

Assumption V

1. Define the scalar ${\mathrm{\gamma }}^{(K)}\equiv \left(\frac{1}{K}\right){\sum }_{k=1}^K{\eta }_k^{-1}$, vector ${\overline{y}}^{(K)}\equiv \left(\frac{1}{K}\right){\sum }_{k=1}^K{\eta }_k^{-1}{y}_k$ and matrix $W^{(K)}\equiv \left(\frac{1}{K}\right){\sum }_{k=1}^K{\eta }_k^{-1}(y_k-{\mathrm{\gamma }}^{(K)-1}{\overline{y}}^{(K)}){(y_k-{\mathrm{\gamma }}^{(K)-1}{\overline{y}}^{(K)})}^T$, then we assume $\underset{K\to \infty }{lim}{\mathrm{\gamma }}^{(K)}$ exists, and there exists ȳ and W such that $\overline{y}=\underset{K\to \infty }{lim}{\overline{y}}^{(K)}$ and $W=\underset{K\to \infty }{lim}{W}^{(K)}$ with probability one (wp1).

2. Define vectors ${\overline{x}}_1^{(K)}\equiv (\frac{1}{K}){\sum }_{k=1}^K{\eta }_k^{-1}{x}_{1,k}$, matrix ${\mathrm{\Xi }}^{(K)}\equiv \left(\frac{1}{K}\right){\sum }_{k=1}^K{\eta }_k^{-1}{x}_{1,k}{x}_{1,k}^T$ and matrix ${\mathrm{\Psi }}^{(K)}\equiv {\mathrm{\Xi }}^{(K)}-{\mathrm{\gamma }}^{(K)-1}{\overline{x}}_1^{(K)}{\overline{x}}_1^{(K)T}$ , then we assume there exists Ψ such that $\mathrm{\Psi }=\underset{K\to \infty }{lim}{\mathrm{\Psi }}^{(K)}$ wp1.

The proof of the following theorem is found in Appendix C.

Theorem III.3

Consider the multivariate EIV model (1) under Assumption I (second-order framework 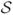) and Assumption IV (weighted covariance). Define ${\mathrm{\gamma }}^{(K)}\equiv \left(\frac{1}{K}\right){\sum }_{k=1}^K{\eta }_k^{-1}$, vector ${\overline{y}}^{(K)}\equiv \left(\frac{1}{K}\right){\sum }_{k=1}^K{\eta }_k^{-1}{y}_k$ and matrix $W^{(K)}\equiv \left(\frac{1}{K}\right){\sum }_{k=1}^K{\eta }_k^{-1}(y_k-{\mathrm{\gamma }}^{(K)-1}{\overline{y}}^{(K)}){(y_k-{\mathrm{\gamma }}^{(K)-1}{\overline{y}}^{(K)})}^T$. The eigendecomposition of $W^{(K)}{\mathrm{\Omega }}_0^{-1}$ is represented as $W^{(K)}{\mathrm{\Omega }}_0^{-1}=GE{G}^{-1}$ with E = diag{e₁, e₂, …, e_2d} where e₁ ≥ … ≥ e_2d are the ordered eigenvalues of $W^{(K)}{\mathrm{\Omega }}_0^{-1}$ and the columns of G are the corresponding eigenvectors. Making the partition $G=\left[\begin{array}{cc}{G}_{11}& G_{12}\\ G_{21}& G_{22}\end{array}\right]$, and assuming $G_{11}^{-1}$ exists, the ML/OLS/GLS estimators A of s and are given as

$$\widehat{A}=G_{21}{G}_{11}^{-1},\widehat{s}={\mathrm{\gamma }}^{(K)-1}\widehat{U}{\overline{y}}^{(K)},$$ (5)

where Û = [−Â, I_d]. Furthermore, provided Assumption V additionally holds then  and ŝ are consistent estimators of A and s, respectively.

IV. Asymptotic Distributions for Parameter Estimators

For the most general case where the covariance matrices {Ω_k, k = 1, …, K} are unrelated and unequal SPD matrices, [36] also derived the asymptotic distributions for the ML estimators of s and A under distributional framework 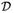. These estimators form the elements of the estimator β̂ for the parameter vector β ≡ [s^T, vec(A)^T]^T. Provided Assumption II (statistical framework 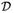) holds, i.e. measurement errors are Gaussian, the result will also be appropriate for the OLS and GLS estimators as given in Definitions III.1(ii) and III.1(iii). We introduce $\underrightarrow{K}$ to denote asymptotically equal in distribution with respect to K. The following is from [36].

Theorem IV.1

Consider the multivariate EIV model (1) under Assumption II (distributional framework 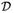), then given β̂ ≡ [ŝ^T, vec(Â)^T]^T is a consistent estimator of β ≡ [s^T, vec(A)^T]^T, defining Δβ ≡ β̂ − β we have $K^{\frac{1}{2}}\mathrm{\Delta }\beta \underrightarrow{K}{N}_{(d^2+d)}(\mathbf{0},B)$, where $B=\underset{K\to \infty }{lim}{B}^{(K)}$, with B^(K) = H^(K)−1 P^(K)(H^(K)−1)^T,

$$H^{(K)}=K^{-1}\sum _{k=1}^K\left[\begin{array}{cc}-{\mathrm{\Phi }}_k^{-1}& -(x_{1,k}^T\otimes {\mathrm{\Phi }}_k^{-1})\\ -\left(x_{1,k}\otimes {\mathrm{\Phi }}_k^{-1}\right)& -(x_{1,k}{x}_{1,k}^T\otimes {\mathrm{\Phi }}_k^{-1})\end{array}\right]$$ (6)

and

$$P^{(K)}=K^{-1}\sum _{k=1}^K\left[\begin{array}{cc}{\mathrm{\Phi }}_k^{-1}& -(x_{1,k}^T\otimes {\mathrm{\Phi }}_k^{-1})\\ -\left(x_{1,k}\otimes {\mathrm{\Phi }}_k^{-1}\right)& L\otimes {\mathrm{\Phi }}_k^{-1}\end{array}\right],$$ (7)

where Φ_k = UΩ_kU^T, U = [−A, I_d], $L={\left({\mathrm{\Lambda }}^T{\mathrm{\Omega }}_k^{-1}\mathrm{\Lambda }\right)}^{-1}+x_{1,k}{x}_{1,k}^T$ and ⊗ denotes the Kronecker product. Given β̂ is a consistent estimator of β, then H and P are consistently estimated by Ĥ^(K) and P̂^(K) respectively, calculated by substituting X̂₁ = [x̂_1,1, …, x̂_1,K] for X₁, and then  and ŝ into (6) and (7).¹

Using this result we are able to present the following corollary for the asymptotic distributions of the estimators in the special case of the weighted covariance property—see Section III-A. We introduce the notation [M]_mn for the (m, n)th element of a matrix M, and specifically use Δa_mn as short-hand for [ΔA]_mn. The proof of the following is found in Appendix D.

Corollary IV.2

Consider the multivariate EIV model (1) under Assumption II (distributional framework 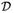) and Assumption IV (weighted covariance). Define vector ${\overline{x}}_1^{(K)}\equiv \left(\frac{1}{K}\right){\sum }_{k=1}^K{\eta }_k^{-1}{x}_{1,k}$, matrix ${\mathrm{\Xi }}^{(K)}\equiv \left(\frac{1}{K}\right){\sum }_{k=1}^K{\eta }_k^{-1}{x}_{1,k}{x}_{1,k}^T$, matrix ${\mathrm{\Psi }}^{(K)}\equiv {\mathrm{\Xi }}^{(K)}-{\mathrm{\gamma }}^{(K)-1}{\overline{x}}_1^{(K)}{\overline{x}}_1^{(K)T}$, matrix Φ₀ = UΩ₀U^T (where U = [−A, I_d]), and matrix ${\mathrm{\Theta }}^{(K)}={\mathrm{\Psi }}^{(K)-1}{({\mathrm{\Lambda }}^T{\mathrm{\Omega }}_0^{-1}\mathrm{\Lambda })}^{-1}{\mathrm{\Psi }}^{(K)-1}+{\mathrm{\Psi }}^{(K)-1}$. Let β̂ ≡ [ŝ^T, vec(Â^T)]^T be constructed from the estimators in (5), then under Assumption V (consistency) $K^{\frac{1}{2}}\mathrm{\Delta }\beta \underrightarrow{K}N(\mathbf{0},B)$, where $B=\underset{K\to \infty }{lim}{B}^{(K)},B^{(K)}\equiv (H_0^{(K)-1}{P}_0^{(K)}{H}_0^{(K)-1})\otimes {\mathrm{\Phi }}_0$ where

$$H_0^{(K)}=\left[\begin{array}{cc}-{\mathrm{\gamma }}^{(K)}& -{\overline{x}}_1^{(K)T}\\ -{\overline{x}}_1^{(K)}& -{\mathrm{\Xi }}^{(K)}\end{array}\right]$$ (8)

$$P_0^{(K)}=\left[\begin{array}{cc}{\mathrm{\gamma }}^{(K)}& -{\overline{x}}_1^{(K)T}\\ -{\overline{x}}_1& {\mathrm{\Xi }}^{(K)}+{({\mathrm{\Lambda }}^T{\mathrm{\Omega }}_0^{-1}\mathrm{\Lambda })}^{-1}\end{array}\right].$$ (9)

This gives the following key asymptotic identities as K → ∞

$$\begin{array}{c}cov\{K^{\frac{1}{2}}\mathrm{\Delta }{s}_m,K^{\frac{1}{2}}\mathrm{\Delta }{s}_n\}\to ({\mathrm{\gamma }}^{-1}+{\mathrm{\gamma }}^{-2}\theta ){[{\mathrm{\Phi }}_0]}_{mn}\\ cov\{K^{\frac{1}{2}}\mathrm{\Delta }{s}_l,K^{\frac{1}{2}}\mathrm{\Delta }{a}_{mn}\}\to {[{\mathrm{\gamma }}^{-1}\mathrm{\Theta }{\overline{x}}_1]}_n{[{\mathrm{\Phi }}_0]}_{\mathit{\text{ml}}}\\ cov\{K^{\frac{1}{2}}\mathrm{\Delta }{a}_{mn},K^{\frac{1}{2}}\mathrm{\Delta }{a}_{m^{\prime }{n}^{\prime }}\}\to {[\mathrm{\Theta }]}_{m{m}^{\prime }}{[{\mathrm{\Phi }}_0]}_{n{n}^{\prime }}.\end{array}$$

where we define $\theta \equiv {\overline{x}}_1^T\mathrm{\Theta }{\overline{x}}_1$ and the limits $\mathrm{\gamma }=\underset{K\to \infty }{lim}{\mathrm{\gamma }}^{(K)}$ and $\mathrm{\Theta }=\underset{K\to \infty }{lim}{\mathrm{\Theta }}^{(K)}$ (which both exist under Assumption V).

We note that in the iid case where Ω_k = σ²I_2d for all k = 1, …, K then the parameter estimation procedures (as outlined in Theorem III.3) and the asymptotic results (as outlined in Corollary IV.2) reduce to the results presented in [22] and thus forms a natural extension to well established GLS results.

V. A symptotic Distributions for TRE and LRE

Given the distributional results of Theorem IV.1 and Corollary IV.2 it is now possible to derive asymptotic distributions for the TRE and LRE—see Definitions II.1 and II.2, respectively. The proof of the following is omitted but follows directly from the linear combination of Gaussian random variables being itself Gaussian. The covariance matrix follows directly from (3), Theorem IV.1 and Corollary IV.2.

Corollary V.1

Under model (1), Assumption II (distributional framework 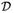) and Assumption III (consistency), for a point x_1,F ∈ ℐ₁ then $K^{\frac{1}{2}}\tau (x_{1,F})\underrightarrow{K}{N}_d(\mathbf{0},T)$ with (m, n)th element given as

$${[T]}_{mn}={[B]}_{mn}+\sum _{j=1}^d({[x_{1,F}]}_j{[B]}_{(j-1)d+m,n}+{[x_{1,F}]}_j{[B]}_{(j-1)d+n,m})+\sum _{j=1}^d\sum _{j^{\prime }=1}^d{[B]}_{(j-1)d+m,(j^{\prime }-1)d+n}{[x_{1,F}]}_j{[x_{1,F}]}_{j^{\prime }},$$ (10)

with B as defined in Theorem IV.1. Further to this, under Assumption IV (weighted covariance) and Assumption V (consistency), where Θ and Φ₀ are as defined in Corollary IV.2

$${[T]}_{mn}=({\mathrm{\gamma }}^{-1}+{\mathrm{\gamma }}^{-1}{\overline{x}}_1\mathrm{\Theta }{\overline{x}}_1^T){[{\mathrm{\Phi }}_0]}_{mn}+\sum _{j=1}^d{\left[x_{1,F}\right]}_j{\left[{\mathrm{\gamma }}^{-1}\mathrm{\Theta }{\overline{x}}_1\right]}_j{[{\mathrm{\Phi }}_0]}_{mn}+\sum _{j=1}^d{[x_{1,F}]}_j{[{\mathrm{\gamma }}^{-1}\mathrm{\Theta }{\overline{x}}_1]}_j{[{\mathrm{\Phi }}_0]}_{nm}+\sum _{j=1}^d\sum _{j^{\prime }=1}^d{[\mathrm{\Theta }]}_{mn}{[{\mathrm{\Phi }}_0]}_{j{j}^{\prime }}{[x_{1,F}]}_j{[x_{1,F}]}_{j^{\prime }}.$$ (11)

To consider distributional results for the LRE, it is necessary to decompose ℓ_F into two parts, ℓ_F = − Aε_1,F + z_F where z_F = − ΔAε_1,F − Δs − ΔAx_1,F. The term −Aε_1,F is a random variable with no dependency on the image registration process, being independent of ΔA and Δs (and hence K, CP locations and CP measurement errors). By contrast, each term in z_F is dependent on the image registration process, being a function of ΔA and Δs. It is important to note z_F and −Aε_1,F are independent. We can now provide the following asymptotic result for z_F, the proof of which is omitted but follows directly from the linear combination of Gaussian random variables being itself Gaussian. The covariance matrix follows directly from (4), Theorem IV.1 and Corollary IV.2.

Corollary V.2

Under model (1), Assumption II (distributional framework ) and Assumption III (consistency) provided ${∊}_{1,F}\underset{=}{\mathrm{d}}{N}_d(\mathbf{0},{\mathrm{\Omega }}_{1,F})$ where ε_1,F is the measurement error associated with localizing a feature in ℐ₁ with true location x_1,F, then $K^{\frac{1}{2}}{z}_F\underrightarrow{K}{N}_d(\mathbf{0},Z)$ with (m, n)th element of Z given as

$${[Z]}_{mn}={[T]}_{mn}+\sum _{j=1}^d\sum _{j^{\prime }=1}^d{[{\mathrm{\Omega }}_{1,F}]}_{j{j}^{\prime }}{[B]}_{(j-1)d+m,(j^{\prime }-1)d+n}.$$ (12)

Further to this, under Assumption IV (weighted covariance) and Assumption V (consistency),

$${[Z]}_{mn}={[T]}_{mn}+\sum _{j=1}^d\sum _{j^{\prime }=1}^d{\mathrm{\Theta }}_{mn}{[{\mathrm{\Phi }}_0]}_{j{j}^{\prime }}{[{\mathrm{\Omega }}_{1,F}]}_{j{j}^{\prime }}.$$ (13)

While the asymptotic distributions presented here are mathematically elegant, experimenters are keen to know the covariance matrices Ω_τ and Ω_ℓ of the TRE τ and LRE ℓ_F, respectively, in their registration procedure. It is therefore necessary to have results for finite K. Consider model (1) under Assumptions II (distributional framework ) and III (consistency), or Assumptions II, IV (weighted covariance) and V (consistency). Let x_1,F ∈ ℐ₁ be the true position of a feature that is localized at y_1,F = x_1,F + ∊_1,F, where ${∊}_{1,F}\underset{=}{\mathrm{d}}{N}_{2d}(\mathbf{0},{\mathrm{\Omega }}_{1,F})$. For “large K” we assume the asymptotics have been approximately met and hence from Corollaries V.1 and V.2, together with the independence of z_F and −Aε_1,F, the TRE τ(x_1,F) and LRE ℓ_F are both approximately d-dimensional normally distributed with zero mean and have respective approximate covariance matrices

$${\mathrm{\Omega }}_{\tau }\approx K^{-1}T,$$ (14)

$${\mathrm{\Omega }}_{\ell }\approx A{\mathrm{\Omega }}_{1,F}{A}^T+K^{-1}Z.$$ (15)

These approximations will be used in Sections VI and VII to investigate in more detail registration problems in single molecule microscopy.

VI. Image Registration Error Analysis for Single Molecule Microscopy

We apply the theory presented thus far in this paper to the important problem of assessing localization errors due to the registration process in a fluorescence microscopy setup. Registration is a common pre-processing step in microscopy experiments. Fiducial markers are used as CPs, these are bright, light emitting objects (e.g. fluorescent beads [8], [42]) that require estimation of their location. One example of a fluorescence microscopy experimental setup is to register a pair of different colored monochromatic images, for example to see if two different protein molecules colocalize e.g. [8], [25], [43], [44]. This is a multimodal registration problem. Fiducial markers are also used for drift correction between successive image frames [7]. This is a multitemporal registration problem.

As will now be discussed, the covariance matrix associated with localizing each CP/fiducial marker in each image is dependent on the number of photons associated with it that are detected at the sensor, and therefore presents us with a HEIV problem of type (1).

A. Measurement Errors

In [26] and [30] are lower bound expressions for the covariance matrix of the error in localizing an isolated point source emitting photons as an inhomogeneous Poisson process in the presence of background and readout noise, which in turn is shown in [26] to be a reasonable estimate for the true covariance matrix. These general expressions can be used with the estimation procedure of [36]—see Section III—for parameter estimation and TRE and LRE second-order moments can be computed with the generalized expressions of (10) and (12), respectively.

When imaging in the absence of background noise and readout noise the covariance matrix for the error in localizing a point source in the object space is given as N⁻¹ J, where N is the number of photons collected from the point source at the detector, and J is a SPD matrix that can be computed from experimental parameters including photon wavelength, numerical aperture and the point spread function of the optical system. For a non-pixelated detector J is diagonal, with pixels introducing off-diagonal terms. In the image space this covariance matrix becomes N⁻¹ ℳ² J, where ℳ is the known system magnification between the object space and the image space (a distance r in the object space is measured as ℳr in the image space). Further to this, it is shown in [45] that even in the presence of typical levels of background and readout noise the covariance matrix N⁻¹ ℳ² J is a suitable approximation to the covariance matrix for errors in localizing a bright (high signal to noise ratio) point source. Conventional fiducial markers used in fluorescence microscopy are typically bright and hence for the purposes of this paper we assume that they can be treated in this way.

We assume the image registration formulation of Section II and model (1) with the use of K fiducial markers for the CPs. The matrix J and system magnification ℳ are specific to the image and hence labeled J_j and ℳ_j, respectively, j = 1, 2. Suppose N_j,k photons are detected at the detector for fiducial marker k in ℐ_j, k = 1, …, K, j = 1,2. The measurement errors ∈_j,k, k = 1, …, K, j = 1, 2, are therefore assumed to have covariance Ω_j,k of the form Ω_j,k = (1/N_j,k)Ω_j,0, where ${\mathrm{\Omega }}_{j,0}\equiv {ℳ}_j^2{J}_j$ is a SPD matrix and universal for all CPs in ℐ_j. This gives the covariance matrix of ${∊}_k\equiv {[{∊}_{1,k}^T,{∊}_{2,k}^T]}^T$ as the block diagonal matrix Ω_k = diag{(1/N_1,k)Ω_1,0,(1/N_2,k)Ω_2,0}.

Consider the two common image registration scenarios described at the beginning of this section. The first is in registering two monochromatic images captured at the same time with two different sensors (multimodal). While the photon count associated with a single fiducial marker at two different wavelengths (i.e. in separate monochromatic images) will be different, it is reasonable to assume that there is a linear relation between the brightness of the marker in each image i.e. a marker that is bright in ℐ₁ is also bright in ℐ₂. Mathematically we say N_2,k = cN_1,k for all k = 1, …, k, where c > 0 is a constant of proportionality, suitable for all k = 1, …, k. The second scenario is performing drift correction by registering two images taken by the same sensor at different times (multitemporal). In this case, provided the brightness of the marker remains constant in the time between captures, then we assume N_1,k ≈ N_2,k (which is mathematically equivalent to the multimodal scenario with c = 1). The constant c need not be known to derive expressions for Ω_τ and Ω_ℓ, we just assume it exists.

With this assumption we have the situation where the covariance matrices of the measurement errors have the weighted co-variance property, i.e. they are scalar multiples of

$${\mathrm{\Omega }}_0=\left[\begin{array}{cc}{\mathrm{\Omega }}_{1,0}& 0\\ 0& c^{-1}{\mathrm{\Omega }}_{2,0}\end{array}\right]$$ (16)

with η_k = 1/N_1,k providing the scaling factor. This gives ${\mathrm{\gamma }}^{(K)}\equiv \left(\frac{1}{K}\right){\sum }_{k=1}^K{\eta }_k^{-1}=\left(\frac{1}{K}\right){\sum }_{k=1}^K{N}_{1,k}={\overline{N}}_1^{(K)}$, the mean photon count for the K CPs in ℐ₁. Fig. 1 summarizes the key steps involved in registering a pair of fluorescence microscopy images.

Fig. 1.

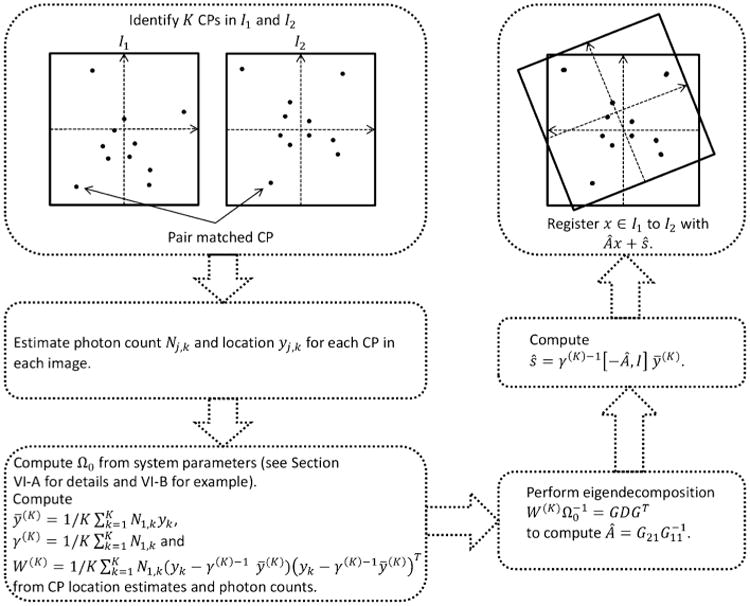
Flow chart summarizing the key steps in registering a pair of fluorescence microscopy images.

B. Microscopy LRE

We now consider the expressions for the TRE and LRE covariance matrices, Ω_τ and Ω_ℓ, respectively. Consider localizing a single molecule in ℐ₁ at point y_1,F, where y_1,F = x_1,F+∈_1,F with the measurement error having covariance Ω_1,F estimable from [26], and x_1,F being the true positional vector. We estimate its location (the registered position) in ℐ₂ as Ây_1,F + ŝ.

We begin by considering the following 2D model.

Assumption (i)

We model the CP measurement errors ${∊}_k\stackrel{\mathrm{d}}{=}{N}_4(0,{\mathrm{\Omega }}_k)$ where Ω_k is given in (2) with ${\mathrm{\Omega }}_{j,k}={\sigma }_{j,k}^2{I}_2=(1/N_{j,k}){ℳ}_j^2{\zeta }_j{I}_2$ where N_j,k is the photon count at the detector associated with CP k in ℐ_j, k = 1, …, K, j = 1, 2. ℳ_j is the known system magnification associated with ℐ_j. ζ_j is a known function of the point spread function, photon wavelength and numerical aperture. In multimodal registration ℳ_j and ζ_j will be different for each image, while in multitemporal registration they will be identical for both images. Ω₀ is of form (16) where ${\mathrm{\Omega }}_{j,0}={ℳ}_j^2{\zeta }_j{I}_2$.

Assumption (ii)

Consider the CP true positions {x_1,k, k = 1, …, K} to be K realizations of a random variable ∈ ℝ² with mean zero and covariance κ² I₂, and let associated photon counts be non-zero, finite and independent of CP positions.

Assumption (iii)

The affine transformation parameter A = SR represents a scaling S = ςI₂, ς ∈ ℝ⁺, combined with a unitary rotation or reflection (or a combination of both)R, i.e. R^T R = RR^T = I₂.

We will make use of the following Lemma, the proof of which is found in Appendix E.

Lemma VI.1

Let CP positions {x_1,k,k = 1, …, K} be K realizations of a random variable 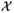∈ ℝ^d with finite mean μ and SPD covariance II, and let weights{η_k, k = 1, …, K} be K realizations of a random variable 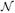with finite non-zero mean and finite variance independent of CP position. Let ${\overline{x}}_1^{(K)}\equiv \left(\frac{1}{K}\right){\sum }_{k=1}^K{\eta }_k^{-1}{x}_{1,k}$ and ${\mathrm{\Psi }}^{(\mathrm{K})}\equiv {\mathrm{\Xi }}^{(K)}-{\mathrm{\gamma }}^{(K)-1}{\overline{x}}_1^{(K)}{\overline{x}}_1^{(K)T}$ where ${\mathrm{\gamma }}^{(K)}\equiv \left(\frac{1}{K}\right){\sum }_{k=1}^K{\eta }_k^{-1}$ and ${\mathrm{\Xi }}^{(K)}\equiv \left(\frac{1}{K}\right){\sum }_{k=1}^K{\eta }_k^{-1}{x}_{1,k}{x}_{1,k}^T$, then ${\overline{x}}_1\equiv \underset{K\to \infty }{lim}{\overline{x}}_1^{(K)}=E\{{\mathcal{N}}^{-1}\}\mu$ and $\mathrm{\Psi }\equiv \underset{K\to \infty }{lim}{\mathrm{\Psi }}^{(K)}=E\{{\mathcal{N}}^{-1}\}\mathrm{\Pi }$, each wp1.

From Assumption (ii) and Lemma VI.1 x̄₁ = 0 and N̄₁ κ² I₂ will provide our estimate of Ψ, where ${\overline{N}}_1=\left(\frac{1}{K}\right){\sum }_{k=1}^K{N}_{1,k}={\mathrm{\gamma }}^{(K)}$. We introduce ${\overline{\sigma }}_j^2\equiv {ℳ}_j^2{\zeta }_j/{\overline{N}}_j$. Using these expressions for x̄₁ and Ψ and with the covariance matrix in Assumption (i) and the form of the transformation parameters in Assumption (iii), then from the definitions in Corollary IV.2 we have the identities Φ₀ = (ς²ζ₁ + c⁻¹ ζ₂)I₂ and $\mathrm{\Theta }={\overline{N}}_1^{-1}{\kappa }^{-4}{({\overline{\sigma }}_1^{-2}+{\varsigma }^2{\overline{\sigma }}_2^{-2})}^{-1}{I}_2+{\overline{N}}_1^{-1}{\kappa }^{-2}{I}_2$. Substituting these expressions into (11) and (13) gives

$${\left[T\right]}_{mn}=({\varsigma }^2{\overline{\sigma }}_1^2+{\overline{\sigma }}_2^2)(1+\frac{r_F^2}{{\kappa }^2}(1+\frac{1}{\frac{{\kappa }^2}{{\overline{\sigma }}_1^2}+\frac{{\varsigma }^2{\kappa }^2}{{\overline{\sigma }}_2^2}}\left)\right){\delta }_{mn},$$

$${[z]}_{mn}={[T]}_{mn}+({\varsigma }^2{\overline{\sigma }}_1^2+{\overline{\sigma }}_2^2)\frac{2{\sigma }_F^2}{{\kappa }^2}(1+\frac{1}{\frac{{\kappa }^2}{{\overline{\sigma }}_1^2}+\frac{{\varsigma }^2{\kappa }^2}{{\overline{\sigma }}_2^2}}){\delta }_{mn}$$

where r_F ≡ ║x_1,F║ is the radial distance of the feature/single molecule from the origin. Given the spread of the CPs (represented by κ) is much greater than the localization accuracy of the individual CPs (represented by σ̄₁ and σ̄₂) and the localization accuracy of the feature (represented by σ_F)—as is typical in microscopy—then the term $1/(\frac{{\kappa }^2}{{\overline{\sigma }}_1^2}+\frac{{\varsigma }^2{\kappa }^2}{{\overline{\sigma }}_2^2})$ and ${\sigma }_F^2/{\kappa }^2$ (both in the order of 10⁻⁶ for a typical microscopy experiment) can be considered negligible. From Corollaries V.1 and V.2 and assuming approximations (14) and (15) we state the following key result:

Proposition VI.2

For large K, under Assumptions (i)–(iii) the (m, n)th element of the covariance matrix of the TRE can be approximated as

$${[{\mathrm{\Omega }}_{\tau }]}_{mn}\approx K^{-1}({\varsigma }^2\frac{{ℳ}_1^2{\zeta }_1}{{\overline{N}}_1}+\frac{{ℳ}_2^2{\zeta }_2}{{\overline{N}}_2})(1+{\left(\frac{r_F}{\kappa }\right)}^2){\delta }_{mn}.$$ (17)

The (m, n) th element of the covariance matrix of the LRE can be approximated as

$${[{\mathrm{\Omega }}_{\ell }]}_{mn}\approx {[A{\mathrm{\Omega }}_{1,F}{A}^T]}_{mn}+K^{-1}({\varsigma }^2\frac{{ℳ}_1^2{\zeta }_1}{{\overline{N}}_1}+\frac{{ℳ}_2^2{\zeta }_2}{{\overline{N}}_2})(1+{\left(\frac{r_F}{\kappa }\right)}^2){\delta }_{mn}.$$ (18)

If the covariance Ω_1,F is itself representable as ${\sigma }_F^2{I}_2=({ℳ}_1^2{\varsigma }_1/N_{1,F})I_2$, where N_1,F is the photon count associated with the feature (molecule) imaged in ℐ₁, then in (18) we replace ${[A{\mathrm{\Omega }}_{1,F}{A}^T]}_{mn}$ with ${\varsigma }^2\frac{{ℳ}_1^2{\zeta }_1}{N_F}{\delta }_{mn}$. The covariance matrices Ω_τ and Ω_ℓ are both given with respect to image space ℐ₂. To express these matrices with respect to the object space coordinates we use ${ℳ}_2^{-2}{\mathrm{\Omega }}_{\tau }$ and ${ℳ}_2^{-2}{\mathrm{\Omega }}_{\ell }$.

Consider (17). We immediately notice that the TRE has an inverse dependence the number of CPs (denoted by K). Given extra CPs have similar localization errors to those already deployed, then increasing the number of CPs will improve the TRE covariance and it vanishes to zero as the number of CPs tends to infinity. It will be the case that for relatively small numbers of CPs the TRE improvements are significant by attempting to introduce more of them into the registration process. However, if we already have a large number of CPs then there is no significant gain in registration performance by small increases in their numbers. Specifically to microscopy, the TRE covariance will also vanish as the mean photon counts tend to infinity. Therefore extending exposure time will improve registration. Diagonal terms of the TRE covariance have dependency on CP measurement errors in both images, while off diagonal terms of the TRE covariance depend only on measurement errors in ℐ₂. In relation to the parameters A and s, the LRE and TRE covariance matrices are independent of rotation and translation and exhibit dependence only on scaling factor ς. The diagonal terms of the Ω_ℓ have lower bound ${\varsigma }^2\frac{{ℳ}_1^2{\zeta }_1}{N_F}$.

Localization accuracy is defined as the standard deviation of the molecule's object space localization error. One derivable quantity of interest to researchers will be the amount by which the registration process affects localization of a feature (single molecule) in object space.

Definition VI.3

Let ${\mathrm{\Omega }}_{1,F}=({ℳ}_1^2{\zeta }_1/N_{1,F})I_2$ be the covariance matrix for the measurement error in localizing a feature at true location x_1,F ∈ ℐ₁ and let Ω_ℓ be the covariance matrix of the LRE, then the localization loss ratio, Δ_F say, has (m, n)th element ${[{\mathrm{\Delta }}_F]}_{mn}\equiv {\left(\frac{{ℳ}_1^2{[{\mathrm{\Omega }}_{\ell }]}_{mn}}{{ℳ}_2^2{[{\mathrm{\Omega }}_{1,F}]}_{mn}}\right)}^{\frac{1}{2}}$.

From (18) we now give the following result for the registration induced error ratio:

Proposition VI.4

Under Assumptions (i)–(iii) the diagonal terms of the registration induced error ratio matrix, Δ_F, for a feature at true location x_1,F ∈ ℐ₁ are given as (for n = 1, 2)

$${[{\mathrm{\Delta }}_F]}_{nn}\approx {(\frac{{\varsigma }^2{ℳ}_1^2}{{ℳ}_2^2}+\frac{N_{1,F}}{K}(1+{\left(\frac{r_F}{\kappa }\right)}^2)\times ({\varsigma }^2\frac{{ℳ}_1^2}{{ℳ}_2^2}\frac{1}{{\overline{N}}_1}+\frac{{\zeta }_2}{{\zeta }_1}\frac{1}{{\overline{N}}_2}\left)\right)}^{\frac{1}{2}}.$$ (19)

Proposition VI.5

If we wish the localization accuracy of a registered feature in ℐ₂ to be restricted to p% more than the localization accuracy in ℐ₁, i.e. [Δ_F] ≤ 1 + (p/100), assuming strict equality in (19), we require the following inequality is satisfied:

$$\frac{1}{K}(\frac{{ℳ}_1^2}{{ℳ}_2^2}\frac{1}{{\overline{N}}_1}+\frac{{\zeta }_2}{{\varsigma }^2{\zeta }_1}\frac{1}{{\overline{N}}_2})\le \frac{1}{N_F(1+{\left(\frac{r_F}{\kappa }\right)}^2)}(\frac{{(1+\frac{p}{100})}^2}{{\varsigma }^2}-1).$$ (20)

Consider a multitemporal registration scenario, i.e. point spread functions, numerical aperture and photon wavelengths can be considered identical ζ₁ = ζ₂, ℳ₁ = ℳ₂ and N_1,k ≈ N_2,k for all k = 1, …, K. Assume A is a rotation with no scaling (i.e ς = 1) and we have an arbitrary translation s. Inequality (20) becomes $\frac{1}{K}(\frac{1}{{\overline{N}}_1}+\frac{1}{{\overline{N}}_2})\le \frac{1}{N_{1,F}(1+{\left(\frac{r_F}{\kappa }\right)}^2)}(\frac{2p}{100}+{\left(\frac{p}{100}\right)}^2)$. For example, suppose we image a single molecule in ℐ₁ with a photon count of N_1,F = 200 on the outer corner of a square ℐ₁ of dimensions l × l, then $r_F^2=l^2/2$. Consider CPs that are uniformly distributed in ℐ₁, then κ² = l²/12 and (r_F/κ)² = 6. To restrict the loss in localization accuracy of the single molecule due to the registration process to within 10% then we require K⁻¹((1/N̄₁) + (1/N̄₂)) ≤ 1.5 × 10⁻⁴. In such a scenario, 10 CPs with a mean photon count of 1350 would be sufficient. A single molecule at the center of ℐ₁ would undergo a loss in localization accuracy of only 0.71%.

C. Non-Diagonal Ω₀

Let us now consider the case where there exists off-diagonal terms in the matrices Ω_1,0 and Ω_2,0—see Section VI-A. Ω₀ is still of form (16) with ${\mathrm{\Omega }}_{j,0}=\left[\begin{array}{cc}{\sigma }_{j,0}^2& {\rho }_{j,0}\\ {\rho }_{j,0}& {\sigma }_{j,0}^2\end{array}\right]$. Assuming the analysis in Section VI-B on the order of magnitude of relative terms still holds, and matrix

$$R=\left[\begin{array}{cc}cos\left(\phi \right)& -sin\left(\phi \right)\\ sin\left(\phi \right)& cos\left(\phi \right)\end{array}\right]$$ (21)

represents a rotation by angle φ, we have the following

$${\left[{\mathrm{\Omega }}_{\tau }\right]}_{11}\approx K^{-1}({\varsigma }^2{\overline{\sigma }}_1^2-{\varsigma }^2{\overline{\rho }}_{1}sin(2\phi )+{\overline{\sigma }}_2^2)$$ (22)

$${\left[{\mathrm{\Omega }}_{\tau }\right]}_{22}\approx K^{-1}({\varsigma }^2{\overline{\sigma }}_1^2+{\varsigma }^2{\overline{\rho }}_{1}sin(2\phi )+{\overline{\sigma }}_2^2)$$ (23)

$${\left[{\mathrm{\Omega }}_{\tau }\right]}_{12}\approx K^{-1}({\varsigma }^2{\overline{\rho }}_{1}cos(2\phi )+{\overline{\sigma }}_2^2)$$ (24)

where ${\overline{\sigma }}_j^2={\sigma }_{j,0}^2/{\overline{N}}_j$, j = 1, 2, and ρ̄₁ = ρ_1,0/N̄₁. Equations (22), (23) and (24) show that when the covariance of the CP measurement errors contain off-diagonal terms, the covariance matrices of the TRE and LRE are dependent on the amount of rotation in the transform. For example, for φ ∈ (0, π/4) then [Ω_τ]₁₁ < [Ω_τ]₂₂, and for φ ∈ (−π/4, 0) we have [Ω_τ]₁₁ > [Ω_τ]₂₂. However, for small rotation angles φ the effect of off diagonal terms is negligible and the results in Propositions VI.2 and VI.4 will still be appropriate.

D. Geometrically Regular Control Point Configurations

In addition to control points that appear to the experimenter at random locations in the image space, it is also useful to consider the use of deterministic, geometrically regular CP locations set by the experimenter. These could take the form of a grid or ellipse (which includes the special case of a circle, provided pair correspondence between the CPs in both images can be guaranteed). We once again take the weighting factor for the covariance matrix (the reciprocal of the photon count) associated with a CP to be a realization of a random variable 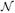and is completely independent of CP location.

Consider a square grid of side length a centered at the origin, where CPs are evenly spaced including positioning at each vertex (i.e. K is always square). It can be shown Ψ = E{ 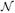⁻¹} (a²/3)I₂. In this situation (18) is valid, replacing κ with a²/3.

We also consider an ellipse centered at the origin with the major axis running along the x axis with major radius a and minor radius b, then it can the shown that Ψ = (1/2) E{ 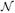⁻¹} diag {a²,b²}. Equation (18) is still valid, however for the case n = m = 1 then κ should be replaced by a. When n = m = 2, k is replaced b. With a > b, this implies that image registration is better resolved in the direction of the major axis as opposed to the direction of the minor axis.

VII. Simulations

Here we seek verification of the results in Section VI through Monte Carlo simulations. We consider a multitemporal registration scenario. ℐ₁ and ℐ₂ each comprise of 512 × 512 pixels, with each pixel being of dimensions 16 μm × 16 μm. The system magnification is ℳ₁ = ℳ₂ = 100, so in object space each pixel corresponds to a square of 0.16 μm × 0.16 μm. We consider the affine transformation T : ℐ₁ → ℐ₂, T(x) = Ax + s with A being a rotation of form (21) with φ = π/6 and s = [480, 480]^T (corresponding to 30 pixels in each direction).

We assume the measurement errors for the bead positions in ℐ_j have mean zero and covariance matrix (ℳ_jζ_j/N_j,k)I₂ where ${\zeta }_j={\lambda }_{j,\mathit{\text{em}}}^2/(4{\pi }^2{n}_F^2)$ [26]. λ_j,em is the wavelength of the photons observed in the jth image and is set as 0.520 μm for j = 1 and 2. n_F is the numerical aperture of the optical system and set to a typical value of 1.4 for both images. N_j,k is the photon count associated with the kth CP in the jth image. We consider a single molecule in ℐ₁ with true position x_1,F = (1600,1200) (giving r_F = ║x_1,F║ = 2000 μm), assuming localization is subject to measurement error with covariance ${\sigma }_F^2{I}_2$, where σ_F = 0.186 μm. Estimators  and ŝ were computed as outlined in Theorem III.3.

Simulations for a multimodal scenario would be carried out in an analogous manner. However, instead of the system parameters (photon wavelength, numerical aperture, system magnification) being the same for both images, they would in general differ between ℐ₁ and ℐ₂. These different values can be easily accounted for by calculating the covariance matrix Ω₀ appropriately and generating measurement errors with this covariance. LRE and TRE covariance terms can be calculated by substituting the system parameters into (17) and (18). Affine transformation parameters A and s are then estimated in an identical way.

A. Distributional Analysis

Fig. 2 is a quantile-quantile (Q-Q) plot for the distribution of the first element of the TRE. The curve is produced by ordering 10000 independent and normalized estimates (with respect to the theoretical variance) into increasing order of the size. The probability of a value less than the jth ordered estimate (or sample quantile) is p_j = j/10001 to a close approximation. The corresponding theoretical quantile of the normal distribution is the value υ_j such that p_j = F(υ_j), where F(·) is the cumulative distribution function of the normal distribution. The values υ₁, …, υ₁₀₀₀₀ are plotted on the x-axis against the ordered estimates for (a) K = 6, (b) 10, (c) 15, (d) 20 uniformly distributed CPs. Even for low numbers of CPs the fit to the derived “large K” distribution is striking, and similar results were seen for the second element of the TRE.

Fig. 2.

Q-Q plot for the first element of the TRE vector with normally distributed CP measurement errors, for (a) K = 6, (b) 10, (c) 15, (d) 20 CPs uniformly distributed in the image space. The (mostly obscured) dashed straight line marks the line of perfect fit.

We note that the LRE ℓ_F is comprised of contributions from the TRE τ and the measurement error ∊_1,F. The elements of the TRE have standard deviation of order $\frac{2}{\sqrt{K}}$ nm, whereas the elements of ∊_1,F have standard deviation of order 2 nm. The $\text{LRE}(\sim 2+(\frac{1}{\sqrt{K}})\text{nm})$ is therefore dominated by the Gaussian measurement error ∊_1,F. For this reason it is more meaningful to focus analysis on the distribution of the TRE.

B. Localization Analysis

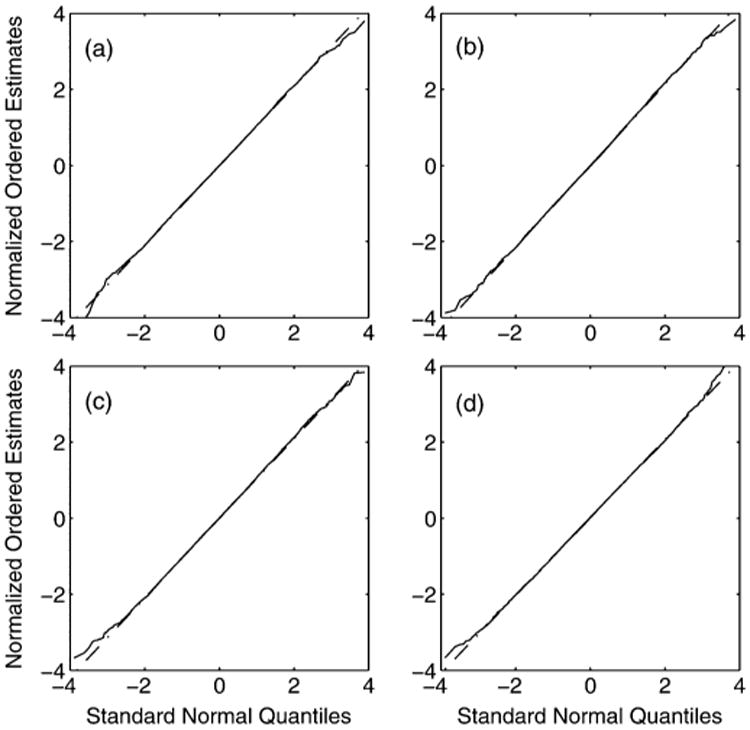
We now consider four different CP configurations; CP locations are (a) normally distributed about the center of ℐ₁ with covariance κ²I₂, κ = 1350 μm, (b) uniformly distributed in ℐ₁, (c) arranged in an ellipse with major radius 4000 μm and minor radius 3000 μm, and (d) arranged in a square grid of side 8100 μm. Due to restrictions on the possible values of K in (d) we consider simulations where K takes the value of the square numbers from 4 to 64 inclusive. For configurations (a)–(d) the sample standard deviation of [ℓ_F]₁ for 100000 Monte Carlo simulations is computed for each value of K, while keeping the same uniform distribution that the CP photon counts are sampled from. The results are plotted in Fig. 3, as are the values predicted by (18). The dashed line marks the theoretical lower bound ${\sigma }_F={\left({\left[{\mathrm{\Omega }}_{1,F}\right]}_{11}\right)}^{\frac{1}{2}}$ of the LRE standard deviation.

Fig. 3.

The sample standard deviation of ℓ_F (from 100000 simulations) in object space dimensions is plotted as a function of the number of CPs K for (a) normally distributed, (b) uniformly distributed, (c) elliptical and (d) grid CP configurations (see Section VII-B for more details). The ‘+’ represents the sample standard deviation of the LRE (in units nanometers). The circles represent the standard deviation as predicted by Corollary V.2. The ‘×’ shows the standard deviation as predicted with (18). The dashed line marks the theoretical bound σ_F.

The accuracy for normally and uniformly distributed CPs (scenarios (a) and (b)) shows some deviation from the large sample results for small K ∼ 9, and in such a circumstance (20) is not totally appropriate. A better interpretation is; at the very least this inequality must be satisfied. However, for larger values of K this provides an excellent guide to experimenters. The elliptical and grid configurations (scenarios (c) and (d)) show a much closer fit for small K compared to the random configurations (secnarios (a) and (b)). This is most likely due to the random positioning of the CPs adding to the overall variance of the parameter estimators. In the deterministic case (20) is an excellent guide to experimenters.

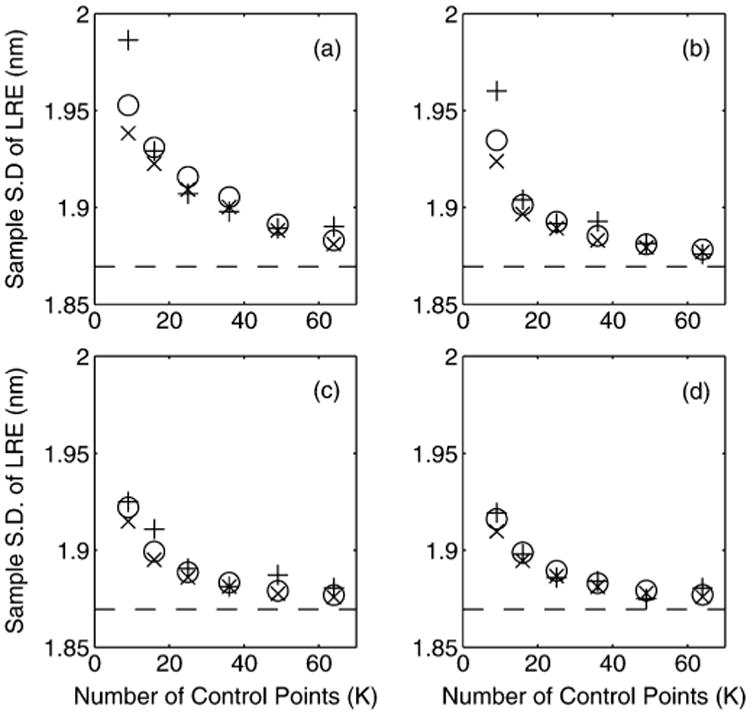
In Fig. 4 we keep the number of CPs constant at K = 16 and change the mean of the uniform distribution from which the photon counts are sampled. For configurations (a)–(d), the sample standard deviation of the first element of the LRE for ℒ_F 100000 Monte Carlo simulations is computed. We also plot the values as predicted by (18). The dashed line marks the theoretical lower bound ${\sigma }_F={({[{\mathrm{\Omega }}_{1,F}]}_{11})}^{\frac{1}{2}}$ of the LRE standard deviation. By increasing the photon count, the asymptotic results can be readily achieved and the key results presented in this paper provide an excellent guide.

Fig. 4.

The sample standard deviation of ℓ_F (from 100000 simulations) in object space dimensions is plotted as a function of N̄₁, the mean photon count for the CPs in I₁, for a constant K = 16 with (a) normally distributed, (b) uniformly distributed, (c) elliptical and (d) grid CP configurations (see Section VII-B for more details). The ‘+’ represents the sample standard deviation of the LRE (in units nanometers). The circles represent the standard deviation as predicted by Corollary V.2. The ‘×’ shows the standard deviation as predicted with (18). The dashed line marks the theoretical bound σ_F.

We have shown in Section VI-B that for a diagonal covariance matrix Ω₀, as is the case in our simulations, then the LRE and TRE are independent of rotation angle and translation in the affine transformation. In Fig. 5 we keep the number of CPs constant at K = 16, the mean of the uniform distribution from which the photon counts are sampled is kept constant and with affine transformation parameter A = R of form (21) change the angle of rotation φ. For each rotation angle the translation is by a random amount. For configurations (a)–(d), the sample standard deviation of the first element of the LRE ℒ_F for 100000 Monte Carlo simulations is computed. We also plot the values as predicted by (18). The dashed line marks the theoretical lower bound ${\sigma }_F={({[{\mathrm{\Omega }}_{1,F}]}_{11})}^{\frac{1}{2}}$ of the LRE standard deviation. It is clear that the standard deviation of the LRE is invariant to rotation angle and translation, as predicted.

Fig. 5.

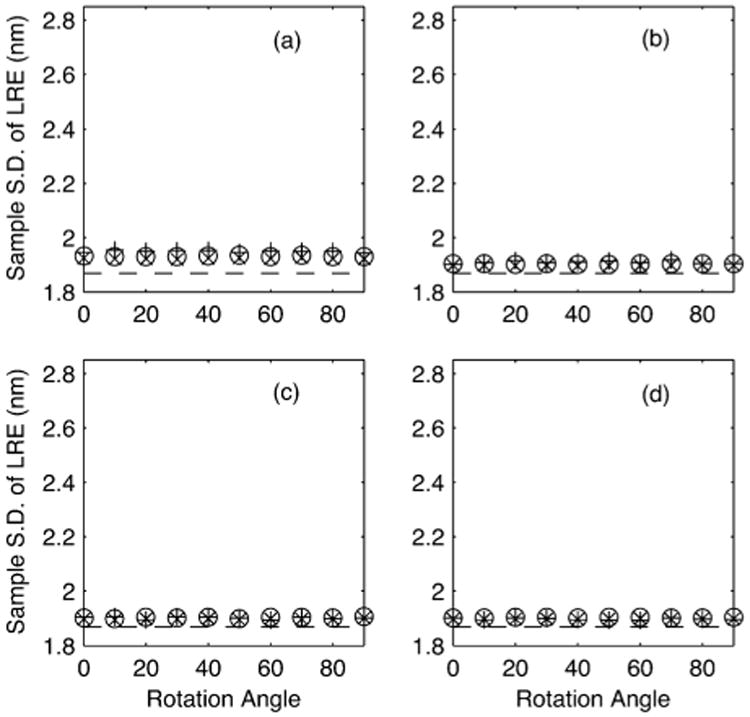
The sample standard deviation of ℓ_F (from 100000 simulations) in object space dimensions is plotted as a function of rotation angle φ (in degrees) when A = R with R of form (21), for a constant K = 16 with (a) normally distributed, (b) uniformly distributed, (c) elliptical and (d) grid CP configurations (see Section VII-B for more details). The ‘+’ represents the sample standard deviation of the LRE (in units nanometers). The circles represent the standard deviation as predicted by Corollary V.2. The ‘×’ shows the standard deviation as predicted with (18). The dashed line marks the theoretical bound σ_F.

C. Non-Gaussian Measurement Errors

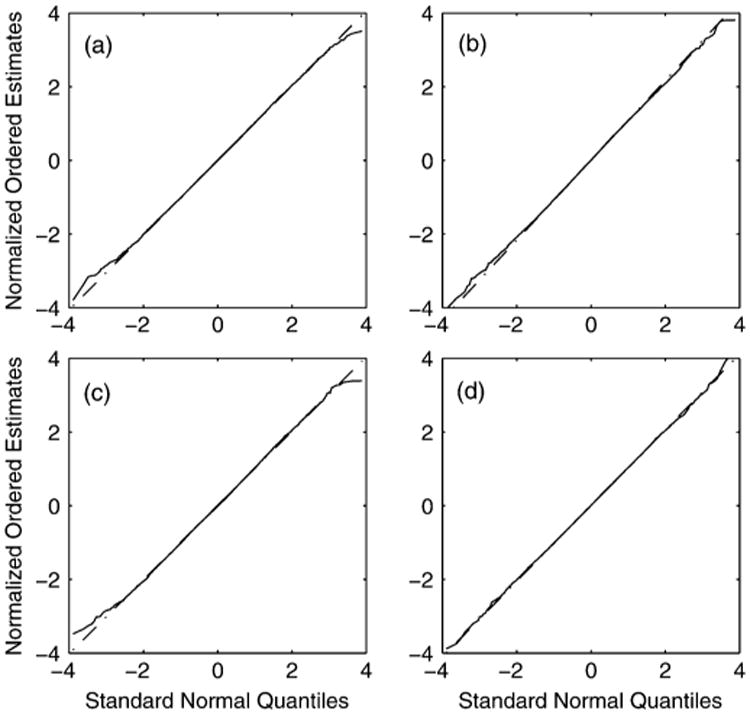
The derived Gaussian distribution for the TRE presented in this paper is given under the assumption that measurement errors in localizing CPs are themselves Gaussian distributed. The measurement errors in a microscopy experiment are often assumed to be Gaussian—which is justified by large sample results and evidence based on the analysis of experimental and simulated data—it is nevertheless useful to know how robust the results of this paper are under deviations away from this Gaussian assumption. We therefore consider the TRE when measurement errors are uniformly distributed, an extreme deviation from Gaussianity.

Fig. 6 gives Q-Q plots to compare the first element of the TRE against the normal distribution. Labels (a)–(d) refer to the same values of K as with Fig. 2. Even with such a pronounced change in the distribution of the CP measurement errors the plots show the normal distribution is still an appropriate approximation for the TRE, although the exact distribution is unknown.

Fig. 6.

Q-Q plot for the first element of the TRE vector with uniformly distributed CP measurement errors, for (a) K = 6, (b) 10, (c) 15, (d) 20 CPs uniformly distributed in the image space. The (mostly obscured) dashed straight line marks the line of perfect fit.

VIII. Imaging Data and Method Comparison

We now apply the algorithm presented in this paper to real imaging data. Analysis has been conducted by performing image registration between a pair of images of the same object space taken by two separate cameras (multimodal registration). We have 599 repeat captures, resulting in 599 pairs of images to register. The registration was performed using 27 TetraSpeck fluorescent beads visible in both fields of view. System parameters were identical for each image, with system magnifications of 63, numerical apertures equal to 1.45 and the photon wavelength distributions peaking at 638 nm.

To calculate the TRE for each of the 599 registrations we need to know the exact coordinates of a point in each image that perfectly map to one another under the affine transformation. Without knowledge of the true transformation parameters this is not available and we instead isolate one of the beads and average its location over the 599 images for each camera. This will give a very high precision estimate of its true location in each image and these coordinates are used as the reference points for the TRE. The TRE is then calculated for each of the 599 registration experiments using two different methods.

The first method is the weighted covariance GLS method presented in this paper (developed in Section III-A and implemented on simulations in Section VII). This method uses the system parameters quoted above and the point spread function to calculate covariance matrix Ω₀ and takes into account both the photon count and location estimates for each bead to compute estimates of the affine transformation parameters A and s—see Fig. 1 for details.

The second method used is the traditional GLS method presented in [22, page 28] (that assumes homoscedastic measurement errors and is equivalent to the ML approach to image registration used by [23]). This method uses just the location estimates for each bead in estimating A and s.

For both methods, the sample standard deviation of the TRE for the x- and y-direction is computed and displayed in Table I. This was repeated 27 times, each time isolating a different bead to act as the reference point.

Table I.

Sample standard deviations of TRE in the x- and y-directions from 599 registration experiments (units: nm), each row is for one of 27 different coordinate points. ‘WCGLS’ columns are using the New weighted covariance generalized least squares presented in This paper. ‘GLS’ columns are using traditional generalized least Squares that assumes homoscedastic measurement errors. ‘GAIN’ Columns give the precentage improvement in the WCGLS method Over the GLS method

WCGLS (x) - nm	GLS (x) - nm	Gain (%)	WCGLS (y) - nm	GLS (y) - nm	Gain (%)
4.142	4.283	3.399	4.003	4.342	8.478
3.942	4.039	2.446	3.762	4.095	8.873
4.030	4.736	17.517	4.111	4.531	10.208
3.657	4.238	15.880	3.640	4.001	9.926
2.972	3.073	3.393	2.659	2.906	9.292
2.709	2.896	6.916	2.361	2.581	9.331
3.124	3.187	2.026	2.846	3.156	10.886
3.913	4.082	4.326	3.801	4.256	11.954
2.338	2.436	4.206	1.842	2.021	9.717
3.436	3.844	11.897	3.194	3.573	11.851
3.743	4.207	12.382	3.555	3.984	12.055
4.279	4.684	9.461	4.355	4.896	12.426
3.363	3.660	8.850	3.302	3.692	11.811
2.865	3.053	6.555	2.441	2.693	10.343
2.472	2.566	3.796	1.976	2.145	8.554
3.623	3.865	6.699	3.300	3.657	10.842
3.404	3.772	10.812	3.403	3.789	11.352
2.757	2.853	3.484	2.364	2.536	7.276
2.896	3.146	8.623	2.733	2.974	8.800
3.154	3.274	3.800	2.859	3.053	6.791
4.674	4.857	3.929	4.401	4.840	9.985
3.449	3.831	11.060	3.462	3.750	8.318
3.282	3.537	7.774	3.162	3.390	7.187
3.282	3.465	5.592	3.085	3.292	6.717
3.687	3.985	8.074	3.572	3.870	8.349
3.987	4.043	1.401	3.799	4.201	10.595
2.590	2.832	9.359	2.183	2.412	10.514

The results show the weighted covariance GLS methods presented here consistently outperforms the traditional GLS method. Comparisons with the theoretical results would be misleading because of a lack of access to the ground truth and photon counts significantly differ across the 599 samples.

IX. Concluding Remarks

We have used a heteroscedastic generalized least squares approach to point-based image registration. This has allowed an asymptotic analysis of the distributional properties of the TRE and the LRE; a new measure of registration success that is of interest in microscopy. By considering the weighted covariance we have derived closed form expressions for both the registration estimators and the large sample TRE/LRE distributions. These distributions can be used for determining confidence intervals of errors induced by registration.

Fluorescence microscopy image registration was used as a motivating example. Here we have derived the TRE and LRE covariance matrices in terms of the number of CPs, their spread in the object space, and associated photon counts. The relative loss in localization accuracy of a imaged single molecule was further derived. When the covariance matrices of the CP measurement errors are multiples of the identity then there is no dependence on the translation or rotation components of the affine transformation. When they have off-diagonal terms then the TRE/LRE are dependent on the rotation part of the affine transformation but still remain independent of the translation. Theoretical results have been verified with Monte Carlo simulations and even for relatively small values of K simulations show excellent agreement with the theory. However, small but notice able discrepancies between the simulations and large sample expressions do occur for small K and in such a situation the results presented here should be considered a useful guide rather than exact.

Using real imaging data the weighted covariance GLS method presented here has been shown to consistently outperform the traditional GLS method.

Biographies

E. A. K. Cohen received the M.Phys. degree in mathematics and physics from the University of Warwick, Coventry, U.K., in 2005 and the Ph.D. degree in 2011 from Imperial College London, U.K., in statistics. He worked as a Signal Processing Scientist at QinetiQ, Malvern, U.K., before starting his Ph.D. in 2007. In 2011, he joined the University of Texas (UT), Dallas, in the Ward-Ober lab based at UT Southwestern Medical Center at Dallas as a Postdoctoral Research Scholar. He is currently a Lecturer in Statistics at Imperial College London. His research interests include multivariate signal and image processing, and their applications to the natural sciences.

R. J. Ober (S'87-M'88-SM'95) received the Ph.D. degree in electrical engineering from the University of Cambridge, U.K., in 1987.

From 1987 to 1990, he was a Research Fellow at Girton College and the Engineering Department, University of Cambridge. In 1990, he joined the University of Texas at Dallas, Richardson, where he is currently a Professor with the Department of Electrical Engineering and the Department of Bioengineering. He is also Adjunct Professor at the University of Texas Southwestern Medical Center, Dallas. His research interests include signal and imaging processing, and their applications to biological problems, fluorescence microscopy and biosensors.

Appendix A.

Table II gives a list of standard abbreviations. Table III gives a list of common operators and functions. Table IV gives a list of standard notations. Table V gives a list of fluorescence microscopy notations.

Table III. Operators and Functions.

cov{·}	covariance matrix of a random vector
Np(μ, Σ)	p-dimensional multivariate normal distribution with mean μ and covariance matrix Σ
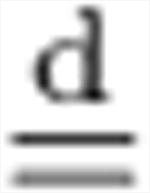
	equal in distribution
ℒ(·)	likelihood function
p(·)	probability density function
vec(·)	vec(Z) of a r × a matrix Z = [z1, …, zs] is the rs × 1 vector $[z_1^T,\dots ,z_s^T]$
E{·}	expectation operator
⊗	Kronecker product
δij	δij equals zero for i ≠ j and equals one for i = j.

Table IV. Key Notation.

Notation	Type	Definition
d	d ∈ {2,3}	dimension of image space
ℐj	subset of ℝd	image space j, j = 1,2
A	ℝd × d	matrix valued affine transformation parameter
s	ℝd	vector valued affine transformation parameter
K	ℕ	number of CPs
xj,k	ℝd	true location of kth CP (k = 1, …K) in ℐj
∊j,k	ℝd	random measurement error associated with localizing kth CP in ℐj
yj,k	ℝd	measured location of kth CP in ℐj, yj,k = xj,k + ∊j,k
Ωj,k	ℝd × d	Ωj,k = cov{∊j,k}
Xj	ℝd × K	Xj = [xj, 1, …, xj,k]
ℰj	ℝd × K	ℰj = [∊j, 1, …, ∊j,k]
Yj	ℝd × K	Yj = [ yj, 1, …, yj,k]
X	ℝ2d × K	$X={[X_1^T,X_2^T]}^T$
ℰ	ℝ2d × K	$ℰ={[{ℰ}_1^T,{ℰ}_2^T]}^T$
Y	ℝ2d × K	$Y={[Y_1^T,Y_2^T]}^T$
Λ	ℝ2d × d	Λ = [Id, AT]T
0	ℝd	0 = [0, 0]T or [0, 0, 0]T
α	ℝ2d	α [0T, sT]T
1K	ℝK	1 = [1, 1, …, 1]T
∊k	ℝ2d	${∊}_k={[{∊}_{1,k}^T,{∊}_{2,k}^T]}^T$
Ωk	ℝ2d × 2d	Ωk = cov{∊k}
τ(·)	ℝd ↦ ℝd	TRE
xj,F	ℝd	true location of a feature in ℐj
∊j,F	ℝd	random measurement error associated with localizing a feature in ℐj
yj,F	ℝd	measured location of a feature in ℐj, yj,F = xj,F + ∊j,F
Ω1,F	ℝd × d	ΩF = cov{∊1,F}
Â	ℝd × d	estimator of A
ŝ	ℝd	estimator of s
ℓF	ℝd	LRE for a feature
ΔA	ℝd × d	ΔA = Â − A
Δs	ℝd	Δs = ŝ − s
Ωτ	ℝd × d	Ωτ = cov{τ}
Ωℓ	ℝd × d	Ωℓ = cov{ℓF}
yk	ℝ2d	$yk={[y_{1,k}^T,y_{2,k}^T]}^T$
U	ℝd×2d	U = [−A, Id]
Φk	ℝd×d	Φk = UΩkUT
β	ℝ(d+d2)	β = [sT, vec(A)T]T
ηk	ℝ+	scalar and matrix valued quantities when we have the property Ωk = ηkΩ0
Ω0	ℝ2d × 2d
γ(K)	ℝ+	${\mathrm{\gamma }}^{(K)}=(1/K){\sum }_{k=1}^K{\eta }_k^{-1}$
γ		γ = limK → ∞ γ(K)
ȳ(K)	ℝ2d	${\overline{y}}^{(K)}=(1/K){\sum }_{k=1}^K{\eta }_k^{-1}yk$
ȳ		ȳ = limK → ∞ ȳ(K)
W(K)	ℝ2d × 2d	$W^{(K)}=(1/K){\sum }_{k=1}^K{\eta }_k^{-1}\times (y_k-{\mathrm{\gamma }}^{(K)-1}{\overline{y}}^{(K)})\times {(y_k-{\mathrm{\gamma }}^{(K)-1}{\overline{y}}^{(K)})}^T$
W		W = limK → ∞ W(K)
${\overline{x}}_1^{(K)}$	ℝd	${\overline{x}}_1^{(K)}=(1/K){\sum }_{k=1}^K{\eta }_k^{-1}{x}_{1,k}$
Ξ(K)	ℝd × d	${\mathrm{\Xi }}^{(K)}=(1/K){\sum }_{k=1}^K{\eta }_k^{-1}{x}_{1,k}{x}_{1,k}^T$
Ψ(K)	ℝd × d	${\mathrm{\Psi }}^{(K)}={\mathrm{\Xi }}^{(K)}-{\mathrm{\gamma }}^{(K)-1}{\overline{x}}_1^{(K)}{\overline{x}}_1^{(K)T}$
Ψ		Ψ = limK → ∞ Ψ(K)
Θ(K)	ℝd × d	${\mathrm{\Theta }}^{(K)}={\mathrm{\Psi }}^{(K)-1}{({\mathrm{\Lambda }}^T{\mathrm{\Omega }}_0^{-1}\mathrm{\Lambda })}^{-1}{\mathrm{\Psi }}^{(K)-1}+{\mathrm{\Psi }}^{(K)-1}$
Θ		Θ = limK → ∞ Θ(K)
θ	ℝ	$\theta ={\overline{x}}_1^T\mathrm{\Theta }{\overline{x}}_1$
Φ0	ℝd × d	Φ0 = UΩ0UT

Table V. Fluorescence Microscopy Notation.

Notation	Type	Definition
Nj,k	ℕ	photon count associated with kth CP in ℐj
Nj	ℤ+	mean photon count for CPs in ℐj
ℳj	ℝ+	system magnification for ℐj
λj,em	ℝ+	photon wavelength associated with ℐj
ζj	ℝ+	known function of the point spread function, photon wavelength and numerical aperture for ℐj
κ2	ℝ+	x/y-direction variance of randomly positioned CPs
R	ℝd ×d	a rotation matrix
ς	ℝ+	scaling constant for A of the form ςR
${\overline{\sigma }}_j^2$	ℝ+	${\overline{\sigma }}_j^2={\mathcal{ℳ}}_j^2{\zeta }_j/{\overline{N}}_j$
rF	ℝ+	radial distance of single molecule from origin of ℐ1

Appendix B.

Proof of Theorem III.2

Under Assumption II, the 4D multivariate Gaussian pdf for measurement vector $y_k={[y_{1,k}^T,y_{2,k}^T]}^T$ is given as

$$p(y_k)={\left(2\pi \right)}^{-\frac{1}{2}}{\left|{\mathrm{\Omega }}_k\right|}^{-\frac{1}{2}}{e}^{-\frac{1}{2}{(y_k-{\mu }_k)}^T{\mathrm{\Omega }}_k^{-1}(y_k-{\mu }_k)}$$

where μ_k = Λx_{1, k} + α, k = 1, …, K, Λ = [I_d, A^T]^T. The likelihood function ℒ(A, s, X₁; Y) for A, s and X₁ is given as

$${\left(2\pi \right)}^{-K/2}\left[\prod _{k=1}^K{\left|{\mathrm{\Omega }}_k\right|}^{-\frac{1}{2}}\right]e^{-\frac{1}{2}{\sum }_{k=1}^K{(y_k-{\mu }_k)}^T{\mathrm{\Omega }}_k^{-1}(y_k-{\mu }_k)}.$$

The parameter values that maximize ℒ(A, s, X₁; Y) are those that minimize the term ${\sum }_{k=1}^K{(y_k-{\mu }_k)}^T{\mathrm{\Omega }}_k^{-1}(y_k-{\mu }_k)$. Noticing

$$\sum _{k=1}^K{(y_k-{\mu }_k)}^T{\mathrm{\Omega }}_k^{-1}(y_k-{\mu }_k)=\sum _{k=1}^K{r}_k^T{\mathrm{\Omega }}_k^{-1}{r}_k=r,$$

it follows that Â_ml = Â_ols, ŝ_ml = ŝ_ols and ${\widehat{X}}_1^{\mathit{\text{ml}}}={\widehat{X}}_1^{\mathit{\text{ols}}}$.

Lemma B.1

Let the kth column of X̂₁ be given as

$${\widehat{x}}_{1,k}={\left({\mathrm{\Lambda }}^T{\mathrm{\Omega }}_k^{-1}\mathrm{\Lambda }\right)}^{-1}{\mathrm{\Lambda }}^T{\mathrm{\Omega }}_k^{-1}(y_k-\alpha ),$$ (25)

then for any fixed A and s, r(s, A, X̂₁; Y) ≤ r(s, A, X₁; Y) and ℒ(A, s, X̂₁; Y) ≥ ℒ(A, s, X₁; Y).

Proof

Let $r_k\equiv {(y_k-{\mu }_k)}^T{\mathrm{\Omega }}_k^{-1}(y_k-{\mu }_k)$, then $\frac{\partial r}{\partial x_{1,k}}=\frac{\partial r_k}{\partial x_{1,k}}=-2\mathrm{\Lambda }{\mathrm{\Omega }}_k^{-1}{y}_k+2{\mathrm{\Lambda }}^T{\mathrm{\Omega }}_k^{-1}\mathrm{\Lambda }{x}_{1,k}+2{\mathrm{\Lambda }}^T{\mathrm{\Omega }}_k^{-1}\alpha$. The conditional estimator x̂_{1, k} is the value of x_{1, k} that gives $\frac{\partial r}{\partial x_{1,k}}=\frac{\partial r_k}{\partial x_{1,k}}=0$. This gives ${\widehat{x}}_{1,k}={\left({\mathrm{\Lambda }}^T{\mathrm{\Omega }}_k^{-1}\mathrm{\Lambda }\right)}^{-1}{\mathrm{\Lambda }}^T{\mathrm{\Omega }}_k^{-1}(y_k-\alpha )$ and the result follows.

The ML estimators (under Assumption II) and OLS estimators (under Assumption I) for A and s are the values that minimize $r(s,A,{\widehat{X}}_1;Y)={\sum }_{k=1}^K{\stackrel{\sim }{r}}_k^T{\stackrel{\sim }{r}}_k$ where ${\stackrel{\sim }{r}}_k={\mathrm{\Omega }}_k^{-\frac{1}{2}}{r}_k$. Substituting in (25) gives

$${\stackrel{\sim }{r}}_k=(I-{\mathrm{\Omega }}_k^{-\frac{1}{2}}\mathrm{\Lambda }{\left({\mathrm{\Lambda }}^T{\mathrm{\Omega }}_k^{-1}\mathrm{\Lambda }\right)}^{-1}{\mathrm{\Lambda }}^T{\mathrm{\Omega }}_k^{-\frac{1}{2}}){\mathrm{\Omega }}_k^{-\frac{1}{2}}(y_k-\alpha ).$$ (26)

We note that $[{\mathrm{\Omega }}_k^{-\frac{1}{2}}\mathrm{\Lambda },{\mathrm{\Omega }}_k^{\frac{1}{2}}{U}^T]$ is a non-singular square matrix and ${\left({\mathrm{\Omega }}_k^{-\frac{1}{2}}\mathrm{\Lambda }\right)}^T{\mathrm{\Omega }}_k^{\frac{1}{2}}{U}^T={\mathrm{\Lambda }}^T{U}^T=0$.

Lemma B.2

Let F and G be equal dimension n × p matrices such that the matrix [F, G] is square nonsingular and F^T G = 0, then I_n = F(F^T F)⁻¹ F^T + G(G^T G) ⁻¹ G^T.

Lemma (B.2) gives

$$I-{\mathrm{\Omega }}_k^{-\frac{1}{2}}\mathrm{\Lambda }{\left({\mathrm{\Lambda }}^T{\mathrm{\Omega }}_k^{-1}\mathrm{\Lambda }\right)}^{-1}{\mathrm{\Lambda }}^T{\mathrm{\Omega }}_k^{-\frac{1}{2}}={\mathrm{\Omega }}_k^{\frac{1}{2}}{U}^T{\mathrm{\Phi }}_k^{-1}U{\mathrm{\Omega }}_k^{\frac{1}{2}}.$$ (27)

Substituting (27) into (26) gives r̃_k = Γ_k(A)^T q̃_k where ${\stackrel{\sim }{q}}_k={\mathrm{\Phi }}_k^{-\frac{1}{2}}{q}_k$ and ${\mathrm{\Gamma }}_k(A)\equiv {\mathrm{\Phi }}_k^{-\frac{1}{2}}U{\mathrm{\Omega }}_k^{\frac{1}{2}}$ is a row orthogonal matrix. Hence Γ_k(A) Γ_k(A)^T = I_2d and ${\stackrel{\sim }{r}}_k^T{\stackrel{\sim }{r}}_k={\stackrel{\sim }{q}}_k^T{\stackrel{\sim }{q}}_k$, giving

$$r(s,A,{\widehat{X}}_1;Y)=q(s,A;Y)$$

under Assumption I.

Appendix C.

Proof of Theorem III.3

This proof borrows from [22]. Consider the Frobenius norm

$${\Vert Q(s,A;Y)\Vert }_F^2=\sum _{k=1}^K{q}_k^T{\mathrm{\Phi }}_k^{-1}{q}_k.$$

Then

$$\frac{\partial }{\partial s}{\Vert Q(s,A;Y)\Vert }_F^2=2\sum _{k=1}^K{\mathrm{\Phi }}_k^{-1}U{y}_k-2\sum _{k=1}^K{\mathrm{\Phi }}_k^{-1}s$$

and consequently by setting equal to zero we conclude for any fixed $A{\Vert Q(s,A;Y)\Vert }_F^2\ge {\Vert Q(\widehat{s},A;Y)\Vert }_F^2$ where

$$\widehat{s}={\left(\sum _{k=1}^K{\mathrm{\Phi }}_k^{-1}\right)}^{-1}\sum _{k=1}^K{\mathrm{\Phi }}_k^{-1}U{y}_k.$$ (28)

Under Assumption IV we have Φ_k = η_kΦ₀ and we can simplify (28) to give ŝ = γ^(K)−1Uȳ^(K),where ${\mathrm{\gamma }}^{\left(K\right)}\equiv \left(\frac{1}{K}\right){\sum }_{k=1}^K{\eta }_k^{-1}$ and ${\overline{y}}^{\left(K\right)}\equiv \left(\frac{1}{K}\right){\sum }_{k=1}^K{\eta }_k^{-1}{y}_k$.

Define v_k ≡ y_k − γ^(K)−1ȳ, k = 1, …, K and the matrix V ≡ [v₁, …, v_K], then it can be shown for any fixed A that

$${\Vert Q(s,A;Y)\Vert }_F^2\ge {\Vert Q(\widehat{s},A;Y)\Vert }_F^2={\Vert Q(0,A;V)\Vert }_F^2$$ (29)

where

$$Q(0,A;V)=[{\mathrm{\Phi }}_k^{-\frac{1}{2}}U{v}_1,\dots ,{\mathrm{\Phi }}_k^{-\frac{1}{2}}U{v}_K]$$

with equality in (29) holding if and only if

$$s=\widehat{s}(A)={\mathrm{\gamma }}^{\left(K\right)-1}U\overline{y}.$$

We now note that under Assumption IV

$$Q(0,A;V)=[\mathrm{\Gamma }(A){\mathrm{\Omega }}_1^{-\frac{1}{2}}{v}_1,\dots ,\mathrm{\Gamma }(A){\mathrm{\Omega }}_K^{-\frac{1}{2}}{v}_K],$$

where

$$\mathrm{\Gamma }(A)\equiv {\mathrm{\Phi }}_k^{-\frac{1}{2}}U{\mathrm{\Omega }}_k^{\frac{1}{2}}={\mathrm{\Phi }}_0^{-\frac{1}{2}}U{\mathrm{\Omega }}_0^{\frac{1}{2}},$$

and hence we can write $Q(0,A;V)=\mathrm{\Gamma }(A){\mathrm{\Omega }}_0^{-\frac{1}{2}}\stackrel{\sim }{V}$ with $\stackrel{\sim }{V}=[{\eta }_1^{-\frac{1}{2}}{v}_1,\dots ,{\eta }_K^{-\frac{1}{2}}{v}_K]$. We note ṼṼ^T = W^(K).

We are required to minimize

$${\Vert Q(0,A;V)\Vert }_F^2={\Vert \mathrm{\Gamma }(A){\mathrm{\Omega }}_0^{\frac{1}{2}}\stackrel{\sim }{V}\Vert }_F^2$$

with respect to A.

Lemma C.1

Let M ∈ ℝ^{m × n} with m ≥ n and rank(M) = r and let P ∈ ℝ^{n × q}, q ≤ r, be a matrix with q orthonormal columns. Then ${\Vert MP\Vert }_F^2=\text{tr}(P^T{M}^{T}MP)$ is minimized for given M, when P = G̃_k where G̃^T is a singular value decomposition (svd) of M and G̃_k = [g_m−k+1, …, g_m] denotes the matrix k of orthonormal right singular vectors of M corresponding to the k smallest singular values.

We note that

$${\Vert \mathrm{\Gamma }(A){\mathrm{\Omega }}_0^{-\frac{1}{2}}\stackrel{\sim }{V}\Vert }_F^2={\Vert {\stackrel{\sim }{V}}^T{\mathrm{\Omega }}_0^{-\frac{1}{2}}{\mathrm{\Gamma }}^T(A)\Vert }_F^2,$$

and Γ^T(A) is a 2d × d matrix with orthonormal columns. Let G̃^T be the svd of ${\stackrel{\sim }{V}}^T{\mathrm{\Omega }}_0^{-\frac{1}{2}}$ where we partition the matrix of right singular vectors

$$\stackrel{\sim }{G}=\left[\begin{array}{cc}{\stackrel{\sim }{G}}_{11}& {\stackrel{\sim }{G}}_{12}\\ {\stackrel{\sim }{G}}_{21}& {\stackrel{\sim }{G}}_{22}\end{array}\right].$$

From Lemma C.1 we have

$${\Vert Q(0,A;V)\Vert }_F^2=\text{tr}(\mathrm{\Gamma }(A){\mathrm{\Omega }}_0^{-\frac{1}{2}}\stackrel{\sim }{V}{\stackrel{\sim }{V}}^T{\mathrm{\Omega }}_0^{-\frac{1}{2}}\mathrm{\Gamma }{(A)}^T)\ge \text{tr}\left({\mathrm{\Omega }}_0^{-\frac{1}{2}}\stackrel{\sim }{V}{\stackrel{\sim }{V}}^T{\mathrm{\Omega }}_0^{-\frac{1}{2}}\right),$$

with equality reached when  is such that $\mathrm{\Gamma }(\widehat{A})=[{\tilde{G}}_{12}^T,{\tilde{G}}_{22}^T]$. From the svd of ${\stackrel{\sim }{V}}^T{\mathrm{\Omega }}_0^{-\frac{1}{2}}$ we have

$$W^{\left(K\right)}{\mathrm{\Omega }}_0^{-1}=\stackrel{\sim }{V}{\stackrel{\sim }{V}}^T{\mathrm{\Omega }}_0^{-1}={\mathrm{\Omega }}_0^{\frac{1}{2}}\stackrel{\sim }{G}{S}^{T}S{\stackrel{\sim }{G}}^T{\mathrm{\Omega }}^{-\frac{1}{2}}=GE{G}^{-1},$$

the eigendecomposition of $W^{\left(K\right)}{\mathrm{\Omega }}_0^{-1}$ where the columns of $G={\mathrm{\Omega }}_0^{\frac{1}{2}}\stackrel{\sim }{G}$ are the eigenvectors of $W^{\left(K\right)}{\mathrm{\Omega }}_0^{-1}$, with inverse

$$G^{-1}={\stackrel{\sim }{G}}^T{\mathrm{\Omega }}_0^{-\frac{1}{2}}.$$ (30)

We have $\mathrm{\Gamma }(\widehat{A})=[{\tilde{G}}_{12}^T,{\tilde{G}}_{22}^T]$ which gives ${\mathrm{\Phi }}_0^{-\frac{1}{2}}U{\mathrm{\Omega }}_0^{\frac{1}{2}}=[{\tilde{G}}_{12}^T,{\tilde{G}}_{22}^T]$, resulting in

$${\mathrm{\Phi }}_0^{-\frac{1}{2}}U=[{\tilde{G}}_{12}^T,{\tilde{G}}_{22}^T]{\mathrm{\Omega }}_0^{-\frac{1}{2}}=[{[G^{-1}]}_{21},{[G^{-1}]}_{22}],$$

with the final equality coming from (30), where we make the partition

$$G^{-1}=\left[\begin{array}{cc}{[G^{-1}]}_{11}& {[G^{-1}]}_{12}\\ {[G^{-1}]}_{21}& {[G^{-1}]}_{22}\end{array}\right].$$

With

$${\mathrm{\Phi }}_0^{-\frac{1}{2}}U=[-{\mathrm{\Phi }}_0^{-\frac{1}{2}}\widehat{A},{\mathrm{\Phi }}_0^{-\frac{1}{2}}]=[{[G^{-1}]}_{21},{[G^{-1}]}_{22}],$$

we have ${\mathrm{\Phi }}_0^{-\frac{1}{2}}={[G^{-1}]}_{22}$ and  = −([G⁻¹]₂₂)⁻¹[G⁻¹]₂₁. Using the block inverse of G we have ${[G^{-1}]}_{21}=-{(G_{22}-G_{21}{G}_{11}^{-1}{G}_{12})}^{-1}{G}_{21}{G}_{11}^{-1}$ and ${[G^{-1}]}_{22}={(G_{22}-G_{21}{G}_{11}^{-1}{G}_{12})}^{-1}$, and it follows that $\widehat{A}=-{\left({[G^{-1}]}_{22}\right)}^{-1}{[G^{-1}]}_{21}=G_{21}{G}_{11}^{-1}$. We have now shown

$${\Vert Q(s,A;Y)\Vert }_F\ge {\Vert Q(\widehat{s},\widehat{A};Y)\Vert }_F$$

for all A and s.

We are left with showing consistency. Let

$$W^{\left(K\right)}\equiv \left(\frac{1}{K}\right)\sum _{k=1}^K{\eta }_k^{-1}(y_k-{\mathrm{\gamma }}^{\left(K\right)-1}{\overline{y}}^{\left(K\right)}){(y_k-{\mathrm{\gamma }}^{\left(K\right)-1}{\overline{y}}^{\left(K\right)})}^T$$

and consider eigendecomposition $W^{\left(K\right)}{\mathrm{\Omega }}_0^{-1}\equiv G^{\left(K\right)}{E}^{\left(K\right)}{G}^{\left(K\right)-1}$ with E^(K) = diag{e₁, e₂, …, e_2d} where e₁ ≥ … ≥ e_2d are the ordered eigenvalues of $W^{\left(K\right)}{\mathrm{\Omega }}_0^{-1}$ and the columns of G^(K) are the corresponding eigenvectors. Under Assumptions I, IV and V(i) it can be shown $W{\mathrm{\Omega }}_0^{-1}\equiv \underset{K\to \infty }{lim}{W}^{\left(K\right)}{\mathrm{\Omega }}_0^{-1}$ exists and is equal to $W{\mathrm{\Omega }}_0^{-1}=\mathrm{\Lambda }\mathrm{\Psi }{\mathrm{\Lambda }}^T{\mathrm{\Omega }}_0^{-1}+I_{2d}$ wp1, where $\mathrm{\Psi }=\underset{K\to \infty }{lim}{\mathrm{\Psi }}^{\left(K\right)},{\mathrm{\Psi }}^{\left(K\right)}\equiv {\mathrm{\Xi }}^{\left(K\right)}-{\mathrm{\gamma }}^{\left(K\right)-1}{\overline{x}}_1^{\left(K\right)}{\overline{x}}_1^{\left(K\right)T},{\mathrm{\Xi }}^{\left(K\right)}\equiv \left(\frac{1}{K}\right){\sum }_{k=1}^K{\eta }_k^{-1}{x}_{1,k}{x}_{1,k}^T$ and Λ = [I_d, A^T]^T. Further to this, Assumption V(ii) implies $W{\mathrm{\Omega }}_0^{-1}$ is positive definite. Under these conditions we give the following as a summary to the results found in [22, Section 3].

Lemma C.2

$W{\mathrm{\Omega }}_0^{-1}$ will have eigendecomposition $W{\mathrm{\Omega }}_0^{-1}=\mathcal{G}E{\mathcal{G}}^{-1}$ where $\mathcal{G}=\underset{K\to \infty }{lim}{G}^{\left(K\right)}$ and $E=\underset{K\to \infty }{lim}{E}^{\left(K\right)}$ each wp1.

Let γ₁ ≥ γ₂ ≥ … γ_d ≥ 0 be the eigenvalues of $\mathrm{\Psi }{\mathrm{\Lambda }}^T{\mathrm{\Omega }}_0^{-1}\mathrm{\Lambda }.\mathrm{\Psi }{\mathrm{\Lambda }}^T{\mathrm{\Omega }}_0^{-1}\mathrm{\Lambda }$ is symmetric hence there exists d × d matrix ψ such that $\mathrm{\Psi }{\mathrm{\Lambda }}^T{\mathrm{\Omega }}_0^{-1}\mathrm{\Lambda }=\psi D_{\mathrm{\gamma }}{\psi }^{-1}$ where D_γ = diag{γ₁, γ₂, …, γ_d}. We therefore have

$${\mathcal{X}}_1{\mathrm{\Lambda }}^T{\mathrm{\Omega }}_0^{-1}\mathrm{\Lambda }\psi =\psi D_{\mathrm{\gamma }}$$

and hence

$$W{\mathrm{\Omega }}_0^{-1}\mathrm{\Lambda }\psi =(I_{2d}+\mathrm{\Lambda }\mathrm{\Psi }{\mathrm{\Lambda }}^T{\mathrm{\Omega }}_0^{-1})\mathrm{\Lambda }\psi =\mathrm{\Lambda }\psi (I_d+D_{\mathrm{\gamma }}).$$

Consequently, we conclude that Λψ are ordered eigenvectors of $W{\mathrm{\Omega }}_0^{-1}$ with eigenvalues E = (I_d + D_γ). By also considering $W{\mathrm{\Omega }}_0^{-1}{\mathrm{\Gamma }}^T(A)={\mathrm{\Gamma }}^T(A)$ we see that the columns of Λψ are the d eigenvectors with the largest corresponding eigenvalues, and the columns of Γ^T(A) are the eigenvectors with the smallest eigenvalues (each equal to one). As such, if we define 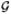to be a matrix whose columns are the eigenvectors of $W{\mathrm{\Omega }}_0^{-1}$, ordered by descending size of their corresponding eigenvalues, then

$${[{\mathcal{G}}_{11}^T,{\mathcal{G}}_{21}^T]}^T={[I_d,A^T]}^T\psi \mathcal{U}$$

for some unitary matrix . From Lemma C.2 this gives

$$\underset{K\to \infty }{lim}\widehat{A}=\underset{K\to \infty }{lim}{G}_{21}^{\left(K\right)}{G}_{11}^{\left(K\right)-1}={\mathcal{G}}_{21}{\mathcal{G}}_{11}^{-1}=A$$

wp1.

Using this result and under Assumption V $\underset{K\to \infty }{lim}\widehat{s}={\mathrm{\gamma }}^{-1}U\overline{y}$ where $\mathrm{\gamma }=\underset{K\to \infty }{lim}{\mathrm{\gamma }}^{\left(K\right)}$ and $\overline{y}=\underset{K\to \infty }{lim}{\overline{y}}^{\left(K\right)}$. By the strong law of large numbers (SLLN), $\underset{K\to \infty }{lim}\left(\frac{1}{K}\right){\sum }_{k=1}^K{\eta }_k^{-1}{∊}_k=0$ wp1, and hence ȳ = x̄ where $\overline{x}=\underset{K\to \infty }{lim}{\overline{x}}^{\left(K\right)}$ with ${\overline{x}}^{\left(K\right)}=\left(\frac{1}{K}\right){\sum }_{k=1}^K{\eta }_k^{-1}{x}_k$. Therefore, with Ux_k = x_{2, k} − Ax_{1, k} = s for all k = 1, …, K, γ⁻¹Uȳ = γ⁻¹Ux̄ = γ⁻¹ γs and $\underset{K\to \infty }{lim}\widehat{s}=s$ wp1.

Appendix D.

Proof of Corollary IV.2

Under Assumptions II, IV, V and IV, and from Theorems III.3 and IV.1, we have that asymptotically in K, $cov\{K^{\frac{1}{2}}\mathrm{\Delta }\beta \}=H^{-1}P{\left(H^{-1}\right)}^T$ where H and P are given by (6) and (7), respectively. Let us define scalar ${\mathrm{\gamma }}^{\left(K\right)}\equiv {\sum }_{k=1}^K{\eta }_k^{-1}$, vector ${\overline{x}}_1^{\left(K\right)}\equiv \left(\frac{1}{K}\right){\sum }_{k=1}^K{\eta }_k^{-1}{x}_{1,k}$ and matrix ${\mathrm{\Xi }}^{\left(K\right)}\equiv \left(\frac{1}{K}\right){\sum }_{k=1}^K{\eta }_k^{-1}{x}_{1,k}{x}_{1,k}^T$. Under Assumption IV it can be shown

$$\begin{array}{c}\left(\frac{1}{K}\right)\sum _{k=1}^K{\mathrm{\Phi }}_k^{-1}={\mathrm{\gamma }}^{\left(K\right)}{\mathrm{\Phi }}_0^{-1},\\ -\left(\frac{1}{K}\right)\sum _{k=1}^K(x_{1,k}\otimes {\mathrm{\Phi }}_k^{-1})=-{\overline{x}}_1^{\left(K\right)}\otimes {\mathrm{\Phi }}_0^{-1},\\ -\left(\frac{1}{K}\right)\sum _{k=1}^K(x_{1,k}^T\otimes {\mathrm{\Phi }}_k^{-1})=-{\overline{x}}_1^{\left(K\right)T}\otimes {\mathrm{\Phi }}_0^{-1}\\ -\left(\frac{1}{K}\right)\sum _{k=1}^K(x_{1,k}{x}_{1,k}^T\otimes {\mathrm{\Phi }}_k^{-1})=-{\mathrm{\Xi }}^{\left(K\right)}\otimes {\mathrm{\Phi }}_0^{-1}\end{array}$$

and

$$\left(\frac{1}{K}\right)\sum _{k=1}^K({\left({\mathrm{\Lambda }}^T{\mathrm{\Omega }}_k^{-1}\mathrm{\Lambda }\right)}^{-1}+x_{1,k}{x}_{1,k}^T)\otimes {\mathrm{\Phi }}_k^{-1}=({\left({\mathrm{\Lambda }}^T{\mathrm{\Omega }}_0^{-1}\mathrm{\Lambda }\right)}^{-1}+{\mathrm{\Xi }}^{\left(K\right)})\otimes {\mathrm{\Phi }}_0^{-1}.$$

Considering the forms of $H_0^{\left(K\right)}$ and $P_0^{\left(K\right)}$ in (8) and (9), respectively, we write $H^{\left(K\right)}=H_0^{\left(K\right)}\otimes {\mathrm{\Phi }}_0^{-1}$ and $P^{\left(K\right)}=P_0^{\left(K\right)}\otimes {\mathrm{\Phi }}_0^{-1}$. Using the mixed-product property of the Kronecker product and the symmetry of H, then

$$H^{\left(K\right)-1}={\left(H^{\left(K\right)-1}\right)}^T=H_0^{\left(K\right)-1}\otimes {\mathrm{\Phi }}_0$$

and

$$B^{\left(K\right)}=H_0^{\left(K\right)-1}{P}_0^{\left(K\right)}{H}_0^{\left(K\right)-1}\otimes {\mathrm{\Phi }}_0.$$

Using the block matrix inverse

$$\begin{array}{c}{\left[H_0^{\left(K\right)-1}\right]}_{11}={\mathrm{\gamma }}^{\left(K\right)-1}+{\mathrm{\gamma }}^{\left(K\right)-2}{\overline{x}}_1^{\left(K\right)T}{\mathrm{\Psi }}^{\left(K\right)-1}{\overline{x}}_1^{\left(K\right)}\\ {\left[H_0^{\left(K\right)-1}\right]}_{12}={\mathrm{\gamma }}^{\left(K\right)-1}{\overline{x}}_1^{\left(K\right)T}{\mathrm{\Psi }}^{\left(K\right)-1}\\ {\left[H_0^{\left(K\right)-1}\right]}_{21}={\mathrm{\gamma }}^{\left(K\right)-1}{\mathrm{\Psi }}^{\left(K\right)-1}{\overline{x}}_1^{\left(K\right)}\\ {\left[H_0^{\left(K\right)-1}\right]}_{22}={\mathrm{\Psi }}^{\left(K\right)-1}\end{array}$$

where ${\mathrm{\Psi }}^{\left(K\right)}={\mathrm{\Xi }}^{\left(K\right)}-{\mathrm{\gamma }}^{\left(K\right)-1}{\overline{x}}_1^{\left(K\right)}{\overline{x}}_1^{\left(K\right)T}$. Results follow by computing $H_0^{\left(K\right)-1}{P}_0^{\left(K\right)}{H}_0^{\left(K\right)-1}$, forming the Kronecker product with Φ₀ and taking limits as K → ∞ under Assumption V.

Appendix E.

Proof of Lemma VI.1

${\overline{x}}_1\equiv \underset{K\to \infty }{lim}\frac{1}{K}{\sum }_{k=1}^K{\eta }_k^{-1}{x}_{1,k}$. With weighting factors {η_k, k = 1, …, K} being independent of points {x_{1, k}, k = 1, …, K} by SLLN

$${\overline{x}}_1=E\left\{{\mathcal{N}}^{-1}\mathcal{X}\right\}=E\left\{{\mathcal{N}}^{-1}\right\}E\left\{\mathcal{X}\right\}=E\left\{{\mathcal{N}}^{-1}\right\}\mu$$

wp1. Let us consider the matrix

$$\mathrm{\Psi }=\mathrm{\Xi }-{\mathrm{\gamma }}^{-1}{\overline{x}}_1{\overline{x}}_1^T,$$

where $\mathrm{\gamma }=\underset{K\to \infty }{lim}\left(\frac{1}{K}\right){\sum }_{k=1}^K{\eta }_k^{-1}$ and $\mathrm{\Xi }\equiv {\sum }_{k=1}{\eta }_k^{-1}{x}_{1,k}{x}_{1,k}^T$. By SLLN γ = E{ ⁻¹}. By SLLN and independence

$$\mathrm{\Xi }=E\left\{{\mathcal{N}}^{-1}\mathcal{X}{\mathcal{X}}^T\right\}=E\left\{{\mathcal{N}}^{-1}\right\}E\left\{\mathcal{X}{\mathcal{X}}^T\right\}.$$

Hence

$$\mathrm{\Psi }=E\left\{{\mathcal{N}}^{-1}\right\}\left(E\right\{\mathcal{X}{\mathcal{X}}^T\}-E\{\mathcal{X}\left\}E{\left\{\mathcal{X}\right\}}^T\right)=E\left\{{\mathcal{N}}^{-1}\right\}\mathrm{\Pi }$$

wp1.