CONCURRENT IDENTITY TRAINING IS NOT NECESSARY FOR ASSOCIATIVE SYMMETRY IN SUCCESSIVE MATCHING

Abstract

Pigeons demonstrate associative symmetry after successive matching training on one arbitrary and two identity relations (e.g., Urcuioli, 2008). Here, we tested whether identity matching training is necessary for this emergent effect. In Experiment 1, one group of pigeons (Dual Oddity) learned hue–form arbitrary matching and two oddity relations which shared sample and comparison elements with the arbitrary relations. A second (Control) group learned the same hue–form matching task and a second (form–hue) arbitrary task which, together with hue oddity, shared only the samples with the hue–form relations. On subsequent symmetry probe trials, four Dual Oddity pigeons exhibited higher probe-trial response rates on the reverse of the positive than negative hue–form baseline trials, demonstrating associative symmetry. None of the Control pigeons, on the other hand, exhibited associative symmetry. Experiment 2 showed that subsequently changing one of the two oddity baseline relations to identity matching in the Dual Oddity group yielded antisymmetry in three of five pigeons. These results are consistent with predictions derived from Urcuioli’s (2008) theory of pigeons’ stimulus class formation and demonstrate that identity training is not necessary for associative symmetry to emerge after arbitrary matching training in pigeons.

Matching-to-sample procedures are usually used to establish conditional relations among physically different stimuli, for example, between A and B, and between B and C stimuli. Subsequent tests evaluate whether the A, B, and C stimuli are then interchangeable with one another (i.e., form an equivalence class) by the demonstration of the reflexivity (AA, BB, and CC), symmetry (BA and CB), and transitivity (AC) properties of equivalence (Sidman & Tailby, 1982). In addition, one may evaluate the emergence of a combined symmetry and transitivity or equivalence (CA) relation.

Studies using standard two-choice matching-to-sample procedures with nonhuman subjects have generally been unsuccessful in finding evidence for equivalence relations (e.g., Lionello-DeNolf, 2009; Sidman et al., 1982) in contrast to data obtained from human participants (Sidman, 1994). The disparity in results has led some authors (Devany, Hayes, & Nelson, 1986; Hayes, 1989; Horne & Lowe, 1996) to argue that language is necessary for participants to show emergent relations. On the other hand, Dube, McIlvane, Callahan and Stoddard (1993; see also McIlvane, Serna, Dube, & Stromer, 2000) argue that the disparity might simply mean that experimenters do not yet know all of the conditions necessary to produce emergent behavior or that other overlooked, but consequential, stimulus features invalidate the desired test.

For example, using two or more stimulus locations during baseline training may invalidate a test by allowing these locations to control responding along with the nominal (i.e., physical) properties of the stimuli (e.g., Iversen, 1997; Iversen, Sidman, & Carrigan, 1986; Lionello & Urcuioli, 1998; Sidman, 1992). For example, consider the following two-alternative procedure. Pigeons are trained to peck (choose) a set of vertical lines on either the left or right side key after observing a red hue on the center key, and to peck (choose) a set of horizontal lines on either the left or right side key after observing a green hue on the center key. Later, in a test for symmetry, pigeons are given a choice between red and green comparison hues on the side keys after observing vertical- or horizontal-lines samples on the center key. Although this test has face validity, it does not, in fact, test for symmetry because the functional stimuli are not simply red, green, vertical lines, and horizontal lines. In other words, red on the left key is functionally different from red on the center key. Likewise, a set of vertical lines on the center key is a functionally different stimulus than the same set of vertical lines on a side key (Lionello & Urcuioli, 1998) and so forth. Thus, the apparent test for symmetry does no such thing because the functional matching stimuli—that is, each [nominal stimulus + its spatial location]—has been altered in the shift from baseline training to testing. Consequently, the drop in performance to chance levels of accuracy on test trials typically observed in this paradigm with nonhuman animals is to be expected.

Interestingly, go/no-go procedures that employ just one location for both sample and comparison stimuli have yielded results that indicate the emergence of symmetry in pigeons when those stimuli are presented either successively (Frank & Wasserman, 2005; Urcuioli, 2008) or simultaneously (Campos, Debert, Barros, & McIlvane, 2011). For example, Frank and Wasserman (2005) and Urcuioli (2008, Experiment 3) trained pigeons on successive (go/no-go) matching in which they learned to peck the singly presented comparison on some (reinforced) sample–comparison trials and not to peck the singly presented comparison on other (nonreinforced) sample–comparison trials. Baseline training consisted of one set of arbitrary relations (e.g., in Frank & Wasserman, a sample picture of a snail was followed on different trials by a comparison picture of either a butterfly or a plant, and a sample picture of a flower was also followed on different trials by a comparison picture of the butterfly or a plant) and two sets of identity relations involving the stimuli appearing in the arbitrary task (e.g., a sample picture of a snail followed by a comparison picture of either a snail or flower, etc.). The measure of performance was the rate of comparison responding on reinforced versus nonreinforced trials. After pigeons were pecking at substantially higher comparison-response rates on reinforced than on nonreinforced trials, the arbitrary baseline relations were reversed on a small set of nonreinforced symmetry-probe trials. On the probes, pigeons pecked the comparisons more often on the reverse of the reinforced baseline combinations than on the reverse of the nonreinforced combinations, a finding indicating associative symmetry¹. In other words, if a reinforced baseline combination was a snail sample followed by a butterfly comparison, then pigeons pecked the snail comparison more often on probe trials beginning with a butterfly sample than on probe trials beginning with the plant sample.

Although it is tempting to conclude that the associative symmetry effect observed by Frank and Wasserman (2005) and by Urcuioli (2008, Experiment 3) came about by holding stimulus location constant (i.e., all stimuli on the same key) and insuring that pigeons saw each matching stimulus as both a sample and as a comparison prior to testing, a follow-up experiment by Urcuioli (2008, Experiment 4) indicated more subtle and complex stimulus control mechanisms at work. In that experiment, pigeons were trained on arbitrary successive matching with red and green sample hues and triangle and horizontal-lines comparison forms. In addition, they were concurrently trained on identity successive matching with the triangle and horizontal forms but on oddity successive matching with the red and green hues (i.e., reinforced trials consisted of a red sample followed by a green comparison and a green sample followed by a red comparison). Although this baseline training regimen also insured that pigeons saw each stimulus as both a sample and a comparison prior to testing, pigeons later exhibited higher comparison response rates on probe trials that were the reverse of the nonreinforced arbitrary matching baseline relations than on probe trials that were the reverse of the reinforced arbitrary matching baseline relations. In other words, if the red sample–triangle comparison combination was reinforced in training but the red sample–horizontal combination was not, in testing pigeons responded more to a red comparison after a horizontal sample than after a triangle sample. In short, they exhibited the exact opposite of associative symmetry—what Urcuioli (2008) called “antisymmetry”.

Together, the symmetry and antisymmetry findings led Urcuioli (2008) to propose a theory of pigeons’ equivalence-class formation whose major assumptions are that (1) the ordinal positions of the stimuli within a successive matching trial control responding together with their nominal properties, (2) baseline training produces stimulus classes consisting of the elements of the reinforced baseline relations, and (3) baseline relations that share [nominal stimulus + ordinal position] elements allow their respective classes to merge.

For example, consider a reinforced trial with red (R) as a sample (i.e., first) followed by triangle (T) as a comparison (i.e., second). If ordinal position also controls responding, the functional stimuli consist of [red + position 1] and [triangle + position 2], or R1 as sample and T2 as comparison, for short. Another reinforced training relation would be green (G) as a sample (i.e., first) followed by horizontal lines (H) as a comparison (i.e., second), or G1 followed by H2. According to Urcuioli (2008), the sample and comparison stimuli comprising each reinforced baseline combination become members of the same stimulus class; in other words, a [R1, T2] and a [G1, H2] class, respectively. Concurrently training hue–hue and form–form identity successive matching using the same stimuli appearing in the arbitrary hue–form task should, by hypothesis, yield the following four additional stimulus classes: [R1, R2], [G1, G2], [T1, T2], and [H1, H2].

Associative symmetry is predicted from the additional assumption that elements common to more than one class produce class merger—e.g., the common T2 element in [R1, T2] and [T1, T2] should cause those classes to merge, and the common R1 element in [R1, T2] and [R1, R2] should do the same. Together, the net result is the following four-member class: [R1, R2, T1, T2]. The same merger-through-common-elements assumption should also result in a four-member [G1, G2, H1, H2] class. Notice that each four-member class contains the elements of an explicitly reinforced arbitrary matching relation (viz., R1→T2 and G1→H2) and its symmetrical counterpart (viz., T1→R2 and H1→G2). Granted, the technically symmetrical relations would be T2→R1 and H2→G1, but these are logically impossible because a stimulus appearing in the second ordinal position cannot, by definition, appear first, and vice versa. Besides, if T1 and T2 are members of the same class, then their nominal components should be substitutable for one another, resulting in the predicted T1→R2 emergent relation (see Sweeney & Urcuioli, 2010; Urcuioli, 2011; and Urcuioli & Swisher, 2012a for other theoretically confirmed predictions).

The counter-intuitive antisymmetry effect—pigeons responding more to the reverse of nonreinforced than reinforced arbitrary matching baseline combinations—can be similarly derived. The theory predicts that training hue–form arbitrary, hue oddity, and form identity relations should yield the following stimulus classes: [R1, T2], [R1, G2], [T1, T2], and [G1, H2], [G1, R2], and [H1, H2], the italics emphasizing those classes assumed to arise from the oddity contingencies. Given that common elements promote class merger and the following common elements: R1 ([R1, T2] and [R1, G2]), T2 ([R1, T2] and [T1, T2]), G1 ([G1, H2] and [G1, R2]) and H2 ([G1, H2] and [H1, H2]), the net result is two 4-member classes: [R1, T2, G2, T1] and [G1, H2, R2, H1]. Notice that each class contains the elements representing the reverse of the nonreinforced arbitrary matching relation (viz., T1→G2 and H1→R2) rather than the elements representing the reverse of the reinforced arbitrary matching relation (viz., T1→R2 and H1→G2). Therefore, antisymmetry is predicted: Pigeons are expected to, and do, show higher comparison response rates on the reverse of the nonreinforced arbitrary matching relations (see also Urcuioli & Swisher, 2012b).

Table 1 summarizes the emergent-relations predictions made by Urcuioli’s (2008) theory regarding associative symmetry and antisymmetry that have so far been tested and confirmed (√). The rows and columns of the table indicate the nature of the successive matching tasks concurrently trained with the arbitrary hue–form matching task. For example, Urcuioli (2008, Experiment 3) trained pigeons on both hue and form identity successive matching along with the hue–form arbitrary task, and later observed associative symmetry (see also Frank & Wasserman, 2005). Urcuioli (2008, Experiment 4) trained pigeons on hue oddity and form identity along with the hue–form arbitrary task, and later observed antisymmetry. Likewise, Urcuioli and Swisher (2012b) observed antisymmetry using hue identity and form oddity as the two concurrently trained tasks along with the hue–form arbitrary task. The remaining theoretical prediction yet to be tested involves concurrently training pigeons on two oddity relations along with the hue–form arbitrary task. As described below, Urcuioli’s (2008) theory predicts that concurrent dual-oddity training should yield associative symmetry.

Table 1.

Confirmed emergent relations predictions (√ - with citations) after arbitrary hue–form successive matching training plus concurrent training on either hue identity or hue oddity successive matching and either form identity or form oddity successive matching.Italicized prediction was tested in Experiment 1 of the present study.

	Form Identity	Form Oddity
Hue Identity	Symmetry √ (Urcuioli, 2008, Exp. 3)	Antisymmetry √ (Urcuioli & Swisher, 2012b)
Hue Oddity	Antisymmetry √ (Urcuioli, 2008, Exp. 4)	Symmetry (Present Experiment 1)

As previously explained, a [R1, T2] and a [G1, H2] class should develop if arbitrary matching training arranges reinforced red sample–triangle comparison and green sample– horizontal comparison combinations. Concurrent training on hue (red/green) oddity arranges for reinforcement on red sample–green comparison and green sample–red comparison trials, and concurrent training on form (triangle/horizontal) oddity arranges for reinforcement on triangle sample–horizontal comparison and horizontal sample–triangle comparison trials. By hypothesis, the four oddity relations should yield [R1, G2], [G1, R2], [T1, H2], and [H1, T2] classes, respectively. Together with the arbitrary matching classes, the common across-class elements are R1 (in the [R1, T2] and [R1, G2] classes), T2 (in the [R1, T2] and [H1, T2] classes), G1 (in the [G1, H2] and [G1, R2] classes), and H2 (in the [G1, H2] and [T1, H2] classes). Assuming class merger via common elements, the net result is two 4-member classes, [R1, T2, H1, G2] and [G1, H2, T1, R2]. Notice that T1 and R2, the stimuli from the reverse of the R1→T2 arbitrary baseline relation, are in one class and H1 and G2, the stimuli from the reverse of the arbitrary baseline relation G1→H2, are in the other class. This should yield associative symmetry in an emergent relations test. In other words, given the reinforced arbitrary baseline relations R1→T2 and G1→H2, pigeons should respond more in testing to the reverse of these relations, namely T1→R2 and H1→G2, than to the reverse of the nonreinforced relations, namely H1→R2 and T1→G2.

If confirmed, this result is noteworthy for other reasons too. First, it would demonstrate associative symmetry even though T1 and T2 are in different stimulus classes, as are R1 and R2, H1 and H2, and G1 and G2. Specifically, note that the R1 and T2 elements are members of one class while T1 and R2 are members of the other class. Second, in their original demonstration of associative symmetry following successive matching training in pigeons, Frank and Wasserman (2005) speculated that “…learning an identity relation might be necessary” (p. 164) for symmetry to emerge. Consistent with this possibility, Frank (2007, Experiment 1) showed that pigeons did not exhibit BA associative symmetry in testing after training on AB, CA, and BD successive matching. Note that this all-arbitrary-matching training procedure guarantees that pigeons see each matching stimulus as both a sample and as a comparison, just as concurrent training on AB, AA, and BB successive matching does. The difference, of course, is that identity training is absent in the former set of trained relations but present in the latter. Moreover, Frank (2007, Experiment 2) showed that BA associative symmetry also did not emerge after training on AB, CC, and DD successive matching. Here, identity training was provided but with stimuli different from those appearing in the arbitrary matching task. Nonetheless, one question remains: Is identity training with the same stimuli appearing in the arbitrary matching task necessary for associative symmetry to emerge?

Experiment 1

Experiment 1 assessed whether associative symmetry would emerge after pigeons were trained on one arbitrary and two oddity successive matching relations (cf. Table 2). In anticipation of positive test results (Urcuioli, 2008), we also ran a separate Control group whose training differed slightly from the Dual Oddity group but in a way that should theoretically preclude associative symmetry.

Table 2.

Baseline successive matching contingencies (first three columns) and nonreinforced probe-test trials (last column) for the two groups in Experiment 1.

Dual Oddity Group
Hue–form Arbitrary	Hue Oddity	Form Oddity	Probe-test Trials
R → T - FI 5 s +	R → R - EXT	T → T - EXT	T → R (√)
R → H - EXT	R → G - FI 5 s +	T → H - FI 5 s +	H → R
G → T - EXT	G → R - FI 5 s +	H → T - FI 5 s +	T → G
G → H - FI 5 s +	G → G - EXT	H → H - EXT	H → G (√)
Control Group
Hue–form Arbitrary	Hue Oddity	Form–hue Arbitrary	Probe-test Trials
R → T - FI 5 s +	R → R - EXT	T → W - EXT	T → R (*)
R → H - EXT	R → G - FI 5 s +	T → B - FI 5 s +	H → R (*)
G → T - EXT	G → R - FI 5 s +	H → W - FI 5 s +	T → G (*)
G → H - FI 5 s +	G → G - EXT	H → B - EXT	H → G (*)

Note. R = red, G = green, W = white, B = blue, T = triangle, H = horizontal, FI = fixed interval schedule, EXT = nonreinforced, + = reinforced. The first and second center-key stimuli in a trial sequence (sample and comparison, respectively) are shown to the left and to the right of the arrows, respectively.

^(√)indicates the probe trials for which higher comparison-response rates are predicted (i.e., associative symmetry).

^(*)indicates that comparison-response rates should be nondifferential across probe-test trials.

Both groups received training on hue–form arbitrary and hue oddity successive matching (left two columns of Table 2). They differed on the third concurrently trained successive matching task. Specifically, Group Dual Oddity received training on form oddity which, together with hue oddity, shared both sample and comparison elements with the hue–form arbitrary task. By contrast, Group Control received training on a form–hue arbitrary matching task involving comparison stimuli that differed from the nominal elements trained in the hue– form arbitrary and hue oddity relations. Specifically, the task consisted of triangle and horizontal samples and blue and white comparisons in which the triangle sample–blue comparison and horizontal sample–white comparison combinations were reinforced. Following acquisition, each group received periodic probe trials in which the order of the nominal samples and comparisons from the hue–form baseline task was reversed (see right column of Table 2).

For the Control group, the six stimulus classes hypothesized to develop from training are [R1, T2], [G1, H2], [R1, G2], [G1, R2], [T1, B2] and [H1, W2]. Here, the only common class elements are R1 (in the [R1, T2] and [R1, G2] classes) and G1 (in the [G1, H2] and [G1, R2] classes, yielding (via class merger) two 3-member classes: [R1, T2, G2] and [G1, H2, R2]. Because the symmetry–probe trials involve triangle sample and red comparison (T1 and R2), and horizontal sample and green comparison (H1 and G2), associative symmetry is not predicted because neither T1 nor H1 are elements of either 3-member class. Therefore, probe-trial responding should be nondifferential for the Control pigeons, as indicated by the asterisks in the right column for this group in Table 2.

In contrast and for the theoretical reasons described earlier, Group Dual Oddity should respond more to the comparisons on probe trials that are the reverse of the reinforced hue–form baseline combinations than on probe trials that are the reverse of the nonreinforced hue–form baseline combinations. This is indicated by the check marks for Group Dual Oddity in the right column of Table 2.

Method

Subjects

Ten experimentally naïve, 1–2 years old pigeons (White Carneau) participated. They were obtained from Double “T” Farms (Glenwood, IA). The pigeons were maintained at 80% of their free-feeding body weights on a food restriction diet. All were fed with Purina ProGrains in the experimental sessions except once per week when the experiment was not run. Water and grit were available at all times in the home cages. The colony room illumination cycle followed a 14h-12h light-dark schedule (lights on at 7 am). Subjects were equally divided into two groups (Dual Oddity and Control) prior to the beginning of the experiment.

Apparatus

Two experimental BRS/LVE (Laurel, MD) pigeon chambers (Model PIP- 016 three-key panel inside a Model SEC-002 enclosure) were used. Each box was equipped with three 2.5-cm response keys. The keys were spaced 5.7 cm apart center-to-center and were aligned horizontally 7.5 cm from the top of the panel. There was a BRS/LVE Model IC-901-IDD stimulus projector behind each key. Each projector was equipped with films and filters for displaying red (R), green (G), blue (B), and white (W) homogeneous fields, and three white horizontal lines (H), and a solid white inverted triangle (T), all on a black background (BRS/LVE Pattern No. 692). A rear-mounted food hopper was located 13 cm below the center key and could be accessed via a 5.8-cm-square opening. The food hopper was illuminated by a small miniature bulb (ESB-28) when raised. A GE #1829 bulb located 7.6 cm above the center key illuminated the chamber. A running blower fan provided ventilation and masking noise to the chamber. An IBM-compatible computer controlled the experimental events in both chambers.

Procedure

Preliminary training

First, pigeons were trained to eat from the raised food hopper. Later, pecks to the center key were shaped by the method of successive approximations. Three sessions were conducted during shaping. In each 60-trial session, two stimuli that would later appear in successive matching were presented equally often in randomized order on the center key: Triangle and horizontal were presented in the first session, blue and white in the second session, and red and green in the third session. Responses were continuously reinforced. The duration of time the food hopper was raised (between 2–6 s) was determined before every session and was held constant within each session in order to maintain subjects’ weights at 80% of their free-feeding weight. Stimulus presentations were separated by a 15-s intertrial interval (ITI) in which the center key went off and the house light remained on (cf. Gibbon, Baldock, Locurto, Gold, & Terrace, 1977).

Next, responses to the center-key stimuli were reinforced on fixed-interval (FI) schedules. For each pair of stimuli, pigeons were given one session with a FI 2-s schedule, one session with FI 3 s, two sessions with FI 5 s, and one session with FI 5 s in which 50% of the trials ended in reinforcement. Blue and white stimuli were presented in the first, red and green in the second, and triangle and horizontal in the third session. The ITI lasted for 15 s, the first 14 s of which were spent in darkness. The house light came on for the last 1 s of the ITI and remained on until the end of the trial. Other procedural details were the same as described for shaping.

Successive matching acquisition

Both groups learned hue–form arbitrary successive matching and hue oddity successive matching that shared sample stimuli (R and G) with the hue–form arbitrary task. The groups differed in terms of the third concurrently trained relations: Dual Oddity pigeons learned form oddity successive matching which, together with hue oddity, shared both sample and comparison elements with the hue–form task. Control pigeons learned a form–hue arbitrary matching task in which the comparison hues (B and W) differed from those in the hue oddity task (viz., R and G). For these pigeons, then, only the sample elements (R and G) were common across the three concurrently trained successive matching tasks.

The left three columns of Table 2 summarize the baseline successive matching contingencies. For all subjects, pecks to the triangle comparison after the red sample (R→T), the horizontal comparison after the green sample (G→H), the green comparison after the red sample (R→G), and the red comparison after the green sample (G→R) were reinforced (reinforced hue– form arbitrary and hue oddity relations), whereas pecks to the horizontal comparison after the red sample (R→H), the triangle comparison after the green sample (G→T), the red comparison after the red sample (R→R), and the green comparison after the green sample (G→G) were not reinforced (nonreinforced hue–form arbitrary and hue oddity relations). For Dual Oddity subjects, pecks to horizontal after triangle (T→H) and triangle after horizontal (H→T) were reinforced (reinforced form oddity relations), whereas pecks to triangle after triangle (T→T) and horizontal after horizontal (H→H) were not reinforced (nonreinforced form oddity relation). For Control subjects, pecks to blue after triangle (T→B) and pecks to white after horizontal (H→W) were reinforced (reinforced form–hue relations), whereas pecks to white after triangle (T→W) and blue after horizontal (H→B) were not reinforced (nonreinforced form–hue relations).

Each matching trial started with the presentation of the sample stimulus on the center key. In order to enhance the chances of attention to the sample, the first sample key peck initiated a FI 5-s schedule. The first peck after 5 s turned off the sample stimulus and initiated a blank 1-s interval after which the comparison stimulus appeared on the same key. On reinforced trials, the first comparison key peck began a 5-s interval after which a comparison peck turned the comparison stimulus off and produced food². On nonreinforced trials, the comparison stimulus went off automatically 5 s after comparison onset. A 15-s ITI, the first 14 s of which the house light was off, followed food presentation (reinforced trials) or comparison offset (nonreinforced trials).

Each 96-trial session consisted of 32 trials each of the hue–form arbitrary, hue oddity, and form oddity (Dual Oddity group) or form–hue arbitrary (Control group) tasks. Each sample– comparison combination was presented eight times in pseudorandom order with the constraint that the same combination could not appear more than twice in a row.

Baseline acquisition was achieved when pigeons exhibited at least a .80 discrimination ratio (DR) for five of six consecutive sessions on each of the three types of trained relations. Only pecks that occurred within 5 s of comparison onset were recorded. Each DR was calculated by dividing the total number of responses to the comparison stimuli on reinforced trials by the sum of responses to the comparison stimuli on reinforced and nonreinforced trials. After reaching criterion, subjects were required to show sustainable performances for at least 10 more sessions (overtraining) and were required to exhibit at least a .80 DR in all tasks for the last five of six overtraining sessions before proceeding to testing.

Successive matching testing

Testing assessed whether or not the baseline hue–form arbitrary relations were symmetrical by presenting periodic probe trials that were the reverse of the hue–form arbitrary relations: T→R and H→G (reverse of the reinforced arbitrary relations), and T→G and H→R (reverse of the nonreinforced arbitrary relations).

Probe trials were interspersed among the three baseline relations. Each 104-trial test session consisted of eight nonreinforced probe trials and 96 baseline trials. Each of the four probe trial types (cf. right column of Table 2) was presented twice in each session. The first probe trial occurred after at least one of each baseline trial type was presented, and subsequent probe trials were separated by at least five baseline trials. Each probe trial ended automatically 5 s after comparison stimulus onset. Eight symmetry test sessions were run in two-session blocks separated by at least five baseline sessions at criterion levels. Associative symmetry was assessed by comparing the number of probe-trial pecks per second to “positive” comparisons (reverse of the reinforced hue–form arbitrary relations) with the number of probe-trial pecks per second to the “negative” comparisons (the reverse of nonreinforced hue–form arbitrary relations). Other procedural details were the same as during successive matching acquisition.

Results and Discussion

Matching acquisition

For the Dual Oddity Group, the average sessions to criterion were 51.8 for hue–form arbitrary matching, 34.2 for hue oddity, and 56.6 for form oddity. Analysis of variance (ANOVA) showed the differences were not statistically significant, F(2, 12) = 0.74. For the Control Group, the corresponding averages were 68.0 for hue–form arbitrary matching, 74.4 for hue oddity, and 58.0 for form–hue arbitrary matching. These differences were not statistically significant, F(2, 12) = 0.35. For the last five sessions of overtraining, the average DRs for the Dual Oddity Group were 0.92 for hue–form arbitrary matching, 0.91 for hue oddity, and 0.90 for form oddity. These differences were not statistically significant, F(2, 12) = 1.06. For the Control group, the corresponding DRs were 0.88 for hue– form arbitrary matching, 0.85 for hue oddity, and 0.91 for form–hue matching. These differences were not statistically significant, F(2, 12) = 2.37.

Symmetry testing

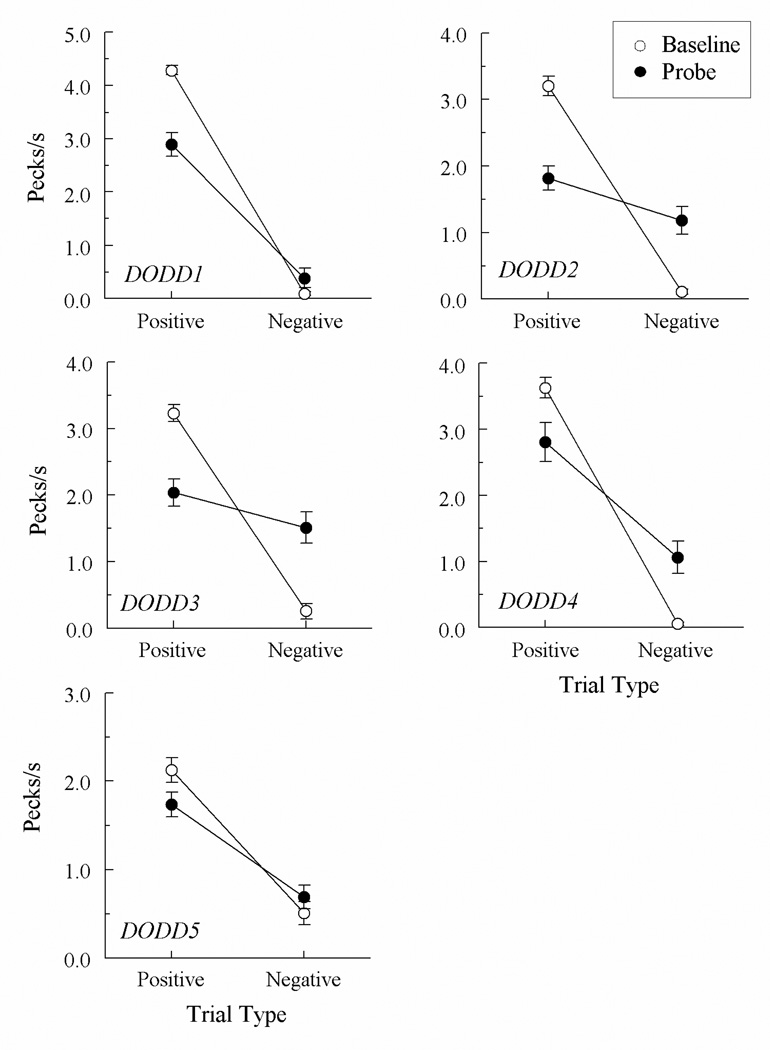
Figure 1 presents the number of comparison pecks per second averaged across the eight test sessions for the baseline trials (hue–form arbitrary matching) and probe trials (form–hue arbitrary matching) for each Dual Oddity pigeon. “Positive” refers to the reinforced baseline trials and the probe trials that were the reverse of these trials. “Negative” refers to the nonreinforced baseline trials and the probe trials that were the reverse of them.

Fig. 1.

Comparison-response rates in pecks per s (± 1 SEM) on the hue–form arbitrary matching baseline trials (open circles) and the nonreinforced form–hue symmetry probe trials (filled circles) averaged over the eight test sessions for each Dual Oddity Group pigeon. “Positive” = reinforced arbitrary baseline trials and test trials in which the samples and comparisons of the reinforced baseline trials were reversed. “Negative” = nonreinforced arbitrary baseline trials and test trials on which the samples and comparisons of the nonreinforced baseline trials were reversed.

All five pigeons exhibited higher comparison response rates on the positive than on the negative baseline trials (open circles). Therefore, baseline responding was maintained during testing. They also exhibited higher comparison response rates on the positive than on the negative symmetry probe trials (filled circles). For four of the five pigeons (DODD1, DODD2, DODD4, and DODD5), the difference between the positive and negative probe-trial response rates was statistically significant: Fs(1, 62) = 80.30, 5.49, 20.46, and 31.61, respectively, indicating associative symmetry. For the other subject (DODD3), it was not: Fs(1, 62) = 2.84, although numerically its difference was also consistent with the pattern indicative of associative symmetry.

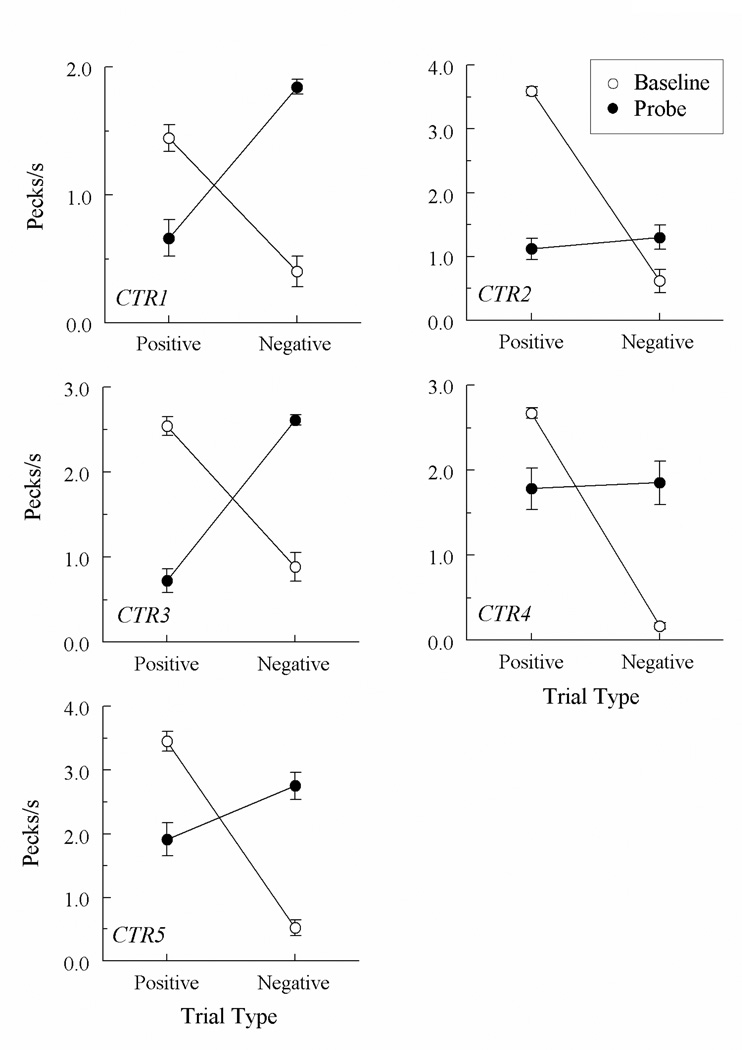
Figure 2 presents the number of comparison pecks per second averaged across the eight test sessions for the baseline trials (hue–form arbitrary matching) and probe trials (form–hue arbitrary matching) for each Control pigeon. Every Control pigeon also exhibited a higher comparison response rate on the positive than on the negative baseline trials (open circles) demonstrating that, like the Dual Oddity pigeons, baseline responding was maintained during testing. On the symmetry probe trials (filled circles), the positive versus negative comparison response rates for pigeons CTR2 and CTR4 were comparable and not statistically significant, Fs(1, 62) = 0.49 and 0.04, respectively, indicating that their arbitrary baseline relations were not symmetrical.

Fig. 2.

Comparison-response rates in pecks per s (± 1 SEM) on the hue–form arbitrary matching baseline trials (open circles) and the nonreinforced form–hue symmetry probe trials (filled circles) averaged over the eight test sessions for each Control Group pigeon. “Positive” = reinforced arbitrary baseline trials and test trials in which the samples and comparisons of the reinforced baseline trials were reversed. “Negative” = non-reinforced arbitrary baseline trials and test trials on which the samples and comparisons of the nonreinforced baseline trials were reversed.

By contrast, pigeons CTR1, CTR3, and CTR5 exhibited significantly higher comparison response rates on the negative than on the positive probe trials, Fs(1, 62) = 60.67, 153.98 and 6.14, respectively. In other words, they responded more to the reverse of the nonreinforced hue– form baseline relations than to the reverse of the reinforced hue–form baseline relations, an antisymmetry effect (Urcuioli, 2008, Experiment 4; Urcuioli & Swisher, 2012b). Interestingly, these three pigeons were all run in the same experimental chamber, whereas CTR2 and CTR4 were both run in the other experimental chamber. Given slight differences in the appearances of the hue center-key stimuli between chambers, we thought that perhaps the explanation for the antisymmetry-like test performances of CTR1, CTR3, and CTR5 was primary stimulus generalization. Specifically, if the blue comparison stimulus appearing in their form–hue baseline task was perceptually similar to the green comparison stimulus appearing on the symmetry probe trials, and if the white baseline comparison stimulus had a yellow color component that made it perceptually similar to the red probe comparison stimulus (Wright & Cumming, 1971), this might account for their pattern of test results. Given these generalization assumptions, these pigeons would be predicted to respond more frequently on T→G (“negative”) than on the T→R (“positive”) probe trials because the former would resemble the reinforced T→B sample–comparison combination in training. Likewise, they should respond more frequently on the H→R (“negative”) than on the H→G (“positive”) probe trials because the former would resemble the reinforced H→W sample–comparison combination in training.

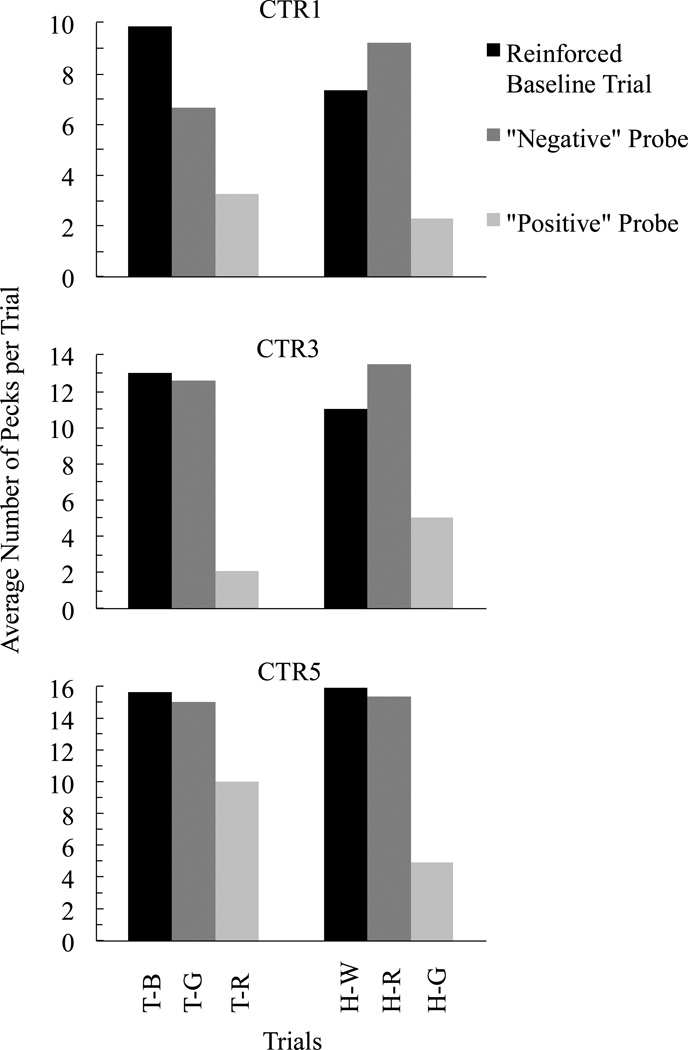
Figure 3 plots the average number of comparison pecks per trial for CTR1, CTR3, and CTR5 on the reinforced form–hue arbitrary matching baseline trials and on the “negative” and “positive” probe trials respectively. (Because comparison pecking on the nonreinforced baseline trials was so low (cf. Fig. 2), those data are omitted for clarity although similar logic would predict relatively few comparison pecks per trial on the T→R and H→G probes given their hypothesized similarity to the nonreinforced T→W and H→B baseline trials.) As can be seen, these pigeons pecked the comparisons on the form–hue symmetry probe trials in a manner very similar to how they pecked comparisons on their form–hue baseline trials. Of course, this analysis is post hoc, and also assumes little or no primary stimulus generalization between the hue comparison stimuli in the other experimental chamber for pigeons CTR2 and CTR4.

Fig. 3.

Average number of pecks to the comparisons per trial on T-B and H-W baseline trials, T-G and H-R “negative” probes trials, and T-R and H-G “positive” probe trials during the eight symmetry tests for Subjects CTR1, CTR3 and CTR5.

Two things are certain, however, given the test results from this experiment. One is that identity matching training is not necessary to observe associative symmetry in arbitrary successive matching by pigeons (cf. Frank, 2007; Frank & Wasserman, 2005). This emergent relation is also observed after training arbitrary matching and two oddity relations that, between them, share samples and comparisons appearing in the arbitrary task, as predicted by Urcuioli’s (2008) theory of pigeons’ stimulus class formation. Second, associative symmetry is not observed if there is incomplete overlap between the samples and comparisons appearing in arbitrary matching and those appearing in the concurrently trained successive matching tasks. This, too, is predicted by the theory given that such incomplete overlap precludes the formation of the stimulus classes containing the symmetrical elements.

Experiment 2

Experiment 1 demonstrated that associative symmetry in pigeons is observed after baseline training on concurrently arbitrary successive matching and two oddity successive matching tasks. Experiment 2 asked whether this effect would reverse (i.e., if antisymmetry would be observed) if one of the baseline tasks was now switched from oddity to identity matching (cf. Table 3). Stated otherwise, would such retraining reorganize the predicted stimulus classes such that they would now contain the elements comprising the symmetrical versions of the nonreinforced arbitrary matching baseline relations?

Table 3.

Baseline successive matching contingencies (first three columns) and nonreinforced probe-test trials (last column) in Experiment 2 for the former DODD pigeons from Experiment 1.

Form Oddity Group
Hue–form Arbitrary	Form Oddity	Hue Identity	Probe-test Trials
R → T - FI 5 s +	T → T - EXT	R → R - FI 5 s +	T → R
R → H - EXT	T → H - FI 5 s +	R → G - EXT	H → R (√)
G → T - EXT	H → T - FI 5 s +	G → R - EXT	T → G (√)
G → H - FI 5 s +	H → G - EXT	G → G - FI 5 s +	H → G
Hue Oddity Group
Hue–form Arbitrary	Hue Oddity	Form Identity	Probe-test Trials
R → T - FI 5 s +	R → R - EXT	T → T - FI 5 s +	T → R
R → H - EXT	R → G - FI 5 s +	T → H - EXT	H → R (√)
G → T - EXT	G → R - FI 5 s +	H → T - EXT	T → G (√)
G → H - FI 5 s +	G → G - EXT	H → H - FI 5 s +	H → G

Note. R = red, G = green, W = white, B = blue, T = triangle, H = horizontal, FI = fixed interval schedule, EXT = nonreinforced, + = reinforced. The first and second center-key stimuli in a trial sequence (sample and comparison, respectively) are shown to the left and to the right of the arrows, respectively.

^(√)indicates the probe trials for which higher comparison-response rates are predicted (i.e., antisymmetry).

Consider, for instance, the same reinforced hue–form arbitrary matching relations and the same hue oddity relations as in Experiment 1. Those sets of relations should yield the following two-member stimulus classes: [R1, T2], [G1, H2], [R1, G2], and [G1, R2]. If the remaining baseline task is switched from form oddity to form identity, this should yield [T1, T2] and [H1, H2] classes. Combining two-member classes sharing common elements (e.g., R1 and T2) produces the following two 4-member stimulus classes: [R1, T2, T1, G2] and [G1, H2, H1, R2]. From these, an antisymmetry effect in testing is predicted. To take one example, although the R1→T2 baseline relation is reinforced and the G1→T2 relation is nonreinforced (cf. Table 3), the prediction is that the reverse of the latter, nonreinforced relation (viz., T1→G2), should produce higher comparison response rates in testing than the reverse of the reinforced relation (viz., T1→R2), as indicated by the check marks in the right column of Table 3. This prediction was tested in Experiment 2 by retraining some of the Dual Oddity pigeons with form identity (top section of Table 3) and the other Dual Oddity pigeons with hue identity (bottom section of Table 3). Theoretically, this should produce antisymmetry in both subgroups (Urcuioli & Swisher, 2012b).

Method

Subjects and Apparatus

The five pigeons in the Dual Oddity group from Experiment 1 were divided into two groups: Form Oddity and Hue Oddity. Specifically, pigeons DODD1, DODD2, and DODD5 from Experiment 1 were renamed FODD1, FODD2, and FODD5, respectively, to reflect the fact that their retraining maintained their form oddity contingencies but switched to hue identity contingencies. Similarly, pigeons DODD3 and DODD4 from Experiment 1 became HODD3 and HODD4, respectively, to reflect the fact that their retraining maintained their hue oddity contingencies but switched to form identity contingencies. The apparatus was the same as in Experiment 1.

Procedure

Successive matching acquisition

The left three columns of Table 3 summarize the baseline successive matching contingencies for the Form Oddity and Hue Oddity groups in this experiment. Both the Form Oddity and Hue Oddity pigeons continued to be trained on the same reinforced, hue–form arbitrary matching relations as in Experiment 1 (viz., R→T and G→H; cf. Table 2). In addition, the Form Oddity pigeons were concurrently trained on form oddity as before but, now, were retrained with hue identity relations. Thus, for them, pecking the red comparison after red sample (R→R), and pecking the green comparison after the green sample (G→G) were now reinforced. By contrast, the Hue Oddity pigeons were concurrently trained on hue oddity as before but, now, were retrained with form identity relations. For them, pecking the triangle comparison after the triangle sample (T→T), and pecking the horizontal comparison after the horizontal sample (H→H) were now reinforced. Other procedural details during successive matching acquisition were the same as in Experiment 1. Similarly, each pigeon was retrained to the same performance criteria as in Experiment 1 and received 10 overtraining sessions after meeting those criteria.

Successive matching testing

As in Experiment 1, testing involved infrequent nonreinforced probe trials involving the reverse of the reinforced hue–form arbitrary relations (T→R and H→G) and the reverse of the nonreinforced hue–form arbitrary relations (T→G and H→R) intermixed among the baseline trials. Other procedural details for testing were identical to those in Experiment 1.

Results and Discussion

Matching acquisition

For the Form Oddity Group, the average sessions to criterion were 6.3 for hue–form arbitrary matching, 49.0 for hue identity, and 12.7 for form oddity. These differences were not statistically significant, F(2, 6) = 2.50. For the Hue Oddity Group, the corresponding averages were 11.5 for hue–form arbitrary matching, 3.5 for hue oddity, and 17.5 for form identity matching. These differences were statistically significant, F(2, 3) = 16.91. Not surprisingly, it took these pigeons longest to learn the form identity task given that their previous baseline relation was form oddity. More importantly, for the last five sessions of overtraining, the average DRs for the Form Oddity Group were 0.93 for hue–form arbitrary matching, 0.91 for hue identity, and 0.93 for form oddity. These differences were not statistically significant, F(2, 6) = 0.12. For the Hue Oddity Group, the corresponding DRs were 0.95 for hue–form arbitrary matching, 0.94 for hue oddity matching, and 0.91 for form identity matching. These differences were also not statistically significant, F(2, 3) = 0.60.

Testing

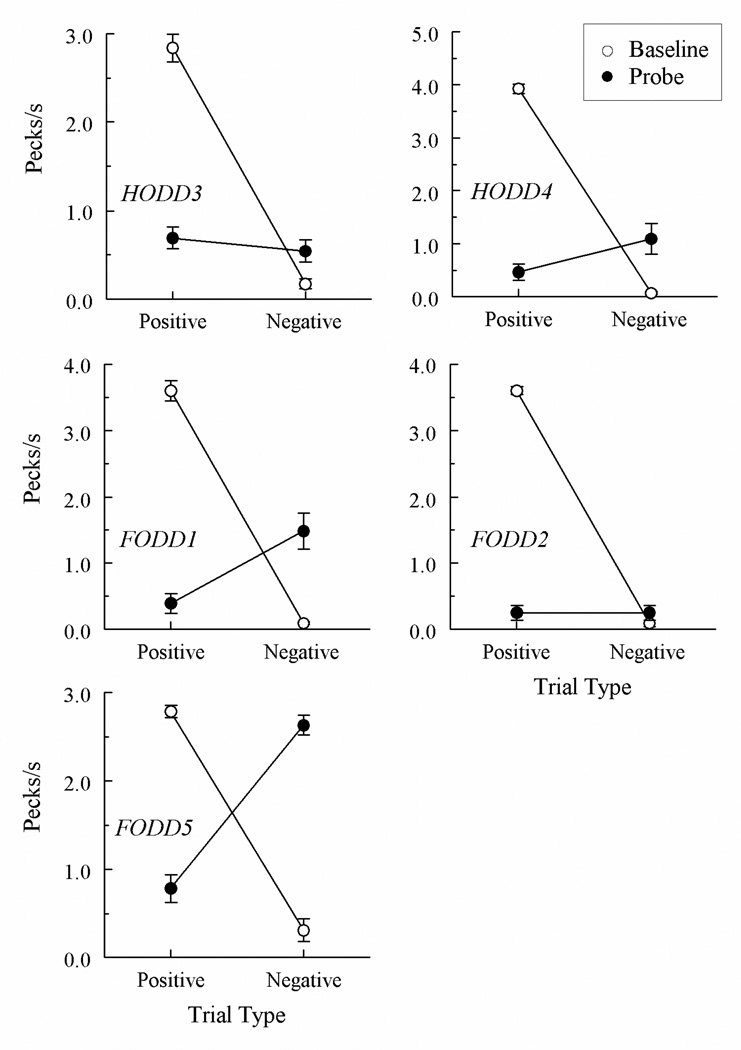
Figure 4 presents the number of comparison pecks per second averaged across the eight test sessions for the baseline hue–form arbitrary matching trials and form–hue probe trials for each Hue Oddity pigeon (top row) and Form Oddity pigeon (middle and bottom rows). “Positive” refers to the reinforced baseline trials and the probe trials that were the reverse of these trials. “Negative” refers to the nonreinforced baseline trials and the probe trials that were the reverse of them.

Fig. 4.

Comparison-response rates in pecks per s (± 1 SEM) on the hue–form arbitrary matching baseline trials (open circles) and the nonreinforced form–hue antisymmetry probe trials (filled circles) averaged over the eight test sessions for each Hue Oddity (HODD) and Form Oddity (FODD) pigeon. “Positive” = reinforced arbitrary baseline trials and test trials in which the samples and comparisons of the reinforced baseline trials were reversed. “Negative” = nonreinforced arbitrary baseline trials and test trials on which the samples and comparisons of the nonreinforced baseline trials were reversed.

All five pigeons maintained their baseline performances by exhibiting higher comparison response rates on the positive than on the negative baseline trials (open circles). Three pigeons (HODD4, FODD1, and FODD5) also exhibited higher comparison response rates on the negative than on the positive symmetry probe trials (filled circles), showing antisymmetry. For FODD1 and FODD5, the difference between the positive and negative probe-trial response rates was statistically significant, Fs(1, 62) = 12.79 and 88.17, respectively. The corresponding difference for HODD4 was not statistically significant when averaged over all eight test sessions, F(1, 62) = 3.65 (p = 0.06), but it was significant when averaged across the first six test sessions, F(1, 46) = 4.45 (data not shown). A likely reason for this 6- versus 8-session discrepancy is that pigeon HODD4 rarely responded on any probe trial during its last two test sessions (viz., all probe-trial responding had extinguished). The probe-trial response-rate differences for pigeons HODD3 and FODD2 were clearly nondifferential and, thus, not statistically significantly, Fs(1, 62) = 0.73 and 0.00, respectively, although the latter pigeon’s probe-trial responding very quickly extinguished in testing, precluding any possibility of observing a positive versus negative probe-trial difference.

In summary, when one of the oddity baseline relations was reversed from Experiment 1 to identity matching in this experiment, three of the five pigeons (FODD1, FODD5, and HODD4) showed an antisymmetry effect, as predicted by Urcuioli’s (2008) theory. This result is especially impressive because these three pigeons (formerly DODD1, DODD5, and DODD4 in Experiment 1) previously showed evidence for associative symmetry (cf. Fig. 1). For them, Experiment 2 can be seen as an intrasubject control condition for Experiment 1 such that the change in baseline contingencies from hue oddity to hue identity or from form oddity to form identity rearranged the elements of their stimulus classes.

Although pigeon HODD3 did not exhibit antisymmetry in this experiment, neither did it exhibit associative symmetry in Experiment 1. Apparently, this pigeon simply learned specific sets of “if-then” relations during baseline training independently of what those relations were. In any event, it is not uncommon to observe the absence of emergent relations following successive matching training in some pigeons (e.g., Urcuioli, 2008, Experiment 4; Urcuioli & Swisher, 2012b).

General Discussion

The results from the two experiments reported here provide additional confirmation of predictions derived from Urcuioli’s (2008) theory of pigeons’ stimulus class formation. One theoretical derivation, in particular, is noteworthy—that is, that concurrent training on arbitrary successive matching along with two oddity matching tasks that, together, involve the samples and comparisons in the arbitrary task, will yield associative symmetry in testing. The test results from Group Dual Oddity in Experiment 1 clearly support that prediction: Four of the five Dual Oddity pigeons responded more to the comparisons on symmetry probe trials that were the reverse of the reinforced arbitrary matching baseline combinations than on probe trials that were the reverse of the nonreinforced arbitrary matching baseline combinations. Furthermore, this finding clearly shows that associative symmetry can emerge without concurrent baseline training on identity matching (cf. Frank, 2007; Frank & Wasserman, 2005; see also Tomonaga, Matsuzawa, Fujita, & Yamamoto, 1991). Rather, instances in which associative symmetry has been observed in successive matching with identity matching as part of baseline training occur because such training permits the development of stimulus classes whose elements overlap with elements in the classes arising from arbitrary matching. That overlap is theoretically important (cf. Urcuioli, 2008) because elements common to more than one class are hypothesized to produce class merger and, consequently, larger classes containing both the elements of the explicitly trained arbitrary relations and the “untrained” symmetrical relations.

Experiment 2 provided additional support for this interpretation by showing that subsequently changing one of the concurrently trained oddity relations to an identity relation reversed the symmetry effect shown by three of the pigeons in Experiment 1. In other words, these pigeons now exhibited antisymmetry, responding more on probe trials that were the reverse of the nonreinforced arbitrary sample–comparison combinations than to the reverse of the reinforced combinations. This represents a within-subject replication of antisymmetry effects previously reported by Urcuioli (2008, Experiment 4) and Urcuioli and Swisher (2012b).

Despite these positive findings, apparent theoretical disconfirmations were observed in the test results from three of the five Control pigeons in Experiment 1 (cf. Fig. 2). Their baseline training should not have yielded stimulus classes and, hence, any emergent relation, associative symmetry or antisymmetry. Nevertheless, these three pigeons unambiguously showed an antisymmetry effect. We have suggested that their test results do not actually represent an emergent effect but, instead, the unwanted contribution of primary stimulus generalization (Honig & Urcuioli, 1981; Wright & Cumming, 1971) between the various hues used as comparison stimuli during baseline training. Nevertheless, it will be important for future research to retest the prediction derived from Urcuioli (2008) by selecting stimuli that minimize the potential for such contribution. Indeed, given the importance of the antisymmetry effect to the theory itself, it is imperative that the results shown by these three pigeons be followed up under better controlled conditions.

The term “stimulus class” incorporates the idea that its members are interchangeable or substitutable for one another not only in training but, more importantly, in new contexts (Dougher & Markham, 1994; Golddiamond, 1962; Sidman, 1994; Urcuioli, 2013). Such interchangeability is readily apparent in the four-member classes that Urcuioli (2008) hypothesizes to underlie associative symmetry following training on hue–form arbitrary successive matching and hue– and form–identity matching with red and green hues and triangle and horizontal-line forms as samples and comparisons: [R1, R2, T1, T2] and [G1, G2, H1, H2]. The explicitly reinforced R1→T2 and G1→H2 relations in training should, and do, yield the symmetrical T1→R2 and H1→G2 relations because the nominal triangle (T) stimuli are interchangeable with one another, as are the nominal horizontal-line stimuli (H), and red (R) and green (G) stimuli. Stated otherwise, T1 and T2 are in the same class as are R1 and R2, G1 and G2, and H1 and H2.

Interestingly, associative symmetry by the Group Dual Oddity pigeons of Experiment 1 was observed despite the fact that each nominal stimulus was a member of the other, “opposing” stimulus class. Training two oddity baseline tasks together with arbitrary hue–form matching theoretically yielded the following four-member classes: [R1, G2, H1, T2] and [G1, R2, T1, H2]. Note that the elements of the explicitly reinforced baseline relation R1→T2 are in one class, but the elements of the symmetrical T1→R2 relation are the in other class. Likewise, the elements of the explicitly reinforced baseline relations G1→H2 are in one class, but the elements of the symmetrical H1→G2 relation are in the other. On one hand, this is not problematic for (i.e., it does not contradict) Urcuioli’s (2008) theory which states that pigeons will respond more in testing to comparisons that are in the same class as their preceding samples than to comparisons that are in a different class than their preceding samples. Clearly, T1 and R2 are in the same class, as are H1 and G2, so by hypothesis these probe-trial combinations should engender higher comparison response rates than the T1→G2 and H1→R2 probe-trial combinations. The data from Experiment 1 are clearly in line with this prediction.

On the other hand, the observed symmetrical relations seem to violate the notion of interchangeability of stimuli within a class as a source of such emergent relations. After all, from a theoretical standpoint, members of one class generated performances in testing that were the reverse of those representing the explicitly trained relations between members of the other class. Certainly, from the standpoint of a naïve observer, the probe-trial performances of the DODD pigeons are evidence for associative symmetry. Given functional stimuli that include ordinal position as one of their components, the theoretical underpinnings of this phenomenon (Urcuioli, 2008), for pigeons at least, involve not only within-class substitutability of the nominal stimuli but also across-class relational substitutability.