Induced Signal Quenching in MAS-DNP Experiments in Homogeneous Solutions

Abstract

The effects of nuclear signal quenching induced by the presence of a paramagnetic polarizing agent are documented for conditions used in magic angle spinning (MAS)-dynamic nuclear polarization (DNP) experiments on homogeneous solutions. In particular, we present a detailed analysis of three time constants: (1) the longitudinal build-up time constant T_B for ¹H; (2) the rotating frame relaxation time constant T_1ρ for ¹H and ¹³C and (3) T₂ of ¹³C, the transverse relaxation time constant in the laboratory frame. These relaxation times were measured during microwave irradiation at a magnetic field of 5 T (140 GHz) as a function of the concentration of four polarizing agents: TOTAPOL, 4-amino-TEMPO, trityl (OX063), and Gd-DOTA and are compared to those obtained for a sample lacking paramagnetic doping. We also report the EPR relaxation time constants T_1S and T_2S, the DNP enhancements, ε, and the parameter E, defined below, which measures the sensitivity enhancement for the four polarizing agents as a function of the electron concentration. We observe substantial intensity losses (paramagnetic quenching) with all of the polarizing agents due to broadening mechanisms and cross relaxation during MAS. In particular, the monoradical trityl and biradical TOTAPOL induce ~40 and 50% loss of signal intensity. In contrast there is little suppression of signal intensity in static samples containing these paramagnetic species. Despite the losses due to quenching, we find that all of the polarizing agents provide substantial gains in signal intensity, and in particular that the net enhancement is optimal for biradicals that operate with the cross effect. We discuss the possibility that much of this polarization loss can be regained with the development of instrumentation and methods to perform electron decoupling.

1. Introduction

Dynamic nuclear polarization (DNP) is a technique to enhance the polarization of nuclear spins by several orders of magnitude and relies on the transfer of the high polarization present in the electron Zeeman reservoir to the nuclear Zeeman reservoir. Accordingly, DNP accelerates otherwise time-consuming experiments or allows observation of spins that are undetectable by conventional magic angle spinning (MAS) nuclear magnetic resonance (NMR) [1–7] and is rapidly becoming a standard technique in chemistry, biochemistry, structural biology, and material sciences [8–11]. An essential requirement is that the samples contain electron spins in the form of paramagnetic centers from which the relatively high Boltzmann polarization (~660 times larger than ¹H) can be transferred to the nuclear spins via microwave driven mechanisms reviewed briefly below. In biochemical applications these paramagnets can in principle be endogenous (protein free radicals [12]), but are usually exogenously additions to the sample [13]. In the latter case the paramagnetic polarizing agent (PA) is co-dissolved in a cryoprotecting glass forming solvent together with the target molecule and both are randomly distributed in the frozen solution. If the sample is heterogeneous the target molecule is in a spatially separate phase (e.g., nanocrystals, amyloid fibrils or membrane protein dispersed in the cryoprotectant) from the polarizing agent. Thus, in a heterogeneous sample, the enhanced polarization is transferred to the molecule of interest by efficient ¹H–¹H spin diffusion across phase boundaries, an example being amyloidiogenic nanocrystals such as GNNQQNY [14, 15], and a polarization gradient can be observed[14]. More recently, heterogeneous samples were further exploited by Emsley and coworkers in applications to microcrystalline analytes dispersed in an organic solvent [16]. In addition, Lesage et al. [17] and Kobayashi, et al. [18] recently demonstrated that it is possible to enhance the NMR signals at a surface and of small ligands bound to a catalytically active surface or mesoporous material using DNP by wetting the surface with a solution containing the polarizing agent. In contrast, in a homogeneous solution of small molecules [19] or proteins [20], which is the case considered here, the distance bridged via spin diffusion is short and a uniform polarization enhancement of all spins in the solvent and of the target molecule is possible [21].

Because polarizing agents must be present within the sample, nuclear spins are subject to interactions with these paramagnetic species. These interactions can manifest themselves as shifts of the nuclear Larmor frequencies due to hyperfine interaction with the electron spin as well as a general shortening of the typical relaxation times encountered in solid state NMR. The former can generally be neglected in MAS DNP, since nuclei subject to strong paramagnetic (first-order) shifts are either filtered by the limited NMR excitation bandwidth or are broadened beyond detection at temperatures around 80 K. Additionally, polarizing agents typically do not induce significant pseudocontact (second-order) shifts due to EPR properties required for efficient DNP. However, nuclei detectable in MAS DNP are subject to reduced relaxation times by incoherent electron-nuclear interactions. The reduction in T₁ and T₂ can be beneficial (e.g., shorter T_1I allows for accelerated acquisition of NMR spectra) or detrimental (e.g., enhanced transverse relaxation that broadens resonances and leads to attenuated (quenched) signal intensities). We observed both of these effects in early experiments using the monoradical TEMPO [22], especially when the electron concentration exceeded 40–60 mM [23]. Importantly, observation of these intensity losses with TEMPO monoradicals stimulated us to develop biradical polarizing agents that function at significantly lower electron concentrations [24–27]. However, until now we have not performed a systemic investigation of the intensity losses comparing the addition of mono and biradical polarizing agents during MAS experiments. Therefore, it is important to investigate these effects using model systems for both homogeneous and heterogeneous samples in order to optimize a variety of DNP parameters, sample preparation methods, design of new polarizing agents, and further the development of DNP as a generally applicable technique.

In this paper we report paramagnet induced intensity losses and enhancements using four polarizing agents - TOTAPOL, 4-amino-TEMPO, trityl (OX063), and Gd-DOTA -- in MAS DNP experiments. We find that all four polarizing agents result in substantial signal losses but also substantial improvements in sensitivity, with enhancements from 11 to 139, and sensitivity enhancements of 15 to 226. The polarizing agent TOTAPOL stands out because it results in the largest gain in sensitivity and does so at a concentration of only 5 to 10 mM that has minimal impact on the resolution while substantially reducing T_B, the build-up time.

An outline of the paper is as follows. In Section 2 we present a brief review of DNP mechanisms and relaxation theory along with a discussion of the polarizing agents chosen for this study. Section 3 describes the instrumentation, sample preparation, and details of data acquisition. In Section 4, we discuss the results in the context of contemporary DNP MAS spectroscopy, along with measurements of T₁, T₂, and T_1ρ. We also include in Section 4 a discussion of enhancement factors, signal quenching, and overall sensitivity enhancement and a discussion of the possibility of decoupling electrons to recover part of the quench nuclear signals.

2. Background and theory

2.1. Mechanisms of DNP

In a MAS DNP experiment using continuous microwave irradiation, the electron-to-nuclear polarization transfer occurs primarily via two different mechanisms: the solid effect (SE) and/or the cross effect (CE). The SE [28–35] relies on formally forbidden excitation of electron-nuclear zero or double quantum transitions which can be selectively excited by fulfilling the SE matching condition

$${\omega }_{\text{mw}}={\omega }_{0S}\pm {\omega }_{0I},$$ (1)

where ω_mw is the microwave frequency and ω_0S and ω_0I are the electron and nuclear Larmor frequencies, respectively. This selectivity can only be achieved efficiently if the overall breadth of the polarizing agent’s EPR line – consisting of both the homogeneous linewidth δ and inhomogeneous breadth Δ – is smaller than the nuclear Larmor frequency: δ, Δ <ω_0I. This prerequisite makes paramagnets with a narrow EPR line like trityl, [36] BDPA [37, 38] or Gd-DOTA [39] ideal polarizing agents for SE DNP [35]. In contrast, the CE [24, 40–47] relies on three-spin flip-flop-flips between two electron spins and one nuclear spin. The flip-flop-flip process is efficient if the net energy involved is vanishing, a condition that is satisfied when the difference in the Larmor frequency of the two electron spins ω_0S,1 and ω_0S,2 matches the nuclear Larmor frequency:

$${\omega }_{0S,1}-{\omega }_{0S,2}=\pm {\omega }_{0I}$$ (2)

In contrast to the SE, where the coherent transfer has to be extrinsically stimulated by application of a microwave field, the coherent electron-nuclear transfer during CE DNP is intrinsically excited by the dipole coupling between the electron spins. As a result, magnetization is exchanged between the electron and nuclear spins even in the absence of microwave irradiation. This electron-electron-nuclear cross relaxation (CR) has a significant impact on nuclear spin-lattice relaxation as will be further discussed below. Given the two electron spins are of equal or similar nature (e.g., two equal monoradicals are interacting in the glassy matrix or two similar radical moieties are tethered in a symmetric biradical) the inhomogeneous breadth of the polarizing agent’s EPR line has to exceed the nuclear Larmor frequency to satisfy (2) while its homogeneous linewidth has to be smaller, so that one electron spin can be selectively saturated: δ <ω_0I < Δ. This condition is met in the case of nitroxide radicals, whose EPR spectra are broadened by the g-anisotropy of the electron and of the ¹⁴N hyperfine interaction. In this case MAS introduces a further complication because spin transitions shift in and out of resonance with the microwave frequency as well as CE conditions as several level (anti-)crossings occur during the rotor period [48, 49].

2.2. Electron-nuclear interactions during MAS DNP

During MAS the coupling of nuclear spins with the electron spins of the polarizing agent is modulated by the sample rotation. Nuclei and unpaired electron(s) within a short distance of one another are strongly coupled leading to paramagnetic shifts and broadening, which effectively reduces the number of nuclear spins detectable by NMR. Concurrently, nuclear spins detectable by NMR exhibit enhanced paramagnetic relaxation. The shortening of T₂ and T_1ρ, even while only minimally impacting resolution in inhomogeneously broadened spectra, leads to an accelerated decay of magnetization during polarization transfer experiments that can reduce the efficiency of homo- and heteronuclear mixing experiments. Therefore, it is crucial to understand the concentration dependent impacts on relaxation times induced by polarizing agents commonly used for MAS DNP.

The existing theory of paramagnetic enhanced relaxation of nuclear spins is mainly based on concepts derived by Solomon and Bloembergen and Morgan [50–53] that invoke incoherent interactions between the dipole moments of electron and nuclear spins. Some of the theory applies to conditions typically satisfied in liquids (e.g. fast isotropic motional averaging due to molecular tumbling). At the other extreme are models that apply to a rigid lattice in which it is assumed that local field fluctuations caused by electron flips are the dominant source of paramagnetic relaxation [50, 54]. In particular, Blumberg has shown that internuclear spin-diffusion plays an important role in longitudinal relaxation in solids doped with paramagnets [54]. However, these models do not account for electron-electron interaction or fluctuations in the local field at the nucleus caused by dynamics of nuclei in the local field gradient of the electron spin or by MAS; accordingly, they are not generally applicable to paramagnetic relaxation effects of nuclei in dielectric or rotating solids. An analytic or numerical derivation of relaxation in DNP samples would need to consider static and dynamic interactions of secular and nonsecular nature between electrons, between electrons and nuclei, as well as between nuclei, all of which span a wide range of magnitude and time-scale. In the absence of a model to treat these effects, we can rely on empirical relaxation data for different DNP polarizing agents.

2.3. Properties of the polarizing agents

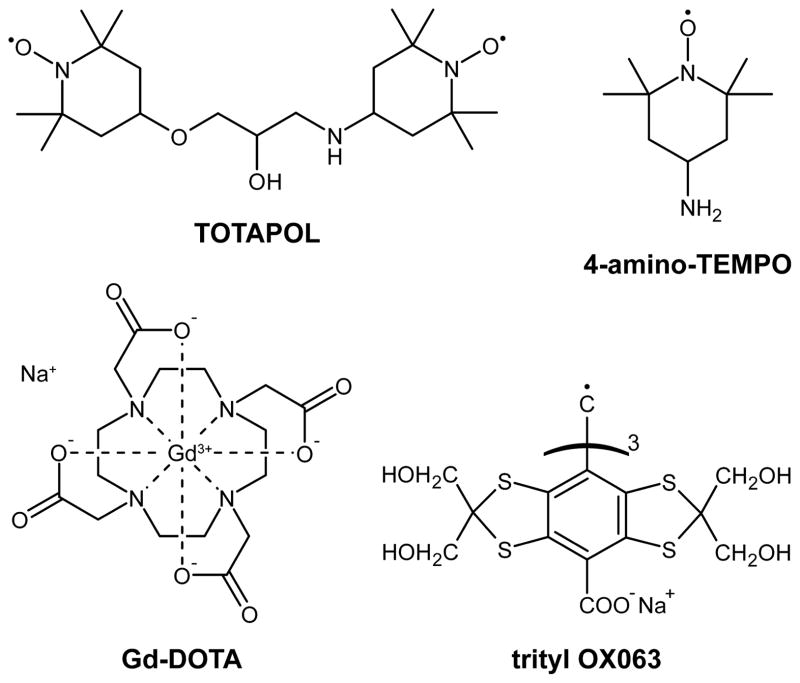
We studied the paramagnetic relaxation effects induced by varying concentrations of TOTAPOL, 4-amino-TEMPO, trityl OX063, and Gd-DOTA in MAS DNP experiments. Each of these paramagnets (see Fig. 1 for their chemical structures) is representative of a certain group of polarizing agents that mediate different DNP mechanisms. Nitroxide-based polarizing agents enable CE DNP with TOTAPOL being an example of a biradical that allows for a relatively strong intramolecular e⁻-e⁻ dipolar coupling at low e⁻ concentrations [26]. In contrast, the monoradical 4-amino-TEMPO requires high concentrations in order to provide the required intermolecular coupling and efficient CE [55]. Trityl OX063 [36] is a radical with a narrow EPR line that is commonly used for SE DNP [33, 35], and Gd-DOTA [39] represents the group of recently introduced high-spin polarizing agents also supporting the SE [56]. In the following sections we report the major differences between these polarizing agents and their respective DNP mechanisms, together with the expected effects on nuclear spin relaxation.

Figure 1.

Polarizing agents investigated in this study.

TOTAPOL (1-(TEMPO-4-oxy)-3-(TEMPO-4-amino)propan-2-ol) was introduced by Song et al. as an efficient biradical polarizing agent for CE DNP [26]. Due to the fact that the CE relies on efficient cross-relaxation (CR) between one electron spin and an electron-nuclear spin pair (vide supra), one expects a pronounced effect on the paramagnet induced nuclear T_1I reduction. Note that the same CR mechanism allowing for CE DNP also leads to efficient paramagnetic relaxation by providing a coherent pathway for nuclear magnetization to the bath via the energy difference of the two electron spins. The e⁻-e⁻ dipole coupling is ~23 MHz [27].

4-Amino-2,2,6,6-tetramethylpiperidine-1-oxyl (4-amino-TEMPO, TEMPAMINE) is a stable, water-soluble, nitroxide radical that exhibits a very similar EPR spectrum to TOTAPOL at 140 GHz [24, 26, 47, 55]. Therefore, the CE is also the active DNP mechanism; however, the two electron spins are located on separate molecules and the crucial e⁻-e⁻ dipole coupling is intermolecular rather than intramolecular. Obviously, the strength of the dipole coupling and hence the efficiency of CR depends strongly on the molecular concentration of the radical in the cryoprotecting matrix, which at 40 mM is ~2 MHz [27]

The stable trityl radical OX063 exhibits a narrow EPR line of ~50 MHz width at 140 GHz [36, 47] due to a small g-anisotropy. The chance of energy matching an electron-electron-proton triplet is small so CR is quenched at high field, and in this case ¹H DNP can be driven by the SE. Paramagnetically enhanced spin-lattice relaxation is caused by local magnetic field fluctuations by random spin flips of the electron spin or by dynamic motion of the nucleus in the local magnetic field gradient of the electron spin.

Gd-DOTA is an extremely stable Gd(III) complex formed by the macrocyclic chelating derivative 1,4,7,10-tetraazacyclododecane-N,N′,N″,N‴-tetraacetate (DOTA) and exhibits a high-spin state of S = 7/2 due to the 4 f ⁷ electronic structure of Gd³⁺, which potentially leads to strong paramagnetic relaxation effects [39, 57, 58]. The electron spin of Gd³⁺ generally experiences a significant zero-field splitting (i.e., electron quadrupole interaction) in the ligand field, with an axially symmetric tensor described by the single constant D = 570 MHz [59]. This interaction leads to a dispersion of the full EPR spectrum over almost 7 GHz. However, because of the half-integer spin state, the central EPR transition (m_S = −1/2 → +1/2) is not influenced by zero-field splitting to first order and exhibits a full width at half maximum (FWHM) of only ~29 MHz at the magnetic field of interest (5 T) [56]. In a previous study we have shown that this narrow transition can be exploited for SE DNP, whereas no signs of CE DNP have been observed [56]. The absence of CE DNP does not, however, automatically indicate that CR is inactive as well. For example, for a very broad EPR line (i.e. the inhomogeneous width greatly exceeding the nuclear Larmor frequency), positive and negative CE conditions cancel each other, leading to negligible CE DNP enhancement; CR might still be active and might lead to efficient relaxation of nuclear polarization toward thermal equilibrium. Nevertheless, we expect CR to be less efficient with Gd-DOTA due to the fact that the probability of finding two dipolar coupled Gd³⁺ sites in the correct orientation and spin states to fulfill the CE matching condition (2) is small, especially in low concentration solutions investigated in this study.

For a further discussion of DNP and its mechanisms, we refer the reader to excellent work on DNP as such by Abragam and Goldman, [8] and reviews about MAS DNP by Maly et al.,[10] and Barnes et al. [9]. Hu has recently published an excellent review focusing on polarizing agents and the related DNP mechanisms [46].

3. Experimental

3.1. Instrumentation

Most of the DNP NMR experiments were performed on a custom-built NMR spectrometer operating at 212 MHz (¹H frequency), courtesy of D. Ruben. A custom-built MAS NMR probe allowed for MAS at cryogenic temperatures (T ≥ 80 K) and features a triple resonance rf circuit (¹H, ¹³C, ¹⁵N) and efficient microwave coupling to the sample using overmoded corrugated waveguides (similar to a design published by Barnes et al.[60]). The probe has a cryogenic sample exchange system that allows efficient screening of multiple samples. Microwaves were generated with a gyrotron oscillator operating at 139.65 GHz with a maximum output power of ~13 W [61–63]. For all experiments the operating conditions were chosen so that ~8 W power was delivered at the probe waveguide entrance. Because the gyrotron operates at a fixed frequency, the magnetic field was swept to the optimal matching condition for each polarizing agent with a cryogenic sweep coil. Optimal DNP fields were determined in previous studies [35, 56], being 4.9798 T for TOTAPOL and 4-amino-TEMPO, 4.9891 T for trityl, and 5.0178 T for Gd-DOTA. Due to their relatively narrow DNP matching conditions, trityl and especially Gd-DOTA require careful adjustment of the magnetic field in order to optimize the enhancement. EPR spectra were recorded on a custom-built pulsed EPR spectrometer operating at 140 GHz. A detailed description of that instrument was published recently [64.]. The experiments comparing intensities of static and spinning samples were performed on a homebuilt 380 MHz/250 GHz spectrometer at ω_r/2π ~ 5 kHz.

3.2. Sample preparation

All samples were prepared by dissolving an appropriate amount of polarizing agent in a mixture of d₈-glycerol/D₂O/H₂O with a volume ratio of 60:30:10 to which 1 M ¹³C-urea was added to provide the required ¹³C for detection of the non-DNP-enhanced signal (off-signal) in 16–128 scans at sufficient S/N for accurate determination of enhancement factors. Samples with varying polarizing agent concentrations were prepared by diluting the most concentrated solution with undoped solvent mixture. 2-¹³C, d₈-glycerol was synthesized by isotope exchange from commercial 2-¹³C glycerol [65]. All other isotope labeled compounds were purchased from Cambridge Isotope Laboratories, Inc. (Andover, MA) and were used without further purification. TOTAPOL was acquired from Dynupol, Inc (Cambridge, MA). We found that TOTAPOL when properly purified and dried is soluble to a maximum concentration of ~50 mM in 60/40 (v/v) glycerol/water mixtures. In contrast to previous reports [66] we have never been able to achieve concentrations of 100 mM or larger. 4-Amino-TEMPO from Sigma-Aldrich (St. Louis, MO) was used without further purification. Trityl OX063 was from Oxford Instruments and Gd-DOTA (Na(Gd[DOTA])·4H₂O) was provided by C. Luchinat and I. Bertini (CERM, Florence, Italy).

Spectra comparing the intensity of static and MAS experiments were obtained from samples composed of d₈-glycerol/D₂O/H₂O with a volume ratio of 30/30/30/10 d₈-glycerol/2-¹³C, d₈-glycerol/ D₂O / H₂O. Since the static ¹³C powder pattern of ¹³C-urea is ~18 kHz in breadth, we used 2-¹³C-glycerol which has line of ~5 kHz. The samples were doped with 20 mM electrons, either 10 mM TOTAPOL or 20 mM trityl.

3.3. Data acquisition and analysis

Samples for DNP NMR studies were contained in a 4 mm OD sapphire MAS rotor from Insaco (Quakertown, PA). The axial sample dimension was restricted by the length of Vespel spacers to the central ~4 mm inside the 8 mm long coil volume. All experiments were performed using a MAS frequency of ω_r/2π = 5 kHz at a temperature of 84 K. Approximately 8 W’s of microwave power (measured at the probe input) were used for all DNP experiments, and signal intensities were detected on ¹³C after a cross-polarization (CP) step from ¹H with 2 ms contact time and ω₁/2π = 83 kHz. Polarization on ¹H and ¹³C was first saturated with a 16-pulse train applied to both channels (ω₁/2π = 50 kHz) after which polarization built up during a microwave irradiation period. The length of this period was varied for determination of the longitudinal DNP build-up time constant T_B (or the longitudinal relaxation time constant $T_1^{\circ }$ in the case of the undoped samples). All other experiments were performed using a fixed recovery period of 1.26 × T_B (or $T_1^{\circ }$), thus allowing for optimal sensitivity in a given experimental time. T₂ was determined by measuring the decay of polarization during a rotor-synchronized Hahn-Echo sequence. Two-pulse phase modulation (TPPM) [67] was used for ¹H decoupling with an rf field strength corresponding to ω₁/2π = 83 kHz during T₂ evolution and acquisition. The ¹H T_1ρ was measured by a spin-lock experiment before the CP sequence, whereas the ¹³C T_1ρ was determined by measuring the magnetization decay during a ¹³C spin-lock after the CP transfer step. In the latter case no ¹H decoupling field was applied since application of typical decoupling fields avoiding Hartmann-Hahn matching resulted in significant shortening of ¹³C T_1ρ. All spin-lock pulses were limited to a maximum duration of 20 ms to prevent extensive energy dissipation in the rf circuit and potential arcing. A timing diagram containing all pulses is shown in Fig. 2. Relaxation or build-up time constants were determined by least-square fitting the signal amplitude (after Fourier transform of the FID/echo) with an exponential function. $T_{1\mathrm{\rho }}^{\circ }$ (of the undoped sample) could not be determined precisely but we ascertain that it is >20 ms because of the absence of detectable decay.

Figure 2.

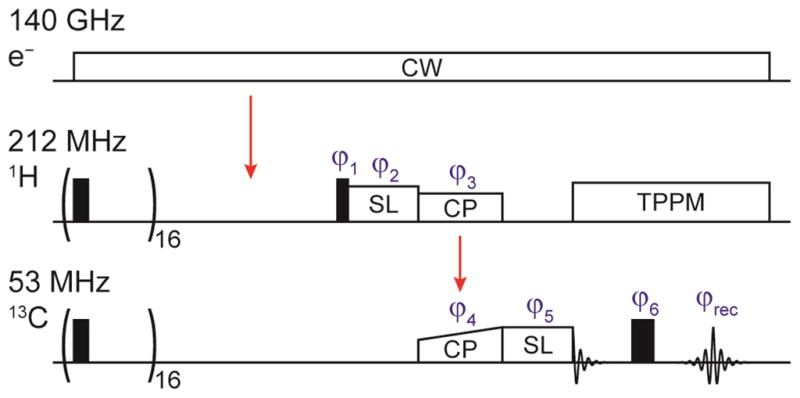
Pulse sequence used for relaxation time measurements. The ¹H and ¹³C spin-lock pulses as well as the Hahn-echo sequence were only used for the respective T_1ρ and T₂ experiments; the pulses not needed for certain experiments having been disabled accordingly. The pathway of polarization transfer is marked by red arrows. The saturation pulses were phase alternated between 0 and 90° phase angle. A phase cycle of ϕ₁ = xx̄, ${\varphi }_2=\text{yy}\overline{\text{yy}}$ ϕ₃ = y, ${\varphi }_4=\text{xxyy}\overline{\text{xxyy}}$ ϕ₅ = xxyy, ϕ₆ = xxyy, and ${\varphi }_{\text{rec}}=\mathrm{y}\overline{\mathrm{y}}\mathrm{x}\overline{\text{xy}}\mathrm{y}\overline{\mathrm{x}}\mathrm{x}$ was used in order to suppress unwanted coherences and artifacts due to experimental imperfections.

EPR experiments were performed on the same sample solutions used for DNP NMR experiments at a temperature of 80 K. Due to a more complicated and time consuming sample changing procedure -- the EPR probe has to be removed from the cryostat, warmed to ambient temperature, and dried to avoid build-up of humidity before returning it into the cold cryostat – the sample space was limited to 3 samples of each polarizing agent. For each compound the smallest, the largest, and an intermediate concentration was chosen. For determination of T_1S a saturation recovery experiment was performed using a long continuous wave (cw) irradiation period followed by a recovery period of varying time during which longitudinal magnetization is built-up and read-out using a Hahn echo sequence π/2−τ −π −τ. Although being theoretically inferior to inversion recovery in terms of sensitivity, saturation recovery minimizes effects of spectral diffusion interfering with longitudinal relaxation due to the incomplete excitation of inhomogeneously broadened spectra. The resulting polarization build-up curve can be fitted using a monoexponential, directly yielding the longitudinal relaxation time constant T_1S. The transverse relaxation time constant T_2S was determined using a Hahn echo experiment with a pulse sequence π/2−τ −π −τ that varies the time τ during which transverse relaxation is occurring. However, in systems with large electron spin concentration and therefore significant electronic spin–spin couplings the transverse magnetization not only decays due to T_2S but also evolves under these couplings; thus care has to be taken to sufficiently refocus these couplings. Otherwise a combination of transverse relaxation and interelectronic spin evolution results in a shortening of the measured echo decay time constant, described by the phase-memory time T_m. In order to determine the actual T_2S, we measured T_m for various microwave field strengths and respective pulse lengths and extrapolated the decay time constant to infinite pulse length (see Fig. S12). This extrapolated value represents the echo decay time constant for an infinitely selective (soft) excitation of a single spin packet and therefore T_2S.

All data recorded and analyzed is compiled in Tables S1–S5 in the supporting information.

4. Results and discussion

4.1. Spectral implications of paramagnetic doping and DNP

In Fig. 3 we show the signal intensities in MAS NMR spectra from an undoped sample of ¹³C-urea in glycerol/water and spectra enhanced by each of the four PA’s with respect to the non-enhanced (off-) signal. The enhanced signal spectra were recorded using the PA concentration yielding the largest enhancement (vide infra). As can be seen in Fig. 7 these concentrations also led to the maximum sensitivity for each polarizing agent.

Figure 3.

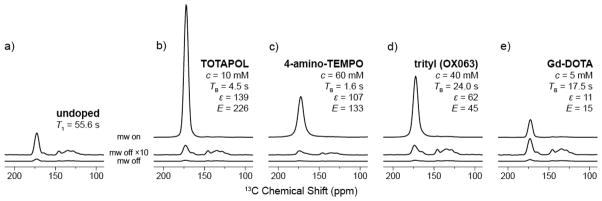
DNP enhanced ¹³C-¹H CP spectra of ¹³C-urea in 60/30/10 (vol.-%) d₈-glycerol/D₂O/H₂O for (a) signal of the undoped sample at equilibrium and (b–e) for each polarizing agent as labeled at the optimal concentration, for maximum enhancement and sensitivity. Off-signals are shown at the same scale as well as multiplied by a factor of 10. Spectra were recorded with a recycle delay of 1.26×T_B and were scaled in order to correct for variations in spectrometer sensitivity as described in supporting information. ω_r/2π = 5 kHz, T = 84 K.

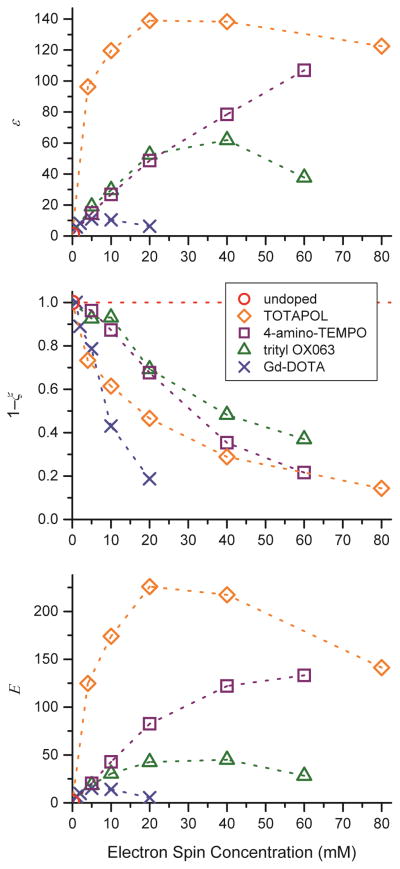
Figure 7.

¹H DNP enhancement ε (top), relative off-signal intensity not affected by paramagnetic bleaching, 1−ζ, following eq. (7) (middle), and effective DNP sensitivity gain E according to eq. (8) (bottom) as a function of electron spin concentration of various polarizing agents.

The signal at 175 ppm in Fig. 3 is the carbonyl group of urea used to measure all of the relaxation, quenching, and enhancement parameters in the text. Signals from 120–150 ppm arise from Vespel and Kel-F used in the rotor and stator assembly, and as expected are not altered by the presence of the polarizing agent; however it varies in intensity due to varying recycle delays. The urea spectrum is inhomogeneously broadened, as expected from a small molecule resident in a glassy matrix, and high electron concentrations of ~60 mM are needed in order to observe noticeable changes in the linewidth.

4.2. Definitions and determination of paramagnet induced relaxation rates

In order to separate relaxation effects induced by paramagnetic polarizing agents from those intrinsic to the sample sans polarizing agent, we calculate the longitudinal DNP build-up rate, Γ̃_B, by subtracting the intrinsic longitudinal relaxation rate of the undoped sample, ${\mathit{\Gamma }}_1^{\circ }$, from the measured overall longitudinal build-up rate, Γ_B, of the doped sample:

$${\stackrel{\sim }{\mathit{\Gamma }}}_{\mathrm{B}}={\mathit{\Gamma }}_{\mathrm{B}}-{\mathit{\Gamma }}_1^{\circ }=\frac{1}{T_{\mathrm{B}}}-\frac{1}{T_1^{\circ }}.$$ (3)

Similarly, the paramagnet induced transverse relaxation rate, Γ̃₂, is obtained by subtracting the intrinsic transverse relaxation rate, ${\mathit{\Gamma }}_2^{\circ }$, of the undoped sample from the measured transverse relaxation rate, Γ₂, of the doped sample:

$${\stackrel{\sim }{\mathit{\Gamma }}}_2={\mathit{\Gamma }}_2-{\mathit{\Gamma }}_2^{\circ }=\frac{1}{T_2}-\frac{1}{T_2^{\circ }}.$$ (4)

where, as usual, $T_1^{\circ }$ and $T_2^{\circ }$ are the longitudinal and transverse relaxation time constants of the undoped sample while T_B and T₂ are the longitudinal DNP build-up time constant and the transverse relaxation time constant. Rate constants are simply obtained as inverse of the respective time constants: ${\mathit{\Gamma }}_i=T_i^{-1}$. All time constants and rates presented were acquired under irradiation with microwaves. Note that T_B (i.e., the build-up time constant with microwave irradiation) and T₁ (i.e., same quantity without microwaves) have been shown to differ for the SE mechanism [33, 35]. Nevertheless we neglect this and only report T_B (≈ T₁). This approximation is reasonable because under similar conditions a maximum discrepancy of ~10 % has been observed [35].

The rotating frame relaxation time constant of the undoped sample, $T_{1\mathrm{\rho }}^{\circ }$, greatly exceeded our maximum spin-locking time for each nucleus and spin-locking field. Therefore we obtained only the respective time constant for the doped samples, T_1ρ, and we conclude $T_{1\mathrm{\rho }}\ll T_{1\mathrm{\rho }}^{\circ }$ in all cases. Therefore we can estimate without significant error:

$${\stackrel{\sim }{\mathit{\Gamma }}}_{1\mathrm{\rho }}={\mathit{\Gamma }}_{1\mathrm{\rho }}-{\mathit{\Gamma }}_{1\mathrm{\rho }}^{\circ }\approx {\mathit{\Gamma }}_{1\mathrm{\rho }}=\frac{1}{T_{1\mathrm{\rho }}},$$ (5)

where Γ̃_1ρ is the paramagnet induced rotating frame relaxation rate and Γ_1ρ and ${\mathit{\Gamma }}_{1\mathrm{\rho }}^{\circ }$ are the experimentally observed rotating frame relaxation rates for the doped and undoped sample.

4.3. T₁ relaxation and build-up of polarization

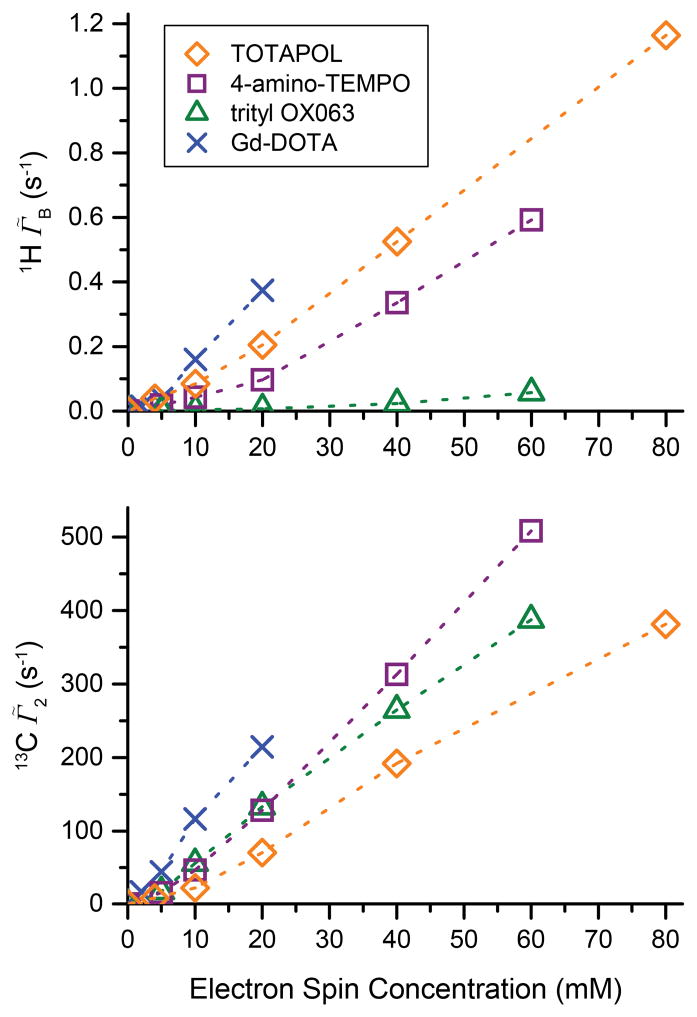
Electron spin concentration dependent build-up time and rate constants are shown in Fig. 4. For the undoped sample, the ¹H $T_1^{\circ }$ was measured as ~54.6 s. Clearly all the paramagnetic samples show a significant reduction of T_B with respect to $T_1^{\circ }$ as is expected. Interestingly, TOTAPOL shows the largest reduction of T_B of all the polarizing agents even at very low electron spin concentrations which is attributed to the efficient intramolecular CR also responsible for CE DNP. Although 4-amino-TEMPO exhibits an EPR spectrum essentially identical to TOTAPOL with a comparable T_1S (see Fig. 5), it leads to a significantly smaller effect on the polarization build-up time constant at low concentrations. This is due to the fact that CR induced by 4-amino-TEMPO relies on intermolecular couplings between nitroxide moieties which are weaker particularly at low molecular concentrations. Even at the largest concentration investigated, 60 mM, the average radical-radical distance is ~30 Å, which corresponds to dipolar coupling of only ~2 MHz compared with the intramolecular coupling of ~25 MHz present in TOTAPOL [26]. Trityl induces only a relatively minor reduction of T_B even at a higher concentration, because the narrow linewidth of trityl does not result in efficient CR. Longitudinal paramagnetic relaxation relies mostly on a fluctuating dipole field at the nuclei caused by electron spin flips or motion. The long T_1S (see Fig. 5) and rigidity of the glassy matrix also translates into inefficient longitudinal paramagnetic relaxation efficiency.

Figure 4.

¹H DNP and paramagnetically enhanced build-up rate constant Γ̃_B and ¹³C transverse relaxation rate constant Γ̃₂ according to eq. (3) (bottom) as a function of electron spin concentration of various polarizing agents. Γ̃_B includes PRE as well as DNP effects (for details see text).

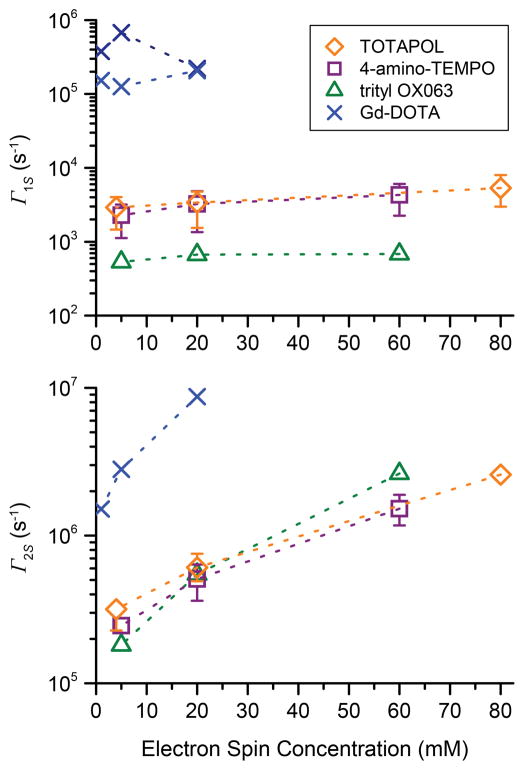
Figure 5.

Electron spin longitudinal relaxation rate constant Γ_1S (top) and transverse relaxation rate constant Γ_2S (bottom) as a function of electron spin concentration of various polarizing agents measured at 140 GHz EPR frequency. Relaxation times of trityl and Gd-DOTA were measured at the maximum of the EPR line. TOTAPOL and 4-amino-TEMPO were measured at four different field positions (4980, 4986, 4994, and 4998 mT; for a figure showing the field position with respect to the EPR spectrum see SI, Fig. S11); data points represent the average (mean) value, error bars indicate the maximum and minimum value. If no error bar is given, the difference between the minimum and maximum value is smaller than the data symbol.

Although CR is expected to be inefficient and SE is supposedly the dominant DNP mechanism for Gd-DOTA, there is a strong reduction in T_B. At electron spin concentrations larger than 10 mM Gd-DOTA induces relaxation rates larger than TOTAPOL. Thus, the S = 7/2 spin state, subject to significant static zero-field splitting in conjunction with the short T_1S of the high-spin system (see Fig. 5), leads to a significant decrease of T_B. Note that we measured a bi-exponential behavior of electron spin-lattice relaxation for Gd-DOTA and provide a fast and a slow relaxation component in Fig. 5 as well as Table S5. This behavior was reported previously by Goldfarb and coworkers [68].

Generally a short T_B is beneficial since it allows for rapid recycling of the NMR experiment and therefore higher sensitivity [69], and the sensitivity increase due to a shorter T_B with respect to $T_1^{\circ }$ is expressed as

$${\kappa }^{\circ }=\sqrt{\frac{T_1^{\circ }}{T_{\mathrm{B}}}}.$$ (6)

This factor κ^∘ is not to be confused with the decrease of T_B with respect to T₁ (i.e., the longitudinal relaxation time of paramagnetically doped samples without microwave irradiation) by excitation of SE DNP as was described in our earlier publications [33, 35]. At the same time, more efficient longitudinal relaxation can compete with polarization build-up by DNP and potentially lead to a lower enhancement. It is important to distinguish between polarizing agents that provide efficient CR and those that operate solely by the SE. While for the SE paramagnetically accelerated nuclear spin-lattice relaxation always prevents development of large DNP enhancements [33, 35], the same is not true for the CE. In the latter case the major part of the strong reduction of T_B is due to CR and indicates an efficient DNP process potentially leading to large enhancement factors. Clearly, the enhancement factor alone understates the sensitivity gain of CE DNP radicals such as TOTAPOL when compared with SE DNP and κ^∘ should always be taken into account when considering DNP efficiency.

4.4. T₂ and homogeneous linewidth

Because the intrinsic $T_2^{\circ }$ might be significantly different in other samples of biological interest and since relaxation rates are additive, the paramagnet induced transverse relaxation rates Γ̃₂ are reported in Fig. 4 as a more intrinsic measure of paramagnetic effects. The paramagnetic effects on the ¹³C nuclear T₂ do not show as strong a dependence on the nature of the paramagnet as is observed for T₁ (see Fig. S9), although the high-spin Gd-DOTA shows a slightly stronger influence compared to the S = 1/2 radicals. The TOTAPOL biradical exhibits about only half of the reduction in T₂ compared to the monoradicals at similar electron spin concentration, indicating that the molecular concentration plays the dominant role in dephasing of nuclear coherence and the biradical character can more or less be neglected. For all PA’s Γ̃₂ shows a strong approximately linear increase with higher polarizing agent concentration. The similarity of transverse relaxation rates induced by different polarizing agents with different electronic spin relaxation properties indicates that a mechanism independent of electronic spin-flips is governing the paramagnetic T₂, pointing to modulation of the electron-nuclear dipole (hyperfine) coupling due to MAS or dynamic (stochastic) motion of the nuclei within the magnetic field gradient of the electron spin as the cause of transverse relaxation; however, the exact nature cannot be determined using the presently available data and further theoretical and experimental work is needed.

Reduction of T₂ is an important consideration when optimizing sample conditions since a short T₂ not only leads to faster magnetization decay during transverse mixing and therefore lower sensitivity, but also leads to increased homogeneous broadening and reduced resolution. Since broadening in homogeneous samples at cryogenic temperatures has been empirically found to be dominated by spectral inhomogeneity [70], the additional broadening by shortening of T₂ will most likely be a minor effect, especially at high field. This is experimentally supported by a previous study performed at 9 T (380 MHz ¹H, 95.6 MHz ¹³C), where it was possible to resolve cross peaks with a width of ~1 ppm of the active site of bacteriorhodopsin (bR) using DNP, even when [TOTAPOL] = 20 mM [21]. However, in the case of bR, the biradical was sterically excluded from the active site by distance of ≥20 Å. Thus, a bulky biradical polarizing agent which is sterically separated from the NMR sites of interest would be requisite for maintaining resolution, and concurrently achieving large ε.

4.5. T_1ρ relaxation

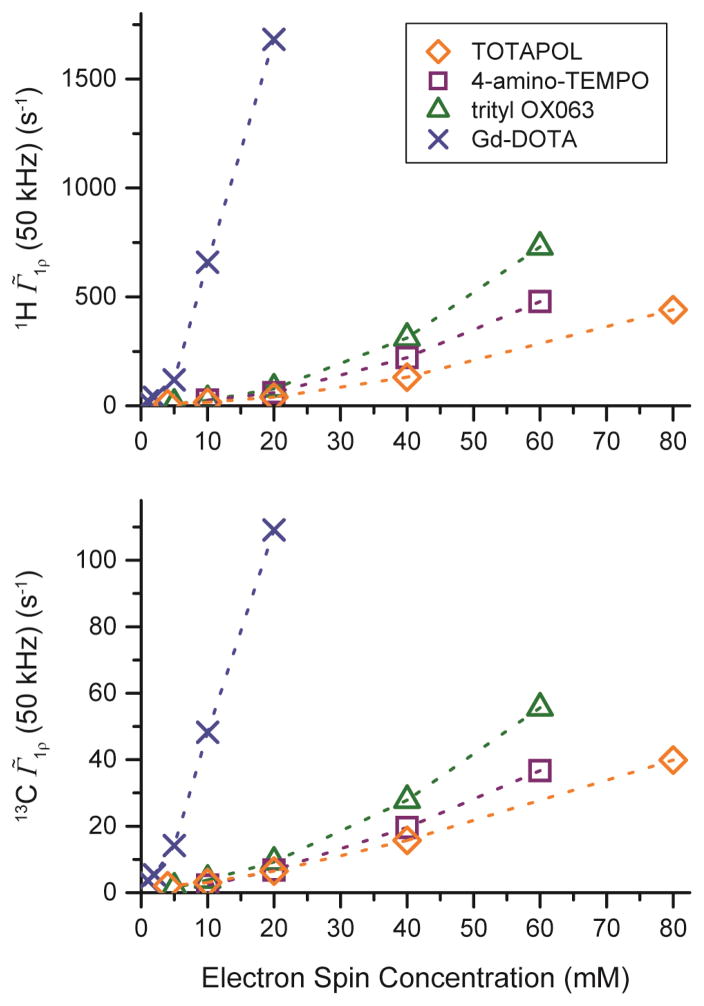
T_1ρ measurements are shown in Fig. 6 for ¹H and ¹³C in spin-lock fields of ω_1I /2π = 50 kHz; both ¹H and ¹³C show a very similar behavior. Increasing the spin-lock field strength to 100 kHz (see Fig. S10) leads to a two-fold decrease of Γ̃_1ρ for all polarizing agents and concentrations investigated, indicating linear relaxation dispersion in that field regime. Gd-DOTA shows a very high Γ̃_1ρ even at low concentrations most probably due to the high-spin properties, whereas the biradical character of TOTAPOL leads to low Γ̃_1ρ even at high electron spin concentrations. It is noteworthy that 4-amino-TEMPO and trityl show similar Γ̃_1ρ ’s at their respective concentrations. This differs from the T_B behavior, where we observed a more pronounced reduction by 4-amino-TEMPO. Clearly, previous arguments we made in order to explain the differences in T_B behavior also have to be considered for T_1ρ relaxation. While for longitudinal relaxation energy matching on the order of the nuclear Zeeman frequency ω_0I = γ_IB₀ is required, in the case of T_1ρ relaxation, the effective field determined by the spin-locking frequency ω_1I = γ_IB₁ is much smaller than the linewidth of either polarizing agent. Therefore, efficient rotating-frame CR can also be induced by the narrow linewidth trityl radical. However, the absolute contribution of rotating-frame CR to the observed Γ̃_1ρ might be slow compared to a direct relaxation process induced by local field fluctuations.

Figure 6.

¹H (top) and ¹³C (bottom) Γ̃_1ρ at a spin-lock field of ω_SL/2π = 50 kHz as a function of electron spin concentration of various polarizing agents.

A quantitative comparison of Γ̃_1ρ shows that the relaxation rates uniformly differ by a factor of ~16 between ¹H and ¹³C at the same spin-locking field strength for all polarizing agents and concentrations. This behavior indicates that a direct paramagnetic effect is responsible for transverse relaxation in the rotating frame, which scales with ${\gamma }_I^2$ [53]. Therefore, relayed effects where paramagnetically enhanced relaxation of ¹H induces relaxation of ¹³C can be neglected. This is further supported by the observation that a spin-locking field of 50 kHz applied to ¹³C sufficiently attenuated ¹H–¹³C interactions without additional application of an ¹H decoupling field.

4.6. DNP enhancement factor

An important measure of the efficiency of DNP is the enhancement factor ε, which is determined as the amplitude ratio between the DNP-enhanced and the non-enhanced signal (on- vs. off-signal). Measured enhancement factors are shown in Fig. 7 (top). Here the efficiency of TOTAPOL biradical as a CE polarizing agent is quite obvious because it yields very high ε even at low electron spin concentrations (< 20mM). Trityl shows slightly larger enhancements than 4-amino-TEMPO for concentrations <40 mM. At higher concentrations, the larger intermolecular electron-electron dipole couplings improve the CE efficiency, thus causing the CE with 4-amino-TEMPO to yield much larger ε than trityl. However, the DNP enhancements at high radical concentration are accompanied by compromised nuclear coherence times (vide supra) and reduced off-signal amplitudes (vide infra), a fact that greatly emphasizes the advantage of biradical polarizing agents. Gd-DOTA shows the smallest enhancements with ε ≈ 11, and we therefore do not expect general applicability of this polarizing agent in typical MAS DNP experiments commonly performed today. However, paramagnetic metal ions might lead to novel applications of DNP, such as investigation of metal centers in enzymes or catalysts in which the benefits of specific localization of the electron spin near the site of interest may be more important than achieving the largest overall enhancement. If absolute enhancement factors are of interest, the superiority of the CE is somewhat exaggerated due to significantly different power dependencies between CE and SE. Enhancements were measured using a moderate microwave power of 8 W for which we have recently shown that the slope of the CE enhancement vs. power dependence is decreased from linearity; however the enhancement is still not saturated [71]. The SE is far from saturation due to the low transition moment of the electron-nuclear double-quantum transition; in fact a linear power dependence is observed [35]; in this previous study we observed signal enhancement factors of up to 92 using trityl under similar conditions but higher microwave power. We have also observed Gd-DOTA enhancement factors of ~20 at the highest microwave power available (data not shown).

4.7. Signal quenching

Although the enhancement factor ε is an easily comparable and a convenient measure for DNP efficiency, it does not incorporate the reduction in the polarization build-up time constant leading to an additional increase of sensitivity due to faster signal accumulation. Concurrently, a certain amount of the signal amplitude is attenuated (quenched) by interactions with the polarizing agent. Accordingly, we introduce the quenching factor

$$\xi =1-\frac{I}{I^{\circ }},$$ (7)

where I and I^∘ are the off-signal amplitudes of the doped and undoped samples, respectively. In Fig. 10 (middle) we plotted (1−ζ) for various concentrations of the four PA’s. We measured the amplitude rather than the area of the peak since amplitude is the most significant measure of signal/noise and hence sensitivity.

In a CPMAS experiment this quenching can have several causes: (i) NMR signals of certain nuclei are shifted outside the excitation or detection bandwidth by paramagnetic shifts, (ii) the amplitude of the NMR signal of the detected nucleus is decreased due to homogeneous broadening by transverse paramagnetic relaxation due to modulation of the electron-nuclear dipole coupling, or (iii) spin-locked coherence of the abundant (proton) spins is decaying during the CP contact time by enhanced T_1ρ relaxation. We cannot distinguish among these signal quenching mechanisms by a simple CPMAS experiment. Similar to a previous model of signal bleaching,[66] we observed that signal quenching induced by trityl, GdDOTA and 4-amino-TEMPO (at concentrations < 40 mM) follows a simple exponential behavior (see Fig. S7) as a function of electron spin concentration [72], implying that each spin bleaches a volume of 28 nm³ for the S = 1/2 systems and 127 nm³ for S = 7/2 GdDOTA (in this bleaching model, we have assumed random overlapping volumes around each PA molecule inside which signal is not observed.) Interestingly, we observed that the signal quenching is proportional to the absolute magnetic moment of a polarizing agent, $\sqrt{S(S+1)}$ (Fig. S8). This indicates that a direct dipolar relaxation mechanism is responsible for signal quenching. Polarizing agents featuring efficient CE (i.e., TOTAPOL, and 4-amino-TEMPO at concentrations ≥ 40 mM) deviate from this model, owing to the fact that CR induces an additional quenching mechanism, probably CE-mediated nuclear depolarization [48, 49]. The characteristic of 4-amino-TEMPO showing the same behavior at low concentrations while converging with TOTAPOL at high concentration is in support of this interpretation. However, the CR induced quenching seems to play only a minor role under DNP relevant conditions (i.e., at 20–40 mM electron spin concentration) compared to the direct quenching process induced by all PA’s.

A detailed description of the exponential quenching model and the derivation of the volumes is presented in the supporting information.

4.8. Overall sensitivity enhancement

We can combine the DNP enhancement factor, quenching factor and the shortening of T_B into a single DNP sensitivity enhancement factor (Fig. 7, bottom) given by

$$E=\epsilon (1-\xi ){\kappa }^{\circ }=\epsilon \frac{I}{I^{\circ }}\sqrt{\frac{T_1^{\circ }}{T_B}}.$$ (8)

E represents the practical sensitivity gain one observes when performing DNP as compared to a MAS NMR experiment performed at the same (cryogenic) temperature without DNP and where no paramagnet has been added to the cryoprotecting solution. The time needed to achieve a specific S/N ratio with DNP is reduced accordingly by a factor of E². Note that (8) does not account for increased Boltzmann polarization nor does it include differences in nuclear T₁ at cryogenic temperature; both would be necessary for comparison of sensitivity to ‘typical’ MAS NMR near ambient temperatures. In such a comparison, E would increase by a factor of ~3.5 due to Boltzmann polarization, but decrease by a factor of about 5 due to nuclear T₁ differences for all polarizing agents and respective concentrations. However, since significant changes in the inhomogeneous linewidth, probe performance, and noise levels in the rf coil and transmission line accompany the reduction in temperature, we do not report absolute changes in sensitivity compared with room temperature experiments.

In this representation the improved performance of biradicals like TOTAPOL becomes even clearer. As illustrated in Fig. 3, a maximum sensitivity gain of a factor of 226 was achieved with ~10 mM TOTAPOL (20 mM electron spins). For 4-amino-TEMPO concentrations of 40 mM or higher are required to reach a substantial, albeit lower, E of 120–130. However, as shown in the preceding sections, paramagnetic relaxation effects at these concentrations are severe and would negatively impact more sophisticated MAS NMR experiments. Polarizing agents operating on the SE were found to exhibit E < 50 in this study. However, as higher microwave field strengths become available, sensitivity is expected to greatly increase due to its strong effect on both ε and κ^∘ [35]. Furthermore, there might be future applications, where doping with biradicals is inappropriate, in which case the SE using polarizing agents like trityl or Gd-DOTA will be the method of choice.

4.9. Signal quenching under static vs. MAS conditions

The observations made in the previous sections of the signal quenching and our inability to (semi-)quantitatively correlate the quenching with the observed relaxation effects raise the question of the main mechanism leading to the observed signal loss. Very recently, studies were conducted by Thurber and Tycko as well as Mentink-Vigier et al. which aimed to investigate the complex implications of MAS on a system which underlies a multitude of highly anisotropic interactions [48, 49]. One of their findings was the theoretical occurrence of an additional quenching mechanism induced by MAS due to (partially) equalized electron spin polarization during nearly adiabatic level (anti-)crossings of a bis-nitroxide electron spin system. Additional signal quenching under MAS not present in static samples has been very recently observed at very low temperatures [73], however, it is not clear that this quenching is induced by the above mechanism.

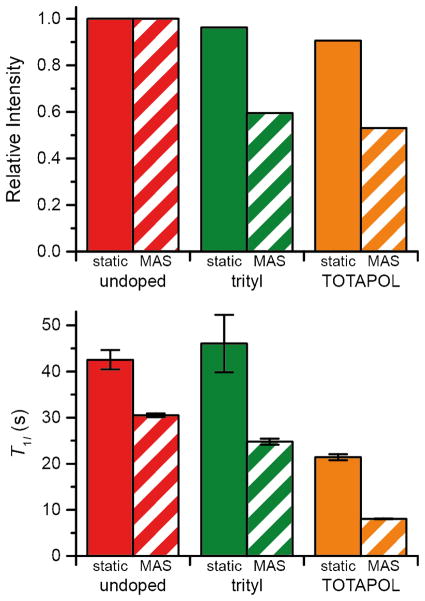
In order to explore the physical basis for the observed signal quenching, we determined the equilibrium signal intensity of a 20 mM trityl sample and a 10 mM TOTAPOL sample under both spinning and static conditions (Fig. 8). Note that there is only 5–10% loss of intensity in the case of the static samples. We anticipated that for TOTAPOL, MAS would result in additional quenching due to the CE depolarization of the nuclear spins without microwave irradiation due to level anticrossings [48, 49]. In the case of trityl, the CE condition is not met for ¹H and this mechanism is not active. Importantly, additional signal loss was observed for both TOTAPOL and trityl during MAS, accompanied by a reduction in the nuclear T₁, pointing to the importance for quenching of the modulation of the electron-nuclear dipole coupling by MAS. For trityl the loss amounts to ~40% and for TOTAPOL ~50%, similar to the quenching ratios reported in Fig. S7. Therefore we conclude that the level anticrossing induced depolarization is not the major quenching mechanism under typically relevant DNP conditions (i.e., at 80–100 K) and moderate MAS frequencies. Data on the polarization build-up for the mono- and biradicals are included in the supporting information (Fig. S13).

Figure 8.

Equilibrium signal intensity (top) and T₁ (bottom) are compared for a 20 mM trityl sample and a 10 mM TOTAPOL (each corresponding to 20 mM electron spins) sample under static and MAS conditions. ω_r/2π = 4975 Hz, and spectra were recorded at 380 MHz. The sample was 30/30/30/10 d₈-glycerol/2-¹³C,d₈-glycerol/D₂O/H₂O.

4.10. Electron Decoupling

The intensity loss that we observe during MAS with all of the polarizing agents amounts to ~50%, and can in principle be partially recovered by decoupling electrons during data acquisition. Since the secular part of the electron-nuclear Hamiltonian is identical to the heteronuclear Hamiltonian - I_zS_z - this is an approach similar to that used to decouple ¹H from ¹³C/¹⁵N, etc. in MAS experiments. However, performing experiments at low temperatures to lengthen electron relaxation times and allow for efficient microwave induced modulation of the magnetization might be required. In addition, it will be necessary to develop decoupling sequences that are effective for lines which are wide compared to γB_1S. For example at 5 T the trityl line has a width of ~50 MHz due to a small g-anisotropy, and is one of the narrowest EPR lines exhibited by a polarizing agent. The instrumentation to perform the experiments will require amplifiers with a bandwidth sufficient to polarize the nuclei, for example at the solid effect condition, and then switch on resonance with the EPR spectrum for decoupling. The pulse forming and phase control would optimally be performed at low frequencies and mixed to the appropriate microwave frequency. Since the blind volume surrounding the paramagnetic center contains several hundred nuclei it is possible to achieve a significant sensitivity gain with this approach.

5. Conclusion

We have documented the effects of the presence of several DNP polarizing agents upon nuclear T₁, T₂, and T_1ρ relaxation times and show that the results may guide the choice of polarizing agent and its concentration. In addition, we showed that attenuation of the spectral intensity occurs in both mono- and biradical polarizing agents. In multidimensional MAS experiments, relaxation of magnetization occurs, for example during coherent mixing periods, evolution of spin coherence, or multiple CP contacts and the details of the type and duration of magnetization transfer will impact the choice of polarizing agent concentration. Polarizing agents employing the SE DNP mechanism generally show a longer longitudinal polarization build-up time compared with CE polarizing agents, which utilize efficient CR for DNP build-up but also for spin-lattice relaxation. Interestingly, the laboratory frame T₂ is less affected by the choice of polarizing agent and is practically invariant of the nature of the electron spin since it shows quantitatively similar polarizing agent concentration dependence for all polarizing agents studied. It is clear from the T₂ measurements that lower polarizing agent concentrations will be optimal when applying long transverse mixing, such as in a REDOR or TEDOR experiment, than would be used based solely on the sensitivity of a CP experiment. In addition, we have characterized the reduction in non-DNP enhanced signal due to paramagnetic dopants and adopted a simple model for the concentration dependence of this effect. We present a measure of overall DNP sensitivity gain that includes the signal quenching, the enhancement factor, and the build-up rate that can be used to optimize a DNP experiment. For multidimensional experiments aimed at providing structural information, the empirically determined relaxation times will determine the optimal combination of experiment, polarizing agent, and its concentration to achieve maximum sensitivity. The results presented here clearly demonstrate that much work remains to be done in the design and implementation of efficient polarizing agents for MAS DNP as well as the continued development of the instrumentation for experiments involving electron decoupling.

Highlights.

• Paramagnet induced quenching and relaxation in MAS-DNP experiments

• Conparison of four fundamentally different polarizing agents

• Optimization of paramagnet concentration

• Cross effect biradicals are superior to monoradicals

• MAS mediates quenching equally for TOTAPOL and trityl