Abstract
A growing literature establishes that high quality early childhood interventions targeted toward disadvantaged children have substantial impacts on later life outcomes. Little is known about the mechanisms producing these impacts. This paper uses longitudinal data on cognitive and personality traits from an experimental evaluation of the influential Perry Preschool program to analyze the channels through which the program boosted both male and female participant outcomes. Experimentally induced changes in personality traits explain a sizable portion of adult treatment effects.
Keywords: cognitive traits, personality traits, externalizing behavior, academic motivation, factor analysis, human capital, human development, early childhood interventions, social experiments, Perry Preschool program, experimentally estimated production functions
A growing literature establishes that early childhood environments substantially impact later life outcomes (e.g., Knudsen et al., 2006, Heckman, 2008 and Almond and Currie, 2011). Less is known about the channels through which early environments operate to produce their long term effects. This paper examines the sources of the success of the Perry Preschool program, a flagship early childhood intervention in the US.1
The Perry program was a randomized trial that targeted disadvantaged, low IQ African American children ages 3–4. After two years, all participants left the program and entered the same public school. Data were collected for treatment and control groups through age 40.
Heckman et al. (2010a) and Conti et al. (2012) show that the Perry program significantly enhanced adult outcomes including education, employment, earnings, marriage, and participation in healthy behaviors, and reduced participation in crime.2 We summarize many of these findings in Table 1. All treatment effects displayed there are statistically significant and survive adjustments for multiple hypothesis testing.3 Heckman et al. (2010b) show that the internal rate of return to the program for both boys and girls is a statistically significant 6–10 percent per year—above the historical return to equity.4 Positive effects of the Perry program have become a cornerstone of the argument for preschool programs (e.g., Shonkoff and Phillips, 2000). Currently, about 30 percent of all Head Start centers nationwide offer a version of the Perry curriculum (ICPSR, 2010).5
Table 1.
Program Treatment Effects
| Variable | Treatment Effect
|
Control Group
|
Treatment Group
|
||||
|---|---|---|---|---|---|---|---|
| Effect | Effect Size | p-value | Mean | Standard Error | Mean | Standard Error | |
| A. Males | |||||||
| CAT total at age 14, end of grade 8 | 0.566 * | 0.652 | (0.060) | 0.000 | (0.164) | 0.566 | (0.204) |
| # of misdemeanor arrests, age 27 | −1.21 ** | −0.363 | (0.036) | 3.03 | (0.533) | 1.82 | (0.445) |
| # of felony arrests, age 27 | −1.12 | −0.324 | (0.101) | 2.33 | (0.554) | 1.21 | (0.342) |
| # of adult arrests (misd.+fel.), age 27 | −2.33 ** | −0.402 | (0.024) | 5.36 | (0.927) | 3.03 | (0.734) |
| Monthly income, age 27 | 0.876 ** | 0.607 | (0.018) | 1.43 | (0.231) | 2.31 | (0.352) |
| Use tobacco, age 27 | −0.119 * | −0.236 | (0.093) | 0.538 | (0.081) | 0.419 | (0.090) |
| # of misdemeanor arrests, age 40 | −3.13 ** | −0.372 | (0.039) | 8.46 | (1.348) | 5.33 | (1.042) |
| # of felony arrests, age 40 | −1.14 * | −0.266 | (0.092) | 3.26 | (0.684) | 2.12 | (0.598) |
| # of adult arrests (misd.+fel.), age 40 | −4.26 ** | −0.373 | (0.041) | 11.7 | (1.831) | 7.46 | (1.515) |
| # of lifetime arrests, age 40 | −4.20 * | −0.346 | (0.053) | 12.4 | (1.945) | 8.21 | (1.778) |
| Employed, age 40 | 0.200 ** | 0.394 | (0.024) | 0.500 | (0.085) | 0.700 | (0.085) |
| Sample | 72 | 39 | 33 | ||||
| B. Females | |||||||
| CAT total, age 8 | 0.565 * | 0.614 | (0.062) | 0.000 | (0.196) | 0.565 | (0.223) |
| CAT total, age 14 | 0.806 ** | 0.909 | (0.014) | 0.000 | (0.209) | 0.806 | (0.204) |
| Any special education, age 14 | −0.262 ** | −0.514 | (0.025) | 0.462 | (0.100) | 0.200 | (0.082) |
| Mentally impaired at least once, age 19 | −0.280 ** | −0.569 | (0.017) | 0.364 | (0.105) | 0.083 | (0.058) |
| # of misdemeanor violent crimes, age 27 | −0.423 ** | −0.292 | (0.032) | 0.423 | (0.284) | 0.000 | (0.000) |
| # of felony arrests, age 27 | −0.269 ** | −0.325 | (0.021) | 0.269 | (0.162) | 0.000 | (0.000) |
| Jobless for more than 1 year, age 27 | −0.292 * | −0.573 | (0.071) | 0.542 | (0.104) | 0.250 | (0.090) |
| Ever tried drugs other than alcohol or weed, age 27 | −0.227 ** | −0.530 | (0.045) | 0.227 | (0.091) | 0.000 | (0.000) |
| # of misdemeanor violent crimes, age 40 | −0.537 ** | −0.364 | (0.016) | 0.577 | (0.289) | 0.040 | (0.040) |
| # of felony arrests, age 40 | −0.383 ** | −0.425 | (0.028) | 0.423 | (0.177) | 0.040 | (0.040) |
| # of lifetime violent crimes, age 40 | −0.574 ** | −0.384 | (0.019) | 0.654 | (0.293) | 0.080 | (0.055) |
| Months in all marriages, age 40 | 39.6 * | 0.539 | (0.076) | 47.8 | (15.015) | 87.5 | (18.853) |
| Sample | 51 | 26 | 25 | ||||
Note: Statistics are shown for the outcomes analyzed in this paper. There are differences in treatment effects by gender although strong effects are found for both. “CAT total” denotes the California Achievement Test total score normalized to control mean zero and variance of one. Test statistics are corrected for the effect of multiple hypothesis testing and threats to validity (see Heckman et al., 2010a, Conti et al., 2012). The reported effect is the difference in means between treatment and control groups. The effect size is the ratio of the effect to the standard deviation of the control group. Stars denote statistical significance:
- 1 percent level,
- 5 percent level,
- 10 percent level. Monthly income is adjusted to thousands of year-2006 dollars using annual national CPI.
Previous studies of Perry focus on estimating treatment effects and do not attempt to explain their sources.6 This paper identifies the psychological skills changed by the Perry program and decomposes the treatment effects on adult outcomes displayed in Table 1 into components attributable to improvements in these skills.
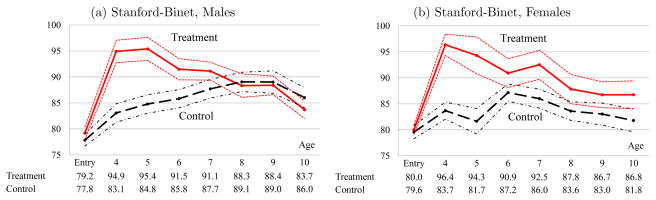
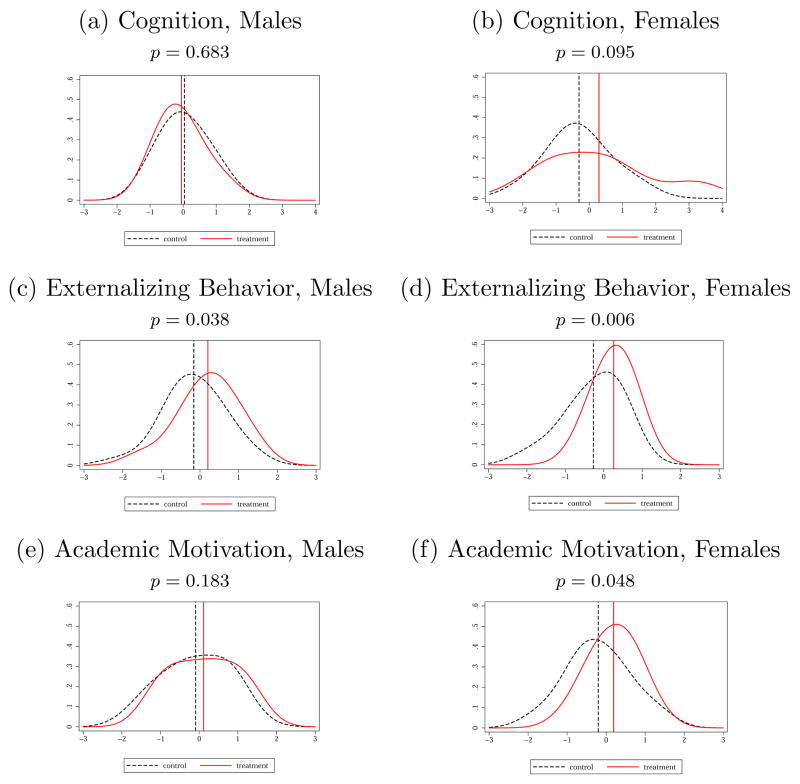
The literature in the economics of education assumes the primacy of cognitive ability in producing successful lifetime outcomes (e.g., Hanushek and Woessmann, 2008). From this perspective, the success of the Perry program is puzzling. Although the program initially boosted the IQs of participants, this effect soon faded. A few years after the program finished, there was no statistically significant difference in IQ between treatments and controls for males and only a borderline statistically significant difference for females (see Figure 1). Consistent with this evidence, we show negligible effects of increases in IQ in producing program treatment effects.
Figure 1. Stanford-Binet IQ Test Scores by Gender and Treatment Status.
Note: Bold lines display mean IQs. Fine lines represent standard errors for the corresponding means (one standard error above and below). For a detailed description of the cognitive measures and results for other IQ tests, see Web Appendix B. Numbers below each chart are treatment and control mean test scores. See panels (a)–(d) of Figure B.6 of Web Appendix B for comparable graphs on the Leiter and PPVT measures of IQ.
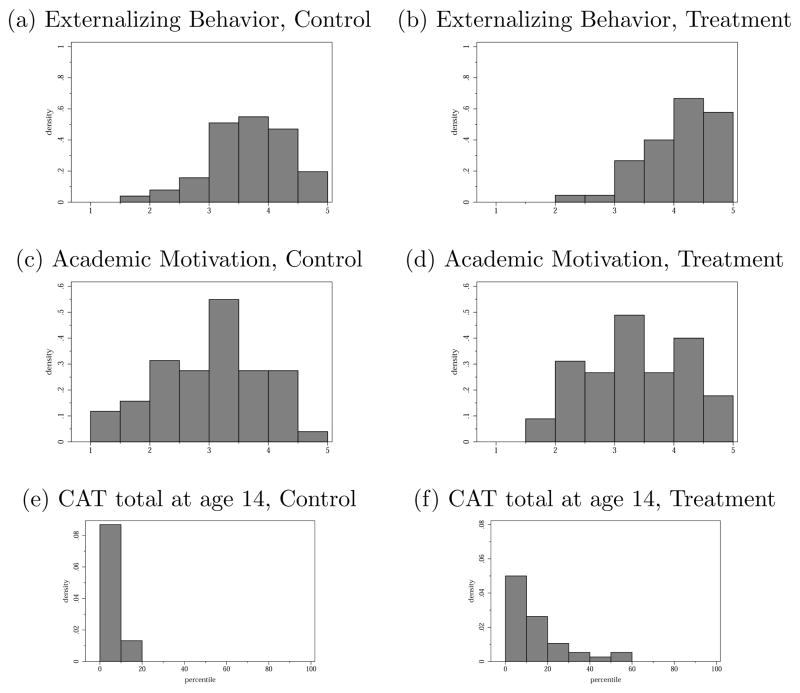
Although Perry did not produce long run gains in IQ, it did create persistent improvements in personality skills.7 The Perry program substantially improved Externalizing Behaviors (aggressive, antisocial, and rule-breaking behaviors), which, in turn, improved a number of labor market outcomes, health behaviors, and criminal activities (see panels (a) and (b) of Figures 2 and 3).8
Figure 2. Histograms of Indices of Personality Skills and CAT scores.
Note: Indices for Externalizing Behavior and Academic Motivation are unweighted averages of measures listed in Table 2. “CAT” is the California Achievement Test score expressed in percentiles of the general population distribution of the scores. See Web Appendix B.4 for description of the CAT. The one-sided p-values for difference in means between treatments and controls are 0.001, 0.043, and 0.000 for Externalizing Behavior, Academic Motivation, and CAT scores respectively. Histograms are based on the pooled sample of males and females. See Figures C.6 and C.7 of Web Appendix C and Figure B.5 of Web Appendix B for the corresponding gender-specific figures.
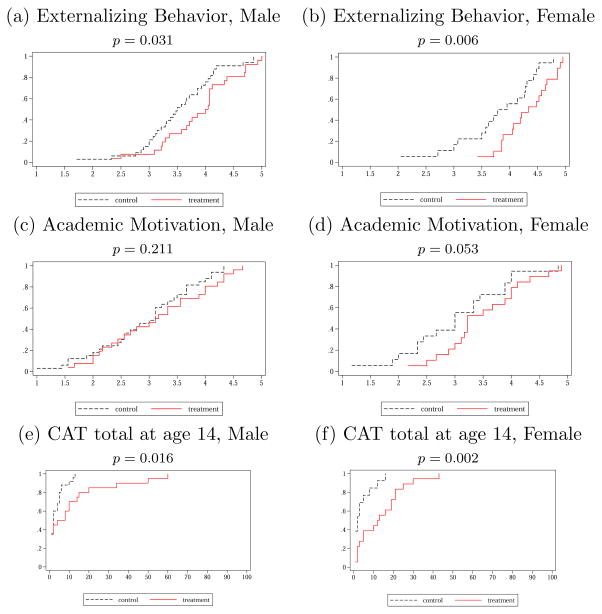
Figure 3. Cumulative Distribution Functions of Indices of Personality Skills and CAT scores by Gender.
Note: Indices for Externalizing Behavior and Academic Motivation are unweighted averages of measures listed in Table 2. “CAT” is the California Achievement Test score expressed in percentiles of the general population distribution of the scores. Numbers above the charts are one-sided p-values testing the equality of means of the indices for the treatment and control groups.
The program also enhanced Academic Motivation (see panels (c) and (d) of Figures 2 and 3), but the effect is primarily for girls.9 This differential enhancement of endowments by gender helps to explain the positive treatment effects for education-related outcomes such as achievement tests and mental impairment for girls. Academic Motivation is not significantly enhanced for boys, and plays no role in explaining their treatment effects.
While the Perry program did not boost long-term IQ, it did boost long-term achievement test scores (see panels (e) and (f) of Figures 2 and 3). The effect is stronger for girls, but also occurs for boys.10 Achievement tests measure acquired knowledge, which is enhanced for children with better cognitive and personality traits. Enhanced personality skills promote learning, which, in turn, boosts achievement test scores.11 This finding is consistent with recent evidence that 30–40 percent of the explained variance in achievement test scores across students is due to personality traits and not IQ.12.
This paper contributes to an emerging literature on the economics of personality. Our demonstration of the powerful role of personality skills is in agreement with a large body of evidence summarized in Borghans et al. (2008) and Almlund et al. (2011).13
Our analysis shows the benefits and limitations of social experiments. The Perry study generated experimentally determined treatment effects for outcomes and skills. However, knowledge that the program enhanced skills and improved a number of outcomes is not enough to establish that the improvement in measured skills caused the improvement in outcomes. Without further assumptions, data from the experiment do not determine the production function relating changes in skills to changes in adult outcomes. The program may also improve unmeasured skills. Changes in measured skills may simply proxy changes in unmeasured skills that affect outcomes. To address this issue, we supplement the treatment effects obtained from the experiment with an econometric model that estimates the relationship between outcomes and experimentally induced changes in measured skills. Our method accounts for measurement error and treatment-induced changes in unmeasured skills. Access to experimental data allows us to test some of its identifying assumptions. Evidence from a series of specification tests supports our econometric procedure.
The paper proceeds in the following way. Section I describes the Perry program and the experiment that evaluated it. Section II presents our econometric model. Section III discusses the variety of measures of psychological traits at our disposal and the need to create low-dimensional summaries of them. It explains how we construct summary measures and test for the validity of the constructed summaries. Section IV presents our analysis of the sources of the Perry treatment effects. Section V concludes. A Web Appendix presents supplementary material.
I. The Perry Program: Design and Background
The Perry program targeted African American children with low IQs and socioeconomic status (Schweinhart and Weikart, 1981). The experiment was conducted during the mid-1960s in the district of the Perry elementary school in Ypsilanti, Michigan. Children began the program at age three and were enrolled for two years.14 Parents were disadvantaged as measured by their income and education. Roughly 47 percent of the children in the study did not have fathers present in the household at age three.
The 123 participants were randomized into treatment and control groups.15 The Perry sample consists of 51 females (25 treatment and 26 control) and 72 males (33 treatment and 39 control). There was relatively little attrition: only 11 participants left the study by the time of the interview at age 40.16
The Perry curriculum is based on the principle of active participatory learning, in which children and adults are treated as equal partners in the learning process, and children engage with objects, people, events, and ideas.17 Abilities to plan, execute, and evaluate tasks were fostered, as were social skills, including cooperation with others and resolution of interpersonal conflicts. The Perry curriculum has been interpreted as implementing the theories of Lev Vygotsky (1986) in teaching self control and sociability.18 A widely implemented program based on these principles — Tools of the Mind — is designed to promote self control.19
Sessions lasted 2.5 hours and were held five days a week during the school year. Teachers in the program, all of whom had bachelor’s degrees (or higher) in education, made weekly 1.5-hour home visits to treatment group mothers with the aim of involving them in the socioemotional development of their children. The control group had no contact with the Perry program other than through annual testing and assessment (Weikart, Bond and McNeil, 1978).
Perry predates Head Start and had no competitors, so there was no control group contamination (see Schweinhart and Weikart, 1981). All eligible parents enrolled their children in the program, so there was no issue of bias arising from noncompliance (Weikart, Bond and McNeil, 1978).
Numerous measures were collected annually from ages 3–15 on a variety of socioeconomic outcomes for treatment and control participants. There were three additional follow-ups at ages 19, 27, and 40. The Perry sample was representative of a particularly disadvantaged cohort of the African American population. About 16 percent of all African American children in the US had family and personal attributes similar to those of Perry participants at the time when the Perry program was conducted.20 The statistically significant treatment effects of the experiment for boys and girls survive rigorous adjustments for multiple hypothesis testing and compromises in the randomization protocol.21
II. Methodology
This paper explains the sources of the Perry treatment effects in terms of improvements in early measures of psychological traits broadly classified into cognitive and personality skills.22 We first estimate treatment effects for these skills. We then estimate the relationship between skills and later life outcomes and decompose treatment effects for adult outcomes into components due to treatment-induced changes in different skills.23
To perform valid decompositions, we need to address two features of the Perry data. First, as previously noted, the randomized design of the Perry study allows us to identify the causal effect of the treatment on measured skills and on adult outcomes, but it does not directly allow us to identify the causal effect of increases in measured skills on outcomes. We use econometric methods to address this problem. Using experimental variation, we can be more confident in the validity of our decompositions because we can test some of the assumptions maintained in our procedure. However, it is necessary to maintain some exogeneity assumptions in order to construct valid decompositions. This section makes those assumptions explicit.
Second, the Perry study has many highly correlated measurements of psychological traits (skills) that are laden with measurement error.24 Moreover, the sample size of the study is small. We would exhaust the available degrees of freedom if we use all available psychological measurements to predict outcomes. Instead, we use factor analysis to create low dimensional, interpretable and informative aggregates that summarize a range of psychological traits and account for measurement error.
Section II.A presents our model for outcomes. Section II.B presents our strategy for reducing numerous error-laden measurements to manageable summary measures and addressing the problem of measurement error. Section II.C discusses identification. We establish what features of the model are overidentified, and hence testable. Section II.D summarizes a simple and robust three-step estimation procedure that is developed more extensively in the appendix.
A. The Outcome Equation
Let D denote treatment assignment. D = 1 if an agent is treated and D = 0 otherwise. Let Y1 and Y0 be the counterfactual outcomes when D is fixed at “1” and “0” respectively. We use the subscript d ∈ {0, 1} to represent variables when treatment is fixed at d. Fixing corresponds to manipulating treatment status d holding everything else constant.25 The observed outcome is
| (1) |
We assume that outcomes are independent across participants conditional on observed pre-program variables X that are assumed not to be affected by the program. We introduce the notion of skills that can be changed by the program and that they produce (in part) the treatment effect. The vector of skills when treatment is fixed at d is given by
, where
 is an index set for skills. We define θ in a fashion analogous to Y : θ = Dθ1 + (1 − D) θ0.
is an index set for skills. We define θ in a fashion analogous to Y : θ = Dθ1 + (1 − D) θ0.
Our analysis is based on the following linear model:
| (2) |
where κd is an intercept, αd and βd are, respectively, |
 |-dimensional and |X|- dimensional vectors of parameters where |Q| denotes the number of elements in Q. While the pre-program variables X are assumed not to be affected by the treatment, their effect on Y can be affected by the treatment. ε̃d is a zero-mean error term assumed to be independent of regressors θd and X.
|-dimensional and |X|- dimensional vectors of parameters where |Q| denotes the number of elements in Q. While the pre-program variables X are assumed not to be affected by the treatment, their effect on Y can be affected by the treatment. ε̃d is a zero-mean error term assumed to be independent of regressors θd and X.
Perry analysts collected a rich array of measures of cognitive and personality skills. However, it is very likely that there are relevant skills that they did not measure. Notationally, let
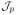 ⊆
⊆
 be the index set of skills on which we have measurements. The measurements may be imperfect so even these skills may not be directly observed. We decompose the term αdθd in equation (2) into components due to skills we measure and skills we do not:
be the index set of skills on which we have measurements. The measurements may be imperfect so even these skills may not be directly observed. We decompose the term αdθd in equation (2) into components due to skills we measure and skills we do not:
| (3) |
where d ∈ {0, 1}, , and εd is a zero-mean error term defined by . Any differences in the error terms between treatment and control groups can be attributed to differences in the skills on which we have no measurements. Without loss of generality we assume that , where means equality in distribution. Note that the error term εd is correlated with the measured skills if measured skills are correlated with unmeasured skills.
We seek to decompose treatment effects into components attributable to changes in the skills that we can measure. Assuming that changes in unmeasured skills attributable to the experiment are independent of X, treatment effects can be decomposed into components due to changes in skills E(Δθj) and components due to changes in parameters :
| 26 | (4) |
Equation (4) can be simplified if treatment affects skills, but not the impact of skills and background variables on outcomes, i.e.
; j ∈
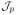 and β1 = β0.27 Under the latter assumption, the term associated with X drops from the decomposition.
and β1 = β0.27 Under the latter assumption, the term associated with X drops from the decomposition.
We establish below that if measured and unmeasured skills are independent in the no-treatment outcome equation, α0 can be consistently estimated by a standard factor analysis. Under this assumption, and if α1 = α0, we can test if the experimentally-induced increments in unmeasured skills are independent of the experimentally induced increments in measured skills.28 The intuition for this test is as follows. The skills for treated participants are the sum of the skills they would have had if they were assigned to the control group plus the increment due to treatment. If measured and unmeasured skill increments are independent, α1 is consistently estimated by a standard factor analysis and we can test if plim α̂1 = plim α̂0 where (α̂0, α̂1) are estimates of (α0, α1).29 Assuming the exogeneity of X, we can also test if plim β̂1 = plim β̂0, where (β̂0, β̂1) are estimates of β0 and β1. We test and do not reject these hypotheses.
Imposing these assumptions simplifies the notation. Equation (3) may be expressed as
| (5) |
In this notation, equation (1) becomes
| (6) |
where τ = τ1 − τ0 is the contribution of unmeasured variables to mean treatment effects, ε = Dε1 + (1 − D) ε0 is a zero-mean error term, and
, j ∈
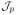 denote the skills that we can measure.
denote the skills that we can measure.
If the θj, j ∈
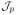 , are measured without error and are independent of the error term ε, least squares estimators of the parameters of equation (6) are unbiased for αj, j ∈
, are measured without error and are independent of the error term ε, least squares estimators of the parameters of equation (6) are unbiased for αj, j ∈
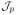 .30 If, on the other hand, the unmeasured skills are correlated with both measured skills and outcomes, least squares estimators of αj, j ∈
.30 If, on the other hand, the unmeasured skills are correlated with both measured skills and outcomes, least squares estimators of αj, j ∈
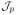 , are biased and capture the effect of changes in the unmeasured skills as they are projected onto the measured components of θ, in addition to the direct effects of changes in measured components of θ on Y.
, are biased and capture the effect of changes in the unmeasured skills as they are projected onto the measured components of θ, in addition to the direct effects of changes in measured components of θ on Y.
Equation (6) is the basis for the decompositions reported in this paper. The treatment effect is
| (7) |
Skill j can explain treatment effects only if it affects outcomes (αj ≠ 0) and, on average, is affected by the experiment ( ). We test both conditions.
Decomposition (7) would be straightforward to identify if the measured variables are independent of the unmeasured variables, and the measurements are accurate. The second term of (7) is easily constructed by using consistent estimates of the αj and the effects of treatment on skills. However, psychological measurements are riddled with measurement error (Cunha and Heckman, 2008). In addition, there are a large number of highly intercorrelated psychological measures that need to be condensed. We address these problems in this paper.
B. Low-Dimensional Characterizations of Skills
One way to summarize the psychological measures is to form simple unweighted indices constructed by taking averages of interpretable groups of items. This way of proceeding is widely used in psychology.31 It is, however, fraught with difficulties. First, there are many ways to form aggregates. Second, the weightings of the measures used to form such aggregates are arbitrary. Third, this approach does not correct for measurement error, except through simple averaging.
This paper forms interpretable aggregates through factor analysis—a statistical method that summarizes the covariability among observed measures using low-dimensional latent variables. The method also accounts for measurement error.32 We use the early measures of skills in the Perry data to extract the latent skills (θj; j ∈
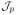 ) in equation (7) where the latent skills are the factors. We use a common measurement system for treated and untreated participants although
, j ∈
) in equation (7) where the latent skills are the factors. We use a common measurement system for treated and untreated participants although
, j ∈
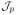 and
, j ∈
and
, j ∈
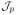 , may differ.
, may differ.
More formally, let the index set for measures associated with factor j ∈
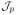 be
be
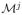 . Denote the measures for factor j in treatment group d by
, d ∈ {0, 1}. Henceforth, let θd denote the vector of factors associated with the skills that can be measured in treatment state d, i.e.,
.
. Denote the measures for factor j in treatment group d by
, d ∈ {0, 1}. Henceforth, let θd denote the vector of factors associated with the skills that can be measured in treatment state d, i.e.,
.
Following the psychometric literature summarized in Gorsuch (1983, 2003) and Thompson (2004), we assume that each measure is associated with at most one factor. We assume that the same measurement equations govern treatment and control groups so that the following equation is assumed to describe the relationship between the measures associated with factor j and the factor:
| (8) |
To simplify the notation, we keep the covariates X implicit. Parameters are measure-specific intercepts. Parameters are factor loadings. The εd in (5) and are mean-zero error terms assumed to be independent of θd, d ∈ {0, 1}, and of each other. The factor structure is characterized by the following equations:
| (9) |
| (10) |
The assumption that the parameters , do not depend on d simplifies the notation, as well as the interpretation of the estimates obtained from our procedure. It implies that the effect of treatment on the measured skills operates only through the latent skills and not through changing the measurement system for those skills. This assumption can be tested by estimating measurement systems separately for treatment and control groups and testing if measurement equation factor loadings and measurement equation intercepts differ between treatment and control groups.33 We do not reject the hypotheses of equality of these parameters across treatment and control groups.34
C. Identification
Identification of factor models requires normalizations that set the location and scale of the factors (e.g., Anderson and Rubin, 1956a).35 We set the location of each factor by fixing the intercepts of one measure—designated “the first”—to zero, i.e. . This defines the location of factor j for each counterfactual condition. We set the scale of the factor by fixing the factor loadings of the first measure of each skill to one, i.e. . For all measures that are related to a factor (i.e. have a non-zero loading on the factor, ), the decomposition of treatment effects presented in this paper is invariant to the choice of which measure is designated as the “first measure” for each factor and to any affine transformations of the measures.36
Identification is established in four steps. First, we identify the means of the factors,
. Second, we identify the measurement factor loadings
, the variances
of the measurement system, and the factor covariance structure Σθd. Third, we use the parameters identified from the first and second steps to secure identification of the measurement intercepts
. Finally, we use the parameters identified in the first three steps to identify the factor loadings α = (αj; j ∈
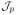 ) and intercept τd of the outcome equations. We discuss each of these steps in turn.
) and intercept τd of the outcome equations. We discuss each of these steps in turn.
1. Factor Means
We identify and from the mean of the designated first measure for treatment and control groups: .
2. Measurement Loadings
From the covariance structure of the measurement system, we can identify: (a) the factor loadings of the measurement system
; (b) the variances of the measurement error terms,
; and (c) the factor covariance matrix, Σθd. Factors are freely correlated. We need at least three measures for each skill j ∈
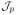 , all with non-zero factor loadings.37 The
can depend on d ∈ {0, 1}, and we can identify
. We test if
, and we do not reject these hypotheses.38
, all with non-zero factor loadings.37 The
can depend on d ∈ {0, 1}, and we can identify
. We test if
, and we do not reject these hypotheses.38
3. Measurement Intercepts
From the means of the measurements, i.e.
, we identify
, mj ∈
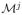 \{1}, j ∈
\{1}, j ∈
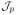 . Recall that the factor loadings
and factor means
are identified. Assuming equality of the intercepts (
) between treatment and control groups guarantees that treatment effects on measures, i.e.
, operate solely through treatment effects on factor means, i.e.
. However, identification of our decomposition requires intercept equality only for the designated first measure of each factor. We test and do not reject
for all mj ∈
. Recall that the factor loadings
and factor means
are identified. Assuming equality of the intercepts (
) between treatment and control groups guarantees that treatment effects on measures, i.e.
, operate solely through treatment effects on factor means, i.e.
. However, identification of our decomposition requires intercept equality only for the designated first measure of each factor. We test and do not reject
for all mj ∈
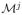 \{1}, j ∈
\{1}, j ∈
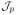 .39
.39
4. Outcome Equation
Adult outcome factor loadings in equation (5) can be identified using the covariances between outcomes and the designated first measure of each skill. We form the covariances of each outcome Yd with the designated first measure of each skill j ∈
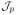 to obtain Cov(Yd,
M1,d) = Σθd
α where α = (αj; j ∈
to obtain Cov(Yd,
M1,d) = Σθd
α where α = (αj; j ∈
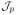 ). By the previous argument, Σθd is identified. Thus α is identified whenever det(Σθd) ≠ 0. Outcome factor loadings α can depend on d ∈ {0, 1}, as they can be identified through Cov(Yd,
M1,d) = Σθd
αd, which can be separately identified for treatments and controls. We test
, and we do not reject these hypotheses.40 Using E(Yd), we can identify τd because all of the other parameters of each outcome equation are identified.
). By the previous argument, Σθd is identified. Thus α is identified whenever det(Σθd) ≠ 0. Outcome factor loadings α can depend on d ∈ {0, 1}, as they can be identified through Cov(Yd,
M1,d) = Σθd
αd, which can be separately identified for treatments and controls. We test
, and we do not reject these hypotheses.40 Using E(Yd), we can identify τd because all of the other parameters of each outcome equation are identified.
D. Estimation Procedure
We estimate the model using a simple three stage procedure. First, we estimate the measurement system. Second, from these equations we can estimate the skills for each participant. Third, we estimate the relationship between participant skills and lifetime outcomes. Proceeding in this fashion makes identification and estimation transparent. In Section IV and Appendix L we show that a one-step procedure produces estimates very similar to those obtained from the three-step procedure. We estimate the model separately for males and females in light of the evidence that there are strong gender differences in program effects.41
We compute p-values using the bootstrap. We draw K = 1000 bootstrap samples of the original data and apply the estimation procedure to each pseudo-sample the same way we apply it to the original data. For a one-tailed test with an upper tail rejection region, the bootstrap p-value is estimated by
| (11) |
where ϱ̂ is the parameter of interest as estimated from the original data, and is the k-th draw from the bootstrap data-generating process satisfying the null hypothesis.42 We describe the details of our estimation procedure in the Appendix.
III. Measures of Cognitive and Personality Skills
This section explains how we condense the data on psychological traits. Using standard psychometric methods, we establish that only three factors are required to explain the available psychological measures. The extracted factors have clear interpretations. After extracting the factors, we test the validity of the derived system.
A. Our Measure of Cognition
A large literature establishes the importance of cognition, as measured by IQ, in explaining a variety of life outcomes (see, e.g., Gottfredson, 1997, and Jensen, 1998, for surveys). We use the Stanford-Binet Intelligence Test (Terman and Merrill, 1960) as our measure of cognition. Mean differences in Stanford-Binet scores between treatment and control groups are plotted by age in panels (a) and (b) of Figure 1. A boost in the IQs of children in the treatment group is observed soon after the program starts at age three. A few years after the program ends, the effect of treatment on IQ essentially disappears for males. A small, borderline statistically significant, positive effect remains for females. In our analysis, we use IQs at ages 7, 8, and 9, since this is the period when the treatment effect on IQ becomes relatively stable for both genders, and IQ becomes rank stable after those ages.43
B. Personality Skills
The most influential taxonomy of personality skills is the Big Five personality inventory (McCrae and John, 1992; John and Srivastava, 1999).44 Unfortunately, the Big Five was developed long after the Perry experiment was conducted. We only have access to psychological measures of personality skills collected before the Big Five was codified.45
Perry Measures of Personality Skills
There are 43 child personality measures in the Perry data. These measures belong to two separate psychological inventories of personality skills: the Pupil Behavior Inventory (PBI) and the Ypsilanti Rating Scale (YRS). These measures are displayed in Tables C.1 and D.1 in the Web Appendix, where their correspondence with Big Five traits is noted.46 The PBI inventory was developed by Vinter et al. (1966) to measure behavioral and attitudinal factors that affect academic success. The YRS measures were developed by the Perry analysts to measure academic potential and socio-emotional skills (Weikart, Bond and McNeil, 1978). The PBI and YRS questionnaires consist of multiple questions called items. They were given to teachers in classes attended by Perry students after the program was completed to assess students in their classes. An example of one of the PBI items is “lying or cheating”, and the possible answers are (1) very frequently, (2) frequently, (3) sometimes, (4) infrequently, and (5) very infrequently. The YRS questionnaire asks questions about socio-emotional skills, such as Academic Potential and Social Development.47
C. Approaches to Summarizing the Data
There are many ways to summarize the available psychological measures in an interpretable fashion. One way is to form indices of measures using the groupings employed by the Perry psychologists.48 The PBI and YRS scales were designed to alert educators of behavioral and motivational problems of children in school. There is considerable overlap among items in the groupings, and the relationship of these measures to more interpretable psychological constructs is unclear.
An intuitively appealing way to construct summary measures is to ignore the groupings used by the Perry psychologists and to select measures from all of their scales based on common sense and previous research in psychology, such as their interpretability in terms of the Big Five. This procedure is called “operationalization” in psychology, and is inherently subjective.49 There are many ways to form such indices leading to a complex model selection problem.
The approach used in this paper is to apply exploratory factor analysis (EFA) to the available measures. EFA is a standard statistical method widely used in psychometrics to allocate measures to factors (e.g., Gorsuch, 2003; Thompson, 2004). It is used to form the Big Five (See Goldberg, 1993). EFA establishes links between a small number of latent factors and the available measures. Each measure is allowed to depend on at most one factor, and the derived factors are allowed to be freely correlated.
Our application of EFA produces three interpretable factors which we interpret as Cognition, Externalizing Behavior, and Academic Motivation.50 The derived factors are consistent with previous research in psychology on the predictive power of psychological traits. We implement EFA in two stages. We first select the number of factors. We then allocate the measures of personality traits to different factors.
D. Exploratory Factor Analysis
We use several accepted procedures to determine the number of factors: the scree test (Cattell, 1966), Onatski’s test (2009), and Horn’s (1965) parallel analysis test.51 Overall, these procedures point to a three-factor characterization for both men and women.52
Exploratory Factor Analysis: Establishing Dedicated Measures
We extract factors following the criteria for EFA laid out by Gorsuch (1983).53 This method is widely used although its application requires judgement on the part of the analyst (see Gorsuch, 2003, and Thompson, 2004). EFA identifies blocks of measures that are strongly correlated within the each block (i.e. satisfy convergent validity), but are weakly correlated between blocks (i.e. satisfy discriminant validity). It discards measures that load on multiple factors. Application of standard EFA methodology to the 46 cognitive and personality Perry measures gives the 13 measures displayed in Table H.2.54
We follow Gorsuch (2003) and Thompson (2004), and derive a fully dedicated system as described by equations (8)–(10) i.e. a system in which each measure is associated with at most one factor. This procedure is called confirmatory factor analysis (CFA), which Gorsuch (2003) and Thompson (2004) advocate as the next step after conducting EFA. It produces the interpretable system displayed in Table 2, based on three factors: Cognition, Externalizing Behavior, and Academic Motivation.55 Externalizing Behavior is proxied by measures of behavior related to lying, stealing, and swearing, as well as being aggressive and disruptive. It has been linked to crime and aggressive behavior.56 Academic Motivation is proxied by measures of student interest, persistence, and initiative in learning and is linked to performance in schools as measured by achievement tests. The personality measures proxying Externalizing Behavior and Academic Motivation are conceptually related to Big Five factors in personality psychology.57
Table 2.
Cognitive and Personality Factors and Their Measures
| Cognition
|
Externalizing behavior
|
Academic Motivation
|
|||
|---|---|---|---|---|---|
| Measures(a) | Age | Measures(a) | Age(b) | Measures(a) | Age(b) |
| Stanford-Binet IQ | 7 | Disrupts classroom procedures | 7–9 | Shows initiative | 7–9 |
| Stanford-Binet IQ | 8 | Swears or uses obscene words | 7–9 | Alert and interested in school work | 7–9 |
| Stanford-Binet IQ | 9 | Steals | 7–9 | Hesitant to try, or gives up easily | 7–9 |
| Lying or cheating | 7–9 | ||||
| Influences others toward troublemaking | 7–9 | ||||
| Aggressive toward peers | 7–9 | ||||
| Teases or provokes students | 7–9 | ||||
|
| |||||
| Cronbach’s alpha(c), males | 0.838 | Cronbach’s alpha, males | 0.906 | Cronbach’s alpha, males | 0.901 |
| Cronbach’s alpha, females | 0.913 | Cronbach’s alpha, females | 0.916 | Cronbach’s alpha, females | 0.896 |
Note:
See Web Appendix B for a detailed description of Stanford-Binet IQ measures. Externalizing Behavior and Academic Motivation are proxied by items of the Pupil Behavior Inventory (PBI) described in Web Appendix C. PBI items are described in this table the same way they appear in the questionnaire. For example, “lying or cheating” and “steals” were the full descriptions of misbehavior that teachers were asked to evaluate.
Each personality measure is an average over non-missing observations at ages 7, 8, and 9.
Cronbach’s alpha (see Cronbach, 1951) is a statistic that captures how well a set of measures proxies a latent skill. Cronbach’s alpha is the lower bound of the internal consistency reliability of measures that are proxies for a skill. The internal consistency reliability is defined as the square of the correlation between the measured scale defined as the sum of the measures and the underlying skill θ (Allen and Yen, 2002). In our case, the correlations between the skills and the scales (equal to the square roots of alphas) range from 0.70 to 0.82 for males and from 0.80 to 0.84 for females. The Cronbach’s alphas can also be interpreted as a correlation between the observed scale and a hypothetical alternative scale measuring the same skill and based on the same number of hypothetical alternative items (Nunnally and Bernstein, 1994). For this table, the alphas (i.e., the correlations) range from 0.84 to 0.91 for males and from 0.90 to 0.92 for females.
The Predictive Power of Externalizing Behavior and Academic Motivation
The factors extracted by the EFA procedure are closely linked to traits that have been shown to be predictive of adult outcomes. This gives us greater confidence in using them to explain the Perry treatment effects.
The recent literature in economics shows that Externalizing Behavior predicts child and adult outcomes (Segal, 2008, 2009).58. The literature in psychology shows that Externalizing Behavior is negatively associated with Academic Achievement.59 Childhood Externalizing Behaviors have also been shown to be related to adolescent and adult delinquency (e.g., Nagin and Tremblay, 1999, and Broidy et al., 2003).
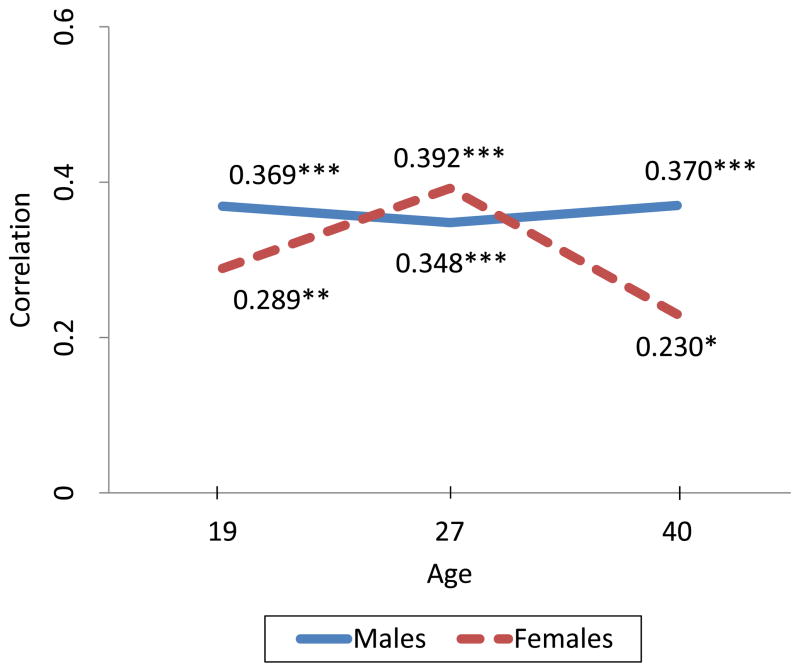
The literature in criminology and psychology demonstrates that early antisocial behaviors are highly predictive of adolescent and adult antisocial behaviors (Gersten et al., 1976; Huesmann et al., 1984; Olweus, 1979). Antisocial behaviors measured between ages 7 and 11 strongly predict criminal behaviors in adulthood (Loeber, 1982; Mofitt, 1993). Meanwhile, disobedient and aggressive behaviors measured as early as ages 3–5 predict later childhood conduct disorders and adolescent arrests (Mofitt, 1993; White et al., 1990). Most children with conduct disorders experience social difficulties in adulthood, whereas only 8 percent of children without conduct disorders experience such difficulties (Zoccolillo et al., 1992). Similarly, many children with antisocial behavior around ages 8–10 become antisocial adults (Coie et al., 1995; Olweus, 1979; Robins, 1978)60 and chronic criminal offenders (Loeber, 1982). Almost all antisocial adults were antisocial children (Robins, 1978). Our analysis confirms previous evidence on the stability of antisocial traits into adulthood. We find stable rank correlations between Externalizing Behavior at ages 7–9 and subsequent measures of crime as late as ages 19, 27, and 40 (see Figure 4). The evidence from the literature in psychology and criminology joined with the evidence from this paper suggests that reducing early externalizing behavior reduces crime.
Figure 4. Spearman’s Rank Correlations between Externalizing Behavior at Ages 7–9 and Number of Arrests by Ages 19, 27, and 40.
Note: *** - 1 percent, ** - 5 percent, * - 10 percent significance levels (one-sided tests).
Academic Motivation, apart from its obvious link to performance in school, has been shown to be a statistically significant predictor of decreased drug use (Bryant et al., 2003, and Razzino et al., 2004) and alcohol consumption (Zimmerman and Schmeelk-Cone, 2003, Simons-Morton, 2004, and Vaughan, Corbin and Fromme, 2009). Since drinking and drug use are associated with crime (Anglin and Perrochet, 1998, and Greenfeld, 1998), youth with higher levels of Academic Motivation are less likely to engage in criminal activities. Flouri and Buchanan (2002) show that for both males and females, low academic motivation in adolescence is positively related to trouble with the police at age 16. Cymbalisty, Schuck and Dubeck (1975) show that for males who have already committed crimes, recidivism decreases with motivation for learning. Therefore, it is expected that experimentally induced enhancements in Academic Motivation would be a source of treatment effects for education and crime outcomes. We confirm such effects for education, but not for crime.
IV. The Effect of Treatment on Traits and the Sources of Treatment Effects
We first study how treatment affects the extracted factors. We then investigate how the factors affect life outcomes. Finally, we decompose adult treatment effects into components corresponding to changes in each factor. The first analysis is based on the output of step two of the three-step estimation procedure described in detail in the Appendix. The second and third analyses are based on the output of the third step of the procedure.
A. The Effect of the Perry Program on Cognitive and Personality Skills
Figure 5 graphs kernel densities of factor scores and presents one-sided p-values for testing the equality of the means for each skill between the treatment and control groups.61 The Perry program has a statistically significant treatment effect on Externalizing Behavior at the 5 percent level for males and at the 1 percent level for females. The effects on Cognition and Academic Motivation are statistically significant at the 10 percent and 5 percent levels, respectively, for females, but are not statistically significant for males. This evidence is consistent with the evidence in Table 1 of a statistically significant treatment effect on achievement test scores, which is much stronger for girls than for boys.
Figure 5. Kernel Densities of Factor Scores.
Note: Probability density functions of Bartlett (1937) factor scores are shown. Densities are computed based on a normal kernel. Numbers above the charts are one-sided p-values testing the equality of factor score means for the treatment and control groups. Higher Externalizing Behavior corresponds to more socially desirable behavior. See Web Appendix L for the empirical CDFs of the factor scores (Figure L.5). Vertical lines locate factor score means for treatment and control groups.
The kernel densities reveal different patterns of the effect of the program on the distribution of skills. The cognition of females is enhanced mostly in the right tail of the distribution (panel b). In contrast, a substantial part of the improvement in Externalizing Behavior for females operates through enhancing low levels of the skill (panel d). Externalizing Behavior in males is improved at all levels. Academic Motivation in females is improved at all levels except for the top percentiles (see panel f). There is no statistically significant difference in the distribution of Cognition for males (panel a).62
B. The Effect of Cognitive and Personality Skills on Outcomes
In order to estimate the effects of factors on outcomes we estimate a model described by a system of equations (5) and (8) conditioning on background variables X. We present estimates of α = (αj, j ∈
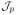 ) in equation (7). Table 3 shows that all three factors (Cognition, Externalizing Behavior, and Academic Motivation) have statistically significant effects on at least one outcome.
) in equation (7). Table 3 shows that all three factors (Cognition, Externalizing Behavior, and Academic Motivation) have statistically significant effects on at least one outcome.
Table 3.
Factor Loadings of Outcome Equations
| Outcome | Cognition | Externalizing Behavior | Academic Motivation | Sample Size | |||
|---|---|---|---|---|---|---|---|
| Coefficient | p-value | Coefficient | p-value | Coefficient | p-value | ||
| Males | |||||||
| CAT total at age 14, end of grade 8 (+) | 0.819 *** | (0.000) | −0.203 | (0.845) | 0.700 *** | (0.000) | 45 |
| # of misdemeanor arrests, age 27 (−) | −0.259 | (0.359) | −1.226 ** | (0.028) | −0.152 | (0.367) | 59 |
| # of felony arrests, age 27 (−) | −0.618 | (0.235) | −1.333 ** | (0.023) | 0.219 | (0.557) | 59 |
| # of adult arrests (misd.+fel.), age 27 (−) | −0.876 | (0.251) | −2.559 ** | (0.014) | 0.067 | (0.549) | 59 |
| Monthly income, age 27 (+) | 0.970 ** | (0.038) | 0.698 ** | (0.046) | −0.257 | (0.670) | 55 |
| Use tobacco, age 27 (−) | −0.179 | (0.121) | −0.332 *** | (0.001) | 0.159 | (0.847) | 57 |
| # of misdemeanor arrests, age 40 (−) | −0.620 | (0.383) | −2.424 * | (0.087) | 0.196 | (0.501) | 59 |
| # of felony arrests, age 40 (−) | −0.628 | (0.266) | −1.755 ** | (0.014) | 0.293 | (0.570) | 59 |
| # of adult arrests (misd.+fel.), age 40 (−) | −1.248 | (0.327) | −4.180 ** | (0.039) | 0.489 | (0.525) | 59 |
| # of lifetime arrests, age 40 (−) | −1.100 | (0.359) | −4.740 ** | (0.030) | 0.239 | (0.519) | 59 |
| Employed, age 40 (+) | 0.277 ** | (0.012) | 0.230 ** | (0.011) | −0.270 | (0.991) | 54 |
| Females | |||||||
| CAT total, age 8 (+) | 0.219 ** | (0.039) | −0.134 | (0.729) | 0.689 *** | (0.000) | 35 |
| CAT total, age 14 (+) | 0.154 | (0.113) | −0.448 | (0.931) | 0.899 *** | (0.001) | 31 |
| Any special education, age 14 (−) | −0.041 | (0.273) | 0.119 | (0.759) | −0.209 * | (0.064) | 37 |
| Mentally impaired at least once, age 19 (+) | −0.039 | (0.283) | 0.227 | (0.948) | −0.308 *** | (0.008) | 33 |
| # of misdemeanor violent crimes, age 27 (−) | 0.083 | (0.778) | −1.080 ** | (0.043) | 0.150 | (0.700) | 37 |
| # of felony arrests, age 27 (+) | 0.021 | (0.609) | −0.451 * | (0.053) | 0.140 | (0.808) | 37 |
| Jobless for more than 1 year, age 27 (−) | 0.139 | (0.920) | 0.048 | (0.608) | −0.465 *** | (0.003) | 36 |
| Ever tried drugs other than alcohol or weed, age 27 (−) | −0.043 | (0.201) | −0.146 | (0.144) | 0.122 | (0.854) | 34 |
| # of misdemeanor violent crimes, age 40 (−) | 0.084 | (0.774) | −1.078 ** | (0.043) | 0.081 | (0.592) | 37 |
| # of felony arrests, age 40 (−) | 0.047 | (0.704) | −0.589 ** | (0.014) | 0.078 | (0.643) | 37 |
| # of lifetime violent crimes, age 40 (−) | 0.096 | (0.807) | −1.220 ** | (0.023) | 0.165 | (0.704) | 37 |
| Months in all marriages, age 40 (+) | 21.748 | (0.111) | 13.591 | (0.289) | 10.453 | (0.280) | 36 |
Note: Regression coefficients for factor scores in Equation (5) are shown with one-sided p-values in parentheses. (+) and (−) denote the sign of the total treatment effect on the corresponding variable. Estimates are corrected based on the bias-correcting procedure described in Equation (A4). “CAT total” denotes the California Achievement Test total score normalized to control mean zero and variance of one. See Tables L.14 and L.15 of Web Appendix L for more detailed versions of this table containing coefficients for background variables. Stars denote significance levels:
- 1 percent,
- 5 percent, and
- 10 percent. Monthly income is adjusted to thousands of year-2006 dollars using annual national CPI.
Different factors affect different outcomes. Cognition primarily affects achievement tests and also affects certain labor market outcomes. Externalizing Behavior affects crime outcomes, labor market outcomes, and health behaviors. Academic Motivation boosts educational outcomes and reduces long-term unemployment.
Treatment effects are generated through changes in skills if (1) skills affect outcomes and (2) skills are enhanced by the intervention. Thus, even though Cognition and Academic Motivation are positively related to the CAT scores of males, the absence of a relationship for males between treatment and both Cognition and Academic Motivation makes this channel either weak or nonexistent.
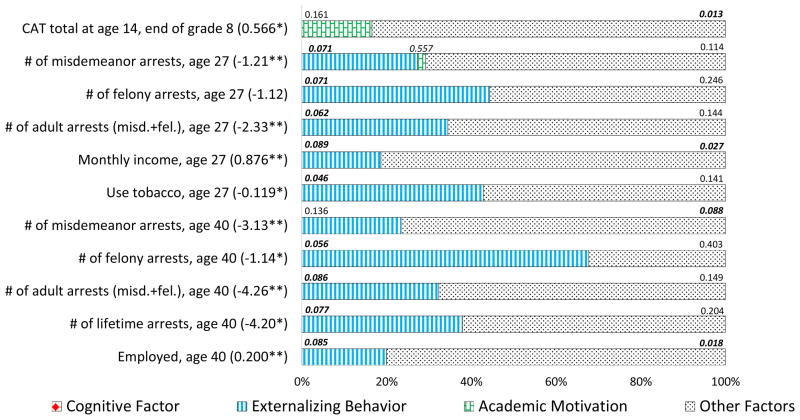
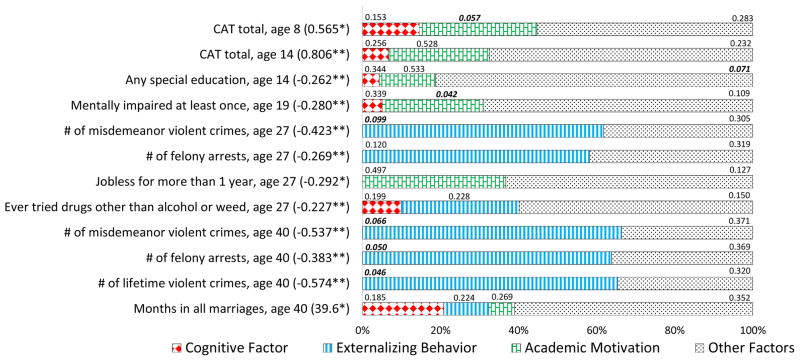
C. Decomposing Treatment Effects on Outcomes by Source
Figures 6 and 7 present our estimated decompositions of treatment effects into experimentally induced improvements in Cognition, Externalizing Behavior, Academic Motivation, and other factors. By “other factors” we mean the residual treatment effect associated with unmeasured skills. We report the percentage of each treatment effect attributable to each component.63 The numbers shown above each component are one-sided p-values for the test of whether the component is zero. We stress that these decompositions are invariant to the choice of normalizing measures and to affine transformations of the measures.64
Figure 6. Decompositions of Treatment Effects on Outcomes, Males.
Note: The total treatment effects are shown in parentheses. Each bar represents the total treatment effect normalized to 100 percent. One-sided p-values are shown above each component of the decomposition. The figure is a slightly simplified visualization of Tables L.10 and L.14 : small and statistically insignificant contributions of the opposite sign are set to zero. See Web Appendix L for detailed information about the simplifications made to produce the figure. “CAT total” denotes California Achievement Test total score normalized to control mean zero and variance of one. Asterisks denote statistical significance: * – 10 percent level; ** – 5 percent level; *** – 1 percent level. Monthly income is adjusted to thousands of year-2006 dollars using annual national CPI.
Figure 7. Decompositions of Treatment Effects on Outcomes, Females.
Note: The total treatment effects are shown in parentheses. Each bar represents the total treatment effect normalized to 100 percent. One-sided p-values are shown above each component in each outcome. The figure is a slightly simplified visualization of Tables L.11 and L.15 : small and statistically insignificant contributions of the opposite sign are set to zero. See Web Appendix L for detailed information about the simplifications made to produce the figure. “CAT total” denotes California Achievement Test total score normalized to control mean zero and variance of one. Asterisks denote statistical significance: * – 10 percent level; ** – 5 percent level; *** – 1 percent level.
We decompose the treatment effect for a number of outcomes: performance on the California Achievement Test (CAT), special education at school and mental impairment, labor market outcomes such as income and employment, health behaviors such as smoking tobacco or using drugs, marriage duration, and crime outcomes. The crime outcomes are especially important since they are the dominant component of Perry program’s total benefit ( e.g., Heckman et al., 2010b). We only decompose treatment effects that have been shown to be statistically significant at the 10 percent level or below after adjusting for the effects of multiple-hypothesis testing on significance levels ( Heckman et al., 2010a, Conti et al., 2012). Proceeding in this fashion leads to somewhat different decompositions for males and females.
The effect of the intervention on life outcomes operates primarily through the program’s enhancement of Externalizing Behavior. Components attributable to changes in this factor are generally statistically significant and, in most cases, explain 20–60 percent of the treatment effects on crime for males and about 40–60 percent for females (see Figures 6 and 7).
The mediating effects of Externalizing Behavior are not only statistically significant, but also economically significant. Reported arrests and registered crimes are only a small fraction of the actual number of crimes. For instance, only one in 15 property crimes and one in five violent crimes actually leads to an arrest.65 We find that experimentally induced reductions in Externalizing Behavior (by one standard deviation) leads to a decline in the total number of lifetime arrests by statistically significant 1.7 (p=0.077) and the number of felony arrests by 0.6 (p=0.056) for males at age 40.66 For females, the total number of felony arrests by age 40 is reduced by 0.31 (p=0.050), and the number of registered lifetime violent crimes is reduced by 0.65 (p=0.046).67 The reduction in actual crimes is likely several times larger than these reductions in the number of arrests and registered crimes. Since Externalizing Behavior is both malleable at early ages (see Figure 5) and strongly predictive of crime (see Table 3), it should not be surprising that crime reduction has been found to be a major benefit of the Perry program.
We also decompose the effect of the program on an achievement test (CAT) for both males and females. For females, enhancements in Academic Motivation explain about 30 percent of the treatment effect on CAT scores at age 8. This estimate is statistically significant at a 10 percent level (p = 0.057). For CAT scores at age 14, the role of Academic Motivation is not precisely determined for males or for females (p = 0.161 and 0.528).
Finally, we decompose a number of education, labor market, and health outcomes. Academic Motivation consistently explains a share of treatment effects for all education-related outcomes, which is not surprising given strong links between Academic Motivation and education outcomes presented in Table 3. However, only some components of these decompositions are precisely determined (e.g. CAT and the status of being mentally impaired for females).
For labor market outcomes, we find that about 20 percent of the treatment effect on monthly income at age 27 (p=0.089) and also about 20 percent of the treatment effect on the probability of employment at age 40 (p=0.085) are explained by early improvements in Externalizing Behavior. Additionally, Externalizing Behavior explains about 40 percent of tobacco use at age 27 (p = 0.046).
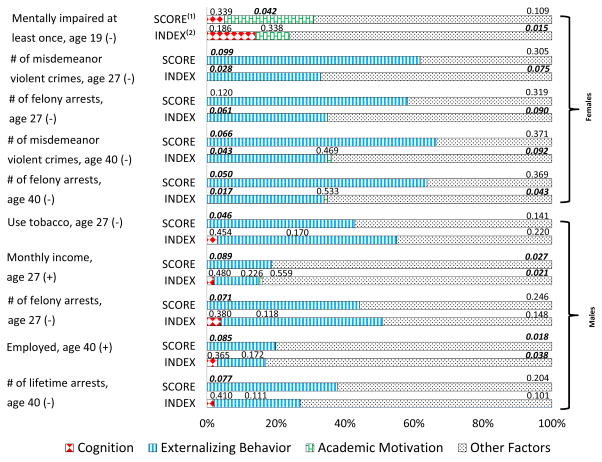
D. Decompositions Based on Indices vs. Decompositions Using Factor Scores
A simple alternative to our factor procedure for summarizing the evidence on the effects of experimentally induced changes in measurements on outcomes is to use indices of the measures in place of factor scores. Such indices, which are unweighted averages over the measures, are commonly used. In making this comparison we take as given the cluster of measures identified by application of EFA (see Table 2). Picking the clusters of the traits in this fashion avoids the serious practical problem that many groupings are possible, and many tests among competing specifications are non-nested. The comparison being made is one between using unweighted averages of measures not correcting for measurement error with a method that extracts factors by weighting the measures by the estimated factor loadings and adjusting for measurement error.
Figure 8 decomposes a selection of the treatment effects for a variety of outcomes for each gender using both indices and factor models.68 For each outcome, we show the results of the two different estimation procedures using a pair of bars. The first bar in each pair corresponds to the estimates from the procedure used in this paper. These bars are identical to those presented in Figures 6 and 7. The second bar in each pair corresponds to the decomposition obtained from estimating equation (7) using indices.
Figure 8. Decompositions of Treatment Effects by Indices versus Factor Scores.
Note: The total treatment effect is normalized to 100 percent. One-sided p-values are shown above each component in each outcome. (1) “SCORE” denotes models where personality traits are measured by factor scores.(1) “INDEX” denotes models where personality traits are measured by indices constructed using unweighted averages over the items. The figure is a slightly simplified visualization of results from Tables L.10, L.11, K.1, and K.2 of the Web Appendix: small and statistically insignificant contributions of the opposite sign are set to zero. See Web Appendix L for detailed information about the simplifications used to produce the figure.
Comparing the first bar with the second bar reveals that even though results of the two procedures lead to similar qualitative conclusions about the role of mediating skills, the estimates of the explained treatment effect components and the associated p-values are numerically different. As is apparent from equation (7), there are two possible sources of difference in the decompositions: (1) different factor loadings αj and (2) different estimates of the treatment effect on the factors:
, j ∈
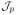 . The approach using indices only partially corrects for attenuation bias by reducing measurement error through simple averaging. Our factor approach explicitly addresses measurement error. Thus the index approach likely generates downward-biased decompositions. Indeed, the shares of the treatment effects explained by Externalizing Behavior are generally smaller for the index-based procedure. The p-values from the index-based procedure are somewhat smaller for females but somewhat larger for males. Most of the comparisons presented in Figure 8 are consistent with this interpretation. 69,70
. The approach using indices only partially corrects for attenuation bias by reducing measurement error through simple averaging. Our factor approach explicitly addresses measurement error. Thus the index approach likely generates downward-biased decompositions. Indeed, the shares of the treatment effects explained by Externalizing Behavior are generally smaller for the index-based procedure. The p-values from the index-based procedure are somewhat smaller for females but somewhat larger for males. Most of the comparisons presented in Figure 8 are consistent with this interpretation. 69,70
E. More Efficient Estimates
The three step estimation procedure used in this paper is simple and intuitive. In general, it is not statistically efficient given that we do not impose cross-equation restrictions across the stages of the estimation. In Web Appendix L, we compare the decompositions obtained from our three-step estimation procedure to those obtained from a one-step maximum likelihood estimation method where the measurement system and outcome equation are estimated jointly.71 The results from both procedures are in close agreement, although p-values from the maximum likelihood procedure are generally lower.72
F. Testing the Validity of the Derived System
The procedure used to create the dedicated factor system is based in part on judgements by the analyst. Such judgements are widely used in the psychometric literature.73 To gain greater confidence in the system created by our EFA analysis, we test the validity of the derived factor structure.
Our application of the EFA methodology yields 13 dedicated measures out of 46 available cognitive and personality measures. The 33 unused measures do not survive the EFA testing criteria. To test the validity of this specification, we run a series of tests on the measurement and outcome equations. We first determine if, conditional on the extracted factors, the unused measures exhibit a treatment effect. If they do not, they are not candidates for explaining the treatment effect for outcomes. We also determine whether, conditional on the extracted factors, the unused measures explain outcomes. Evidence from both types of tests support the low-dimensional specification of equations (5) and (8)–(10) derived from applying EFA. Web appendix M presents a detailed discussion of these tests.
G. A Framework for Unifying Diverse Studies of Child Development
The framework developed in this paper facilitates the interpretation of diverse treatment effects within and across programs as the manifestations of program-induced changes in a low-dimensional set of skills of participants. This framework can be used to unify the interpretation of the treatment effects across different studies with different interventions applied to different populations. By focusing on the channels through which the different programs produce their effects, we gain a deeper understanding of the traits that matter and how they can be affected by various influences on the child. Systematic application of this framework will enable the intervention literature to move beyond meta analyses to understand the common mechanisms producing success in children and how different interventions boost different traits to different degrees. This framework also offers a basis for unifying observational studies of family influence with intervention studies.74 Investments made by families boost θ as do the investments made in intervention programs. Using the framework developed and applied in this paper, we can in principle compare family investments and interventions in terms of their effects on θ.
V. Conclusions
Using experimental data from an influential early childhood program, we analyze the sources of program treatment effects. Coupling experimental variation with an econometric model, we estimate the role of enhancements in Cognition, Externalizing Behavior, and Academic Motivation in producing the Perry treatment effects. Persistent changes in personality skills play a substantial role in producing the success of the Perry program. The reduction in Externalizing Behavior, which explains the bulk of the effects of Perry program on criminal, labor market, and health behavior outcomes, is especially strong.75
We offer a new understanding of how a few hours per day of preschool at ages three and four with a curriculum that promotes social competency, planning, and organization can significantly and beneficially affect life outcomes. The importance and malleability of these skills deserves greater emphasis in public policies designed to promote skills and alleviate poverty.76
Appendix on the Three Step Estimation Procedure
Step 1
For a given set of dedicated measurements, and choice of the number of factors, we estimate the factor model using measurement system (8)–(10).
Step 2
We use the measures and factor loadings estimated in the first step to compute a vector of factor scores for each participant i. We form unbiased estimates of the true vector of skills for agent i. The factor measure equations contain X which we suppress to simplify the expressions. Notationally, we represent the measurement system for agent i as
| (A1) |
where ϕ represents a matrix of the factor loadings estimated in first step and Mi is the vector of stacked measures for participant i subtracting the intercepts
of equation (8). The dimension of each element in equation (A1) is shown beneath it, where
 = ∪j∈
= ∪j∈
 is the union of all the index sets of the measures
is the union of all the index sets of the measures
 , j ∈
, j ∈
 . The error term for agent i,
ηi, has zero mean and is independent of the vector of skills θi. Cov(ηi,
ηi) = Ω. The most commonly used estimator of factor scores is based on a linear function of measures: θS,i = L′Mi. Unbiasedness requires that L′ϕ = I|p|, where I|p| is a |p|-dimensional identity matrix.77 To achieve unbiasedness, L must satisfy L′ = (ϕ′Ω−1
ϕ) −1
ϕ′Ω−1. The unbiased estimator of the factor is:
. The error term for agent i,
ηi, has zero mean and is independent of the vector of skills θi. Cov(ηi,
ηi) = Ω. The most commonly used estimator of factor scores is based on a linear function of measures: θS,i = L′Mi. Unbiasedness requires that L′ϕ = I|p|, where I|p| is a |p|-dimensional identity matrix.77 To achieve unbiasedness, L must satisfy L′ = (ϕ′Ω−1
ϕ) −1
ϕ′Ω−1. The unbiased estimator of the factor is:
Factor score estimates can be interpreted as the output of a GLS estimation procedure where measures are taken as dependent variables and factor loadings are treated as regressors. By the Gauss-Markov theorem, for a known ϕ the proposed estimator is the best linear unbiased estimator of the vector of skills θi.78
Step 3
The use of factor scores instead of the true factors to estimate equation (5) generates biased estimates of outcome coefficients α. Even though estimates of θi are unbiased, there is still a discrepancy between the true and measured θi due to estimation error. To correct for the bias, we implement a bias-correction procedure. Because we estimate the variance of θ and the variance of the measurement errors in the first step of our procedure, we can eliminate the bias created by the measurement error.
Consider the outcome model for agent i:
| (A2) |
where (θi,
Zi)
 εi and E(εi) = 0. For brevity of notation, we use Zi to denote pre-program variables, treatment status indicators, and the intercept term of equation (5). From equation (A1), the factor scores θS,i can be written as the skills θi plus a measurement error Vi, that is,
εi and E(εi) = 0. For brevity of notation, we use Zi to denote pre-program variables, treatment status indicators, and the intercept term of equation (5). From equation (A1), the factor scores θS,i can be written as the skills θi plus a measurement error Vi, that is,
| (A3) |
Replacing θi with θS,i yields Yi = αθS,i + γZi + εi − αVi. The linear regression estimator of α and γ is inconsistent:
| (A4) |
This is the multivariate version of the standard one-variable attenuation bias formula. All covariances in A can be computed directly except for the terms that involve θ. The covariance Cov(θ, θ) is estimated in step (1). Using equation (A3), we can compute Cov(Z, θS) = Cov(Z, θ). Thus, A is identified. Our bias-correction procedure consists of pre-multiplying the least squares estimators (α̂, γ̂) by A−1, thus providing consistent estimates of (α, γ).79 A one step maximum likelihood procedure, while less intuitive, directly estimates the parameters without constructing the factors and accounts for measurement error. It is justified in large samples under standard regularity conditions. It produces estimates very close to those obtained from the three step procedure but with smaller standard errors. See Web Appendix L.
Supplementary Material
Acknowledgments
We thank three anonymous referees for helpful comments. Lena Malofeeva, then at the HighScope Foundation, worked with us in supplying the Perry data and interpreting it for us. We are deeply grateful for her assistance and the cooperation of the HighScope Foundation. Versions of this paper were presented at numerous conferences and seminars starting in 2006 that are listed in the Web Appendix. We thank participants at these meetings for useful comments. We are grateful to Clancy Blair, Dan Benjamin, Martin Browning, Sarah Cattan, Kenneth Dodge, Angela Duckworth, Amy Finklestein, Miriam Gensowski, Matt Gentzkow, Maryclare Griffen, Jeff Grogger, Emir Kamenica, Costas Meghir, Jörn-Steffen Pischke, Devesh Raval, Brent Roberts, Cullen Roberts, Tino Sanandaji, Larry Schweinhart, Sandra Waxman, Ben Williams, and Junjian Yi for helpful comments. We are grateful to Christopher Hansman, Kegon Tan Teng Kok, Min Ju Lee, Xiliang Lin, Yun Pei, and Ivana Stosic for excellent research assistance. This research was supported in part by the American Bar Foundation, the JB & MK Pritzker Family Foundation, Susan Thompson Buffett Foundation, NICHD R37HD065072, R01HD54702, a grant to the Becker Friedman Institute for Research and Economics from the Institute for New Economic Thinking (INET), and an anonymous funder. We acknowledge the support of a European Research Council grant hosted by University College Dublin, DEVHEALTH 269874. The views expressed in this paper are those of the authors and not necessarily those of the funders or persons named here. Supplementary materials are placed in a Web Appendix (http://jenni.uchicago.edu/Perry/).
Footnotes
The formal name of the program is the “HighScope Perry Preschool Program” (see Schweinhart et al., 2005).
The small sample size of the Perry experiment (123 participants) has led some researchers to question the validity and relevance of its findings (e.g., Herrnstein and Murray, 1994, and Hanushek and Lindseth, 2009). Heckman et al. (2010a) use a method of exact inference that is valid in small samples. They find that Perry treatment effects remain statistically significant even after accounting for multiple hypothesis testing and compromised randomization.
One of the outcomes, the number of felony arrests for males at age 27, is borderline statistically significant at the 10% level.
The historical post-World War II stock market rate of return to equity is 5.8 percent (DeLong and Magin, 2009).
Although not necessarily with the same quality of staff and background of participants as in the original program.
See Weikart (1967); Weikart, Bond and McNeil (1978); Berrueta-Clement et al. (1984); Schweinhart, Barnes and Weikart (1993).
Reduction in crime is a major benefit of the Perry program (Belfield et al., 2006; Heckman et al., 2010b).
See Figure C.7 of the Web Appendix for breakdowns by gender.
See Cunha and Heckman (2008) and Cunha, Heckman and Schennach (2010) for evidence that personality traits boost acquisition of cognition as measured by achievement tests.
Borghans et al. (2011a) show that achievement test scores are explained, in part, by both personality traits and IQ. See also Heckman and Kautz (2012)
See also Bowles and Gintis (1976, 2001); Heckman, Stixrud and Urzúa (2006); Segal (2008, 2009).
The first entry cohort was enrolled for only one year of the program, beginning at age four.
Heckman et al. (2010a) describe the protocol and develop statistical procedures for testing treatment effects which take into account the peculiarities of the Perry randomization protocol.
Five control and two treatment group participants died; two control and two treatment group participants were missing.
See Web Appendix A for more information on the Perry curriculum.
The curriculum of the Perry program was also grounded, in part, in the research on cognitive development by Jean Piaget (Piaget and Inhelder, 2000) and in the progressive educational philosophy of John Dewey (Dewey, 1997).
See Tough (2009) for a popular exposition of the Tools of the Mind program. See Bodrova and Leong (2007) for a complete description of the Tools of the Mind program. Diamond et al. (2007) present a recent evaluation of the program that demonstrates that it enhanced self-control by participants. For a discussion of the Vygotskian foundations of the Perry program see Sylva (1997).
Anderson (2008) adjusts test statistics for the Perry program treatment effects for the effects of multiple hypothesis testing. He claims that the program only affected girls. Heckman et al. 2010(a) critically evaluate this conclusion and his procedures. They establish statistically significant program treatment effects for both boys and girls. Heckman et al. 2010(b) show that the rate of return to the program is statistically significantly different from zero for both boys and girls.
Throughout the paper we assume that the Perry program has either positive or no effect on outcomes and use one sided p-values to test hypotheses. The literature shows that high-quality intervention programs targeting disadvantaged children generally show either beneficial or no effects from the program. For example, Gray and Klaus (1970), Lazar et al. (1982), Campbell and Ramey (1994, 1995), Yoshikawa (1995), and Reynolds et al. (2001) document beneficial effects of intervention programs targeting disadvantaged children. Barnett (1995) reviews a variety of early intervention programs and shows that there were mainly beneficial effects on children’s development outcomes, although some programs had no treatment effects. He explains the lack of treatment effects as a consequence of the difference in program quality. Baker, Gruber and Milligan (2008) investigate the effects of Quebec’s universal childcare program and find a number of adverse effects of this program on children’s socio-emotional skills, possibly casting doubt on use of one-sided p-values in this paper. The program they study is a warehousing child-care program, not a high quality early intervention program. Ramey and Ramey (2010) show that low quality childcare program can have adverse effects. The Perry program was of extremely high quality and targeted highly disadvantaged children who generally lacked adequate parenting. Therefore, we should expect positive or no effects from the program.
These are called mediation analyses in the statistics literature. See, e.g., Pearl (2011). Such analyses have been used for decades in economics. See, e.g., Klein and Goldberger (1955) and Theil (1958).
For evidence on the extent of measurement error in these traits see Cunha and Heckman (2008) and Cunha, Heckman and Schennach (2010).
The distinction between fixing and conditioning traces back to Haavelmo (1943). See Pearl (2009) and Heckman and Pinto (2012a) for recent discussions.
Alternative decompositions are discussed in Appendix E.3
These are called structural invariance or autonomy assumptions in the econometric literature. See, e.g., Hurwicz (1962). These assumptions do not rule out heterogenous responses to treatment because θ1 − θ0 may vary in the population.
See Appendix J for details.
If skill increments are not independent, then in general even if α1 = α0, plim α1 ≠ plim α0. This test is valid in general even when α0 cannot be consistently estimated. See Appendix J. A distinct test of autonomy (H0 : α1 = α0) is possible if we maintain full exogeneity (i.e. measured skills are independent of unmeasured skills in both treatment regimes).
Web Appendix G shows that the estimates of α in equation (6) are unbiased if measured and unmeasured skills are independent.
See the review in Borghans et al. (2008)
See, e.g., Wansbeek and Meijer (2000). Table L.1 in Web Appendix L gives estimates of the measurement error for the psychological measures used in this paper. In some measures, up to 80 percent of the variance is measurement error.
See Web Appendix E.2 and the discussion in Section II.C.
We refer the reader to Web Appendix E for a more detailed discussion of identification.
See Web Appendix E.3 for a proof. If α1 ≠ α0, we acquire another term in the decomposition that is not invariant to affine transformations of the measures used to extract factors. However, even in this case, the treatment effect arising from measured skills in (7) is invariant. See also James J. Heckman and Rodrigo Pinto 2012(b) for a more general analysis of the combinations of parameters identified under monotonic transformations of the measures.
Having three measures allows us to form three covariances and to solve for the three unrestricted parameters of the three-measurement system. With two measures, we form one covariance which cannot, by itself, be used to identify the two unrestricted parameters of the two measurement system. See T. W. Anderson and H. Rubin (1956b).
Table L.4 in the Web Appendix. Proof of identification of this more general model is given in Appendix E.
See Wasserman (2006) for details.
Measures of IQ from alternative tests, the Leiter and the PPVT, evolve in a fashion similar to scores on the Stanford-Binet test (see panels (a)-(d) of Figure B.6 of Web Appendix B). Among IQ measures available in the Perry data, Stanford-Binet is the most established one. The Stanford-Binet IQ test is widely used and has high reliability (see Santrock, 2008). Web Appendix B presents a detailed description of the test. Borghans et al. (2008) and Almlund et al. (2011) discuss the evidence on the rank stability of IQ after age 10 or so.
However, even the Big Five is not universally accepted. See Borghans et al. (2008), and Almlund et al. (2011), for surveys of personality psychology literature.
The traits can be related to the Big Five (see Tables C.1 and D.1 of the Web Appendix)
We thank Angela Duckworth for helping us make this correspondence.
Although measures are missing on the PBI and YRS, the longitudinal structure of the Perry experiment allows us to use closely adjacent measures by age to impute the missing data. See Web Appendices C and D.
There are nine such groupings. We list the corresponding measures within groups in Tables C.1 and D.1 of the Web Appendix.
The interpretation of a factor is derived from the interpretation of the measures from which it is extracted.
Web Appendix H provides additional details about the criteria used in the literature to choose the number of factors. The Guttman-Kaiser rule (Guttman, 1954, and Kaiser, 1960, 1961) suggests 7–9 factors. This rule is well known to overestimate the number of factors (see Zwick and Velicer, 1986, Gorsuch, 2003, and Thompson, 2004) and this makes it less informative than the other methods. We do not use it in this paper.
See Web Appendix H.1 for the algebra of factor rotation and for the definition of various factor selection criteria. We use direct quartimin oblique rotation. We find that other widely recognized oblique rotation methods such as geomin, lead to similar results and the same choice of measures as quartimin (see Table L.7 of the Web Appendix, which shows the same pattern as the direct quartimin solution in Table H.2 of Appendix H). This result is in line with the literature showing that widely recognized methods of oblique rotation produce similar results (Fabrigar et al., 1999).
Measures are retained if they are strongly related to one and only one factor. For statements about the standard EFA methodology, see Tabachnick and Fidell (2001), Thompson (2004), and Costello and Osborne (2005).
The factor loadings for the dedicated system are presented in Table L.8 of Web Appendix L.
Externalizing behavior is linked to the Big Five traits of Agreeableness, Neuroticism and Conscientiousness. (see Almlund et al., 2011)
See Almlund et al. (2011) for a discussion of these relationships.
For more information about externalizing behaviors, see Achenbach (1978), Campbell et al. (1996), and Brunnekreef et al. (2007).
See Richman, Stevenson and Graham, 1982, Egeland et al., 1990, Jimerson, Egeland and Teo, 1999, and Jimerson et al., 2002.
Robins (1978) estimates that 36–41 percent of children with antisocial behaviors become highly antisocial adults.
Cognition is uncorrelated with Externalizing Behavior, while Academic Motivation correlates with both Externalizing Behavior and Cognition (see Table L.9 of Web Appendix L).
We also test for gender differences in skills and find that differences are not statistically significant. In other words, for each skill and for each treatment group we cannot reject the null hypothesis of equality of skills between males and females. See Figure L.1 of Web Appendix L.
Figures 6 and 7 are slightly simplified representations of the results presented in Tables L.10 and L.11 of the Web Appendix. To simplify the exposition, for the figures in the main text, contributions opposite in sign to those of the total treatment effect are set to zero. These contributions are small and statistically insignificant. Thus the figures in the text are an accurate summary of the essential information in the tables. Appendix L explains the methodology for constructing the figures and shows (see Figure L.2) that the the figures presented in the text closely approximate the actual decomposition.
See Web Appendix E.
Heckman et al. (2010b) estimate that the average victimization to arrest ratio in Midwestern urban areas is 15.0 for property crimes and 5.3 for violent crimes.
Control group means for the number of total lifetime and felony arrests for males are 12.4 and 3.2, with standard errors 1.9 and 0.7.
Tables L.10 and L.11 of the Web Appendix present the effects in terms of absolute levels rather than in relative levels as shown in Figures 6 and 7. Control group means for the number of lifetime felony arrests and number of registered lifetime violent crimes are .42 and .65 respectively, with standard errors 0.18 and 0.29.
We present a full comparison of indices with factors in Appendix L for all treatment effects analyzed in this paper. See Figures L.6 and L.7 to be compared to Figures 6 and 7 respectively.
Upward bias may arise for the following reason. An index uses equal weights for all measures. It may happen that for some particular outcome, measures that are more predictive of that outcome have relatively higher weights in the index compared to their weights on the true factor scores. Then the index will be more predictive of that particular outcome than the factor score. If the effect of using an index outweighs the attenuation bias due to measurement error, it may happen that a decomposition based on an index is biased upwards. There are only two instances of this occurring in Figure 8 (tobacco use and felony arrests for males).
A related issue, somewhat tangential to the main point of this paper, is the decomposition that results from using achievement test scores in place of IQ test scores in constructing our decomposition. As noted by Borghans et al. 2011(a,b), 30–40 percent of the variation in achievement test scores is attributable to variation in personality scores. Thus the common practice of assuming that achievement tests proxy intelligence is misleading. When we use the CAT scores at ages 7–9 in place of IQ scores at those ages, and construct an “Achievement” cognition factor, we overstate the importance of “Cognition” as a source of treatment effects. See Tables L.12 – L.13, Figure L.3, and the discussion in Web Appendix L.
Tables L.5 and L.6 of the Web Appendix L show the full set of estimates for the decompositions.
See Gorsuch (2003) and Thompson (2004).
For a template of this program see Cunha and Heckman (2009).
Our analysis cannot rule out the possibility that the initial enhancement of IQ in the Perry program permanently boosted personality traits (e.g. by giving participants more understanding of their environment and promoting self confidence and other traits) even though the initial IQ surge faded. To examine this possibility would require estimating the state space model of Cunha and Heckman (2008) to examine the transient dynamics of the model. This would be a formidable empirical challenge for a sample the size of the Perry study.
Since we analyze one program in one site with one level of program intensity, we are unable to determine the external validity of our evidence for other sites or intensity levels, nor can we discuss how easy it is to go to scale with the program. An analysis of these questions for early childhood outcomes is possible using data from ICPSR (2010) because roughly 30 percent of Head Start centers adopt some version of the Perry curriculum.
The method is due to Bartlett (1937) and is based on the restricted minimization of mean squared error, subject to L′ϕ = I|
 |.
|.
Web Appendix F discusses other estimators considered in the literature. Note that the assumption that ϕ is known can be replaced with the assumption that ϕ is consistently estimated and we can use an asymptomatic version of the Gauss-Markov theorem replacing “unbiased” with “unbiased in large samples”.
See Croon (2002) for more details on this bias correction approach.
The paper was presented at a Public Policy and Economics Seminar at the Harris School, University of Chicago, October, 2009, attended by Diane Schatzenbach.
Contributor Information
James Heckman, Henry Schultz Distinguished Service Professor of Economics and Public Policy, University of Chicago; Professor of Science and Society, University College Dublin; Senior Fellow, American Bar Foundation; The University of Chicago, Department of Economics, 1126 E. 59th St., Chicago, IL 60637.
Rodrigo Pinto, Ph.D. Candidate in Economics, University of Chicago; The University of Chicago, Department of Economics, 1126 E. 59th St., Chicago, IL 60637.
Peter Savelyev, Assistant Professor of Economics, Vanderbilt University and Health Policy Associate of the Robert Wood Johnson Center for Health Policy at Meharry Medical College; Vanderbilt University, Department of Economics, PMB 351819, 2301 Vanderbilt Place, Nashville, TN 37235-1819.
References
- Achenbach Thomas M. The Child Behavior Profile: I. Boys Aged 6–11. Journal of Consulting and Clinical Psychology in the Schools. 1978;46(3):478–488. doi: 10.1037//0022-006x.46.3.478. [DOI] [PubMed] [Google Scholar]
- Allen Mary J, Yen Wendy M. Introduction to Measurement Theory. Prospect Heights, IL: Waveland Press; 2002. [Google Scholar]
- Almlund Mathilde, Duckworth Angela, Heckman James J, Kautz Tim. Personality Psychology and Economics. In: Hanushek EA, Machin S, Wößmann L, editors. Handbook of the Economics of Education. Vol. 4. Amsterdam: Elsevier; 2011. pp. 1–181. [Google Scholar]
- Almond Douglas, Currie Janet. Human Capital Development before Age Five. In: Ashenfelter Orley, Card David., editors. Handbook of Labor Economics. 4B. North Holland: Elsevier; 2011. pp. 1315–1486. Chapter 15. [Google Scholar]
- Anderson Michael. Multiple Inference and Gender Differences in the Effects of Early Intervention: A Reevaluation of the Abecedarian, Perry Preschool and Early Training Projects. Journal of the American Statistical Association. 2008;103(484):1481–1495. [Google Scholar]
- Anderson Theodore W, Rubin Herman. Statistical Inference in Factor Analysis. In: Neyman J, editor. Proceedings of the Third Berkeley Symposium on Mathematical Statistics and Probability. Vol. 5. Berkeley: University of California Press; 1956a. pp. 111–150. [Google Scholar]
- Anderson TW, Rubin H. Statistical inference in factor analysis. Proceedings of the third Berkeley Symposium on mathematical statistics and probability; 1956b. p. V. [Google Scholar]
- Anglin M Douglas, Perrochet Brian. Drug Use and Crime: A Historical Review of Research Conducted by the UCLA Drug Abuse Research Center. Substance Use and Misuse. 1998;33(9):478–488. doi: 10.3109/10826089809059325. [DOI] [PubMed] [Google Scholar]
- Baker Michael, Gruber Jonathan, Milligan Kevin. Universal Child Care, Maternal Labor Supply, and Family Well-Being. Journal of Political Economy. 2008;116(4):709–745. [Google Scholar]
- Barnett W Steven. Long-Term Effects of Early Childhood Programs on Cognitive and School Outcomes. The Future of Children. 1995;5(3):25–50. [PubMed] [Google Scholar]
- Bartlett Maurice S. The Statistical Conception of Mental Factors. British Journal of Psychology. 1937;28(1):97–104. [Google Scholar]
- Belfield Clive R, Nores Milagros, Steven Barnett W, Schweinhart Lawrence. The High/Scope Perry Preschool Program: Cost-Benefit Analysis Using Data from the Age-40 Followup. Journal of Human Resources. 2006;41(1):162–190. [Google Scholar]
- Berrueta-Clement John R, Schweinhart Lawrence J, Barnett Steven W, Epstein Ann S, Weikart David P. Changed Lives: The Effects of the Perry Preschool Program on Youths Through Age 19. Ypsilanti, MI: High/Scope Press; 1984. [Google Scholar]
- Bodrova Elena, Leong Deborah J. Tools of the Mind: The Vygotskian Approach to Early Childhood Education. Upper Saddle River: Pearson Education, Inc; 2007. [Google Scholar]
- Borghans Lex, Duckworth Angela L, Heckman James J, Weel Baster. The Economics and Psychology of Personality Traits. Journal of Human Resources. 2008;43(4):972–1059. [Google Scholar]
- Borghans Lex, Golsteyn Bart HH, Heckman James J, Humphries John Eric. Identification Problems in Personality Psychology. In: Ferguson E, Heckman JJ, Corr P, editors. Personality and Individual Differences. Vol. 51. 2011a. pp. 315–320. Special Issue on Personality and Economics. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borghans Lex, Golsteyn Bart HH, Heckman James J, Humphries John Eric. Unpublished manuscript. University of Maastricht and University of Chicago; 2011b. IQ, Achievement, and Personality. (revised from the 2009 version) [Google Scholar]
- Bowles Samuel, Gintis Herbert. Schooling in Capitalist America: Educational Reform and the Contradictions of Economic Life. New York: Basic Books; 1976. [Google Scholar]
- Bowles Samuel, Gintis Herbert. Inheritance of Economic Status: Education, Class, and Genetics. In: Smelser Neil J, Baltes Paul B., editors. International Encyclopedia of the Social & Behavioral Sciences. Oxford, UK: Pergamon; 2001. pp. 4132–4141. [Google Scholar]
- Broidy Lisa M, Nagin Daniel S, Tremblay Richard E, Bates John E, Brame Bobby, Dodge Kenneth A, Fergusson David, Horwood John L, Loeber Rolf, Laird Robert, Lynam Donald R, Moffitt Terrie E, Pettit Gregory S, Vitaro Frank. Developmental Trajectories of Childhood Disruptive Behaviors and Adolescent Delinquency: A Six-Site, Cross-National Study. Developmental Psychology. 2003;39(2):222–245. doi: 10.1037//0012-1649.39.2.222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunnekreef J Agnes, De Sonneville Leo MJ, Althaus Monika, Minderaa Ruud B, Oldehinkel Albertine J, Verhulst Frank C, Ormel Johan. Information processing profiles of internalizing and externalizing behavior problems: evidence from a population-based sample of preadolescents. Journal of Child Psychology and Psychiatry. 2007;48(2):185–193. doi: 10.1111/j.1469-7610.2006.01695.x. [DOI] [PubMed] [Google Scholar]
- Bryant Alison L, Schulenberg John E, O’Malley Patrick M, Bachman Jerald G, Johnston Lloyd D. How Academic Achievement, Attitudes, and Behaviors Relate to the Course of Substance Use During Adolescence: A 6-Year, Multiwave National Longitudinal Study. Journal of Research on Adolescence. 2003;13(3):361397. [Google Scholar]
- Campbell Frances A, Ramey Craig T. Effects of Early Intervention on Intellectual and Academic Achievement: A Follow-Up Study of Children from Low-Income Families. Child Development. 1994;65(2):684–698. Children and Poverty. [PubMed] [Google Scholar]
- Campbell Frances A, Ramey Craig T. Cognitive and School Outcomes for High-Risk African-American Students at Middle Adolescence: Positive Effects of Early Intervention. American Educational Research Journal. 1995;32(4):743–72. [Google Scholar]
- Campbell Susan B, Pierce Elizabeth W, Moore Ginger, Marakovitz Susan, Newby Kristin. Boys’ externalizing problems at elementary school age: Pathways from early behavior problems, maternal control, and family stress. Development and Psychopathology. 1996;8:701–719. [Google Scholar]
- Carneiro Pedro, Heckman James J. Human Capital Policy. In: Heckman James J, Krueger Alan B, Friedman Benjamin M., editors. Inequality in America: What Role for Human Capital Policies? Cambridge, MA: MIT Press; 2003. pp. 77–239. [Google Scholar]
- Cattell Raymond B. The Scree Test for the Number of Factors. Multivariate Behavioral Research. 1966;1(2):245–276. doi: 10.1207/s15327906mbr0102_10. [DOI] [PubMed] [Google Scholar]
- Coie John, Terry Robert, Lenox Kari, Lochman John, Hyman Clarine. Childhood peer rejection and aggression as predictors of stable patterns of adolescent disorder. Development and Psychopathology. 1995;7:697–713. [Google Scholar]
- Conti Gabriella, Heckman James, Moon Seong, Pinto Rodrigo. Unpublished manuscript. The University of Chicago, Department of Economics; 2012. Long-term Health Effects of Early Childhood Interventions. [Google Scholar]
- Costello Anna B, Osborne Jason W. Best Practices in Exploratory Factor Analysis: Four Recommendations for Getting the Most From Your Analysis. Practical Assessment, Research & Evaluation. 2005;10(7) [Google Scholar]
- Cronbach Lee J. Coefficient Alpha and the Internal Structure of Tests. Psychometrika. 1951;16(3):297–334. [Google Scholar]
- Croon Marcel A. Using predicted latent scores in general latent structure models. Lawrence Erlbaum Associates, Inc; 2002. [Google Scholar]
- Cunha Flavio, Heckman James J. Formulating, Identifying and Estimating the Technology of Cognitive and Noncognitive Skill Formation. Journal of Human Resources. 2008;43(4):738–782. [Google Scholar]
- Cunha Flavio, Heckman James J. The Economics and Psychology of Inequality and Human Development. Journal of the European Economic Association. 2009;7(2–3):320–364. doi: 10.1162/jeea.2009.7.2-3.320. [DOI] [PMC free article] [PubMed] [Google Scholar]; Presented as the Marshall Lecture, European Economics Association; Milan, Italy. August 29, 2008. [Google Scholar]
- Cunha Flavio, Heckman James J, Schennach Susanne M. Estimating the Technology of Cognitive and Noncognitive Skill Formation. Econometrica. 2010;78(3):883–931. doi: 10.3982/ECTA6551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cymbalisty Bohdan Y, Schuck Solomon Z, Dubeck John A. Achievement level, institutional adjustment and recidivism among juvenile delinquents. Journal of Community Psychology. 1975;3(3):289–294. [Google Scholar]
- DeLong J Bradford, Magin Konstantin. The U.S. Equity Return Premium: Past, Present and Future. Journal of Economic Perspectives. 2009;23(1):193–208. [Google Scholar]
- Dewey John. Experience and Education. New York: Free Press; 1997. [Google Scholar]
- Diamond Adele, Barnett Steven, Thomas Jessica, Munro Sarah. Preschool Program Improves Cognitive Control. Science. 2007;318(5855):1387–1388. doi: 10.1126/science.1151148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Egeland Byron, Kalkoske Mark, Gottesman Natan, Erickson Martha F. Preschool behavior problems: Stability and factors accounting for change. Journal of Child Psychology and Psychiatry. 1990;31:891–910. doi: 10.1111/j.1469-7610.1990.tb00832.x. [DOI] [PubMed] [Google Scholar]
- Fabrigar Leandre R, Wegener Duane T, MacCallum Robert C, Strahan Erin J. Evaluating the Use of Exploratory Factor Analysis in Psychological Research. Psychological Methods. 1999;4:272–299. [Google Scholar]
- Flouri Eirini, Buchanan Ann. Father Involvement in Childhood and Trouble With the Police in Adolescence: Findings From the 1958 British Cohort. Journal of Interpersonal Violence. 2002;17(6):689–701. [Google Scholar]
- Gersten Joanne C, Langner Thomas S, Eisenberg Jeanne G, Simcha-Fagan Ora, McCarthy Elizabeth D. Stability and Change in Types of Behavioral Disturbance of Children and Adolescents. Journal of Abnormal Child Psychology. 1976;4(2) doi: 10.1007/BF00916516. [DOI] [PubMed] [Google Scholar]
- Goldberg Lewis R. The Structure of Phenotypic Personality Traits. American Psychologist. 1993;48(1):26–34. doi: 10.1037//0003-066x.48.1.26. [DOI] [PubMed] [Google Scholar]
- Gorsuch Richard. Factor Analysis. Hillsdale, NJ: Lawrence Erlbaum Associates; 1983. [Google Scholar]
- Gorsuch Richard L. Factor Analysis. In: Weiner Irving B, Freedheim Donald K, Schinka John A, Velicer Wayne F., editors. Handbook of psychology: Research methods in psychology. Vol. 2. Chapter 6. Hoboken, NJ: John Wiely & Sons, Inc; 2003. pp. 143–164. [Google Scholar]
- Gottfredson Linda S. Why g Matters: The Complexity of Everyday Life. Intelligence. 1997;24(1):79–132. [Google Scholar]
- Gray Susan W, Klaus Rupert A. The Early Training Project: A Seventh-Year Report. Child Development. 1970;41(4):909–924. [PubMed] [Google Scholar]
- Greenfeld Lawrence A. Alcohol and Crime: An Analysis of National Data on the Prevalence of Alcohol Involvement in Crime. US Department of Justice, Bureau of Justice Statistics Statistical data; 1998. p. 168632. [Google Scholar]
- Guttman Louis. Some necessary conditions for common-factor analysis. Psychometrika. 1954;19:149–161. [Google Scholar]
- Haavelmo Trygve. The Statistical Implications of a System of Simultaneous Equations. Econometrica. 1943;11(1):1–12. [Google Scholar]
- Hanushek Eric, Lindseth Alfred A. Schoolhouses, Courthouses, and Statehouses: Solving the Funding-Achievement Puzzle in America’s Public Schools. Princeton, NJ: Princeton University Press; 2009. [Google Scholar]
- Hanushek Eric, Woessmann Ludger. The Role of Cognitive Skills in Economic Development. Journal of Economic Literature. 2008;46(3):607–668. [Google Scholar]
- Heckman James J. Policies to Foster Human Capital. Research in Economics. 2000;54(1):3–56. [Google Scholar]
- Heckman James J. Schools, Skills and Synapses. Economic Inquiry. 2008;46(3):289–324. doi: 10.1111/j.1465-7295.2008.00163.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heckman James J, Pinto Rodrigo. Unpublished manuscript. University of Chicago; 2012a. Causal Analysis After Haavelmo: Definitions and a Unified Analysis of Identification. [Google Scholar]
- Heckman James J, Pinto Rodrigo. Unpublished manuscript. University of Chicago; 2012b. Econometric Mediation Analysis. [Google Scholar]
- Heckman James J, Kautz Tim. Hard evidence on soft skills. Labour Economics. 2012;19(4):451–464. doi: 10.1016/j.labeco.2012.05.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heckman James J, Stixrud Jora, Urzúa Sergio. The Effects of Cognitive and Noncognitive Abilities on Labor Market Outcomes and Social Behavior. Journal of Labor Economics. 2006;24(3):411–482. [Google Scholar]
- Heckman James J, Moon Seong Hyeok, Pinto Rodrigo, Savelyev Peter A, Yavitz Adam Q. Analyzing Social Experiments as Implemented: A Reexamination of the Evidence From the HighScope Perry Preschool Program. Quantitative Economics. 2010a;1(1):1–46. doi: 10.3982/qe8. First draft, September, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heckman James J, Moon Seong Hyeok, Pinto Rodrigo, Savelyev Peter A, Yavitz Adam Q. The Rate of Return to the HighScope Perry Preschool Program. Journal of Public Economics. 2010b;94(1–2):114–128. doi: 10.1016/j.jpubeco.2009.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herrnstein Richard J, Murray Charles A. The Bell Curve: Intelligence and Class Structure in American Life. New York: Free Press; 1994. [Google Scholar]
- Horn John L. A rationale and test for the number of factors in factor analysis. Psychometrika. 1965;30(2):179–185. doi: 10.1007/BF02289447. [DOI] [PubMed] [Google Scholar]
- Huesmann L Rowel, Eron Leonard D, Lefkowitz Monroe M, Walder Leopold O. Stability of Aggression Over Time and Generations. Developmental Psychology. 1984;20(6):1120–1134. [Google Scholar]
- Hurwicz Leonid. On the Structural Form of Interdependent Systems. In: Nagel E, Suppes P, Tarski A, editors. Logic, Methodology and Philosophy of Science. Stanford University Press; 1962. pp. 232–239. [Google Scholar]
- ICPSR. Head Start Impact Study, 2002–2006: Spring 2003 Center Director Interview Data Codebook. University of Michigan; Ann Arbor, MI: Inter-University Consortium for Political and Social Research (ICPSR); 2010. [Google Scholar]
- Jensen Arthur R. The g Factor: The Science of Mental Ability. West-port, CT: Praeger; 1998. [Google Scholar]
- Jimerson Shane, Egeland Byron, Teo Adrian. A Longitudinal Study of Achievement Trajectories: Factors Associated with Change. Journal of Educational Psychology. 1999;91(1):116–126. [Google Scholar]
- Jimerson Shane R, Ferguson Phillip, Whipple Angela D, Anderson Gabrielle E, Dalton Michael J. Exploring the Association Between Grade Retention and Dropout: A Longitudinal Study Examining Socio-Emotional, Behavioral, and Achievement Characteristics of Retained Students. The California School Psychologist. 2002;7:51–62. [Google Scholar]
- John Oliver P, Srivastava Sanjay. The Big Five Trait Taxonomy: History, Measurement and Theoretical Perspectives. In: Pervin LA, John OP, editors. Handbook of Personality: Theory and Research. Chapter 4. New York: The Guilford Press; 1999. pp. 102–138. [Google Scholar]
- Kaiser Henry F. The application of electronic computers to factor analysis. Educational and Psychological Measurement. 1960;20:141–151. [Google Scholar]
- Kaiser Henry F. A note on Guttman’s lower bound for the number of common factors. British Journal of Statistical Psychology. 1961;14:1–2. [Google Scholar]
- Klein Lawrence Robert, Goldberger Arthur Stanley. An Econometric Model of the United States, 1929–1952. Amsterdam: North-Holland Publishing Company; 1955. [Google Scholar]
- Knudsen Eric I, Heckman James J, Cameron Judy, Shonkoff Jack P. Economic, Neurobiological, and Behavioral Perspectives on Building America’s Future Workforce. Proceedings of the National Academy of Sciences. 2006;103(27):10155–10162. doi: 10.1073/pnas.0600888103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazar Irving, Darlington Richard, Murray Harry, Royce Jacqueline, Snipper Ann, Ramey Craig T. Lasting Effects of Early Education: A Report from the Consortium for Longitudinal Studies. Monographs of the Society for Research in Child Development. 1982;47(2/3):1–151. i+iii+v–vii+ix–xiv+ [Google Scholar]
- Loeber Rolf. The Stability of Antisocial and Delinquent Child Behavior: A Review. Child Development. 1982;53(6):1431–1446. [PubMed] [Google Scholar]
- McCrae Robert R, John Oliver P. An introduction to the five-factor model and its applications. Jounral of Personality. 1992;60(2):175–215. doi: 10.1111/j.1467-6494.1992.tb00970.x. [DOI] [PubMed] [Google Scholar]
- Moffitt Terrie E. Adolescence-Limited and Life-Course-Persistent Antisocial Behavior: A Developmental Taxonomy. Psychological Review. 1993;100(4):674–701. [PubMed] [Google Scholar]
- Nagin Daniel, Tremblay Richard E. Trajectories of Boys Physical Aggression, Opposition, and Hyperactivity on the Path to Physically Violent and Nonviolent Juvenile Delinquency. Child Development. 1999;70(5):1181–1196. doi: 10.1111/1467-8624.00086. [DOI] [PubMed] [Google Scholar]
- Nunnally Jum C, Bernstein Ira H. Psychometric Theory. New York: McGraw-Hill; 1994. [Google Scholar]
- Olweus Dan. Stability of Aggressive Reaction Patterns in Males: A Review. Psychological Bulletin. 1979;86(4):852–875. [PubMed] [Google Scholar]
- Onatski Alexei. Testing hypotheses about the number of factors in large factor models. Econometrica. 2009;77(5):14471479. [Google Scholar]
- Pearl Judea. Causality: Models, Reasoning, and Inference. 2. New York: Cambridge University Press; 2009. [Google Scholar]
- Pearl Judea. The Mediation Formula: A Guide to the Assessment of Causal Pathways in Nonlinear Models.” Forthcoming in. Causality: Statistical Perspectives and Applications 2011 [Google Scholar]
- Piaget Jean, Inhelder Bärbel. The Psychology of the Child. New York: Basic Books; 2000. [Google Scholar]
- Ramey Craig T, Ramey Sharon Landesman. Children’s Right to Thrive: The Foundational Years. Georgetown University; 2010. Unpublished manuscript. [Google Scholar]
- Razzino Brian E, Ribordy Sheila C, Grant Kathryn, Ferrari Joseph R, Bowden Blake S, Zeisz Jennifer. Gender-related processes and drug use: Self-expression with parents, peer group selection, and achievement motivation. Adolescence. 2004;39(153):167–177. [PubMed] [Google Scholar]
- Reynolds Arthur J, Temple Judy A, Robertson Dylan L, Mann Emily A. Long-term Effects of an Early Childhood Intervention on Educational Achievement and Juvenile Arrest: A 15-Year Follow-up of Low-Income Children in Public Schools. JAMA. 2001;285(18):2339–2346. doi: 10.1001/jama.285.18.2339. [DOI] [PubMed] [Google Scholar]
- Richman Naomi, Stevenson James E, Graham Philip Jeremy. Preschool to school: A behavioural study. San Diego: Academic Press; 1982. [Google Scholar]
- Robins Lee N. Sturdy childhood predictors of adult antisocial behaviour: replications from longitudinal studies. Psychological Medicine. 1978;8:611–622. doi: 10.1017/s0033291700018821. [DOI] [PubMed] [Google Scholar]
- Santrock John W. A Topical Approach to Life-Span Development. 4. New York: McGraw-Hill; 2008. [Google Scholar]
- Schweinhart Lawrence J, Weikart David P. Effects of the Perry Preschool Program on Youths Through Age 15. Journal of Early Intervention. 1981;4(1):29–39. [Google Scholar]
- Schweinhart Lawrence J, Montie Jeanne, Xiang Zongping, Steven Barnett W, Belfield Clive R, Nores Milagros. Lifetime Effects: The High/Scope Perry Preschool Study Through Age 40. Ypsilanti, MI: High/Scope Press; 2005. [Google Scholar]
- Schweinhart LJ, Barnes Helen V, Weikart David. Significant Benefits: The High-Scope Perry Preschool Study Through Age 27. Ypsilanti, MI: High/Scope Press; 1993. [Google Scholar]
- Segal Carmit. Classroom Behavior. Journal of Human Resources. 2008;43(4):783–814. [Google Scholar]
- Segal Carmit. Misbehavior, Education, and Labor Market Outcomes. Universitat Pompeu Fabra, Department of Economics and Business; 2009. Unpublished manuscript. [Google Scholar]
- Shonkoff Jack P, Phillips Deborah. From Neurons to Neighborhoods: The Science of Early Child Development. Washington, DC: National Academy Press; 2000. [PubMed] [Google Scholar]
- Simons-Morton Bruce. Prospective association of peer influence, school engagement, drinking expectancies, and parent expectations with drinking initiation among sixth graders. Addictive Behaviors. 2004;29(2):299–309. doi: 10.1016/j.addbeh.2003.08.005. [DOI] [PubMed] [Google Scholar]
- Sylva Kathy. Lasting Differences: The High/Scope Preschool Curriculum Comparison Study through Age 23. High/Scope Press; 1997. The Quest for Quality in Curriculum. A commentary to the book by Lawrence J. Schweinhart & David P. Weikart, 1997. [Google Scholar]
- Tabachnick Barbara G, Fidell Linda S. Chapter Principal components and factor analysis. 4. Boston: Allyn and Bacon; 2001. Using multivariate statistics; pp. 582–633. [Google Scholar]
- Terman Lewis Madison, Merrill Maud A. Stanford-Binet Intelligence Scale: Manual for the Third Revision Form L-M. Boston: Houghton Mifflin; 1960. [Google Scholar]
- Theil Henri. Economic Forecasts and Policy. Amsterdam: North-Holland Publishing Company; 1958. [Google Scholar]
- Thompson Bruce. Exploratory and confirmatory factor analysis : understanding concepts and applications. Washington, DC: American Psychological Association; 2004. [Google Scholar]
- Tough Paul. Can the Right Kinds of Play Teach Self-Control? New York Times; 2009. [Google Scholar]
- Vaughan Ellen L, Corbin William R, Fromme Kim. Academic and social motives and drinking behavior. Psychology of Addictive Behaviors. 2009;23(4):564–576. doi: 10.1037/a0017331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vinter RD, Sarri Rosemary C, Vorwaller Darrel J, Shafer Walter E. Pupil Behavior Inventory: A Manual for Administration and Scoring. Ann Arbor, MI: Campus Publishers; 1966. [Google Scholar]
- Vygotsky Lev S. Thought and language. In: Kozulin Alex., editor. Chapter The genetic roots of thought and speech. Cambridge: MIT Press; 1986. [Google Scholar]
- Wansbeek Tom, Meijer Erik. Measurement Error and Latent Variables in Econometrics. Vol. 37. Washington D.C: Advanced Textbooks in Economics; 2000. [Google Scholar]
- Wasserman Larry. All of Nonparametric Statistics. Springer Texts in Statistics. New York: Springer Science+Business Media; 2006. [Google Scholar]
- Weikart David P. Preliminary Results From a Longitudinal Study of Disadvantaged Preschool Children. Presented at the 1967 convention of the Council for Exceptional Children; St. Louis, MO. 1967. Unpublished manuscript, ERIC No. ED 030 490. [Google Scholar]
- Weikart David P, Bond James T, McNeil Judy T. The Ypsilanti Perry Preschool Project: Preschool Years and Longitudinal Results Through Fourth Grade. Ypsilanti, MI: Monographs of the High/Scope Educational Research Foundation; 1978. [Google Scholar]
- White Jennifer L, Moffitt Terrie E, Earls Felton, Robins Lee, Silva Phil A. How Early Can We Tell?: Predicators of Childhood Conduct Disorder and Adolescent Delinquency. Criminology. 1990;28:507–533. [Google Scholar]
- Yoshikawa Hirokazu. Long-Term Effects of Early Childhood Programs on Social Outcomes and Delinquency. The Future of Children. 1995;5(3):51–75. [PubMed] [Google Scholar]
- Zimmerman Marc A, Schmeelk-Cone Karen H. A longitudinal analysis of adolescent substance use and school motivation among African American youth. Journal of Research on Adolescence. 2003;13(2):185–210. [Google Scholar]
- Zoccolillo Mark, Pickles Andrew, Quinton David, Rutter Michael. The outcome of childhood conduct disorder: implications for defining adult personality disorder and conduct disorder. Psychological Medicine. 1992;22:971–986. doi: 10.1017/s003329170003854x. [DOI] [PubMed] [Google Scholar]
- Zwick William R, Velicer Wayne F. Comparison of five rules for determining the number of components to retain. Psychological Bulletin. 1986;99(3):432–442. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.