Electron Spin-Lattice Relaxation Mechanisms of Rapidly-Tumbling Nitroxide Radicals

Abstract

Electron spin relaxation times at 295 K were measured at frequencies between 250 MHz and 34 GHz for perdeuterated 2,2,6,6-tetramethyl-4-piperidone-1-oxyl (PDT) in five solvents with viscosities that result in tumbling correlation times, τ_R, between 4 and 50 ps and for three ¹⁴N/¹⁵N pairs of nitroxides in water with τ_R between 9 and 19 ps. To test the impact of structure on relaxation three additional nitroxides with τ_R between 10 and 26 ps were studied. In this fast tumbling regime T₂⁻¹ ∼ T₁⁻¹ at frequencies up to about 9 GHz. At 34 GHz T₂⁻¹ > T₁⁻¹ due to increased contributions to T₂⁻¹ from incomplete motional averaging of g-anisotropy, and T₂⁻¹ − T₁⁻¹ is proportional to τ_R. The contribution to T₁⁻¹ from spin rotation is independent of frequency and decreases as τ_R increases. Spin rotation dominates T₁⁻¹ at 34 GHz for all τ_R studied, and at all frequencies studied for τ_R = 4 ps. The contribution to T₁⁻¹ from modulation of nitrogen hyperfine anisotropy increases as frequency decreases and as τ_R increases; it dominates at low frequencies for τ_R > ∼ 15 ps. The contribution from modulation of g anisotropy is significant only at 34 GHz. Inclusion of a thermally-activated process was required to account for the observation that for most of the radicals, T₁⁻¹ was smaller at 250 MHz than at 1 to 2 GHz. The significant ¹⁵N/¹⁴N isotope effect, the small H/D isotope effect, and the viscosity dependence of the magnitude of the contribution from the thermally-activated process suggest that it arises from intramolecular motions of the nitroxide ring that modulate the isotropic A values.

1. Introduction

Nitroxide T₂ has been studied extensively, both experimentally and theoretically, to understand motional dynamics in fluid solutions [1-4]. Early studies of T₁ focused primarily on ∼9.5 GHz [5-7]. The utility of T₁ to measure oxygen concentrations in membranes [8-10] and tissues [11] and the use of nitroxides for in vivo imaging [12,13] has motivated characterization of the frequency dependence of T₁. In 1990 it was reported that T₁ was smaller at 2.5 GHz than at ∼9.5 GHz for stearic acid spin labels in lipids at 27°C [14]. Subsequently, it was shown that T₁ for spin-labeled lipids and for the small molecules CTPO (3-carbamoyl-2,2,5,5-tetramethyl-3-pyrroline-1-oxyl) and tempone (2,2,6,6-tetramethyl-4-piperidone-1-oxyl) increased from ca. 2.5 GHz to 35 GHz, but then became smaller at ca. 95 GHz [15,16]. The frequency dependence up to 35 GHz was modeled in terms of spin rotation, modulation of nitrogen hyperfine anisotropy and g anisotropy, and generalized spin diffusion [17]. Multifrequency measurements for triarylmethyl (trityl) radicals showed that modulation of intra- and inter-molecular electron-proton interactions had significant impact on T₁ at 250 MHz but not at ∼9.5 GHz [18], which highlights the need to study the frequency dependence of relaxation.

Extrapolation of the trend for nitroxide T₁ between 2.5 and 35 GHz [15,16] predicts that in the frequency range used for in vivo EPR (250 MHz to 1 GHz) T₁ would be less than 0.1 μs. However, it has long been known that lines in the spectra of Fremy's salt ((SO₃)₂NO²⁻) in aqueous solution at 60 MHz are Lorentzian with T₁= T₂ = 0.5 μs [19]. Rapid-scan EPR of perdeuterated 2,2,6,6-tetramethyl-4-piperidone-1-oxyl (PDT, 1a) in aqueous solution at 250 MHz [20] found T₂ = 0.5 μs. Since T₂ ≤ T₁, T₂ puts a lower limit on T₁. These results motivate examination of nitroxide T₁ at frequencies lower than 2.5 GHz to determine the dominant relaxation mechanisms at these lower frequencies.

Recently we reported T₁ and T₂ for aqueous solutions of a nitronyl nitroxide and of PDT at five frequencies between 250 MHz and 34 GHz [21] in the fast motional regime where the tumbling correlation time, τ_R, is less than about 25 ps. These studies have now been extended to a wider range of nitroxides and solvents to investigate i) the relative importance of spin rotation and modulation of nitrogen hyperfine anisotropy when τ_R = 4 to 50 ps at ambient temperature, ii) whether additional mechanisms contribute to relaxation at frequencies lower than ∼9.5 GHz, and iii) the thermally-activated process that is proposed to have maximum impact on T₁ at 1 to 2 GHz, and has been observed previously in both the fast [21] and slow tumbling regimes [22]. T₁ and T₂ were measured by pulsed methods for the nitroxides shown in Figure 1, at frequencies between 250 MHz and 34 GHz.

Figure 1.

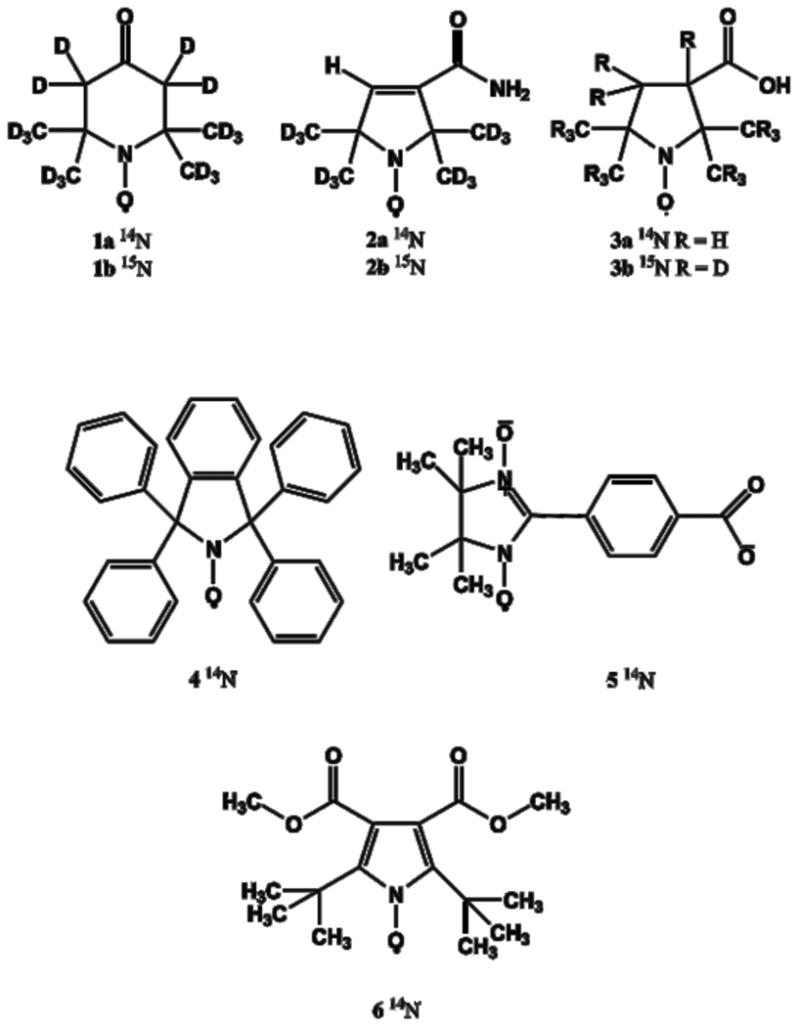
Nitroxide Structures.

Spin-lattice relaxation mechanisms

The importance of spin-rotation (Eq. 1) in the fast tumbling regime was recognized in early discussions of T₁⁻¹ for nitroxides and semiquinones [23-25].

$${({T_1}^{\mathit{\text{SR}}})}^{-1}=\frac{{\displaystyle \sum _{i=1}^3}{(g_i-g_e)}^2}{9{\tau }_R}$$ (1)

where i = x,y,z and g_e is 2.0023. (T₁^SR)⁻¹ is independent of resonance frequency and decreases as τ_R increases.

Modulation of the large anisotropic (dipolar) nitrogen nuclear hyperfine coupling by molecular tumbling (the END process, Eq. 2) is a major contributor to nitroxide relaxation in certain motional regimes [5,6,17].

$${({T_1}^A)}^{-1}=\frac{2}{9}I(I+1)\sum _i{(A_i-\overline{A})}^{2}J(\omega )$$ (2)

where A_i is a component of the nitrogen hyperfine coupling in angular frequency units, Ā is the average nitrogen hyperfine, I is the nitrogen nuclear spin, ω is the resonance frequency, and J(ω) is the Bloembergen, Purcell, Pound (BPP) spectral density function (Eq. 3).

$$J(\omega )=\frac{{\tau }_R}{1+{(\omega {\tau }_R)}^2}$$ (3)

In the rapid-tumbling regime the BPP spectral density function is indistinguishable from the Cole-Davidson spectral density function that has been found to give better agreement than BPP with the temperature dependence of nitroxide T₁⁻¹ [26,27].

The frequency dependence of (T₁^A)⁻¹ depends on τ_R (Eq. 3). For τ_R in the range of 4 to 50 ps, ωτ_R changes from < 1 at 250 MHz to > 1 at 34 GHz. For ωτ_R > 1, (T₁^A)⁻¹ increases as ω decreases. For ωτ_R << 1, (T₁^A)⁻¹ is independent of ω and increases as τ_R increases. Because (T₁^A)⁻¹ is proportional to γ² I(I+1), where γ is the gyromagnetic ratio, the ratio [(T₁^A)⁻¹(¹⁴N)]/[(T₁^A)⁻¹(¹⁵N)] = 1.36. The ¹⁵N/¹⁴N isotope effect on T₁⁻¹ provides a test of the contribution from the END mechanism [27,28].

Modulation of g anisotropy by molecular tumbling is described by Eq. (4) [5,6].

$${({T_1}^g)}^{-1}=\frac{2}{5}{(\frac{{\mu }_B\omega }{g\beta })}^2\left\{\frac{{(\mathrm{\Delta }g)}^2}{3}+{(\delta g)}^2\right\}J(\omega )$$ (4)

where Δg = g_zz − 0.5(g_xx+g_yy), δg = 0.5(g_xx − g_yy), and μ_B is the electron Bohr magneton. This contribution enhances relaxation for radicals with larger g anisotropy, particularly at higher microwave frequency.

The enhancement of electron spin T₁⁻¹ by thermally-activated methyl rotation has been demonstrated in a variety of solid samples [29-32]. Nuclear spin-lattice relaxation enhancement by thermally-activated processes has been studied extensively in NMR [33-36]. For nitroxides in viscous water/glycerol solutions at 1.9, 3.1, and 9.2 GHz at room temperature, T₁⁻¹ was larger than predicted by Eqs. (1) – (4) [22]. The additional process dominated relaxation for τ_R > ∼3×10⁻⁹ s, and the magnitude of the contribution increased with decreasing frequency between 9.2 and 1.9 GHz. This contribution was modeled as a thermally-activated process, Eq. (5).

$${({T_1}^{\mathit{\text{therm}}})}^{-1}=C_{\mathit{\text{therm}}}\left(\frac{\omega }{{\omega }_{\mathit{\text{ref}}}}\right)\frac{{\tau }_{\mathit{\text{therm}}}}{1+{(\omega {\tau }_{\mathit{\text{therm}}})}^2}$$ (5)

where τ_therm = τ_c⁰ exp(E_a/RT), E_a is the activation energy, τ_c⁰ is the pre-exponential factor, C_therm is the coefficient for the contribution of the thermally-activated process, and ω_ref = 9.5 GHz. Data as a function of temperature would be needed to separately evaluate E_a and τ_c⁰. Since experiments were performed at a single temperature, these parameters were combined into a single variable τ_therm, which was found to be about 1.0×10⁻¹⁰ s. This thermally-activated process was also required to model the frequency dependence of T₁⁻¹ for two nitroxides in the rapid-tumbling regime [21].

Nitroxides studied

Several of the radicals selected for this study (Figure 1) have been used for in vivo imaging: PDT (1a) to monitor redox activity [37], mono-hydrogenated deuterated CTPO (mHCTPO, 2a) [38] for in vivo imaging of local oxygen concentration [39,40], and 3-carboxy-2,2,5,5-tetramethyl-1-pyrrolidinyloxyl radical (carboxy-proxyl, 3a) for in vivo O₂ quantitation in mouse brain [41-43]. T₁ and T₂ for 1a – 3a, along with their ¹⁵N derivatives (denoted as 1b-3b) have been investigated previously at ∼9.5 GHz [28]. Other nitroxides with different ring structures, and g- and A- anisotropies were selected for comparison. The phenyl isoindoline nitroxide (4)[26] contains no methyl groups and the central ring is expected to be more rigid than in 1a – 3a. Nitroxides that are similar to 4, including some that are isotopically labeled, have recently been investigated for in vivo O₂ quantitation [44,45]. The nitronyl nitroxide 5 was included because the nitrogen hyperfine splittings are smaller than for 1a – 3a and the g anisotropy is larger [21]. 6 has smaller nitrogen hyperfine splittings than 1a – 3a due to extensive delocalization of the unpaired electron into the aromatic ring, the ring is expected to be more rigid, and the four ring methyls of 1a – 3a are replaced by two t-butyl groups.

Relaxation times T₁ and T₂ for 1 to 6 were measured at frequencies between 250 MHz and 34 GHz. For 1a τ_R was varied by changing solvent, including both nonpolar organics and water:glycerol mixtures.

2. Experimental

Samples

1b with > 98% isotope purity were purchased from CDN Isotopes (Quebec, Canada). 1a [28], 3a [46], 3b [46], 4 [26], and 5 [21] were prepared as reported. 2a and 2b were prepared as previously reported [47] and provided by Prof. Howard Halpern (University of Chicago). 6 was prepared as reported [48], and was a gift from Prof. Andre Rassat.

For slower tumbling radicals, 4, 1a in 44% glycerol, and 1a in 69% glycerol, solutions were 0.2 mM. Most solutions were 0.4 to 0.5 mM (Table 1). Between 0.2 mM and 0.5 mM in aqueous solution of 1a – 3a in water there is only a 5 to 15% increase in T₁⁻¹ due to Heisenberg exchange [28], so the higher concentrations were used to improve signal-to-noise (S/N), particularly at the lower frequencies. The contribution from Heisenberg exchange is expected to be independent of resonance frequency so it will not alter the frequency dependence of T₁⁻¹ that is the focus of this study.

Table 1. Nitroxide Parameters.

	FW	Solvent	Conc. mM	τC ps	Aiso G	Axx G	Ayy G	Azz G	gxx	gyy	gzz	Lit.
1a	186	Toluene	0.4	4	14.5	4.1	5.1	33.6	2.0094	2.0063	2.0023	[67]
1a	186	Water	0.5	9	16.3	5.5	6.3	35.9	2.0092	2.0061	2.0022	[56]
1a	186	Light Mineral Oil	0.5	9	14.5	4.1	5.1	33.6	2.0094	2.0063	2.0023	[67]
1a	186	44% Glycerol	0.2	19	16.3	5.5	6.3	35.9	2.0092	2.0061	2.0022	[56]
1a	186	69% Glycerol	0.2	50	16.3	5.5	6.3	35.9	2.0092	2.0061	2.0022	[56]
1b	187	Water	0.5	9	22.6	7.7	8.8	50.3	2.0092	2.0061	2.0022	[56]
2a	195	Water	0.5	13	16.3	5.5	6.3	35.9	2.0092	2.0061	2.0022	[68]
2b	196	Water	0.5	13	22.6	7.7	8.8	50.3	2.0092	2.0061	2.0022	[68]
3a	186	Water	0.5	19	16.3	5.5	6.3	35.9	2.0092	2.0061	2.0022	[68]
3b	202	Water	0.5	19	22.9	7.7	8.8	50.3	2.0092	2.0061	2.0022	[68]
4	410	Toluene	0.2	26	13.4	3.2	3.2	31.8	2.0090	2.0058	2.0020	[26,27]
5	276	2 mM NaOH	0.5	25	8.1	3.6	3.6	18.6	2.0110	2.0065	2.0021	[69]
6	310	Toluene	0.5	10	4.7	0.4	0.4	13.2	2.0094	2.0060	2.0024	[26]

O₂ was removed by one of three methods, depending on sample tube size [21]. Briefly, for large-diameter samples used at lower microwave frequencies, the samples were bubbled with N₂ and then flame-sealed. Samples in 4 or 6 mm OD tubes for experiments at 1 to 3 GHz were degassed by several freeze-pump-thaw cycles. N₂ was passed over the outside of samples in thin Teflon tubing supported in quartz EPR tubes for experiments at 9 or 34 GHz.

Spectroscopy

Relaxation times were measured at 250 MHz [49], L-band (1.0, 1.5, and 1.9 GHz) [50], S-band (2.5 and 3.0 GHz) [50], X-band (∼9.5 GHz) [51] and Q-band (34.5 GHz) using locally-constructed pulsed EPR spectrometers and resonators and on a Bruker E580 with 9 and 34 GHz bridges and resonators [21]. Measurements were made at 21° ± 2° C. The relaxation times for 1a in 69% glycerol and for 4 at ∼640 MHz were obtained on a spectrometer that will be described separately. Each measurement was performed at least three times. The S/N for T₁ was 80-100, except for 1a in 69% glycerol at 630 MHz and for 4 at 640 MHz and 250 MHz where S/N was lower because relaxation times were of the same order as the resonator ringdown time. T₂ was measured as the time constant of 2-pulse echo decays. Most T₁ measurements were by 3-pulse inversion recovery, and some were also measured by long-pulse saturation recovery. The spin echo decay and saturation recovery curves fit well with a single exponential, using a least squares criterion. A potential complication in the measurement of T₁ by inversion recovery is the need to distinguish T₁ from nitrogen T_1N, which also can contribute to the return of magnetization to equilibrium [16]. At long τ_R, T_1N is shorter than T₁, but becomes equal to T₁ for short τ_R [6]. If the S/N is low, it may be difficult to distinguish between one- and two-component decays. At lower resonance frequencies, the inversion recovery curves fit well with a single exponential, as expected when ωτ_R ≤ ∼1 [6]. For slower tumbling radicals at ∼9.5 GHz and most radicals at 34 GHz, two components were observed in the fits to the inversion recovery curves, as expected for ωτ_R > 1 [52,53]. The longer relaxation time is assigned as T₁. The uniform penalty (UPEN) fitting procedure [54,55] was used to confirm the presence of two contributions to the exponential decays at 34 GHz. Values of T₁ at ∼9.5 GHz for 1a in 69% glycerol, 3a, and 4 obtained by saturation recovery with pump times that are long relative to T₁ were in good agreement with values obtained by inversion recovery, which confirmed that the inversion recovery experiments were accurately reporting T₁.

Values of T₁ and T₂ for each of the nitrogen hyperfine lines at each of the frequencies studied are listed in supplementary Tables S1 and S2. As observed previously, there is a systematic m_I dependence of both T₁ and T₂ [28]. Values of T₁ decrease in the order m_I = +1 (low-field) ≥ m_I = 0 (center field) > m_I = −1 (high-field) for ¹⁴N and m_I = 0.5 > m_I= −0.5 for ¹⁵N (Table S1). In tumbling regies where the END process (Eq. 2) is the dominant contribution to T₁⁻¹ the ratio of T₁ for ¹⁴N m_I = 1 to m_I = −1 is about 1.2, which is in good agreement with prior results [28]. The m_I dependence is smaller at concentrations above 0.5 mM (Table S3) where Heisenberg exchange may be significant, and in tumbling regimes where the END mechanism (Eq. 2) is a smaller fraction of the combined contributions to T₁⁻¹ Since the available models for the END mechanism do not include an m_I dependent contribution, the values of T₁⁻¹ plotted in Figures 2, 4, and 5, and included in the modeling, are m_I = 0 (¹⁴N) or the average for m_I = ±0.5 (¹⁵N).

Figure 2.

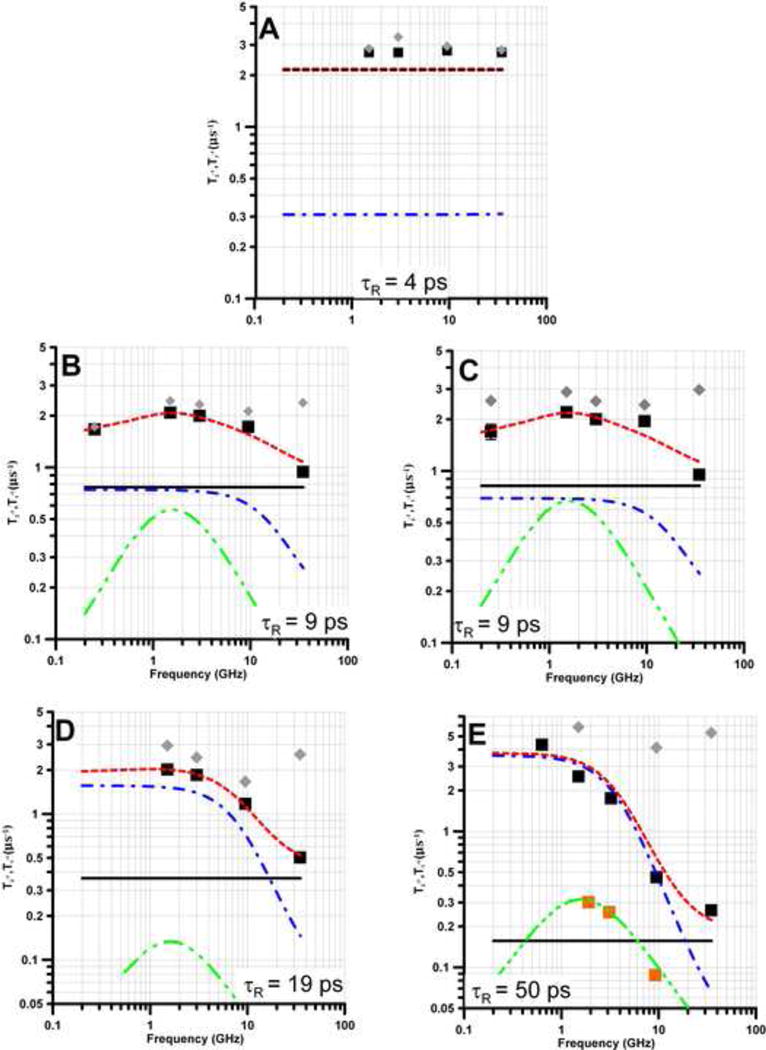
Frequency Dependence of T₁⁻¹ (■) and T₂⁻¹ ( ) for PDT (1a) in solvents that result in τ_R between 4 and 50 ps. (A) toluene, (B) water, (C) light mineral oil, (D) 44% glycerol in water, and (E) 69% glycerol in water. Spin lattice relaxation is modeled as the sum ( ) of contributions from spin rotation (Eq. 1, ), the modulation of g- and A-anisotropy (Eq. 2 - 4, ), and a thermally-activated process (Eq. 5, ). In (E) the gold squares and fit line are the contribution from the thermally-activated process observed previously for τ > ∼ 3×10⁻⁹ s [22]. In (A) the contribution from spin rotation is indistinguishable from the fit line.

Figure 4.

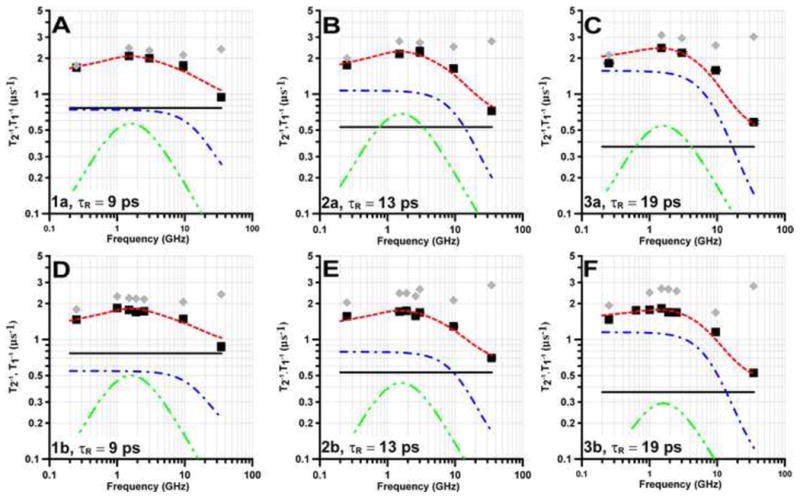
Frequency dependence of T₁⁻¹ (■) and T₂⁻¹ ( ) in water for the m_I = 0 lines of (A) 1a, (B) 2a, (C) 3a or the m_I = ± 0.5 lines of (D) 1b, (E) 2b, and (F) 3b. Spin lattice relaxation is modeled as the sum ( ) of contributions from spin rotation (Eq. 1, ), the modulation of g- and A- anisotropy (Eq. 2 – 4, ) and a thermally-activated process (Eq. 5 ).

Figure 5.

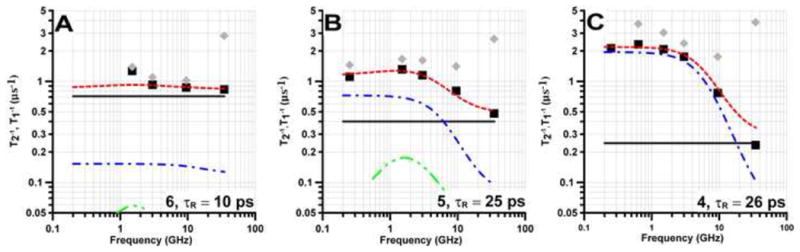
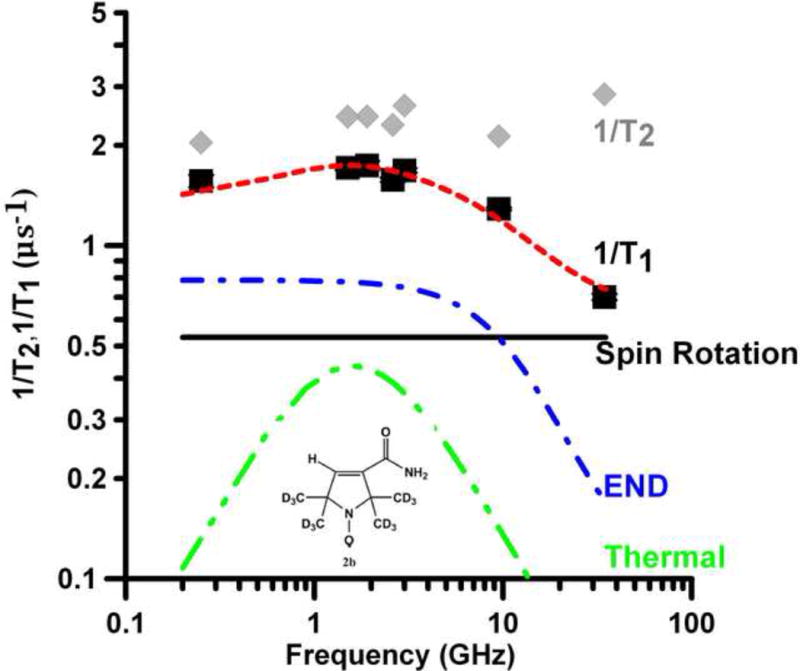
Frequency dependence of T₁⁻¹ (■) and T₂⁻¹( ) for the m_I =0 lines of (A) 6 in toluene, (B) 5 in 2 mM aqueous NaOH and (C) 4 in toluene. Spin lattice relaxation is modeled as the sum ( ) of contributions from spin rotation ( ), the modulation of g- and A- anisotropy ( ) and a thermally activated process ( ).

Modeling the frequency dependence of 1/T₁

The g- and nitrogen A-values are summarized in Table 1. A-values for 1b to 3b were calculated from the values for the ¹⁴N analogs multiplied by the ratio of the gyromagnetic ratios for ¹⁵N/¹⁴N = 1.40. For 6 immobilized in sucrose octaacetate, simulation of the ∼9.5 GHz spectrum (unpublished data) gave a well-defined A_zz = 13.2 G. Values of A_xx = A_yy = 0.4 G were estimated by assuming that A_xx = A_yy and using A_iso = 4.7 G in toluene. Values of τ_R for all radicals, except 5, were calculated from the m_I dependence of T₂ at X-band [28]. The uncertainties in τ_R are about ±20%. The value of τ_R = 4 ps for PDT (1a) in toluene is in good agreement with the literature value of 5 ps [56]. The value of τ_R for 5 is taken from [21]. The T₁⁻¹ data in Figures 2, 4, and 5 are modeled as the sum of contributions from spin rotation ((Eq. 1, solid black line), modulation of A- and g-anisotropy by molecular tumbling (Eq. 2 – 4, blue dashed line) and a thermally-activated process (Eq. 5, green dashed line). The sum of the contributions is the red fit line. The contribution from modulation of g-anisotropy is negligible except at 34 GHz. For 1 - 4 and 6, there are no adjustable parameters in the calculations of the contributions to relaxation from Eq. (1) – (4). The only adjustable contribution to T₁⁻¹ was from the thermally-activated process, Eq. (5). Independent variation of C_therm and τ_therm did not give significantly improved fit to the data, so τ_therm was fixed at 1.0×10⁻¹⁰ s [21]. The contribution of the END process for nitronyl nitroxide 5 was discussed in [21].

3. Results and Discussion

Much of the prior work on electron spin lattice relaxation of nitroxides has focused on lower temperatures and/or relatively long tumbling correlation times [5,6,15,22,26,27,56,57]. Understanding relaxation in the faster tumbling regime provides exciting new insights for designing small molecule spin probes for applications to in vivo imaging and dynamic nuclear polarization (DNP).

Relaxation times were measured at 0.25, 1.5, 2.5 to 3.0, 9.4 to 9.5 and 34 GHz, with the exception of 1a in 69% glycerol for which the lowest frequency data were measured at ca. 0.63 GHz (Figures 2). For 1b – 3b relaxation times also were measured at 1.0 and 1.9 GHz. Relaxation times for 1a in water and for 5 are reproduced from [21]. At ∼9.5 and 34 GHz the T₁ for 1a in water is in good agreement with values for 0.5 mM natural abundance tempone reported in [15]. The values of T₁ reported for tempone in water at 2.5 – 3.2 GHz [15] are about 40% shorter than observed for 1a. The greater difference at lower frequencies may be due in part to the factor of ∼1.5 H/D isotope effects previously reported for nitroxide T₁ in solution [22,27]. For the natural isotope abundance analogue of 2a, the values of T₁ reported in [15] are about 10% longer than observed for 2a in this study, which is smaller than the H/D isotope effect expected [22].

Interpretation of frequency dependence of relaxation

The frequency dependence of T₁⁻¹ (■) and T₂⁻¹ ( ) for PDT (1a) in five solvents (toluene, water, light mineral oil, 44% glycerol in water, and 69% glycerol in water) is shown in Figure 2. For τ_R < ∼20 ps and resonance frequencies ≤ 9 GHz, T₁⁻¹ ∼ T₂⁻¹ as expected in the fast tumbling regime. At 34 GHz, T₂⁻¹ − T₁⁻¹ is substantial (Figure 2) due to increased contributions from incomplete motional averaging of g-anisotropy. The slope of the plot of T₂⁻¹ − T₁⁻¹ vs τ_R is 2.3×10¹⁷ s⁻² (Figure 3). Calculation of the predicted slope of the plot based on the A, B, and C terms in the Kivelson model of linewidths [58,59] and typical g and A hyperfine anisotropy predicts a slope of 1.6×10¹⁷ s⁻². Given the approximations in the model and the range of solvents and nitroxides included in the plot, the agreement is good, which lends credence to the values of τ_R.

Figure 3.

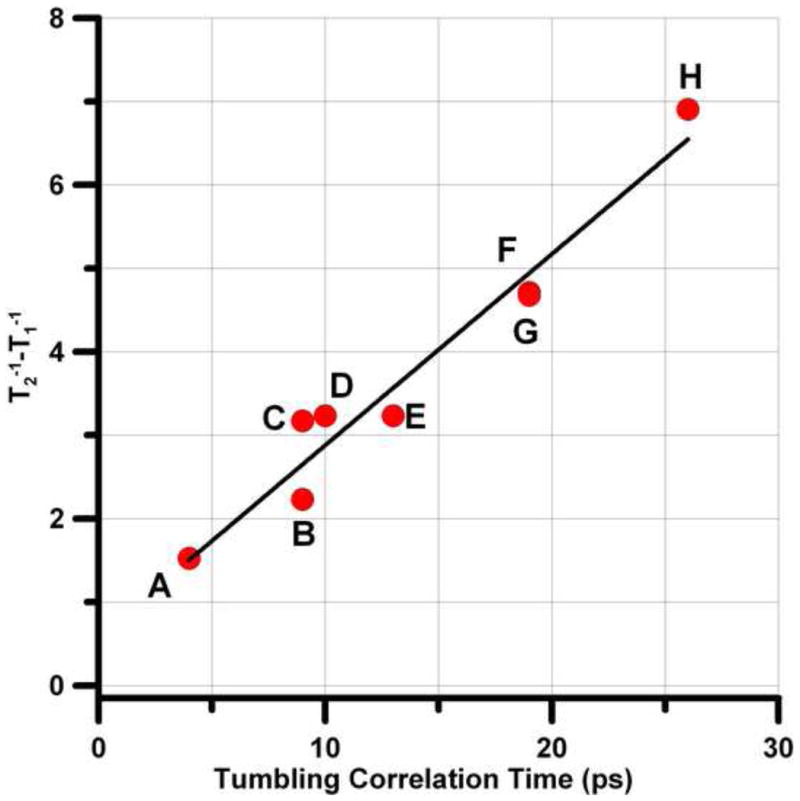
Dependence of T₂⁻¹ − T₁⁻¹ on τ_R for the high-field ¹⁴N hyperfine line at Q-band for: A, 1a in toluene; B, 1a in water; C, 1a in light mineral oil; D, 6 in toluene; E, 2a in water; F, 3a in water; G, 1a in 44% glycerol; H, 4 in toluene. The slope of the least-squares fit line is 2.3×10¹⁷ s⁻².

As τ_R increases the frequency-independent contribution from spin rotation (Eq. (1) decreases (Figure 2). At τ_R = 4 ps spin rotation dominates T₁⁻¹ and relaxation is independent of frequency (Figure 2A). The agreement between experiment and calculation at τ_R = 4 ps is not as good as at longer τ_R. For the small PDT molecule (1a) in low-viscosity toluene, Heisenberg exchange due to nitroxide-nitroxide collision, which is not included in the simulation, may contribute more to relaxation than for other samples studied. In contrast to the dependence for spin rotation, as τ_R increases the contribution from modulation of A and g-anisotropy increases. As τ_R increases from 4 ps to 50 ps, the relaxation at frequencies less than 34 GHz changes from domination by spin rotation to domination by modulation of A anisotropy. The frequency at which the contribution from modulation of A changes from frequency independent to frequency dependent is a strong function of τ_R (Eq. 2-4). The longer the value of τ_R, the lower the frequency at which the change in slope occurs. Thus the agreement between the observed and calculated frequency dependence of T₁⁻¹ is a validation of the model and of the values of τ_R. For τ_R = 9 ps, in either water (Fig. 2B) or light mineral oil (Fig. 2C), T₁^-1 is smaller at 250 MHz than at 1-2 GHz. This frequency dependence is not predicted by the spin rotation (Eq. 1) or modulation of A or g-anisotropy (Eq. 2-4). Modeling of the relaxation rates therefore included a contribution from a thermally-activated process, Eq. (5). The effect of the thermally-activated process is maximum when ω = 1/τ_therm, which was observed to occur at about 1.6 GHz (Fig. 2 and 4), and corresponds to τ_therm = 1.0×10⁻¹⁰ s. This is the same value of τ_therm that was used to model the frequency dependence of T₁⁻¹ for tempol with τ_R > ∼3×10⁻⁹ s (300 ps) in viscous water:glycerol mixtures [22]. The value of τ_therm was fixed at 1.0×10⁻¹⁰ s and the coefficient C_therm (Table 3) was adjusted to match the experimental data for T₁⁻¹ The value of C_therm was similar in water (Fig. 2B) or light mineral oil (Fig. 2C), which indicates that the process does not require a protic solvent. C_therm is smaller in 44% glycerol (Fig. 2D), which demonstrates a dependence on viscosity. For comparison, the contributions to T₁⁻¹ from the thermally-activated process for tempol with τ_R > ∼3×10⁻⁹ s in viscous water:glycerol mixtures [22] is shown as orange squares in Fig. 2E, and is negligibly small relative to the contributions from modulation of A and g anisotropy at τ_R = 50 ps.

Table 3. Values of C_therm^a.

Ctherm (×1016) s−2
	Solvent	14N MI = 0	14N average MIb	15N average MIc	14N/15Nd
1a	Water	7	7.7		1.4
	Light mineral oil	8.6	8.5
	44% Glycerol	3.8	4.5
1b	Water			5.7
2a	Water	8.2	9.0		1.7
2b	Water			5.2
3a	Water	6.5	9.0
3b	Water			3.5	2.6
4	Toluene	<0.7
5	2 mM NaOH	2.8
6	Toluene	0.7

^aUncertainties are about 10% for τ_R ∼ 10 ps and increase to ∼25% for τ_R > 25 ps.

^bBased on modeling of average T₁⁻¹ for m_I = +1,0,−1

^cBased on modeling of average T₁⁻¹ for m_I = ±1/2

^dCalculated from values obtained for average T₁⁻¹ for all m_I lines

The frequency dependence of relaxation in water for ¹⁴N/¹⁵N pairs of radicals is shown in Fig. 4. These radicals have τ_R in the range of 9 to 19 ps. At 34 GHz spin rotation (Eq. 1) dominates T₁⁻¹ which is about the same for ¹⁴N and ¹⁵N (Fig. 4). As seen in Fig. 2 the contribution from (T₁^A)⁻¹ (Eq. 2) increases as frequency decreases from 34 to about 3 GHz. If the END process were the only relaxation mechanism, the dependence on nuclear spin I and the hyperfine coupling constants, A, would cause the ratio of [T₁⁻¹(¹⁴N)]/[T₁⁻¹(¹⁵N)] to be 1.36 [27]. For the pairs 1a/1b, 2a/2b, and 3a/3b the ratios of relaxation rates increase, as expected, as the contribution from the END process increases (Table 2) and is in the range of 1.3 to 1.4 where the END process dominates. The limiting value of (T₁^A)⁻¹ at low frequency increases as τ_R increases (Eq. 2). Because of the increasing role of the END process at lower frequencies, T₁⁻¹ becomes more frequency dependent as τ_R increases.

Table 2.

Frequency dependence of (T₁⁻¹ for ¹⁴N m_I = 0)/(T₁⁻¹ for ¹⁵N m_I = ±0.5)^a and of the relative contributions from relaxation mechanisms.^b,^c

Freq. (GHz)	1a/1b		2a/2b		3a/3b
33.9	1.05	SR > END > THM	1.00	SR > END > THM	1.12	SR > END > THM
9.4-9.5	1.16	SR > END > THM	1.28	END > SR > THM	1.38	END > SR > THM
2.5-3.0	116	SR ∼ END > THM	1.35	END > SR ∼ THM	1.32	END > SR ∼ THM
1.5	1.18	SR∼ END ∼ THM	1.27	END > SR ∼ THM	1.34	END > SR ∼ THM
0.25	1.13	SR ∼ END > THM	1.12	END > SR > THM	1.25	END > SR > THM

^aUncertainties in ratios of T₁ are 5 to 7%.

^bAbbreviations for relaxation mechanisms are spin rotation (SR), modulation of A anisotropy (END), and thermally-activated process (THM).

^cThe contributions from relaxation mechanisms are displayed quantitatively in Figure 4.

For the two nitroxides with smaller nitrogen hyperfine couplings, 6 and nitronyl nitroxide 5, the contribution to T₁⁻¹ from (T₁^A)⁻¹ is substantially reduced (Fig. 5A,B). Even though τ_R for 5 in water (25 ps) is about the same as for 4 in toluene (26 ps), T₁⁻¹ for 5 at low frequencies is about a factor of two smaller than for 4, due to the decreased contribution from (T₁^A)⁻¹. Nitroxide 6 has nitrogen hyperfine couplings that are less than 1/3 of those for 1 – 4. The τ_R for 6 in toluene (10 ps) (Figure 5A) is intermediate between those for 1a (τ_R = 9 ps) (Fig. 4A) and 2a (τ_R = 13 ps) (Fig. 4B) in water, so the contributions from spin rotation are similar. However, the contribution from (T₁^A)⁻¹ for 6 in toluene is so much smaller than for 1 or 2 in water that T₁⁻¹ for 6 is approximately equal to the value predicted for spin rotation alone (Fig. 5A).

Analogous to what was observed for 1a in water and mineral oil (Fig. 2B,C) T₁⁻¹ for 1b, 2a, 2b, 3a, 3b, and 5 at 250 MHz is smaller than at 1-2 GHz (Fig. 4 and 5), which cannot be accounted for by Eq. (1) – (4). The enhanced relaxation at 1-2 GHz is attributed to a thermally-activated process. C_therm is larger for 1a - 3a (containing ¹⁴N) than for 1b - 3b (containing ¹⁵N) (Table 3), which indicates a nitrogen isotope effect on C_therm. The nitrogen isotope effect is observed independent of whether the T₁⁻¹ for ¹⁴N is analyzed for m_I = 0 or for the average of all three nitrogen hyperfine lines. For the pairs 1a/1b and 2a/2b the only substitution is ¹⁴N to ¹⁵N. For the pair 3a/3b H is substituted by D as well as ¹⁴N by ¹⁵N so the larger ratio of values of C_therm for 3a/3b (2.6) than for 1a/1b or 2a/2b (1.4 or 1.7) suggests that there is an additional H/D isotope effect.

Potential assignments of the thermally-activated process

The characteristic time for the thermally-activated process is about 1×10⁻¹⁰ s, which is longer than the τ_R of (10 to 50)×10⁻¹² s. Thus the thermally-activated process is modulating an interaction that is not averaged by τ_R, which therefore excludes modulation of anisotropic dipolar couplings. The values of C_therm decrease with increasing solvent viscosity, in the order 1a in water > 1a in 44% glycerol > tempol in highly viscous solvents [22]. Values of C_therm for 1a – 3a are substantially larger than for 4, 5, or 6. The nitroxide rings for 4 - 6 are expected to be less flexible than for 1 – 3 because of bulkier substituents for 4 and 5 and the additional double bond in 6. Because of the higher molecular weight of 4, τ_R = 26 ps even in low-viscosity toluene. The contribution from (T₁^A)⁻¹ is so large for 4 that it is difficult to determine whether the contribution from the thermally-activated process is small or absent, but it cannot be as large as for 1a – 3a. These observations suggest that the thermally-activated process is modulation of the nitrogen isotropic A.

One possible mechanism for modulation of g or A is conformational changes of the geometry at the nitroxide nitrogen. Substantial temperature dependence of nitroxide g and A-values in fluid solution has been observed and attributed to fast exchange between conformations [60]. For 1a, 1b the interconversion of twist-crossover conformations averages axial and equatorial methyl group on the ENDOR timescale above about 230 K in a doped crystal [61] and results in equal hyperfine couplings to all twelve methyl protons in fluid solution [28]. The lifetime of about 1×10⁻⁷ s at 230 K predicts a lifetime at 298 K that is substantially longer than 1×10⁻¹⁰ s. For 5-member ring nitroxides interconversion of ring conformations is slow on the EPR time scale at 298K and inequivalent couplings are observed for axial and equatorial methyls [62]. The large differences in rates of interconversion for 5- and 6- member ring nitroxides and estimates of lifetimes substantially longer than 10⁻¹⁰ s at 298 K indicate that interconversion of ring conformations is too slow to be assigned as the thermally-activated process for nitroxide relaxation. Recent molecular dynamics calculations have shown that the intramolecular out-of-plane motion of the N-O moiety is a ‘soft’ mode [63,64]. For both 5- and 6-member ring nitroxides the angle between the N-O group and the plane of the molecule can vary by ±10° within a low-energy range of about 0.5 kcal/mole [64]. This angular variation is sufficient to cause substantial changes in the isotropic g and A values. Modulation of either or both of these parameters is an effective spin-lattice relaxation process. Modulation of isotropic A and g would be consistent with a nitrogen isotope effect on C_therm. The dependence of C_therm on viscosity could indicate that a smaller range of orientations is encompassed by these motions when solvent viscosity is higher. The value of τ_therm is approximately what is predicted for methyl rotation at room temperature based on ENDOR studies of tempone [61]. In these sterically hindered molecules methyl rotation may couple to the motion of the NO bond and be involved in the bond angle variation that dominates the thermally-activated process.

Other potential contributions to relaxation

The discussion of the role of the thermally-activated process (Eq 5) in the relaxation for these rapidly tumbling nitroxides assumes that this process is the same as the one that contributes to the frequency-dependent relaxation of tempol for τ_R > ∼3×10⁻⁹ s in viscous water:glycerol mixtures [22]. At those long values of τ_R the contributions to T₁⁻¹ from spin rotation and modulation of g and A anisotropy become very small. Robinson and co-workers proposed generalized spin diffusion (GSD) as the process that dominated spin-lattice relaxation for slowly tumbling nitroxides [17], which raises the question whether GSD might also contribute for rapidly tumbling samples. The GSD mechanism contributes to relaxation by modulation of electron-nuclear interspin distances via diffusion of solvent nuclei or intramolecular motions, which would have a large H/D isotope effect. In Ref. [19] it was shown that for Fremy's salt in water at 60 MHz the relaxation rate was the same in H₂O and D₂O. It was also shown previously that at ∼9.5 GHz for τ_R < 5×10⁻⁹ s there was no difference in relaxation rate for a nitroxide in water:glycerol or in D₂O:glycerol-d₈ mixtures [22]. Thus, solvent diffusion does not appear to be an effective relaxation mechanism for the nitroxides studied here. Furthermore, the proposed frequency dependence of GSD does not predict smaller relaxation rates at 250 MHz than at higher frequencies, so it is not an alternative to the thermally-activated process.

In an early discussion of potential relaxation processes for Fremy's salt, Lloyd and Pake [19] proposed that modulation of spin-orbit coupling by solid-state-like processes would be significant. The temperature dependence at ∼9.5 GHz of T₁⁻¹ for tempone in glycerol, 1:1 water:glycerol, decalin, and 3-methylpentane did not exhibit a discontinuity in the region of the glass transition temperature, which was interpreted as indicating that solid-state mechanisms persisted at higher temperatures [27]. In the slow tumbling regime the temperature dependence was modeled with contributions from Raman and local-mode processes. In glycerol, the most viscous of the solvents studied, these processes dominated relaxation at room temperature. However, in the fast tumbling regime these contributions are much smaller than the contributions from spin rotation and modulation of g- and A-anisotropy.

4. Conclusions

Understanding electron spin relaxation has been a goal of magnetic resonance spectroscopists from the earliest days of the field. Most prior studies of electron spin lattice relaxation in fluid solution were performed at ∼9.5 GHz and τ_R was varied by changing temperature [5,6,27,56,65,66]. The frequency dependence of relaxation is a powerful way to distinguish contributions from proposed mechanisms. The contribution from spin rotation is independent of ω, and decreases as τ_R increases. The contribution from modulation of g- and A-anisotropy (END process) depends on both ω and τ_R. The contribution from the thermally-activated process depends on ω, but not τ_R. For rapidly tumbling nitroxides, T₁ decreases with decreasing ω between about 34 and 3 GHz [15] as previously reported, because of the frequency dependence of the END process. However, this trend does not continue at lower frequencies because the END process becomes frequency independent. The frequency dependence of T₁⁻¹ between 34 and 3 GHz is smaller when τ_R = 10 ps than when τ_R = 50 ps. The thermally-activated process has maximal impact on T₁ in the range of 1 to 2 GHz. These three processes are sufficient to model T₁⁻¹ over the full frequency range studied. The net effect of the contributions from spin rotation, modulation of anisotropy by tumbling, and the thermally-activated process is that for small rapidly tumbling nitroxides there is a maximum in relaxation rate at about 1 to 2 GHz and relaxation rates become smaller again at lower frequency. Consequently, relaxation rates at very low frequency (e.g., 60 MHz, 250 MHz) are similar to those at ∼9.5 GHz, which is fully consistent with the earliest estimates of nitroxide relaxation rates.

In addition to understanding relaxation mechanisms, a goal of this work is to guide synthesis of application-specific nitroxide radicals. To maximize nitroxide relaxation times at low microwave frequencies, such as for in vivo studies, the nitroxide should be designed to minimize nitrogen hyperfine, thus reducing the effect of the END process (Eq. 2). If the contributions from the END process are decreased, increasing molecular size to increase τ_R is advantageous. The radical should be as rigid as possible to minimize the impact of the thermally-activated process.

Research highlights.

• T₁ and T₂ were measured for 6 nitroxides between 250 MHz and 34 GHz.

• Tumbling correlation times were between 4 and 50 ps.

• Spin rotation dominates at 34 GHz.

• Modulation of anisotropy and thermally-activated process are important.

• Thermally-activated process for ¹⁴N > ¹⁵N and decreases with increasing viscosity.