Abstract
Amorphous HES/disaccharide (trehalose or sucrose) formulations, with and without added polyols (glycerol and sorbitol) and disaccharide formulations of human growth hormone (hGH), were prepared by freeze drying and characterized with particular interest in methodology for using high precision density measurements to evaluate free volume changes and a focus on comparisons between “free volume” changes obtained from analysis of density data, fast dynamics (local mobility), and PALS characterization of “free volume” hole size. Density measurements were performed using a helium gas pycnometer, and fast dynamics was characterized using incoherent neutron scattering spectrometer. Addition of sucrose and trehalose to hGH decreases free volume in the system with sucrose marginally more effective than trehalose, consistent with superior pharmaceutical stability of sucrose hGH formulations well below Tg relative to trehalose. We find that density data may be analyzed in terms of free volume changes by evaluation of volume changes on mixing and calculation of apparent specific volumes from the densities. Addition of sucrose to HES decreases free volume, but the effect of trehalose is not detectable above experimental error. Addition of sorbitol or glycerol to HES/trehalose base formulations appears to significantly decrease free volume, consistent with the positive impact of such additions on pharmaceutical stability (i.e., degradation) in the glassy state. Free volume changes, evaluated from density data, fast dynamics amplitude of local motion, and PALS hole size data generally are in qualitative agreement for the HES/disaccharide systems studied. All predict decreasing molecular mobility as disaccharides are added to HES. Global mobility as measured by enthalpy relaxation times, increases as disaccharides, particularly sucrose, are added to HES.
Keywords: Freeze drying, Pharmaceutical stability, Glass dynamics, Density, Free volume, PALS
1. Introduction
Pharmaceutical protein formulations are often freeze-dried (lyophilized) with stabilizers such as sucrose and trehalose to achieve good pharmaceutical stability, thereby allowing satisfactory storage stability [1,2]. Here, the term, “pharmaceutical stability” refers resistance to irreversible change by either chemical degradation or physical changes such as aggregation in protein systems. Two hypotheses, not necessarily mutually exclusive, have been proposed to describe the mechanism of protein stabilization in dried solid state: (1) water substitution and (2) glass dynamics [3]. The former hypothesis is attributed to the ability of disaccharides to form hydrogen bonds at specific sites of the protein and thus “substitutes” for the stabilization provided by water that is lost during drying [4,5]. The glass matrix stabilization hypothesis is based on formation of a rigid inert matrix, normally disaccharide, which dilutes the protein in the matrix and limits the mobility of protein molecules, thereby minimizing protein–protein interaction as well as reducing mobility of both the protein and of potential reactants in the system [6,7]. The focus of protein stabilization in this work is on the glass dynamics in the amorphous systems and physical properties that may reflect the dynamics and therefore potentially are predictive of pharmaceutical stability trends.
Historically, the glass transition temperature, Tg (a global mobility parameter correlated with onset of viscous flow), has been used as a predictor of molecular mobility and thus reactivity. While some studies showed excellent correlation between Tg and physical/chemical stability [8,9], examples of poor correlations can also be found [10,11]. Global mobility is perhaps better characterized by the structural relaxation time, frequently measured using calorimetry, and while generally correlations with stability are better than those comparisons based on Tg, the correlations are far from perfect [2,3,11]. Glassy systems have also been shown to have motions on small time and small length scales involving intra-molecular reorientations; these motions are often classified as local mobility or β-relaxations [12]. Only in recent years has the potential role of local molecular motions in controlling pharmaceutical stability in protein formulations been extensively explored [13–15]. It has been demonstrated that the addition of glycerol to a trehalose based formulation suppresses local mobility, specifically the “fast dynamics” as observed by inelastic neutron scattering, and improves the stability profile of horseradish peroxidase and yeast alcohol dehydrogenase, even though the overall Tg of the formulation was reduced [14]. The optimal glycerol concentration was found at 5% w/w [14]. Similar observations were also found for protein A–E, HER2 antibody, serum albumin, human growth hormone (hGH), and immunoglobulin G (IgG) [15].
Simple theory [16] suggests that mobility of a molecule or group of atoms should be related to the freedom of movement of the molecule or group of atoms, that is, related to the volume available to the moving unit to move freely without concerted movement of neighboring groups of atoms or molecules. Thus, the probability of large length scale motion increases dramatically as the “free space” increases. This “free space” is denoted “free volume”, and although the concept is too simple to apply to real molecules in quantitative fashion, the concept has intuitive appeal and perhaps qualitative validity. For example, using simple free volume theory, one can derive the well-known “VTF” equation, which does represent structural relaxation and viscosity in highly viscous systems [17]. One parameter that is related to free volume is the size of “holes” in an amorphous system, as measured by Positron Annihilation Lifetime Spectroscopy (PALS). The lifetime of a positron increases as the size of the void or hole increases. While the average size of the holes do not necessarily correlate directly with total free volume since the hole density may vary, the PALS lifetime has been studied as a measure of free volume and dynamics in the glass [17,18].
In principle, the density of an amorphous solid also reflects free volume, and with high precision density measurements [19], trends in free volume can be studied. For example, it was shown that annealing formulations below their glass transition temperature for times on the order of 1 or 2 days can result in small yet significant increases in density values compared to non-annealed samples [19]. It is significant to note that annealing does stabilize against degradation in protein and small molecule pharmaceuticals, and annealing does decrease global mobility as measured by enthalpy relaxation calorimetry [6,21]. Recent evidence also suggests that stability of proteins and small molecules in disaccharide formulations (IgG [20] and sodium ethacrynate [21]) correlates with the density of the amorphous solids. However, in a series of samples where the atomic composition varies, density may vary simply due to variation in average atomic density. This is not an issue when annealed samples are compared to non-annealed samples since the composition is constant, and changes in density between samples do mean differences in free volume. However, many applications involve studying trends with formulation, and in these applications, variations in composition will contribute to density variations. When compositions are very similar, the assumption is that such variations are minor. However, this assumption needs support, and when the assumption fails, the density values themselves cannot be used directly to establish trends in free volume. Clearly, alternate methodology for analysis of density data for systems of variable composition is needed to relate density data to free volume.
We have two major objectives with this study. First, we wish to provide methodology to properly analyze density data in terms of free volume. We accomplish this by first assessing the influence of variable atomic composition on density and apply this methodology to hGH/disaccharide systems. We then demonstrate the value of apparent specific volume and volume changes on mixing, both calculated from density data, as measures of changes in free volume in a series of samples. Secondly, we compare the various measures of mobility (enthalpy relaxation times and mean amplitudes of motion from neutron scattering) and free volume (from density measurements and PALS data) in complex freeze-dried formulations. Many of the formulations involve hydroxyethylstarch (HES). The rationale for studying HES formulations is that this polymer has been used as a protectant in the storage of frozen cells, can be used as part of a stabilizer system for pharmaceuticals and vaccines, and it is a FDA approved product for clinical use as a plasma volume expander [22,23]. The high Tg of HES [23] is an added bonus in that HES will increase the Tg’ of the formulation and allow easier freeze drying. We also study formulations that involve addition of low levels of polyols (glycerol and sorbitol) to HES/trehalose formulations. Previous studies [14,15,24] have shown that addition of low levels of polyols to protein/disaccharide formulations can dampen “fast dynamics” and can improve the storage stability of proteins.
2. Materials and methods
Materials were obtained, and freeze-dried samples were prepared as previously described [25]. High precision densities were determined by He pycnometry, fast dynamics by neutron scattering, and free volume “hole size” was obtained by Positron Annihilation Lifetime Spectroscopy (PALS), all as described below:
2.1. Density
The densities of the freeze-dried samples were obtained using a helium pycnometer (AccuPyc 1330 Gas Pycnometer, Micromeritics Instruments Corporation, Norcross, USA), which was described previously [19]. In order to prevent moisture uptake by the hygroscopic amorphous samples, sample preparation and measurements were carried out inside a glove bag. The glove bag was purged with nitrogen gas throughout the measurement to maintain a humidity level of <5% RH. Briefly, about 100 mg of sample was loaded (gently packed) into a 1 mL aluminum cup, and the cup was then transferred into the pycnometer measurement chamber for analysis. Prior to measurement, the sample was purged with helium for about 30 min (99 sequential purges). Thereafter, an average of 20 density measurements was collected for one sample. At least three independent analyses were carried out for each sample. All measurements were carried out at room temperature, about 23 °C. Calibration of the pycnometer was first carried out using a standard sphere with known volume followed by crystalline sucrose (99 sequential purges and 20 measurements). Our measurements of crystalline sucrose gave a density value of 1.586 ± 0.001 g/mL (literature value was 1.5854 g/mL [19]), and amorphous sucrose and trehalose were measured at 1.503 and 1.507, respectively (literature values [19] are 1.506 and 1.504, respectively). Periodic confirmation of reliable operation was carried out by measuring crystalline sucrose density between sample measurement series. Standard error of the mean of a set of replicates was normally about 0.2%, except for measurements with hGH systems where standard errors averaged about 0.8%, presumably because the sample size used was much smaller than optimum due to scarce hGH supply.
2.2. Neutron scattering characterization of fast dynamics
The high flux backscattering (HFBS) spectrometer at the National Institute of Standards and Technology (NIST) Center for Neutron Research on the NG2 beam line was used to study the fast dynamics. The HFBS spectrometer operates with an incident neutron wavelength of 6.271 Å and a kinetic energy of 2.08 meV. The accessible momentum transfer (Q) range is 0.25–1.75 Å−1. Approximately 300 mg of freeze-dried sample was loaded into sealed neutron scattering sample cells in a dried glove box. In these studies, the spectrometer operates in the fixed-window scanning mode where the elastic scattering intensity (I) is recorded as a function of Q while the sample is heated at 1 K/min from 4 K to about 330 K (all temperatures were below the glass transition temperature of the tested formulations).
The elastic scattering intensity was analyzed using DAVE software (available for download at http://www.ncnr.nist.gov/dave). Dynamic data are obtained through the temperature-dependent decrease in elastic scattering intensity, under the assumption that the decrease is due to increased inelastic scattering. The inelastic scattering can be described in terms of the intermediate scattering function,
| (1) |
where A(Q, t) is the Debye Waller Factor (DWF) and φ(Q, t) is a relaxation function that is generally found to have the form Exp[−t/τ(Q)]β in the regime of interest. Under Gaussian approximation, an effective DWF can be defined as:
| (2) |
Thus, a mean-squared displacement (〈u2〉) can be extracted from neutron scattering as the Q2 dependence of the logarithm of the intensity drop in the elastically scattered signal. In this way, the Q-dependence of the incoherent elastic scattering intensity was analyzed to give hydrogen–weighted Debye-Waller factors and 〈u2〉 values.
The hydrogen-weighted mean-square atomic displacement, (〈u2〉, was obtained at temperatures throughout the range reported above. In order to remove small artifacts of the coherent scattering signal, a scattering intensity baseline was removed such that the temperature-dependent values of 〈u2〉 extrapolate to zero at 0 K.
2.3. Positron Annihilation Lifetime Spectroscopy (PALS)
The PALS measurements were carried out at the positron facility of the North Carolina State University with a typical fast–fast bulk PALS system. In each PALS measurement, the [22] Na positron source was sandwiched between the sample pallet (Kapton sealed) and a piece of copper. The samples were exposed to the ambient environment only for about a minute while putting together the sample–source–copper sandwich. Then, samples were put back into the containers and sealed again during the acquisition of the PALS spectra. In this set up, roughly half of the positrons emitted by the source were implanted to the copper and the other half were into the sample. We also need to note that a fraction of the positrons (~15%) were absorbed by the Kapton sealing layer of the samples and of the source. At least 2 × 106 annihilation events were collected in each PALS histogram. The spectra were best fitted with three lifetime components. The first and the second lifetime (~250 ps and ~400 ps, respectively) are due to the short lived positrons from the sample, the Kapton seal, and the copper, which are not relevant to the hole volume in which we have interest. The third lifetime (1.2–1.7 ns) is solely due to the positronium (i.e., bound state of a positron and an electron) annihilation in the sample and can be correlated to the free volume hole size using the well–accepted Tao-Eldrup model [25,26]. Nearly all data reported represent the mean of two or three replicates.
3. Analysis of density data in terms of “Free Volume” concepts
3.1. Correction of densities for differences in atomic densities
The density of a solid reflects not only the mass of the constituent atoms but also the volume of those atoms and the space between atoms, the latter including the volume available for motion of the atom or groups of atoms without requiring concerted motion of neighbors, which we may term “free volume”. Thus, at least in principle, density measurements may provide information on free volume and therefore may correlate with dynamics in the glassy state. However, in most stability applications of interest, we are interested in comparing stability in a series of formulations where the chemical composition is varied, meaning the atomic densities vary. Thus, density measurements for these samples include not only the variation in free volume, but also include the variation due to variation in atomic densities.
While there is no practical way to calculate this effect with high accuracy since the atomic volumes vary depending on details of their bonding to other atoms, we can estimate the effect by calculating the van der Waals density, defined as the total mass of the molecule divided by the total van der Waals volume, the latter being taken from literature tabulations [28]. If the compositions of the systems being compared differ only slightly, the calculation would be expected to have useful accuracy. The procedure is as follows:
Density is grams/cm3, or grams per molecule divided by cm3/ molecule. However, grams per molecule is M/N0, where M is the gram molecular weight and N0 is Avogadro’s number, 6.023 × 1023. Further, we may write,
| (3) |
where mi is the number of i type atoms of volume Vi, in Å3. Thus,
| (4) |
where the term, 1024, comes from conversion of volume in cm3 to volume in Å3. We now define the relative van der Waals volume as volume per atom divided by the van der Waals volume of hydrogen, VH, and use the symbol, νi. Thus,
| (5) |
Using Girolami’s value [28] of 1.15 Å for the van der Waals radius of hydrogen, the value of VH is calculated to be 6.4 Å3. Thus, introducing the value of N0, the van der Waals density may be calculated by
| (6) |
where Vs is the sum of the relative volumes of the constituent atoms. Van der Waals radii and relative volumes, νi, for the atoms of interest for our formulations, as given by Girolami [28] are given below in Scheme 1.
Scheme 1.
van der Waals radii, relative volume (to H), and atomic weight
Using the data above and Eq. (6), van der Waals densities may be calculated for each component in the formulation, and the van der Waals density of the formulation is then obtained by a weight fraction average of the densities of each component. We find that the van der Waals densities calculated by the above procedure produces densities are systematically low for the formulation components of interest, i.e., 1.304 (sucrose) and 1.230 (hGH). However, what we require is a prediction of the density ratio of the formulation to that of a comparator (i.e., pure hGH) to address the issue of what portion of the density change with formulation arises from changes in free volume. As a check on the accuracy of the above procedure for estimating the impact of varying atomic density on density of formulations, we evaluate the ratio of the van der Waals density of a “reference” material (sucrose) to the van der Waals density of the compound of interest, here sorbitol and six amino acids representative of the most common residues found in proteins. We then calculate the ratio of the experimental density of crystalline sucrose to that of the compound of interest and then compare the experimental and calculated ratios.2 The assumption is that the van der Waals densities should represent crystalline densities as a first approximation except for a constant multiplicative factor. Thus, ratios of sucrose to “amino acid” density evaluated from van der Waals estimation should be close to the corresponding experimental density ratio of crystalline material. The range of densities, both calculated van der Waals values and experimental values, is about 27%, which is excellent agreement. However, the average difference between the van der Waals density ratios for amino acids (i.e., sucrose/amino acid) and experimental density ratio (sucrose/ amino acid) is about 2.5%, with the experimental ratio being higher. That is, “on average”, the van der Waals approach underestimates the impact of added disaccharide on the density of a protein/disaccharide formulation, with the error being about 0.025w2, where w2 is the weight fraction of disaccharide in the formulation. Thus, we conclude that the van der Waals approach is reliable only for applications involving relatively large density differences (i.e., more than about 2%) where variations in average atomic densities between samples are moderate.
3.2. Volume change on mixing from densities
One can determine the volume change on mixing two solids from the densities of the pure components and the mixture. Such data can address free volume changes in a series of formulations in that a negative volume of mixing would mean loss of free volume upon mixing, and these data are not subject to approximations such as the density comparisons using the van der Waals densities. Density is mass per unit volume, and the reciprocal of density is the specific volume, ν′. The initial specific volume, , is calculated from the sum of the component specific volumes,
| (7) |
where wi is the weight fraction of component i of specific volume, , and di is the density of component i. For the mixture, the specific volume is , where the subscript “m” means “mixture”, and the volume change on mixing one gram of total material, , is
| (8) |
where is the “weight average sum” of the specific volumes of the pure components, either in the amorphous or crystalline state. If there is a loss of free volume on mixing, the value of will be negative. Clearly, the loss of free volume on mixing will be less if, for example, the crystalline state is used to compute , since essentially by definition, the crystalline state has zero free volume.
To relate the change in specific volume on mixing to free volume, we consider volume to be composed of volume occupied by the atoms, or “van der Waals volume”, which could be approximated by the specific volume of the crystalline state, and free volume. Thus, upon mixing, the “van der Waals volume” will cancel, and the volume change will reflect changes in free volume of at least one component. For example, consider a two component system composed of “solvent” (component 1, weight fraction w1) and “solute” (component 2, weight fraction w2). We may write,
| (9) |
is the change in specific volume on mixing; the specific free volume of component 1 (solvent) in pure state; the specific free volume of component 2 (solute) in pure state; , nominally if crystal is chosen as pure state.
Thus, the change in specific volume on mixing will contain contributions in free volume changes from both solvent and solute. However, if the crystalline state is used for the specific volume of the solute, , and the value of will be less negative.
3.3. Apparent specific volume of solute from densities
Similar to the definition of the apparent molal volume [29], which is defined on a per mol basis, the apparent specific volume of the solute, may be defined based on a per gram basis. The corresponding apparent molal volume of the solute is calculated as the product of the molecular weight of the solute (component 2) and the apparent specific volume. We define apparent specific volume by,
| (10) |
where V is the volume of one gram of the “solution”, here an amorphous solid, m is the mass, one gram, m2 is the mass of solute, and is the specific volume of the pure “solvent” (component 1). Note that the solvent may actually be a multi-component system; for example, the solvent may be a 1:1 weight ratio of HES/trehalose. When the total mass is one gram, we may use w2 to denote the weight fraction of solute and since the specific volume is the reciprocal of density, we write,
| (11) |
where d is the density of the mixture. The partial specific volume, V̄2, may be calculated from the apparent specific volume and the concentration dependence of the apparent specific volume,
| (12) |
and when ,
| (13) |
If the free volume decreases on adding the solute to the solvent, the apparent specific volume of the solute should be less than the specific volume of the pure solute (i.e., pure component 2). As with volume changes on mixing, one might compare the apparent specific volume with either the specific volume of the amorphous or the crystalline solute. Using the crystalline state and observing an apparent specific volume less than the specific volume of the crystalline solute would indicate a reduction in free volume of the solvent. Taking the specific volume as the sum of the “van der Waals volume”, which depends only on atomic densities, and the free volume of each component, solvent and solute, we may write the apparent specific volume in terms of free volumes,
| (14) |
where is the specific van der Waals volume of component 2 (solute); the specific “free volume” of the solvent in its “pure state”; ν′free the specific “free volume” in the resulting solution.
We may also express the result in the form,
| (15) |
where is the specific free volume of solute in pure state, =0 if crystal, the change in specific free volume of solute when added to solution and is the change in specific free volume of solvent when w2 gram of solute are added.
The apparent specific volume of solute and the volume change on mixing solute and solvent may be related by combining the defining equations to give,
| (16) |
Noting again that the apparent specific volume and the partial specific volume differ by the derivative of apparent specific volume with respect to solute weight fraction, we may write,
| (17) |
When the volume change on mixing is linear in w2, the derivative and ratio in square brackets in Eq. (17) are equal, meaning that the apparent specific volume is independent of composition, and the apparent and partial specific volumes are therefore identical.
4. Results and discussion
4.1. Density and loss of free volume on mixing in HES systems
Density data as well as volume changes on mixing and apparent specific volumes are summarized in Table 1 and Figs. 1–3. In comparison with apparent specific volumes, the specific volumes of the polyols, sorbitol and glycerol are also provided in Table 1 for both their amorphous and crystalline states. Note that except for one system, 5%HES with 1% glycerol, none of the systems in Table 1 showed DSC evidence of phase separation [25] (i.e., two Tg’s). We suggest that when investigating the perturbation of a small amount of polyol on a “matrix system” (i.e., HES/disaccharide system), apparent specific volumes perhaps offer the most natural or intuitive interpretation, but of course, the actual information content is the same for the changes in volume on mixing. However, when investigating mixtures over the entire range of compositions, such as the HES/disaccharide systems without polyols over the range from pure HES to pure disaccharide, volume changes on mixing are the preferred quantity to compare since there is no obvious choice for “solute”.
Table 1.
Densities, volume change on mixing (ΔVmixing), and apparent specific volumes for freeze-dried hydroxyethylstarch (HES)/trehalose/polyol systems. Uncertainties given are estimated standard errors of the mean.
| Sample composition freeze-dried (HES) | Density, g/cc ± std. error | ΔVmixing cc/g ± 0.002 | cc/g± std error |
|---|---|---|---|
| HES/sorbitol systems | |||
| 5%HES | 1.464 ±0.001 | – | |
| 5%HES, 0.5% Sorb | 1.472 ±0.002 | −0.004 | 0.64 ± 0.01 |
| 5%HES, 1% Sorb | 1.476 ±0.002 | −0.007 | 0.65 ± 0.01 |
| HES/1%trehalose/sorbitol systems | |||
| 5%HES, 1% Treh | 1.462 ±0.002 | 0.003 | – |
| 5%HES, 1% Treh, 0.5% Sorb | 1.477 ±0.004 | 0.004 | 0.59 ± 0.02 |
| 5%HES, 1% Treh, 1% Sorb | 1.487 ±0.001 | −0.009 | 0.60 ± 0.01 |
| HES/3%trehalose/sorbitol systems | |||
| 5%HES, 3% Treh | 1.480 ±0.001 | −0.001 | − |
| 5%HES, 3% Treh, 0.5% Sorb | 1.492 ±0.001 | −0.006 | 0.59 ± 0.01 |
| 5%HES, 3% Treh, 1% Sorb | 1.4921 ± 0.0004 | −0.008 | 0.626 ± 0.003 |
| Sorbitol amorphous | 1.4445a | 0.692 | |
| Sorbitol crystalline | 1.4767a | 0.677 | |
| HES/glycerol systems | |||
| 5%HES, 0.5% glycerol | 1.458 ±0.006 | −0.007 | 0.71 ± 0.03 |
| 5%HES, 1% glycerol | 1.448 ±0.004 | −0.011 | 0.73 ± 0.01 |
| HES/1%trehlose/glycerol systems | |||
| 5%HES, 1% Treh, 0.5% glycerol | 1.463 ±0.005 | −0.005 | 0.68 ± 0.03 |
| 5%HES, 1% Treh, 1% glycerol | 1.459 ±0.005 | −0.011 | 0.70 ± 0.02 |
| HES/3%trehalose/glycerol systems | |||
| 5%HES, 3% Treh, 0.5% glycerol | 1.468 ±0.004 | −0.002 | 0.77 ± 0.03 |
| 5%HES, 3% Treh, 1% glycerol | 1.466 ±0.005 | −0.007 | 0.73 ± 0.02 |
| Glycerol amorphous | 1.2610b | 0.793 | |
| Glycerol crystalline | 1.336c | 0.748 | |
| HES/disaccharide systems | |||
| 4%HES, 1%trehalose | 1.473 ±0.002 | −0.001 | − |
| 2.5%HES, 2.5%trehalose | 1.485 ±0.002 | −0.000 | − |
| 1%HES, 4%trehalose | 1.494 ±0.002 | 0.002 | − |
| 5%Trehalose | 1.507 ± 0.004 | 0 | − |
| 4%HES, 1% sucrose | 1.481 ±0.003 | −0.004 | − |
| 2.5%HES, 2.5% sucrose | 1.500 ± 0.004 | −0.008 | − |
| 1%HES, 4% sucrose | 1.500 ± 0.003 | −0.002 | − |
| 5% Sucrose | 1.503 ± 0.003 | − | − |
Fig. 1.
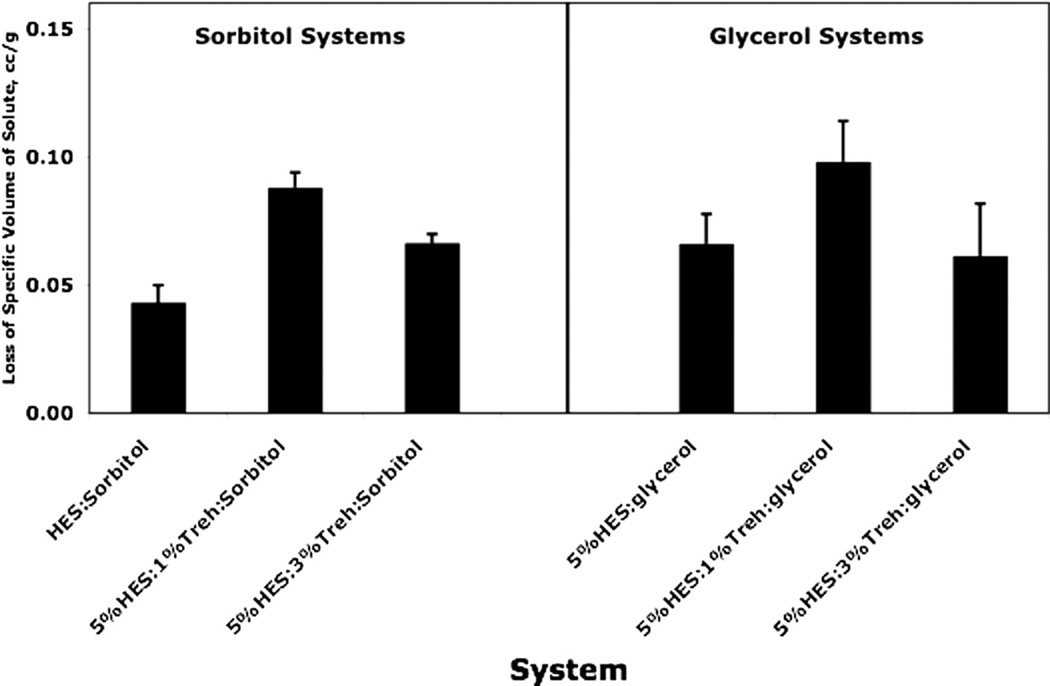
Decrease in apparent specific volume at room temperature of 1% polyol on mixing with hydroxyethylstarch/trehalose systems, as calculated from densities in Table 1: difference between amorphous polyol specific volume and apparent specific volume of mixture (apparent loss of specific volume of polyol on mixing). Error bars reflect estimated standard errors evaluated from corresponding standard errors in density using propagation of errors.
Fig. 3.
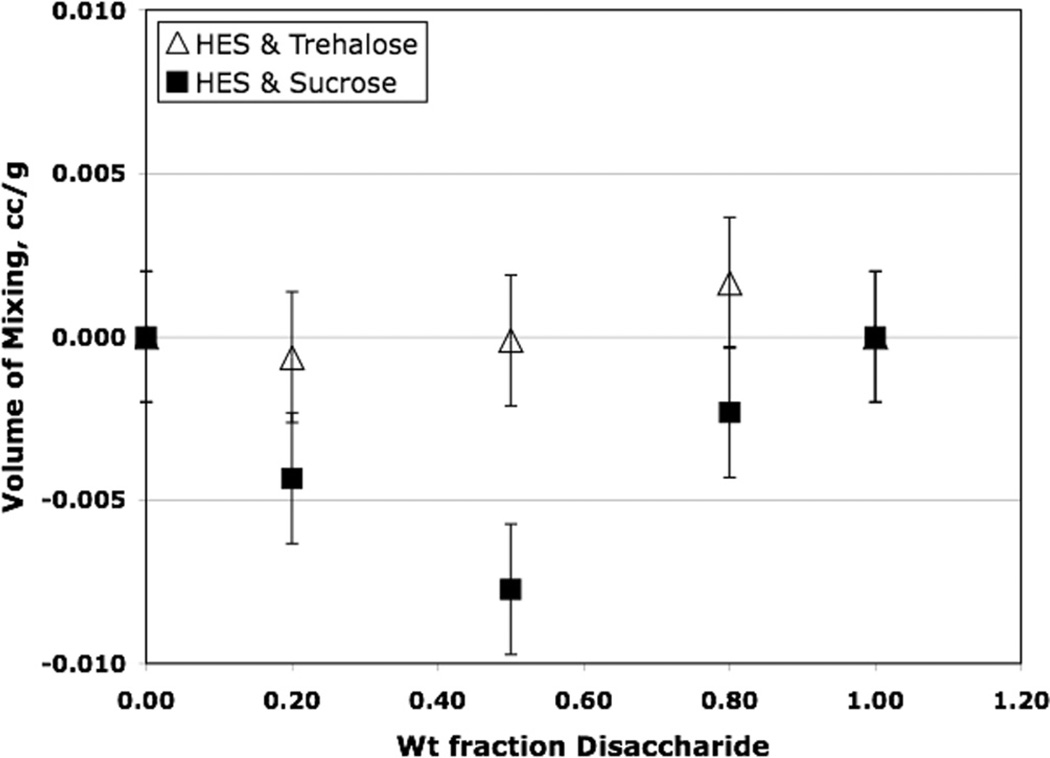
Volume change on mixing hydroxyethylstarch (HES) with amorphous disaccharides at room temperature evaluated from density data in Table 1. Error bars represent standard errors as estimated from corresponding errors in density measurements using propagation of errors. Open triangles = HES/trehalose; filled squares = HES/sucrose.
Note that the apparent specific volumes are nearly independent of concentration over the limited concentration range investigated. This also means that the partial specific volume is essentially equal to the apparent specific volume (Eq. (12)) over this concentration range. Our view is that interpretation of the apparent specific volumes should be based on a comparison of the apparent specific volume of a polyol with the specific volume of the pure polyol. If the apparent specific volume is significantly lower than the specific volume of the pure polyol, there is a loss of “free volume” upon dissolving the polyol “solute” in the solvent, which may be a mixture of HES and trehalose. If the comparison is made with the specific volume of the crystalline polyol, all of the loss may be attributed to loss of free volume of the “solvent matrix”. On the other hand, if comparison is made with the amorphous specific volume, loss of free volume may be both loss in the solvent and in the polyol, and the loss would be greater in magnitude than if the comparison is made with the crystalline specific volume. Note that for sorbitol containing systems, but not the glycerol containing systems, the apparent specific volumes are all less than both the specific volume of the amorphous solid and the crystalline solid.
The change in volume on mixing tabulated (Table 1) uses the amorphous state of all components in the initial state. Note that with two exceptions, the 5%HES/1%trehalose system without polyol and the 1%HES/4%trehalose systems, all volume changes on mixing in Table 1 are negative. Neither of these systems involve a polyol. For both polyol containing systems, there is a loss of free volume on mixing the polyol with the HES/disaccharide. Of course, because it is the same set of density data used to compute volume changes on mixing as used to compute apparent specific volumes, and volume changes on mixing and apparent specific volume are related by Eq. (16), we must have essentially the same observation made regarding changes in free volume. The change in volume on mixing and the apparent specific volume just offer alternate ways of thinking about the data.
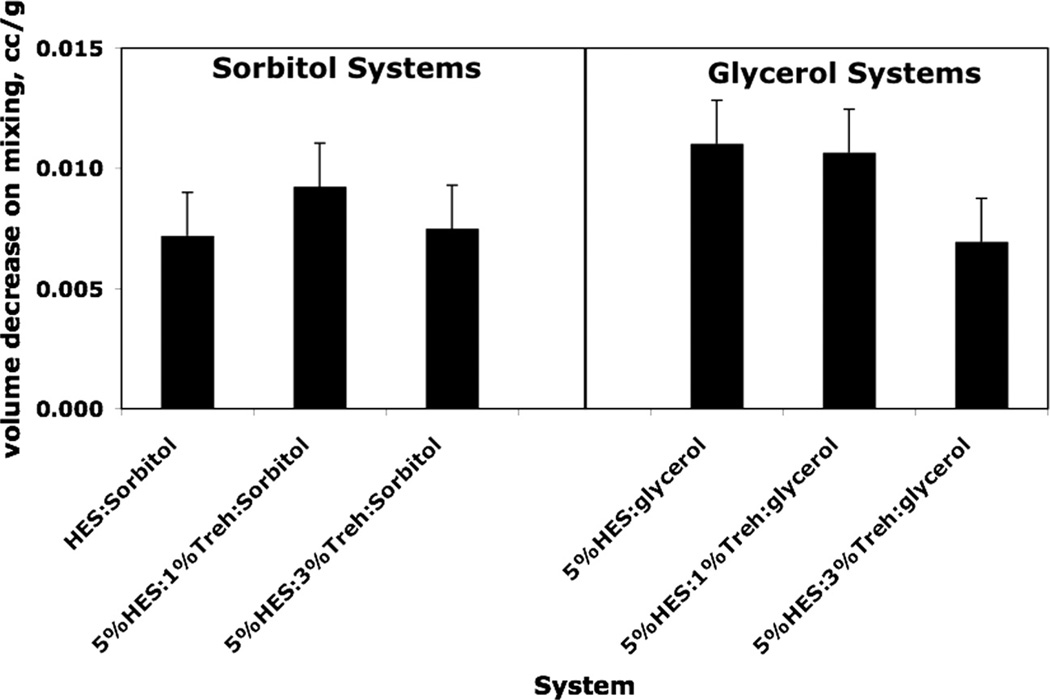
Figs. 1 and 2 show graphically the variation in apparent specific volume and volume changes on mixing for HES/trehalose/polyol systems. In both cases, it is the amorphous state of the polyol that is used in the calculation. It is clear that there is a loss of free volume on adding 1% polyol to the HES/trehalose “solution”. The effects are small, however, as the free volume in amorphous sucrose (measured by the difference in specific volume between amorphous and crystalline phases) is about 0.034 cc, about three times the maximum loss shown in Fig. 1 and Fig. 2. While the effect is relatively small and error bars are large, the effect is still significant in the sense that the difference between the measured loss of free volume and zero (i.e., no loss of free volume) is much larger than the standard error in the value. For loss of volume measured by apparent specific volume, the largest losses are for the 5%HES/1%trehalose systems, but the differences are not always larger than the combined standard errors. For apparent specific volume changes on mixing, the differences with trehalose level are not as apparent, particularly for glycerol systems. However, considering both Figs. 1 and 2, it seems clear that free volume is decreased on adding a small amount of polyol to HES/trehalose systems, which assuming free volume and stability are related, would suggest stabilization by the polyol, as observed [14,15,24] with other systems, the effect perhaps being largest with 5%HES/1%trehalose.
Fig. 2.
Analysis of density data: volume change on mixing amorphous polyols with hydroxyethylstarch/trehalose (HES) systems. The volume decrease on mixing 1% polyol with HES/trehalose is calculated from density data (Table 1) using density of amorphous polyol to evaluate initial volume. Error bars represent standard errors of the mean calculated from corresponding density errors using propagation of errors.
Fig. 3 compares the volume changes on mixing HES with sucrose and trehalose. Amorphous disaccharide densities are employed to generate these data (see also, Table 1). It seems clear that while the volume changes on mixing for trehalose systems are very small and show no systematic trend above the estimated standard error, the volume changes on mixing for sucrose systems are negative and do appear to be significant, particularly at 1:1 weight ratios. Again, the effect is small compared to the free volume in amorphous sucrose, only about 33% of the estimated free volume in amorphous sucrose, but seems sufficiently large to impact stability. For example, in saccharide formulations of a monoclonal antibody, annealing resulted in about a 30% decrease in free volume and about a 30% increase in aggregation stability [6]. Thus, based on these results, assuming free volume correlates with pharmaceutical stability, we would expect significantly better stability in HES/sucrose formulations than in the corresponding compositions with trehalose.
4.2. Density and free volume in disaccharide/hGH systems
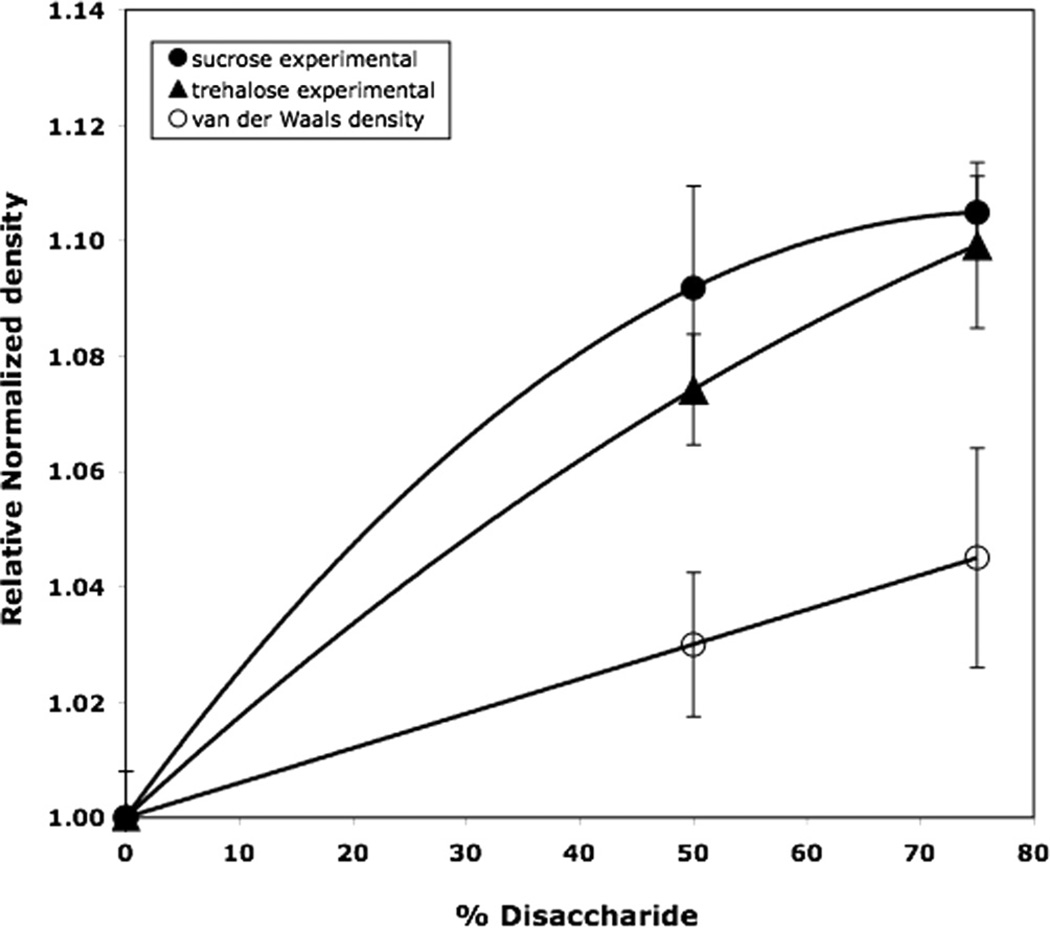
Fig. 4 illustrates the effect of disaccharide addition to human growth hormone (hGH) on relative density and therefore on “free volume”. The graph plots measured density divided by the measured density of human growth hormone without disaccharide for hGH/trehalose and hGH/sucrose systems. The plot also includes the corresponding ratios evaluated from the calculated “van der Waals densities”, where van der Waals densities were evaluated as described earlier. All error bars represent standard errors. Addition of disaccharide increases the density of hGH, with the effect being marginally larger for sucrose than for trehalose systems (P = 0.2). However, as noted earlier, variation in atomic densities arising from composition variation also increases this density ratio, as also shown in Fig. 4. It does seem clear, however, that that the increase in experimental density ratio is significantly greater than that for the calculated from van der Waals densities. The implication is that much, or most, of the density increase on adding disaccharide arises from a decrease in free volume. Moreover, the effect of sucrose is slightly greater than the effect of trehalose (P = 0.2). Thus, we would expect addition of sucrose and trehalose to stabilize hGH, with the effect of sucrose being slightly greater, in complete agreement with experimental stability data [11]. Unusually large variation in replicates for the hGH containing samples, probably arising from the use of small samples for density measurements, means large standard errors of the mean and precludes a more quantitative analysis of the data.
Fig. 4.
Effect of disaccharide content on density of human growth hormone (hGH) formulations: comparison of experimental data for sucrose and trehalose systems with calculated effect of changing atomic density with added disaccharide. The effect of variable average atomic density was estimated from calculated van der Waals densities. Relative normalized density means density normalized to the value obtained for hGH without saccharide. All disaccharide containing systems contained sodium phosphate buffer, but the density measurement for hGH alone did not contain buffer. Thus, the value of density for hGH (zero disaccharide) was evaluated from the measured value for pure hGH (1.282) and handbook literature values for density of phosphate salts to give the value for zero disaccharide used in the plot (1.327). Error bars indicated standard errors evaluated from density errors using propagation of errors. Error estimate in the van der Waals density is about 2.5%. ANOVA comparing sucrose with trehalose systems gave a P value of 0.20 (Tukey’s HSD).
4.3. Comparison of various measures of dynamics in HES systems
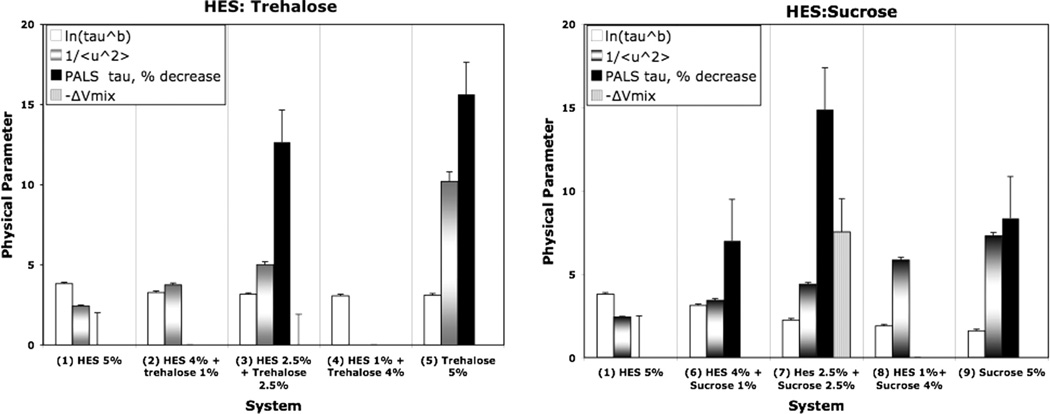
Table 2 and Fig. 5 compare the various physical parameters relevant to dynamics in the amorphous solid for the HES/disaccharide formulations studied. The open bars represent the natural log of the structural relaxation time constant, τβ where an increase means lower global mobility in the systems (i.e., longer time required for the movement involved in relaxation). The variable texture bars denote the reciprocal of the mean amplitude of motion on a nanosecond time scale as measured by neutron scattering, where an increase means a decrease in local mobility on a short time scale. The solid bars denote the positron lifetimes measured by the PALS in ns, relative to pure HES or positron where an increase means greater mobility if the hole size correlates with free volume and mobility. The striped bars show the volume decrease on mixing a 1:1 weight ratio of HES/disaccharide. Thus, as mobility decreases, the open bars (lnτβ) should increase, the textured bars (1/〈u2〉) should increase, the solid bars (PALS lifetime ratios) should increase, and the volume loss on mixing, −ΔVmix, should increase if mixing causes loss of free volume and free volume and mobility are coupled. Error bars represent standard error estimates in all cases. As the composition proceeds from pure HES to pure disaccharide, the structural relaxation time (open bars) decreases, slightly for trehalose and significantly for sucrose, meaning global mobility increases with increasing disaccharide content. The textured bars (1/ 〈u2〉) measuring the magnitude of local rigidity of structure increase significantly for both trehalose systems and sucrose systems, slightly greater for trehalose systems at corresponding compositions. Thus, local mobility decreases as we proceed from pure HES to pure disaccharide, the effect being slightly greater for trehalose systems. Note that this trend suggests trehalose/ HES systems have less free volume than sucrose/HES systems. However, the loss of volume on mixing evaluated from density data shows no loss of volume on mixing with trehalose but a small but significant loss of volume on mixing with sucrose, suggesting that sucrose/HES systems have lower free volume and therefore should promote superior stability. Finally, the PALS data (% decrease in lifetime from pure HES) show significant decreases in positron lifetimes from pure HES as disaccharide is added. This means smaller “hole size” in the free volume cavities as disaccharide is added, in agreement with the analysis of density data and the neutron scattering mean amplitudes of motion. There does not seem to be a systematic difference between trehalose and sucrose systems, and no systematic trend with level of disaccharide is evident. Finally, the global mobility data are not consistent with mobility measured by the other methods. As disaccharide is added, the (global) mobility increases (i.e., ln τβ decreases), but the other measures of mobility indicate that addition of disaccharide decreases mobility. Evidently, trends in global mobility are not the same as trends in mobility measured by the other techniques, including methods such as free volume from density, neutron scattering, and PALS lifetimes. It should be noted that historically, global mobility is often well correlated with stability, but in many cases, particularly when the system is being examined well below Tg, trends in global mobility and trends in stability go in opposite direction where stability trends and local mobility trends often correlate reasonably well [20].
Table 2.
Reciprocal of mean-square amplitude of hydrogen motion on a nanosecond time scale as determined by neutron backscattering and positron annihilation lifetimes (PALS) for hydroxyethylstarch (HES)–disaccharide systems. Error bars for 〈u2〉 are calculated as the standard deviation from the fitted (smoothed) curve. PALS results are the means of at least two independent runs where the standard error averaged about 0.02 ns.
| Formulation | 〈u2〉−1 (Å−2) |
PALS lifetime | ||
|---|---|---|---|---|
| 40 °C | 50 °C | 60 °C | ns (±0.02) | |
| HES | 2.44 ± 0.04 | 2.25 ± 0.04 | 2.08 ± 0.03 | 1.47 |
| HES/sucrose 4:1 | 3.43 ±0.10 | 3.15 ± 0.08 | 2.89 ± 0.07 | 1.37 |
| HES/sucrose 1:1 | 4.42 ±0.16 | 4.05 ± 0.13 | 3.70 ±0.11 | 1.25 |
| HES/sucrose 1:4 | 5.85 ±0.18 | 5.38 ± 0.15 | 4.94 ±0.12 | – |
| Sucrose | 7.28 ±0.19 | 6.72 ± 0.17 | 6.17 ±0.14 | 1.35 |
| HES/trehalose 4:1 | 3.74 ±0.12 | 3.40 ± 0.10 | 3.08 ± 0.08 | − |
| HES/trehalose 1:1 | 5.05 ± 0.20 | 4.54 ± 0.16 | 4.09 ±0.13 | 1.28 |
| Trehalose | 10.2 ±0.6 | 9.1 ± 0.5 | 8.2 ± 0.4 | 1.24 |
Fig. 5.
Comparison of relaxation dynamics (ln τ β) [τ in h], reciprocal of fast dynamics amplitude (1/〈u2〉), % decrease in PALS lifetime from base hydroxyethylstarch (HES) for HES/disaccharide systems, and loss of volume on mixing 1:1 systems (µL/g). Relaxation times at 40 °C were taken from a previous report (Ref. [25]), fast dynamics refers to the mean square of the amplitude of motion (Å2) evaluated from neutron scattering at 40 °C, and PALS refers to positron annihilation lifetimes (ns). Error bars indicate estimated standard errors. Note that ΔVmix for trehalose systems is essentially zero so all that is shown on the plot is the error bar.
5. Conclusions
We conclude that density measurements can be interpreted in terms of “free volume” and therefore are potentially relevant to pharmaceutical stability in the amorphous solid state, but when the atomic composition in a series of samples being compared varies, variation in mean atomic density can confound interpretation of density variation in terms only of variation in free volume. The contribution of variable mean atomic density on density variation can be estimated easily using procedures from the literature to calculate “van der Waals density”, but the calculated results may have a residual error on the order of 2% in density, thus precluding applications to problems where density variations are similar or smaller in magnitude. However, without any assumptions, apparent specific volumes and volume changes on mixing may be evaluated from density data, and with plausible assumptions, these quantities may be related to free volume changes upon mixing components, which then may be applied to stability problems. We find that addition of polyols in small amounts to HES/disaccharide systems generally decreases free volume, as determined by examination of either apparent specific volume or volume changes on mixing, and so should stabilize reactive molecules dispersed in these matrices. Sucrose appears to be more effective in reducing free volume of a base HES system than trehalose, and so sucrose should be a better stabilizer. Sucrose is indeed more effective than trehalose in stabilizing hGH at temperatures well below the system Tg [11]. Free volume changes, calculated from density data, fast dynamics evaluated from neutron scattering, and PALS lifetimes, generally are in qualitative agreement for the HES/disaccharide systems studied in that all predict decreasing molecular mobility as disaccharides are added to HES. Global mobility as measured by enthalpy relaxation times, however, predicts higher mobility as disaccharides, particularly sucrose, are added to HES. We conclude that, at least in these formulations, global mobility is not necessarily predictive of variation in local dynamics or “free volume” and therefore may not accurately predict stability variations, a conclusion with ample support in the literature from other formulation studies [3,14,15,20,24].
6. Uncited reference
[27].
Acknowledgement
We acknowledge funding from NIH/NIBIB under Grant R01 EB006398-01A1.
Footnotes
The calculation is illustrated for glycine and tyrosine, representing two extremes, good and poor agreement of density ratios. Van der Waals densities (g/cm3) are 1.304 (sucrose), 1.296 (glycine), and 1.268 (tyrosine). Corresponding experimental crystalline densities (Handbook values) are 1.585 (sucrose), 1.601 (glycine), and 1.456 (tyrosine). Thus, the ratios of van der Waals densities, (sucrose)/(amino acid) are 1.006 (glycine) and 1.028 (tyrosine). The corresponding ratios of crystalline densities are 0.990 (glycine) and 1.088 (tyrosine).
References
- 1.Carpenter JF, Crowe LM, Crowe JH. Stabilization of phosphofructokinase with sugars during freeze-drying: characterization of enhanced protection in the presence of divalent cations. Biochimica et Biophysica Acta. 1987;923:109–115. doi: 10.1016/0304-4165(87)90133-4. [DOI] [PubMed] [Google Scholar]
- 2.Pikal MJ, Freeze drying. In: Encyclopedia of Pharmaceutical Technology. Swarbrick J, editor. New York: Informa Healthcare; 2007. pp. 1807–1833. [Google Scholar]
- 3.Chang L, Pikal MJ. Mechanisms of protein stabilization in the solid state. Journal of Pharmaceutical Sciences. 2009;98(9):2886–2908. doi: 10.1002/jps.21825. [DOI] [PubMed] [Google Scholar]
- 4.Crowe JH, Crowe LM, Carpenter JF. Preserving dry biomaterials: the water replacement hypothesis, Part 1S. Biopharm. 1993;6:28–37. [Google Scholar]
- 5.Pérez-Moral N, Adnet C, Noel TR, Parker R. Characterization of the rate of thermally-induce aggregation of β-lactoglobulin and its trehalose mixtures in the glass state. Biomacromolecules. 2010;11(11):2985–2992. doi: 10.1021/bm100785d. [DOI] [PubMed] [Google Scholar]
- 6.Wang B, Cicerone MT, Aso Y, Pikal MJ. The impact of thermal treatment on the stability of freeze-dried amorphous pharmaceuticals: II. Aggregation in an IgG1 fusion protein. Journal of Pharmaceutical Sciences. 2009;99(2):683–700. doi: 10.1002/jps.21960. [DOI] [PubMed] [Google Scholar]
- 7.Yoshioka S, Yukio A. Correlations between molecular mobility and chemical stability during storage of amorphous pharmaceuticals. Journal of Pharmaceutical Sciences. 2007;96(5):960–981. doi: 10.1002/jps.20926. [DOI] [PubMed] [Google Scholar]
- 8.Buitink J, Dries IJvd, Hoekstra FA, Alberda M, Hemminga MA. High critical temperature above Tg may contribute to the stability of biological systems. Biophysical Journal. 2000;79:1119–1128. doi: 10.1016/S0006-3495(00)76365-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chang BS, Beauvais RM, Dong A, Carpenter JF. Physical factors affecting the storage stability of freeze-dried interleukin-1 receptor antagonist: glass transition and protein conformation. Archives of Biochemistry and Biophysics. 1996;331(2):249–258. doi: 10.1006/abbi.1996.0305. [DOI] [PubMed] [Google Scholar]
- 10.Davidson P, Sun W. Effect of sucrose/raffinose mass ratios on the stability of co-lyophilised protein during storage above the Tg. Pharmaceutical Research. 2001;18:474–479. doi: 10.1023/a:1011002326825. [DOI] [PubMed] [Google Scholar]
- 11.Pikal MJ, Rigsbee DL, Roy M, Galreath D, Kovach KJ, Wang B, Carpenter JF, Cicerone MT. Solid state chemistry of proteins: II. The correlation of storage stability of freeze-dried human growth hormone (hGH) with structure and dynamics in the glassy solid. Journal of Pharmaceutical Sciences. 2008;97(12):5106–5121. doi: 10.1002/jps.21374. [DOI] [PubMed] [Google Scholar]
- 12.Sixou B, Faivre A, David L, Vigier G. Intermolecular and intramolecular contributions to the relaxation process in sorbitol and maltitol. Molecular Physics. 2001;99:1845–1850. [Google Scholar]
- 13.Cicerone MT, Tellington A, Trost L, Sokolov AP. Substantially improved stability of biological agents in dried form. BioProcess International. 2003;1(1):36–47. [Google Scholar]
- 14.Cicerone MT, Soles CL. Fast dynamics and stabilization of proteins: binary glasses of trehalose and glycerol. Biophysical Journal. 2004;86(6):3836–3845. doi: 10.1529/biophysj.103.035519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cicerone MT, Douglas JF. β-relaxation governs protein stability in sugar-glass matrices. Soft Matter. 2012;8(10):2983–2991. [Google Scholar]
- 16.Cohen MH, Turnbull D. Molecular transport in liquids and glasses. Journal of Chemical Physics. 1959;31:1164–1169. [Google Scholar]
- 17.Dlubek G, Shaikh MQ, Krause-Rehberg R, Paluch M. Effect of free volume and temperature on the structural relaxation in polymethylphenylsiloxane: a positron lifetime and pressure-volume-temperature study. Journal of Chemical Physics. 2007;126:024906. doi: 10.1063/1.2406077. [DOI] [PubMed] [Google Scholar]
- 18.Kilburn K, Claude J, Sweitzer T, Alam A, Ubbink J. Carbohydrate polymers in amorphous states: an integrated thermodynamic and nanostructural investigation. Biomacromolecules. 2005;6:864–879. doi: 10.1021/bm049355r. [DOI] [PubMed] [Google Scholar]
- 19.Kikuchi T, Wang BS, Pikal M. High-precision absolute (true) density measurements on hygroscopic powders by gas pycnometry: application to determining effects of formulation and process on free volume of lyophilized products. Journal of Pharmaceutical Sciences. 2011;100(7):2945–2951. doi: 10.1002/jps.22521. [DOI] [PubMed] [Google Scholar]
- 20.Wang B, Tchessalov S, Cicerone MT, Warne NW, Pikal MJ. Impact of sucrose level on storage stability of proteins in freeze-dried solids: II. Correlation of aggregation rate with protein structure and molecular mobility. Journal of Pharmaceutical Sciences. 2009;98(9):3145–3166. doi: 10.1002/jps.21622. [DOI] [PubMed] [Google Scholar]
- 21.Wang B, Pikal MJ. The impact of thermal treatment on the stability of freeze dried amorphous pharmaceuticals: I. Dimer formation in sodium ethacrynate. Journal of Pharmaceutical Sciences. 2009;99(2):663–682. doi: 10.1002/jps.21959. [DOI] [PubMed] [Google Scholar]
- 22.Bakaltcheva I, Ganong J, Holtz B, Peat R, Reid T. Effects of high-molecular-weight cryoprotectants on platelets and the coagulation system. Cryobiology. 2000;40:283–293. doi: 10.1006/cryo.2000.2247. [DOI] [PubMed] [Google Scholar]
- 23.Roy S, Henderson I, Nayar R, Randolph TW, Carpenter JF. Effect of pH on stability of recombinant botulinum serotype A vaccine in aqueous solution and during storage of freeze dried formulations. Journal of Pharmaceutical Sciences. 2008;97:5132–5146. doi: 10.1002/jps.21409. [DOI] [PubMed] [Google Scholar]
- 24.Chang L, Shepherd D, Sun J, Tang X, Pikal MJ. Effect of sorbitol and residual moisture on the stability of lyophilized antibodies: implications for the mechanism of protein stabilization in the solid state. Journal of Pharmaceutical Sciences. 2005;94(7):1445–1455. doi: 10.1002/jps.20363. [DOI] [PubMed] [Google Scholar]
- 25.Chieng N, Mizuno M, Pikal MJ. Relaxation dynamics of complex lyophilized formulations: comparison of relaxation times measured by isothermal calorimetry with data estimated from the width of the glass transition temperature region. European Journal of Pharmaceutics and BioPharmaceutics. doi: 10.1016/j.ejpb.2013.04.003. submitted for publication. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Tao SJ. Positronium annihilation in molecular substances. Journal of Chemical Physics. 1972;56:5499–5510. [Google Scholar]
- 27.Eldrup M, Lightbody D, Sherwood JN. The temperature dependence of positron lifetimes in solid pivalic acid. Journal of Chemical Physics. 1981;63:51–58. [Google Scholar]
- 28.Girolami GS. A simple “Back of the Envelope” method for estimating the densities and molecular volumes of liquids and solids. Journal of Chemical Education. 1994;71(11):962–964. [Google Scholar]
- 29.Lewis GN, Randall M, Pitzer KS, L Brewer. Thermodynamics. New York, NY: McGraw Hill Publishers; 1961. [Google Scholar]
- 30.Naoki M, Ujita K, Kashima S. Pressure-volume-temperature relations and configurational energy of liquid, crystal and glasses of D-sorbitol. Journal of Physical Chemistry. 1993;97:12356–12362. [Google Scholar]
- 31.Blazhnov IV, Malomuzh NP. Temperature dependence of density, thermal expansion coefficient and shear viscosity of supercooled glycerol as a reflection of its structure. Journal of Chemical Physics. 2004;121:6435–6441. doi: 10.1063/1.1789474. [DOI] [PubMed] [Google Scholar]
- 32.Ubbelohde AR. Melting and Crystal Structure. Oxford: Clarendon; 1965. [Google Scholar]