Structural Optimization by Quantum Monte Carlo: Investigating the Low-Lying Excited States of Ethylene

Abstract

We present full structural optimizations of the ground state and of the low lying triplet state of the ethylene molecule by means of Quantum Monte Carlo methods. Using the efficient structural optimization method based on renormalization techniques and on adjoint differentiation algorithms recently proposed [Sorella, S.; Capriotti, L. J. Chem. Phys. 2010, 133, 234111], we present the variational convergence of both wave function parameters and atomic positions. All of the calculations were done using an accurate and compact wave function based on Pauling’s resonating valence bond representation: the Jastrow Antisymmetrized Geminal Power (JAGP). All structural and wave function parameters are optimized, including coefficients and exponents of the Gaussian primitives of the AGP and the Jastrow atomic orbitals. Bond lengths and bond angles are calculated with a statistical error of about 0.1% and are in good agreement with the available experimental data. The Variational and Diffusion Monte Carlo calculations estimate vertical and adiabatic excitation energies in the ranges 4.623(10)–4.688(5) eV and 3.001(5)–3.091(5) eV, respectively. The adiabatic gap, which is in line with other correlated quantum chemistry methods, is slightly higher than the value estimated by recent photodissociation experiments. Our results demonstrate how Quantum Monte Carlo calculations have become a promising and computationally affordable tool for the structural optimization of correlated molecular systems.

1. INTRODUCTION

Quantum Monte Carlo (QMC) methods have been successfully applied to tackle the electronic structure of molecules and solids where electron correlation plays an important role.^1,2 In the past decade, a rapid improvement of algorithms opened the door to the QMC study of the ground state properties of several highly correlated systems in chemistry and physics, such as transition metal complexes,^3,4 graphene,⁵ hydrogen bonding systems,^6–8 dispersive interactions,⁹ and high pressure hydrogen.¹⁰

The success of these stochastic methods is due to their capability to correctly describe the electronic states of the system and, at the same time, due to the possibility of their handling a relatively large number of atoms. The good scaling properties with the number of electrons together with the excellent portability of the algorithms on high performance parallel computers make these methods particularly promising for quantum chemistry calculations of large and correlated systems. The calculations proposed in the present work are based on highly compact and correlated variational wave functions inspired by Pauling’s resonating valence bond (RVB) representation of the chemical bond: the Jastrow Antisymmetrized Geminal Power (JAGP), as introduced in refs 11 and 12. This resonating valence bond ansatz is able to correctly describe the statical and dynamical correlation of a large variety of molecular systems.^3,5,6,9,13

One historical difficulty with QMC methods is efficiently evaluating forces, due to problems arising from the stochastic noise. Several solutions have been proposed, like those based on the zero-variance principle,¹⁴ on correlated sampling,¹⁵ and on the introduction of particular coordinate transformations.¹⁶ However, all of these approaches have the inconvenience of becoming unfeasible for large systems, due to the fact that the number of coordinate derivatives increases linearly with the system’s size. Recently, an efficient scheme to compute forces with quantum Monte Carlo has been proposed by means of the so-called adjoint algorithmic differentiation,¹⁷ through which full structural optimization of systems of few atoms can be performed with small computational overhead.

In the present paper, we apply this technique to study the ground and excited state properties of ethylene. Besides its important role in industry and medicine, ethylene has been the subject of many experimental and high level computational works since it represents the prototype for a double carbon bond in organic molecules.¹⁸ In addition, its singlet to triplet interconversion is a model for the photochemistry of larger conjugated organic molecules and polymers.

Since the early investigations of the properties of ethylene’s ¹A_g ground state (N), the first singlet excitation (V), the vertical triplet excitation (T), and Rydberg states, identified by Mulliken and Wilkinson,^18,19 were an interesting and quite challenging subject because of the significant change in the geometrical structure induced by the electronic excitations. While the dominant line in ethylene’s spectrum has been recognized as the V(¹B_1u)←N(¹A_g) singlet excitation with an estimated energy of about ~7.6 eV,^19,20 many experimental studies, through optical²¹ and low-energy electron impact spectroscopies,^22–25 have assigned to the vertical triplet excitation T(³B_1u)←N(¹A_g) an energy gap between 4.32 and 4.70 eV. A lower bound of the gap equal to 4.3 eV has been also reported by ion impact spectroscopy.²⁶ The adiabatic vertical excitation, namely, the energy gap between the equilibrium ground state and the triplet state at its equilibrium geometry T(³A₁)←N(¹A_g), has been recently identified during the dissociation dynamics of ethylene sulfide SC₂H₃ by Qi et al. Through the time-of-flight (TOF) spectra of photofragments from photodissociation, they were able to produce ethylene’s T state near its equilibrium geometry ³A₁, estimating an energy gap T ←N of about 2.52(13) eV.²⁷ Many computational efforts have been spent to identify the N, V, and T states of ethylene and to evaluate the vertical excitations between the singlet (¹A_g) and the low lying vertical (³B_1u) and adiabatic (³A₁) triplets.^28–34

In the present work, we use variational Monte Carlo methods to fully optimize the wave functions and the molecular geometries of ethylene in both the singlet and triplet states. The vertical and adiabatic triplet excitation energies will be estimated using the variational Monte Carlo (VMC) and lattice regularized diffusion Monte Carlo (LRDMC)^35,36 methods, comparing the obtained results with the available experimental data and with other quantum chemistry calculations.

2. QUANTUM MONTE CARLO METHODS

Variational Monte Carlo methods are based on the stochastic evaluation of the energy functional

$$E\left[{\Psi }_{\mathrm{T}}\right(\{\overline{\alpha },\overline{\mathbf{R}}\}\left)\right]=\frac{\int \mathrm{d}\overline{\mathbf{r}}{\Psi }_{\mathrm{T}}^{\ast }(\overline{\mathbf{x}};\{\overline{\alpha },\overline{\mathbf{R}}\left\}\right)\widehat{H}{\Psi }_{\mathrm{T}}(\overline{\mathbf{x}};\{\overline{\alpha },\overline{\mathbf{R}}\left\}\right)}{\int \mathrm{d}\overline{\mathbf{r}}{\mid {\Psi }_T(\overline{\mathbf{x}};\{\overline{\alpha },\overline{\mathbf{R}}\left\}\right)\mid }^2}$$ (1)

with respect to a trial wave function ${\Psi }_{\mathrm{T}}(\overline{\mathbf{x}};\{\overline{\alpha },\overline{\mathbf{R}}\left\}\right)=\langle \overline{\mathbf{x}}\mid {\Psi }_{\mathrm{T}}\left(\right\{\overline{\alpha },\overline{\mathbf{R}}\left\}\right)\rangle$, where $\overline{\mathbf{x}}$ is the 6N-dimensional vector of the electronic Cartesian $\overline{\mathbf{r}}=\{{\mathbf{r}}_i,i=1,\dots ,N\}$ and spin coordinates, $\overline{\alpha }$ is a set of independent wave function parameters, $\overline{\mathbf{R}}=\{{\mathbf{R}}_a,a=1,\dots ,M\}$ is the vector of the nuclear coordinates, and $\widehat{H}$ is the molecular Hamiltonian. In order to stochastically evaluate the functional eq 1, it is convenient to rewrite the integrand as the product of two local functions:

$$E\left[{\Psi }_{\mathrm{T}}\right(\{\overline{\alpha },\overline{\mathbf{R}}\}\left)\right]=\int \mathrm{d}\overline{\mathbf{r}}{E}_L\left(\overline{\mathbf{x}}\right)\Pi \left(\overline{\mathbf{x}}\right)$$ (2)

the local energy $E_{\mathrm{L}}\left(\overline{\mathbf{x}}\right)=(\langle \overline{\mathbf{x}}\mid \widehat{H}\mid {\Psi }_{\mathrm{T}}(\{\overline{\alpha },\overline{\mathbf{R}}\})\rangle )∕(\langle \overline{\mathbf{x}}\mid {\Psi }_{\mathrm{T}}(\{\overline{\alpha },\overline{\mathbf{R}}\})\rangle )$, i.e., the energy of a single electronic configuration $\overline{\mathbf{x}}$, and ${\Pi }_{\left(\overline{\mathbf{x}}\right)}=\left({\mid {\Psi }_{\mathrm{T}}(\overline{\mathbf{x}};\{\overline{\alpha },\overline{\mathbf{R}}\left\}\right)\mid }^2\right)∕(\int \mathrm{d}r{\mid {\Psi }_{\mathrm{T}}(\overline{\mathbf{x}};\{\overline{\alpha },\overline{\mathbf{R}}\left\}\right)\mid }^2)$, which is the probability to visit that particular configuration in space. The integral written in the form of eq 2 can now be evaluated as the mean value of the local energy, $E\sim {\langle E_{\mathrm{L}}\left(\overline{\mathbf{x}}\right)\rangle }_{\Pi \left(\overline{\mathbf{x}}\right)}$, calculated on a number $\mathcal{N}$ of electronic configurations $\overline{\mathbf{x}}$, sampled with probability $\Pi \left(\overline{\mathbf{x}}\right)$. The error associated with this estimation will be equal to ${\left(\right(1∕\mathcal{N}\left)\right({\langle {E_{\mathrm{L}}}^2\left(\overline{\mathbf{x}}\right)\rangle }_{\Pi \left(\overline{\mathbf{x}}\right)}-\langle E_L\left(\overline{\mathbf{x}}\right)\rangle {{}_{\Pi \left(\overline{\mathbf{x}}\right)}}^2\left)\right)}^{1∕2}$, decreasing as the square root of the number of samples of the configuration space independently of the dimension of the system. Expression 1 can be minimized with respect to the set of parameters $\overline{\alpha }$ obtaining

$$E_{\mathrm{VMC}}=\underset{\overline{\alpha }}{\min }E\left[{\Psi }_{\mathrm{T}}\right(\{\overline{\alpha },\overline{\mathbf{R}}\}\left)\right]$$ (3)

According to the variational principle, E_VMC represents the lowest upper bound of the ground state energy E₀ for a given variational wave function. The $\overline{\alpha }$ set of parameters of the many-body wave function can be optimized using stochastic evaluation of the energy derivatives recently developed.^9,37,38

The QMC methods also include a variety of projection methods such as diffusion² and Green’s function³⁹ Monte Carlo that can go beyond the variational ansantz having direct access to the lowest energy eigenvalue given the nodal surface determined by ${\Psi }_{\mathrm{T}}\left(\overline{\mathbf{x}}\right)$. In particular, the lattice regularized diffusion Monte Carlo^35,36 method can offer two advantages with respect to the traditional diffusion Monte Carlo (DMC) algorithms. First of all, it is size-consistent, so that it maintains its efficiency during the correlated metropolis sampling even for systems with a large number of electrons.³⁶ The second important advantage is that the LRDMC method preserves the variational principle even when used in combination with nonlocal pseudopotentials.³⁶ Both projection methods introduce a systematic error either by the discretization τ of the imaginary time propagator (DMC) or by the spatial discretization of the molecular Hamiltonian on a lattice grid of step a (LRDMC). These errors are overcome by extrapolating the estimated energy, for different a or τ steps, to the continuum limit a, τ→0.

3. STRUCTURAL OPTIMIZATION AND FORCE CALCULATION IN VMC

The structural optimization of molecular systems within the VMC scheme corresponds to minimizing expression 3 with respect to both sets of parameters $\{\overline{\alpha },\overline{\mathbf{R}}\}$, the parameters of the electronic wave function, and the coordinates of the nuclei:

$$E_{\mathrm{VMC}}^{\mathrm{OPT}}=\underset{\{\overline{\alpha },\overline{\mathbf{R}}\}}{\min }E[\overline{\mathbf{R}};{\Psi }_{\mathrm{T}}(\{\overline{\alpha },\overline{\mathbf{R}}\}\left)\right]$$ (4)

where we have explicitly written the dependency of the energy functional E from $\overline{\mathbf{R}}$ through the Hamiltonian $\widehat{H}\left(\overline{\mathbf{R}}\right)$. The optimization requires the evaluation of the force vectors acting along all of the coordinates $\overline{\mathbf{R}}$ of the nuclei, defined as

$${\mathbf{F}}_a\left(\overline{\mathbf{R}}\right)=-{\nabla }_{{\mathbf{R}}_a}{E}_{\mathrm{VMC}}\left(\right\{\overline{\mathbf{R}};\overline{\alpha }\left(\overline{\mathbf{R}}\right)\left\}\right)$$ (5)

where $\overline{\alpha }\left(\overline{\mathbf{R}}\right)$ implicitly depends on $\overline{\mathbf{R}}$ since the minimum energy condition (eq 3) has to be satisfied at fixed $\overline{\mathbf{R}}$. In general, the calculation of forces in QMC is done through two approaches. A first method is the finite difference approach for which the derivatives of the energy functional with respect to the atomic displacements are defined through a space discretization, leading to the equation

$${\mathbf{F}}_a\left(\overline{\mathbf{R}}\right)=-\underset{\Delta {\mathbf{R}}_a\to 0}{\lim }\frac{E_{\mathrm{VMC}}\left(\right\{{\overline{\mathbf{R}}}^{\prime };\overline{\alpha }\left({\overline{\mathbf{R}}}^{\prime }\right)\left\}\right)-E_{\mathrm{VMC}}\left(\right\{\overline{\mathbf{R}};\overline{\alpha }\left(\overline{\mathbf{R}}\right)\left\}\right)}{\Delta {\mathbf{R}}_a}$$ (6)

where ${\overline{\mathbf{R}}}^{\prime }=\overline{\mathbf{R}}+\Delta {\mathbf{R}}_a$ is the new geometrical configuration after the displacement ΔR_a of the ath nucleus, and $E_{\mathrm{VMC}}\left(\right\{{\overline{\mathbf{R}}}^{\prime };\overline{\alpha }\left({\overline{\mathbf{R}}}^{\prime }\right)\left\}\right)$ is the variational energy (eq 3) evaluated in the new positions ${\overline{\mathbf{R}}}^{\prime }$ with the optimized wave function ${{\Psi }^{\prime }}_{\mathrm{T}}\left(\right\{{\overline{\alpha }}^{\prime },{\overline{\mathbf{R}}}^{\prime }\left\}\right)$. Unfortunately, in QMC, the values of the energy for the two structural geometries are affected by a stochastic error that propagates in the calculation of forces, increasing when ΔR_a → 0. For this reason, the finite difference approach is usually carried out using the correlated sampling technique. This technique reduces the stochastic error when evaluating energy differences by estimating both of the variational energies in eq 6 using the same Monte Carlo random walk.¹⁵

The second approach for evaluating forces is to directly estimate the analytic derivative of eq 5 that gives the expression

$$\begin{array}{cc}\hfill {\mathbf{F}}_a\left(\overline{\mathbf{R}}\right)=& -\frac{\partial }{\partial {\mathbf{R}}_a}{E}_{\mathrm{VMC}}\left(\right\{\overline{\mathbf{R}};\overline{\alpha }\left(\overline{\mathbf{R}}\right)\left\}\right)\hfill \\ \hfill & -\frac{\partial }{\partial \overline{\alpha }\left(\overline{\mathbf{R}}\right)}{E}_{\mathrm{VMC}}\left(\right\{\overline{\mathbf{R}};\overline{\alpha }\left(\overline{\mathbf{R}}\right)\left\}\right)\times \frac{d\overline{\alpha }\left(\overline{\mathbf{R}}\right)}{d{\mathbf{R}}_a}\hfill \end{array}$$ (7)

The second term in this definition can be neglected for the Euler conditions $(\partial E_{\mathrm{VMC}}∕\partial \overline{\alpha }(\overline{\mathbf{R}})=0)$ at the energy minimum (eq 3). For this reason, we are left with the equation ${\mathbf{F}}_a\left(\overline{\mathbf{R}}\right)=-\partial E_{\mathrm{VMC}}∕\partial {\mathbf{R}}_a$, which following the notation introduced in section 2 can be rewritten as the sum of two contributions:^40,41

$$\begin{array}{cc}\hfill {\mathbf{F}}_a\left(\overline{\mathbf{R}}\right)=& -{\langle \frac{{\mathit{dE}}_{\mathrm{L}}\left(\overline{\mathbf{x}}\right)}{d{\mathbf{R}}_a}\rangle }_{\Pi \left(\overline{\mathbf{x}}\right)}\hfill \\ \hfill & +2\{{\langle E_{\mathrm{L}}\left(\overline{\mathbf{x}}\right)\rangle }_{\Pi \left(\overline{\mathbf{x}}\right)}{\langle \frac{d\ln \left[{\Psi }_{\mathrm{T}}\right(\overline{\mathbf{x}}\left)\right]}{d{\mathbf{R}}_a}\rangle }_{\Pi \left(\overline{\mathbf{x}}\right)}\hfill \\ \hfill & -{\langle E_{\mathrm{L}}\left(\overline{\mathbf{x}}\right)\frac{d\ln \left[{\Psi }_{\mathrm{T}}\right(\overline{\mathbf{x}}\left)\right]}{d{\mathbf{R}}_a}\rangle }_{\Pi \left(\overline{\mathbf{x}}\right)}\}\hfill \\ \hfill =& {\mathbf{F}}_a^{\mathrm{H}-\mathrm{F}}\left(\overline{\mathbf{R}}\right)+{\mathbf{F}}_a^{\mathrm{P}}\left(\overline{\mathbf{R}}\right)\hfill \end{array}$$ (8)

that are respectively the Hellmann–Feynman (H–F) ${\mathbf{F}}_a^{\mathrm{H}-\mathrm{F}}\left(\overline{\mathbf{R}}\right)$ and Pulay (P) ${\mathbf{F}}_a^{\mathrm{P}}\left(\overline{\mathbf{R}}\right)$ terms. The Pulay term is exactly zero in two cases: when working with an exact eigenstate in the limit of complete basis sets and if the trial wave function is expanded into an originless basis set such as plane waves. In our case, the Pulay term cannot be neglected as discussed in ref 40.

Our approach to the evaluation of the analytic eq 8 in the VMC frame is characterized by the introduction of three ingredients. The first of these ingredients is the space warp coordinate transformation (SWCT), that together with the second ingredient of our procedure, which is the reweighting method defined in ref 41, is able to reduce the variance of the forces.¹⁷ When using pseudopotentials in the SWCT scheme, the analytic calculation of derivatives becomes prohibitive. To overcome this drawback, we used the adjoint algorithm differentiation (AAD), obtaining overall a computational cost that does not grow linearly with the system size, at variance with the methods based on the numerical derivative. In the next paragraphs, we will briefly describe these three techniques that lead to a new expression of the force components, as described by Sorella and Capriotti in ref 17.

Space Warp Coordinate Transformation

To derive our convenient analytic expression of the force components, we used the Space Warp Coordinate Transformation first introduced to calculate atomic forces within the VMC and DMC methods within the finite difference approach.^14–16,42 In ref 17 it is shown that the introduction of this transformation in the definition of the energy functional, used with the reweighting method, has the advantage of reducing the variance and also treating nonlocal pseudopotentials. Within this transformation scheme, each ionic displacement ΔR_a is followed by the translation of the electronic positions around the nuclei, through the equations:

$$\{\begin{array}{c}{{\mathbf{r}}^{\prime }}_i={\mathbf{r}}_i+\Delta {\mathbf{R}}_a{\omega }_a\left({\mathbf{r}}_i\right)\hfill \\ {\omega }_a\left({\mathbf{r}}_i\right)=\frac{F\left(r_{\mathit{ia}}\right)}{\sum _{b=1}^{M}F\left(r_{\mathit{ib}}\right)}\hfill \end{array}$$ (9)

where F(r_ia) should be a function that decays rapidly; in this case, it is taken to be $1∕r_{\mathit{ia}}^4$ as proposed in ref 15, with r_ia = ∣r_i – R_a∣. Within the SWCT, the energy functional (eq 1), after the displacement of a single nuclei $\Delta {\overline{\mathbf{R}}}_a$, assumes the form

$$E\left[{\Psi }_{\mathrm{T}}\right(\left\{{\overline{\mathbf{R}}}^{\prime }\right\}\left)\right]=\frac{\int \mathrm{d}\overline{\mathbf{r}}{J}_{\Delta {\mathbf{R}}_a}\left(\overline{\mathbf{r}}\right){\mid {\Psi }_{\mathrm{T}}\left({\overline{\mathbf{x}}}^{\prime }\right)\mid }^2{E}_{\mathrm{L}}^{\Delta {\mathbf{R}}_a}\left({\overline{\mathbf{x}}}^{\prime }\right)}{\int \mathrm{d}\overline{\mathbf{r}}{J}_{\Delta {\mathbf{R}}_a}\left(\overline{\mathbf{r}}\right){\mid {\Psi }_{\mathrm{T}}\left({\overline{\mathbf{x}}}^{\prime }\right)\mid }^2}$$ (10)

where $J_{\Delta {\mathbf{R}}_a}\left(\overline{\mathbf{r}}\right)$ is the Jacobian of the transformation (eq 9) and both the local energy and the wave function depend on the new nuclear displacement both directly and through the transformed electronic coordinates ${\overline{\mathbf{x}}}^{\prime }$. Equation 10 can be easily differentiated with respect to ΔR_a in the limit of ΔR_a →0, leaving us with the differential expression of the force acting on the ath nucleus:

$$\begin{array}{cc}\hfill {\mathbf{F}}_a=& -{\langle \frac{{\mathit{dE}}_{\mathrm{L}}\left(\overline{\mathbf{x}}\right)}{d{\mathbf{R}}_a}\rangle }_{\Pi \left(\overline{\mathbf{x}}\right)}\hfill \\ \hfill & +2\{{\langle E_{\mathrm{L}}\left(\overline{\mathbf{x}}\right)\rangle }_{\Pi \left(\overline{\mathbf{x}}\right)}{\langle \frac{d\ln \left[J^{1∕2}\right(\overline{\mathbf{r}}\left){\Psi }_{\mathrm{T}}\right(\overline{\mathbf{x}}\left)\right]}{d{\mathbf{R}}_a}\rangle }_{\Pi \left(\overline{\mathbf{x}}\right)}\hfill \\ \hfill & -{\langle E_{\mathrm{L}}\left(\overline{\mathbf{x}}\right)\frac{d\ln \left[J^{1∕2}\right(\overline{\mathbf{r}}\left){\Psi }_{\mathrm{T}}\right(\overline{\mathbf{x}}\left)\right]}{d{\mathbf{R}}_a}\rangle }_{\Pi \left(\overline{\mathbf{x}}\right)}\}\hfill \end{array}$$ (11)

This analytic expression is the sum of the two different contributions previously introduced, the Hellmann–Feynman term, which is simply the mean value of the derivative of the local energy, and the Pulay term, which is fundamental for accurate force evaluations, as demonstrated in ref 40.

Taking into account the fact that the electronic coordinates also depend on the nuclear displacement within the SWCT, the total derivatives in eq 11 can be written in terms of partial derivatives of the local energy and of the wave function logarithm:

$$\begin{array}{cc}\hfill \frac{d}{d{\mathbf{R}}_a}& E_{\mathrm{L}}\left(\overline{\mathbf{x}}\right)={\partial }_{{\mathbf{R}}_{\mathrm{a}}}{E}_{\mathrm{L}}\left(\overline{\mathbf{x}}\right)+\sum _{i=1}^N{\omega }_a\left({\mathbf{r}}_i\right){\partial }_{{\mathbf{r}}_i}{E}_{\mathrm{L}}\left(\overline{\mathbf{x}}\right)\hfill \\ \hfill \frac{d}{d{\mathbf{R}}_a}& \ln \left[J^{1∕2}\right(\overline{\mathbf{r}}\left){\Psi }_{\mathrm{T}}\right(\overline{\mathbf{x}}\left)\right]\hfill \end{array}$$ (12)

$$\begin{array}{cc}\hfill =& {\partial }_{{\mathbf{R}}_a}\ln \left[{\Psi }_{\mathrm{T}}\right(\overline{\mathbf{x}}\left)\right]+\sum _{i=1}^N[{\omega }_a\left({\mathbf{r}}_i\right){\partial }_{\mathbf{r}i}\ln \left[{\Psi }_{\mathrm{T}}\right(\overline{\mathbf{x}}\left)\right]\hfill \\ \hfill & +\frac{1}{2}{\partial }_{\mathbf{r}i}{\omega }_a\left({\mathbf{r}}_i\right)]\hfill \end{array}$$ (13)

The force components 11 with the expansions 12 and 13 are the analytic local expressions that we have to sample within our VMC schemes. Although these expressions present an elegant form, they still have an unbounded variance, as described in the next paragraph, so that to obtain a meaningful average some manipulations have to be made.

Reweighting Methods

As anticipated, the Hellmann–Feynman term has unbounded variance when the electron–atom distance vanishes. In our case, this problem is overcome by the fact that the Hellmann–Feynman contribution defined in eq 11 depends on the local energy and not only on the Coulomb potential, which means that with a trial wave function satisfying the electron–ion cusp conditions (as shown in section 4), it remains finite even when the electron ion distance r_ia approaches zero. The H–F term containing only the first derivative of the local energy diverges at most as 1/r_ia, and the variance is therefore finite in three dimensions as $\int \mathrm{d}{\mathrm{r}}^{3}1∕r_{\mathit{ia}}^2$ converges.

Parallel to the variance problem appearing when the electron–ion distances approach zero, there exists also a more subtle infinite variance problem when a sample configuration $\overline{\mathbf{x}}$ approaches the nodal surface, i.e. $\overline{\mathbf{x}}:{\Psi }_{\mathrm{T}}\left(\overline{\mathbf{x}}\right)=0$. Both the H–F and the Pulay terms diverge when a sampled electronic configuration $\overline{\mathbf{x}}$ approaches the nodal surface of the wave function. In this situation, both the local energy and the partial derivative of the logarithm of the wave function are proportional to the inverse of this distance 1/d, while the density probability $\Pi \left(\overline{\mathbf{x}}\right)\simeq d^2$, leading to an unbound variance of their product in the Pulay term or in the local energy derivative that appear in the H–F term (≃ 1/d²), although the mean values remain well-defined. This problem was first tackled by Attaccalite and Sorella in ref 41 with the so-called reweighting method in which a new probability distribution is defined ${\Pi }_{\epsilon }\left(\overline{\mathbf{x}}\right)={\mid {\Psi }_{\mathrm{G}}\left(\overline{\mathbf{x}}\right)\mid }^2$ depending on a guiding function

$${\Psi }_{\mathrm{G}}\left(\overline{\mathbf{x}}\right)=\frac{R_{\epsilon }\left(\overline{\mathbf{x}}\right)}{R\left(\overline{\mathbf{x}}\right)}{\Psi }_{\mathrm{T}}\left(\overline{\mathbf{x}}\right)$$ (14)

where the function $R\left(\overline{\mathbf{x}}\right)$ is a measure of the distance between the electronic configuration $\overline{\mathbf{x}}$ and the nodal surface and therefore is assumed to vanish proportionally to ${\Psi }_{\mathrm{T}}\left(\overline{\mathbf{x}}\right)$ as d → 0. As the nodes of the wave function only depend on its determinantal part, schematized here by a single Slater determinant A, we can assume that the $R\left(\overline{\mathbf{x}}\right)$ depends only on A:⁴¹

$$R\left(\overline{\mathbf{x}}\right)={\left(\sum _{i,j=1}^N{\mid A_{i,j}^{-1}\mid }^2\right)}^{-1∕2}$$ (15)

To regularize the probability density close to the nodal surface, $R_{\epsilon }\left(\overline{\mathbf{x}}\right)$ is defined as

$$R_{\epsilon }\left(\overline{\mathbf{x}}\right)=\{\begin{array}{cc}\hfill R\left(\overline{\mathbf{x}}\right)\hfill & R\left(\overline{\mathbf{x}}\right)\ge \epsilon \hfill \\ \hfill \epsilon {\left[\frac{R\left(\overline{\mathbf{x}}\right)}{\epsilon }\right]}^{R\left(\overline{\mathbf{x}}\right)∕\epsilon }\hfill & R\left(\mathbf{x}\right)<\epsilon \hfill \end{array}$$ (16)

where ε is a positive small number chosen to reduce the number of electron configurations that approach the nodal surface. This renormalization has the advantage of satisfying the continuity of the derivate of the ${\Psi }_{\mathrm{G}}\left(\overline{\mathbf{x}}\right)$ when $R\left(\overline{\mathbf{x}}\right)=\epsilon$, ensuring that Ψ_G stays as close as possible to the trial wave function. In this new scheme, the Hellmann–Feynman and Pulay terms are written as

$${\mathbf{F}}_a^{\mathrm{H}-\mathrm{F}}=-\frac{1}{\langle S\left(\overline{\mathbf{x}}\right)\rangle {}_{{\Pi }_{\epsilon }}\left(\overline{\mathbf{x}}\right)}{\langle S\left(\overline{\mathbf{x}}\right)\frac{{\mathit{dE}}_{\mathrm{L}}\left(\overline{\mathbf{x}}\right)}{d{\mathbf{R}}_a}\rangle }_{{\Pi }_{\epsilon }\left(\overline{\mathbf{x}}\right)}$$ (17)

$$\begin{array}{cc}\hfill {\mathbf{F}}_a^{\mathrm{P}}=& \frac{2}{{\langle S\left(\overline{\mathbf{x}}\right)\rangle }_{{\Pi }_{\epsilon }\left(\overline{\mathbf{x}}\right)}}\hfill \\ \hfill & \times {\{\frac{{\langle S\left(\overline{\mathbf{x}}\right)E_{\mathrm{L}}\left(\overline{\mathbf{x}}\right)\rangle }_{{\Pi }_{\epsilon }\left(\overline{\mathbf{x}}\right)}}{{\langle S\left(\overline{\mathbf{x}}\right)\rangle }_{{\Pi }_{\epsilon }\left(\overline{\mathbf{x}}\right)}}\langle S\left(\overline{\mathbf{x}}\right)\frac{d\ln \left[J^{1∕2}\right(\overline{\mathbf{r}}\left){\Psi }_{\mathrm{T}}\right(\overline{\mathbf{x}}\left)\right]}{d{\mathbf{R}}_a}\rangle }_{{\Pi }_{\epsilon }\left(\overline{\mathbf{x}}\right)}\hfill \\ \hfill & -{\langle S\left(\overline{\mathbf{x}}\right)E_{\mathrm{L}}\left(\overline{\mathbf{x}}\right)\frac{d\ln \left[J^{1∕2}\right(\overline{\mathbf{r}}\left){\Psi }_{\mathrm{T}}\right(\overline{\mathbf{x}}\left)\right]}{d{\mathbf{R}}_a}\rangle }_{{\Pi }_{\epsilon }\left(\overline{\mathbf{x}}\right)}\}\hfill \end{array}$$ (18)

where the reweighting factor $S\left(\overline{\mathbf{x}}\right)={\left({\Psi }_{\mathrm{T}}\right(\overline{\mathbf{x}})∕{\Psi }_{\mathrm{G}}(\overline{\mathbf{x}}\left)\right)}^2$ is proportional to d² and cancels out the divergence of the integrand, solving the problem of unbounded variance in the VMC scheme.

Adjoint Algorithm Differentiation

Although the reweighting method cures the variance problems of eq 11, we are still left with the computational challenge of evaluating the derivatives of the local energy and of the logarithms that appear in eqs 12 and 13. The presence of pseudopotentials and SWCT makes the practical implementation of the analytic derivatives extremely complicated. To overcome this drawback, we efficiently computed the derivative using the third feature of our structural optimization method which is the adjoint algorithmic differentiation procedure.¹⁷ The idea beyond the algorithmic differentiation is that a derivate can always be written using the chain rule as the propagation of the derivatives of simpler functions that are known (polynomials, cosines, sines, etc). Following the chain rule, intermediate results can be stored in memory and used to calculate other derivatives that share the same intermediate values. These procedure can be applied either in a backward or forward sweep, as described in ref 43. A clear example on how the calculation of the kinetic energy derivatives is done through the AAD can be found in ref 17. In summary, the inclusion of AAD is a very convenient way to deal with analytical derivatives using pseudopotentials and SWCT. The computational overload for calculating forces in the proposed scheme does not have any linear dependence on the system size and allows us to optimize wave functions and geometries of large molecular systems.

4. VARIATIONAL WAVE FUNCTION

The trial wave function used in this investigation is the Jastrow antisymmetrized geminal power,¹¹ which is an implementation of Pauling’s valence bond picture.⁴⁴ This wave function is built as the product between an antisymmetric geminal power (AGP)^45,46 and a Jastrow factor $J\left(\overline{\mathbf{r}}\right)$ and includes both static and dynamical electron correlation effects. It has been demonstrated that the JAGP^11–13,41 is a compact and reliable wave function for describing the bonding properties of organic molecular systems like graphene sheets⁵ and benzene molecules,⁴⁷ and in reproducing the weak binding energies in van der Waals interactions⁹ and hydrogen bonds.⁶

For molecular systems of N electrons in a spin singlet state, i.e., N/2 = N^↑ = N^↓, the AGP is written as the product

$${\Psi }_{\mathrm{AGP}}\left(\overline{\mathbf{x}}\right)=\widehat{A}\left[\prod _{i=1}^{N∕2}{\Phi }_{\mathrm{G}}\right({\mathbf{x}}_i^{\uparrow };{\mathbf{x}}_i^{\downarrow }\left)\right]$$ (19)

where $\overline{\mathbf{x}}$ is the whole set of Cartesian and spin coordinates of the N electrons and $\widehat{A}$ is the antisymmetrization operator. The two electron wave functions that appear in the definition 19 are the Geminal pairing functions

$${\Phi }_{\mathrm{G}}({\mathbf{x}}_i;{\mathbf{x}}_j)={\varphi }_{\mathrm{G}}({\mathbf{r}}_i,{\mathbf{r}}_j)\frac{1}{\sqrt{2}}(\mid {\uparrow \rangle }_i\mid {\downarrow \rangle }_j-\mid {\uparrow \rangle }_j\mid {\downarrow \rangle }_i)$$ (20)

written as a spin singlet multiplied by a spatial part ϕ_G(r_i,r_j), which is a linear combination of products of two atomic orbitals:

$${\varphi }_{\mathrm{G}}({\mathbf{r}}_i,{\mathbf{r}}_j)=\sum _{a,b=1}^M\sum _{\mu ,\nu }{\lambda }_{{\mu }_a{\nu }_b}{\Psi }_{{\mu }_a}\left({\mathbf{r}}_i\right){\Psi }_{{\nu }_b}\left({\mathbf{r}}_j\right)$$ (21)

the indices μ and ν represent the quantum numbers (n,l,l_z) of the orbitals centered on the ath and bth atoms.

These pairing functions couple electrons belonging to different atoms according to the matrix λ_μaνb in a resonating valence bond scheme, similar to that proposed a b by Anderson in the study of oxide superconductors.⁴⁸

The 1A_g ground state of the ethylene molecule can be correctly described using the AGP (eq 21) wave function because it is a singlet state. To represent molecular excitations with total spin S > 0, like the two triplet states ³B_1u and ³A₁ of ethylene, it is necessary to apply the generalized antisymmetric geminal power wave function (GAGP), introduced by Coleman in 1965.^49,50 Assuming that the number of spin-up electrons exceeds the number of electrons with opposite spin N^↑ > N^↓, the GAGP is built as the antisymmetric product:

$${\Psi }_{\mathrm{GAGP}}\left(\overline{\mathbf{x}}\right)=\widehat{A}\left[\prod _{i=1}^{N\downarrow }{\Phi }_{\mathrm{G}}\right({\mathbf{x}}_i^{\uparrow };{\mathbf{x}}_i^{\downarrow }\left)\prod _{s=1}^S{\Phi }_s\right({\mathbf{x}}_{N^{\downarrow }+s}^{\uparrow }\left)\right]$$ (22)

that along with N^↓ geminal functions 21, contains S = (N^↑ – N^↓) single electron wave functions:

$${\Phi }_s\left({\mathbf{x}}_i\right)=\sum _{a=1}^M\sum _{\mu }{\lambda }_{{\mu }_a}^s{\Psi }_{{\mu }_a}\left({\mathbf{r}}_i\right)\mid \uparrow \rangle s=1,\dots ,S$$ (23)

One fundamental ingredient of the JAGP is the Jastrow factor¹³ that includes a homogeneous interaction that treats the electron–electron and electron–nucleus cusps conditions⁵¹ and a non homogeneous contribution that introduces dynamical correlations between electrons and nuclei. In our representation, the Jastrow factor is written as the product of three terms, J = J₁J₂J_3/4. The first term is the one-body Jastrow factor:

$$\begin{array}{cc}\hfill J_1(\overline{\mathbf{R}},\overline{\mathbf{r}})=& \exp \left(\sum _{a,1}\right\{-{\left(2Z_a\right)}^{3∕4}\xi \left({\left(2Z_a\right)}^{1∕4}{r}_{\mathit{ia}}\right)\hfill \\ \hfill & +{\Xi }_a\left({\mathbf{r}}_i\right)\left\}\right)\hfill \end{array}$$ (24)

where r_ia = ∣r_i – R_a∣ is the distance between the ith electron and the ath nucleus, Z_a is the atomic charge, M is the number of atoms in the molecular compound, and N is the total number of electrons. This factor includes both the homogeneous interaction between the electron and the nuclei through the function ξ(r) = B/2(1 – e^−r/B), and the non homogeneous term built from the linear combination of atomic orbitals $\Xi \left({\mathbf{r}}_i\right)={\Sigma }_{{\mu }_a}{g}_{{\mu }_a}{x}_{{\mu }_a}\left({\mathbf{r}}_i\right)$.

The second term is the purely homogeneous two-body factor

$$J_2\left(\overline{\mathbf{r}}\right)=\exp \left\{\sum _{i<j=1}^N\xi \right(r_{\mathit{ij}}\left)\right\}$$ (25)

that depends only on the distances r_ij = ∣r_i – r_j∣ between electron pairs, treating the electron–electron cusp conditions of the JAGP wave function through the function ξ(r_ij) = b/2(1 – e^−r_ij/b).

The last term is the three/four-body Jastrow J_3/4 that includes the electron–electron–nuclei correlation

$$J_{3∕4}\left(\overline{\mathbf{r}}\right)=\exp \left\{\sum _{i<j=1}^N\varpi \right({\mathbf{r}}_i,{\mathbf{r}}_j\left)\right\}$$ (26)

where

$$\varpi ({\mathbf{r}}_i,{\mathbf{r}}_j)=\sum _{a,b=1}^M\sum _{{\mu }_a{\nu }_b}{g}_{{\mu }_a{\nu }_b}{\chi }_{{\mu }_a}\left({\mathbf{r}}_i\right){\chi }_{{\nu }_b}\left({\mathbf{r}}_j\right)$$ (27)

The contributions with a = b represent the three-body terms that consider correlations between electrons occupying shells of the same atom, whereas terms with a ≠ b are four-body terms that consider the coupling between orbitals of different atomic centers, crucial for the correct description of dispersive interactions.⁶

5. COMPUTATIONAL DETAILS

The computational investigation of our systems has been carried on using the TurboRVB package developed by Sorella⁵² that includes a complete suite of variational and diffusion quantum Monte Carlo programs for wave function and geometry optimization of molecules and solids.

All-Electron Calculations—JAGP

As starting points for the construction of the all-electron basis sets of the AGP wave functions, we used the cc-pVDZ and cc-pVTZ basis sets.^53,54 We considered only s, p, and d shells for the carbon atoms and the s and p shells for hydrogen atoms. We included only the terms of the contractions with smaller exponents, since the electron–nuclei cusps are already described through the Jastrow factor. Finally, we obtained the following contracted basis sets: 8s4p1d composed of (8s4p1d)/[3s2p1d] orbitals for the carbon atom and (4s1p)/[2s1p] contracted orbitals for the hydrogen atoms and 9s5p2d built of (9s5p2d)/[4s3p2d] orbitals for the carbon atom and (5s2p)/[3s2p] orbitals for the hydrogen atoms. For the Jastrow factor J_3/4, we used an uncontracted Gaussian basis set of (2s2p) orbitals and (1s1p) for carbon and hydrogen atoms, respectively.

The wave function was optimized through different steps using the linear method described in refs 9 and 37. As a first step, we optimized only the λ coefficients of the JAGP and the J₂ Jastrow factor. In the second step, we optimized only the J₁ and J_3/4 terms, keeping all other parameters fixed. Finally, we fully relaxed all of the parameters of the wave function including the exponents and coefficients of the atomic orbital basis sets. During the optimization procedure, we used an increasing statistical accuracy for each step, ranging from 6.4 × 10³ to 3.2 × 10⁵ Monte Carlo (MC) steps per electron. VMC and LRDMC calculations at the energy minimum were carried on using 5.1 × 10⁷ and 1.3 × 10⁷ MC steps per electron, respectively. LRDMC energies were extrapolated in the limit a→0 using the following set of lattice space discretizations: a = {0.05, 0.10, 0.15, 0.2} [au].

All-Electron Calculations—JAGPn*

Together with the standard JAGP wave function optimization, we have also employed the JAGPn* method introduced recently in ref 13. The method adopts a projection scheme to reduce the total number of parameters (in particular the λ matrix) in the JAGP wave function. The optimization of the parameters is performed under the constraint of keeping fixed the number n of molecular orbitals considered in the AGP expansion to an appropriate number. For ethylene’s ground state, we considered n = 8 (corresponding to the minimum number of molecular orbitals, i.e., a single Slater determinant) and the optimal value n = n* = 12, which corresponds to the number of occupied orbitals of the totally dissociated molecule, as described in ref 13. For the triplet states of ethylene, the minimum number of molecular orbitals is equal to n = 9, whereas n* = 12 as in the singlet case. As a starting point for these optimization procedures, we used molecular orbitals previously obtained through density functional theory (DFT) calculations with the B3LYP hybrid functional. All parameters were optimized with the same procedure described above for the JAGP with maximum statistics of 3.2 × 10⁵ MC steps per electron.

Pseudopotential Calculations

To investigate the influence of the explicit treatment of core electrons on the geometrical and electronic properties, we have employed different pseudopotentials: a scalar-relativistic energy consistent pseudopotential (SR-ECP),⁵⁵ a smooth relativistic norm-conserving pseudopotential (SR-NCP),⁵⁶ and a norm-conserving pseudopotential generated through a Hartree–Fock Hamiltonian (HF-NCP).⁵⁷ As basis sets, we used contracted Gaussian orbitals. For hydrogen atoms, we have used a (4s3p)/[1s1p] basis set, whereas for carbon atoms the basis set was gradually increased to verify the convergence of ethylene’s excitation energies: keeping fixed to 5 the number of primitive Gaussians per shell, the number of contracted orbitals was varied from (5s5p5d)/[1s1p1d] to (5s5p5d)/[2s2p2d]. The basis set for the Jastrow factor was fixed to (2s2p)/[1s1p] contracted orbitals for the hydrogen atoms. For carbon atoms, we tested three different contracted basis sets: (4s3p)/[1s1p], (4s3p)/[1s2p], and (4s3p)/[2s2p]. Wave functions were optimized following a multistep procedure similar to that employed for the all-electron case but using final statistics of 1.6 × 10⁵ MC steps per electron. VMC and LRDMC calculations at the energy minimum were carried on using 2.6 × 10⁷ and 1.3 × 10⁷ MC steps per electron, respectively. LRDMC energies were extrapolated in the limit a → 0 using the following set of lattice space discretizations: a = {0.1,0.2,0.3,0.4} [au].

Structural Optimization

During the geometry optimizations, when possible, we enforced molecular symmetries to reduce the number of force components and of independent parameters. The final 500 structural optimization steps were made with 6.4 × 10⁵ MC steps per electron, corresponding to an error of 3 × 10⁻⁴ [au] on the mean values of the force components over the last 200 steps. This last accurate optimization step required about 2 h on eight quad-core Opteron CPUs.

6. RESULTS AND DISCUSSION

6.1. Geometry Optimization by Variational Monte Carlo

The ¹A_g Ground State of Ethylene

Geometry relaxation of the ground state structure of the ethylene molecule was performed starting from the ground state experimental geometry reported in ref 58 (R_CH = 1.086 Å, R_CC = 1.337 Å, θ_HCH = 117.62°). We carried out a full wave function and geometry optimization using different basis sets, as described in the computational details.

The number of the total variational parameters was varying from 237 to 1216, ranging from the smallest pseudopotential calculation to the largest basis set employed in all-electron calculations.

The structural parameters of the optimized geometries for the ¹A_g state are reported in Table 1. In all cases, both the R_CC and R_CH bond lengths and the θ_HCH angle are compatible with the available experimental data and with high level quantum chemistry calculations such as CCSD(T).³⁰ For the all-electron calculations, it is very interesting to see that the equilibrium geometry of the molecule is basically consistent within 0.001 Å with the best CCSD(T) quantum chemistry method. Nevertheless, the JAGP (n = 8) results are also in good agreement with the available experimental data.

Table 1. Equilibrium Structure of the ¹A_g State^a.

basis setsb		RCC [Å]	RCH [Å]	θHCH [deg]
all-ele.	8s4p1d (AGP)	1.3288(9)	1.0788(7)	117.04(11)
	8s4p1d (n = 8)	1.3262(9)	1.0801(6)	117.03(11)
	9s5p2d (n = 8)	1.3257(9)	1.0798(6)	117.09(11)
	8s4p1d (n = 12)	1.3305(9)	1.0798(6)	117.16(11)
	9s5p2d (n = 12)	1.3313(9)	1.0793(6)	117.03(11)
SR-ECP	[1s1p1d]	1.3303(3)	1.0783(2)	116.89(5)
	[2s1p1d]	1.3282(8)	1.0786(16)	116.82(14)
	[1s2p1d]	1.3295(6)	1.0787(3)	117.07(9)
	[2s2p]c	1.3284(12)	1.0791(9)	116.94(9)
	[2s2p1d]	1.3289(6)	1.0790(5)	117.01(9)
	[2s2p2d]	1.3283(3)	1.0789(2)	117.08(5)
SR-NCP	[1s2p1d]	1.3347(11)	1.0809(12)	117.09(22)
HF-NCP	[1s2p1d]	1.3353(11)	1.0808(13)	117.09(22)
CCSD(T)30		1.3307(3)	1.0809(3)	117.12(3)
LDA34		1.3266	1.0958	116.66
MP234		1.3386	1.0848	116.64
MP231		1.331046	1.080564	117.3
B3LYP34		1.3289	1.0850	116.52
B3LYP60		1.324	1.085	116.32
exptl58		1.3370	1.0860	117.62
exptl61		1.330(5)	1.079(5)
exptl62		1.334(2)	1.081(2)	117.36(17)
exptl63		1.336	1.076	118.02
exptl59		1.339	1.085	117.8

^aIn this table, we report the structural optimization of the ¹A_g ground state of the C₂H₄ molecule for different basis sets.

^bFor the pseudopotential basis sets, we have indicated only the carbon atom contracted orbitals made of (5s5p5d) primitive Gaussians. The hydrogens’ basis set was fixed to (4s3p)/[1s1p] contracted Gaussian orbitals.

^cThis basis set is built of (4s4p)/[2s2p] contracted orbitals for the carbon atom and (2s2p)/[1s1p] orbitals for the hydrogen atoms. The three-body Jastrow factor is built with (3s2p)/[2s2p] orbitals for the carbon atoms and (2s1p)/[1s1p] orbitals for the hydrogens.

For the pseudopotential calculations, we made an extended study of the basis set convergence using the energy consistent pseudopotential with scalar-relativistic corrections (SR-ECP).⁵⁵ As shown in Table 1, the relaxed geometrical parameters do not seem to be significantly affected by the basis set. In particular, even with the smallest basis set (4s4p)/[2s2p] for carbon atoms, bond distances and angles are all compatible within the converged ones, and the introduction of d orbitals in the basis set does not seem to be crucial for the correct description of the ground state geometry. Further calculations were done with the well converged middle size basis set (5s5p5d)/[1s2p1d], to test the SR-NCP⁵⁶ and the HF-NCP⁵⁷ norm-conserving pseudopotentials. As shown in Table 1, both the norm-conserving pseudopotentials display a slight elongation of the R_CC (in the range 1.333–1.335 Å) and R_CH bonds with respect to the all-electron and the SR-ECP optimizations, regardless of the inclusion of relativistic corrections.

In summary, all of the converged equilibrium geometries obtained with the JAGP are compatible with the most recent MP2, B3LYP, and CCSD(T) results within deviations of less than 0.002 Å on the R_CC and R_CH bond lengths. The predicted equilibrium R_CC bond falls in the lower limit of the experimental values, which spread in a range between 1.330 and 1.339 Å. This demonstrates the possibility to obtain full geometry relaxation of small molecules at the quantum Monte Carlo level, by using a relatively compact and fully optimized AGP wave function.

The Adiabatic ³A₁ Triplet State of Ethylene

Starting from the ¹A_g optimized ground state geometry, we built the ³B_1u JAGP triplet wave function and performed a full geometry optimization up to complete relaxation into the ³A₁ lowest energy triplet state.

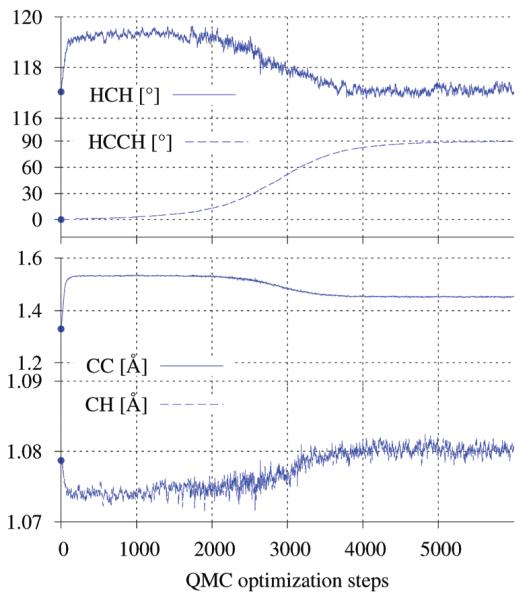
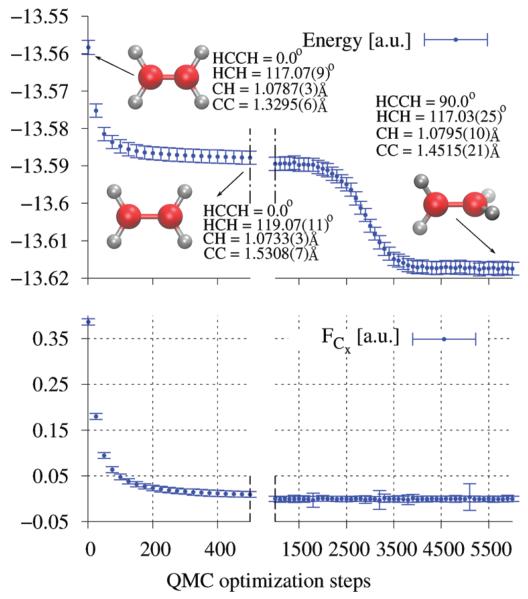
In Figure 1, we can follow this geometrical relaxation as a function of the optimization steps for the SR-ECP pseudopotential case with the (5s5p5d)/[1s2p1d] contracted basis set. During the first steps of optimization, the molecule is kept planar so that we can identify a first quick energy drop due to the elongation of the R_CC bond from 1.33 Å to 1.53 Å, as shown in Figure 2. After these first steps, the planar symmetry is broken and the ethylene molecule slowly starts to rotate around the R_CC bond, and at the same time, a contraction of the bond occurs. The ³A₁ adiabatic triplet state is eventually reached, displaying a D_2d symmetry with an optimized R_CC distance of 1.4515(21) Å.

Figure 1. Variation of ethylene’s structural parameters during the ³A₁← ³B_1u geometrical optimization.

Figure 2. Energy and force convergence during the structural optimization ³A₁← ³B_1u.

The points reported are mean values obtained from 50 consequential optimization steps. The force component showed in the figure is the one acting on a C atom along the C–C bond.

In Table 2, we report the extensive basis set study of the equilibrium geometries of the ³A₁ adiabatic triplet in the case of the SR-ECP pseudopotential. The effect of the basis set is similar to what is observed for the ground state equilibrium, and also for the adiabatic triplet, the relaxed R_CC bond lengths obtained through the two norm-conserving pseudopotentials SR-NCP and HF-NCP are slightly longer than the SR-ECP and the all-electron predictions. We can also infer from Table 2 a good agreement between our predicted adiabatic triplet geometry and the most recent MP2, B3LYP, and CCSD(T) equilibrium geometries. Unfortunately, to the best of our knowledge, no experimental information is available for the geometrical parameters of this state.

Table 2. Equilibrium Structure of the ³A₁ State^a.

basis setsb		RCC [Å]	RCH [Å]	θHCH [deg]
all-ele.	8s4p1d (AGP)	1.4533(8)	1.0775(6)	117.10(9)
	8s4p1d (n = 9)	1.4492(10)	1.0811(6)	116.91(14)
	9s5p2d (n = 9)	1.4478(10)	1.0805(7)	116.94(14)
	8s4p1d (n = 12)	1.4526(10)	1.0804(6)	117.05(10)
	9s5p2d (n = 12)	1.4509(9)	1.0804(6)	117.20(15)
SR-ECP	[1s1p1d]	1.4494(9)	1.0801(4)	116.77(10)
	[2s1p1d]	1.4515(9)	1.0799(9)	117.01(19)
	[1s2p1d]	1.4515(21)	1.0795(10)	117.03(25)
	[2s2p1d]	1.4485(53)	1.0793(38)	116.61(59)
	[2s2p2d]	1.4507(37)	1.0799(20)	116.99(36)
SR-NCP	[1s2p1d]	1.4556(11)	1.0820(6)	117.03(10)
HF-NCP	[1s2p1d]	1.4562(13)	1.0822(7)	116.97(13)
LDA34		1.42	1.1014	115.38
MP234		1.4604	1.0847	116.98
MP231		1.449148	1.080469	117
B3LYP34		1.4473	1.0880	116.44
CCSD(T)64		1.451	1.080	117.1
CCSD(T)33		1.456

^aIn this table, we report the structural optimization of the ³A₁ excited state of the C₂H₄ molecule with fixed dihedral angle HCCH = 90°.

^bFor the pseudopotential basis sets we have indicated only the Carbon atom contracted orbitals made of (5s5p5d) primitive gaussians. The hydrogens’ basis set was fixed to (4s3p)/[1s1p] contracted Gaussian orbitals.

6.2. Excitation Energies

The ³B_1u← ¹A_g Vertical Triplet Excitation of Ethylene

In Table 3, we report the energies of the ground state and first excited states for all-electron wave functions, calculated on both the VMC and LRDMC levels on the optimized equilibrium geometries reported in Table 1.

Table 3. All-Electron Energy Calculations^a.

basis set	1Ag [Hartree]	3B1u [Hartree]	3A1 [Hartree]	3B1u ← 1Ag [eV]	3A1 ← 1Ag [eV]
VMC
8s4p1d (n = 8)/(n = 9)	−78.5217(4)	−78.3553(4)	−78.4171(4)	4.528(16)	2.846(16)
9s5p2d (n = 8)/(n = 9)	−78.5249(4)	−78.3578(4)	−78.4190(4)	4.547(16)	2.882(16)
8s4p1d (n = 12)	−78.5287(4)	−78.3595(4)	−78.4182(4)	4.604(16)	3.007(16)
9s5p2d (n = 12)	−78.5303(4)	−78.3613(4)	−78.4207(4)	4.598(16)	2.982(16)
8s4p1d (AGP)	−78.5246(4)	−78.3561(4)	−78.4173(4)	4.585(16)	2.920(16)
LRDMC
8s4p1d (n = 8)/(n = 9)	−78.5663(5)	−78.3999(6)	−78.4588(6)	4.527(21)	2.925(21)
9s5p2d (n = 8)/(n = 9)	−78.5685(6)	−78.4015(5)	−78.4612(5)	4.544(21)	2.919(21)
8s4p1d (n = 12)	−78.5717(6)	−78.4013(5)	−78.4600(5)	4.637(21)	3.039(21)
9s5p2d (n = 12)	−78.5743(5)	−78.4037(3)	−78.4619(3)	4.642(19)	3.058(19)
8s4p1d (AGP)	−78.5726(5)	−78.4019(5)	−78.4631(5)	4.645(19)	2.979(19)
GVB-2 (cc-pVTZ)b	−78.56236(18)	−78.39401(18)	−78.45124(18)	4.581(7)	3.024(7)
HF(cc-pVDZ/cusp)c				4.501(17)	3.014(26)
MR-CISD+Qd	−78.451288	−78.285126		4.52
MR-AQCCd	−78.432429	−78.266543		4.51

^aIn this table, we report the absolute energies of the ¹A_g, ³B_1u, and ³A₁ states of ethylene, evaluated with all-electron calculations. The geometries are those reported in Tables 1 and 2. The energy differences do not consider the zero point energies of the states. The all-electron calculations were made using n = 8 molecular orbitals for the ground state and n = 9 orbitals for the triplet states, corrisponding to single Slater determinants.

^bDMC results from ref 31. We reported the lowest energy calculations with an identical basis set. The ground state geometry (R_CC = 1.331046 Å, R_CH = 1.080564 Å, HCH = 117.3°) and the adibatic triplet geometry (R_CC = 1.449148 Å, R_CH = 1.080469 Å, HCH = 117°) are both optimized on the MP2 level with the cc-pVTZ basis set.

^cDMC results from ref 34 with geometry optimized on the MP2 level and uncorrected with the addition of 0.1388 eV (3.2 kcal/mol)³³ of ZPE energy to compare them with our results.

^dResults from ref 32 with fixed geometry (R_CC = 1.339 Å, R_CH = 1.086 Å, HCH = 117.6°); the MR-CISD+Q calculations refer to the QZ basis set reported for REF(12,12,1p) determinants, while the MR-AQCC calculations refer to the TZ basis reported for REF(12,12,1p).

It is important to emphasize that the absolute energies in Table 3 clearly demonstrate the high variational quality of our all-electron JAGP wave function for both the VMC and LRDMC approaches, if compared to the reported multi-reference,³² coupled cluster,²⁹ and DMC results.^31,34

The vertical excitation energies seem to be sensitive to the number of molecular orbitals considered in the JAGPn* wave function, an increase of about 0.1 eV passing from n = 8/n = 9 to n = n* = 12. As shown in Table 1, increasing the number of molecular orbitals affects the ground state’s equilibrium geometry by stretching the C๛C bond by about 0.005 Å. This geometrical difference is not relevant for the energy of the singlet state since the structure is close to the singlet minimum, but it is significative for the energy of the triplet state because at that distance the triplet energy surface is rather steep and the stretching of the C๛C bond corresponds to a lowering of the triplet energy. This dependency on the R_CC bond length has already been shown in previous works through the calculation of the potential energy surface (PES) of the ground state of ethylene.²⁸

A similar trend is observed when comparing the pseudopotential results reported in Table 4. The values of the VMC vertical gap predicted by the SR-ECP calculations are in the range 3.020(10)–3.053(10) eV, which is similar to what was obtained in all-electron calculations (3.039(21)–3.058(19) eV). In the case of the two norm-conserving pseudopotentials, the gap is about 0.1 eV smaller. Similarly to what discussed above about the JAGP (n = 12) results, this can be interpreted as an effect of the ground state geometries, since for these pseudopotentials a slightly longer R_CC bond (Table 1) is reported.

Table 4. Pseudopotential Energies of the Ethylene Electronic States^a.

carbon atoms’ basis sets			VMC			LRDMC
pseudo	AGP (5s5p5d)	3/4bodyJas. (4s3p)	1Ag [Hartree]	3B1u ← 1Ag [eV]	3A1 ← 1Ag [eV]	1Ag [Hartree]	3B1u ← 1Ag [eV]	3A1 ← 1Ag [eV]
SR-ECP	[1s1p1d]	[1s2p]	−13.7254(1)	4.686(5)	3.067(5)	−13.7472(3)	4.623(10)	3.048(10)
	[2s1p1d]	[1s2p]	−13.7269(1)	4.688(5)	3.091(5)	−13.7477(3)	4.677(10)	3.037(10)
	[1s2p1d]b	[1s1p]	−13.7276(1)	4.645(5)	3.012(5)	−13.7479(3)	4.628(10)	3.037(10)
	[1s2p1d]b	[1s2p]	−13.7277(1)	4.626(5)	3.001(5)	−13.7481(3)	4.626(10)	3.031(10)
	[1s2p1d]b	[2s2p]	−13.7286(1)	4.642(5)	3.012(5)	−13.7483(3)	4.645(10)	3.037(10)
	[2s2p1d]	[1s2p]	−13.7281(1)	4.648(5)	3.018(5)	−13.7476(3)	4.634(10)	3.020(10)
	[2s2p2d]	[1s2p]	−13.7289(1)	4.658(5)	3.034(5)	−13.7483(3)	4.648(10)	3.053(10)
SR-NCP	[1s2p1d]	[1s2p]	−13.6945(1)	4.555(5)	2.993(5)	−13.7155(3)	4.568(10)	3.015(10)
HF-NCP	[1s2p1d]	[1s2p]	−13.6924(1)	4.549(5)	3.012(5)	−13.7130(3)	4.533(10)	2.988(10)

^aThe geometrical structures used for each base are those reported in Tables 1 and 2. As in Table 3, the energy values of the adiabatic triplet excitations are not corrected with the ZPE.

^bThese basis sets share the same optimized geometry of the (5s5p5d)/[1s2p1d] basis set.

In the recent article by Anderson, the ethylene vertical triplet excitation has been calculated by DMC using a generalized valence bond (GVB) wave function and considering two different ground state geometries. For the “long” experimental geometry reported in ref 59 that displays a C๛C bond R_CC = 1.339 Å, they estimate a vertical excitation in the range 4.4721(69)–4.5090(69) eV, whereas for the “short” geometry, optimized at the MP2 level (R_CC = 1.331046 Å), the energy gap ranges between 4.5554(69) eV and 4.6200(60) eV. The dependence on the R_CC geometrical parameter is therefore similar to what was observed by us.

In conclusion, all of our VMC and LRDMC all-electron and pseudopotential calculations predict a vertical triplet excitation energy which spreads in a range compatible with the various experimental measurements, which indicate lower and upper bound values of 4.20²⁵ eV and 4.68²⁴ eV, respectively (Table 5).

Table 5. Excitation Energies^a.

	3B1u← 1Ag [eV]	3A1← 1Ag [eV]
VMC (all-ele)	4.598(16)	2.843(16)
VMC (SR-ECP)	4.626(5)	2.862(5)
VMC (HF-NCP)	4.549(5)	2.873(5)
VMC (SR-NCP)	4.555(5)	2.854(5)
LRDMC (all-ele)	4.642(19)	2.919(19)
LRDMC (SR-ECP)	4.626(10)	2.892(10)
LRDMC (HF-NCP)	4.533(10)	2.849(10)
LRDMC (SR-NCP)	4.568(10)	2.876(10)
CIS65		1.995
LDA34	4.874	2.953
MP234	4.549	2.970
B3LYP34	4.462	2.667
MR-CI28	4.597	2.780
CCSD(T)33	4.514	2.845
DMC (HF-ECP)34	4.523(13)	2.862(13)
DMC (CASSCF-ECP)34	4.488(13)	2.879(13)
DMC (HFall)34	4.501(26)	2.875(18)
DMC (GVB)31	4.6027(13)	2.9102(61)
DMC (CAS2–2)66	4.49(2)
PDb		2.52(13)
EELSc	4.2
IISd	4.3
EELSe	4.32
OSf	4.60
LEEISg	4.68

^aThe adiabatic excitation energy is corrected with the difference between the singlet and triplet zero point energies, which has been estimated to be 0.1388 eV (3.2 kcal/mol).³³ The all-electron values reported are related to the 9s5p2d basis set with n = 12 molecular orbitals. The pseudopotential calculations all refer to the same (5s5p5d)/[1s2p1d] basis set for the carbon atom.

^bPhotodissociation experiment ref 27.

^cElectron energy loose spectroscopy ref 25.

^dIon impact spectroscopy ref 26.

^eElectron energy loose spectroscopy ref 67.

^fOptical absorption spectroscopy ref 21.

^gLow-energy electronimpact spectroscopy ref 24.

The ³A₁ ← ¹A_g Adiabatic Triplet Excitation of Ethylene

The adiabatic singlet–triplet excitation energies are reported in Table 3 for all-electron calculations and in Table 4 for the pseudopotential calculations, without zero point energy (ZPE) corrections.

All of the results are in the range of 2.890(16)–3.053(16) eV and are compatible with previous DMC calculations using HF and GVB wave functions, which give respectively a value of 3.014(26)³⁴ eV and 3.024(7)³¹ eV, and with CCSD(T) calculations (2.9835 eV).³³

In Table 5, some of our singlet–triplet excitations are summarized together with the ones obtained using other methods and experimental data. In this table, the adiabatic excitations are corrected with the difference between the ground ¹A_g state and the adiabatic ³A₁ triplet state ZPE energies, estimated to be 0.139 eV by a mixture of coupled cluster and experimental frequency calculations.³³ These results obtained by different fully correlated computational methods are in disagreement with the value of 2.52(13) eV predicted by photodissociation experiments.²⁷

7. CONCLUSIONS

In this work, we have applied modern QMC optimization techniques to study the geometrical and electronic properties of the ethylene molecule in its singlet and triplet states.

The recently introduced methods, to perform efficient structural optimization by QMC,¹⁷ have been shown to be able to describe the equilibrium geometries with a statistical accuracy of about 0.1% and with a reasonable computational effort. Since the computational demand of these QMC techniques scales as the third–fourth power of the number of electrons, these results indicate that these methods are willing to become competitive with respect to other quantum chemistry methods for the evaluation of geometrical and electronic properties of large molecules.

The obtained geometrical ethylene parameters, such as the equilibrium R_CC bond lengths in singlet and triplet states, appear to be unaffected by the choice of the basis sets used for the Jastrow factor and for the AGP part of the wave function. The use of different pseudopotentials seems to slightly affect the R_CC distance, introducing some shift (~0.1 eV) on the calculated vertical excitations.

It is worth to remark that, thanks to the high correlation and variational complexity of the JAGP wave function, the VMC results are in most cases very close to the LRDMC extrapolated data. This indicates the completeness of JAGP and its capability to quantitatively describe, even at the variational level, the electronic properties of molecules. The results obtained are in agreement with those reported by other DMC, CCSD(T), and MP2 calculations for both the vertical and adiabatic singlet–triplet excitations. In particular, our results confirm that the theoretical estimation of the adiabatic excitation, considering zero point energy corrections, is in the range of 2.85–2.91 eV, at variance with the value of 2.52(13) eV estimated by photodissociation experiments. These discrepancies deserve further experimental and theoretical investigation.