Abstract
It is of fundamental import to be able to easily distinguish between the viscoelastic properties of a molecular gel (non-covalent cross-linked three dimensional polymer structure) and a brush (polymer structure that emanates from a surface in three-dimensions sans cross-linking). This has relevance in biology and in designing surfaces with desired chemical and viscoelastic properties for nano- and genomic-technology applications. Agarose and thiol tagged poly(ethylene glycol) were chosen model systems as they are known, on adsorption, to behave like a molecular gel and brush, respectively. Here, we focus on their viscoelastic differences using a quartz crystal microbalance with dissipation monitoring (QCM-D). Changes in resonance frequency and dissipation for three overtones using QCM-D were fitted with the Voigt viscoelastic model to calculate the shear viscosity and shear modulus for the adsorbed agarose gel and the PEG brush. At a surface coverage of 500 ng/cm2, the shear viscosities and shear moduli were 0.0025 ± 0.0002 Pa-s and 2.0 ± 0.17 × 105 Pa and 0.0010 ± 0.0001 Pa-s and 5.0 ± 0.3 × 104 Pa for the gel and brush, respectively. Thus, the adsorbed agarose gel layer was far more rigid than that of covalently bound PEG brush due to its cross-linked network. Also, the diffusivity of agarose and PEG in solution was compared during adsorption onto a bare gold surface. The estimated value for the effective diffusivity of the PEG (without a thiol tag) and of the agarose gel was of the order of 10−11 and 10−15 m2/s, respectively. This low diffusivity for agarose supports the contention that it exists as a molecular gel with a H-bonded cross-linked network in aqueous solution. With the methods used here, it is relatively easy to distinguish the differences in viscoelastic properties between an adsorbed gel and brush.
Introduction
Several polymers and biopolymers spontaneously form gels via formation of a cross-linked network in water that is called a hydro-gel.1 When a cross-linked network is formed due to non-covalent forces then it is known as a molecular gel (e.g. agarose).2 Whereas, a layer consisting of individual non-linked polymers or biopolymers dangling into a solvent with one end attached to a surface is frequently referred to as a brush (e.g. thiol-tagged PEG chemisorbed onto gold).3 It is important to characterize the physical properties of interfacial materials such as gels and brushes under various environmental conditions. Polymers and gels with biomimetic properties are used in designing intelligent biomaterials.4 Incorporation of different macromolecules such as DNA, proteins or drugs into polymer and biological films and interfaces has become a major research interest in the last decade5. Bioactive proteins can be directly integrated into the architecture of films while maintaining their native secondary structure.6 Enzymes have been incorporated into synthetic polymeric membranes so as to effect a commercially relevant conversion (Wu et al7). However, the physical properties of the interface are a major factor that controls these processes.
In trying to understand the transport of large biological molecules (~ 40 kDa) from the cytoplasm to the nucleus through a “molecular machine” called the nuclear pore complex (NPC) 8a, 8b, a controversy has arisen regarding the state of a group of unstructured molecules called nucleoporins (FG-nups for short). They are long fibril like proteins without known secondary structure with a large number of phenylalanine-glycine (FG) repeats. That cargo molecules bind to carrier molecules called Kayopherins that then selectively bind to the FG-nups is also known.8b Two different hypotheses have been offered for the state of the FG-nups: One group suggests that they are gel-like,8c while another suggest that they are more like a brush without cross-linking among the FG-nups8b, 8d. This question of “gel” versus “brush” is the basis for investigating this viscoelastic study. In order to determine whether a self-assembled layer of FG-nups is a gel or a brush, it is important to know the respective viscoelastic properties of each.
Harden et al.9 have used a coupled two-fluid model to study the hydrodynamic properties of concentrated polymer solutions and gels. Viscoelastic properties of adsorbed polymer layers under compression have been estimated by Luckham et al.10 with a Surface Force Apparatus (SFA). Kampf et al.11 have studied the shear force of an adsorbed polymer layer and chemically cross-linked polymer layer using a surface force balance (SFB). Researchers have also used other experimental techniques such as spectroscopic ellipsometry (SE),12 atomic force microscopy (AFM),13 surface plasmon resonance (SPR)14 and quartz crystal microbalance with dissipation monitoring (QCM-D)14–18 to determine the physical properties of such interfaces. QCM-D is a high resolution mass sensor that can operate both in the liquid and the gas phase. It has been used to study adsorption of proteins,19 polyelectrolytes,20 liquid vesicle adsorption21 and antibody-antigen interactions22. The technique measures the total mass of protein and associated hydrodynamically coupled water. In a QCM-D, an AC voltage is pulsed across a gold plated AT-cut piezoelectric quartz crystal23 via two gold electrodes, causing it to oscillate in shear mode at its fundamental resonant frequency, f0. The dampening of the shear wave due to the adsorbed mass on the gold surface is recorded as the dissipation factor (D), simultaneously with resonant frequency of the crystal. This together with a model provides information about the viscoelastic properties of the adsorbed film. Höök et al.24 used the Voigt viscoelastic model to study the viscoelasticity of an adsorbed Mytilus edulis foot protein (Mefp-1) film both before and after cross-linking of the adsorbed layer by NaIO4. Munro et al.25 also used the same viscoelastic model to analyze QCM-D data to determine the shear modulus and shear viscosity of adsorbed poly(acrylamide) films.
As far as we are aware, there are no previous publications comparing the viscolelastic properties of adsorbed gels and brushes at the liquid-solid interface. In the present work, we have used QCM-D to measure the adsorption and dissipation of agarose and PEG onto gold and have compared their physical properties as representative of a molecular gel and brush, respectively. The choice of agarose was based on the fact that is it well-known, well-studied and easy to manipulate. Also, more importantly, since it is comprised of natural marine polysaccharide molecules it could be a close model to the FG-nups. Both have a high aspect ratio and are unstructured. The frequency and dissipation for three overtones were fitted with the Voigt viscoelastic model in order to calculate their shear viscosity and shear modulus. The structural differences between agarose and PEG were determined by AFM imaging.
Materials and Methods
Soluton preparation
Separate aqueous solutions at 500 μg/ml of thiol tagged poly(ethylene glycol) (average molecular weight 30 kDa, 2M40R01, Nektar Therapeutics, Al, USA), poly(ethylene glycol) (without thiol tag, average molecular weight 35 kDa, 81310, Fluka) and agarose (average molecular weight 600 kDa26, gel point 36 ± 15°C, A9539, Sigma) were prepared in a buffer containing 20 mM Hepes (4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid) potassium salt, 110 mM potassium acetate, 2 mM Magnesium chloride at pH 7.4. Agarose was dissolved in the buffer by boiling in a water bath for 5 minutes and then cooling to room temperature.
Surface preparation
Polished, gold coated AT-cut quartz crystals with fundamental frequencies of ~5 MHz (D300, Q-Sense AB, Goteborg, Sweden) were cleaned by immersion in a 1:1:5 mixture of H2O2 (30%), NH3 (25%), and distilled water at 60 °C for 20 min. The cleaned crystals were then washed with distilled water ethanol mixture (50:50) and then dried with nitrogen gas.
QCM-D experiment
Mass and dissipation measurements were performed using a QCM-D (Q-Sense D300 system, Q-Sense AB, Goteborg, Sweden) in batch mode at 24 ± 0.1°C. Six drops of the sample solution were passed through the sensor loop. A decrease in the frequency and an increase in the dissipation were recorded with time. Four separate resonant frequencies (overtones, n) were used to drive the oscillation of the shear wave through the crystal: 5 MHz (fundamental overtone, n=1), 15 MHz (n = 3), 25 MHz (n = 5) and 35 MHz (n= 7). The applied voltage for each resonant frequency was sequentially pulsed across the sensor crystal, allowing the shear wave to dissipate and obtaining the simultaneous measurement of the absolute dissipation. The dissipation factor, D, is defined as
| (1) |
where Edissipated is the energy dissipated during one oscillation period, and Estored is the energy stored during the oscillation. The quartz crystals used were AT- cut with gold coating (Q-Sense). The dissipation factor, D0 for a typical crystal was of the order of 10−6. Without adsorbate, the crystal, when immersed in aqueous solution, oscillated at its resonant frequency, f0. When material adsorbed onto the crystal, the resonance frequency was lowered to f and dissipation increased from D0 to D. The decrease in frequency (Δf = f0−f) and increase in dissipation (ΔD = D0−D) with time were recorded. The QCM-D technique has been described in detail by Rohdal et al.27 Since the noise at 5 MHz was particularly large, we, as others have done previously,15–17 neglected these data and focused on the overtones (n > 1).
Atomic force microscopy experiment
500 μg/ml of agarose and thiol tagged PEG solutions were allowed to adsorb separately onto gold plated glass cover slip for eight hours and then were washed by distilled water. The samples were then left to dry for 12 hours. Images of the samples were then taken in air using an AFM (MFP-3D, Asylum Research, Santa Barbara, USA) with silicon cantilevers (AC240TS, Olympus, Tokyo, Japan).
Theory
Viscoelastic Modeling
The Voigt element consists of a parallel combination of a spring and a dashpot to represent the elastic (storage) and inelastic (damping) behavior of a material, respectively. Using the Voigt model, Voinova et al.28a solved the wave equation describing the physical characteristics of a viscoelastic film, whose complex shear modulus (G) is defined as:
| (2) |
where μf and 2Πfηf are G′ and G″, respectively. μf and ηf are the elastic shear (storage) modulus and the shear viscosity (loss) modulus, respectively.
Voinova et al.28a assumed that the oscillating quartz plate is covered by a viscoelastic film, of uniform thickness df and density, ρf, that adjoins to a semi infinite Newtonian liquid under “no-slip” conditions. The change in resonance frequency, Δf, and in dissipation factor, ΔD, for an oscillating quartz plate can be obtained from the imaginary and the real part of the solution of the wave equation28a, 28b. Thus, from Ref. 28b,
| (3) |
| (4) |
where
| (5) |
| (6) |
| (7), (8) |
dq and ρq are the quartz thickness and density, respectively. f0 is the fundamental resonance frequency and f = n×f0 (with n =1, 3,5 and 7 are the overtone numbers ( n >1)). ρl and ηl are the bulk liquid density and viscosity, respectively. To obtain the unknown shear modulus and shear viscosity of the adsorbed layer, ρl and ηl were assumed known. The temporal change in frequency and change in dissipation were fitted according to Eqs. (3) and (4) using the Qtools software (QSense) to calculate the value of shear viscosity and shear modulus of the adsorbed viscoelastic layer. The best fit between Voigt model and experimental data for three overtones (n =3, 5 and 7) was obtained by minimizing the error function (χ2), given by 28b:
| (9) |
where ΔfnVoigt and ΔDnVoigt are model values and Δfnmeasured and ΔDnmeasured are the experimental values. σnf and σnD are the standard deviation for f and D at harmonic n. Note that this analysis is for constant parameters and ignores the possibility of frequency-dependent viscoelastic properties as other have done previously15, 17, 28b. More details about Voigt viscoelastic model are that paper reported by Stengel et al.28b. Domak et al.29 has studied the swelling of a polystyrene brush using similar visoelastic modeling.
Adsorption and diffusion
Motschmann et al.30 have developed the equations for adsorption of a solute onto solid substrate assuming (i) adsorption is diffusion controlled, (ii) solute reaching the surface is immediately adsorbed and removed from solution, and (iii) at t = 0, concentration of solute at the solid surface is zero and the solute concentration in the solution C0 is homogeneous. Using Fick’s second law and integrating the flux at the solid surface, the following equations were developed by Motschmann et al.30:
| (10) |
and
| (11) |
and
| (12) |
ΔM(t) (kg/m2) is the mass adsorbed with time and D is the diffusivity (m2/s). The diffusivity of the solute can be estimated from the slope of the plot of ΔM versus t1/2. More details on this model have been described elsewhere30, 31.
Results and Discussion
QCM-D response (change in mass and dissipation)
The decrease in frequency with time for adsorption of agarose and thiol tagged PEG is shown in Fig. 1a and b, respectively. After introduction of 500 μg/ml thiol tagged PEG solution into the sensor loop, adsorption equilibrium was reached in about one hour. However, adsorption of 500 μg/ml agarose was very slow because of its low diffusion rate and the lower molar concentration. Adsorption of agarose gel was so slow that it did not reach an asymptotic value even after 25 h (inset in Fig. 1a). In both cases, mass adsorbed, as measured by the QCM-D method, includes not only the solute molecules but also associated hydrodynamically-coupled water molecules. Such long times of adsorption can lead to evaporation of water molecules through the sensor loop and dry the adsorbed layer. This will cause an error in measured viscoelastic properties of the adsorbed layer. So, we have taken data at short times (up to ~8 h, arbitrarily chosen) for viscoelastic modeling of the adsorbed layer of the agarose gel
Fig. 1.
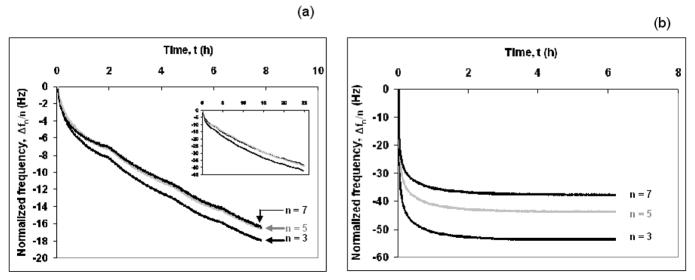
Adsorption of (a) the agarose gel and (b) the thiol tagged PEG brush onto gold. The normalized frequency (Δfn/n) decreases as a function of time for the three overtones (n = 3, 5 and 7; f0 = 5 MHz). Dark lines are for n = 3, 7 and grey lines are for n = 5. T = 24.0 ± 0.1°C.
According to the Sauerbrey equation,32 a decrease in the frequency is proportional to the adsorbed mass, ΔM, given that the mass is small compared to the mass of the crystal, and is sufficiently rigid and/or thin to have negligible internal friction. If the Sauerbrey equation holds then,
| (13) |
where C is the mass sensitivity constant (C= 17.7 ngcm−2Hz−1 at 5 MHz) and n is the overtone number (n= 1, 3, 5 and 7). Thus, the normalized frequency (Δf/n) is independent of the overtone number if the adsorbed layer obeys the Sauerbrey equation. For agarose, the decrease in the normalized frequencies, for three different overtones was very similar, whereas for the thiol tagged PEG, it was clearly different (Fig. 1). This indicates that the agarose gel was more rigid and obeyed the Sauebrey equation more closely than the thiol tagged PEG brush. However, the applicability of Sauerbrey equation has been questioned because the adsorbed layers were not perfectly rigid, and might not have been thin enough to meet the assumptions on which the equation is based.33 To test this, the adsorbed mass was calculated for both the gel and the brush using the Sauerbrey equation and the Voigt viscoelastic model and are summarized in Table 1. To calculate the adsorbed mass using the Voigt viscoelastic model, the Δf and ΔD values obtained from the adsorption data of agarose and thiol tagged PEG were fitted according to Voigt model using Qtools software (QSense AB, Goteborg, Sweden). The model fit for the agarose gel and the PEG brush is shown in Fig. 2a and b, respectively where it appears to predict the observed behavior well. The adsorbed mass was calculated from the Voigt model at 24±0.1°C. and is plotted against the square root of time as shown in Fig. 3. The PEG (with and without thiol) appears to saturate on the surface after about 3 h (t1/2 ≈ 1.73 h1/2) and 2.3 h (t1/2 ≈ 1.50 h1/2), respectively, while the agarose gel continues to adsorb even after 8 h. After 6 h the adsorbed amount for the thiol-terminated PEG brush and non thiol-terminated PEG and the agarose gel were 1800, 600 and 950 ng/cm2, respectively. The adsorption kinetics (profile) of the non-thiol-terminated PEG was similar to that of the thiol-terminated PEG but with much lower amount adsorbed. The hydrophobic methylene groups of the non-thiol-terminated PEG interacted randomly and without orientation with the hydrophobic gold electrode of the QCM-D. The adsorbed mass ratios after 8 h, as predicted by the Voigt model (ΔMVoigt) to those predicted by the Sauerbrey equation (ΔMSauerbrey) (n=7) are 1.9 to 2.7 for the gel and the brush, respectively (Table 1). This suggests that, because of the viscoelastic nature of both adsorbed layers, it is inappropriate to use the Sauerbrey equation.
Table 1.
Comparison of the adsorbed mass calculated from the Sauerbrey and the Voigt models after 8 ha.
| Solute | Δf/n experiment (Hz) | Δf/n from Voigt fit (Hz) | ΔMSauerbrey (ng/cm2) | ΔMVoigt (ng/cm2) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| n = 3 | n = 5 | n = 7 | n = 3 | n = 5 | n = 7 | n = 3 | n = 5 | n = 7 | ||
| Agarose | 17.1 ± 0.5 | 16.2 ± 0.6 | 16.1 ± 0.6 | 16.9 ±0.5 | 16.1 ± 0.6 | 16.0 ± 0.5 | 303 ± 9 | 287 ± 10 | 285 ± 10 | 554 ± 12 |
| PEG (Thiol tagged) | 53.5 ± 1.2 | 43.4 ± 1.2 | 37.5 ± 1.3 | 53.1 ± 1.2 | 43.5 ± 1.1 | 37.3 ± 1.3 | 947 ± 21 | 768 ± 21 | 664 ± 22 | 1778 ± 27 |
The density and viscosity of the bulk solution were assumed to be 1000 kg/m3 and 0.001 Pa-s, respectively. The assumed value of 1200 kg/m3 for density of the adsorbed layer gave the best fit for the Voigt viscoelastic model. The listed data are the averages of four experimental runs. The value of error function (χ2) for the agaorse gel varied from 3.4–4.0×107 whereas that for PEG brush (thiol tagged) varied from 7.9–8.7×107 as per Eq. (9).
Fig. 2.
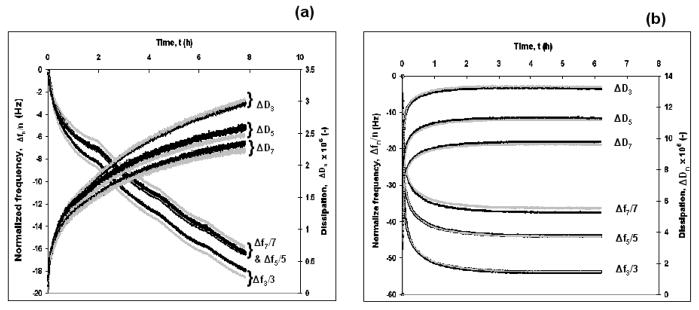
The normalized frequency, Δfn/n, and dissipation, ΔDn, for adsorption of (a) the agarose gel and (b) the thiol tagged PEG brush. The data (dark lines) were fitted according to the Voigt viscoelastic model28 (grey lines). T = 24.0 ± 0.1°C.
Fig. 3.
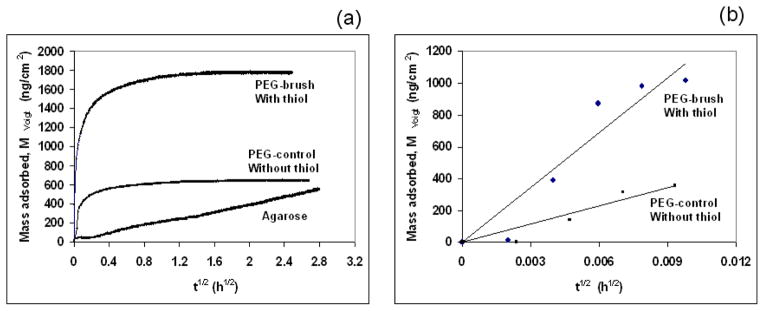
Estimation of effective diffusion coefficients at 24.0 ± 0.1°C. (a) Mass adsorbed calculated from the Voigt viscoelastic model versus t1/2 according to Eq. (12). (b) Initial slope for thiol tagged PEG (PEG brush) and without thiol tagged PEG (PEG control). The origin of the time axis was shifted to the time of injection to avoid the distortion of square root dependence.
Diffusion
As mentioned above, the mass adsorbed was obtained from the Voigt model and is plotted against t1/2 (Fig. 3) to estimate the diffusivity of the solute from Eq. (12). Only initial adsorption of thiol terminated PEG and PEG without thiol was diffusion-controlled whereas that for the agarose gel was diffusion-controlled all the time because the plot was slowly increasing and linear throughout the period. Hence, the effective diffusivity of thiol terminated PEG was calculated from the initial slope (Eq. 12, inset Fig. 3) whereas an estimate of the effective diffusivity for the agarose included linear slope for all time. The initial slope of the plot for thiol tagged PEG was 103,000–119,000 ng cm−2 h−1/2 and that for the agarose gel was 190–200 ng cm−2 h−1/2. The estimated effective diffusivity of the thiol terminated PEG (~30 kDa) was 9.3–12.1 × 10−10 m2/s whereas that for agarose gel varied from 3.1–3.7 × 10−15 m2/s. Since the thiol tagged PEG was chemisorbed onto gold, whereas the agarose gel was physisorbed onto gold, it was important to determine the diffusivity of PEG without the thiol group (control; ~ 35 kDa). The slope of the plot for PEG (without thiol, control) was 30,500–39,000 ng cm−2 h−1/2 (inset of Fig. 3). The estimated diffusivity of PEG (without thiol) varied from 8.8–11.2 × 10−11 m2/s. The estimated diffusivity (~10−11 m2/s) of PEG matches well with the diffusivity of other polymer and biopolymers reported in the literature.36 Researchers have also reported the diffusivity of high molecular weight biopolymers (cellulose in 1,4-dioxane, dextran in ethanediol) to be of the order of 10−11 m2/s.36 We would expect the diffusivity of agarose (~600 kDa) to be of the order of 10−11–10−12 m2/s if it did not form a cross-linked gel network. Four orders of magnitude lower diffusivity for agarose suggests the presence of a hydrogen bonded cross-linked network in aqueous solution. As mentioned above, is also called a molecular gel. In both cases, for gel and brush, as mentioned above, the QCM-D measured both the solute molecules together with the associated hydrodynamically-coupled water molecules. This, of course, would affect an estimate of the actual value of the diffusivities for the gel or brush alone but would not affect the overall conclusion because the estimated diffusivity of thiol tagged PEG is four orders of magnitude higher than that of agarose gel. Since the gel is expected to imbibe more water that the brush its diffusivity would likely be even lower than estimated from Fig. 3 and the theory (Eqs. (10–12)). Thus, their difference in diffusivity would be even larger than reported here, so our conclusions are conservative. With respect to the differential diffusion between the thiol-tagged and the non-thiol-tagged PEG molecules (30 and 35 kDa, respectively), we suspect that the former exhibits a larger diffusivity not only because it is lighter but also because it is driven by the covalent reaction with the gold surface. Also, the surface density at long times for the thiol-terminated PEG on gold was ~1800 ng/cm2. At this high concentration, we expect that it will behave like a brush.
Difference in dissipation between the agarose gel and the PEG brush
The increase in dissipation versus decrease in normalized frequency during adsorption for the agarose gel and the PEG brush is shown in Fig. 4a and b, respectively. The steepness of the slope of the plots during adsorption of a solute is an inverse measure of rigidity of the adsorbed layer. The plots of ΔD versus Δf/n are initially linear, then, the slopes decrease, indicating coverage-induced structural changes of the adsorbed layer. A decrease in the slope indicates that the adsorbed layer becomes more rigid due to an increase in packing density of the adsorbed layer. The slope of the ΔD versus Δf/n plot for the agarose gel varies from 0.21 × 10−6–0.15 × 10−6 Hz−1 over the range of (Δf/n) from 0–17 Hz, whereas that for the thiol tagged PEG brush varies from 0.28 × 10−6–0.25 × 10−6 Hz−1 over the range from 0–40 Hz. The lower slope for agarose gel indicates that it was more rigid than thiol tagged PEG brush.
Fig. 4.
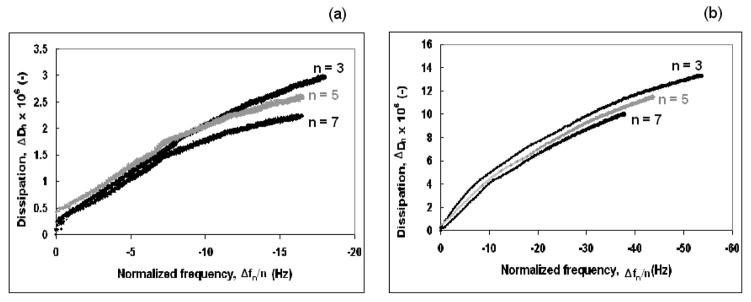
Change in Dissipation, ΔDn, versus normalized frequency change, Δfn/n, for adsorption of (a) the agarose gel and (b) the thiol tagged PEG brush onto gold at 24.0 ± 0.1°C. The change in slope of the curves indicates coverage-induced changes in the structure of the adsorbed molecules. Dark lines are for n = 3, 7 and grey lines are for n = 5.
Shear modulus and shear viscosity
The shear viscosity, ηf, and shear modulus, μf, of the two layers were determined, from fits of Eqs. (3) and (4) to the data using known parameter values for dq, ρq, ρl and ηl (Fig. 5). These values were higher for the agarose gel than for the thiol tagged PEG brush (Fig. 5a and b) at 24 ± 0.1 °C. At low coverage, as expected the effective viscosity of the adsorbed layers was close to that of pure water (0.00091 Pa s) at 24°C. As the coverage increased, the viscosity increased to a maximum of ~0.0027 kg/m3 for the agarose gel and to ~0.0014 kg/m 3 for the thiol tagged PEG brush. Both the gel and the brush exhibited two-stage behavior. With an increase in the mass adsorbed, the shear modulus, μf first increases sharply and then plateaued to ~ 2.1 × 105 Pa for the agarose gel. For the PEG brush, however, a modest increase in μf was observed for both stages. At a coverage of 1750 ng/cm2, the shear modulus reached a value of ~1.25 × 105 Pa, well below that of agarose at a coverage of only 500 ng/cm2. These values are similar in order to those reported in the literature for an adsorbed Mytilus edulis foot protein (Mefp-1) film.24 Moreover, to compare the viscoelasticity of the two adsorbed layers at constant surface coverage of say, 500 ng/cm2, one can see clearly the very large difference between the values of the shear modulus, μ, and viscosity, η in Fig. 5. Since the values of the two parameters (μ and η) diverge for the gel and the brush with increasing coverage clearly, the difference become more pronounced! The change in slope in Fig 5a and b coincides with the change in slope for dissipation versus normalized frequency plot in Fig. 4. It should be noted, though, for the Voigt viscoelastic modeling, the density of the adsorbed layers was arbitrarily kept constant (1200 kg/m3). However, at low coverages, the density of the adsorbed layers is expected to be lower than 1200 kg/m3. For a given adsorbed mass, a decrease in the adsorbed layer density would result in an increase in the adsorbed layer thickness. This would not primarily influence the shear viscosity and shear modulus as demonstrated by Larsson et al.34
Fig. 5.
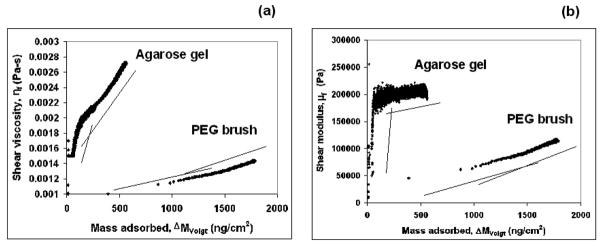
Variation in (a) shear viscosity, ηf, and (b) shear modulus, μf, as a function of mass adsorbed as calculated by the Voigt model, ΔMVoigt, at 24.0 ± 0.1°C. The lines are used to indicate the changes in slope due to coverage-induced changes in structure of the adsorbed molecules. dq = 3.34 × 10−4 m; ρq = 2650 kg/m3; ρl = 1000 kg/m3 and ηl = 0.001 Pa.s.39
Difference in structure of agarose gel and PEG brush
AFM images of the agarose gel and the PEG brush are shown in Fig. 6a and b, respectively. Unlike PEG, the agarose layer was found to have a cross-linked network. Arnott et al.35 suggested that an agarose coil-to-double helix transition is the origin of the gelation process. The double helices join together to form a cross-linked network of gel. This cross-linked network gave rise to higher rigidity of the agarose layer which is reflected in the higher shear viscosity and shear modulus values as compared with those for the PEG brush. Since the AFM images were taken in air, this could somewhat mask the actual size of the structures in water. The cross-linked nature of the agarose gel is the major distinguishing feature with respect to the PEG brush.
Fig. 6.
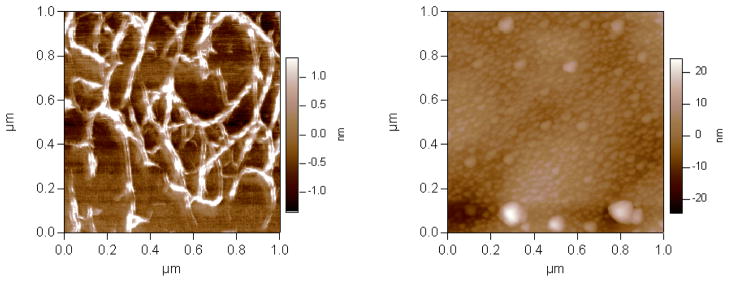
AFM images of (a) the agrose gel and (b) the thiol tagged PEG brush adsorbed onto gold. These images were collected in non-contact mode in air.
Conclusions
Because of recent interest in nano- and genomic-technology, we have developed and tested a methodology to determine the difference in the viscoelastic properties of a gel and a brush. QCM-D analysis is a powerful surface characterization technique that can monitor the physical properties of interfacial polymer networks. A QCM-D was employed here to analyze the physical properties of an agarose gel and a thiol-tagged PEG brush. The agarose formed a molecular gel in aqueous solution which had a rigid cross-linked network which was reflected in its relatively low dissipation values, high shear modulus and high shear viscosity. The PEG brush on the other hand, exhibited much larger values for ηf and μf. These differences were observed in spite of the fact that the adsorbed mass for the PEG brush was greater than three times that of the agarose gel at all times (Fig. 3). Due to the rigidity of the agarose gel, it obeyed the Sauerbrey equation somewhat better than did the thiol-tagged PEG brush. Also, both sets of data were predicted by the Voigt model fairly well. The resultant parameters obtained from these fits for the shear viscosity and shear modulus were within the range reported in literature. For example, these values are similar in order to those reported in the literature for an adsorbed Mytilus edulis foot protein (Mefp-1) film.24 The estimated effective diffusion coefficients of PEG sans thiol group was of the order of 10−11 m2/s whereas that for agarose was of the order of 10−15 m2/s. The very low diffusivity of agarose supports the idea that a molecular gel was formed in aqueous solution. This comparative analysis between a gel and brush could be useful in determining the physical properties of other interfacial molecules such as neurofilaments37 or the unstructured FG-NSP1 proteins8,38 lining the entrance to the nuclear pore complex for which structural differences (gel or brush) matters.
Acknowledgments
This work was supported by the National Institute of Health Grant Number R01GM071329 and US Department of Energy (DE-FG02-90ER14114 and DE-FG02-05ER46249). Brian Chait and Michael Rout are thanked for suggesting the problem.
References
- 1.Terech P. Encyclopedia of Surface and Colloid Science. Marcel Dekker; New York: 2002. [Google Scholar]
- 2.Terech P, Wiess RG. Molecular Gels. Kluwer Academic Publishers; The Netherlands: 2004. [Google Scholar]
- 3.Milner ST. Science. 1991;251:905–914. doi: 10.1126/science.251.4996.905. [DOI] [PubMed] [Google Scholar]
- 4.Peppas N, Huang Y. Pharmaceutical Research. 2002;19:578–587. doi: 10.1023/a:1015389609344. [DOI] [PubMed] [Google Scholar]
- 5.Gil ES, Hudson SM. Progress in Polymer Science. 2004;29:1173–1222. [Google Scholar]
- 6.Chen J, Thomas E, Ober C, Mao G. Science. 1996;273:343–346. doi: 10.1126/science.273.5273.343. [DOI] [PubMed] [Google Scholar]
- 7.Wu DR, Belfort G, Cramer SM. I & EC Research. 1990;29:1612–1621. [Google Scholar]
- 8.(a) Rout M, Aitchison J, Suprapto A, Hjertaas K, Zhao Y, Chait B. J Cell Biol. 2000;148:635–651. doi: 10.1083/jcb.148.4.635. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Rout MP, Aitchison JD, Magnasco MO, Chait BT. Trends in Cell Biology. 2003;13:622–628. doi: 10.1016/j.tcb.2003.10.007. [DOI] [PubMed] [Google Scholar]; (c) Frey S, Richter R, Görlich D. Science. 2006;314:815–817. doi: 10.1126/science.1132516. [DOI] [PubMed] [Google Scholar]; (d) Lim R, Huang N, Köser J, Deng J, Lau K, Schwarz-Herion K, Fahrenkrog B, Aebi U. PNAS. 2006;103:9512–9517. doi: 10.1073/pnas.0603521103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Harden J, Pleiner H, Pincus P. J Chem Phys. 1991;94:5208–5221. [Google Scholar]
- 10.Ansarifar MA, Luckham PF. Colloid and Polymer Science. 1989;267:736–740. [Google Scholar]
- 11.Kampf N, Raviv U, Klein J. Macromolecules. 2004;37:1134–1142. [Google Scholar]
- 12.Extrand CW. Polym Eng Sci. 1994;34:390–394. [Google Scholar]
- 13.Domke J, Radmacher M. Langmuir. 1998;14:3320–3325. [Google Scholar]
- 14.Reimhult E, Larsson C, Kasemo B, Höök F. Anal Chem. 2004;76:7211–7220. doi: 10.1021/ac0492970. [DOI] [PubMed] [Google Scholar]
- 15.Irwin E, Ho J, Kane S, Healy K. Langmuir. 2005;21:5529–5536. doi: 10.1021/la0470737. [DOI] [PubMed] [Google Scholar]
- 16.Vogt B, Lin E, Wu W, White C. J Phys Chem B. 2004;108:12685–12690. [Google Scholar]
- 17.Tammelin T, Merta J, Johansson L, Stenius P. Langmuir. 2004;20:10900–10909. doi: 10.1021/la0487693. [DOI] [PubMed] [Google Scholar]
- 18.Plunkett MA, Wang ZH, Rutland MW, Johannsmann D. Langmuir. 2003;19:6837–6844. [Google Scholar]
- 19.Baba A, Kaneko F, Advincula RC. Colloids Surf A. 2000;173:39–49. [Google Scholar]
- 20.Rodahl M, Höök F, Fredriksson C, Keller CA, Krozer A, Brzezinski P, Voinova M, Kasemo B. Faraday Discuss. 1997;107:229–246. doi: 10.1039/a703137h. [DOI] [PubMed] [Google Scholar]
- 21.Reimhult E, Höök F, Kasemo B. Phys Rev E. 2002;66:051905(1–4). doi: 10.1103/PhysRevE.66.051905. [DOI] [PubMed] [Google Scholar]
- 22.Blonder R, Ben-Dov I, Dagan A, Willner I, Zisman E. Biosensors & Bioelectronics. 1997;12:27–644. doi: 10.1016/s0956-5663(97)00022-5. [DOI] [PubMed] [Google Scholar]
- 23.Reed C, Kanazawa K, Kaufman J. Journal of Applied Physics. 1990;68:1993–2001. [Google Scholar]
- 24.Höök F, Kasemo B, Nylander T, Fant C, Sott K, Elwing H. Anal Chem. 2001;73:5796–5804. doi: 10.1021/ac0106501. [DOI] [PubMed] [Google Scholar]
- 25.Munro JC, Frank CW. Macromolecules. 2004;37:925–938. [Google Scholar]
- 26.Marszalek P, Li H, Fernandez J. Nature Biotechnology. 2001;19:258–262. doi: 10.1038/85712. [DOI] [PubMed] [Google Scholar]
- 27.Rodahl M, Kasemo B. Rev Sci InstrumHKN. 1996;6:3238–3241. [Google Scholar]
- 28.(a) Voinova M, Rohdal M, Jonson M, Kasemo B. Physica Scripta. 1999;59:391–396. [Google Scholar]; (b) Stengel G, Höök F, Knoll W. Anal Chem. 2005;77:3709–3714. doi: 10.1021/ac048302x. [DOI] [PubMed] [Google Scholar]
- 29.Domack A, Prucker O, Rühe J, Johannsmann D. Physical Review E. 1997;56:680–689. [Google Scholar]
- 30.Motschmann H, Stamm M, Toprakcioglu C. Macromolecules. 1991;24:3681–3688. [Google Scholar]
- 31.(a) Aimel C, Sikka M, Schneider J, Tsao Y, Tirrell M, Mays J. Macromolecules. 1995;28:3125–3134. [Google Scholar]; (b) Bird R, Stewart W, Lightfoot E. Transport Phenomena. Wiley; New York: 1960. [Google Scholar]
- 32.Saurbrey ZZ. Phys. 1959;155:206–222. [Google Scholar]
- 33.Ward MD, Buttry DA. Science. 1990;249:1000–1007. doi: 10.1126/science.249.4972.1000. [DOI] [PubMed] [Google Scholar]
- 34.Larsson C, Rodahl M, Höök F. Anal Chem. 2003;75:5080–5087. doi: 10.1021/ac034269n. [DOI] [PubMed] [Google Scholar]
- 35.Arnott S, Fulmer A, Scott W, Dea I, Moorhouse R, Rees D. J Mol Biol. 1974;90:269–272. doi: 10.1016/0022-2836(74)90372-6. [DOI] [PubMed] [Google Scholar]
- 36.Brandrup J, Immergut Edmund H, Grulke Eric A, Abe Akihiro, Bloch Daniel R. Polymer Handbook. 4. John Wiley & Sons; New York: 2005. [Google Scholar]
- 37.Brown HG, Hoh JH. Biochemistry. 1997;36:15035–15040. doi: 10.1021/bi9721748. [DOI] [PubMed] [Google Scholar]
- 38.Rout MP, Aitchison JD, Magnasco MO, Chait BT. Trends in Cell Biology. 2003;13:622–628. doi: 10.1016/j.tcb.2003.10.007. [DOI] [PubMed] [Google Scholar]
- 39.Rodahl M, Kasemo B. Sensors and Actuators A. 1996;54:448–456. [Google Scholar]


