Abstract
Endovenous laser ablation (EVLA) is a commonly used and very effective minimally invasive therapy to manage leg varicosities. Yet, and despite a clinical history of 16 years, no international consensus on a best treatment protocol has been reached so far. Evidence presented in this paper supports the opinion that insufficient knowledge of the underlying physics amongst frequent users could explain this shortcoming. In this review, we will examine the possible modes of action of EVLA, hoping that better understanding of EVLA-related physics stimulates critical appraisal of claims made concerning the efficacy of EVLA devices, and may advance identifying a best possible treatment protocol. Finally, physical arguments are presented to debate on long-standing, but often unfounded, clinical opinions and habits. This includes issues such as (1) the importance of laser power versus the lack of clinical relevance of laser energy (Joule) as used in Joule per centimeter vein length, i.e., in linear endovenous energy density (LEED), and Joule per square centimeter vein wall area, (2) the predicted effectiveness of a higher power and faster pullback velocity, (3) the irrelevance of whether laser light is absorbed by hemoglobin or water, and (4) the effectiveness of reducing the vein diameter during EVLA therapy.
Keywords: Endovenous laser ablation
Introduction
Endovenous laser ablation (EVLA) has become a common minimally invasive therapy to manage leg varicosities. Clinically, scientifically, and commercially, it is a fascinating therapy. Clinically, because EVLA took over surgical stripping as a result of its very high success rate with minimal complications at all laser wavelengths, laser powers, and pullback velocities used [1]. Scientifically, because the consented mechanism of action, i.e., achieving irreversible thermal injury of the vein wall, may be reached by several mechanisms of which the individual contribution is still under debate [2, 3]. Commercially, because gaps in knowledge of the mechanism of action created space for a wide variety of treatment protocols, frequently introduced as new and more effective laser wavelengths. Yet, and despite all efforts since 1999 [4], it is still unknown whether an optimal protocol can be defined.
There are two main modes of action in EVLA proposed so far, both related to the conversion of absorbed laser light energy into heat. The first is heating of blood, vein wall, and perivenous tissue by direct absorption of the laser power emitted from the fiber and scattered by the blood towards the other tissues, where the generated heat in the blood also diffuses to the vein wall [5–7]. When direct absorption of laser light by the blood close to the fiber tip generates temperatures in excess of 100 °C, steam bubbles will be generated and spread within the lumen in the same way as mentioned below (under (c)). The second mode of action is heating of the vein wall by heat transfer from the hot black layer of carbonized blood sticking to the fiber tip. This transfer may be (a) via direct contact between the hot tip and the vein wall [4, 8], (b) via diffusion through the blood [5–11], (c) by boiling steam bubbles which are formed in the hot carbonized layer, grow, detach, and travel downstream from the tip to condense near or at the wall [12, 13], or (d) by Planck's black body radiation [7].
This review aims at increasing the knowledge of the physics surrounding EVLA amongst clinical users of the technique. We suppose that limited awareness of EVLA-related physics may have left too much room for inadequately substantiated claims from industrial parties concerning the efficacy and safety of specific laser settings. This may also have hampered the development of an internationally consented best treatment protocol. We will therefore review (some of) the physics involved in EVLA and will analyze the contribution of the main modes of action of EVLA in an optical–thermal computational simulation model. Finally, physical arguments are presented to debate on certain long-standing, but unfounded, clinical opinions and habits.
Presentation of this paper is in two parts plus two appendices. Part I includes details surrounding the two mechanisms of action proposed so far, as well as a brief presentation of the two computational models of EVLA. Part II addresses important issues for debate within the EVLA community. Appendix 1 presents the underlying physics of the optical–thermal interaction of laser-irradiated tissue, and Appendix 2 presents an estimate of steam production by a laser-irradiated hot carbonized blood layer of about 1,000 °C.
Part I. Mechanisms
Optical–thermal response of laser-irradiated tissue
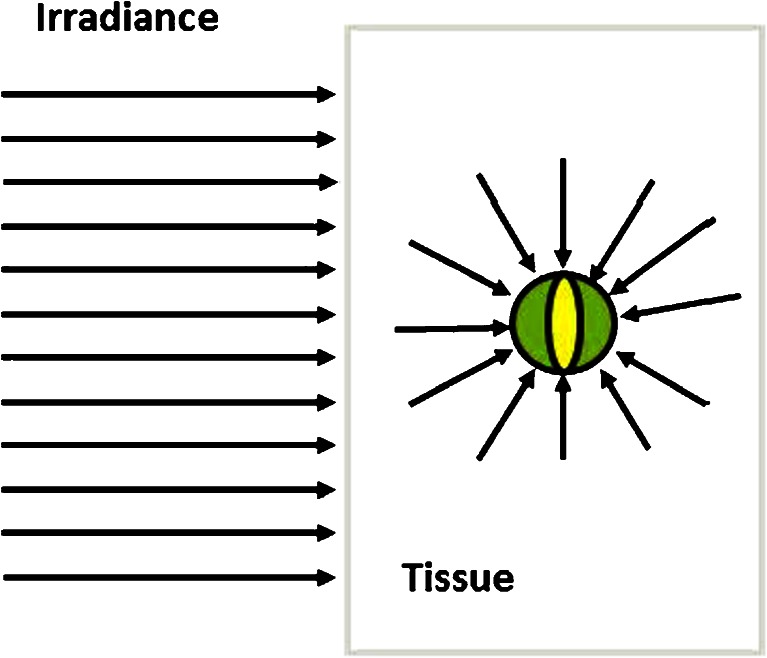
The optical–thermal response of laser-irradiated blood, vein wall, and perivenous tissue aims to assess the temperature distribution of these tissues when irradiated by laser light. There are two separate mechanisms. First, the optical interaction, where the laser power is incident on an area of the tissue, i.e., the irradiance (Watt/area), propagates into the tissue, and rearranges itself into a spatial fluence rate distribution (Fig. 1) due to the tissue's absorption and reduced scattering coefficients, μ a, μ ′s (see Table 1 for definitions). Second, the thermal interaction, where the absorbed part of the laser fluence rate in an infinitesimal small tissue volume (Fig. 1), which equals the product of fluence rate and absorption coefficient, see also Eq. (8) in Appendix 1 below, is converted into heat and causes an increased temperature in that volume. Flows of heat (Watt/area) then develop which propagate from hotter to cooler tissue locations by heat conduction (see Appendix 1). These heat flows (or fluxes) affect the temperature distribution within the tissue. The temperature controls the energy stored in that small tissue volume. Finally, the rate of change of energy that is stored in the small tissue volume (Fig. 1) follows from combining (a) the absorbed power in that tissue volume (the product of fluence rate and absorption coefficient, Eq. (8) in Appendix 1 below) and (b) heat conduction into or out of that volume. This is the bio-heat equation which describes this mechanism of optical–thermal tissue response as a conservation law of power in that infinitesimal volume (Watt/vol) as follows:
| 1 |
Fig. 1.
Definition of laser fluence rate. The tissue is irradiated by a collimated laser beam of power P incident on tissue area A, i.e., with irradiance P/A (Watt/area). The infinitesimally small volume inside the tissue, here the green sphere at tissue location r (coordinate r not shown), receives a continuous stream of collimated and diffuse photons through its surface (represented by the arrows). The fluence rate is defined as all the incoming laser power divided by the (yellow) cross-sectional area of the sphere (Watt/area)
Table 1.
Definitions, symbols, and physical units of important physical parameters in optical–thermal modeling
| Physical term | Symbol (unit) | Description |
|---|---|---|
| Absorption coefficient | μ a (m−1) | Fraction of absorbed light after traveling over an infinitesimally small distance through the medium |
| Scattering coefficient | μ s (m−1) | Fraction of scattered light after traveling over an infinitesimally small distance through the medium |
| Reduced scattering coefficient | μ s′ (m−1) | A parameter incorporating the scattering coefficient and the scattering anisotropy factor g. It equals μ s(1 g) |
| Irradiance | E (Watt/area) | Incident laser power (P) on area (A) of the tissue, where E = P/A. |
| Radiant exposure | H (Joule/area) | Incident laser energy on area (A) of the tissue. The radiant exposure is the irradiance times irradiation time or H = E ⋅ t |
| Fluence rate | Φ(r) (Watt/area) | The total amount of collimated and diffuse light power entering the surface of an infinitesimal small sphere inside the tissue, at tissue coordinate r, divided by the cross-sectional area of that sphere |
| Fluence | Ψ(r) (Joule/area) | The total amount of collimated and diffuse light energy entering the surface of an infinitesimal small sphere inside the tissue, at tissue coordinate r, divided by the cross-sectional area of that sphere. The fluence is the fluence rate times the irradiation time, or Ψ(r) = Φ(r) ⋅ t. |
| Specific heat capacity | c (Joule kg−1 °C−1) | Amount of heat (Joule) required to raise the temperature of 1 kg of a medium by 1 °C in the absence of any heat loss |
| Thermal conductivity | k (Watt m−1 °C−1) | The thermal energy that is conducted in 1 s (Joule/s = Watt) over 1 m driven by a difference in temperature of 1 °C |
| Temperature | T (°C) | A thermal measure of the average kinetic energy (or thermal vibrations) of particles or matter or radiation, independent of the amount of material |
| Laplace differential operator | Δ (m−2) | In Cartesian coordinates: . |
The plus sign denotes heat diffusion into the infinitesimal volume and the minus sign, out of the volume. In Appendix 1, we give a brief survey of the underlying physics of optical–thermal laser–tissue interaction, including the derivation of the bio-heat equation in Appendix 1, Eq. (9), which is the basis for the two existing computational models of EVLA [5–7], explained below in “Computational models of EVLA therapy.”
Heating the vein wall by heat transfer from the hot layer of carbonized blood
When a fiber tip emits laser light in air or in clear water, the tip will not be heated up. However, when embedded in blood, the tip will be covered by a thin layer of carbonized blood, virtually immediately after switching on the laser power, because the blood close to the tip absorbs the power, heats up, coagulates, denatures, and subsequently reduces to carbon particles of high temperatures, typically over 200 °C [14], which forms a thin carbonized blood layer that sticks to the fiber tip. The layer absorbs a substantial part (measured about 45 %) of the emitted light [10], which causes very high temperatures, on the order of 1,000 °C [15–17].
There are at least four mechanisms by which the hot tip may transfer its heat to the vein wall: (a) by direct contact, (b) by heat conduction, (c) by steam bubbles and the heat-pipe principle, and (d) by Planck's black body radiation.
Direct contact between the hot fiber tip and the vein wall
Direct contact between hot tip and vein wall occurs when bare fibers are used. These contact points show as carbonization of the tissue, and because of the temperatures of over 200 °C, prolonged contact may perforate the vein wall, an adverse effect of the use of bare fibers [12, 16, 17]. Remarkably, this direct contact mechanism has been suggested as the primary mechanism of action. First, by Navarro et al. in their patent, filed in 1999 [4], and more recently by Fan and Anderson [8]. The latter authors, however, discarded three important alternative mechanisms not yet identified as an EVLA mechanism in 1999. First, apparently unaware of the fact that steam bubbles are a consequence of the hot carbonized layer, they argued against steam bubbles as an EVLA contributor because these bubbles (indeed) cannot cause the very high tip temperatures (see also “Steam bubbles and the heat-pipe principle” below). Second, optical–thermal interaction of laser light by blood and vein wall was ignored, in part due to penetration depth estimates of 0.2 to 0.3 mm, rather than 1.1 to 1.2 mm, based on blood absorption and scattering at 980 and 1,320 nm [5, 18]; see also Table 2 below. Third, heating the vein wall by conduction from the hot fiber tip was neither mentioned [11]. In our opinion, it is unlikely that direct tip–wall contact is the main EVLA interaction mechanism, first because EVLA procedures are effective without direct tip–wall contact [19], and, second, it seems unlikely that a line of denatured vessel wall of about 0.6 mm width can achieve permanent closure of the entire vein.
Table 2.
Optical parameters, i.e., absorption coefficient, μ a, and reduced scattering coefficient, μ′s, for venous blood (75 % HbO2), vein wall, and perivenous tissue for the various wavelengths, λ, as used in our model computations [23]
| λ (nm) | μ a (1/mm) | μ′s (1/mm) | ||||
|---|---|---|---|---|---|---|
| Blood | Vein wall | Perivenous tissue | Blood | Vein wall | Perivenous tissue | |
| 810 | 0.21 | 0.2 | 0.017 | 0.73 | 2.4 | 1.2 |
| 840 | 0.21 | 0.18 | 0.019 | 0.75 | 2.33 | 1.18 |
| 940 | 0.28 | 0.12 | 0.027 | 0.64 | 2.13 | 1.1 |
| 980 | 0.21 | 0.1 | 0.030 | 0.6 | 2.0 | 1.0 |
| 1,064 | 0.12 | 0.12 | 0.034 | 0.58 | 1.95 | 0.98 |
| 1,320 | 0.3 | 0.3 | 0.045 | 0.54 | 1.8 | 0.9 |
| 1,470 | 3.0 | 2.4 | 0.35 | 0.52 | 1.7 | 0.84 |
| 1,950 | 10.0 | 7.5 | 0.35 | 0.52 | 1.7 | 0.84 |
Heat conduction
Heat conduction is described by a flow (or flux) of heat (Watt/area) that propagates from a hotter to a colder tissue location. The temperature gradient is the driving force of this flow with the thermal conductivity (Watt per meter per degree Celsius) as proportionality factor, accounting for the effectiveness of the medium (here tissue) to facilitate this thermal transport process. The heat conduction part of the bio-heat equation follows from the gradient of the heat flow over the infinitesimal volume (it is instructive to consider the x-direction only, the small volume then is a small area and an infinitesimal small length in the x-direction), which becomes a diffusion equation in the temperature of that volume (see Appendix 1, section “Heat conduction”, for more details).
Steam bubbles and the heat-pipe principle
The condition of a 1,000 °C carbonized layer on the fiber tip facilitates heterogeneous nucleation in the tiny pores of the layer because the associated (thermal) energy content allows the formation of a considerable amount of small steam bubbles per second from residues of blood soluble gases, in Appendix 2 estimated to be at least several cubic millimeters per second. These bubbles then grow, detach, and travel downstream from the fiber tip. Travel distances of about 20 mm have been observed [13]. During their travel, the bubbles cause additional motion and stirring in the fluid, which promotes the convective transfer of heat to the near surroundings. The bubbles may condense already during their travel, and by condensation, they release their latent heat of vaporization. As a consequence, the volume of blood in which steam bubbles travel readily achieves a high temperature of about 100 °C.
A fluid flow and heat transfer process, in which evaporation takes place in one part of the volume and condensation in another part, resembles a heat pipe. Heat pipes were developed in the 1940s of the last century for industrial applications because of their remarkable efficiency of heat transport [20]. When a bubble is formed, the liquid around it is superheated, i.e., in blood at a temperature exceeding the saturation (steam) temperature of 100 °C. The energy content of the liquid is used for bubble growth, and only when sufficient energy is available does the bubble detach and move to colder spots in the vein lumen. In an industrial heat pipe, the condensed bubble content moves as a liquid film back to the hot part of the heat pipe, where superheating, bubble formation, propagation, condensation, and moving back keep occurring. This results in a much faster and more effective transfer of heat than is possible by diffusion. In a vein, the condensed bubble content is a small amount of water, which is readily transported away from the location of the fiber tip, where the EVLA treatment takes place because of the pullback velocity.
When bubbles are noncondensing over 20 mm, the volume in which they move must be at 100 °C. Because tissue becomes irreversibly injured if a temperature of 75 °C occurs during 1 s, or 70 °C during 10 s, suggested by the thermal rate process theory (Fig. 13.19 of [14]), pullback velocities of a few millimeters per second warrant the conclusion that the vein wall will be long enough in close contact with a volume of liquid close to 100 °C consisting of steam bubbles and hot carrier liquid to become irreversibly injured. It should also be noted that heat loss mechanisms such as thermal conduction and convection create a temperature gradient around the steam bubbles, thus also at the vein wall; however, the temperature of the steam bubbles is not influenced by these heat loss mechanisms. Since this is a very effective mode of heat transfer, it has been postulated, albeit not proven, to be the most important mode of action of EVLA [9, 12].
In case the heat pipe mechanism of creation and moving of steam bubbles fails to occur, the hot carbonized layer at the fiber tip becomes deprived from this effective cooling mechanism. The immediate consequence is the generation of a steam bubble close to the fiber tip. By the absence of bubble transport, the steam bubble stays and grows. The thermal conductivity of steam is low so that the temperature of the carbonized layer will increase even more than otherwise. Eventually, the fiber tip may start to glow and even melt. We have observed this process in vitro in the laboratory and are currently assessing the conditions under which it occurs. Melting of the fiber tip has been observed clinically [8, 9] and obviously is an undesirable event during EVLA treatment.
Planck's black body radiation
A medium at surface temperature T emits a spectrum of “black body” radiation with a heat flow proportional to T 4. The wavelength of maximum heat flow also depends on T. The sun's surface of about 6,000 °C, emitting visible light with a maximum in the yellow, is a good example. However, fiber tip temperatures of about 1,100 °C turn out to be too low to produce a significant thermal effect at the vein wall, due to the very low radiated power of 0.023 W over the whole black body spectrum (maximum emission at 2,650 nm and wavelengths of half maximum at 1,600 and 4,800 nm. The wavelengths are, however, well absorbed by water) [7].
Computational models of EVLA therapy
Mordon's model
The first computational model of EVLA was by Mordon et al. [5, 6]. Mordon's model uses solutions of Eq. (1), or Eq. (9) of Appendix 1, incorporating for the fluence rate an approximate analytical solution of the transport equation of light propagation in an absorbing and scattering medium [21]. The assumption is that the laser light emitted out of the fiber is from a point source at r = 0 with power P (Watt), implying that the fluence rate at radial distance r from the source is given by
| 2 |
where μ a, μ ′s are the absorption and reduced scattering coefficients (see Table 1 for definitions). Mordon's model additionally includes that a blood temperature in excess of 100 °C is approximated by keeping it to 100 °C. The efficacy of EVLA was related to the computed maximum temperature of the inner vein wall.
Our model
The second computational model for EVLA was developed by our group [7]. We used the same fluence rate distribution, Eq. (2), in Eqs. (1) and (9), as Mordon did, but we also included the thermal effects of the thin layer of carbonized blood. We used that the source term of absorbed laser power in this layer is given by 0.45P/(layer volume), incorporating that the black layer absorbs about 45 % of the power, virtually independent of wavelength, measured between 450 and 1,650 nm [10]. Furthermore, the strong heat transfer from fiber tip to vein wall by the steam bubbles and the heat-pipe principle have been approximately incorporated by raising the thermal conductivity of blood 200 times when blood temperature exceeds 95 °C. Although this tends to restrict calculated blood temperatures to about 100 °C, temperatures in excess of that value do occur in the simulations. As in Mordon's model, EVLA efficacy was related to the maximum temperature of the inner vein wall. Some results of computations with our model are shown below.
We acknowledge that EVLA modeling still lacks a realistic mathematical account of the effects of steam bubbles. This computational fluid dynamics project, although in progress, is a very complex numerical problem which requires simultaneously solving several coupled partial differential equations, including the Navier–Stokes equation, for describing the production, growth, propagation, and condensation of steam bubbles, in combination with the bio-heat Eq. (9) and Eq. (2).
Part II. Issues for debate
Clinical relevance of laser power, laser energy, and Joule per cm vein length in linear endovenous energy density (LEED)
A photon of light at a specific wavelength either behaves as an electromagnetic wave or as a particle; see, e.g., the book chapter by Walsh [22]. Importantly, a photon has energy (Joule) whose value is proportional to the frequency of the associated wave, hence inversely proportional to the wavelength. Thus, a photon, once absorbed by a tissue molecule, elevates the energy of that molecule which is expressed as a very brief temperature rise. Clinically, two cases are important. The first is a continuous stream of photons interacting with a volume of tissue; the photon stream then is represented by the fluence rate of laser power (Watt/area); see Fig. 1 and Table 1. The second is a short pulse of photons interacting with the same tissue volume; the photon stream then is represented by the fluence of laser energy, the product of fluence rate and pulse duration (Joule/area). We stress that the term fluence denotes the total energy of all photons that enter the infinitesimal spherical volume inside the tissue divided by the sphere's cross-sectional area (see Fig. 1 and Table 1). Unfortunately, fluence often is misused to denote the radiant exposure (Joule/area), the total energy of laser light that is incident on a tissue surface, the product of irradiance and irradiation time (Table 1).
So, in the first case of continuous wave laser irradiation (laser light given during at least 0.1 s), it is laser power, not laser energy, which causes the thermal response of the irradiated tissue; see Eq. (8) of Appendix 1.
Therefore, the frequently used linear endovenous energy density (LEED), in units of Joules per centimeter of vessel treated, does not properly represent the setting of EVLA procedures. LEED originates from the ratio of laser power (Watt) and pullback velocity (centimeter per second).
| 3 |
Obviously, crucial information disappears when two essential parameters are amalgamated into one, here by taking their ratio. Using LEED, without specifying power or pullback velocity, would imply that, e.g., for 25 Joule/cm at 1,470 nm, one cannot distinguish between, say, 10 Watt given with 0.4 cm/s, and most likely resulting in permanent vein closure, and 1 Watt with 0.04 cm/s, most likely without much clinical effect. Our model simulates at 2 mm inner wall diameter, a maximum increase in inner vein wall temperature of 79 and 42 °C, respectively. The first temperature will certainly result in irreversible damage of the vein wall, but with the second temperature, irreversible damage is not certain. Interestingly, however, this result at 1 Watt, 0.04 cm/s gives a surprisingly high inner wall temperature of 62 °C, assuming an initial temperature of 20 °C, which is close to coagulation temperatures.
These parameters are both essential since (1) the laser power (fluence rate), rather than laser energy, is the source for the thermal response of EVLA, and (2) the pullback velocity determines the time period during which the laser power affects a location on the vein wall. In addition, we acknowledge that the diameter of the vein treated during EVLA should also be considered an essential parameter for EVLA efficacy.
In conclusion, we strongly recommend to always provide the two parameters, laser power and pullback velocity, in all future papers on EVLA and avoid the use of laser energy (Joule), in LEED, in (the incorrect usage of) “fluence”, as well as in Joule per square centimeter.
Laser power versus pullback velocity ratios
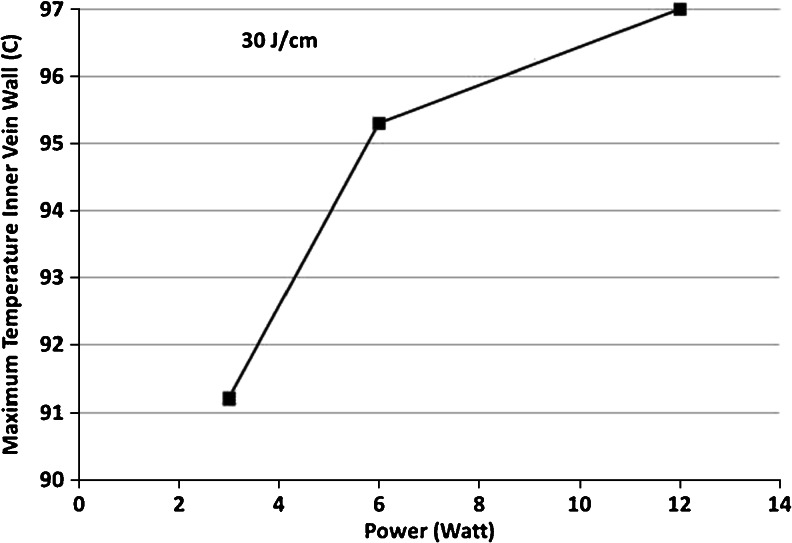
Comparing the efficacy of a combination of various powers and pullback velocities requires EVLA outcomes at constant power/velocity ratios, i.e., at constant Joule per centimeter values, Eq. (3). Our model predictions [23] suggest an interesting and perhaps clinically relevant outcome. The maximum temperature during EVLA with a 1,470 nm laser, of a 2 mm inner vein wall diameter, simulated with a power/velocity ratio of 30 Joule/cm [24], at three different power settings (3, 6, and 12 Watt), necessitating appropriate pullback velocities (1, 2, and 4 mm/s), showed that the highest power setting and fastest pullback velocity resulted in the highest inner vein wall temperature (Fig. 2). This simulation thus predicts a better EVLA efficacy at higher power and higher velocity combinations and underscores the value of reporting both parameters.
Fig. 2.
Maximum temperatures at the inner vein wall at 1,470 nm at various laser powers (3, 6, 12 Watt) and pullback velocities (1, 2, 4 mm/s), at a power/velocity ratio of 30 Joule/cm, Eq. (3)
Influence of target chromophore and wavelength on efficacy of EVLA
Laser light causes a rise in temperature when it is absorbed by a tissue chromophore. Table 2 gives absorption and reduced scattering coefficients of the blood, vein wall, and perivenous tissue that we used in our model [23]. The absorption target of the shorter wavelengths (810, 940, 980, and 1,064 nm) was assumed to be the hemoglobin in intravascular red blood cells. In contrast, wavelengths of over 1,200 nm are absorbed by water and more so with increasing wavelength [24–26]. From this, it was proposed that the absorption target of the longer wavelength lasers (1,320, 1,470–1,500, and 1,950 nm) had to be water in the endothelial cells [25]. Physiologically, however, this is questionable reasoning, since blood cells also contain water, over 60 % [27] that equally absorbs these longer wavelengths. So, with sufficient laser power, the irradiated blood volume will always heat up to coagulation temperatures, irrespective of whether (most of) the laser light was absorbed by hemoglobin or by water.
Consistent with this conclusion are the findings of comparative EVLA studies, which demonstrated that all wavelengths are equally effective in obliterating veins, although patients treated with longer wavelengths reported less postoperative pain, used fewer painkillers, and/or were less likely to have ecchymoses [26, 28–30]. However, laser power, pullback velocity, and/or type of fiber tip also varied, and longer wavelength treatments were favored by lower power settings. Thus, to contribute this favorable effect to wavelength only is illegitimate. A randomized controlled trial, comparing short- and long-wavelength EVLA with the same laser parameters (power, pullback speed, and fiber), is needed to ascertain if long wavelengths are indeed superior to short wavelengths in terms of patient-reported outcomes.
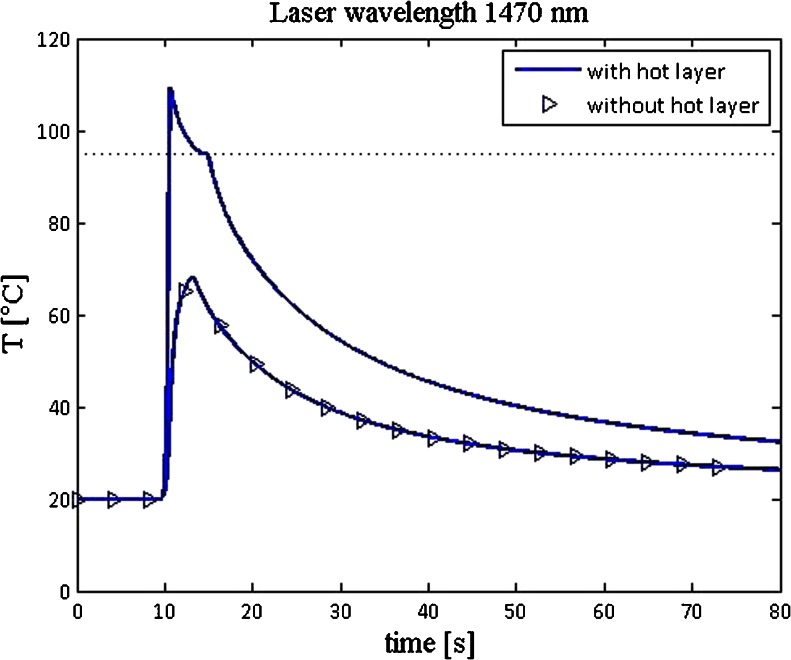
Model simulations at 1,470 nm with commonly used settings for power and pullback velocity showed, quite interestingly, that a hot fiber tip doubles the temperature increase at the inner vein wall compared to the simulated situation of keeping the tip at room temperature [23] (Fig. 3).
Fig. 3.
Computations of vein wall temperatures in a 3 mm diameter vein, using a 0.6 mm diameter laser fiber, 15 Watt of power, and 0.2 cm/s pullback velocity, as a function of time. The computations give the temperature at a fixed inner vein wall position, 2 cm above the fiber tip's starting position at t = 0, so the tip is closest to that vein wall position at 10 s after laser switch-on and start of pullback. The computations are either with the hot tip layer included (normal line) or simulated with this layer kept at room temperature (line with symbols) (from [23])
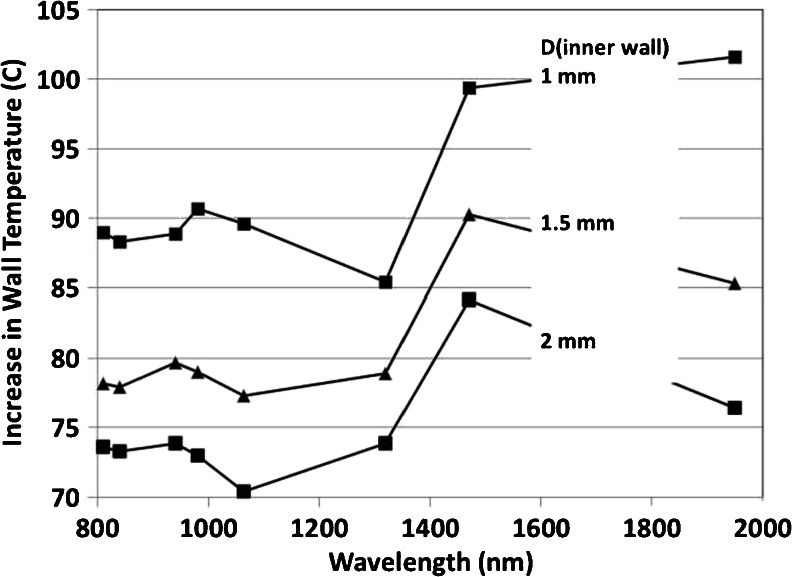
This phenomenon explains, at least in part, why differences in wavelengths have little, if any, influence on the efficacy of the procedure, here expressed by the maximum temperature of the inner vein wall. Nevertheless, our model simulations [23] do predict a slightly increased EVLA efficacy at 1,470 nm, compared to EVLA with the shorter wavelengths (about 10 °C greater rise in vein wall temperature), for all vein diameters larger than 1 mm considered in the model (Fig. 4). However, the reliability of this interesting prediction has yet to await the full mathematical introduction of the effects of steam bubbles.
Fig. 4.
Inner vein wall temperature increases versus wavelength simulated for inner vein diameters of 1, 1.5, and 2 mm, at 15 Watt, 2 mm/s
Vein diameter reduction
It is thought that the amount of intraluminal blood volume affects destruction of the vein wall. A higher blood volume is assumed to absorb a larger amount of light power, hence limiting the power that reaches the vein wall and thus reducing the vein wall's increase in temperature. In vitro and in vivo studies have been performed to demonstrate the importance of reducing the blood volume of the vein, expressed as emptying the vein of its blood [31, 32] by tumescent anesthesia and Trendelenburg positioning.
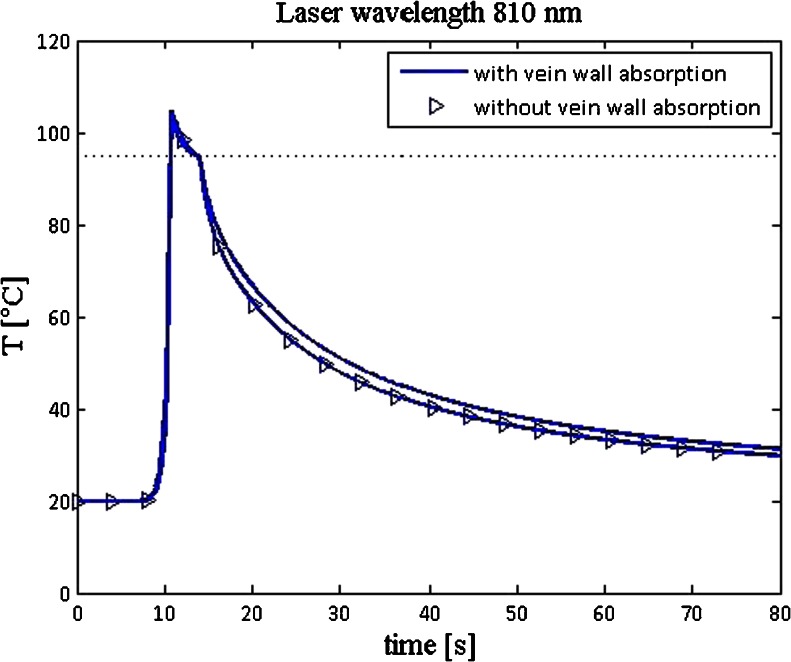
In a recent review, Vuylsteke et al. [2] stated that direct energy absorption by the vein wall is the most efficient mechanism of EVLA. However, an interesting prediction of our model [23] is that direct absorption of the laser light power by the vein wall had little effect on the increase in wall temperature (Fig. 5).
Fig. 5.
Temperature profiles at the inner vein wall, 3 mm diameter, as a function of time, with vein wall absorption included (lines) and with zero vein wall absorption (lines with symbols), at 810 nm, 15 Watt, 2 mm/s (from [23])
Nevertheless, our model does show a progressive increase in vein wall temperature during EVLA with progressive diminution of vein diameter (Fig. 4), however, with a different explanation for this phenomenon than Vuylsteke's [2]. According to our model, it is caused by the combination of two separate heat flows to the vein wall, which originate from two independent heat sources at or near the fiber tip. The hot carbonized layer on the fiber tip is the first heat source, and the hot blood surrounding the fiber tip, heated by direct absorption of the emitted laser light, is the second heat source. This latter mechanism is obviously also included in Mordon's model [5, 6], although not explicitly mentioned as a source for the thermal effects. In conclusion, our model predictions confirm the beneficial effects of diameter reduction of the vein lumen as proposed by Vuylsteke's group [2, 31, 32].
Discussion
EVLA is a fascinating therapy in clinical phlebology, and there are several ways to express this perception. One is to address the great efficacy of any EVLA protocol, seemingly irrespective of the chosen laser wavelength, power, and pullback velocity, perhaps a consequence of overtreatment by the collective effects of all contributing mechanisms. However, another is the recognition expressed in this paper that despite its great efficacy, EVLA-related physics is still poorly disseminated.
In part, this may be due to the small number of medical physicists and biomedical engineers involved in phlebology, compared to other laser-related clinical specialties. Nevertheless, the two computational models developed to simulate EVLA procedures under varying experimental conditions (power, pullback velocity, vein diameter) have significantly contributed to the identification of the various EVLA mechanisms and how these affect EVLA efficacy, particularly the importance of the hot fiber tip and the unimportance of direct absorption of laser power by the vein wall. Furthermore, we hypothesize that predictions by the future model, in which the effects of steam bubbles will have been fully incorporated, may result in identifying the most efficient protocol for EVLA therapy.
Concomitantly, the function and effects of the different fiber tips have to be assessed too and in more experimental detail than has been done so far. For example, it is essential to experimentally verify whether the hypothesis is true that a carbonized layer will not occur on a bare (centered) fiber when the treated vein is more or less “emptied” of blood by Trendelenburg position and tumescence anesthesia [2]. This requires comparing transmission spectra and microscopy of clinically used versus new fibers [10]. This part of EVLA-related research might confirm or refute the importance of having a very hot tip as well as its subsequent production of steam bubbles. Our model showed a hot tip to be a viable and clinically important EVLA mechanism (Fig. 3), whereas the steam bubbles it produces have been previously touted to be the most important EVLA mechanism [9, 12].
In conclusion, we showed that laser power, not energy, pullback velocity, and vein diameter during EVLA procedures determine the thermal response of EVLA. The total energy (Joule) given during EVLA contains insufficient information to identify the clinical setting of the procedure, so reporting LEED (Joule per centimeter) or Joule per square centimeter vein wall is without much clinical value. However, in the spirit of the Joule per square centimeter, it could perhaps be an interesting thought to adjust the laser power to the vein wall diameter, attempting to reduce the incidence of perforation, extravasation of blood, and postoperative pain. Whether hemoglobin or water is the EVLA target chromophore is irrelevant because blood consists of over 60 % water and about 15 % hemoglobin. Thus, the previously stated superiority of longer EVLA wavelengths is flawed, not only on this theoretical basis, but also because patient-reported outcomes [26, 28–31] are based on unequal laser parameter settings (power, pullback velocity, and/or fiber type), actually applying lower power levels at the longer wavelengths. A smaller vein diameter during EVLA, by Trendelenburg positioning and tumescent anesthesia, is confirmed to be beneficial, not because the vein wall may absorb more scattered laser light but because the vein wall is closer to the two heat sources, i.e., the hot tip with its constant production of steam bubbles and the thin layer of hot blood immediately surrounding this tip.
Appendix 1: optical–thermal laser–tissue interaction
Table 1 summarizes some key terms used in optical–thermal modeling to facilitate understanding the following sections.
Optical laser–tissue interactions
Laser irradiation by a collimated laser beam of power P (Watt), covering a tissue area of A (square meter), implies an irradiance (or incident power per area) of E = P/A (Watt per square meter). When the laser beam is coupled into an optical fiber and the fiber end is kept in air, the emitted light has a divergence which can be as large as 23° (with respect to the fiber axis, thus 46° full divergence); however, when kept in water, or blood, as in EVLA, the divergence angle is smaller, say around 17°, due to the small refractive index difference between fiber material and blood. The sinus of this angle is called the numerical aperture (NA) of the fiber [33]. In EVLA therapy, (bare) fibers usually have a 0.6 mm diameter.
It is commonly assumed that tissue, including blood, is an isotropic (equal properties in all directions) and homogeneous medium that has wavelength-dependent absorbing and scattering properties. Molecules like hemoglobin, melanin, bilirubin, and water display strong absorption in the UV region so tissue penetration between 200 and 400 nm is only up to tens of micrometers. Blue, green, and yellow light (400–550 nm) is absorbed primarily by hemoglobin and melanin. Red and near-infrared light (600–1,400 nm) penetrates several millimeters in tissues, where scattering additionally limits this penetration. Still longer wavelengths become absorbed intensely by water, and therefore tissue penetration of longer wavelengths is progressively reduced.
Inside the tissue, the collimated beam attenuates exponentially with tissue depth due to absorption and scattering of the photons. The scattered light is the source for the diffuse light distribution in the tissue. Scattering changes the angle of propagation of a photon. On average, the scattering angle of a photon is much more often in forward than in backward directions relative to its original direction of propagation, which is expressed by the dimensionless anisotropy factor g, having values between −1 and 1, and which are about 0.8 for tissues and over 0.99 for blood [18].
The theory of light propagation in an absorbing and scattering medium is complex, and an exact formulation of this theory has not even been achieved so far. As a next best, the photons are assumed to be particles that interact with randomly distributed absorbing and scattering centers within the tissue, neglecting the possible effects of their electromagnetic wave-like properties. Even then, photon propagation requires solving the transport integro-differential equation, with only very few known analytical solutions. Here, Monte Carlo numerical techniques are commonly used to find solutions relevant for the clinical anatomy [34]. However, a frequently used approximation, also employed to simulate EVLA therapy [5–7, 23], is the diffusion approximation, where the transport equation has been reduced to a diffusion equation (including second-order spatial derivatives, in Cartesian coordinates expressed in Table 1), assumed to be valid only when scattering dominates over absorption [21]. Equation (2) is the example used in the two EVLA models. The most important parameter describing the laser light power distribution within the tissue is the laser light fluence rate, Φ(r) (Watt per square meter); see Fig. 1 and Table 1. Coordinate r denotes the radial distance between the origin of a frame of reference (in EVLA, the fiber tip in the center of the vein) and the infinitesimal small volume of tissue.
Since the fluence rate includes scattered photons from all directions, a thought-provoking example is wide beam irradiation of tissue, which may result in a fluence rate near the inside tissue surface that exceeds the incident irradiance significantly, even up to a factor of eight (Fig. 6.8, page 175, of [21]).
Thermal laser–tissue interactions
Heat conduction
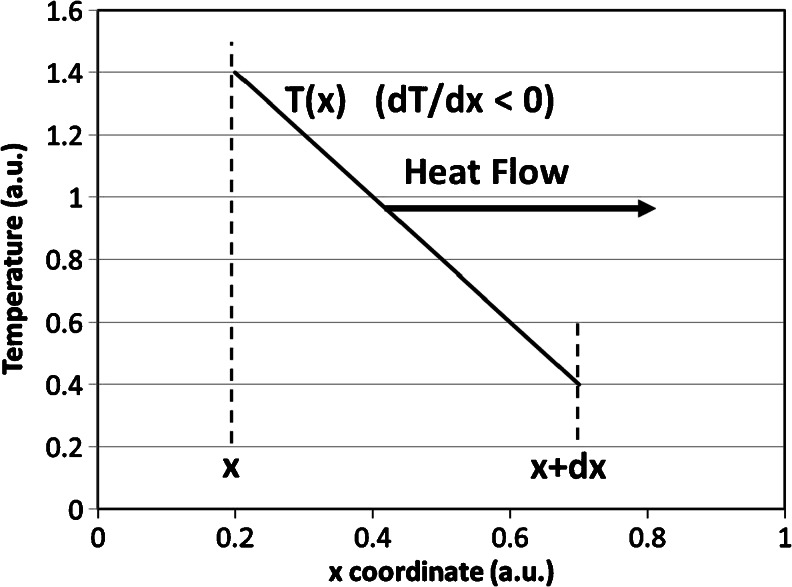
Part of the fluence rate, Φ(r) (Watt per square meter), will become absorbed in the infinitesimal volume at coordinate r (Fig. 1) and converted into heat; see Eq. (8) below. A local increase in temperature results which causes the heat to flow to surrounding regions that are cooler, a mechanism called heat conduction [35]. Different media may differ in their ability to facilitate this thermal transport process. This is expressed in the thermal conductivity (k), (Watt per meter per degree Celsius). First, the flow of heat, the official physics term is a flux of heat (Watt/area), at position x follows from taking the flow proportional to the temperature gradient over a small distance (dx) in the x direction, i.e., the temperature at x + dx minus the temperature at x divided by dx, with the thermal conductivity as proportionality coefficient. Because heat flows from higher to lower T, the flow of heat is proportional to minus the temperature gradient, thus to − dT / dx, or (Fig. 6)
| 4 |
Fig. 6.
Cartoon of Fourier's law of thermal diffusion, relating the negative gradient of the temperature (T) to the heat flow (or heat flux, in Watt/area) by Eq. (4). The temperature versus x-coordinate curve is linearized between x and x + dx because dx is assumed to be infinitesimally small
This equation is known as Fourier's law of thermal diffusion (Fig. 6).
Our aim is to derive the bio-heat equation, Eqs. (1) and (9) below, whose solution, T(r, t), is the space- and time-dependent temperature of the infinitesimal small tissue volume (Fig. 1), where t denotes the irradiation time. This requires an expression for the conduction (diffusion) of heat into or out of that small volume.
In one direction, say the x direction, the stored energy will change because of the heat flow that enters at x + dx minus the heat flow that enters at x, divided by distance dx, hence the negative gradient of the heat flow. Thus, from Eq. (4), a second-order derivative over coordinate x occurs, which is mathematically a diffusion equation, basically expressing the curvature of T in the x direction, as follows:
| 5 |
In three dimensions, second-order differentials then also occur in the other two coordinate directions (see Table 1), which are generally abbreviated by the Laplace second-order differential diffusion operator Δ.
The bio-heat equation: conservation of power in an infinitesimal volume
First, from Eq. (1), we recall that the state of the tissue is characterized by its stored energy, which is directly related to its temperature [35] and which may vary with position and time. As before, Fig. 1, we consider an infinitesimal volume of tissue at coordinate r. The stored energy in that volume (Joule/volume) then is given as follows:
| 6 |
Parameters ρ and c (Table 1) are, respectively, the tissue density (kilogram per cubic meter) and the specific heat capacity (Joule per kilogram per degree Celsius) at r. We now consider the change in the stored energy/volume in a short time period dt, which is expressed as follows:
| 7 |
We assumed that ρc is independent of time. The source for this rate of change in stored energy is the absorbed part of the fluence rate in that infinitesimal volume, which can be derived to equal the product of absorption coefficient and fluence rate, called the source term [36].
| 8 |
Finally, the rate of change in stored energy in the infinitesimal volume during dt, Eq. (7), can be written as the sum of the absorbed power within that volume, Eq. (8), and the change in power in that volume due to heat diffusion, Eq. (5), which is called the bio-heat equation.
| 9 |
Operator Δ is positive when the infinitesimal sphere is colder than its surrounding (i.e., heat will be flowing in) and negative when it is hotter (i.e., heat will be flowing out). The result is a time- and space-varying temperature profile within the tissue volume, T(r,t), where t denotes the time since the laser was switched on.
Appendix 2: steam production by a 1,000 °C layer of carbonized blood
There are two ways to estimate the vapor production by the carbonized layer. In the first, this layer is assumed to be at 1,000 °C when the laser has just been switched off. If all the energy contained in this layer is used to vaporize water, the following estimate shows that about 30 mm3 of steam is formed.
The carbonized layer is about 30 μm thick [10] and has a diameter of 0.6 mm, thus a volume of 30 ⋅ 10− 6 ⋅ π ⋅ (0.3 ⋅ 10− 3)2 ∼ 10− 11 m3. From thermodynamics [37], it is known that conversion of x kilograms of water into x kilograms of steam requires an energy of x Dh (Joule), with specific enthalpy of vaporization Dh ~ 2.2 × 106 Joule/kg. The available energy of a layer of volume V at a temperature of 900 °C above 100 °C, the temperature of steam, is denoted by ρ ⋅ c p ⋅ V ⋅ 900 ≈ 0.04 Joule , using ρ = 1,000 kg/m3 and c p ~ 4.2 · 103Joule/kg/°C. Thus, 0.04 Joule creates 0.04/2.2 · 10−6 = 1.8 · 10−8 kg of steam. With a ρ of steam of about 0.6 kg/m3, this implies ~3 · 10−8m3 or 30 mm3 of steam. This estimate shows that steam bubbles can be created by the “rest” energy residing in the layer of carbonized blood at 1,000 °C just after switching off the laser.
The second estimate is obtained assuming the amount of energy given per second to the carbonized layer by the laser, 45 % of the emitted laser power [10] minus Planck's radiation, equals the energy per second given off by this layer to the blood. Per second, this is about 4 Joule, if 10 Watt is the laser power and about 5 % is assumed to represent Planck's black body radiation (which is one of the cooling mechanisms for the carbonized layer; the others are heat conduction and convection). With the same estimate as above for 0.04 Joule, 4 Joule produces 100 times more, thus 3,000 mm3 or 3 cm3, steam vapor per second. However, the heat needed to heat up the blood to 100 °C must be subtracted from this value. Again, with the above estimate, a cylinder of fresh blood with a length of (say) 3 mm (assuming a 3 mm/s pullback velocity) and a 0.6 mm diameter has a volume close to 10−9 m3 and requires ρ ⋅ c p ⋅ V blood ⋅ 100 ≈ 0.4 Joule/s to be heated up to 100 °C. This is one tenth of the available energy per second, so vapor production by the laser-irradiated carbonized layer occurs without any doubt.
References
- 1.van den Bos R, Arends L, Kockaert M, Neumann M, Nijsten T. Endovenous therapies of lower extremity varicosities: a meta-analysis. J Vasc Surg. 2009;49:230–239. doi: 10.1016/j.jvs.2008.06.030. [DOI] [PubMed] [Google Scholar]
- 2.Vuylsteke ME, Mordon SR. Endovenous laser ablation: a review of mechanisms of action. Ann Vasc Surg. 2012;26:424–433. doi: 10.1016/j.avsg.2011.05.037. [DOI] [PubMed] [Google Scholar]
- 3.van Gemert MJC, van der Geld CWM, Bruijninckx CMA, Verdaasdonk RM, Neumann HAM (2012) Comment to Vuylsteke ME and Mordon SR. Endovenous laser ablation: a review of mechanisms of action. Ann Vasc Surg 2012;26:424-33. Ann Vasc Surg 26:881–883 [DOI] [PubMed]
- 4.Navarro L, Navarro N, Salat CB, Gomez JF, Min RJ (2002) Endovascular laser device and treatment of varicose veins. US 6,398,777 B1; patent filed in 1999, granted in 2002
- 5.Mordon SR, Wassmer B, Zemmouri J. Mathematical modeling of 980-nm and 1320-nm endovenous laser treatment. Lasers Surg Med. 2007;39:256–265. doi: 10.1002/lsm.20476. [DOI] [PubMed] [Google Scholar]
- 6.Mordon SR, Wassmer B, Zemmouri J (2006) Mathematical modeling of endovenous laser treatment (ELT). Biomed Eng Online 5:26 [DOI] [PMC free article] [PubMed]
- 7.van Ruijven PWM, Poluektova AA, van Gemert MJC, Neumann HAM, Nijsten T, van der Geld CWM (2014) Optical-thermal mathematical model for endovenous laser ablation of varicose veins. Lasers Med Sci. doi:10.1007/s10103-013-1451-x [DOI] [PubMed]
- 8.Fan CM, Anderson RR. Endovenous laser ablation: mechanism of action. Phlebology. 2008;23:206–213. doi: 10.1258/phleb.2008.008049. [DOI] [PubMed] [Google Scholar]
- 9.Disselhoff BCVM, Rem AI, Verdaasdonk RM, der Kinderen DJ, Moll FL (2008) Endovenous laser ablation: an experimental study on the mechanism of action. Phlebology 23:69–76 [DOI] [PubMed]
- 10.Amzayyb M, van den Bos RR, Kodach VM, de Bruin DM, Nijsten T, Neumann HAM, van Gemert MJC (2010) Carbonized blood deposited on fibres during 810, 940 and 1,470 nm endovenous laser ablation: thickness and absorption by optical coherence tomography. Lasers Med Sci 25:439–447 [DOI] [PMC free article] [PubMed]
- 11.van den Bos RR, Kockaert MA, Neumann HAM, Bremmer RH, Nijsten T, van Gemert MJC (2009) Heat conduction from the exceedingly hot fiber tip contributes to the endovenous laser ablation of varicose veins. Lasers Med Sci 24:247–251, Erratum 2009;24:679 [DOI] [PubMed]
- 12.Proebstle TM, Lehr HA, Kargl A, Espinola-Klein C, Rother W, Bethge S, Knop J. Endovenous treatment of the greater saphenous vein with a 940-nm diode laser: thrombotic occlusion after endoluminal thermal damage by laser-generated steam bubbles. J Vasc Surg. 2002;35:729–736. doi: 10.1067/mva.2002.121132. [DOI] [PubMed] [Google Scholar]
- 13.van der Geld CWM, van den Bos RR, van Ruijven PWM, Nijsten T, Neumann HAM, van Gemert MJC. The heat-pipe resembling action of boiling bubbles in endovenous laser ablation. Lasers Med Sci. 2010;25:907–909. doi: 10.1007/s10103-010-0780-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Thomsen S, Pearce JA (2011) Thermal damage and rate processes in biologic tissues. In: Welch AJ, van Gemert MJC (eds) Optical–thermal response of laser-irradiated tissue, 2nd edn. Springer, Dordrecht, Chapter 13, page 497
- 15.Verdaasdonk RM, Holstege FC, Jansen ED, Borst C. Temperature along the surface of modified fiber tips for Nd:YAG laser angioplasty. Lasers Surg Med. 1991;11:213–222. doi: 10.1002/lsm.1900110304. [DOI] [PubMed] [Google Scholar]
- 16.Meissner OA, Schmedt CG, Hunger K, Hetterich H, Sroka R, Rieber J, Babaryka G, Steckmeier BM, Reiser M, Siebert U, Mueller-Lisse U. Endovascular optical coherence tomography ex vivo: venous wall anatomy and tissue alterations after endovenous therapy. Eur Radiol. 2007;17:2384–2393. doi: 10.1007/s00330-007-0593-2. [DOI] [PubMed] [Google Scholar]
- 17.Weiss RA. Comparison of endovenous radiofrequency versus 810 nm diode laser occlusion of large veins in an animal model. Dermatol Surg. 2002;28:56–61. doi: 10.1046/j.1524-4725.2002.01191.x. [DOI] [PubMed] [Google Scholar]
- 18.Bosschaart N, Edelman G, Aalders MCG, van Leeuwen TG, Faber DJ (2014) A literature review and a novel theoretical approach on the optical properties of whole blood. Lasers Med Sci. doi:10.1007/s10103-013-1446-7 [DOI] [PMC free article] [PubMed]
- 19.Vuylsteke ME, Van Dorpe J, Roelens J, De Bo T, Mordon S, Fourneau I (2010) Intraluminal fibre-tip centering can improve endovenous laser ablation: a histological study. Eur J Vasc Endovasc Surg 40:110–116 [DOI] [PubMed]
- 20.Grooten MWM, van der Geld CWM. Predicting heat transfer in long R-134a filled thermosyphons. ASME J Heat Transfer. 2009;131:051501–051509. doi: 10.1115/1.3000969. [DOI] [Google Scholar]
- 21.Star WM. Diffusion theory of light transport. In: Welch AJ, van Gemert MJC, editors. Optical-thermal response of laser-irradiated tissue. 2. Dordrecht: Springer; 2011. pp. 145–201. [Google Scholar]
- 22.Walsh JT. Basic interactions of light with tissue. In: Welch AJ, van Gemert MJC, editors. Optical-thermal response of laser-irradiated tissue. 2. Dordrecht: Springer; 2011. pp. 13–15. [Google Scholar]
- 23.Poluektova AA, Malskat WSJ, van Gemert MJC, Vuylsteke ME, Bruijninckx CMA, Neumann HAM, van der Geld CWM (2014) Some controversies in Endovenous Laser Ablation of varicose veins addressed by optical–thermal mathematical modeling. Lasers Med Sci. doi:10.1007/s10103-013-1450-y [DOI] [PubMed]
- 24.Almeida J, Mackay E, Javier J, Mauriello J, Raines J. Saphenous laser ablation at 1470 nm targets the vein wall, not blood. Vasc Endovasc Surg. 2009;43:467–472. doi: 10.1177/1538574409335916. [DOI] [PubMed] [Google Scholar]
- 25.Goldman MP, Mauricio M, Rao J. Intravascular 1320-nm laser closure of the great saphenous vein: a 6- to 12-month follow-up study. Dermatol Surg. 2004;30:1380–1385. doi: 10.1111/j.1524-4725.2004.30431.x. [DOI] [PubMed] [Google Scholar]
- 26.Vuylsteke M, De Bo T, Dompe G, Di Crisci D, Abbad C, Mordon S. Endovenous laser treatment: is there a clinical difference between using a 1500 nm and a 980 nm diode laser? A multicenter randomised clinical trial. Int Angiol. 2011;30:327–334. [PubMed] [Google Scholar]
- 27.Beilin LJ, Knight J, Munco-Faure AD, Anderson J. The sodium, potassium, and water content of red blood cells of healthy human adults. J Clin Invest. 1966;45:1817–1825. doi: 10.1172/JCI105485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Proebstle TM, Moehler T, Gul D, Herdemann S. Endovenous treatment of the great saphenous vein using a 1,320 nm Nd:YAG laser causes fewer side effects than using a 940-nm diode laser. Dermatol Surg. 2005;31:1678–1683. doi: 10.2310/6350.2005.31308. [DOI] [PubMed] [Google Scholar]
- 29.Kabnick LS. Outcome of different endovenous laser wavelengths for great saphenous vein ablation. J Vasc Surg. 2006;43:88–93. doi: 10.1016/j.jvs.2005.09.033. [DOI] [PubMed] [Google Scholar]
- 30.Doganci S, Demirkilic U. Comparison of 980 nm laser and bare-tip fibre with 1470 nm laser and radial fibre in the treatment of great saphenous vein varicosities: a prospective randomised clinical trial. Eur J Vasc Endovasc Surg. 2010;40:254–259. doi: 10.1016/j.ejvs.2010.04.006. [DOI] [PubMed] [Google Scholar]
- 31.Desmyttere J, Grard C, Mordon S. A 2 years follow-up study of endovenous 980 nm laser treatment of the great saphenous vein: Role of the blood content in the GSV. Med Laser Appl. 2005;20:283–289. doi: 10.1016/j.mla.2005.08.003. [DOI] [Google Scholar]
- 32.Vuylsteke ME, Martinelli T, Van Dorpe J, Roelens J, Mordon S, Fourneau I. Endovenous laser ablation: the role of intraluminal blood. Eur J Vasc Endovasc Surg. 2011;42:120–126. doi: 10.1016/j.ejvs.2011.03.017. [DOI] [PubMed] [Google Scholar]
- 33.Verdaasdonk RM, Borst C. Optics of fiber and fiber probes. In: Welch AJ, van Gemert MJC, editors. Optical-thermal response of laser-irradiated tissue. New York: Plenum Press; 1995. p. 624. [Google Scholar]
- 34.Jacques SL. Monte Carlo modeling of light transport in tissue (steady state and time of flight) In: Welch AJ, van Gemert MJC, editors. Optical-thermal response of laser-irradiated tissue. 2. Dordrecht: Springer; 2011. pp. 109–144. [Google Scholar]
- 35.Diller KR. Laser generated heat transfer. In: Welch AJ, van Gemert MJC, editors. Optical-thermal response of laser-irradiated tissue. 2. Dordrecht: Springer; 2011. pp. 353–361. [Google Scholar]
- 36.Welch AJ, van Gemert MJC, Star WM. Definitions and overview of tissue optics. In: Welch AJ, van Gemert MJC, editors. Optical-thermal response of laser-irradiated tissue. 2. Dordrecht: Springer; 2011. p. 52. [Google Scholar]
- 37.Bird RB, Stewart WE, Lightfoot EN. Transport phenomena. New York: Wiley; 1960. [Google Scholar]