Bayesian Model Selection in Complex Linear Systems, as Illustrated in Genetic Association Studies

Summary

Motivated by examples from genetic association studies, this paper considers the model selection problem in a general complex linear model system and in a Bayesian framework. We discuss formulating model selection problems and incorporating context-dependent a priori information through different levels of prior specifications. We also derive analytic Bayes factors and their approximations to facilitate model selection and discuss their theoretical and computational properties. We demonstrate our Bayesian approach based on an implemented Markov Chain Monte Carlo (MCMC) algorithm in simulations and a real data application of mapping tissue-specific eQTLs. Our novel results on Bayes factors provide a general framework to perform efficient model comparisons in complex linear model systems.

1. Introduction

Genetic association studies aim to detect statistical associations between genetic variants (most commonly, single nucleotide polymorphisms, or SNPs) and phenotypic traits. Genetic associations are complicated in nature: multiple SNPs may simultaneously affect a single phenotype, the genetic effects of a SNP with respect to a phenotype may exhibit a large degree of heterogeneity in different environmental conditions (known as gene-environment interactions), and a single SNP may affect multiple phenotypes through gene networks. Statistical analysis of genetic associations under these complex settings has become increasingly important because it can yield a comprehensive understanding of the roles played by genetic variants in a biological system. To illustrate, we briefly introduce two motivating examples.

Motivating Example 1: Multiple-Tissue eQTL Mapping

eQTLs (expression quantitative trait loci) are genetic variants associated with gene expression phenotypes and play important roles in transcriptional regulation processes. Most recently, eQTL data have been collected from multiple tissue/cell types (e.g., the NIH GTEx project). One important goal is to identify eQTLs across tissues and investigate how their effects vary in different cellular environments. Biologically, it is expected that a proportion of eQTLs are active (i.e., effect size ≠ 0) only in certain tissues but silent (i.e., effect size = 0) in others, a classic case of gene-environment interaction; for tissues in which an eQTL is active, the regulatory environments of the target gene are likely similar, and the effects of the eQTL are expected to show low heterogeneity. In addition, because a single gene is typically subject to many regulatory elements, it is highly likely that there exist multiple eQTLs for any given gene. Finally, in the most popular experimental design of this type, multiple tissue samples are collected from the same set of individuals, and intraindividual correlations of gene expressions need to be accounted for. Under this setting, it is challenging to simultaneously identify multiple and potentially tissue-specific eQTLs.

Motivating Example 2: Fine-Mapping in a Genetic Association Meta-Analysis

Genetic association studies with limited sample sizes are underpowered to detect modest association signals. Nevertheless, genuine genetic associations typically show consistent effect sizes in many independent studies. Meta-analysis therefore becomes critically important to aggregate sample sizes and increase power for detecting associations. Currently, most existing meta-analytic approaches in genome-wide association (GWA) studies analyze one SNP at a time. In a meta-analytic setting, the simultaneous mapping of multiple genetic associations, especially in a predefined genomic region, remains a statistical challenge.

Although identifying non-zero genetic associations can be naturally formulated as a model-selection problem, most available approaches (Fridley (2009); Wilson et al. (2010); Wu et al. (2009); Mitchell and Beauchamp (1988); Guan and Stephens (2011)), applicable only to single multiple linear regression models, are inadequate for addressing the situations described in our motivating examples. This is mainly because, in both cases, observed data form subgroups (viz., different tissue types in eQTL mapping and individual GWA studies in the meta-analysis). We not only require a complex model system to account for these subgroup structures (in likelihood computation), but we also require variable selections to be performed either with respect to (as in the case of tissue-specific eQTLs) or integrating among (as in meta-analysis) the intrinsic subgroup structures. Furthermore, as we have shown in both examples, there typically exists a priori information on the correlations of non-zero effects. Effectively utilizing this prior information would greatly improve the performance of model selection and make the results easy to interpret.

In this paper, we describe a general system of linear models that is capable of addressing both of the motivating examples. We consider the problem of formulating model (variable) selection through prior specification under this linear system and propose Bayesian solutions to conduct model comparison and model selection via Bayes factors. We illustrate our Bayesian approach through simulation studies and a real example of tissue-specific eQTL mapping. We want to emphasize that our results on Bayes factors, discussed in section 4, are completely general and can be readily applied to a wide range of model comparison, hypothesis testing and model selection problems.

2. A System of Simultaneous Multivariate Linear Regressions (SSMR)

We describe a very general linear model system for which many commonly used linear models become special cases. It naturally applies in the complex scenarios in genetic association studies we have discussed. Unless otherwise specified, all of the results presented in this paper apply to this most general form of the linear model system.

2.1 Model Description and Notation

We consider a system of simultaneous multivariate linear regressions (SSMR) consisting of a set of s separate multivariate linear regression equations, i.e.,

$${\mathit{Y}}_i={\mathit{X}}_{c,i}{\mathit{B}}_{c,i}+{\mathit{X}}_{g,i}{\mathit{B}}_{g,i}+{\mathit{E}}_i,{\mathit{E}}_i~\mathrm{M}\mathrm{N}(\mathbf{0},\mathit{I},{\mathbf{\Sigma }}_{\mathbf{i}}),i=1,\dots ,s,$$ (1)

where “MN” denotes the matrix-variate normal distribution, and each composing linear equation describes one of the s non-overlapping subgroups of observed data. For subgroup i with n_i subjects, Y_i is an n_i × r matrix with each row representing r quantitative measurements from one subject. We denote X_i = (X_c,iX_g,i) as the n_i × (q_i + p) design matrix, in which X_g,i (n_i × p) represents the data matrix of p explanatory variables of interest (e.g., genotypes of interrogated genetic variants), and X_c,i (n_i × q_i) represents the data of q_i additional variables (including the intercept) to be controlled for; matrices B_g,i (p × r) and B_c,i (q_i × r) contain the regression coefficients for the explanatory and the controlled variables, respectively. Finally, E_i is an n_i × r matrix of residual errors in which each row vector is assumed to be independent and identically distributed as N(0, Σ_i) (i.e., E_i ~ MN(0, I, Σ_i)). Although the same set of r response variables and p explanatory variables are assumed to be measured in all s subgroups, we allow each composing linear model to control for a different set of covariates. Furthermore, the residual errors are assumed to be independent across subgroups. In addition, we denote 𝒴 := {Y₁, …, Y_s}, 𝒳 := {X₁, …, Xs} and ℰ := {Σ₁, … Σ_s}. (Throughout the paper, we refer to ℰ as “error variances”.)

The SSMR model is a generalization of a class of linear systems; some commonly used special cases include the following:

1. Multiple Linear Regression: s = 1 and r = 1.

2. Multivariate Linear Regression (MVLR): s = 1. This is a suitable model for describing multiple-tissue eQTLs for which different tissue samples are obtained from the same set of individuals (Motivating Example 1).

3. Systems of Simultaneous Linear Regressions (SSLR): r = 1. This model can be applied to fine mappings of genetic variants in a meta-analytic setting (Motivating Example 2).

The general SSMR model is also uniquely important for many genetics/genomics applications. One such example is the meta-analysis of genetic variants with respect to multiple phenotypes.

We introduce the vectorized regression coefficients ${\mathit{\beta }}_g:=\left(\begin{array}{c}\hfill \text{vec}({\mathit{B}}_{g,1}^{\prime })\hfill \\ \hfill ⋮\hfill \\ \hfill \text{vec}({\mathit{B}}_{g,s}^{\prime })\hfill \end{array}\right)$ and ${\mathit{\beta }}_c:=\left(\begin{array}{c}\hfill \text{vec}({\mathit{B}}_{c,1}^{\prime })\hfill \\ \hfill ⋮\hfill \\ \hfill \text{vec}({\mathit{B}}_{c,s}^{\prime })\hfill \end{array}\right)$, which are mathematically convenient to work with. We use the notation 𝕀(β_g,i) to denote an indicator function of the i-th component of β_g, such that 𝕀(β_g,i) = 1 if β_g,i ≠ 0 and 0 otherwise. Furthermore, we define the following indicator vector:

$$\xi ({\mathit{\beta }}_g):=(𝕀({\beta }_{g,1}),𝕀({\beta }_{g,2}),\dots ).$$ (2)

In this paper, ξ(β_g) is our quantity of interest for model selection.

To perform Bayesian inference based on the SSMR model, we assign prior distributions for β_g, β_c, and Σ. For β_g, we assume a multivariate normal prior,

$${\mathit{\beta }}_g~\mathrm{N}(\mathbf{0},{\mathit{W}}_g).$$ (3)

The variance-covariance matrix W_g plays a central role in our framework, and we defer a detailed discussion of it to section 3. For the regression coefficients of controlled variables, we assume

$${\mathit{\beta }}_c~\mathrm{N}(\mathbf{0},{\mathbf{\Psi }}_c),$$ (4)

where matrix Ψ_c is assumed to be diagonal. When performing an inference, we consider the limiting condition ${\mathbf{\Psi }}_c^{-1}\to \mathbf{0}$ (i.e., each composing coefficient in β_c is effectively assigned an independent at prior). Furthermore, we assume β_g and β_c are a priori independent. Finally, we assign an independent inverse Wishart prior, with parameters m_i (a positive scalar) and H_i (a positive-definite r × r matrix), for each composing Σ_i ∈ ℰ, i.e.,

$${\mathbf{\Sigma }}_i~\mathrm{I}{\mathrm{W}}_r({\nu }_i{\mathit{H}}_i,m_i),$$ (5)

where ν_i = m_i − q_i − r − 1, and we require ν_i > 0. If r is small relative to the sample size, Σ_i can be sufficiently learned from the data. In such cases (as in the simulations and the data application of this paper), we consider the limiting condition H_i → 0 and ν_i → 0. As r is large, setting H_i and ν_i requires context-dependent considerations, we discuss this briefly in the discussion.

3. Prior Specification for Structured Model Selection in SSMR

At its most basic level, a model/variable selection problem in the SSMR model can be formulated as an inference on ξ(β_g) (defined in Equation (2)). Throughout this paper, we refer to a candidate model as a particular configuration of ξ(β_g). In our Bayesian framework, a prior distribution on the space of candidate models, Pr(ξ(β_g)), is used to prioritize (or in the extreme case, enforce) a certain class of preferred models. For instance, the intrinsic (sub)group structure and the sparse property of preferred candidate models can be quantified by Pr(ξ(β_g)). Given a candidate model, we use the multivariate normal prior (3) to fully specify the prior distribution on β_g, for which a positive semidefinite covariance matrix W_g is sufficient. In this presentation, we use matrix W_g to serve two primary purposes:

1. articulate the structure of the given candidate model ξ(β_g).

2. convey context-dependent a priori correlation information on non-zero elements of β_g to aid model selection.

The first point provides convenience in mathematical representations, and the second point highlights the fact that matrix W_g incorporates a source of prior information that complements what is conveyed in Pr(ξ(β_g)).

The idea of using matrix W_g to represent a candidate model is similar to the use of the “spike-and-slab” prior in Bayesian variable selection: for a regression coefficient β ∈ β_g, it is convenient to represent Pr(β = 0) = 1 by a degenerate normal (prior) distribution β ~ N(0, 0) (i.e., a spike), and accordingly, a non-zero marginal prior variance on β (i.e., a slab) indicates the corresponding variable is included. Thus, information about ξ(β_g) can be directly obtained from the main diagonal of a given (singular) matrix W_g.

The off-diagonal of matrix W_g defines context-dependent prior correlations between (nonzero) regression coefficients. Incorporating this information in the inference enables “borrowing strength” across correlated components in β_g, thereby improving the efficiency of model selection. Given a specific context and a candidate model, the qualitative dependence relationships between any two coefficients in β_g are typically determined. Much recent research has been devoted to further quantifying such correlation structures (Scott-Boyer et al. (2012); Guan and Stephens (2011); Wen and Stephens (2011). We provide a brief summary of some existing prior specification approaches in various genetic settings in Appendix A of the Web Supplementary Materials.

3.1 Parameterization of Wg for Model Selection

To better facilitate model selection, we propose to parameterize W_g = (Γ_g, Λ_g), where Γ_g is a binary matrix consisting of entry-wise non-zero indicators and is identical in size and layout to W_g; Λ_g = {w_ij} is an indexed set of numerical values quantifying each non-zero entry in the Γ_g matrix. For a given candidate model, the main diagonal of Γ_g corresponds to ξ(β_g). The off-diagonal of Γ_g represents the qualitative prior dependence relationships between coefficients in β_g and can always be deterministically specified given its diagonal and a specific application context. Mathematically speaking, there always exists a context-dependent injection from ξ(β_g) to Γ_g.

Given the prior probability Pr(ξ(β_g)) for a candidate model, we now have a principled way to specify a prior distribution on matrix W_g, i.e.,

$$p({\mathit{W}}_g)=p({\mathrm{\Lambda }}_g|\xi ({\mathit{\beta }}_g))·\mathrm{P}\mathrm{r}(\xi ({\mathit{\beta }}_g)).$$ (6)

3.2 Scale-Invariant Prior Formulation

In practice, it is often desirable that inference results be invariant to linear transformations of response variables (the g-prior for multiple linear regressions and the conjugate prior commonly used in the MVLR model both have this property, see also Servin and Stephens (2007); Wen and Stephens (2011)). To achieve this in the SSMR model, we scale each element in β_g by its corresponding marginal residual standard error (in the MVLR, the residual standard error for a given regression coefficient is represented as the square root of the corresponding diagonal element in its residual variance-covariance matrix). More formally, we define a vector of scale-free standardized effects by ${\mathbf{b}}_g:={\mathbf{S}}^{-\frac{1}{2}}{\mathit{\beta }}_g$, where S is a diagonal matrix permuted from ${\oplus }_{i=1}^s(\mathit{I}\otimes \text{diag}({\mathbf{\Sigma }}_i))$ to match the order of elements in β_g. (Throughout this paper, we use “⊗” and “⊕” to denote Kronecker product and direct sum of matrices, respectively). Under this setting, a multivariate normal prior distribution b_g ~ N(0, U_g) induces a normal prior distribution on β_g with mean 0 and

$${\mathit{W}}_g={\mathit{S}}^{\frac{1}{2}}{\mathit{U}}_g{\mathit{S}}^{\frac{1}{2}}.$$ (7)

With (7), we are able to handle the desired scale-invariant prior formulation as a special case of the original scale formulation.

4. Results on Bayes Factors

We derive Bayes factors to facilitate model comparisons and selections in the SSMR model. At the most fundamental level, Bayes factors enable us to compare the supporting evidence from observed data for a set of competing models (which are not necessarily nested). In the case that posterior model probabilities are of direct interest, Bayes factors can typically be utilized as computational devices in the place of marginal likelihood, which is sometimes more difficult to compute. In what follows, we discuss the Bayes factors derived from the SSMR model, assuming the multivariate normal prior (3) is fully specified. Let H₀ denote the trivial null model, where β_g ≡ 0. Then, for an alternative target model characterized by its prior variance W_g, we formally define a null-based Bayes factor (Liang et al. (2008)) as follows:

Definition 1: Under the SSMR model, for a positive definite W_g, the Bayes factor is defined as

$$\mathrm{B}\mathrm{F}({\mathit{W}}_g)=\underset{{\mathbf{\Psi }}_c^{-1}\to 0}{\text{lim}}\frac{P(\mathit{𝒳}|\mathit{𝒴},{\mathit{W}}_g)}{P(\mathit{𝒳}|\mathit{𝒴},H_0)}.$$ (8)

For technical reasons, the above definition requires W_g to be full rank; we will extend this definition to allow for a singular W_g matrix later in section 4.1.3.

4.1 Analytic Results of Bayes Factors

We start by introducing some necessary additional notation. We use β̂_g to denote the maximum likelihood estimate (MLE) of β_g and denote its variance by V_g := Var(β̂_g). Under the SSMR model, both β̂_g and V_g have closed-form expressions: β̂_g depends only on observed data 𝒳 and 𝒴, while V_g depends on 𝒳 and ℰ (their explicit functional forms can be found in Appendix B of the Web Supplementary Materials).

4.1.1 Exact Bayes Factors with Known Error Variances

In the general case of the SSMR model, when the error variances are considered known, rather than being assigned priors, the exact Bayes factor can be analytically expressed. We summarize this result in the following lemma:

Lemma 1: In the SSMR model, if ℰ is known, the Bayes factor in definition 1 can be analytically computed by

$$\mathrm{B}\mathrm{F}({\mathit{W}}_g)={|\mathit{I}+{\mathit{V}}_g^{-1}{\mathit{W}}_g|}^{-\frac{1}{2}}·\text{exp}(\frac{1}{2}{\mathit{\beta ̂}}_g^{\prime }{\mathit{V}}_g^{-1}[{\mathit{W}}_g{(\mathit{I}+{\mathit{V}}_g^{-1}{\mathit{W}}_g)}^{-1}]{\mathit{V}}_g^{-1}{\mathit{\beta ̂}}_g).$$ (9)

The derivation of Lemma 1 is mostly straightforward; the details are provided in Appendix B.1 of the Web Supplementary Materials.

Note 1: The Bayes factor naturally addresses potential collinearity in predictors. In particular, the evaluation of the Bayes factor does not require the involved design matrices to be full rank (the details are explained in Appendix C of the Web Supplementary Materials). As a result, when highly correlated explanatory variables are included in the model, the Bayes factor can still be stably computed without special computational treatments.

Note 1 is extremely relevant for genetic applications, where genotypes of many spatially close genetic variants are often highly correlated.

4.1.2 Approximate Bayes Factors with Unknown Error Variances

In more realistic settings, error variances are typically unknown and additional integrations with respect to ℰ are necessary for Bayes factor evaluations. Except for a very few special cases, the exact Bayes factor generally is analytically intractable. Alternatively, we apply Laplace’s method to pursue analytic approximations of the Bayes factor. Laplace’s method has been widely applied in computing Bayes factors in other similar settings (Kass and Raftery (1995); Raftery (1996); DiCiccio et al. (1997); Saville and Herring (2009); Wen and Stephens (2011)). In the case of the SSMR model, applying Laplace’s method yields an analytic approximation that maintains the exact functional form of (9) – only with the unknown Σ replaced by an intuitive point estimate. More specifically, ABF substitutes each Σ_i ∈ ℰ in (9) with the following Bayesian shrinkage estimate

$${\mathbf{\Sigma ̌}}_i=\frac{{\nu }_i}{n_i+{\nu }_i}{\mathit{H}}_i+\frac{n_i}{n_i+{\nu }_i}[{\alpha }_i{\mathbf{\Sigma ̂}}_i+(1-{\alpha }_i){\mathbf{\Sigma ̃}}_i],$$ (10)

where Σ̂_i and Σ̃_i denote the MLEs of error variances estimated from the residuals under the target and the null models, respectively, parameters ν_i and H_i are defined in the inverse-Wishart prior of Σ_i, and parameter α_i ∈ [0, 1] serves as a tuning parameter and has an impact on the finite-sample accuracy of the resulting Bayes factor approximations. We further denote α = (α₁, …, α_s) and ℰ̌ := {Σ̌₁, …, Σ̌_s}.

Other relevant quantities in (9) that are functionally related to ℰ include V_g and potentially W_g (e.g., in the scale-invariant prior formulation). We denote V̌_g and W̌_g as the corresponding plug-in estimates of V_g and W_g by ℰ̌.

The result of the approximate Bayes factor is summarized in the following proposition:

Proposition 1: Under the SSMR model, when ℰ is unknown, applying Laplace’s method leads to the following analytic approximation of the Bayes factor

$$\mathrm{A}\mathrm{B}\mathrm{F}({\mathit{W}}_g,\mathit{\alpha }):=|\mathit{I}+{\mathit{V̌}}_g^{-1}{\mathit{W̌}}_g{|}^{-\frac{1}{2}}·\text{exp}(\frac{1}{2}{\mathit{\beta ̂}}_g^{\prime }{\mathit{V̌}}_g^{-1}\left[{\mathit{W̌}}_g{(\mathit{I}+{\mathit{V̌}}_g^{-1}{\mathit{W̌}}_g)}^{-1}\right]{\mathit{V̌}}_g^{-1}{\mathit{\beta ̂}}_g).$$ (11)

It follows that

$$\mathrm{B}\mathrm{F}({\mathit{W}}_g)=\mathrm{A}\mathrm{B}\mathrm{F}({\mathit{W}}_g,\mathit{\alpha })·\prod _{i=1}^s(1+O(n_i^{-1})).$$

Proof. See derivation in Appendix B.2 of the Web Supplementary Materials.

As long as α resides in an s-simplex, the above proposition holds. There are two notable extreme cases concerning the choice of α values:

1. α₁ = ⋯ = α_s = 1. The resulting ℰ̌ only relates to the MLEs estimated from the target model, i.e., ${\mathbf{\Sigma ̌}}_i=\frac{{\nu }_i}{n_i+{\nu }_i}{\mathit{H}}_i+\frac{n_i}{n_i+{\nu }_i}{\mathbf{\Sigma ̂}}_i$. Under the usual asymptotic settings, where n_i ≫ p and n_i ≫ r and when the mean model is correctly specified, ${\mathbf{\Sigma ̌}}_i\stackrel{a.s.}{\to }{\mathbf{\Sigma }}_i$. By the continuous mapping theorem, it follows that the resulting ABF almost surely converges to the true value.

2. α₁ = ⋯ = α_s = 0. Σ̌_i only relies on the MLE of Σ_i estimated from the trivial null model, i.e., ${\mathbf{\Sigma ̌}}_i=\frac{{\nu }_i}{n_i+{\nu }_i}{\mathit{H}}_i+\frac{n_i}{n_i+{\nu }_i}{\mathbf{\Sigma ̃}}_i$. Indeed, β̂_g can also be analytically expressed as a simple analytic function of the MLEs of the regression coefficients obtained from the null model. As a result, computing this particular ABF only requires fitting the trivial null model – a scenario analogous to computing score statistics in hypothesis testing (the details are further explained in Appendix F.1 of the Web Supplementary Materials).

Notwithstanding their having the same asymptotic order of error bounds, different α values affect the accuracy of the approximations in finite-sample situations. To examine the performance of ABFs with various α values, we carry out numerical experiments with small sample sizes. In summary, we find that the resulting ABF with all α_i = 1 tends to be anti-conservative compared with true values (most likely because Σ̂_i is prone to overfitting in these cases), whereas setting all α_i = 0 understandably yields conservative approximations. Interestingly, setting α_i = 0.5 for all subgroups gives consistently accurate numerical results in our simulation setting. Finally, we confirm that as sample sizes grow, all approximations become increasingly accurate, regardless of α values. The details of the numerical comparisons and the results are given in Appendix E of the Web Supplementary Materials.

4.1.3 Singular Prior Distributions

To extend the definition of Bayes factors for a singular W_g, we first define

$${\mathit{W}}_g^{†}(\lambda )={\mathit{W}}_g+\lambda \mathit{I},\lambda >0,$$ (12)

where W_g is only required to be positive semidefinite. We then are able to extend definition 1 to include a singular W_g matrix:

Definition 2: Under the SSMR model, for a positive semidefinite W_g, the Bayes factor is defined as

$$\mathrm{B}\mathrm{F}({\mathit{W}}_g)=\underset{\lambda \to 0}{\text{lim}}\mathrm{B}\mathrm{F}({\mathit{W}}_g^{†}(\lambda )).$$ (13)

This definition is based on the following important intuition: Bayes factors are expected to vary very smoothly over a continuum of models. This is not only desirable but also critically important for selecting models consistently when using Bayes factors. We obtain the following result regarding the existence of the limits:

Proposition 2: For the SSMR model, the limiting Bayes factors in definition 2 are always well defined, provided that W_g is positive semidefinite.

Proof. See Appendix D of the Web Supplementary Materials.

Proposition 2 directly extends the results of Lemma 1 and Proposition 1 to allow for a singular W_g matrix. Moreover, when approximating Bayes factors using Laplace’s method, the functional form of the result remains the same; however, we now compute the MLE of the unknown Σ_i for the target model, subject to the linear restrictions imposed by the singular W_g matrix. The details are explained in Appendix D of the Web Supplementary Materials.

4.2 Connections to Frequentist Test Statistics and the BIC

Previous studies by Wakefield (2009); Johnson (2005, 2008); Wen and Stephens (2011) have shown in certain linear model systems (all being regarded as special cases of the SSMR model) that Bayes factors are linked to commonly used frequentist test statistics. We also identify approximate Bayes factors for the SSMR model as being connected to the multivariate Wald statistic and Rao’s score statistic, depending on the choice of α value. The main consequence of this connection is that under specific prior specifications of W_g, Bayes factors and the corresponding test statistics yield the same ranking for a set of models.

Bayes factors are also naturally linked to the Bayesian Information Criterion (BIC, Schwarz (1978)). Under the SSMR model, we show (in Appendix F of the Web Supplementary Materials) that the BIC can be derived as a very rough (i.e., with error bound O(1) in log scale) approximation to both the exact and the approximate Bayes factors for most W_g matrices. Because the BIC is known to be asymptotically consistent as a model selection criterion, based on this connection, we conclude that our Bayes factors also enjoy this property.

A detailed explanation of both connections is given in Appendix F of the Web Supplementary Materials.

4.3 Bayes Factors of Candidate Models

Based on the results of BF(W_g) and Equation (6), we can compute the Bayes factor of a given candidate model, ξ(β_g), by

$$\mathrm{B}\mathrm{F}(\xi ({\mathit{\beta }}_g))=\int p({\mathrm{\Lambda }}_g|\xi ({\mathit{\beta }}_g))\mathrm{B}\mathrm{F}({\mathit{W}}_g)d{\mathrm{\Lambda }}_g,$$ (14)

which essentially integrates out the effect sizes of non-zero regression coefficients. In many genetic applications, it is feasible and effective to model p(Λ_g | ξ(β_g)) by a finite discrete distribution (Servin and Stephens (2007); Stephens and Balding (2009); Wen and Stephens (2011)). In these cases, the integration in (14) is replaced by a summation, and the computation is efficient.

5. Bayesian Model Selection Procedure and the MCMC Algorithm

Based on the results discussed in the previous sections, we are now ready to describe the full Bayesian model selection procedure based on the SSMR model. Assuming the goal of inference is ξ(β_g), the following prior information is required to be specified in a context-specific manner:

1. prior distribution in the space of candidate models, Pr(ξ(β_g)).

2. injection from ξ(β_g) to Γ_g, i.e., specification of prior qualitative dependence/independence structures.

3. probability distribution p(Λ_g | ξ(β_g)), i.e., quantification of prior correlation and marginal variance specified in Γ_g.

Then, based on Equation (14) and relevant discussions on Bayes factor computations, it is straightforward to perform full Bayesian model selection under the general SSMR model. If the number of the candidate models, 2^rps in total, is computationally manageable, we can enumerate all possible models and evaluate their posterior probabilities directly. However, in most practical settings, the candidate model space is enormous, we then need the MCMC algorithm to efficiently traverse the model space.

For the sake of simplicity but without loss of generality, we give a detailed description of a particular version of this algorithm for the commonly used MVLR model in Appendix H of the Web Supplementary Materials. Aided by a novel proposal distribution proposed by Guan and Stephens (2011), we observe that the implemented Markov chain achieves fast mixing and generates accurate results even in very high-dimensional settings. The performance of the algorithm is demonstrated through simulations and real data applications in sections 6 and 7.

6. Simulation Studies

We perform simulation studies to examine and demonstrate the performance of the proposed Bayesian methods in a variety of settings. In these simulations, we focus on the scenario of mapping eQTLs across a handful of tissue types using a common set of individuals, which is best described by an MVLR model with large p (number of candidate genetic variants), small n (sample size), and small r (number of tissue types) values. Moreover, we allow each covariate (SNP) to have different (zero or non-zero) effects in r subgroups (tissues); however, within a covariate, we simulate a scenario in which non-zero effects across subgroups are highly correlated.

6.1 Simulation Settings

We create two simulation settings that differ in the generation of covariates. In the first setting, we simulate p = 250 independent covariates for n = 100 unrelated individuals. The causal SNPs (i.e., the covariates that are associated with the phenotype in at least one of the r subgroups) are independently assigned by a Bernoulli(0.03) distribution. In the second setting, we focus on correlated covariate data. More specifically, we take real SNP genotype data from 100 Caucasian samples of the 1000 Genomes project. We select 105 genomic regions across chromosome 22 that average 30 kb in size. The two consecutive regions are approximately 300 kb apart, and within each region, we select 15 SNPs whose minor allele frequencies are greater than 5%. Between and within these genomic regions, the genotypes present various degrees of spatial correlations (also known as linkage disequilibrium, or LD). In this setting, the regions harboring causal SNPs are assigned by a Bernoulli(0.03) distribution, and we randomly assign a single causal SNP within the selected region.

Given the covariate data, we simulate quantitative (gene expression) phenotype data in r = 3 subgroups (tissue types) for each individual using the following scheme. For each SNP, we represent its binary association states by an r-vector (e.g., γ = (100) indicates a causal and tissue-specific eQTL for which association only presents in the first tissue type), and collectively, {γ_i : i = 1, …, p} represents the true ξ(β_g). We randomly assign each causal SNP a non-zero configuration according to a discrete distribution. More specifically, among seven possible non-zero configurations, γ = (111) is assigned a probability of 0.50, and the others are assumed equally likely (i.e., with probability 1/12 each), conditioning on γ ≠ (000). This distribution is motivated by the observation from the real multiple-tissue eQTL data, where most identified eQTLs are found to have consistent effects in all tissues. For each simulated γ ≠ (000), we first generate a mean effect from β̄ ~ N(0, 1); then, non-zero genetic effects are subsequently drawn from $\beta ~N(\mathrm{\beta ̄},\frac{{\mathrm{\beta ̄}}^2}{100})$. With this procedure, the nonzero βs for a causal SNP across tissues are highly correlated, albeit with some non-negligible heterogeneity. Finally, the residual errors for each individual are independently simulated from a multivariate normal distribution, e ~ N(0, Σ), with $\mathrm{\Sigma }=\left(\begin{array}{ccc}\hfill 1.00\hfill & \hfill 0.24\hfill & \hfill 1.20\hfill \\ \hfill 0.24\hfill & \hfill 1.44\hfill & \hfill 1.08\hfill \\ \hfill 1.20\hfill & \hfill 1.08\hfill & \hfill 2.25\hfill \end{array}\right)$ prefixed. We generate 200 and 500 data sets for simulated independent and real correlated genotypes, respectively.

6.2 Bayesian Model Selection

We perform inference on the binary indicator vector ξ(β_g). We assume that genetic effects are a priori independent across SNPs but correlated among tissues within a single covariate if they are non-zero. This prior relationship is precisely formulated by an injection: ${\mathbf{\Gamma }}_g={\oplus }_{i=1}^p[{\gamma }_i\otimes {\gamma }_i^{\prime }]$, and the factorization of prior probability, $\text{Pr}(\xi ({\mathit{\beta }}_g))={\prod }_{i=1}^p\text{Pr}({\gamma }_i)$.

In all cases, we assume the default prior probability Pr (γ = (000)) = 0.99 for each covariate, which encourages an overall sparse ξ(β_g). By default, all possible non-zero configurations for γ are assigned with equal prior probability, $0.01\times \frac{1}{2^r-1}$.

To specify the distribution Λ_g | ξ(β_g), we follow Wen and Stephens (2011); Flutre et al. (2013) and model the joint prior distribution of a pair of non-zero effects within a covariate by a multivariate normal $\left(\begin{array}{c}\hfill {\beta }_1\hfill \\ \hfill {\beta }_2\hfill \end{array}\right)~N[0,(\begin{array}{cc}\hfill {\omega }^2+{\varphi }^2\hfill & \hfill {\omega }^2\hfill \\ \hfill {\omega }^2\hfill & \hfill {\omega }^2+{\varphi }^2\hfill \end{array}\left)\right]$, where parameter ϕ describes the prior heterogeneity of the effects, and parameter ω characterizes the magnitude of the average prior effect, and the prior correlation between the pair can be computed by ω²/(ω² + ϕ²) (details explained in Appendix A.3 of the Web Supplementary Materials). Furthermore, instead of fixing a single (ϕ, ω) value for all covariates, we assume that (ϕ_i, ω_i) for covariate i is independently and uniformly drawn from the following set

$$L:=\{({\varphi }^{(l)},{\omega }^{(l)}):(0.05,0.20),(0.10,0.40),(0.20,0.80),0.40,1.60)\},$$

where the various levels of ω values cover a range of potentially small, modest, and large average effects and the relatively small ϕ value quantifies our prior belief of low heterogeneity across non-zero effects. It is worth emphasizing that even with a single grid value, the prior would allow for a range of actual effect sizes, and multiple grid points (which form a mixture normal distribution) are helpful for describing a longer-tailed distribution of effect size. It should also be noted that all the priors we use in the inference are different from the true generative distributions used in the simulations.

For likelihood calculation of a given ξ(β_g), we compute a Bayes factor (14) in which BF(W_g) is approximated by ABF(W_g, α = 0.5). We use the MCMC algorithm described in section 5 to conduct posterior inference.

For simulated independent genotype data, we use the posterior inclusion probability of each SNP configuration to assess its relative importance. In the case of correlated covariate data, it might not be plausible to identify the true association based on observed data (e.g., in a scenario in which multiple covariates are perfectly correlated). Therefore, we focus on assessing the importance of preselected genomic regions and compute the posterior probability that a given region harbors a genetic variant with particular configurations. These quantities are computed by combining SNP-level posterior inclusion probabilities and posterior model probabilities using the inclusion-exclusion principle.

6.3 Methods for Comparison

We compare our Bayesian model selection method (BMS) with two other methods: single variable analysis, which examines one covariate at a time while accounting for the subgroup structure (Wen and Stephens (2011); Flutre et al. (2013)), and the regularized regression approach LASSO (Tibshirani (1996)).

The single variable procedure can be viewed as a special case of the general MVLR model with p = 1. For each SNP, we compute the single-SNP posterior probability of each configuration based on the corresponding ABF values and use it to assess the importance of each SNP configuration. For the real genotype data, we analyze one region at a time and further compute a regional posterior probability based on single-SNP Bayes factors, assuming at most one causal SNP in a region, a method described in (Servin and Stephens (2007); Flutre et al. (2013)).

We center the phenotype data and apply the LASSO procedure to estimate β_g by

$$\text{arg}\underset{{\mathit{\beta }}_g}{\text{min}}[(\text{vec}(\mathit{Y})-(\mathit{I}\otimes \mathit{X}){\mathit{\beta }}_g)\prime (\text{vec}(\mathit{Y})-(\mathit{I}\otimes \mathit{X}){\mathit{\beta }}_g)+\lambda \sum _j|{\beta }_{g,j}|],$$ (15)

where I is the r × r identity matrix and λ is the tuning shrinkage parameter. If λ is sufficiently large, LASSO produces sparse estimates of β_g; whereas, if λ is set to 0, the solution becomes the usual least squares estimate/MLE for the MVLR model. Given a particular λ value, for the simulated independent genotype data, we identify the true and false positives of non-zero β_g estimates; whereas, for the real genotype data, following Guan and Stephens (2011), we further denote that a region is positively identified if any SNP within that region is selected by LASSO. We then record the full solution paths from LASSO for a range of λ values using the lars package (version 1.1) implemented in R.

6.4 Simulation Results

In both simulation settings, we represent the results in Figure 1 by plotting curves of the trade-off between true and false positives from all three experimental methods. Each point on the curve is obtained by accumulating true and false positives across independent simulated data sets using a common threshold (either of the posterior inclusion probability or the shrinkage tuning parameter) within a method. In both simulation settings, the Bayesian model selection method (BMS) always yields as many or more true positives than the other comparable methods for any given false-positive value.

Figure 1.

Plots of the trade-offs between true positives and false positives for all three compared methods in two simulation settings. Panel A is based on simulated independent covariate data, and Panel B shows the results for correlated covariate data taken from real genotypes. In both cases, the proposed Bayesian model selection method (BMS) achieves superior performance. LASSO seems to severely underperform when covariates are correlated.

Many previous publications have reported that multivariate methods are superior to single-variable analysis in selecting candidate variables in multiple linear regression models. We observe that a similar pattern also holds for multivariate linear regressions in our simulation settings. Guan and Stephens (2011) provide some very intuitive explanations for the superiority of multivariate methods vs. single-variable methods, even when covariates are all independent. Their arguments also naturally apply in our context. Although this result is largely expected, it serves as a reassuring sanity check that our implementation of the MCMC algorithm is fast mixing in this nontrivial setting (one could expect that a poor-mixing Markov chain would yield results inferior to those obtained from a single-variable analysis).

We conduct additional simulations to investigate the performance difference between BMS and LASSO. First, we observe that the accuracy of LASSO is affected by correlated error structures characterized by Σ, which is not accounted for in (15). Similar observations also have been made by Rothman et al. (2010). Second and more importantly, BMS utilizes additional correlation information on effect sizes within a single covariate through priors, whereas LASSO does not. We provide the details of these additional simulations and their results in Appendix I of the Web Supplementary Materials.

Finally, we notice that BMS performs in a stable manner even when covariate data are (highly) correlated, while LASSO greatly underperforms in such a setting.

7. Real Data Application

We apply the Bayesian model selection method to map eQTLs across multiple tissues on a real data set originally published by Dimas et al. (2009). In this experiment, the investigators genotyped 75 unrelated western European individuals. Expression levels from this set of individuals were measured genome-wide in primary fibroblasts, Epstein-Barr virus-immortalized B cells (LCLs), and T cells. The expression data went through quality control and normalization steps by the original authors, and we further select a subset of 5,011 genes that are highly expressed in all 3 cell types and perform additional quantile-normalizations for each gene in each cell type. For demonstration purposes, we map eQTLs for each gene separately and narrow the search for eQTLs in the cis-region (i.e., the coding region and its close neighborhood) of each gene (note, this is also the strategy adopted in the original publication).

The setting of this data set is similar to that of our simulations. We use the MVLR model described in section 6.2 to jointly infer the association states of all cis-SNPs in three cell types for each selected gene. More specifically, we assume the following independent priors for each SNP: Pr(γ = (000)) = 0.99, $\text{Pr}(\gamma =(111))=0.01\times \frac{1}{2}$, and the rest of the six possible tissue-specific configurations are assigned probability mass $(0.01\times \frac{1}{2}\times \frac{1}{6})$ each. This prior setup reflects our prior beliefs that the vast majority of cis-SNPs are not eQTLs and that among eQTLs, most are likely to behave in a tissue-consistent manner. Finally, we use the same prior distribution of p(Λ_g | ξ(β_g)) described in section 6.2.

Remark 1. It is important to note that genome-wide expression-genotype data are typically informative about the distributions of configurations of γ and effect-size grids in L. In other words, those distributional parameters can be effectively estimated by pooling information across all genes using a hierarchical model approach (Veyrieras et al. (2008); Flutre et al. (2013)). In fact, the hyperparameters we select here are closely related to the estimations from fitting such a hierarchical model; however, these details are not our focus in this paper.

We apply the MCMC algorithm described in section 6.2 to the set of 5,011 selected genes. We identify 510 “eQTL genes” whose inferred best posterior model contains at least one candidate cis-SNP. In total, 539 eQTLs are identified from this set of the best posterior models, and 382 are inferred as tissue-consistent. Using the posterior maximum probability models, we are also able to confidently identify 28 genes with multiple cis-eQTLs accounting for linkage disequilibrium (LD), suggesting the involvement of multiple regulatory elements in transcriptional regulation processes.

One of the unique advantages of our Bayesian method is its ability to perform fine mapping on interesting genomic regions harboring true causal eQTLs. We demonstrate this feature through the analysis of gene C21orf57 (HGNC symbol YBEY, Ensemble ID ENSG00000182362). From a total of 236 cis-SNPs, our Bayesian analysis identifies three genomic regions centered around SNPs rs12329865 and rs2839265 and a SNP pair in perfect LD (rs2839156, rs2075906). The best posterior models consist of one SNP from each region, and the three regions have marginal posterior inclusion probabilities of 0.66, 0.38, and 0.89, respectively. More interestingly, our results suggest that the three distinct eQTL regions have completely different tissue activity configurations. We summarize these results in Table 1. We further examine the effect sizes of the identified signals in each cell type separately, and the results (shown in appendix J of the Web Supplementary Materials) are strongly consistent with the conclusions of our tissue specificity inference.

Table 1.

Potential eQTLs identified by the Bayesian model selection procedure using only genotyped SNPs. Genotypes of SNPs rs2075906 and rs2839156 are highly correlated. The two models [rs12329865, rs2075906, rs2839265] and [rs12329865, rs2839156, rs2839265] have the highest posterior model probabilities (0.200 and 0.204, respectively).

SNP	Position	Configuration	Posterior inclusion prob.
rs12329865	chr 21:47583506	LCL only	0.662
rs2075906	chr 21:47625544	consistent	0.447
rs2839156	chr 21:47641196	consistent	0.444
rs2839265	chr 21:47867318	Fibroblast only	0.378

As a comparison, we also applied the remMap method (Peng et al. (2010), R implementation version 0.10) to the genotype-expression data of the gene C21orf57. The remMap method implements a penalized multivariate regression algorithm which assumes the same MVLR model. There are two tuning parameters required by the remMap method: one controls the sparsity of ξ(β) and the other controls the sparsity of the residual error variance matrix. These two parameters are selected using a BIC procedure implemented in the R package. In the end, remMap does not select any eQTLs. Given the strength of the signals identified by the Bayesian procedure and the results from the single SNP analysis, this is a little surprising. Nevertheless, we noted in a similar context of mapping eQTL for mutiple genes, Scott-Boyer et al. (2012) also observed this overly conservative behavior of the remMap method. We suspect that the non-trivial LD patterns presented in the SNP data might be one of the contributing factors here. As Peng et al. (2010) noted, complex correlation structures in predictors lead to the remMap procedure selecting very small models. In addition, like the LASSO procedure, the remMap method does not utilize the correlation information on eQTL effect sizes across tissues.

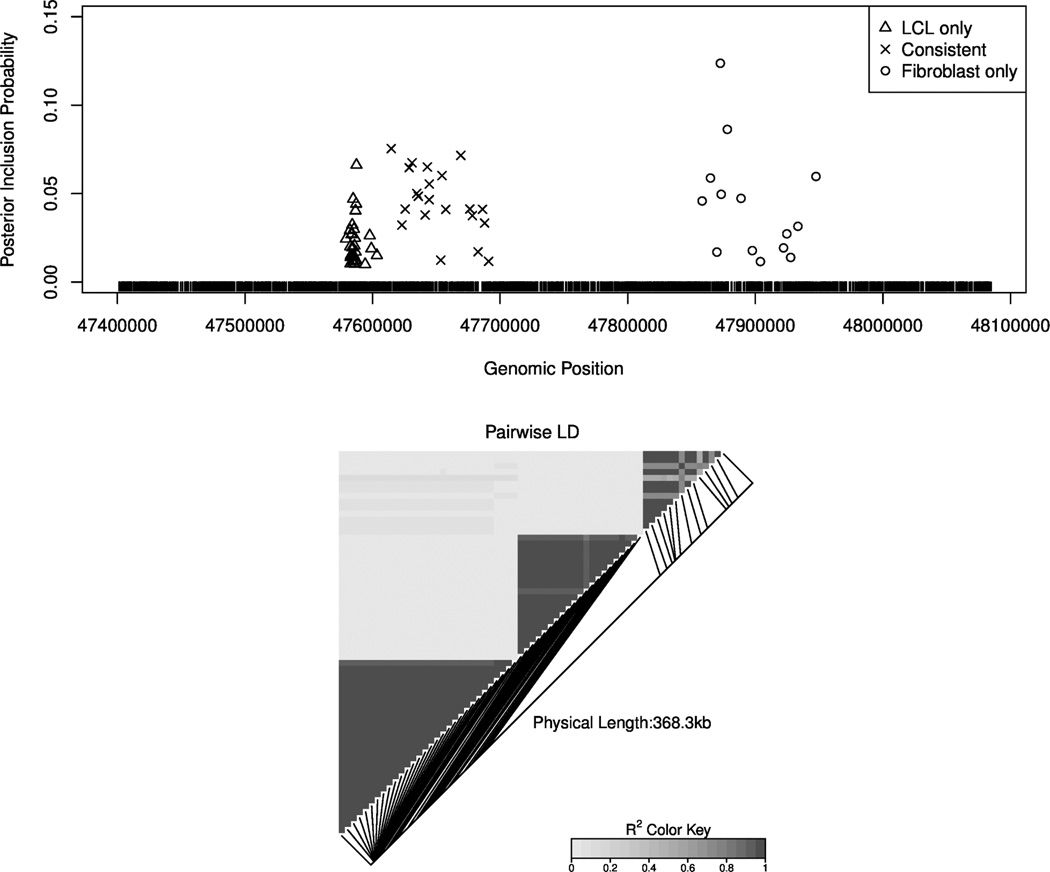
To refine the identified genomic regions and rule out potential spurious associations identified with low-density SNPs, we perform genotype imputation to obtain additional genotypes of untyped SNPs using the 1000 Genome European panel and software package IMPUTE v2 (Howie et al. (2009)). In the end, we accumulate genotypes from 4797 SNPs, roughly a 20-fold increase, for the same cis-region. We rerun the MCMC algorithm on the imputed data set and plot the marginal posterior inclusion probabilities of top-ranked SNPs according to their genomic positions and inferred configurations in Figure 2. The plot clearly indicates three adjacent however distinct genomic regions with a much improved resolution. We note that although the individual SNP inclusion probabilities decrease significantly from the previous analysis, the inclusion probabilities of the three regions all increase in some degree: the probability of the LCL only eQTL region increases from 0.66 to 0.68, the probability of the consistent eQTL region increases from 0.89 to 0.95 and the the probability of the Fibroblast only eQTL region increases from 0.38 to 0.61. Figure 2 also shows SNP genotypes are highly correlated within each region, and it is impossible to distinguish the true causal variants based on association analysis. Therefore, it seems only logical to report interesting regions rather than individual variants in such settings.

Figure 2.

eQTL fine-mapping for gene C21orf57 with a dense SNP set. The top panel plots SNPs with marginal posterior inclusion probabilities ≥ 0.01. The different symbols indicate the different activity configurations of potential eQTLs. The ticks on the X-axis label the positions of interrogated SNPs (genotyped and imputed) in this region. Three distinct genomic regions that harbor three different eQTLs with different tissue configurations can be clearly identified from the plot. The inferred high posterior probability models typically contain one SNP from each of the three regions. The bottom panel displays the correlations, measured by r², between the SNPs plotted in the top panel (produced by R package LDheatmap). It should be clear that genotype correlations within each identified genomic region are quite high, and between the regions, the SNPs are much less correlated.

8. Discussion

The general statistical problem we have considered in this paper is related to the problem of structured variable selection. Our Bayesian approach provides a general framework to specify both group structures (through Pr(ξ(β_g))) and prior correlations on non-zero effects (through p(Λ_g | ξ(β_g))) in a hierarchical fashion. Compared with regularization-based model selection methods such as group LASSO (Yuan and Lin (2006)) and fused LASSO (Tibshirani et al. (2005)), our method is more flexible and conceptually easier to apply. For example, in the multiple-tissue eQTL mapping example, the association patterns within a SNP across multiple tissues are rather complex; neither group LASSO (which encourages the whole group to be selected) nor sparse group LASSO (which encourages only a few members in the group to be selected) is suitable in this context.

One of our main contributions in this paper is the results involving Bayes factors. Although we have focused mostly on model selection, our novel results can be directly applied to hypothesis-testing settings (e.g., in gene-based genetic association testing). It should be noted that although we have described our results exclusively assuming quantitative Gaussian response variables, our results can be naturally extended to the generalized linear models. We give a brief argument for this extension in appendix G of the Web Supplementary Materials.

Our simulations and data application both focus on the problem of mapping eQTLs across multiple tissues. We note that although many sophisticated statistical methods have been developed for mapping multiple (cis and trans) eQTLs (Scott-Boyer et al. (2012); Xu et al. (2009)), almost none of them considers the mapping problem in a multiple-tissue context. As shown by Flutre et al. (2013) and Ding et al. (2010), naively applying single tissue mapping method one tissue at a time not only lacks of power in detecting tissue-consistent eQTLs but also can be dangerous in inferring tissue-specific eQTLs. Our statistical framework naturally fills this gap. The SSLR model can be naturally applied to the fine-mapping problem in genetic association meta-analysis. Furthermore, a prior requiring genuine association signals to display low within-group heterogeneity seems most appropriate in this context.

In our examples, we deal with relatively small r value by using a non-informative inverse- Wishart prior. It should be noted that our Bayes factor results can be applied in the situation where r is also high dimensional. In principle, a strong and informative prior on Σ is sufficient (see Equation (10)). However in practice, constructing a reasonable and strongly informative prior for a covariance matrix in high-dimensional is challenging and the context of the applications should always be carefully considered. A useful statistical technique in specifying the inverse-Wishart prior in high dimensional settings is to utilize its connection to Gaussian graphical models (Dawid and Lauritzen (1993); Carvalho and Scott (2009)) which can be extremely helpful to systematically describe the complex relationships among a large number of variables.

Finally, although we have demonstrated our approach exclusively in the genetic/genomic context, the statistical approaches presented in this paper are general enough to apply to model selection problems in other contexts, such as graphical model inference and Bayesian causal inference, to name a few examples.