Improved Cross Validation of a Static Ubiquitin Structure Derived from High Precision Residual Dipolar Couplings Measured in a Drug-Based Liquid Crystalline Phase

Abstract

The antibiotic squalamine forms a lyotropic liquid crystal at very low concentrations in water (0.3-3.5% w/v), which remains stable over a wide range of temperature (1-40 °C) and pH (4-8). Squalamine is positively charged, and comparison of the alignment of ubiquitin relative to 36 previously reported alignment conditions shows that it differs substantially from most of these, but is closest to liquid crystalline cetyl pyridinium bromide. High precision residual dipolar couplings (RDCs) measured for the backbone ¹H-¹⁵N, ¹⁵N-¹³C′, ¹H^α-¹³C^α, and ¹³C′-¹³C^α one-bond interactions in the squalamine medium fit well to the static structural model previously derived from NMR data. Inclusion into the structure refinement procedure of these RDCs, together with ¹H-¹⁵N and ¹H^α-¹³C^α RDCs newly measured in Pf1, results in improved agreement between alignment-induced changes in ¹³C′ chemical shift, ³J_HNHα values, and ¹³C^α-¹³C^β RDCs and corresponding values predicted by the structure, thereby validating the high quality of the single-conformer structural model. This result indicates that fitting of a single model to experimental data provides a better description of the average conformation than does averaging over previously reported NMR-derived ensemble representations. The latter can capture dynamic aspects of a protein, thus making the two representations valuable complements to one another.

Over the past four decades, dynamic behavior of folded proteins has been increasingly recognized as a fundamental aspect of biological function.^1,2 Quantitative analysis of NMR relaxation rates in terms of order parameters can provide the amplitudes and rates of these motions on the ns time scale and faster.^2,3 Analysis of NMR residual dipolar couplings (RDCs) in proteins that are weakly aligned relative to the magnetic field can quantify the amplitude and direction of such motions, including those that take place in the functionally important μs time regime.⁴⁻¹³ To provide an experimental view of the conformational space actually sampled by the protein, sophisticated analyses of such RDCs are used to depict the structure as an ensemble of conformations. The “fuzziness” in such ensembles can make it difficult to recognize functionally significant backbone rearrangements associated with, e.g., allosteric activation or target binding. For evaluating the latter, it can be more informative to consider the much narrower defined time-averaged conformation. We demonstrate for ubiquitin, a benchmark in such studies, that calculating a single, average structure validates parameters not used in deriving it better than do ensemble calculations. Our results also indicate that the amplitude of slow-time-scale backbone motions across elements of secondary structure is poorly defined by the RDCs, which fit equally well or better to a single static structure or to a very narrow ensemble of X-ray structures than to much wider RDC-derived ensemble representations.

When an isotopically enriched protein is immersed in a dilute lyotropic liquid crystalline suspension, RDCs are readily observed for one-bond ¹⁵N-¹H, ¹³C-¹H, ¹³C-¹³C, and ¹³C-¹⁵N interactions.^14,15 Key to their accurate measurement is that the protein alignment is kept very weak, such that the RDCs are scaled down by about 3 orders of magnitude relative to their static values. The RDC values, including their sign, are then obtained from the difference in ¹J splitting observed under aligned and isotropic conditions.^14,15

When using a diagonalized representation of the molecular alignment tensor (Saupe matrix), the relation between the orientation of an internuclear vector and its RDC, D^PQ, takes a simple trigonometric form:

1

where θ and ϕ are spherical angular coordinates of vector PQ in the frame of the diagonalized alignment tensor; D_a reflects the strength of the alignment, expressed in Hz, for internuclear pairs of types P and Q, e.g., ¹⁵N-¹H; and R is the rhombicity or asymmetry of the alignment. D_a also absorbs the magnitude of the static P-Q dipolar coupling and the effect of any uniform axially symmetric motion of the P-Q vectors. Equation 1 does not account for residue by residue variability in the amplitude of internal dynamics, nor for any asymmetry of the internal motion.

The symmetric and traceless 3×3 Saupe matrix describing the average molecular alignment contains five independent elements, and up to five linearly independent alignments in principle can be generated for any given protein. For each such alignment, the corresponding eq 1 maps out a cone of possible P-Q bond vector orientations that are compatible with a given D^PQ dipolar coupling.¹⁶ In the absence of internal dynamics, or under the above assumption of uniform, axially symmetric internal motion, the cones of possible bond vector orientations will all share a common point of intersection, uniquely defining the orientation of the P-Q vector (or its inverse) in the molecular frame.

In practice, the assumption of uniform and isotropic internal dynamics does not apply and, next to the presence of measurement error in the RDCs, can be responsible for the failure to find a common intersection between the five sets of cones for any given internuclear vector. Indeed, the amplitude, anisotropy, and direction of the anisotropy of internal dynamics are encoded in the five independent sets of RDC measurements. Many studies have focused on extracting this dynamic information out of such extensive sets of RDCs.⁴⁻¹³ Backbone ¹⁵N-¹H RDCs in ubiquitin have been reported for 36 different alignment conditions, effectively covering the five-dimensional alignment tensor space.¹⁷ Quantitative evaluation of the accuracy at which dynamics can be extracted from RDCs remains challenging, and a gradual decrease in the amplitude of backbone dynamics obtained from RDC analysis is observed when comparing more recent studies, based on a wider range of alignment conditions and increasingly sophisticated computational methods,^11,12,18 to earlier ones. Here, we report ubiquitin RDCs measured at very high precision in a new liquid crystalline medium, consisting of a dilute (3 mg/mL) suspension of the antibiotic squalamine (Scheme 1), as well as newly measured ¹D_HN, ¹D_CαHα, and ¹D_CαCβ couplings in Pf1 medium. Ubiquitin has a large electric dipole moment and aligns strongly in charged alignment media, such as squalamine and Pf1, complicating accurate RDC measurement. ¹H-¹H decoupling alleviated this problem.¹⁹ These new data complement those previously used for deriving a conventional, single-model solution NMR structure of ubiquitin (PDB 1D3Z),²⁰ and result in an improved structural model with cross-validation statistics better than any of the prior static or ensemble descriptions.

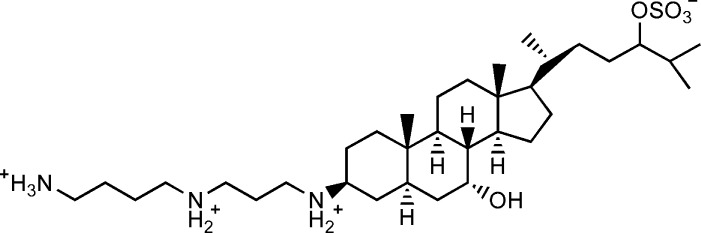
Scheme 1. Structure of Squalamine and Ionization States of Its Polar Groups at Neutral pH.

Squalamine is an aminosterol compound with a broad spectrum of antimicrobial activity, originally discovered in the tissue of dogfish shark.²¹ It displays potent activity against both Gram-negative and -positive bacteria, fungi, and multiple viruses,²² and its effectiveness as an antiangiogenic agent in cancer therapy has also been reported.²³ While studying the effect of squalamine on fibril formation of the protein α-synuclein, we found that upon addition of phosphate buffer, its ¹H NMR spectrum effectively vanished, while causing a small splitting of the D₂O lock signal, similar to that observed in various lyotropic liquid crystalline suspensions and asymmetrically compressed gels, commonly used for alignment of biological macromolecules.^18,24,25 The liquid crystalline behavior was stabilized by addition of hexanol, with an optimal molar ratio of squalamine/hexanol of ∼3. Samples at 12 mg/mL squalamine concentration yielded a ²H quadrupole splitting of ∼10 Hz and remained stable over a wide range of temperature (1-40 °C) and pH, extending from <4 to >8. Addition of ubiquitin to this liquid crystalline suspension yielded an alignment too strong for convenient measurement of RDCs. To bring the ¹D_NH RDCs into the optimal range of ±25 Hz, the squalamine concentration needed to be reduced to 3 mg/mL (yielding a ²H quadrupole splitting for the HDO lock solvent of 1.7 Hz). Other proteins were found to align considerably weaker.

The presence of the liquid crystal had no significant impact on the ¹⁵N transverse relaxation properties and yielded multinuclear NMR spectra at very high resolution (Figure 1). Comparison to 36 sets of prior RDCs¹² indicates that the newly recorded data are most similar to those recorded in cetyl pyridinium bromide (Table S3), a lamellar liquid crystalline phase also characterized by a net positive surface charge.³⁰⁻³²

Figure 1.

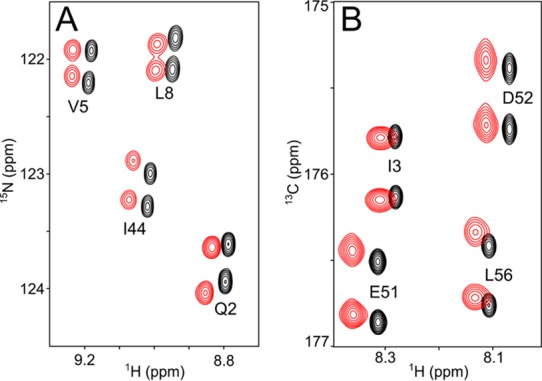
Small regions of NMR spectra of uniformly ²H/¹⁵N/¹³C-enriched ubiquitin (0.5 mM) in the absence (black) and presence (red) of 3 mg/mL liquid crystalline squalamine dilactate, pH 6.0, 10 mM sodium phosphate, 1.1 mM hexanol, 20 mM imidazole-d₄, 35 °C. Aligned and isotropic spectra have been offset relative to one another in the ¹H dimension by 0.03 ppm for display purposes. (A) Small region of the ¹³C′-coupled ¹H-¹⁵N 2D TROSY spectrum, recorded at 500 MHz ¹H frequency. The relative displacement of doublet components corresponds to (¹J_NC′ + ¹D_NC′) in the ¹⁵N dimension, and to (²J_HC′ + ²D_HC′) in the ¹H dimension. The average signal-to-noise ratio (S/N) for correlations in the aligned spectra is ∼400:1. (B) Small region of the 3D HNCO spectrum recorded at 600 MHz ¹H frequency, projected on the ¹H-¹³C plane over the 113-124 ppm ¹⁵N chemical shift range. The relative displacement of doublet components in the ¹³C dimension corresponds to (¹J_C′Cα + ¹D_C′Cα).

Refinement of a protein model in terms of a structural ensemble rather than a single static structure effectively adds, at least, three degrees of freedom to the two parameters (θ and ϕ) that define each bond vector orientation relative to the molecular frame. These correspond to the width of the distribution (effectively representing the generalized order parameter), the asymmetry of the disorder, and the direction of the asymmetry in terms of an azimuthal angle. The question then arises whether, with these additional degrees of freedom, such a distribution leads to a more accurate model of the average structure, which should be reflected in improved validation statistics. We compared the results of a new structure calculation of ubiquitin, which now includes the RDCs measured in both the squalamine and Pf1 media, in addition to all experimental restraints previously used to derive the “static” ubiquitin structure (PDB 1D3Z), with the various ensembles derived previously from much larger sets of RDCs. For independent validation, we resort to three quite different sets of parameters not used in the present or any of the prior structure determinations, all measured at very high accuracy: (1) previously reported residual ¹³C′ chemical shift anisotropy (RCSA),²⁸ obtained by ¹³C′ shift measurement on the same sample under magic angle spinning and static conditions (estimated random error ≤2 ppb);²⁸ (2) newly measured ¹D_CαCβ couplings in Pf1 (Table S2); (3) ³J_HNHα values (Table S1), newly collected using a multiquantum scheme that eliminates relaxation effects.^29,33 The same validation analysis is used for the original 1D3Z entry, various ubiquitin ensembles, and a number of high-quality crystal structures.^12,18,26,34

The ¹³C′ chemical shift anisotropy (CSA) tensor is highly asymmetric and its orientation relative to the peptide bond is tightly defined by prior solution and solid state NMR data.³⁵⁻³⁷¹D_CαCβ couplings were measured in uniformly perdeuterated ubiquitin while using ²H decoupling, thereby avoiding the rapid transverse relaxation of ¹³C^α in protonated proteins, and yielding highly precise ¹J_CαCβ splittings. ³J_HNHα couplings were not used directly in any of the prior or current structure calculation protocols, but ϕ angle restraints derived from these and related couplings³⁸ were used in most of these.

Table 1 shows how well the validation parameters are predicted by various NMR and X-ray ubiquitin models, either when considering all residues (2-70) for which atomic coordinates are available in a set of 15 high-resolution X-ray structures, or when separating out the “rigid” subset with small (≤0.4 Å) root-mean-square differences (rmsd) in backbone atomic coordinates, or the “dynamic” subset of residues with large rmsd (>0.4 Å) in the X-ray ensemble.

Table 1. Experimental Validation Statistics for Different Structural Representations of Ubiquitin^a.

structure	current (2MJB)	1D3Z20	2KOX18	2NR226	1UBQ27,d	⟨X-ray⟩d,e
RCSAb (ppb)	6.5/15.7/8.9b	7.2/14.9/9.4b	9.2/17.5/11.1b	10.6/17.4/12.1b	11.6/24.7/14.3b	6.2/13.9/8.1b
QNHc (%)	5.9/8.3/6.6	8.9/15.3/10.5	6.5/7.7/6.8	18.1/35.9/22.8	14.7/28.3/17.6	11.6/14.6/12.2
QCαCβ(%)	9.3/22.2/11.7	10.8/29.4/14.6	10.5/21.1/12.4	12.5/16.9/13.2	17.3/37.8/21.3	9.9/14.3/10.4
3JHNHαf (Hz)	0.43/0.77/0.50	0.49/0.56/0.50	0.58/0.89/0.65	0.84/1.43/0.97	0.66/1.17/0.77	0.50/0.83/0.57

^aFor Q2-V70. Predicted ¹³C′ RCSA values are based on the alignment tensor obtained from an SVD fit of the ¹D_NH RDCs, previously reported in conjunction with the RCSA values,²⁸ to the corresponding structural model or ensemble of models. There are no RCSA-fitted adjustable parameters used in this comparison.

^bThe first number corresponds to residues with ≤0.4 Å backbone coordinate (N, C^α, C′) rmsd in the X-ray ensemble; the 2d number to residues with >0.4 Å rmsd (7-11, 32-35, 46, 47, 52, and 70); the 3d number to all residues.

^c“Working” Q-factor for the four sets of ¹D_NH RDCs used. Entries 2NR2, 1UBQ and ⟨X-ray⟩ were determined without RDCs, and the reported values are free Q factors; 1D3Z was determined without Pf1 and squalamine ¹D_NH values, making Q_NH an average between free and working; 2KOX lacked squalamine ¹D_NH, but the working RDCs spanned the entire five-dimensional alignment space.

^dQ-factors and ³J_HNHα rmsd for the X-ray structures have the H^N atom modeled to locate in the plane bisecting the C′-N and N-C^α bonds, at the same out-of-peptide-plane angle observed in the newly derived NMR structure. These values are ∼5% (for 1UBQ) and 16% (for ⟨X-ray⟩) lower than for in-peptide-plane H^N.

^eEnsemble of 15 chains from high resolution (≤1.8 Å) X-ray structures, listed in Table S5, superimposed by best fitting the backbone atoms of residues 2-70, and alignment tensor and Q-factor determined from an RDC fit to this ensemble.

^fRmsd relative to ³J_HNHα predicted using “rigid” Karplus equation coefficients.²⁹

For the X-ray structures, which lack crystallographic coordinates for H atoms, fits of ¹D_NH RDCs and ³J_HNHα couplings to such structures are sensitive to the method used for modeling these H-atoms into the structure. For both ¹D_NH and ³J_HNHα, we find significantly better fits to crystal structures when adding the H^N atoms at the same out-of-peptide-plane angle that is observed in our newly derived static NMR structure, over adding H^N atoms in their idealized in-plane positions (Table S5), and this method is used for the data presented in Table 1. A modest further improvement in validation statistics can be achieved by optimizing the relative weights in the X-ray ensemble (Tables S9, S10).

For all three types of structures, static NMR, dynamic NMR ensembles, and X-ray ensemble, we find that the validation parameters fit significantly better to the “rigid” subset of residues than to the dynamic ones (Table 1). The fact that for the “rigid” residues, which differ by only 0.27 Å in backbone coordinate rmsd to their mean, the fits to the X-ray ensemble score much better than for any of the individual X-ray structures likely is dominated by the averaging of the small errors in backbone coordinates, not from true dynamics. Our static NMR structure shows validation statistics very similar to the X-ray ensemble, demonstrating that it is possible to generate a single, low energy model that predicts the validation parameters for the “rigid” residues as well as the X-ray ensemble.

When focusing on the 13 most dynamic residues, the newly calculated static model no longer outscores the dynamic RDC-derived NMR ensemble (2KOX in Table 1), indicating that neglecting dynamics for these 13 residues in our static model has an adverse impact on the validation parameters comparable to that of the additional degrees of freedom introduced by fitting RDCs to a dynamic ensemble. Remarkably, as can be seen in Table 1 (2NR2 column), for the dynamic residues a sophisticated molecular dynamics based refinement protocol that utilizes as experimental restraints only NOEs and ¹⁵N-derived S² values, referred to as Minimal-Under-restraining-Minimal-Over-restraining or MUMO,²⁶ results in errors of the validation parameters that are comparable to what is obtained when including large numbers of RDC constraints but a less elaborate computational refinement procedure. This result, which represents a significant improvement over an analogous earlier protocol^12,18,26,34 (see Table S8), suggests that it should be possible to further enhance the quality of NMR-derived structural ensembles by including RDC restraints in the MUMO protocol.

Of note, our findings do not detract from the intrinsic ability to derive dynamic information from RDCs. We simply show that extracting this additional information by generating ensemble representations can go at the expense of a decrease in the accuracy of the average structure. Thus, our results indicate that for globular proteins the best average structure compatible with the NMR data is obtained by calculating a single model that best fits the experimental restraints. Even for the quite mobile residues in ubiquitin, the static model calculated with full disregard of dynamics falls close to the various ensemble averages, with comparable validation statistics. Provided a sufficient number of high accuracy RDC data are available, measured under multiple alignment conditions, the multiconformer ensemble then potentially can complement such a model to define amplitudes and directions of motions. However, our finding that the narrow X-ray ensemble (Figure 3B) validates the NMR parameters better than RDC-derived NMR ensembles highlights the practical difficulty in generating molecular models that accurately depict the amplitude of dynamics from RDCs.

Figure 3.

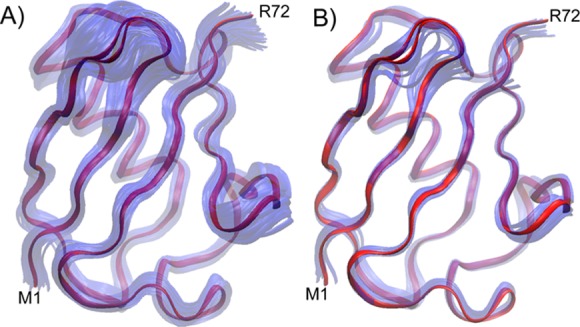
Overlayed backbone representations of the newly derived NMR structure (red) with (A) the NMR ensemble representation (2KOX) (in transparent blue) and (B) with the 15 highest-resolution X-ray structures of ubiquitin. Structures are superimposed by best-fitting the residues with most-ordered backbone coordinates in the X-ray ensemble (see Table 1, footnote b).

Figure 2.

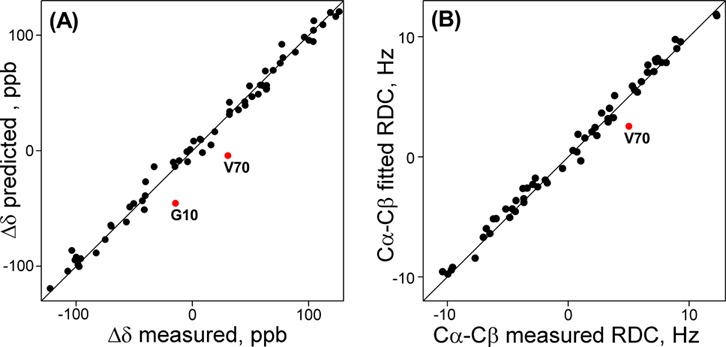
Comparison of observed NMR parameters not used in the structure determination with values predicted from the new static ubiquitin model, refined using all restraints previously used for deriving PDB entry 1D3Z, supplemented by newly measured backbone RDCs in squalamine and Pf1 media. (A) ¹³C′ RCSA values. (B) ¹D_CαCβ RDCs, measured in Pf1 medium. ¹³C′ RCSA of G10 and ¹D_CαCβ of V70 (both classified as dynamic) agree better with ensemble representations of ubiquitin (Figure S4).

Supporting Information Available

Experimental procedures and additional data. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States