Quantum Mechanical/Molecular Mechanical Free Energy Simulations of the Self-Cleavage Reaction in the Hepatitis Delta Virus Ribozyme

Abstract

The hepatitis delta virus (HDV) ribozyme catalyzes a self-cleavage reaction using a combination of nucleobase and metal ion catalysis. Both divalent and monovalent ions can catalyze this reaction, although the rate is slower with monovalent ions alone. Herein, we use quantum mechanical/molecular mechanical (QM/MM) free energy simulations to investigate the mechanism of this ribozyme and to elucidate the roles of the catalytic metal ion. With Mg²⁺ at the catalytic site, the self-cleavage mechanism is observed to be concerted with a phosphorane-like transition state and a free energy barrier of ∼13 kcal/mol, consistent with free energy barrier values extrapolated from experimental studies. With Na⁺ at the catalytic site, the mechanism is observed to be sequential, passing through a phosphorane intermediate, with free energy barriers of 2–4 kcal/mol for both steps; moreover, proton transfer from the exocyclic amine of protonated C75 to the nonbridging oxygen of the scissile phosphate occurs to stabilize the phosphorane intermediate in the sequential mechanism. To explain the slower rate observed experimentally with monovalent ions, we hypothesize that the activation of the O2′ nucleophile by deprotonation and orientation is less favorable with Na⁺ ions than with Mg²⁺ ions. To explore this hypothesis, we experimentally measure the pK_a of O2′ by kinetic and NMR methods and find it to be lower in the presence of divalent ions rather than only monovalent ions. The combined theoretical and experimental results indicate that the catalytic Mg²⁺ ion may play three key roles: assisting in the activation of the O2′ nucleophile, acidifying the general acid C75, and stabilizing the nonbridging oxygen to prevent proton transfer to it.

Introduction

The hepatitis delta virus (HDV) ribozyme belongs to a family of five distinct small ribozymes known as the nucleolytic ribozymes.^1,2 These ribozymes perform site-specific cleavage and ligation reactions in RNA and can utilize nucleobases in catalysis.^1,3,4 The HDV ribozyme is found in closely related genomic and antigenomic forms⁵ as well as an extended family of HDV-like ribozymes.⁶⁻⁸ The pK_a’s of specific functional groups in ribozymes can be shifted toward neutrality to aid in general acid–base catalysis.⁹⁻¹⁴ An active site cytosine, termed “C75” in the genomic HDV ribozyme, has a pK_a shifted toward neutrality and has been shown to be critical for its self-cleavage reaction, acting as the general acid by donating a proton to the O5′ oxyanion of the leaving group.^15,16 A role for C75 in proton transfer in the cleavage reaction of the genomic HDV ribozyme has been further supported by molecular dynamics (MD) and quantum mechanical/molecular mechanical (QM/MM) calculations.¹⁷⁻²⁰ In addition to nucleobase catalysis, the HDV ribozyme uses a metal ion in its cleavage reaction,^16,21,22 a strategy characteristic of the large ribozymes.^23,24 The catalytic divalent ion binds to a groove of extreme negative potential, where it interacts with a reverse G·U wobble²⁵ and the pro-R_P oxygen of the scissile phosphate.²² In the case of the HDV ribozyme, both divalent and monovalent ions can catalyze the reaction, although the rate is ∼25-fold slower in the case of monovalent ions alone.²¹ The use of both metal ion and nucleobase catalysis in a single ribozyme is unusual²⁶ and thus has generated significant interest in understanding the mechanistic details.

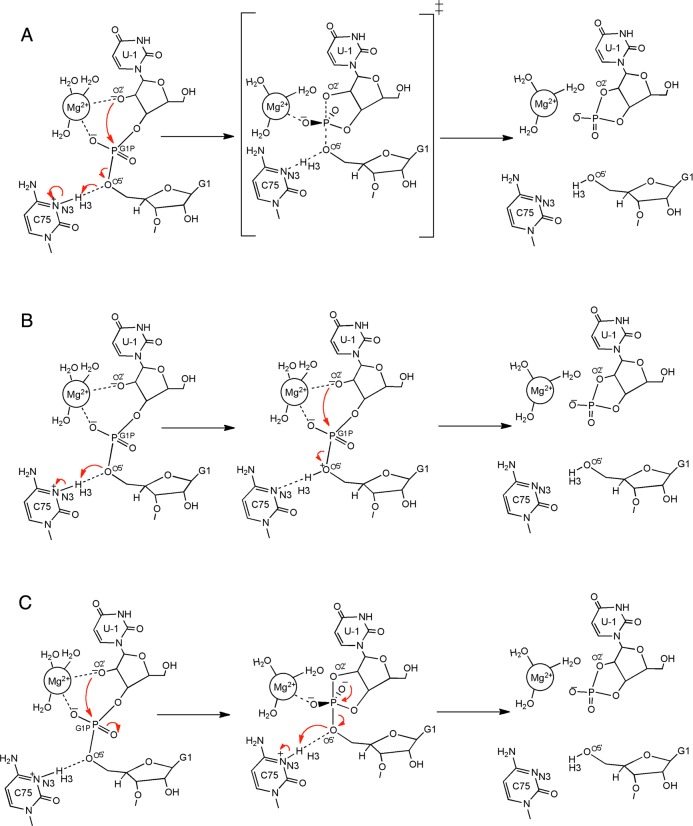
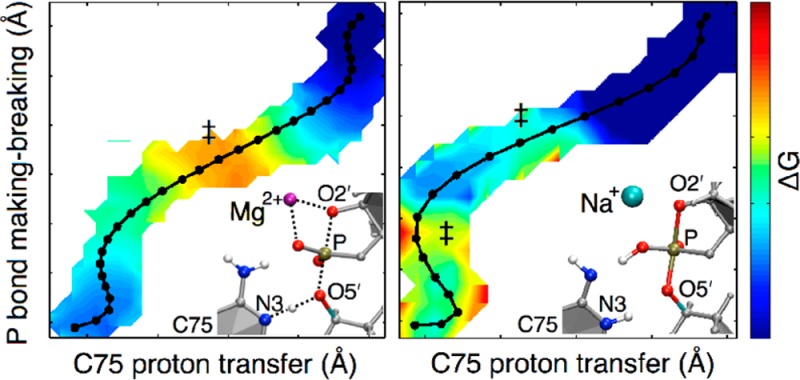
In a previous study, we performed QM/MM calculations on the HDV ribozyme.¹⁹ The active site of the HDV ribozyme and several possible mechanisms are depicted in Figure 1. Those calculations indicated that the mechanism of the self-cleavage reaction is concerted with a phosphorane-like transition state (TS) when a divalent metal ion, such as Mg²⁺ or Ca²⁺, is bound at the catalytic site (Figure 1A). In contrast, the self-cleavage reaction was found to be sequential with a phosphorane intermediate (PI) when a monovalent ion, such as Na⁺, is at this site (Figure 1C with a Na⁺ rather than Mg²⁺ at the catalytic site). Electrostatic potential calculations suggested that the divalent metal ion at the active site lowers the pK_a of protonated C75, aiding its proton donation and thus facilitating the concerted mechanism, in which the proton is partially transferred to the leaving group in the phosphorane-like TS. These observations are supported by several experimental studies, including measurements of the pK_a at different Mg²⁺ and Na⁺ concentrations and proton inventories in the presence of Mg²⁺ or Na⁺ alone.^10,11,27 In this previous study, however, we emphasized that the results were only qualitatively meaningful because of the limitations of the methodology. Specifically, we optimized structures for the minima and transition states and calculated the minimum energy path (MEP) without including entropic contributions or conformational sampling. The potential energy surface for such large systems is expected to be complex, with numerous stationary points, and the reactant, product, and transition states identified by this methodology may be biased toward the starting configuration. Moreover, the inclusion of entropic contributions is essential for obtaining free energy barriers that are related to experimentally measured rate constants.

Figure 1.

Plausible reaction pathways explored in this study. (A) The concerted mechanism, in which the reaction passes through a phosphorane-like TS, which is depicted as the middle structure. The minimum energy pathway obtained in our previous study¹⁹ corresponds to this pathway. (B) A sequential pathway that passes through a bridging O5′ proton-transferred intermediate, which is depicted as the middle structure. (C) A sequential pathway that passes through a nonprotonated phosphorane intermediate, which is depicted as the middle structure. Note that all of the pathways are reversible but are shown only in one direction for clarity.

An alternative approach that avoids these limitations is to combine QM/MM calculations with free energy simulations to generate the underlying free energy surface for the reaction.²⁸⁻³⁵ Exploring the entire free energy surface of the system is typically computationally prohibitive, however, because of the multidimensionality of these types of complex systems and the expense of the QM/MM calculations. A variety of methods have been developed to sample only the relevant portions of the free energy surface, thereby providing a computationally tractable approach for generating the minimum free energy path (MFEP). For example, Hummer and co-workers combined the finite temperature string method³⁶ with umbrella sampling simulations³⁷ to investigate the catalytic reaction in the ribonuclease H enzyme.³³ The key strategy of this method is to start with an initial guess reaction path described by an initial string in the multidimensional phase space and to repeatedly update the string on the basis of umbrella sampling simulations for points along the string. In this manner, the regions of phase space relevant to the reaction are sampled, and the string evolves toward the MFEP.

In the present study, we use this finite temperature string umbrella sampling approach to investigate the mechanism of the HDV ribozyme self-cleavage reaction. We explore three possible reaction mechanisms for the self-cleavage reaction with a Mg²⁺ ion bound at the catalytic site. As described below, all three initial reaction paths, which correspond to three different mechanisms, evolve toward the same MFEP, thereby illustrating the robustness of the approach in identifying the thermodynamically favorable mechanism. We also examine the reaction with a Na⁺ ion rather than a Mg²⁺ ion at the catalytic site and further illustrate that the mechanism is different in the presence of monovalent versus divalent ions. In contrast to previous calculations, these QM/MM free energy calculations provide estimates of the free energy barriers for comparison to experimental data and lead to different mechanistic predictions, such as an additional proton transfer reaction occurring to stabilize the phosphorane intermediate when Na⁺ is at the catalytic site. Furthermore, these calculations lead to several hypotheses regarding the role of the catalytic metal ion. To test one of the hypotheses generated by these calculations, we perform kinetic and NMR experimental measurements to determine the pK_a of the attacking O2′ in the presence of divalent or monovalent cations. The combined theoretical and experimental results provide a number of new key insights into the mechanism of the HDV ribozyme and, in particular, the roles of the catalytic metal ion.

Methods

QM/MM Free Energy Simulations

The simulations were based on the precleaved crystal structure (PDB ID 3NKB)¹⁶ solved with wild-type sequences and a Mg²⁺ ion bound at the catalytic site, as in our previous QM/MM calculations.¹⁹ The initial modeling performed on the crystal structure, particularly on the scissile phosphate and the upstream nucleotide, is discussed in our previous studies.^19,20,38 Several recent studies support the positioning of the active site nucleotides and metal ions in this model.^22,25 The nucleotides at positions 1 and 2 were modified from their deoxy forms, which were present to prevent degradation during crystallography, by addition of 2′-hydroxyls with ideal bond lengths and bond angles. The residues C75 and C41 were kept protonated at their N3 positions to reflect the active form of the ribozyme, as discussed elsewhere.^38,39 The Accelrys Discover Studio Visualizer 2.0 program was used to add the hydrogen atoms. The ribozyme, along with its 10 crystallographically resolved Mg²⁺ ions, was immersed in an orthorhombic box containing rigid TIP3P waters,⁴¹ and Na⁺ ions were added to neutralize the system. Additional Na⁺ and Cl^– ions were added to provide a physiological ionic strength of 0.15 M. The starting structures along the initial guess pathways for the QM/MM free energy simulations were obtained after classical molecular dynamics (MD) equilibration of the solvent and the monovalent Na⁺ and Cl^– ions, followed by deletion of all solvent molecules and ions further than 20 Å from the ribozyme. The MD simulations were performed using the Desmond program⁴² in conjunction with the AMBER99 force field,⁴³ periodic boundary conditions, and the Ewald treatment⁴⁴ of long-range electrostatics. The details of these classical MD simulations are provided in refs (20) and (38).

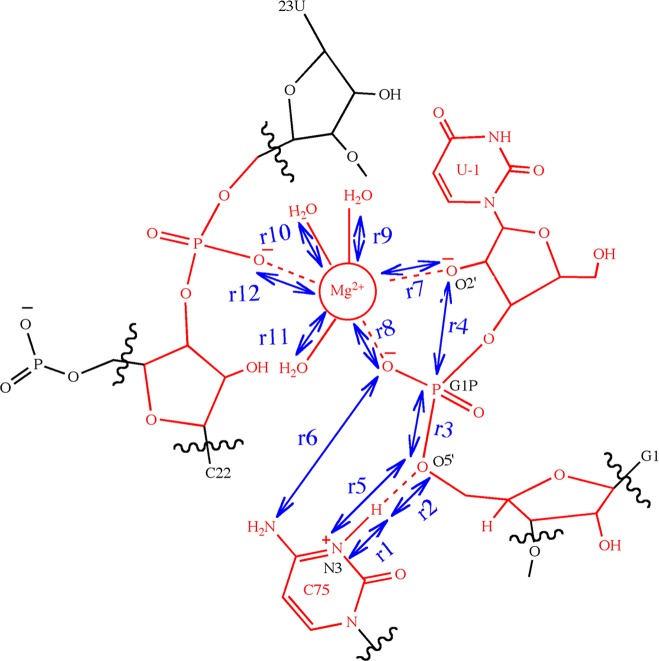
The QM/MM interface between Q-Chem⁴⁵ and CHARMM⁴⁶ was used to perform the QM/MM free energy simulations. The QM region consisted of 87 atoms, as used in our previous study¹⁹ and depicted in Figure 2. The O2′ of the U-1 residue remained deprotonated throughout all of these simulations to drive the nucleophilic attack on the scissile phosphate. The deprotonation of the U-1 2′-OH was assumed to occur prior to the nucleophilic attack and was not considered explicitly in these simulations because the identity of the general base is unknown, although it may be a hydroxide anion ligated to the Mg²⁺ ion. As will be discussed at the end of the Results, we did however investigate this possible mechanism for deprotonation of the U-1 2′OH by propagating additional QM/MM molecular dynamics trajectories. In the free energy simulations, the QM atoms were treated with density functional theory (DFT) using the 6-31G** basis set and the B3LYP functional. The MM region was described by the AMBER99 force field,⁴³ and link atoms were utilized to treat the QM–MM boundary. The simulations were performed using Langevin dynamics with a 1 fs time step. During the simulations, all atoms lying outside a sphere of radius 20 Å centered at the phosphorus atom of the scissile phosphate remained fixed.

Figure 2.

Schematic illustration of the active site of the genomic HDV ribozyme and the reaction coordinates included in the string calculations. The QM region for the QM/MM calculations consists of the 87 atoms shown in red, including the U-1 base and sugar, the G1 phosphate (the scissile phosphate) and sugar, the protonated C75 base, the U23 phosphate, the sugar of C22, the active site Mg²⁺ ion, and the three crystallographic waters coordinating to the Mg²⁺ ion. The reaction coordinates included in the string calculations are indicated by the blue double-headed arrows. In total, 12 active site distances were considered, although r1, r2, r3, and r4 were found to be the most important. The reaction paths are typically projected onto collective coordinates, namely, the difference of r1 and r2 (r1 – r2) and the difference of r3 and r4 (r3 – r4).

The multidimensional free energy surface and the MFEP were determined by combining umbrella sampling simulations with a finite temperature string method.³³ In this method, an M-dimensional curve corresponding to the initial string, S₀(ξ) = (f₀¹(ξ), ..., f₀(ξ)), is constructed along an initial guess reaction pathway from the reactant to the product state. Here M is the number of reaction coordinates, ξ is the reduced length along the curve (0 ≤ ξ ≤ 1), and each function f₀ⁱ(ξ) represents the value of the ith reaction coordinate at ξ. The reactant and product states correspond to f₀(0) and f₀ⁱ(1), respectively, for i = 1 to M. The initial string along ξ is then divided equally into N images at positions ξ_j with j = 1 to N, where each image corresponds to certain values of the M reaction coordinates. Umbrella sampling is performed for each image, with harmonic restraints centered at S₀(ξ_j) for each of the M reaction coordinates. After 100 fs of MD, the string is updated by fitting the average reaction coordinates of each image along ξ to a new curve. The N images are redistributed along this updated string with equal spacings to obtain the new centers of the restraining potentials, S₁(ξ_j) with j = 1 to N, for the umbrella sampling. This process of updating the string on the basis of umbrella sampling simulations is repeated until the string is converged. We considered the string to be converged when the root-mean-square deviation (RMSD) of all coordinates of the latest string from the mean value of the previous 10 iterations, summed over all images, fell below a threshold of 0.1 Å. Finally, the results are unbiased using the multidimensional weighted histogram analysis method (WHAM)⁴⁷ with a convergence threshold of 0.001 kcal/mol.

We utilized this method to explore the possibility of three different reaction mechanisms of the HDV ribozyme self-cleavage reaction. Independent sets of simulations were performed for each case, starting with an initial guess string associated with each proposed reaction mechanism. The following three mechanisms were investigated: (A) a concerted mechanism, in which the reaction passes through a single phosphorane-like transition state (Figure 1A); (B) a sequential mechanism, in which the reaction passes through a bridging O5′ proton-transferred intermediate (Figure 1B); and (C) another sequential mechanism, in which the reaction passes through a phosphorane intermediate (Figure 1C). The initial string in simulation set A was constructed from configurations along the minimum energy path obtained in our previous QM/MM calculations.¹⁹ The initial strings for simulation sets B and C were generated from interpolation between representative structures along the respective pathways. For these three simulation sets A, B, and C, a Mg²⁺ ion was bound at the catalytic site, as in the crystal structure. We also investigated the impact of the valency of the catalytic metal ion on the reaction mechanism by replacing the Mg²⁺ ion at the catalytic site with a Na⁺ ion in certain calculations. On the basis of our previous QM/MM calculations,¹⁹ the initial string for this simulation set, denoted as D, was chosen to be similar to that for simulation set C, passing through a phosphorane intermediate.

For each of these four sets A, B, C, and D, independent simulations were performed using the finite temperature string method with umbrella sampling as described above. Twelve atom-to-atom active site distances were used as reaction coordinates, as illustrated in Figure 2. Note that many of these distances did not change significantly along the initial strings but were included in case they were found to be important during the finite temperature string calculations. The inclusion of reaction coordinates that do not change substantially during the reaction does not increase the computational cost significantly. Restraining potentials with a force constant of 100 kcal mol^–1 Å^–2 were used for the umbrella sampling simulations. For set A, initially 15 images along the reaction pathway were used, and later the number of images was increased to 30 to ensure better resolution of the MFEP. In all other sets, 21 images along the reaction pathway were used. To obtain the starting configurations for the production simulations, the configurations representing the images along the initial strings for each of the sets were subjected to 150 fs of QM/MM equilibration with harmonic restraints applied to the reaction coordinates. The total simulation times for sets A, B, C, and D were 52 ps, 66 ps, 37 ps, and 56 ps, respectively. A limitation of this approach is that such relatively short simulation times do not enable comprehensive sampling of conformational space. As will be shown below, however, the qualitatively different initial strings for simulation sets A, B, and C resulted in similar MFEPs and overall mechanisms, providing a degree of validation for the convergence of these simulations in terms of the qualitative behavior. Set D corresponds to a different ion at the catalytic site (i.e., Na⁺ instead of Mg²⁺) and results in a different MFEP and mechanism, illustrating the flexibility of the approach in terms of identifying different mechanisms.

Measurements of O2′ pK_a

The pK_a of O2′ was determined using two different experimental methods. The first method measured the dependence of the cleavage rate of a chimeric oligonucleotide with a single ribose linkage on pH using kinetic assays, and the second method measured the dependence of the ¹H chemical shift of 3′-adenosine monophosphate (3′AMP) on pH using proton NMR spectroscopy.

In the first method, the chimeric DNA/RNA with the same sequence as used in a previous study,⁴⁸ 5′-d(CGACTCACTAT)rU*d(GGAAGAGATG), was obtained from IDT (Coralville, IA). The “*” denotes the site of the only RNA linkage in the chimeric oligonucleotide. The sequence U*G was chosen for the ribose linkage in order to correspond with the −1 and +1 nucleotides at the cleavage site of the HDV ribozyme. The chimeric oligonucleotide was 5′-³²P-labeled using T4 polynucleotide kinase (New England Biolabs) and [γ-³²P]ATP and subsequently purified on a 10% polyacrylamide/7 M urea gel before being used for the kinetic assays.

The cleavage assays in the presence of Na⁺ or K⁺ were performed similarly to those previously described.⁴⁸ Reactions were conducted at 23 °C in the presence of 3.16 M monovalent ion. The reaction was performed at a particular pH by using the appropriate concentration of the corresponding metal hydroxide (NaOH or KOH). The total M⁺ ion concentration was maintained at 3.16 M at various pH values by addition of appropriate amounts of the corresponding metal chloride (NaCl or KCl).

Cleavage assays in the presence of Ca²⁺ were performed under an inert argon atmosphere to avoid the precipitation of Ca²⁺ as calcium carbonate. Solid Ca(OH)₂ and CaCl₂ (Sigma-Aldrich, 99.99% purity) were used to make stock solutions of 10 mM and 20 mM, respectively, using degassed water under an argon atmosphere. The solutions were made fresh for each new set of experiments and stored under argon. For each pH tested, the total Ca²⁺ concentration was maintained at 10 mM, which is relevant to typical HDV ribozyme experiments.^10,49 Higher Ca²⁺ concentrations were not attempted because of precipitation of Ca(OH)₂.

For each metal ion, the reaction was initiated by the addition of a premixed solution of metal hydroxide and metal chloride to the 5′-³²P-labeled chimeric substrate. Subsequently, 3 μL aliquots were removed at regular intervals and neutralized by addition to an equal volume of 100 mM Tris-HCl buffer (pH 7.0). The solution was then diluted with an equal volume of 20 mM EDTA and 90% formamide and placed on dry ice to prevent further reaction. The reactant and product were fractionated on a 10% polyacrylamide/7 M urea gel, and the fraction of the cleaved substrate with respect to time was quantified using a Typhoon PhosphorImager (Molecular Dynamics). Data from the cleavage of the chimeric substrate were fit to a single-exponential equation:

1

where f_cleaved is the fraction of substrate cleaved at time t, k_obs is the observed first-order rate constant, and A is the fraction of the substrate cleaved at completion. For reactions at lower pH, which had slower observable rates (<10^–3 min^–1), early time points corresponding to the initial reaction rate were taken and fitted to a linearized form of eq 1:

2

where A is the amplitude of the reaction, as in eq 1, and Ak_obs is the slope of the line. For reactions in the presence of monovalent ions, the reactions went to completion, leading to A ≈ 1. In the presence of Ca²⁺, the reaction showed complete cleavage of substrate (A ≈ 1) at high pH (≥11.5) in an Ar atmosphere. Reactions carried out at the same pH but in the presence of atmospheric CO₂ showed similar rates but gave only partial cleavage of substrate (A ≈ 0.5–0.6). Thus, CO₂ present in air was found to affect the amplitude but not the rate of the reaction. The reaction performed under an argon atmosphere at pH 11.0 in the presence of Ca²⁺ went to 70% completion, so a value of 0.7 was used for A in eq 2 for slow reactions (pH < 11.0).

The rate–pH profiles obtained were fitted to the following equation:

3

where k_max is the maximal observed rate constant, n is the Hill coefficient, and the pK_a corresponds to the value of the pH at which k_obs is equal to k_max/2. Fits were performed with nonlinear least-squares using a Marquardt algorithm in KaleidaGraph (Synergy Software).

To test whether the pK_a measured from the kinetic method was associated, at least in part, with the deprotonation of a calcium-bound water, we directly measured the pK_a of the 2′-OH of 3′AMP using NMR spectroscopy. We chose to use 3′AMP because a ribose linkage such as that in the above chimeric oligonucleotide would be cleaved at high pH during the NMR experiment. Similar studies on 3′AMP have been carried out previously by Chattopadhyaya and co-workers⁵⁰ but under different ionic conditions. NMR data were collected on a Bruker AV-3-600 spectrophotometer at 25 °C. Even though it required water suppression, we chose to determine pK_a’s in 90% H₂O solutions rather than 100% D₂O because pure D₂O solutions generally shift pK_a values of N-linked protons higher by ∼0.4–0.6 units.^10,51 The 3′AMP was obtained from Sigma-Aldrich (St. Louis, MO). Solutions of 3′AMP (∼1–2 mM) were prepared in 10% D₂O and contained 4,4-dimethyl-4-silapentane-1-sulfonic acid (DSS) as an internal standard. Water suppression was achieved through presaturation using the noesygppr1d pulse sequence. Each NMR-detected pH titration consisted of 12–15 points, each of which was prepared independently. Appropriate volumes of sodium or calcium hydroxide were used to bring the solution to the required pH in a total volume of 500 μL. Throughout the titration, the total final concentration of sodium ions was kept constant at 0.5 M and that of calcium ions was kept constant at 10 mM by adding appropriate volumes of sodium chloride and calcium chloride. Sodium ion concentrations higher than 0.5 M, corresponding to pH 13.7, were avoided because of NMR tuning issues associated with high ionic strength solutions, while the pH was limited to 12.2 in the presence of calcium ions to avoid precipitation of calcium hydroxide. The calcium hydroxide-containing samples were degassed under inert argon to avoid precipitation of calcium carbonate. Degassing by bubbling argon into the NMR tube or degassing only the buffers gave similar results. The pH of each solution was measured after each NMR spectrum was acquired and was found to agree with calculated values. All solutions were prepared freshly on the day that the NMR experiments were performed. The chemical shift of the H1′ peak was monitored as a function of pH because this peak is relatively well isolated from the water peak.

Plots of observed chemical shift versus pH were used to determine the pK_a according to the following equation:

4

where δ_A is the chemical shift at high pH, δ_AH is the chemical shift at low pH, and δ_obs is the observed chemical shift at a given pH. As stated above, the highest pH attainable in the presence of 0.5 M Na⁺ was 13.7, and that in the presence of 10 mM Ca²⁺ was 12.2. Because of incomplete ionization of the 2′-OH of AMP at these pH values, the high-pH baseline was not well-defined for either the Na⁺ or Ca²⁺ experiments. To determine the value of δ_A, we used a linearized form of eq 4 as previously described:⁵⁰

5

where a_H⁺ is the activity of the proton and K_a is the acid dissociation constant. A plot of δ_obs versus (δ_AH – δ_obs)a_H+ gives a straight line with a y-intercept of δ_A. This value of δ_A was then used in eq 4 to obtain the pK_a.

To compare the changes in protonation as a function of pH for sodium and calcium ions on the same scale, the fraction of protonated species was plotted as a function of pH according to the following equation:

6

where f_AH is the fraction of protonated species and the other parameters were determined from eq 4.

Results and Discussion

As discussed in the Introduction, our previous QM/MM calculations¹⁹ implicated a concerted reaction pathway for the HDV ribozyme when a Mg²⁺ ion is at the catalytic site. Figure 3 depicts the initial (dashed) and final (solid) strings from the three sets of simulations with Mg²⁺ at the catalytic site: A (green), B (purple), and C (red). The strings are projected in the two-dimensional (2D) space of the collective reaction coordinates (r1 – r2) and (r3 – r4). As shown in Figure 2, (r1 – r2) is associated with proton transfer from N3(C75) to O5′(G1), and (r3 – r4) is associated with the P(G1)–O2′(U-1)/P(G1)–O5′(G1) bond forming/breaking. Figure 3 indicates that the strings from all three sets converged to a similar reaction pathway corresponding to a concerted mechanism (i.e., a predominantly straight line along the diagonal in the 2D space of these two collective reaction coordinates). The initial string for set B (dashed purple curve) is in a very different region of configurational space than the initial strings for sets A and C (dashed green and dashed red curves) because the mechanism associated with the initial string for set B has an intermediate with the proton transferred to the 5′-bridging oxygen. In contrast, the mechanisms associated with the initial strings for sets A and C have a phosphorane-like TS and phosphorane intermediate, respectively, which are located in similar regions of configurational space. The converged strings for sets A and C (solid green and solid red curves) are nearly indistinguishable. To conserve computational resources, the string calculations for set B were terminated after the reaction pathway indicated by the latest string (solid purple curve) was determined to be qualitatively similar to that obtained from sets A and C and continuing to evolve in that direction. Details regarding the convergence of the strings are provided in the Supporting Information.

Figure 3.

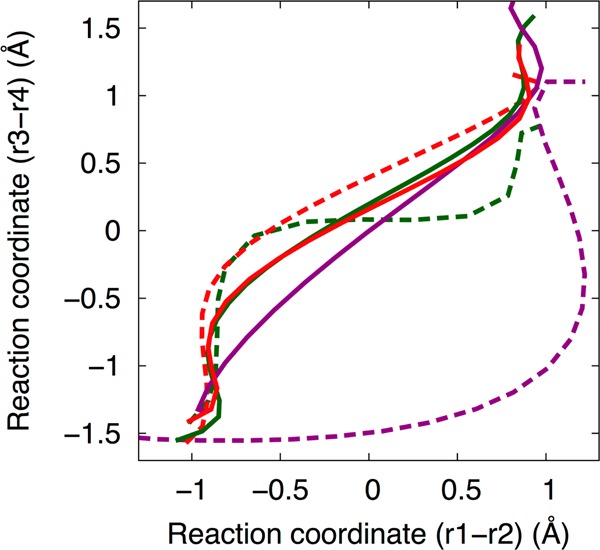
The initial (dashed lines) and final (solid lines) strings from the three sets of simulations with Mg²⁺ bound at the catalytic site: A (green, initial path is a concerted mechanism), B (purple, initial path is sequential with a proton transferred intermediate), and C (red, initial path is sequential with a phosphorane intermediate). The three initial paths are depicted in Figure 1, but the final paths all correspond qualitatively to pathway A in Figure 1. The strings are projected in the space of the collective coordinates (r1 – r2) and (r3 – r4), corresponding to the proton transfer reaction to the O5′ and the oxygen–phosphorus bond breaking/forming, respectively. The strings from sets A and C have converged to a similar path. The string from set B is still evolving, as described in the text, but is already close to the converged strings from A and C.

The 2D free energy profile of the self-cleavage reaction obtained from set A is depicted in Figure 4A. The 2D surface was constructed by projecting the free energy along the (r1 – r2) and (r3 – r4) collective reaction coordinates. The dashed and solid black lines indicate the initial and converged strings, respectively. The free energy surface implicates a concerted mechanism for the reaction without stable intermediates. Specifically, the MFEP (solid black line) is a predominantly straight line along the diagonal with a single maximum in free energy. The 1D free energy profile along the converged string, which corresponds to the MFEP, is depicted in Figure 4B. The free energy barrier along this string is ∼13 kcal/mol. This barrier is consistent with the experimental observation that the intrinsic rate constant of the HDV ribozyme catalytic reaction is 10²–10⁴ s^–1 when the general base is extrapolated to the fully functional deprotonated O2′ form as used in the reactant state for the calculations.¹⁰ This range of experimental rate constants corresponds to a free energy barrier of 11–14 kcal/mol using transition state theory (TST), assuming a prefactor of ∼1 ps^–1 in the TST rate constant expression. In this qualitative analysis, we are neglecting the corrections associated with dynamical recrossings and Jacobian factors related to the choice of reaction coordinates, but these effects are not expected to significantly alter the qualitative rate constant. The free energy profiles along the converged strings for sets B and C are similar and are provided in the Supporting Information.

Figure 4.

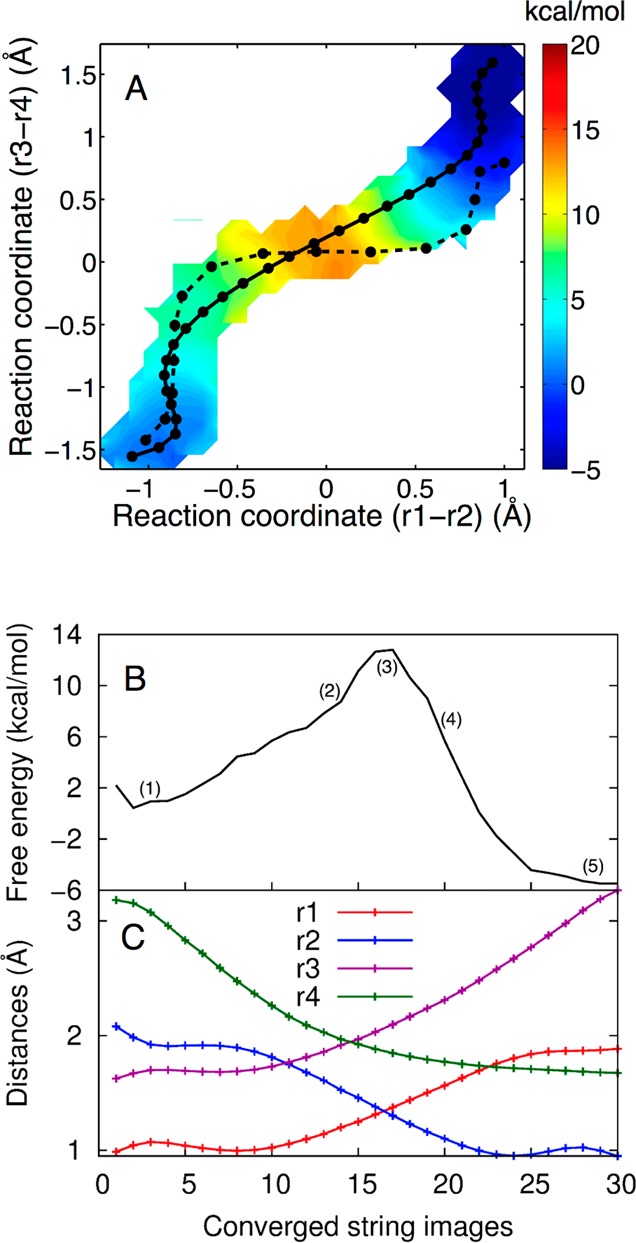
(A) The 2D free energy surface obtained from set A, where Mg²⁺ is bound at the catalytic site, projected in the (r1 – r2) and (r3 – r4) space. The initial string (dashed black line) corresponds to the MEP obtained in our previous study.¹⁹ The converged string (solid black line) corresponds to the MFEP obtained from set A. Both the MEP and MFEP correspond to a concerted mechanism with a phosphorane-like TS, but the MFEP is more synchronous than the previously obtained MEP. Each circle corresponds to an image along the string. The color scale denotes free energy in units of kcal/mol. (B) The 1D free energy profile along the MFEP obtained from set A, where Mg²⁺ is bound at the catalytic site. (C) Values of the most important reaction coordinates, r1, r2, r3, and r4, along the MFEP. Each circle corresponds to an image along the string.

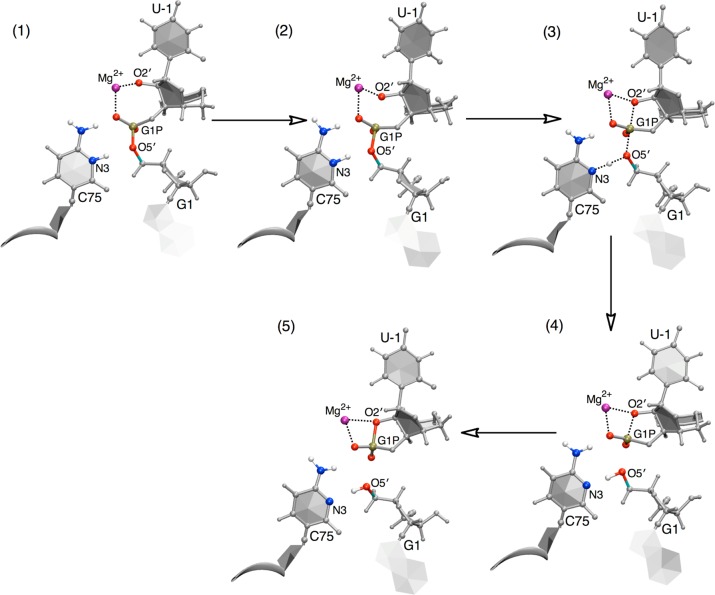
Figure 4C depicts the changes in the most important reaction coordinates involved in the self-cleavage reaction along the MFEP. The reaction coordinates shown here are as follows: r1 (the N3–H3 distance), r2 (the O5′–H3 distance), r3 (the P–O5′ distance), and r4 (the P–O2′ distance), as depicted in Figure 2. The other eight reaction coordinates do not change significantly along the MFEP, as depicted in Figure S7 in the Supporting Information. The mechanism of the reaction is further illustrated in Figure 5 in terms of representative structures along the MFEP. According to Figure 4B, the cleavage reaction in the HDV ribozyme is concerted, evolving from the reactant state to the product state through a single TS. Furthermore, Figures 4C and 5 provide detailed mechanistic information along the MFEP. In the early stages of the reaction (i.e., over the first three points in Figure 4C), the r2 coordinate (blue curve in Figure 4C) decreases, mainly as a result of a decrease in the proton donor–acceptor distance (i.e., a decrease in the distance between O5′ and N3). Simultaneously, the r4 coordinate decreases as the O2′ begins to attack the scissile phosphate. In Figure 4A, these two movements are manifested as an initial increase in (r1 – r2) as well as an increase in (r3 – r4) in the early stages of the MFEP to prime the system prior to the overall concerted mechanism. Following this initial preparation, the O2′ continues to move toward the phosphorus, as indicated by the further decrease of the r4 coordinate in Figure 4C. This attack, as depicted in structure 2 of Figure 5, primes the local geometry for the subsequent proton transfer from N3(C75) to O5′(G1). Subsequently, movements along (r3 – r4) and (r1 – r2) are concerted, as manifested by the diagonal, nearly linear MFEP with a slope of ∼1 between −0.5 and +0.5 Å for the two collective coordinates (Figure 4A, solid line). Moreover, the scissile phosphate evolves into a phosphorane-like geometry in the TS region, as depicted in structure 3 of Figure 5. In the TS region, r4 ≈ r3, suggesting that the P–O2′ and P–O5′ bonds are half formed and half broken, and r1 ≈ r2, suggesting that the proton H3 is midway between the donor N3(C75) and the acceptor O5′(G1). In other words, the two collective reaction coordinates (r1 – r2) and (r3 – r4) are both approximately zero in the TS region. Finally, the proton fully transfers to the O5′ of G1, as shown in structure 4 of Figure 5, and subsequently the P–O2′ and P–O5′ bonds are completely formed and broken, respectively, as shown in structure 5 of Figure 5. We emphasize that the structures in Figure 5 do not represent stationary points along the reaction pathway but rather represent selected structures along a concerted pathway comprising a single TS between two stable minima.

Figure 5.

Representative structures along the MFEP obtained from set A, where Mg²⁺ is bound at the catalytic site. The structures are numbered according to the locations along the MFEP identified in Figure 4B. The MFEP passes through a single transition state, which is phosphorane-like, as depicted in the reaction pathway in Figure 1A and represented here by structure 3. Note that these structures do not represent stationary points but rather represent selected structures along a concerted pathway.

The MFEP described above is consistent with the results from our previous theoretical study¹⁹ with Mg²⁺ bound at the catalytic site. In that study, we used QM/MM methods to generate an MEP for the HDV ribozyme self-cleavage reaction with a Mg²⁺ ion at the catalytic site. The MEP was generated by identifying a TS (i.e., a first-order saddle point) on the potential energy surface and following the paths of steepest descent to the reactant and product minima. When Mg²⁺ was bound at the catalytic site, the mechanism was found to be concerted with a phosphorane-like TS. We searched for stable intermediates but were unsuccessful for this case. One key limitation associated with this previous study was the lack of conformational sampling and hence the neglect of entropic contributions. In the present study, the MFEP was also determined to correspond to a concerted mechanism with a phosphorane-like TS.

Although both the MEP and the MFEP correspond to an overall concerted mechanism, we observed certain differences in the specific pathways followed. The most important difference is that the previously determined MEP (dashed black line in Figure 4A) was characterized as concerted but asynchronous. Specifically, the proton transfer coordinate in the MEP remained nearly constant during the initial O2′ attack on the scissile phosphate, which was followed by proton movement with a nearly constant P(G1)–O2′(U-1) distance to generate a phosphorane-like TS with the proton partially transferred. This reaction pathway was still considered to be concerted, however, because there was a single TS. In contrast, the MFEP is more synchronous, as indicated by the solid black line in Figure 4A and by Figures 4C and 5. Specifically, in the TS region of Figure 4A, the MFEP (solid line) is nearly linear with a slope of ∼1, whereas the MEP (dashed line) is nearly linear with a slope of ∼0. Moreover, the distance between the proton donor, C75(N3), and the proton acceptor, G1(O5′), decreases from ∼3.0 Å in structure 1 to ∼2.7 Å in structure 2 of Figure 5. The previous MEP calculations did not exhibit this decrease in the proton donor–acceptor distance during the initial O2′ attack on the scissile phosphate. This decrease in the proton donor–acceptor distance is likely to facilitate the proton transfer, leading to earlier proton motion and a more synchronous mechanism.

Furthermore, the MFEP indicates that the reaction is modestly exergonic, whereas the previously determined MEP indicated that the reaction is highly endothermic. Although a direct comparison of free energy and potential energy profiles is not meaningful, the entropic differences between the reactant and product states are unlikely to be large enough to account for this difference. The procedure used to generate the MEP probably resulted in a local minimum for the product state, whereas the finite temperature string umbrella sampling method used to generate the MFEP included conformational sampling and therefore was able to identify a more stable product structure, as shown in Figure 4A,B. Note that these calculations do not include the separation of the U-1 product fragment from the rest of the ribozyme following self-cleavage, which would further impact the entropic contributions to the overall process.

In contrast to the concerted mechanism observed when a Mg²⁺ ion is bound at the catalytic site, the previous QM/MM MEP calculations indicated that the mechanism is sequential with a phosphorane intermediate when a monovalent ion is at the catalytic site. The free energy simulations from set D are consistent with this hypothesis but, as discussed below, differ from the previous MEP calculations in the protonation state of the intermediate. The initial string for set D (Na⁺ ion at the catalytic site) corresponds to a sequential mechanism with a phosphorane intermediate, similar to the initial string used for set C (Mg²⁺ ion at the catalytic site). Figure 6 compares the initial string (dashed lines) and the converged string (solid lines) from set D in the presence of Na⁺ (blue lines) to those from set C in the presence of Mg²⁺ (red lines). Again the strings are projected in the 2D space of the collective coordinates (r1 – r2) and (r3 – r4). Although the initial strings are similar for set C (Mg²⁺ ion at the catalytic site) and set D (Na⁺ ion at the catalytic site), the converged MFEP for set C corresponds to a concerted mechanism with a phosphorane-like TS, as discussed above, whereas the converged MFEP for set D corresponds to a sequential mechanism with a phosphorane intermediate indicated by an additional minimum on the free energy surface, as discussed below. In Figure 6, the red and blue circles indicate the positions of the phosphorane-like TS structure and the phosphorane intermediate structure, respectively.

Figure 6.

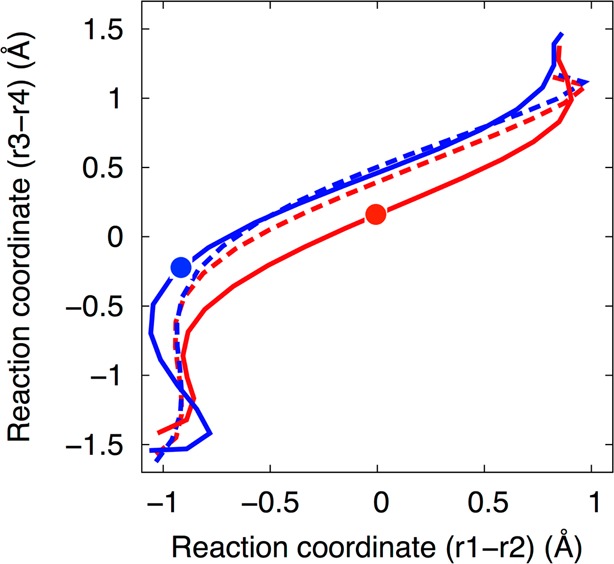
The initial (dashed lines) and final (solid lines) strings from sets C (red, Mg²⁺ at the catalytic site) and D (blue, Na⁺ at the catalytic site). The results for set C (both the solid and dashed red lines) are reproduced from Figure 3. The strings are projected in the space of the collective coordinates (r1 – r2) and (r3 – r4). The converged string from set D is distinct from the converged string from set C. The red circle indicates the position of the phosphorane-like transition state structure (free energy maximum for the concerted mechanism with Mg²⁺), while the blue circle indicates the position of the phosphorane intermediate structure (free energy minimum for the sequential mechanism with Na⁺).

The 2D free energy surface obtained from set D is depicted in Figure 7A. The dashed and solid black lines indicate the initial and converged strings, respectively. In this case, the free energy surface exhibits a minimum corresponding to a phosphorane intermediate structure. Figure 7B depicts the 1D free energy profile along the MFEP and also illustrates that the self-cleavage reaction in the presence of a Na⁺ ion at the catalytic site occurs by a sequential mechanism with a phosphorane intermediate. The first and second free energy barriers obtained from this free energy profile are ∼3.5 kcal/mol and ∼2 kcal/mol, respectively.

Figure 7.

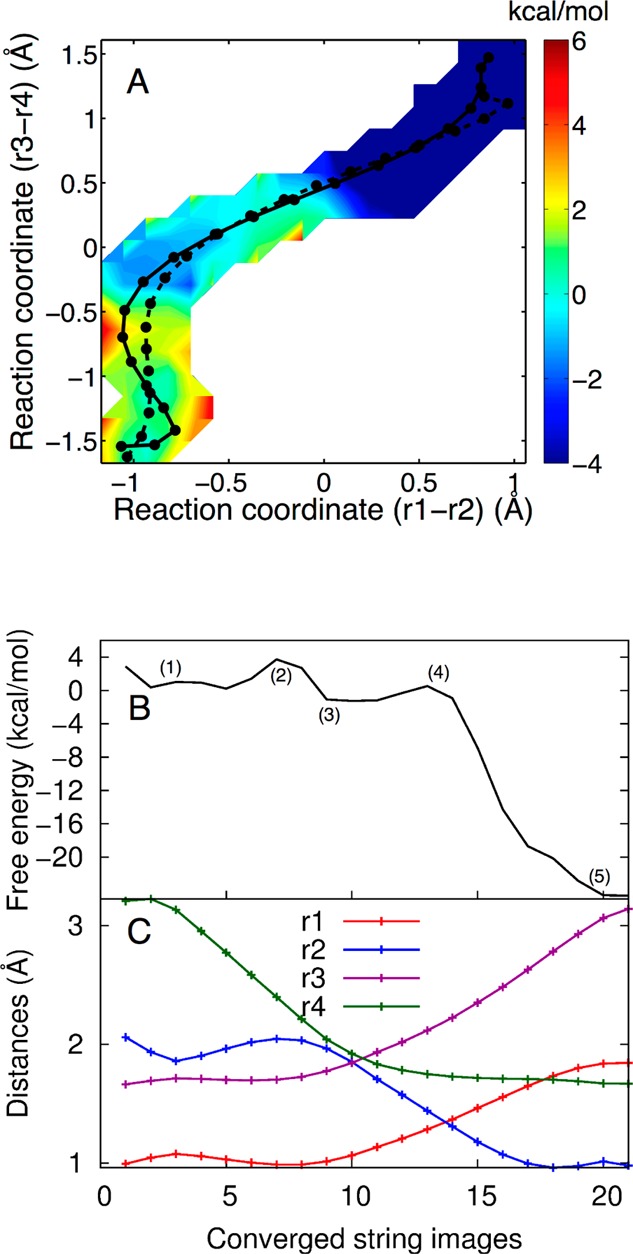
(A) The 2D free energy surface obtained from simulation set D, where a Na⁺ ion is at the catalytic site, projected in the (r1 – r2) and (r3 – r4) space. The initial and converged strings are illustrated on the surface as the dashed and solid black lines, respectively. In this case, the MFEP (solid black line) is sequential, passing through a phosphorane intermediate. Each circle corresponds to an image along the string. The color scale denotes free energy in units of kcal/mol. (B) The 1D free energy profile along the MFEP obtained from set D, where a Na⁺ ion is at the catalytic site. (C) Values of the most important reaction coordinates, r1, r2, r3, and r4, along the MFEP. Each circle corresponds to an image along the string.

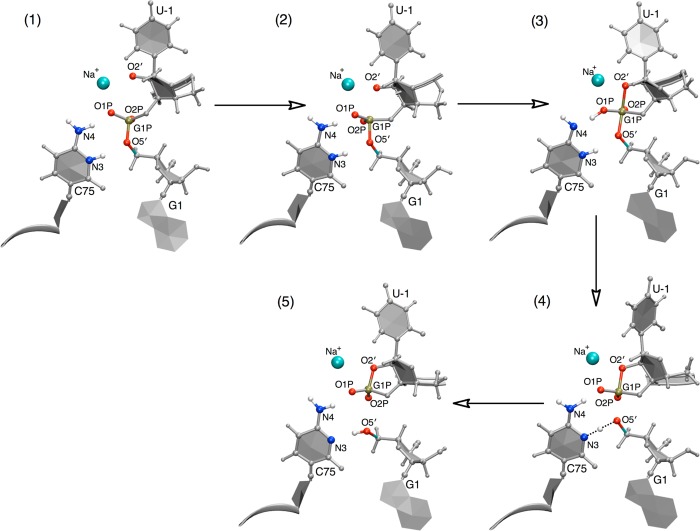
The detailed mechanism of the self-cleavage reaction with a Na⁺ ion at the catalytic site is depicted in Figures 7C and 8. Initially the O2′ attacks the scissile phosphate to form a structure in which the P–O2′ and P–O5′ bonds are half formed and half broken, respectively, as indicated by the decrease in the r4 coordinate (i.e., the P–O2′ distance) at the beginning of the MFEP in Figure 7C. Structure 2 of Figure 8 corresponds approximately to the TS for the first step. This part of the mechanism is similar to that observed in the MFEP obtained with a Mg²⁺ ion at the catalytic site. Next, the P–O2′ distance decreases further, and a proton is transferred from the exocyclic amine of C75 (N4 in Figure 8) to the nonbridging oxygen of the scissile phosphate, denoted as the pro-R_P oxygen (O1P in Figure 8), to make a stable pentacoordinated monoanionic phosphorane structure (structure 3 of Figure 8). This structure corresponds to the intermediate minimum observed in the free energy profiles shown in Figure 7A,B. This part of the mechanism is different from that observed with a Mg²⁺ ion at the active site and is also different from that observed in our previous MEP calculations with a Na⁺ ion at the active site. Following this step, the P–O2′ distance decreases a bit further and the P–O5′ distance increases substantially, leading to the transfer of the proton from the pro-R_P oxygen (O1P) back to N4 of C75 as well as initiating the proton transfer from N3(C75) to O5′(G1). Structure 4 of Figure 8 corresponds approximately to the TS for the second step [i.e., the proton transfer reaction from N3(C75) to O5′(G1)]. Finally, once the proton (H3) is transferred to O5′(G1), the P–O2′ and P–O5′ bonds are completely formed and broken, respectively.

Figure 8.

Representative structures along the MFEP obtained from simulation set D, where Na⁺ is at the catalytic site. The structures are numbered according to the locations along the MFEP identified in Figure 7B. The MFEP passes through a phosphorane intermediate, as represented here by structure 3, which is similar to the intermediate depicted in Figure 1C but with protonation at the pro-R_P oxygen (O1P) rather than at N4 of C75. Note that these structures do not represent stationary points but rather simply represent selected structures along a sequential pathway.

These free energy calculations indicate that the mechanism is concerted when Mg²⁺ is at the catalytic site and sequential when Na⁺ is at the catalytic site. An explanation for these different mechanisms is that the proton H3 of C75⁺ is less acidic with a monovalent ion than with a divalent ion at the catalytic site. Indeed, solution and crystallographic experiments have measured lower pK_a’s for C75 in the presence of Mg²⁺ ions than in the presence of Na⁺ ions.^10,11,27 In particular, kinetics experiments indicate that the pK_a of C75 decreases from 7.25 to 5.9 upon the binding of a Mg²⁺ ion at the catalytic site⁵² and is ∼7.5 in the presence of Na⁺ up to a concentration of 1 M without Mg²⁺.²⁷ As a result, it is more difficult to transfer the proton H3 of C75⁺ from N3(C75) to O5′(G1) when Na⁺ is at the catalytic site, and a protonated phosphorane monoanion intermediate is formed prior to this proton transfer reaction.

A new aspect of the mechanism illustrated by these free energy calculations is the transfer of a proton from the exocyclic amine of C75 to the pro-R_P oxygen to generate a protonated phosphorane monoanion intermediate. There is experimental support for the occurrence of such proton transfer to generate a monoanionic phosphorane in the monovalent ion mechanism of the genomic HDV ribozyme. While proton inventory measurements on this ribozyme in the presence of Mg²⁺ gave an inventory of 2, consistent with a concerted reaction mechanism,⁵³ those in the presence of 1 M Na⁺ gave an inventory of 1,²⁷ supporting a stepwise pathway such as that shown in Figure 7. In addition, we observed a normal thio effect at the pro-R_P oxygen in the presence of 1 M Na⁺, where the thio effect is the ratio of rate constants with oxo and thio at this oxygen (k_O/k_S).²² Observation of a thio effect supports the importance of the role of the pro-R_P oxygen in the mechanism in the absence of divalent ion coordination and thus is consistent with the stepwise mechanism. We also note that studies by Anslyn and Breslow on dinucleotide cleavage in the presence of imidazole buffer and no divalent ions support a similar stepwise mechanism with a protonated, monoanionic phosphorane intermediate.⁵⁴ These observations suggest that divalent ions, in addition to acidifying the general acid, interact with the pro-R_P oxygen and stabilize charge development at the scissile phosphate, preventing proton transfer to a nonbridging oxygen in the HDV ribozyme mechanism. This idea is supported by recent metal ion rescue experiments that establish an interaction between the pro-R_P oxygen and divalent metal ion in the transition state.²² Moreover, it is notable that the Mg²⁺ remains within 2.1 Å of the pro-R_P oxygen throughout the MFEP.

The proton transfer from N4 of C75 to the pro-R_P oxygen (O1P) observed during formation of the monoanionic phosphorane intermediate with Na⁺ at the catalytic site is reasonable on the basis of energetic considerations. According to high-level gas-phase quantum calculations,^55,56 the neutral imino tautomer of cytosine shown in structure 3 of Figure 8 has been estimated to be only slightly higher in energy (0.8 kcal/mol) than the standard amino tautomer of cytosine, suggesting that this species is energetically accessible. Second, the pK_a of the amino group (N4) of cytosine is significantly acidified, from a pK_a of 18 to 9, upon protonation at the imino nitrogen (N3) as determined by proton exchange NMR measurements.⁵⁷⁻⁵⁹ Estimates of the pK_a of the nonbridging oxygens of the dianionic phosphorane species are near 14.^60,61 Thus, protonation at the N3 of C75 could acidify the N4 enough to allow proton transfer to the pro-R_P oxygen, which is basic in the phosphorane intermediate. Protonation at one atom facilitating transfer at another could be a general catalytic strategy for enhancing ribozyme mechanism.⁶²

The rate of the HDV ribozyme catalytic reaction has been experimentally measured to be ∼25-fold higher in the presence of Mg²⁺ ions than in the presence of only Na⁺ ions.²¹ However, the QM/MM free energy simulations indicate that the free energy barrier for the self-cleavage reaction is significantly higher with a Mg²⁺ ion at the catalytic site than with a Na⁺ ion at the catalytic site. These free energy barriers are only qualitatively meaningful, but nevertheless, this substantial difference in free energy barriers suggests that the rate constant for self-cleavage should be smaller in the presence of Mg²⁺ ions. This result from the simulations can be reconciled with the experimental data by considering the initial deprotonation of the 2′-OH nucleophile. On the basis of simple electrostatic arguments concerning stabilization of the negatively charged O2′, the initial deprotonation of 2′-OH is expected to be more thermodynamically favorable with Mg²⁺ than with Na⁺.

To test this hypothesis, we measured the pK_a of the O2′ in the presence of monovalent and divalent ions using kinetic and NMR methods. First, we used the kinetic method of Li and Breaker,⁴⁸ in which we utilized a chimeric 22-mer with a single internal ribose linkage. This oligonucleotide was 5′-end-labeled, and its self-cleavage was monitored as a function of pH in the presence of various monovalent and divalent ions. Li and Breaker reported pK_a values in the presence of 0.5 to 3.16 M K⁺ but not in the presence of Mg²⁺ because of precipitation of magnesium hydroxide above pH ∼9. We repeated their studies in 3.16 M K⁺ and then measured the pK_a in 3.16 M Na⁺, which is the monovalent ion we used in prior HDV ribozyme experiments. We then conducted measurements in the presence of Ca²⁺ as the divalent ion, as its hydroxide has a higher K_sp than magnesium hydroxide, allowing studies up to pH 12.3, equivalent to 10.0 mM Ca(OH)₂. We previously observed that HDV ribozyme kinetics are similar for Mg²⁺ and Ca²⁺, with nearly indistinguishable rate–pH profiles and slightly faster rates in the presence of identical concentrations of Ca²⁺, suggesting that this is a reasonable approach.^10,49 Molar amounts of monovalent ion and millimolar amounts of divalent ion correspond to the concentrations of these ions used in our HDV ribozyme experiments.^10,21

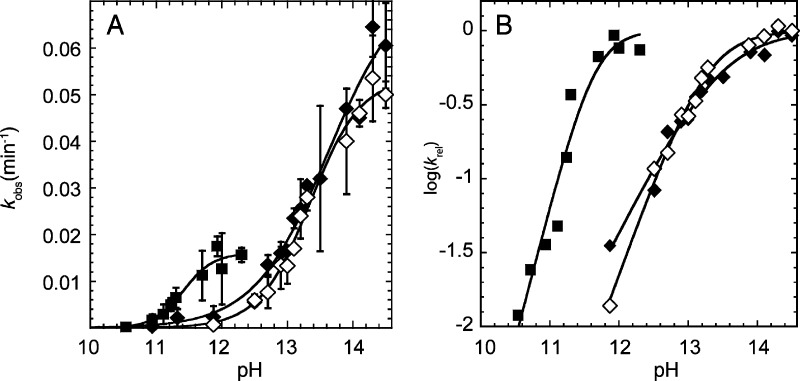
Sample PAGE gels and kinetic traces in the presence of Na⁺ and Ca²⁺ are provided in Figure S8 in the Supporting Information, and rate–pH profiles are provided in Figure 9. Cleavage experiments yielded a single product by PAGE analysis, and the reactions went to completion (Figure S8). As shown in Figure 9A, a plot of rate versus pH in the presence of 3.16 M K⁺ has a sigmoidal shape. Fitting of this plot to a standard rate–pH profile equation (eq 3) yielded a pK_a of 13.3 in 3.16 M K⁺, in good agreement with Li and Breaker,⁴⁸ and measurements in the presence of 3.16 M Na⁺ provided a pK_a of 13.6, indicating little dependence of the pK_a of the O2′ on the identity of the monovalent ion, as expected. Our experiments and simulations focus on Na⁺. Extrapolation of the pK_a value with Na⁺ from 3.16 M to 1 M monovalent ion conditions,⁴⁸ which were used in our earlier experiments on the genomic HDV ribozyme,^10,21 leads to an O2′ pK_a that is ∼0.5 units higher at ∼14.1. The rate–pH profiles in the presence of Ca²⁺ yielded a much lower pK_a of 11.4 (Figure 9). Thus, using kinetic measurements we found that the pK_a of the O2′ is shifted ∼2.7 units lower in the presence of millimolar amounts of divalent ions compared with molar amounts of sodium ions.

Figure 9.

Determination of the pK_a of the 2′-OH by the kinetic method. (A) Plot of k_obs as a function of pH in the presence of 3.16 M Na⁺ (◆), 3.16 M K⁺ (◇), and 10 mM Ca²⁺ (■). (B) Plot of log(k_rel) as a function of pH using the same symbols as in panel A. k_rel was obtained by normalizing the data in panel A to the k_max value from the fit. The pK_a values were determined by fitting the rate versus pH plots in panel A to eq 3 and were found to be 13.6, 13.3, and 11.4 in the presence of 3.16 M Na⁺, 3.16 M K⁺, and 10 mM Ca²⁺_, respectively. (Note that for panel A, the pK_a is the pH where k_obs = k_max/2, while for panel B the pK_a is the pH near the flex point.) The Hill coefficients determined from the fits of the data in panel A to eq 3 were found to be 0.8, 1.1, and 1.9 for Na⁺, K⁺, and Ca²⁺, respectively. These Hill coefficients are apparent in the relative slopes in panel B. The value of k_max is ∼3-fold higher for monovalent ions than divalent ions, as revealed in panel A, but the pK_a values are unaffected by k_max differences as they are determined entirely from the shape of the curves. The origin of the k_max difference is unclear, but this difference could reflect different interactions of divalent and monovalent ions with this 22-mer.

The above kinetic method is not necessarily specific to the pK_a of the O2′ because deprotonation of a calcium-bound water that could act as a general base might also be detected. We thus utilized the approach used by Chattopadhyaya and co-workers⁵⁰ to directly measure the pK_a of the O2′ in 3′AMP by ¹H NMR spectroscopy. Although we used methods similar to theirs, we conducted our experiments in 90% H₂O rather than 100% D₂O, kept the ionic strength constant throughout the titration, and explored different cations and cation concentrations (see Methods). We first conducted the experiments in the presence of 0.5 M Na⁺. As reported previously,⁵⁰ the chemical shift versus pH profile did not yield a sigmoidal curve because of incomplete ionization of the 2′-OH at the highest pH attainable (Figure S9A in the Supporting Information). We used eq 5 to estimate the chemical shift at high pH (Figure S9C) and then fit the data in Figure S9A to eq 4. This method yielded a pK_a of 13.2 in the presence of 0.5 M Na⁺, which is similar to the pK_a of 13.38 previously reported for 3′AMP in Na⁺ as determined by ¹H NMR spectroscopy.⁵⁰

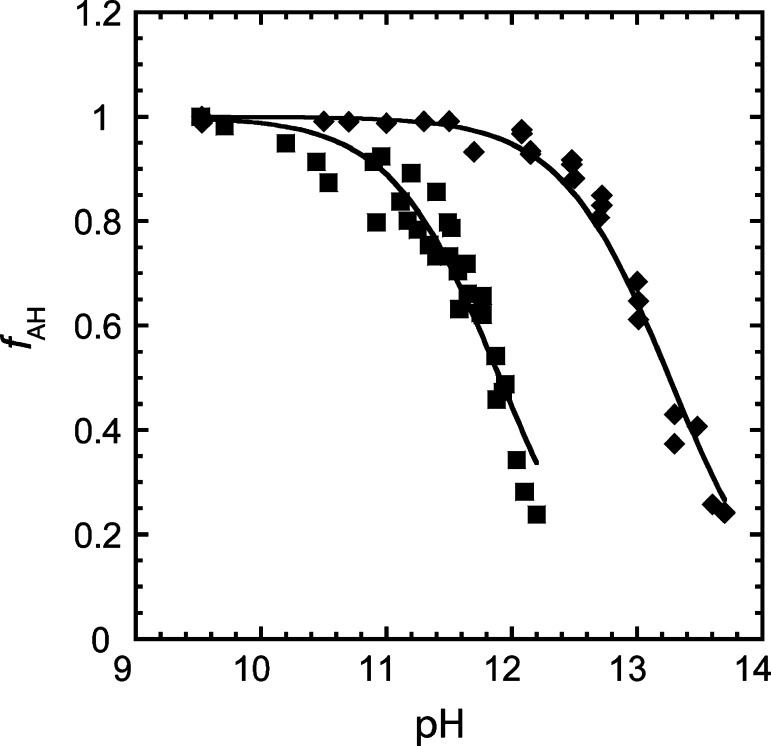
Subsequently, we carried out NMR experiments in the presence of calcium ions. As in our kinetic assays, we kept the concentration of Ca²⁺ constant at 10 mM throughout the titration. As in the presence of Na⁺, the chemical shift value at high pH was estimated from eq 5 (Figure S9D). In the presence of Ca²⁺, the pK_a was found to be shifted to 11.9 (Figure S9B), which is in good agreement with the value of 11.4 from our kinetic assay under identical divalent ion conditions. Thus, using NMR spectroscopy we found that the pK_a of the O2′ is shifted ∼1.3 units lower in the presence of millimolar amounts of divalent ions compared with molar amounts of sodium ions. This result is clearly visualized in the difference in the flex points of the NMR species plots provided in Figure 10. Additionally, the difference in the pK_a values in the presence of Ca²⁺ and Na⁺ determined by NMR spectroscopy is in reasonable agreement with the difference obtained by kinetics, especially considering that lower baselines had to be estimated for the NMR method. Both methods clearly show that deprotonation of the 2′-OH is considerably more favored in Ca²⁺ than Na⁺. Lastly, we note that the pK_a in the presence of Ca²⁺ ions measured using the kinetic method may be a result of convolution due to the deprotonation of the 2′-OH and a calcium-bound water both having similar pK_a values. Indeed, the Hill coefficient from the fit of the kinetic data is close to 2 (Figure 9), suggesting that more than one deprotonation event is being measured, as opposed to the NMR experiment, which is specific to the nucleotide.

Figure 10.

Fraction of protonated species as a function of pH in the presence of 0.5 M Na⁺ (◆) and 10 mM Ca²⁺ (■) as determined by the NMR method. The fraction of protonated species at a given pH was generated using eq 6. The pK_a values were determined by fitting δ_obs vs pH plots to eq 4, as shown in Figure S9 in the Supporting Information, and were found to be 13.2 and 11.9 in the presence of 0.5 M Na⁺ and 10 mM Ca²⁺_, respectively.

Overall, the experimental results are consistent with the hypothesis generated by the simulations, namely that 2′-OH deprotonation is less favorable in the presence of only monovalent ions than when a divalent ion is bound at the catalytic site. For both types of ions, the shapes of the rate–pH profiles of the HDV ribozyme reaction reflect participation of C75 in the rate-limiting step; thus, 2′-OH deprotonation does not appear to be rate-limiting in either case but rather is in rapid equilibrium. Thus, we can estimate the observed rate constant, k_obs, as the product of an equilibrium constant K_eq associated with O2′ activation and a rate constant k_cleavage associated with self-cleavage: k_obs = K_eqk_cleavage. We can use the following three observations to qualitatively estimate the impact of this pre-equilibrium on the observed rate constant: (1) the experimental observation of a ∼25-fold slower overall rate in the case of monovalent ions alone;²¹ (2) the experimentally measured O2′ pK_a that is ∼1.3–2.7 units lower for divalent ions than for sodium ions under typical reaction concentrations; and (3) the calculated free energy barriers for the self-cleavage reactions with Mg²⁺ or Na⁺ at the catalytic site. Given the calculated free energy barriers for the self-cleavage reaction (∼13 kcal/mol and ∼3.5 kcal/mol for divalent and monovalent ions, respectively) in conjunction with the pK_a differences that favor deprotonation in the presence of Mg²⁺ by ∼1.8–3.8 kcal/mol, the 2′-OH activation in the presence of Na⁺ is expected to be disfavored by an additional ∼8–10 kcal/mol to render the observed rate ∼25-fold slower with Na⁺. Such an effect could arise from an inability of Na⁺ to effectively orient the O2′ for attack on the adjacent phosphorus. In contrast, Mg²⁺ at the active site appears to act as a Lewis acid and directly coordinate the nucleophilic O2′ of U-1, which may provide not only enhanced acidity of the O2′, as indicated in the experiments herein, but also proper orientation for attack.^16,19 Along these lines, we note that the monovalent and divalent ions are within 2.3 and 2.1 Å respectively, of the deprotonated O2′ throughout the MFEPs, indicating closer approach of the divalent ion and greater stabilization throughout. Moreover, these distances represent direct interactions of the Na⁺ and Mg²⁺ with the O2′ (i.e., without a water bridge); thus, the differential energetics for dehydrating these ions and the O2′ within the active site may also influence the pre-equilibrium process.

Another effect that could contribute to the pre-equilibrium constant in the overall observed rate constant is the relative probability that a Mg²⁺ ion versus a Na⁺ ion occupies a binding site that allows interaction with the O2′. To investigate this effect, we analyzed a series of 25 ns classical MD trajectories from our previous work.^20,38 Specifically, we analyzed two independent trajectories of the HDV ribozyme with a Mg²⁺ ion at the catalytic site and two independent trajectories in which the catalytic Mg²⁺ ion was replaced by two Na⁺ ions in the bulk. In the latter case, we observed that a Na⁺ ion moved into the active site region during the equilibration stage. The charge isodensity plots illustrating positive charge in the active site region and the associated cumulative distribution functions for metal ion occupancy are depicted in Figures S10 and S11 in the Supporting Information, respectively. These plots indicate that the Mg²⁺ ion is highly localized with 100% occupancy of a binding site that allows strong interaction with the O2′ of U-1. In contrast, the Na⁺ ion is more delocalized with multiple binding sites that often do not allow the ion to interact with the O2′. These observations suggest that the pre-equilibrium constant is significantly decreased for the Na⁺ ion relative to the Mg²⁺ ion because of the lower probability that the Na⁺ ion occupies a binding site that allows it to interact with the O2′. It is interesting to note that Ke and co-workers solved a structure of the HDV ribozyme in the precleaved state with the heavy monovalent ion Tl⁺ and found that the ion interacts in a nonproductive way with the O2′ and pro-S_P oxygen, which would be consistent with an unfavorable conformation in the presence of monovalent ions.⁶³

To complete this study, we performed additional QM/MM molecular dynamics simulations to investigate the plausibility of a hydroxide ion bound to the catalytic Mg²⁺ ion acting as a general base and activating the O2′ of U-1. The starting structures for these simulations were obtained from the solvated precleaved crystal structure following equilibration of the solvent and ions. In these starting structures, the O2′ of U-1 was protonated, the Mg²⁺ ion was directly coordinated to the O2′, and one of the Mg²⁺-coordinated crystallographic water molecules was replaced by a hydroxide ion. The QM region consisted of the U-1 sugar, the phosphate, the atoms C5′ and O5′ of G1, the catalytic Mg²⁺ ion, the two Mg²⁺-coordinating water molecules, and the hydroxide ion. Two independent MD trajectories, in which different water molecules were replaced by a hydroxide ion, were propagated for 300 and 900 fs, respectively. In both trajectories, we observed that the hydroxide ion moved to a position that enabled it to interact strongly with the O2′ either directly or by a Grotthuss-type mechanism(64,65) to abstract the proton from the O2′. Movies of these two trajectories are available. These QM/MM molecular dynamics trajectories suggest that a hydroxide ion ligated to the catalytic Mg²⁺ can potentially act as a general base, thereby activating the O2′. A dual role of a partially hydrated Mg²⁺ ion as a Lewis acid and a Brønsted base, such as that observed here, is consistent with earlier experiments and models^10,25 and is also consistent with the kinetic-based pK_a studies conducted herein, where a Hill coefficient of approximately 2 was observed.

Concluding Remarks

We carried out QM/MM free energy simulations to investigate the mechanism of the self-cleavage reaction in the HDV ribozyme. We explored the possibility of three different reaction mechanisms with a Mg²⁺ ion bound at the catalytic site. Our simulations indicated that the self-cleavage reaction for this case is concerted with a phosphorane-like TS. The free energy barrier of the reaction along the concerted pathway is ∼13 kcal/mol, which is consistent with values extrapolated from experimental studies. In contrast to our previous MEP calculations, the inclusion of conformational sampling and entropic effects resulted in a modestly exergonic reaction and a concerted mechanism that is synchronous, with the proton transfer and oxygen–phosphorus bond breaking/forming occurring simultaneously. Furthermore, although these free energy simulations were initiated with the O2′ already deprotonated, separate QM/MM molecular dynamics trajectories beginning with a protonated O2′ provided evidence that a Mg²⁺-bound hydroxide ion could potentially activate the O2′ via deprotonation, thereby suggesting a Brønsted base as well as a Lewis acid role for the catalytic partially hydrated Mg²⁺.

We also investigated the reaction with a Na⁺ ion instead of a Mg²⁺ ion at the catalytic site. Our results indicated that the self-cleavage reaction is sequential in this case, passing through a phosphorane intermediate. The free energy barriers along this sequential path are much lower, ∼3.5 and 2 kcal/mol for the first and second steps, respectively. In contrast to our previous MEP calculations, we observed a proton transfer from the exocyclic amine (N4) of N3-protonated C75 to the nonbridging pro-R_P oxygen of the scissile phosphate to stabilize the phosphorane intermediate. This new observation is consistent with previous experimental data.

To explain the experimental observation that the rate is ∼25-fold slower with Na⁺ than with Mg²⁺, we hypothesized that the activation of the O2′ nucleophile of the U-1 nucleobase by deprotonation and orientation is more disfavored when Na⁺ is at the catalytic site than when Mg²⁺ is bound at the catalytic site. In addition to providing greater electrostatic stabilization of the negatively charged O2′, Mg²⁺ directly coordinates to the O2′ as a Lewis acid, thereby increasing its acidity and potentially facilitating an in-line attack. This hypothesis is supported by our experimental measurements of the pK_a of the O2′ nucleophile in the presence of monovalent and divalent ions ions. In particular, the pK_a of the O2′ was measured to be ∼1.3–2.7 units lower in the presence of divalent ions rather than monovalent ions. In addition, analysis of the metal ion distribution functions in the active site region from classical MD simulations indicates that Na⁺ populates the site near the O2′ much less frequently than does Mg²⁺. Overall, the combined theoretical and experimental data suggest that the initial 2′-OH deprotonation step is in rapid equilibrium, with a significantly lower equilibrium constant in the presence of monovalent ions compared with divalent ions.

Thus, the catalytic partially hydrated Mg²⁺ ion may play multiple key roles in the mechanism: assisting in the activation of the O2′ nucleophile of the U-1 nucleobase by Lewis acid and Brønsted base catalysis, acidifying the general acid C75, and stabilizing the nonbridging oxygen so as to prevent proton transfer to it. The studies herein indicate that the proton may be transferred to a nonbridging oxygen in the phosphorane intermediate in the absence of divalent ions, most likely because the above roles are altered without divalent ions present. Further experiments relating rates to specific atomic substitutions at active site residues will be performed to examine the significance of these functional roles.

Supporting Information Available

Two-dimensional free energy surfaces and mechanistic analysis for simulation sets B and C; convergence analysis for simulation sets A, B, C, and D; average values of all reaction coordinates for the final iterations of simulation sets A, B, C, and D; autoradiograms and plots of the chimeric substrate cleavage with respect to time in the presence of Na⁺ and Ca²⁺; determination of the pK_a of the 2′-OH of 3′AMP by ¹H NMR spectroscopy; charge isodensity plots of metal ions at the active site; and cumulative distribution functions of the occupancy of metal ions at the active site. This material is available free of charge via the Internet at http://pubs.acs.org.

Two WEOs are available in the HTML version of this paper. These two MPG files are movies of the QM/MM molecular dynamics trajectories illustrating that a hydroxide ion ligated to the catalytic Mg²⁺ can potentially activate the O2′ via deprotonation. One movie depicts direct deprotonation of the O2′ by the hydroxide ion, while the other depicts a Grotthuss-type mechanism in which the hydroxide ion first deprotonates another water molecule ligated to the Mg²⁺ and the resulting hydroxide ion subsequently deprotonates the O2′.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States