Reconstructing virus structures from nanometer to near-atomic resolutions with cryo-electron microscopy and tomography

Abstract

The past few decades have seen tremendous advances in single particle electron cryo-microscopy (cryo-EM). The field has matured to the point that near-atomic resolution density maps can be generated for icosahedral viruses without the need for crystallization. In parallel, substantial progress has been made in determining the structures of non-icosahedrally arranged proteins in viruses by employing either single particle cryo-EM or cryo-electron tomography (cryo-ET). Implicit in this course has been the availability of a new generation of electron cryo-microscopes and the development of the computational tools that are essential for generating these maps and models. This methodology has enabled structural biologists to analyze structures in increasing detail for virus particles that are in different morphogenetic and biochemical states. Furthermore, electron imaging of frozen, hydrated cells, in the process of being infected by viruses, has also opened up a new avenue for studying virus structures “in situ”. Here we present the common techniques used to acquire and process cryo-EM and cryo-ET data and discuss their implications for structural virology both now and in the future.

Introduction

Many viruses are composed of a highly symmetric capsid shell that serves as a container for their genome. In the past few decades, structures of icosahedrally arranged capsid shells solved by electron cryo-microscopy (cryo-EM) have progressed from low-resolution (30–50 Å) to well beyond the subnanometer resolution threshold (<10 Å). However, the imposition of icosahedral symmetry to reconstruct the capsid shell structure conceals the structures of the protein components that do not have such an arrangement (i.e. non-icosahedral). These protein components can play key roles in a virus’ life-cycle, from packaging its genome, to infecting its host cell, and even viral genome transcription. To recover these features, it is necessary to reconstruct the virus structure without any imposed symmetry. While it may seem conceptually easy to identify these special features of a virus from raw images, in reality this process is extremely difficult and relies on specialized software that is powerful enough to detect these features. Once such non-icosahedrally organized components can be resolved, their structures can also be determined at subnanometer resolutions.

The single particle approach to virus reconstruction usually assumes a high degree of structural homogeneity in the virus sample, which may not be true in some cases (e.g. for the tegument proteins of a Herpes virus or the unevenly distributed envelope spikes of HIV). To address this issue, electron cryo-tomography (cryo-ET) has found a niche for visualizing extremely heterogeneous samples. Unlike the single particle approach, cryo-ET obtains structural information by collecting a series of images of the same specimen area at different tilt-angles and reconstructing them into a 3-D map, much in the same way that modern medical X-ray computed tomography (CT) scanner provides a 3-D view of the human body. Cryo-ET followed by post-tomographic averaging of computationally extracted tomographic subvolumes can provide a 3-D density map of homogeneous molecular components in a heterogeneous virus structure. This approach can also provide snapshots of a biological process in situ. For example, it is possible to study the structural changes in viruses that accompany infection, capsid assembly, capsid maturation, and other processes in the virus life cycle. While the level of detail garnered from this approach is far lower than that possible with cryo-EM in the current state of the technology, there is still much that can be learned about virus-host cell interactions even at these low resolutions.

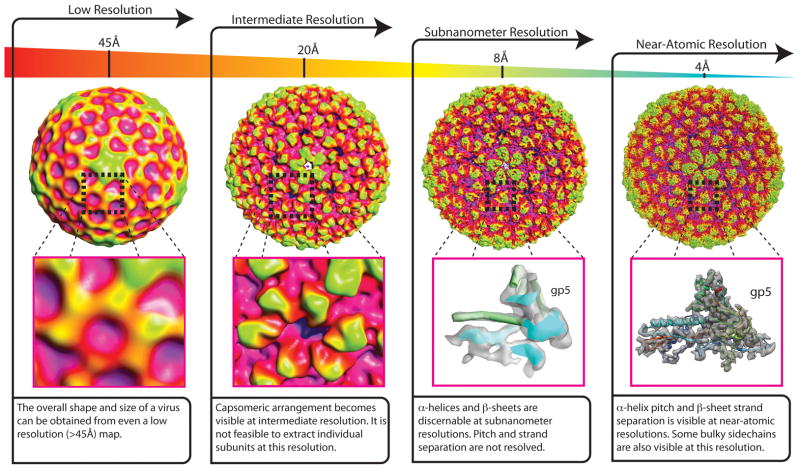
Regardless of the tools used to generate a 3-D virus reconstruction, the ultimate goal is to produce an atomic model of the protein components of the virus. The structural detail of the reconstruction is a function of the resolution of the map (Figure 1). In a low-resolution map (20–40 Å), only shape and overall arrangement of the virus capsomeres can be determined. At subnanometer resolutions (<10Å), α-helices and β-sheets become visible in the map and as the cryo-EM reconstructions push towards near-atomic resolutions, Cα backbones and some bulky side chains can be delineated in the map (beyond 4.5 Å).

Figure 1.

Features visible as a function of resolution, with Bacteriophage P22 Procapsid shown for reference [EMD-1824]. At low-resolutions (~45Å) very basic information about the shape and size of a virus are apparent in the 3-D reconstruction. As the resolution of the reconstruction increases to near 20Å, it becomes possible to identify the arrangement of capsomeres in the capsid shell. At subnanometer resolutions (<10Å), α-helices and β-sheets become visible. As the resolution of a reconstruction pushes towards near-atomic resolutions, α-helix pitch and β-sheet strand separation are apparent. Additionally it is possible to visualize bulky side-chains in the protein subunits that comprise the map.

In this chapter, we will introduce both cryo-EM and cryo-ET, with a focus on how to process the data generated by these techniques. Specifically, we will discuss single particle reconstructions of both icosahedral and non-icosahedral components of virus particle, and tomography of pleomorphic specimens containing homogeneous components (e.g. a virus envelope with protein spikes and cells infected with viruses). We will also address how these results can be validated and interpreted, including annotation and model building. Additionally, in line with such a rapidly evolving field, we will cover selected emerging techniques that will likely play a role in structural virology in years to come.

Section 1: Cryo-electron Microscopy and Tomography

Light microscopes have been used for centuries to observe objects that are too small for the human eye to resolve. In the 1930s, with the advent of the electron microscope, it became possible to visualize objects that were beyond the range of resolvability by conventional light microscopes. While the principles that dictate the behavior of these two instruments are similar, the main difference lies in the fact that electron microscopes use electrons (not light) as an illuminations source. As resolvability is inversely proportional to the wavelength of the illumination source (4000–7000Å for light, 0.025Å for 200KeV electrons), electron microscopes have the distinct advantage that they can potentially resolve features tens of thousands of times smaller than even the best light microscope.

Electron microscopy has been implemented for a variety of applications, but here we focus on the use of transmission electron microscopy (TEM) in cryo-EM for reconstructing virus particles. Cryo-EM first started in the mid 1970’s (Taylor and Glaeser, 1974; Taylor and Glaeser, 1976) (Chiu and Glaeser, 1977) and during the 1980s was refined using a rapid plunge-freezing procedure (Adrian et al., 1984; Chiu, 1986; Dubochet et al., 1988; McDowall et al., 1983). This rapid freezing procedure has the advantage that the sample is frozen quickly enough that ice crystals do not have time to form, resulting in a thin vitrified ice layer embedding the sample of interest. These ice-embedded specimens can be readily imaged in an electron microscope as long as the sample is kept at a temperature that is below the phase transition temperature of the vitreous ice (−133°C). However, while it is possible to preserve the specimen at these low temperatures, vitrified specimens are extremely sensitive to the electron beam and can tolerate only limited electron exposure. It has been shown by a number of radiation damage studies that the optimal temperature for imaging frozen, hydrated specimen is in the range −193°C (Bammes et al., 2010; Comolli and Downing, 2005; Iancu et al., 2006), and in general, the electron exposure used for single particle cryo-EM ranges from 15–25 e/Ų.

In biological cryo-EM, the images collected on the microscope can be interpreted in terms of the weak phase object approximation (WPOA) (Erickson and Klug, 1971; Unwin and Henderson, 1975). The WPOA makes two assumptions: the electrons are elastically scattered by the specimen (they suffer no energy loss) and the phase change of the scattered electrons is slight. The phase variations of the scattered electrons in the object plane, which carry the specimen’s density information, are converted into spatial intensity variations in the image plane through interference. As a result, the specimen must be very thin in order to satisfy the assumptions of the WPOA. Under the WPOA, the 2-D image can be treated as the projection of the original 3-D object’s density function, modulated by a sinusoidal contrast transfer function (CTF). In practice, in addition to this phase-contrast, there is also a small amount (~10% or less) of amplitude modification, which is expressed in a form of a co-sinusoidal function.

If the sample is not thin enough to satisfy the WPOA assumptions, it becomes very difficult to restore the original object’s CTF from the collected 2-D particle images. Even though there have been theoretical predictions, based on the WPOA, for the maximum attainable resolution as a function of specimen thickness (Ho et al., 1988; Schmid et al., 1994; Zhou and Chiu, 2003), no systematic experimental verification has yet been reported. Interestingly, the 3.6 Å resolution map of human adenovirus, reconstructed by cryo-EM, is almost identical to the structure determined by X-ray crystallography (Liu et al., 2010a), demonstrating that at 900 Å the WPOA assumptions have not been violated.

In addition to the CTF, there are numerous instrument factors that affect the image, including the spatial and temporal coherence of the electron source, instability of the lens and specimen holder, and the point spread function of the recording media. All of these factors act to dampen the high frequency information in the images and thus the likelihood that the data will be useful for a high-resolution reconstruction. This dampening can be expressed analytically as the product of a series of envelope functions which can be approximated simply as a Gaussian function E(s)=exp(−Bs²), with its width at half maximum set to the experimental B-factor (Saad et al., 2001). In the course of image reconstruction, all of the parameters inherent in the CTF and the envelope function have to be determined on a per particle basis (Jiang and Chiu, 2007).

Section 2: Single Particle Reconstruction Methods

The goal of any single particle virus reconstruction is the generation of a 3-D density map of the virus from the 2-D projection images produced by the electron microscope. The ability to start with 2-D projections of an object and then work back to a full 3-D density function is entirely based on the central section theorem (Glaeser et al., 2007). This theorem states that the Fourier transform (FT) of a 2-D projection of a 3-D object is identical to a central section of the FT of the 3-D object. The section is perpendicular to the direction of projection and passes through the origin. Thus, the original 3-D object can be recovered by filling a volume in Fourier space with many of these central sections and then computing the inverse FT of this volume.

The theory behind the single particle approach for cryo-EM is that by collecting thousands of images of a homogeneous virus particle in different orientations, the 2-D particle images can, with sufficient angular sampling, be used to reconstruct its 3-D structure. In order to obtain a 3-D reconstruction from 2-D images, views of the specimen in sufficiently different directions is required. In single particle imaging, multiple copies of a randomly oriented specimen are distributed throughout the vitreous ice layer. Thus, imaging any area will provide different views of the specimen. The assumption of homogeneity predicts that the differences that are observed in the raw images are due to projections of the particles in these different orientations. In the case of a specimen that has a preferred orientation on the grid (e.g. only top views), tilting the grid to a fixed angle during imaging (random conical tilt) can circumvent the problem by generating views from different directions. A few fixed angles can be used in order to increase the number of views from different directions. Unfortunately, as a consequence of both these approaches, by combining multiple images together on the basis of homogeneity, any heterogeneity in the data will be averaged out and not appear in the final reconstruction.

As mentioned above, the particle images are convoluted with the CTF and envelope function of the electron microscope. As such, the computational tasks required for this process are to determine the orientation of each of the individual particle images and correct any image defects prior to reconstructing the data. Since a virus particle is typically made up of both icosahedrally and non-icosahedrally arranged components, the methods of reconstruction differ depending on whether icosahedral symmetry is assumed. We will discuss the various methods used to determine both icosahedrally and non-icosahedrally arranged structures in the virus particles.

2.1 Reconstructing Icosahedral Viruses

In the 1970’s, DeRosier, Crowther, and Klug developed algorithms that we still use today for reconstructing 3-D maps of icosahedral virus particles from electron micrographs (Crowther, 1971; Crowther et al., 1970a). These methods use common lines to find the orientations of the 2-D particles and Fourier-Bessel inversion to compute the 3-D map as described below. This approach was first applied to Tomato Bushy Stunt Virus (TBSV), which was prepared using the traditional negative stain procedure. From just 6 particles, even though the particles had shrunk by 10% as a result of the negative staining procedure, the overall morphology of TBSV could still be determined from the reconstruction. In the 40 years following these first reconstructions, the resolutions of icosahedral virus reconstructions have improved to the point that the once lumpy densities representing virus capsomers can now be resolved at near-atomic resolutions, detailing the intricate structures that comprise them (Figure 1)(Chen et al., 2011). These advances were made possible by numerous improvements in cryo-specimen preservation, the coherence and stability of the electron beam, and particularly in the software used to process the data. While there are many options when it comes to choosing a software package for virus reconstruction, all of them follow a common path of particle image preparation, 2-D image orientation determination, and 3-D map synthesis. The differences in these programs lie in the algorithms they use for alignment and reconstruction.

2.1.1 Initial Data Preparation

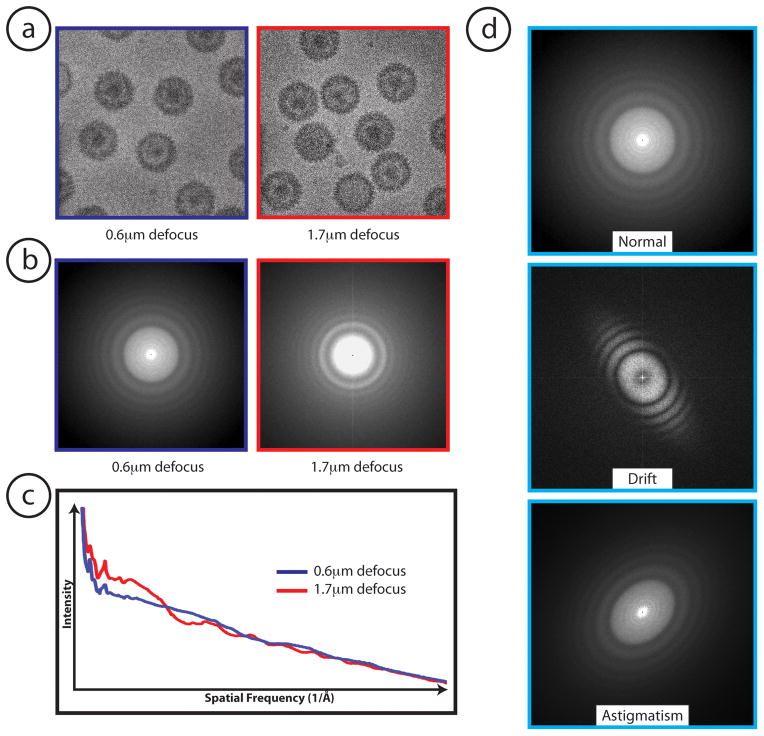
The first step in any single particle reconstruction is determining the quality of the individual micrographs or CCD frames (Figure 2a) and selecting the best ones for further processing. The quality of a micrograph can be judged visually by an experienced microscopist or through inspection of the Thon rings in the power spectrum (Fourier transform) of the micrograph figure 2b. It is a common practice to exclude images that contain aberrations as seen in figure 2d. Once a subset of good CCD frames has been selected, particles in these frames are individually selected (boxed) and stored as individual particle images. Next, the CTF parameters and the damping functions for each micrograph can be determined from the circularly averaged power spectrum (Figure 2c) of the boxed particles from the micrograph. From such a power spectrum, it is possible to estimate the signal-to-noise ratio (SNR) at any resolution (spatial frequency) of the data. Images that have a poor SNR at the desired resolution are typically removed from further consideration. While there are programs that can automatically or semi-automatically determine these CTF parameters (fitctf in EMAN, ctffind3/ctftilt, and tf ed in SPIDER), many users often choose to visually inspect the output and/or manually refine the parameters using a GUI program (ctfit in EMAN, robem in AUTO3DEM, bshow in BSOFT, and ctfmatch in SPIDER)(Heymann et al., 2008b; Ludtke et al., 1999; Mindell and Grigorieff, 2003; Shaikh et al., 2008; Yan et al., 2007).

Figure 2.

Image pre-processing and data assessment. (a) Typical electron micrographs of herpes simplex virus type I collected on a 300kV electron cryomicrosope. Higher contrast (right side of figure 2a) as a result of defocus is visible in the real space images. (b) Differences in defocus are also visualized in Fourier space, where images further from focus have tighter Thon rings. (c) Power spectrum curves from boxed herpes particles at different defocuses, which can be used to fit contrast transfer function (CTF) curves of the corresponding micrographs (d) Comparison between a normal image and images with aberrations (e.g. drift, astigmatism). For the purposes of quality control, images that contain these aberrations are typically excluded prior to processing the data for a 3-D reconstruction.

2.1.2 Building an Initial Model

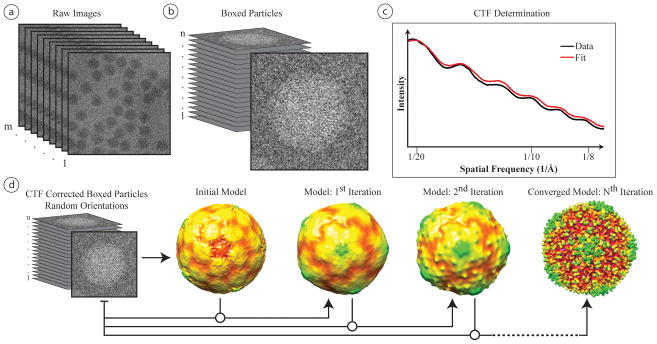
After the CTF parameters of the boxed particles have been determined, the next stage of the process is to start the iterative refinement for each of the 5 spatial parameters (orientations) of each particle image (Figure 3). The first step of this process generally requires an initial 3-D model for comparison. One way to obtain an initial model is to download an icosahedral virus density map from the electron microscopy data bank (EMDB: http://www.emdatabank.org), scale its dimensions to approximately match the current data set, and then low pass filter the map to keep only the icosahedral shape and size information. It is important when selecting a virus from the EMDB to choose a different virus than the one under study as virtually eliminates all possibility of model bias in the reconstruction. Alternatively, an initial model can be generated from the raw data by randomly assigning icosahedral orientations to a few hundred particles and reconstructing a 3-D density that has approximately the right size for the target particle (Liu et al., 2007). A more sophisticated approach involves computing the self-common lines of a handful of particle images, thereby determining their icosahedral orientations without using any reference model (the particle itself is the reference; see below) from which an adequate initial model can be built (Fuller et al., 1996). In the early days of cryo-EM, model bias was a big concern for 3-D virus reconstruction, as refining a model from an inaccurate starting model could provide erroneous results. However, with improvements in both image quality and alignment/reconstruction software, researchers can routinely achieve subnanometer resolution maps for most virus capsids using the methods above, thus minimizing the possibility of model bias. As secondary structural elements (SSEs) in the reconstruction become apparent in these subnanometer resolution reconstructions, the question of model bias is virtually inexistent because it is unlikely for a map suffering from model bias to reach such a resolution.

Figure 3.

Generalized schematic for single particle reconstruction. (a) A single cryo-EM micrograph or CCD frame can contain anywhere from just a few to hundreds of particles. (b) The first step in reconstruction is to box the individual particles from all micrographs. Depending upon the software used, it may be necessary to invert the particles contrast prior to alignment and reconstruction. (c) Once boxed, the power spectrum of the boxed particles of a micrograph can be used to determine the particles’ CTF. (d) Using the determined CTF parameters, the particles can be aligned to a model and then reconstructed to a better-resolved map. The first step in this process is to build an initial model, as discussed in text. While there are a variety of different alignment schemes used in single particle virus reconstruction, the general approach is to align the single particle images to references projected from either an initial model or a previously reconstructed model, and then iteratively refine this model until it converges.

2.1.3 Particle Orientation and Center Determination

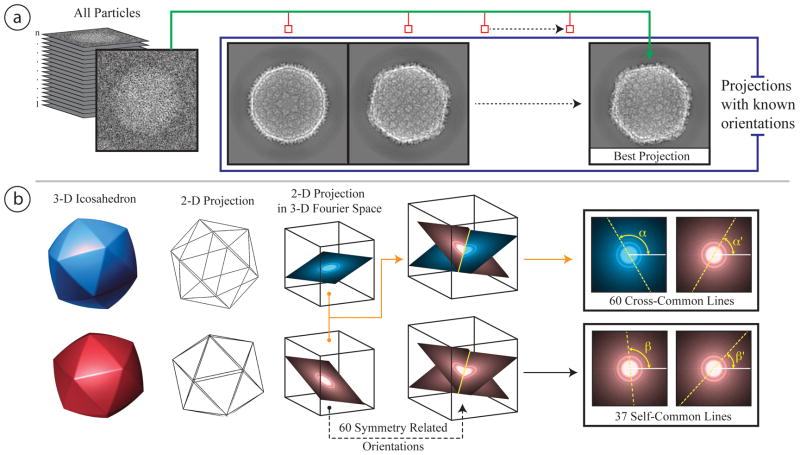
The most time consuming aspect of generating a 3-D virus map is the process of iteratively refining the orientation and center parameters (Figure 3d). This procedure involves comparing the particles images with some 2-D references projected from a 3-D model (either an initial model or a model computed from a previous iteration) to determine their centers and orientations. Accuracy in determining the center and orientation of each particle image is an important factor in the quality of the 3-D reconstruction. While there are a variety of ways to determine these parameters, the most frequently used methods are projection matching and common lines (Figure 4)(.

Figure 4.

Single particle 2D alignment methods. (a) Schematic of projection matching method. By comparing individual raw single particle images to projections made of a model at known orientations, it is possible to define classes of particles that can then be averaged together to obtain a 3-D electron density map. (b) Cross-common line method. According to central section theorem, the Fourier transforms of any two images/projections intersect along a line where the values are identical. If the two images are generated from two totally different orientations, the intersection line is called cross common line (top of figure 4b). Considering the icosahedral symmetry of a virus particle, there are 60 pairs of cross common lines between the two images. If the orientations of the two images are only related to its icosahedral symmetry, they are actually the same image. The intersection line is called self-common line. There are 37 unique pairs of self-common lines for an icosahedral particle image.

2.1.3.1 Projection Matching and Class Averages

In the projection matching method, unique 2-D projections are generated from the 3-D model for all possible views at a given angular step size. The initial model can be obtained as described in section 2.12 and can be updated using a reconstruction produced at the end of each refinement cycle during this iterative process. These projections are compared against the pre-centered raw particle images in order to determine the orientations of the raw particle data. The orientation of the particle is assumed to be the same as the orientation of the projection it matches most closely. However, before this comparison can be made, in order to fully utilize the information in a raw image, the CTF must be deconvoluted from the raw particle images (equivalently, the CTF could be applied to the projection images). As the resolution of the map is dependent on how accurate the particle orientations are, a finer angular step size is required in order to refine the model to higher resolutions. Unfortunately, as these projections are sampled in 3-D space, the number of projections increases cubically with finer step size. In the process of refining a model to higher resolution, there is a trade-off between resolution and computation time, as the requirement for precise orientation determination requires an ever-increasing number of comparisons to be made.

Projection matching can be carried out either in real or Fourier space. In order to speed up the computation, the alignment is typically performed in both Fourier and real space and involves determining a particle’s projection angles (θ, φ) and in-plane rotation angle (ω) separately and refining the pre-determined center (x and y). Different software packages implement these 3 steps in variety of ways, each using different mathematical principles.

One approach to projection matching is to find the best in-plane rotation angle (ω) for a given projection, use this angle to refine the center, and then use these two results to find the best match among all the projections. To find the in-plane rotation angle, both the raw particle image and the model projection are converted to polar coordinates. Then a 1-D FT of an annulus of the data is computed and the in-plane rotation is determined by the highest correlation between the 1-D FTs of the raw particle image and model projection. After in-plane alignment, the center of the particle is refined using the convolution theorem to compare the 2-D FTs of the image and projection. Given the in-plane rotation and center between the image and the projection, a correlation score can be computed. Applying these steps to a single raw particle image and each of the model projections will result in a set of scores. The particle orientation is assigned to the in-plane rotation, center, and projection with the best score (Ludtke et al., 1999).

In order to minimize the error propagation implicit in the process of sequential parameter search, another approach is to perform the local center refinement and global in-plane rotation search simultaneously. As a result, this method calculates the rotational correlation between an image and a projection for each of the possible center positions in the neighborhood of the image’s predetermined center (Joyeux and Penczek, 2002). This simultaneous search is time-consuming because of the large number of possible center positions in this neighborhood. To speed up computation, FRM2D converts the operations of rotation and two-dimensional translation into rotating both image and projection and translating the image center in one-dimension (Cong et al., 2003). Thus, it calculates two rotational correlations for each possible center in one dimension, reducing the total number of rotational correlations. Furthermore, even though the rotations in FRM2D are decomposed into Fourier-Bessel coefficients, which effectively reduce interpolation errors, this decomposition takes CPU time to complete. Overall, FRM2D increases the speed of orientation determination moderately, while avoiding interpolation and propagation errors.

The polar Fourier transform (PFT) is another approach that uses a different sequence of steps for determining the orientation parameters (Baker and Cheng, 1996). First, the pre-centered particle image is converted to polar coordinates (Γ, r) and a 1-D FT for each annulus of data is computed. The values in an annulus have a fixed radius r in the Cartesian image but different Γ angles and the 1-D FTs of this data are rotationally invariant (invariant in the in-plane rotation ω in the Cartesian image). As a result, the best matching projection can be determined first, and this provides the 2 Euler angles (θ, φ) associated with the projection. Next the in-plane rotation ω can be determined by rotational correlation between the best matching projection and the raw particle image. Given the 3 Euler angles, cross correlation can be used to refine the image center. This method is very fast, but may suffer from interpolation and propagation errors because of the 3 separate searches. Furthermore, as this method only uses amplitude information from the 1-D FTs (phase information is ignored), its use for high-resolution reconstructions may be limited.

Once the centers and orientations of the individual particles have been determined, it is possible to generate 2-D class-averages using a variety of software packages (e.g. EMAN, SPIDER, Frealign, Imagic, etc.). These class-averages are an average of all particles that matched the same projection during the process of projection matching and have the advantage of increasing the SNR above that of a single image. It is important to note that prior to averaging, the CTF must be deconvoluted in the individual single particle images. Otherwise, the average of images with different CTF parameters would result in the loss of signal at specific spatial frequencies. These class averages can then be used for reconstructing a 3-D volume (Section 2.1.4).

2.1.3.2 Common Lines

Another approach to particle orientation determination relies on the central section theorem, which assumes that planes in Fourier space intersect at the origin. In the case of cryo-EM, the individual images recorded in the microscope are projections of randomly oriented objects, and the Fourier transform of these individual particle images exist as 2-D planes in a 3-D Fourier volume. For any two planes in Fourier space, the line at which the planes intersect is known as a common line (Figure 4b). For icosahedral viruses, each of the 60 equivalent icosahedral orientations defines a plane in Fourier space that is related to each other through this symmetry (Figure 4b). The line at which any two of these planes intersect is known as a self-common line. For any icosahedral particle there are 37 self common lines, including 12 from the five-fold symmetries, 10 from the three-folds, and 15 from the two-folds. Therefore, there is a great deal of information inherent in a single icosahedral particle with which the Fourier amplitudes and phases of two particles can be matched to each other (provided the particle’s center is correctly identified).

The self common line method works best for icosahedral viruses as it relies on the symmetry inherent in the particle. Additionally, as a result of the icosahedral symmetry in these particles, it is possible to determine the particle’s center either from a center of mass calculation or from the cross correlation of an image and the same image rotated by 180°. To determine the individual particles’ orientations, an exhaustive search is performed for all possible orientations. The accuracy of an orientation is judged by the phase residual, which is a score that measures the discrepancy of the self common lines for the given orientation. The orientation with the smallest phase residual is assumed to be the correct one. Subsequently, the predetermined center of the particle can be further refined based on this orientation (Fuller et al., 1996). Since the self common lines method uses the individual raw image themselves as reference images, it does not require an initial model, thus freeing it of model bias. Unfortunately, the accuracy of the self common lines method for determining particle centers and orientations, is limited by the small number of self common lines (37 of them) and error propagation from one step to the next, which precludes its use for studies with excessively noisy images.

In the same vein as the self common line approach is cross common lines (Figure 4b). Unlike the self common line method, which uses the particle itself as a reference, cross common lines occur between a particle and another particle. The references in the cross common line method can be either projections from a 3-D model/map or other single particle images whose orientations are known. Cross common lines can use multiple references instead of only one reference (the image itself, as in self common lines), which makes it possible to use all of the information in the 2-D Fourier transform. To determine a particle’s orientation, the cross common line method also uses the phase residuals of the cross common lines to judge if an orientation is correct. As more references are included in the comparison, the phase residual will be more sensitive to variation in the orientation when searching near the true orientation. While this approach allows for the orientation to be determined very accurately, it also increases the possibility of inaccurately determining the true orientation (i.e. very small radius of convergence) when a large angular step size is used in an exhaustive search. This small radius of convergence requires a very exhaustive and simultaneous search of the center and orientation parameters, a process that was once nearly impossible to achieve (Fuller et al., 1996). Fortunately, as more computational resources have become available, the cross common line method can now be exploited for accurate single particle orientation determination.

The cross common lines method was eventually implemented in the refinement loop of SPIDER (Shaikh et al., 2008). However it requires an accurate determination of the particle’s center in the image, so that the search can be mostly limited to orientation space (θ, φ, ω). The multi-path simulated annealing (MPSA) optimization algorithm was later developed to use cross common lines to globally determine both center and orientation simultaneously by minimizing the phase residual of the cross common lines between the raw image and reference projections (Liu et al., 2007). The core of the MPSA algorithm relies on a Monte Carlo optimization scheme, which is formulated to optimally search a very small portion of the 5-D (2-D for center, 3-D for orientation) space, saving a tremendous amount of CPU time as compared with the exhaustive search methods. However, as a result of the Monte Carlo approach, there is no guarantee that the search result represents the true global minimum (i.e. the correct center and orientation). Nevertheless, the speed of the MPSA algorithm enables it to perform the same search multiple times and the consistency of these results/solutions (reaching the same orientation) can confirm the determined orientation as a global minimum.

Since both the center and orientation parameters are determined simultaneously in the common line approach, there is no error propagation as compared with the other sequential methods. This characteristic of the cross common line approach permits the accuracy of the orientation search to extend far beyond the resolution range used in the orientation search. However, as most of cross common lines do not overlap with the 2-D Fourier space grid points, the method suffers from interpolation errors in the high resolution data. While it may be possible to overcome this interpolation errors by oversampling the 2-D Fourier transform of the images, this process will inevitably have larger memory demands.

2.1.4 Reconstructing a 3-D Volume

The only requirement for reconstructing a 3-D volume is a set of single particle images (or class averages) and their corresponding orientations. The resolution of the 3-D map will depend on the total number of particles, accuracy of the orientations, the quality of the data, and many other factors (e.g. weighting scheme, interpolation method, CTF correction, etc). Discussed below are the methods by which these maps are synthesized, either in Fourier or real space.

2.1.4.1 Fourier Space Reconstructions

The most direct way to build a 3-D model from 2-D projections is through an inverse Fourier transform. Here, as in common lines, the central section theorem is used, but this time as a straightforward application for computing a particle’s 3-D volume from a set of 2-D projections. The direct Fourier inversion technique takes the FTs of the particle images, and inserts these 2-D FTs into an empty 3-D matrix, according to the previously determined particle centers and orientations. Once all the 2-D FTs have been inserted into this volume, it is possible to generate a real space 3-D map by computing the inverse FT of this 3-D Fourier volume. In this method, CTF correction must be applied to the individual particles before inserting the 2-D FTs into the 3-D Fourier volume (class averages must already have corrected CTFs as well). As with many of the particle alignment protocols, errors in interpolation can limit the pursuit of high-resolution. Since this procedure requires a 2-D section to be placed in a 3-D volume, interpolation is inevitable because the grid points (voxels) do not overlap. While 3-D oversampling can potentially limit the effect of interpolation errors, the massive memory and computational resources required for large virus particles often constrains the use of this approach for high-resolution reconstructions.

An alternative method, Fourier-Bessel synthesis, can partially address the memory and interpolation issues that arise from the direct Fourier inversion approach. This method uses cylindrical coordinates ρ(r, φ, z) in real space or F(R, Φ, Z) in Fourier space (Crowther, 1971; Crowther et al., 1970a; Fuller et al., 1996). Each of the inserted FT of the particle images F(R, Φ, Z), at a given cylindrical annulus (R and Z are constant in an annulus), can be expanded into a Φ-related Fourier-Bessel series, which overcomes the data interpolation problem in the Φ direction. The expansion coefficients can be determined by least square fitting, so long as the total number of particle images is greater than the number of the expansion coefficients, as determined by targeted reconstruction resolution. Once the coefficients are determined, the real space density ρ(r, φ, z) can be synthesized in two sequential steps of 1-D integration/summation that requires only a very small amount of memory. Even though Fourier-Bessel synthesis is still susceptible to interpolation errors, the memory requirements of this approach are significantly lower than for direct Fourier inversion.

A third method for reconstruction is spherical harmonics, which is similar to the Fourier-Bessel method but uses spherical coordinates ρ(r, θ, φ) and/or F(R, Θ, Φ) instead of cylindrical coordinates (Liu et al., 2008a). The advantage of spherical coordinates is that the method is less susceptible to interpolation errors. However this comes at the cost of significantly increased CPU time for the reconstruction. This method expands each of the inserted 2-D Fourier transforms into a series of spherical harmonic coefficients at a given Fourier shell radius (R is held constant). The two dimensional expansion coefficients can also be obtained through least square fitting, and then the density map ρ(r, θ, φ) can be synthesized from these coefficients. Just as with Fourier-Bessel synthesis, the Cartesian coordinates for the real space 3-D map are interpolated from the spherical coordinates of the spherical harmonic method.

2.1.4.2 Real Space Reconstruction (Back Projection)

Conceptually, the images collected on the microscope can be visualized as a flattening process by which a 3-D object becomes a 2-D image. If this process were directly reversible, then the 2-D image could be stretched back into 3-D space by recovering the height information, which was lost due to this flattening, from any non-parallel projection of a similar object. While the process described above appears to be relatively straightforward, non-uniform sampling caused by the conversion from polar to Cartesian coordinates when the 2-D images are “stretched” back into 3-D space overweights the low-resolution components, resulting in a blurred 3-D map. This overweighting can be corrected using FTs to apply a windowed ramp filter to the 2-D images prior to back projecting. As this filtering process requires both forward and backward FTs, back projection requires one extra Fourier inversion for each image compared to the direct Fourier inversion method described above, which quickly increases computation times. However, the back projection method requires half the memory needed by direct Fourier inversion, making it desirable for problems that are intractable due to memory constraints. Furthermore, and most importantly, simple linear interpolation is often sufficient for the back projection approach, while more complicated approaches are needed for interpolating high-resolution data in Fourier space reconstruction methods above (Section 2.1.4.1) (Stark et al., 1981).

2.1.5 Processing and Refining a 3-D Map

Once a reconstruction cycle is complete, the 3-D map may need additional processing before the next iteration of refinement. In some cases, to enhance the visibility of structural features, it may be necessary to boost the high-resolution components and/or filter out noise at specific spatial frequencies of the map. The real space noise outside the capsid and any density within the capsid (if not of interest) can be removed by masking the 3-D volume. As masking can cause edge artifacts, a soft mask is preferred over a sharp mask. In addition, normalizing the density map can help reduce any artifacts that may result from masking the 3-D volume. These steps are important for minimizing any noise in the reference projections used in the subsequent refinement iterations. This iterative refinement process stops when the 3-D map no longer shows any improvement.

2.1.6 Post-Processing of 3-D Volumes

2.1.6.1 Map Sharpening

Upon inspection of a refined 3-D map, it may appear as if certain features are not adequately resolved in the volume. While this can have many potential causes (e.g. preferred orientations in the data, uneven weighting, interpolation errors), it is possible to recover much of the missing information by “sharpening” the map. The process of map sharpening scales specific spatial frequencies (resolutions) above others. One such sharpening procedure is accomplished by multiplying by an appropriate B-factor curve (i.e. exp(Bs²)) in Fourier space to preferentially scale-up the high resolution components. As there is no precise criterion for choosing the proper B-factor, a more objective way to sharpen the map is to scale the power spectrum of the map to match the structure factor of the virus (Schmid et al., 1999).

2.1.6.2 Non-Crystallographic Symmetry (NCS) Averaging

The icosahedral symmetry in many virus capsids means there are 60 copies of the asymmetric unit in each particle. Thus, not only can this symmetry be used to determine orientation, but also to increase the SNR of the data thereby improving the resolution of the reconstruction. Additionally, each of the 60 icosahedral asymmetric units may be comprised of several protein subunits (typically given by the virus T-number). Provided that these subunits are found in similar conformations it is possible to average them together to further increase the SNR of the data, thus improving the map’s resolution. As this local averaging does not follow the overall icosahedral symmetry of the capsid, it cannot be performed during reconstruction and must be done afterwards. The process of extracting and averaging similar subunits is called “non-crystallographic symmetry (NCS) averaging”, which is borrowed from a term in X-ray crystallography. NCS averaging was first used in cryo-EM to improve a subnanometer resolution reconstruction of herpes simplex virus (Zhou et al., 2000) and has since been used to enhance several near atomic resolution reconstructions (Settembre et al., 2011; Zhang et al., 2010b) (See Table 1).

Table 1.

Selected Examples of Near-Atomic Resolution Structures

Virus	EMD/PDB	Particles	Reported Resolution (A)	Program (algorithm)	Symmetry
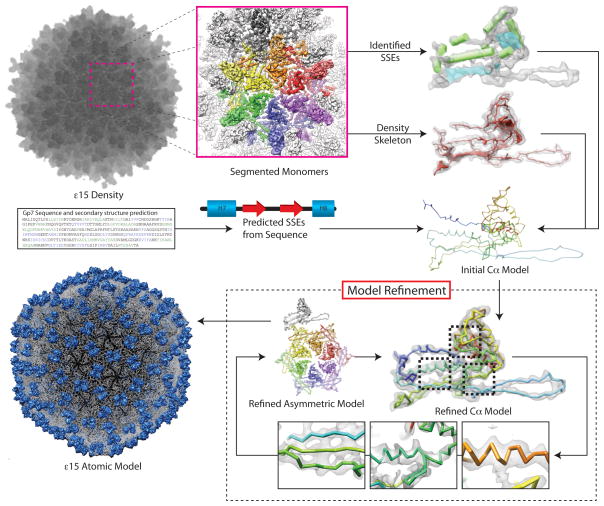
Epislon-15 phage (Jiang et al., 2008)	5003/3C5B	36259	4.5 (FSC 0.5)	EMAN (projection matching, direct Fourier inversion)	Icosahedral
P-SSP7 phage (Liu et al., 2010b)	1713/2XD8	~36,000	4.6 (FSC 0.5)	MPSA (cross common line with optimization), EMAN (direct Fourier inversion)	Icosahedral
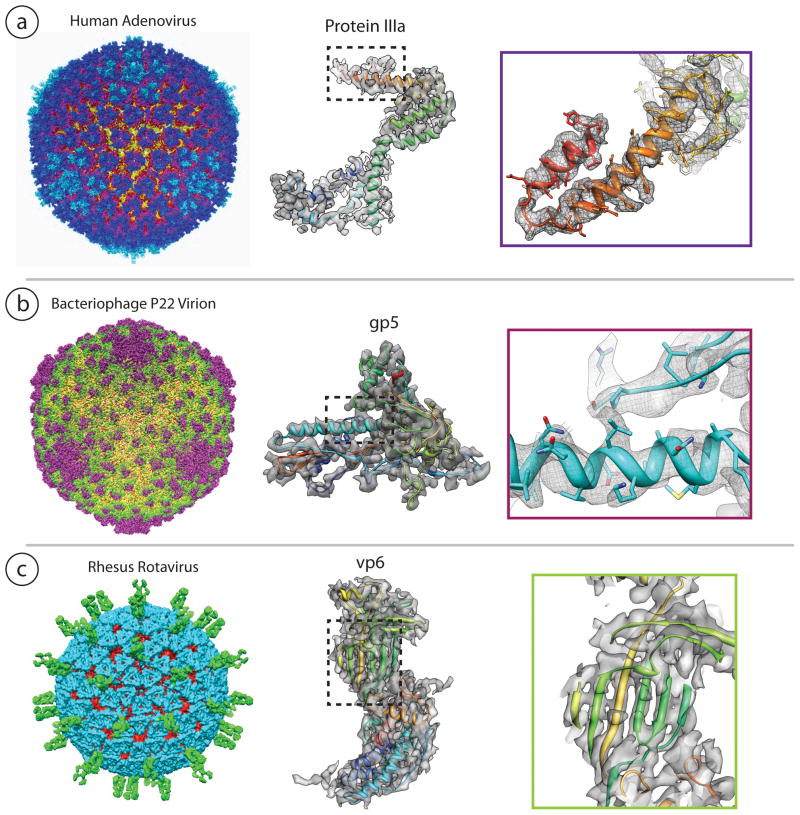
Human Adenovirus (Liu et al., 2010a)	5172/3IYN	31815	3.6 (FSC 0.5)	IMIRS (common lines, astigmatism correction, spherical harmonics reconstruction, map sharpening)	Icosahedral
Bovine Papilloma Virus (Wolf et al., 2010)	5155/3IYJ, 5156 (with NCS)	3977	4.9 (FSC 0.5), 4.2 (NCS, FSC 0.5)	Frealign (projection matching, per particle defocus refinement, interpolation in Fourier space, map sharpening) multiple programs for NCS	Icosahedral NCS
Aquareovirus infectious subvirion particle (VP3, VP6) (Zhang et al., 2010)	5160/3IYL	18646	3.3 (FSC 0.143)	CTFFIND, IMIRS, Frealign, map sharpening	Icosahedral NCS
P22 phage procapsid (Chen et al., 2011)	1824/2XYY	23400	3.8 (FSC 0.5)	EMAN	Icosahedral
P22 phage (Chen et al., 2011)	1826/2XYZ	18300	4 (FSC 0.5)	EMAN	Icosahedral
Cytoplasmic polyhedrosis virus (Cheng et al., 2011)	5233/3IZ3	29000	3.9 (FSC 0.143)	EMAN, IMIRS, ISAF	Icosahedral
T7 phage (Ionel et al., 2011)	1810/2XVR	5100	10.8 (FSC 0.5), 9 (FSC 0.143)	Bsoft, Spider, XMIPP	Icosahedral
Rotavirus (Settembre et al., 2011)	5199/3IYU (scaffold, VP6), 3N09 (VP7, VP4)	4187	6.5 (FSC 0.5), 4.3 (FSC 0.143), 3.8 (NCS, FSC 0.143)	Frealign (projection matching, per particle defocus refinement)	Icosahedral NCS

2.1.6.3 Visualization and Segmentation

Once a finalized 3-D volume has been obtained, using any of the methods described above (Section 2.1.4), the data can be visualized with a variety of programs, including Chimera (Pettersen et al., 2004), Amira and Avizo. These programs allow the user to manipulate the volume in 3-D and some even support the use of stereographic presentation so that the 3-D maps can be visualized in a “true 3-D” environment.

One of the most important steps in interpreting and annotating a map is segmentation, a process that enhances visualization of the density maps. While it is possible in some cases to directly segment the data based on the discontinuities observed between densities, for the majority of cases, segmentation is performed based on X-ray data of the molecule or homologous structures, biochemical experiments, biological information, or other supporting experimental evidence. Amira and Avizo are two commercially available programs that are designed for manual segmentation. Alternatively, densities can be segmented manually using “color zone” tools, or semi-automatically using Segger (Pintilie et al., 2010) as part of the Chimera suite.

For high-resolution maps (<5Å), further interpretation and validation are often needed but have the distinct advantage of being able to produce accurate Cα backbone traces of the proteins in the map. As the resolution of a reconstruction approaches atomic resolution, it becomes possible to visualize and model the complex side-chain interactions in these proteins (Section 4).

2.1.7 Selected Examples of Near Atomic Resolution Structures

Table 1 is a selected compilation of the near-atomic resolution virus structures solved by single particle cryo-EM. The structures of these viruses were solved by a variety of computational procedures and software packages. While crystal structures exist for some of the structures, in other cases they have yet to be solved. Where crystal structures are available they demonstrate remarkable structural similarities both in their backbone traces and in some of their side chain densities. In the case of adenovirus, the cryo-EM map resolves more of the connective density representing the cementing capsid proteins than is visible in the corresponding crystal map. In the case of P22, the detailed structural changes between the procapsid, which contains scaffolding proteins, and the mature phage, which contains the viral DNA, clearly illustrates the structural mechanism of phage maturation. These are just a few examples of the knowledge gained about the structural features and assembly of virus capsids, while only a few such structures have been solved to date, more are expected to come in the future and likely at higher resolutions.

2.2. Reconstructing Particles Without Imposing Symmetry

In the traditional application of cryo-EM for studying virus particles, any features/proteins that do not satisfy the condition of being icosahedrally arranged will be lost. However, there are a variety of situations where the assumption of icosahedral symmetry prevents the visualization of certain virus features such as the genome packaging complex of some dsDNA viruses. Furthermore, these non-icosahedrally ordered features may have their own symmetry which is obscured by the symmetry mismatch with the icosahedral capsid shell. Symmetry mismatch in complex macromolecular assemblies has been recognized by structural biologists for over 30 years in structural biology (Hendrix, 1978), and by biochemists for even longer. This problem arises when two objects that have different symmetries (e.g. 5-fold and 12-fold) are part of the same macromolecular complex. Essentially, the symmetry averaging for either of the objects must be decoupled because assigning one symmetry to the whole complex would obscure the subunit arrangement of the other component. The problems in directly visualizing such symmetry mismatches have recently been solved thanks to the tremendous advancements in both data acquisition and the software used to process the data. Unfortunately, in order to achieve a resolution equivalent to an icosahedral map, a symmetry-free map requires at least 60 times as much data.

In general, to correctly determine a particle’s symmertry-free orientation, the non-icosahedrally arranged components need to have enough signal to overcome both the noise in cryo-EM images, as well as the signal from the other components in the particle (e.g. capsid proteins, nucleic acids). Ideally, if these components have a large mass, their signal is sufficient for them to be identified in the particle images. When this is not the case, the use of defocus adjustment to increase contrast in the micrographs can enhance the ability of identifing these features in the projection images. Unfortunately, as discussed above, one potential downside of defocus-based contrast enhancement is the loss of high-resolution information. Although solutions may be forthcoming from a variety of alternative electron optics methodologies (e.g. a Zernike phase plate), their application in low-contrast cryo-EM situations is still in its infancy. Such methodologies are discussed in Section 5.

When available, the crystal structures of viral proteins are often docked into the cryo-EM density map to paint a picture of how these complex macromolecular machines function. In the case of the T4 phage, the capsid and tail were reconstructed separately by cryo-EM and then the crystal structures of their component proteins were docked into the density maps to gain an understanding of how the individual parts contribute to the function of this complex molecular machine (Leiman et al., 2010). However, new developments in data processing have now made it possible to resolve the structure of complex viruses as a single entity without imposing any symmetry, removing the need to separate the components prior to cryo-EM imaging. The following section describes how these advancements are implemented for symmetry-free subnanometer resolution reconstructions and how they have the potential to be extended to even higher resolutions.

2.2.2 Initial Data Preparation

The same data that is used for high-resolution icosahedral reconstructions can also be used for a symmetry-free reconstruction. For viruses that have extended asymmetric protrusions, such as a bacteriophage tail, the particle images may need to be adjusted prior to processing. Specifically, the box with which the particle image was initially selected may need to be enlarged to accommodate the tail structure. Furthermore, as a result of this larger box, it may be necessary to downsample the images if memory and computation power are limited.

For any data collection scheme designed to see asymmetric features, to enhance contrast, the individual images are typically acquired in a range of 3–5 μm defocus. However, there is no specific defocus value that is optimum for every specimen, so the defocus value is often determined empirically. It is good practice to collect a series of images of a new sample across a broad range of defocus values and choose a defocus value that accentuates the asymmetric feature (as judged by visual inspection). However, discerning the asymmetric components in raw images is not always necessary because some symmetry-free reconstruction programs can identify the true asymmetric orientation even when the feature is not readily apparent in the raw images (Liu et al., 2010c). Thus, the defocus target for acquiring the images should also depend on the desired resolution because of the need for a tradeoff between visualizing the feature in the raw micrographs and retaining the high-resolution information which is lost at higher defocus. A subnanometer resolution, symmetry-free reconstruction will likely demand closer to focus imaging than if the target is 25Å.

2.2.3 Building an Initial Model

Just as for an icosahedral reconstruction, a symmetry-free reconstruction requires an initial model for starting the orientation search. This initial model must simulate the nonicosahedral components and comes with the same caveat as before of not biasing the final 3-D reconstruction. There are three common ways to create an initial model for symmetry-free virus reconstructions. The first involves creating a chimeric model comprised of the icosahedral particle reconstruction combined with a model of the nonicosahedral feature produced by low pass filtering a known structure for the isolated component itself or an equivalent (Agirrezabala et al., 2005). The second approach uses a simple geometric shape that mimics the approximate shape of the non-icosahedral feature (e.g. a cylinder for the tail of P22 and Epsilon15 (Chang et al., 2006; Jiang et al., 2006)). The third, and most direct, method uses an icosahedral reconstruction map to find the general shape of the non-icosahedrally arranged components (Liu et al., 2010c). By lowering the isosurface threshold (generally 10–20 fold), the map’s non-icosahedral features become faintly visible at each of their icosahedrally related positions (usually the vertices) and can be extracted as an initial model (Figure 6). The lower display threshold is needed because imposing icosahedral symmetry to the non-icosahedrally symmetric features reduces their relative contribution to the overall density of the map.

Figure 6.

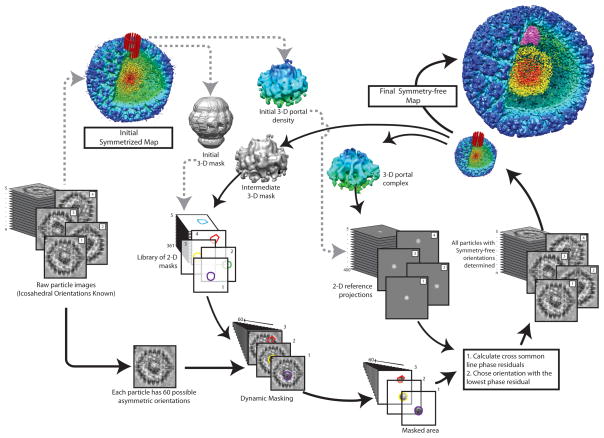
A flowchart for symmetry-free reconstruction using the dynamic masking technique. Starting with a collection of single particle images (whose icosahedral orientations are known) and the icosahedrally reconstructed map, a 3-D initial model and mask of the interested asymmetric features can be extracted and generated (red cylindrical area). The 3-D mask is used to generate a series of 2-D masks for the raw particle data. After these 2-D masks are dynamically applied to a particle image to extract the interested asymmetric features, the resulting masked images are aligned to reference projections of the 3-D model. This process is iterated, each time generating a new 3-D mask and model from the intermediate 3-D symmetry free reconstruction, until the asymmetric map converges.

2.2.4 Determining the Asymmetric Orientation

Currently available software can determine the asymmetric orientation of a particle in two ways. The first method, which does not make any assumptions about the symmetry of the particle, finds the orientation by exhaustively searching every possible orientation. While this approach is conceptually easy to understand, the exhaustive approach to orientation determination necessitates a large, homogeneous search space that is very time-consuming to process because of the non-icosahedral constraints. The second method takes advantage of prior knowledge about the icosahedral organization present in many viruses, and splits the process of asymmetric orientation determination into two steps. The first step determines the particle’s icosahedral orientation, at which point the asymmetric orientation search is limited to the 60 equivalent icosahedral orientations. The problem of symmetry-free alignment then becomes a process of determining which one of the 60 possible choices is the “true” asymmetric orientation of the particle. Care must be exercised with this second approach for two reasons; it assumes that the icosahedral orientation is correctly assigned, and the second step of this alignment procedure does not correct for errors in the first step.

To accurately determine the asymmetric orientation of a single particle image, there needs to be enough contrast in the image to distinguish the non-icosahedral component from the other densities/features in the image. If the component contributes a significant part of the molecular mass of the whole particle (e.g. the tail in bacteriophage Epsilon15 (Figure 7)) it is relatively easy to find these orientations. In the event that this does not hold true, it is necessary to increase the signal of the non-icosahedrally arranged component relative to the other components. One way to enhance this contrast is to subtract the known icosahedrally symmetric components (i.e. the capsid shell) from the image. This is accomplished by projecting the 3-D icosahedral map in the same orientation as a given raw particle image. This projection, which, as a result of icosahedral averaging does not display the non-icsosahedrally symmetric feature, can be subtracted from the raw particle image. Conceptually, the density that remains should correspond to the non-icosahedrally symmetric component alone. In practice, there are many factors that can reduce the effectiveness of this procedure, notably inaccuracy in the icosahedral orientation for projecting the image to be subtracted and improper scaling of its density to match that of the raw particle image.

Figure 7.

Selected symmetry free cryo-EM density maps. (a) Bacteriophage T7 [EMD-1163]. This is the first symmetry-free reconstruction of a whole virus. An oblique view (left) and coronal slice (right) are shown. (b) Bacteriophage epsilon-15 [EMD-1175]. This is the first reconstruction to clearly show the genome organization and DNA packaging/injection apparatus in the context of the virion. (c) Cyanophage P-SSP7 [EMD-1715]. This symmetry-free reconstruction is the first to show how the symmetry-mismatch between 5-fold capsid and 12-fold portal structure is accommodated. (d) Human herpes virus type I B-capsid [EMD-5259]. This symmetry-free reconstruction represents the first such reconstruction for a non-tailed virus particle. The green circle shows the 5-fold vertex where the portal is located (left). The green portal density can be easily visualized in the cutaway map.

Another way to enhance the contrast is by using a dynamic 2-D mask to remove portions of the raw image that do not contain the non-icosahedrally symmetric component (Liu et al., 2010b) (Figure 6). This 2-D mask is generated by projecting a 3-D mask encompassing a volume that is believed to contain the non-icosahedrally symmetric feature, at each of the previously determined icosahedral positions and orientations for a given single particle image. Depending upon the orientation with which the 3-D mask is projected, the resulting 2-D mask will take on a variety of shapes, hence a dynamic mask. To facilitate this process, a library of all possible 2-D masks is generated before beginning the orientation search process. Typically these masks are projected with an angular spacing of 5–10°. While it is possible to use a smaller angular step size, which would remove more of the undesirable signal, this would require more masks and would take longer to process. In contrast to the subtraction technique, this dynamic masking technique does not remove any of the undesirable signal (i.e. capsid proteins, nucleic acids) in the projection that overlaps with the non-icosahedrally symmetric components in the 2-D projection image.

The choice of which of the above approaches to use depends upon the scientific question at hand, and whether the 2-D images would benefit from contrast enhancement. Once the 2-D raw particle images have been modified, the process of alignment and refinement can proceed. Just as for an icosahedral orientation search, alignment for symmetry-free reconstructions can either be in real space by projection matching or in Fourier space by common lines but without imposing any icosahedral symmetry in the alignment procedure.

2.2.5 Reconstructing Asymmetric Density Maps

Once the asymmetric particle orientations have been determined, the reconstruction can be performed either in real space (back projection) or in Fourier space (direct Fourier inversion, Fourier-Bessel method, etc.). The reconstruction procedure is basically the same as for icosahedral reconstruction (see Section 2.1), but since no symmetry is imposed in the process, it is more sensitive to preferred orientations. Since only one of the 60 symmetry-related planes is inserted into the 3-D Fourier volume during reconstruction, it is possible to undersample this volume, resulting in artifacts in the 3-D map. As before, these symmetry-free reconstructions are refined until no further improvement is seen in the 3-D volume. Similarly, masking, normalizing, and the other processing steps described for icosahedral reconstructions can be applied to these symmetry-free 3-D maps.

2.2.6 Selected Examples of Symmetry-free Structures

Spherical viruses are composed of both icosahedrally and non-icosahedrally arranged proteins and nucleic acids. In the past few years, developments in image processing software have enabled cryo-EM to solve the structures of these non-icosahedral components (Table 2). These advances have opened up a new area of structural virology where it is possible to understand the complex structural organization of all the viral components regardless of their underlying symmetry. Furthermore, the resolutions of these studies are gradually moving towards the subnanometer mark, where it becomes possible to detect alpha helices and beta sheets. An example of the value of these maps is the light they have cast on the longstanding puzzle as to how the differing symmetries of the DNA packaging machinery and the capsid shell accommodate each other at a single unique vertex (Chen et al., 2011; Jiang et al., 2006; Lander et al., 2006; Liu et al., 2010c; Murata et al., 2010; Parent et al., 2010). Furthermore, the maps of the full and empty capsids of P-SSP7 phages have revealed the structural changes that occur in the nozzle proteins to trigger genome release upon infecting its host cell (Liu et al., 2010c).

Table 2.

Selected Examples of Symmetry-free Structures

Virus	EMD/PDB	Particles	Reported Resolution (Å)	Program (algorithm)
T7 phage procapsid (Agirrezabala et al., 2005)	1161	4460	24 (FSC 0.5)	SPIDER
T7 phage (Agirrezabala et al., 2005)	1163	4785	25 (FSC 0.5)	SPIDER
Epsilon-15 phage (Jiang et al., 2006)	1175	15000	20 (FSC 0.5)	EMAN, SAVR
P22 phage (Chang et al., 2006)	1222	16000	20 (FSC 0.5)	EMAN
P22 phage (Chang et al., 2006)	1220	20267	17 (FSC 0.5)	EMAN, SPIDER
K1E phage (Leiman et al., 2007)	1333	6105	16.6 (FSC 0.4)	EMAN, SPIDER
Phi29 phage (Tang et al., 2008)	1420	12682	7.8 (FSC 0.5)	EMAN, Frealign, AUTO3DEM
P-SSP7 phage (Liu et al., 2010b)	1715	15000	9.2 (FSC 0.5)	MPSA, EMAN
P22 phage procapsid (Chen et al., 2011)	1827	43850	8.7 (FSC 0.5)	MPSA, EMAN
HSV-1 B-capsid (Rochat et al., 2011)	5259	2308	25 (FSC 0.5)	MPSA, EMAN

Section 3: Tomographic Reconstruction Methods

From both scientific and biomedical standpoints it is particularly important to understand the structure of viruses while they are interacting with their host cells. Unfortunately, the two methods described in Section 2 are of limited use for determining the structure of these viruses in their most native state, as they assume that the particles under study are structurally homogeneous. Therefore, any differences in the 2-D images are assumed to be due to different particle orientations. However, the structures of virus particles within cells are frequently heterogeneous, and so combining 2-D images of different particles into a 3-D volume is not necessarily appropriate. In addition, the environment occupied by every virus particle in a cell is unique, so there are no exact copies in different orientations. Additional problems arise because the single particle based approaches do not work well in the context of the overlapping densities of viruses, organelles, tissues, and other biological materials. Because of these considerations, cryo-ET is the method of choice for imaging infected cells.

3.1 Specimen and Data Considerations

While it is often assumed, in reality no virus is completely icosahedral and many have no icosahedral components at all. For example, influenza (Orthomyxoviridae) surrounds its genome with a flexible helical capsid that is enclosed by a pleomorphic envelope, and human immuno-deficiency virus (HIV) has an envelope that encircles its non-icosahedral nucleocapsid. As highlighted in Section 2.2, even icosahedral viruses have nonsymmetrical components. For example, herpesviruses have an icosahedral capsid inside irregular tegument and envelope layers. In all these cases, the shapes and sizes of the membranes, their relationship to the capsids, and the distribution of the glycoproteins will vary from particle to particle. Similarly, viruses infecting their host cells will exhibit non-uniform properties as each virus is in a different step of infection. Fortunately, heterogeneity, polymorphism, flexibility, and labile structures pose less of a problem for cryo-ET.

Cryo-ET offers the opportunity to study whole cell preparations. For this reason, specimen thickness becomes an important consideration as specimens can become impenetrable to the electron beam if they are too thick (e.g. over 1μm). For very thick specimens, one solution is cryo-sectioning (Al-Amoudi et al., 2004). In this procedure, the sample of interest is cooled very rapidly to liquid nitrogen temperature at very high pressures and usually in the presence of a cryoprotectant. Freezing at high-pressure slows the formation of ice crystals and allows the formation of vitreous ice, which preserves structural features in the specimen. Ultra-thin cryosections are cut from the block of frozen material and transferred to a specimen grid for imaging in the EM. While this approach may seem ideal, the sections invariably contain many artifacts that are caused by the sectioning process and can complicate data interpretation (Dubochet et al., 1988). Furthermore, as the optimal sectioning thickness is less than the diameter of many viruses (~750 Å), this approach may not provide the full picture of the virus structure in the cells.

3.2 Cryo-ET Data Collection

In contrast to single particle data collection, where the sample is imaged at a fixed angular position, the sample in tomography is rotated around an axis during imaging (Figure 8). This allows for images of the same specimen area to be acquired at different tilt angles. Usually the microscope is mechanically limited to a tilt range of ±70°, but specimen thickness or other factors may further constrain this range to ±60°. Within this range, the specimen can be tilted by a constant angular increment (typically 1° or 2°) or by a variable step that is proportional to the cosine of the current tilt angle (Saxton scheme) (Saxton et al., 1984). In the Saxton scheme, the angular step is larger at low tilt angles and smaller at high tilt angles, which results in more even sampling in Fourier space.

Figure 8.

Generalized schematic for a tomographic reconstruction. (a) Schematic of a cryo-tomographic holder, which enables the sample to be tilted at a specified angle. Most holders allow for the sample to be tilted in the range of ±60° to ±70°. (b) A series of tilted images are collected with a step size of 2°. (c) Images from a typical tilt series are not aligned with respect to each other due to mechanical imperfections in the TEM. Fiducial markers, typically gold nano-particles, can be used to aid in alignment as they appear as high density dots in micrographs. The aligned image stack can be used to reconstruct a tomogram (d). From the tomogram, the individual virus particles attached to the cell can be computationally extracted into subvolumes, aligned, and averaged. Shown here is bacteriophage epsilon-15 attached to its Salmonella host cell [EMD-5216] (e).

In order to minimize damage to the specimen, the total electron exposure must be kept as low as possible. It has been established that low-resolution structures can be preserved up to an electron exposure of ~100 e/Ų (Bammes et al., 2010). Therefore, this total electron dose must be divided among all the images (usually 60–150) in a typical tomogram. Consequently, each image will receive an exposure of only ~1 e/Ų, which is less than 5% of the exposure normally used for single particle cryo-EM. As a result of this low exposure, each image is very noisy and has low contrast, which makes alignment and CTF correction very difficult. One way to improve the contrast is to image at a higher defocus (typically at least 3–10 μm). This facilitates alignment of the images but does not necessarily help with CTF correction. As a result, CTF correction is usually not performed for tomography, which limits the resolution to the first zero of the CTF. Another significant limitation to the resolution is the angular step that is used in collecting the tilt-series (Crowther et al., 1970b). Ideally, a small angular step would be used for finer sampling (higher resolution data collection), but this is not possible because of the limited total exposure that must be partitioned among all the images.

3.3 Processing the 2-D Data (Tilt-series)

Subtle mechanical imperfections in the microscope stage can cause the specimen to shift as the stage is tilted during tomography. Thus, before a volume can be reconstructed, the individual images in a tilt-series must be aligned to each other. To facilitate this alignment, gold particles (fiducials), which appear as high-density dots in the images, can be applied to the specimen, (figure 8). As the fiducial markers are fixed relative to the specimen, tracking their position across a tilt-series allows the individual images to be shifted into alignment with each other (Amat et al., 2008; Brandt et al., 2001b; Heymann et al., 2008a; Kremer et al., 1996; Lawrence et al., 2006; Mastronarde, 1997; Nickell et al., 2005). The gold particles must be large enough for them to be visible under the imaging conditions used for tomography but not too large, as it is harder to accurately determine the center of a larger, non-spherical gold fiducial, potentially introducing errors in alignment. As thicker specimens may need larger gold particles in order for them to be visible (especially at higher tilt), a reasonable starting point is to use gold particles that are ~15 pixels wide (usually 100–200Å, depending on imaging conditions) and make adjustments as dictated by the specimen. Alternatively, a mixture of sizes can be used.

Fiducial based alignment algorithms perform an initial coarse alignment using cross correlation between the images, but they can also be aligned by visual inspection. This simplifies the process of locating the corresponding fiducials in each image. The more widely distributed the fiducial markers are throughout the volume of the specimen, the better the global alignment of the images will be. Even though three points are sufficient to define a plane, selecting more fiducials will allow the software to provide a better solution. Once individual fiducials have been selected in the 0°-tilt image, the software can use these coordinates and the initial tilt angles for each image supplied in the readout from the EM stage to predict the positions of these same fiducials in the other images. However when the software fails to locate and center a fiducial accurately, user intervention is necessary. The user should examine the software solution and adjust the outliers (visually inspect the fiducials with large errors and make sure they are accurately centered on the gold particle). Once all the selected fiducials have been accurately positioned, their coordinates are used to transform the 2-D images (translate, rotate, scale, distort) before reconstructing the 3-D volume (i.e. a tomogram).

While it is relatively easy to use gold fiducials to align tilt-series, there are algorithms for marker-free alignment (Brandt et al., 2001a; Castano-Diez et al., 2007; Castano-Diez et al., 2010; Liu et al., 1995; Sorzano et al., 2009; Winkler, 2007; Winkler and Taylor, 2006; Zheng et al., 2007). These methods can align the images by cross-correlation or by tracking identifiable features in the specimen itself. For example, membranes, which contain lipids with large positive head groups, tend to have good contrast in the images. Indeed, any prominent features in a sample that are evenly distributed in the tilt-series images can act as markers for fiducial-free alignment. Aligning the images in this way is essentially the same process as is used for fiducial based alignment, but an advantage of this method is that the resulting 3-D reconstructions do not have the “shadows” that are a characteristic of gold fiducials and have the potential to obscure regions of interest (Figure 8). In addition, marker-free alignment does not suffer from possible movement of the gold beads under the electron beam (Wright et al., 2006), which would cause inaccurate tilt-series alignment.

The aligned images are typically reconstructed into a volume by using weighted back projection rather than the Fourier-based methods (section 2.1.4). In general, reconstructed volumes from cryo-ET are much larger than those from single particle cryo-EM, so back projection, which requires half the computer memory as Fourier methods, is preferred. The weighting function used for this back projection is as previously described in Section 2.1.4, but the ramp function in this case is the radius in Fourier space at a defined cutoff (Gilbert, 1972). Thus, the Fourier amplitudes are weighted by their distance from the origin, and then zeroed after a certain resolution. Other methods to obtain the 3-D density include iterative and algebraic algorithms, such as ART and SIRT (Lakshminarayanan and Lent, 1979; Marabini et al., 1998). ART (algebraic reconstruction technique) and SIRT (simultaneous iterative reconstruction technique) iteratively minimize the differences between the projections from 3-D and the 2-D data, similar to the iterations of projection matching as discussed in section 2.1 (Figure 3). These iterative methods have higher computational demands, so they have been used less frequently that the weighted back projection approach.

All 3-D volumes derived by cryo-ET suffer from missing wedge artifacts. This is due to the lack of tilted views from 70° to 90° (or even from 60° to 90°, as mentioned above). The missing views result in a missing wedge of data in 3-D Fourier space. As a consequence, the densities in the final tomogram are elongated in the direction parallel to the electron beam in real space. Nonetheless, a great deal of insight can still be gained from the 3-D map even in the presence of these artifacts. While there is a great deal of information that can be directly extracted from an individual tomogram, for the purposes of this chapter, we will focus exclusively on computationally extracting subvolumes from this 3-D map for further processing. Various implementations of this approach are available and have been applied to different specimens (Table 3) (Bartesaghi et al., 2008; Bostina et al., 2011; Nicastro et al., 2006; Schmid, 2011).

Table 3.

Selected Examples of Cryo-ET Reconstructions

Virus	EMD/PDB	Particles	Reported Resolution (Å)	Program (algorithm)
Vacinnia virus (Sougrat et al., 2007)	n/a	n/a	n/a	IMOD
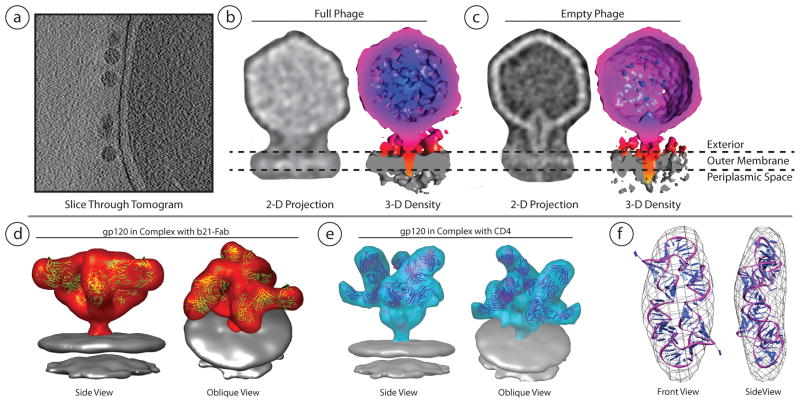
Human Immunodeficiency Virus Env (Liu et al., 2008)	5019	4741	19 (FSC 0.5)	Inspect3D, Protomo, IMOD
Human Immunodeficiency Virus Env+Antibody (Liu et al., 2008)	5018	4323	22 (FSC 0.5)	Inspect3D, Protomo, IMOD
Human Immunodeficiency Virus Env+Antibody+CD4 (Liu et al., 2008)	5020	4900	23 (FSC 0.5)	Inspect3D, Protomo, IMOD
Epsilon-15 phage (Chang et al., 2010)	5216, 5217, 5218, 5219	83, 85, 44, 10	n/a	IMOD, EMAN (Tomohunter)
Sulfolobus turreted icosahedral virus (Fu et al., 2010)	n/a	n/a	n/a	IMOD
P-SSP7 Phage (Liu et al., 2010b)	1714	29	24 (FSC 0.5)	IMOD, EMAN (Tomohunter)
Maloney Murine Leukemia Virus RNA (Miyazaki et al., 2010)	1806	38	n/a	IMOD, EMAN (Tomohunter)
Epsilon-15 Phage (Murata et al., 2010)	5203, 5204, 5208	132	32, 38, 26 (FSC 0.5)	IMOD, EMAN (Tomohunter)
Poliovirus (Bostina et al., 2011)	n/a	n/a	n/a	SPIDER, IMOD

After reconstructing a tomogram of a polymorphic specimen, identical or homogeneous components can be recognized, such as virus glycoproteins or capsids. In contrast to overlapping densities in the 2-D images for single particle cryo-EM, the different densities are discernible in 3-D, which simplifies processing this data. These components are candidates for extraction into subvolumes for 3-D alignment, classification, and averaging to improve the visibility of features in the volume. Each subvolume should contain one copy of the component of interest, and the subvolumes can originate from a single tomogram or from several tomograms.

Processing the subvolumes to enhance the structural features normally requires 3-D alignment and averaging. However, if the particles are not identical, classification is necessary. This case would require iterative refinement by alternating the alignment and classification steps because of the interdependence between these two steps. Accurate alignment needs homogeneous structures, while accurate classification needs accurate alignment to determine differences due to structure instead of orientation. To improve the 3-D alignment, an initial visual inspection can roughly classify the subvolumes (for example, on the basis of particle diameter, presence of DNA in the capsid, or other coarse features) before aligning. An example of this classification is illustrated for bacteriophage Epsilon15 attached to ghost cells that were visually separated on the basis of the presence of DNA in the capsids prior to alignment (Chang et al., 2010).

3.4 Aligning and Averaging Subvolumes

One approach to 3-D alignment is an exhaustive search of all rotations. The subvolumes are rotated around three axes, and each transformation is compared against a fixed (not rotated) reference subvolume (e.g. an initial or intermediate model). The reference can be a 3-D map derived from the single particle method (section 2.2), downloaded from EMDB, or another subvolume. The rotation that results in the best match between the two subvolumes is retained as the correct alignment. Once all the subvolumes have been aligned, they can be averaged together to increase the SNR of the data, reduce the effect of the missing wedge, and increase the resolution of the total aggregate subvolume. Reduction in the missing wedge is accomplished by averaging particles that have their missing wedges in different orientations so that the gaps in the structural information are effectively filled when these particles are combined. Similarly, the angular step between each of the tilted images, which is fixed by the angular step-size at which the tilt-series was collected, can be reduced by combining particles derived from tilt-series which have images taken at different tilt angles or rotations.

Cross correlation is frequently used to align objects in 3-D. This is accomplished by determining the orientation that maximizes the product from multiplying the 3-D Fourier transforms of the two subvolumes. However, each subvolume extracted from the tomogram has a wedge of missing data in Fourier space and multiplication by this artifact will ablate any signal (zero times anything is zero). This produces a very strong directional signal and, if left unaccounted for, the process of maximizing the cross correlations will preferentially align the missing wedges rather than the two objects themselves. In order to compensate for this misleading scoring function, the cross correlation has to be scaled by the fraction of data that is not eliminated by the missing wedge (Schmid and Booth, 2008). Counting the number of nonzero amplitudes is easy to understand but not straightforward to accomplish computationally. Fortunately, it is possible to simplify this problem using Parseval’s theorem, so that instead of counting the number of nonzero amplitudes in Fourier space, the cross correlation map in real space is normalized (Schmid, 2011). By Parseval’s theorem, scaling the cross correlation map in real space is equivalent to scaling the intensity or power (i.e. sum of the squared magnitudes) in Fourier space. Hence, the magnitudes of the data voxels in the product (representing cross correlation in Fourier space) will be scaled up when there are fewer nonzero voxel and scaled down when there are more nonzero voxels. This approach reduces the tendency to align the missing wedges of the particles, thus producing more reliable results.

A similar algorithm minimizes the dissimilarities between the two subvolumes and uses masks to restrict the comparison to only the region where the data in the two subvolumes overlap (Bartesaghi et al., 2008). This general dissimilarity function can take the form of a cross correlation or other scoring functions. Changing the Cartesian coordinates into spherical coordinates allows the use of the convolution theorem (spherical harmonics) to compute the rotational transformation that produces the best match, similar to the polar Fourier transform for 2-D alignment (Section 2.1.3). The same is performed in Cartesian coordinates to find the best translational transformation. The main advantage of this approach is that by using spherical harmonics, the slower exhaustive search can be avoided.

Another method for determining subvolume orientations is similar to the projection-matching scheme applied to 2-D images for single particle reconstruction (section 2.1.3), and requires an initial reference model (Förster et al., 2005). The reference model is rotated around all three axes to generate a set of 3-D references. Next, a missing wedge is applied to these 3-D references, by multiplying by a 3-D mask in Fourier space, so that the missing wedge effect is the same as that in the actual data. Then the individual subvolumes are compared with all the 3-D references, and the alignment having the highest cross correlation coefficient is assigned to the subvolume. This is analogous to comparing the 2-D particle images with the 3-D model projections to find their orientations for single particle cryo-EM.

As with the normalized cross correlation map method, comparing the subvolume to all the references represents an exhaustive search. However, prior knowledge about the specific sample can be used to optimize the computation by limiting the search space. For example, searching for the icosahedral orientation of a virus capsid can be limited to one of the 60 equivalent rotations rather than to a complete sphere. Similarly, aligning the glycoproteins on the envelope of a virus, may only require an exhaustive search in the neighborhood of the glycoprotein’s axis (Förster et al., 2005). An exhaustive search can also be hastened by beginning with downsampled volumes and a large search step size. Once the approximate orientations are known, the original data can be processed with a finer step size to improve its accuracy.

Subvolumes that are aligned in 3-D can be averaged together. The algorithm to combine them must take into account the missing wedge. In the 3-D FT of subvolumes, voxels in the missing wedge have a value of 0, and combining these voxels with data voxels would reduce the average, resulting in an improper weighting of the data. One implementation uses the Fourier amplitudes to weight the sum of the real and imaging voxels in Fourier space (Schmid and Booth, 2008). Another method keeps track of all the transformations required to align the subvolumes, applies the transformations to the corresponding sub-areas extracted from the raw tilt series, and reconstructs a 3-D subvolume (Walz et al., 1997).

3.5 Classification of Subvolumes

Many tomograms consist of a mixture of particles with different structures. Therefore, separation of the structural forms is necessary prior to performing subvolume averaging as described above. Classification relies on accurate alignment, so after a preliminary visual classification, alignment, and averaging, a more objective and accurate classification can be used for refinement. For example, a modified maximum likelihood algorithm separated newly assembled Sulfolobus turreted icosahedral viruses (STIV) inside the cell into empty and full capsids (Fu et al., 2010). Another algorithm uses the cross correlation peak scaled by the number of non-zero amplitudes, which can also be used for alignment (above), to separate subvolumes into different groups (Schmid et al., 2006). In addition, an all-vs-all dissimilarity function between two subvolumes (above) can be used in a hierarchical ascending classification technique (Bartesaghi et al., 2008). After classifying the subvolumes into new groups with any of these algorithms, the next iteration would refine the alignment. As in the single particle cryp-EM, iteration stops when there are no further improvements.

Iterative processing of carboxysomes is one such example of particle classification (Schmid et al., 2006). Selected subvolumes were grossly classified into 9 arbitrary classes based on diameter, as determined by a 1-D radial density plot. Then all-vs-all alignment and averaging was performed on the subvolumes in each class, resulting in 9 averaged class subvolumes. Next the subvolumes were compared against these averaged class subvolumes to generate a new classification of the subvolumes. At the end, the initial 9 classes were reduced to 7 stable classes by alternating alignment and classification in an iterative refinement. Compared to the original subvolumes, the 7 averaged subvolumes provided more interpretable information.

3.6 Selected Examples of Cryo-ET Reconstructions

Cryo-ET is the method of choice for studying heterogeneous samples. In the case of the archaea bacteria Sulfolobus infected by STIV, cryo-ET showed a novel pyramid structure and distribution of capsids in different assembly states in the cytoplasm (Fu et al., 2010). Cryo-ET with subvolume averaging has emerged as a powerful method for studying the structures of virus particles and infected cells. When applied to the study of the trimeric HIV glycoprotein (gp120) (Figure 9d), the averaged densities showed how gp120 changes conformation in order to interact with cellular receptors, subsequently leading to membrane fusion and infection (Liu et al., 2008b). Furthermore, the study challenged the proposed structural conformation based on X-ray crystallography (Chen et al., 2005). Another example of subvolume averaging focused on a virus-cell interaction, where snapshots of epsilon15 phages infecting their bacterium host (Chang et al., 2010) (Figure 9a,b,c), revealed a tubular density spanning the bacterium periplasmic space. For the first time, this density has shown what is believed to be the conduit for viral DNA to enter the cell.

Figure 9.

Selected tomographic subvolume averages. (a) Slice through a reconstructed tomogram showing the bacteriophage epsilon-15 at the surface of its Salmonella host cell. (b–c) Shown are averaged 3-D maps of epsilon-15 attached to the cell before release of its genome (b) and after genome release (c). (d–e) Structure of the HIV gp120 surface glycoproteins: (d) in complex with b12-Fab (green, PDB ID: 2NY7) EMD-5018 (red) and EMD-5022 (gray), (e) in complex with CD4 and 17b-Fab (blue, PDB ID: 1GC1) EMD-5020 (cyan) and EMD-5022 (gray). (f) Orthogonal views of the averaged RNA density of Moloney Murine Leukemia Virus fitted to the ensemble of [ΨCD]2 NMR structures. This average represents the smallest structure solved to date by cryo-ET (43kDa).

Section 4: Data Validation and Interpretation

No matter what their resolution, both cryo-EM and cryo-ET reconstructions allow researchers unparalleled access to virus structure and function. However, as these reconstructions have not yet reached atomic resolutions, it is often necessary to use a variety of field-specific computational tools for analyzing these density maps. Interpreting and validating a 3-D electron density map depends on a variety of factors: the resolution of the map, availability of related structures, biochemical data and other experimental information. Here we discuss the tools used and process behind interpreting and validating the 3-D structural information that results from these studies.

4.1 Map Validation

Conceptually, perhaps the most direct method for validating a cryo-EM reconstruction is to compare the structure to known atomic models or homologous structures. Generally, structures of individual components can be fit visually or computationally and assessed for their agreement to the density map (see Section 4.4 for details). In a number of examples, such as Herpese Simplex Virus, Hepataitis B and Rice Dwarf Virus, the subnanometer resolution cryo-EM density maps were actually published before the availability of their corresponding crystal structures (Baker et al., 2003; Böttcher et al., 1997; Zhou et al., 2001). These subsequent atomic models bore out the structural model determined from the density map for the individual capasid proteins. Recently, work on rotavirus and adenovirus have also clearly demonstrated the outstanding match between the cryo-EM density map, model and available crystal structures at near-atomic resolutions (Liu et al., 2010a; Zhang et al., 2008).

While no validation methods are rigorously implemented in cryo-EM, several techniques have begun to emerge. One method uses tilted pairs, in which the same specimen area is imaged at 0°-tilt and 10°-tilt (Rosenthal and Henderson, 2003). Once the orientations the particles in this tilt-pair have been determined, the accuracy of the alignment can be assessed by verifying that the orientations differ by 10°. In addition to assessing the accuracy of the reconstruction, this method can also provide the handedness of the virus particle. An alternative approach uses a range of resolutions to determine the orientations of the particles (e.g. 15–1000 Å) before reconstructing them using the entire range of spatial frequencies in the data. If the resolution of the reconstruction is found to be higher than what was used to orient the particles (e.g. 10 Å), one can be assured that the higher resolution information in the map is real and not due to alignment of noise by the software.

Bootstrapping has also been used to measure the validity of a 3-D reconstruction by generating a 3-D variance map, which can approximate the potential error at each voxel in the reconstruction (Penczek et al., 2006). Using the same particles and particle orientations that go into the final reconstruction, a new set of 2-D images is created in which a fraction of the particles are replaced by duplicates of the other images. This process is repeated multiple times (tens to thousands), reconstructing a 3-D model for each iteration. These reconstructions are combined to produce a 3-D density representative of the error at each voxel in the volume (a variance map). The variance map generated through this process shows the error present in each voxel of the final reconstruction. This error/variance can prove useful in interpreting the density map, as regions of high variance are likely to correspond to flexible regions in the structure (Chen et al., 2008; Zhang et al., 2010a).

4.2 Segmenting Cryo-EM and Cryo-ET Maps

Segmentation is the process of isolating specific regions of density in a 3-D map so that they can be extracted and visualized/processed separately. This process can be performed on any volume and the features that can be segmented depend on the resolution of the data (Figure 1). While it may only be possible to segment the capsid shell at low resolutions (~40 Å), at subnanometer resolutions, the protein subunits in the capsid shell can be approximately identified and extracted for further analysis. As the data reaches near-atomic resolutions it becomes possible to unambiguously identify specific protein subunits in the virus and extract them for further processing (Section 2.1.6.2).

Segmentation can be accomplished with completely interactive tools like Amira and UCSF Chimera (Pettersen et al., 2004) or automated routines like Segment3D (Ludtke et al., 1999). Semi-automated tools like VolRover (Baker et al., 2006b) and Segger (Pintilie et al., 2010) can take advantage of symmetry inherent in the sample, while other methods can be used to segment, average and classify multiple copies of a subunit within a tomogram (Forster et al., 2008). Regardless of technique, a mask is generally created for one or more subunits that defines its boundaries and can be used to separate it from the reconstruction. It is important to note that this process of segmentation is often imprecise and can lead to erroneous results, particularly in lower resolution reconstruction. In the case of epsilon-15, the initial 9 Å map failed to resolve the globular density on top of the major capsid protein as a second capsid protein, which was subsequently identified in the 4.5Å resolution structure of the virus (Jiang et al., 2008; Jiang et al., 2006).

4.3 Identifying Structural Features in a Density Map

The availability of high-resolution cryo-EM density has stimulated the development of a number of specialized tools for structural analysis and model building (Table 4). In principle, many of these tools are not specific for subnanometer resolution density maps and, while the results may not be as accurate, can be readily applied to lower resolution data.

Table 4.

Computational tools used in the validation and analysis of cryo-EM density maps

Function	Program Name (Reference)
Segmentation	Amira (Visage Imaging, GmbH)
	Avizo (VSG, France)
	Chimera (Pettersen et al., 2004)
	CoDiv (Volkmann, 2002)
	EMAN (Ludtke et al., 1999; Tang et al., 2007)
	Segger (Pintilie et al., 2010)
	VolRover (Baker et al., 2006)
Rigid body fitting	Chimera (Pettersen et al., 2004)
	CoFi (Volkmann and Hanein, 1999)
	DockEM (Roseman, 2000)
	EMFit (Rossmann, 2000)
	Foldhunter (Jiang et al., 2001)
	Mod-EM (Topf and Sali, 2005)
	Situs (Wriggers et al., 1999)
	UROX (Siebert and Navaza, 2009)
Flexible fitting	DireX (Schröder et al., 2007)
	Flex-EM (Topf et al., 2008)
	MDFF (Trabuco et al., 2009)
	NMFF (Tama et al., 2004)
	NORMA (Suhre et al., 2006)
	Yup.scx (Tan et al., 2008)
	Situs (Rusu et al., 2008)
SSE Identification	Helixhunter (Jiang et al., 2001)
	Sheetminer/Sheetracer (Kong and Ma, 2003; Kong et al., 2004)
	SSEHunter (Baker et al., 2007)
Modeling	Coot (Emsley and Cowtan, 2004)
	EM-IMO (Zhu et al., 2010)
	Gorgon (Baker et al., 2011)
	Modeller (Topf et al., 2006; Topf and Sali, 2005)
	O (Jones et al., 1991)
	Rosetta (Baker, 2006; DiMaio et al., 2009)
Visualization	Amira (Visage Imaging, GmbH)
	Avizo (VSG, France)
	Chimera (Pettersen et al., 2004)
	PyMol (DeLano Scientific LLC, USA)
	VMD (Humphrey et al., 1996)

In subnanometer resolution density maps secondary structural elements (SSEs) begin to be resolved (Baker et al., 2010a; Chiu et al., 2005). In general, α-helices appear as long rod-like densities and β-sheets appear as thin, flat sheets at ~8 Å resolution. Around 7 Å resolution, connections between SSEs begin to be resolved, although not to the point to unambiguously identify the protein backbone trace. At ~5 Å resolution, the pitch of α-helices begin to become visible and β-sheets transform from flat densities to a series of interconnected strands and when pushed to near-atomic resolutions, large charged sidechains become visible. Based on these observations, a number of tools have been developed to directly analyze and model protein structure at subnanometer resolutions. Helixhunter (Jiang et al., 2001) was the first computational tool to detect α-helices in a density map and was later followed by SheetMiner and SheetTracer (Kong and Ma, 2003; Kong et al., 2004) for detecting β-sheets. SSEHunter offers a comprehensive solution to detect α-helices and β-sheets (Baker et al., 2007), as well as the connections between the secondary structure elements (Ju et al., 2007).

While SSEs can be used to describe gross protein structure at subnanometer resolutions, they can also be important in identifying structural and functional domains within a protein. In adapting fold recognition software, such as DejaVu (Kleywegt and Jones, 1997) and COSEC (Mizuguchi and Go, 1995), a set of SSEs can be queried against a structural database to identify potential structural homologues in the absence of structural similarity. This is particularly useful in identifying common structural motifs in seemingly unrelated proteins, as in the case of the capsid proteins from herpes simplex virus-1 and bacteriophages (Baker et al., 2005). Furthermore, these SSEs can be used as landmarks for fitting atomic models to the density map (Abeysinghe et al., 2010).

4.4 Model Fitting to Cryo-EM Density Maps

When a known atomic model is available, fitting it to a cryo-EM density map provides a valuable means for analyzing structure and function in a macromolecular assembly (reviewed in (Rossmann et al., 2005)). Fitting known structures is not restricted by the resolution of the density map and has been used both in the highest resolution single particle reconstructions (Zhang et al., 2008) and in relatively low-resolution cryo-ET reconstructions (Zanetti et al., 2006). Over the past two decades, a number of fitting routines have evolved for use in cryo-EM, including Situs (Wriggers et al., 1999), Foldhunter (Jiang et al., 2001), CoFi (Volkmann and Hanein, 1999), UROX (Siebert and Navaza, 2009) and EMFit (Rossmann, 2000). Generally, these tools use a rotational and translational search of a given model within the density map in which a scoring metric is used to measure the agreement of the model with the density. However, each program utilizes a slightly different metric and reports a variety of fitting scores, so it is important to visually inspect the fit and assess the results in the context of all available structural information.

Traditionally, the aforementioned fitting methods treat an atomic model as a rigid body when fitting it to the density map. However, with flexible fitting methods, such as DireX (Schröder et al., 2007), Flex-EM (Topf et al., 2008), MDFF (Trabuco et al., 2009), NMDF (Tama et al., 2004), Norma (Suhre et al., 2006) and Yup (Tan et al., 2008) atomic models are morphed to best fit the density map. This type of fitting is particularly useful when fitting homologous structures, or structures in different conformations to the density map (Trabuco et al., 2010). In these flexible fitting methods, an atomic model is generally first fit to a density map as a rigid body and then allowed to deform over time to better fit the density map. The flexible deformation can be accomplished through a variety of algorithms, including normal modes, molecular dynamics and geometric constraints. Again, flexible fitting can be used at any resolution, though higher resolution density maps offer more well-resolved features that can increase the accuracy of the fit.

4.5 Deriving Protein Models from Cryo-EM Density Maps

In addition to model fitting, computational modeling tools can be used to construct a structural model for a protein or domain in a density map (Table 4). In this context, a cryo-EM density map becomes a constraint for constructing and evaluating models generated by computational tools such as Modeller and Rosetta (Baker et al., 2006a; DiMaio et al., 2009; Topf et al., 2005; Topf et al., 2006). If a structural homologue is known, constrained comparative modeling creates an initial sequence-structure alignment and model (Topf et al., 2005; Topf et al., 2006; Zhu et al., 2010). The alignment and model are then allowed to “evolve” in an effort to improve the model’s fit to the cryo-EM density map. An example of this was in the near-atomic resolution structure of grass carp reovirus, where EM-IMO was used to build and refine protein structures in the virus based on the mammalian Reovirus crystal structures and using the cryo-EM density map as a constraint.

In the absence of a structural homologue, a structural model for a small protein or domain may be constructed using a similar constrained ab initio modeling approach. Rather than using an initial structural template, ab initio modeling constructs a gallery of potential models, typically with Rosetta (Bradley et al., 2005), and then evaluates their fit to the density map along with a variety of other model-based scores (Baker et al., 2006a). This procedure was used to construct a model for HSV-1 VP26, a small capsid protein bound to the tips of hexon subunits (Baker et al., 2006a). However, it should be noted that this procedure only works on relatively small proteins or domains (<200 amino acids). A recent extension of this procedure has been used to build and refine full atomic models of entire macromolecular assemblies using density constraints, though an initial structural template of all of the components is required (DiMaio et al., 2009; Ludtke et al., 2008).

In both of the above density-constrained modeling approaches, resolution is a key determinant in of the accuracy of the models (Topf et al., 2005). At lower resolutions, a density map provides only basic information about shape and may only be able to discriminate between possible protein folds. At higher resolutions, accuracy increases and even allows for optimal sidechain fitting at near-atomic resolutions.

4.6 De Novo Modeling

Single-particle cryo-EM reached another milestone in 2008 when the first near-atomic resolution structures of Rotavirus (3.88Å) (Zhang et al., 2008), GroEL (4.2Å) (Ludtke et al., 2008), Cytoplasmic Polyhedrosis Virus (4.0Å) (Yu et al., 2008) and bacteriophage epsilon15 (4.5Å) (Jiang et al., 2008) were reported. At this resolution, the pitch of the α-helices and separation of the β-strands could be seen unambiguously, and when combined with computational techniques, Cα backbone models could be built directly from the cryo-EM density maps (Baker et al., 2010b; Jiang et al., 2008; Ludtke et al., 2008). However, these de novo models relied almost entirely on visual interpretation of the density and manual structure assignment, as they did not have the resolution to utilize standard X-ray crystallographic methods for model construction. Current state-of-the-art reconstructions have continued to push towards higher resolutions and have now made it possible to resolve atomic details (Baker et al., 2010b; Grigorieff and Harrison, 2011; Zhou, 2011).

At these near-atomic resolutions, SSE detection coupled with density skeletonization (Abeysinghe et al., 2008; Ju et al., 2007) and sequence analysis can be used for constructing de novo structural models directly from a density map without the aid of an existing structural template (described in (Baker et al., 2010a) and (Baker et al., 2010b)). In de novo modeling, SSEs are used as anchors for establishing a topological model for a protein (Figure 10). Once a topology has been established, individual atoms can be placed on annotated SSEs and along the density skeleton, in a similar manner to the techniques used in X-ray crystallography. While many model building toolkits, such as Coot (Emsley and Cowtan, 2004) and O (Jones et al., 1991), offer a mechanism for placing atoms within a density map, none are specifically tailored to cryo-EM or near-atomic resolution density maps. Gorgon, a molecular modeling toolkit designed for subnanometer resolution density maps from cryo-EM and X-ray crystallography, provides a comprehensive suite of utilities that implement a complete protocol for Cα model construction (Baker et al., 2011). The streamlined procedure provided by Gorgon has made it possible to construct complete backbone traces in a fraction of the time required by the original de novo methods (Chen et al., 2011).

Figure 10.

De novo modeling. A schematic diagram illustrates the process of building a de novo backbone model directly from the cryo-EM density map of bacteriophage epsilon 15 without the aid of a structural template. Once an individual protein has been segmented from the density map, SSEs are identified along with a corresponding density skeleton. This density skeleton provides a set of possible topological paths that link the observed SSEs. From the sequence of the protein in question, secondary structure prediction yields a linear array of SSEs. Using a modified graph matching approach, SSEs from the density map are correlated to those in the sequence based on relative size, position and connectivity. From this, an initial topological model can be created by placing Cα atoms along the density skeleton of the specified path. This model is then iteratively optimized with respect to visible density features and interactions with neighboring subunits in order to produce a final model.

At resolutions where sidechain density becomes visible, computational and de novo modeling protocols can be extended to compute full atomic models (Zhang et al., 2010a). Essentially, a Cα backbone trace is first transformed into a full model and then iteratively refined to fit the density and satisfy biochemical and geometric constraints. This process can either be done manually using interactive software like Coot and O or completely automated with refinement routines in Rosetta (Dimaio et al., 2011). However, a density map may not necessarily have uniform resolution throughout the map and thus only partial full atom maps can be generated for the protein (Chen et al., 2011). Regardless of the technique used to construct the model, model validation techniques at this resolution (4.5 to 3.0 Å) are still limited and will require future efforts to determine their reliability and limit.

Section 5: Conclusion and Future Directions

The ability to study large macromolecular complexes in near native environments at subnanometer resolutions is one of the driving forces behind the development and growth of cryo-EM in the past decade. The success of cryo-EM for homogeneous samples spurred the development of cryo-ET for studying heterogeneous samples where the assumptions of single particle cryo-EM do not hold. Both of these techniques have opened the door to the study of the structures and conformational changes that occur in the life cycle of viruses (Chen et al., 2011; Liu et al., 2010c). While it took nearly 40 years to see the first near-atomic resolution virus structure from cryo-EM, the technology has advanced to the point that subnanometer resolution reconstructions are now routine for most virus capsid structures (Grigorieff and Harrison, 2011; Zhou, 2011). Nevertheless, even though the field has matured dramatically in the past few years, there is still a great deal of knowledge to be gained by pushing the resolution of these techniques even further. History has shown that these incremental improvements in resolution are the result of years of technological advances in both the microscope and in the software used to acquire and process the data. However, as the scientific community begins to embrace the utility of cryo-EM and cryo-ET as tools for structural biology, these advancements are likely to come at a hastened pace. Below we discuss what is on the horizon for virus reconstruction in an era of high-resolution imaging and reconstruction.

5.1 Single Particle Reconstruction at Atomic Resolutions

From a simplistic statistical perspective, pushing these reconstructions to higher resolutions would only require more data. Most of the near atomic resolution maps discussed were reconstructed using 20,000–30,000 single particle images, and the assumption of icosahedral symmetry equates this to roughly 1.2–1.8 million projections that go into these single reconstruction. From a theoretical standpoint (Rosenthal and Henderson, 2003), to improve the resolution of these maps from near-atomic to atomic resolutions (4 Å to 3 Å), more than 10 times the current number of single particle images will be needed (assuming a crystallographic B-factor of 100Ų). Collecting such massive, high-quality, datasets can be facilitated an automated imaging system that can operate continuously and efficiently (Carragher et al., 2000; Nakamura et al., 2010; Potter et al., 1999; Stagg et al., 2006; Zhang et al., 2009). The sheer magnitude of these datasets will require tapping into large scale computing resources (CPU power, memory, and storage) to align and reconstruct the 3-D electron density maps. While it may be possible to process this data using the hundreds of CPUs available on modern day graphics cards (GPUs), doing so will require the current software to be updated accordingly.

Not only will atomic resolution cryo-EM reconstructions require magnitudes more data, but these images must be of high-quality as well. Specifically, the individual images must have detectable signal up to and beyond 3.0 Å so that the alignment software can extract this information for a reconstruction. There are numerous factors that need to be considered when targeting a 3.0 Å resolution reconstruction (e.g. microscope, image recording medium, alignment/reconstruction algorithm). On the instrument side, the electron optical system and the cryo-specimen holder have to be very stable, with coherent illumination but without drift or lens aberration. The current generation of microscopes appear to perform well, out to at least to ~2.8 Å, and substantial improvement seems unlikely in the near future. Improvements can also be anticipated at the detector level. The CCDs currently in use do not directly record electrons but employ a scintillator to convert the electrons into photons, which are then recorded by the CCD. Unfortunately this process blurs the electron signal into an area of photons, effectively increasing background noise. The modulation transfer function of the CCD reduces the signal transfer substantially and loses practically all high-resolution information beyond the 0.5–0.6 Nyquist frequency of the detector. Direct electron detection devices (DDD) and electron counters have recently shown the potential to improve the signal transfer efficiency substantially (Deptuch et al., 2007; McMullan et al., 2009; Milazzo et al., 2005; Milazzo et al., 2010). This offers the possibility of enhancing the high-resolution signal recorded on the detector by a factor of 5 or more. Such an improvement will in turn reduce the number of particle images needed to achieve a specific resolution by the same factor. Furthermore, the enhanced high-resolution contrast it provides may also improve the accuracy of the particle center and orientation determination. All these benefits will contribute to pushing the resolution of the reconstruction of biological specimens towards the resolving limit of the microscope.

It is unlikely that hardware improvements alone will solve all high-resolution reconstruction issues. Other parameters like as defocus variation within a micrograph, magnification scaling for different particle images, depth of focus, etc. must also be considered in order to achieve these resolutions. In the few near-atomic resolution virus maps solved to date, attempts have been made to address these issues in the software used for alignment and reconstruction. Achieving atomic resolutions may also necessitate avoiding even the slightest error propagation in alignment, so all of these parameters may need to be refined at the same time, together with the 5 orientation parameters as discussed above. To handle this simultaneous, high dimensional refinement, optimized search algorithms will be required for processing the data.

5.2 High-resolution Symmetry-free Reconstruction

Current technology can generate subnanometer resolution symmetry-free reconstructions of virus particles from single particle cryo-EM images. In terms of resolution, symmetry-free reconstructions of viruses are lagging far behind those where icosahedral symmetry is assumed. The reason for this is; the sheer magnitude of data needed (60 times more than for an equivalent resolution in an icosahedral reconstruction), together with ambiguity in correctly determining the true asymmetric orientation. As for icoshedral reconstructions, part of this problem will be solved as the systems that automate image acquisition become mainstream. However, while it has been assumed that software can always determine the true asymmetric orientation of each particle image for symmetry-free reconstructions, there is no guarantee that this orientation is correct. Maximizing the number of images where a true asymmetric orientation can be unambiguously identified will require more sensitive algorithms and possibly advanced EM technology. Nevertheless, regardless of any improvement made in data collection and image processing, structural homogeneity is a requirement, a reality that should be considered for any specimen before attempting high-resolution asymmetric reconstruction.

5.3 CTF Correction in Cryo-ET

Some viruses may contain structurally homogeneous components that are not uniformly distributed, such as the glycoproteins on the envelopes of HSV and HIV. While these components have been reconstructed using cryo-ET, these results have been limited to ~20 Å resolution (Liu et al., 2008b), due largely in part to the defocus gradient in tilted images as well as limitations in electron exposure. For cryo-ET, the difficulty in determining the defocus of the images (a major contributor to the CTF) is a result of the low dose per image, making correction of the CTF difficult. While potential solutions to this problem have been proposed by correcting the CTF along strips of data parallel to the tilt axis (Fernandez et al., 2006; Winkler and Taylor, 2003; Xiong et al., 2009), these methods have not yet been widely adopted in the field. In the event that the CTF can be accurately corrected for cryo-ET, it will become possible to process the data extracted from these volumes to higher resolutions and potentially into the subnanometer range.

5.4 Model Validation

Modeling cryo-EM or cryo-ET maps is an essential pipeline in the methodology described here. When used properly, these tools can provide amazing insight into the structure and function of individual proteins, macromolecular complexes, organelles and even cells as illustrated in recent literature. However, the accuracy with which one can analyze a density map is a function of the map itself. Size, complexity and quality all play critical roles in the ability to analyze a density map regardless of resolution. Another important consideration comes from the need to understand the limitations imposed by resolution when annotating structural features. While one would not expect to see side chain density or strand separation at 9 Å resolution, the absence of such features at 3.5Å resolution may indicate potential problems in the reconstruction. It is certain that the development of computational tools for modeling and annotating remains a necessity in order to make this process faster and the results more accurate.

5.5 Phase Plate Electron Microscopy

With current technology, there is a trade-off between high contrast and high-resolution information. One promising technology to achieve both is phase plate electron microscopy, which was initially proposed nearly 65 years ago (Boersch, 1947). One advantage of a phase plate electron microscope is that it dramatically enhances the low-resolution contrast of cryo-EM images because of the conversion of the contrast transfer function from a sine to a cosine function. The theory behind phase plate electron microscopy is that, by altering the electron beam, it is possible to shift the phase of the scattered electron beam, relative to the unscattered beam, thus dramatically enhancing the image contrast. Many devices have been proposed to induce this phase shift (Cambie et al., 2007; Danev and Nagayama, 2001; Thon, 1971), and Zernike-type phase plates have already begun to show very promising results for cryo-EM (Danev and Nagayama, 2008; Murata et al., 2010). While there are many technical challenges to implementing this type of device, preliminary results suggest that it may be possible to reduce the data required for a subnanometer reconstruction by a factor of 3 (Murata et al., 2010). Zernike phase contrast cryo-EM has also proven to be valuable for cryo-ET. For components that have proven difficult to study by conventional cryo-EM due to the weak signal from the low-resolution component of the particle image, phase contrast microscopy may provide the necessary means to resolve their structures at resolutions beyond the current limit.

5.6 Conclusion

Cryo-EM, cryo-ET, and image processing software have been used to determine the structures of many viruses. This includes, not only, the icosahedral capsids, but also portals, tails, glycoproteins, and other components without icosahedral symmetry. Analyses of these results have provided virologist and structural biologist with valuable insight into how viruses work. These structural studies have been enormously enriched by the use of the techniques above that have developed over the past 40 years. Furthermore, the future holds enormous potential for visualizing viruses interacting with their host cells, which will extend our picture of the life-cycles of these fascinating biological systems and make their structural investigation of interest to an even wider community.

Figure 5.

Selected near-atomic resolution cryo-EM density maps. The left column of the figure is the whole virus density map, the middle is the segmented subunit density map of the virus, and the right column is a close-up that shows their detailed features. (a) Human Adenovirus [EMD-5172]. The Protein IIIa density shows more connecting density than the X-ray density map. (b) Bacteriophage P22 [EMD-1826]. Individual bulky side chains are visible in the gp5 subunit of P22. (c) Rotavirus [EMD-5199]. At near atomic resolution, the separations of beta strands in VP6 [EMD-1461] can be clearly seen.

Abbreviations

1-D

One dimension; one dimensional

2-D

Two dimensions; two dimensional

3-D

Three dimensions; three dimensional

EM

Electron microscope; electron microscopy

Cryo-EM

Electron cryo-microscopy

Cryo-ET

Electron cryo-tomography

CT

Computed tomography

CTF

Contrast transfer function

SNR

Signal-to-noise ratio

SSE

Secondary Structural Elements

GUI

Graphical user interface

CCD

Charge-coupled device

DDD

Direct detection device

ZPC

Zernike phase contrast

FSC

Fourier shell correlation

FT

Fourier transform

EMDB

Electron microscopy data bank (www.emdatabank.org)

WPOA

Weak phase object approximation