Abstract
Many real networks exhibit a layered structure in which links in each layer reflect the function of nodes on different environments. These multiple types of links are usually represented by a multiplex network in which each layer has a different topology. In real-world networks, however, not all nodes are present on every layer. To generate a more realistic scenario, we use a generalized multiplex network and assume that only a fraction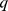 
of the nodes are shared by the layers. We develop a theoretical framework for a branching process to describe the spread of an epidemic on these partially overlapped multiplex networks. This allows us to obtain the fraction of infected individuals as a function of the effective probability that the disease will be transmitted 
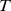. We also theoretically determine the dependence of the epidemic threshold on the fraction 
of shared nodes in a system composed of two layers. We find that in the limit of 
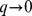the threshold is dominated by the layer with the smaller isolated threshold. Although a system of two completely isolated networks is nearly indistinguishable from a system of two networks that share just a few nodes, we find that the presence of these few shared nodes causes the epidemic threshold of the isolated network with the lower propagating capacity to change discontinuously and to acquire the threshold of the other network.
Introduction
Although the study of isolated networks allows us to understand how network topology affects network activity [1], most real-world networks are not isolated, instead they interact with other networks. In recent years, many researchers have studied how interconnections between networks produce phenomena that are absent in isolated networks [2]. A system composed of interconnected networks, often called a network of networks [3]–[6], retains connectivity links within each individual network but adds dependency links that connect each network to other networks in the system. This interdependency is the cause of many real-world multiple network phenomena, such as failure cascades [7], avalanches [8], and traffic overloads [9]. Very recently physicists have begun to consider a particular class of network of networks in which the nodes have multiple types of links across different layers [10]–[16]. These so-called multiplex networks were introduced in the social sciences several years ago [17] and provide a new way to advance the study of network complexity. They enable us to determine how the interplay between layers affects the dynamic processes running through them. This multiplex network approach has proven to be a successful tool in modeling a number of real-world systems, e.g., the European air transport system [18], [19] and the global cargo ship network [20].
The study of propagation processes in multiplex networks is a rapidly evolving research area. In particular, because of the urgent need for control strategies, the study of the propagation of disease epidemics has been the focus of much recent work. One of the most successful models used to describe the propagation of recurrent diseases is the susceptible-infected-susceptible (SIS) model. Research using the SIS model on multiplex networks [21]–[23] has found that the dynamics of the disease across a multiplex system is characterized by a critical point that is lower than the critical point of each isolated layer. Very recently Cozzo et al. [24] studied the SIS model in a multiplex network using a contact-contagion formulation with a rate of infection within each layer and a rate of infection between layers. They found that the critical point of the total system is always dominated by one of the layers. Although the SIS model can describe the propagation dynamics for recurrent diseases in which individuals are constantly being reinfected, there are many diseases in which ill individuals either die or after recovery become immune to future infections. For this class of disease, the favorite approach to describing the spreading process is the susceptible-infected-recovered (SIR) model [25]–[27]. At present there are only a few instances in which the SIR model has been applied to a network of networks. Dickison et al. [28] use the SIR model to numerically explore two interacting networks in order to determine the probabilities that the disease will spread within each individual network and between the networks of the system. Marceau et al. [29] developed an analytical approach that captures the dynamic interaction between two different SIR propagations over a multiplex network. Yagan et al. [30] studied the SIR model in a multiplex network with two different information layers, a virtual layer and a physical layer, each with different propagation speeds. They found that, even when the disease does not propagate in a particular layer, an epidemic can occur in the conjoint virtual-physical network.
In social interactions, individuals are not necessarily present in all layers of a society. To allow for this significant constraint, we use a partially overlapped multiplex network in which only a fraction of individuals are present in all layers. Our goal is to study how this overlapping fraction affects the spreading of such nonrecurrent diseases as influenza, the H5N5 flu or the Severe Acute Respiratory Syndrome (SARS) [31]. We use the SIR model over a partially overlapped multiplex network. In the SIR model each individual of the population can be in one of three different states: susceptible, infected, or recovered. Infected individuals transmit the disease to its susceptible neighbors with a probability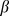 
and recover after a fixed time 
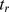. The spreading process stops when all the infected individuals are recovered. The dynamic of the epidemic is controlled by the transmissibility 
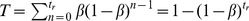, which is a measure of disease virulence, i.e., the effective probability that the disease will be transmitted across any given link. As in the SIR model, an individual cannot be reinfected, the disease spreads through branches of infection that have a tree-like structure, and thus can be described using a generating function formalism [32], [33] that holds in the thermodynamic limit.
We first examine some of the concepts of the generating function formalism for an isolated network, and we then extend this formalism to the partially overlapped multiplex network. In the generating function framework, the relevant magnitude that provides information about the process is the probability 
that a branch of infection can extend throughout the network [34], [35]. When a branch of infection reaches a node of connectivity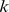 
across one of its links, the branch can only expand through its remaining 
connections. Thus the probability that a node of connectivity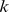 
belongs to a branch of infection is proportional to 
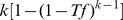, since the probability to reach a node through a link is proportional to its connectivity. Thus 
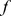verifies the self-consistent equation 
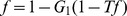in isolated networks, where 
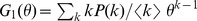is the generating function of the underlying branching process [33], 
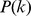is the degree distribution, and 
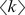is the average degree of the network. In the steady state of the epidemics, the branches of infection form a single cluster of recovered individuals made up of nodes that were infected by some of its connections. Thus the fraction of nodes in the cluster of infection of an isolated network is given by 
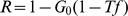, where 
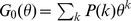is the generating function of the degree distribution. Within this formalism we find that the self-consistent equation has a nontrivial solution above the critical transmissibility 
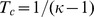, where 
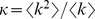is the branching factor and 
is the second moment of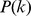 
. Since 
can be used to measure the connectivity dispersion of the network, we find that the critical threshold is very small for heterogeneous networks. At this critical threshold, the fraction of recovered individuals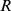 
overcomes a second-order phase transition where at 
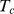and below 
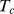the disease cannot spread and above 
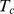the disease infects a significant fraction of the population and becomes an epidemic. Therefore an epidemic occurs only if the number of recovered individuals in the steady state reaches or exceed a minimum size 
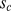. In this letter, we use 
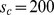for all our simulations [36].
Method
In our model we use an overlapping multiplex network formed by two layers, A and B, of the same size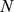 
, where an overlapping fraction 
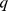of shared individuals is active in both layers. Figure 1(a) shows schematically the partially overlapped network. The dashed lines that represent the fraction 
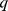of shared individuals should not to be interpreted as interacting or interdependent links but as the shared nodes and their counterpart in the other layer.
Figure 1. Scheme of a SIR epidemic process in a partially overlapped multiplex network.
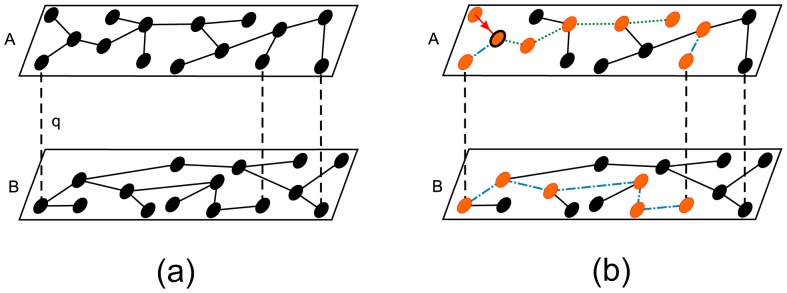
Partially overlapped multiplex network with layer size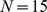 
and fraction of shared nodes 
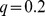. The total size of the network is 
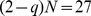individuals. The dashed lines are used as a guide to show the fraction 
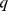of shared nodes. (a) Before the spreading dynamics, all individuals are in the susceptible stage represented by black circles. (b) In the steady state of the epidemic, the recovered individuals are denoted by orange circles. The branches of infection start in the link denoted by a red arrow, which leads to an infected orange node denoted with a black contour. Two branches expand through the two available links of that node. One of the branches denoted by green dotted lines corresponds to a branch of infection that only spreads through layer A that is described by the first term of 
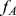in Eq. (1). The other branch denoted in blue dash-dotted lines is a branch of infection that spreads through both layers and is described by the second term of 
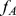in Eq. (1). An analogous interpretation holds for the terms of 
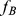of Eq. (1).
For the simulation, we construct each layer using the Molloy Reed algorithm [37], we choose randomly a fraction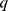 
of nodes in each of the layers that represent the same nodes. In our model of the SIR process we assume that the transmissibility is the same in both layers because there is only one disease and all individuals in the system spread equally. We begin by infecting a randomly chosen individual in layer A. The spreading process then follows the SIR dynamics in both layers, the overlapped nodes in both layers have the same state because they represent the same individuals. After all infected nodes infect their susceptible neighbors with probability 
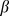in both layers, the time is increased in one, and the states of the nodes are updated simultaneously. Note that because there are shared nodes the branches of infection can cross between the two layers. Thus the probability that, following a random link, a node belonging to the infected cluster will be reached in each layer can be written
 |
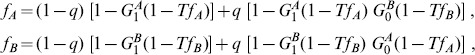(1) |
where 
and 
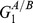are the generating functions defined above for layer A and B, respectively. In Eq. (1) both 
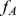and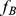 
are written as the sum of two terms that takes into account all possible spreading of the branches of infection. The first term corresponds to those branches of infection that only spread within their own layer, while the second term takes into account those branches that spread through both layers. Figure 1(b) shows how a node is reached through an ingoing link marked by an arrow. The disease spreads through both available outgoing links of that node in layer A and develops two branches of infection. The green dotted line denotes the branch that stays in layer A and corresponds to the first term of Eq. (1) for 
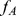. The second term of Eq. (1) for 
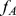is indicated by the blue dot-dashed branch that reaches layer B through a shared node and then spreads to its neighbors on that layer. After the shared node is infected, the branch spreads through five links in layer B and reaches another shared node that allows the branch of infection to spread back to layer A. An analogous interpretation holds for the terms of 
.
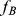Results
The solution of Eq. (1) for all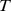 
above and at criticality is given by the intersection of 
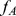and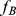 
, which can be derived by solving the determinant equation 
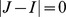, where 
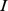is the identity and 
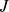is the Jacobian matrix of Eq. (1). The only possibility to have a non-epidemic regime is that none of the branches of infection spread, i.e.
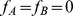. Therefore below and at criticality 
, an evaluation of the Jacobian matrix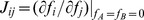 
given by
 |
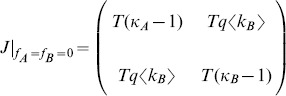(2) |
allow us to obtain a quadratic equation for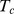 
with only one stable solution [38] given by,
 |
(3) |
where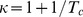 
is the total branching factor and 
, 
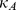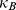are the isolated branching factors of layer A and B respectively. For 
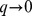we recover the isolated network result 
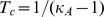, which is compatible with our model in which the infection starts in layer A and, because 
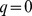, the disease never reaches layer B. In contrast, when 
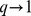, we find 
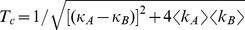. Note that 
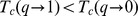. In general, 
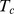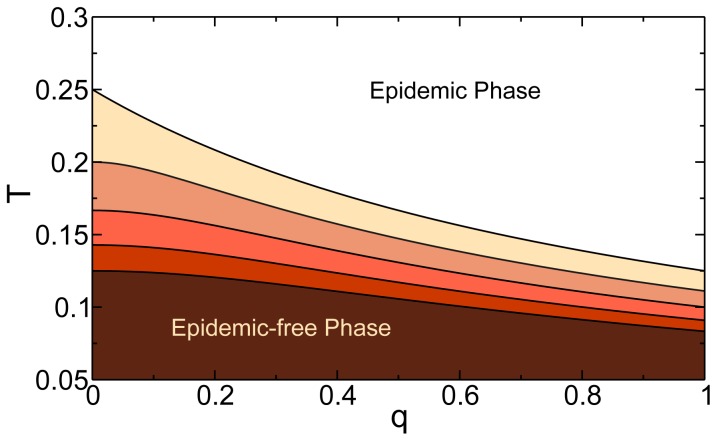
decreases as a function of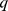 
. This is the case because an increase in the overlapping between layers causes an increasing in the dispersion of the degrees of the nodes, therefore the total system becomes more heterogeneous in degree making the total branching factor to increase, i.e., the total branching factor is equal to or bigger than the branching factor of the isolated layers. Figure 2 shows this behavior with a plot of a phase diagram in the plane 
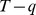for Erdös-Rényi (ER) layers [39] whose degree distribution is Poissonian 
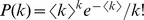and its branching factor is given by 
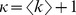. Figure 2 shows the critical lines 
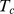given by Eq. (3) as a function of the overlapping fraction 
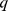when one of the layers is fixed at 
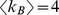for the different average connectivities 
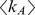of layer A. The colored areas correspond to the epidemic-free phase for a given connectivity in layer A, and the region above the critical lines belongs to the epidemic phase. The left and right extremes of the critical lines correspond to the limits 
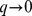and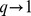 
for Eq. (3) mentioned above.
Figure 2. Dependence of the epidemic threshold of the SIR model with the overlapping fraction and topology of the layers.
Phase diagram in the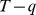 
plane for two Erdös-Rényi layers with 
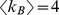and different values of 
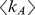. The black full lines correspond to 
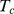obtained theoretically from Eq. (3) for 
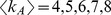from top to bottom. The limit 
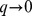corresponds to a disease spreading in layer A when it is isolated and the limit 
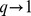represents the fully overlapped multiplex network. Colored regions correspond to the epidemic-free phase for each value of 
, while the region above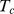 
corresponds to the epidemic-phase.
In the steady state, the fraction of nodes reached by the branches of infection, i.e., the recovered individuals in each layer, can be written
 |
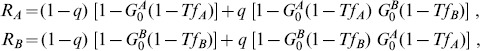(4) |
and the total fraction of recovered individuals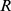 
is given by
 |
(5) |
where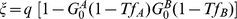 
is the fraction of shared nodes that have recovered in the steady state. The factor 
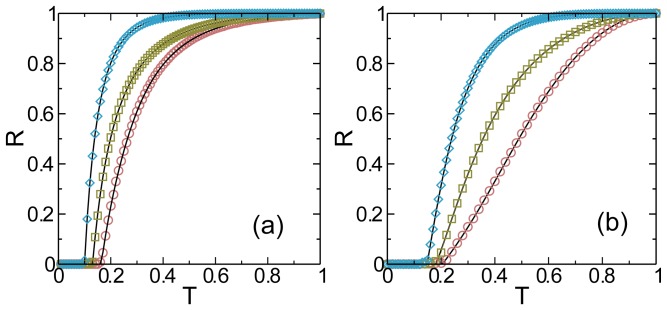
appears because the total number of individuals in the system is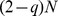 
. Figure 3 plots the total fraction 
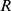of recovered individuals, obtained from Eq. (5), as a function of 
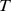for different values of the overlapping fraction 
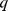and compares it with simulation results for 
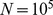nodes and 
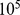realizations. Figure 3 shows the results for (a) two ER layers with 
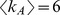and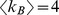 
and (b) two power law distributed layers with an exponential cutoff 
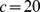, where 
, and exponents 
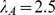and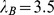 
. In both cases we observe the typical second order phase transition of the SIR process with the transmissibility 
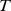as the control parameter—with perfect agreement between the theory and the simulations. As the overlapping fraction 
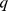increases [see Eq. (3)] the critical threshold moves to the left and the increase in 
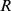becomes more abrupt but the second-order character of the SIR for isolated networks is preserved [40]. In the case of the power-law distributed layers, when 
, 
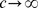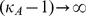, which eliminates any dependence of the critical threshold on 
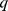, as can be inferred from Eq. (3).
Figure 3. Theoretical predictions and simulations for the fraction of recovered individuals in the steady state of the epidemics.
Total fraction of recovered individuals in the steady state of the SIR model with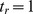 
for (a) two Erdös-Rényi layers with 
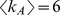and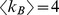 
and for (b) two power law layers with exponential cutoff 
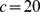with 
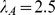and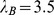 
, the minimum and maximum values of 
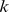where set as 
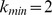and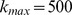 
, respectively, for both layers. In both panels full black lines correspond to theory given by Eq. (5) and simulations results are given for 
in pink circles, 
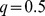in green squares and 
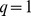in blue diamonds. All simulations were done with a total system size of 
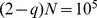and over 
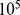realizations.
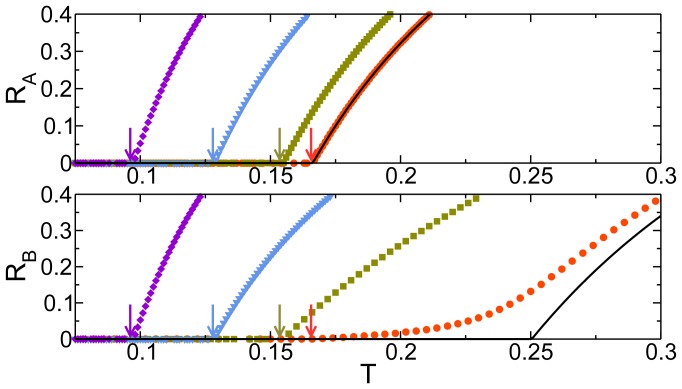
Finally we investigate the effect of the overlapping fraction by observing the epidemic in each layer separately, shown in Fig. 4. When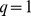 
, the threshold [see Eq. (3)] is at its minimum and both layers have the same fraction of recovered nodes. This is the case because the layer with the bigger isolated threshold (or the smaller isolated branching factor) can be infected by either its own infection branches or by those coming from the other layer. This second possibility decreases with 
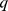. For lower values of 
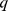the epidemic threshold increases because the total branching factor is lower and the layer with the lower isolated threshold cannot as effectively infect the other layer. As a consequence, when 
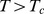the fraction of recovered individuals of the layers detach from each other and show a difference that increases as 
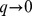[see Eq. (3)]. In this limit, the joined threshold approaches quadratically the threshold of the isolated layer with the higher branching factor. Thus no matter how small the overlapping fraction is, when 
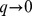the epidemic threshold of the system is given by the lower isolated threshold that corresponds to the layer with the higher propagation capability. This limit is consistent with the results found in Ref. [24] for the SIS model in which the epidemic threshold of the system is dominated by the layer with the lower isolated threshold. Thus although a system of two completely isolated layers is indistinguishable from a system of two layers that share only a few nodes (
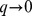), the isolated epidemic threshold of the less propagating layer will change discontinuously and acquire the isolated threshold of the other layer.
Figure 4. Effect of the overlapping fraction in the SIR epidemic threshold on individual layers.
Fraction of recovered individuals vs the transmissibility in the steady state of the SIR model. The values were obtained theoretically from Eq. (4) for two Erdös-Rényi layers with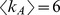 
, 
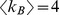and different overlapping fraction values. In orange circles 
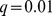, in green squares 
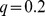, in blue triangles 
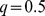and in violet diamonds 
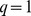. In the upper panel we plot 
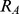and in the bottom panel we plot 
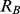. The arrows indicate the threshold 
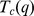and are used as a guide to show that 
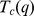is the same for 
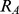and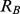 
. The black full lines denote 
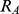(up) and 
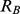(down) when both networks are isolated and 
.
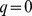Discussion
In summary, we have studied a SIR epidemic propagation model in a partially overlapped multiplex network formed by two layers that share a fraction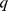 
of nodes. We find that the epidemic threshold 
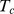of the multiplex network depends on both the topology of each layer and the overlapping fraction 
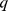. Using of a generating function framework, we find the equation for the threshold 
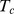and also the equation for the recovered individuals in the steady state of the spreading process. Our analytical predictions are in agreement with extensive simulation results. Finally, we analyze the fraction of recovered individuals in the steady state as a function of the transmissibility 
for layer A and layer B separately. When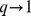 
, we find that the epidemic threshold is at its minimum and, because all individuals belong to both layers, that both layers have the same fraction of recovered nodes for all 
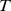. As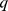 
decreases, the total branching factor of the system decreases and the epidemic threshold increases, and when 
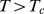the fraction of recovered individuals in both layers detach from each other. When 
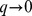, the epidemic threshold of the system is dominated by the isolated epidemic threshold of the layer with the larger propagation capability and thus it reaches a higher value. Thus although a system of two completely isolated layers is indistinguishable from a system of two layers that share only a few nodes, the presence of these few shared nodes causes the epidemic threshold of the isolated network with the lower propagating capability to discontinuously change to the threshold of the other network. This result may have important implications for the implementation of non-pharmaceutical interventions to control the propagation of diseases on real scenarios. Our study suggests that vaccinating or isolating only that layer with the higher propagation capacity can drastically reduce the total branching factor of the network, as can be seen from Eq. (3). As a consequence, the epidemic threshold of the system increases significantly, and the risk that a disease epidemic will propagate across the entire network is reduced.
Acknowledgments
The authors thank L. D. Valdez for his useful comments. This work is part of a research project of UNMdP and FONCyT (Pict 0293/2008). CB, LGAZ, PAM and LAB wish to thanks Professor H. E. Stanley for a careful proofreading of the manuscript. One of us, LAB, wishes to thank DTRA for the travel support that allow us to accomplish this research.
Funding Statement
The authors have no support or funding to report.
References
- 1.Barrat A, Barthélemy M, Vespignani A (2008) Dynamical Processes on Complex Networks. Cambridge University Press.
- 2.Erez T, Hohnisch M, Solomon S (2005) Statistical economics on multi-variable layered networks. In: Economics: Complex Windows. Springer Milan, pp. 201–217.
- 3. Gao J, Buldyrev SV, Havlin S, Stanley HE (2011) Robustness of a network of networks. Physical Review Letters 107: 195701. [DOI] [PubMed] [Google Scholar]
- 4. Gao J, Buldyrev SV, Stanley HE, Havlin S (2012) Networks formed from interdependent networks. Nature Physics 8: 40–48. [DOI] [PubMed] [Google Scholar]
- 5. Dong G, Gao J, Du R, Tian L, Stanley HE, et al. (2013) Robustness of network of networks under targeted attack. Physical Review E 87: 052804. [DOI] [PubMed] [Google Scholar]
- 6. Valdez LD, Macri PA, Stanley HE, Braunstein LA (2013) Triple point in correlated interdependent networks. Physical Review E 88: 050803 (R).. [DOI] [PubMed] [Google Scholar]
- 7. Buldyrev SV, Parshani R, Paul G, Stanley HE, Havlin S (2010) Catastrophic cascade of failures in interdependent networks. Nature 464: 1025–1028. [DOI] [PubMed] [Google Scholar]
- 8. Baxter GJ, Dorogovtsev SN, Goltsev AV, Mendes JFF (2012) Avalanche collapse of interdependent networks. Physical Review Letters 109: 248701. [DOI] [PubMed] [Google Scholar]
- 9. Brummitt CD, D'Souza RM, Leicht EA (2012) Suppressing cascades of load in interdependent networks. Proceedings of the National Academy of Sciences 109: 680–689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Lee KM, Kim JY, Cho WK, Goh KI, Kim IM (2012) Correlated multiplexity and connectivity of multiplex random networks. New Journal of Physics 14: 033027. [Google Scholar]
- 11. Brummitt CD, Lee KM, Goh KI (2012) Multiplexity-facilitated cascades in networks. Physical Review E 85: 045102 (R).. [DOI] [PubMed] [Google Scholar]
- 12. Gómez S, Díaz-Guilera A, Gómez-Gardeñes J, Pérez-Vicente CJ, Moreno Y, et al. (2013) Diffusion dynamics on multiplex networks. Physical Review Letters 110: 028701. [DOI] [PubMed] [Google Scholar]
- 13. Kim JY, Goh KI (2013) Coevolution and correlated multiplexity in multiplex networks. Physical Review Letters 111: 058702. [DOI] [PubMed] [Google Scholar]
- 14. Cozzo E, Arenas A, Moreno Y (2012) Stability of boolean multilevel networks. Physical Review E 86: 036115. [DOI] [PubMed] [Google Scholar]
- 15. Gómez-Gardeñes J, Reinares I, Arenas A, Floria LM (2012) Evolution of cooperation in multiplex networks. Scientific Reports 2 620: srep00620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kivelä M, Arenas A, Barthélemy M, Gleeson JP, Moreno Y, et al. (2013) Multilayer networks. Http://arxiv.org/abs/1309.7233.
- 17.Wasserman S, Faust K (1994) Social Network Analysis. Cambridge University Press.
- 18. Cardillo A, Zanin M, Gómez-Gardeñes J, Romance M, García del Amo AJ, et al. (2013) Modeling the multi-layer nature of the european air transport network: Resilience and passengers re-scheduling under random failures. The European Physical Journal Special Topics 215: 23–33. [Google Scholar]
- 19. Cardillo A, Gómez-Gardeñes J, Zanin M, Romance M, Papo D, et al. (2013) Emergence of network features from multiplexity. Scientific Reports 3: 1344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Kaluza P, Kölzsch A, Gastner MT, Blasius B (2010) The complex network of global cargo ship movements. Journal of the Royal Society: Interface 7: 1093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Saumell-Mendiola A, Serrano MÁ, Boguñá M (2012) Epidemic spreading on interconnected networks. Physical Review E 86: 026106. [DOI] [PubMed] [Google Scholar]
- 22.Sahneh F, Scoglio C, Chowdhury F (2013) Effect of coupling on the epidemic threshold in interconnected complex networks: A spectral analysis. In: American Control Conference (ACC), 2013. pp. 2307–2312.
- 23. Granell C, Gómez S, Arenas A (2013) Dynamical interplay between awareness and epidemic spreading in multiplex networks. Physical Review Letters 111: 128701. [DOI] [PubMed] [Google Scholar]
- 24. Cozzo E, Baños RA, Meloni S, Moreno Y (2013) Contact-based social contagion in multiplex networks. Physical Review E 88: 050801 (R).. [DOI] [PubMed] [Google Scholar]
- 25.Bailey NTJ (1975) The Mathematical Theory of Infectious Diseases. Griffin, London.
- 26. Colizza V, Barrat A, Barthélemy M, Vespignani A (2006) The role of the airline transportation network in the prediction and predictability of global epidemics. Proceedings of the National Academy of Sciences 103: 2015–2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Colizza V, Vespignani A (2007) Invasion threshold in heterogeneous metapopulation networks. Physical Review Letters 99: 148701. [DOI] [PubMed] [Google Scholar]
- 28. Dickison M, Havlin S, Stanley HE (2012) Epidemics on interconnected networks. Physical Review E 85: 066109. [DOI] [PubMed] [Google Scholar]
- 29. Marceau V, Noël PA, Hébert-Dufresne L, Allard A, Dubé LJ (2011) Modeling the dynamical interaction between epidemics on overlay networks. Physical Review E 84: 026105. [DOI] [PubMed] [Google Scholar]
- 30. Yagan O, Qian D, Zhang J, Cochran D (2013) Conjoining speeds up information diffusion in overlaying social-physical networks. IEEE JSAC Special Issue on Network Science 31: 1038. [Google Scholar]
- 31. Colizza V, Barrat A, Barthélemy M, Vespignani A (2007) Predictability and epidemic pathways in global outbreaks of infectious diseases: the sars case study. BMC Medicine 5: 34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Callaway DS, Newman MEJ, Strogatz SH, Watts DJ (2000) Network robustness and fragility: Percolation on random graphs. Physical Review Letters 85: 5468. [DOI] [PubMed] [Google Scholar]
- 33. Newman MEJ, Strogatz SH, Watts DJ (2001) Random graphs with arbitrary degree distributions and their applications. Physical Review E 64: 026118. [DOI] [PubMed] [Google Scholar]
- 34. Braunstein LA, Wu Z, Chen Y, Buldyrev SV, Kalisky T, et al. (2007) Optimal path and minimal spanning trees in random weighted networks. I J Bifurcation and Chaos 17: 2215–2255. [Google Scholar]
- 35. Valdez LD, Buono C, Macri PA, Braunstein LA (2013) Social distancing strategies against disease spreading. FRACTALS 21: 1350019. [Google Scholar]
- 36. Lagorio C, Migueles MV, Braunstein LA, López E, Macri PA (2009) Effects of epidemic threshold definition on disease spread statistics. Physica A 388: 755–763. [Google Scholar]
- 37. Molloy M, Reed B (1995) A critical point for random graphs with a given degree sequence. Random Structures and Algorithms 6: 161–180. [Google Scholar]
- 38.Alligood KT, Sauer TD, Yorke JA (1997) CHAOS: An Introduction to Dynamical Systems. Springer.
- 39. Erdős P, Rényi A (1959) On random graphs. i. Publications Mathematicae 6: 290–297. [Google Scholar]
- 40. Newman MEJ (2002) Spread of epidemic disease on networks. Physical Review E 66: 016128. [DOI] [PubMed] [Google Scholar]