Abstract
It has long been appreciated that Mg2+ is essential for the stabilization of RNA tertiary structure. However, the problem of quantitative prediction for the ion effect in tertiary structure folding remains. By using the virtual bond RNA folding model (Vfold) to generate RNA conformations and the newly improved tightly bound ion model (TBI) to treat ion-RNA interactions, we investigate Mg2+-facilitated tetraloop-receptor docking. For the specific construct of the tetraloop-receptor system,the theoretical analysis shows that the Mg2+-induced stabilizing force for the docked state is predominantly entropic and the major contribution comes from the entropy of the diffusive ions. Furthermore, our results show that Mg2+ ions promote tetraloop-receptor docking mainly through the entropy of the diffusive ions. The theoretical prediction agrees with experimental analysis. The method developed in this paper, which combines the theory for the (Mg2+) ion effects in RNA folding and RNA conformational sampling, may provide a useful framework for studying the ion effect in the folding of more complex RNA structures.
Introduction
In RNA tertiary structure, a GNRA hairpin tetraloop (TL) interacts with specific helix to form a tetraloop-receptor (TL-R) complex through long-range contacts.1,2,3 Tetraloop-receptor complex is a frequently occurring basic building block for RNA tertiary structure. Therefore, understanding the mechanism of its formation can provide useful insights into the physical mechanism for the assembly of tertiary folds. Because the formation of a tetraloop-receptor involves significant build-up of RNA backbone charges, the folding driving force is intrinsically sensitive to the ionic condition of the solution.1,4-8
Several recent experiments have uncovered a number of novel ion effects in the formation of tetraloop-receptor motif.1,5,9-23 Davis et al used NMR to study the role of metal ions in stabilizing the tetraloop-receptor solution structure and found the stable native structure of the tetraloop-receptor formed under a wide ionic condition.5 Qin at al used site-directed spin labeling to explore the tetraloop-receptor conformational changes. The experimental data demonstrated that base unstacking is an intrinsic feature of the solution tetraloop-receptor complex formed in the presence of Mg2+.24 Meulen and Butcher studied the tetraloop-receptor folding in salt solution using isothermal titration calorimetry (ITC) and found a significant difference in the kinetic and thermodynamic profiles of the system when it’s stabilized by K+ versus Mg2+ ions.23 The result further suggested that the tertiary folding in physiological conditions may involve a complex interplay between K+- and Mg2+-induced stabilization23. Downey and co-workers investigated the effect of pressure and cosolutes on the tetraloop-receptor docking using FRET (fluorescence resonance energy transfer)10 and found that (a) hydrostatic pressure slightly destabilizes the GAAA tetraloop-receptor interaction and (b) increasing the nondenaturing cosolutes favors the formation of the tetraloop-receptor tertiary structure.
Motivated by the need to understand the conformational distribution and folding pathways, a series of FRET experiments have been performed for the tetraloop-receptor docking in the monovalent and multivalent solutions.1,13,17,22,25-27 These single molecule experiments led to several important findings. One of the remarkable findings is the entropic effect as the dominant driving force for tetraloop-receptor docking.25 In contrast to the entropic effect, with increasing [Mg2+], the Mg2+-induced changes of the activation enthalpy and the overall exothermicity for docking are both negligible.22 Moreover, in the transition state, Mg2+-induced tetraloop-receptor docking arises from reducing the entropic barrier and the overall entropic penalty for docking.22 This conclusion contradicts with the conventional notion that the ion-dependent folding stability comes from charge neutralization and the resultant reduction in Coulomb repulsion energy.25,26,28-33
The above experiments have provided useful results on the ion dependence of the docking enthalpy and entropy.13,15-17,19,22,23,25,26 Inspired by the deep insights from the experimental findings, we here develop a theory to analyze the quantitative roles for the different components of the driving force for docking. The detailed mechanism for tetraloop-receptor docking is determined by the complex interplay between multiple factors, such as the electrostatic energy, the conformational entropy, the solvent polarization energy and the entropies of the bound and diffusive ions. The three-dimensional atomic structures of the free form (undocked) and the native form (docked) of the tetraloop-receptor complex have been experimentally determined.34-40 These structures have provided invaluable information about the energetics for the folding of the tetraloop-receptor. However, to fully understand the forces that promote the formation of the structure, we need to go beyond the structures and understand the folding thermodynamics and kinetics of the system. This requires the information about the free energy landscape of the complete conformational ensemble, including the conformational ensembles for the free and the docked states. In the present study, we investigate the full electrostatic free energy landscape of the tetraloop-receptor docking in Na+ and Mg2+ mixed solution.
One of the extensively studied tetraloop-receptor system in experiments (such as the single molecule FRET experiment) consists of three minimal elements: a GAAA tetraloop, an 11-nt receptor in a helix, and a 7-nt poly(U) loop/linker between the tetraloop and the receptor.1,13,17,22,25-27 We choose the above minimal tetraloop-receptor construct as a paradigm system for our study. To generate the conformational ensemble, we sample the three-dimensional (3D) structures of the docked and the undocked tetraloop-receptor in using the virtual bond-based RNA folding model (Vfold model).41-43 In the Vfold model, RNA virtual bonds (P-C4-P bonds) are configured on a diamond lattice and RNA conformations are enumerated through 3D self-avoiding random walks of RNA virtual bonds on the diamond lattice. An advantage of the Vfold model is that it can treat chain connectivity and exclude volume interferences within a loop/junction and between loop and loop and between loop and helix. For each conformation of the tetraloop-receptor docked and undocked states, we use the tightly bound ion (TBI) model44-49 to calculate the electrostatic free energy in a Mg2+ solution. The TBI model is a statistical mechanics-based polyelectrolyte theory that can treat ion fluctuation and correlation effects for counterions around a nucleic acid structure. For multivalent ions such as Mg2+ ions, whose correlation and fluctuation effects may be strong, the TBI theory leads to better predictions for the ion-effect in folding thermodynamics than mean-field theories such Poisson-Boltzmann Equation.44-49 Here we used a combined Vfold/TBI approach. A unique advantage of such a combined theory is its ability to predict (a) the full energy landscape and (b) the detailed ion dependence of each enthalpic and entropic component as determined from the conformation ensemble. Our results show that the dominant Mg2+-induced driving force comes from the decrease in the entropic penalty of the diffusive ions upon docking and the increase of the compactness of the structures in the undocked conformational ensemble. The conclusion supports the experimental findings. Furthermore, we found that the Coulomb interaction also plays a (weaker) role in promoting the tetraloop-receptor docking. The theory-experiment agreement suggests that the new theoretical method here may be reliable and can be useful for further treatment of the ion-dependent folding of more complex RNA tertiary structures.
Methods and Theory
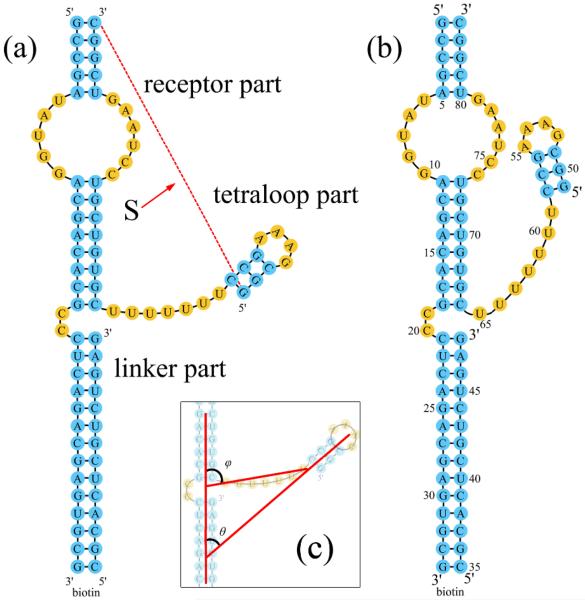
We consider two states for the tetraloop-receptor system: the docked (F) and the undocked (U) state (see Fig. 1a). In the undocked state, the tetraloop is freely oriented. In the docked state, the tertiary interactions such as the hydrogen binding and base staking are stabilized between the docked tetraloop and receptor.17,22 In our calculation, we focus on the ion-dependence of the electrostatic free energy landscape. The tetraloop-receptor docking stability ΔGdock is determined by the free energy difference between the docked (ΔG(F)) and the undocked (ΔG(U)) states:
| (1) |
Figure 1.
The GAAA tetraloop-receptor system. The GAAA tetraloop and the receptor are connected by a U7 single-stranded linker. (a) The undocked state; (b) The docked state; (c) The definition of the structure parameters θ and φ.
I. Structure model
In order to compare the theoretical predictions with the experimental data, we focus on an isolated GAAA tetraloop-receptor system (shown in Fig. 1a and b) similar to the one used in the experiment.22,25,26 The only difference between our system and the experimental construct is that the DNA strand22,25,26 connected to a biotin in the experiment is replaced by an RNA strand in our calculation, so the RNA duplex can be conveniently modeled as an A-form helix. Since the tetraloop-receptor docking site is relatively distant from the modified RNA duplex, we believe such a minor change would not cause notable changes to the results.
The tetraloop-receptor system shown in Fig. 1 has three parts: the receptor, the linker and the tetraloop. The receptor part is formed by three long helices connected by an internal loop (receptor) and a short C2 bulge loop. The linker part is a long U7 flexible loop and the tetraloop part contains a GAAA tetraloop and the attached helix. One of the key issues for the structure modeling is how to sample the conformations for the docked and the undocked states. We use the experimentally determined structures (PDB ID: 1GID)37 for the docked state. In the undocked state, we use the solution structure of the isolated tetraloop receptor (PDB ID: 1TLR)38 for the receptor. Experimental structure determination shows that the tetraloop structure is unchanged before and after docking, so we used the same PDF structure (PDB ID: 1GID)37 for the tetraloop for the docked and the undocked states. In both states, the flexible U7 linker gives an ensemble of 3D conformations for the system. In the undocked state, the end of the U7 linker connected to the tetraloop is free while the other end is fixed. As the U7 loop samples the different conformations in the 3D space, the tetraloop attached to the linker moves accordingly in the 3D space. For the docked state, the tetraloop is fixed in the 3D space according to the PDB structure of the docked complex (PDB code: 1GID),37 so both ends of the linker loop are fixed while the remaining five uracil nucleotides in the loop are flexible.
The Vfold model generates 2628 and 5985453 complete sets of conformations for the docked and undocked states, respectively. To classify the conformations, we define three structure parameters: the angle θ and the end-to-end distance S between the tetraloop helix and the receptor helix and the angle φ between the end-to-end vector and the receptor helix (see Fig. 1c).
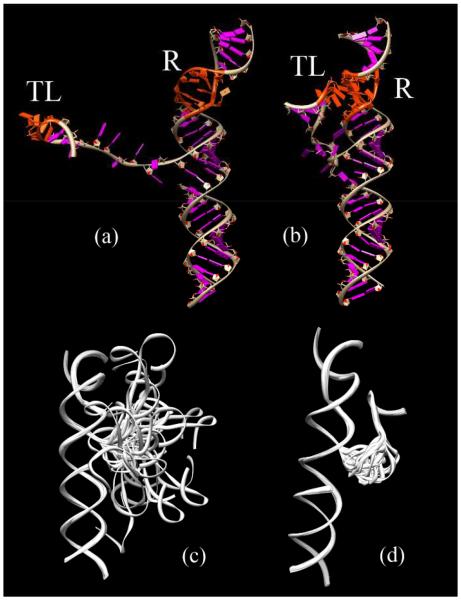
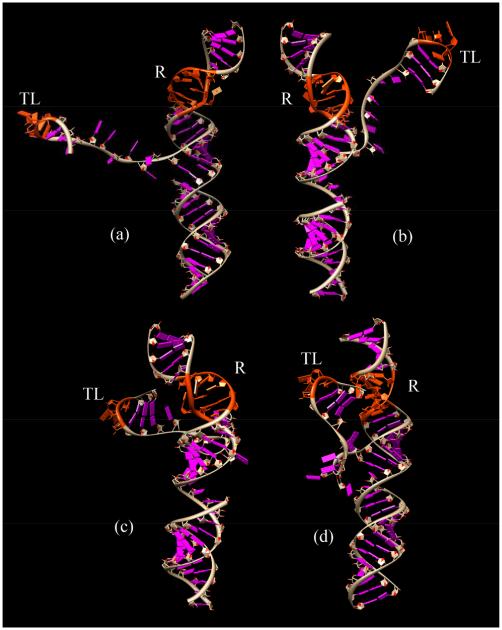
Given the large number of conformations in the docked and undocked states, it is computationally impractical to consider all the conformations in the free energy calculation. We use Monte Carlo method to sample conformations from the complete ensemble. To ensure the broad coverage of the conformational sampling for the docked and the undocked states, we uniformly divide the conformational space into 30 clusters according to the tetraloop-receptor distance S. In each cluster, we randomly select 30 conformations. For the docked state, the structure of the tetraloop-receptor complex is rigid (PDB ID: 1GID), therefore, we fix the distance S according to the experimentally determined structure of the complex. This leads to only one conformational cluster according to the S value. It is important to note that although there is only one cluster for the docked state, the tether loop connecting the tetraloop and the receptor can sample a large number of conformations. Our calculation for the docked state accounts for such loop-generated conformational ensemble. To verify the validity of the conformational sampling, we perform four independent sets of Monte Carlo samplings to generate four groups of docked and undocked conformational ensembles. In each group, there are 900 conformations for the undocked states and 30 conformations for the docked case. Figs. 2c and d show subsets (30 structures) of the conformational ensembles for the undocked and the docked states.
Figure 2.
Representative structures for (a) the undocked state and (b) the docked state. “TL” represents the GAAA tetraloop, and “R” represents the receptor, both the GAAA tetraloop and the receptor parts are marked with red color. (c) and (d) show the conformational ensemble of the undocked and the docked states, respectively.
II. Electrostatic free energies of the tetraloop-receptor system
For each given tetraloop-receptor conformation, we use the tightly bounding ion model (TBI)44-49 to calculate the electrostatic free energy of the system. In contrast to other models, the TBI model has the advantage of accounting for the fluctuation in ion distribution and the correlations between multivalent ions in the close vicinity of the RNA surface. The model can also treat solvent polarization through the Generalized Born model (GB). See the Supporting Information (SI) for the details of the TBI model.
The TBI model gives the electrostatic free energy and ion binding properties for each tetraloop-receptor conformation. The Boltzmann-weighted average over all the conformations gives the net free energy, enthalpy and entropy of the docked and the undocked states respectively. More importantly, the model can provide quantitative results for the different energetic components, from which we determine the roles of the different forces in tetraloop-receptor docking. For each conformation j, we compute the total free energy and its components: the Coulomb energy , the polarization energy and the entropic free energy . For a given state M (the docked or undocked state), we calculate the free energy ΔGT(M) from the conformational ensemble (see SI).
The Coulomb energy ΔGE(M) and the polarization energy ΔGP(M) are given by the following equations:
| (2) |
and
| (3) |
where is the electrostatic free energy for the jthconformation in the ith cluster for state M. is calculated from the TBI model (see SI). and are the Coulomb energy and the polarization energy for the jth conformation in the ith cluster in state M, respectively. and are calculated from the TBI model (see SI). The entropic free senergy ΔGS(M) can be calculated as:
| (4) |
Here, the entropic free energy contains two parts: the first part is from the ion entropy ΔGS_ion(M), including both the bound and the diffusive ions; the second part is from the conformational entropy ΔGS_conf(M). The ion entropy can be calculated from the following equation:
| (5) |
where is the entropic free energy for the jth conformation in the ith cluster in state M. Because the entropic free energy is for a fixed conformation, it represents the entropy from the ions (without the conformational entropy). The conformational entropy part can be obtained from the difference between the total entropic free energy and the ionic entropic free energy:
| (6) |
The TBI model is used to calculate the electrostatic free energy for the docked and the undocked states in various [Mg2+] with the 0.1M NaCl background at 37°C (the experimental condition).22 The docking free energy, i.e., the free energy difference between the docked and the undocked states, is determined from Eq. 1.
Results
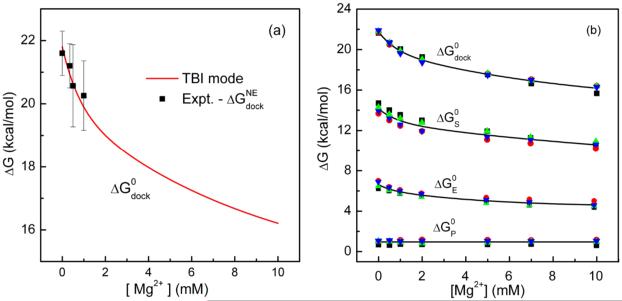
Our focus here is the [ion]-dependence of the free energy landscape. Fig. 3a shows the comparison of the experimental data22 and our predicted results for the [ion]-dependence of the docking free energy ΔGdock. The experimental data includes both the electrostatic contribution and the nonelectrostatic contribution . In the solved tetraloop-receptor structure, the tetraloop binds by base stacking and hydrogen bonding to the minor groove of the receptor. The energies of base stacking and hydrogen bonding are not accounted for in the ion electrostatics calculations. Other nonelectrostatic interactions may include the nonpolar solvation energy. Our estimation for the change of the solvent accessible surface area between the docked and the undocked states a nonpolar solvation free energy of proximately 11 kcal/mol (see SI). The hydrogen bonding/base stacking network and the nonpolar solvation energy constitute the major portion of the nonelectrostatic free energy .
Figure 3.
The total docking free energy ΔGdock and its components. (a) Comparison between the predicted electrostatic free energy for docking ΔGdock and the experimental data for the total docking free energy minus 20.6 kcal/mol.22 Here the non-electrostatic contribution () of −20.6 kcal/mol accounts for the tertiary interaction energy between the tetraloop and the receptor. (b) The total docking free energy (ΔGdock) and the corresponding component free energies as a function of the Mg2+ concentration in the background of 0.1M NaCl at 37°C. ΔGS, ΔGE and ΔGP are respectively the entropic free energy, the Coulomb energy and the solvent polarization energy contributions.
Assuming the nonelectrostatic free energy to be independent of the ion concentration, we can extract as the difference between the total docking free energy ΔGdock and the electrostatic free energy at any ion concentration as the reference state45: . Here ΔGdock is the experimental docking free energy at the reference ionic condition and is calculated from our TBI model.Choosing 0.5mM Mg2+ and 100mM Na+ mixed solution at 37°C as the reference solution condition, is found to be 20.6 kcal/mol. The good theory-experiment comparison as shown in Fig. 3a supports our approach to the [ion]-independent nonelectrostatic free energy .
I. Free energy components
Fig. 3b shows the docking free energy ΔGdock and its components as functions of [Mg2+]. The components include the entropic free energy ΔGS, the Coulomb energy ΔGE and the polarization energy ΔGP, each of them can be computed from Eq. 1. The results shown in Fig. 3b include four sets of data from the four aforementioned Monte Carlo-generated conformational ensembles. The agreement between the four sets of results suggests that our Monte Carlo sampling may be reliable.
The different free energy components have different [Mg2+]-dependence. Similar to the docking free energy ΔGdock, the entropic free energy ΔGS and the Coulomb energy ΔGE decrease with increasing [Mg2+] while the polarization free energy ΔGP keeps nearly constant.
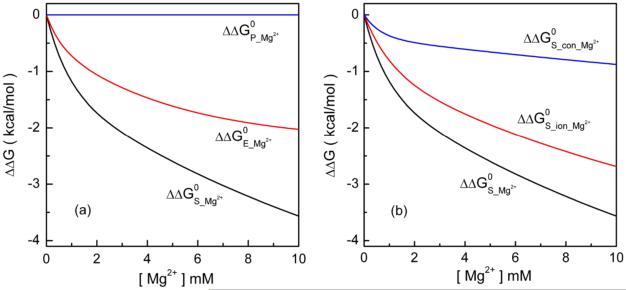
To further highlight the effect of Mg2+ ions in the docking process, we also calculate the Mg2+ ion-induced docking free energy change:30
| (7) |
where ΔG(obs)[Mg2+] and ΔG(obs)[0] are the docking free energies with and without Mg2+ ions, respectively. As shown in Fig. 4a, ΔΔGP keeps nearly zero in the different [Mg2+], suggesting that Mg2+ does not cause significant changes in the solvent polarization effect in the docking process. Both the Coulombic free energy ΔΔGE and the entropic free energy ΔΔGS decrease with increasing [Mg2+] and ΔΔGS decreases more rapidly than ΔΔGE. From 0 mM to 10 mM [Mg2+] at 37°C, ΔGE and ΔGS decrease by about 2 kcal/mol and 3.5 kcal/mol, respectively, contributing about 40% and 60% to the total change of the docking free energy (5.6 kcal/mol). The main contribution comes from the entropic effect. The conclusion is in accordance with the experimental finding.22
Figure 4.
(a) The Mg2+-induced free energy changes: (a) The entropic free energy ΔΔGS, the Coulomb free energy ΔΔGE and the polarization energy ΔΔGP; (b) The conformational entropy contribution ΔΔGS_conf and the ionic entropy contribution ΔΔGS_ion.
II. Entropic effect
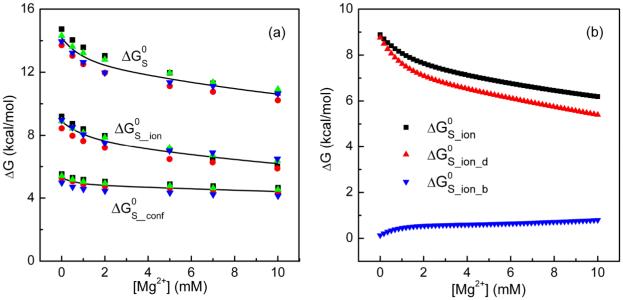
In our calculations, the entropic contribution is divided into two parts: the ion entropy contribution ΔGS_ion and the conformational entropy contribution ΔGS_conf (see Fig. 5a). To further clarify the effect of the different types of ions, we calculate the entropic free energies for the diffusive (ΔGS_ion_d) and the bound ions (ΔGS_ion_b) separately (see Fig. 5b).
Figure 5.
The different components of the entropic free energy. (a) ΔGS_ion and ΔGS_conf are the free energies for the ion entropy and the conformational entropy, respectively. (b) The different components for the ion entropic free energies ΔGS_ion: the diffusive ions ΔGS_ion_d and the bound ions ΔGS_ion_b.
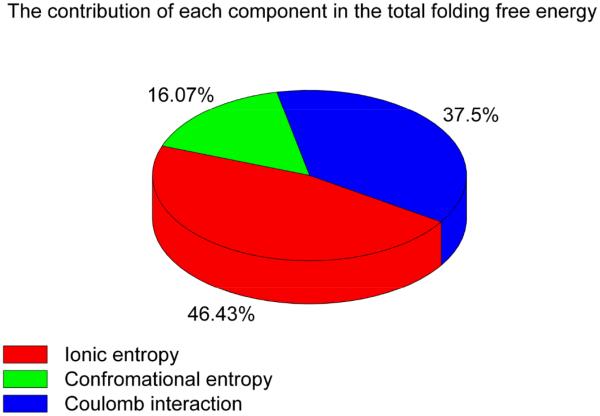
Fig. 5 reveals several important features for the Mg2+-induced entropic free energy changes. First, the entropic free energy for the diffusive ions (ΔGS_ion_d) is significantly larger than that for the bound ions (ΔGS_ion_b). Therefore, the ion entropy effect is dominated by the diffusive ions. Second, the entropic free energies ΔGS, ΔGS_ion and ΔGS_conf decrease with increasing [Mg2+]. Such a [Mg2+]-dependence indicates a Mg2+-induced entropic forces in the stabilization of the docked state. Third, the changes of ΔGS_ion and ΔGS_conf from [Mg2+]=0mM to [Mg2+]=10mM are approximately 2.6 kcal/mol and 0.9 kcal/mol (shown in Fig. 5b), respectively. Then result shows that ion entropy (ΔGS_ion) contributes nearly 75% of the net entropy change for the docking of the tetraloop-receptor system. Fourth, with increasing [Mg2+], ΔGS_ion_d decreases much faster than the total ionic contribution ΔGS_ion, while ΔGS_ion_b, which gradually increases, shows an opposite trend. In Fig. 6, we show the percentage contribution of each component in the total docking free energy.
Figure 6.
The percentage of each component contribution in the total docking free energy at 10mM [Mg2+] with 0.1M [Na+] background at 37°C.
III. Ion uptake
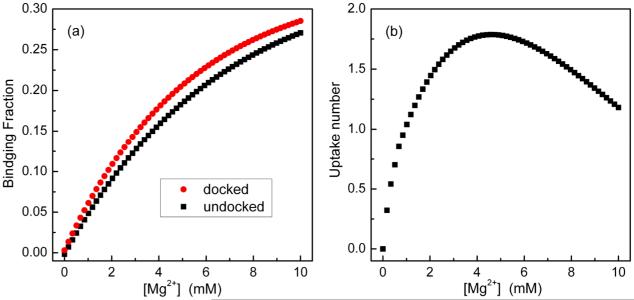
We calculate the ensemble-averaged binding fraction fb for both the docked and the undocked states. The uptake number for the docking is equal to
| (8) |
where fb(F) and fb(U) are the binding fraction of the Mg2+ ions in the docked and the undocked states (see Fig. 7a) and Na is the number of nucleotides in the RNA (Na is 84 for the tetraloop-receptor system).
Figure 7.
(a) The binding fraction for the docked and the undocked states as a function of the Mg2+ concentration in the background of 0.1M NaCl at 37°C. (b) The uptake number of Mg2+ as a function of [Mg2+].
As shown in Fig. 7b, at [Mg2+]=0mM, the uptake number of the counterions is about 0; with increasing [Mg2+], the uptake number of ion rises and quickly reaches the maximum value (≈1.7 at [Mg2+]=4.5mM); when the [Mg2+] further increases, the uptake number slowly decreases and becomes 1 at [Mg2+]=10mM. This tendency is (qualitatively) consistent with the experimental measurements.17,22,25
IV. Bound iondistribution
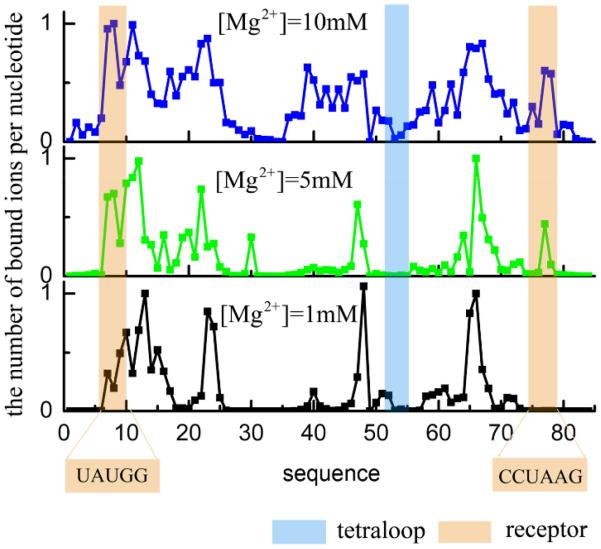
To understand the bound ions distribution, we calculate the mean binding fraction on each nucleotide (see Fig. 8) for representative structures (see Fig. 10b for [Mg2+]=1mM, c for 5mM and d for 10mM). The results show that the bound ions mainly distribute in the grooves of the helices. In addition, we find that the binding fraction on the receptor increases notably with increasing [Mg2+] while the binding fraction on the tetraloop is relatively small, especially at low [Mg2+].
Figure 8.
The ion distribution for the lowest energy tetraloop-receptor structure (see Figs. 10b, c and d) in the different Mg2+ concentrations with 0.1M NaCl background at 37°C. The distribution is calculated as the Boltzmann average over all the possible ion binding models for the given RNA structure.
Figure 10.
The undocked structures with the lowest electrostatic free energy in the different Mg2+ concentrations with the fixed background of 0.1M NaCl: (a) 0mM, (b) 1mM, (c) 5mM and (d) 10mM.
Discussions
I. Docking free energy
The tetraloop-receptor docked complex involves significant tertiary interactions such as hydrogen bonding and base stacking interactions between the tetraloop and the receptor.17 The tertiary contacts can drastically decrease the free energy of the docked state. For example, the net free energy difference between the docked and the undocked states is no more than 1 kcal/mol under certain condition ([Mg2+]<0.35 mM, [Na+]=100mM and 37°C)19,22 suggesting significant cancellation between the electrostatic interactions and the (non-electrostatic) tertiary contacts. In the current analysis, we focus on the electrostatic free energy because our primary goal is to understand the role of ions. If invoking a transition-state analysis, the free energy difference between the transition state and the undocked states (the free energy barrier of docking)is about 17 kcal/mol in the same solution condition.22,25,26 Here, in the transition state the tetraloop and receptor are assumed to be in close proximity but the tertiary interactions are largely unformed.22 Experiment data further suggest that the free energy barrier of docking mainly comes from the entropic effect.22
In our calculation, we focus on the ion-dependent electrostatic free energies and the theory does not account for the tetraloop-receptor tertiary interaction energies. Therefore, effectively, our predicted electrostatic docking free energy reflects the difference between the undocked state and a special state. In this special state, the tetraloop-receptor native conformation has formed but the tertiary interactions have not yet established. Except for the conformational change of the receptor, this special state is close to the proposed transition state.22 Therefore, the theoretical prediction for the docking free energy is comparable to the experimental result for the free energy difference between the transition state and the undocked state. Our predicted docking free energies are higher than the experimental results and the difference is nearly independent of [Mg2+]. For example, in 1mM Mg2+ and 100mM Na+ mixed solution at 37°C, our calculated (electrostatic) docking free energy is about 20.3 kcal/mol. The experimentally measured free energy is about 0.34 kcal/mol for the net docking free energy and about 16 kcal/mol for the kinetic barrier. There is about 4 kcal/mol difference between the predicted (electrostatic) docking free energy and the measured kinetic barrier.22 Moreover, we find this free energy difference is nearly independent of [Mg2+]. We propose the difference may come from two sources.
The tertiary structure of the docked tetraloop-receptor can form significant hydrogen bonding and base stacking.17,37,38 Some hydrogen bonds may have already formed in the transition state, which lowers the free energy barrier. This may be a major reason to cause the 4 kcal/mol difference. Furthermore, the receptor can be more flexible in the undocked state than in the docked state, causing an additional entropy cost.
In our model, the tetraloop and receptor structures are assumed to be fixed (PDB) structures. However, the receptor loop can be flexible in the undocked state. The flexible receptor becomes rigid in the docked state. Neglecting this additional conformational entropy change can also contribute to the 4 kcal/mol difference.22,38
Despite the difference between the predicted docking free energy and the experimental data for the free energy barrier, the [Mg2+]-independent nonelectrostatic 4 kcal/mol difference does not change our results about the (electrostatic) [Mg2+]-dependence of the docking free energy and the different free energy components.
II. Effect of ion entropy
Consistent with the experimental analyses,22 our results (Figs. 3b and 4) suggest that the ion entropy provides the major force for Mg2+-facilitated docking. Furthermore, by dissecting the ion entropy into diffusive and bound ion contributions, we found that the entropic force for tetraloop-receptor docking predominantly comes from the diffusive ions (Fig. 5b).
Fig. 5b shows that ΔGS_ion_b, the contribution from the entropy of the bound ions to the docking free energy, gradually increases with [Mg2+] and tends to stabilize at high [Mg2+]. This result suggests that entropically, ΔGS_ion_b opposes docking. More ions are bound to the docked state due to the higher RNA charge density in the (more compact) docked state than the undocked state, causing a net decrease in the entropy for the bound ions and hence an increase in the entropic free energy ΔGS_ion_b. The effect becomes weaker with increasing [Mg2+] because the entropy loss for ion binding becomes smaller in higher [Mg2+]. Moreover, in a high [Mg2+] solution, both the undocked and the docked states involve significant charge neutralization, thus the increase in the number of bound ions in the docking process is limited. In contrast, in a low [Mg2+] solution, docking would induce a significant uptake of counterions.
Compared to the bound ions, the entropy of the diffusive ions promotes the docking process (Fig. 5b). With increasing [Mg2+], more cations bind to the RNA molecule, causing stronger charge neutralization. RNA charge neutralization leads to a more uniform distribution (large entropy) of the diffusive ions. The larger entropy of the diffusive ions lowers the free energy of the system. This effect is more pronounced for the docked state than for the undocked state due to the stronger charge neutralization effect in the docked state. Therefore, the diffusive ion entropy promotes the tetraloop-receptor docking. This conclusion agrees with the analysis based on the experimental data.22
III. Conformational entropyeffect
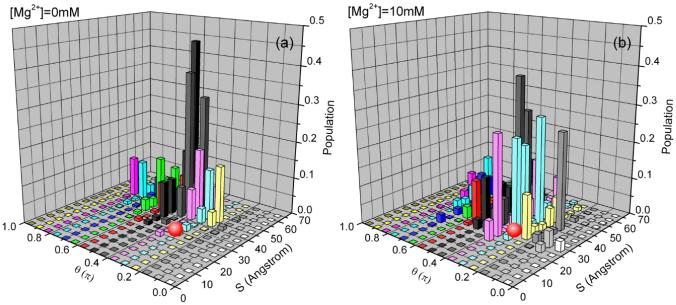
Fig. 6 shows that the conformational entropy occupies a small fraction of the docking free energy. Furthermore, Fig. 4b shows that the Mg2+ can induce a stabilizing force from the conformational entropy. As shown in Fig. 9, a higher [Mg2+] causes a higher probability for the close approach (small S) between the tetraloop and the receptor. The overall conformational distribution is shifted toward the more compact state in the vicinity of the docked structure (denoted by a red ball in Fig. 9). Indeed, as shown in Fig. 10, the low free energy conformations become more compact in higher [Mg2+]. Thus, from the point of view of the conformational entropy, increasing [Mg2+] tends to stabilize the docked state.
Figure 9.
The conformational distribution of the undocked state in the different Mg2+ concentrations with 0.1M NaCl background at 37°C. The calculation is based on the 4 sets independent Monte Carlo generated conformational ensembles. The figure shows the trend for the change of the populational distribution with increasing [Mg2+] according to the structural parameters S (x axis) and θ (y axis) (shown in Fig. 1). The docked state (the red ball) is shown for reference. To calculate the populational distribution, we first uniformly divide the conformational space into 30 clusters according to the distance S (see Fig. 1), we then uniformly divide each cluster into 30 sub-regions according to the angle θ (see Fig. 1). We calculate the average electrostatic free energy for the conformations in each subspace (S, θ) using the formula ΔGS,θ = (ΣiΔGi · e−ΔGi/kT)/(Σie−ΔGi/kT), where ΔGi is the free energy for the ith conformation in subspace (S, θ ). The z-axis in the figure shows the population of each subspace: P(S, θ) = exp[−(ΔGS,θ − ΔGmin)/kT], where ΔGmin is the minimum electrostatic free energy in the whole space.
IV. Effect of Coulomb interaction
In our calculation, the change of the Coulomb free energy ΔGE from [Mg2+]=0.35mM to [Mg2+] =1mM is about 0.7 kcal/mol. This value is within the error bar of the experimental measurement.22 The similar viewpoint for the minor difference of the Coulomb energy between the experimental data and theoretical calculations was also reported for DNA systems.50-52
The Coulomb energy effect in the docking process can stem from several Coulomb effects. First, ions can neutralize RNA backbone charge to reduce Coulomb repulsion between the tetraloop and the receptor. Second, Mg2+ ions can promote docking through the Coulomb correlation effect. For a compact (docked) structure, compared to the undocked structure, the higher negative charge density of the RNA would cause significant ion binding and thus high concentration of counterions around the RNA surface. The high concentration of counterions leads to strong correlation (coupling) between ions. In the docking process, the (correlated) Mg2+ ions bound to the tetraloop part (including the connected helix stem) and those bound to the receptor part (including the connected helix stems) can self-organize to reach a low correlated Coulomb energy, and such a low-energy state is beyond charge neutralization effect. This Coulomb correlation effect can add additional Coulomb effect to promote the docking by lowering the Coulomb energy of the system.
Conclusion
Using a physics-based RNA folding model (Vfold) to sample the conformations of the flexible loop in 3D space, we generate the conformational ensembles of both the docked and the undocked states. Using the TBI theory for ion-RNA interactions, we predict the electrostatic thermodynamics of the tetraloop-receptor system in a salt solution with the different [Mg2+]. The docking free energy landscape and the component contributions demonstrate that the ion entropy provides the major stabilizing force for tetraloop-receptor docking. Further detailed theoretical analysis indicates that the dominant contribution to the ion entropy force comes from the redistribution of the diffusive ions. Through the electrostatic screening/charge neutralization effect, the Coulomb force can also play a (albeit minor) role in the docking process. The predicted results are consistent with the experimental data and analysis. The method presented here may provide a paradigm for studying the folding of more complex RNA structures.
Supplementary Material
Acknowledgments
This research was supported by NSF grants MCB0920067 and MCB0920411 and NIH grant GM063732. Most of the computations in this research were performed on the HPC resources at the University of Missouri Bioinformatics Consortium (UMBC).
References
- 1.Downey CD, Fiore JL, Stoddard CD, Hodak JH, Nesbitt DJ, Pardi A. Biochemistry. 2006;45:3664. doi: 10.1021/bi0520941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Qin PZ, Butcher SE, Feigon J, Hubbell WL. Biochemistry. 2001;40:6929. doi: 10.1021/bi010294g. [DOI] [PubMed] [Google Scholar]
- 3.Davis JH, Tonelli M, Scott LG, Jaeger L, Williamson JR, Butcher SE. J Mol Biol. 2005;351:371. doi: 10.1016/j.jmb.2005.05.069. [DOI] [PubMed] [Google Scholar]
- 4.Maderia M, Horton TE, DeRose VJ. Biochemistry. 2000;39:8193. doi: 10.1021/bi000140l. [DOI] [PubMed] [Google Scholar]
- 5.Davis JH, Foster TR, Tonelli M, Butcher SE. RNA. 2007;13:76. doi: 10.1261/rna.268307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Qiua X, Parsegian VA, Rau DC. Proc. Natl. Acad. Sci. U.S.A. 2010;107:21482. doi: 10.1073/pnas.1003374107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kirmizialtin S, Pabit SA, Meisburger SP, Pollack L, Elber R. Biophys. J. 2012;102:819. doi: 10.1016/j.bpj.2012.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chen AA, Marucho M, Baker NA, Pappu RV. MethodsEnzymol. 2009;469:411. doi: 10.1016/S0076-6879(09)69020-0. [DOI] [PubMed] [Google Scholar]
- 9.Hamill S, Pyle AM. Molecular cell. 2006;23:831. doi: 10.1016/j.molcel.2006.07.017. [DOI] [PubMed] [Google Scholar]
- 10.Downey CD, Crisman RL, Randolph TW, Pardi A. J. Am. Chem. Soc. 2007;129:9290. doi: 10.1021/ja072179k. [DOI] [PubMed] [Google Scholar]
- 11.Erat M. l. C., Sigel RKO. Inorg.Chem. 2007;46:11224. doi: 10.1021/ic701627t. [DOI] [PubMed] [Google Scholar]
- 12.Laederach A, Shcherbakova I, Jonikas MA, Altman RB, Brenowitz M. Proc. Natl. Acad. Sci. U.S.A. 2007;104:7045. doi: 10.1073/pnas.0608765104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Fiore JL, Hodak JH, Piestert O, Downey CD, Nesbitt DJ. Biophys. J. 2008;95:3892. doi: 10.1529/biophysj.108.134346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ishitani R, Yokoyama S, Nureki O. Curr. Opin. Struct. Biol. 2008;18:330. doi: 10.1016/j.sbi.2008.05.003. [DOI] [PubMed] [Google Scholar]
- 15.Qu X, Smith GJ, Lee KT, Sosnick TR, Pan T, Scherer NF. Proc. Natl. Acad. Sci. U.S.A. 2008;105:6602. doi: 10.1073/pnas.0801436105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Vander Meulen KA, Davis JH, Foster TR, Record MT, Jr., Butcher SE. J. Mol. Biol. 2008;384:702. doi: 10.1016/j.jmb.2008.09.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Fiore JL, Kraemer B, Koberling F, Edmann R, Nesbitt DJ. Biochemistry. 2009;48:2550. doi: 10.1021/bi8019788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhang Y, Zhao X, Mu Y. J. Chem. Theory Comput. 2009;5:1146. doi: 10.1021/ct8004276. [DOI] [PubMed] [Google Scholar]
- 19.DePaul AJ, Thompson EJ, Patel SS, Haldeman K, Sorin EJ. Nucleic Acids Res. 2010;38:4856. doi: 10.1093/nar/gkq134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Duncan CD, Weeks KM. PloS one. 2010;5:e8983. doi: 10.1371/journal.pone.0008983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Woodson SA. Annu. Rev. Biophys. 2010;39:61. doi: 10.1146/annurev.biophys.093008.131334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Fiore JL, Holmstrom ED, Nesbitt1 DJ. Proc. Natl. Acad. Sci. U.S.A. 2012;109:2902. doi: 10.1073/pnas.1114859109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Vander Meulen KA, Butcher SE. Nucleic Acids Res. 2012;40:2140. doi: 10.1093/nar/gkr894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Qin PZ, Feigon J, Hubbell WL. J. Mol. Biol. 2005;351:1. doi: 10.1016/j.jmb.2005.06.007. [DOI] [PubMed] [Google Scholar]
- 25.Holmstrom ED, Fiore JL, Nesbitt DJ. Biochemistry. 2012;51:3732. doi: 10.1021/bi201420a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Fiore JL, Holmstrom ED, Fiegland LR, Hodak JH, Nesbitt DJ. J. Mol. Biol. 2012;423:198. doi: 10.1016/j.jmb.2012.07.006. [DOI] [PubMed] [Google Scholar]
- 27.Hodak JH, Downey CD, Fiore JL, Pardi A, Nesbitt DJ. Proc. Natl. Acad. Sci. U.S.A. 2005;102:10505. doi: 10.1073/pnas.0408645102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bowman JC, Lenz TK, Hud NV, Williams LD. Curr. Opin. Struct. Biol. 2012;22:262. doi: 10.1016/j.sbi.2012.04.006. [DOI] [PubMed] [Google Scholar]
- 29.Leipply D, Draper DE. Biochemistry. 2010;49:1843. doi: 10.1021/bi902036j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Grilley D, Soto AM, Draper DE. PNAS. 2006;103:14003. doi: 10.1073/pnas.0606409103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Li PT, Vieregg J, Tinoco I., Jr. Annu. Rev. Biochem. 2008;77:77. doi: 10.1146/annurev.biochem.77.061206.174353. [DOI] [PubMed] [Google Scholar]
- 32.E.Drape D, Grilley D, Soto A. Annu. Rev. Biophys. Biomol. Struct. 2005;34:221. doi: 10.1146/annurev.biophys.34.040204.144511. [DOI] [PubMed] [Google Scholar]
- 33.Jr IT, Bustamante C. J. Mol. Biol. 1999;293:271. doi: 10.1006/jmbi.1999.3001. [DOI] [PubMed] [Google Scholar]
- 34.Heus H, Pardi A. Science. 1991;253:191. doi: 10.1126/science.1712983. [DOI] [PubMed] [Google Scholar]
- 35.Costa M, Michel F. o. EMBO J. 1995;14:1276. doi: 10.1002/j.1460-2075.1995.tb07111.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Jucer FM, Pardi A. RNA. 1995;1:219. [PMC free article] [PubMed] [Google Scholar]
- 37.Cate JH, Gooding AR, Podell E, Zhou K, Golden BL, Kundrot CE, Cech TR, Doudna JA. Science. 1996;273:1678. doi: 10.1126/science.273.5282.1678. [DOI] [PubMed] [Google Scholar]
- 38.E.Butcher S, Dieckmann T, Feigon J. EMBO J. 1997;16:7490. doi: 10.1093/emboj/16.24.7490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Krasilnikov AS, Yang X, Pan T, Mondragón A. Nature. 2003;421:760. doi: 10.1038/nature01386. [DOI] [PubMed] [Google Scholar]
- 40.Davis JH, Tonelli M, Scott LG, Jaeger L, Williamson JR, Butcher SE. J. Mol. Biol. 2005;351:371. doi: 10.1016/j.jmb.2005.05.069. [DOI] [PubMed] [Google Scholar]
- 41.Cao S, Chen SJ. Nucleic Acids Res. 2012;40:4681. doi: 10.1093/nar/gks052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Cao S, Chen SJ. RNA. 2011;17:2130. doi: 10.1261/rna.026658.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Cao S, Chen S-J. Nucleic Acids Res. 2006;34:2634. doi: 10.1093/nar/gkl346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Tan Z-J, Chen S-J. Met. Ions Life Sci. 2011;9:101. [PMC free article] [PubMed] [Google Scholar]
- 45.Tan ZJ, Chen SJ. Biophys. J. 2011;101:176. doi: 10.1016/j.bpj.2011.05.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Tan ZJ, Chen SJ. Biophys. J. 2008;94:3137. doi: 10.1529/biophysj.107.122366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Tan ZJ, Chen SJ. Biophys. J. 2007;92:3615. doi: 10.1529/biophysj.106.100388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Tan ZJ, Chen SJ. The Journal of chemical physics. 2005;122:44903. doi: 10.1063/1.1842059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.He Z, Chen S-J. J. Chem. Theory Comput. 2012;8:2095. doi: 10.1021/ct300227a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Delcourt SG, Blake RD. J. Biol. Chem. 1991;266:15160. [PubMed] [Google Scholar]
- 51.Erie D, Sinha N, Olson W, Jones R, Breslauer K. Biochemistry. 1987;26:7150. doi: 10.1021/bi00396a042. [DOI] [PubMed] [Google Scholar]
- 52.Misra VK, Draper DE. J. Mol. Biol. 1999;294:1135. doi: 10.1006/jmbi.1999.3334. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.