The role of mechanics in actin stress fiber kinetics

Abstract

The dynamic responses of actin stress fibers within a cell's cytoskeleton are central to the development and maintenance of healthy tissues and organs. Disturbances to these underlie a broad range of pathologies. Because of the importance of these responses, extensive experiments have been conducted in vitro to characterize actin cytoskeleton dynamics of cells cultured upon two-dimensional substrata, and the first experiments have been conducted for cells within three-dimensional tissue models. Three mathematical models exist for predicting the dynamic behaviors observed. Surprisingly, despite differing viewpoints on how actin stress fibers are stabilized or destabilized, all of these models are predictive of a broad range of available experimental data. Coarsely, the models of Kaunas and coworkers adopt a strategy whereby mechanical stretch can hasten the depolymerization actin stress fibers that turn over constantly, while the models of Desphande and co-workers adopt a strategy whereby mechanical stress is required to activate the formation of stress fibers and subsequently stabilize them. In three-dimensional culture, elements of both approaches appear necessary to predict observed phenomena, as embodied by the model of Lee, et al. After providing a critical review of existing models, we propose lines of experimentation that might be able to test the different principles underlying their kinetic laws.

Introduction

Stress fibers (SFs) are bundles of microfilaments cross-linked by α-actinin. These actin filaments are arranged with “graded polarity”: their rapidly growing (barbed) ends predominate at the ends of the SFs and gradually change orientation from one end to the other [1]. Four kinds of structures are included in the SF family, as observed in cells cultured on two-dimensional (2D) substrata: dorsal and ventral SFs, transverse arcs and perinuclear caps that differ in their attachment to focal adhesions (FAs) and their myosin content. Focal adhesions are complex protein assemblies by which SFs are linked to the extracellular matrix [2]. We will be concerned in 2D with ventral SFs that are composed of contractile actin-myosin segments similar to muscle sarcomeres and that are attached to focal adhesions at their ends, and note that the nature of stress fibers and FAs in 3D is still an open question.

The formation of both SFs and FAs requires mechanical force and can be retarded by inhibition of actin-myosin contractility [3, 4]. Although the mechanism of SF assembly is still unclear, a number of experimental approaches have revealed interesting facts about the dependence of SF assembly and orientation on the form of the attachment of a cell to a substrate and the contractile forces that it develops. When cells adhere to designed micropatterns, it is observed that for the most part they organize long SFs that link to FAs attached to the adhesive surface [5, 6]. Allowing cells to attach to an array of flexible microposts allows the determination not only of the dependence of cell shape on the disposition of the posts but also the force exerted by the cells measured in terms of the bending of the posts [7]. The cells on the microposts displayed the following properties: steady state average force per post, F_avg^SS, increases with increasing post stiffness; for 5×5 (or smaller) arrays of posts, F_avg^SS increases with increasing numbers of posts, but decreases for arrays with 10×10 (or more) posts; the distribution of SFs is determined by the pattern of the posts (Figure 1); and forces exerted on the posts is greater at the cell periphery than in its interior [8]. While much progress has been made recently on extending these technologies to incorporate additional loading and topographical schemes (e.g., [9-16]), these observations suffice as a backdrop for the foregoing discussion.

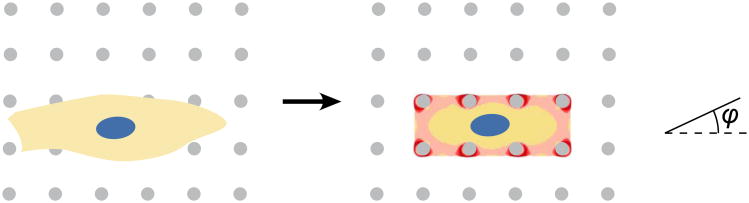
Figure 1.

The models of Deshpande, et al., predict stabilization of stress fibers in the direction of stretch, and involve an explicit dependence of disassembly rate on stress when stress drops below an isometric level. In the classic experiment it was first designed to model, cells placed on micropillar arrays develop a stress fiber distribution η(x_i, φ, t) at each point x_i that varies with stress, with time t since initiation of a signal triggering stress fiber growth, and with direction φ. Shades of red in the cartoon represent relative values of stress fiber concentration at each point, averaged over the predicted orientation distribution (cf. [84]); grey circles in the cartoon represent positions of flexible micropillars patterned with proteins that enable cell adhesion.

Motivated by the fact that endothelial cells are constantly subjected to pulsatile stretch, studies of cells on flexible substrata have shown that SFs gradually align in a direction of minimal substrate deformation (Figure 2). Hence, for uniaxial deformation the SFs oriented perpendicular to the direction of stretch while for equibiaxial stretch, as expected from symmetry, there was no reorientation in the substrate plane, but the cells formed a “tent-like” protrusion normal to the plane [17, 18]. For simple stretch the SFs oriented obliquely (∼65°-75°) to the direction of stretch.

Figure 2.

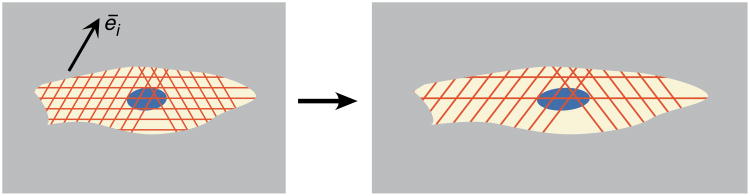
The models of Kaunas, et al., predict strain-driven destabilization of stress fibers (red). Each family i of stress fibers is defined by its orientation ē_i and the time and resolved strain at which it formed. Stress fibers degrade over time to supply F-actin for the formation of new stress fibers, which occurs in all directions equally. In the classic experiment it was first designed to model, cells cultured on a flexible, planar substratum can align perpendicular to the direction of periodic uniaxial straining due to increasing dissociation rates associated with straining.

Tissue cells normally reside in a 3D environment embedded in an extracellular matrix. It is therefore, important to test their response to external force in this condition, and a number of coupled experimental and analytical systems have been constructed for this purpose [19-26]. Fibroblasts in engineered tissue constructs (ETCs) show three kinds of responses to simple stretch of the ETC [27] (Figure 3). Reinforcement responses consisted of extension of cellular processes and augmentation of SFs along the direction of stretch. Retraction responses resulted in retraction of cellular processes and diminution of the density of SFs measured as “fibrosity”, described below. Finally some cells first retracted and then underwent a reinforcement response.

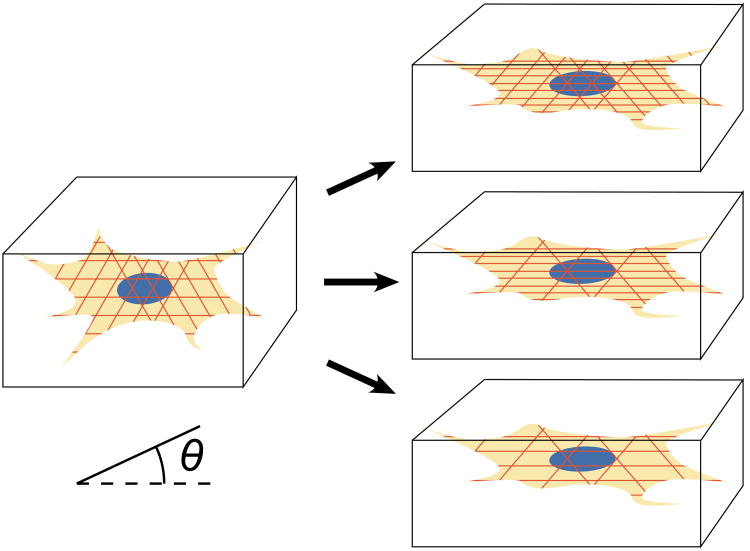
Figure 3.

The model of Lee, et al., predicts strain-dependent dissociation of stress fibers, and stress-dependent growth and stabilization. In the experiments it was designed to model, cells in three-dimensional engineered tissue constructs exhibited one of three responses to a stretch-and-hold experiment: reinforcement, involving growth of stress fibers in the direction of stretch (top); retraction, involving dissociation of stress fibers in all directions (bottom); and retraction followed by reinforcement. These responses can be predicted based upon the statistical variance of the initial pre-stretch of stress fibers.

The overall responses of cells to their mechanical environments has been the focus of a great number of theoretical efforts, and a broad range of models exist to predict changes in cell polarity as a function of mechanical environment, topographical cues, and interactions with neighboring cells and extracellular matrix (cf. [28-38]). However, the actin stress fiber dynamics that might underlie these responses are much less well understood. These latter phenomena are the focus of this review.

Three models have been developed to explain the three kinds of observations described above for the effects of force and adhesion on SF organization in cells [27, 39, 40]. Although closely related conceptually, each model suggests a different mechanism for control of SF orientation. The essential qualities of the models are captured by the kinetic laws that are proposed for dependence SF assembly and fragmentation on applied stretch or stress generated by the cells. Here we discuss and compare these models in terms of their kinetic laws.

Models for Assembly and Fragmentation of Stress Fibers

Several models have been proposed to account for the effects of externally applied or cell-generated contractile stresses or strains on the development and disposition of cellular SFs. The models are essentially phenomenological. They do not explicitly account for the signaling processes and molecular mechanisms that link force to structural changes in a cell. Nevertheless, these models provide a useful explanatory framework and provide guidance for further investigation into the molecular events that translate force into cellular molecular changes. In comparing these models we concentrate on the kinetic laws upon which they are based. The central feature of each of the models is the dependence of the rate of assembly or fragmentation of SFs (and FAs) on the magnitude and orientation of the stress or the strain experienced by the cells. Based on currently available data it is not possible to distinguish stress from strain as the primary cause of SF remodeling.

Model of Deshpande et al

Deshpande and coworkers have proposed models that attempt a comprehensive and detailed account of the force dependence of the assembly and disassembly of SFs and FAs [8, 39, 41-44]. The model in many ways builds upon the cardiomyocyte model of Nickerson et al. [45], but, significantly, adds remodeling of stress fibers and the capacity for this orientation distribution to evolve over time, and employs a greatly simplified model of calcium handling. As suggested by earlier experimental observations the central tenet of the model is that the development and maintenance of SFs requires the exertion of cell-generated contractile force or of forces externally applied to the cells. A motivation for the model of SF kinetics was experimental observation of the patterns of SF assembly in cells that have been grown on specialized substrates such as micropatterns of integrins that confine adherent cells to specified shapes and areas [5, 6] and to arrays of microposts that not only confine the interactions of the cell to small areas at the tips of the microposts but also yield measurements of the forces exerted by the cells [7] (Figure 1). Key to the development of the models was the observation that there exists no simple relationship between the magnitudes and orientations of the force vectors and the features of the cytoskeleton revealed by fluorescence microscopy. The purpose of the models is to account the observed effects of the compliance of the substratum, the dependence on the size of a cell of the forces exerted at its periphery, and the influence of cell shape on the orientations of the SFs [39]; however, the model and its extensions have now been applied to interpret the responses of cells to a broad range of stimuli (e.g., [46-51]). There are three components of the model:

1. An activation signal, C, that could arise in response to a mechanical perturbation or a biochemical signal, e.g., an increase in cytoplasmic calcium ion concentration, and that decays exponentially over time, $C(t_i)=\mathit{exp}\left(\frac{-t_i}{\theta }\right).$ Here t_i is the time since the most recent activation signal and θ is the relaxation time for the decay of the signal. Note that it is possible, even likely, that in some instances the activation signal could be spread out over a time interval, say, from t=0 to t=T. Then, C(t) would be replaced by a convolution integral: $C(\tau )={\int }_0^{T}f(t)\mathit{exp}\left(\frac{-(t-\tau )}{\theta }\right)dt$ where f(t) is the time course of the signal over the interval.

2. A kinetic law for the assembly and disassembly of SFs along the direction φ:

   $$\frac{d\eta (\phi )}{dt}=[(1-\eta (\phi ))\frac{C(t){\overline{k}}_f}{\theta }]-[(1-\frac{\sigma (\phi )}{{\sigma }_0(\phi )}\eta (\phi )\frac{{\overline{k}}_b}{\theta }]$$ (1)

   Here η(φ) (0 ≤ η ≤ 1) is a non-dimensional measure of the extent to which actin and myosin are incorporated into a SF and σ(φ) is the tension in the SFs along direction φ (Figure 1). The isometric stress at activation level η is taken to be a linear function of η, σ₀(φ) = η(φ)σ_max, where σ_max is the stress at maximum activation level. According to this equation the rate of fiber assembly along the direction φ is proportional to the signal strength, the extent of actin and myosin as yet not activated, and a non-dimensional rate constant, K̄_f. The rate of SF disassembly, in addition to the non-dimensional rate constant, K̄_b is proportional to the activation level, i.e., the fraction of actin and myosin in SFs, and the difference between the stress and the isometric stress along the direction φ. Thus, the SFs are stable at the isometric stress level but disassemble at a rate that increases as the stress decreases from that level. SF assembly depends only implicitly on stress through C(t) (the strength of which can in principle vary with stress, but could also arise independently of mechanical perturbations through the action of chemical messengers). In contrast there is an explicit dependence of disassembly rate on stress.

3. The stress is controlled by the effect of myosin cross-bridge mechanics on the SF contraction rate embodied in a version of the Hill equation (a force generating contractile element in series and parallel with elastic elements) [52]. For a sufficiently fast shortening rate, the stress vanishes, $\frac{\sigma (\phi )}{{\sigma }_0(\phi )}=0,$ providing the maximum rate of SF disassembly. Under isometric conditions or if the stress fibers are being extended, $\frac{\sigma (\phi )}{{\sigma }_0(\phi )}=1,$ and the SFs are stable. Between the upper and lower strain rate thresholds, $\frac{\sigma (\phi )}{{\sigma }_0(\phi )}$ decreases in proportion to the rate of contraction yielding intermediate rates of SF disassembly that increase as $\frac{\sigma (\phi )}{{\sigma }_0(\phi )}$ decreases.

For this model the orientation distribution of stress fibers (η(φ)) depends on the orientation distribution of isometric stress, σ₀(φ) which, in turn, depends on the rigidity of the sites at which the cell is attached to the substratum. Near sites of stiff attachment cellular contractile force can rapidly develop local isometric stress. At these locations high σ₀(φ) is correlated with high η(φ). In contrast, when attachment is compliant or in regions of the cell distant from stiff attachments both σ₀(φ)and η(φ) are diminished [39]. Note that in this model based on linear elasticity a cell could in principle develop high isometric stress even near a soft attachment site. The model supposes that by the time this could have happened, the stimulus, C(t), would have decayed, and so both cell-exerted forces and the formation of SFs would remain low. A detailed comparison of the model with cells on microneedles has more recently appeared [8].

As for SFs, forces exerted by or on the cell play an important role in the assembly of FA that link the SFs to the external environment of the cell (e.g., [53-57]). Therefore, the kinetic model for the formation-fragmentation kinetics of SFs has been augmented by a force-dependent model for the assembly of FAs [42]. Force enters this model through its effect on the conformation of the integrins that link the SFs to a substrate surface or to the extracellular matrix. The integrins can be in either a low-affinity or a high-affinity state for binding to their ligands, e.g., an extracellular matrix protein such as collagen. Exertion of force converts integrin molecules from the former to the latter state. That is, the chemical potential of the high affinity molecules is taken to depend explicitly on the force exerted on them. As high affinity integrin molecules bind to their ligands, molecules are converted from the low to the high affinity state to maintain equilibrium between the two forms. Hence, FAs assemble in response to force as more and more integrin molecules bind to the extracellular ligands. The model has been used to explain the disposition of SFs and FAs on patterned substrates and could explain such experimental observations as the formation of high concentrations of SFs and FAs at the periphery of convex ligand patterns and the formation of highly aligned SFs along the non-adhered edges of cells on concave ligand patterns [43].

A central result described below, one that motivates the models of Kaunas, et al., is the orientation of stress fibers perpendicular to the direction of cyclic uniaxial stretching for cells cultured on a 2D substratum, for certain frequencies of cyclic stretching. These results are described in detail in the next section. The model of Deshpande et al. rationalizes the perpendicular orientation of SF relative to the cyclic uniaxial stretching of cells [44] in the following way. The model shows that the stress generated perpendicular is greater than that parallel to the direction of stretch, consistent with the higher actin polymerization levels in that direction. The authors explain that the main reason for the perpendicular orientation of the SFs after cyclic uniaxial stretch is, however, due to the dissociation of SFs during the unloading phase of each stretch cycle [44]. During the unloading phase the SF in the stretch direction undergo the maximum decrease of stress and therefore experience the maximum extent of dissociation. The fibers perpendicular to the stretch direction do not contract and so do not dissociate. Similarly, the observation that higher cyclic stretching frequencies yield greater levels of SF alignment is attributed to the larger contraction strain rates at higher frequencies. There is greater dissociation of SF at the higher contraction strain rates and so greater alignment perpendicular to the stretch direction. This explanation differs substantially from that arising from the model of Kaunas, et al., and an effort will be made to rectify the two viewpoints in the discussion that follows.

Model of Kaunas et al

A model for stretch-induced SF turnover was introduced by Kaunas, et al., to account for the following observations:

1. Endothelial cells and actin SFs become oriented perpendicular to the principal direction of cyclic pure uniaxial stretch, but not cyclic equibiaxial stretch. SF alignment occurs over hours and its time course correlates with the activation pattern of stretch-induced signal transduction.

2. The extent of SF alignment depends on magnitude of cyclic stretch and level of contractile activity.

3. Cells exert isometric contractile stress that pre-stretches SFs to a common level among members of an endothelial cell population, suggesting that SF pre-stretch is maintained at a physiologically prescribed homeostatic level. Kaunas, et al., presume the homeostatic level of stretch to be set during the initial assembly of the SFs at the value of 1.1. Note that their modeling results were insensitive to this pre-stretch level in the range 1.1 to 1.3.

4. The actin cytoskeleton is in a constant state of assembly and disassembly.

5. Perturbing the level of stretch in SF by suddenly stretching or compressing the matrix disrupts SF.

6. For cells stretched on a 2D substratum, all available F-actin and myosin is incorporated into SFs, and the rate of growth of new SFs is thus governed by the disassembly rate of old SFs.

The simplest of their models proposed to account for these observations centers on a strain-dependent kinetic law for SF disruption. Using an assumption of affine deformation for stress fibers within a cell, the SFs in a cell are grouped into families with the same orientation and time and conditions of growth. Then, the rate law for the i^th family is

$$\frac{d{\Phi }^i}{dt}=k^i{\Phi }^i,$$ (2)

where, for SF family i oriented in a particular direction ē_i (Figure 2), Φⁱ is the mass fraction equivalent to η in the model of Deshpande et al., and kⁱ is the rate constant for disassembly that depends on stretch as follows:

$$k^i=k_0[1+k_1{\left(\frac{{\alpha }^i-{\alpha }_0}{{\alpha }_0}\right)}^2],$$ (3)

in which αⁱ is the current stretch of i^th family SFs. The model supposes that prior to an imposed stretch, the SF are pre-stretched to a homeostatic level, α₀. Then, αⁱ − σ₀ is the deviation of the stretch from the homeostatic level. In this model reassembly of SFs is isotropic and occurs immediately as F-actin and myosin become available through SF disassembly, modeling the observation that, unlike tests conducted in 3D, all available F-actin and myosin is incorporated in SFs and SF assembly is thus limited by the disassembly rate.

This model has been applied to interpret the effects on SF organization in cells that are subjected to cyclic equibiaxial or uniaxial stretches of flexible substrata on which they are tightly bound (Figure 2). Prior to stretch, SFs are presumed to be pre-stretched to the homeostatic level, α₀, at which the SF was originally assembled. Due to a stretch of the substrate to a level λ in the direction of a particular family of SFs, all SF in that family of SFs are stretched to the level α_i = α₀λ. The rate constant for overstretched or understretched SFs increases dramatically, causing them to fragment. The F-actin and myosin immediately reassemble into new SFs at the new homeostatic level of stretch. Hence, an equibiaxial stretch causes SF turnover to a new homeostatic level, but does not change the net orientations of the SFs. Similarly, cyclic equibiaxial stretching does not cause a change in SF orientation. In contrast, experimental observations show that cyclic uniaxial stretching causes SFs to align perpendicular to the level of stretch. According to the model this occurs because the SFs oriented in the direction of stretch fragment most rapidly and so are replaced by SFs along directions with slower fragmentation rates, i.e., perpendicular to the stretch direction (least stretch perturbation).

A more recent version of the model incorporates a stochastic model in which the kinetic equation (2) is replaced with a stochastic law and in which stretches in SFs relax viscoelastically to a set-point level α₀ [58]. The probability of disassembly over a time Δt of the i^th family of stress fibers that has persisted to time t scales with the kⁱ as in Equation (3), with the stretch relative to the set-point decaying over time. Much data exist for cellular reorientations in response to stretch of their 2D substratum with different frequencies, directions, and magnitudes and directions of stretch [59, 60], and the modified model predicts the range of these as a trade-off between SF turnover and SF relaxation.

Model of Lee, et al

The experimental measurements on which the previous models are based were carried out on cells adherent to 2D planar tissue culture substrata. Cells such as fibroblasts and endothelial cells, however, normally reside in 3D, compliant extracellular matrices. It is therefore important to investigate the effects of force on cells that reside within tissues. There are substantial advantages to using engineered tissue constructs (ETCs) for this purpose, including the ability to apply fluorescent labels to components of the cytoskeleton such as actin and other constituents of SF and to focal adhesion such as talin or vinculin and to control the cell density and composition of the ETC.

Lee, et al., assembled ETCs from chicken embryo fibroblasts and collagen using technology applied previously for analyzing cell mechanics [22, 26, 61-64]. Ring-shaped ETCs formed over a few days of culture as the cells compressed and stiffened the collagen matrix. To enable study of stretch-induced changes to actin cytoskeletal dynamics, an instrument was constructed that allowed observation of the effects of stretching an ETC on the shapes of myofibroblast cells within it and on the disposition of their fluorescence-labeled actin cytoskeletons observed with a scanning confocal fluorescent microscope [27]. As ETCs were held isometrically following a stretch, two kinds of cellular responses were observed: retraction and reinforcement (Figure 3). Retraction responses consisted in fragmentation of actin SF and retraction of filopodia-like cellular protrusions. These responses were observed for SF and filopodia-like cellular protrusions oriented in all directions relative to the stretch direction. Reinforcement responses consisted of increase of the size and number of SFs and extension of cellular protrusions, both mainly in the direction of the applied stretch. Furthermore, it appeared that F-actin was transferred from fragmenting SFs during retraction responses to “reservoirs” and that these reservoirs diminished during reinforcement responses, presumably due to transfer of F-actin to growing SFs.

In a single tissue construct, cells could be observed exhibiting retraction responses, reinforcement responses, or reinforcement following retraction, but retraction following reinforcement was a very rare event. Two basic premises, consistent with principles previously discussed, support a model to account for these observations:

1. Ample experimental observations support concept that SFs are normally stable within a range of pre-stretch [27, 39, 40]. When they are either compressed or stretched beyond this range, SFs fragment.

2. Within the range of pre-stretch over which SFs are stable to fragmentation, stress promotes SF assembly.

The experimental measurements to be modeled characterize the level of SFs in terms of a “fibrosity” parameter, φ, derived from the power spectrum of a spatial Fourier analysis of confocal scanning microscopy images of cells with fluorescence labeled actin filaments in ETCs [27, 65]. The fibrosity, φ, yields an estimate of the total length of image features with thickness in the range of SFs. In the context of the model φ has a significance comparable to η and to Φ in the Deshpande et al. and the Kaunas models.

The model considers SF dynamics and the time variation of fibrosity in three distinct stages. The first is the development of the orientation and pre-stretch distribution of a population of SFs prior to the application of a stretch. This is treated as an input to the model, and appears to vary from cell to cell within a single tissue construct based upon the time history of the local mechanical environment. In the implementations presented in [27, 39, 40], two limiting shapes representative of cells seen in ETCs were modeled: a spindle shaped cell modeled as having a rectangular form with its long axis and SFs aligned with the stretch direction. Here, the SFs were shared among N compartments of equal width, each running the length of the cell and assigned pre-stretch values selected from a normal distribution. The other limiting case was less elongated cells that prior to stretch displayed SFs and protrusions oriented randomly, modeled in [27, 39, 40] with a circular form containing uniformly distributed radial SFs with pre-stretches also selected from a normal distribution. Each semicircle was divided into N sectors and within each sector SFs were assigned a random pre-stretch value. In each case, ${\lambda }_n^0$ (n = 1,2, … N) is the randomly assigned initial pre-stretch value of the n^th sector.

The second stage was stretch-induced SF depolymerization, which was taken to be rapid relative to the other two stages and relative to the observation frequency; the timescale for SF depolymerization in response to a rapid stretch is on the order of 30 seconds [27, 39, 40] [66]. SFs fragment if, following stretch of the ETC, they have stretch values λ_n outside the allowable range λ_min ≤ λ_n ≤ λ_max. For this work λ_min = 0.95 and λ_max = 1.25 defines the allowable range. In the implementation in [27, 39, 40], the Poisson's ratio of ETCs that relates transverse contraction to axial extension was found to be approximately 1, so that axial and transverse strains were comparable (ε_I = −ε_II) so that, assuming affine deformation of the ETC, the SF stretch ${\lambda }_n^f$ following ETC stretch of a magnitude (1+ε_I) was ${\lambda }_n^f={\lambda }_n^0(1+{\varepsilon }_I(\mathit{cos}2{\theta }_n))$ for a sector oriented at an angle θ_n from the stretch direction (cf. Figure 3); the assumption of affine deformation is appropriate for ETCs in which the cell population is close to the percolation threshold [22, 62, 63].

The final stage was stress-induced SF assembly. The effects of stretch and stress on SF fragmentation and assembly are treated separately. SF stretched beyond the range of stable pre-stretch, as described above, fragment rapidly on the time scale of the measurements, and so the kinetics of fragmentation are not explicitly described [9]. The normal stress, σ_n, near adhesions sites in the n^th sector, just prior to SF fragmentation, drives SF growth in that sector:

$$\frac{d{\phi }_n}{dt}=\frac{({\phi }_{\mathit{max}}-{\phi }_n)}{{\tau }_G}f({\sigma }_n)$$ (4)

where τ_g is a time constant, φ_max is an upper limit of SF density and the function f(σ_n) that determines SF growth rates is

$$f({\sigma }_n)=\{\begin{array}{cc}(\frac{{\sigma }_n}{{\sigma }_g}-1),& {\sigma }_n\ge {\sigma }_g\\ 0,& {\sigma }_n<{\sigma }_g\end{array},$$ (5)

in which σ_g is a threshold tensile stress needed for assembly of SFs to occur.

It is straightforward to see how this model accounts for the three characteristic patterns of observed responses to stretch. That stretch along one cell axis could cause fragmentation of SF both parallel and perpendicular to the stretch direction is due to two features of the model: first, that Poisson contraction causes a transverse compressive strain nearly equal to the stretch strain and, second, that SF fragmentation can be triggered not only by stretch beyond the upper limit of pre-stretch stability, λ_max, but also by compression to a level below the lower limit, λ_min. For a circular model cell with very uniform SFs pre-stretch and therefore relatively few SFs with pre-stretch values near λ_max and λ_min, imposed stretch will cause fragmentation only of the few SF that are nearly parallel or perpendicular to the stretch direction and are near the pre-stretch limit values. With little fragmentation, the dominant response will, then, be monotonic reinforcement. In contrast, a cell that has a high variance in the distribution of pre-stretch and therefore many SFs near λ_max and λ_min and also a cell that simply has very high or very low pre-stretch values over all, will incur extensive SF fragmentation in response to stretch. This, in turn, will reduce the stress at adhesion sites and so diminish the driving force for SF growth. Hence, this cell could undergo a monotonic retraction response. A cell with intermediate variance in SF pre-stretch will experience both significant SF fragmentation and also stress-promoted re-growth of SF and therefore will display first a retraction and then reinforcement. This argument could also be cast in terms of the variance in SF orientation. Non-spindle-shaped cells often have a few groups of commonly oriented SF. Hence, by chance some of these cells could have a preponderance of SF oriented parallel or perpendicular to the stretch direction that would respond to stretch by extensive fragmentation and so experience monotonic retraction. Conversely other cells could have most of their SF oriented so that they would experience little fragmentation in response to stretch and so would be dominated by growth of SF along the direction of stretch, thereby displaying monotonic reinforcement. This model, therefore, explains the observations of the three kinds of responses cells in ETCs to stretch and also that retraction was seen to occur for SF oriented in any direction while reinforcement occurred mainly in the direction of the applied stretch [27].

Discussion

The three models that we have discussed were formulated to account for the amount and the orientation of SFs in cells adherent to 2D substrata subjected to cyclic uniaxial and biaxial stretch [40, 44]; in cells that were grown on microposts arrays or patterned substrates [8, 39, 43]; and in cells in 3D ETCs subjected to simple stretch [27]. Each model interprets SF reorientation in terms of a different dependence of SF fragmentation and assembly on stress or stretch. Although current experimental data in the literature are not sufficient, the models do lend themselves to a series of experiments that might help to distinguish amongst the three different dependences. In the following, we compare predictions of the models and propose experiments that might illuminate the ranges of validity of some of their basic assumptions.

Steady state predictions and kinetic model parameters

For the Kaunas model SF fragmentation depends on the orientation and magnitude of stretch [40]. The rate of fragmentation of SFs increases in proportion to the extent of stretch beyond their homeostatic set-point (Equations 2 and 3). The assembly of SFs is continuous (constitutive) and isotropic. The net result for cells subjected to uniaxial stretch is that SFs oriented along the stretch direction fragment preferentially and are replaced by SFs that experience minimal stretch oriented perpendicular to the direction of stretch. As expected from symmetry, equibiaxial stretch does not influence the orientation of SFs but does increase their turnover rate. Examination of steady states often provides useful insights into the behavior of kinetic models. The Kaunas model could in principle yield steady states in which orientation-dependent fragmentation balances isotropic assembly of SF. For the Kaunas model the rate of SF fragmentation under stretch is specified by Eq. 2. In principle, this could be balanced by the constituent and isotropic reassembly of SF, to yield a steady state. Turnover of SF as described above is acknowledged in the Kaunas model without, however, specifying a kinetic scheme. Nevertheless, one could use measurements at constant stretch to test whether the rate of SF fragmentation varied as specified in Eq. 2. Although the version of the model discussed above does not provide sufficient detail for this to be instructive quantitatively, such measurements would permit validation of the form of Eq. 2.

The Deshpande model, having been formulated to account for a variety of static and dynamic responses of SFs to stretch, is more complex [39]. For cells in static culture the fragmentation of SFs depends on stress generated by actin-myosin contractile force. In Equation 1 there are two terms that depend explicitly on, φ, the orientation of the SFs. One is the extent of SF assembly (the “activation level”), η(x_i, φ, t) the other, the difference between the stress in the direction φ, σ(φ), and isometric stress, ${\sigma }_0(\phi ):1-\frac{\sigma (x_i,\phi ,t)}{{\sigma }_0(x_i,\phi ,t)}.$ Hence, SF fragmentation in any direction φ is proportional to the density of SFs and to the difference between the current stress and the isometric stress in that direction. For SF assembly, orientation dependence is explicit only in the term 1 − η(x_i, φ, t); SF assembly tends to increase along the directions less populated with SF. The activation signal could vary with φ, but this is not made explicit. It may be useful to examine the steady state behavior of this model. Suppose for the Deshpande model (Eq. 1) that the activation signal is maintained at a steady state level, C̄, and also recall that σ₀ = ησ_max where σ_max is a function of C̄. Let $\frac{{\overline{k}}_f}{{\overline{k}}_b}=K,$ and not that it is possible for K (and either of the rate constants) to also a function of C̄. Then, by setting η=0, one obtains the following for the steady-state level of SF assembly: ${\eta }^{SS}=\frac{K\overline{C}+\frac{\sigma }{{\sigma }_{\mathit{max}}}}{K\overline{C}+1}.$ When the steady-state signal level is high, η^ss → 1, as expected. When $K\overline{C}\ll \frac{\sigma }{{\sigma }_{\mathit{max}}},$ then ${\eta }^{SS}\approx \frac{\sigma }{{\sigma }_{\mathit{max}}},$ and so, under these conditions the steady state level of SF assembly is proportional to σ. This relationship could be tested experimentally by measuring η^ss and $\frac{\sigma }{{\sigma }_{\mathit{max}}}$ at varying low levels of C̄ (and σ_max(C̄). Conversely, it would be interesting to measure η^ss varying $\frac{\sigma }{{\sigma }_{\mathit{max}}}$ mechanically under isotonic conditions while maintaining C̄ constant, as will be discussed in the next section.

For the model of Lee, et al., the only formal steady state occurs when φ_n =φ_max (Eq. 4). When the ETC is stretched there is fragmentation of SF that are extended beyond the range of stable pre-stretch. This is supposed to happen rapidly, while orientation-specific re-assembly of SF under the influence stress occurs more slowly as described by Eq. 5. The model is insufficiently detailed to permit the definition of steady state conditions. Nevertheless, it would be possible to test equation Eq. 5 by measuring the rate of SF assembly at different constant levels of strain under isotonic conditions as described in the following section.

Isotonic “creep” responses

In ETCs it is possible to carry out not only isometric but also isotonic measurements, using feedback control of the force applied to the construct. In principle this allows a distinction between responses to stretch/strain from those to stress. In a series of isometric steady states with varying extents of stretch (strain is constant but stress can vary), strain dependent phenomena should scale with the extent of stretch, but not with the force, which is uncontrolled. In a series of isotonic steady states (stress is constant but strain can vary) with varying extents of force, stress dependent phenomena should scale with the extent of force, but not with strain, which is uncontrolled. Eq. 1 predicts for the Deshpande model that SF fragmentation should increase as the force is decreased, while Eq. 4 for the model of Lee et al. predicts that the rate of SF assembly should increase as the force is increased. Correspondingly, Eq. (1) and also the model of Lee et al. predict that SF fragmentation should increase with increasing stretch. It could be difficult, however, to distinguish between enhancement of assembly and inhibition of fragmentation.

As mentioned, isotonic tests are possible in 3D ETCs, but only under certain conditions. For ETCs with cell populations near the percolation threshold and thus undergoing nominally affine deformation, the stress absorbed by cells in such an experiment can be estimated from relatively straightforward calibrations on ETCs from which cells have been selectively removed (cf. [21, 22, 26, 61, 64]). Additionally, single-cell pulling and poking experiments (e.g., [67, 68]), magnetic actuation of micropillars and microtissues [69], and creep loading of flexible substrata offer promising approaches to approximate isotonic conditions.

Fluorescence photobleaching and recovery measurements (FPR or FRAP) [70] could help to distinguish among different responses to stress and strain. These measurements measure the rate of fluorescence recovery after a fluorescence-labeled component of a SF has been photobleached by a brief pulse of light. Recovery of SF fluorescence results from replacement of the bleached molecule with an unbleached molecule that has diffused to the observed SF after termination of the bleaching pulse. The rate of recovery is expected to be dominated by the rate of dissociation of the bleached molecule from the SF although it is also possible that the rate could be influenced by the rate of incorporation of the unbleached molecule into the SF. In either case the rate of recovery yields a measure of the SF kinetic stability. One would expect that as the SF is destabilized, the rate of exchange should increase. Hence, one could test the effects of stretch on the kinetics of membrane fragmentation by carrying out photobleaching measurements on cells in ETCs held at different levels of stretch. These measurements are complicated, however, by the ability of the cells to adapt to different stretch and force levels. One way to evade this problem would be to inhibit actin-myosin interactions, e.g., with blebbistatin [71], so that the tension of the cells is entirely controlled by the force exerted on the ETC.

For the model of Desphande, et al., measurement of η^ss while varying $\frac{\sigma }{{\sigma }_{\mathit{max}}}$ mechanically under isotonic conditions while maintaining C̄ constant would allow direct calibration of the rate constants K̄_f and K̄_b and evaluation of the range of validity of Eq. 1. Even though SF appear to be static in non-locomoting cells that have accommodated to a bed of microneedles or a patterned substrate, it is likely that they are in a state continual turnover, as suggested by photobleaching measurements, for example on α-actinin and myosin light chain that show recovery times in the range of tens of seconds to a few minutes [2, 72-74].

For the model of Kaunas, et al., the connection to an isotonic experiment is more difficult because the model does not depend upon stress state, but rather only upon strain state. However, a creep load applied to a flexible planar substratum upon which cells are cultured would still provide a useful assay of the underlying kinetic Eq. (2) and Eq. (3). The polymer substrata of interest are typically designed to be largely elastic over the timescale of experiments, to avoid complications associated with viscoelastic relaxation in oscillatory experiments, but enhancement of viscoelasticity is possible by tuning cross-linking of or coating extracellular matrix proteins upon substrata. ETCs are inherently viscoelastic as well [61, 66]. In both cases, nonlinear viscoelasticity is expected, but the responses of ETCs can be approximated incrementally with linear viscoelasticity over broad ranges [75, 76] provided that loads are applied sufficiently slowly [77]. In such cases, the axial strain ε applied to cells in an isometric test of a 3D ETC or 2D viscoelastic substratum would follow, for a standard viscoelastic solid (e.g., [78]):

$$\in =\sigma (C_1+C_2\mathit{exp}(-t/\tau ))$$ (5)

where τ is a relaxation time constant and C₁ and C₂ are constitutive parameters that could be characterized. Alternatively, strains could be estimated using optical approaches. Isotonic loading would then allow, in conjunction with the fluorescence photobleaching recovery (FRAP) experiments suggested above, estimation of rate constants from Eq. (3) and assessment of the functional form of the dependence of rate constants upon strain. The constant k_o would play a dominant role at later times (relative to τ) in a creep test, and the quantification and the constant k₁ would play an increasingly important role at earlier times.

The model of Lee, at al., does not have parameters that can be calibrated usefully under creep conditions. However, some basic assumptions could be tested. Specifically, the model would predict that as the cells stretch over time, stress fibers will dissociate, and that sufficient stress will lead to alignment of cells and stress fibers into the direction of applied loading. The functional form of Eq. 5 could then be evaluated from SF assembly rates measured at a series of strain levels under isotonic conditions.

Cell reorientation and predictions of 3D experiments

For the kinds of observations reported in 3D ETCs, it appears that SF do not reorient in response to stretch or stress simply by rotation of the cell or by rotation of SF within the cell. Rather, reorientation of SF to a preferential direction defined relative to stretch or stress requires the fragmentation of SFs not oriented in the preferred direction and their assembly in the preferred direction. The three models that we have discussed accomplish this in different but closely related ways.

According to the Kaunas model fragmentation of SFs occurs preferentially along the direction of stretch for uniaxial cyclic stretch [40]. Note that for these experiments there is no lateral compression for uniaxial stretch and so there is no driving force for preferential fragmentation perpendicular to stretch. At the same time there is continuous and rapid isotropic assembly of SFs. The net result of fragmentation parallel to stretch and isotropic assembly is net reorientation of SF perpendicular to stretch.

Wei, et al., used the Deshpande model to account for the same experimental observations [44]. According to their model SFs should be stabilized along the direction of stretch during the loading phase of the cyclic stretch. They assert, however, that the dominant effect is rapid fragmentation during the unloading phase of the cycle. There is no corresponding effect on the SF perpendicular to the uniaxial stretch. Hence, the net effect is reorientation of the SF perpendicular to the stretch direction. Note that Chen, et al., reinforce this idea by describing rapid SF fragmentation during the unloading phase of a stretch and unload experiment [9]. Hence, the principal difference between these two proposed mechanisms for reorientation is that fragmentation occurs during the loading phase of cyclic stretch for the former and during the unloading phase for the latter.

This might be tested by varying the relative durations and rates of loading and unloading. Suppose that loading and unloading occur at the same rate and that the duration of loading is kept constant in a series of measurements for which the duration of unloading is shortened. The interpretation by Wei, et al., would predict less fragmentation. According to the Kaunas model, however, supposing that fragmentation occurs during loading, there should be no effect on fragmentation by shortening the duration of unloading and keeping the duration of loading constant. Conversely, if the duration of unloading is kept constant and the duration of loading is varied, there should be greater fragmentation for longer loading periods according to Kaunas but no effect according to the interpretation of Wei.

One challenge with this experiment is that the magnitude of stretch increases with the duration of the loading phase. Hence, both duration and stretch magnitude vary. As the period of loading is increased there should be greater assembly of SF along the direction of stretch according to the interpretation of Wei, et al. This should be observable as well. In any event, this challenge would not affect testing of the fundamental difference, namely that one model predicts that fragmentation occurs during loading while the other, that it occurs during unloading.

The stress exerted by the SF at the attachment sites of the cell to the extracellular matrix plays distinct and complementary roles in the models of Lee, et al., and of Deshpande. The model of Lee, et al., emphasizes the role of stresses greater than a threshold in accelerating SF assembly (Eq. 4) while the Deshpande model focuses on an increased rate of fragmentation of SF as stresses decrease below the isometric level (Eq. 1).

According to the model of Lee, at al., fragmentation of SFs depends explicitly on the magnitude and direction of stretch while SF assembly depends on the magnitude and direction of stress [27]. Due to the incompressibility of the ETCs a simple stretch along one direction causes a corresponding (Poisson) compression in the transverse direction. An important feature of this model is the provision for a range of allowed pre-stretch levels. This allows for diverse behaviors of cells in response to stretch. Therefore, along the direction of stretch or perpendicular to it SF that are, respectively, strained or compressed beyond the allowed pre-stretch range rapidly fragment. According to Eq. (4) the assembly of SFs is favored along direction of low SF density (fibrosity, φ_max − φ_n) and high stress (σ_n > σ_g). Thus, for cells with a narrow range of pre-stretch values, stretching the ETC extends few SF outside the allowed range, and so there is very little fragmentation. The cells respond to stretch by simple reinforcement (SF assembly) along the direction of stretch. For relatively isotropic cells with a wide range of pre-stretch values stretch causes extensive SF fragmentation along parallel and transverse directions. As a result the SF density is too low to permit the build-up of sufficient contractile force to enhance directional assembly of SF. These cells, then, experience simple retraction. Cells with an intermediate distribution of pre-stretches undergo a moderate level of SF fragmentation followed by a reassembly of SF along the direction of stress, and so exhibit retraction followed by reinforcement. For this model there is a formal steady state under static conditions when φ_n = φ_max. Under these conditions there is no stretch-induced fragmentation and the SFs are at their maximum level. This model does not explicitly allow steady states that result from a balance of SF fragmentation and assembly. It would be useful, however, to test Eq. 4 by measuring the rate of SF assembly at different constant levels of stress under isotonic conditions.

Testing and extending the models

To extend and test the models for SF fragmentation and assembly it is necessary to provide more detailed molecular mechanisms. Fragmentation by stretch might result simply from the detachment of SFs from their anchorage to FAs. Detachment might uncap filaments and so allow them to depolymerize from their barbed ends. Moreover, the release of tension might otherwise destabilize the actin filaments, e.g., by interfering with the actin-myosin contractile apparatus. It is also possible, however, and perhaps more likely, that stretch beyond a threshold activates proteins that specifically disassemble actin filaments [79]. For example, ADF/cofilin and gelsolin sever actin filaments, while other proteins, e.g., capping protein, limit filament growth by binding to the rapidly growing (barbed) end of actin filament. Stretch activated Ca²⁺ channels could cause an increase in cytoplasmic Ca²⁺ concentration that would activate gelsolin, leading to fragmentation of actin filaments. Alternatively, ADF/cofilin could be activated to depolymerize actin filaments by a Ca²⁺-independent mechanism, e.g., dephosphorylation. Although the mechanism for SF assembly is not well understood, there is a great deal of information about the molecular mechanisms for the formation of dendritic actin networks based on the protein complex Arp2/3 and long actin filaments nucleated by formins [80]. It seems clear that the assembly of ventral SFs and of FAs is coordinated and dependent on cellular contractile force [42, 43, 55]. The nucleation of SF and FA assembly might depend on the initial mechanical interactions of actin filaments with integrins and other FA components [81].

The most direct approach to testing the effects of specific proteins in the fragmentation and assembly of SF is to use genetic or molecular biological methods to increase or decrease their concentration in the cell. The interpretation of these types of experiments is sometimes complicated by adaptation mechanisms in cells that reduce the phenotypic consequences of mutations. It is therefore useful to design mutant protein molecules that can be rapidly activated or inhibited, e.g., by light. For example, using light sensitive plant proteins it has been possible to create cells with photoactivatable versions of the small GTPase protein Rac1 [82, 83]. Exposure to activating light caused relocation of the modified Rac1 from the cytoplasm to the cell membrane and extension of lamellipodia.

Conclusions

We have discussed three models that seek to account for the effects of force and stretch on the stability and orientation of SF in cells. Orientation and re-orientation of SF are related to the orientation of stretch applied to cells and contractile stress generated by the cells. At the heart of each model is a rate law for the effect of stretch and stress on the assembly and fragmentation of SF. The models of Kaunas and of Lee et al. posit that stretch beyond specified homeostatic levels accelerates fragmentation of SF, while the Deshpande model supposes that SFs are stable at a maximal homeostatic stress level and that the rate of SF fragmentation increases as the level of stress decreases from this level due to cell contraction. The Kaunas model supposes that SF assembly is continuous, rapid and isotropic, and the Deshpande model is similar except for a possible dependence of an excitation signal on cell orientation. The model of Lee et al. proposes that the rate of SF assembly increases with stress, which provides an additional orientation constraint. The Deshpande model is the most complex and has been applied to a wide range of observations. Nevertheless, the extent to which each of the models can account for any of the observations is not yet clear. Further experimental work including both tests of the functions of specific proteins using molecular biological approaches and mechanical and photobleaching studies can determine which aspects of the proposed rate laws do apply to the control of SFs in cells.