Adaptation disrupts motion integration in the primate dorsal stream

Summary

Sensory systems adjust continuously to the environment. The effects of recent sensory experience—or adaptation—are typically assayed by recording in a relevant subcortical or cortical network. However, adaptation effects cannot be localized to a single, local network. Adjustments in one circuit or area will alter the input provided to others, with unclear consequences for computations implemented in the downstream circuit. Here we show that prolonged adaptation with drifting gratings, which alters responses in the early visual system, impedes the ability of area MT neurons to integrate motion signals in plaid stimuli. Perceptual experiments reveal a corresponding loss of plaid coherence. A simple computational model shows how the altered representation of motion signals in early cortex can derail integration in MT. Our results suggest that the effects of adaptation cascade through the visual system, derailing the downstream representation of distinct stimulus attributes.

The visual system, like other sensory systems, is strongly influenced by experience. Visual circuitry undergoes striking changes if normal experience is perturbed during development (Hensch 2005). In adulthood, circuitry is altered by repeated exposures to a stimulus (e.g. perceptual learning; Fahle and Poggio, 2002), loss of afferent input (e.g. retinal lesions; Dreher et al., 2001) and even the stimulus history of the preceding seconds (adaptation).

Adaptation has been shown to affect neuronal responses in the retina, lateral geniculate nucleus (LGN), primary visual cortex (V1), and in higher cortex (including areas V2, MT, V4, and IT cortex; Kohn 2007, Webster 2011). Although adaptation effects are evident throughout the visual system, they are typically assayed in distinct ways at each processing stage. For instance, retinal studies focus on changes in sensitivity to light intensity or contrast (Demb, 2008), whereas those in IT cortex investigate how exposure to a particular visual object alters complex selectivity there (e.g. Sawamura et al., 2006).

Natural visual experience provides input that will alter the representation of both low-level features (e.g. contrast and orientation) and more complex ones (e.g. object form and motion). It is not known whether these adjustments occur independently, or whether altered sensitivity to low-level features affects the representation of more complex ones. Perceptual studies suggest “cross-adaptation” can be substantial. For instance, adapting to line curvature can alter the perceived emotion of a face stimulus (Xu et al., 2008, 2012) and the perceived global form of an object (Dickinson et al., 2010); altered contrast and luminance sensitivity can give rise to a percept of illusory motion (Backus and Oruc, 2005). Such effects might be expected given our understanding of the computations underlying complex form (Riesenhuber et al., 1999; Cadieu et al., 2007) and motion selectivity (Rust et al., 2006). These involve the precise pooling of signals representing elemental features, followed by non-linear operations. As a result, experience-driven changes in the representation of low-level features could disrupt the computations performed by downstream circuits. Alternatively, downstream circuits might be endowed with mechanisms that allow them to compute quantities of interest, even in the face of adapted input.

Here we test how adapting with drifting sinusoidal gratings affects the ability of macaque area MT neurons to integrate motion signals. MT is a midlevel visual area, strongly involved in motion processing (Born and Bradley, 2005). MT receives most of its input from V1, both directly and via other cortical areas. Both V1 and MT contain direction-selective neurons, but they differ in their selectivity for pattern or plaid stimuli—composed by the addition of two gratings with offset directions of motion (Movshon et al., 1985). Direction-selective V1 neurons typically respond to both components of the pattern, and are thus termed component direction selective (CDS). Some MT neurons are also CDS, but an appreciable fraction encodes the direction of the pattern and not its constituent elements (pattern direction selective or PDS). This form of motion integration has been studied extensively, and models to explain how MT pattern selectivity might be built from V1 inputs have been proposed (Simoncelli and Heeger 1998; Perrone 2004; Rust et al. 2006; Beck and Neumann 2011; Nishimoto and Gallant 2011).

The effects of adaptation on V1 and MT neurons have been explored in a number of studies. In V1, adaptation with a drifting grating induces a stimulus-specific loss of responsivity, when the stimulus is confined to the spatial receptive field (Movshon and Lennie, 1979; Muller et al., 1999, Dragoi et al., 2000). Adaptation with larger gratings can induce either stimulus-specific suppression or facilitation (Webb et al., 2005; Wissig and Kohn, 2012; Patterson et al., 2013a). In MT, grating adaptation also changes responsivity in a stimulus-specific manner (Kohn and Movshon, 2004). Importantly, these effects are spatially specific within an MT neuron’s receptive field: a small adapter reduces neuronal responsivity to gratings presented at the same location, but not to gratings presented elsewhere within the receptive field (Kohn and Movshon 2003). This strongly suggests that MT effects are inherited from earlier stages of processing, where receptive fields are smaller.

We used the inheritance of grating adaptation effects in MT and the distinct computations performed there to test how altering early sensory signals affects downstream processing. We show that motion integration in MT is strongly disrupted by adaptation, as is the perceptual coherence of plaid stimuli. These results can be explained by a fixed pooling by MT neurons of an altered representation of motion signals in the early visual system.

Results

We recorded spiking activity from 170 MT neurons in 4 anesthetized macaque monkeys. MT receptive fields were located 4–8 degrees from the fovea.

Grating adaptation reduces pattern selectivity in MT

We measured MT responses to gratings and plaids, before and after prolonged (40 s) adaptation with a drifting grating. For most measurements (n=133 cells) we used a fixed stimulus ensemble (see Methods) rather than tailoring stimuli to individual cells. This approach reveals how adaptation alters the representation of a particular stimulus ensemble by cells with diverse preferences (Wissig and Kohn, 2012). We quantified neuronal pattern selectivity using a standard pattern index (PI, see Methods). PDS cells were defined as having a PI greater than 1.28; CDS cells had a PI less than −1.28 (Smith et al. 2005). Otherwise, cells were defined as unclassified.

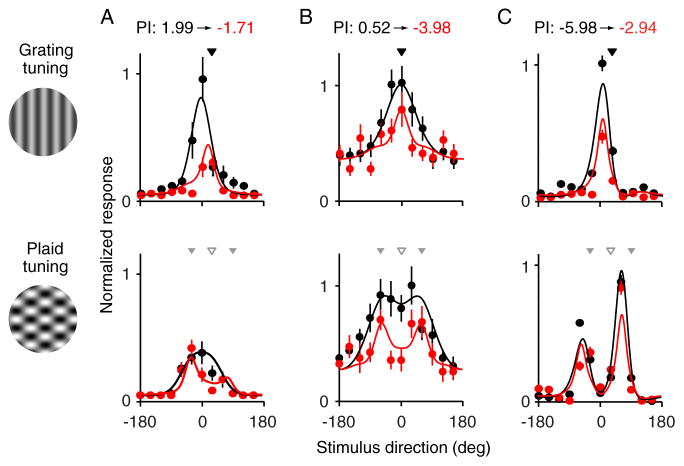
Figure 1A shows the responses of a PDS cell adapted near its preferred direction (black arrowhead). Peak responsivity to gratings (top) was reduced after adaptation (red compared to black). However, responses to gratings matched to the adapter were largely unaffected, thus causing a shift in preferred direction toward the adapted direction. Adaptation caused a notable change in plaid tuning (bottom), converting the unimodal, PDS tuning (black) to a bimodal, CDS one (red). Responsivity was reduced most for plaids drifting in the adapted direction (open gray arrowhead); responses to plaids containing component motion in the adapted direction (filled gray arrowheads) were not strongly affected. The PI was reduced from 1.99 to −1.71 after adaptation, a conversion from significant pattern to component selectivity.

Figure 1.

Tuning of MT neurons for gratings and plaids, before and after grating adaptation. (A) The responses of a PDS cell, before (black) and after (red) adaptation. Responses to drifting gratings are shown on top; responses to plaids on bottom. The direction of the grating adapter is indicated by black arrowhead; in the bottom plot, the open gray arrowhead indicates the adapted direction and the filled gray arrowheads indicate the plaid directions which contain component motion in the adapted direction. All responses are normalized by the peak pre-adaptation grating response. Solid lines show the fits of the model shown in Figure 3. Error bars indicate SEM. (B) Responses of an unclassified unit. The offset of this cell is due to a high spontaneous firing rate. (C) Responses of a CDS neuron.

Figure 1B shows an unclassified cell, also adapted near its preferred direction. After adaptation, responses to gratings were reduced (top). Plaid tuning (bottom) developed two peaks offset by 120 degrees after adaptation, resulting in CDS tuning. The PI fell from 0.52 to −3.98. For a CDS cell (Figure 1C), adaptation near the preferred direction also led to weaker responses to drifting gratings (top). Selectivity for plaids, however, was not strongly altered (bottom): the PI increased from −5.98 to −2.94, but tuning remained CDS. Thus, tuning in this sample of example cells spanned a range from PDS to CDS before adaptation, but all cells were CDS after adaptation.

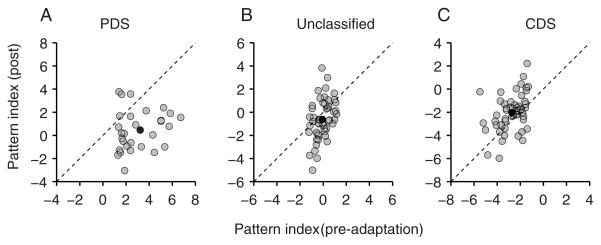
Across our population of MT cells (n=133), adaptation led to a notable reduction in pattern selectivity. The PI fell from −0.39 to −0.93 on average (p=0.005; paired-sample t-test). The PI decreased most for PDS cells, from 3.23±0.36 to 0.44±0.31 (p<0.0001; Figure 2A), and the proportion of PDS cells dropped from 23% of units before adaptation to 13% after. Unclassified cells showed a weaker but still significant loss of pattern selectivity. The PI of these cells fell from −0.10±0.10 to −0.66±0.25 (p=0.02; Figure 2B), and their proportion increased from 38 to 41%. Most CDS cells remained component-selective after adaptation, with the average PI increasing from −2.75±0.15 to −1.99±0.22 (p=0.0005) and their proportion from 39 to 46% (Figure 2C).

Figure 2.

Effects of grating adaptation on MT pattern selectivity. (A) A comparison of the pattern index (PI) before and after adaptation for PDS cells. Almost every neuron had a lower PI after adaptation, and many neurons became strongly CDS (PI<−1.28). (B,C) PIs before and after adaptation for unclassified and component cells. Black dots indicate the mean PI for each cell type. See also Figure S4.

To be sure that our results did not depend on the particular parameters of our stimulus ensemble, we performed further experiments in which we matched the spatial and temporal frequency of the adapter and test stimuli to the preferences of individual cells (n=37). In these experiments, grating spatial frequency ranged from 0.25–1.75 cycles/degree and drift rate from 1–8.5 Hz. Under these conditions, adaptation also reduced pattern selectivity. The PI of PDS cells fell from 2.55±0.30 to 0.92±0.51 (p=0.017; n=9). For unclassified cells, the PI fell from 0.01±0.25 to −0.89±0.49 (p=0.08; n=9). For CDS neurons, there was no notable change in the PI (from −2.93 ±0.30 to −2.54±0.30, p=0.28; n=19). Thus, the loss of MT pattern selectivity does not require using stimuli with a particular spatial or temporal frequency. Because we found no notable differences between the results obtained with the common and optimized ensembles, we pooled the data in further analysis.

Although the disruption of pattern selectivity in PDS cells was substantial on average, the strength of the effect depended on the offset of the neuron’s preference from the adapter. The strongest effects were evident for cells adapted near their preferred direction: of those adapted 0–60 degrees from their preferred direction (n=16), 25% became CDS and only 19% remained PDS. Cells adapted opposite to their preference (120–180 deg offset; n=8) showed weaker but still significant effects: 25% became CDS and 37.5% remained PDS. The weakest effects were observed for cells with preferences in between (60–120 deg offset; n=15), for which only 7% became CDS and nearly half (47%) remained PDS.

In summary, prolonged grating adaptation sharply reduced MT pattern selectivity. The effect was strongest in PDS cells, particularly those adapted in their preferred- or null-direction. Unclassified and CDS cells showed weaker effects. We conclude that adaptation with drifting gratings can disrupt the ability of MT cells to integrate motion signals.

V1 adaptation effects can explain the disruption of MT pattern selectivity

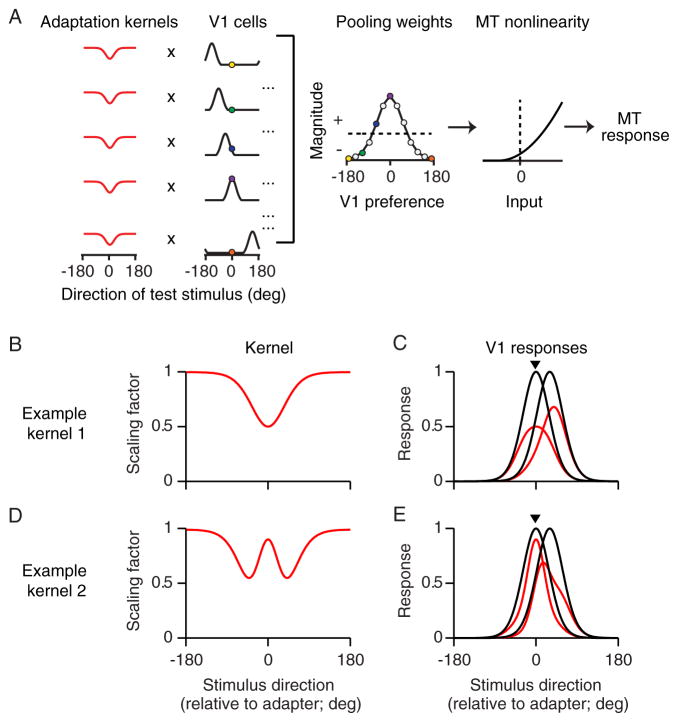
To understand how grating adaptation could disrupt MT pattern selectivity, we used a simplified version of a recently developed model (Figure 3A; Rust et al., 2006). The first stage of our model consisted of a bank of direction-selective V1 neurons with evenly distributed preferences. Direction-selective V1 cells are known to project directly to MT (Movshon and Newsome, 1996), and to contribute strongly to direction-selectivity there (Ponce et al., 2008; Born and Bradley, 2005). These V1 responses were weighted by a positive or negative factor (pooling weights) and summed. The sum was then passed through a nonlinearity to generate the MT response. Thus, the model has a simple feedforward, linear-non-linear architecture. Pattern selectivity in the model is determined by the weights: a broad profile with balanced excitatory and inhibitory weights generates PDS responses, whereas a narrow weighting profile dominated by excitation results in CDS responses (Rust et al., 2006; Jazayeri et al., 2012).

Figure 3.

Explaining how grating adaptation alters MT pattern selectivity. (A) The model consists of a bank of direction selective V1 neurons, a linear weighting profile, and a nonlinearity which transforms the summed input to an MT firing rate. Adaptation is implemented by applying the same adaptation kernel (red) to the tuning of each V1 neuron. Colored dots indicate the responses of the respective V1 neurons to one direction of motion (left) and how these responses are weighted by the MT neuron (center). (B) A sample adaptation kernel, which implements broadly-tuned, stimulus-specific suppression. (C) Tuning of two sample V1 neurons before (black) and after (red) applying the kernel in (B). (D) A second adaptation kernel. It pairs a broadly-tuned, stimulus-specific suppression with a local disinhibition, which weakens effects for stimuli similar to the adapter. (E) Tuning of two sample V1 neurons before (black) and after (red) applying the kernel in (D).

We implemented adaptation effects in the model by altering responsivity in V1. We did so because adaptation is known to have strong effects in V1, and because grating adaptation effects in MT are inherited from the early visual system (Kohn and Movshon 2003). Effects were implemented with an adaptation kernel, which defined how the response to each stimulus was altered by adaptation. We applied the kernel by pointwise multiplying the kernel’s scaling factor for each stimulus with the corresponding response on each V1 tuning curve.

Kernels of different shapes can account for the wide-range of adaptation effects previously reported in V1. For instance, the example kernel shown in Figure 3B reduces responses to stimuli matched to the adapter by half, and responses to offset test stimuli much less strongly. When this kernel was applied to a neuron whose preference matched the adapter (Figure 3C), it caused a loss of peak responsivity. When applied to a neuron whose preference is offset slightly from the adapter, the kernel also caused a shift in tuning away from the adapter, a frequently observed effect in V1 (Kohn, 2007; Webster, 2011).

The example kernel shown in Figure 3D pairs broadly tuned suppression with a more sharply tuned disinhibition, which weakens effects for stimuli most similar to the adapter. When applied to a V1 neuron whose preference matched the adapter (Figure 3E), this kernel resulted in maintained responsivity and narrower tuning. For a neuron with an offset preference, the kernel caused tuning to shift toward the adapter. These effects are observed in V1 when large grating stimuli are used and the targeted neurons have substantial surround suppression (Wissig and Kohn, 2012; Patterson et al., 2013a)—a suppressive influence recruited by stimuli falling outside the classical receptive field (Cavanaugh et al., 2002). Large adapters weaken surround suppression in a stimulus-specific manner, a form of disinhibition which partially offsets the loss of responsivity typically reported after adaptation.

To determine which type of V1 adaptation effects could disrupt pattern selectivity, we fit the model in Figure 3A to the pre- and post-adaptation responses of each cell, by maximum likelihood. We parameterized the adaptation kernel as a difference-of-Gaussians function, allowing for both facilitory and suppressive effects (see Methods). The model accurately captured the measured responses. The median fit quality was 0.81 (median absolute deviation, 0.06), where a value of 0 represents a model which always predicts the mean response across all stimuli and a value of 1 represents a “perfect” model which predicts the measured responses (see Patterson et al., 2013a, and references therein). Fit quality did not differ among PDS, CDS, and unclassified cells (0.82, 0.81, 0.80, respectively; p>0.1 for all comparisons).

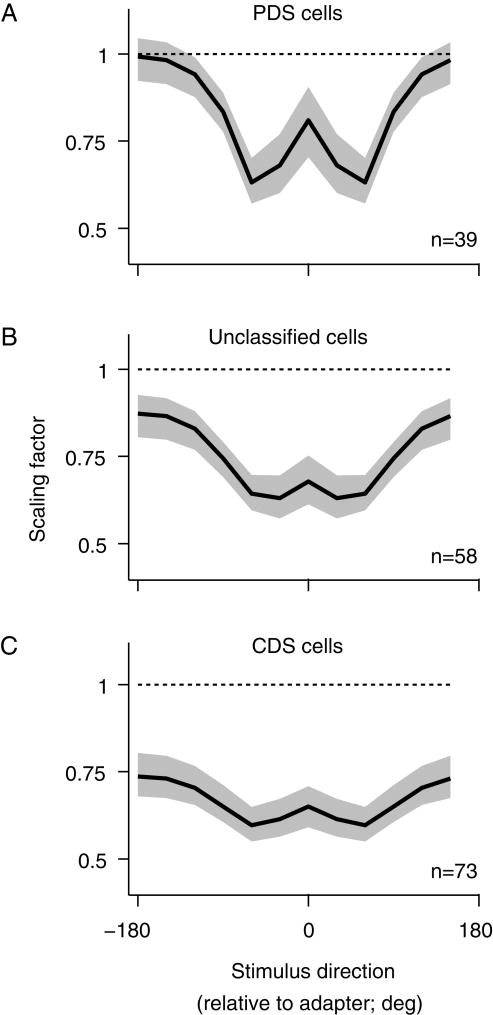
Figure 4 shows the average kernels applied to the V1 stage of the model, for each type of MT neuron. The kernels depended both on pattern selectivity (F=6.74, p=0.0012) and the offset of the stimulus from the adapter (F=4.66; p=0.0001; 2 factor ANOVA). The kernels for PDS cells (Figure 4A) showed a broadly tuned loss of responsivity, which was notably weaker for stimuli near the adapter (0 deg). This disinhibition was particularly evident in preferred- and flank-adapted PDS cells (Supplementary Figure 1). The kernels for CDS cells (Figure 4C) showed only a suppressive effect of adaptation, which was strongest for stimuli similar to the adapter but also significant for offset stimuli. Kernels for unclassified cells had an intermediate form (Figure 4B).

Figure 4.

Model adaptation kernels. (A) The average (geometric mean) adaptation kernels for MT PDS cells (black). The gray shading indicates 68% confidence intervals. (B) Kernel for unclassified cells. (C) Kernel for CDS cells. See also Figures S1, S2, and S3.

The kernels for PDS cells would induce effects that are seen in strongly surround-suppressed V1 neurons (Figure 3D,E), given the large gratings we used in our experiments (7.4 deg). This suggests that PDS cells receive preferential input from surround-suppressed V1 neurons, a conclusion also reached by numerous previous studies (van den Berg and Noest 1993; Livingstone et al. 2001; Pack et al., 2003; Rust et al., 2006; Tsui et al., 2010). The kernels fit to CDS cells would induce V1 effects seen in cells with little surround suppression (Figure 3B,C). To confirm that the adaptation kernels for CDS and PDS cells corresponded to effects in these two subpopulation of V1 neurons, we measured pre- and post-adaptation responses in V1. This confirmed the presence of tuned disinhibition for populations of surround-suppressed V1 neurons, but not for V1 neurons lacking surround suppression (Supplementary Figure 2).

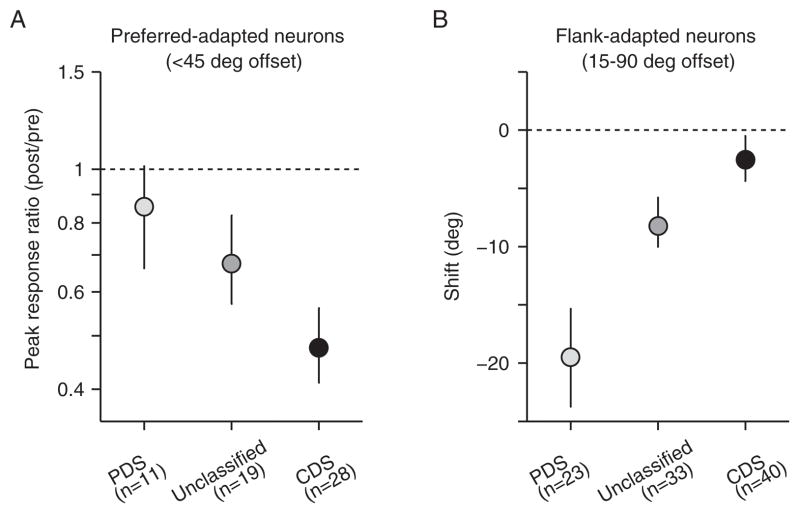
If PDS and CDS neurons inherit effects from different subsets of V1 neurons, this should be evident in how adaptation alters their tuning for grating motion. PDS neurons should show effects similar to those seen in strongly surround-suppressed V1 neurons; CDS neurons should show effects seen in V1 neurons without surround suppression. To test this prediction, we fit von Mises functions to the grating tuning curves and extracted the peak evoked response and tuning preference of each MT cell (as in Kohn and Movshon, 2004). PDS cells adapted within 45 deg of their preferred direction showed no loss of responsivity (Figure 5A): the peak response ratio (after adaptation compared to before) was 0.85 (p=0.85 for difference from 1). In contrast, the peak responsivity of the corresponding CDS and unclassified MT cells was reduced strongly by adaptation, with ratios of 0.67 (p<0.0001) and 0.47 (p<0.001; p=0.02 for difference with PDS cells). Adaptation also had distinct effects on the direction preference of CDS and PDS cells. The tuning of flank-adapted PDS cells (preferences offset by 15–90 deg from the adapter) shifted strongly toward the adapter (−19.5 deg, p<0.001; Figure 5B). This was not the case for flank-adapted CDS cells (−3.1 deg, p=0.20).

Figure 5.

Effects of adaptation on MT grating tuning differ across cell types. (A) Peak responsivity ratio (post/pre) for neurons adapted within 45 degrees of their preferred direction. Note that peak responsivity was affected, on average, more strongly than in Kohn and Movshon (2004); this is likely due to the use of lower contrast test stimuli here. (B) Shifts in direction preference in cells adapted 15–90 degrees away from their preferred direction. Error bars indicate 68% confidence intervals. See also Figures S2 and S3.

Thus, adaptation-induced changes in grating tuning depended strongly on MT pattern selectivity. PDS, but not CDS, cells showed effects consistent with those previously observed in V1, when surround suppression is recruited. We conclude that the disruption of MT pattern selectivity by grating adaptation can be explained by effects induced in V1, if PDS receive inputs from V1 neurons with surround suppression.

Understanding how V1 adaptation can alter MT pattern selectivity

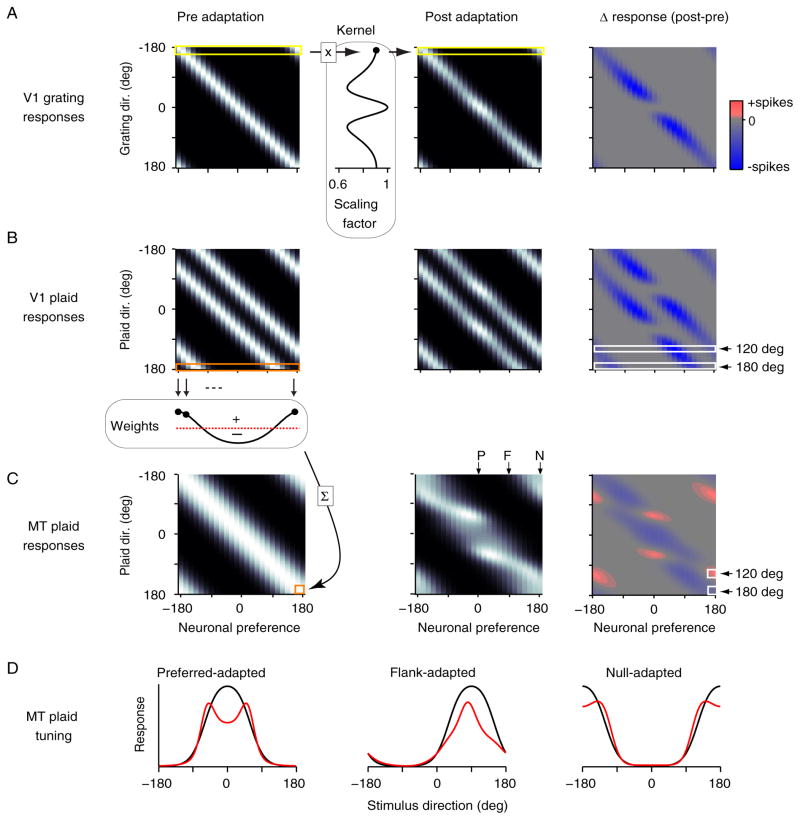
Why does the adaptation kernel shown in Figure 4A disrupt motion integration in MT? To provide intuition, we conducted simulations using a kernel similar to that which fit our data.

We begin by considering V1 responses to gratings before adaptation. Each column in Figure 6A (left) shows the response of one V1 neuron to a full range of grating directions (ordinate), with whiter colors indicating stronger responses. The main diagonal structure arises because each neuron fires most to its preferred stimulus, by definition. The adaptation kernel (inset) produces a distorted V1 population response (center). Specifically, the kernel defines how the response to each stimulus is scaled after adaptation. The scaling is minimal for stimuli either matched to the adapter (0 deg.) or very different from it (±180 deg), and strongest for stimuli in between. Comparing the pre- and post-adaptation V1 responses reveals a loss of spiking activity (blue colors in right panel), particularly for neurons that prefer the stimuli which are most strongly scaled (roughly ±60 deg).

Figure 6.

Intuition for why V1 adaptation disrupts MT pattern tuning. (A) Left: V1 population responses to drifting gratings, before adaptation. The abscissa indicates the preference of each modeled V1 neuron; the ordinate indicates grating direction. Whiter colors correspond to stronger responses. Inset: The adaptation kernel applied to V1 responses. Responses to each stimulus (row of the panel in A; response to one stimulus highlighted in yellow box) are scaled by the factor indicated by filled circle. Center: Post-adaptation V1 responses to drifting gratings. Right: Difference between responses before and after adaptation. Gray indicates no change in response strength; blue indicates a reduction in spiking activity. (B) V1 responses to plaid stimuli. Right: White boxes indicate responses to two plaid stimuli considered in (C). (C) Left: MT responses to plaid stimuli before adaptation. Inset: The weighting profile for the MT neuron preferring 180 deg motion. The response to a 180 deg plaid, shown in an orange square box at the bottom right of the panel, is defined by the weighted sum of V1 responses to that stimulus (orange rectangle in A). Center: MT responses to plaids after adaptation. Letters (P,F,N) indicate the post-adaptation tuning curves illustrated in (D). Right: Difference between responses before and after adaptation. Red indicates an increase in response strength; blue indicates a decrease. White boxes highlight the plaid directions indicated. (D) Sample MT tuning curves for plaids, before (black) and after (red) adaptation. See also Figure S3.

V1 responses to plaids are straightforward. Both before and after adaptation, they are made simply by summing the responses to each of the component gratings (±60 deg because we used 120 deg plaids). As a result, there are two clusters of activity in V1 for each plaid, involving neurons whose preferences are 120 degrees apart (Figure 6B, left and center). For each stimulus, adaptation thus causes a loss of spiking activity that is distributed across a broader range of neurons (right panel).

MT responses are determined by a weighting of the V1 population response. For instance, the responses of an MT neuron preferring 180 degree motion are defined by the illustrated weighting profile (inset). Its response to its preferred plaid (orange square in Figure 6C) is defined by the weighted sum of the V1 response to that stimulus (orange rectangle in Figure 6B). Because we focus on PDS cells, the weighting profiles produce MT responses to plaids that are unimodal before adaptation (Figure 6C; left). After adaptation, MT responses to plaids show evidence of both response suppression (blue in right panel) and enhancement (red).

Why do responses to some plaid stimuli increase? This arises when the loss of V1 responsivity is in neurons that are negatively weighted by an MT cell. For instance, the MT neuron which prefers 180 degree plaids responds more strongly to a 120 degree plaid after adaptation (indicated with white box in Figure 6C, right). This is because the loss of V1 responsivity for this plaid occurs for V1 neurons that are weighted negatively (white rectangle in Figure 6B, right). In contrast, this MT neuron’s response to a 180 deg plaid decreases, because positively-weighted V1 neurons show the greatest loss of responsivity for this stimulus.

The consequences of this altered responsivity for the plaid tuning of preferred-, flank- and null-adapted MT neurons can be appreciated by taking vertical slices through the population responses. Preferred- and null-adapted neurons showed a loss of PDS tuning, with the PI dropping from 2.23 to −1.33 and 0.18, respectively (Figure 6D). For flank-adapted neurons, there is little change in pattern selectivity (PI increased to 2.62).

In summary, the V1 adaptation kernel can explain how pattern selectivity is altered by adaptation for MT neurons with a range of offsets. Changes in pattern selectivity arise because MT pooling involves both positive and negative weighting of weaker V1 responses, resulting in stronger responses to some plaids and weaker responses to others.

Grating adaptation reduces perceived plaid coherence

The disruption of MT pattern selectivity by adaptation provides a clear perceptual prediction. It suggests that grating adaptation should make plaids appear transparent, meaning the two gratings should appear to drift over each other. To test this, we measured whether human subjects perceived plaid stimuli as coherent (a single pattern) or transparent, before and after adaptation. In order to make the most direct comparison with our physiological findings, we used the same stimulus and adaptation parameters (see Methods).

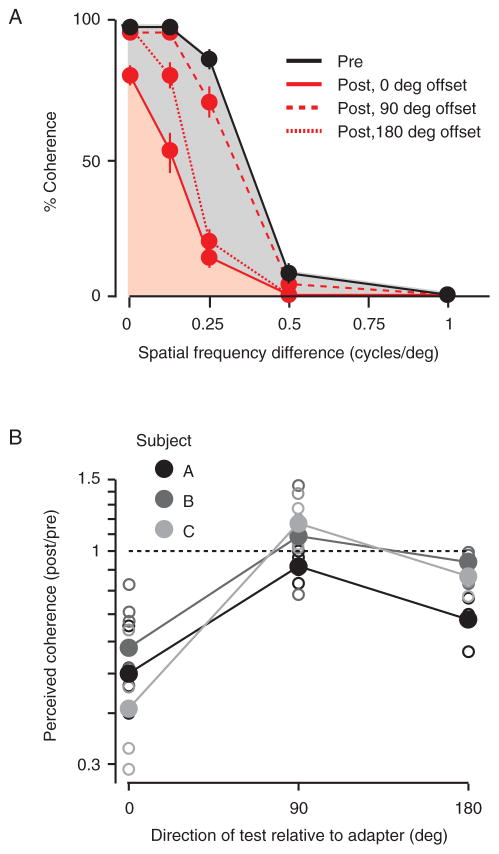
To produce stimuli with differing degrees of perceived coherence, we manipulated the difference in spatial frequency of the two grating components. Differences in spatial frequency, like other component features, can bias perception towards transparency whereas similarities bias towards coherence (Adelson and Movshon 1982; Smith, 1992). Consistent with this description, unadapted subjects were less likely to report the plaid as coherent, when the spatial frequency difference between gratings was larger (Figure 7A, black, data for a single subject). This was also true after adaptation (red lines), but there was a marked reduction in the perceived coherence for some stimuli. For plaids whose direction matched the grating adapter (0 deg offset; red solid line), two gratings with a difference of 0.25 cyc/deg were perceived as coherent on 88% of trials before adaptation but only 14% after. The coherence of plaids drifting opposite to the adapted direction was also strongly reduced (180 deg offset; red dotted line), but there was little effect on plaids drifting orthogonally to the adapter (red dashed line).

Figure 7.

Grating adaptation reduces the perceptual coherence of plaid stimuli. (A) Psychometric function for one subject. Perceived coherence (proportion of trials in which subjects report a single direction of motion) is plotted as a function of the spatial frequency difference of the two component gratings. Data before adaptation are in black. The red solid line shows the effects when the grating adapter is matched to the pattern direction of motion; red dashed line when it is offset by 90 degrees; and red dotted line when its direction of motion is opposite to the test stimuli. Error bars indicate SEM across sessions. (B) Effects of adaptation on perceived coherence across all subjects. Open symbols show data from each session; filled symbols show the average data for each subject. Perceived coherence is measured as the area under the psychometric function after adaptation, compared to before.

We quantified the change in perceived coherence across subjects (n=3) by calculating the ratio of the area under the psychometric functions (post/pre). We did not calculate coherence thresholds because these were sometimes undefined after adaptation, due to the strong loss of coherence. All subjects showed a strong reduction in perceived coherence when the adapter matched the pattern direction of the plaid (Figure 7B; filled symbols indicate averages across sessions, open symbols are data from each session). The geometric mean ratio was 0.49 (p<0.0001 for difference with 1, bootstrap test). There was a weaker but still clear loss of perceived coherence after null adaptation (0.82, p<0.0001). For test stimuli whose pattern motion was orthogonal to the grating direction, there was a small increase in perceived coherence (mean ratio 1.06, p=0.06).

In summary, grating adaptation reduced the perceived coherence of plaids whose pattern motion matched or was opposite to the adapter direction. Adaptation did not alter the coherence of plaids drifting in an orthogonal direction. These results are consistent with the neuronal changes in pattern selectivity and with effects predicted by a model for generating MT pattern selectivity, given the V1 adaptation kernels we derived.

Discussion

Grating adaptation reduces pattern selectivity in macaque MT, and disrupts the perceptual coherence of plaid stimuli for human subjects. The loss of pattern selectivity can be explained by adaptation-induced changes in V1 population responses and a fixed (unadapted) pooling rule for generating selectivity in MT. This explanation makes use of an independently-derived model for generating MT pattern selectivity and is consistent with previous evidence that PDS cells receive input from strongly surround-suppressed V1 neurons, with the influence of surround suppression on V1 adaptation effects, and with previous evidence that grating adaptation effects in MT are inherited from early cortex.

Our findings reveal two important principles of adaptation. First, the effects of adaptation are not limited to the features of the adapter (e.g. direction of one-dimensional motion), but cascade through the visual system to disrupt the representation of more complex stimulus features (e.g. pattern selectivity). Downstream networks appear unable to generate their typical selectivity in the face of altered input from early cortex, at least in the case of pattern selectivity in MT. Second, the effects of adaptation can depend strongly on the functional properties of a neuron. The responsivity of preferred-adapted PDS cells was maintained after adaptation, and the preference of flank-adapted neurons shifted strongly toward the adapter. Neither effect was evident for CDS cells. Thus, nearby cortical neurons may adapt in strikingly different ways, presumably because of differences in the properties of their inputs.

Explaining the loss of MT pattern selectivity

To explain the loss of MT pattern selectivity after adaptation, we fit a simplified variant of a model proposed by Rust et al., (2006). We chose this model because it has a simple, feedforward pooling architecture. Further, the components of the model respect the known physiology, including input to MT from direction-selective V1 neurons (Movshon and Newsome, 1996) and an exponentiating nonlinearity for relating summed synaptic input to spiking responses (Priebe and Ferster, 2008). Alternative models of MT pattern selectivity share its motif of broad pooling of V1 inputs and the inhibitory influence from neurons “outside” the pool (Simoncelli and Heeger, 1998; Perrone, 2004; Tsui et al., 2010; Beck and Neumann, 2011; Nishimoto and Gallant, 2011). Thus we would expect that pattern selectivity in these models would also be disrupted by distorting the representation of motion signals in V1.

We altered responses at the V1 stage of our model, because of the spatial specificity of adaptation effects in MT (Kohn and Movshon, 2003). Of course, MT receives input from other areas, including V1, V2, and V3 (Maunsell and van Essen 1983; Born and Bradley 2005), as well as from thalamic nuclei (Lyon et al., 2010). The precise locus of grating adaptation effects in this complex network is unknown. However, because many of these areas rely strongly on input from V1 (Rodman et al. 1989), placing the locus of adaptation effects at some later (or earlier) stage of processing need not alter our results, so long as it is where receptive fields are small and prior to the integration of motion signals to compute pattern selectivity.

We used an adaptation kernel to define how V1 responses to different stimuli are altered. Variations in kernel form can reproduce the broad array of effects previously reported in V1 (Figure 3). Benucci et al. (2013) used a similar “stimulus-based” kernel, as well as a “neuron-based” kernel (adjusting the gain of each neuron depending on the relationship between its preference and the adapter), to explain adaptation effects in V1 population spiking responses. The stimulus-based kernel was consistently larger and thus more important for accounting for the measured responses, providing support for this choice in our model. Their stimulus-based kernel did not include evidence of disinhibition for stimuli similar to the adapter, but this is entirely expected given the brief (32 ms) stimulus duration used. The influence of surround suppression is only evident after adaptation lasting at least several hundred milliseconds (Patterson et al., 2013a).

To fit the Rust et al. (2006) model to our data, we simplified it by removing its tuned and untuned normalization signals. Rust et al. found these signals necessary to sharpen pattern selectivity and explain response magnitude for a more diverse set of stimulus conditions than we considered (see also Nishimoto and Gallant, 2012; Tsui et al., 2010). However, these signals are not required for producing pattern selectivity (Jazayeri et al., 2012). Although we did not include a tuned normalization signal, it was implicit in determining the shape of our adaptation kernels. This signal likely corresponds to surround suppression, whose weakening we suggest underlies the minimal loss of responsivity for stimuli similar to the adapter.

Central to our explanation is the proposal that MT pattern cells are “unaware” of adaptation-induced changes in their inputs. That is, there are no compensatory mechanisms in MT that mitigate the distorted representation of component motion in V1. This is an instantiation of the adaptation coding catastrophe or decoding ambiguity (Schwartz et al., 2007; Series et al., 2009). The existence of strong visual aftereffects (e.g. the tilt, motion, and direction aftereffects) supports this proposal, since these require that higher areas must be at least partly unaware of the altered representation in early cortex. Were this not the case, the distorted representation of sensory stimuli in early cortex would not give rise to aberrant percepts after adaptation.

Alternative models

Our model assumes that CDS and PDS neurons in MT receive input from V1 neurons with different adaptation properties. We also considered the possibility that there is instead a single set of V1 adaptation effects, with the differences between CDS and PDS cells arising from their distinct weighting of V1 input. Several factors argue strongly against this possibility. First, the weighting profile cannot be freely manipulated to produce different adaptation effects in MT. For each neuron, the relationship between grating and plaid tuning, before adaptation, places strong constraints on the weighting profile. Second, the different effects of adaptation on the grating tuning curves of CDS and PDS cells cannot be reproduced by differential weighting of a common set of V1 adaptation effects, at least in in the context of a simple, feedforward model (see Supplementary Figure 3 for further discussion).

Our model builds PDS and CDS cells directly from V1 inputs. An alternative would be to build PDS cells from CDS cells in MT, driven in turn by V1 (Simoncelli and Heeger, 1998). This hierarchical model might in principle also explain our results, if adaptation effects were implemented in V1 so as to maintain their spatial specificity. However, this model faces two challenges. First, the pattern computation is spatially specific within at MT receptive field (Majaj et al., 2006), suggesting the integration of motion signals occurs before spatial pooling. Second, we found that the responses of preferred-adapted CDS cells to gratings are strongly reduced after adaptation, whereas those of PDS cells are maintained (Figure 5A). A feedforward, hierarchical model would thus require somehow undoing this strong loss of responsivity in CDS cells.

Finally, like most models of pattern selectivity, ours ignores the rich recurrent circuitry between MT cells. Recurrent circuitry can modulate the effects of inherited adaptation (Teich and Qian, 2003; Kohn and Movshon, 2004). We cannot exclude that it contributes to the effects we measured. However, our simulations show that recurrent circuitry is not needed to account for the disruption of pattern selectivity in MT.

Relation to previous work

Our study is not the first to compare adaptation effects across stages of processing. However, previous work has focused mostly on testing whether the magnitude of altered responsivity in one area can be explained by that in a preceding stage (e.g. McClelland et al., 2010). Some studies have measured the spatial specificity of adaptation effects, to infer whether these are inherited or generated locally. For instance, whereas the effects induced in MT by prolonged grating adaptation appear to be inherited (Kohn and Movshon, 2003), those induced by brief presentations of coherent dots appear to be locally generated (Priebe et al., 2002). This is perhaps because of the different drive provided by dot and grating stimuli to early cortical networks (Basole et al., 2003).

In work more similar to ours, Dhruv and Carandini (2013) compared how adaptation alters the spatial receptive fields of neurons in V1 and the thalamus of the mouse. Like us, they find that effects in a downstream network can be explained by the fixed pooling of adapted input from an upstream one. Our study extends these observations to stages of the primate cortical motion processing stream. More importantly, our study is the first, to our knowledge, to show that the fixed pooling of altered feedforward input can disrupt novel selectivity generated in the downstream network.

Previous work has shown that grating adaptation reduces MT neuronal peak responsivity only slightly and causes direction preference to shift toward the adapter (Kohn and Movshon, 2004), effects that preceding V1 studies had not reported. However, more recent work has revealed that “MT-like” effects can be induced in V1 when large grating stimuli are used (i.e. a size typically used in MT), because of the weakening of V1 surround suppression by adaptation (Webb et al., 2005; Wissig and Kohn, 2012; Patterson et al. 2013a). Indeed a direct comparison of adaptation effects in V1 and MT with identical stimulus ensembles confirmed little difference between these areas (Patterson et al., 2013b). Here we extend these previous findings by showing that adaptation effects on MT direction tuning depend strongly on pattern selectivity.

Our perceptual experiments revealed an adaptation-induced loss of plaid coherence that mirrored neuronal effects in MT. Others have reported a similar effect when the pattern direction of the plaid matched that of the grating adapter (Movshon et al., 1985; Burke et al., 1994). Other work has shown that perceptual coherence is reduced at low contrasts (Smith, 1992; Delicato and Derrington, 2005) and higher speeds (Hedges, 2011). Adaptation reduces perceived contrast (Graham 1989) and alters perceived speed (Thompson, 1981), so these effects may also be related to our perceptual results. Importantly, the correspondence between neuronal and perceptual effects suggests the anesthetic we used was not responsible for our observations. Previous work has also found similar pattern selectivity (Movshon et al., 2003) and adaptation effects (e.g. Priebe et al., 2002) in anesthetized and awake animals.

Implications

Many models of visual processing involve the selective pooling of the upstream signals, followed by some nonlinearity (Priebe and Ferster, 2008). For instance, models of V4 and IT perform this computation iteratively, with a “MAX” nonlinearity at each processing stage (Riesenhuber and Poggio, 1999; Cadieu et al., 2007). By distorting the early sensory representation, adaptation could easily disrupt form selectivity in these models. Whether this occurs in IT remains to be experimentally tested. However, adaptation can clearly provide an important tool for testing models and understanding how selectivity in higher cortex is built.

The distortion caused by cascading adaptation effects poses distinct challenges for interpreting perceptual and imaging results. For instance, the finding that grating adaptation can reduce perceived plaid coherence has been taken as evidence for the existence of a motion channel sensitive to the plaid intersections, or ‘blobs’ (Burke et al. 1994; Born and Bradley, 2005). Our data suggest instead that the loss of plaid coherence arises from a distorted representation of simple motion signals in early cortex, and the way these are combined to generate pattern selectivity in MT. Thus, inferring the existence of high-level feature detectors, using adaptation with simpler stimuli, can be misleading if it is not based on an understanding of the relevant computations. A similar cautionary note is relevant for fMRI research (Krekelberg et al., 2006), which often assumes that stimulus-specific adaptation effects indicate neuronal selectivity for a feature. Our results show instead that changes in responsivity—across stimuli or features—can result from the cascading of adaptation effects through multilayered circuits.

The cascading of adaptation effects also raises questions about their function. One common proposal is that adaptation decorrelates the neuronal representation (Barlow and Foldiak, 1989; Benucci et al., 2013). This emphasizes a benefit for the immediate representation of a visual feature, without regard to how this is used by downstream networks to perform further computation. Perhaps this is so: the visual system may adapt to the prolonged exposure to a grating by altering responses in early cortex, ignoring the consequences for networks encoding more complex motion (e.g. plaids), if these are not part of the adapting ensemble. However, this strikes us as unlikely. Most natural visual experience will involve adaptation to both simple and complex features. This suggests that understanding the benefits afforded by adaptation effects will require considering how they cascade through the visual system.

Finally, we focused on the effects of prolonged adaptation, but similar issues are likely relevant to experience-based modulation of cortical networks more generally. For instance, phantom limb percepts may arise from higher cortical areas misinterpreting aberrant input from lower areas (Flor et al. 2006). By understanding in greater detail how plasticity effects cascade through cortical networks we may be better able to develop ways of treating such conditions.

Experimental Procedures

Detailed methods have been described previously (Patterson et al. 2013a). In brief, monkeys (M.fascicularis) were pre-medicated with 0.05 g/kg atropine and 1.5 mg/kg diazepam. Ketamine (10 mg/kg) was administrated to induce anesthesia. Animals were intubated and anesthesia was maintained with 1.0–2.5% isoflurane in a 98% O₂/2% CO₂ mixture. Surgery was performed to insert a catheter in the saphenous vein of each leg and animal were then placed in a recording stereotax. A craniotomy and durotomy were performed over visual cortex to allow the insertion of electrodes. Anesthesia during recordings was provided by an intravenous infusion of sufentanil citrate (6–18 μg/kg/hr, adjusted as needed); vecuronium bromide (0.15 mg/kg/hr) was administered to suppress eye movements. Vital signs were monitored constantly to ensure adequate anesthesia and animal well-being. At the end of the experiment, the monkey was euthanized with an overdose of sodium pentobarbital (65 mg/kg) and perfused to preserve the brain for histological processing. All procedures were approved by the IACUC of the Albert Einstein College of Medicine at Yeshiva University.

Stimuli and recording methods

Extracellular responses in MT were collected with an array of up to 7 microelectrodes and tetrodes (Thomas Recording, ~300 micron interelectrode spacing). The raw response was filtered (0.5–10 kHz) and events that exceeded a voltage threshold were digitized at 40 kHz and sorted offline (Plexon Offline Sorter). Sorting yielded between 9 and 25 units at a single recording site (i.e. across up to 7 tetrodes and electrodes). To ensure that our results were not sensitive to isolation quality, we analyzed a subset of our data with the best isolation. These revealed a similar loss of MT pattern selectivity to that seen in the full data set (Supplementary Figure 4).

Visual stimuli were displayed on a linearized CRT monitor (1024 x 768 pixels; 100 Hz frame rate; ~ 40cd/m² mean luminance; 80 cm from the animal) using EXPO. MT spatial receptive fields were measured with a rapid (250 ms presentation), sequential presentation of gratings (2 deg in diameter) drifting in one of four directions, positioned at a range of locations that spanned the entire monitor. We used these measurements to center our experimental stimuli over the aggregate MT RF.

For most neurons, we used a fixed ensemble of grating and plaid stimuli. Gratings (6.25 Hz, 1 cycle/degree) were 7.4 degrees in diameter and presented at half (test stimuli) or full (adapter) contrast. Gratings were presented at 12 directions of drift (30 degree steps). Plaid stimuli were composed of two half contrast gratings, offset in their direction of motion by 120 degrees. Pre-adaptation or control responses were measured with a pseudo-random sequence of 1 second stimulus presentations, separated by 5 seconds of gray screen. We then adapted cells with a 40 second presentation of a drifting grating, and measured responses to test stimuli separated by 5 seconds of top-up adaptation. Pre and post-adaptation spontaneous activity was measured during the display of a gray screen, interleaved with other stimulus condition.

Analysis

Firing rates were measured between 0.1 s and 1 s following stimulus onset. The initial 0.1 s of the response was excluded because pattern selectivity develops during this time (Pack and Born 2001; Smith et al. 2005). We analyzed responses from all well-tuned, responsive cells. We defined these by fitting responses to gratings with a von Mises function by maximum likelihood, and retained for further analysis cells for which the pre-adaptation fit quality was >0.7 and the post-adaptation quality was >0.5 (where 0 is the quality achieved by a model based on the average response across all conditions and 1 is achieved by a model base on the measured responses, Patterson et al., 2013a). We also excluded (1) cells for which the pre- and post-adaptation preference differed by more than 50 degrees, as this indicated recording instability (Kohn and Movshon 2004); and (2) cells whose peak stimulus-firing rate did not exceed the spontaneous firing plus one half times the standard deviation of that rate.

Pattern selectivity was calculated for each neuron by comparing the measured responses with a predicted component (the linear sum of two tuning curves, each offset by 60 degrees from the plaid direction) and pattern response (equivalent to the grating tuning curve). Pre- and post-adaptation grating responses were used to predict pre- and post-adaptation plaid responses, respectively. The partial correlation with the plaid prediction, R_p, is

$$R_p=\frac{(r_p-r_c{r}_{pc})}{\sqrt{(1-r_c^2)(1-r_{pc}^2)}}$$ Eq 1

where r_p and r_c are the correlations of the measured plaid responses with the pattern and component predictions, respectively, and r_pc is the correlation between the pattern and component predictions. R_cis defined similarily, but substituting r_c for r_p and vice-versa. Partial correlations were converted to Z-scores using Fisher’s r-to-Z transform,

$$Z_p=\frac{0.5ln\left(\frac{1+R_p}{1-R_p}\right)}{\sqrt{1/df}}$$ Eq 2

where df indicates the degrees of freedom. The pattern index (PI) was defined as Z_p – Z_c.

Model

To model the effects of adaptation on MT pattern selectivity, we used a simple variant of a cascade model described in Rust et al (2006). The first stage consisted of 12 direction-selective V1 neurons with 50 degree bandwidths and uniformly spaced preferred directions. V1 responses to 120 degree plaids were defined as the summed responses to the two component gratings.

MT input, I_MT, was calculated by summing weighted V1 responses as follows:

$$I_{MT}(\theta )=\sum _n{w}_n{R}_{V{1}_n}(\theta )$$ Eq 3

where w_n are the weights for each neuron, and R_V1n is the response of the n^th V1 neuron. To reduce the number of free parameters, we assumed a weighting profile defined by a difference of circular Gaussians function. Each Gaussian was determined by its peak height, bandwidth, and peak location (6 parameters). In addition, we allowed for a constant offset to the inhibitory profile. The predicted responses was generated by passing I_MT(θ) through a threshold nonlinearity to generate the MT response (R_MT):

$$R_{MT}(\theta )={ke}^{{pI}_{MT}(\theta )}$$ Eq 4

where k provides an overall scaling of responsivity and p defines the steepness of the nonlinearity.

We implemented adaptation effects at the V1 stage, by defining an adaptation kernel, k_a(θ), using a difference of circular Gaussian function:

$$k_a(\theta )=a_g+a_{\mathit{exc}}{e}^{b_{\mathit{exc}}(cos(\theta -{\theta }_{\mathit{adapt}})-1)}-a_{\mathit{inh}}{e}^{b_{\mathit{inh}}(cos(\theta -{\theta }_{\mathit{adapt}})-1)}$$ Eq 5

where a_exc and b_exc define the gain and width of the facilitory component of the kernel, and a_inh and b_inh do the same for the suppressive component. The parameter a_g allows for untuned facilitation (a_g>1) or suppression (a_g<1). The peak of each Gaussian was fixed at the direction of the adapting grating, θ_adapt, since adaptation effects are strongest for stimuli that match the adapter. We constrained the kernels to have values between 0.2 and 2, because these correspond to maximum range of effects we have observed in previous recordings in V1 (Patterson et al., 2013a). V1 neurons were adapted by multiplying the direction tuning function of each neuron by the adaptation kernel:

$$R_{V{1}_n\mathit{adapt}}(\theta )=R_{V{1}_n}(\theta )k_a(\theta )$$ Eq 6

We fit model to the responses by maximum likelihood, under the assumption of Poisson spiking statistics (Patterson et al., 2013a). We fit the mean raw responses (not subtracting spontaneous activity) to avoid cases where the evoked response was negative.

The simulations of Figure 6 used this model with the following parameters: k=1 and p=2.5 for the nonlinearity; the excitatory component of weighting profile had an amplitude of 1 and a width of 0.7, and its inhibitory component had an amplitude of 0.68 and a width parameter of 0.05; an adaptation kernel with a_g=1.05, a_exc=0.65, b_exc=4, a_in=0.7, and b_in=0.8. For display reasons only, we used a bank of 24 V1 neurons for these simulations.

Psychophysics

We measured psychometric functions for plaid coherence in three subjects (2 naive). We manipulated coherence by altering the spatial frequency difference between the two component gratings (120 deg offset): one of the components was set at either 1 or 2 cycles/degree; the other component ranged between 1 and 2 cycles/degree. We used two base spatial frequencies to preclude this cue from aiding performance: both increments and decrements in frequency corresponded to a greater difference between the two components. All gratings drifted at 6.25 Hz; component gratings were presented at half contrast, the adapter at full contrast. Stimuli were presented at an eccentricity of 4 degrees and were 7.4 deg in diameter.

Before testing, subjects were familiarized with the stimuli. Psychometric functions were collected under 4 conditions: a pre-adapt (control) condition where test stimuli (1 s presentation, 5 s interstimulus interval) were preceded by a gray screen, and three adaptation conditions where the test stimuli were preceded by a grating drifting in the same direction, 90 degrees offset, or 180 degrees offset from the pattern motion of the test plaids. The adaptation conditions used an adapt top-up design identical to the physiological experiments. Subjects maintained fixation at the center of the screen throughout the session and were instructed to indicate with a button press whether they perceived each stimulus as having one direction of motion or two. Subjects were instructed to report their first percept upon viewing the test stimulus, and the short presentation duration minimized any rivalrous percepts (Hupe and Rubin, 2003). We evaluate the statistical significance of effects using a bootstrap procedure: we combined pre- and post-adaptation data from each subject and sampled ‘pre’ and ‘post’ responses (equal in number within and across sessions to the true data) from this pot, with replacement. Significance was determined by the rank value of the true data with respect to the sampled distribution.