Tumor-Immune Dynamics Regulated in the Microenvironment Inform the Transient Nature of Immune-Induced Tumor Dormancy

Abstract

Cancer in a host induces responses that increases the ability of the microenvironment to sustain the growing mass e.g. angiogenesis, but cancer cells can have varying sensitivities to these sustainability signals. Here we show that these sensitivities are significant determinants of ultimate tumor fate, especially in response to treatments and immune interactions. We present a mathematical model of cancer-immune interactions that modifies generalized logistic growth with both immune-predation and immune-recruitment. The role of a growing environmental carrying capacity is discussed as a possible regulatory mechanism for tumor growth, and this regulation is shown to modify cancer-immune interactions and the possibility of achieving immune-induced tumor dormancy. This mathematical model qualitatively matches experimental observations of immune-induced tumor dormancy as it predicts dormancy as a transient period of growth that necessarily ends in either tumor elimination or tumor escape. Since dormant tumors may exist asymptomatically and may be easier to treat with conventional therapy, understanding the mechanisms behind tumor dormancy may lead to new treatments aimed at prolonging the dormant state or converting an aggressive cancer to the dormant state.

Major Findings

We demonstrate, using a mathematical model, how the sensitivity of tumor cells to immune-mediated environmental signals can significantly alter tumor dynamics and thus treatment outcomes. Moreover, immune-induced tumor dormancy is predicted to be a transient period of tumor growth that must necessarily end in either tumor elimination or tumor escape, in agreement with several experimental observations.

Quick Guide to Equations and Assumptions

Since we focus on cancer dormancy induced by immune predation, the cancer-immune interactions considered are immune predation of, and immune recruitment by, cancer cells. The cancer, C(t) and immune, I(t) populations are assumed to exhibit generalized logistic growth. Without immune predation, C(t) will grow until it reaches the carrying capacity K_C. We consider the carrying capacity to be dictated by the growth regulatory signal emitted by the environment and sensed by the cells. The immune compartment I(t) impedes tumor growth through cytotoxic actions targeted at the cancer cells. These actions are contained in the predation term Ψ(I, C), which acts to modulate the growth rate of C(t). The equation governing cancer growth is thus

$$\frac{\mathrm{d}C}{\mathrm{d}t}=\frac{\mu }{\alpha }\left(1+\Psi (I,C)\right)C\left(1-{\left(\frac{C}{K_C}\right)}^{\alpha }\right),C\left(0\right)=C_0.$$ (1)

Here μ and α are parameters that capture the growth rate and sensitivity of cancer cells to environmental regulatory signals.

The immune population is assumed to consist of cytotoxic cells e.g. CD8⁺ T cells, natural killer cells, and macrophages that are known to directly target cancer cells. The immune response is assumed to grow towards a theoretical limit, or carrying capacity K_I through proliferation and recruitment from the blood, spleen, and bone marrow. With parameter r, we allow for both immune cell- and cancer cell-mediated recruitment; the latter through, for example, the production of danger-associated molecules and necrosis (1). The equation governing immune growth is thus

$$\frac{\mathrm{d}I}{\mathrm{d}t}=\lambda (I+\mathit{rC})\left(1-\frac{I}{K_I}\right),I\left(0\right)=I_0,$$ (2)

where λ is the immune growth rate parameter.

Immune predation of cancer cells is assumed to contain both fast and slow dynamics, expressed as

$$\Psi (I,C)=-\theta \left(\frac{I^{\beta }}{\varphi C^{\beta }+I^{\beta }}+∊{\log }_{10}(1+I)\right),$$ (3)

where Ψ(0,0)=0 by definition. The fast saturation behavior observed in some cancer-immune lysis assays (2,3) is described by the first, ratio-dependent term (4). Although this form has been suggested to better capture the cytotoxic effects of T cells, this term alone neglects innate immunity, which should not exhibit saturation (compare, for example, the percent lysis curves for cytotoxic T cells versus NK cells in (2,3,5)). The second term accounts for innate immunity, and allows for a slow increase in the saturation limit with increasing immune presence, as seen when the lysis assays are performed at larger ratios (3,5,6). The logarithm transforms the cytotoxic actions of the innate immunity into a range appropriate for Ψ. For small immune populations, we assume that the innate and adaptive effects can be combined into the ratio-dependent term, but for large populations, innate immunity should still have a small cytotoxic effect. Thus we assume ∊=0.01.

Introduction

Tumor growth is defined by interactions with the local environment. Immune cells can both promote tumor growth through inflammatory mechanisms and inhibit growth through direct cytotoxic effects (7). Other stromal cells contribute to a tumor-promoting environment by increasing the local vasculature and by forming a supportive niche for cancer cell proliferation and invasion (8). The intercellular signaling between cancer and stromal cells can trigger pro-survival pathways in both cancer cells and host stroma, including endothelial cells, fibroblasts, and immune cells (8).

Inherently, there is variability in the intercellular signaling, which may modulate macroscopic measurements such as tumor diameter. This variability may arise from many factors, including cell sensitivities to intercellular signals and the rates at which cells respond to those signals. One example of environmental regulation is demonstrated by dormant and fast-growing tumor clones that exhibit similar growth kinetics in vitro, but display strikingly different growth rates in vivo (9). Here we demonstrate that intercellular signaling may act to regulate tumor growth. We focus on the sensitivity of cancer cells to growth regulatory signals from the tumor microenvironment and the altered tumor dynamics resulting from treatment-induced disruption of these signals. We demonstrate that the variable sensitivities of cancer cells to stromal intercellular signaling may fundamentally control tumor dynamics, even to the point of inducing an immune-induced dormant state, with clear implications for therapeutic efficacies.

Immune-induced cancer dormancy is a state of cancer progression where the cancer is maintained in a viable, but non-expanding, state (10), often described as an ‘equilibrium’ phase in immunoediting nomenclature (11). Although this state may persist for days to decades, its immunologic realization is one of transience, i.e., the eventual elimination of the disease or the development of immune-resistance followed some time later by tumor escape.

In contrast, mathematical models typically describe the dormant state by a stable equilibrium point (or limit cycle) with a basin of attraction (12-17). This implies that the dormant state can attract tumor trajectories and maintain itself for long times. Such analyses neglect the transient nature of the dormant state, however, and require external perturbations to the system to explain the eventual escape from dormancy. Recent mathematical explorations of possible escape mechanisms include random fluctuations in immune presence (18), intercellular communication of learned cancer cell resistance (19), and immunoediting or evolution in cancer cell phenotypes (20).

Here, without considering specific escape mechanisms, we present a formalism that contains one long-term dormancy-associated equilibrium, and that predicts tumor dormancy will generally end in either tumor elimination or tumor escape. The equilibrium point is a saddle node with a separatrix that divides two attractor regions of ultimate tumor fate. We show the duration of dormancy is determined by tumor-immune dynamics and the proximity of the tumor trajectory to the separatrix.

This model is simple enough to analytically investigate, yet complex enough to capture all qualitative behaviors of tumor growth, including tumor dormancy. Using parameter sets estimated by a Markov Chain Monte Carlo algorithm, we demonstrate that the sensitivity of cancer cells to environmental signals is a prominent factor in determining tumor fate. We generate four parameter sets: one assuming a constant environmental signal, producing a static carrying capacity, and three assuming a variable environmental signal, giving rise to a dynamic carrying capacity. These four sets fit the experimental tumor growth data equally well, but when the variable signals are disrupted, the differing cancer cell sensitivities predict different tumor growth fates. Interestingly, these four sets predict drastically different results for the same treatment, ranging from rapid tumor elimination to tumor escape.

These results may explain both the high variability of treatment success among patients, as well as the observation of accelerated repopulation after treatment (21,22), a phenomenon arising here from disruption of growth regulatory signals in the microenvironment. These same signals are shown to ultimately determine if dormancy will be possible, with higher tumor sensitivities to these signals corresponding to decreased likelihood of dormancy when these signals are disrupted, as may happen from therapy or chronic microenvironmental perturbations such as low-dose radiation exposure (23).

Materials and Methods

Experimental Data

Basic tumor growth dynamics in the absence of an anti-cancer immune response are estimated from experimental measurements of a subcutaneous fibrosarcoma induced by 3-methylcholanthrene. Tanooka et al. (24) induced the sarcomas in wild-type WBB6F₁/J and C₃H/He mice. Volume measurements were taken once the resulting tumors reached a palpable size. We note that WB mice are mast cell deficient, which inhibits the host’s inflammatory response.

Estimation of Model Parameters

Parameters are estimated using a Markov Chain Monte Carlo (MCMC) algorithm (25,26). From an initial guess, a Markov chain of permitted parameter sets is created by randomly perturbing the previous parameter set and accepting this perturbed set with a probability determined by a measure of goodness of fit. Here we use the sum of squared deviations between model prediction and experimental measurements. Each parameter is perturbed and tested for acceptance independently, except parameters μ and α, which are handled together since they are inherently related in equation (1). The algorithm is repeated ten times with each run having 20,000 iterations. Final parameters are those that provide the best fits.

Parameters are estimated under the assumption of no immune predation (Ψ=0). The results assuming a constant or dynamic carrying capacity are listed in Tables 1 and 2, respectively. Immune size and growth rate values are chosen to approximately match those of the tumor since methods to measure immune system checkpoint blockades and other size-determining factors remain elusive.

Table 1.

Parameter values for model simulations. C(t) and I(t) measure cell number, but their values are plotted in terms of cellular mass diameter in mm according to the formula diameter $\left(\mathrm{X}\right)=2{\left(\frac{X}{{10}^6}\frac{3}{4\pi }\right)}^{1∕3}$ mm.

Parameter	Value	Interpretation
μ	0.16 days−1	cancer growth
α	0.72	cancer growth
λ	0.22 days−1	immune growth
r	1·10−3	immune recruitment
θ	2.5	predation strength
β	0.5	predation saturation
ϕ	50	predation saturation
ε	0.01	innate immunity predation strength
KC	3.92·1010 Cell num	cancer carrying capacity
KI	3.92·1010 Cell num	immune carrying capacity

Table 2.

Tumor growth parameter sets estimated by the MCMC parameter fitting method assuming a dynamic carrying capacity. The last column gives the maximum value of K_C, a value used when a constant carrying capacity is forced on the system.

	Growth Rate and Sensitivity		Dynamic Carrying Capacity			Constant Carrying Capacity
	μ	α	p	q	KC(0)	$K_C={\left(\frac{p}{q}\right)}^{3∕2}$
Set 1	0.28	1.08	0.90	7.97·10−8	1.12·108	3.79·1010
Set 2	0.23	1.03	34.5	3.14·10−6	8.47·105	3.64·1010
Set 3	0.19	1.44·10−5	0.73	5.98·10−8	2.90·107	4.27·1010

Mathematical Analysis

The nonlinear system given by equations (1)-(3) describes a two-compartment model for cancer-immune interactions. The general form Ω=1+Ψ allows for immune modulation of tumor growth, which may be stimulatory or inhibitory, depending on Ω. It should be noted that this form fundamentally differs from classic predator-prey-type models where immune effectors only inhibit tumor growth and are stimulated directly by tumor presence (4,13,17,27,28). In contrast to decaying oscillations or limit cycle behaviors, our model predicts tumor elimination or escape, with only transient periods of dormancy. This is partially due to the assumed form of the immune response, which, once initiated, will progress to a maximal response that is independent of the cancer population.

Stability Analysis of the System Equilibrium Points and Possible Cancer-Immune Dynamics

The dynamical system described by equations (1) and (2) is simple enough to allow for analytic investigation of system stability. The system has four equilibrium points: (I,C)=(0,0), (K_I,0), (K_I,K_C), and $(K_I,\stackrel{‒}{C})$ where $\stackrel{‒}{C}$ satisfying $1+\Psi (K_I,\stackrel{‒}{C})=0$ is given by

$$\stackrel{‒}{C}=K_I{\left(\frac{1}{\varphi }\left(\frac{\theta }{1-∊\theta {\log }_{10}(1+K_I)}-1\right)\right)}^{\frac{1}{\beta }},$$ (4)

and represents a cancer equilibrium state that, once obtained, will persist for a long time. We note that Ψ(I,C) is not differentiable at (0,0) but that we can classify this point based on physical arguments and a topologically equivalent system. The equilibria stability, based on the Jacobian, are as follows: (0,0) is an unstable point, (K_I,0) is a stable point if 1+Ψ(K_I,0)<0 otherwise it is a saddle point, and (K_I,K_C) is a stable point if 1+Ψ(K_I,K_C)>0 otherwise it is a saddle point. The point $(K_I,\stackrel{‒}{C})$ with $0<\stackrel{‒}{C}<K_C$ is a saddle point if (K_I,0) and (K_I,K_C) are both stable. The two restrictions guaranteeing the attractor states bound immune predation strength as follows, ensuring a dormancy-associated equilibrium point:

$${\theta }_{\min }={\left[1+∊{\log }_{10}(1+K_I)\right]}^{-1}<\theta <{\left[\frac{K_I^{\beta }}{\varphi K_C^{\beta }+K_I^{\beta }}+∊{\log }_{10}(1+K_I)\right]}^{-1}={\theta }_{\max }.$$ (5)

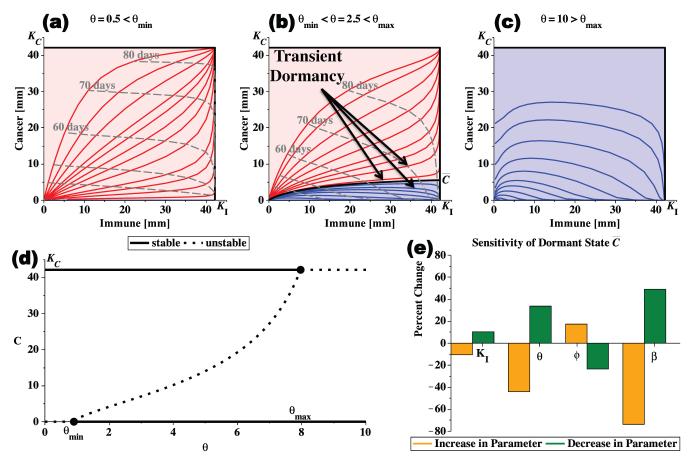
Under this condition, a large immune response is strong enough to eliminate small tumors but not large tumors, resulting in a possible dormant tumor of size $\stackrel{‒}{C}$. It guarantees the existence of all possible tumor outcomes: tumor elimination, tumor escape, and long-term tumor dormancy followed by elimination or escape. Three sample cancer-immune phase portraits are shown in Figure 1. The long-term dormant state increases as immune efficacy increases from θ_min to θ_max and trajectories that pass near the separatrix have transient dormant states.

Figure 1.

The progression of the immune-cancer phase plane as immune efficacy θ increases. If θ<θ_min, immune predation is weak and all cancers reach the carrying capacity K_C (a). If θ_min<θ<θ_max, a dormant cancer state exists as a saddle point between two stable equilibria creating two basins of attraction, one representing cancer elimination (lower blue region) and one representing cancer escape (upper red region) (b). The separatrix is the black curve separating the two basins of attraction, and leads to the dormancy-associated equilibrium point $(K_I,\stackrel{‒}{C})$. Finally, if θ>θ_max, all cancers are eventually eliminated (c). In (d), a bifurcation diagram shows the stability of the cancer equilibrium points as immune efficacy θ increases. In (e), the sensitivity of the size of the dormant state, $\stackrel{‒}{C}$, to changes of 10% in the immune model parameters K_I, θ, ϕ, and β, is shown. Analyses completed with parameter values from Table 1 unless otherwise stated.

Bifurcation and Sensitivity Analysis of Tumor Dormancy

If θ<θ_min (or 1+Ψ(K_I,0)>0) then the immune response is weak and (K_I,0) is a saddle point with all tumors escaping immune control (Figure 1(a)). In this case, $\stackrel{‒}{C}$ is negative and thus unphysical. If θ>θ_max (or 1+Ψ(K_I,K_C)<0) then the immune response is strong and (K_I,K_C) is a saddle point, implying that all tumors are eliminated (Figure 1(c)). In this case, $\stackrel{‒}{C}>K_C$, and since we only consider tumor growth in the positive quadrant bounded by the carrying capacity, we neglect this dormant equilibrium point. Furthermore, if θ=θ_min (or 1+Ψ(K_I,0)=0), then $\stackrel{‒}{C}=0$, and if θ=θ_max (or 1+Ψ(K_I,K_C)=0), then $\stackrel{‒}{C}=K_C$. Thus, θ is a bifurcation parameter with two transcritical bifurcations. A bifurcation diagram demonstrating the transitions and stability of the equilibrium points is shown in Figure 1(d). Since the range [θ_min,θ_max] guarantees the existence of all possible tumor outcomes, we focus on it for the remainder of the discussion.

Ranges of Immune Efficacy Guaranteeing Tumor Dormancy

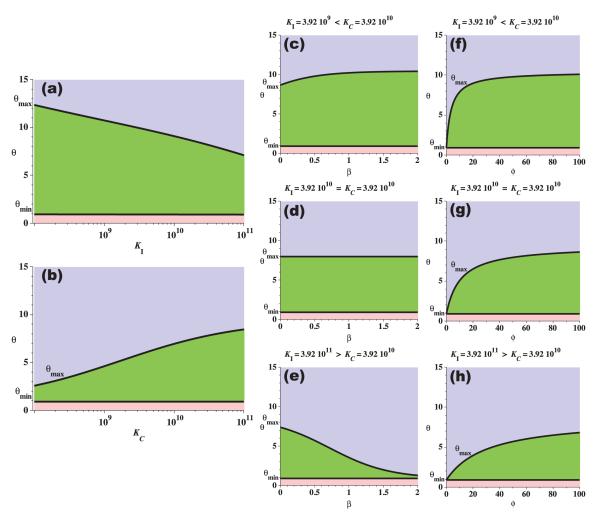
Figure 2 shows the dependence of the range [θ_min,θ_max] on parameters K_I, K_C, β, and ϕ. As the immune carrying capacity increases, the upper bound on immune efficacy decreases since the same amount of cancer cell predation can be mediated by either a large and weakly effective immune presence or a small but strongly effective immune presence. Similarly, as the cancer carrying capacity increases, the upper bound on immune efficacy increases, as stronger immune predation is required to eliminate the larger tumor. The effects of the immune predation shape parameters, (β,ϕ), on the range [θ_min,θ_max] depends on the relative size of the two carrying capacities. Notice that if K_C=K_I then β has no effect on [θ_min,θ_max]. If this is not the case, however, then if K_I<K_C, increasing β increases θ_max, and if K_I>K_C, increasing β decreases θ_max. This behavior results from the shape of the fast saturation kinetic in the cell-kill term, which is a function of the ratio $K_I/K_C$ (see equation (3)). Parameter ϕ also controls the shape of the fast saturation kinetic. If ϕ=0, then θ_min=θ_max, and as ϕ increases, the upper bound also increases. Notice that for all these cases, the lower bound, θ_min, is essentially constant, suggesting that there exists a strictly positive threshold for immune predation efficacy below which long-term tumor dormancy cannot exist.

Figure 2.

The dependence of the range [θ_min,θ_max] on model parameters K_I, K_C, β, and ϕ. In all figures the three shaded areas represent regions describing distinct tumor outcomes: all tumors are eliminated in the (light blue) upper regions; tumor elimination, tumor escape, and long-term tumor dormancy are all possible in the (green) middle regions; and all tumors escape in the (pink) lower regions. The range of θ permitting a long-term dormant cancer state decreases as immune carrying capacity increases (a), and increases as cancer carrying capacity increases (b), for fixed (β,ϕ) in the predation term. The effects of changes in β and ϕ on the range [θ_min,θ_max] depend on both K_I and K_C, (c-h). Unless otherwise stated, parameter values are from Table 1.

Discussion of Simulations and Results

Numerical simulations of tumor growth are presented with and without immune predation. Simulations are computed numerically in MAPLE (www.maplesoft.com) using the parameter values in Tables 1 and 2 as appropriate.

Tumor Growth is Regulated by Signals from the Microenvironment

We investigate the effect of environmental signaling on tumor dormancy. When a tumor grows, it modifies the local environment, through angiogenesis, to increase the nutrient supply to that area. In this way, the carrying capacity increases with tumor mass. This effect can be modeled by a differential equation that describes the growth of the cancer carrying capacity, K_C(t), in response to the growing tumor, C(t). The functional form as first proposed by Hahnfeldt et al. (29) is

$$\frac{\mathrm{d}{K}_C}{\mathrm{d}t}=\mathit{pC}\left(t\right)-{\mathit{qK}}_C\left(t\right)C{\left(t\right)}^{\frac{2}{3}},$$ (6)

where p and q are growth stimulation and inhibition constants, respectively.

Replacing the constant carrying capacity in equation (1) with a dynamic capacity as described above, creates an extension of the mathematical model given by equations (1)-(3). By comparing these two models, we will demonstrate that disturbance of the support signals from the tumor environment can significantly alter tumor growth dynamics. This formulation attempts to capture some of the effects stromal cells (including immune cells) can have on the proliferation rate, viability, differentiation state, and invasiveness of cancer cells (30).

Parameter estimation for tumor growth in the absence of immune predation is performed with the experimental data of Tanooka et al. (24) using an MCMC parameter estimation algorithm. Parameter sets are estimated 1) for the tumor growth model assuming a constant carrying capacity given by equation (1); and 2) the tumor growth model assuming a dynamic carrying capacity given by equations (1) and (6). Table 1 lists the estimated parameter values used for the constant carrying capacity model, referred to as set 0 (μ, α, and K_C from Table 1), and Table 2 lists three possible parameter sets for the dynamic carrying capacity model, referred to as sets 1, 2, and 3.

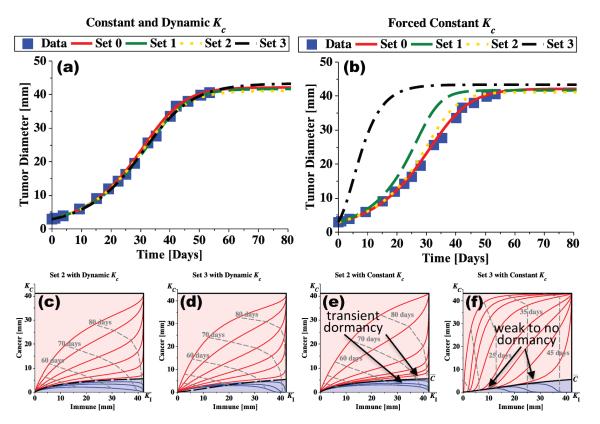
As can be seen from Figure 3, both models and all parameter sets fit the experimental data equally well. When microenvironmental regulation of tumor growth is disturbed, however, sets 1 and 3 no longer fit the data. Microenvironmental signaling is disrupted in the model by forcing the dynamic carrying capacity to be constant and equal to the maximum possible value for each parameter set (these values are listed as K_C in Table 2). Doing so removes early damping of tumor growth, providing a strongly pro-tumor environment. Its effect is different for the three parameter sets. Parameter set 2 still fits the data well but sets 1 and 3 predict much faster tumor growth. More specifically, the rate at which the environment increases either its vascularization, the sensitivity of the stromal cells to the pro-angiogenic or other growth factors, or the sensitivity of the tumor cells to the signaled levels of environmental support, all contribute to tumor-specific inherent variabilities that determine basic tumor growth dynamics.

Figure 3.

Tumor microenvironmental growth signals modulate tumor growth. In (a), tumor growth is predicted by fitting growth parameters to the experimental data of Tanooka et al. (24). Set 0 (Table 1) assumes a constant carrying capacity, while sets 1, 2, and 3 (Table 2) allow for a dynamic carrying capacity. All curves fit the experimental data equally well. In (b), the same parameter sets are used but a constant carrying capacity is forced on sets 1, 2, and 3 after the parameter fitting using $K_C={\left(\frac{p}{q}\right)}^{\frac{3}{2}}$ (values from Table 2). Note that set 2 still fits the data well while sets 1 and 3 do not. This indicates that the tumor described by set 2 is not sensitive to the local environmental growth cues, while sets 1 and 3 are very sensitive. Cancer-immune phase portraits for sets 2 and 3 demonstrate the same general behavior when the dynamic carrying capacity is allowed (c, d) but demonstrate significantly different behavior when a constant carrying capacity is enforced (e, f) simulating a disrupted environmental signal. After disruption, set 2 still allows immune-induced transient periods of tumor dormancy whereas set 3 no longer predicts any significant dormant periods.

These results highlight the important fact that the same tumor growth curve can be observed for three different tumors, each with different cellular proliferation rates and different sensitivities to the regulatory signals originating from their different environments. At the same time, when these signals are altered, the resulting changes in growth dynamics can be drastic.

Altering the balance of the tumor and microenvironmental compartments, e.g. by selective reduction of tumor burden by therapy, leaving the microenvironmental support nearly intact (or enhanced (23)), may accelerate tumor repopulation; a problematic phenomenon familiar to clinicians that remains poorly understood (21, 22, 31). In this regard, Figure 3 shows how the rate of tumor regrowth depends on the signaling sensitivities of the tumor cells.

Another possible interpretation of our disrupted regulatory signals comes from Hu et al. (32). They found that when tumor-associated and arthritis-associated (inflammatory) fibroblasts were coinjected with breast cancer cells, tumor weight was increased. This contribution may explain our simulations for how enhanced capacity leads to accelerated growth in sets 1 and 3. Typically, these stromal cells would develop their pro-tumor associations over time as the tumor grows (modeled here by the dynamic capacity), but in these in vivo experiments, the stromal cells are already pro-tumorigenic and are thus capable of supporting a tumor faster (modeled here by the forced-constant capacity).

Additionally, the ability of the immune response to induce tumor dormancy may be lost when environmental regulatory signals are disrupted. Using parameter set 2, simulations of tumor growth with disrupted signals results in a growth curve similar to the data, and the resulting tumor-immune phase portraits, shown in Figure 3(c and e), are similar for both the dynamic and the (disrupted) forced-constant carrying capacity models. This suggests that the tumor represented by parameter set 2 is not very sensitive to regulation signals produced by the microenvironment, and that the cancer cells proliferate at a rate consistent with the growth curves. This allows the immune response to achieve transient dormant states in both the dynamic and (disrupted) forced-constant capacity models.

By contrast, the cancer-immune phase portraits for set 3 in Figure 3(d and f) demonstrate a lost ability of the immune response to induce tumor dormancy, due to the tumor being very sensitive to growth regulation signals emanating from the local microenvironment. Also, disrupting the regulatory signals for set 3 causes the tumor to grow much faster than the experimental data. These observations suggest that immune-mediated tumor dormancy is dependent on the sensitivity of cancer cells to environmental regulatory signals.

The Success of Immunotherapy Depends on Tumor Sensitivity to Environmental Regulatory Signals

To elucidate the role of variability in signaling sensitivity to treatment success, we now consider immunotherapies that increase the immune effectiveness of the cytotoxic T cells, achieved conceivably, for instance, by checkpoint blockade targeted antibodies to cytotoxic T-lymphocyte antigen 4 (CTLA-4) and programmed cell death protein 1 (PD-1). These therapies release the immunological block that limits the immune response, allowing the development of a large specifically targeted T cell response to the cancer. We simulate the effects of these treatments by allowing a large immune response to develop with an increased recruitment ability (r) and an increased cytotoxic efficacy (θ). Treatment occurs after the tumor is initially detected (at t=0) with no appreciable initial immune presence (I(0)=0). In Figure 4(a and b) the experimental data for tumor growth without predation is included to reference the initial growth trend.

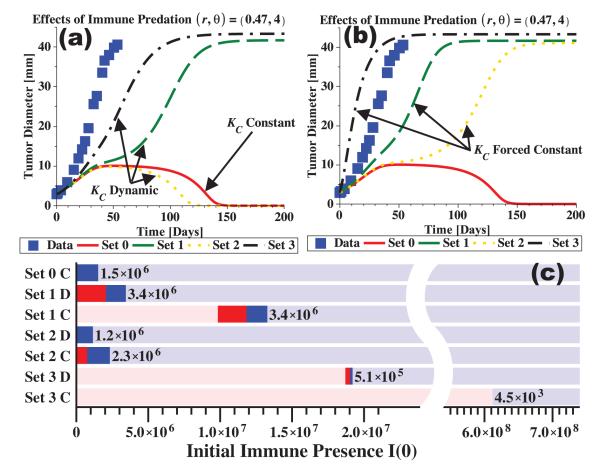
Figure 4.

Immunotherapy treatment is simulated by an increased immune recruitment rate, r, and an increased predation efficacy, θ. Treatment is given at the time of tumor detection (here t=0) and is assumed to be immediately effective with no decay. Any immune presence at detection is ignored (I(0)=0). In (a, b) the data points show the growth trend with no immune interaction (as in Figure 3). The dynamic carrying capacity model with parameter sets 1, 2, and 3 are shown in (a) along with the constant capacity model with parameter set 0. In (b), the dynamic capacity models are forced to have constant capacities, disrupting the regulatory signal to the tumor. All curves are modified to different extents by immune predation when compared to the data (no predation). In (c), tumor fate is indicated for increasing initial immune presence, I(0). From left to right, the pink regions represent tumor escape with no dormancy, the red regions represent tumor escape after dormancy, the blue regions represent tumor elimination after dormancy, and the light blue regions represent tumor elimination with no dormancy. Dormancy is defined as a period of non-growth lasting at least 30 days. The width of each dormancy range (red plus blue region) is labeled to the right of each range. Parameter sets 1, 2, and 3 are used with the dynamic capacity (D) and constant capacity (C) models. Parameter values are r=0.47 and θ=4 together with the values from Tables 1 and 2.

Including strong immune predation in the tumor growth simulations of Figure 4 results in the parameter sets all predicting different outcomes for the same treatment, mimicking real-world inter-patient variability. A striking comparison can be seen between the case with no immune predation, where all curves fit the data equally well (Figure 3(a)), and the case with strong immune predation, where each curve predicts a different outcome (Figure 4(a)). Note also that while set 2 indicates elimination happens faster than in the constant capacity model (set 0), set 1 indicates a short dormant period before escape, and set 3 indicates escape at only a slightly slower rate than the experimental reference. Thus, with environmental growth regulation signals intact, these simulations suggest that the tumor may either escape, be eliminated, or be transiently dormant before elimination or escape. Such results may explain why patient responses to immunotherapies are quite varied, and shed light on the connection between regulatory sensitivities and treatment response.

With the loss of environmental growth regulation, however, all tumors are predicted to escape (Figure 4(b)). Disrupting the regulatory signals by forcing the dynamic capacity to be constant results in tumor escape: 1) with a short dormant period (set 2), 2) at a slightly slower rate than the reference (set 1), or 3) at a faster rate than the reference (set 3). Again, forcing the dynamic carrying capacity to be constant simulates a reduction of tumor burden with little modification of environmental support. When regulation is disrupted, only tumor escape is predicted, implying that a stronger dose, or combinations of therapies may be required to eliminate the tumor upon recurrence.

Dormancy Depends on Tumor Cell-Inherent Sensitivities and Parameters of the Immune Response

As discussed above, immune-mediated tumor dormancy is dependent not only on immune effectiveness, but also on the sensitivity of cancer cells to environmental regulatory signals. To demonstrate this, we examine the initial immune presence required to induce a period of dormancy in our simulations. We define dormancy as a period of at least 30 days within the first 150 days of growth wherein the effective tumor growth rate is small, i.e., $\left(\frac{1}{C}\frac{\mathrm{d}C}{\mathrm{d}t}\right)<0.04$, and the tumor size is moderate, i.e., between 1 and 30mm in diameter. This definition excludes dormant regions where the tumor has effectively been eliminated or where the tumor has grown to the maximal size.

In Figure 4(c) predicted tumor fate for an initial immune presence is indicated by color for each model (i.e., for ‘constant’ and ‘dynamic’ carrying capacities) for parameter sets 0, 1, 2, and 3 as appropriate. The dormancy windows, i.e., ranges of initial immune presence guaranteeing tumor dormancy, are indicated by the red (escape afterwards) and blue (elimination afterwards) regions. Pink regions correspond to tumor escape and light blue regions to elimination. Parameter values are r=0.47 and θ=4 as used in the rest of Figure 4 to simulate immunotherapy. As can be seen, the constant carrying capacity model with parameter set 0 predicts only elimination, with dormancy occurring for small initial immune presence. When a dynamic carrying capacity is used, however, the three parameter sets (sets 1D, 2D, and 3D) predict different outcomes with different dormancy windows. After disrupting the growth regulation signals (sets 1C, 2C, and 3C), these dormancy windows tend to shift to the right, indicating that a higher initial immune presence is required to obtain dormancy. For comparison, the left-most color of Figure 4(c) corresponds to outcomes predicted in Figure 4(a and b). Since parameter set 3 requires a much higher initial immune presence to obtain dormancy, and the size of the window is small compared to those predicted by sets 1 and 2, we conclude that dormancy is harder to achieve in this instance due to high sensitivity to environmental regulation.

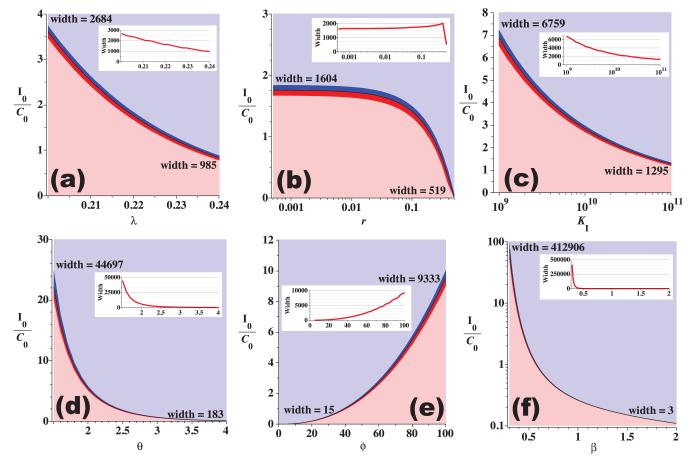
Dormancy is explored further through the parameter sensitivity analysis shown in Figure 5 using the constant carrying capacity model and parameters from Table 1. Each immune parameter is varied and the resulting tumor fate is indicated by color for ranges of initial immune presence. Under the assumption that large dormancy windows at low levels of initial immune presence correspond to more easily achieved dormancy, these sensitivities may suggest treatment strategies targeted at obtaining and maintaining the dormant state.

Figure 5.

Parameter sensitivity for immune system parameters (λ (a), r (b), K_I (c), θ (d), ϕ (e), and β (f)) using the model with constant carrying capacities and parameter values from Table 1 (set 0). The lower (pink) regions indicate tumor escape, the upper (light blue) regions indicate tumor elimination, and the mid-regions indicate that the tumor either escaped (red) or was eliminated (blue) after a period of at least 30 days of dormancy. Vertical axes indicate the initial immune presence relative to the initial cancer presence. Theoretically, tumor dormancy should be easier for the immune response to achieve when the required initial presence I₀ is small and the width of the dormancy region (red and blue middle regions) is large. The width of the dormancy regions (measured in initial immune presence) is indicated at the left and right endpoints of the curves as well as on the inset line graphs.

Conclusions

The analysis presented here demonstrates that in most cases, immune-induced tumor dormancy is a transient state that necessarily ends in either elimination or escape. This result contrasts with behavior predicted by many predator-prey-type models wherein dormancy is described by decaying oscillations converging to a limit cycle or steady-state, that, once obtained, is maintained for long time. The transient nature of the dormant state described here complements the immunoediting hypothesis since the equilibrium stage must end in either tumor elimination or escape, and qualitatively matches real-world observations (33).

Cancer and immune cell behaviors are constantly evolving through autocrine and paracrine cytokine feedback loops in the microenvironment. Tumor escape from immune-induced dormancy can involve selective editing of cancer cell immunogenicity (34) and accumulated resistance to apoptotic signals from immune cells or chemotherapeutics (6,35). Additionally, the local cytokine milieu can determine the anti-tumor or pro-tumor polarization of the immune response (5,36,37). These phenomena are now being investigated through mathematical models of both tumor escape mechanisms (18-20) and immune polarization. The model presented here does not explicitly address these phenomena, yet captures the transient nature of dormancy in a comparatively simple framework.

With this model, we investigated the range of immune efficacy required to guarantee the existence of a dormant state. Obtaining this state, however, is not guaranteed as we also demonstrated how growth regulatory signals emanating from the tumor microenvironment play a significant role in determining tumor fate. The regulatory mechanism of a carrying capacity that grows with the tumor may be disturbed after debulking treatments that leave the microenvironment unaltered or possibly enhanced. We found that for tumors that are highly sensitive to these regulatory signals, tumor regrowth may be accelerated, offering one possible rationale for the phenomenon of accelerated repopulation frequently observed in the clinic following treatment.

Variability in tumor sensitivities, in turn, may account for unpredictable outcomes following therapy, and thus may serve as a proxy for patient variability. The mathematical model discussed here is the first, to our knowledge, to incorporate such variability and predict outcomes that qualitatively match those seen in the clinic. Tracking variability in sensitivity to environmental regulatory signals may well improve our understanding of why treatments work for some patients but not others.