Abstract
Background
The phase-amplitude coupling (PAC) between distinct neural oscillations is critical to brain functions that include cross-scale organization, selection of attention, routing the flow of information through neural circuits, memory processing and information coding. Several methods for PAC estimation have been proposed but the limitations of PAC estimation as well as the assumptions about the data for accurate PAC estimation are unclear.
New Method
We define boundary conditions for standard PAC algorithms and propose “oscillation-triggered coupling” (OTC), a parameter-free, data-driven algorithm for unbiased estimation of PAC. OTC establishes a unified framework that treats individual oscillations as discrete events for estimating PAC from a set of oscillations and for characterizing events from time windows as short as a single modulating oscillation.
Results
For accurate PAC estimation, standard PAC algorithms require amplitude filters with a bandwidth at least twice the modulatory frequency. The phase filters must be moderately narrow-band, especially when the modulatory rhythm is non-sinusoidal. The minimally appropriate analysis window is ~10 seconds. We then demonstrate that OTC can characterize PAC by treating neural oscillations as discrete events rather than continuous phase and amplitude time series.
Comparison with existing methods
These findings show that in addition to providing the same information about PAC as the standard approach, OTC facilitates characterization of single oscillations and their sequences, in addition to explaining the role of individual oscillations in generating PAC patterns.
Conclusions
OTC allows PAC analysis at the level of individual oscillations and therefore enables investigation of PAC at the time scales of cognitive phenomena.
1.0 Introduction
The mammalian brain is a complex system with a distributed organization of sensory, motor, and executive computation centers across large areas of the cortex. While the distributed organization allows for parallel and specialized processing of information, it requires a mechanism for binding information from different computations into a coherent, unitary mental experience (von der Malsburg, 1981, Engel and Singer, 2001). The multipurpose, functional organization of local brain circuits also requires a mechanism for achieving dynamic, context-dependent cognitive and attentional control, a mechanism for the efficient routing of information between different brain computation centers, as well as a robust and efficient mechanism for coding the information in the dynamics of neural discharge (Phillips and Singer, 1997, Kelemen and Fenton, 2010). Various forms of neural synchrony, the coordinated synchronized activation of same-function cells and the active desynchronization of different-function cells have been proposed as this fundamental mechanism of neural computation (von der Malsburg and Schneider, 1986, Buzsaki, 2010). In the recent decade, phase-amplitude synchrony of field potential oscillations, the coupling between the phase of a slow oscillation and the amplitude of a faster oscillation, has received significant attention as a candidate synchronizing mechanism and is the subject of the present work.
In phase-amplitude coupling (PAC), the amplitude of a fast signal (e.g. gamma 30–100 Hz) is modulated by the phase of a slow signal (e.g. theta 5–12 Hz). This interaction is sometimes called “nesting” because the fast oscillation is precisely fitted within the cycle of the slower oscillation (Lakatos et al., 2005). The term phase-amplitude cross-frequency coupling (CFC) has also been used for this phenomenon, because the interaction happens between two distinct oscillatory bands (Bragin et al., 1995). This particular property makes PAC principally different from other synchrony measures such as amplitude synchrony (assessed by cross -correlation) or phase synchrony (assessed by phase locking statistics) because it reflects the dynamical relationship between two oscillations that are generated by distinct neurophysiological mechanisms. As the oscillations have different biophysical origins, the consequent PAC is not easily attributed to the spurious occurrence of synchrony caused by volume conduction, selection of reference or synchronized noise. The concept of a cross-scale organization of neural activity (Jensen and Colgin, 2007, Le Van Quyen, 2011) offers a possible neural mechanism for integrating information between several functionally distinct networks, to accomplish perceptual binding, selective attention, cognitive control and the recruitment of computational and representational cell assemblies. Neural activity in macroscopic (slow oscillations), mesoscopic (high frequency oscillations) and microscopic (single neuron activity) scales are braided together such that a progressively faster activity occurs within a specific, short time window of a slower activity. Indeed, several conceptual and theoretical frameworks have been proposed for the computational role of PAC (Knight and Canolty, 2010). Given the growing interest, and the substantial value in PAC as a mechanism for neural computation it is important for the broader neuroscience community to understand how to accurately measure and interpret PAC, and appreciate the limitations of the current methods.
This paper is written in two parts. The first part is an analysis of the standard approach to computing PAC. We examine the assumptions and by parametric analyses, identify the filter and temporal requirements for estimating PAC accurately. The second part introduces a novel approach to estimate, measure and characterize PAC. It operates on two time scales, one is global, and like traditional methods it is only robust when applied to long time series of data, on the order of many seconds. The approach also allows the characterization of PAC on short time scales, as short as a single oscillation.
2.0 Materials and Methods
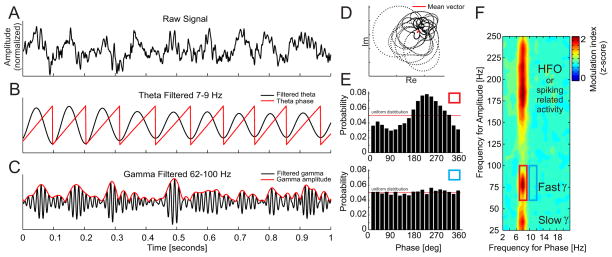
Multiple algorithms for quantifying PAC have been proposed (Fig. 1). The common starting point of all algorithms is an extraction of the phase and the amplitude information from the sampled signal x(t). This can be accomplished by band-pass filtering the signal into the bands of interest, for example theta 7–9 Hz and fast gamma 62–100 Hz followed by the Hilbert transform (Fig. 1 A–C). There are other methods for extraction of phase and amplitude information, for example convolution of the signal with a complex wavelet but since these methods lead in principle to the same result (LeVan Quyen et al., 2001) we use the Hilbert transform approach throughout our study. The Hilbert transform converts a band-pass filtered time series into a complex analytical time series. The instantaneous phase φ(t) and amplitude A(t) time series are then extracted from the analytic signal by taking the argument or modulus, respectively. The relationship between the phase and the amplitude time series, often referred to as the modulation index can then be studied by means of circular statistics, i.e. by computing the mean vector of the complex composite signal: (Fig. 1d); (Canolty et al., 2006). Another method to calculate the modulation index calculates the phase relationship between the instantaneous phase time series φ(t) and φA(t), where φA(t) is the instantaneous phase extracted from the amplitude time series A(t) (Penny et al., 2008). Other methods to calculate the modulation index are based on analysis of the power spectral density of the amplitude time series A(t) (Cohen, 2008) or coherence spectrum between A(t) and the original signal x(t) (Colgin et al., 2009). Most recently, a method based on the analysis of the phase-amplitude distribution was proposed (Tort et al., 2010). This measure computes a normalized Kullback-Leibler (KL) divergence between the phase-amplitude distribution and the uniform distribution (Fig. 1E). Since in the first, review part of this paper, we primarily focus on the initial steps of the algorithm, i.e. selection of filters for extraction of the phase and the amplitude information, we refer the interested reader to an extensive review and comparison of the above methods (Tort et al., 2010). The first part of the present report has mainly used modulation index estimates that are based on the phase-amplitude histogram (Tort et al., 2010).
Figure 1.
Phase-amplitude coupling analysis applied to an LFP recording from rat CA1. [A] A raw signal is pass-band filtered in a low frequency range (7–9 Hz) and [B] the signal phase is extracted. The raw signal is also filtered in a high frequency range (62–100 Hz) and [C] the signal amplitude is extracted. When amplitude is phase modulated, the [D] mean vector of the composite signal created by the combination of the low frequency phase and the high frequency amplitude information will be non-zero and will point to the preferred phase of the modulation. The strength of the coupling (modulation index) corresponds directly to the mean vector length. A modulation index can also be estimated by [E] binning the phase time series into equal bins (here twenty 18° bins) and averaging the corresponding amplitude values within each bin. High modulation index values correspond to [E top] a large deviation of the resulting distribution from the uniform distribution. On the contrary, low modulation index values correspond to [E bottom] small deviations from the uniform distribution. Repeating the above steps for a range of slow and fast frequencies [F] results in a comodulogram that describes the extent to which the phase of oscillations at frequencies on the x-axis modulates the amplitudes of oscillations at frequencies on the y-axis.
It is not always certain, a priori, what frequency bands are involved in PAC, and thus PAC estimation typically begins with construction of a comodulogram to reveal the frequency bands that can be observed to interact in a particular dataset. The comodulogram analysis varies the frequency of both filters used to separately extract the amplitude A(t) and the phase φ (t) series from one signal and computes the modulation index for all combinations of the two series (Fig. 1F).
To test the significance of the modulation index (MIraw), surrogate tests can be used (Hurtado et al., 2004). All surrogate techniques follow a similar approach. One of the time series (for example the phase time series) is randomly shuffled to create a new phase time series with broken temporal relationships between the phase and amplitude information. The shuffled phase time series is then used with the observed amplitude time series to estimate a surrogate modulation index. This procedure is repeated several hundred times to obtain the null distribution of surrogate modulation index values. A normalized modulation index (MInorm) is then obtained as a z-score: , where μ and σ are the mean and standard deviation obtained from the null distribution.
2.1 Subjects
All procedures were performed in accordance with National Institutes of Health guidelines and were approved by the SUNY, Downstate and NYU animal use committees. Data were collected from adult male Long-Evans rats and adult male C57bl/6J mice that were obtained from a commercial breeder (Taconic Farms, Germantown, NY).
2.2 Electrophysiology
The recordings of action potentials and local field potentials from urethane-anesthetized rats have been described (Olypher et al., 2006). Briefly, rats were anesthetized with urethane (1.25 g/kg i.p.) and supplemented as necessary. Hydration was maintained by a saline drip and the EKG was monitored to ensure stable physiological function. The rat was mounted in a stereotaxic frame, the scalp was cut and retracted and a burr hole was drilled in the skull overlying each dorsal hippocampus. Stereotaxic micromanipulators positioned a 30-gauge stainless steel cannula for infusing 1 μl of saline with tetrodotoxin (5ng/μl) into one hippocampus (relative to bregma: anteroposterior, 3.5; mediolateral, 2.6; dorsoventral, 3.5). Additional micromanipulators were used to lower tetrodes made from four twisted 25-um nichrome wires, to the pyramidal cell layers in the dorsal and ventral hippocampus opposite to the injected side.
The methods for recording LFPs in freely-moving animals have been described (Fenton et al., 2008, Kelemen and Fenton, 2010). Briefly, for the recordings from rats, tetrodes were assembled in a custom microdrive, implanted under Nembutal anesthesia (50mg/kg i.p.) and fixed to the skull with bone screws and dental cement. Tetrodes were directed to the dorsal hippocampus (AP: −4.0 mm, ML: −2.5 mm, DV: −1.9 mm below the brain surface). One week after surgery, the tetrodes were moved toward the hippocampus pyramidal cell layer until action potentials from CA1 place cells could be recorded. Extracellular LFPs were acquired from one wire of the tetrode using a commercial recording system (dacqUSB, Axona Ltd., St. Albans U.K.). LFPs were band-pass filtered (0.1–300 Hz) and digitized at 2 kHz. For the LFP recordings from mice, a six-contact electrode was created by twisting insulated 75-μm nichrome wires such that the spacing between the tips was 250 μm. The electrode was implanted, similar to the rat, so that the recording contacts spanned the CA1 and dentate gyrus subfields of the dorsal hippocampus (AP: −1.8 mm, MI: 1.3 mm, DV: 1.6 mm). The recording sites were localized to specific hippocampal dendritic and cell layers according to electrophysiological landmarks, in particular the theta oscillation maximum that is at the hippocampal fissure. This localization was confirmed by the theta phase reversal between stratum radiatum and stratum lacunosum moleculare and by histological verification. All LFPs were recorded from freely moving mice or rats in a circular arena that was 40 cm in diameter for mice and 81 cm for rats. During the recordings the rats foraged for 20-mg food pellets (Bio-serve, Frenchtown, NJ) that were scattered onto the arena from an overhead feeder on a pseudo-random schedule with period ~25 seconds. All analyses were performed on the rat data, except for what is presented in Figure 7 A1, A2, which is from mouse.
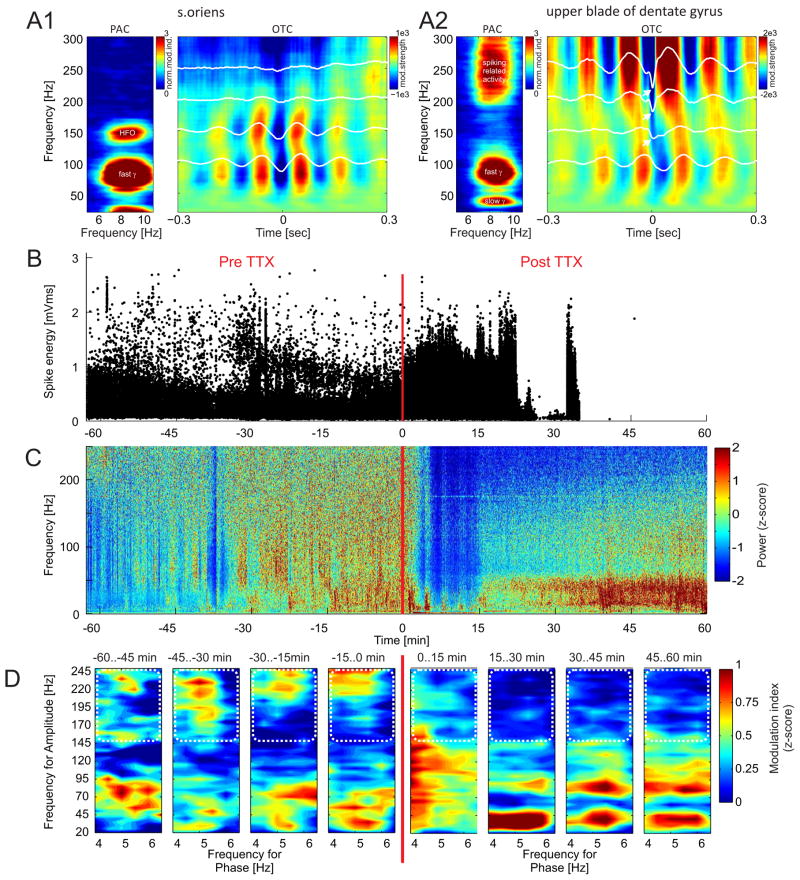
Figure 7.
Origin of > 100 Hz high frequency oscillations. [A1 left] A standard PAC comodulogram obtained from stratum oriens of mouse CA1 shows a narrow-band peak at ~150 Hz that corresponds to typical high frequency oscillations (HFOs). [A1 right] The corresponding OTC comodulogram shows modulation in the same band. [A2 left] The PAC comodulogram from the upper blade of the dentate gyrus shows a wide-band, significant PAC above 200 Hz. [A2 right] The corresponding OTC comodulogram shows abrupt changes in the typically smooth OTC profiles (white lines) for frequencies above 150 Hz, pointing to the spike-related activity that is phase-locked to the slow theta rhythm. [B] Under urethane anesthesia, TTX was injected into the dorsal hippocampus of a rat while using the same electrode to record action potentials and LFPs from the ventral hippocampus. The recording site was at least 5 mm from the dorsal injection site. TTX blocked action potentials in the ventral hippocampus ~20 min after TTX injection. [C] The TTX injection also suppressed LFP power at all frequencies during the 20 min after injection. Afterwards, relative to pre-injection levels, there was a wideband increase of power below 50 Hz while the oscillations across the rest of the spectrum recovered to only a modest decrease from the pre-injection levels. [D] Before TTX, the comodulogram for 15-min intervals shows 4–6 Hz theta phase modulation of oscillation amplitudes both below 100 Hz and above 150 Hz. After TTX, the phase-amplitude modulation above 150 Hz disappeared, in apparent correspondence with the blockade of local action potentials. The high frequency region of interest is shown by the white dotted line.
Before any analysis, each LFP was z-score normalized by subtracting its mean and then dividing by its standard deviation. This was done to remove electrode-specific differences in the absolute magnitude of electrophysiological signals. This ensured that differences in electrode quality such as impedance and placement did not influence quantitative estimations.
3.0 Results
Part I
3.1 Analysis of the component steps of PAC estimation methods
3.1.1 Filters
Filters used for the extraction of oscillatory signals of interest are perhaps the most crucial part of the PAC algorithm to use properly. Several aspects of filters such as the filter center frequency, bandwidth, filter type, filter transition band and filtering algorithm have to be considered carefully. In the majority of published work, these properties are entrusted to various public toolboxes such as EEGLAB (Delorme and Makeig, 2004).
3.1.2 Filter frequency and bandwidth
Filter center frequency is typically selected based on known physiological bands (e.g. hippocampal theta oscillations 5–12 Hz, gamma oscillations 30–100 Hz). Another option is to parametrically search through a wide range of frequencies (Canolty et al., 2006). In this scenario, LFP signals are filtered using an array of filters with center frequencies that cover the range of oscillations of potential interest and the modulation index is estimated for each phase-amplitude filter pair (Fig. 1F). While this approach may be comprehensive, it is however, extremely computationally intensive. As an example, the filter for extracting phase information can be varied from 2 to 20 Hz with step of 1 Hz and the filter for extracting the amplitude information can be varied between 25 and 250 Hz with step of 5 Hz. This strategy yields 874 filter combinations for which the modulation index needs to be estimated.
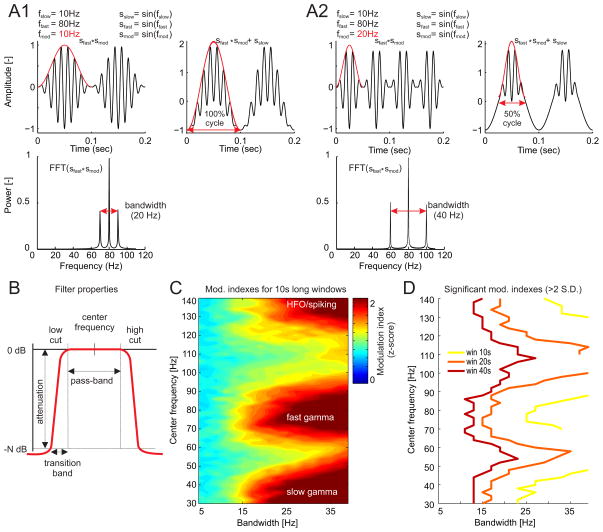
The filters for extracting the frequency-specific amplitude information have to be sufficiently wide to capture the amplitude fluctuations of the fast oscillations. In PAC, by definition, the amplitude of the high frequency signal gets modulated during a time-limited window. According to the Heisenberg-Gabor limit, the bandwidth of the modulated signal increases as this time-limited window decreases, to limit the phase interval in which the amplitude is modulated. Because many physiologists are not familiar with the Heisenberg-Gabor limit, we conducted a numerical analysis to illustrate this fact and identify the minimum bandwidth of the filter that is required to capture the amplitude fluctuations of a fast signal within the cycle of a slow signal, as required for estimating PAC. A synthetic signal is shown on the right side of Fig. 2A1. It has PAC that resembles what can be observed physiologically. It was constructed by adding a fast oscillation (e.g. a 80 Hz sine wave) to a slow oscillation (e.g. 10 Hz sine wave) and multiplying the fast oscillation by a modulatory oscillation (e.g. a 10 Hz sine wave) s′ = sslow + sfast × smod. This signal can be simplified to isolate the PAC component by ignoring the slow oscillation s′ = sfast × smod, which is the simplest synthetic signal (Berman et al., 2012) for the present purpose of evaluating the filter bandwidth requirement for detecting PAC in an arbitrary signal (Fig. 2A1 left).
Figure 2.
Effect of the amplitude filter bandwidth on modulation index estimation. [A1 top] In this synthetic signal, an 80 Hz sinusoid sfast is modulated by a 10 Hz sinusoid smod (red line shows signal amplitude) across 100 % of the slow sinusoidal cycle sslow. Modulated 80 Hz sinusoids sfast × smod exhibit [A1 bottom] three peaks in the power spectra with total bandwidth of 20 Hz. [A2 top] Increasing the modulatory frequency to 20 Hz, by narrowing the time window in which the amplitude is modulated [A2 bottom] increases the bandwidth to 40 Hz. [B] Pass-band filter properties, filter center frequency and filter pass-band width were varied in a range of 30–140 Hz and 5–40 Hz, respectively and [C] the normalized modulation index was computed for all these combinations using 10-s long windows. The data were the same as those used for computing the comodulogram in Fig. 1F. The theta filter (2 Hz pass-band width) was the same for all combinations and was centered on the theta peak (~ 8 Hz). Notice that significant modulation indexes (> 2 S.D.) for both slow-gamma and fast-gamma bands can only be observed for filter bandwidths above 15 Hz. [D] Since longer analysis windows result in stronger surrogate tests, the minimum filter bandwidth required for observing significant modulation can be lowered, but its value is still above 10 Hz for all bands of interest.
The spectra of s′ can be shown analytically to have three frequency components ( ). This is illustrated in Fig. 2A1 bottom. It has a total bandwidth of 20 Hz, which is double the modulatory frequency. The signals in Fig. 2A2 result from narrowing by 50%, the time during which the fast signal is modulated by the slow signal period, which amounts to increasing the modulatory frequency from 10 Hz to 20 Hz while keeping both the slow and fast frequency components constant. The spectra of this PAC component signal shows that the bandwidth doubled to 40 Hz (Fig. 2A2 bottom). Consistent with this relationship, the bandwidth of the filter for extracting the amplitude information from a modulated signal needs to be at least twice the frequency of the modulatory signal in order to characterize the modulation of the amplitude within the period of the slower oscillation.
To directly evaluate this claim in LFP data, we used a series of parametrically-varying filters (Fig. 2B) for extracting the amplitude series and computing the normalized modulation indexes for a single LFP (Fig. 2C). These filters were defined by combinations of the center frequency (30–140 Hz, steps 2 Hz) and filter bandwith (5–40 Hz, steps 2 Hz). The filter for extracting phase information was centered at 8 Hz with 2 Hz bandwidth. Both of these values were estimated from the theta peak in the power spectrum of the LFP recorded from hippocampus in the freely moving rat. We used several window lengths ranging from 5 to 40 seconds because longer analysis windows provide more robust statistical results (higher normalized modulation index) and therefore narrower amplitude filters might be sufficient in these cases. While this is indeed the case (Fig. 2D), we were only able to observe significant modulation index estimates (> 2 S.D.) for bandwidths > 25 Hz in the case of 10 s long analysis windows and > 15 Hz in the case of 20 s long analysis windows. This analysis demonstrates that estimating PAC is sensitive to the bandwidth of the filter that is used for extracting amplitude. The results also demonstrate that estimating PAC is sensitive to the duration of the data segments that are analysed. Indeed, we were unable to observe significant PAC at any band and for any filter bandwidth we tried when this LFP was segmented into 5 s long analysis windows. We performed a detailed examination of how the the analysis window impacts PAC estimation in section 3.1.5 below.
While the amplitude filter is required to be wideband, we also need to avoid merging sub-bands of the higher frequencies, because they may have different physiological origins, different phase coupling, and may potentially convey different information (Colgin et al., 2009). This is especially the case for hippocampal gamma oscillations, where multiple sub-bands have been identified (Belluscio et al., 2012).
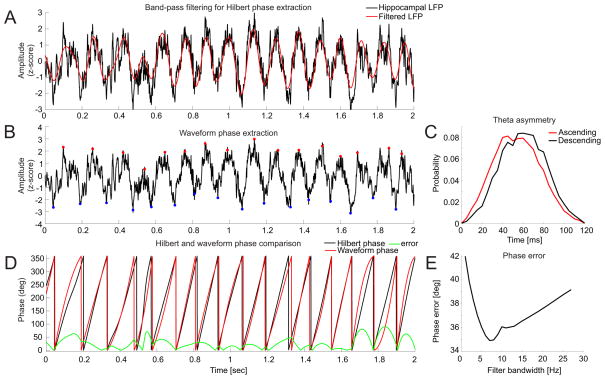
The filters used for extracting the phase information are typically very narrow in order to extract a nearly sinusoidal waveform, which is necessary for robust phase estimation (Chavez et al., 2006). When this narrowband condition is not met, the signal might contain additional fundamental frequencies and therefore several centers of rotations in the phase plane, in which case the phase of the signal cannot be reliably defined. In this regard, a particular challenge to PAC estimation is that neural oscillations, such as hippocampal theta, are not purely sinusoidal (Buzsaki et al., 1985, Belluscio et al., 2012) and therefore filters that are too narrow will necessarily cause errors in the phase estimate. In order to quantify the phase error caused by the narrow band-pass filter used for the phase estimation we compared the phase estimation using two different methods, by the Hilbert method (Fig. 3A)and by waveform analysis (Fig. 3B) (Belluscio et al., 2012). Because the waveform analysis uses wide-band signals to estimate the signal phase, we set this phase to be the reference. We then varied the bandwidth of the band-pass filter used by the Hilbert method and computed the error as the average difference between the two methods (Fig. 3D). The resulting phase error was minimized for a phase filter bandwidth of approximately 7 Hz (Fig. 3E).
Figure 3.
Error in the phase estimate of non-sinusoidal signals such as hippocampus theta oscillations. [A] The phase obtained from using a narrow pass-band filter followed by the Hilbert transform was compared with [B] the “reference” phase obtained from the signal using waveform analysis. Waveform analysis reveals [C] an asymmetry of the ascending and descending phases of hippocampus theta oscillations because the ascending phase is faster than the descending phase. [D] Comparing the phases obtained using the two methods provides a function to estimate the error in the phase estimate from the Hilbert transform. [E] The average error is plotted for a range of bandwidths of the phase filter. The plot shows the error is minimized for a filter bandwidth of about 7 Hz.
3.1.3 Filter transition band
An important property of a filter is its transition band, also known as the filter “roll-off”. The transition band is the bandwidth (specified in Hz) after which the filter attenuates the power of the signal by a required amount (specified in decibels - dB). The transition band is directly related to the length of a digital filter (number of filter coefficients). A shorter transition band (sharper filter) requires more coefficients and therefore longer computation time. Importantly, although a shorter transition band provides for a sharper filter, it is also more prone to ringing artifacts such as the generation of false oscillations in the filtered signal when there is a sharp edge transition in the input signal (Kramer et al., 2008). A filter with a wider transition band, although it is less precise in defining the frequencies of interest, is also less prone to the ringing artifact from a sharp edge transition. Ringing artifacts are especially important to consider as they can generate what look like high frequency gamma-like oscillations in LFP data.
3.1.4 Filter type
Generally, there are two types of digital filters - Finite Input Response (FIR) and Infinite Input Response (IIR) filters. IIR filters such as the Butterworth, Chebyshev or Elliptic filter are based on analog electronic filters and their main advantage is performance. Because IIR filters work with feedback, their transition band is shorter than the transition band of the FIR filter of the same length. This means that for a defined width of the transition band of the filter, the filter uses fewer coefficients and the computation time required to filter a signal is therefore shorter than with a FIR filter. This slight advantage of IIR filters (which is weakened by the advance of computing power in modern computers) is outweighed by a crucial disadvantage of IIR filters – the nonlinear phase response in the pass band. This essentially means that different frequencies contained in the filtered signal are time-shifted by a variable amount of time. This results in a distortion of the phase relationships in the signal, which is a serious problem when phase relationships are the subject of study. The nonlinear phase response can be corrected by the so called “forward-backward” filtering algorithm, which filters the signal in two consecutive steps “forward” and “backward”. In this case, all time shifts introduced in the first step are removed in the second step. While this approach makes the filtered signal zero-phase distorted it also introduces two related problems. First, the algorithm doubles the filter order so the execution time is several times longer than in the case of standard filtering. According to our benchmarks, the Matlab implementation of the forward-backward algorithm (filtfilt) takes over seven times longer to compute than the standard (filter) algorithm. Second, the algorithm squares the amplitude response, which can increase the pass-band ripple of the filter. FIR filters introduce a phase delay as well, but importantly, the phase delay is constant over the pass-band of the filter. Correction of the phase delay is then simply performed by shifting the signal by a constant number of samples.
Taken together, FIR filters provide crucial advantages over IIR filters when phase relationships are the subject of study. While it is difficult or impossible to provide any hard values for the bandwidths of filters that should be generally used for phase and amplitude estimation in PAC analysis, the amplitude filters need to be at least twice as wide as the frequency of the modulatory rhythm while phase filters need to be wide enough to capture any possible non-sinusoidal characteristics of the signal, as well as be sufficiently narrow band in order to allow robust phase estimates. Within these guidelines, it is necessary to select the filter properties that are appropriate for the specific signals that are being investigated.
3.1.5 Window size
Numerically, to estimate PAC, the modulation index can be computed from a time series of a minimum length given by a single cycle of the slow oscillation that provides the phase information. However, robust estimates can only be obtained by the analysis of multiple cycles in order to rule out the possibility of spurious coupling between phase and amplitude as a result of noise fluctuations. Generally, as illustrated in Figs. 2D and 4B, longer windows provide more robust evaluation of the coupling strength. In other words, it is less likely to measure a high coupling strength (high modulation index) as a result of noise for a long window rather than for a short window. This aspect is crucial when estimating PAC from signals with high amounts of background noise such as scalp EEG. If for example, the 50/60 Hz line noise is present in the EEG, it is unlikely to be modulated by the phase of the slower oscillation, rather by definition it is independent of it. In terms of the coupling algorithm logic, the amplitude of the line noise is constant across various phases of the slow oscillation, but this can only be determined when a sufficiently high number of slow oscillation cycles are analyzed. Longer runs of data are therefore needed for robust estimation of PAC. In contrast, the use of long data windows assumes stationarity of the variables of interest within the windows, which is unlikely for many applications, especially for cognitive variables like attention, memory, and decisions, which may have sub-second dynamics.
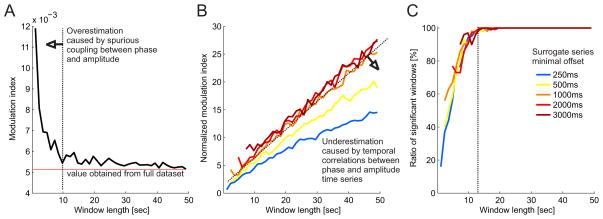
Figure 4.
Effect of data window length on modulation index estimates. [A] The modulation index was computed for data window lengths in the range 2–50 s. Each window was composed from randomly selected theta cycles (N=2000 corresponding to 10% of the theta cycles with the highest individual modulation indexes). The process was repeated 100 times for each window length. The raw modulation index shows a converging trend towards the modulation index value that is obtained from all the available theta cycles. The elevated modulation index values below window sizes of 10–15 s indicates overestimation which is likely caused by spurious coupling between the short phase and amplitude time series. [B] Normalized modulation index values computed for a range of minimal surrogate offsets 250–3000 ms indicate underestimation for surrogate shifts shorter than 1000 ms due to temporal correlations between the phase and amplitude time series. [C] The percentage of windows with a significant normalized modulation index (S.D. > 2) increases with the window length. With a window length > 10 seconds, most modulation index values were significant.
We investigated what the minimum appropriate window length might be for suitable analysis of PAC in the rat hippocampal LFP. We did this by extracting theta (7–9 Hz) phase and slow gamma (20–40 Hz) amplitude information from the hippocampal LFP and on the basis of the slow theta oscillation phase, we divided both signals into individual cycles. We then computed modulation indexes separately for all theta cycles and selected as our dataset, the 10% of cycles with the highest individual modulation indexes. We then combined the data from these individual cycles into analysis windows (N = 100) that ranged from 2.5 to 50 seconds, computed the modulation index for each of these windows, and finally, averaged the results from all the windows. With analysis windows shorter than about 10 seconds, the overall average tended to diverge from the mean modulation index estimated from the dataset of selected theta cycles (Fig. 4A). This can be attributed to the presence of spurious coupling between phase and amplitude information in short time windows. We then computed the normalized modulation indexes using the same surrogate procedure as described above (Fig. 4B). As expected, longer time windows provided more robust PAC estimates. Significant PAC values were only obtained for windows longer than approximately 5 seconds. We also varied the minimum surrogate series offset to investigate its effect on the estimate of PAC. For minimum surrogate offsets smaller than 1 second, the normalized modulation indexes tended to underestimate PAC. This can be assigned to the increased temporal correlations between the data and surrogate phase and amplitude time series when the surrogate offsets are small. Finally, we computed the ratio of windows with significant modulation index (> 2 S.D.) for different window lengths. For window lengths > 12 seconds, most of the modulation index estimates were significant.
Taken together, robust modulation index estimates can be observed for analysis windows of at least several seconds long (practically over 10 seconds) with minimal surrogate offsets of about 1 second. These requirements make it difficult to investigate PAC associated with sub-second events, such as what might be expected for cognitive events like attentional shifts, decision, and associative learning between transient stimuli and reinforcement. Our research program, is in fact interested in studying the electrophysiological correlates of such fast timescale cognitive events (Kelemen and Fenton, 2010; 2013), which motivated us to explore an alternative, event-based framework for estimating PAC and characterizing PAC-associated oscillation events as short as a single oscillation.
Part II
3.2 An event-based parameter-free approach to estimating PAC
As demonstrated above, an important limitation of current PAC algorithms is the time resolution. Several seconds (> 10 seconds practically) of data are needed for robust PAC estimation and appropriate statistical validation of the result using surrogate tests (Fig. 4). A second limitation of these algorithms is the requirement to define all the filter properties a priori, either as anticipated “typical” values of known physiological bands (such as theta and gamma rhythms) or by a wide parameter search through a range of frequencies, such as is provided by the comodulogram. A third challenge to the algorithm is the necessity to extract the phase of the slow rhythm, which can be challenging in the presence of noise and the reality of non-sinusoidal oscillations (Fig. 3). Here we propose an event-based parameter-free algorithm for estimating PAC that circumvents these limitations (Fig. 5).
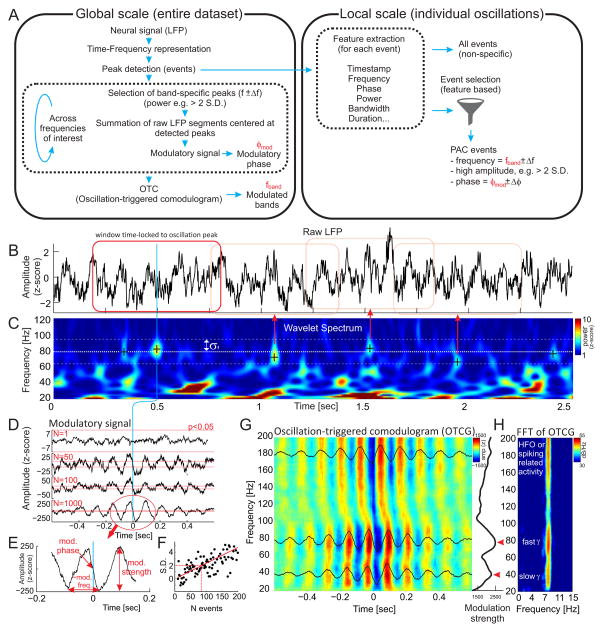
Figure 5.
Oscillation triggered coupling (OTC) analysis. [A] The OTC algorithm operates at two temporal scales – the “global” scale, which estimates the general properties of PAC (modulated bands, preferred phases of coupling) and the “local” scale of individual oscillations. Oscillations that are initially used to create the oscillation triggered comodulogram (OTCG) at the global scale can be filtered using various criteria (e.g. specific frequency, phase and power) in order to obtain the specific events that are responsible for generating phase-amplitude coupling. [B] In the first step, the raw LFP signal is transformed into [C] a z-score normalized wavelet spectra. Individual oscillations are detected as local maxima in time-frequency space. [D] Time stamps of large (> 2 S.D. from mean power) and frequency-specific (f ± σf) oscillations are then used as trigger points for summing the time windows of the raw LFPs centered at these time stamps. The development of the OTC signal is displayed as a function of increasing numbers of summed event windows N=1, 50, 100 and 1000. Notice that the amplitude and smoothness of the resulting OTC signal increases with the number of events. This indicates there is a systematic relationship between the peaks of detected oscillations and the phase of the slow rhythm. The red dotted horizontal lines mark the significant amplitude threshold of the OTC signal, which was computed from a surrogate test using random trigger points. [E] The resulting OTC signal displays several important properties. Its peak-to-peak amplitude corresponds to the strength of coupling, its phase at time 0 (middle of the time window) corresponds to the preferred phase of the coupling and its frequency corresponds to the modulatory rhythm. [F] In order to obtain a significant amplitude of the modulatory signal, approximately 70 events (corresponding to approx. 30 seconds of data) need to be added to the summation. [G] The above process can be repeated for a range of frequency bands (e.g. 20–200 Hz) to obtain the oscillation -triggered comodulogram (OTCG). The profile of the modulation strength (peak-to-peak amplitude of the modulatory signal) across frequencies (G right) shows peaks in the slow (~40 Hz) and fast (~80 Hz) gamma bands (red arrows). [H] The same peaks can be also observed in the FFT spectra computed from all frequency-specific modulatory signals. The FFT also shows that the wave pattern of the OTC corresponds to a single modulatory frequency of ~8 Hz (theta) that is present across the whole frequency range (20–200 Hz).
The central idea of this algorithm is to treat oscillations as time- and frequency- specific events, rather than continuous variables, as in the standard PAC algorithms we reviewed and characterized above. This event-based approach, we call “oscillation-triggered coupling” (OTC) has features that resemble those in the detection of single unit activity from extracellular action potential recordings. The OTC approach works on two distinct, complementary time scales. The “global” scale (Fig. 5A left), similar to standard PAC analysis, estimates the overall properties of phase-amplitude coupling such as the frequencies of the modulatory rhythms (e.g. delta or theta), the frequencies of modulated bands (e.g. slow gamma, fast gamma and high frequency oscillations) as well as the preferred phases of coupling for the individual modulated bands. The “local” scale (Fig. 5A right), uses the global scale properties of phase-amplitude coupling to filter all oscillatory events into subtypes, that can be characterized, for example, by being theta-modulated or non-modulated slow and fast gamma oscillations.
3.2.1 Global scale of OTC
The goal of the OTC algorithm at the global scale is to extract the overall properties of the phase-amplitude coupling using oscillatory events. The essential idea comes from the approach to signal filtering that is based on event-triggered averaging, like what is used for study of event-related potentials (ERP In a). signal with phase-amplitude coupling, by definition, the amplitude of the fast oscillation is phase locked to a particular phase of the slow oscillation. If such a bias is reliable, then identifying the peaks of the higher frequency oscillations as events and superimposing the raw (unfiltered) LFP segments centered on these peaks should reveal any modulatory slow frequency signals due to constructive interference in the averaging, whereas inconsistent modulatory relationships will average out due to destructive interference (Chrobak and Buzsaki, 1998).
The first step of the OTC algorithm is to transform the LFP signal (Fig. 5B) into a time-frequency representation (Fig. 5C). We do this by convolving the LFP signal s(t) with a group of frequency-specific Morlet wavelets w(t, f0) followed by squaring such as E(t, f0) = |w(t, f0) * s(t)|2, where symbol * denotes convolution. The Morlet wavelet is defined as , where σf = 1/2πσt (σt and σf denoting standard deviation in the time and frequency domains, respectively), normalization factor ensures that the total wavelet energy is 1, and practically (Tallon-Baudry et al., 1997). The resulting signals are then normalized (using a z score) in order to remove the 1/f nature of the spectral power. While a time-frequency representation can also be obtained by band-pass filtering the LFP, we prefer to use Morlet wavelets because of their Gaussian shape in both the time and frequency domains. This provides a straightforward estimation of their time-frequency resolution, which is crucial for understanding the limits of the time-frequency resolution of the method. As a concrete example, such a wavelet with center frequency f0 = 7 Hz (typical theta frequency) would have duration (2σt) of 318 ms and spectral bandwidth (2σf) of 2 Hz. At 40 Hz (typical slow gamma frequency), this would lead to 2σt = 56 ms and 2σf = 11 Hz. At 80 Hz (typical fast gamma frequency), this would lead to 2σt = 28 ms and 2σf = 23 Hz. Finally, at 160 Hz (typical high-frequency oscillation frequency), this would lead to 2σt = 14 ms and 2σf = 46 Hz.
In the next step, oscillatory events are detected as local peaks in the normalized time-frequency space. To reveal the modulatory signal ŝ for a specific band (for example 80 Hz; thick dashed line in Fig. 5C), events with large enough power within the band of interest are used as time locking points to superimpose segments of raw LFP that are time locked to the centers of the selected segments. In our analysis we define the band as f ∓ σf, where σf denotes the frequency resolution of the Morlet wavelet at frequency f. We also select only those events with power higher than the 95th percentile in the band of interest in order to reduce the effect of noise in estimating the modulatory signal. The modulatory signal ŝ is then defined as
where n = 1..N corresponds to time stamps of the selected power peaks within the band of interest and T corresponds to the time window around the time stamp, which is taken into the sum. The sum is selected here instead of the average so that the amplitude of the resulting signal also reflects the total number of detected oscillatory events, which is related to the strength of phase-amplitude coupling as will be demonstrated shortly. Fig. 5D shows the results of the process when different numbers of events are selected for the sum. As expected, the amplitude of the resulting signal increases with the number of events because there is a systematic occurrence of power peaks at specific phases of the slower rhythm. Furthermore, as the number of events is increased, the signal also becomes smoother because all activity that is not phase-locked to the power peaks is washed out by the summation. The resulting modulatory signal (Fig. 5D bottom) has several important properties (Fig. 5E). First, its base frequency (or frequencies in the case of multiple modulatory rhythms) corresponds to the frequency of the modulatory rhythm. Second, the phase of the modulatory signal at time 0 (corresponding to the location of power peaks) marks the preferred phase of coupling. Third, the peak-to-peak amplitude of the signal reflects the strength of the coupling.
The significance of the result can be determined using a surrogate test. By summing the same number of time windows but with random time stamps, we can estimate the peak-to-peak amplitude of the chance modulatory signal. Repeating this process several hundred times provides a null distribution, against which the peak-to-peak amplitude of the original modulatory signal can be compared to obtain z scores and significance intervals (red dashed lines in Fig. 5D; notice that the significance of the result increases as the number of events added to the sum increases). A similar approach can also be used to find out how many events need to be averaged in order to obtain a significant result (Fig. 5F). We computed a z score using the peak-to-peak amplitude of the original modulatory signal and the parameters from the null distribution after parametrically varying the number of randomly selected oscillatory events for the OTC analysis. The significance level of p < 0.05 could be reached after averaging approximately 80 events, corresponding to ~30 seconds of data. Repeating the above steps for a range of frequencies (e.g. 20 to 200 Hz) generates the data for an oscillation-triggered comodulogram (OTCG) as shown in Figure 5G. The OTCG contains the same information as the standard PAC comodulogram. This can be verified by comparing Figure 1F with 5G, H, which were computed from the same LFP data. In addition, the OTC shows the modulatory phase for each frequency band. Computing the peak-to-peak value of the modulatory signal for each frequency results in a relationship between the modulated frequency and the strength of coupling (a modulation strength profile, the black line at the right of Fig. 5G). Analysis of this relationship provides information about the potentially distinct modulated bands such as slow and fast gamma, which appear as peaks in the modulation strength profile (red arrow heads). A similar result can be obtained by taking the FFT of the frequency-specific modulatory signal (Fig. 5H). If a strong modulatory rhythm is present, the FFT should display a peak at this frequency.
Thus the OTCG provides global estimates of the modulatory frequency or frequencies, ranges of the modulated bands, the preferred phases of modulation as well as the modulatory strength across various bands.
3.2.2 Local scale of OTC
The pattern in the OTCG in Fig. 5G illustrates the important point that the peak times of the detected frequency-specific oscillation events are sufficient to reveal phase-amplitude coupling patterns. This event-based approach contrasts with the standard PAC methods, which use the whole LFP signal, not only the frequency-specific peak oscillatory events.
If we are able to separate phase-modulated oscillations from random power fluctuations, we would be able to better explain the origin of the phase-amplitude coupling that is measured by standard PAC methods, study the phase-amplitude coupling at the resolution of single oscillations, and importantly, at the scale that is relevant for ongoing neural computations and behavior (Buzsaki, 2010, Kelemen and Fenton, 2010, 2013). With this in mind we now return to the frequency-specific power peaks that were detected (Fig. 5C) to explore and characterize them as individual oscillations. An example of a single, isolated oscillation is shown in Figure 6A. Several features of each oscillation can be extracted, such as the peak power, bandwidth (distance between the two closest power minima above and below the power peak in the frequency domain), duration (time interval between the two closest power minima before and after the power peak in the time domain) and center frequency (corresponding frequency of the power peak). Furthermore, the corresponding instantaneous phase and amplitude of the modulatory frequency (such as theta) can be extracted for example by filtering the LFP using a band-pass filter centered at the modulatory frequency (obtained from the OTCG) followed by the Hilbert transform. By knowing the frequency and phase together with other features of each detected oscillation, we can compute a phase-frequency histogram. Of all the features we analyzed, the total number of high power (>95th percentile power) oscillations per unit time (Fig. 6B top, left) shows the strongest modulatory pattern in both slow (25–60 Hz) and fast (60–100 Hz) gamma bands. This confirms what was already observed in the OTCG (compare Fig. 6B with Fig. 5G). These patterns are much stronger than the patterns associated with the power of the oscillations (Fig. 6B top, right), their duration (Fig. 6B bottom, left) or bandwidth (Fig. 6B bottom, right). These observations suggest that the actual appearance of the high-power oscillatory events at the preferred phase is the most important contributor to modulation index estimates of PAC.
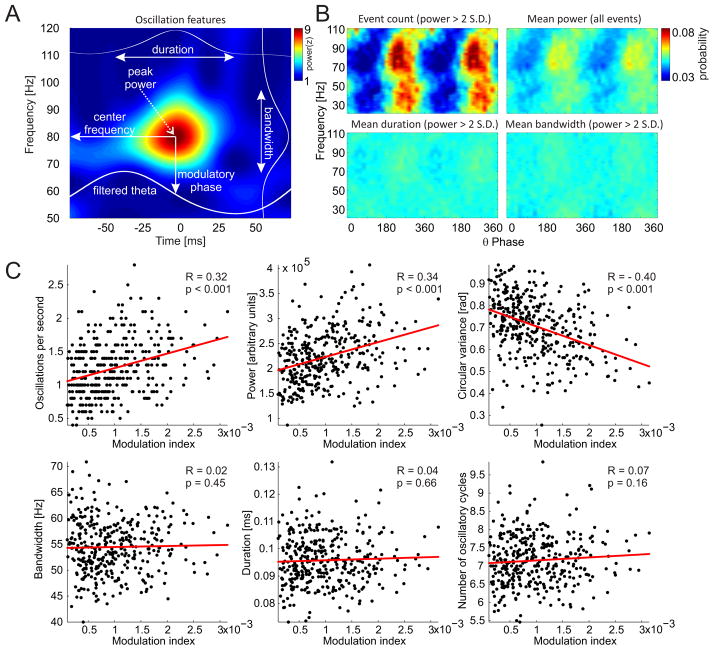
Figure 6.
The relationship of the standard PAC modulation index to the features of oscillatory events. [A] Each oscillatory event can be described by several features including its peak power, center frequency, bandwidth, duration and corresponding phase of the slow oscillation (theta). [B] The frequency-phase histogram of the number of high power (> 2 S.D. from mean power) events (top, left) reveals a strong phase modulation of the event occurrence as well as a clear separation and phase-specificity of slow (20–60 Hz) and fast (60–100 Hz) gamma band events. The histogram of the average power of all events (top, right) also displays a theta phase-modulated pattern but it is weaker than in the case of high power event counts. The average duration and bandwidth of oscillations show only weak phase-modulated patterns. All histograms were independently normalized for each frequency. [C] The standard PAC modulation indexes within the fast gamma band (70–90 Hz) were computed from 10 s sliding data windows and compared to the average features of the fast gamma oscillatory events that happened within the same time windows. Higher modulation indexes were positively and significantly (p < 0.001) correlated with the more frequent appearance of oscillatory events (top, left) as well as the power of these events (top, middle). As expected, modulation indexes were negatively correlated with the circular variance (spread) of oscillatory events across the phases of the modulatory rhythm (top, right). Modulation indexes were not correlated with the bandwidth (bottom left), duration (bottom middle) and number of consecutive cycles (bottom right) of the specific oscillatory events.
To further evaluate the hypothesis that the modulation index is an estimate of the number of phase-locked high power frequency-specific events, we extracted the features of oscillations from the same windows that were used for calculating the standard PAC modulation index (Fig. 6C). Because the modulation index cannot be robustly estimated from time windows smaller than 10 seconds (Fig. 4), we averaged the features of the multiple individual oscillations within each 10 s analysis window. We selected only the high power (>95th percentile power) oscillatory events with a corresponding theta phase that was close (< 60°) to the modulatory phase that was obtained from the OTCG (Fig. 6C top, left). To investigate the relationship between power of the oscillation events and the modulation index (Fig. 6C top, middle) we didn’t apply the power threshold. To investigate the relationship between the circular variance of the oscillation events and the modulation index (Fig 6C top, right) we did not apply a phase threshold. As expected, high modulation indexes were positively and significantly correlated with higher numbers of high-power phase-modulated oscillatory events (Fig. 6C top, left), and with increased power of phase-modulated oscillatory events (Fig. 6C top, middle). In addition, high modulation indexes were negatively correlated with the circular variance of the high-power oscillatory events (Fig. 6C top, right). The remaining features of the isolated oscillations (bandwidth, duration and number of cycles of the oscillation) were independent of the modulation index.
3.3 An example: Investigating high-frequency oscillations with OTC
We now provide an example of using OTC to investigate cross-frequency coupling in the hippocampal LFP. This example was selected because it illustrates some of the utility of the OTC approach. The gamma rhythm originally referred to the 35–85 Hz band (Bressler and Freeman, 1980). In more recent work, authors have subdivided the gamma band into slow (< 50 Hz) and “high” or “fast” (> 50 Hz) components. Furthermore, fast gamma was recently extended up to 140 Hz (Csicsvari et al., 1999, Canolty et al., 2006, Colgin et al., 2009). However, it is also necessary to be cautious when analyzing frequencies above 100 Hz because they can be contaminated by the wideband spectral content of action potentials and associated after potentials (Colgin et al., 2009, Ray and Maunsell, 2011, Belluscio et al., 2012, Schomburg et al., 2012, Scheffer-Teixeira et al., 2013). Indeed, because these signals are typically only defined by their spectral properties, there has been some controversy because it is unclear whether signals in the LFP above 100 Hz represent a unitary set of phenomena. Because OTC resembles spike-triggered averaging (in OTC, the trigger is an oscillatory event), we performed OTC analyses of the high frequency components of the LFP. By directly analyzing the modulated signals it should be apparent with OTC whether the >100 Hz theta-modulated signals are from true oscillatory activity or from spiking-related activity.
To investigate the performance of OTC in the > 100 Hz high frequency range, we analyzed LFP signals recorded from CA1 stratum oriens and the upper blade of the dentate gyrus of the mouse hippocampus because of their activity patterns in the high frequency range. The standard PAC comodulogram from CA1 stratum oriens (Fig. 7 A1 left) shows a narrow-band peak around 150 Hz that is modulated by a ~9 Hz theta rhythm. The OTC comodulogram from the same data (Fig. 7 A1 right) reveals the modulated activity at the same frequency band with the preferred phase located at the trough of the theta oscillation. The PAC comodulogram from the upper blade of the dentate gyrus (Fig. 7 A2 left) shows significantly phase modulated activity in a higher and wider frequency range > 200 Hz. The OTC comodulogram shows modulated activity in the same range (Fig. 7 A2 right) but in addition it shows a clear nonlinearity in the otherwise smooth OTC profile (white arrows in Fig. 7 A2 right), which are located around the trough of the theta oscillation. This suggests the presence of an abrupt voltage change that is systematically phase-locked to the theta oscillation. As can be seen from the figure, the spike-like profile of the activity can be best seen in the highest frequency range, however, its impact on the smoothness of the OTC profile can be clearly traced even to the range of HFOs and perhaps slower frequencies.
To further investigate whether action potential -related activity contributes to standard PAC, as has been debated in the literature, we took advantage of a published data set in which action potentials had been blocked without eliminating LFPs at gamma frequencies and below (Olypher et al., 2006). We performed standard PAC analysis on the LFP signals obtained from the ventral hippocampus after tetrodotoxin (TTX) was injected into the dorsal hippocampus of the urethane-anesthetized rat. TTX caused an abrupt block of action and local field potentials in the dorsal hippocampus where the drug diffused (Olypher et al., 2006). The TTX caused a delayed cessation of action potentials in the ventral hippocampus (Fig. 7B), and a transient, 15-min reduction in the power in the LFPs of the ventral hippocampus (Fig. 7C) that was coincident with a loss of excitation-inhibition coupling (Olypher et al., 2006). Before TTX, the standard PAC comodulogram from LFPs in the ventral hippocampus shows clear modulation of the amplitude of fast oscillations >150 Hz by theta phase ~4–6 Hz. After TTX, the modulation in this range disappeared during the intervals that action potentials were eliminated (Fig. 7D).
4.0 Discussion
4.1 Properties of standard PAC algorithms
We investigated the boundary conditions for the appropriate estimation of phase-amplitude coupling in LFP recordings. We demonstrated the importance of filter properties and analysis window size for estimating PAC. Because these properties define the time-frequency resolution of the analyses, it is necessary to consider them carefully. Phase filters should be narrow band to obtain meaningful phase information but not excessively narrow to distort non-sinusoidal shapes of rhythms such as hippocampal theta (Fig. 3), whereas the amplitude filters for extracting the instantaneous amplitude should be at least twice as wide as the frequency of the modulatory rhythm (Fig. 2). The minimum window length for robust computation of PAC is ~10 seconds (Fig. 4). Shorter windows lead to overestimates of coupling and lower significance of the modulation index. We emphasize that we are not suggesting any fixed values for these parameters, but rather methods for estimating ideal bandwidths of phase and amplitude filters, which will be use-specific when optimized for different types of neural signals and particular experimental questions.
4.2 Interpreting previous work
Although all filter properties such as bandwidth, transition band and attenuation strongly affect PAC estimation, they have often been entrusted (Canolty et al., 2006, Tort et al., 2009, Voytek et al., 2010) to third party software such as the EEGLAB, which does not allow for sufficient optimization for unbiased PAC estimation. Using the EEGLAB filters, PAC has been estimated from different bands using filters with very different properties (bandwidth, transition band and attenuation of the filter). As an example, in one of the first papers describing PAC (Canolty et al., 2006) it was claimed that 4-Hz wide filters were used to extract the phase and amplitude information. Because it is not possible to measure significant amounts of PAC with amplitudes filtered with narrower bandwidths than the frequency of the modulatory rhythm (Fig. 2), there appears to be an inconsistency. The problem lies in the filtering routine of the EEGLAB package (EEGFILT). This routine computes the transition band of the filter as a ratio of the low-pass and high-pass frequencies and therefore the total bandwidth of the filter scales with increasing frequency. This results in a higher total bandwidth of the filter than intended (4 Hz), which, was serendipitous because it made it possible to detect PAC. Filters with unnecessarily wide bandwidth can also merge physiologically distinct bands and may be responsible for apparent conflicts in the literature about the identity of discrete oscillatory bands. As an example, the continuing controversy concerning the distinction between the common “gamma” rhythm and oscillations above ~100 Hz can be seen in recent papers. While (Colgin et al., 2009) refers to “fast gamma” as a rhythm occupying 65–140 Hz in hippocampus CA1, others observe two rhythms occupying the very same band in the same region of the hippocampus - “mid-frequency gamma” 50–90 Hz and “fast gamma” or “epsilon band” 90–150 Hz (Belluscio et al., 2012).
4.3 Origin of >100 Hz high frequency oscillations
The origin of oscillatory activity above the traditional gamma range (> 100 Hz) is not fully understood. Some of the activity such as hippocampal sharp wave associated ripples (140–220 Hz) is a bona fide oscillation that is distinct from fast gamma (Sullivan et al., 2011). The additional high-frequency spectral content can be explained by both high frequency oscillations (HFOs) and components of extracellular action potentials (Ray and Maunsell, 2011, Belluscio et al., 2012). The ambiguity is further complicated because both potential sources can be theta-phase modulated resulting in increased modulation index in both cases (Fig. 7). Strategies to dissociate modulated HFOs from modulated spike-related activity were recently proposed (Tort et al., 2013). Modulated HFO activity can be distinguished in the raw LFP signal, and is confined to a fairly narrow frequency range compared to the wideband contribution of spike-related activity. Importantly, the OTC analysis which we propose here can directly detect nonlinearities in the oscillation-triggered modulatory signal and therefore dissociate PAC caused by oscillatory activity or spike-related activity (Fig. 7). Finally, when single neuron activity is available, the phase distribution of average firing rates with the phase distribution of amplitudes in the high frequency range can be compared. Our TTX-injection experiments (Fig. 7) demonstrated that abolishing spiking activity removed modulated activity above 150 Hz and therefore argues that this band is associated with spike-related activity. Modulated spike-related activity can provide valuable information about the global organization and discharge features of large cell populations (Schomburg et al., 2012).
4.4 PAC as neural computation
The notion that PAC itself is a neural computation has gained support as significant amounts of PAC have been reported in various species and across multiple brain areas, including rat hippocampus (Bragin et al., 1995, Tort et al., 2008, Tort et al., 2009), mouse hippocampus (Buzsaki et al., 2003), human neocortex (Canolty et al., 2006), human hippocampus (Axmacher et al., 2010) and monkey auditory cortex (Lakatos et al., 2005). PAC may be a mechanism for routing the flow of information through neural circuits (Colgin et al., 2009), memory processing (Tort et al., 2009, Axmacher et al., 2010), the selection of attention (Schroeder and Lakatos, 2009) and decision (Tort et al., 2008). However, the physiological bases of PAC are not well understood. Perisomatic basket cells in the hippocampus might play a role in the spatiotemporal organization of cell assemblies by firing theta rhythmic trains of action potentials at gamma frequency and therefore contribute to both rhythms and their phase-amplitude and phase-phase relationships (Buzsaki et al., 1983, Belluscio et al., 2012).
As demonstrated here, the hippocampus LFP of the freely-behaving rat offers a particularly robust example of PAC, which can be understood as a mechanism of neural computation. The phase of the hippocampal theta oscillation modulates the amplitude of hippocampal gamma oscillations. In turn, gamma oscillations provide millisecond-scale “windows of opportunity” when the discharge probability of hippocampal pyramidal cells is the greatest (Leung and Buzsaki, 1983, Colgin et al., 2009, Mizuseki et al., 2009). Because of conduction delays, slow oscillations like theta, may synchronize functionally-coupled networks over longer distances (Buzsaki and Draguhn, 2004, Uhlhaas et al., 2006). In contrast, fast oscillations like gamma might transiently synchronize action potential discharge into same-function assemblies over relatively short spatial scales (Kajikawa and Schroeder, 2011) that can be as long as a few hundred microns (Harris et al., 2003, Kelemen and Fenton, 2010). The interplay between the two oscillations might then provide a mechanism for spatial integration from a local to a global scale. In this scheme, the faster gamma oscillations that emerge at the specific phase of the slower theta oscillations might recruit subsets of cells that signal the same information and organize them into a cell assembly of co-active cells for neuronal information processing. Theta oscillations might then serve as an integration mechanism between multiple functional networks, each associated with a particular gamma episode, across longer periods of time (Jensen and Colgin, 2007). Another framework for understanding PAC as neural computation is based on the idea of phase coding, where PAC is a mechanism for encoding different information at different phases of the theta cycle. In this scenario, gamma oscillations appearing at specific phases of theta oscillations may enable activation of distinct neural ensembles, which encode distinct representations (Lisman and Idiart, 1995, Colgin et al., 2009) as is necessary for many higher order neurological and cognitive functions. These notions predict that single oscillations with a specific set of features that might include the modulatory frequency and phase, amplitude and duration would define and thus correlate with specific network-level computations. Accordingly, it may be valuable to investigate the utility of a multi-dimensional feature parameter space to classify individual oscillatory events into unitary event clusters in an attempt to identify their sensory and/or behavioral correlates. The example in Fig. 8, shows that a set of individual oscillatory events that have been characterized by local-scale OTC analyses can be investigated within the framework of a oscillatory event parameter space, which would also make it possible to apply standard methods of dimensionality reduction like principal component analysis (PCA) and then to examine the time course of these event sequences as trajectories through this state space. Such an effort, that treats oscillations in the LFP as unitary events would be similar to what is now routine for action potentials and their classification into single unit waveform clusters for investigating the neural dynamics and the neural correlates of cognitive variables.
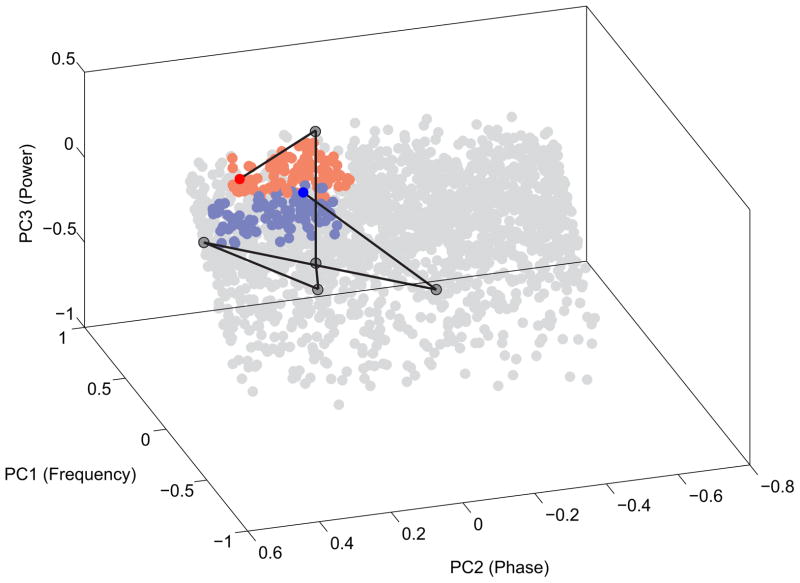
Figure 8.
Oscillatory events and their temporal dynamics represented in a multidimensional parameter space. Each oscillatory event from a rat CA1 recording can be characterized as an event in a multi-dimensional features space. The features we used to describe the individual oscillations were frequency, power, band-normalized power, bandwidth, duration, number of oscillatory cycles, energy of the oscillation, and corresponding instantaneous theta phase and amplitude. The 9 dimensions of this feature space were reduced to 3 dimensions using principal component analysis (PCA). The first three principal components (in decreasing order of importance) were frequency, phase and power which altogether accounted for ~90% of the variance in the dataset. Only a random subset (N=2000) of the events from the 45 min recording was plotted in the PCA space. The blue dots represent phase-modulated (105° ± 60°), slow gamma (39 Hz ± 10 Hz) with significant power (> 95th percentile from power mean). The red dots represent phase-modulated (80° ± 60°), fast gamma (76 Hz ± 10 Hz) events with significant power (> 95th percentile from power mean). All threshold values were obtained from the OTCG. The black line represents an example trajectory (a sequence of events) through the space that connects the two indicated fast and slow gamma events across several events with different frequency, phase and power specificity. The line corresponds to~200 ms.
4.5 Looking for correlates of cognitive variables
Time resolution is an important limitation of all published PAC studies. We estimate the smallest window size for a robust modulation index estimate to be ~10 seconds. However, such long windows assume stationarity, which is hardly the case because many oscillations appear and disappear within the period of the modulatory rhythms like theta or delta. Furthermore, long time windows are typically beyond the cognitive behavioral scales of several hundred milliseconds to a few seconds, which is the most crucial obstacle for linking PAC and cognitive processes. On the other hand, shorter time windows, while appropriate for investigating cognitive phenomena, are nonetheless more prone to overestimating the modulation index due to spurious coupling between phase and amplitude and don’t provide statistically strong estimates (Fig. 4). This fundamental limitation can be partially overcome with a trial-based experimental design (Tort et al., 2008), which can reduce the analysis window below 1 second. Even a 1-second resolution, however, only allows tracking of neural network “states” that are reflected in PAC, rather than individual phase-amplitude coupled “events” that are hypothesized to be linked to particular cognitive processing steps. To overcome this limitation, in particular for assessing the relationship between PAC and cognitive variables, we suggest an event-based algorithm like the OTC method, for detecting individual phase-modulated oscillations. Importantly, this method requires few prior assumptions about the input data. Indeed, this data-driven approach can be used where all global properties of PAC such as separate bands of phase-modulated oscillations, preferred phases of modulation and frequency of the modulatory signal emerge from the data, independent of most preconceptions (Fig. 5). We used the OTC method to extract features of individual modulated oscillations (Fig. 6). Such features such as the peak power, bandwidth, duration and associated phase of the modulatory rhythm may have predictive value and can provide a means to dissect modulated and non-modulated oscillations at functionally different bands such as slow and fast gamma or HFOs. Detecting modulated oscillations at behaviorally, or cognitively relevant time scales, such as a single theta cycle, is crucial for further understanding the role of PAC in brain function in general, and in cognitive information processing in particular.
Highilghts.
Boundary conditions are determined for appropriate use of standard PAC algorithms
Oscillation triggered coupling (OTC) estimates PAC by treating oscillations as events
The occurrence of high power phase and frequency specific oscillations explains PAC
OTC can separate phase locked oscillatory activity from spiking related activity
Acknowledgments
Supported by NIMH grants R01MH084038 and R01MH099128.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
7.0 References
- Axmacher N, Henseler MM, Jensen O, Weinreich I, Elger CE, Fell J. Cross-frequency coupling supports multi-item working memory in the human hippocampus. Proc Natl Acad Sci U S A. 2010;107:3228–3233. doi: 10.1073/pnas.0911531107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Belluscio MA, Mizuseki K, Schmidt R, Kempter R, Buzsaki G. Cross-Frequency Phase-Phase Coupling between Theta and Gamma Oscillations in the Hippocampus. J Neurosci. 2012;32:423–435. doi: 10.1523/JNEUROSCI.4122-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berman JI, McDaniel J, Liu S, Cornew L, Gaetz W, Roberts TP, Edgar JC. Variable bandwidth filtering for improved sensitivity of cross-frequency coupling metrics. Brain connectivity. 2012;2:155–163. doi: 10.1089/brain.2012.0085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bragin A, Jando G, Nadasdy Z, Hetke J, Wise K, Buzsaki G. Gamma (40–100 Hz) oscillation in the hippocampus of the behaving rat. J Neurosci. 1995;15:47–60. doi: 10.1523/JNEUROSCI.15-01-00047.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bressler SL, Freeman WJ. Frequency analysis of olfactory system EEG in cat, rabbit, and rat. Electroencephalography and clinical neurophysiology. 1980;50:19–24. doi: 10.1016/0013-4694(80)90319-3. [DOI] [PubMed] [Google Scholar]
- Buzsaki G. Neural syntax: cell assemblies, synapsembles, and readers. Neuron. 2010;68:362–385. doi: 10.1016/j.neuron.2010.09.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsaki G, Buhl DL, Harris KD, Csicsvari J, Czeh B, Morozov A. Hippocampal network patterns of activity in the mouse. Neuroscience. 2003;116:201–211. doi: 10.1016/s0306-4522(02)00669-3. [DOI] [PubMed] [Google Scholar]
- Buzsaki G, Draguhn A. Neuronal oscillations in cortical networks. Science. 2004;304:1926–1929. doi: 10.1126/science.1099745. [DOI] [PubMed] [Google Scholar]
- Buzsaki G, Leung LW, Vanderwolf CH. Cellular bases of hippocampal EEG in the behaving rat. Brain Res. 1983;287:139–171. doi: 10.1016/0165-0173(83)90037-1. [DOI] [PubMed] [Google Scholar]
- Buzsaki G, Rappelsberger P, Kellenyi L. Depth profiles of hippocampal rhythmic slow activity (‘theta rhythm’) depend on behaviour. Electroencephalography and clinical neurophysiology. 1985;61:77–88. doi: 10.1016/0013-4694(85)91075-2. [DOI] [PubMed] [Google Scholar]
- Canolty RT, Edwards E, Dalal SS, Soltani M, Nagarajan SS, Kirsch HE, Berger MS, Barbaro NM, Knight RT. High gamma power is phase-locked to theta oscillations in human neocortex. Science. 2006;313:1626–1628. doi: 10.1126/science.1128115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chavez M, Besserve M, Adam C, Martinerie J. Towards a proper estimation of phase synchronization from time series. J Neurosci Methods. 2006;154:149–160. doi: 10.1016/j.jneumeth.2005.12.009. [DOI] [PubMed] [Google Scholar]
- Chrobak JJ, Buzsaki G. Gamma oscillations in the entorhinal cortex of the freely behaving rat. J Neurosci. 1998;18:388–398. doi: 10.1523/JNEUROSCI.18-01-00388.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MX. Assessing transient cross-frequency coupling in EEG data. J Neurosci Methods. 2008;168:494–499. doi: 10.1016/j.jneumeth.2007.10.012. [DOI] [PubMed] [Google Scholar]
- Colgin LL, Denninger T, Fyhn M, Hafting T, Bonnevie T, Jensen O, Moser MB, Moser EI. Frequency of gamma oscillations routes flow of information in the hippocampus. Nature. 2009;462:353–357. doi: 10.1038/nature08573. [DOI] [PubMed] [Google Scholar]
- Csicsvari J, Hirase H, Czurko A, Mamiya A, Buzsaki G. Oscillatory coupling of hippocampal pyramidal cells and interneurons in the behaving Rat. J Neurosci. 1999;19:274–287. doi: 10.1523/JNEUROSCI.19-01-00274.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delorme A, Makeig S. EEGLAB: an open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J Neurosci Methods. 2004;134:9–21. doi: 10.1016/j.jneumeth.2003.10.009. [DOI] [PubMed] [Google Scholar]
- Engel AK, Singer W. Temporal binding and the neural correlates of sensory awareness. Trends Cogn Sci. 2001;5:16–25. doi: 10.1016/s1364-6613(00)01568-0. [DOI] [PubMed] [Google Scholar]
- Fenton AA, Kao HY, Neymotin SA, Olypher A, Vayntrub Y, Lytton WW, Ludvig N. Unmasking the CA1 ensemble place code by exposures to small and large environments: more place cells and multiple, irregularly arranged, and expanded place fields in the larger space. J Neurosci. 2008;28:11250–11262. doi: 10.1523/JNEUROSCI.2862-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris KD, Csicsvari J, Hirase H, Dragoi G, Buzsaki G. Organization of cell assemblies in the hippocampus. Nature. 2003;424:552–556. doi: 10.1038/nature01834. [DOI] [PubMed] [Google Scholar]
- Hurtado JM, Rubchinsky LL, Sigvardt KA. Statistical method for detection of phase-locking episodes in neural oscillations. J Neurophysiol. 2004;91:1883–1898. doi: 10.1152/jn.00853.2003. [DOI] [PubMed] [Google Scholar]
- Jensen O, Colgin LL. Cross-frequency coupling between neuronal oscillations. Trends Cogn Sci. 2007;11:267–269. doi: 10.1016/j.tics.2007.05.003. [DOI] [PubMed] [Google Scholar]
- Kajikawa Y, Schroeder CE. How local is the local field potential? Neuron. 2011;72:847–858. doi: 10.1016/j.neuron.2011.09.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelemen E, Fenton AA. Dynamic grouping of hippocampal neural activity during cognitive control of two spatial frames. PLoS Biol. 2010;8:e1000403. doi: 10.1371/journal.pbio.1000403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelemen E, Fenton AA. Key features of human episodic recollection in the cross-episode retrieval of rat hippocampus representations of space. PLoS Biol. 2013;11:e1001607. doi: 10.1371/journal.pbio.1001607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kramer MA, Tort AB, Kopell NJ. Sharp edge artifacts and spurious coupling in EEG frequency comodulation measures. J Neurosci Methods. 2008;170:352–357. doi: 10.1016/j.jneumeth.2008.01.020. [DOI] [PubMed] [Google Scholar]
- Lakatos P, Shah AS, Knuth KH, Ulbert I, Karmos G, Schroeder CE. An oscillatory hierarchy controlling neuronal excitability and stimulus processing in the auditory cortex. J Neurophysiol. 2005;94:1904–1911. doi: 10.1152/jn.00263.2005. [DOI] [PubMed] [Google Scholar]
- Le Van Quyen M. The brainweb of cross-scale interactions. New ideas in psychology. 2011;29:57–63. [Google Scholar]
- Le Van Quyen M, Foucher J, Lachaux J, Rodriguez E, Lutz A, Martinerie J, Varela FJ. Comparison of Hilbert transform and wavelet methods for the analysis of neuronal synchrony. J Neurosci Methods. 2001;111:83–98. doi: 10.1016/s0165-0270(01)00372-7. [DOI] [PubMed] [Google Scholar]
- Leung LW, Buzsaki G. Spectral analysis of hippocampal unit train in relation to hippocampal EEG. Electroencephalogr Clin Neurophysiol. 1983;56:668–671. doi: 10.1016/0013-4694(83)90034-2. [DOI] [PubMed] [Google Scholar]
- Lisman JE, Idiart MA. Storage of 7 +/− 2 short-term memories in oscillatory subcycles. Science. 1995;267:1512–1515. doi: 10.1126/science.7878473. [DOI] [PubMed] [Google Scholar]
- Mizuseki K, Sirota A, Pastalkova E, Buzsaki G. Theta oscillations provide temporal windows for local circuit computation in the entorhinal-hippocampal loop. Neuron. 2009;64:267–280. doi: 10.1016/j.neuron.2009.08.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olypher AV, Klement D, Fenton AA. Cognitive disorganization in hippocampus: a physiological model of the disorganization in psychosis. J Neurosci. 2006;26:158–168. doi: 10.1523/JNEUROSCI.2064-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penny WD, Duzel E, Miller KJ, Ojemann JG. Testing for nested oscillation. J Neurosci Methods. 2008;174:50–61. doi: 10.1016/j.jneumeth.2008.06.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips WA, Singer W. In search of common foundations for cortical computation. Behav Brain Sci. 1997;20:657–683. doi: 10.1017/s0140525x9700160x. discussion 683–722. [DOI] [PubMed] [Google Scholar]
- Ray S, Maunsell JH. Different origins of gamma rhythm and high-gamma activity in macaque visual cortex. PLoS Biol. 2011;9:e1000610. doi: 10.1371/journal.pbio.1000610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheffer-Teixeira R, Belchior H, Leao RN, Ribeiro S, Tort AB. On high-frequency field oscillations (>100 Hz) and the spectral leakage of spiking activity. J Neurosci. 2013;33:1535–1539. doi: 10.1523/JNEUROSCI.4217-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schomburg EW, Anastassiou CA, Buzsaki G, Koch C. The spiking component of oscillatory extracellular potentials in the rat hippocampus. J Neurosci. 2012;32:11798–11811. doi: 10.1523/JNEUROSCI.0656-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schroeder CE, Lakatos P. Low-frequency neuronal oscillations as instruments of sensory selection. Trends Neurosci. 2009;32:9–18. doi: 10.1016/j.tins.2008.09.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sullivan D, Csicsvari J, Mizuseki K, Montgomery S, Diba K, Buzsaki G. Relationships between hippocampal sharp waves, ripples, and fast gamma oscillation: influence of dentate and entorhinal cortical activity. J Neurosci. 2011;31:8605–8616. doi: 10.1523/JNEUROSCI.0294-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tallon-Baudry C, Bertrand O, Delpuech C, Permier J. Oscillatory gamma-band (30–70 Hz) activity induced by a visual search task in humans. J Neurosci. 1997;17:722–734. doi: 10.1523/JNEUROSCI.17-02-00722.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tort AB, Komorowski R, Eichenbaum H, Kopell N. Measuring phase-amplitude coupling between neuronal oscillations of different frequencies. J Neurophysiol. 2010;104:1195–1210. doi: 10.1152/jn.00106.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tort AB, Komorowski RW, Manns JR, Kopell NJ, Eichenbaum H. Theta-gamma coupling increases during the learning of item-context associations. Proc Natl Acad Sci U S A. 2009;106:20942–20947. doi: 10.1073/pnas.0911331106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tort AB, Kramer MA, Thorn C, Gibson DJ, Kubota Y, Graybiel AM, Kopell NJ. Dynamic cross-frequency couplings of local field potential oscillations in rat striatum and hippocampus during performance of a T-maze task. Proc Natl Acad Sci U S A. 2008;105:20517–20522. doi: 10.1073/pnas.0810524105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tort AB, Scheffer-Teixeira R, Souza BC, Draguhn A, Brankack J. Theta-associated high-frequency oscillations (110–160Hz) in the hippocampus and neocortex. Progress in neurobiology. 2013;100:1–14. doi: 10.1016/j.pneurobio.2012.09.002. [DOI] [PubMed] [Google Scholar]
- Uhlhaas PJ, Linden DE, Singer W, Haenschel C, Lindner M, Maurer K, Rodriguez E. Dysfunctional long-range coordination of neural activity during Gestalt perception in schizophrenia. J Neurosci. 2006;26:8168–8175. doi: 10.1523/JNEUROSCI.2002-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- von der Malsburg C. The correlation theory of brain function (MPI Biophysical Chemistry, internal report 81–82) In: Domany E, et al., editors. Reprinted in Models of neural networks II. Berlin: Springer; 1981. 1994. [Google Scholar]
- von der Malsburg C, Schneider W. A neural cocktail-party processor. Biol Cybern. 1986;54:29–40. doi: 10.1007/BF00337113. [DOI] [PubMed] [Google Scholar]
- Voytek B, Canolty RT, Shestyuk A, Crone NE, Parvizi J, Knight RT. Shifts in gamma phase-amplitude coupling frequency from theta to alpha over posterior cortex during visual tasks. Frontiers in human neuroscience. 2010;4:191. doi: 10.3389/fnhum.2010.00191. [DOI] [PMC free article] [PubMed] [Google Scholar]