Cortical activity in the null space: permitting preparation without movement

Abstract

Neural circuits must perform computations and then selectively output the results to other circuits. Yet synapses do not change radically at millisecond timescales. A key question then is: how is communication between neural circuits controlled? In motor control, brain areas directly involved in driving movement are active well before movement begins. Muscle activity is some readout of neural activity, yet remains largely unchanged during preparation. Here we find that during preparation, while the monkey holds still, changes in motor cortical activity cancel out at the level of these population readouts. Motor cortex can thereby prepare the movement without prematurely causing it. Further, we found evidence that this mechanism also operates in dorsal premotor cortex (PMd), largely accounting for how preparatory activity is attenuated in primary motor cortex (M1). Selective use of “output-null” vs. “output-potent” patterns of activity may thus help control communication to the muscles and between these brain areas.

Brain areas are highly interconnected yet perform different functions. At the heart of many fundamental questions in neuroscience is the question of how different brain circuits effectively modulate their connections on and off to allow selective communication^{1, 2}. In this study, we ask one such question about how selective communication operates: how can we plan a course of action, while still waiting for the right moment to act^3–6?

We employed the monkey motor system to test a new candidate mechanism for controlling output from one set of neural circuits to another. When a monkey is cued regarding the path of an upcoming reach but required to withhold the movement until a go cue, preparatory activity is present before the go cue in both PMd and M1^7–9 (Fig. 1). Preparatory activity is relevant to the upcoming movement: it is tuned for a variety of movement parameters^{7, 10–13}, predicts reaction time^{14, 15}, predicts movement variability¹⁶, and if disrupted delays the movement¹⁷. Preparatory activity is prevalent in PMd, somewhat less prevalent in M1, present but modest in the spinal cord^{18, 19}, and essentially absent in the muscles. This pathway therefore provides an ideal testing ground, because the central mystery is readily apparent: each area drives movement^{9, 20–22}, yet PMd and even M1 are also active in the absence of movement²³. Given this pathway of PMd to M1 to the spinal cord, and PMd’s direct projection to the spinal cord as well, how is preparatory activity attenuated at each of these stages?

Figure 1.

Illustration of task and of typical data. a. Layout of maze task. One typical trial shown. The same mazes were repeated many times; each maze is hereafter called a ‘condition.’ b. Top, task timeline. The monkey initially touched a central spot, then a target and (typically) barriers appeared. On some trials, two inaccessible distractor ‘targets’ also appeared. After the Go cue, the monkey made a curved reach (which left a white trail on the screen) around the barriers to touch the accessible target. Middle, trial-averaged deltoid EMG. Bottom, firing rate of one PMd neuron. Times are target onset, go cue, and movement onset. Flanking traces show s.e.m. Maze ID100, neuron J-PM48, EMG recording J-PD10.

It is often assumed that ‘gating’ of preparatory activity is performed at the target site. For example, preparatory activity might simply lie below some spinal activation threshold, or await a boost in spinal gain²⁴. Yet this would not explain the empirical observation that preparatory activity is not a weaker (and thus potentially sub-threshold) version of movement activity^25–28. A related hypothesis has been that preparatory activity is held at bay by a switch^{29, 30}, such as an inhibitory gate³¹, as is the case in the brainstem oculomotor system³². However, we have recently shown that there are no clear signs of a simple inhibitory gating mechanism within PMd or M1^{28, 33}. Thus, it has remained unclear how neural activity during preparation can be kept local, even though activity in those same neurons can drive movement moments later⁵. Here we test a new candidate mechanism for controlling when circuits communicate and when they functionally decouple. We find that a population-level mechanism operating in PMd can largely account for how preparatory activity is prevented from reaching M1, and that the same mechanism operating in both areas can largely account for how preparatory activity is prevented from reaching the muscles.

Results

The activity of the muscles is some function of neural activity. Whatever this function is, it must accommodate M1 and PMd changing their firing rates during motor preparation without movement occurring prematurely. Here, we consider a simple possibility. The simplest type of relationship between the neural activity of a brain area ‘A’ and its target is a linear one. That is, each target muscle would be driven by a linear combination of neural firing rates³⁴:

$$M=WN$$ (1)

where M, W and N are matrices. Each row of M contains the activity of one muscle, and each row of N contains the activity of one neuron. Columns correspond to the activities at different times and for different movements. W contains the weights for the linear mapping from neurons to muscles. That is, W specifies the weighted sum of neurons’ firing rates that drives each muscle.

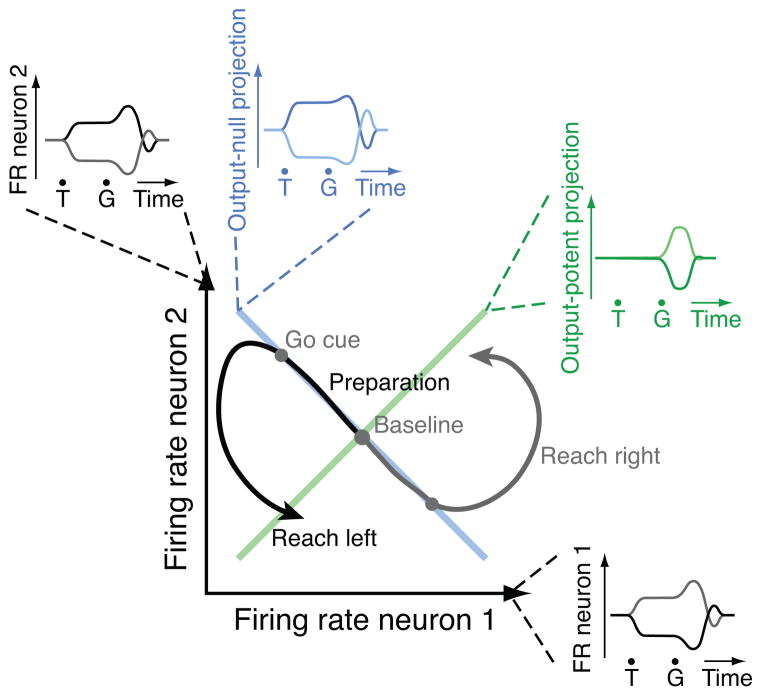
To build intuition about this model, consider the following extreme, un-physiologically simplified situation. Imagine that just two excitatory neurons synapsed directly on a muscle, and this muscle produced force proportional to the sum of its two inputs. As long as the sum of the two inputs remained constant, the muscle would produce a constant amount of force–no ‘gate’ or ‘switch’ is required. The activity of these two neurons can be represented as a point in a two-dimensional firing rate space. Their pattern of activity over time is a trajectory through this space^35–37. In the state space, the constant-sum line forms an ‘output-null’ dimension (Fig. 2, blue line). The muscle’s force output will change only if there is a change in the sum of the neurons’ firing rates; we term the direction in which that sum changes the ‘output-potent’ dimension (Fig. 2, green line). This idea also generalizes to more complex cases: if one of these hypothetical neurons had a net inhibitory effect, the dimensions would be switched. With many neurons, we would expect multiple output-null dimensions. If there were multiple independent muscles, we would need multiple output-potent dimensions. This is all to say that activity in the output-potent dimensions would be read out by the target muscle or brain area, while activity in output-null dimensions would not be visible to the target. Formally, any activity changes in output-null dimensions fall in the null space of W. Conversely, activity changes in output-potent dimensions fall in the row space of W.

Figure 2.

Simplified output-null model. For illustration, assume a muscle receives input from two neurons and produces a response that is the linear sum of the inputs. If the sum is constant (“Output-null dimension”), the muscle cannot distinguish between input 1 being high and 2 low, or vice versa. When the sum changes (“Output-potent dimension”), muscle output will change. If preparatory neural activity changes only within the output-null dimension (two different reaches illustrated), then the muscle’s activity remains constant; when neural activity changes in the output-potent dimension also, movement ensues. Insets: PSTHs for the neurons, and PSTH-like views of output-potent and output-null dimensions. T, target onset, G, go cue.

The existence of output-potent and output-null dimensions is likely inevitable, as there are more neurons than muscles. The key question is whether the brain exploits these dimensions to control when circuits communicate (as opposed to relying on nonlinear thresholds or a time-varying gain). The hypothesis that output-null dimensions are used to control communication leads to two predictions. First, if this mechanism operates between cortex and the muscles, then during motor preparation changes in neural firing rates should occur in combinations that produce changes in output-null dimensions, but do not produce changes in the dimensions that are output-potent with respect to the muscles (Fig. 2). Second, if this same mechanism operates between cortical areas, we would expect PMd preparatory activity to preferentially occupy dimensions that are output-null with respect to M1. If this latter prediction is correct, this could help produce the well-known reduction in preparatory activity between PMd and M1.

Exploitation of output-null dimensions is unlikely to leave any particular signature at the level of single neurons. As illustrated in the model (Fig. 2, black insets), changing state along the output-null dimension corresponds to activity changes in most of the relevant neurons. Such activity cancels out only at the level of the population output. Intriguingly, though, this model tends to produce neurons with mismatches in tuning between the preparatory and movement periods, as has been observed previously^25–28. Thus, if one averages over neurons based on their preferred reach condition during movement, their preparatory tuning largely averages away (Supplementary Fig. 1). This mismatch is suggestive, but forms only an indirect test and is neither necessary nor sufficient to demonstrate that such a model is correct (Methods). Testing this hypothesis requires both knowing the population response and estimating the output-null and output-potent dimensions.

To test our hypothesis, we used a variant of a standard delayed reaching task with two monkeys (Fig. 1, Methods). We recorded the population response using both single- and multi-unit neural activity (using single moveable electrodes and silicon electrode arrays) and muscle activity (using percutaneous electrodes). Importantly, trial-averaged data were used except where noted – the primary goal of these analyses was to explain how there can be preparatory tuning without movement, not to explain trial-by-trial variability. Thus, all repeats of the same condition were averaged to produce a single rate versus time. The same reaches were required every day and monkeys were highly practiced. Repeated reaches to the same targets were thus extremely similar to one another over the course of months (Supplementary Fig. 2). Data from different days were therefore combined.

As a basic test for the plausibility of exploiting output-null dimensions, we can search for neuron pairs whose preparatory activity might cancel out. Activity for one such pair of neurons (Fig. 3a, left, center) illustrates a partial canceling out. When the two neurons’ activity is added together (right), the sum has less preparatory tuning than either but retains the movement activity. In this example, the canceling out is quite incomplete because only two neurons were used; the effect might be much greater with more neurons.

Figure 3.

Examples suggesting potential output-null structure. a. When the weighted activity of the left neuron is added to the activity of the center neuron, the result (right) has less preparatory activity than either input. This pair thus illustrate the output-null idea, though with more neurons a more complete cancellation occurs. Constant c was set to 0.37. Conditions colored based on preparatory activity of left neuron. b. Example readouts of real data. Each panel shows a linear, two-dimensional readout of real data, exhibiting the predicted structure (compare with Fig. 2). Each trace corresponds to a single, trial-averaged condition. Preparatory activity shown in blue, movement activity shown in green, and state at Go cue shown as grey circles. Red ellipse shows 2 s.d. of the preparatory activity. As in the model, preparatory activity for different conditions is mostly spread out in one dimension, while movement-epoch activity travels through both dimensions. Dimensions found using jPCA³⁸.

Similarly, we can take linear combinations (weighted sums) of many neurons’ activity. These linear combinations represent possible linear readouts of the population. Some readouts revealed structure in the data that strongly resembles the hypothesized structure (see Fig. 2). One such pair of readouts is shown for each of two monkeys (Fig. 3b). Each trace represents one trial-averaged reach condition, e.g., the average response for many leftwards reaches. In these examples, preparatory activity (blue) for the various conditions is spread out in one dimension but confined in the other – the red ellipse showing the envelope of preparatory activity is very elongated. Movement activity (green), in contrast, sweeps through both dimensions. These projections illustrate that the hypothesis in Figure 2 is plausible. Preparatory activity is strongly present in the population, yet a downstream target could be largely insensitive to this preparatory activity if it received inputs in a particular combination: the linear combination described by the sum of the two dimensions shown (the short axis of the red ellipse). Note that this does not mean that preparatory activity is functionless. To the contrary, in this case preparatory activity appears to set the initial direction and amplitude of the subsequent movement activity^{25, 38}.

Two caveats are worth stressing. First, a two-dimensional view may be insufficient to fully test the hypothesis. Second, to properly interpret these results, one wishes to have some independent means for identifying which dimensions are output-null versus output-potent. We therefore designed a mathematical method for estimating output-potent and output-null dimensions. We then tested the degree to which preparatory activity avoids the output-potent dimensions. We first test for this structure in PMd/M1 (considered together) with respect to the muscles. We then turn to the question of communication between PMd and M1.

Analysis of PMd/M1 to muscles

The core logic of this analysis is to use EMG data to help identify which neural dimensions (linear readouts) are most likely to be output-potent and which dimensions are most likely to be output-null. We can then test our central prediction: preparatory activity should avoid leaking into the output-potent dimensions, and should mainly be present in output-null dimensions. To avoid circularity, putative output-null and output-potent dimensions are identified using only movement activity, by finding neural dimensions in which activity resembles the EMG recordings. Only then is preparatory activity examined.

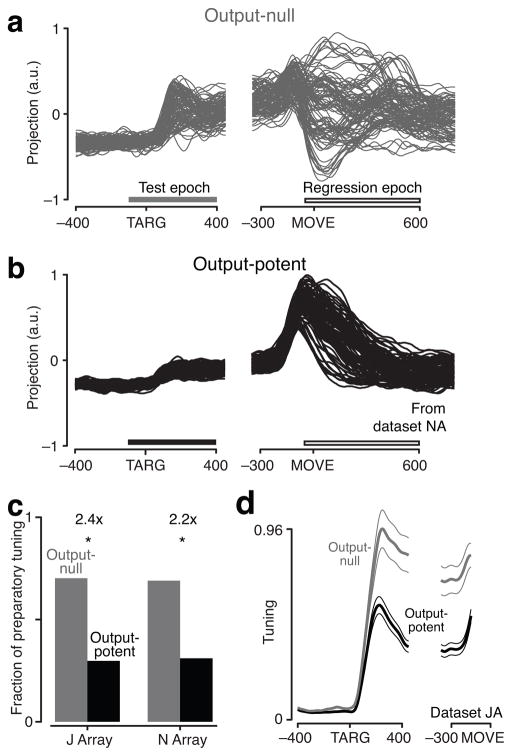
Figure 4 shows the results of this analysis. An explanation of the analysis follows, with the full derivation in Methods. Output-null and output-potent readouts can be plotted as PSTHs (as in the blue and green insets in Fig. 2), since they are made by simply adding and subtracting neurons’ responses (see Fig. 3a). Each trace corresponds to a different condition, and is a readout of the trial-averaged responses of individual neurons. Two such readouts are shown: one readout of a putative output-null dimension (Fig. 4a), and one readout of a putative output-potent dimension (Fig. 4b). Both reveal strong movement-related activity. However, by construction, only for the output-potent dimension did movement activity resemble muscle activity (“regression epoch” in Fig. 4a–b). The output-null dimension also contained strong movement-epoch activity, but due to the particular pattern of tuning and the temporal structure of the response, it correlated only weakly with muscle activity.

Figure 4.

Output-null results for cortex to muscles. a. Neural activity in one output-null dimension for one dataset (JA-2D1). All activity is trial-averaged, and each trace represents the response for a different condition. b. Neural data in one output-potent dimension. Dimensions were identified relative to EMG activity. This pair of example dimensions has a tuning ratio of 9.2. Bars indicate “test epoch” (−100 to +400 ms from target onset), where the tuning ratio was computed, and “regression epoch” (−50 to +600 ms from movement onset), where dimensions were identified. c. Fraction of preparatory tuning (across conditions and times) in output-null (gray) and output-potent (black) dimensions for each dataset. Tuning ratios indicated above bars; all values were significantly greater than unity. d. Tuning at each time-point, in the output-null and output-potent dimensions. Flanking traces indicate s.e.m. computed via resampling of conditions.

With the dimensions identified, our prediction was that preparatory activity would be weaker in the output-potent dimension, to avoid prematurely causing muscle contractions. This is indeed what was observed (compare Fig. 4a and b for the “test epoch”): preparatory activity in the output-null dimension was more strongly tuned and more different from baseline (the sign of this change is arbitrary). A similar effect was found in all datasets tested. Preparatory tuning – the spread of the mean firing rates across different conditions – was always weaker in the output-potent dimensions (Fig. 4c; explained below).

The analysis in Figure 4 was performed as follows. We first found the putative muscle readouts (W from equation 1) using neural and EMG activity from the movement epoch. As described above, if the output-null hypothesis is correct, then when we apply these same ‘muscle readouts’ to preparatory activity the result should have little tuning and should hold steady at baseline (as in Fig. 4a). If the output-null hypothesis is incorrect, and movement is prevented via a threshold nonlinearity or time-varying gain, then the ‘muscle readouts’ will contain preparatory tuning at the same strength as other, output-null readouts. This latter expectation also holds if equation (1) is an inappropriate simplification that fails to capture the key relationship.

In principle, W can be found using linear regression. However, because different neurons have correlated activity patterns (mathematically, N is nearly rank deficient), W cannot be found directly. One standard solution to this problem is to use dimensionality reduction first; this solution is sometimes called Principal Component Regression. The low-dimensional version of the model is:

$$\stackrel{\sim }{M}=\stackrel{\sim }{W}\stackrel{\sim }{N}$$ (2)

where M̃ and Ñ are the low-dimensional versions of the data matrices M and N, found via Principal Component Analysis (PCA). W̃ captures the relationship between them. Unlike N, Ñ has orthogonal (uncorrelated) rows, and so regression is viable and W̃ can be found. We can choose the number of rows for Ñ and M̃; these values were chosen as six and three, respectively (three dimensions for M̃ captured 77–92% of the variance). This produces three ‘muscle readouts’ (putative output-potent dimensions), and three putative output-null dimensions.

To find W̃ , we considered only the activity during the movement. W̃ was then found using linear regression. The result of all of the above is to identify a reasonable estimate for how the muscles could read out a weighted sum of neurons’ firing rates.

Our overarching goal was to test whether one must propose that preparatory activity is reduced by a nonlinearity (threshold or low gain), or whether significant reduction occurs due to the structure of W. That is, we ask whether the preparatory activity in N falls mainly in the null space of W and is therefore not read out by the muscles. To test this, we compared the activity in the ‘muscle readouts’ (output-potent dimensions) with the activity in the output-null dimensions, which cannot pass through W̃. Mathematically, the space of ‘muscle readouts’ is the row space of W̃ , and the output-null dimensions form the null space of W̃.

As our test, we measured whether more preparatory activity survives in the putative output-null dimensions or in the putative output-potent dimensions. To avoid circularity, these spaces were identified based on movement activity; only then was preparatory activity tested. Figure 4c was produced by taking the strength of preparatory tuning in the output-null dimensions divided by the strength of preparatory tuning in the output-potent dimensions (the “tuning ratio,” Methods).

Consider the data in Figure 3b. The tuning ratio asks how elongated the ellipse is, and whether it is in fact aligned with the output-null dimensions. If our hypothesis is correct, then the tuning ratio should be considerably greater than one. As shown in Figure 4c, the tuning ratio ranged from 2.8 to 8.2.

We employed extensive simulations to verify that this analysis detects exploitation of output-null dimensions during preparation when appropriate but does not do so when such structure is absent. We created simulated datasets, varying how strongly the preparatory activity was confined to the output-null dimensions. The simulated neural and muscle activity (Fig. 5b, d) qualitatively resembled our recorded neural and muscle activity (Fig. 5a, c). We analyzed this simulated data using the method described above. Our method correctly detected how strongly the preparatory activity was confined to output-null dimensions, and rarely produced false positives (Fig. 5e–h; the results lie nearly along the line y=x, or below). This was true even when nonlinearities were introduced to simulate firing rate saturation and floor effects (i.e., when firing rates were always positive and median firing rates were low; see Fig. 5b, d). As a mathematical note, this nonlinearity changes the relationship between neural and muscle activity to M = f(WN), with f a non-time-varying nonlinearity that is not responsible for ‘gating.’ The method was also robust when “errors” were made in applying the analysis with the wrong dimensionality (Fig. 5g–h), or when unequal numbers of output-null and output-potent dimensions were present in the data (Supplementary Fig. 3). When results differed substantially from the true underlying value, the results were nearly always underestimates, meaning that the results reported in Figure 4 are most likely conservative.

Figure 5.

Testing analysis method on simulated data. Simulations produced artificial neural and EMG “recordings” with the desired strength of output-null structure (Methods). Our analysis was run on this artificial data to quantify accuracy. a. Example real neural recording. Each trace shows trial-averaged response for one condition. Conditions color-coded according to preparatory activity level. b. Example simulated neuron. Qualitatively, it exhibits similar response complexity to real neuron. c. Example real EMG recording. d. Example simulated EMG recording. Qualitatively, it exhibits similar response complexity to real muscle. e. Analysis of data produced without distorting nonlinearities. Dot indicates median measured effect size for set of 50 simulations. Error bars encompass 68% of simulations (equivalent to 1 s.d.). Grey line shows unity. f. Analysis of data distorted with floor effects and saturating nonlinearities. g. Analysis of same data as in f, but underlying dimensionality was “underestimated” during analysis: two output-null and two output-potent instead of three and three. h. Same as g, but dimensionality overestimated as four output-null and four output-potent. In essentially all cases, adding nonlinearities to the data or misestimating dimensionality (including unequal numbers of output-null and output-potent dimensions; Supplementary Fig. 3) resulted in underestimates, not overestimates, of true effect size. Our results are thus likely conservative.

Returning to the real data, the tuning ratio was greater than unity in all four datasets obtained from two monkeys (Fig. 4c). This indicates that preparatory tuning remained mostly within the output-null dimensions, avoiding the output-potent dimensions. This dimensional preference was large – on average, the tuning ratio was 4.5 (geometric mean). Using conservative Monte Carlo simulation-derived statistics (Methods), all four datasets were statistically significant (J: p=0.006; N: p=0.030; JA: p=0.011; NA: p=0.021). To gain a sense of how the effect evolves over the course of a trial, we also measured the tuning depth separately at each time point for output-null and output-potent dimensions (dataset J shown in Fig. 4d, all datasets shown in Supplementary Fig. 4).

Moreover, this effect was present on a trial-by-trial basis. We performed a trial-by-trial analysis, which was conceptually similar to our main analysis, but instead of using trial-averaged data (where all repeats of the same condition were averaged over), we preserved the data for each trial. The observed trial-by-trial tuning ratios were greater than unity for both datasets for which we had simultaneous recordings: 2.1 for monkey J (p=0.027), and 2.7 for monkey N (p=0.002). These ratios were smaller than those found using trial-averaged data, likely in part because trial-by-trial state estimation is noisier; this tends to reduce effect sizes. Nonetheless, these results confirm that preparatory activity is preferentially confined to the output-null dimensions even when trial-by-trial variability is taken into account.

Analysis of PMd to M1

Our second prediction was that this same principle might operate as a more general mechanism to modulate communication between one cortical area and another. A natural place where such a mechanism might operate is between PMd and M1. M1 is more tightly coupled to the spinal cord than is PMd, contributing approximately twice the number of spinal projections³⁹. M1 exhibits preparatory activity, but considerably less than PMd. We tested whether PMd might avoid driving M1 during preparation by confining its preparatory activity to the dimensions that are output-null with respect to M1.

We performed the same analysis as above, except with PMd as the ‘source’ area (N) and M1 as the ‘target’ (M). As predicted, we found that PMd preparatory activity lay preferentially in output-null dimensions with respect to M1 (Fig. 6; two datasets had sufficient recordings from both areas for this analysis). This was the case in both monkeys, with an average tuning ratio of 2.3 (JA: p=0.017; NA: p=0.029; see also Supplementary Fig. 5). Thus, these cortical areas appear to exploit the output-null vs. output-potent distinction. However, this effect was not as large as that seen for the muscles. This is consistent with the observation that M1 is active during movement preparation, just less so than PMd. Also consistent with that observation, we found that both PMd and M1 independently exhibit the output-null effect with respect to muscles when analyzed separately (Supplementary Table 1). However, as analyzing PMd or M1 alone splits the dataset in half, the results were somewhat less reliable.

Figure 6.

Output-null results for PMd to M1. Format as in Figure 4. a. Neural activity in one PMd output-null dimension for one dataset (NA-D4). b. Neural activity in one PMd output-potent dimension. Dimensions were identified relative to M1 activity. This example pair of dimensions has a tuning ratio of 3.8. c. Fraction of preparatory and baseline tuning (across conditions and times) in output-null (gray) and output-potent (black) dimensions for each dataset. Both ratios were significantly greater than unity. d. Tuning at each time-point, in the output-null and output-potent dimensions. Flanking traces indicate s.e.m. computed via resampling of conditions.

Thus, it appears that an output-null space effect can account for much of the loss of preparatory activity between PMd and M1, and also between each area and the periphery. Moreover, this control of communication was specific, as expected given that PMd has stronger preparatory activity than M1. When the same analysis was performed with reversed source/target roles, M1 preparatory activity did not preferentially lie in output-null dimensions with respect to PMd (Fig. 7a; mean tuning ratio 1.1; p>0.2 for both monkeys). In addition to the simulations, this confirms that the analysis does not intrinsically produce tuning ratios greater than one; in cases where no effect is expected, the method reports the correct value of ~1.

Figure 7.

Controls for output-null analysis. a. Results of output-null analysis, with M1 as ‘source’ and PMd as ‘target’. As expected, no substantial effect was found. b. Muscle activity over time relative to key epochs. Each muscle’s activity was first normalized by its range. Heavy trace indicates mean across muscles. Width of thin traces shows mean tuning depth (assessed as standard deviation across conditions). Red bar shows epoch used to identify output-potent dimensions. Effect size computed using only preparatory data (black bar). Monkey J. c. Black bars show measured effect size for each dataset. Blue bars show effect size due to neurons with strong preparatory tuning preferentially contributing to output-null dimensions. Chance is unity. d. Neurons’ contributions to the output-null and output-potent dimensions. For each neuron, a space preference index was computed, which is +1 if the neuron contributes solely to output-potent dimensions and −1 if the neuron contributes solely to output-null dimensions. Histogram of values from the data are plotted in black (dataset J). Chance distribution is plotted in purple. Horizontal bars (above) show ±1 SD. Dots indicate means. Values for examples below indicated by green arrowheads. e. PSTH for example neuron that mainly contributed to output-null dimensions. Unit J36. f. Same as e, for neuron that contributed almost equally to output-null and output-potent dimensions. Unit J2. g. Same as e, for neuron that mainly contributed to output-potent dimensions. Unit J149.

Basic controls

In addition to the simulations, we tested directly whether the main analyses were sensitive to the precise dimensionality used. For the cortex-to-muscles analysis, we verified that results were similar using a dimensionality of 2 or 4 for M̃ (always using twice as many dimensions for Ñ). In 10 of 12 cases (4 datasets × 3 dimensionalities) the expected-direction effect was observed. In the two remaining cases, very small and statistically insignificant opposite-direction effects were obtained; no statistically significant opposite-direction effects were found. For the PMd-to-M1 analysis, the relevant dimensionality was higher: PMd and M1 both had dimensionalities of ~7–15, as in other datasets^{25, 35, 40}. We therefore retained 14 dimensions for PMd in our main PMd-to-M1 analysis (this captured 64–67% of the variance, approximately where the variance captured per dimension leveled off), and 7 for M1. We verified that effects were similar with a PMd dimensionality of 10, 12, 16, and 18. In all 20 cases (4 datasets × 5 dimensionalities), the expected-direction effect was observed.

Notably, our datasets included both curved and straight reaches. This provided a wider variety of movements, but curved reaches might conceivably differ from straight reaches in some important way. We therefore repeated our analyses on the 1/3 of our data consisting of straight reaches (with no virtual barriers presented). Our effect sizes were reduced, as expected when analyzing smaller amounts of data, but the same effect direction was always observed. For the cortex-to-muscles analysis, the tuning ratios were 1.9, 2.8, 2.8*, 1.3 (dataset J, N, JA, NA; star indicates p<0.05). For the PMd-to-M1 analysis, the tuning ratios were 1.5 and 2.0* (JA, NA). Since these effect sizes were smaller than when using the full range of conditions, replications of this work using only straight reaches would likely require a larger number of neurons to reliably obtain statistical significance.

Controls for interpretation

There are two possible interpretations of the above results. First, the activity of different neurons may appropriately co-vary (e.g., one neuron’s rate increases while the other’s decreases, as in Fig. 2) in order to avoid prematurely causing movement. This would make the output-null dimensions a true population-level phenomenon, one that could not be observed directly by examining one neuron at a time^41–43. Alternatively, the output-null and output-potent dimensions might correspond to segregated populations of neurons. That is, output-potent dimensions might include only neurons that are quiet during preparation. We reiterate that our dimension identification did not use preparatory activity; it used only time points when EMG activity was already strong (Fig. 7b, only the “regression epoch” was used for dimension identification). However, it remains possible that some other response feature of the strongly preparatory-tuned neurons excluded them from output-potent dimensions. If true, use of the null space might not be a true ‘population level’ effect; it is already well known that some neurons have stronger preparatory tuning than others.

To distinguish these possibilities, we measured whether strongly preparatory-tuned neurons mainly contributed to output-null dimensions. To obtain this measurement, each neuron’s contribution to the output-null dimensions was multiplied by the strength of its preparatory tuning, then these values were added across neurons. This yields a measure of the total amount of preparatory tuning feeding into the output-null dimensions, before any canceling out. A similar number was produced for the output-potent dimensions. If our results were merely due to preparatory-tuned neurons mainly contributing to the output-null dimensions, we would expect the above tuning-strength value to be much greater for the output-null dimensions than for the output-potent dimensions. This was not the case. The ratio of these two values can be compared with our measured effect sizes (Fig. 7c). Across the six datasets, only ~4% of the measured effect was due to this kind of neuron segregation (blue bars). The remaining 96% of the observed effect is due to the responses of different neurons canceling out in output-potent dimensions (as in Fig. 2). This indicates a fundamentally population-level effect, involving coordination across many neurons such that a change in the activity of one neuron is countered by a change in the activity of another.

The above control tells us that neurons with strong preparatory tuning contribute almost equally to output-null and output-potent dimensions. However, we still do not know the following: do separate sets of neurons (perhaps projection vs. local neurons, or inhibitory vs. excitatory neurons) contribute to the output-null and output-potent dimensions? Or is the situation as in Figure 2, where the same neurons contribute to the output-null and output-potent dimensions, just with different weights? To test for segregated populations, for each unit we computed a “space preference index,” defined as how strongly that neuron contributed to the output-potent dimensions minus how strongly it contributed to the output-null dimensions, normalized by the sum of the two contributions. This index will be +1 if the neuron is solely involved in output-potent dimensions, −1 if it is solely involved in output-null dimensions, and intermediate if the neuron contributes to both sets of dimensions. If two distinct sets of neurons made up the output-null and output-potent dimensions, many neurons would have space preference indices near +1 or −1. In our data, however, the distribution of space preference indices over neurons (Fig. 7d and Supplementary Fig. 6, black histograms) is unimodal, peaks at approximately zero, and looks nearly identical to the distribution expected by chance (purple line; SDs shown as bars above distributions). Individual neurons that happened to contribute more to output-null or output-potent dimensions did not show any systematic qualitative differences in their responses (Fig. 7e–g). This indicates that output-null and output-potent dimensions are not made up of segregated groups of neurons. Instead, they are different linear combinations of the same neurons.

Discussion

While it was previously known that preparatory activity is attenuated along the PMd-M1-spinal cord pathway, it was not known how it is attenuated⁵. We tested a novel model, the output-null hypothesis. This model posits that, even if cortical activity is related straightforwardly to the activity of that area’s target, it is still relatively simple to control communication without resorting to strong nonlinearities or gates: activity which should not be read out by the target can be structured to change only in the source area’s output-null dimensions, avoiding the output-potent dimensions. While this may not be the only control mechanism at work, the following is clear: the structure of preparatory activity is such that it largely cancels out in the dimensions most likely to be relevant to the downstream target. Thus, exploitation of output-null dimensions appears to be at least part of the mechanism that helps to prevent premature contraction of the muscles during movement preparation, and to modulate communication between motor cortical areas.

The magnitude of the effect we measured cannot account fully for the observed reduction of preparatory activity between cortex and the muscles; EMG typically shows very little preparatory activity while the output-potent dimensions still show some. If the relationship between cortex and the muscles were perfectly linear – and if we identified the output-null and output-potent dimensions perfectly – then it would be mathematically necessary that cortical preparatory activity only occupy output-null dimensions. In the real data effects were not this strong, yet the output-null mechanism accounted for more than 75% of the reduction. This is consistent with a relationship between cortex and muscles that is not too far from linear in our task. While other mechanisms such as target gating may be important, use of output-null dimensions greatly reduces the burden on other possible mechanisms.

M1, of course, receives many inputs from areas other than PMd. Some of these other inputs are likely rich in preparatory activity too, but others may not be. It therefore might have been that preparatory signals from PMd were simply diluted out in M1. However, given the strong PMd-to-M1 projection, it made sense to ask whether there is an output-null effect. Our data suggest that there is. It is thus likely that this is one of the reasons that M1 has less preparatory activity than PMd.

The idea of output-potent dimensions helps make sense of several previously puzzling facts. For example, individual neurons⁴⁴, even corticomotor neurons^45–47, exhibit heterogeneous patterns of activity that often do not resemble muscle responses. Instead, the net input that the lower motor neurons and muscles receive is likely a weighted sum of these neurons’ responses^{34, 47, 48}. This diverse group of neurons could thus contribute to movement generation even though the individual responses do not resemble muscle activity. While individual neurons may exhibit confusing responses, the population-level/dynamical systems view may provide insight about how a circuit performs its key computations^{37, 38, 43}.

It has also been known for some time that preparatory activity in neurons does not correlate strongly with movement-epoch activity^25–28. This is inconsistent with the view of preparatory activity as a sub-threshold version of movement activity. However, in light of the output-null hypothesis, this finding makes sense; movement activity should be largely orthogonal to preparatory activity, and thus this poor correlation should be expected. Importantly, though, this orthogonality does not imply that preparatory activity is unrelated to the upcoming movement activity. As recently shown^{25, 38}, and as visible in Figure 3b, the preparatory state is correlated with the phase and amplitude of the subsequent neural trajectory during movement. This relationship is clear at the population level, even though it is hidden at the single-neuron level. This may allow M1 and PMd to “set up” the neural trajectory that will be needed to produce the correct movement^{25, 35, 37, 38}.

In the dynamical systems view³⁷, “setting up” unfolds as follows. When preparation begins, neural activity goes from a relatively less controlled baseline state to a relatively more controlled state¹⁴, remaining within the output-null dimensions throughout. This preparatory process appears to be necessary, even if the preparatory trajectory can differ under different circumstances⁴⁹: when preparation is absent^{14, 49}, disrupted¹⁷ (D. J. O’Shea, et al. Dynamics of primate premotor cortical recovery following optogenetic disruption of motor preparation. 2013 Neuroscience Meeting Planner, Society for Neuroscience), or incorrect⁴⁹, reaction time is slowed relative to a ‘correctly’ prepared reach. Moreover, trial-by-trial differences in hand speed¹⁶ and movement timing⁵⁰ depend on details of the preparatory state. After preparation, a presently unidentified mechanism enables active dynamics. These dynamics are simple and strongly rotational, and produce the movement-epoch neural trajectory³⁸. This portion of the neural trajectory travels through both output-null and output-potent dimensions, but the present results suggest that only output-potent dimensions drive the spinal cord and muscles.

Why, though, should neural activity change in output-null dimensions during movement? We speculate that to achieve the required neural trajectory in output-potent dimensions it may be necessary to make use of output-null dimensions as well. For example, to describe the pendulum in a grandfather clock it is not enough to know the position; when the pendulum is centered, it could be swinging either left or right. The oscillation of a second variable (velocity), out of phase with the position, is needed. If position forms an output-potent dimension (because it drives the clock), then velocity forms an output-null dimension – it is needed to produce the sine wave in position, but does not drive the clock directly. In the motor cortices, having output-potent dimensions available might make it possible to have simpler, smoother, less nonlinear dynamics, which would be consistent with the smooth tuning curves exhibited by neurons in these areas^{25, 38}. Somehow the cortex must learn how to attain preparatory activity patterns that initialize the dynamics while remaining in the output-null dimensions; how it does so is a topic for future research.

The present results do not rule out contributions by other mechanisms, such as nonlinearities in the spinal cord, in preventing preparatory activity from causing movement. However, the magnitude of the effects shown here does imply that the output-null mechanism likely forms a major component in producing this functionality. Nonlinearities are almost certainly present in the system, but given the present results they need not be the primary mechanism for controlling functional connectivity in the motor system. Even without relying on nonlinearities, it appears that these brain areas ‘know’ how to communicate or keep to themselves.

Methods

Subjects

Animal protocols were approved by the Stanford University Institutional Animal Care and Use Committee. Subjects were two adult male macaque monkeys (Macaca mulatta), J and N, trained to perform a delayed reach task on a fronto-parallel screen for juice reward. Use of two monkeys is standard practice in the field. In a sterile surgery, the monkeys were implanted with a head restraint and standard recording cylinder located over M1 and caudal PMd. After single-electrode recordings were completed, EMG was recorded, then two 96-electrode silicon arrays (Blackrock Microsystems, Salt Lake City, UT) were implanted in M1 and caudal PMd of both monkeys (estimated from local anatomical landmarks; Supplementary Fig. 7).

Task apparatus and design

Our basic methods have been described previously^{14, 28}. Both monkeys performed a variant of the center-out delayed-reach task, called the ‘maze’ task. This task required both straight reaches and reaches that curved around virtual barriers. Here, the maze task simply provides a way of evoking a variety of reaches (27 or 108 conditions depending on dataset), providing a large set of patterns of neural and muscle activity. Each monkey saw the same mazes every day and performed highly consistent movements during the entire data collection period (4–9.5 months; Supplementary Fig. 2).

For monkey J, each 108-condition dataset consisted of four sub-datasets of different mazes (27 conditions per sub-dataset). These sub-datasets were analyzed separately and the results averaged to obtain the reported values.

Neural recordings and EMG

Neural and EMG recordings were performed using previously described techniques^{14, 28}. Neural recordings were made in the range of medio-lateral locations that best produced shoulder or upper arm movements when microstimulation was delivered. Datasets J^{25, 33, 38} and N^{33, 38} have appeared in previous work, as have subsets of JA^{25, 38} and NA³⁸. For the four datasets (J, N, JA, NA), 197, 107, 192, or 118 units passed tuning criteria for the cortex-to-muscles analyses: 3 spikes/s during preparation and 5 spikes/s during movement, assessed as firing rate range across conditions. For the PMd-to-M1 analyses, 95 (120) neurons [JA (NA)] for PMd and 97 (103) neurons for M1 passed tuning criteria. Results were similar when no preparatory tuning criterion was used. All single-electrode recordings were from well-isolated single units, and the number of recordings was set before these analyses were formulated. For array recordings, spike sorting was performed offline using a custom software package (now available online as MKsort; https://github.com/ripple-neuro/mksort); both single units (JA: 47, NA: 22) and stable multi-unit isolations were included. The median number of trials per condition was 13, 11, 18, or 48 (J, N, JA, NA), dictated by how long stable recordings could be maintained. When array datasets were combined, data from the single best recording day was used for any given electrode.

For monkey J, percutaneous EMG recordings were made from trapezius, latissimus dorsi, pectoralis, triceps brachii, medial and lateral aspects of the biceps brachii, and anterior, medial and posterior aspects of the deltoid. For monkey N, EMG recordings were made from proximal, middle and distal aspects of the trapezius, latissimus dorsi, pectoralis, triceps brachii, medial and lateral aspects of the biceps, and anterior, medial and posterior aspects of the deltoid. Recordings from the triceps (both monkeys) and latissimus dorsi (monkey N) were modulated very weakly during the task and were therefore excluded from subsequent analyses.

Working hypothesis

We begin with three conditions, which must hold for our analysis to produce a positive result. Condition 1: activity of neurons in M1 and PMd causally affects muscle activity via indirect and/or direct connections, and the descending command signals include some spatiotemporal details of the muscle activity. Condition 2: before or within the spinal cord, descending signals converge and produce a net motor command which is approximately (perhaps very approximately) a linear combination of the individual-neuron signals. Condition 3: the relationship between neural and muscle activity is similar during movement preparation and actual movement (e.g., there is no dramatic gating in the impact of descending signals between these two epochs).

If these conditions hold, the below predictions follow; the final prediction is tested directly. First, we should be able to identify the linear combinations of neurons which influence the muscles (output-potent dimensions) via linear regression between neural data and EMG (since the relationship is quasi-linear). Second, not all changes in neural activity should influence the muscles, since most linear combinations of neurons do not affect the output-potent dimensions. Finally, in the absence of nonlinearities or time-varying gating mechanisms, any preparatory activity in M1 and PMd must remain in the output-null dimensions to avoid causing movement.

If any of the three conditions above were substantially violated, the analysis would have returned a negative result. If condition 1 were violated (if neural activity did not contain details of muscle activity), we would identify random dimensions as output-null and output-potent and would see similar levels of preparatory activity in both sets of dimensions. If conditions 2 or 3 were violated (nonlinearity or nonstationarity), there would be no reason for preparatory activity to avoid output-potent dimensions.

PCA and preprocessing of data

To compare neural activity with EMG, we constructed two data matrices: N and M. N contained neural data and was of size n by c*t_pv, with n the number of neurons, c the number of conditions, and t_pv the number of time points per condition during preparation (−100 to +400 ms from target onset) and movement (−50 to +600 ms from movement onset; Fig. 7b, Supplementary Fig. 8). Time points were spaced 10 ms apart. M contained EMG data and was of size m by c*t_v, with m the number of muscle recordings and t_v the number of time points during movement. Following standard procedures to prepare for Principal Component Analysis (PCA) each row of N and M was normalized by its range (maximum minus minimum across all times and conditions), and the row means were subtracted off. To accommodate the known lag between motor cortical activity and muscle activity, M was advanced by 50 ms relative to N^{34, 46} (the movement period for the muscle data therefore began at movement onset).

To obtain the low-dimensional model (equation 2), we performed PCA on N and M. PCA produces a new matrix, with (fewer) rows which are linear combinations of the original rows and which capture the maximum variance possible. That is:

$$\stackrel{\sim }{N}\approx PN,\stackrel{\sim }{M}\approx QM$$ (3)

where P and Q are coefficients matrices resulting from PCA performed on N and M. Since PCA is linear, the low-dimensional model still satisfies the original goal: muscle activity is specified as a linear combination of neurons’ activity. To demonstrate this formally, substituting and rearranging equations (2) and (3) yields M ≈ Q*W̃PN, where Q* is the pseudoinverse of Q. Since Q*W̃P simplifies to a matrix, M and N are related linearly in the low-dimensional model (modulo the residuals lost in PCA), as intended.

For a later step, M̃ must have half as many rows as Ñ. Therefore, the first k rows of P and k/2 rows of Q were retained. This value k was chosen as 6, discussed below.

Intuitively, PCA identifies natural patterns of covariation in the neural or EMG data. For EMG recordings, these patterns are traditionally referred to as “muscle synergies”⁵¹. The final result of preprocessing is well-behaved matrices M̃ and Ñ that can be used to identify putative output-null and output-potent dimensions.

When performing the output-null analysis from PMd to M1, the procedure differed in three ways from the above description. First, N contained only the PMd data and M contained the M1 data. Second, k, the dimensionality of N, was set to 14. Finally, no lag was used between the data in N and M (the epoch used was −50 to +600 ms for both).

Output-null analysis

In the computations below, we first identified the weighted sums of neurons (neural dimensions) that appear most likely to activate the muscles, i.e., output-potent dimensions. This was accomplished by finding dimensions in which neural activity during the movement period resembles EMG activity. We then determined whether, as predicted, neural activity during the delay period avoids these output-potent neural dimensions.

A formal explanation follows. We assumed the linear model from equation (1): M = WN. Since N is nearly rank-deficient, we reduced the dimensionality of the data as described above; we obtain equation (2): M̃ = W̃Ñ. Since all data is trial-averaged, no noise term is necessary. M̃ and Ñ are data matrices, so W̃ can be found directly (see next section). W̃ is our estimate of the mapping from neural to muscle activity. Critically, W̃ is found using movement data only.

The output-potent dimensions are then the row space of W̃ , denoted W̃_potent. The output-null dimensions are the null space of W̃ , denoted W̃_null. The row space and null space were found using Singular Value Decomposition. We then found the projections into the output-null and output-potent spaces:

$${\stackrel{\sim }{N}}_{\mathit{null}}={\stackrel{\sim }{W}}_{\mathit{null}}{\stackrel{\sim }{N}}_{\mathit{preparatory}}$$ (4)

$${\stackrel{\sim }{N}}_{\mathit{potent}}={\stackrel{\sim }{W}}_{\mathit{potent}}{\stackrel{\sim }{N}}_{\mathit{preparatory}}$$ (5)

Finally, we assessed how strongly ‘tuned’ neural activity was (how strongly it varied across time and condition) in the output-null and output-potent dimensions. This measure was:

$$\mathit{tuning}\mathit{ratio}=\frac{1}{\mathrm{\gamma }}·\frac{{\Vert {\stackrel{\sim }{N}}_{\mathit{null}}\Vert }_F^2}{{\Vert {\stackrel{\sim }{N}}_{\mathit{potent}}\Vert }_F^2}$$ (6)

in which ${\Vert •\Vert }_F^2$ indicates the squared Frobenius norm of a matrix (that is, each element of the matrix is squared, then all these values are summed). To make the Frobenius norm equivalent to variance, we subtracted off each row’s mean from Ñ_null and Ñ_potent before taking the norm. As a technical point, for the ratio to be meaningful the norms should be taken on matrices with the same number of elements; this is why the dimensionality of M̃ was chosen as k/2 during preprocessing.

A normalization term (1/γ), derived from the data, helped ensure that the initial dimensionality reduction step could not “build in” a result. The term was found to be important in case there were unequal numbers of (real, underlying) output-null and output-potent dimensions (Supplementary Fig. 3). γ was defined as:

$$\mathrm{\gamma }=\frac{{\Vert {\stackrel{\sim }{W}}_{\mathit{null}}{\stackrel{\sim }{N}}_{\mathit{movement}}\Vert }_F^2}{{\Vert {\stackrel{\sim }{W}}_{\mathit{potent}}{\stackrel{\sim }{N}}_{\mathit{movement}}\Vert }_F^2}$$

That is, γ was the main measure taken on the movement epoch data. This defines the “natural” scaling of the row space and null space in the data. 1/γ ranged from 1.17–1.74, and all results were in the same direction without this term (Supplementary Fig. 9, 10).

Importantly, the tuning ratio is expected to be greater than one if the central hypothesis, including its basic assumption of approximate linearity, is roughly correct. If the central hypothesis is not roughly correct, there is no expectation that the tuning ratio should be greater than one. This is underscored by a variety of simulations (see below).

Finding W̃

To avoid overfitting, we used regularized regression (Ridge regression) on the low-dimensional data (equation 2) to find W̃. Again, only peri-movement data were used in this regression. The regularization parameter was chosen via cross-validation. The regressions accounted for an average of 65% of the variance of M̃ using W̃Ñ. The three output-null dimensions, as expected, correlated less well with EMG activity (mean R²=0.18 for output-null vs. R²=0.60 for output-potent). These values were somewhat modest, both because the regression was performed on low-D data and because regularization was used.

Note that W contains both positive and negative coefficients. Some of the negative coefficients likely reflect real net inhibition on the muscles, either because the neurons themselves are inhibitory or because of intervening inhibitory interneurons. However, since the mean is subtracted off from each neuron’s firing rate before PCA, negative coefficients can simply mean that a neuron is modulated below its baseline. In addition, if a neuron a tends to anti-vary with a neuron p that has a net positive effect on the muscles, a will receive a negative coefficient – even though it does not itself have a direct effect on the muscles.

Statistics

For our main statistical measure, a Monte Carlo simulation was performed in which dimensions in the low-D neural space were chosen randomly as output-null or output-potent, then the tuning ratio for this random partitioning was measured. This was repeated 10,000 times to generate a distribution of random effect sizes. This process estimates the likelihood that a given effect size (i.e., an apparent avoidance of output-potent dimensions during the preparatory period) would occur by chance. The distribution of random effect sizes was then compared with the size of the measured effect. This class of statistical method generates a ‘null hypothesis’ distribution but not error bars, which is why error bars are not shown in Figure 4c or 6c.

For display purposes only (Fig. 4d and 6d), a separate bootstrap statistic was used. We asked whether a small number of outlier conditions could somehow be driving our effects. We therefore resampled conditions at the final step (after PCA and space identification), and re-computed our measure.

Trial-by-trial output-null analysis

For this analysis, instead of using trial-averaged data, we preserved the data for each trial. Thus N and M were wider than in the main analysis, by a factor equal to the number of trials per condition. We used Factor Analysis instead of PCA to reduce the neural dimensionality, since PCA is inappropriate for single-trial data⁵². Larger bins of 60 ms were required; the time points used were −120 to +360 ms from target onset and 0 to +660 from movement onset. Since simultaneous EMG data were not available, and movements were highly consistent, we repeated the mean EMG as a proxy for trial-by-trial EMG in the regression step. This analysis required large-scale simultaneous neural recordings, and therefore only the array datasets (JA, NA) were used. Because Factor Analysis requires a large amount of data per dimension estimated, this analysis could only be performed for cortex-to-muscles.

Simulation details

We created simulated neural and EMG data containing varying, known levels of output-null structure. We first produced random vectors with the desired structure in low-dimensional space. One set of vectors was chosen for preparation (one per condition), then another set of vectors was chosen for movement (three vectors per condition, to use as waypoints for the time-varying movement activity). All dimensions of these data were randomly projected out as simulated “neurons”; output-potent dimensions (only) were randomly projected out as simulated “muscles”. Both neurons and muscles then received a baseline offset, and the resulting firing rates were cubic spline interpolated and rectified to form a PSTH-like timecourse resembling the real data.

To match the real data’s noise level after smoothing, noise was added from a second-order gamma function with 11 trials per neuron per condition, or fourth-order gamma function with 11 trials per muscle per condition. As in the real data, 27 conditions were simulated. Simulated muscle recordings were delayed by 50 ms relative to simulated neurons. When nonlinearities were required (Fig. 5f–h, Supplementary Fig. 3) the mean firing rates for neurons and muscles were chosen to be near zero, causing floor effects, and a weakly saturating nonlinearity was simulated by raising neural firing rates and muscle responses to the power of 0.8. Simulations were run 50 times for each parameter set.

The simulated data also allowed us to assess the impact of the 1/γ term. This normalization made the analysis both more precise and more accurate (Supplementary Fig. 3), especially when simulating unequal numbers of output-null and output-potent dimensions.

In addition, we asked whether standard models of motor cortex might incidentally yield results similar to what we found in the data. We therefore performed the output-null analysis on data generated from a “velocity-tuned” model. This model produced simulated neurons that were tuned for hand velocity and speed during movement^53–55, and endpoint during preparation (this model has been used previously^{25, 38}). This model implicitly assumes a gating mechanism, since there is an unexplained transition between preparatory and movement activity. Activity was structured to have preparatory and movement tuning with a low correlation, as in the real data. Firing rate distributions for the simulated neurons were based on real datasets. When the output-null analysis was performed on this model, it did not produce consistent positive results. This confirms that our effects are not simply an incidental consequence of velocity tuning.

Brief proof that changes in tuning between preparation and movement are likely, but neither necessary nor sufficient, to demonstrate use of output-null dimensions

Confining preparatory activity to output-null dimensions tends to produce neurons with ‘mismatched’ tuning between preparation and movement (see Fig. 2). However, mismatched tuning is neither necessary nor sufficient to indicate that an output-null mechanism is at work; this is why our main analysis was needed.

A counterexample to necessity follows. Imagine that output-null dimensions had ‘matched’ tuning and contained most of the total variance. Most neurons would be dominated by the high-variance output-null activity. The correlation between preparatory and movement tuning would therefore remain large.

Regarding sufficiency, consider Fig. 3b. Imagine that the neural data spanned only these two dimensions, and that the variance ellipse for preparation was round (i.e., the red ellipse was a circle). The rotational structure during movement indicates that there is still mismatched tuning, since after 180° of rotation the tuning has inverted. But, if preparatory activity equally spans both dimensions (and there are only two dimensions), then an output-null mechanism cannot be at work. Thus, mismatched tuning is insufficient to indicate an output-null mechanism.

Supplementary Material

1. Supplementary Table 1.

Output-null effect of each brain area separately to the muscles. Significant values starred. Most half-datasets did not have enough statistical power to reach significance, but 7/8 exhibited the expected greater-than-unity tuning ratio. It is not clear which area by itself “should” exhibit stronger effects, since preparatory activity is presumably reduced stepwise from PMd to M1 to the muscles (PMd has stronger preparatory activity, and M1 is more strongly connected to the muscles⁵⁶). In the data, there may be a trend for effects in PMd to be stronger than in M1, though we did not have the statistical power to resolve any such difference. One sub-dataset, M1 from dataset J, exhibits a vanishing and non-significant wrong-direction effect.

10. Supplementary Figure 1.

Tuning is mismatched between the preparatory and movement epochs. Each panel represents firing rate data from one dataset. For each neuron, firing rates were first averaged over trials, then conditions were sorted based on the neuron’s firing rate at movement onset. The reddest trace shows the average across neurons for each neuron’s “most preferred” condition. The greenest trace shows the average across neurons for each neuron’s “least preferred” condition; the other two traces represent the 33rd and 67th percentile conditions. Very little preparatory tuning remains after this procedure, indicating that tuning is mismatched between the preparatory and movement epochs. Each neuron’s response was normalized by its range before averaging. Target, target onset; Move, movement onset. Scale bar indicates 200 ms.

11. Supplementary Figure 2.

Behavioral consistency within and across days. Single-electrode neural data were collected over many days, and it is important that behavior was similar over time. In particular, since EMG data were recorded late during single-electrode data collection, and array recordings were performed after that, this figure compares behavior during neural data collection and EMG data collection. (a) All reaches for a particular maze for dataset J (single electrode recordings for monkey J). Blue shows reaches made during one neuron worth of neural recording, red during one muscle worth of EMG recording. Note that some blue traces are hidden by the red traces. The same EMG session is shown as in Figure 1. The neural recording day was chosen to be the most distant possible from the EMG day, 4.5 months apart. Behavior for this example maze was slightly more different between days than typical. The scale bar is 40 mm. (b) The speed profile for each reach, aligned to movement onset (black tick). Colors as in (a). Scale bars are 100 ms and 0.5 m/s. (c–d) Same for dataset N (single electrode recordings for monkey N). The days were again chosen to be maximally far apart, ~3 months. (e–f) Same for dataset JA (array recordings for monkey J). Days were 9.5 months apart. (g–h) Same for dataset NA (array recordings for monkey N). Days were 1.2 months apart.

2. Supplementary Figure 3.

Output-null method on additional simulated data. Plots are as in Figure 5. These plots illustrate algorithm performance when the simulated data contains unequal numbers of output-null and output-potent dimensions, and how the analysis performs with (right) and without (left) the 1/γ term. (a–b) Four output-potent dimensions and two output-null dimensions were present in the simulated data. The analysis assumed three and three. Though false positives were present without the 1/γ term (a), using the term prevented false positives (b). (c–d) Four output-null dimensions and three output-potent dimensions were present in the simulated data, but the analysis assumed three and three. Again, false positives are absent, and the 1/γ term helps to reduce underestimation of the effect size. (e–f) Three output-potent and six output-null dimensions were present in the simulated data. The analysis assumed three and three. We note that this situation, of having only a few output-potent dimensions and many output-null dimensions, is likely to be the true one. Here, again, the analysis produces reasonable results with a mild underestimation of the effect size.

3. Supplementary Figure 4.

Output-null results from cortex to muscles as a function of time. This figure is similar to Figure 4d, but shows all datasets and all time points. We measured the tuning depth at each time point in the putative output-null dimensions (gray) and output-potent dimensions (black). As predicted, in all four datasets, the tuning depth during preparation was greater in the output-null dimensions than in the output-potent dimensions. This confirms that during movement preparation, the pattern of activity preferentially avoids the dimensions that cause muscle activity. Importantly, however, the effects shown here are smaller than the effects shown in Figure 4c because the present analysis cannot factor in the shift in the across-condition mean that occurs at target onset. Note that here the variance across conditions is shown, which effectively squares the ratio of how strong movement-epoch tuning appears relative to preparatory tuning; preparatory activity thus looks weaker than it would in a PSTH. Flanking traces indicate s.e.m.s computed via resampling of conditions.

4. Supplementary Figure 5.

Output-null results from PMd to M1 as a function of time. These plots are similar to Supplementary Figure 4, but show the output-null results for PMd to M1 instead of both areas to the muscles. Again, note that this analysis underestimates the true effect size because it cannot factor in the shift in the across-condition mean that occurs at target onset, which is a major source of the effect size especially for monkey N.

5. Supplementary Figure 6.

Analysis of neurons’ projections into the output-null and output-potent spaces. For each neuron, a space preference index was computed, which is +1 if the neuron contributes solely to output-potent dimensions and −1 if the neuron contributes solely to output-null dimensions. If there were two populations of neurons, where one population contributed mostly to output-null dimensions and the other contributed mostly to output-potent dimensions, we would expect a distribution with a peak near each extremum. The histogram of the values from the data are plotted in black, one panel per dataset. The null distribution (computed from random vectors in the same-dimensional space) is plotted in purple. One standard deviation above and below zero is plotted as horizontal bars above, with dots indicating the means. In each dataset, the empirical distribution is nearly identical to the random distribution. This indicates that there are not two separate populations of neurons driving the differences between the output-null and output-potent dimensions.

6. Supplementary Figure 7.

Recording locations. Left, monkey J; right, monkey N. Top panels show outlines of the entry points where single-electrode recordings were made. Note that many recordings were made deep in the central sulcus, underneath the outlined areas. Bottom panels show the locations of the electrode arrays. For scale in the bottom panels, the arrays were square, 4.2 mm on a side.

7. Supplementary Figure 8.

Muscle activity over time relative to key epochs. Plots as in Figure 7b, but for each monkey (J, left; N, right). Each muscle’s activity was first normalized by its range (over all times and conditions). The heavy trace indicates the mean of these values across all muscles at each time point. This therefore gives a general idea of how average activity changed over time (muscle activity rose more strongly than it fell). To obtain an estimate of tuning depth with time, the standard deviation was taken across conditions (different reach shapes) at each time point for each normalized muscle. These values were then averaged across muscles at each time point. The width of the thin traces around the mean show this value, at one standard deviation. Muscle activity was only used in our main analysis to identify output-potent dimensions and output-null dimensions. To do so, we only used activity from the peri-movement epoch (red bar). Specifically, we used 0 to +650 ms from movement onset. Note that the muscle is already responding strongly by this time point. Effect size was computed using only preparatory data (black bar).

8. Supplementary Figure 9.

Output-null results from cortex to muscles as a function of time, without the 1/γ term. These plots are similar to the plots in Supplementary Figure 4, but the tuning in each space has not been normalized by the movement-epoch tuning. The 1/γ term was important in simulations to produce accurate results, and we therefore believe that Supplementary Figure 4 represents the most quantitatively interpretable effect sizes. However, we wished to show that the central effect was not somehow created by normalization. The current analysis demonstrates that the central effect survives without the 1/γ term. Again, note that this analysis underestimates the true effect size because it cannot factor in the shift in the across-condition mean that occurs at target onset. This limitation appears to be particularly important in the monkey N dataset.

9. Supplementary Figure 10.

Output-null results from PMd to M1 as a function of time, without the 1/γ term. These plots are similar to Supplementary Figure 5, but as in Supplementary Figure 9, the values are not normalized by the movement-epoch tuning. Again, note that this analysis underestimates the true effect size because it cannot factor in the shift in the across-condition mean that occurs at target onset, which is a major source of the effect size in monkey N.