Abstract
Performing micromanipulation and delicate operations in submillimeter workspaces is difficult because of destabilizing tremor and imprecise targeting. Accurate micromanipulation is especially important for microsurgical procedures, such as vitreoretinal surgery, to maximize successful outcomes and minimize collateral damage. Robotic aid combined with filtering techniques that suppress tremor frequency bands increases performance; however, if knowledge of the operator’s goals is available, virtual fixtures have been shown to further improve performance. In this paper, we derive a virtual fixture framework for active handheld micromanipulators that is based on high-bandwidth position measurements rather than forces applied to a robot handle. For applicability in surgical environments, the fixtures are generated in real-time from microscope video during the procedure. Additionally, we develop motion scaling behavior around virtual fixtures as a simple and direct extension to the proposed framework. We demonstrate that virtual fixtures significantly outperform tremor cancellation algorithms on a set of synthetic tracing tasks (p < 0.05). In more medically relevant experiments of vein tracing and membrane peeling in eye phantoms, virtual fixtures can significantly reduce both positioning error and forces applied to tissue (p < 0.05).
Index Terms: Micro/nano robots, dexterous manipulation, motion control, medical robots and systems, vision-based control
I. Introduction
In biology and microsurgery, proper manipulation of extremely small anatomical features often requires precision and dexterity that exceeds the capability of an unaided operator. Physiological tremor, or high-frequency involuntary hand movements with amplitudes of over 100 μm [1], is a large contributing factor to the difficulty of micromanipulation. Furthermore, lower frequency drift in gross hand positioning over time, caused by poor depth perception through the microscope and the relatively low bandwidth of the eye-hand feedback loop, reduces pointing accuracy [2]. Many robotic platforms have been introduced to improve manipulation during surgery, especially vitreoretinal microsurgery as extraordinarily precise micromanipulations are required to avoid sight-damaging trauma. Tiny structures commonly manipulated in the eye include veins less than 100 μm in diameter and membranes only several microns thick.
To address micromanipulation challenges in retinal surgical procedures, a variety of assistive robots have been proposed. Specific instruments such as the intraocular tool developed by Ikuta et al. [3] combine an actively-jointed forceps with optical fiber optic illumination. Master/slave robots developed for eye surgery include the JPL Robot Assisted MicroSurgery (RAMS) system [4], the Japanese occular robot of Ueta et al. [5], and the multi-arm stabilizing micromanipulator of Wei et al. [6]. Retinal surgery with the da Vinci master/slave robot has been investigated [7] and led to the design of a Hexapod micropositioner accessory for the da Vinci end-effector [8]. The Johns Hopkins SteadyHand Eye-Robot [9] cooperatively shares control with an operator by application of force to the robot arm holding the instrument. A unique MEMS pneumatic actuator called the Microhand allows grasping and manipulation of the retina [10] while the Microbots of Dogangil et al. aim to deliver drugs directly to the retinal vasculature via magnetic navigation [11].
Another class of micromanipulators for retinal surgery is active handheld micromanipulators, best exemplified by the Micron device [2] depicted in Fig. 1. Micron incorporates motors between the handle and the tip, effectively creating a fully active handheld tool in which the end-effector can actuate semi-independently of the hand motion within a limited range of motion (1×1×0.5 mm). Recently we proposed a virtual fixture framework for handheld micromanipulators that integrates both tremor compensation and motion scaling [12]. This paper expands upon that work by formulating a more general spline representation for virtual fixtures, integration of vision-based control with dense stereo vision, a new feedforward controller derived from [13], and extensions from planar surfaces to naturally curved surfaces. Additional evaluation, including a vein-tracing to mimic canulation and an extension of the membrane peeling experiment of [14], are explored. Furthermore, unlike previous work that presented results from novices [12–14], all results presented in this paper are completely new and performed by experienced surgeons.
Fig. 1.

Micron micromanipulator, shown without housing to illustrate the piezoelectric motors between the handle and tip, which enable the tip to actuate independently of the handle (or hand) motion.
Our contributions are threefold: (1) the derivation of a virtual fixture framework based on position, rather than force, control for handheld micromanipulators, (2) the integration of visual information to generate fixtures in real-time that enforce task-specific behaviors for individual surgical procedures, and (3) the evaluation of the virtual fixture framework in both synthetic tracing tasks and realistic retinal procedures. Section II covers background material and introduces Micron and the system setup. Section III presents the derivation of position-based virtual fixtures for Micron. In Section IV, we test our system with medically relevant retinal experiments: synthetic task tracing, vein cannulation tracing, and membrane peeling. Finally, we conclude in Section V with a discussion of results and directions for future work.
II. Background
In general, robotic aids for surgical micromanipulation can be grouped into three categories: tremor compensation, motion scaling, and virtual fixtures. Tremor compensation is a key component of many surgical robots [2], [4], [5], [9] and aims to suppress frequency bands dominated by tremor in order to eliminate unwanted high-frequency motion while preserving the operator’s lower-frequency intended movements. In master/slave robots, tremor compensation can be achieved by inserting various filters between the hand motion and the drive mechanism. Cooperative robots such as SteadyHand accomplish this mechanically by utilizing the inherent stiffness of the robot arm to damp high-frequency movement. Motion scaling reduces all movements so the tip only moves a set fraction of the hand movement. Scaling behavior is often used in master/slave robots [4], [5], and recent developments in handheld micromanipulation use a low-pass shelving filter [2] that acts as relative motion scaling.
Virtual fixtures, in contrast to tremor compensation or motion scaling behaviors that operate in the general case, instead improve specific motions or tasks [15]. Proposed originally by Rosenberg as a method to overlay abstract sensory information onto a force-reflecting master workspace to address latency in teleoperation [16], virtual fixtures were also found to reduce cognitive load and increase performance. In surgical operations, virtual fixtures have been used to constrain robot end-effectors to pre-defined areas, orientations, or behaviors for increased safety [17–21]. Integrating vision-based control with virtual fixtures [15] allows for more complex virtual fixtures constructed from anatomy [22], [23]. Most relevant to retinal surgery, Dewan et al. proposed virtual fixtures generated from dense stereo to guide the tip and orientation of the SteadyHand robot along an eye phantom retina [24] while Lin et al. employed virtual fixtures in a simulated retinal cannulation task [25].
In most formulations of virtual fixtures, the user manipulates a robot arm that is attached to the instrument directly or remotely via teleoperation. Forces on the robot arm are shaped and transformed to velocity commands at the instrument tip via the active virtual fixture. If the robot is non-backdriveable, strict adherence to the virtual fixture can be enforced by ensuring that velocity components are zero in directions that move the tip away from the fixture. Unlike most virtual-fixture-enabled robots, Micron is not manipulated by the operator through the application of forces to a joystick control or robot arm. It is a fully handheld device that purely senses position; thus, the input to the virtual fixtures must be handle (or hand) motion. This fundamental difference, the use of position instead of force as the control input, necessitates the development of a unique formulation of virtual fixtures specifically designed for handheld micromanipulators.
A. Micron Manipulator
The robotic system used in this research is Micron, a previously reported 3 DOF micromanipulator [2] that has motors positioned between the handle and the instrument tip as depicted in Fig. 1. The motors are three Thunder® piezoelectric actuators arranged in a radially symmetric pattern, allowing for tip movement independent of hand motion within a region of approximately 1×1×0.5-mm, centered on the handle. The operator uses Micron under a surgical microscope (Zeiss OPMI 1). A 27 gauge hypodermic needle (418 μm outer diameter) is attached to Micron and a 127 μm nitinol wire is inserted into the needle to serve as a very fine instrument tip. The entire setup can be seen in Fig. 2.
Fig. 2.
System setup with (a) Micron, (b) ASAP position sensors, (c) surgical microscope, (d) image injection system, (e) stereo cameras, and (f) phantom half eyeball.
Low-latency, high-bandwidth positioning information is obtained from custom optical tracking hardware named ASAP [26]. Two Position Sensitive Detectors (PSDs) act as analog cameras, tracking three LEDs on the actuated shaft of the instrument and one LED on the Micron handle. By frequency-modulating at a very high rate, the 3D positions of the LEDs can be triangulated accurately, yielding 6-DOF pose information for the Micron tip and handle. ASAP has a workspace of 4 cm3 and measures poses at a rate of 2 kHz with errors of less than 10 μm RMS. Such high-bandwidth and accurate positioning information allows Micron to measure and control tip motion very precisely. A block diagram of the vision and control systems is shown in Fig. 3
Fig. 3.
Block diagram of the control and vision system. The vision system registers the cameras to ASAP and generates virtual fixture geometry from the anatomy. The control system includes feedback and feedforward paths for more precise control of the instrument tip. The virtual fixture controller uses the filtered hand motion to enforce the subspace constraints of the fixtures.
B. Control System and Notation
The tip of Micron in 3D space is defined as PT ∈ ℝ3. As Micron actuates, the tip will move independently of the hand (or handle) motion, so it is important to define a measure of how much the tip has moved. We define the null position as the 3D tip position PN ∈ ℝ3 under the assumption that Micron is off; i.e., PN exactly reflects the hand motion. One can think of PN as being mechanically tied to the handle; thus PT = PN unless Micron actuates the tip. Fig. 4 graphically depicts the difference between the null position PN and the actual tip position PT. With high-rate, low-bandwidth ASAP sensors, Micron performs position-based control using closed-loop feedback with approximated linear inverse kinematics to bring the tip position PT coincident with the goal PG. The ASAP controller C(s) in Fig. 3 uses PID for feedback control.
Fig. 4.

Example of handheld micromanipulation with position-based virtual fixtures, which drives the tip position PT to a goal position PG on the virtual fixture V. The goal position is calculated by the orthogonal projection Mo of the null position PN. The null position is the location of the tip position if the actuators were turned off. It is a natural selection for choosing the goal position because it is nominally the center of the actuator range of motion and exactly reflects the hand motion. Note: not to scale.
C. Feedforward Tremor Compensation
When a 3D goal PG is specified in handheld operation, typical tremor disturbance in the hand motion PN is 90% rejected by a 2nd order low-pass Butterworth filter F(s) with a corner frequency of 2 Hz. However, the remaining 10% of tremor represents 10–20 μm deviations of the tip position from the goal, making it the largest contributing factor in the error reported for hard virtual fixtures [12]. Analysis revealed that a 3-ms latency in the Micron manipulator plant G(s) is largely responsible for tip positioning error [13]. We denote T as the latency between when the ASAP controller C(s) sends a command to the Micron manipulator G(s) and when the effect is seen in the tip position. During this time, tremor at the handle is moving the null position with a velocity ṖN, and to a first-order approximation, the latency in actuation introduces error PΔ at the tip position that accumulates over time T:
| (1) |
To address this latency, a feedforward control path was designed to anticipate, estimate, and compensate for the error PΔ before it is seen by the feedback loop. As shown in Fig. 3, a constant-acceleration Kalman filter K(s) is run at 2 kHz to optimally estimate the position, velocity, and acceleration states of the tip and handle. The velocity of the handle ṖN, which represents tremor velocity, is used by the tremor prediction module P(s) to estimate tip error PΔ caused by the T delay in actuation G(s). Although P(s) could employ a nonlinear algorithm to predict ṖN(t) such as the double adaptive bandlimited multiple Fourier linear combiner [27], we found a simple predict-current-velocity at time t works well, e.g., ṖN(t + k) = ṖN(t) ∀ k ∈ [0, T]. Once P(s) integrates the velocity, the predicted error PΔ is used as a feedforward term to adjust the goal position PG to form the latency-compensated goal position . Combined with the existing feedback control strategy, an additional 50% reduction in error is seen, for a total tremor rejection rate of 95%.
D. Vision-System
Vision-based control of the manipulator is necessary because the anatomy of interest is localized via intraoperative imagery. Stereo cameras (PointGrey Flea2) attached to the microscope view the same workspace as the operator and capture up to 1024×768 resolution video at up to 50 Hz. The cameras track both the tip of the instrument and anatomical targets. However, traditional image-based visual servoing techniques [28] operating at the low camera rates cannot provide the high bandwidth and low latencies needed for active control of handheld micromanipulators. Instead, the control loop must use the much faster 2 kHz ASAP positioning system. Thus, virtual fixtures are generated stereo images, transferred to the ASAP coordinate frame, and the resulting geometry is passed to the virtual fixture controller V(s) that runs at 2 kHz in the Micron control system. The registration between the ASAP measurement system and the stereo cameras is maintained using a recursive least squares calibration procedure between the sensed tip position.
III. Position-Based Virtual Fixtures
Represented as a subspace defined in 3D Euclidean space by the stereo vision cameras, the virtual fixture V must constrain the tip position PT of Micron, using only the hand motion of the operator PN to guide and position the instrument tip on the virtual fixture. In the case of hard virtual fixtures, the tip of Micron should always lie on the subspace representing the fixture; in the case of soft virtual fixtures, the error between the hand motion and the virtual fixture should be scaled. In all cases, a tremor filter F(s) smoothes the tip movement. The remainder of this section devises virtual fixtures that modify the behavior of the tip PT while using the handle motion PN as the indicator of operator intention.
A. Point Virtual Fixture
We begin the formulation of virtual fixtures for Micron by considering the simplest fixture possible: fixing Micron’s tip to a single goal point PG ∈ ℝ3 in space. While the point virtual fixture is active, the control system should enforce:
| (2) |
regardless of where or how the operator moves the handle (within Micron’s range of motion). The control from Sec. II.B and II.C drives and maintains the tip at the goal position. In response to shifting anatomy, moving the virtual fixture is possible by setting a new goal point PG. To avoid high-frequency oscillations, large changes in PG should be smoothed with either filtration (lowpass, Kalman, etc.) or trajectory planning.
B. Higher-Order Virtual Fixtures
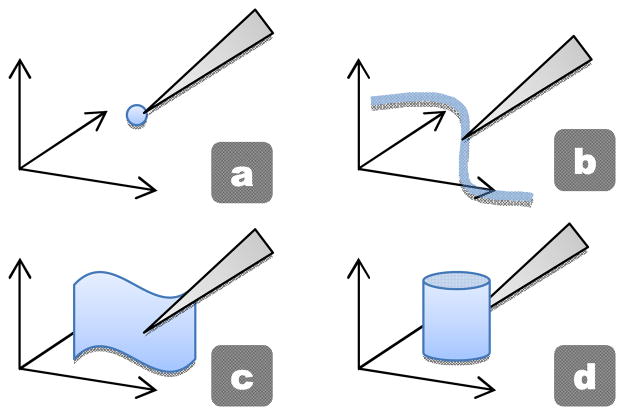
Higher-order subspaces can be built on top of the point virtual fixture to obtain more interesting behaviors. Each additional level adds a degree of freedom to the tip motion. For instance, a line virtual fixture allows the tip to freely travel along a line while restricting motion orthogonal to the line. Likewise, we can define the hierarchy of virtual fixtures as seen in Fig. 5: point, curve, surface, and volume. It is worth considering medical relevance for each type virtual fixture:
Fig. 5.
Virtual fixtures constraining the tip to a subspace with increasing degrees of freedom: (a) point, (b) curve, (c) surface, and (d) volume.
Point (0 DOF): Steadying cannula during injection
Curve (1 DOF): Following path for laser ablation, guiding suture/needle along a blood vessel
Surface (2 DOF): Maintaining a constant standoff distance, navigating in narrow crevices
Volume (3 DOF): Restricting the tip to prevent tissue contact outside of designated “safe” volumes
We assert that all virtual fixtures can be implemented easily with just the point virtual fixture. The key to implementing higher-order fixtures with point fixtures is selecting the correct point on the higher-order virtual fixture. Geometrically, it is most intuitive to select a point on the virtual fixture as close as possible to the operator’s intended position. Thus for an arbitrary virtual fixture V, the nearest goal position PG is the orthogonal projection of PN onto the virtual fixture V. We define this orthogonal projection by the mapping Mo: ℝ3 → ℝ3 that selects the goal point PG as the closest point from the null position PN to the virtual fixture V:
| (3) |
For simple geometric structures (lines, planes, circles, cylinders, etc.), analytic solutions for Mo exist. For more complex shapes, numerical solutions are available [30].
C. Tremor Suppression
In point virtual fixtures, all degrees of freedom are proscribed by the fixture, eliminating unwanted tremor. However, for higher-order virtual fixtures, tremor parallel to the subspace is not affected by the orthogonal projection Mo. A suppression filter F between the 3D null position PN and the orthogonal projection Mo reduces tremor in the tip position:
| (4) |
Furthermore, virtual fixtures generated by noisy video should be filtered as well to reduce high-frequency motions.
D. Motion Scaling
So far we have described hard fixtures where the tip position cannot deviate from the constraint imposed by the virtual fixture. However, it is also possible to derive soft virtual fixtures that share control between the virtual fixture and the operator. An additional parameter λ ∈ [0,1] defines how much the operator can override the virtual fixture. In our formulation, λ represents the proportion of the hand motion PN vs. the goal point PG that Micron uses to actuate the tip:
| (5) |
In essence, λ functions as a weighted average of the goal and null position. λ = 0 corresponds to a hard virtual fixture where the operator can only control where on the virtual fixture the tip moves, while λ = 1 disables virtual fixtures entirely and leaves the operator in complete control (see Fig. 6). For values of λ between 0 and 1, (6) can be directly manipulated into a motion scaling paradigm:
| (6) |
| (7) |
| (8) |
Fig. 6.
Effect of motion scaling parameter λ on the tip position. (a) Hard virtual fixture (λ = 0). (b) Soft virtual fixture with λ = 1/2; control is shared 50% between virtual fixture and hand motion. (c) Fixtures off (λ = 1).
By introducing the error e as the difference between the null position PN controlled by the operator and the goal point PG calculated by the virtual fixture, it is clear the parameter λ directly represents the motion scaling factor. Thus, we can see that sharing control between the virtual fixture and the operator yields motion-scaling behavior, e.g., Fig. 6b.
E. Generalizable Spline Virtual Fixtures
When applying the position-based virtual fixture framework to surgical environments, simple geometric shapes such as those used in our previous work [12] will not suffice; a more general fixture representation is necessary to model the complex nature of anatomical structures. A suitable representation is one of piecewise curves, or splines, which have the beneficial property of representing continuous curves and surfaces with low dimensionality and have been used with virtual fixtures [22], [24]. Additionally, the orthogonal mapping Mo can be calculated numerically for splines [29]. Fitting splines can be done directly in image space [30], or after a point-cloud representation of the anatomy of interest has been extracted. Because virtual fixtures must be available in the 3D ASAP coordinate system, the latter approach is taken. Although a variety of spline representations may be used, we use basis-splines (B-splines) to describe general anatomy because of their versatile yet simple representation, with widespread support for fitting and evaluation. Surfaces such as the retina can be represented by a B-spline surface. Encoding a notion of “side” to the surface allows for volumetric fixtures, such as forbidding the tip to pass through the B-spline surface virtual fixture representing the retina.
F. Generalized Position-Based Virtual Fixtures
To summarize the framework that incorporates virtual fixtures, tremor suppression, and motion scaling for handheld micromanipulators based on position control, the generalized control law is:
| (9) |
| (10) |
| (11) |
First, (9) selects the goal point on the virtual fixture closest to the tremor suppressed null position. Eq. (10) then calculates the error between what the virtual fixture and where the operator is currently pointing. Finally, (11) drives the tip to either the virtual fixture or, if λ is non-zero, scales the error to achieve motion scaling about the fixture.
G. Visual Cues to Maintain Eye-Hand Coordination
A final consideration in our formulation of position-based virtual fixtures is one of practical implementation. The input to virtual fixtures is the null position, which is measured by the ASAP sensors but is unseen by the operator. Hard virtual fixtures force the tip to the fixture regardless of any hand movement, removing all error and effectively disrupting the eye-hand coordination feedback loop. With the eye-hand feedback loop broken, the operator will unknowingly drift away from the virtual fixture until the virtual fixture is no longer within Micron’s range of motion. At this point, active control becomes impossible because the motors have saturated. Thus it is imperative to provide a surrogate sense of error to restore eye-hand coordination.
In order to prevent this unbounded drifting behavior, we display visual cues that indicate the 3D location of the unseen null position. As shown in Fig. 7, we choose visual cues in the form of two circles: a green one to show the goal location and a blue one to show the null position, which reflects the actual hand movements. The distance between the circle centers represents the error Micron is currently eliminating. Z error is displayed by varying the radius of the null position circle, e.g., a growing radius represents upward drift. The operator is instructed to keep the two circles roughly coincident to avoid saturation of the actuators.
Fig. 7.

Micron enforcing a point hard virtual fixture with visual cues: green represents the goal, blue represents the null position. (a) Nearly coincident circles is desirable, indicating Micron is near the center of the range of motion. (b) The position and size of the blue circle indicates drift. Here, the operator has drifted left, down, and upwards in the X, Y, and Z directions, respectively. If Micron was turned off, the tip would snap to the blue circle.
IV. Evaluation
In order to assess the performance of the proposed virtual fixture framework in surgically relevant situations, three experiments were performed in phantoms by surgeons under a board-approved protocol: basic synthetic tracing, vein cannulation tracing, and retinal membrane peeling. Whereas previously reported results involved only novices [2], [12], all experiments presented here involved trained surgeons. Statistical significance was assessed via two-tailed t-test.
A. Synthetic Tracing above Rubber Slide
Similar to [2], we performed simple synthetic tracing tasks above a rubber slide to assess general micromanipulation performance. As shown in Fig. 8, the rubber slide had a laser-etched target consisting of four crosses arranged as the corners of a 600-μm square, with a circle of 500-μm diameter in the middle. Three tasks were performed at 29X magnification (see Fig. 8):
Fig. 8.
(a) Laser etched target onto rubber surface (b) Generating a 3D circle virtual fixture from the tracked target (c) White-painted, tapered tip of Micron.
Hold Still: Hold the tip of the instrument 500 μm above a fiducial on a plane for 30 s. A point fixture located above the top right cross was used.
Circle Tracing: Trace a circle with a 500 μm offset from rubber surface two times. A 3D circle fixture derived from the tracked rubber target was used.
Move and Hold: Move between the four corners of a square sequentially, pausing at each corner. Four plane segments oriented vertically and connecting each of the four corners were used, forming a compound box fixture.
To construct the virtual fixtures for each case, hierarchical template matching is used to locate the target. Once the target is located in both images, the center of the target can be backprojected into 3D using the camera registration. Individual virtual fixtures (point, circle, box) are derived from the 3D location of the target and the relative distances of the components. All tracking and virtual fixture generation happens at 50 Hz with a custom resolution of 504×324.
For each task, four different scenarios were performed by three trained surgeons in random order:
Unaided: Micron was inactive (turned off).
Aided with Shelving Filter: Micron implemented a tremor-suppressing shelving filter [2].
Aided with Soft Virtual Fixtures: Micron implemented virtual fixtures with the motion scaling factor λ = 1/5, so errors were reduced by 5X.
Aided with Hard Virtual Fixtures: Micron implemented virtual fixtures but no motion scaling (λ = 0).
Each set of synthetic experiments on the rubber slide was performed by three surgeons at least once, for a total of seven sets and 84 trials. Visual cues were displayed on a 3D monitor. Error was measured at 2 kHz as the Euclidean distance between the tip position sensed by the ASAP optical trackers and the closest point on the virtual fixture.
B. Vein Cannulation Tracing in Eyeball Phantom
To evaluate the virtual fixture framework in a manner more relevant to surgery, we present a new task simulating vein cannulation in which drugs need to be injected into tiny retinal vessels. An eye phantom with a curved vein was constructed; the curved “vein” was a hair painted red and taped on a yellow paper background that was firmly glued to the inside of half of a table-tennis ball (see Fig. 9). Under 11X magnification, the surgeon was asked to follow a 10-mm segment of the curved vein, maintaining a vertical distance of 500 μm from the spherical surface. The same four scenarios as the synthetic tracing experiments were performed by a single vitreoretinal surgeon for a total of seven sets (28 trials).
Fig. 9.

(a) Half eyeball phantom with a dyed hair tapped to yellow paper affixed to the inside of a ping pong ball with green-painted tip of Micron visible. (b) 3D reconstruction and 3D spline representation of the vein, with dark blue representing low Z positions and dark orange representing high Z positions. Although the vein lies on the surface, it is visualized with red; additionally, the vein is represented as a tube for illustration, in reality it is much flatter.
The vision system for the vein tracing experiment uses 1024×768 stereo images captured at 30 Hz to perform a dense 3D reconstruction using the fast Semi-Global Block Matching (SGBM) algorithm [31]. The vein is localized with color trackers, filtered with blob analysis, skeletonized with morphological and distance transforms, and fit to a B-spline in the XY image space and XZ direction based on the disparity map. The B-spline is then backprojected to form a full 3D representation of the vein on the surface (see Fig. 9). Because the anatomy of greatest interest is often occluded by the tip, partially observed splines are matched with Iterative Closet Point (ICP) [32] to the initial un-occluded spline and occluded sections are filled in with linear interpolation. Full disparity maps and 3D spline representations are updated at 2 Hz and provided to the virtual fixture controller.
C. Retinal Membrane Peeling with Plastic Wrap Phantom
For evaluation of the virtual fixtures in contact with tissue, we use our framework in the task of retinal membrane peeling, a challenging microsurgical task that can involve membranes as thin as 5 μm. In contrast to [2], which used rubber as a phantom retina, we use a sorbothane slide to better mimic retinal tissue deformation, and place 12-μm plastic wrap on top to simulate a membrane (Fig. 10). Dense stereo reconstructs 640×480 resolution disparity maps at 10 Hz; a plane is fit locally at the tip of Micron to measure Z displacement from the surface.
Fig. 10.

Peeling of simulated retinal membrane (12-μm plastic wrap on sorbothane slab).
Unlike the previous tracing tasks that focus on positioning, the goal of the peeling experiment is to minimize force applied to the tissue. A force sensor below the sorbothane slide measured both downward and upward force at 2 kHz. However, force information is used only for evaluation: all control of Micron is vision-based using Z displacement measured by the stereo cameras. During the procedure, tremor suppression and velocity limiting smooth tremor while peeling. A volumetric soft virtual fixture extending from 50 μm above the surface to 50 μm below the surface scales motions in the Z direction with λ = 1/3 to increase precision during the engagement of the membrane. To limit downward force while in contact with tissue, a hard-stop virtual fixture prevents the tip from penetrating more than 50 μm below the surface. Visual cues indicate when hard stops are reached. An experienced vitreoretinal surgeon performed 10 unaided and 10 aided trials in random order.
D. Results
For tracing tasks, Figs. 11–14 show representative trace histories of the tip locations in black for each task and scenario on the target represented by thick, light green lines. Figure 15(a) presents mean 3D RMS error for all tracing tasks and Table I shows maximum error. It is important to note that the Vein Tracing task has a higher incidence of saturation, and thus more error, because of the lower magnification and the greater tip traversal required (almost 10 mm, compared to the 0.5-mm circle). In fact, 98% of the error during the Vein Tracing task with hard virtual fixtures occurs while the manipulator is in saturation.
Fig. 11.
Hold Still results (a) unaided (b) aided with shelving filter (c) aided with soft fixtures (d) aided with hard fixtures.
Fig. 14.
Vein Tracing results (a) unaided (b) aided with shelving filter (c) aided with soft fixtures (d) aided with hard fixtures.
Fig. 15.

(a) Mean 3D RMS error across seven trials of each combination of task and scenario, with standard deviation error bars. Hard fixtures significantly reduce error compared to unaided and shelving filter scenarios (p < 0.05). (b) Maximum upwards and downwards force per trial, averaged over 10 randomized unaided and aided runs each. Virtual fixtures significantly reduce both upwards and downwards force (p < 0.05).
In all cases, mean RMS error and maximum error for hard virtual fixtures is significantly less than in the unaided case for 3D measurements (p < 0.05). Mean error of hard virtual fixtures for 3D is significantly less than the state-of-the-art shelving filter from [2] (p < 0.05). Fig. 16b shows the average maximum upwards and downwards forces measured during the peeling experiments. Vision-based virtual fixtures significant reduce forces, and downward forces are greatly reduced by the hard-stop virtual fixture (p < 0.05).
V. Discussion
The new position-based virtual fixture formulation presented here is necessary for the class of fully-handheld micromanipulators such as Micron that use handle position as input to the control system. Virtual fixtures are generated in real time from stereo cameras attached to the microscope, providing task-dependent behaviors to the operator. Visual cues are displayed to the operator to maintain eye-hand coordination and help guide the operator.
Hard virtual fixtures totally constrain the tip, enforcing constraints that should never be violated, e.g., forbidden areas or snap-to behaviors. Implementation of soft virtual fixtures under our formulation provides intuitive motion scaling. In all cases, tremor suppression filters compensate for unwanted high-frequency motion. Furthermore, the virtual fixture framework easily adapts to general parameterizations such as splines to model complex anatomy. Using Micron as a test platform, virtual fixtures have been validated with medically relevant artificial tests such as vein tracing to significantly reduce tip positioning error. In retinal membrane peeling with tissue contact, virtual fixtures can reduce forces significantly using only visual information.
Future work includes extensions to orientation-based virtual fixtures, which would be helpful to enforce a remote center of motion or to perform laser therapies. A new Micron prototype with a larger range of motion should reduce saturation and improve performance. Further testing in more realistic situations ex vivo and in vivo is necessary in order to fully validate the efficacy of the proposed work in retinal surgery.
Fig. 12.
Circle Tracing results (a) unaided (b) aided with shelving filter (c) aided with soft fixtures (d) aided with hard fixtures.
Fig. 13.
Move and Hold results (a) unaided (b) aided with shelving filter (c) aided with soft fixtures (d) aided with hard fixtures. Deviations from the virtual fixtures in (c) and (d) result from saturation of the actuators, caused by tremor or drift in excess of the range of motion of Micron.
Acknowledgments
This work was supported in part by the National Institutes of Health (grant nos. R01 EB000526, R21 EY016359, and R01 EB007969), the National Science Foundation (Graduate Research Fellowship), and the ARCS Foundation.
Contributor Information
Brian C. Becker, The Robotics Institute, Carnegie Mellon University, Pittsburgh, PA 15213 USA.
Robert A. MacLachlan, The Robotics Institute, Carnegie Mellon University, Pittsburgh, PA 15213 USA.
Louis A. Lobes, Jr., The Department of Ophthalmology, University of Pittsburgh Medical Center, Pittsburgh, PA 15213 USA
Gregory D. Hager, The Computer Science Department, Johns Hopkins University, Baltimore, Maryland 21218 USA.
Cameron N. Riviere, Email: camr@ri.cmu.edu, The Robotics Institute, Carnegie Mellon University, Pittsburgh, PA 15213 USA.
References
- 1.Singh SPN, Riviere CN. Physiological tremor amplitude during retinal microsurgery. Proc IEEE Northeast Bioeng Conf. 2002:171–172. [Google Scholar]
- 2.MacLachlan RA, Becker BC, Cuevas Tabares J, Podnar GW, Lobes LA, Jr, Riviere CN. Micron: An actively stabilized handheld tool for microsurgery. IEEE Trans Robot. 2012;28(1):195–212. doi: 10.1109/TRO.2011.2169634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ikuta K, Kato T, Nagata S. Micro active forceps with optical fiber scope for intra-ocular microsurgery. IEEE Micro Electro Mech Syst. 1996:456–461. [Google Scholar]
- 4.Das H, Zak H, Johnson J, Crouch J, Frambach D. Evaluation of a telerobotic system to assist surgeons in microsurgery. Computer Aided Surgery. 1999;4(1):15–25. doi: 10.1002/(SICI)1097-0150(1999)4:1<15::AID-IGS2>3.0.CO;2-0. [DOI] [PubMed] [Google Scholar]
- 5.Ueta T, Yamaguchi Y, Shirakawa Y, Nakano T, Ideta R, Noda Y, Morita A, Mochizuki R, Sugita N, Mitsuishi M. Robot-assisted vitreoretinal surgery: Development of a prototype and feasibility studies in an animal model. Ophthalmol. 2009;116(8):1538–43. doi: 10.1016/j.ophtha.2009.03.001. [DOI] [PubMed] [Google Scholar]
- 6.Wei W, Goldman RE, Fine HF, Chang S, Simaan N. Performance evaluation for multi-arm manipulation of hollow suspended organs. IEEE Trans Robot. 2009;25(1):147–157. [Google Scholar]
- 7.Bourla DH, Hubschman JP, Culjat M, Tsirbas A, Gupta A, Schwartz SD. Feasibility study of intraocular robotic surgery with the da Vinci surgical system. Retina. 2008;28(1):154–158. doi: 10.1097/IAE.0b013e318068de46. [DOI] [PubMed] [Google Scholar]
- 8.Mulgaonkar AP, Hubschman JP, Bourges JL, Jordan BL, Cham C, Wilson JT, Tsao TC, Culjat MO. A prototype surgical manipulator for robotic intraocular micro surgery. Stud Health Technol Inform. 2009;142(1):215–7. [PubMed] [Google Scholar]
- 9.Uneri A, Balicki M, Handa J, Gehlbach P, Taylor RH, Iordachita I. New Steady-Hand Eye Robot with micro-force sensing for vitreoretinal surgery. Proc IEEE Int Conf Biomed Robot Biomechatron. 2010:814–819. doi: 10.1109/BIOROB.2010.5625991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hubschman JP, Bourges JL, Choi W, Mozayan A, Tsirbas A, Kim CJ, Schwartz SD. The Microhand: a new concept of micro-forceps for ocular robotic surgery. Eye. 2009;24(2):364–367. doi: 10.1038/eye.2009.47. [DOI] [PubMed] [Google Scholar]
- 11.Dogangil G, Ergeneman O, Abbott JJ, Pané S, Hall H, Muntwyler S, Nelson BJ. Toward targeted retinal drug delivery with wireless magnetic microrobots. Proc IEEE Intl Conf Intell Robot Syst. 2008:1921–1926. [Google Scholar]
- 12.Becker BC, MacLachlan RA, Hager GD, Riviere CN. Handheld micromanipulation with vision-based virtual fixtures. Proc IEEE Int Conf Robot Autom. 2011:4127–4132. doi: 10.1109/ICRA.2011.5980345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Becker BC, MacLachlan RA, Riviere CN. State estimation and feedforward tremor suppression for a handheld micromanipulator with a Kalman filter. Proc IEEE Intl Conf Intell Robot Syst. 2011:5160–5165. doi: 10.1109/IROS.2011.6094935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Becker BC, Maclachlan RA, Lobes LA, Jr, Riviere CN. Vision-based retinal membrane peeling with a handheld robot. Proc IEEE Int Conf Robot Autom. 2012:1075–180. doi: 10.1109/ICRA.2012.6224844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bettini A, Marayong P, Lang S, Okamura AM, Hager GD. Vision-assisted control for manipulation using virtual fixtures. IEEE Trans Robot. 2004 Dec;20(6):953–966. [Google Scholar]
- 16.Rosenberg LB. Virtual fixtures: Perceptual tools for telerobotic manipulation. IEEE Virt Reality Ann Int Symp. 1993:76–82. [Google Scholar]
- 17.Funda J, Taylor RH, Eldridge B, Gomory S, Gruben KG. Constrained cartesian motion control for teleoperated surgical robots. IEEE Trans Robot Autom. 1996;12(3):453–465. [Google Scholar]
- 18.Davies BL, Harris SJ, Lin WJ, Hibberd RD, Middleton R, Cobb JC. Active compliance in robotic surgery—the use of force control as a dynamic constraint. Proc Inst Mech Eng, Part H: J Eng Med. 1997;211(4):285–292. doi: 10.1243/0954411971534403. [DOI] [PubMed] [Google Scholar]
- 19.Park S, Howe R, Torchiana D. Virtual fixtures for robotic cardiac surgery. Proc Med Image Comput Comput Assist Interv. 2001:1419–1420. [Google Scholar]
- 20.Moore CA, Jr, Peshkin MA, Colgate JE. Cobot implementation of virtual paths and 3D virtual surfaces. IEEE Trans Robot Autom. 2003;19(2):347–351. [Google Scholar]
- 21.Kapoor A, Li M, Taylor RH. Constrained control for surgical assistant robots. Proc IEEE Int Conf Robot Autom. 2006:231–236. [Google Scholar]
- 22.Li M, Ishii M, Taylor RH. Spatial motion constraints using virtual fixtures generated by anatomy. IEEE Trans Robot. 2007;23(1):4–19. [Google Scholar]
- 23.Ren J, Patel RV, McIsaac KA, Guiraudon G, Peters TM. Dynamic 3-D virtual fixtures for minimally invasive beating heart procedures. IEEE Trans Med Imag. 2008;27(8):1061–1070. doi: 10.1109/TMI.2008.917246. [DOI] [PubMed] [Google Scholar]
- 24.Dewan M, Marayong P, Okamura AM, Hager GD. Vision-based assistance for ophthalmic micro-surgery. Proc Med Imag Comput Comput Assist Interv. 2004:49–57. [Google Scholar]
- 25.Lin HC, Mills K, Kazanzides P, Hager GD, Marayong P, Okamura AM, Karam R. Portability and applicability of virtual fixtures across medical and manufacturing tasks. Proc IEEE Int Conf Robot Autom. 2006:225–231. [Google Scholar]
- 26.MacLachlan RA, Riviere CN. High-speed microscale optical tracking using digital frequency-domain multiplexing. IEEE Trans Instrum Meas. 2009;58(6):1991–2001. doi: 10.1109/TIM.2008.2006132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Veluvolu KC, Latt WT, Ang WT. Double adaptive bandlimited multiple Fourier linear combiner for real-time estimation/filtering of physiological tremor. Biomed Sig Proces Con. 2010;5(1):37–44. [Google Scholar]
- 28.Hutchinson S, Hager GD, Corke PI. A tutorial on visual servo control. IEEE Trans Robot Autom. 1996;12(5):651–670. [Google Scholar]
- 29.Chen XD, Yong JH, Wang G, Paul JC, Xu G. Computing the minimum distance between a point and a nurbs curve. Computer-Aided Design. 2008;40(10–11):1051–1054. [Google Scholar]
- 30.Richa R, Poignet P, Liu Chao. Three-dimensional motion tracking for beating heart surgery using a thin-plate spline deformable model. Int J Robot Res. 2010;29(2–3):218–230. [Google Scholar]
- 31.Hirschmuller H. Stereo processing by semiglobal matching and mutual information. IEEE Trans Pattern Anal Mach Intell. 2008;30(2):328–341. doi: 10.1109/TPAMI.2007.1166. [DOI] [PubMed] [Google Scholar]
- 32.Besl PJ, McKay ND. A method for registration of 3-D shapes. IEEE Trans Pattern Anal Mach Intell. 1992;14(2):239–256. [Google Scholar]