Marriage Meets the Joneses: Relative Income, Identity, and Marital Status

Abstract

This paper investigates the effect of relative income on marriage. Accounting flexibly for absolute income, the ratio between a man's income and a local reference group median is a strong predictor of marital status, but only for low-income men. Relative income affects marriage even among those living with a partner. A ten percent higher reference group income is associated with a two percent reduction in marriage. We propose an identity model to explain the results.

Low-income men are less likely to marry. Among 25-34-year-old white men in the 2000 Census, for example, 34 percent of those in the bottom quarter of the income distribution are married, compared with 67 percent of those in the top quarter of the income distribution. For blacks, the numbers are 16 percent and 50 percent respectively.¹ The decline in marriage since 1960 has been most pronounced at the bottom of the income distribution.²

Marriage is tied to important outcomes, including the stability of partnerships, the health and well-being of couples, and a wide range of outcomes for children. Burstein (2007) summarizes four recent reviews and concludes that “[W]hile causation is nearly impossible to prove, the very strong associations must at least be acknowledged.(p.387)” There are reasons to believe that, by raising the social and financial costs of exit, marriage offers benefits beyond those realized by cohabiting couples.³ Furthermore, there may be externalities associated with declining aggregate marriage rates, and these may be most acutely felt at the bottom of the income distribution. Marriage promotion is also a key underpinning of recent anti-poverty efforts (Lerman, 2002).⁴ Understanding why couples, and particularly low-income couples, choose to marry or not marry is therefore of heightened policy interest.

Previous explanations for low and declining marriage rates for low-income men emphasize on the role of economic security in determining whether a man is “marriageable.” Here we explore the possibility that, conditional on absolute income, income relative to a local reference group is an important determinant of the marriage decision. We build on Easterlin's (1980) suggestion that income relative to aspirations affects marriage and childbearing. Specifically, we hypothesize that individuals perceive a threshold income required for marriage, and that this threshold is influenced by an individual's local reference group.

The results suggest that relative income is a strong predictor of marital status. After carefully accounting for cost-of-living-adjusted absolute income, low-income men are less likely to be married when they are farther from the median income in their reference group. High-income men, on the other hand, are largely unaffected by relative income concerns. A ten percent increase in reference group income reduces the probability of marriage by about two percent. We explore metropolitan area reference groups determined by race and education.

Our theoretical framework builds on Akerlof and Kranton's (2000) model of identity. We hypothesize that one benefit of marriage is the utility couples gain from thinking of themselves in the category of “married people.” This category entails certain prescriptions for behavior and characteristics, including a particular standard of living associated with marriage. When couples are far from achieving this norm, they benefit less from marrying, and therefore are less likely to do so. We posit that the income threshold varies across local race/ethnicity and education groups, allowing us to separately identify the effects of absolute and relative income.

This paper contributes to a growing literature which attempts to isolate the causal influence of relative income on a diverse set of behaviors and outcomes. Recent and historic work has explored the link between relative income and subjective well-being (Card et al. (2008), Clark et al. (2008), Luttmer (2005), and others), health outcomes and health behaviors (Miller and Paxson (2006), Eibner and Evans (2005), and others), female labor supply (Neumark and Postlewaite, 1998)), consumption and savings (Denizer et al, 2000, Kosicki, 1987, Duesenberry, 1949), homeownership (Withers, 1998), suicide (Daly, Wilson, and Johnson, 2007), social capital (Fischer and Torgler, 2006), and even soccer performance (Torgler and Schmidt, 2007). To our knowledge, we are the first to systematically examine the link between relative income and the marriage decisions of individuals.

The paper proceeds as follows. Section I discusses the link between income and marriage. In Section II, we develop a simple theoretical framework which incorporates the notion of identity to the marriage decision. We discuss the “middle class marriage ideal” in Section III. Section IV describes the data and empirical strategy, and section V reports results. Section VI concludes.

I. Income and Marriage

Our analysis focuses on the years 1980–2000. During that period, there was a roughly 15 percentage point decline in marriage for young white men across the income distribution. Declines for black men were 11 to 18 percentage points and greatest in the second quartile of the income distribution. These changes represent a larger percentage change in marriage at the bottom of the income distribution for all groups.

As noted by Burstein (2007), economic models suggest reasons why the poor might be either more or less likely to marry. The classic economic model of marriage posited by Becker (1981) hinges on specialization in home production. The gains from specialization and public goods (Lam, 1988) might be particularly important to a disadvantaged couple. On the other hand, if men's incomes are low relative to women's at the bottom of the distribution, the gains from specialization are muted and marriage becomes less likely among disadvantaged couples. Furthermore, tax policy and means-tested social insurance programs may discourage marriage, and the disincentives might be particularly pronounced at the bottom of the income distribution.⁵

The structure of marriage markets also plays a potentially important role in discouraging marriage at the bottom of the income distribution. Loughran (2002) and Gould and Paserman (2003) document the negative effect of rising male income inequality on marriage rates, arguing that income dispersion extends the female search process. Willis (1999) suggests that uneven sex ratios and adequate support for single mothers can lead to an equilibrium in which low-income men remain unmarried and father children with multiple partners.

The existing economic models of specialization and marriage markets suggest that low-income men may be less likely to form long-term partnerships. However, economic theory is less well-developed on how income affects the decision to marry once such partnerships are formed.⁶ Unmarried cohabitation is an increasingly common status; in the 2002 National Survey of Family Growth 50 percent of women aged 15 to 44 had cohabited at some point and 59 percent of marriages were preceded by cohabitation (Stevenson and Wolfers, 2007). A large majority of cohabiters expect or hope to marry (Lichter, 2006). Still, a majority of cohabiting unions do not transition to marriage in five years, either because of dissolution or inertia. More than a fifth of cohabiting couples in 2002 had been living together at least five years (Stevenson and Wolfers, 2007). These facts imply that barriers to marriage exist among co-residing couples.

Qualitative work by Gibson-Davis, Edin, and McLanahan (2005) suggests that financial status affects the marriage decision even among co-residing couples with children.⁷ Although all of the couples in the Gibson-Davis et al. study have young children together and a majority co-reside, many opt to postpone marriage for financial reasons. Respondents repeatedly point to markers of a middle class lifestyle as pre-requisites for marriage, though the perceived necessities vary across individuals. Examples include a washer-dryer, a single-family house with a garage, a couples “own place”, a car, and a big wedding. We posit that the financial resources viewed as necessary for marriage depend on an individual's local reference group.

The Gibson-Davis et al. study suggests that marriage is associated with a set of prescriptions (norms) for behavior and financial status. Without the financial wherewithal to meet these expectations, cohabitation is preferable to marriage. One married couple in the study, for example, is embarrassed to publicly acknowledge their marriage because they lack financial independence and still live at home. The idea of social norms affecting decisions can be formalized using an Akerlof and Kranton (2000) identity framework, and we use this framework below to model the marriage decision.

The notion that marriage is associated with the realization of financial norms is not new. Easterlin (1980) posits that couples aspire to a certain standard of living before marrying. Wilson (1987), Oppenheimer, Kalmjin, and Lim (1997), and Brown and Kesselring (2003) argue that male “marriageability” is contingent on steady employment or a minimum level of earnings. Qualitative work by Edin (2000) also points to the importance of financial stability as a precursor to marriage.

Less clear is how such financial prescriptions are determined. Easterlin (1980) suggests that financial aspirations stem from the standard of living one experienced as a young adult. But the Gibson-Davis et al. respondents reference a set of norms extending beyond their own life experiences. Here we analyze local reference groups - those comprised of others in one's own metropolitan area, race/ethnicity, and education category. We are guided by the theme of a “middle class lifestyle” that runs throughout the Gibson-Davis et al. study; we assume that the ideal income targeted by men is that of the median fully employed man in his local reference group.

II. A Model of Income, Identity, and Marriage

Suppose a locality has an equal number of men and women in the marriage market. Each person is endowed with income drawn from the same distribution. Suppose further that the desirability of men and women is represented by their incomeY_i. We abstract from the matching process and assume men and women are matched by the level of income such that within each couple the man and the woman have equal levels of income. The couples may decide to cohabit or marry. The value of marrying is determined by background characteristics (such as age, education, race, income, characteristics of peers) which in turn affect the financial returns and personal returns to marriage. For example, married couples might receive financial benefits or incur costs because of tax and welfare policies that interact with their level of income. The personal returns include social rewards for marriage from family and friends as well as the psychic benefit of marrying for one's self-image.

Following the model of identity outlined in Akerlof and Kranton (2000), we describe “married people” as one group c in a set of social categories C with which men and women may choose to identify. Prescriptions P describe the ideal characteristics and behavior for each category. For example, married people might be expected to have a high level of income, to live in their own residence apart from extended family, to stay home instead of going to the bar, and to exhibit high levels of paternal involvement in childrearing.

We assume the category “cohabiting people” has no set of prescriptions. While this is a simplification, the financial hurdle for cohabitation is likely to be much lower than that for marriage. In a study of the relationship between education, marriage and cohabitation, Thorton, Axinn, and Teachman (1995) posit that schooling and the associated earning power may be less important for cohabitation than for marriage. The qualitative evidence from Gibson-Davis, Edin, and McLanahan (2005) also suggests that cohabitation involves weaker financial prescriptions; many respondents already lived together but viewed their economic situation as inadequate for marriage.

An individual's self-image I_i depends on the match between his or her behavior and characteristics with the ideals prescribed for his or her category. In our simple model, we focus on the prescription that married people have a certain minimum level of income. We also allow a random error term ε_i with mean zero to affect an individual's self image associated with any given category. Thus, an individual's utility can be described by:

$$U_i=U_i(Y_i,I_i)$$

where I_i=I_i (Y_i, c_i, P, ε_ic), ∂U_i/∂Y_i>0, and ∂U_i/∂I_i>0 That is, in general an individual's utility depends on his income and self-image. Self-image, in turn, is a function of interactions between an individual's income, the category with which he identifies, the prescriptions for that category, and a random error term.

Suppose that the financial prescription for a married person is at least Y_ideal, where Y_ideal is the median income of a given reference group. The identity payoff for a married person is then:

$$I_i={\mathrm{I}}_{\mathrm{m}ar}-t\left(\max (0,1-\frac{Y_i}{Y_{\mathit{ideal}}})\right)+{\epsilon }_{\mathit{imar}},$$

, where t is a positive scalar describing the identity loss associated with falling below the “marriage ideal”. The identity payoff for cohabiting is:

$$I_i=I_{\mathit{cohab}}+{\epsilon }_{\mathit{icohab}}$$

and we assume I_mar > I_cohab. In other words, on average a married person meeting the ideal has a higher self-image than a cohabiting person.

In making the decision whether to marry, an individual compares the utility from cohabiting and marriage. The self-image gained through marriage (relative to cohabitation) is

$$I_i({\mathrm{I}}_{\mathrm{m}ar}-I_{cohab})-t\left(\max (0,1-\frac{Y_i}{Y_{\mathit{ideal}}})\right)+({\epsilon }_{\mathit{imar}}-{\epsilon }_{\mathit{icohab}})$$

The gains to self-image through marriage tend to increase with the average gain in self-image from marriage and an individual's income. The gains decrease with a higher “marriage ideal” and a higher penalty t for deviating from the norm.

This framework provides some simple comparative statics. The gain to marriage is increasing in Y_i for $Y_i<Y_{\mathit{ideal}}(\frac{\partial I}{\partial Y_i}=t∕Y_{\mathit{ideal}})$ and constant in Y_i for $Y_i>Y_{\mathit{ideal}}(\frac{\partial I}{\partial Y_i}=0)$. Similarly, an increase in the marriage ideal Y_ideal is associated with a decrease in the gain to marriage for low values of Y_i but no change in the gain for high values of Y_i. A higher level of t strengthens the relationship between Y_i and marriage below the marriage ideal, and reduces the overall marriage rate holding other factors constant.

III. Middle-Class Marriage Ideals

The model assumes that Y_ideal is the median income of a relevant reference group. The level of income perceived to be required for marriage is unobservable and presumably differs across individuals. The qualitative evidence described by Gibson-Davis et al. suggests that low-income couples view a middle class lifestyle as a prerequisite to marriage, which we define as the median income of a fully employed (full-time, full-year) man in a relevant reference group. Our main analysis assumes the relevant reference group is fully employed male workers in the man's metropolitan area, education group and race/ethnicity group, though we also explore other reference groups.⁸ These “middle class marriage ideals” determined by median reference group income serve as proxies for the income thresholds required for marriage.

Table 1 shows the average reference group median by year, race/ethnicity and education. For all three race/ethnicity groups, the reference group median falls over time for men with some college, high school, or less than high school. Reference group medians for college graduates are generally increasing over time. These patterns are not surprising given the well-documented rise in the return to schooling over the period.

Table 1.

Reference Group Medians and Fraction Under Median

Native White Non-Hispanic Men
Average Reference Group Median				Fraction Under Median
	1980	1990	2000		1980	1990	2000
<HS	37,798	32,594	30,104	<HS	0.72	0.74	0.70
HS exactly	41,536	37,520	36,284	HS exactly	0.64	0.66	0.67
SC	44,848	43,816	43,175	SC	0.68	0.69	0.70
CG+	58,697	63,034	66,151	CG+	0.79	0.77	0.78
All	47,690	46,773	49,078	All	0.71	0.71	0.72

Native Black Non-Hispanic Men
Average Reference Group Median				Fraction Under Median
	1980	1990	2000		1980	1990	2000
<HS	28,007	26,730	24,835	<HS	0.73	0.84	0.79
HS exactly	31,031	28,137	27,830	HS exactly	0.63	0.71	0.68
SC	35,712	34,707	34,376	SC	0.65	0.71	0.69
CG+	45,049	47,653	48,695	CG+	0.72	0.75	0.73
All	33,336	32,576	33,271	All	0.67	0.73	0.70

Native Hispanic Men
Average Reference Group Median				Fraction Under Median
	1980	1990	2000		1980	1990	2000
<HS	30,077	26,477	22,738	<HS	0.66	0.71	0.64
HS exactly	33,896	30,581	28,247	HS exactly	0.58	0.62	0.59
SC	39,098	38,121	36,429	SC	0.63	0.64	0.65
CG+	48,120	51,461	50,989	CG+	0.75	0.73	0.72
All	36,217	34,946	33,896	All	0.63	0.65	0.64

Table 1 also shows the fraction of the sample with income below the reference group median. We expect more than half of men to fall under this hypothesized marriage ideal because it represents the earnings of all fully employed (full-time and full-year) men ages 18–64 in the race/ethnicity and education group. In the sample, 58–84 percent of men have incomes below their reference group median, with the exact fraction depending on the reference group and year.⁹

Appendix Table 1 shows selected reference group medians (i.e. hypothesized marriage ideals) for the ten largest metropolitan areas in the sample. Even among very large metropolitan areas, there is substantial variation in reference group medians across metro areas and over time. For example, in 1980, the median fully employed white man without a high school education in Detroit earned a third more than the median such man in Boston. By the year 2000, this disparity was reduced by half. For white college graduates, the reference group median increased over time in all large cities, but grew by 30 percent in San Francisco and only 6 percent in Detroit. There is similar variation across areas for black and Hispanic men. In the empirical analysis below, we exploit variation in reference group medians across metropolitan areas to estimate the effect of relative income on marriage.

Appendix Table 1.

Sample Reference Group Medians and Fraction Under Median For Largest Metropolitan Areas (2000 dollars)

	Native Non-Hispanic White Men				Native Non-Hispanic Black Men				Native Hispanic Men
	1980 <HS	2000 <HS	1980 CG+	2000 CG+	1980 <HS	2000 <HS	1980 CG+	2000 CG+	1980 <HS	2000 <HS	1980 CG+	2000 CG+
Reference Group Median Incomes
Metropolitan Area
Boston	34,895	30,644	55,901	67,722	27,919	26,558	46,523	56,180	21,628	24,515	39,791	48,315
Chicago	46,523	36,670	61,093	69,459	32,663	30,031	46,674	49,847	37,221	24,515	49,151	48,008
Dallas	36,116	29,632	58,372	68,539	24,198	23,493	40,721	46,987	27,826	21,450	48,279	51,073
Detroit	47,000	35,751	66,890	71,502	40,000	26,558	54,116	54,137	42,715	27,579	54,581	56,282
Houston	43,035	32,686	65,128	73,544	28,547	24,515	46,523	48,012	30,244	23,493	51,616	51,073
Los Angeles	41,872	33,708	64,674	73,544	30,244	25,536	47,895	55,577	32,570	22,472	48,884	52,094
New York	39,547	36,772	63,674	77,222	27,919	27,579	46,081	51,073	24,430	23,493	46,523	51,073
Philadelphia	38,140	32,686	59,326	67,416	30,244	24,515	46,523	45,965	25,651	23,493	52,047	51,073
San Francisco	44,756	36,129	62,820	81,716	34,895	28,601	49,000	61,287	39,942	26,558	49,791	61,287
Washington	39,547	32,686	71,186	78,652	30,244	27,579	53,500	59,244	38,523	24,515	60,477	64,351
Fraction Under Reference Group Median
Metropolitan Area
Boston	0.74	0.69	0.78	0.75	0.71	0.79	0.71	0.70	0.61	0.66	0.58	0.57
Chicago	0.71	0.78	0.76	0.74	0.80	0.92	0.70	0.70	0.64	0.68	0.68	0.64
Dallas	0.69	0.72	0.75	0.76	0.71	0.82	0.68	0.66	0.58	0.62	0.70	0.70
Detroit	0.76	0.74	0.78	0.77	0.82	0.91	0.71	0.72	0.72	0.75	0.73	0.75
Houston	0.65	0.76	0.75	0.79	0.68	0.82	0.64	0.75	0.56	0.62	0.69	0.70
Los Angeles	0.73	0.77	0.80	0.78	0.86	0.91	0.72	0.75	0.71	0.70	0.76	0.74
New York	0.76	0.80	0.79	0.75	0.80	0.86	0.78	0.70	0.73	0.74	0.68	0.66
Philadelphia	0.76	0.76	0.80	0.78	0.82	0.88	0.73	0.69	0.63	0.79	0.81	0.75
San Francisco	0.80	0.75	0.80	0.73	0.87	0.90	0.76	0.71	0.78	0.74	0.77	0.67
Washington	0.74	0.72	0.84	0.82	0.73	0.80	0.76	0.79	1.00	0.72	0.75	0.73

Note: There are multiple areas with the same median in each year because reported incomes tend to clump at $1000 intervals in the raw data. <HS Refers to less than high school; CG+ referes to four-year college graduate or more.

IV. Data and Empirical Strategy

We use the 5% IPUMS sample of the 1980–2000 U.S. Censuses to investigate the determinants of marriage. We limit our analysis to residents of 109 metropolitan areas for which we have complete data; the metropolitan areas are matched to be as geographically consistent as possible across three sample years.¹⁰ We use samples for three demographic groups: native born non-Hispanic white men, native born non-Hispanic black men, and native born Hispanic men.¹¹ The samples are restricted to ages 25–34 so that respondents are likely to have completed school and are observed at a point likely to be close to the timing of their marriage decision. We exclude the foreign born population because some of these individuals may derive norms and expectations about marriage from their home countries.

A limitation of the Census sample is that it is a repeated cross-section rather than a panel. Therefore, we do not know a man's income at the time of the marriage decision, and we cannot evaluate how the exact timing of the marriage decision relates to the income trajectory for an individual. However, we believe that this disadvantage is outweighed by the very large sample sizes; there are more than 1.2 million young men in the non-Hispanic white sample. The large samples allow us to precisely estimate the effects of relative income on marital status while controlling very flexibly for absolute income and a number of other potential confounders.

We use reported total real income last year for each man in the Census sample as a proxy for his income at the time of the marriage decision.¹² Income is top-coded and bottom-coded in the public use data. To minimize the effect of top- and bottom-coding, and to exclude negative reported incomes, we drop men in the top and bottom one percent of each metropolitan area's income distribution in each year.¹³

The dependent variable, married, is equal to one if the man is categorized in the Census data as currently married with a spouse present in the household. We also show in a specification check that the results are similar if one treats “ever married” as the outcome and that the results are not driven by divorce patterns among young men.¹⁴

As noted above, our main analysis assumes that the couple aspires to male income of at least the median income of a fully employed (full-time and full-year) man within a particular reference group. Throughout the analysis, reference groups are assumed to operate within metropolitan areas. Norms that are perpetuated at a national level (for example, through television) are not identified here.

According to the theoretical model, the ratio of one's own income to the marriage ideal should affect the marriage decision, but only for those below the ideal. The preferred baseline specification is as follows:

$$\begin{array}{c}\hfill \hfill \\ \hfill {\mathit{Married}}_{iremt}={{\beta }_1}^{\ast }{{\mathit{under}}_i}^{\ast }\frac{Y_i}{Y_{refme{d}_{remt}}}+{{\beta }_2}^{\ast }{(1-unde{r}_i)}^{\ast }\frac{Y_i}{Y_{refme{d}_{remt}}}+{{\beta }_3}^{\ast }{\mathit{under}}_i\hfill \\ \hfill {{\beta }_4}^{\ast }{X}_i+{{\beta }_5}^{\ast }{W}_{mt}+{{\gamma }_{{\mathrm{ycat}}_{irt}}}^{\ast }{{\mathrm{educ}}_{ie}}^{\ast }{\mathit{year}}_i+{\sigma }_{{\mathrm{age}}_i}+{\theta }_m+{\epsilon }_i\hfill \end{array}$$

where Married_iremt indicates that the individual i in race group r in education group e in metro area m in year t is married, under_i is an indicator suggesting i is below the reference group median, $\frac{Y_i}{Y_{refme{d}_{remt}}}$ is the ratio of i's income to the reference group median, X_i is a vector of individual characteristics, and W_mt is a vector of time-varying metropolitan area characteristics. Individual characteristics and metropolitan area characteristics are described in more detail below. In addition, γycatirt is a vector of dummies indicating income categories adjusted for cost-of-living (corresponding to the year- and race-specific percentile rank in the national housing-price-adjusted income distribution) in year t interacted with education and year categories. Thus, the model flexibly accounts for absolute income and allows the effect of income to vary by education group-year cell. These variables also imply that we have flexibly accounted for time trends and education group-specific changes in national marriage rates over time. We also include individual age dummies,σ agei, metropolitan area fixed effects, θ m, and an error term ε_i.¹⁵

The key coefficients are β₁, the effect of the ratio for those under the ideal, and β₂, the effect of the ratio for those above the ideal. The theoretical framework predicts that β₁ is positive and β₂ is zero. To our knowledge, we are the first to distinguish between the effect of relative income for men lying above and below a hypothesized ideal. We also report the “slope change,” β₂ – β₁, which we expect to be negative.

The main source of variation stems from a man's relative income – how his income relates to the middle-class marriage ideal determined by his local reference group. We hypothesize that a low-income man is less likely to marry if he lives in a metropolitan area in which similar men have high incomes, holding his own income and income rank constant. A sufficiently high-income man, on the other hand, is theoretically unaffected by others in his reference group. The specification described above is designed to capture the effect of a change in relative income holding absolute income constant and to distinguish the effect of relative income for men above and below the reference group median.

The variation exploited in the analysis stems from differences in metropolitan area income distributions, while holding an individual's income constant. For example, an inflow of highly productive reference group workers into a man's metropolitan area could increase the reference group median income without affecting the man's income. An increase in the compensation of the more highly paid workers in a man's metropolitan area could increase the reference group median income without affecting the man's income or income rank.

It would be ideal for the purposes of estimation if such changes in the income distribution of an individual's reference group arose randomly. However, we are forced to rely on observed (and potentially non-random) differences in reference group income distributions. Bias could arise if the forces that lead to these reference group income differences also directly affect marriage propensities of young low-income men. For example, a white high school graduate earning 20,000 dollars in a city where the typical white high school graduate earns 40,000 may have undesirable but unobservable qualities compared to a similar man earning 20,000 dollars in a city where a typical white high school graduate earns 30,000. We cannot fully overcome the limitations imposed by an observational study, but in the work below we do our best to control for observable characteristics of both men and metropolitan areas.

To address concerns about the endogeneity of relative income, we incorporate a rich set of metropolitan area control variables. All models include metropolitan area fixed effects to account for unobserved characteristics of cities that do not change over time. We also control for demographic and socioeconomic characteristics of the metropolitan residents – fraction native black, fraction native Hispanic, fraction foreign-born, fraction with a high school degree, fraction with some college, fraction with a college degree or more, fraction under 18, and fraction under 65. We control for the male employment-to-population ratio and predicted male and female employment levels based on 1980 industrial mix. We include additional controls for the race/ethnicity specific sex ratios in the metropolitan area, the ACCRA housing price index, the log of real housing-price-adjusted AFDC/TANF benefits for a family of three in the state, and the log of the metropolitan area population.¹⁶ We also consider potential alternative explanations for our results, though in the absence of an experimental design we cannot definitively rule out the possibility that unobserved factors are shaping marriage decisions and affecting the reference group income distribution at the same time.

Our theoretical framework abstracts from marriage market considerations and the search process. Though we believe relative and absolute income are both likely to influence the probability that a man finds a partner, it is the decision to marry conditional on partnership that is of interest here. Empirically, partnership is not observable in all cases, so we address the marriage market and search issues in two ways. First, we control for factors that are likely to affect the probability that a man is matched with a partner.¹⁷ Second, in section V.B. below, we replicate the main analysis restricting the sample to those men already living with a partner. We expect marriage market search considerations to be considerably dampened for co-residing men.

Table 2 shows means for each of the three samples. After excluding the top and bottom one percent of each metropolitan area's income distribution, those living in group quarters, and those in excluded metropolitan areas, the final sample of native non-Hispanic white men is 1.2 million observations. For black men, the final sample size is roughly 160,000 and for Hispanic men the sample is almost 77,000. Marriage rates have fallen substantially over time for all three groups and are lowest in the sample of black men.

Table 2.

Sample Means of Key Variables

	White Sample (N=1,215,527)			Black Sample (N=160,203)			Hispanic Sample (N=76,803)
	1980	1990	2000	1980	1990	2000	1980	1990	2000
Individual Characteristics
Married (and living with spouse)	0.65	0.56	0.51	0.51	0.36	0.35	0.64	0.50	0.44
Divorced	0.03	0.03	0.03	0.09	0.08	0.06	0.05	0.06	0.05
Married Ever	0.76	0.66	0.60	0.68	0.51	0.47	0.77	0.63	0.56
Married (household head sample)	0.74	0.67	0.60	0.65	0.55	0.49	0.76	0.66	0.60
Cohabiting (household head sample)	0.05	0.10	0.14	0.08	0.17	0.21	0.06	0.13	0.18
Residential Father (household head sample)	0.54	0.48	0.43	0.57	0.51	0.48	0.64	0.56	0.52
Total Income, $2000	38,142	37,867	39,811	26,797	24,012	26,607	30,878	29,588	30.019
Age	29.34	29.58	29.71	29.22	29.49	29.64	29.06	29.21	29.22
Employed	0.92	0.93	0.92	0.81	0.81	0.79	0.88	0.88	0.84
Employed Full-Time Full-Year	0.72	0.74	0.76	0.57	0.58	0.62	0.62	0.63	0.65
High School Exactly	0.32	0.32	0.27	0.40	0.42	0.40	0.35	0.38	0.36
Some College	0.26	0.31	0.32	0.25	0.32	0.35	0.26	0.33	0.34
College Graduate or More	0.33	0.30	0.37	0.13	0.13	0.16	0.14	0.12	0.16
Ratio of Income to Ref.Group Median if Under	0.60	0.60	0.59	0.54	0.52	0.55	0.58	0.57	0.59
Ratio of Income to Ref.Group Median if Over	1.31	1.36	1.43	1.36	1.34	1.38	1.35	1.39	1.44
MSA Characteristics
MSA-Year Race/Ethnicity-Specific Sex Ratio	1.03	1.01	1.01	1.20	1.18	1.19	1.04	1.03	1.04
MSA-Year Fraction Black	0.12	0.12	0.12	0.18	0.18	0.18	0.09	0.09	0.09
MSA-Year Fraction Native Hispanic	0.04	0.05	0.06	0.04	0.04	0.06	0.13	0.14	0.16
MSA-Year Fraction Native Other	0.01	0.02	0.03	0.01	0.01	0.03	0.02	0.03	0.04
MSA-Year Fraction Immigrant	0.08	0.10	0.13	0.08	0.11	0.14	0.13	0.18	0.22
MSA-Year Fraction Under 18	0.28	0.25	0.26	0.28	0.25	0.26	0.28	0.26	0.27
MSA-Year Fraction Under 65	0.89	0.88	0.88	0.90	0.89	0.89	0.90	0.89	0.89
MSA-Year Fraction High School Exactly	0.34	0.32	0.31	0.33	0.32	0.30	0.32	0.29	0.28
MSA-Year Fraction Some College	0.17	0.26	0.28	0.16	0.25	0.27	0.20	0.28	0.28
MSA-Year Fraction College Grad	0.18	0.23	0.27	0.18	0.23	0.28	0.19	0.23	0.27
MSA-Year Male Emp.-to-Pop. Ratio (ages, 18–64)	0.82	0.82	0.78	0.82	0.81	0.78	0.82	0.81	0.76
Male Predicted Emplovment Demand Index	0.66	0.60	0.60	0.66	0.61	0.60	0.65	0.61	0.61
Female Predicted Employment Demand Index	0.38	0.41	0.43	0.38	0.42	0.43	0.38	0.42	0.43
Housing Price Index	70.79	122.84	176.20	70.31	122.30	172.00	71.89	129.71	172.88
Real Housing-Price-Adjusted AFDC Benefit, $2000	781.39	597.79	424.44	699.44	540.85	383.64	819.57	657.03	475.00
Population	769,95.2	884,396	898,573	868,969	983,872	1,008,410	1,055,140	1,348,875	1,485,750

Notes: White Sample refers to native non-Hispanic white men ages 25–34; Black sample refers to native non-Hispanic black men; Hispanic sample refers to native Hispanic men. Married Now refers to men married and living with a spouse. Cohabition and residential fatherhood are based on subsamples of household heads and their partners; see text for details.

V. Results

A. Baseline Analysis

The model suggests that relative income matters to the marriage decision. In particular, we posit that a man is more likely to marry when his income approaches the median income of fully employed workers in his reference group. The ratio of income to the reference group median is expected to predict marital status below the reference group median, but not above it.

In Table 3, we examine the relative income hypothesis in a linear probability model. Column I simply relates the log of real income to marital status for non-Hispanic white men. An additional log point of income raises the probability of being married by 12.5 percentage points, holding many individual and metropolitan area characteristics constant. This result is consistent with the large literature suggesting that absolute income is an important predictor of marriage.

Table 3.

Effect of Ratio to Median of Income Fully Employed in Reference Group on Marital Status, By Race/Ethnicity, Native Born Men Ages 25–34

Dependent Variable: Married
	White Non-Hispanic (mean=0.57)	White Non-Hispanic (mean=0.57)	White Non-Hispanic (mean=0.57)	White Non-Hispanic (mean=0.57)	Black Non-Hispanic (mean=0.40)	Hispanic (mean=0.51)
	I	II	III	IV	V	VI
Ratio Income/Ideal if Under Reference Group Median			0.4677** (0.0079)	0.3813** (0.0251)	0.1619** (0.0375)	0.2644** (0.0546)
Ratio Income/Ideal if Over Reference Group Median			0.0572** (0.0051)	−0.0298* (0.0143)	0.0254 (0.0153)	−0.0404 (0.0242)
Under Reference Group Median		−0.0816** (0.0036)	−0.4171** (0.0121)	−0.3995** (0.0270)	−0.1603** (0.0364)	−0.3142** (0.0577)
Log (Real Total Income)	0.1254** (0.0024)	0.0969** (0.0028)	−0.0377** (0.0022)
Employed	0.0694** (0.0025)	0.0762** (0.0025)	0.0790** (0.0025)	0.0777** (0.0025)	0.0760** (0.0049)	0.0535** (0.0076)
Employed Full Time Full Year	0.0669** (0.0026)	0.0697** (0.0026)	0.0477** (0.0026)	0.0461** (0.0028)	0.0172** (0.0037)	0.0205** (0.0044)
CMSA Sex Ratio (within race/ethnicity group)	0.3693** (0.0915)	0.3851** (0.0871)	0.4090** (0.0722)	0.4112** (0.0781)	0.1369* (0.0522)	0.0731 (0.0948)
CMSA Housing Price Index	−0.0002* (0.0001)	−0.0002* (0.0001)	−0.0002* (0.0001)	−0.0001+ (0.0001)	0.0001 (0.0002)	0.0001 (0.0002)
Log (Real Adjusted AFDC Benefits)	−0.0179 (0.0117)	−0.0176 (0.0115)	−0.0230* (0.0114)	−0.0253* (0.0112)	−0.0298 (0.0298)	−0.0385 (0.0322)
Adjusted Income*Education Dummies*Year Dummies				yes	yes	yes
Age Dummies	yes	yes	yes	yes	yes	yes
Year*Ed Croup Dummies	yes	yes	yes
Additional Time-Varying CMSA controls	yes	yes	yes	yes	yes	yes
CMSA Dummies	yes	yes	yes	yes	yes	yes
Slope Change			−0.4105** (0.0099)	−0.4111** (0.0281)	−0.1365** (0.0343)	−0.3048** (0.0558)
Number of Observations	1,215,509	1,215,509	1,215,509	1,215,527	160,203	76,803
Number of CMSA-Year Cells	330	330	330	330	255	123
R-squared	0.13	0.13	0.14	0.14	0.14	0.15

Notes: Standard errors in parentheses are clustered on CMSA.

^{+, *,**}indicate staistical significance at the 10, 5, and 1 percent level respectively. Regression sample excludes top and bottom 1 percent of income distribution in each metro area-year-racegroup and those not living in households under the 1980 definition. Additional CMSA controls include race/ethnicity distribution in CMSA (fraction native non-Hispanic black, fraction native Hispanic, fraction native non-Hispanic non-white non-black, fraction foreign born), age distribution in CMSA (fraction under 18, fraction under 65), education distribution in CMSA (fraction high school exactly, fraction some college exactly, fraction college graduate or more), predicted employment demand for men, predicted employment demand for women, and log of population. Education Groups include less than high school, high school exactly, some college, and college graduate or more.Reference Group Median is median income of full-time full-year male workers ages 18–64 in the CMSA-year-race/ethincity-education group. Adjusted income dummies reflect adjustment for cost of living as described in text.

Column II of Table 3 indicates that, controlling log-linearly for his own income, a man is 8.2 percentage points less likely to be married if his income falls below the reference group median. The theoretical framework implies that is the ratio of income to the reference group median that affects marital status. As shown in column III, the ratio of a man's own income to the ideal has a highly significant relationship to marriage below the ideal. The ratio between income and the ideal is also statistically significant for men above the ideal, but the coefficient is much smaller and the slope change is highly significant.

The evidence in the third column is consistent with the idea that relative income is important, but could also reflect an underlying non-linear relationship between income and marriage. We prefer a more flexible specification. We calculate income percentile groups of the national income distribution and interact these with year*education indicators.¹⁸ Thus, we include nearly 1200 income dummy variables into the model to allow the effect of income percentile to vary by year and education group. These variables also account for national changes in the propensity for different income groups and education groups to marry over time.

The results are consistent with the theoretical predictions. Column IV of Table 3 shows that the ratio of a man's income to the median reference group income significantly increases the probability of marriage below the reference group median, but not above it. The magnitude of the coefficient suggests that moving one's income from 70 to 80 percent of the marriage ideal, for example, increases the probability of marriage by 3.8 percentage points. In contrast, moving from 120 to 130 percent slightly decreases the probability of marriage, conditional on absolute income. The estimated slope change is large and statistically significant. We prefer the model in column IV of Table 3 because it is conservative, and we treat it as our baseline model.

The baseline results focus on two groups of men: those above and below the hypothesized ideal. Figure 1 offers more detail. Among white men, the effect of relative income is most pronounced for those with income levels between one quarter and three quarters of the level of the reference group median. The effect of relative income is muted for the poorest men in the sample; it is possible that these men do not aspire to the reference group median. For each ratio category above one, the effect is statistically indistinguishable from zero.

Figure 1.

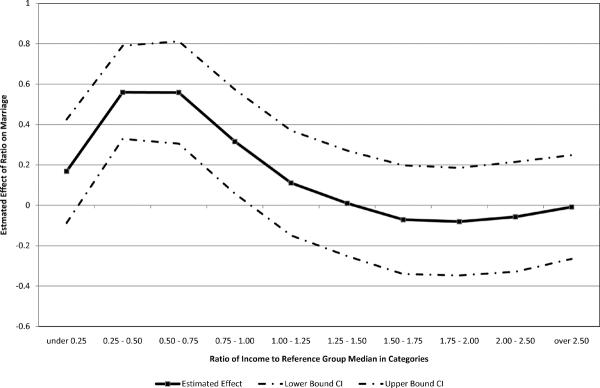
Effect of Ratio by Ratio Category Native Non-Hispanic White Men

Another way of examining the information is to look by decile in the metropolitan area-race-education group income distribution. Roughly seventy percent of men lie below the reference group median, so it is in the bottom seventy percent of the distribution that we expect relative income to matter. That is indeed what we see in Figure 2, with the largest effect around the third decile.

Figure 2.

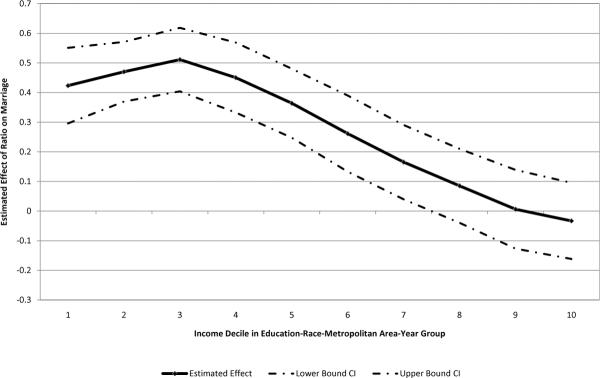
Effect of Ratio by Income Decile Native Non-Hispanic White Men

We also examine the effect of relative income for different race/ethnicity groups. Column V of Table 3 shows the baseline analysis repeated non-Hispanic black men. For black men, the results accord well with the prediction of the model: a positive effect of the ratio below the reference group median, a small and statistically insignificant effect of the ratio above it, and a statistically significant slope change. Black men are more likely to be married when their income approaches the median of fully employed men in their reference group. Above the reference group median relative income has little effect once absolute income is held constant. The story is similar for Hispanic men, as shown in column VI of Table 3. The probability of marriage depends on the median income of a reference group, but only when a man is below that income.¹⁹

In sum, the baseline model indicates that relative income is linked to marital status for those below the median of a local reference group, but not for those above the median. The association is robust to the inclusion of flexible controls for absolute income. As will be documented below, the relationship persists across many alternative specifications and sample restrictions. First, however, we discuss alternative explanations for our results.

B. Marriage Markets, Cohabitation, and Fatherhood

We have documented a relationship between marital status of young men and their income relative to a local reference group. Our proposed explanation is that couples gain utility by achieving a certain level of financial security before marriage, and that this level is determined in part by those around them. The notion that couples postpone marriage until they can achieve a middle class lifestyle is supported by previous qualitative literature (Gibson-Davis et al., 2005). Nevertheless, there are other potential reasons that the marriage decisions of young men could be linked to the incomes of those around them.

One important class of explanations relates to the marriage market. A man whose relative income falls becomes a less desirable mate compared to his peers even if his purchasing power remains constant. Furthermore, if income inequality is high, a standard search model predicts that women will choose a higher “reservation income” in searching for a mate and will search longer, as has been shown in empirical work by Loughran (2002) and Gould and Paserman (2003).

We believe marriage market considerations are potentially important and we examine this issue in several ways. First, we control for a man's decile rank in his metropolitan area-race group or metropolitan area-race-education group. The thought experiment represented by this specification is one in which the earnings of middle-income and high-income men increase, but low-income men maintain their income and income rank. Inclusion of rank controls slightly attenuates the results, as shown in columns II and III of Appendix Table 2, but the pattern retains is statistical significance.²⁰

Appendix Table 2.

Exploring Alternative Explanations

	I	II	III	IV	V	VI	VII	VIII	IX	X	XI	XII
	Baseline	Control for Rank in Race/Eth Group	Control for Rank in Race/Eth- Education Group	Controls for Inequality Interacted with “Under”	Drop Controls For Employment Status	Restrict to FTFY workers	Assume Housing is 50 percent of expenditure	No Cost-of Living Adjustment	No Housing Price Control	Control for Income/ Housing Price Index	Assume Pre- marriage Income is 90% of Observed	Restrict to Ages 25 and 26
Panel A. Native Non-Hispanic White Men
Ratio Income/Ideal if Under Ref. Median	0.3813** (0.0251)	0.3010** (0.0308)	0.3230** (0.0312)	0.3829** (0.0260)	0.4029** (0.0249)	0.4151** (0.0263)	0.3772** (0.0250)	0.3726** (0.0301)	0.3732** (0.0245)	0.3792** (0.0245)	0.2163** (0.0303)	0.4398** (0.0423)
Ratio Income/Ideal if Over Ref. Median	−0.0298* (0.0143)	−0.0275* (0.0133)	−0.0332** (0.0125)	−0.0303* (0.0139)	−0.0335* (0.0151)	−0.0207 (0.0142)	−0.0241+ (0.0124)	−0.0242+ (0.0134)	−0.0326* (0.0136)	−0.0259+ (0.0137)	−0.0252+ (0.0140)	0.0400 (0.0296)
Panel B. Native Non-Hispanic Black Men
Ratio Income/Ideal if Under Ref. Median	0.1619** (0.0375)	0.1607** (0.0380)	0.1335** (0.0398)	0.1695** (0.0393)	0.1796** (0.0384)	0.1349** (0.0415)	0.1833** (0.0435)	0.1318** (0.0326)	0.1630** (0.0370)	0.1624** (0.0377)	0.1581** (0.0369)	0.1257+ (0.0721)
Ratio Income/Ideal if Over Ref. Median	0.0254 (0.0153)	0.0074 (0.0158)	0.0113 (0.0156)	0.0318+ (0.0161)	0.0178 (0.0150)	−0.0081 (0.0199)	0.0266 (0.0163)	0.0310+ (0.0161)	0.0257+ (0.0154)	0.0254 (0.0153)	0.0170 (0.0226)	0.0637 (0.0478)
Panel C. Native Hispanic Men
Ratio Income/Ideal if Under Ref. Median	0.2644** (0.0546)	0.2539** (0.0542)	0.2515** (0.0581)	0.2646** (0.0546)	0.2794** (0.0545)	0.2614** (0.0623)	0.2583** (0.0543)	0.2364** (0.0630)	0.2670** (0.0552)	0.2652** (0.0556)	0.1592* (0.0639)	0.2201* (0.0930)
Ratio Income/Ideal if Over Ref. Median	−0.0404 (0.0242)	−0.0511+ (0.0269)	−0.0443 (0.0264)	−0.0380 (0.0239)	−0.0421+ (0.0243)	−0.0294 (0.0378)	−0.0317 (0.0228)	−0.0402+ (0.0219)	−0.0398 (0.0245)	−0.0398 (0.0238)	−0.0366 (0.0231)	−0.0540 (0.0601)

Notes: Standard errors in parentheses are clustered on CMSA.

^{+, *,**}indicate statistical significance at the 10, 5, and 1 percent level respectively. Each column within a panel represents a separate regression. Regressions based on baseline specifications and include adjusted income category dummies interacted with year and education and all other controls. See text for more details.

Second, in column IV of Appendix Table 2 we directly control for inequality, which we believe should affect the willingness of women to choose a man with a particular level of income. We allow the effect of both income inequality in the metropolitan area and income inequality in the race/ethnicity-education group to differ based on whether the man is above or below the reference group median. The results are not sensitive to the inclusion of these variables.

Third, we consider a subsample of men who are already residing with a partner. We believe search considerations should be considerably dampened for this group. It should be noted that there are several limitations to this analysis. First, for unmarried men, a cohabiting relationship can only be observed in the Census if the man or his partner is the household head. We limit the analysis to men who are household heads or have partners or spouses who are household heads (the household head sample). This introduces selection bias to the extent that the decision to form a separate household is linked to the decision to co-reside with a partner. In addition, the 1980 Census does not distinguish between unmarried partners and roommates. For consistency across all three Census years, we define an unmarried man as cohabiting if he has either a female roommate or an unmarried partner.²¹

We start by replicating the baseline analysis for the household head sample in column I of Table 4. The household head sample is substantially smaller than the overall sample for all three groups, suggesting that a substantial fraction of young men do not maintain their own households. There is a significant slope change in the household head sample for whites, blacks, and Hispanics, though the effect is muted compared to the full sample.

Table 4.

Effect of Reference Group Median on Cohabitation and Family Structure

	I	II	III	IV	V	VI	VII
Panel A. Native Non-Hispanic White Men
	Full Household Sample (N=1,038,546)				Co-residing Sample (N=809,675)		Co-residing With Kids Sample (N=520,609)
Dependent Variable:	Married (mean=0.68)	Non-Material Cohabiting (mean=0.09)	Non-Co-residing (mean=0.23)	Co-residing With Kids (mean=0.48)	Married (mean=0.88)	Co-residing With Kids (mean=0.63)	Married (mean=0.96)
Ratio Income/Ideal if Under Marriage Ideal	0.2551** (0.0285)	−0.0721** (0.0128)	−01827** (0.0215)	0.2707** (0.0236)	0.1129** (0.0187)	0.2237** (0.0242)	0.0568** (0.0106)
Ratio Income/Ideal if Over Marriage Ideal	−0.0102 (0.0119)	0.0124* (0.0057)	−0.0024 (0.0091)	0.0170 (0.0128)	−0.0256** (0.0094)	−0.0036 (0.0105)	0.0001 (0.0055)
Slope Change	−0.2653** (0.0243)	0.0845** (0.0117)	0.1804** (0.0172)	−0.2537** (0.0208)	−0.1385** (0.0172)	−0.2273** (0.0202)	−0.0566** (0.0089)
Panel B. Native Non-Hispanic Black Men
	Full Household Head Sample (N=113,840)				Co-residing Sample (N=82,658)		Co-residing With Kids Sample (N=60,366)
Dependent Variable:	Married (mean=0.57)	Non-Marital Cohabiting (mean=0.15)	Non-Co-residing (mean=0.28)	Co-residing With Kids (mean=0.52)	Married (mean=0.79)	Co-residing With Kids (mean=0.72)	Married (mean=0.88)
Ratio Income/Ideal if Under Marriage Ideal	0.0793+ (0.0433)	−0.0447+ (0.0260)	−0.0351 (0.0409)	0.0359 (0.0381)	0.0637+ (0.0322)	0.0121 (0.0403)	0.0539 (0.0325)
Ratio Income/Ideal if Over Marriage Ideal	−0.0254 (0.0180)	0.0197+ (0.0117)	0.0065 (0.0145)	0.0042 (0.0155)	0.0395* (0.O160)	O.0032 (0.0141)	−0.0268* (0.0119)
Slope Change	−0.1047** (0.0348)	0.0644** (0.0226)	0.0417 (0.0326)	−0.0317 (0.0311)	−0.1031** (0.0273)	−0.0089 (0.0343)	−0.0806** (0.0294)
Panel C. Native Hispanic Men
	Full Household Head Sample (N=56,673)				Co-residing Sample (N=45,303)		Co-residing With Kids Sample (N=32,735)
Dependent Variable:	Married (mean=0.66)	Non-Marital Cohabiting (mean=0.13)	Non-Co-residing (mean=0.21)	Co-residing With Kids (mean=0.56)	Married (mean=0.83)	Co-residing With Kids (mean=0.71)	Married (mean=0.93)
Ratio Income/Ideal if Under Marriage Ideal	0.2324** (0.0533)	−0.0891* (0.0427)	−0.1422** (0.0506)	0.1518* (0.0571)	0.1319* (0.0502)	0.0653 (0.0613)	0.0942** (0.0347)
Ratio Income/Ideal if Over Marriage Ideal	−0.0405 (0.0270)	0.0117 (0.0139)	0.0282 (0.0245)	−0.0017 (0.0251)	−0.0332 (0.0205)	−0.0232 (0.0247)	−0.0109 (0.0140)
Slope Change	−0.2729** (0.0526)	0.1008* (0.0435)	0.1704** (0.0498)	−0.1534* (0.0614)	−0.1651** (0.0496)	−0.0421 (0.0636)	−0.1051** (0.0345)

Notes: Standard errors in parentheses are clustered on CMSA.

^{+, *, **}indicate statistical significance at the 10, 5, and 1 percent level respectively. Household head sample includes men reported as household heads or partners/roomates of female household heads. Coresiding sample includes members of household head sample who are married or living with a partner or female roommate. Coresiding with kids sample includes members of coresiding sample who have a partner with children living in the household. Each column of a given panel represents a separate regression. Regressions include adjusted income category dummies interacted with year and education group and all other baseline controls.

It is helpful to consider whether those whose marriage decisions are affected by relative income would otherwise be living with a partner or not. The answer differs by race/ethnicity group, as shown in columns II and III. For whites and Hispanics, it appears that relative income most often moves low-income men from the category of non-co-residing to the category of married. For black men, on the other hand, it appears that a majority of those whose marriage decisions are affected by relative income would otherwise be living with a partner. These findings are unsurprising given the relatively high rates of non-marital cohabitation for black men.

We now return to the question of whether relative income considerations drive marriage decisions for men living with a partner. As shown in column V of Table 4, the ratio of a man's income to the reference group median is linked to marriage among co-residing men in all three groups. Comparing columns I and V, we see that the effect of relative income is more modest for co-residing men, especially white and Hispanic men. If one were willing to assume that the difference in the effect of relative income between co-residers and all household heads is largely driven by search, and that search is not a major determinant of marriage for men once they live with a partner, search considerations explain perhaps half of the effect of relative income for white and Hispanic men and little of the effect for black men.²²

For white, black, and Hispanic men, there is a positive effect of the income ratio below the median and a zero or negative effect above the median for co-residing men, suggesting that relative income considerations affect marriage even for men who live with a partner. For men living with a partner and children, the effects are smaller, but for all groups there is a statistically significant slope change as predicted by the model.

It is worth comparing the effect of relative income on marriage to its effect on fatherhood, though there are some limitations to the fatherhood analysis as well. A man is listed as having children in the household if he lives with his own children or his step-children; the latter label is endogenous to the marriage decision. Also, it is not possible to observe fatherhood if the man does not live in the same household as his children. Our solution is to describe the man as living with children if he lives with a female partner who has children (regardless of whether they are described as his own). The outcome observed is co-residential social fatherhood.

For white men, the effects of relative income on marriage and on fatherhood are quite similar. This likely stems from the fact that marriage and fatherhood are tightly linked in this population. Among black men, on the other hand, there is no apparent relationship between relative income and fatherhood. For this group, relative income appears to affect the decision to marry but not the decision to live with a woman and children.²³

Our reading of the evidence is that while marriage market considerations are important, they are not the full story. Controlling for metropolitan area characteristics that could affect the marriage market does not substantively affect the results. We see a smaller but statistically and economically significant effect of relative income even among co-residing men of all three race/ethnicity groups. Even among those already living with their partners, men are more likely to be married as their income approaches a reference group median.

C. Alternative Explanations

Aside from marriage market considerations, there are other reasons we could see an association between a man's relative income and his propensity to be married. For example, stable employment is frequently cited as a necessary condition for marriage (e.g. Wilson, 1987). In the baseline, we control for employment status and whether the man works full-time and worked a full year in the previous calendar year. Omitting these controls does not substantively change the results, as shown in column V of Appendix Table 2. We also repeat the analysis restricting to men who are full-time full-year workers; the results are similar to the baseline though a bit muted for black men (see column VI).

Another possibility is that we have not fully accounted for differences in absolute income in our models. Our preferred model includes over one thousand dummy variables indicating real cost-of-living adjusted income – each category representing a percentile of the national housing-price adjusted income distribution in a given year and interacted with year and education group. Nevertheless, it is possible that the income category dummy variables do not appropriately account for cost-of-living differences across metropolitan areas. In the baseline, we adjust for cost-of-living differences by assuming 0.36 of expenditures are affected by housing prices, as suggested by Albouy (2008). We experiment with alternative adjustments for cost of living in columns VII and VIII of Appendix Table 2 and the results are not substantively affected. In column IX, we drop the control for the housing price index and in column X we include a control for the man's income divided by the housing price index in his area. None of these alternative approaches to accounting for housing price differentials across metropolitan areas make a substantive difference to the results.

A final concern is that men may receive a wage boost when they are married because of employer discrimination or because they increase their productivity. Unfortunately, the Census data do not allow us to examine how the trajectory of income relates to the timing of marriage. Even in longitudinal data, it would be difficult to distinguish between a boost to earnings around the time of marriage caused by employer discrimination and an exogenous boost to earnings which pushes a couple towards marriage.²⁴ We use two methods to investigate whether this concern is important. First, we simulate a world in which each man receives an unexpected earnings bonus at the time of marriage due to employer favoritism. Specifically, married men are assumed to have been earning only 90 percent of observed income at the time of the marriage decision. We then repeat the analysis using the lower income for married men, and the resulting coefficients on the ratio*under variable are smaller but retain their statistical significance (see column XI of Appendix Table 2).

In the final column of Appendix Table 2, we restrict the sample to men that are ages 25 and 26 only. We assume these men are relatively close to the timing of their marriage decision, and that their wages are less likely to reflect employer discrimination (which may not happen instantaneously). The basic pattern in the results holds even for the youngest men in the sample, though standard errors are larger and statistical significance is weakened.

Though the evidence is highly suggestive of link between relative income and marriage, we cannot prove that the relationship is causal. To do so, one would need to randomly assign reference group income without changing a man's own income or the characteristics of his metropolitan area. There may be unobservable characteristics of individual men that are correlated with reference group income; we believe this is the most likely threat to identification. For example, a low-income man living in a high-income area may be less able, less motivated, or less attractive in some unobservable way than a man who earns the same real income in another city where there are fewer opportunities for men like him. We do not have an experimental design, so our results should be interpreted with the same caution as those derived from any observational study. It is also important to note that even if a causal relationship between relative income and marriage could be definitively established, the identity story proposed here is only one possible explanation.

D. Alternative Marriage Ideals and Reference Groups

In Appendix Table 3, we experiment with alternatives to the median of the reference group and alternative reference groups. We report results using alternative benchmarks between the 20^th and 80^th percentile of reference group income. For white men, the slope change is more pronounced when using the 40^th to 60^th percentile rather than higher or lower percentiles. The slope change for black men is most dramatic using an 80^th percentile hypothesized ideal, suggesting that our baseline specification may be understating the effect of relative income for this group.²⁵ We also try using a more narrowly defined age group for the reference group, 25–49 year-olds. Though this reduces the sample available to estimate reference group medians, the results are quite similar to the baseline.

Appendix Table 3.

Exploring Alternative Ideals and Reference Groups

	I	II	III	IV	V	VI	VII	VIII	IX	X	XI
	Baseline (Median)	Use 20th Percentile	Use 30th Percentile	Use 40th Percentile	Use 60th Percentile	Use 70th Percentile	Use 80th Percentile	Reference Group is 25–49 FTFY workers	Randomly Generated Reference Group Median	Reference Group is Defined by Race/Eth.	Reference Group is Defined By Education
Panel A. Native Non-Hispanic White Men
Ratio Income/Ideal if Under Ref. Percentile	0.3813** (0.0251)	0.1142** (0.0323)	0.2128** (0.0288)	0.2782** (0.0463)	0.2698** (0.0549)	0.2070** (0.0387)	0.1085** (0.0290)	0.3900** (0.0276)	−0.0058 (0.0037)	0.2866** (0.0404)	0.3663** (0.0322)
Ratio Income/Ideal if Over Ref. Percentile	−0.0298* (0.0143)	−0.0307** (0.0051)	−0.0297** (0.0065)	−0.0288** (0.0096)	−0.0454** (0.0151)	−0.0641** (0.0185)	−0.0924** (0.0219)	−0.0286+ (0.0154)	−0.0065+ (0.0039)	−0.0123 (0.0157)	−0.0179 (0.0136)
Slope Change	−0.4111** (0.0281)	−0.1449** (0.0318)	−0.2425** (0.0285)	−0.3070** (0.0426)	−0.3151** (0.0520)	−0.2711** (0.0369)	−0.2008** (0.0195)	−0.4186** (0.0302)	−0.0007 (0.0013)	−0.2990** (0.0409)	−0.3842** (0.0389)
Panel B. Native Non-Hispanic Black Men
Ratio Income/Ideal if Under Ref. Percentile	0.1619** (0.0375)	0.1140* (0.0491)	0.2881** (0.0621)	0.3113** (0.0777)	0.4018** (0.0888)	0.4584** (0.0705)	0.4356** (0.0569)	0.1499** (0.0415)	0.0021 (0.0083)	0.2207** (0.0577)	0.3345** (0.0747)
Ratio Income/Ideal if Over Ref. Percentile	0.0254 (0.0153)	0.0438** (0.0154)	0.0736** (0.0226)	0.0905** (0.0261)	0.0675* (0.0260)	0.0358 (0.0319)	0.0118 (0.0447)	0.0245 (0.0166)	−0.0022 (0.0081)	0.0754** (0.0207)	0.0404+ (0.0204)
Slope Change	−0.1365** (0.0343)	−0.0702 (0.0484)	−0.2145** (0.0482)	−0.2208** (0.0612)	−0.3342** (0.0840)	−0.4226** (0.0667)	−0.4238** (0.0629)	−0.1255** (0.0371)	−0.0044 (0.0037)	−0.1453** (0.0463)	−0.2941** (0.0704)
Panel C. Native Hispanic Men
Ratio Income/Ideal if Under Ref. Percentile	0.2644** (0.0546)	0.0343 (0.0475)	0.2110** (0.0544)	0.2621** (0.0639)	0.1960* (0.0863)	0.2606** (0.0695)	0.1954** (0.0560)	0.2291** (0.0655)	0.0003 (0.0123)	0.2846** (0.0620)	0.3298** (0.0809)
Ratio Income/Ideal if Over Ref. Percentile	−0.0404 (0.0242)	0.0037 (0.0175)	0.0198 (0.0211)	0.0173 (0.0274)	−0.0214 (0.0419)	−0.0518 (0.0536)	−0.0765 (0.0712)	−0.0533* (0.0258)	0.0041 (0.0118)	−0.0120 (0.0293)	0.0185 (0.0242)
Slope Change	−0.3048** (0.0558)	−0.0306 (0.0407)	−0.1912** (0.0512)	−0.2448** (0.0625)	−0.2174* (0.0916)	−0.3124** (0.0818)	−0.2719** (0.0808)	−0.2824** (0.0700)	0.0039 (0.0044)	−0.2967** (0.0620)	−0.3113** (0.0777)

Notes: Standard errors in parentheses are clustered on CMSA.

^{+, *,**}indicate statistical significance at the 10, 5, and 1 percent level respectively. Each column within a panel represents a separate regression. Regressions use baseline specification with changes as indicated and include adjusted income category dummies interacted with year and education and all other controls. See text for more details.

One might worry that the regression results stem from a particular functional form or artifact of the data. To investigate this possibility, we perform a falsification exercise in which we randomly generate reference group medians using a normal distribution with the same mean and standard deviation as the actual distribution of reference group medians in the race/ethnicity-education-year cell. Using this approach, we find that the ratio of a man's income to the median of a randomly selected reference group does not predict marriage (column IX of Appendix Table 3). This null result suggests that it is variation in relative income within race/ethnicity-education-year cells that is driving the main findings.

We also experiment with reference groups based on metropolitan area-race/ethnicity groups and metropolitan area-education groups. Both alternatives are consistent with the model for all three groups, as shown in the final columns of Appendix Table 3.

Finally, we explore empirically based kink points, as described in the appendix. These points of flattening in the income-marriage relationship are positively correlated with the reference group median, lending some validity to the use of the reference group median in our analysis.

E. Robustness

Appendix Table 4 investigates the sensitivity of the results to a variety of alternative specifications. First, we use the dependent variable “ever married” and find similar results, as shown in column II. We show in column III that the pattern is not driven by an effect of relative income on divorce, which is unsurprising given the relatively low rates of divorce among this age group. In columns IV and V we experiment with different ways of trimming the tails of the income distribution. Neither including the full sample nor excluding the top and bottom ten percent substantively changes the results. In column VI, we allow the effect of age to vary by year. In column VII, we include a control for the log of income in addition to the detailed percentile dummies. In column VIII, we control for metropolitan area-specific time trends. In column IX, we flexibly control for the rates employment rate in the man's metropolitan area-race/ethnicity-income group.²⁶ In column X, we allow the dummy for “under the median” to interact with the man's employment status and full time status and with the metropolitan area sex ratio, housing price index, and AFDC benefit level. None of these modifications affects the results very much.

Appendix Table 4.

Sensitivity Analysis

	I	II	III	IV	V	VI	VII	VIII	IX	X	XI
	Baseline	Dependent Variable is Ever Marriec	Dependent Variable is Divorced	Full Sample Including Tails	Drop Top and Bottom 10 percent	Include Age *Year Dummies	Control for Log (Income) and Income Dummies	Include Metro Area-Specific Time Trends	Drop Largest Metro Areas	Control for Employment in Reference Group	Interact Controls With Under Dummy
Panel A. Native Non-Hispanic White Men
Ratio Income/Ideal if Under Ref. Median	0.3813** (0.0251)	0.3431** (0.0244)	0.0071 (0.0091)	0.3395** (0.0311)	0.3340** (0.0308)	0.3828** (0.0252)	0.3894** (0.0252)	0.3890** (0.0264)	0.4572** (0.0340)	0.3786** (0.0252)	0.3851** (0.0260)
Ratio Income/Ideal if Over Ref. Median	−0.0298* (0.0143)	−0.0479** (0.0169)	0.0041 (0.0031)	−0.0223** (0.0049)	−0.0414+ (0.0233)	−0.0294* −0.0142	−0.0257+ (0.0143)	−0.0269+ (0.0147)	0.0231 (0.0195)	−0.0290* (0.0144)	−0.0202 (0.0125)
Panel B. Native Non-Hispanic Black Men
Ratio Income/Ideal if Under Ref. Median	0.1619** (0.0375)	0.1057** (0.0352)	−0.0260 (0.0185)	0.1641** (0.0397)	0.2025** (0.0431)	0.1620** (0.0374)	0.1637** (0.0375)	0.1660** (0.0391)	0.2139** (0.0387)	0.1712** (0.0398)	0.1835** (0.0393)
Ratio Income/Ideal if Over Ref. Median	0.0254 (0.0153)	−0.0065 (0.0150)	−0.0140* (0.0061)	0.0044 (0.0049)	0.0587* (0.0280)	0.0253 (0.0153)	0.0267+ (0.0154)	0.0274+ (0.0153)	0.0474** (0.0179)	0.0286+ (0.0156)	0.0100 (0.0161)
Panel C. Native Hispanic Men
Ratio Income/Ideal if Under Ref. Median	0.2644** (0.0546)	0.2461** (0.0590)	0.0337 (0.0328)	0.2624** (0.0625)	0.2394** (0.0586)	0.2651** (0.0547)	0.2680** (0.0544)	0.2431** (0.0619)	0.3411** (0.0583)	0.2645** (0.0546)	0.2827** (0.0591)
Ratio Income/Ideal if Over Ref. Median	−0.0404 (0.0242)	−0.0014 (0.0183)	0.0370+ (0.0202)	−0.0041 (0.0081)	−0.0721* (0.0335)	−0.0404 (0.0245)	−0.0380 (0.0245)	−0.0444+ (0.0247)	0.0022 (0.0293)	−0.0406+ (0.0239)	−0.0455+ (0.0235)

Notes: Standard errors in parentheses are clustered on CMSA.

^{+, *,**}indicate statistical significance at the 10, 5, and 1 percent level respectively. Each column within a panel represents a separate regression. Regressions use baseline specification with changes as indicated and include adjusted income category dummies interacted with year and education and all other controls. See text for more details.

F. Magnitude of the Effects

The coefficients in the regression model do not immediately provide a sense of the magnitude of the estimated effects. To do so, we use the model to predict marriage rates if the median income of the reference group increased by ten percent (holding absolute income and all other factors constant). The results suggest that a ten percent increase in the hypothesized “marriage ideal” reduces marriage by one to three percent depending on the race/ethnicity group, education level and year. Details are reported in Appendix Table 5.

Appendix Table 5.

Quantifying the Magnitude of the Effects

Native non-Hispanic White Men
	Predicted Marriage Rates Using Actual Ref. Group Median			Predicted Marriage Rates Using 10% Higher Median			Percent Change
	1980	1990	2000	1980	1990	2000	1980	1990	2000
Less Than HS	0.640	0.489	0.418	0.628	0.477	0.406	−0.020	−0.024	−0.027
HS Exactly	0.670	0.547	0.471	0.657	0.534	0.458	−0.020	−0.024	−0.028
Some College	0.642	0.569	0.512	0.628	0.555	0.498	−0.022	−0.024	−0.028
College Grad+	0.619	0.550	0.514	0.604	0.536	0.500	−0.025	−0.027	−0.028
All	0.643	0.550	0.497	0.629	0.537	0.483	−0.022	−0.025	−0.028
Native non-Hispanic Black Men
	Predicted Marriage Rates Using Actual Ref. Group Median			Predicted Marriage Rates Using 10% Higher Median			Percent Change
	1980	1990	2000	1980	1990	2000	1980	1990	2000
Less Than HS	0.393	0.224	0.177	0.386	0.219	0.171	−0.018	−0.023	−0.030
HS Exactly	0.486	0.332	0.312	0.478	0.324	0.304	−0.017	−0.022	−0.025
Some College	0.508	0.415	0.388	0.500	0.406	0.379	−0.017	−0.021	−0.023
College Grad+	0.530	0.418	0.403	0.521	0.408	0.394	−0.017	−0.023	−0.023
All	0.475	0.352	0.338	0.467	0.345	0.329	−0.017	−0.022	−0.024
Native Hispanic Men
	Predicted Marriage Rates Using Actual Ref. Group Median			Predicted Marriage Rates Using 10% Higher Median			Percent Change
	1980	1990	2000	1980	1990	2000	1980	1990	2000
Less Than HS	0.625	0.390	0.337	0.618	0.383	0.331	−0.013	−0.019	−0.019
HS Exactly	0.640	0.463	0.409	0.632	0.455	0.402	−0.012	−0.017	−0.018
Some College	0.616	0.509	0.456	0.607	0.501	0.447	−0.015	−0.017	−0.020
College Grad+	0.557	0.464	0.405	0.546	0.454	0.395	−0.019	−0.022	−0.024
All	0.619	0.465	0.413	0.610	0.456	0.405	−0.014	−0.018	−0.020

Note: Results based on baseline model. Reference group medians have been artifically increased by ten percent and the status of under the reference group median and the ratio of income to the median have been recalculated for each individual.

VI. Conclusion

The primary contribution of this paper is to document a relationship between relative income and marriage, conditional on absolute income. We find that income relative to a threshold determined by a local reference group is an important determinant of marriage for men below the threshold, but not those above it. The association is robust to the inclusion of a number of controls and alternative specifications.

We propose an identity model to explain the relationship between relative income and marriage. Alternative models might also predict a link between relative income and marriage, conditional on absolute income. For example, the (unobservable) price of “spousal labor” (Grossbard-Shechtman, 1993) might be higher in a marriage market with richer men.²⁷ There might also be marriage market and search considerations that are not fully captured by our control variables, and we cannot rule out the possibility that the relationship is due to unobservable characteristics of men that are associated with where they live. Nevertheless, the results are consistent with an identity framework, and the identity framework is corroborated by previous qualitative work.

In the context of the identity model, the evidence presented here suggests that men falling below an idealized norm of marriage choose to defer marriage rather than face an identity loss for failing to fulfill the prescriptions associated with marriage. A man's “marriageability” appears to be related not only to his absolute level of income, but to income relative to a middle-class ideal determined by a local reference group. The model predicts that raising reference group incomes by ten percent reduces marriage by about two percent.

One possibility we have not explored is that the financial ideal associated with marriage may be endogenous to marriage rates. As marriage becomes more rarefied and the financial gap between married and unmarried couples widens, the marriage ideal may increase. The resulting cycle is difficult to identify empirically, but suggests the role of relative income may be understated here.

Finally, we note that while marriage has been proposed as an anti-poverty measure, our results imply that anti-poverty (or, more precisely, anti-inequality) measures may increase marriage rates. On the other hand, as long as it remains difficult for low-income couples to “keep up with the Joneses,” the evidence suggests that these couples are likely to defer marriage until their high financial expectations are reached.

VII. Appendix: Empirically Based Kink Points

For each metropolitan area-education-race-year group, we explore potential kink points at 1000 dollar intervals between the 20^th and 80^th percentiles of the reference group income distributions. The empirical kink point is that which generates the largest statistically significant slope change in the income-marriage relationship.

For white men, in 1171 of 1308 metropolitan area-education-race-year cells (representing about 97.5% of the population), there is a statistically significant flattening of the income-marriage relationship evident in the data. The empirical kink points vary widely, and only about a third are between the 40^th and 60^th percentiles of the reference group income distribution. This is likely due to the small sample available to estimate each kink point. However, the reference group median is near the median of the empirical kink points: among metropolitan area-education-race-year cells with an estimated kink point, 50 percent are below the reference group median (46 percent when weighted by population).

Furthermore, empirical kink points are highly correlated with the reference group median income. The correlation is 0.66, ranging from 0.33 to 0.75 within education-year groups. In a regression setting with the empirical kink point as the dependent variable and including metropolitan area dummies and education*year dummies , the coefficient on the reference group median is 0.82 and is highly significant (see Appendix Table 6). This coefficient implies that the empirical kink point increases $820 with each $1000 increase in reference group income.

Appendix Table 6.

Predicting Empirical Kink Points

Dependent Variable: Empirical Kink Point
	White Non- Hispanic	White Non- Hispanic	Black Non- Hispanic	Black Non- Hispanic	Hispanic	Hispanic
	Unweighted	Weighted	Unweighted	Weighted	Unweighted	Weighted
	I	II	III	IV	V	VI
Reference Group Median	0.8211** (0.1482)	0.8196** (0.1905)	0.6371** (0.1938)	0.5676 (0.3820)	0.6930* (0.2573)	0.6579 (0.4770)
Year*Ed Group Dummies	yes	yes	yes	yes	yes	yes
CMSA Dummies	yes	yes	yes	yes	yes	yes
Number of Observations	1171	1171	474	474	255	255
R-Squared	0.540	0.671	0.573	0.595	0.564	0.604

Notes: Standard errors in parentheses are clustered on CMSA.

^{+, *,**}indicate staistical significance at the 10, 5, and 1 percent level respectively. The unit of observation is the metropolitan area-race/ethnicity-education-year cell. Weighted regressions are weighted by estimated reference group population.

For black and Hispanic men, empirical kink points are more difficult to estimate, presumably because of the smaller sample size in each metropolitan area-education-race-year cell. For black men, significant kink points can be identified in 474 of 1006 cells, representing about 60 percent of the population. For Hispanic men, there is a significant flattening in 255 of 480 cells, representing about 70 percent of the population. The correlation between empirical kink points and reference group medians is around 0.66 in both cases, though the weighted regressions do not have statistically significant coefficients after controlling for metropolitan area and education*year dummies. The point estimates suggest that the empirical kink point increases by $560–$700 with each $1000 increase in reference group income after controlling for metropolitan area and education*year.

In sum, there is a flattening of the income-marriage relationship for most sub-groups in the sample. These empirical kink points tend to be higher in metropolitan areas and years in which the reference group median is higher.